 Open Access Article
Open Access ArticleAdvancing microfluidic design with machine learning: a Bayesian optimization approach†
Ivana
Kundacina‡
 *a,
Ognjen
Kundacina‡
*a,
Ognjen
Kundacina‡
 b,
Dragisa
Miskovic
b,
Dragisa
Miskovic
 b and
Vasa
Radonic
b and
Vasa
Radonic
 a
a
aUniversity of Novi Sad, BioSense Institute, Dr Zorana Djindjica 1, 21000 Novi Sad, Serbia. E-mail: ivana.kundacina@biosense.rs
bThe Institute for Artificial Intelligence Research and Development of Serbia, Fruskogorska 1, 21000 Novi Sad, Serbia
First published on 31st January 2025
Abstract
Microfluidic technology, which involves the manipulation of fluids in microchannels, faces challenges in channel design and performance optimization due to its complex, multi-parameter nature. Traditional design and optimization approaches usually rely on time-consuming numerical simulations, or on trial-and-error methods, which entail high costs associated with experimental evaluations. Additionally, commonly used optimization methods require many numerical simulations, and to avoid excessive computation time, they approximate simulation results with faster surrogate models. Alternatively, machine learning (ML) is becoming increasingly significant in microfluidics and technology in general, enabling advancements in data analysis, automation, and system optimization. Among ML methods, Bayesian optimization (BO) stands out by systematically exploring the design space, usually using Gaussian processes (GP) to model the objective function and guide the search for optimal designs. In this paper, we demonstrate the application of BO in the design optimization of the microfluidic systems, by enhancing the mixing performance of a micromixer with parallelogram barriers and a Tesla micromixer modified with parallelogram barriers. Micromixer models were made using Comsol Multiphysics software® and their geometric parameters were optimized using BO. The presented approach minimizes the number of required simulations to reach the optimal design, thus eliminating the need for developing a separate surrogate model for approximation of the simulation results. The results showed the effectiveness of using BO for design optimization, both in terms of the execution speed and reaching the optimum of the objective function. The optimal geometries for efficient mixing were achieved at least an order of magnitude faster compared to state-of-the-art optimization methods for microfluidic design. In addition, the presented approach can be widely applied to other microfluidic devices, such as droplet generators, particle separators, etc.
1 Introduction
Microfluidics is a multidisciplinary field that involves the science and technology of fluid manipulation, typically within channels that have at least one dimension on the micrometer scale.1–3 Chemical4,5 and biological research,6–8 as well as medical diagnostics9–11 widely use microfluidics, due to its ability to control conditions in miniaturized devices operating with small volumes of fluids with high precision. Microfluidic devices can integrate multiple functions into a single, compact system, often referred to as a “lab-on-a-chip”, which enables complex processes like mixing, particle separation, droplet generation and detection.12,13 Among these, microfluidic mixers are essential components designed to ensure that fluids within the microchannels are thoroughly mixed, which can be challenging due to the laminar flow regime.14,15The designing methods of micromixers often rely on passive mixing strategies, with microchannels enriched with different geometric features like herringbone structures,16,17 or staggered obstacles18,19 to induce chaotic advection and enhance mixing. Another approach enables mixing by increasing the contact area between fluids using suitable channel geometry – serpentines,20,21 twisted channels,22 zigzag channels,23etc. One of the common examples of passive micromixers is the Tesla micromixer, which utilizes specially designed channel structures to direct fluid flow and create vortices that enhance mixing.24 Modified Tesla micromixers are frequently encountered in the literature due to their versatility and efficiency. These modifications often aim to optimize mixing performance by adjusting geometric parameters, making them suitable for a wide range of applications and flow conditions.25,26 On the other hand, active mixing strategies involve acoustic waves,27,28 electric and magnetic fields29,30 or electro- and magneto-hydrodynamic forces,31,32 as an external mixing actuator. However, although active mixers enable faster mixing and shorter mixer length than passive ones, their integration into complex systems is a challenging task. Recent studies are focused on finding a suitable compact geometry for a microfluidic mixer that will enable efficient mixing performances and easy integration into miniaturized systems.33,34
Machine learning (ML) is a promising tool to enhance the design and operation of microfluidic components, while also improving success rates and accelerating their commercialization.35–38 Recent studies propose different ML-based solutions for applications in droplet microfluidics39 such as convolutional autoencoders for droplet stability prediction,40 deep neural networks (DNNs) for modeling droplet flow,41 and convolutional neural networks for mixing characterization in binary-coalesced droplets.42 Various types of DNNs were used for bubble detection in channels of microfluidic devices for point-of-care diagnostics,43 for gas bubble detection and tracking in microfluidic chips studying CO2 displacement and gas–liquid exchange processes,44 and for predicting the response time of a rotating microfluidic biosensor designed to detect complex reactive proteins.45 Another application of ML is proposed in the field of nanoparticle synthesis in microfluidics where decision trees were used to optimize synthesis parameters.46 Additionally, tree-based ensemble methods were adopted to predict viscous fingering phenomena in Hele-Shaw cells, providing accurate predictions of flow instabilities.47 ML can also contribute to achieving uniform operation across different devices, reducing the need for manual intervention. In that sense, reinforcement learning was applied for flow control of continuous and segmented flow microfluidic systems.48 Beyond conventional ML-based techniques, Bayesian decision-making has been applied to microfluidic chip design to model uncertainty in the design space and select the most reliable configuration, as demonstrated in a routing-based digital microfluidic biochip synthesis method.49
Even though there is a significant interest in experimental applications, a large part of the field is focused on ML-based surrogate models that approximate computationally demanding computational fluid dynamics (CFD) simulations. For example, various types of DNNs were used to reduce the computational complexity of simulations that determine the mixing index of micromixers,50 velocity field and concentration profile of mixers,51 swirling flow pattern in cyclone separators,52 and concentrations in microfluidic concentration gradient generators.53 The end goal of these approaches is to utilize the DNN-based simulation approximations to increase the speed of manual optimization of design parameters.
To automate the design optimization process, there is an increasing number of approaches that employ various optimization algorithms to find the best set of design parameters. Similar to manual optimization, these approaches attempt to accelerate the process by incorporating ML-based surrogate models that approximate the simulations. For instance, a genetic algorithm with a DNN surrogate was proposed to optimize the mixer geometry.54 In ref. 55, a DNN surrogate is used to predict the droplet generation outcomes, while the device design is refined through a coordinate descent-like optimization procedure. A similar concept is proposed for the design optimization of single and double emulsion droplet generators,56 utilizing DNNs and boosted decision trees to predict droplet size and stability. Design optimization of micromixers with a Cantor fractal baffle, proposed in ref. 57, uses the simulated annealing optimization algorithm with a response surface analysis surrogate model. Additionally, reinforcement learning was explored for microfluidic mixer optimization, with a DNN as an efficient surrogate, allowing for the exploration of vast design spaces.58 Multi-objective optimization techniques, like the NSGA-II variant of the genetic algorithm, were used for fractal-based micromixer designs, to balance the objectives like mixing efficiency, pressure drop, and energy costs.59 NSGA-II with a Kriging interpolation surrogate model was used to minimize the required pumping power while maximizing the mixing efficiency of a mechanical micromixer.60 Similarly, ref. 61 proposes the optimization of a Cantor fractal-based AC electric micromixer in a multi-objective setting, using a response surface analysis-based surrogate. Despite these advancements in leveraging DNNs and other ML techniques to speed up optimization, there are remaining challenges related to approximation errors and the extensive simulations required for training. More specifically, using ML based surrogate models introduces approximation errors, introducing the mismatch between the function being optimized, and the real optimization goal. Additionally, a large number of simulations are required for creating a dataset for ML model training. The number of simulations required to establish the datasets for DNN/ML model training varies from 1890 and 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 for Newtonian and non-Newtonian fluids in a micromixer, respectively, in ref. 50; 20
700 for Newtonian and non-Newtonian fluids in a micromixer, respectively, in ref. 50; 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for a concentration gradient generator in ref. 53; 10
000 for a concentration gradient generator in ref. 53; 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 images for a velocity field and concentration profile in ref. 51; 10
513 images for a velocity field and concentration profile in ref. 51; 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for micromixers in ref. 58; 888 and 998 for flow-focusing droplet generation in ref. 55; etc. On the other hand, using the exact CFD simulations within optimization algorithms is highly demanding, since they require a large number of objective function evaluations. For example, the approach in ref. 54 requires 600
000 for micromixers in ref. 58; 888 and 998 for flow-focusing droplet generation in ref. 55; etc. On the other hand, using the exact CFD simulations within optimization algorithms is highly demanding, since they require a large number of objective function evaluations. For example, the approach in ref. 54 requires 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulations, while the approach in ref. 59 requires 40
000 simulations, while the approach in ref. 59 requires 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulations for micromixer design optimization. In this study, we focus on maximizing precision by using exact simulations while minimizing their number to improve efficiency. This strategic balance ensures an optimization process that is both highly accurate and resource efficient.
000 simulations for micromixer design optimization. In this study, we focus on maximizing precision by using exact simulations while minimizing their number to improve efficiency. This strategic balance ensures an optimization process that is both highly accurate and resource efficient.
To address the shortcomings of the mentioned optimization algorithms, Bayesian optimization (BO) has emerged as a powerful alternative for sequential optimization of complex, computationally intensive functions requiring minimal evaluations by using a probabilistic model to guide the search for optimal solutions.62 When combined with Gaussian processes (GP),63 it efficiently models the underlying function and identifies the most promising points for evaluation, leading to a more strategic exploration of the search space. This approach avoids the need to separately train a surrogate model, which is crucial for preventing unnecessary simulations and the associated risks of approximation errors and overfitting. Recent studies use BO for a wide range of applications such as microneedle design for biologic fluid sampling,64 chemical design,65 detector design in particle physics,66etc.
In this paper, we propose an ML-based tool for designing a micromixer using BO combined with GP. The micromixer model is created using Comsol Multiphysics®, while the BO algorithm is implemented in Python. First, we demonstrate the applicability of BO using a micromixer with parallelogram barriers, focusing on the optimization of four geometric parameters. To illustrate a higher-dimensional example, we apply the method to a Tesla micromixer modified with parallelogram barriers, optimizing nine parameters. In both cases, significant improvements in mixing performance are achieved through geometric optimization. Even though the presented study is focused on using the exact CFD simulations for design optimization, this approach can also use a surrogate model as an approximative model, further reducing the computational complexity. To showcase the effectiveness in reducing the number of required simulations, we provide a comparison of the proposed approach with state-of-the art evolutionary algorithms. The stability of BO is demonstrated through repeated experiments, confirming its consistent convergence despite small variability in the convergence speed.
2 Bayesian optimization
Bayesian optimization is an ML-based approach aimed at optimizing complex or even unknown objective functions, especially those that are expensive to evaluate, noisy, or those that lack analytical expressions or gradients.62,67 BO excels in scenarios where only a limited number of evaluations can be performed, due to the high costs of direct experimentation or simulations, making it ideal for applications in fields like hyperparameter tuning, experimental design, and engineering simulations.68 Formally, the goal of BO is to solve the problem presented in eqn (1):| max f(x), for x ∈ A, | (1) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m denotes the optimization variable, the input set A ⊂
m denotes the optimization variable, the input set A ⊂ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m represents the possible values of x, typically defined as a hyper-rectangle or a multi-dimensional simplex, and the objective function f is usually continuous. The objective function represents the metric we aim to maximize, such as efficiency or performance, while the optimization variable x represents the input parameters being tuned to achieve the objective within the constraints of the input set A. The dimensionality m defines the number of elements in x, corresponding to the parameters being tuned. BO constructs a probabilistic model, typically using GP regression,63 to approximate the objective function during the iterative procedure of finding the global optimum. GP regression is a statistical technique used to predict outcomes and their uncertainties by modeling the relationships between inputs and outputs. In BO, it specifically models the objective function values and associated uncertainty based on the observed parameter values. In each iteration of the optimization process, the GP model is updated with observations gathered from previous evaluations, and the BO strategically identifies the next point to evaluate based on the current GP model. For this purpose, BO uses an acquisition function, a mathematical tool that balances exploring uncertain areas in the search space with exploiting regions that appear promising. In other words, it manages the trade-off between selecting parameters for which the GP model exhibits high uncertainty to discover new possibilities and choosing parameters similar to those already found to produce high objective values. It is important to note that BO does not attempt to approximate the entire objective function but focuses only on regions where it is most likely to find an optimal solution based on the model's current knowledge. This targeted approach increases the computational efficiency of the method, which is especially important for functions that are expensive to evaluate.
m represents the possible values of x, typically defined as a hyper-rectangle or a multi-dimensional simplex, and the objective function f is usually continuous. The objective function represents the metric we aim to maximize, such as efficiency or performance, while the optimization variable x represents the input parameters being tuned to achieve the objective within the constraints of the input set A. The dimensionality m defines the number of elements in x, corresponding to the parameters being tuned. BO constructs a probabilistic model, typically using GP regression,63 to approximate the objective function during the iterative procedure of finding the global optimum. GP regression is a statistical technique used to predict outcomes and their uncertainties by modeling the relationships between inputs and outputs. In BO, it specifically models the objective function values and associated uncertainty based on the observed parameter values. In each iteration of the optimization process, the GP model is updated with observations gathered from previous evaluations, and the BO strategically identifies the next point to evaluate based on the current GP model. For this purpose, BO uses an acquisition function, a mathematical tool that balances exploring uncertain areas in the search space with exploiting regions that appear promising. In other words, it manages the trade-off between selecting parameters for which the GP model exhibits high uncertainty to discover new possibilities and choosing parameters similar to those already found to produce high objective values. It is important to note that BO does not attempt to approximate the entire objective function but focuses only on regions where it is most likely to find an optimal solution based on the model's current knowledge. This targeted approach increases the computational efficiency of the method, which is especially important for functions that are expensive to evaluate.
BO starts with an initial probability distribution, known as the prior of the GP model, which represents assumptions about the properties of the objective function before observing any data. After observing new data points, GP regression updates the posterior probability distribution of the objective function. The posterior distribution is a concept from Bayesian statistics, representing an updated belief about a function based on its prior distribution and the newly observed data. The posterior at each point f(x) is characterized by a mean function μ(x) and a variance σ2(x), representing the predicted objective function value and the predictive uncertainty, respectively. The posterior mean interpolates previously observed points, while the variance determines the width of the confidence intervals, typically expressed as μ(x) ± 1.96 σ(x), which contains the true function value f(x) with 95% probability. The variance is zero at observed points and increases as we move away from them, reflecting the model's confidence at points where data is available and its growing uncertainty in unexplored regions of the parameter space.
When making predictions and quantifying uncertainty, the GP model relies on a covariance matrix, which contains the covariances between pairs of observed points, quantifying how changes in one observed point are expected to relate to changes in another. The elements of this matrix are determined by evaluating a kernel function Σ(xi, xj) at each pair of points (xi, xj). The kernel function is a mathematical tool which computes the similarity between two points, ensuring that points close to each other in input space exhibit strong correlations. This function also reflects the underlying assumption of the GP model about the smoothness of the objective function, which dictates how gradually the function is expected to change as the input parameters vary. Commonly used kernels in GP models include the linear kernel, the rational quadratic kernel, the Gaussian or radial basis function (RBF) kernel, and the Matérn kernel,69 used in our approach. The Matérn kernel is particularly suitable for modeling functions with moderate smoothness, offering more flexibility than the other mentioned kernels that assume higher degrees of smoothness. Since microfluidic flows often exhibit moderate smoothness due to laminar flow conditions and diffusion processes, the Matérn kernel enables the GP model to capture essential variations in mixing performance without overfitting to noise. For the specific case where the smoothness parameter is set to 5/2, which we used in our work, the Matérn kernel is given by eqn (2):
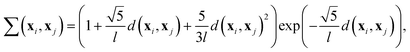 | (2) |
Once the kernel function is specified, a GP regression model can be formulated. Given a set of n observed data points X = [x1, x2,…,xn] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m×n with corresponding objective function values y = [y1, y2,…,yn] ∈
m×n with corresponding objective function values y = [y1, y2,…,yn] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n, the GP provides a posterior distribution over possible functions that fit the data. The mean μ(x) and variance σ2(x) predictions at a new point x are given by eqn (3) and (4):
n, the GP provides a posterior distribution over possible functions that fit the data. The mean μ(x) and variance σ2(x) predictions at a new point x are given by eqn (3) and (4):
| μ(x) = k(x, X)TK(X, X)−1y, | (3) |
| σ2(x) = ∑(x, x) − k(x, X)TK(X, X)−1k(x, X), | (4) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n is the covariance vector between the new point x and the observed points in X, and K(X, X) ∈
n is the covariance vector between the new point x and the observed points in X, and K(X, X) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×n is the covariance matrix consisting of pairwise covariances among all observed points. Both the elements of the covariance matrix and the covariance vector are computed using the kernel function Σ(xi, xj). As mentioned above, the mean μ(x) gives the best estimate of the function value at the newly observed point x, while the variance σ2(x) reflects the uncertainty in this prediction. These formulas form the foundation for making predictions and refining the GP regression model.
n×n is the covariance matrix consisting of pairwise covariances among all observed points. Both the elements of the covariance matrix and the covariance vector are computed using the kernel function Σ(xi, xj). As mentioned above, the mean μ(x) gives the best estimate of the function value at the newly observed point x, while the variance σ2(x) reflects the uncertainty in this prediction. These formulas form the foundation for making predictions and refining the GP regression model.
Acquisition functions guide the input space search of the optimization process to the most promising regions by determining the next point to be evaluated and observed. These functions use the mean and variance predictions from the GP model to balance the exploration of uncertain areas and the exploitation of regions where the objective function is expected to be high. Exploration refers to investigating areas with high uncertainty to learn more about the objective function, while exploitation focuses on refining the GP model only in regions already known to perform well. Common acquisition functions include expected improvement (EI), probability of improvement, and upper confidence bound. In our work, we employed the EI acquisition function, which prioritizes selecting points with the highest expected gain over the current best observation x* (ref. 62) The EI formula for a potential next point x is presented with eqn (5):
 | (5) |
In summary, BO uses past data and statistical modeling to identify the most efficient way to explore and optimize challenging problems, by ensuring that the search focuses on the most promising regions. It operates through an iterative process fitting a GP model to observed data available at the current iteration to approximate the objective function. An acquisition function utilizes the model's predictions to balance exploration of new areas and exploitation of known promising regions, selecting the next point to evaluate. The objective function is evaluated at this new point, and the resulting data is added to the existing observed data. This updated dataset is used to refine the model, and the cycle continues until a stopping criterion is met, such as reaching a maximum number of iterations or achieving convergence in the objective function value. In the following sections, the potential of the BO approach in microfluidics will be examined on the example of improving the mixing performance of a micromixer with parallelogram barriers and a high-dimensional scenario will be examined on the example of a Tesla micromixer with parallelogram barriers.
3 Micromixer configurations
3.1 Design of a micromixer with parallelogram barriers
The design of the microfluidic mixer with parallelogram barriers is illustrated in Fig. 1. The micromixer is proposed for two liquids with parallel flows that enter through two separate inlets and mix along the micromixer, exiting through a single outlet. It contains 8 pairs of parallelogram barriers positioned on both sides of the channel. Each parallelogram barrier is described with a barrier height l and barrier width p, while the distance between each barrier is described with the parameter d. The angle α represents the inclination angle of the barrier, relative to the channel wall. The micromixer channel width is set to 1 mm, with barriers starting 5.5 and 5 mm at the upper and lower wall, respectively. The total length of the proposed microfluidic mixer is 30 mm. Considering potential manufacturing limitations and constraints in the design, the ranges of parameter values used in simulations were limited as follows: the angle of inclination α from 10 deg to 170 deg, the barrier length l from 10 μm to 500 μm, the barrier width p from 10 μm to 1000 μm, and the distance between barriers d from 410 μm to 1800 μm. The influence of each mentioned parameter on mixing performances was examined using CFD simulations in Comsol Multiphysics® software. | ||
| Fig. 1 Layout of the micromixer with parallelogram barriers. Blue color presents a microchannel with mixing liquids. | ||
3.2 Tesla micromixer modified with parallelogram barriers
Another example of a passive micromixer, with nine geometric parameters, is the Tesla micromixer modified with parallelogram barriers. This design combines the advantages of Tesla's established mixing principles with barrier geometry to achieve superior mixing performance. The design and its geometric parameters are illustrated in Fig. 2. The Tesla mixer, in general, consists of units containing dividing barriers, which split the flow, and subsequently recombine it again in the vortex zone. These units are arranged in a mirrored pattern, creating a sequence of structures that promote efficient fluid interaction along the micromixer. Key parameters and their ranges used in the BO process include: the length of the vortex zone P (300–1200 μm); the distance between the channel wall and divider G (200–600 μm); the divider length K (300–700 μm); the angle of channel inclination α (10–40 deg); the angle of the divider β (5–15 deg); the angle of barrier inclination γ (30–150 deg); the barrier length l (20–180 μm); the barrier width p (20–180 μm); and the distance between parallelogram barriers d (220–500 μm). The radius of the half-circle is equal to the channel width (200 μm).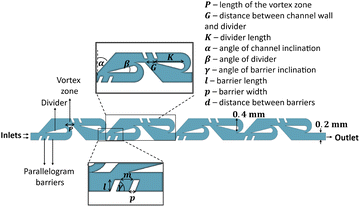 | ||
| Fig. 2 Tesla mixer modified with parallelogram barriers and parameters used in BO. Blue color presents a microchannel with mixing liquids. | ||
3.3 Comsol model
For micromixing simulations, Laminar flow and Transport of Diluted Species physics interfaces in Comsol Multiphysics® software were utilized,70 together with Heat Transfer in the Fluids physics interface for examining the influence of temperature variation on the mixing performance. The Laminar flow interface models fluid dynamics within microchannels governed by the Navier–Stokes equation for conservation of momentum and the continuity equation for conservation of mass, while Transport of Diluted Species simulates the mixing of dilute solute in solvents governed with Fick's laws of diffusion and convection for coupled transport with a flow field. The Heat Transfer in the Fluids interface models the thermal behavior based on Fourier's law of heat conduction and principles of convective heat transfer.The fluid was modeled as water, incorporating temperature-dependent density and dynamic viscosity functions available in Comsol. The Reynolds' number (Re) was calculated according to eqn (6):71
 | (6) |
| MI = 1 − σ/σ0, | (7) |
 , with N representing the number of data points on the cross-section, c0 is the normalized concentration for completely mixed liquids ci, is the mass fraction at a point i while σ0 is the maximum variance over the data range.72 Specifically, in our case c0 has a value of 0.5 mol m−3, while σ0 is equal to 0.5 mol m−3. Simulations were performed using physics controlled fine mesh. To demonstrate that the chosen fine mesh provides an optimal balance between accuracy and computational efficiency, a mesh convergence test was performed. Five physics-controlled mesh configurations, each with a different number of mesh cells, were tested on the micromixer with parallelogram barriers with the initial parameters (α = 45 deg, l = 250 μm, p = 500 μm, d = 1500 μm, Re = 1), and their corresponding mixing indices were compared, Fig. 3.
, with N representing the number of data points on the cross-section, c0 is the normalized concentration for completely mixed liquids ci, is the mass fraction at a point i while σ0 is the maximum variance over the data range.72 Specifically, in our case c0 has a value of 0.5 mol m−3, while σ0 is equal to 0.5 mol m−3. Simulations were performed using physics controlled fine mesh. To demonstrate that the chosen fine mesh provides an optimal balance between accuracy and computational efficiency, a mesh convergence test was performed. Five physics-controlled mesh configurations, each with a different number of mesh cells, were tested on the micromixer with parallelogram barriers with the initial parameters (α = 45 deg, l = 250 μm, p = 500 μm, d = 1500 μm, Re = 1), and their corresponding mixing indices were compared, Fig. 3.
 | ||
| Fig. 3 Mesh convergence test. Parameters of the micromixer with parallelogram barriers: α = 45 deg, l = 250 μm, p = 500 μm, d = 1500 μm, and Re = 1. | ||
4 BO approach for design optimization
The schematic in Fig. 4 illustrates the BO workflow applied to micromixer design. In this process, new design parameters are iteratively proposed through BO, aiming to maximize the mixing performance. Each proposed design is simulated using Comsol Multiphysics 6.0®, and the mixing performance is quantified by calculating the MI, which serves as the BO objective function. In each iteration, a GP model is used to approximate the relationship between design parameters and the MI based on all the observed data. The model predicts the mean and uncertainty for untested designs, and the acquisition function balances the exploration of uncertain design regions and the exploitation of promising ones to propose the next design. This procedure is repeated for a predefined number of iterations (Nit), with each iteration refining the design based on the updated GP model. Over time, this approach converges toward an optimal micromixer design, maximizing the mixing performance through efficient exploration and exploitation of the design space. | ||
| Fig. 4 Schematic representation of the BO workflow. Iterative design and evaluation of micromixers in Comsol Multiphysics® to achieve optimal design and mixing performance. | ||
The proposed workflow is primarily implemented in Python using open-source tools, except for proprietary Comsol Multiphysics® software used for microfluidic simulations. Specifically, we utilized the Scikit-Optimize library for BO,73 which provides essential BO building blocks such as kernel and acquisition function implementations, tell function for evaluating new observations and updating the GP model, and ask function for determining the next parameters to evaluate.
To integrate Python with Comsol Multiphysics®, we employed the MPh library.74 This library includes features such as the start function to initialize the Comsol Multiphysics® software and the load function to read a Comsol model file containing the desired microfluidic design. The entire optimization process is automated and iterates for a predefined number of cycles. In each iteration, Scikit-Optimize's ask function suggests a new set of parameters that maximize the acquisition function, balancing the exploitation and exploration of the parameter space. The MPh library then modifies the Comsol model accordingly using the parameter function. The updated Comsol model is simulated using the build and solve functions, and the results are exported to a CSV file using the export function. Our Python program reads this file, computes the MI according to eqn (7), and sends this value, along with the corresponding parameters, as a new observation to Scikit-Optimize's tell function to update the GP model. Finally, the Comsol software is reset to its original state using the clear and reset functions from the MPh library, preparing it for the next iteration. After the optimization process, the optimal solution is retrieved using the get_result function from the Scikit-Optimize library.
This workflow can also be adapted for other numerical solvers, whether open-source or proprietary, as long as an integration interface is available or can be developed to perform functions similar to those in the MPh library.
5 Results and discussion
The results are structured to first provide an illustrative example that explains the BO process for optimization of a single parameter, demonstrating how the method operates. Then, we compare multiple kernel functions and use the best-performing one in the remaining experiments. This is followed by a more complex scenario where four parameters of the micromixer with parallelogram barriers are optimized for different values of Re. Moreover, the proposed approach is compared with a traditional evolutionary optimization method in terms of the number of iterations required for convergence. Finally, a high-dimensional example of nine-parameter optimization is presented for the case of the Tesla micromixer modified with parallelogram barriers.5.1 Illustrative example
In order to illustrate how the proposed method works, a one-parameter optimization example is provided for the micromixer with parallelogram barriers, while keeping all other parameters fixed. Specifically, we optimize the parameter α, while the selected values for the other parameters in this example are p = 500 μm, l = 250 μm, and d = 1500 μm, with Re = 5.The results in Fig. 5 show BO results after 14 executed iterations, upon which the optimal MI is achieved. The graph displays the GP model representing the underlying objective function with its variance, estimated from 14 observations of the MI for different angle values. The green line represents the mean of the GP model for the parameter α, with green areas indicating the 95% confidence intervals. The red dots mark the observed values, while the blue line represents the values of the EI acquisition function. The blue dot indicates the maximum of the EI function, which corresponds to the next parameter value to be evaluated in the optimization process. Although the confidence intervals are wider for multiple angle values between 20 and 140 degrees, the selected point has the highest EI due to its larger expected MI value, despite a narrower confidence interval, exemplifying a balance between exploration and exploitation. We observe that the confidence intervals approach zero near the previously observed parameter values, making these regions less favorable for exploration, as reflected by the low values of the EI function.
From the microfluidic point of view, in the case of Re = 5, the results show that as the α increases, the mixing performance decreases until approx. 30 deg, after which α does not influence the mixing performance. Afterward, the MI increases again for values larger than 140 deg. Additionally, it can be seen that there is a slight difference in mixing performance depending on the barrier orientation. For sharper angles, where the barrier is aligned with the flow direction, the resulting mixing is slightly better. Other geometric parameters of the micromixer with parallelogram barriers also significantly influence micromixing performance. The barrier width p shows a linear dependence on mixing efficiency, with larger values leading to better mixing. Similarly, greater barrier height l exhibits an exponential increase in mixing efficiency, while the greater distance between barriers d results in a linear decline in mixing performance. Results of one-parameter optimization for parameters p, l and d are presented in Fig. S1–S3.†
5.2 Comparison of different kernel functions for BO
As mentioned in section 2, the kernel function has an important role in GP modeling. To justify the choice of the Matérn kernel experimentally, we performed BO using four different kernel functions: linear, Matérn, rational quadratic, and RBF to optimize four design parameters of the micromixer with parallelogram barriers for Re = 5. The results, shown in Fig. 6, indicate that the Matérn kernel performs the best, achieving the highest MI equal to 0.82 after 33 simulations. The RBF kernel is a close second, reaching a MI of 0.79 after 36 simulations. In contrast, the rational quadratic and linear kernels converge to lower final values, with slower progress observed for the linear kernel. These findings highlight the superiority of the Matérn kernel for this optimization task, with the RBF kernel providing a competitive alternative. | ||
| Fig. 6 Comparison of BO performance using different kernel functions (linear, Matérn, rational quadratic, and RBF) for optimizing four design parameters at Re = 5 (RBF = radial basis function). | ||
5.3 Optimizing four geometric parameters of the micromixer with parallelogram barriers
In this section, we have explored the simultaneous optimization of four geometric parameters, p, d, l and α, using BO to achieve an optimal micromixer design across different Re values. The optimization was done for Re values equal to 0.1, 1, 5, 10 and 100, where different mixing mechanisms are dominant, resulting in significant variations in the corresponding MI objective function landscape. Based on these variations in certain regions of the optimization space, we have empirically selected the following length-scale hyperparameters for the Matérn kernel, as they provided the best results: 1.0, 1.0, 0.01, 0.001, and 1.0 for Re values of 0.1, 1, 5, 10, and 100, respectively. A smaller length-scale better adapts to rapidly changing objective function values, which is the case in specific regions for Re = 5 and 10.The BO process produces a GP model of the MI for each of the mentioned Re values, mapping the 4D input parameter space to a 1D output space. While a full representation of this GP model would require a 5D plot, which is not practical for visualization, the optimization results are instead visualized using two 3D surface plots for each Re value. In these plots, MI is presented as a function of two geometric parameters, with the other two parameters kept fixed, and the plot values are calculated directly from the GP model. The optimal solution is marked with a red dot. Fig. 7a, c, e and g illustrate the relationship between α and l (with parameters p and d fixed to the optimal values obtained in the optimization process), while Fig. 7b, d, f and h present the surface for parameters p and d (with values of α and l fixed), corresponding to Re = 1, 5, 10 and 100, respectively. The case of Re = 0.1 is not discussed, since complete mixing occurred across all parameter sets (driven entirely by molecular diffusion), implying that the barrier geometry had no impact on mixing performance at such low Re.
In the case of Re equal to 1, Fig. 7a shows that optimal MI values, close to 1, are achieved with α values around 10 deg, and with l close to 500 μm. As α increases beyond 100 deg or l deviates from 500 μm, the mixing performance declines significantly. On the other hand, optimal MI values are achieved when p is close to 1000 μm and d is between 1200 and 1500 μm, Fig. 7b. At Re = 1 the flow is highly laminar with no turbulence or chaotic advection occurring. Mixing primarily occurs through molecular diffusion, which is a slow process, and it is often insufficient for efficient mixing, especially over short distances. The role of the barrier geometry becomes important because these features can induce localized disruptions in the smooth, laminar flow. The barriers enhance mixing by stretching and folding the fluid flow, which increases the contact area between different fluid streams and accelerates the diffusion process between them.
At Re = 5, Fig. 7c and d indicate that optimal mixing occurs with α near 10 deg and l around 500 μm, while p and d values near 1000 μm and 1100 μm, respectively, yield the highest MI values. Although the flow remains laminar, advection becomes more influential in the mixing process. The barriers introduce disturbances that create recirculation zones and stretch the fluid interfaces, promoting enhanced mixing by intensifying diffusion through advective motion.
For Re = 10, Fig. 7e and f show similar trends, with optimal mixing achieved at α close to 10 deg and l around 500 μm. The best MI values are found with p near 1000 μm and d around 1300 μm. Though the flow is still laminar, advection plays an even stronger role. The barrier geometry amplifies recirculation and the stretching of fluid layers, significantly boosting the efficiency of diffusion. Moreover, as it can be seen in Fig. 7e, the MI function is particularly nonlinear for Re = 5, highlighting the need for using the efficient optimization algorithms such as BO.
Finally, for the case when Re is equal to 100, the analysis shows that l values close to 500 μm result in optimal performance when the barrier angle α approaches 170 deg, Fig. 7g. At higher Re, the barrier's orientation opposite to the flow direction further enhances mixing efficiency by generating stronger vortices and more chaotic flow patterns. For the parameters p and d, the analysis indicates that the optimal mixing performance occurs when d is close to 1200 μm for all values of p, Fig. 7h. In this case, the dominant mixing mechanism shifts from diffusion to advection and inertial effects, driven by the high flow velocities.
Table 1 summarizes the sets of optimal parameters proposed by BO for different Re, along with the calculated pressure drop for each case. As it was previously discussed, the results indicate a decrease in mixing performance as Re increases due to the shift from diffusion to advection and inertial effects in mixing mechanisms at higher Re. Although some studies focus on further optimizing the pressure drop to minimize resistance, in this case, the values remain significantly below the critical thresholds59,60,75 that would create substantial flow resistance within the micromixer, and it will not be further discussed.
| Re | α [deg] | l [μm] | p [μm] | d [μm] | Δp [Pa] | MI |
|---|---|---|---|---|---|---|
| 0.1 | 13 | 394.54 | 739.66 | 1697.39 | 0.00018 | 0.99 |
| 1 | 10 | 500 | 840.49 | 1242.75 | 0.23 | 0.99 |
| 5 | 10 | 500 | 1000 | 1299.00 | 2.1 | 0.82 |
| 10 | 10 | 500 | 1000 | 1100 | 39.1 | 0.60 |
| 100 | 170 | 500 | 1000 | 1100 | 656.1 | 0.54 |
In order to better illustrate the BO process, we have selected four representative iterations and displayed concentration profiles in the micromixer for different sets of geometric parameters, Fig. 8. The simulation results present the mixing of concentrations 0 and 1 mol m−3 for Re = 5. These results show the progress of the BO process through four iterations, beginning with the randomly chosen initial set of parameters and concluding with the optimal set of parameters. In the first iteration, the micromixer shows poor performance with MI = 0.17, indicating ineffective mixing, Fig. 8a. As BO iteratively refines the parameter selection, subsequent figures reveal gradual improvements in the MI, increasing to 0.43 and 0.61, Fig. 8b and c, respectively. By the final iteration, the optimization converges on the best configuration, Fig. 8d, achieving a significantly higher mixing index, MI = 0.82 and demonstrating the effectiveness of BO in navigating complex design spaces and improving micromixer performance.
Finally, we performed a sensitivity analysis over the parameter space to identify the parameters with the greatest influence on the resulting MI, providing deeper insights into design optimization. Namely, the plots in Fig. 7 cannot fully represent the GP model of MI, as they require fixing two parameters for visualization in 3D. Instead of focusing on a specific set of input conditions or local effects, we conducted a global sensitivity analysis for each Re value, offering a comprehensive metric that captures how much each parameter influences the MI estimated by the GP model, across the entire parameter space.
We employed Sobol sensitivity analysis,76 which quantifies the contributions of individual parameters and their interactions to the variance of the output. Firstly, we generated 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 samples of four design parameters using quasi-random Sobol sampling, systematically varying one parameter at a time while holding the others constant. Next, we calculated the MI for each sampled parameter set using the trained GP model. Finally, we applied Sobol sensitivity analysis over the created dataset, utilizing the variance decomposition procedure to estimate sensitivity indices.
920 samples of four design parameters using quasi-random Sobol sampling, systematically varying one parameter at a time while holding the others constant. Next, we calculated the MI for each sampled parameter set using the trained GP model. Finally, we applied Sobol sensitivity analysis over the created dataset, utilizing the variance decomposition procedure to estimate sensitivity indices.
In Table 2 we present the total sensitivity indices for each parameter at different Re values. These indices quantify the influence of each parameter on the resulting MI, either directly or through interactions with other parameters. Higher sensitivity indices indicate a greater overall impact of the parameter on the outcome. For Re = 1, the influence of barrier length l dominates, accounting for 0.76 of the variance, as diffusion is the primary mixing mechanism. As Re increases to 5 and 10, the significance of α grows (0.42 and 0.36, respectively), reflecting its role in shaping flow patterns for moderate advection-driven mixing. For Re = 100, α and p become dominant, emphasizing their impact on chaotic advection and flow disruption at higher velocities. In addition, parameter d shows the lowest influence on the mixing performance for all Re.
| Re | α | l | p | d |
|---|---|---|---|---|
| 1 | 0.15 | 0.76 | 0.05 | 0.06 |
| 5 | 0.42 | 0.79 | 0.15 | 0.06 |
| 10 | 0.36 | 0.86 | 0.19 | 0.05 |
| 100 | 0.63 | 0.40 | 0.55 | 0.10 |
5.4 Convergence analysis and comparison with evolutionary optimization methods
We compare the proposed BO approach with several evolutionary algorithms commonly used in microfluidic device and sensor design, including the genetic algorithm (GA),77 differential evolution (DE),78 evolution strategies (ES),79 and particle swarm optimization (PSO).80 We compared the results of each algorithm using the setup outlined in subsection 5.3, focusing on the task of optimizing four design parameters of the micromixer with parallelogram barriers to maximize the MI, with Re = 5. GA employed a population size of 20, with a crossover probability of 0.5 and a mutation probability of 0.2. DE also used a population size of 20, with a crossover probability of 0.25 and a differential weight of 1.0. PSO utilized a smaller population of 5 particles, with an inertia weight approach for velocity updates. ES was configured with a (μ, λ) evolutionary strategy, where μ = 10 and λ = 100, a population size of 10, a crossover probability of 0.6, and a mutation probability of 0.3.During the execution of each algorithm, MI encountered during Comsol simulations were recorded to track the progress. Unlike existing studies that rely on trained surrogate models to reduce computational costs, we employed direct simulations for a more accurate comparison. Fig. 9 presents the cumulative maximum MI achieved by each algorithm over the number of performed simulations. BO reached the optimal solution after 33 simulations, significantly outperforming the other methods. None of the evolutionary algorithms achieved the optimal MI within 100 simulations, although all showed a steady increase over time. When we allowed all algorithms to continue running until they reached the solution proposed by BO, PSO required 289 simulations, DE needed 580, while GA and ES did not achieve the optimal solution within 1000 simulations. These results highlight the advantages of BO in terms of convergence speed and efficiency, especially in scenarios involving computationally expensive evaluations.
The primary reason for the superiority of BO over evolutionary algorithms in terms of convergence speed is that BO leverages the GP model to predict the objective function and guide the optimization process more effectively.62 This allows BO to identify promising regions of the parameter space and converge to the optimal solution in far fewer iterations compared to evolutionary algorithms, which rely on stochastic population-based search strategies. Evolutionary algorithms excel at exploring large, high-dimensional, and complex search spaces, particularly when the global optimum lies in a small region of the parameter space. However, they lack a probabilistic model to effectively narrow down the search space.81 Consequently, these algorithms require significantly more iterations to achieve comparable solutions, making them less efficient for problems where objective function evaluations are computationally expensive.
Theoretical computational complexities of BO and evolutionary algorithms are based on fundamentally different factors (e.g., generation and population sizes for evolutionary algorithms in contrast to the number of observed points in BO). To address this, we experimentally compare their time and memory complexities. We note that the experiments were conducted using a laptop computer with an AMD Ryzen 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 U processor running at 2.00 GHz and 16 GB of RAM. Table 3 presents additional metrics for comparing the performance of BO and evolutionary algorithms.
700 U processor running at 2.00 GHz and 16 GB of RAM. Table 3 presents additional metrics for comparing the performance of BO and evolutionary algorithms.
| Metric | BO | DE | ES | GA | PSO |
|---|---|---|---|---|---|
| Iterations to optimum | 33 | 580 | >1000 | >1000 | 289 |
| Time to optimum [s] | 1219 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
>32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261 261 |
>33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 019 |
9727 |
| MI at 33rd iteration | 0.82 | 0.27 | 0.24 | 0.38 | 0.20 |
| Time to 100 iterations [s] | 3510 | 3245 | 3137 | 3211 | 3335 |
| Algo. time [s] (100 iter.) | 604 | 4.67 | 7.33 | 3.61 | 3.14 |
| Sim. time [s] (100 iter.) | 2906 | 3241 | 3130 | 3207 | 3332 |
| Peak memory usage [MB] | 3048 | 2626 | 2644 | 2633 | 2663 |
• The first row of the table provides a reference to the previously discussed results by showing the number of iterations (i.e., simulations) required by each algorithm to reach the optimal solution.
• The second row displays the total time to reach the optimum, a critical metric of practical interest. This time is expectedly correlated with the number of iterations required to reach the optimum for each algorithm. BO demonstrates the best performance for this metric, achieving the optimum in the shortest total time.
• The third row introduces an alternative comparison metric: the objective function value at a specific iteration, in this case, the 33rd iteration, when BO first reached the optimum. Here as well, BO demonstrates the best performance, achieving a significantly higher objective function value compared to the evolutionary algorithms.
• To compare computational efficiency per iteration, the fourth row includes the execution time required for 100 iterations of each algorithm. The results show that the times are relatively similar, with BO exhibiting higher times. To better understand this, the execution time is decomposed into two components: the time required for the algorithm itself, and the simulation time required for 100 Comsol simulations. These are detailed in the subsequent rows, followed by the peak RAM memory usage of each algorithm. A key observation is that simulation time overwhelmingly dominates algorithm execution time, which is expected given the computational cost of running simulations. Notably, algorithm execution time is independent of simulation complexity. For more complex Comsol models, this difference would become even more pronounced. As anticipated, the algorithm time for BO is higher than for evolutionary algorithms. This is because BO involves training a GP model on the observed data and maximizing the acquisition function to guide optimization, while evolutionary algorithms focus on devising a broad search strategy during their execution. As discussed, this guidance explains the faster convergence of BO. Despite being higher, the algorithm time for BO is still significantly lower than the simulation time, highlighting that the computational overhead introduced by BO remains relatively negligible compared to the cost of running simulations. Similarly, peak memory usage is higher for BO due to the additional resources needed for GP model training. In contrast, evolutionary algorithms have similar memory usage, as most of the memory is consumed by the Comsol model and the Python libraries, which are shared across implementations. It is worth noting that all the displayed memory usages are well within the capacity of computational hardware configurations of standard laptop computers, and do not pose a bottleneck.
• Lastly, the slightly lower simulation time for BO during 100 iterations can be attributed to its tendency to explore parameter values similar to the optimal ones after reaching the 33rd iteration. By chance, the simulation of these parameter combinations happens to be faster than the more diverse combinations proposed by evolutionary algorithms. However, this does not strictly imply that simulation times for BO will always be lower, as they depend on the specific parameter combinations and their associated simulation costs.
5.5 Optimizing nine geometric parameters of the Tesla mixer modified with parallelogram barriers
Further application of BO to more complex designs is demonstrated through a nine-parameter optimization of the Tesla micromixer modified with parallelogram barriers, described in subsection 3.2. Results of BO are presented in Table 4 for Re = 1, 5, 10 and 100, where excellent mixing performances can be seen with MI values close to 1 for all Re.| Re/Param. | K [μm] | G [μm] | P [μm] | α [deg] | β [deg] | p [μm] | l [μm] | γ [deg] | d [μm] | MI |
|---|---|---|---|---|---|---|---|---|---|---|
| Re = 1 | 700 | 460.66 | 1200 | 40 | 7.87 | 20 | 180 | 150 | 474.35 | 0.97 |
| Re = 5 | 673.59 | 223.6 | 536.27 | 35.24 | 14.13 | 96.77 | 166.29 | 137.85 | 448.85 | 0.96 |
| Re = 10 | 700 | 600 | 546.93 | 10.49 | 5 | 187.17 | 180 | 141.23 | 435.59 | 0.92 |
| Re = 100 | 679.6 | 596.62 | 488.96 | 31.23 | 14.42 | 92.14 | 147.44 | 143.79 | 268 | 0.85 |
The results highlight the non-linear nature of the objective function, as evidenced by the fact that the optimal parameter values predominantly fall within the interior of the parameter intervals rather than at their boundaries. This suggests a complex interplay between parameters, where the optimal solution emerges from a balance of influences rather than being constrained by extreme values.
The model successfully converged within 70 iterations for the nine-parameter micromixer optimized using BO, indicating that the convergence properties did not significantly change with the increase in dimensionality.
Fig. 10 presents the concentration profiles of Tesla mixers modified with parallelogram barriers after BO for Re = 1, 5, 10 and 100.
 | ||
| Fig. 10 Concentration profiles of Telsa micromixers modified with parallelogram barriers optimized using BO for different Re (a) Re = 1; (b) Re = 5; (c) Re = 10; (d) Re = 100. | ||
In addition, results of the Sobol method for global sensitivity analysis are presented in Table 5. Namely, for Re = 1, the barrier width p plays a dominant role in enhancing mixing (1.01), together with the length of the vortex zone P (0.7) and the moderate impact of barrier length l (0.39). Other parameters have negligible effects on average because global sensitivity analysis evaluates the impact of each parameter by averaging its influence over the entire parameter space. Parameters with localized effects in specific regions may appear to have little to no influence when assessed across the full range of possible values. For Re = 5, the barrier length l (0.70) and barrier inclination angle γ (0.57) emerge as the most influential parameters. This indicates that at low-to-moderate flow rates, the interplay between barrier geometry and flow direction becomes critical for enhancing mixing. For Re = 10, the barrier length l (0.78) and angle of barrier inclination γ (0.46) were shown as the most influential parameters. This suggests that at moderate flow rates, parallelogram barriers dominantly influence mixing performance. Other parameters remain insignificant on average. For Re = 100, the barrier length l (0.79) and barrier inclination angle γ (0.60) continue to dominate, reflecting their importance also under high flow conditions. Notably, the distance between the wall and divider G (0.07) becomes more significant, likely due to stronger inertial effects and increased flow complexity. Parameters like the channel inclination α, divider angle β, and distance between barriers d and divider length K remain negligible on average across all Re.
| Re | K | G | P | α | β | p | l | γ | d |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.01 | ≈0 | 0.70 | ≈0 | ≈0 | 1.01 | 0.39 | 0.03 | ≈0 |
| 5 | ≈0 | 0.01 | 0.04 | ≈0 | 0.05 | ≈0 | 0.70 | 0.57 | ≈0 |
| 10 | 0.02 | 0.01 | ≈0 | ≈0 | 0.04 | 0.09 | 0.78 | 0.46 | ≈0 |
| 100 | ≈0 | 0.07 | ≈0 | ≈0 | ≈0 | ≈0 | 0.79 | 0.60 | ≈0 |
5.6 Practical considerations
The described optimization approach is applicable to any microfluidic design regardless of the Comsol model complexity. While the presented BO process can be applied directly to experiments for real-world accuracy, this approach can be expensive, as each iteration assumes the fabrication of a new microfluidic device. To address this, we propose a two-stage process: the first stage utilizes simulations to identify an optimal design under idealized conditions. The second stage involves real-world fine-tuning on a narrower parameter set, incorporating fabrication constraints and testing a limited number of designs to achieve improved performance under practical conditions. This strategy balances efficiency with real-world applicability.In practice, material properties such as surface roughness, hydrophilicity and hydrophobicity as well as fabrication accuracy and temperature affect the mixing performance, thus, including these factors can improve simulation accuracy.
In that sense, BO can play a significant role in the post-fabrication process. Simulations can evaluate how specific parameter variations affect mixing performance, offering valuable insights into how manufacturing imperfections influence the outcome. This capability not only refines the design process but also makes the approach more accessible and practical for experimental applications. In order to prove the applicability of BO for different scenarios and illustrate the importance of an accurate simulation model, the influence of material properties, fabrication accuracy and temperature on mixing performance is examined and presented below.
The optimization was done for Re = 5 and results are presented in Table 6. In the case of hydrophilic walls (no-slip boundary condition), the optimized design achieves a MI of 0.82, indicating better mixing efficiency in comparison with hydrophobic walls (slip boundary condition) where the MI is 0.71. This outcome can be attributed to the stronger fluid–wall interaction, which promotes layered streamlines necessary for effective diffusive mixing. However, this leads to a higher pressure drop (Δp = 2.1 Pa), as the no-slip condition increases resistance to flow. On the other hand, for hydrophobic walls (slip condition), the optimized design results in a lower MI, reflecting reduced mixing efficiency. This is likely due to the weaker interaction between the fluid and the channel walls. Nevertheless, the slip condition reduces the pressure drop to Δp = 0.1 Pa, demonstrating smoother and faster flow with lower resistance.
| Boundary condition/parameters | α [deg] | l [μm] | p [μm] | d [μm] | Δp [Pa] | MI |
|---|---|---|---|---|---|---|
| No-slip | 10 | 500 | 1000 | 1299 | 2.1 | 0.82 |
| Slip | 10 | 482.3 | 1000 | 1800 | 0.1 | 0.71 |
| Parameters | α [deg] | l [μm] | p [μm] | d [μm] | MI |
|---|---|---|---|---|---|
| Optimized model | 10 | 500 | 1000 | 1299 | 0.82 |
| Deviation of α | 9.5 | 500 | 1000 | 1299 | 0.74 |
| Deviation of l | 10 | 475 | 1000 | 1299 | 0.60 |
| Deviation of p | 10 | 500 | 950 | 1299 | 0.79 |
| Deviation of d | 10 | 500 | 1000 | 1234 | 0.82 |
| Deviation (Δ = 5%) | 9.5 | 475 | 950 | 1299 | 0.56 |
 | ||
| Fig. 11 Examining the temperature influence on the MI for different inflow velocities. Results of optimization for 4, 20 and 80 °C. | ||
It is evident from results that temperature, inflow rates and boundary conditions have a significant impact on the mixing index. Therefore, before the optimization itself it is necessary to know the manufacturing technology, the materials that will be used, the operating temperature and expected inlet flows and to include them as initial conditions in the model.
5.7 Limitations and future work
Although the results presented in this work are promising, there are a few limitations to consider. One limitation of BO is that it performs well when optimizing up to approximately 20 parameters.82 Additionally, GP models can face computational challenges as the number of observations grows, due to the cubic scaling of covariance matrix inversion. However, in real-world microfluidic design problems, these limitations are typically not significant, as we do not expect scenarios requiring optimization with a large number of parameters or evaluations. If needed, methods like sparse GP can mitigate computational demands without significantly sacrificing accuracy.83 In our work, the dimensionality and number of evaluations were manageable, so we successfully used the proposed GP approach.Another potential limitation involves the selection of the kernel function and its hyperparameters. Although the Matérn kernel function performed well in our study with minor adjustments to the length-scale hyperparameter, selecting the appropriate kernel and fine-tuning its hyperparameters is necessary for highly nonlinear and rapidly changing objective functions. For example, when using the Matérn kernel, a smaller length-scale hyperparameter allows the model to capture rapid changes in the objective function between closely spaced points, with increasing uncertainty as the distance from observed data points grows. This complexity can further increase if the rate of change of the objective function differs significantly across different axes, as this may require using distinct length-scale hyperparameters for each parameter being optimized to accurately model variations along different dimensions. Generally, this process requires iterative optimization and some familiarity with the function being modeled.
Additionally, while multi-objective optimization is not necessary for our specific case, it is crucial in certain microfluidic design problems such as simultaneous optimization of mixing efficiency, pressure drop, and energy costs for fractal-based micromixers,59 or minimization of required pumping power while maximizing mixing efficiency for mechanical micromixers.60 Multi-objective BO is used to maximize several objectives at the same time. However, in microfluidic design, it is common to encounter objectives that compete with each other. For instance, one might aim to maximize mixing efficiency while minimizing pressure drop. To handle such competing objectives uniformly within the multi-objective BO framework, we typically reframe them for consistent treatment. For example, objectives that need to be minimized, like pressure drop, are transformed into maximization problems by negating their values. This approach ensures that all objectives fit within the standard framework of maximizing multiple outcomes simultaneously. A naive approach to implement this would be to optimize the sum of multiple objective functions using the proposed BO approach, but this can lead to suboptimal solutions where trade-offs between objectives are not properly managed. Researching multi-objective BO tailored for microfluidic design could therefore be a promising topic for further investigation. Similarly, handling constraints directly in the optimization process is not currently considered and could also be explored in future studies.
6 Conclusions
In this paper, we presented an ML-based tool for optimizing the design of two micromixers based on BO. The proposed approach was applied to optimize the geometric parameters of the micromixer with parallelogram barriers and the Tesla micromixer modified with parallelogram barriers, resulting in significant improvements in micromixing performance. BO has demonstrated consistent and stable convergence, providing efficient optimization without the need to train a separate surrogate model. Instead, the original CFD simulations were used, ensuring high precision while maintaining satisfactory optimization speed. The ability to directly use simulations simplifies the implementation of BO, making it a practical and effective solution for microfluidic design. The results confirmed that BO reduces the number of required simulations compared to state-of-the-art evolutionary algorithms. Future work may explore extending this approach to multi-objective optimization, further enhancing its applicability to a wider range of microfluidic systems.Data availability
The data presented in this study are available on request from the corresponding author. Email: E-mail: ivana.kundacina@biosense.rs.Author contributions
Ivana Kundacina: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization; Ognjen Kundacina: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization; Dragisa Miskovic: writing – review & editing, supervision; Vasa Radonic: resources, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This research was supported by the Science Fund of the Republic of Serbia, #Grant No. 7750276, Microfluidic lab-on-a-chip platform for fast detection of pathogenic bacteria using novel electrochemical aptamer-based biosensors – MicroLabAptaSens. IK and VR, and OK and DM acknowledge the financial support of the Ministry of Science, Technological Development, and Innovations of the Republic of Serbia GA No. 451-03-66/2024-03/ 200358 and GA No. 451-03-66/2024-03/ 200025, respectively.Notes and references
- J. K. Nunes and H. A. Stone, Chem. Rev., 2022, 122, 6919–6920 CrossRef CAS PubMed.
- S. Battat, D. A. Weitz and G. M. Whitesides, Lab Chip, 2022, 22, 530–536 RSC.
- M. I. Hajam and M. M. Khan, Biomater. Sci., 2024, 12, 218–251 RSC.
- Y. Liu and X. Jiang, Lab Chip, 2017, 17, 3960–3978 RSC.
- A.-G. Niculescu, C. Chircov, A. C. Bîrcă and A. M. Grumezescu, Nanomaterials, 2021, 11, 864 CrossRef CAS PubMed.
- Y. Yang, Y. Chen, H. Tang, N. Zong and X. Jiang, Small Methods, 2020, 4, 1900451 CrossRef CAS.
- A. Nikshad, A. Aghlmandi, R. Safaralizadeh, L. Aghebati-Maleki, M. E. Warkiani, F. M. Khiavi and M. Yousefi, Life Sci., 2021, 265, 118767 CrossRef CAS PubMed.
- Y. Zeng, J. W. Khor, T. L. van Neel, W. Tu, J. Berthier, S. Thongpang, E. Berthier and A. B. Theberge, Nat. Rev. Chem., 2023, 7, 439–455 CrossRef PubMed.
- S. Regmi, C. Poudel, R. Adhikari and K. Q. Luo, Biosensors, 2022, 12, 459 CrossRef CAS PubMed.
- A. Burklund, A. Tadimety, Y. Nie, N. Hao and J. X. J. Zhang, Adv. Clin. Chem., 2020, 95, 1–72 CAS.
- S. Preetam, B. K. Nahak, S. Patra, D. C. Toncu, S. Park, M. Syväjärvi, G. Orive and A. Tiwari, Biosens. Bioelectron.:X, 2022, 10, 100106 CAS.
- B. Sharma and A. Sharma, Adv. Eng. Mater., 2021, 24, 2100738 CrossRef.
- N. Azizipour, R. Avazpour, D. H. Rosenzweig, M. Sawan and A. Ajji, Micromachines, 2020, 11, 599 CrossRef PubMed.
- X. Wang, Z. Liu, B. Wang, Y. Cai and Q. Song, Anal. Chim. Acta, 2023, 1279, 341685 CrossRef CAS PubMed.
- S. Razavi Bazaz, A. Sayyah, A. H. Hazeri, R. Salomon, A. Abouei Mehrizi and M. Ebrahimi Warkiani, Chem. Eng. Sci., 2024, 293, 120028 CrossRef CAS.
- B. Hama, G. Mahajan, P. S. Fodor, M. Kaufman and C. R. Kothapalli, Microfluid. Nanofluid., 2018, 22, 54 CrossRef.
- R. B. Channon, R. F. Menger, W. Wang, D. B. Carrão, S. Vallabhuneni, A. K. Kota and C. S. Henry, Microfluid. Nanofluid., 2021, 25, 31 CrossRef CAS.
- E. H. T. Cunegatto, F. S. F. Zinani, C. Biserni and L. A. O. Rocha, Int. J. Heat Mass Transfer, 2023, 215, 124519 CrossRef CAS.
- M. Antognoli, D. Stoecklein, C. Galletti, E. Brunazzi and D. Di Carlo, Lab Chip, 2021, 21, 3910–3923 RSC.
- E. Tripathi, P. K. Patowari and S. Pati, Chem. Eng. Process., 2021, 162, 108335 CrossRef CAS.
- D. Zhou, L. Qin, J. Yue, A. Yang, Z. Jiang and S. Zheng, Int. J. Heat Mass Transfer, 2023, 212, 124273 CrossRef CAS.
- S. Akar, A. Taheri, R. Bazaz, E. Warkiani and M. Shaegh, Chem. Eng. Process., 2021, 160, 108251 CrossRef CAS.
- C.-H. D. Tsai and X.-Y. Lin, Micromachines, 2019, 10, 583 CrossRef PubMed.
- B. Abolpour, R. Hekmatkhah and R. Shamsoddini, Microfluid. Nanofluid., 2022, 26, 46 CrossRef.
- M. Juraeva and D.-J. Kang, Micromachines, 2022, 13, 1375 CrossRef PubMed.
- P. T. Le, S. H. An and H.-H. Jeong, Chem. Eng. J., 2024, 483, 149377 CrossRef CAS.
- H. Bachman, C. Chen, J. Rufo, S. Zhao, S. Yang, Z. Tian, N. Nama, P.-H. Huang and T. J. Huang, Lab Chip, 2020, 20, 1238–1248 RSC.
- Z. Chen, L. Shen, X. Zhao, H. Chen, Y. Xiao, Y. Zhang, X. Yang, J. Zhang, J. Wei and N. Hao, Appl. Mater. Today, 2022, 26, 101356 CrossRef.
- H. Ding, X. Zhong, B. Liu, L. Shi, T. Zhou and Y. Zhu, Microfluid. Nanofluid., 2021, 25, 26 CrossRef CAS.
- R. Zhou, A. Surendran and J. Wang, Sens. Actuators, A, 2021, 326, 112733 CrossRef CAS.
- P. Modarres and M. Tabrizian, ACS Appl. Nano Mater., 2020, 3, 4000–4013 CrossRef CAS.
- X. Xiao, T. Li and C. N. Kim, Chem. Eng. Res. Des., 2018, 139, 12–25 CrossRef CAS.
- A. Agarwal, A. Salahuddin, H. Wang and M. J. Ahamed, Microsyst., 2020, 26, 2465–2477 CrossRef.
- A. Pradeep and T. G. S. Babu, in Advanced Microfluidics-Based Point-of-Care Diagnostics, CRC Press, Boca Raton, 2022, pp. 271–292 Search PubMed.
- J. Park, Y. W. Kim and H.-J. Jeon, Biosensors, 2024, 14, 613 CrossRef PubMed.
- J. Zhou, J. Dong, H. Hou, L. Huang and J. Li, Lab Chip, 2024, 24, 1307–1326 RSC.
- G. Antonelli, J. Filippi, M. D'Orazio, G. Curci, P. Casti, A. Mencattini and E. Martinelli, Biosens. Bioelectron., 2024, 263, 116632 CrossRef CAS PubMed.
- D. McIntyre, A. Lashkaripour, P. Fordyce and D. Densmore, Lab Chip, 2022, 22, 2925–2937 RSC.
- S. Srikanth, S. K. Dubey, A. Javed and S. Goel, Sens. Actuators, A, 2021, 332, 113096 CrossRef CAS.
- J. W. Khor, N. Jean, E. S. Luxenberg, S. Ermon and S. K. Y. Tang, Soft Matter, 2019, 15, 1361–1372 RSC.
- P. Hadikhani, N. Borhani, S. M. H. Hashemi and D. Psaltis, Sci. Rep., 2019, 9, 8114 CrossRef PubMed.
- A. Arjun, R. R. Ajith and S. Kumar Ranjith, Biomicrofluidics, 2020, 14, 034111 CrossRef CAS PubMed.
- M. T. Doganay, P. Chakraborty, S. M. Bommakanti, S. Jammalamadaka, D. Battalapalli, A. Madabhushi and M. S. Draz, Lab Chip, 2024, 24, 4998–5008 RSC.
- J. Shi, L. You, Y. Wang and B. Peng, Geoenergy Sci. Eng., 2024, 243, 213391 CrossRef CAS.
- A. Jemmali, S. Kaziz, F. Echouchene and M. H. Gazzah, IEEE Sens. J., 2024, 24, 9299–9307 CAS.
- K. Nathanael, S. Cheng, N. M. Kovalchuk, R. Arcucci and M. J. H. Simmons, Chem. Eng. Res. Des., 2023, 193, 65–74 CrossRef CAS.
- A. A. Lendhe, N. Raykar, B. S. Kale and K. S. Bhole, Int. J. Interact. Des. Manuf., 2024, 18, 7183–7239 CrossRef.
- O. J. Dressler, P. D. Howes, J. Choo and A. J. deMello, ACS Omega, 2018, 3, 10084–10091 CrossRef CAS PubMed.
- J. Shi, P. Fu and W. Zheng, Analyst, 2022, 147, 1076–1085 RSC.
- M. T. Birtek, M. M. Alseed, M. R. Sarabi, A. Ahmadpour, A. K. Yetisen and S. Tasoglu, Biomicrofluidics, 2023, 17, 044101 CrossRef CAS PubMed.
- J. Wang, N. Zhang, J. Chen, G. Su, H. Yao, T.-Y. Ho and L. Sun, Lab Chip, 2021, 21, 296–309 RSC.
- L. H. Queiroz, F. P. Santos, J. P. Oliveira and M. B. Souza, Digit. Chem. Eng., 2021, 1, 100002 CrossRef.
- N. Zhang, Z. Liu and J. Wang, Micromachines, 2022, 13, 1810 CrossRef PubMed.
- D. de O. Maionchi, L. Ainstein, F. P. dos Santos and M. B. de Souza Júnior, Int. J. Heat Mass Transfer, 2022, 194, 123110 CrossRef.
- A. Lashkaripour, C. Rodriguez, N. Mehdipour, R. Mardian, D. McIntyre, L. Ortiz, J. Campbell and D. Densmore, Nat. Commun., 2021, 12, 25 CrossRef CAS PubMed.
- A. Lashkaripour, D. P. McIntyre, S. G. K. Calhoun, K. Krauth, D. M. Densmore and P. M. Fordyce, Nat. Commun., 2024, 15, 83 CrossRef CAS PubMed.
- H. Lv, X. Chen and X. Zeng, Chaos Solit. Fractals, 2021, 148, 111048 CrossRef.
- Y. Chen, T. Sun, Z. Liu, Y. Zhang and J. Wang, Micromachines, 2024, 15, 901 CrossRef PubMed.
- J. Wang, N. Zhang, J. Chen, V. G. J. Rodgers, P. Brisk and W. H. Grover, Lab Chip, 2019, 19, 3618–3627 RSC.
- F.-J. Granados-Ortiz and J. Ortega-Casanova, Phys. Fluids, 2021, 33, 063604 CrossRef CAS.
- H. Lv, X. Chen, X. Li, Y. Ma and D. Zhang, Int. Commun. Heat Mass Transfer, 2022, 131, 105867 CrossRef CAS.
- D. R. Jones, M. Schonlau and W. J. Welch, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, The MIT Press, 2006 Search PubMed.
- C. Tarar, E. Aydın, A. K. Yetisen and S. Tasoglu, Sens. Diagn., 2023, 2, 858–866 RSC.
- J. Guo, B. Ranković and P. Schwaller, Chimia, 2023, 77, 31 CrossRef CAS PubMed.
- E. Cisbani, A. Del Dotto, C. Fanelli, M. Williams, M. Alfred, F. Barbosa, L. Barion, V. Berdnikov, W. Brooks, T. Cao, M. Contalbrigo, S. Danagoulian, A. Datta, M. Demarteau, A. Denisov, M. Diefenthaler, A. Durum, D. Fields, Y. Furletova, C. Gleason, M. Grosse-Perdekamp, M. Hattawy, X. He, H. van Hecke, D. Higinbotham, T. Horn, C. Hyde, Y. Ilieva, G. Kalicy, A. Kebede, B. Kim, M. Liu, J. McKisson, R. Mendez, P. Nadel-Turonski, I. Pegg, D. Romanov, M. Sarsour, C. L. da Silva, J. Stevens, X. Sun, S. Syed, R. Towell, J. Xie, Z. W. Zhao, B. Zihlmann and C. Zorn, J. Instrum., 2020, 15, P05009–P05009 CrossRef.
- P. Frazier, A Tutorial on Bayesian Optimization, arXiv, 2018, preprint, arXiv:1807.02811, DOI:10.48550/arXiv.1807.02811.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175 Search PubMed.
- M. G. Genton, J. Mach. Learn. Res., 2002, 2, 299–312 Search PubMed.
- COMSOL Multiphysics Reference Manual, 2024.
- E. L. Upp and P. J. LaNasa, Fluid Flow Measurement: A Practical Guide to Accurate Flow Measurement, Gulf Professional Publishing, 2nd edn, 2002 Search PubMed.
- W. Raza, S. Hossain and K.-Y. Kim, Micromachines, 2020, 11, 455 CrossRef PubMed.
- T. Head, MechCoder, G. Louppe, I. Shcherbatyi, fcharras, Z. Vinícius, cmmalone and C. Schröder, Zenodo, 2018, preprint, Zenodo:v0.5.2, DOI:10.5281/zenodo.1207017.
- J. Hennig, M. Elfner, A. Maeder and J. Feder, Zenodo, 2024, preprint, Zenodo:v1.2.4, DOI:10.5281/zenodo.11539226.
- X. Zhang and Z. Zhang, Micromachines, 2019, 10, 653 CrossRef PubMed.
- I. M. Sobol′, Math. Comput. Simul., 2001, 55, 271–280 CrossRef.
- J. H. Holland, Sci. Am., 1992, 267, 66–73 CrossRef.
- R. Storn and K. Price, Journal of Global Optimization, 1997, 11, 341–359 CrossRef.
- H.-G. Beyer and H.-P. Schwefel, Nat. Comput., 2002, 1, 3–52 CrossRef.
- D. Wang, D. Tan and L. Liu, Soft Comput., 2017, 22, 387–408 CrossRef.
- T. H. W. Bäck, A. V. Kononova, B. van Stein, H. Wang, K. A. Antonov, R. T. Kalkreuth, J. de Nobel, D. Vermetten, R. de Winter and F. Ye, Evol. Comput., 2023, 31, 81–122 CrossRef PubMed.
- R. Moriconi, M. P. Deisenroth and K. S. Sesh Kumar, Mach. Learn., 2020, 109, 1925–1943 CrossRef.
- J. Quinonero-Candela and C. E. Rasmussen, J. Mach. Learn. Res., 2005, 6, 1939–1959 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00872c |
| ‡ Authors equally contributed. |
| This journal is © The Royal Society of Chemistry 2025 |




