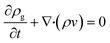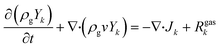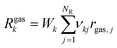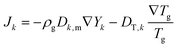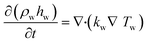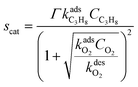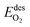Design of microcombustor–thermoelectric coupled device using a CFD-based multiphysics model for power generation
Neha
Yedala
and
Niket S.
Kaisare
 *
*
Department of Chemical Engineering, Indian Institute of Technology Madras, Chennai 600036, India. E-mail: nkaisare@iitm.ac.in
First published on 2nd May 2024
Abstract
Catalytic combustion in micro-reactors can be coupled with thermoelectric power generator (TEG) modules for distributed and portable power generation, especially in niche applications. The efficiency of such an integrated device can be improved by operating the microcombustor at lean flow rates or using more efficient heat sinks. However, these lead to incomplete fuel conversion and eventually extinction instability. In contrast, high flow rates are detrimental to the TEG module owing to high temperatures. In this work, the TEG modules are coupled with a more efficient symmetric heat recirculating reactor (S-HRR) and a water-cooled heat sink to address this tradeoff between combustion stability and electrical efficiency. Specifically, we provide a detailed analysis of power generation from the integrated device and the impact of design parameters of the inner wall material and flue gas recirculation channel gap-size. We also present operating parameters for stable operation, based on combustion extinction limits and maximum operating temperature limitation of the TEG module and finally make a comparison of energy associated with various streams in the integrated device.
1. Introduction
Owing to the high energy density of hydrocarbon-based fuels, extracting and utilizing thermal energy from their combustion in micro-combustors (i.e., reactors with channel diameters < 1 mm) can be a potential source for distributed power generation.1–3 Such micropower generation is relevant for use in mission-critical niche applications and in remote areas, where onsite power generation may be desirable. The continuous power generated may (for example) be used to recharge portable devices such as laptops, mobile phones, GPS units, etc. in mission-critical applications. The power required to charge these devices is about 5–50 W.1–3 Alternatively, micropower generation may provide a cheaper and (relatively) reliable source of electricity in poorer regions, or during times of natural disasters when procuring fuel may be easier than other alternatives. Although these fuels have more than an order of magnitude higher energy density than batteries, the energy density of a power generating device is determined by the weight or volume of all the systems integrated. Hence, a microcombustion-based integrated device that provides high energy density and ensures good efficiency considering the overall system remains a key challenge.1–3 This work is one of the contributions towards that aim. Power generation from microcombustors integrated with thermoelectric power generating (TEG) modules is investigated in this work. TEG modules are light-weight and compact, easy to integrate with a microcombustor, and facilitate vibration-free operation.4,5 These devices do not require recharging but refueling with hydrocarbon fuels.Several research groups have presented proof-of-concept demonstrations. Vican et al.6 developed a micropower generator fuelled by hydrogen, with a Swiss-roll reactor integrated into a thermoelectric (TEG) module. Federici et al.7 demonstrated power generation of ∼0.6 W from combustion of hydrogen and propane in a catalytic parallel plate reactor. Merotto et al.8 designed a meso-scale combustor filled with catalyst pellets, coupled with two TEG modules; with water-cooled heat sinks attached, this device produced ∼9.8 W of power.8 Kumar and co-workers presented power generation of ∼5 W from coupled devices with various reactor designs designed to promote stable homogeneous combustion.9,10 In these studies, the gaseous fuel is supplied from domestic (commercial) or lab-grade gas cylinders, and the integrated reactor-TEG device typically has length ∼10 cm.
While there have been experimental demonstrations, model-based design and analysis is missing. This work focuses on using a multiphysics model developed in our previous work26 for design and analysis to improve the combustion efficiency, power output, and overall performance of the coupled device. The power generated from a TEG module is proportional to the temperature difference between the hot (microcombustor) side and the cold (heat-sink) side.4,7 Finned heat sinks, CPU cooler fans, and water-cooled heat sinks are employed on the cold side of the TEG to maintain lower temperatures.11–13 While lower cold-side temperatures improve the TEG efficiency, they can destabilize combustion in the microreactor. For example, combustion in straight channel microcombustors in the presence of high energy extracting devices such as TEG and heat sinks often leads to lower fuel conversion.14,15 Therefore, heat recirculating (HR) combustion or excess-enthalpy combustion is promoted.16,17 The basic principle underlying HR combustion is that the combustion can be stabilized by the transfer of heat from the reaction zone to the unburnt mixture. It has been proved that the heat addition to unburnt mixtures allows the stable combustion of lean mixtures outside their flammability limits.18
Kumar and co-workers9,10,19 analyzed multiple configurations of homogeneous HR microreactors coupled with TEG for power generation. A U-shaped combustor, with extended flow channels to accommodate a greater number of modules to extract heat from the exhaust, was designed by Bensaid et al.20 Wang et al.21 performed a simulation study on a new design with the TEG module placed between the inlet and recirculation channel side, so that the heat rejected on the cold-side can be absorbed by the incoming cold feed. A reactor with stepped corners and recirculation channels on either side was designed and coupled with TEGs by Kumar and co-workers.9,22 Microreactors coupled with thermo-photo-voltaic (TPV) devices have also been investigated in a similar manner.23
Although HR facilitates combustion at lean flow rates, it may lead to higher surface temperatures. Such conditions are not suitable for TEG coupling.24 In other words, stable combustion requires high temperatures but efficient TEG performance requires optimum heat recycle and proper thermal management.25 Hu et al.24 studied the impact of using copper-based thermal spreaders and exhaust gas recirculation for proper thermal management of stand-alone microcombustors for controlling the outer-wall temperatures. However, the actual skin temperatures and, hence, the overall device performance can significantly differ from the stand-alone operation of the microcombustor. In order to perform a detailed numerical analysis of the coupled device, a model for integrated microreactor-TEG device, comprising a TEG model that can be thermally coupled with the microreactor model, was proposed in our previous work.26 Using this model, we presented a comparison between two HR reactors, viz., the U-bend and symmetric-HRR for integration with TEG modules.25 We reported that S-HRR, when used with finned coolers, gave higher skin temperatures due to improved transfer of excess enthalpy from reactants to products, thus limiting the operating regime. However, if additional heat is extracted from the cold-side (e.g., using water-cooled heat-sinks), S-HRR could prove advantageous and the overall power generation could be increased.25
Since the power generated is proportional to the temperature difference across the TEG module,15 water-cooled heat sinks have been used experimentally.9,11,27 Aravind et al.27 found that a water-cooled heat sink is the most efficient, even accounting for the energy required to run the water pump for circulation of cooling water. The net power generated from the integrated device was higher in the water-cooled heat sink compared to the fin-fan type heat sink in.27 A catalytic microreactor-TEG device coupled with a water-cooled heat sink examined for small-scale battery back-up demonstrated the potential of this technology to provide high power densities with leaner fuel concentrations.28 Although several experimental reports exist in the literature, simulation-based analysis and design of integrated microdevices has not received equivalent attention. Therefore, the performance of the catalytic S-HRR coupled with TEG and water-cooled heat sink is studied in this work. To improve fuel conversion, avoid breakthrough, and obtain higher power outputs at leaner compositions, the design parameters of inner wall conductivity and gap size of the recirculation channel of S-HRR are varied, and their impact on coupled device performance is analyzed in this work.
Thermal conductivity of the wall plays a vital role in the stability of microreactors. Unlike the straight channel reactor, HR reactors can sustain combustion with poor-conducting walls even at high heat losses.29 However, the outer walls of the microreactor determine the heat transfer to the TEG device. Hence, steel is regarded as an optimal compromise for the exterior walls considering both the factors of stable combustion and heat transfer to the coupled device. In the individual microcombustor, Federici et al.29 and Chen et al.30 found that the conductivity of the inner wall of S-HRR impacts the stability more significantly than the conductivity of the outer wall. The critical heat loss coefficient increased by an order of magnitude when the inner wall conductivity is reduced, despite conductive outer walls.29 This was also demonstrated by Lee et al.31 using quartz and steel reactors for homogeneous combustion inside a U-bend heat recirculating reactor with combustion space at the U-turn of the reactor. They also studied the effect of gap size on homogeneous combustion and reported that preheating of incoming reactants was suppressed when the gap-size was increased, for the same mean velocity and heat recirculation area.31 However, since the system considered in this study is catalytic, the microcombustor is integrated with TEG and heat sinks, and the geometry is different, it is difficult to draw parallels. While the effects of conductivity of the inner wall and gap-size have been analyzed for stand-alone HR microreactors, their impact on the integrated device has not been analyzed, to the best of our knowledge. Towards this end, the effect of changing the inner wall material from steel to ceramic and the effect of increased recirculation channel gap size on propane conversion, power generation, and extinction velocities are discussed in this work, followed by the comparison of operating regimes and energy analyses for the cases considered.
2. Model description and solution methodology
2.1. Symmetric-heat recirculating geometry integrated with a water-cooled heat sink
The schematic of the integrated device, with one S-HRR coupled with two TEG modules, is shown in Fig. 1(a). The two TEG modules, placed on either face of the S-HRR, draw electric power due to the Seebeck effect. The S-HRR heats the TEG modules via copper thermal spreaders, whereas water-cooled heat sinks are coupled to the cold side of TEG modules. The S-HRR is 5 cm in length (see Fig. 1b), with a central 4 cm section coated with catalyst on the inner walls. The walls are 800 μm thick; the gap size of the catalytic channel is 600 μm, and the gap size of each of the recirculation channels is 300 μm for the nominal case. Copper spreaders promote temperature uniformity in the axial direction, eliminate hot-spots and provide skin temperatures that are acceptable for TEG coupling.7,32 Each copper spreader has a length of 4 cm and thickness of 3.2 mm. Each HiZ-2 TEG module (Fig. 1c) is 3 cm in length and 3 cm in width, with a semiconductor height of 3.8 mm and ceramic wafer thickness of 1 mm. These are coupled on either side of S-HRR, placed on the copper spreaders as shown in Fig. 1(a). The TEG geometry and physical properties are the same as those used in our previous work.26 There, we presented simulations of a straight-channel microreactor coupled with a TEG module, and validated them with the corresponding experiments of Federici et al.7 Our model in Yedala and Kaisare26 was able to predict power vs. voltage characteristics of this device with good agreement with experiments. Therefore, the same coupled microdevice model is now used for analyzing the integrated device in the current study.A water-cooled heat sink with a footprint area equivalent to the HiZ-2 module is coupled on the cold side, as shown in Fig. 1(a). The heat sink consists of two copper walls separated by a gap width of 1 mm for the circulation of cooling water. This 2D model of the heat sink is intended to provide cold-side temperatures close to 35–40 °C, similar to the heat sink used in the experiments of Aravind et al.9 However, it needs to be emphasized that the actual device temperature is determined by solving the multi-physics model for the S-HRR, TEG, and cooling water sink simultaneously. In section 3.3, the gap size of recirculation channels on either side is increased to 600 μm to double the recirculation volume.
2.2. Model description and solution methodology
The model for the TEG module and its subsequent coupling with a catalytic microreactor was described in our previous work.26 Here, we briefly summarize the details of the coupled device. The fuel–air mixture is modeled as ideal gas, the flow is laminar, and species diffusion and Soret diffusion effects are included. A flat inlet profile at desired composition and temperature is assumed at the reactor inlet and the downstream pressure is atmospheric. To simulate catalytic combustion of lean premixed propane–air mixtures in the coupled microdevice, we solve the mass, momentum, energy and species conservation equations in 2D in ANSYS FLUENT using the SIMPLE algorithm. The resulting conservation equations include:where
The energy conservation in the solid is given by
The boundary conditions are as follows. At all the inner walls of the microreactors, the no-slip condition (u = 0) is imposed. The inner walls of the inlet channel are catalytic:
| Jk,y|wall− + Rcatk = 0, |
The subscripts wall+ and wall− represent the solid-side and gas-side of the wall-interface, respectively. When the fluid–solid interface is non-catalytic (e.g., in the recirculating channel):
| Jk,y|wall− = 0 |
All the external walls lose heat to the surroundings due to convection and radiation:
| Qlost = h∞(Tw − T∞) + σε(T4w − T4∞) |
whereas the surface reaction rate is given by the following reduced-order model from:34
The kinetic rate parameters are given in Table 1, whereas the activation energy for oxygen desorption is taken from ref. 35 and evaluated as:
The mixture properties for the gas-phase are computed as the mass-weighted average of species properties. Thermal conductivity, viscosity and diffusivity of each species are estimated by kinetic theory; and piece-wise polynomials are used to calculate species' specific heats. The reactor material is considered to be stainless steel for the nominal case, whose thermal conductivity and emissivity are 16 W m−1 K−1 and 0.8, respectively. In section 3.2, the inner walls or dividing walls of S-HRR are modeled as ceramic, whose conductivity is 2 W m−1 K−1.
The copper spreaders and the ceramic wafers enclosing the TEG module solid blocks are modeled with a 2D energy balance equation. The thermal conductivity of copper spreaders37 and ceramic wafers26 are 388 W m−1 K−1 and 10 W m−1 K−1, respectively. The interfaces between the microreactor wall and copper spreader, between the copper spreader and ceramic wafer, between the TEG block and ceramic wafer, and between the ceramic wafer and water-cooled heat sink, are set to be thermally coupled walls to create the coupling between the sub-units. The uncovered external walls on the reactor and copper spreaders (i.e., the walls that are exposed to the atmosphere) are assumed to lose heat to the atmosphere via convection (h∞ = 20 W m−2 K−1) and radiation (∈ = 0.8).
The model for a TEG module developed in our previous work,26 with its temperature dependent aggregate (thermal and electrical) properties, is summarized below for completeness. The TEG module, which comprises an assembly of all p- and n-type semiconductors, is modeled as a single semiconductor block sandwiched between ceramic wafers. The aggregate properties of the TEG block were determined by fitting the manufacturer data as temperature dependent polynomials. The contact resistance at the hot-side and cold-side junctions is negligible. Therefore, the 2D energy conservation equation is solved in the bulk of the semiconductor block given by
| ∇·(kM∇T) + Sv = 0 | (1) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) M) and Thomson (
M) and Thomson (![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) I(Th − Tc)) effects, where
I(Th − Tc)) effects, where ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) M and
M and ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) denote the aggregate internal resistance and Thomson coefficient of the module. The electrical current (I), voltage (V) and power drawn (P) are evaluated at steady state using the following equations:
denote the aggregate internal resistance and Thomson coefficient of the module. The electrical current (I), voltage (V) and power drawn (P) are evaluated at steady state using the following equations: | (2) |
| V = IRload | (3) |
| P = VI | (4) |
Interfaces between the TEG block and ceramic wafers on either side are set to be thermally coupled walls. These walls on the hot-side and cold-side of the TEG have copper interconnects that link adjacent thermocouples; these are modeled using a thin wall resistance model with the source terms of the Peltier effect given by (αMhThI) and (αMcTcI).
We refer the interested reader to our previous work26 for detailed model development and validation. Specifically, the model for the standalone TEG module was validated using the experiments of Wang et al.11 and Chen et al.38 After validation, the TEG module and the combustor were coupled by setting the interface between the TEG and combustor as a thermally coupled wall in ANSYS FLUENT. The coupled wall boundary condition ensures that the heat transferred from the wall of the copper spreader equals the flux entering the TEG module. The coupled device model (microcombustor thermally integrated with the TEG module) was validated with the experiments of Federici et al.7 as presented in our previous work.26
Finally, the water-cooled heat sink is modeled using mass, momentum, and energy conservation. Liquid water is the working fluid and the walls are made of copper. No-slip boundary condition is used at the fluid–solid interface. The inlet velocity of cooling water is varied as 0.27, 0.54 or 0.81 ms−1 and the inlet temperature is 27 °C.
2.3. Grid independence
The conservation equations are solved with the boundary conditions mentioned in the previous section, until the system reaches steady-state and the solution is converged. Convergence is ensured by verifying that the scaled residuals fall by at least two orders of magnitude and the conservation of mass and energy in the entire domain are satisfied. We also ensure the monitored profiles of weighted averages of temperature/species at multiple locations are constant for several thousand iterations.Before proceeding to the results, the solution is verified grid-independent. Half geometry is simulated owing to the symmetry of the device along the center-line (indicated by the dash-dot line in Fig. 1(a)). The geometry of S-HRR coupled with the TEG and water-cooled heat sink, i.e., shown in Fig. 1(a), is meshed into a grid size of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 elements, consisting of 250 axial and 20 radial divisions in the reactor fluid zone; the copper spreader domain has 200 axial and 20 radial divisions; wall zones are meshed into 10 radial divisions; TEG bulk is divided into 20 radial divisions and 150 axial divisions with 10 radial divisions in the ceramic wafers; 10 radial divisions in copper walls, 20 radial divisions in the flow channel with 150 axial divisions in the heat sink section. Radial divisions alone and axial divisions alone are increased to form meshes with a grid size of 57
820 elements, consisting of 250 axial and 20 radial divisions in the reactor fluid zone; the copper spreader domain has 200 axial and 20 radial divisions; wall zones are meshed into 10 radial divisions; TEG bulk is divided into 20 radial divisions and 150 axial divisions with 10 radial divisions in the ceramic wafers; 10 radial divisions in copper walls, 20 radial divisions in the flow channel with 150 axial divisions in the heat sink section. Radial divisions alone and axial divisions alone are increased to form meshes with a grid size of 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 elements and 63
020 elements and 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 elements, respectively. Specifically, radial divisions are increased to 30 in the reactor fluid zone, TEG bulk, cooling water channel, and copper spreader; 20 in the reactor, ceramic and sink-copper walls with the same number of axial divisions to form a second mesh with 57
820 elements, respectively. Specifically, radial divisions are increased to 30 in the reactor fluid zone, TEG bulk, cooling water channel, and copper spreader; 20 in the reactor, ceramic and sink-copper walls with the same number of axial divisions to form a second mesh with 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 elements. In the third mesh, radial divisions are retained the same as the nominal mesh size, but axial divisions are increased to 500 in the reactor bulk, 200 in the copper spreader, and 150 in the TEG module and heat sink to form a mesh of size 63
020 elements. In the third mesh, radial divisions are retained the same as the nominal mesh size, but axial divisions are increased to 500 in the reactor bulk, 200 in the copper spreader, and 150 in the TEG module and heat sink to form a mesh of size 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 elements. The centerline temperatures and TEG hot-side temperatures did not vary significantly with mesh size. Therefore, the nominal mesh size of 32
820 elements. The centerline temperatures and TEG hot-side temperatures did not vary significantly with mesh size. Therefore, the nominal mesh size of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 elements is used for all the simulations.
820 elements is used for all the simulations.
For the parametric study, we varied the operating conditions as in Table 2. A stable solution was obtained under nominal conditions, with a given cooling water flow rate. Thereafter, the equivalence ratio and inlet velocity are varied until the extinction point, akin to natural parameter continuation.
| Parameter | Operating range |
|---|---|
| Inlet velocity | 5–0.8 m s−1 |
| Equivalence ratio | 0.9–0.6 |
| Cooling water flowrate | 1.5–0.5 lpm |
| Thermal conductivity | 16 W m−1 K−1 (steel walls) 2 W m−1 K−1 (ceramic inner walls) |
3. Results and discussion
3.1. Operation of the coupled device
Fig. 2 depicts the hot-side (solid lines) and cold-side (dashed lines) temperatures at the two faces of the TEG, obtained with S-HRR coupled at the hot-side and water-cooled heat sink coupled at the cold-side under various operating conditions. The effect of inlet velocity of the feed is shown at three different equivalence ratios of 0.7 (square symbols), 0.8 (circles), and 0.9 (triangles). The cooling water flow rate is maintained at 0.5 lpm, which ensures cold side temperatures at 40 °C. Flow rates below 0.5 lpm resulted in higher temperatures at the cold side of the TEG module and lower power generation, and therefore were not considered further. A significant increase in the hot-side temperatures with the increase in the fuel flow rate is observed. In contrast, the corresponding cold-side temperatures do not vary significantly. Downward arrows at the left of each curve in Fig. 2 indicate the extinction velocities, i.e., the lowest inlet velocity of the propane–air mixture required for sustained operation of the coupled system. The extinction velocities shift to much lower inlet velocities when the equivalence ratio of the fuel is increased. Due to flow of cooling water in the heat sink, the cold-side temperatures are lower. Compared to the previous work,25 where the sink-side heat loss coefficients were considered to be 200 W m−2 K−1 and 500 W m−2 K−1 to represent finned cooling, using a water-cooled heat sink resulted in lower cold-side temperatures, and hence, a higher temperature difference across the TEG modules. | ||
| Fig. 4 (a) Net power generated from the two TEG modules integrated on either side of S-HRR and (b) propane conversion vs. inlet velocity. The three curves represent different values of equivalence ratios. The operating conditions are the same as those in Fig. 2. | ||
Since the microreactor is operated under fuel-lean conditions, formation of partially oxidized products was not considered. Thus, the reactor outlet contains CO2, H2O, O2, N2 and unconverted propane. Propane conversion exceeded 80% in all simulations considered. Fig. 4(b) shows that breakthrough is observed at low velocities and low equivalence ratios because of high heat removal from the system. Therefore, higher equivalence ratios are required for the operation of the present system when low emissions and higher power extraction are the targets. However, the trade-off between skin temperatures and conversion always exists.
The device efficiency under various operating conditions is another key performance parameter. Two kinds of efficiencies are defined: thermoelectric efficiency (ηTEG) and overall efficiency (ηoverall). ηTEG is the ratio of electrical energy generated by TEG (and delivered to the load resistance) to the energy provided by the microreactor to TEG at the hot-side,
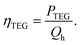 | (5) |
 | (6) |
 | ||
| Fig. 5 Thermoelectric (ηTEG, solid line) and overall (ηoverall, dashed line) efficiencies of the S-HRR–TEG coupled with a water-cooled heat sink, at ϕ = 0.7 and various inlet velocities. | ||
The water-cooled heat sinks ensure lower cold-side temperatures. Thus, the desired operating conditions shift to higher equivalence ratios and inlet velocities, resulting in higher hot-side temperatures. This increased difference between hot- and cold-side temperatures across the TEG modules results in higher power generated, ηTEG and ηoverall. For a safe operating condition of equivalence ratio of 0.7 and inlet velocity of 3.5 ms−1 (Th = 241 °C and Tc = 42 °C), ηTEG and ηoverall are 4.7% and 3.1%. Considering propane conversion also, the efficiency  is found to be 3.5%, which is comparable to the recent studies of Abedi et al.28 and Aravind et al.9
is found to be 3.5%, which is comparable to the recent studies of Abedi et al.28 and Aravind et al.9
The performance of this integrated device is limited by the low efficiency of the TEG module, which is a major bottleneck for widespread adoption. Several efforts are being made by researchers to discover TEG materials with higher figures of merit.39 Zheng et al.39 and Twaha et al.13 reviewed various methods and structure modifications to improve TEG module efficiency and allow higher operating temperatures. Nonetheless, the design of the integrated device can be optimized to improve combustion efficiency, lower emissions and better thermal integration. Some of the strategies for reactor design are discussed in the rest of this section.
3.2. Effect of changing the inner wall material
While the coupled device shows good power generation, the issue of incomplete propane conversion needs to be addressed. The unique S-HRR geometry allows us to modify the inner walls of the microcombustor while retaining the same outer walls. Alternatively, the gap-size of the recirculating channel can be varied. We will analyze the two strategies in this section.Federici et al.29 and Chen et al.30 reported that the inner S-HRR wall can have a large impact on the stability of stand-alone microcombustors, with more insulating walls providing higher propane conversion and stability. Hence, we compare the performance of the integrated device when steel inner walls (kw = 16 W m−1 K−1) are replaced by ceramic (kw = 2 W m−1 K−1). The left panels in Fig. 6 (i.e., panels (a.1), (a.2) and (a.3)) show the contours for the nominal case (steel inner walls), whereas the right panels (i.e., panels (b.1), (b.2) and (b.3)) show the corresponding contours for ceramic inner walls. These contours help with a visual comparison of the two cases. Propane concentration is high at the inlet and the initial non-catalytic region. Ceramic inner walls result in heat localization, as indicated by higher temperature in Fig. 6(b.1) compared to Fig. 6(a.1). The propane concentration drops to zero significantly upstream in the S-HRR with ceramic inner walls (Fig. 6–b.2), which reinforces the advantage of heat recirculation on fuel conversion. The increase in temperature and conversion also results in an increase in velocity for both cases.
 | ||
| Fig. 6 The effect of the inner wall material on the contours of temperature (top), propane mass fraction (middle) and velocity (bottom). The inner dividing of the S-HRR wall is steel in the left panels (a.1–a.3) and ceramic in the right panels (b.1–b.3). In the middle and bottom panels, only the flow channels of S-HRR are shown. The inlet velocity is 3.5 ms−1, ϕ = 0.7 and other conditions the same as in Fig. 2. | ||
The centerline temperature and reaction rate are plotted in Fig. 7 for a quantitative understanding of these two cases at the same operating equivalence ratio of 0.7 and inlet velocity of 3.5 ms−1. Specifically, the temperature profiles along the centerlines of the reaction and recirculation channels are shown. Although the TEG temperatures are lower, insulating inner walls result in higher temperatures and a hot-spot in the inner channel of the microcombustor. On comparing Fig. 7(a) and (b), higher temperatures and a hot-spot are observed in the combustor with ceramic inner walls, owing to the weaker axial conduction in ceramic dividing walls. The gap between the dashed and solid lines near the combustor inlet is indicative of the amount of heat recirculation possible in the S-HRR. Clearly, the excess enthalpy transfer from the recirculation to the reaction channel in the pre-reaction zone (near the inlet) is higher in the S-HRR with insulating walls. This eventually results in increased reaction rates (blue lines with right-axis in Fig. 7) and, hence, a steeper increase in the temperatures in the catalytic channel. The temperature and propane contours in Fig. 6 also support this understanding. This indeed results in higher skin temperatures on the copper spreaders and will impact the power and fuel conversion, which will be discussed further.
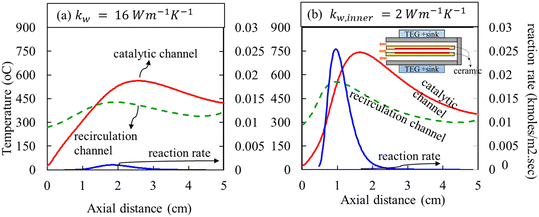 | ||
| Fig. 7 Temperature profiles along the centerlines of the catalytic (solid lines) and the recirculation (dashed lines) channels of the S-HRR when the inner dividing wall is (a) steel and (b) ceramic, respectively. Blue solid lines show the reaction rates on the right axis. These conditions correspond to those in Fig. 6. | ||
Fig. 8 compares the power generated and propane conversion at various inlet velocities for steel and ceramic inner walls. Although operating a pump to circulate cooling water requires some power, this is not included in the electric power reported in this figure. Solid and dashed lines represent steel and ceramic walls, respectively, at ϕ = 0.7 (squares) and 0.6 (diamonds). Higher power and higher propane conversion are obtained with ceramic inner walls for the same rate of fuel input because of increased hot-side skin temperatures and increased magnitudes of (Th − Tc). Furthermore, it was interesting to note that stable device operation was only observed with ceramic inner walls at a lower equivalence ratio of ϕ = 0.6, unlike the reactor with steel inner walls. The extinction velocity also decreased for ceramic inner walls (thus increasing the region of stable operation), as observed from the downward arrows Fig. 8. Comparison of solid (steel) and dashed (ceramic) lines in Fig. 8(b) at ϕ = 0.7 shows profound improvement in propane conversions. The power generated and conversions are shown only at the leaner equivalence ratios because the ceramic inner walls are advantageous under leaner conditions. At higher equivalence ratios, the higher skin temperatures are undesirable.
3.3. Effect of increased recirculation channel gap size
We now analyze the effect of doubling the gap-size of the outer channel to 600 μm in Fig. 9. Increasing the gap-size can promote higher propane conversion by reducing the transverse heat transfer from the hot central channel to the endothermic TEG module. The residence time of the product stream increases, which could promote transfer of excess enthalpy to the inlet. The contours of temperature and propane mass fraction follow a qualitatively similar behavior to the nominal case in Fig. 6(a.1) and (a.2); however, with an increased gap-width of the recirculating channel, the maximum temperature as well as propane conversion increases.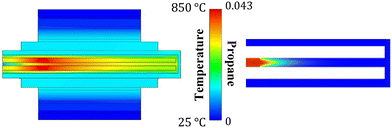 | ||
| Fig. 9 Effect of increased gap-size of the recirculating channel to 600 μm on contours of temperature and propane mass fraction. All other conditions are as in Fig. 6(a), with only the recirculation channel width increased from 300 to 600 μm. | ||
Fig. 10 provides a direct comparison of the temperature profiles for the two cases, i.e., gap-size of 300 μm and 600 μm. Note that the centerline temperature and reaction rate in Fig. 10(a) are the same as in Fig. 7(a) and have been repeated to aid the reader. With the higher gap-width, the difference between centerline temperatures of the catalytic (solid line) and recirculating (dashed lines) channels increases, as observed in Fig. 10(b). This increased isolation of the reaction channel results in higher temperatures. The reaction zone moves upstream, and the reaction rate is increased. Although the temperature is higher, increased isolation of the reaction zone from the TEG module results in slightly lower skin temperatures.
 | ||
| Fig. 10 Temperature profiles along the centerlines of the catalytic (solid lines) and the recirculation (dashed lines) channels of the S-HRR when the gap-size of the recirculation channel is (a) 300 μm and (b) 600 μm. The other conditions are the same as Fig. 7. | ||
Fig. 11 compares the power generated and propane conversion vs. inlet velocity for three different equivalence ratios of 0.5 (diamonds), 0.7 (squares) and 0.9 (triangles) for the microcombustor–TEG coupled with a water-cooled heat sink. Solid lines represent the nominal gap-size of 300 μm, whereas dotted lines represent gap-size of 600 μm. It is exciting to observe combustion at an equivalence ratio of 0.5 with conversions close to 90% as depicted by Fig. 11(a.1) and (b.1) for the higher recirculation channel gap size of 600 μm. At the equivalence ratio of 0.5, considering the safe operating temperature, 5.1 W power can be generated at an inlet velocity of 6 ms−1 (Th = 254.6 °C and Tc = 44.6 °C). As noted earlier, an equivalence ratio of ϕ = 0.7 or higher is required for the nominal design with 300 μm gap-size, whereas with an increase gap-size of 600 μm, stable device operation can be achieved at ϕ = 0.5 as well. Further, Fig. 11(a.2) and (a.3) show that the operation zone of the integrated device expands when a wider recirculation channel (600 μm) is used. In the range of intermediate velocities, the power generated from the 600 μm gap size reactor is close to that from the gap size of 300 μm. Consequently, the operating velocity space for stable operation increases at this gap width. Propane conversion is also influenced by doubling the gap-width of the recirculation channel. The effect is more pronounced towards lower equivalence ratios and low velocities. In several cases, complete conversion is observed, indicating the usefulness of this strategy to obtain high conversions, reduce propane break-through and deliver higher power.
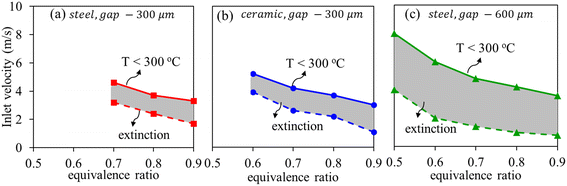
3.4. Operating regime diagrams
Fig. 12(a) shows the operating regime for the nominal case, i.e., where the parameters are at their nominal values, the inner walls are steel (kw = 16 W m−1 K−1) and the gap-size of the recirculation channel is 300 μm. The effect of the other two design parameters is examined; i.e., using ceramic walls (circles, Fig. 12b) and increasing the gap-size to 600 μm retaining the steel inner walls (triangles, Fig. 12c). The lower branch represents extinction, below which stable operation is not sustained, whereas the upper branch represents inlet velocity at which the temperature reaches 300 °C. This limit of 300 °C skin-temperature is chosen due to material stability of the TEG module. Thus the shaded region bound between the extinction and material stability limits represents the preferrable operating regime for each of the cases considered. Although the operating space is very narrow for the nominal case considering the trade-off between the constraints, the strategies for improved S-HRR performance are validated by the results in Fig. 12(b) and (c). With ceramic inner walls (Fig. 12(b)), a small increment in the preferred operating regime is observed. However, a significant expansion of the operating regime is observed in Fig. 12(c) when the recirculation channel gap size is doubled. The extinction branch shifted to lower velocities, while the upper limit branch simultaneously shifted to higher velocities. Thus, increased residence time in the recirculation channel and increased isolation of the inlet (reaction) channel simultaneously resulted in moderation of skin temperature, extension of the material stability limit as well as enabled higher propane conversions.The energy input to the system is in form of chemical energy. The energy released on propane combustion is given by Pchemical = ṁ × LHV × XC3H8, where LHV is the lower heating value and XC3H8 is propane conversion. A part of this energy is harnessed via the TEG as electrical energy (PTEG), a part is lost by heat loss to the surroundings (Ploss), a part is used in the heat sink to raise the sensible heat of the coolant water (Psink) and the rest is rejected as the sensible heat of the exhaust (Pout), such that:
| Pchemical = PTEG + Pout + Ploss + Psink. | (7) |
Fig. 13 also indicates that the net heat loss through the exposed surfaces accounts for ∼12% of the net energy flow for all three cases. This may be considered as an indicator of an efficient device design, since a large fraction of the microcombustor surface is exposed to the power-consuming device (i.e., TEG). The sensible heat of hot exhaust gases (Pout) shows an interesting behavior. There is only a slight increase in the sensible heat of exhaust gases when ceramic walls (case-B) were used. However, case-C with 600 μm gap-width has a higher energy associated with the exhaust. As explained in Fig. 10(b), higher temperature in the recirculation channel is the reason for high energy of the exhaust in case C. This higher temperature, and hence increased heat recirculation, is the reason for higher conversion. Finally, it is interesting to observe that most of the energy is rejected to the water-cooled sink, as observed in previous studies.28,40 This is the energy that traverses through the TEG module via conduction, and results in lower efficiency, ηTEG.
4. Conclusions
Thermoelectric power generation in an integrated device comprising a symmetric heat recirculating microcombustor coupled with two TEG modules was presented in this work. The use of a water-cooled heat sink resulted in a comparatively high electric power generation. Under nominal conditions, an overall efficiency of 3.5% with a power generation of 4.6 W, sufficient to charge a personal-portable device for niche applications, was obtained. Despite a large amount of heat removal by cooling water, S-HRR ensured stable combustion and sustained operation of the coupled device. A detailed analysis of the effect of inlet parameters revealed that the system is susceptible to extinction, characterized by incomplete propane conversion at lower flow rates and equivalence ratios.In order to overcome the limitation of incomplete propane conversion, the role of reactor design parameters was analyzed. Specifically, the thermal conductivity of the inner wall of the S-HRR and the gap-size of the recirculation channel were varied, to ensure improved heat recirculation and better performance. In the presence of ceramic inner walls, heat recirculation from outgoing fluid to incoming fluid was higher, resulting in high skin temperatures. This strategy improved power generation and propane conversion under lean conditions. On the other hand, increasing the recirculation channel volume by doubling the gap size increased the residence time of the recirculating fluid for heat exchange with incoming reactants. This strategy enabled sustained combustion and power generation at remarkably low velocities and equivalence ratios compared to other cases examined in this work. This led to even higher propane conversion, although it had only a marginal effect on the generated power or the overall device efficiency. The operating regimes were mapped for all three cases, which revealed significant broadening of the operating regime compared to the nominal gap size. Therefore, potential ways of generating higher power from microcombustors using lower fuel concentrations while maintaining low emissions were presented. Finally, detailed analysis of the net energy flow revealed that over three-quarters of the chemical energy is available as sensible heat of the exhaust gases and the cooling fluid. A part of this energy can be further recovered by coupling additional TEG modules downstream, indicating further opportunities to increase the net power generated from a couple device.
Nomenclature
| A j | Pre-exponential factor for reaction j (s−1) |
| C | Molar concentration (mol cm−3) |
| D k,m | Diffusion coefficient of species k in the mixture (m2 s−1) |
| D T,k | Thermal diffusion coefficient of species k (m2 s−1) |
| E | Activation energy (J mol−1) |
| h | Specific sensible enthalpy (J kg−1) |
| h ∞ | Heat loss coefficient (W m−2 K−1) |
| I | Current (ampere) |
| J | Diffusion flux vector (kg m−2 s−1) |
| k | Thermal conductivity (m−1 K−1) |
| k ads, kdes | Adsorption/desorption rate constants (s−1) |
| ṁ | Mass flow rate (kg s−1) |
| N R | Number of gas-phase reactions |
| N S | Number of surface reactions |
| p | Pressure (Pascal) |
| P | Electric power (Watt) |
| Q | Heat flow into the thermoelectric module (Watt m−2) |
| R M | Internal electrical resistance of the module (Ω) |
| R load | Electrical resistance of the load (Ω) |
| R | Universal gas constant (J mol−1 K−1) |
| R k | Rate of formation of species k (mol cm−3 s−1) |
| s | Rate of catalytic reaction (mole cm−2 s−1) |
| S 0j | Sticking coefficient for reaction j |
| S v | Volumetric heat generation or consumption source (W m−3) |
| t | Time (s) |
| T | Temperature (K or °C) |
| v | Velocity (m s−1) |
| V | Voltage (Volts) |
| W | Molecular weight (kmol kg−1) |
| y | Transverse coordinate |
| Y | Mass fraction |
| Z | Figure of merit |
Subscripts
| c | Cold-side |
| g | Gas |
| h | Hot-side |
| M | Thermoelectric module |
| ∞ | Ambient |
| w | Wall |
Greek symbols
| α | Seebeck coefficient (V K−1) |
| β j | Temperature exponent of reaction j |
| ε | Emissivity |
| μ | Viscosity (kg m−1 s−1) |
| ν | Stoichiometric coefficient |
| ρ g | Density of gas (kg m−3) |
| ρ w | Density of solid wall (kg m−3) |
| η | Efficiency |
| ϕ | Equivalence ratio |
| τ | Thomson coefficient (V K−1) |
| Γ | Catalyst site density (mol cm−2) |
| σ | Stefan–Boltzmann constant (W m−2 K−4) |
Conflicts of interest
The authors declare that they have no known conflict of interest that could influence the work reported in this paper.References
- A. C. Fernandez-Pello, Micropower generation using combustion: Issues and approaches, Proc. Combust. Inst., 2002, 29(1), 883–899, DOI:10.1016/s1540-7489(02)80113-4.
- N. S. Kaisare and D. G. Vlachos, A review on microcombustion : Fundamentals, devices and applications, Prog. Energy Combust. Sci., 2012, 38, 3112–3359, DOI:10.1016/j.pecs.2012.01.001.
- Y. Ju and K. Maruta, Microscale combustion : Technology development and fundamental research, Prog. Energy Combust. Sci., 2011, 37(6), 669–715, DOI:10.1016/j.pecs.2011.03.001.
- B. Orr, A. Akbarzadeh, M. Mochizuki and R. Singh, A review of car waste heat recovery systems utilising thermoelectric generators and heat pipes, Appl. Therm. Eng., 2016, 101, 490–495, DOI:10.1016/j.applthermaleng.2015.10.081.
- K. V. Selvan and M. S. Mohamed Ali, Micro-scale energy harvesting devices: Review of methodological performances in the last decade, Renewable Sustainable Energy Rev., 2016, 54, 1035–1047, DOI:10.1016/j.rser.2015.10.046.
- J. Vican, B. F. Gajdeczko, F. L. Dryer, D. L. Milius, I. A. Aksay and R. A. Yetter, Development of a microreactor as a thermal source for microelectromechanical systems power generation, Proc. Combust. Inst., 2002, 29, 909–916, DOI:10.1016/S1540-7489(02)80115-8.
- J. A. Federici, D. G. Norton, T. Brüggemann, K. W. Voit, E. D. Wetzel and D. G. Vlachos, Catalytic microcombustors with integrated thermoelectric elements for portable power production, J. Power Sources, 2006, 161(2), 1469–1478, DOI:10.1016/j.jpowsour.2006.06.042.
- L. Merotto, C. Fanciulli, R. Dondè and S. De Iuliis, Study of a thermoelectric generator based on a catalytic premixed meso-scale combustor, Appl. Energy, 2016, 162, 346–353, DOI:10.1016/j.apenergy.2015.10.079.
- B. Aravind, G. K. S. Raghuram, V. R. Kishore and S. Kumar, Compact design of planar stepped micro combustor for portable thermoelectric power generation, Energy Convers. Manage., 2018, 156, 224–234, DOI:10.1016/j.enconman.2017.11.021.
- S. Yadav, P. Yamasani and S. Kumar, Experimental studies on a micro power generator using thermo-electric modules mounted on a micro-combustor, Energy Convers. Manage., 2015, 99, 1–7, DOI:10.1016/j.enconman.2015.04.019.
- C. C. Wang, C. I. Hung and W. H. Chen, Design of heat sink for improving the performance of thermoelectric generator using two-stage optimization, Energy, 2012, 39(1), 236–245, DOI:10.1016/j.energy.2012.01.025.
- M. Chen, L. A. Rosendahl and T. Condra, A three-dimensional numerical model of thermoelectric generators in fluid power systems, Int. J. Heat Mass Transfer, 2011, 54(1–3), 345–355, DOI:10.1016/j.ijheatmasstransfer.2010.08.024.
- S. Twaha, J. Zhu, Y. Yan and B. Li, A comprehensive review of thermoelectric technology: Materials, applications, modelling and performance improvement, Renewable Sustainable Energy Rev., 2016, 65, 698–726, DOI:10.1016/j.rser.2016.07.034.
- S. K. Chou, W. M. Yang, K. J. Chua, J. Li and K. L. Zhang, Development of micro power generators - A review, Appl. Energy, 2011, 88(1), 1–16, DOI:10.1016/j.apenergy.2010.07.010.
- K. F. Mustafa, S. Abdullah, M. Z. Abdullah and K. Sopian, A review of combustion-driven thermoelectric (TE) and thermophotovoltaic (TPV) power systems, Renewable Sustainable Energy Rev., 2016, 71, 572–584, DOI:10.1016/j.rser.2016.12.085.
- I. Schoegl and J. L. Ellzey, Superadiabatic combustion in conducting tubes and heat exchangers of finite length, Combust. Flame, 2007, 151(1–2), 142–159, DOI:10.1016/j.combustflame.2007.01.009.
- V. Shirsat and A. K. Gupta, A review of progress in heat recirculating meso-scale combustors, Appl. Energy, 2011, 88(12), 4294–4309, DOI:10.1016/j.apenergy.2011.07.021.
- K. Maruta, J. K. Parc, K. C. Oh, T. Fujimori, S. S. Minaev and R. V. Fursenko, Characteristics of Microscale Combustion in a Narrow Heated Channel, Combust., Explos. Shock Waves, 2004, 40(5), 516–523 CrossRef.
- B. Aravind, B. Khandelwal, P. A. Ramakrishna and S. Kumar, Towards the development of a high power density, high efficiency, micro power generator, Appl. Energy, 2020, 261, 114386, DOI:10.1016/j.apenergy.2019.114386.
- S. Bensaid, M. Brignone, A. Ziggiotti and S. Specchia, High efficiency Thermo-Electric power generator, Int. J. Hydrogen Energy, 2012, 37(2), 1385–1398, DOI:10.1016/j.ijhydene.2011.09.125.
- F. Wang, J. Zhou, G. Wang and X. Zhou, Simulation on thermoelectric device with hydrogen catalytic combustion, Int. J. Hydrogen Energy, 2012, 37(1), 884–888, DOI:10.1016/j.ijhydene.2011.04.029.
- U. W. Taywade, A. A. Deshpande and S. Kumar, Thermal performance of a micro combustor with heat recirculation, Fuel Process. Technol., 2013, 109, 179–188, DOI:10.1016/j.fuproc.2012.11.002.
- G. Bagheri and S. E. Hosseini, Impacts of inner/outer reactor heat recirculation on the characteristic of micro-scale combustion system, Energy Convers. Manage., 2015, 105, 45–53, DOI:10.1016/j.enconman.2015.07.056.
- X. Hu, Z. Shen and Y. Wang, On the design of a hydrogen micro-rectangular combustor for portable thermoelectric generators, Chem. Eng. Process., 2024, 195, 109611, DOI:10.1016/j.cep.2023.109611.
- N. Yedala and N. S. Kaisare, Integration of heat recirculating microreactors with thermoelectric modules for power generation : a comparative study using CFD, React. Chem. Eng., 2021, 6(12), 2327–2341, 10.1039/d1re00382h.
- N. Yedala and N. S. Kaisare, Modeling of Thermal Integration of a Catalytic Microcombustor with a Thermoelectric for Power Generation Applications, Energy Fuels, 2021, 35, 5141–5152, DOI:10.1021/acs.energyfuels.0c03943.
- B. Aravind, D. K. Saini and S. Kumar, Experimental investigations on the role of various heat sinks in developing an efficient combustion based micro power generator, Appl. Therm. Eng., 2019, 148, 22–32, DOI:10.1016/j.applthermaleng.2018.11.016.
- H. Abedi, F. Migliorini, R. Dondè, S. De Iuliis, F. Passaretti and C. Fanciulli, Small size thermoelectric power supply for battery backup, Energy, 2019, 188, DOI:10.1016/j.energy.2019.116061.
- J. A. Federici and D. G. Vlachos, A computational fluid dynamics study of propane/air microflame stability in a heat recirculation reactor, Combust. Flame, 2008, 153(1–2), 258–269, DOI:10.1016/j.combustflame.2007.09.009.
- J. Chen, L. Yan, W. Song and D. Xu, Effect of heat recirculation on the combustion stability of methane-air mixtures in catalytic micro-combustors, Appl. Therm. Eng., 2017, 115, 702–714, DOI:10.1016/j.applthermaleng.2017.01.031.
- M. J. Lee, S. M. Cho, B. Choi and N. Kim, Scale and material effects on flame characteristics in small heat recirculation combustors of a counter-current channel type, Appl. Therm. Eng., 2010, 30(14–15), 2227–2235, DOI:10.1016/j.applthermaleng.2010.06.003.
- D. G. Norton, E. D. Wetzel and D. G. Vlachos, Thermal management in catalytic microreactors, Ind. Eng. Chem. Res., 2006, 45(1), 76–84, DOI:10.1021/ie050674o.
- C. K. Westbrook and F. L. Dryer, Simplified Reaction Mechanisms for the Oxidation of Hydrocarbon Fuels in Flames, Combust. Sci. Technol., 1981, 27(1–2), 31–43, DOI:10.1080/00102208108946970.
- S. R. Deshmukh and D. G. Vlachos, A reduced mechanism for methane and one-step rate expressions for fuel-lean catalytic combustion of small alkanes on noble metals, Combust. Flame, 2007, 149(4), 366–383, DOI:10.1016/j.combustflame.2007.02.006.
- V. R. Regatte, G. Selle and N. S. Kaisare, The role of homogeneous chemistry during Ignition of propane combustion in Pt-catalyzed microburners, Int. J. Spray Combust. Dyn., 2012, 4(2), 155–174, DOI:10.1260/1756-8277.4.2.155.
- N. S. Kaisare, S. R. Deshmukh and D. G. Vlachos, Stability and performance of catalytic microreactors: Simulations of propane catalytic combustion on Pt, Chem. Eng. Sci., 2008, 63(4), 1098–1116, DOI:10.1016/j.ces.2007.11.014.
- ANSYS Inc. (US), Ansys Users' Guide, ANSYS Inc., 2013, (November), http://148.204.81.206/Ansys/150/ANSYS, Fluent Users Guide.pdf Search PubMed.
- M. Chen, L. A. Rosendahl, T. J. Condra and J. K. Pedersen, Numerical modeling of thermoelectric generators with varing material properties in a circuit simulator, IEEE Trans. Power Delivery, 2009, 24(1), 112–124, DOI:10.1109/TEC.2008.2005310.
- X. F. Zheng, C. X. Liu, Y. Y. Yan and Q. Wang, A review of thermoelectrics research - Recent developments and potentials for sustainable and renewable energy applications, Renewable Sustainable Energy Rev., 2014, 32, 486–503, DOI:10.1016/j.rser.2013.12.053.
- K. Hanamura, T. Kumano and Y. Iida, Electric power generation by super-adiabatic combustion in thermoelectric porous element, Energy, 2005, 30, 347–357, DOI:10.1016/j.energy.2004.05.010.
| This journal is © The Royal Society of Chemistry 2024 |