Open Access Article
Open Access ArticleUnderstanding specific ion effects and the Hofmeister series†
Kasimir P.
Gregory‡
 ab,
Gareth R.
Elliott‡
ab,
Gareth R.
Elliott‡
 a,
Hayden
Robertson
a,
Hayden
Robertson
 a,
Anand
Kumar
a,
Anand
Kumar
 c,
Erica J.
Wanless
c,
Erica J.
Wanless
 a,
Grant B.
Webber
a,
Grant B.
Webber
 d,
Vincent S. J.
Craig
d,
Vincent S. J.
Craig
 b,
Gunther G.
Andersson
b,
Gunther G.
Andersson
 c and
Alister J.
Page
c and
Alister J.
Page
 *a
*a
aDiscipline of Chemistry, School of Environmental and Life Sciences, The University of Newcastle, Callaghan, New South Wales 2308, Australia. E-mail: alister.page@newcastle.edu.au
bDepartment of Materials Physics, Research School of Physics, Australian National University, Canberra, ACT 0200, Australia
cFlinders Institute of Nanoscale Science and Technology, College of Science and Engineering, Flinders University, South Australia 5001, Australia
dSchool of Engineering, The University of Newcastle, Callaghan, New South Wales 2308, Australia
First published on 9th May 2022
Abstract
Specific ion effects (SIE), encompassing the Hofmeister Series, have been known for more than 130 years since Hofmeister and Lewith's foundational work. SIEs are ubiquitous and are observed across the medical, biological, chemical and industrial sciences. Nevertheless, no general predictive theory has yet been able to explain ion specificity across these fields; it remains impossible to predict when, how, and to what magnitude, a SIE will be observed. In part, this is due to the complexity of real systems in which ions, counterions, solvents and cosolutes all play varying roles, which give rise to anomalies and reversals in anticipated SIEs. Herein we review the historical explanations for SIE in water and the key ion properties that have been attributed to them. Systems where the Hofmeister series is perturbed or reversed are explored, as is the behaviour of ions at the liquid–vapour interface. We discuss SIEs in mixed electrolytes, nonaqueous solvents, and in highly concentrated electrolyte solutions – exciting frontiers in this field with particular relevance to biological and electrochemical applications. We conclude the perspective by summarising the challenges and opportunities facing this SIE research that highlight potential pathways towards a general predictive theory of SIE.
1. Introduction
The presence of ions in a solution has a direct effect on its physicochemical properties. Electrolytes, encompassing acids, bases and salts, are key components in myriad contexts: cleaning agents,1–5 fertilisers,6 batteries7–9 and broader geophysical phenomena.10–15 Even life itself runs on electrolytes, which stabilise and regulate proteins, enzymes16–27 and cells,28 as well as balance acidity levels29 and fluid retention.30 In the majority of these applications, the electrolyte's effect is dependent not only on the ions’ charges or concentrations, as suggested by widely-used theories (e.g. Debye–Hückel theory), but also on their identity. For example, KF is poisonous to humans, whilst KI is used to treat hypothyroidism; clearly the identity of the anion matters here. Such phenomena, in which the ion's identity is intrinsic to its effect on the properties of a system, are collectively known as specific ion effects (SIEs). Specific ion effects are the rule, rather than the exception.SIEs were first systematically studied by Lewith and Hofmeister in the period 1887–1891, who found a consistent ordering of ions’ abilities to precipitate proteins from blood serum and hen egg white in aqueous solutions:31,32
| Anions: C4H4O62− > SO42− > HPO42− > C3H5O(CO2)33− > CH3CO2− > HCO3− > CrO42− > Cl− > NO3− > ClO3− |
| Cations: Li+ > K+ ≈ Na+ > NH4+ > Mg2+ |
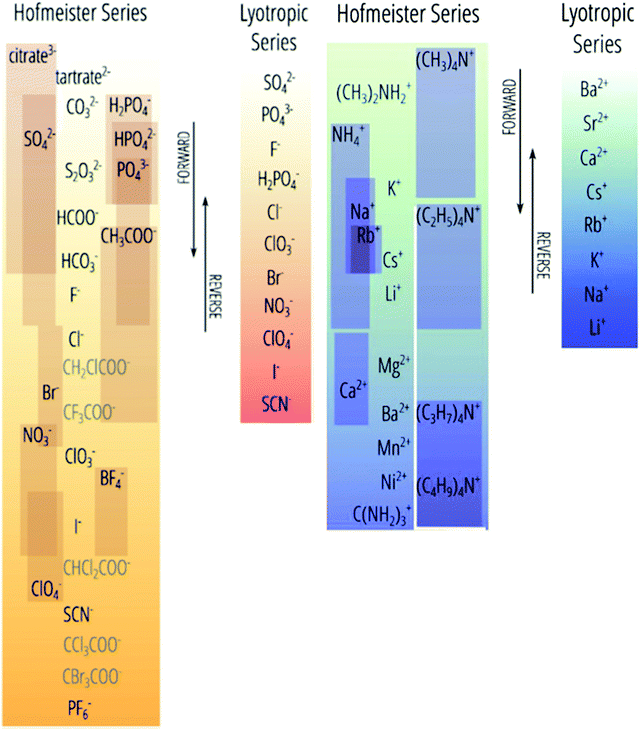 | ||
| Fig. 1 The Hofmeister series versus its deviations (with the latter indicated by individual boxes). The top(anions)/bottom(cations) end of this series, historically called kosmotropes, generally precipitate proteins from (aqueous) solution. The bottom(anions)/top(cations) ions are historically called chaotropes, which generally solubilise proteins.41 We prefer the terms charge diffuse ions and charge dense ions over chaotrope and kosmotrope respectively. Reprinted with permission from ref. 41 and 47 with permission from Elsevier, copyright 2017. | ||
There are many curious disconnects between the SIE field and the broader chemical and physiological literature. For instance, Pearson's hard and soft acids and bases (HSAB) theory48 has many parallels with the Hofmeister series, yet is rarely discussed in the context of SIE despite having arguably stronger theoretical foundations.49,50 Similarly, the work of Wright and Diamond20 is often overlooked by the field, despite its sound theoretical discussions on potential origins of SIEs in terms of electrostatic and competitive interactions.
This perspective aims to review recent advances in our theoretical understanding of SIEs and summarise the current challenges facing this fundamentally important field of research. SIEs are commonly attributed solely to the anion or cation, with disregard for the presence of a counterion. We address the shortcomings of this assumption in this perspective, and recount historical explanations, theoretical treatments, and correlations between SIEs and ionic properties in Section 2. However, SIEs are clearly counterion-dependent and are known to be responsible for deviations and even reversals in Hofmeister trends.33,44,45 Counterions must be considered explicitly if SIE are to be understood completely. Counterion-induced deviations, and those caused by other relevant physicochemical conditions, are therefore discussed in Section 3. Many SIEs occur at an interface, meaning that the synergies between SIEs and interfacial structure/properties must be elucidated carefully, if SIEs are to be fully understood; we discuss recent advances in this respect in Section 4. The complexity of SIEs is compounded in mixed-salt systems (of particular relevance to SIEs in biochemical contexts), and so we examine the manifestation of SIEs in mixed salt systems in Section 5. The fact that SIEs occur not only in water, but in nonaqueous solvents as well suggests that SIEs occur fundamentally due to some inherent property of ions themselves that is apparently modulated by the solvent environment. With this in mind, we discuss recent advances concerning nonaqueous SIEs in Section 6. The electrostatic environments in concentrated electrolytes differ fundamentally from weak electrolytes, for instance, by exhibiting variable electrostatic decay lengths. Recent investigations have demonstrated this phenomenon to be ion specific and so Section 7 reviews recent progress in this respect. Finally, we summarise the recent progress and current challenges for the field in Section 8.
At this point it is also important to make our conventions in terminology clear. In the manner of Mazzini and Craig,41 we will use the phrase “specific ion effect” (or SIE) in reference to any physicochemical phenomenon that depends on the identity of the ion. A Hofmeister effect or series refers to a SIE that conforms to the original ion ordering reported by Hofmeister, above (either whole, or with few exceptions). A reverse Hofmeister effect or series refers to a SIE that occurs in the opposite order to that reported by Hofmeister. Similarly, Lyotropic effects or series are those that are consistent with the conventional ordering of the Lyotropic series (either whole, or in part) and the label ‘reverse’ is used in the same manner here.46 When discussing general interactions between an ion and a dissolved protein, polymer, surface or other chemical species, the term cosolute is used to address these moieties.
2. Aqueous specific ion effects
2.1. Historical explanations
The genesis of the Hofmeister effect was Hofmeister's own experiments concerning the solubility of egg proteins in aqueous electrolyte solutions.31,32 Two key observations from these original experiments have had far-reaching consequence. Firstly, given the timescale over which the effects were observed by Hofmeister and Lewith (several hours or days in some circumstances), it is likely they are thermodynamic in origin (as opposed to kinetic). Secondly, trends in an ions’ abilities to precipitate five different solutes were consistent, suggesting that the effect was general. Indeed, Hofmeister effects are known to influence myriad phenomena, including surface tension,51 zeta potentials,52 buffers,53 upper and lower critical solution temperatures (UCSTs and LCSTs respectively) of thermoresponsive polymers,36,54–56 ion-binding to proteins57 and membranes,58 transport across membranes,59 molecular forces,60,61 electrolyte viscosity,62–66 enzyme activity,16–27 bacterial growth,67 bubble stability,14 and others.62,65,68–75Hofmeister hypothesised32 that the behaviour of each ion derived from its capacity to adsorb water. On this basis, ions were subsequently categorised as kosmotropes (which are strongly hydrated, thereby bringing order to the solution) and chaotropes (which are weakly hydrated, thereby disrupting order in the solution), respectively. As shown in Fig. 1, the Hofmeister series orders ions from kosmotropes (highest anions, lowest cations) to chaotropes (lowest anions, highest cations). Kosmotropes precipitate (“salt-out”) proteins, while chaotropes solubilise (“salt-in”) proteins. However, despite the pervasive historical use of the kosmotrope and chaotrope terms, they are often misleading considering the relative standard molar entropies of many ions.45,66 We therefore prefer to use the terms ‘charge diffuse ion’ instead of chaotrope and ‘charge dense ion’ instead of kosmotrope. Salting-in and salting-out terms are also useful in regard to describing an ion's impact on precipitation, yet are system dependent (Section 3), so require caution when used more generally. Similarly, as Fig. 1 indicates, the positions of ions on this scale are not invariant; they may change based on the system and the effect in question (the most common variations are indicated by the sliding boxes containing some ions in the series).
Various models and mechanisms have been proposed since Hofmeister's initial ion–water adsorption model. Various cavity models75,76 have attempted to explain SIEs purely in terms of the ion's influence on the solvent. These models are based on the work required to make a cavity in a liquid. On this basis, Melander and Horváth's model75 explains salting-out behaviour in terms of ion surface tension increments, and a protein salting-out constant (which is a measure of a protein's susceptibility to being salted out, related to the “hydrophobic” and electrostatic interactions). Pica and Graziano77,78 have used theories grounded in a solvent-excluded volume effect to describe the thermodynamics of poly(N-isopropylacrylamide) (pNIPAM) hydration. On the other hand, other models, such as Baldwin's,79 hypothesised that ions precipitate proteins via interactions at nonpolar functional groups, while they salt-in proteins via interactions at peptide groups. In polymer systems, Rogers et al.80 have postulated that weakly hydrated ions preferentially bind to the centre of macromolecular chains where the solvation structure is most disrupted. A recognition that the counterion was important led Collins in 1997 to develop the Law of Matching Water Affinities (LMWA),81 which attempts to explain SIEs via the fact that associated ion pairs will preferentially form if they have similar absolute enthalpies of hydration (Fig. 2). Collins also considered the relationship between the charge density and observed Hofmeister effects. More recently, Lo Nostro and Ninham29 have posited that SIEs are the product of three key considerations:
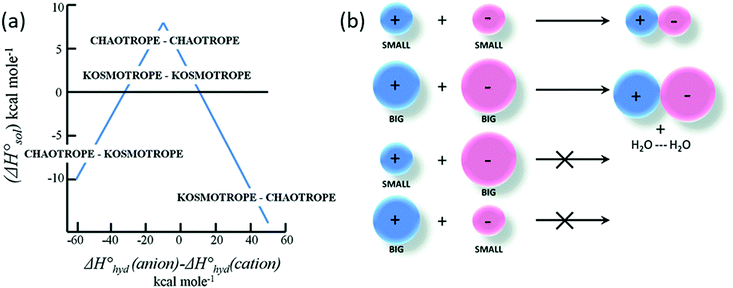 | ||
| Fig. 2 The Law of Matching water affinities. (a) Plot of the enthalpy of hydration of the salt vs. the difference in the enthalpy of hydration of the anion and cation (a so-called ‘volcano plot’). When the anion and cation have similar enthalpies of hydration they are likely to form ion-pairs (above the x-axis). (b) Schematics: a small (big) cation would form a contact ion pair with a small (big) anion, whereas a small (big) cation would not form a contact ion pair with a big (small) anion.82 Reproduced from ref. 82 with permission from the Royal Society of Chemistry, copyright 2014. | ||
i. Cation–anion pairing and their interactions with both cosolute and solvent molecules.
ii. “Local” interactions between the ion and the cosolute drive ions to adsorb specifically. Many-body quantum mechanical dispersion forces that are missing from standard theories can account for this. These and specific hydration are dependent on the dielectric properties of the ion, cosolutes and solvent.
iii. Concurrent phenomena allow anomalies such as reordering the series of ionic efficacy and series inversions.
Many investigations focus on ion–protein interactions in conjunction with ion–solvent interactions.79,81,83–95 Like Collins,81 later work has emphasised the importance of moving “Beyond Hofmeister” to overcome the limitations of separating the anion and the cation series.33
2.2. Ion solvation in water
The local solvation environment around dissolved ions has long been hypothesised to be the origin of SIEs in aqueous electrolytes. Whilst ionic solvation structures have been studied extensively in this context, both experimental and theoretical approaches have revealed the aqueous solvation structure of ions to be deceptively complex. Neutron diffraction experiments96 have supported the now conventional explanation of the Hofmeister effect for proteins, i.e. that salting-in or salting-out is caused by the competition between the dissolved salt and the protein for waters of hydration. Similarly, X-ray diffraction has indicated that water hydrogen bond strength changes upon NaCl dissolution.97 However, there is ongoing debate regarding the influence ions have on water's native structure beyond their first solvation shell. A range of techniques indicate that ions do not significantly affect the water structure beyond their first solvation shell. These include femtosecond mid-infrared pump–probe spectroscopy,98 terahertz absorption spectroscopy,99 and molecular dynamics (MD)99,100 studies. On the other hand, alternate conclusions, viz. that well hydrated ions influence the structure of water well beyond the first solvation shell, were reached on the basis of femtosecond infrared spectroscopy.101 Neutron diffraction experiments102 also imply that ion solvation is not limited to a single solvation shell, with salts disordering the tetrahedral structure of water in a similar manner to changes in pressure and temperature. Quantum chemical molecular dynamics103 simulations indicate Na+ and Cl− ions have distinct effects; while the disruption caused by Na+ is limited to the cation's first solvation shell, Cl− influences hydrogen bonding within the solvent over larger length scales. A potential caveat here is that the timescale of these simulations (∼20 ps) is comparable to the estimated residence times of water molecules around these ions.104–106 The disruptions observed may therefore not truly reflect the ions’ effects on experimental timescales. Thus, the range over which an ion perturbs the structure of the solvent is still to be determined, and likely to be ion specific and concentration dependent (Sections 3.1 and 7).Classical theories regarding salt interactions in aqueous solution, such as Born energies of solution and ion transfer,107,108 Debye–Hückel (DH) theory,109 and the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory of colloidal interaction,110–112 have been developed largely to account for deviations in ideality, rather than to explain SIEs. They therefore generally fail to account for such subtle structural effects, and have significant limitations.113 DH theory treats the electrostatic potential within an electrolyte solution via a linearisation of the Poisson–Boltzmann equation, and assumes that ions are non-polarisable point charges that undergo complete dissociation in a featureless, homogenous dielectric “solvent”. Whilst DH theory is often considered capable of only accounting for phenomena in dilute aqueous environments (<10−3 M), for long-range electrostatic interactions it is often adequate up to concentrations of ∼0.5 M.114 The extended DH model of Stokes and Robinson,115 which includes a description of the ionic radius, is accurate up to ∼0.1 M. Similarly, specific ion interaction theory was developed from DH theory to estimate single ion activity coefficients at even higher concentrations (∼10 M) via interaction coefficients.116,117 The Pitzer Method118 has become an increasingly popular tool for determining the thermodynamic properties of electrolytes119–122 and is considered the best model for predicting ion activity coefficients to date.123,124 Nevertheless, it too is based on DH theory, although it also accounts for the hydrated size of individual ions and their short-range binary and ternary interactions via a virial expansion (thereby requiring additional empirical parameterisation). The necessity for additional empirical parameters at high concentration in DH theory arises ultimately from the rudimentary assumptions of DH theory itself. In fact, some authors125 contend that the early successes of DH theory, despite its assumptions, are responsible for our current poor understanding of electrolyte solutions at high concentrations. We discuss more advanced theoretical treatments of concentrated electrolyte solutions in Section 7. The fact that properties such as ion size, shape, polarisability and charge density are ignored in DH theory fundamentally limits its utility in the context of SIEs.
2.3. Correlations with electrolyte properties
The nature of an ion's effect on a system is determined by the properties of the ion as well as the solute and solvent. In fact, the ubiquity of the Hofmeister series indicates that the properties of the ion are fundamental to its origin. Collins and Washabaugh126 had listed 30 properties of salt solutions by 1985, which has since expanded, with many, such as ion size, polarisability and hydration free energy following Hofmeister trends to some extent.124,127,128 Variations and exceptions are frequent however, meaning well-defined Hofmeister ion parameters have not been well established. Leontidis129 covered these properties in a recent review, positing that the Hofmeister series originates from a combination of ionic charge distribution, size, shape, and hydrophobicity (Fig. 3). A study by Mazzini and Craig42 showed consistent trends for anions (Hofmeister series) and cations (reverse Lyotropic series) with respect to their electrostrictive volume in eleven different protic and aprotic solvents. This suggests ions alone exhibit a SIE series that is independent of the solvent; that is, there exists a fundamental SIE series. Investigations128,130–133 of the intermolecular forces134 driving SIEs have elucidated and aided the search for relevant ion properties. The discussion below considers the correlation of fundamental ion properties with observed SIEs.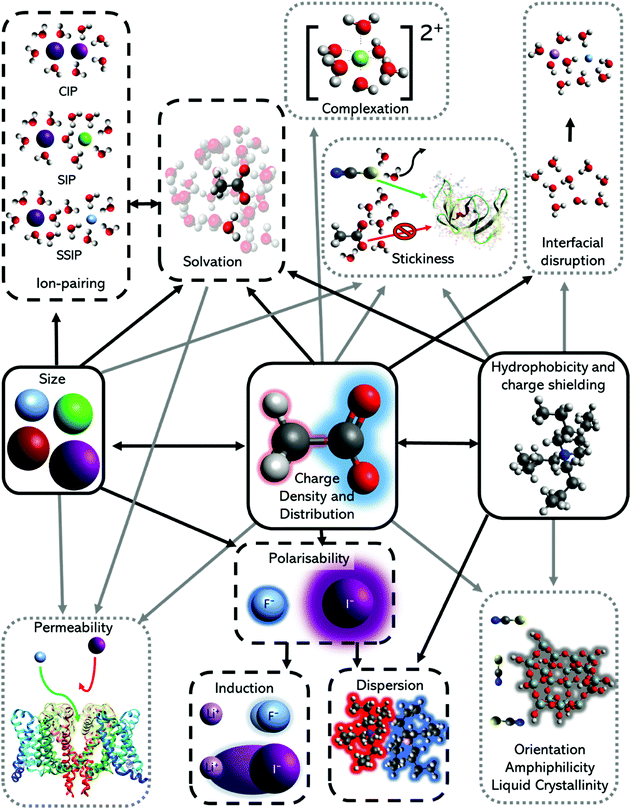 | ||
| Fig. 3 The major ion properties (solid black box) linked to the effects studied widely (dashed black box) and sparsely (dotted grey box). Stickiness is a term to describe the ease at which an ion can lose or share their hydration shells, and therefore adhere to interfaces. It is resultant from a combination of ion hydration, complexation ability and surface polarity. Adapted from ref. 129 with permission from Elsevier, copyright 2017. | ||
The location of the charge within a polyatomic ion is of utmost importance. When the maximal charge density of an ion is located on a distal moiety, the magnitude of the interaction strength appears to be directed through this site (e.g., CH3COO−). This is discussed in detail below in Section 2.3.3. However, in cases where the charge density has a maximum on an internal atom, this can effectively cause a shielding of charge. The latter is evident in tertiary ammonium cations (which often show a reverse Hofmeister series),41 and also for tetraphenylphosphonium and tetraphenylarsonium cations and tetraphenylborate anions. In these cases, higher order interactions (e.g. dispersion, induction, exchange) become the driving intermolecular force governing their effects.128 Notably, for the tetraphenyl ions, both the cationic and anionic derivatives show little difference in common measures of the strength of specific ion interactions such as viscosity B coefficients, limiting molar conductivities, enthalpies of hydration and Gibbs energies of transfer, indicating a charge independence for these ions.66,128,140
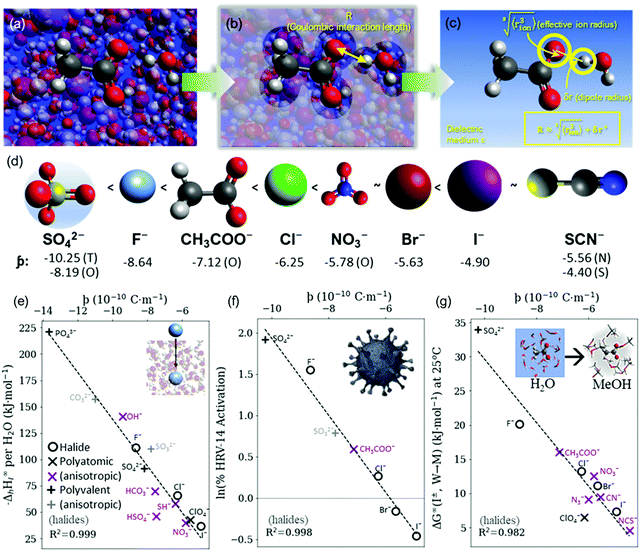 | ||
Fig. 4 (a) In bulk electrolyte solutions (b) where single ion–solvent interaction have a length of R, (c) the interaction distance may be approximated by the effective radius of the ion's charge site 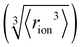 and the solvent dipole (δr+). Given the partial charge on the solvent dipole is effectively constant and and the solvent dipole (δr+). Given the partial charge on the solvent dipole is effectively constant and 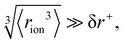 the electrostatic interaction as calculated by Coulomb's Law can be approximated by the radial charge density of the ion. An ion's radial charge density is calculated as the electrostatic interaction as calculated by Coulomb's Law can be approximated by the radial charge density of the ion. An ion's radial charge density is calculated as 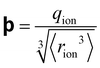 . (d) Example ϸ values in 10−10 C m−1 are shown for commonly investigated anions. Both the total (T) and oxygen (O) values are provided for SO42−, and both nitrogen (N) and sulfur (S) values for SCN−. Example correlations for (e) hydration enthalpies,66 (f) viral activities22 and (g) Gibbs energies of transfers.66 Reproduced from ref. 128 with permission from the Royal Society of Chemistry, copyright 2021. . (d) Example ϸ values in 10−10 C m−1 are shown for commonly investigated anions. Both the total (T) and oxygen (O) values are provided for SO42−, and both nitrogen (N) and sulfur (S) values for SCN−. Example correlations for (e) hydration enthalpies,66 (f) viral activities22 and (g) Gibbs energies of transfers.66 Reproduced from ref. 128 with permission from the Royal Society of Chemistry, copyright 2021. | ||
The utility of the ϸ parameter is greater for anions than it is for cations (even when accounting for the increased atomic radii at a solvent's negative dipole in the Coulomb's Law approximation).128 This suggests that electrostatic interactions are more determinant in aqueous solutions for anions than cations. This is somewhat counterintuitive, considering their generally larger size and hence greater polarisability. For the cations there is more pronounced competitive behaviour between distinct components of the ion–solvent interactions (viz. electrostatics, dispersion, induction, exchange). The result is that cation-induced SIEs are increasingly subject to non-Coulombic phenomena (especially when additional co-solutes are present). Notably, the dispersion and electrostatic components of the cation–solvent interaction are generally inversely related and charge-dependent, whereas for anions, these components are directly related and charge independent.
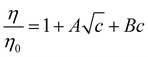 | (1) |
Experimentally it is not possible to directly measure the contribution of each ion to the viscosity B coefficient to determine ionic B coefficients. An additivity assumption, that the contribution of each ion to the B coefficient is independent, allows ionic B coefficients to be determined relative to a reference anion or cation. In aqueous solution, KCl is often chosen as the reference salt with each of the ionic B coefficients assigned half the total B coefficient for KCl, as K+ and Cl− have similar ionic mobilities. In other solvents, a different choice of reference ions is often required. The ionic B coefficients for simple monatomic ions correlate with the cube of the crystal radius of ions, with smaller ions having positive B coefficients and larger ions leading to more negative ionic B coefficients. The more negative the ionic B coefficient the more “structure breaking” the ion. Ionic viscosity B coefficients have been correlated with structural hydration entropies,143 partial molar entropies,144 ionic partial molar volumes145 and, for anions, lyotropic numbers.146 Further, the variation of the B coefficients for an ion in different solvents are related to the molar volume of the solvents. Mazzini and Craig41 have examined the ordering of ionic B coefficients in a number of solvents and found that the alkali metals follow a reverse lyotropic series for most solvents and the large ammonium cations follow a reverse Hofmeister series. For the anions a Hofmeister series is evident in a number of solvents but not in water.41 For further details the interested reader is referred to the excellent and comprehensive review of Jenkins and Marcus on viscosity B coefficients.147
The pKa and pKb of the respective conjugate acid and base of a salt is important to consider in understanding SIEs. Not only are they indicative of the degree of dissociation of the ions in solution, but they also describe whether hydrolysis of the ions might occur. For example, citrate buffers modulate the pH between 3.0–6.2 and NaHCO3 neutralises acids toward a pH of 8.4. This affects various components of the system, including the cosolute (whether it has an effective positive or negative charge), the ion protonation state (i.e., PO43−, HPO42−, H2PO4− or H3PO4), and the need to account for additional ions (i.e., OH− or H3O+) in any analysis, modelling or prediction.
A related and common misconception is that strong electrolytes completely dissociate in water.149 This is understandable considering the initial success of DH theory, and its underlying assumption that the salt is completely dissociated. However, molecular dynamics150 and Monte Carlo151 simulations, X-ray diffraction,152 conductivity151,153 and transference data,154 as well as osmotic and vapour pressure measurements125,155 indicate that this is not always the case in alkyl halide solutions (up to 20–30% of the ions could exist as ion-pairs or clusters at concentrations of 1 m).150 Heyrovska claims that the degree of dissociation and ion hydration numbers are the two parameters required to explain activity155,156 and similarly Shi and Beck157 suggest a correlation exists between free energy and the ion-association affected hydration numbers. Free ions and associated ion-pairs are speculated to exhibit different SIEs, so a deeper knowledge of degree of dissociation may elucidate some SIE phenomena, especially where cation–anion interactions appear to have substantial impact (see Section 3.3).154,158 Bruce and Bui et al.159–163 have recently made substantial efforts in improving this mechanistic understanding for SIE, especially for cations and mixed salt (see Section 5) systems. Additionally, Judd et al.164 have suggested that ion pair formation does not necessarily correlate with ion–ion binding affinity by using an eicosyl sulfate ionic surfactants as a probe.
We also note here that the concept of ion-pairing in electrolyte solutions can be ambiguous. Considering the dynamic behaviour of ions in solution, the relatively-static (statistical) picture of an ion–pair fails to encompass the range of ion–ion interactions occurring in reality, which will include contact, solvent-separated and solvent–solvent separated “ion–pairs” (CIP, SIP and SSIP respectively, see Fig. 3),165 as well as larger clusters,150,152 which can have lifetimes on the same timescale as ion–water interactions.104–106 The term ion–ion correlations could be used to encompass this range of behaviour. The interested reader is directed to the comprehensive review of Marcus and Hefter.165
| Classification of bases | |
|---|---|
| Hard | Soft |
| H2O, OH−, F− | I−, SCN−, S2O32− |
| CH3COO−, PO43−, SO4− | R3P, R3As, (RO)3P |
| Cl−, CO3−, ClO4−, NO3− | CN−, RNC, CO |
| ROH, R2O, RO− | R2S, RSH, RS− |
| NH3, RNH2, N2H4 | C2H4, C2H6 |
| H−, R− | |
| Borderline | |
| C6H5NH, C5H5N, N3−, Br−, NO2−, SO32−, N2 | |
| Classification of acids | |
|---|---|
| Hard | Soft |
| H+, Li+, Na+, K+ | Cu+, Ag+, Au+, Tl+, Hg+ |
| Be2+, Mg2+, Ca2+, Sr2+, Mn2+ | Pd2+, Cd2+, Pt2+, Hg2+, CH3Hg+, Co(CN)32−, Pt4+, Te4+ |
| Al3+, Se3+, Ga3+, In3+, La3+ | Tl3+, Tl(CH3)3, BH3, Ga(CH3)3 |
| N3+, Cl3+, Gd3+, Lu3+ | GaCl3, GaI3, InCl3 |
| Cr3+, Co3+, Co3+, Fe3+, As3+, CH3Sn3+ | RS+, RSe+, RTe+ |
| Si4+, Tl4+, Zr4+, Th4+, U4+, Pu4+, Ce3+, Hf4+, WO4+, Sn4+ | I+, Br+, HO+, RO+ |
| UO22+, (CH3)2Sn2+, VO2+, MoO2+ | I2, Br2, ICN, etc. |
| BeMe2, BF3, B(OR)3 | Trinitrobenzene, etc. |
| Al(CH3)3, AlCl3, AlH3 | Chloranil, quinones, etc. |
| RPO2+, ROPO2+ | Tetracyanothylene, etc. |
| RSO2+, ROSO2+, SO3 | O, Cl, Br, I, N, RO−, RO2− |
| I7+, I5+, Cl7+, Cr6+ | M0 (metal atoms) |
| RCO+, CO2, NC+ | Bulk metals |
| HX (hydrogen bonding molecules) | CH2, carbenes |
| Borderline | |
| Fe2+, CO2+, Ni2+, Cu2+, Zn2+, Pb2+, Sn2+, Sb3+, Bi3+, Rh3+, Ir3+, B(CH3)3, SO2, NO+, Ru2+, Os2+, R3C+, C6H5+, GaH3 | |
Table 1 shows that HSAB theory encompasses not only ions that are traditionally the focus of SIE studies, but also transition metal ions and non-ionic molecules. Nevertheless, despite its generality, HSAB remains a qualitative categorisation; it does not allow for differentiation between acids and bases in the same category. Pearson167 recognised a need for a two-parameter quantitative description of ions and proposed a strength factor (S, based on gas phase reaction data) paired with a “softness” parameter, σ, such that the equilibrium constant (K) for an acid (A)-base (B) reaction,
| A(aq) + B(aq) ⇌ A:B(aq) | (2) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = SASB + σAσB K = SASB + σAσB | (3) |
Pearson highlighted, however, a lack of quantitative precision using this approach, despite its qualitative utility, and that parameters for the weaker aquo-ions (e.g., M(H2O)n+) would be of more practical use than bare ions. This is especially relevant for strongly coordinated cations (e.g., Mg2+).
Gregory et al.45 showed that the Lewis acidity and basicity indices deduced by Marcus66,168 could be correlated with observed SIE.38 This hypothesis has been further investigated by Miranda-Quintana and Smiatek in terms of protein stabilisation for zwitterions and osmolytes.169 For anions it appears these Lewis basic properties relate to the anion's charge density.128
3. Anomalous SIEs in aqueous solutions
Since so many SIE follow the Hofmeister series, it is useful to investigate those that do not – that is, those that qualitatively differ from the order of the Hofmeister series. Such ‘anomalies’ occur frequently and complicate the study of SIEs as it becomes increasingly difficult to find recurring trends. The origins of these anomalies themselves are, in many cases, not well understood. Do they deviate due to competing effects that become dominant given certain conditions,43 or are they the product of a fundamentally different underlying mechanism? Some anomalies may in fact be a result of incomplete series reversals, or competing mechanisms (see, for instance, Fig. 5). Commonly, it is reported that SIEs are more pronounced for anions than they are for cations. This is a broad generalisation that should be taken with a grain of salt (pun intended), since in some cases the physical conditions of the system itself can be responsible, and indeed the influence or effect of cations can be more pronounced than anions.170,171 In this section we examine how subtle changes within aqueous electrolytes (e.g., pH, ion concentration, presence of a cosolute, counterion and temperature), can each cause SIEs to deviate from the Hofmeister series. Understanding these phenomena remains a principal barrier preventing a complete understanding of SIEs. | ||
| Fig. 5 The salt concentration dependence of the double-layer pressure between two surfaces separated by 20 Å showing separate (a) anion and (b) cation influences.172 (c) The cloud-point temperature of lysozyme as a function of anion type and concentration.25 (a) and (b) reprinted from ref. 172 with permission from the American Chemical Society, copyright 2011. (c) Reprinted from ref. 25 with permission from the National Academy of Sciences, copyright 2009. | ||
3.1. Concentration and pH-induced series reversals
Beyond SIEs in concentrated electrolytes (see Section 7), several studies have demonstrated the delicate interplay between ion concentration and pH on Hofmeister trends (or even on ‘simple’ sodium chloride behaviour173). In one study the effect of pH and salt concentration on the reversal of the Hofmeister series for lysozyme was discussed by Boström et al.172 At pH values above the isoelectric point the direct series was followed, but below this the reverse series was followed. At low salt concentrations, the adsorption of more polarisable anions was enhanced by ion-surface dispersion interactions, whereas at high concentrations there was enhanced adsorption of the cations. This is a charge reversal phenomenon; anion adsorption screens surface forces, while cation adsorption increases them (Fig. 5(a) and (b)). Boström et al. posit that the entropic terms, for anions at low concentration and for cations at high concentration, were the driving forces for the Hofmeister series.172 Salis et al.174 also reported electrophoretic mobility measurements on lysozyme suspensions to help explain how solution pH can invert the Hofmeister series. The reversal was predicted by a complex interplay of ionic size, hydration, and dispersion forces. Additionally, it impacted the charge on the amino acid groups, as well as the ionic composition of the solution. Specific buffer effects (a buffer subset of SIE) that can modulate Hofmeister effects in biological systems were reviewed by Salis and Monuzzi.175Fig. 5(c) displays a very rich concentration dependence on the behaviour of lysozyme in electrolyte solutions. Zhang and Cremer25 claimed ionic volume and polarisability to be the properties determining the liquid–liquid phase transition, suggesting that charge diffuse ions raise the cloud point temperature sharply due to ion pairing with lysozyme. Upon saturation, however, a maximum was reached, and the behaviour reversed due to a decrease in interfacial tension. For chloride, the phase transition continues to rise due to a continual increase in the interfacial tension. pH effects have also been observed in polymer systems. For instance, in a multi-responsive poly(2-(diethylamino)ethyl methacrylate) and poly(2-(2-methoxyethoxy) ethyl methacrylate) copolymer brush system, Johnson et al. utilised pH effects to alter the SIE observed on the thermal response.176 They indicated that the overall SIE could be quenched by a balance of competing stabilising and destabilising effects of the ions on each individual monomer identity. Section 3.2 further discusses how cosolute identity may alter SIE.
Fig. 6 shows three different concentration dependent specific ion influences on polymer behaviour.177 An elastin-like polypeptide (ELP) has the general structure (VPGXG)-n, where the monomeric unit is Valine-Proline-Glycine-X-Glycine, X denotes a variable amino acid and n denotes the number of monomer units. The uncharged ELP-V5A2G3-120, which has a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio of Valine, Alanine and Glycine guest residues with 120 monomer units, does not show any reversal behaviour due to salt concentration (Fig. 6(a)). The charge diffuse ions cause an increase in the LCST, while the charge dense ions show a decrease in the LCST. A positively charged KV6-112 peptide/moiety, with a 1
3 ratio of Valine, Alanine and Glycine guest residues with 120 monomer units, does not show any reversal behaviour due to salt concentration (Fig. 6(a)). The charge diffuse ions cause an increase in the LCST, while the charge dense ions show a decrease in the LCST. A positively charged KV6-112 peptide/moiety, with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 ratio of lysine to valine, shows charge diffuse ions causing the largest change in LCST at low concentrations (Fig. 6(b)), but these plateau, while charge dense ions continue decreasing the LCST causing a series inversion at ∼0.4 M. This is one example of a concentration dependent Hofmeister reversal.
6 ratio of lysine to valine, shows charge diffuse ions causing the largest change in LCST at low concentrations (Fig. 6(b)), but these plateau, while charge dense ions continue decreasing the LCST causing a series inversion at ∼0.4 M. This is one example of a concentration dependent Hofmeister reversal.
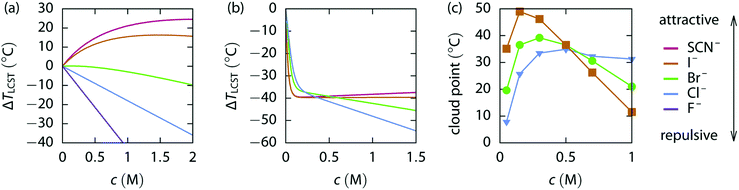 | ||
| Fig. 6 LCST change vs. the concentration of various sodium salts for (a) uncharged ELP V5A2G3–120, (b) weakly positive ELP KV6-112 and (c) the UCST for weakly positive PAU.177 Reproduced from ref. 177 with permission from the Royal Society of Chemistry, copyright 2018. | ||
A similar reversal is shown in Fig. 6(c) for the positively charged poly(allylamine)-co-poly(allylurea) (PAU). At low salt concentrations, charge diffuse ions increase the cloud point temperature most significantly. However, increasing the concentration further begins to decrease the cloud point, most dramatically for the charge diffuse ions, but only minimally for charge dense ions. This results in a series inversion at ∼0.5 M. This concentration reversal is explained via a charge screening effect.177 At low concentrations this is described as an ion-specific screening and bridging effect (causing collapse) while at high concentrations (Section 7), the same strong ion specific direct interactions now govern re-entrant swelling.
3.2. Cosolute-induced series reversals
Cosolute-dependent Hofmeister reversal has been reviewed by Paterová et al.,178 who state that traditional explanations of Hofmeister ordering of ions in terms of their bulk hydration properties is inadequate. NMR spectroscopy and MD simulations on a specific amino acid (triglycine) showed that uncapping the N-terminus (RNH3 to RNH2+) caused the ordering of the anions to reverse (Fig. 7). No appreciable binding was observed for SO42−, Cl− and Br− for the terminated triglycine, while I− and SCN− had some weak binding (KD > 1000 mM). The apparent dissociation constants (KD in mM) for the non-terminated triglycine were in the order SO42− (70 ± 30) < Cl− (290 ± 240) < Br− (890 ± 560) < I− (>1000) < SCN− (>1000). This demonstrates the importance of the cosolute on the chemical and physical properties associated with SIEs and may have the same fundamental origins as those associated with pH changes.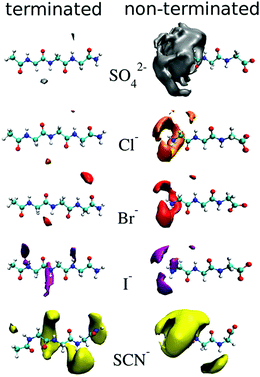 | ||
| Fig. 7 Density maps of ions about terminated (left) and non-terminated (right) triglycine at an isovalue three times the aqueous bulk ion density.178 Reprinted from ref. 178 with permission from the American Chemical Society, copyright 2013. | ||
A similar reversal was observed by Schwierz et al.179,180 who investigated colloidal coagulation kinetics. A direct Hofmeister series was followed for a partial set of anions for both negatively charged hydrophobic surfaces and positively charged polar surfaces. Conversely, a reversal in the Hofmeister series was observed at negatively charged polar surfaces and positively charged non-polar surfaces. This is understood as a transient phenomenon for surfaces of intermediate polarity or charge. It implies that the surface determines whether the dominant ion will be the anion or the cation. Similar conclusions have been reached by Okur et al.,33 who investigated Hofmeister effects on protein surfaces. Franks et al., investigating zeta potentials and yield stresses, observed a forward cation Hofmeister series existing at silica surfaces181 (K+ > Na+ > Li+), whilst a reverse series occurred at alumina surfaces182 (Li+ > Na+ > K+). These were corroborated theoretically by Parsons et al.183 using a modified Poisson Boltzmann analysis, indicating an interplay of hydration, non-electrostatic potentials and ion size underpinning these effects. SIE occurring at such surfaces indicates that even the vessel choice (i.e., silica glassware) requires consideration. Indeed, surface functionalisation can be used as a means of masking specific ion effects (on the surface) entirely.184
3.3. Counterion-induced series reversals
As alluded to in the Introduction (Section 1), SIEs are not independent of the counterion despite common assumptions and the implicit assumption of the Hofmeister series itself. A simple example is provided in Fig. 8.185 Here, the activity of NaF and NaSCN are vastly different across all concentrations. The activity of NaSCN is greater than the activity of KSCN, when SCN− is the common counterion, however this is reversed when F− is the counterion (i.e., γ(NaSCN) > γ(KSCN; γ(KF) > γ(NaF)). Also, the activity of NaSCN is greater than activity of NaF when Na+ is the common counterion, but this is reversed when K+ is the counterion (i.e., γ(NaSCN) > γ(NaF); γ(KF) > γ(KSCN)).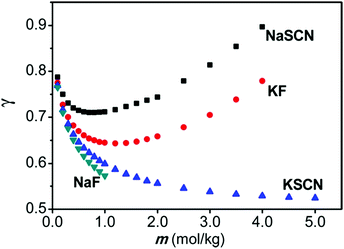 | ||
| Fig. 8 Activity coefficients of NaF, NaF, NaSCN and KSCN electrolyte solutions. Reprinted from ref. 185 with permission from the American Chemical Society, copyright 2013. | ||
Similarly, HSAB theory (see Section 2.3.6) recognises counterion reversals, but in a more generalised way. Soft acids form complexes with different ligand atoms in order of decreasing stability, i.e. C ∼ S > I > Br > Cl ∼ N > O > F; whilst there is a strong, but incomplete inversion of this stability series for hard acids.186 The argument for an incomplete inversion is that some soft bases are still strong proton acceptors.
Gregory et al.45 investigated the energetic mechanisms of counterion induced reversals in a solvent cluster model via a density functional theory (DFT) approach using generalised Kohn–Sham energy decomposition analysis (GKS-EDA).187 In the presence of a counterion that has had its energy included as part of the solvation environment, there is negligible counterion effect on the direct interaction strength between anions or cations and the model pNIPAM fragment. However, when simultaneously considering the energetics of both the cation and anion interacting at the respective C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–H moieties of the pNIPAM fragment (Fig. 9(a)), a cationic reversal takes place if an ion–pair is forced at the amide N–H moiety (Fig. 9(b)), whereas an anionic reversal takes place if an ion-pair is forced at the C
O and N–H moieties of the pNIPAM fragment (Fig. 9(a)), a cationic reversal takes place if an ion–pair is forced at the amide N–H moiety (Fig. 9(b)), whereas an anionic reversal takes place if an ion-pair is forced at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety (Fig. 9(c)).
O moiety (Fig. 9(c)).
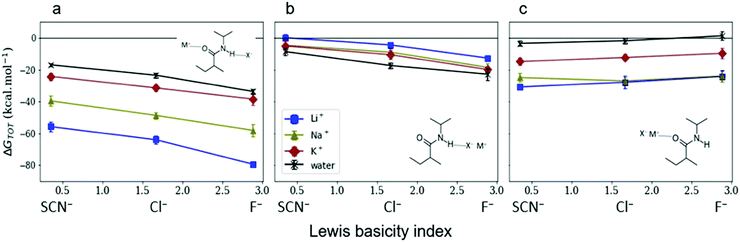 | ||
Fig. 9 GKS-EDA (M062X/cc-pVDZ) interaction energies between (a) dissociated salts and associated salts at (b) the N–H and (c) the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O sites of a NIPAM monomer in water. Black atoms in the inset structures indicate GKS-EDA fragments considered. All data is the average of 10 independent configurations; error bars denote 1 standard deviation. Reprinted with permission from ref. 45 with permission from the American Chemical Society, copyright 2019. O sites of a NIPAM monomer in water. Black atoms in the inset structures indicate GKS-EDA fragments considered. All data is the average of 10 independent configurations; error bars denote 1 standard deviation. Reprinted with permission from ref. 45 with permission from the American Chemical Society, copyright 2019. | ||
Furthermore, Mazzini and Craig44 showed these counterion reversals appear in nonaqueous solutions when considering the Gibbs free energy of dissolution of salts (negative values indicate solubility) versus the difference in the constituent ions’ absolute free energies of solvation (negative values indicate the anion is more soluble than the cation, Fig. 10). In these circumstances counterion reversals can be more pronounced for aprotic solvents. In water (and other protic solvents) the inversion is most evident for the F− anion, whilst the other cation–anion combinations fall onto the same trend. In propylene carbonate (PC) (and other aprotic solvents) no singular trend appears, but the F− ion shows a very different trend.
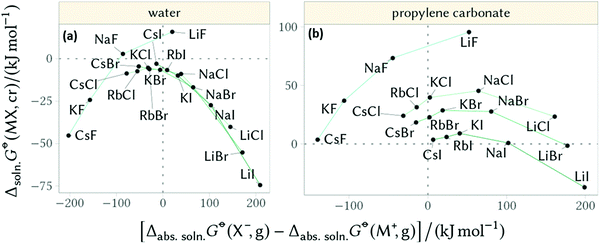 | ||
| Fig. 10 Gibbs free energy of dissolution of salts versus the difference in the constituent ions’ absolute free energies of solvation for (a) water and (b) propylene carbonate. Adapted from ref. 44 with permission from the American Chemical Society, copyright 2018. | ||
3.4. Stimuli-induced series anomalies
Whilst there has been previous work on light-responsive polymers generally,188–190 only recently191 have studies investigated the Hofmeister series in light responsive (azobenzene) salts. UV-activation causes the cation to adopt a cis-conformation and greatly decreases the LCST of pNIPAM (Fig. 11(a)). For azobenzene cation salts, it is difficult to distinguish the behaviour of different anions under visible light, where the cation adopts a trans-conformation (Fig. 11(b)). Thus, UV light acts to amplify both the ion specificity of the salts and the magnitude of their effect. This was explained as the cis-conformation permitting more dissociation, providing anions with more dynamic freedom. Equivalent systems for alkali metal cations, with a common light responsive anion, showed very little ion specificity and, if anything, the UV-induced cis-conformation decreased ion-specificity.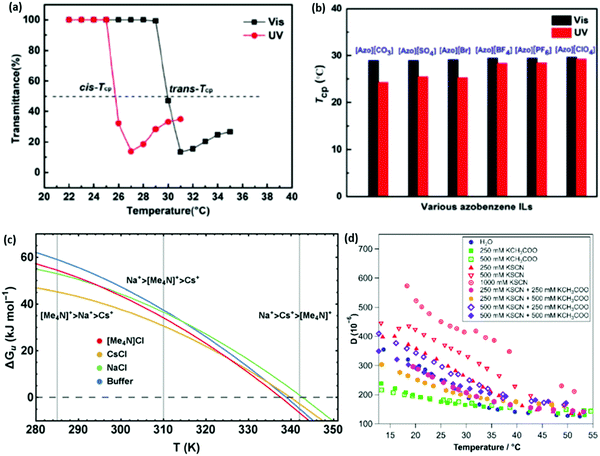 | ||
Fig. 11 (a) A large shift in the temperature of the phase transition in pNIPAM is observed depending on the light-responsive conformation of the azobenzene cation.191 (b) The magnitude of the ion specific change in the temperature of the phase transition is seen to be more pronounced when the salts are in a UV-induced cis-conformation.191 (c) Stability curves, ΔGu(T), of RNase A in buffered solutions of 4 M NaCl, CsCl, and [Me4N]Cl illustrating the temperature dependence of the Hofmeister series.192 (d) The dissipation of an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mol% p(MEO2MA-stat-OEGMA300) brush with changing temperature in various mixtures of thiocyanate and acetate potassium salts.193 (a and b) Reproduced from ref. 191 with permission from Wiley Materials, copyright 2021. (c and d) Reproduced from ref. 192 and 193 respectively, with permission from the Royal Society of Chemistry, copyright 2016 and 2019 respectively. 20 mol% p(MEO2MA-stat-OEGMA300) brush with changing temperature in various mixtures of thiocyanate and acetate potassium salts.193 (a and b) Reproduced from ref. 191 with permission from Wiley Materials, copyright 2021. (c and d) Reproduced from ref. 192 and 193 respectively, with permission from the Royal Society of Chemistry, copyright 2016 and 2019 respectively. | ||
Senske et al.192 reported a Hofmeister series reversal due to temperature changes using a novel thermodynamic analysis. It was found that protein stability curves, ΔGu(T), for each ion were impacted by the temperature, such that their respective curves intersected, presenting temperature dependent ion rankings (Fig. 11(c)). This was attributed to differing enthalpic and entropic contributions to the excess free energy. It is claimed this classification may be extrapolated beyond ions to neutral cosolutes as well. Quartz crystal microbalance with dissipation monitoring (QCM-D) measurements performed by Johnson et al.193 also displayed a subtle temperature dependence on the ion ordering for the dissipation of an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mol% p(MEO2MA-stat-OEGMA300) brush (Fig. 11(d)). For example, at low temperatures lower dissipation values for the brush were observed in a 250 mM KSCN + 500 mM KCH3COO salt mixture when compared with a 250 mM KSCN + 250 mM KCH3COO salt mixture or pure 250 mM KSCN salt, however at high temperatures the opposite was observed. However, in this case it is difficult to decouple the SIEs from the effect of ionic strength and steric crowding, as noted by the authors,193 as the brush in higher ionic strengths seemingly exhibits slightly higher dissipations at elevated temperatures when it is expected to be in a collapsed state. A recent study by Yao et al.194 on ubiquitin proteins, showed both temperature and pH (Section 3.1) dependent SIE via static light scattering data as well as concentration dependent trends via differential scanning calorimetry (DSC).
20 mol% p(MEO2MA-stat-OEGMA300) brush (Fig. 11(d)). For example, at low temperatures lower dissipation values for the brush were observed in a 250 mM KSCN + 500 mM KCH3COO salt mixture when compared with a 250 mM KSCN + 250 mM KCH3COO salt mixture or pure 250 mM KSCN salt, however at high temperatures the opposite was observed. However, in this case it is difficult to decouple the SIEs from the effect of ionic strength and steric crowding, as noted by the authors,193 as the brush in higher ionic strengths seemingly exhibits slightly higher dissipations at elevated temperatures when it is expected to be in a collapsed state. A recent study by Yao et al.194 on ubiquitin proteins, showed both temperature and pH (Section 3.1) dependent SIE via static light scattering data as well as concentration dependent trends via differential scanning calorimetry (DSC).
4. SIEs at the liquid–vapour interface
Ions at the vapour–liquid interface are of fundamental interest for understanding SIEs, and the presence of an interface increases the complexity of ion specificity (Fig. 12). In this respect the vapour–liquid interface is the simplest to consider. Classical models of electrolytes suggest that the sharp discontinuity at the interface between two dielectric media forces (point charge) ions away from the interface, due to image charge repulsion. This results in a depletion of ions from solvent–vapour interfaces.195 As elucidated in Sections 2.2 and 7 however, treating ions as point charges ignores ion specificity completely. Experimental196 and computational results197–199 deviate from this classical picture, indicating that more polarisable ions have a greater affinity for the vapour–solvent interface.Levin200 explained this phenomenon via the cavitational energy required for an ion to reside at the water–vapour interface. Polarisable ions can redistribute their charges to stay hydrated at the interface to balance the electrostatic penalty accompanying ion adsorption. On the other hand, less-polarisable ions are less able to redistribute their charge, and so become depleted at the water–vapour interface. Nevertheless, the correlation between these ion specific trends and ion polarisability is weak,201,202 and investigation of ionic adsorption at solvent surfaces remains an active area of research. Ion-specific adsorption at the liquid–vapour interface has also been explained in terms of the competition between ions’ bulk solvation and interfacial affinity. Colussi et al.201 found an inverse correlation between the dehydration free energy of an anion and its affinity for the air/water interface. Their results indicate strongly hydrated ions prefer to remain in the bulk solvent, while weakly hydrated ions will be driven to the liquid–vapour interface.
At the surface of an electrolyte solution, the Gibbs adsorption equation relates increasing203 surface tension values of an electrolyte solution with a depletion of the ions from the interface (if an electrolyte is treated as a binary system).195 However, separate ion contributions are essential to understand ion-specific adsorption, and it is impossible to directly infer these from surface tension measurements (which reflect the influence of both cation and anion). Pegram and Record204–206 have utilised surface tension data to determine single ionic partition coefficients (Kp) at the water–vapour interface (relative to Na2SO4 at 0). These coefficients show similarity to reported Hofmeister series. Nevertheless, these Kp values only account for anion–cation interactions indirectly. Further, the impact of ions on the interfacial tension is not strictly additive, reflecting ion specific effects of the counterion (see Section 3.3).14 Work by Craig et al.13,14,207 with similarities to Collins’ LMWA (Section 2.1)81,126 suggested if the cation and anion had similar properties (i.e., α or β) they would inhibit bubble coalescence, whilst different would allow properties would allow coalescence. The assignment of α and β properties was related to each ions Kp values and indicates ion pairs inhibit coalescence while partitioned ions do not.14 Modelling by Duignan208 explained these results with a modified Poisson–Boltzmann equation. An electrostatic surface potential arises from the coexisting enhancement and depletion of each ion. This allows for bubble coalescence due to a reduced Gibbs-Marangoni pressure.
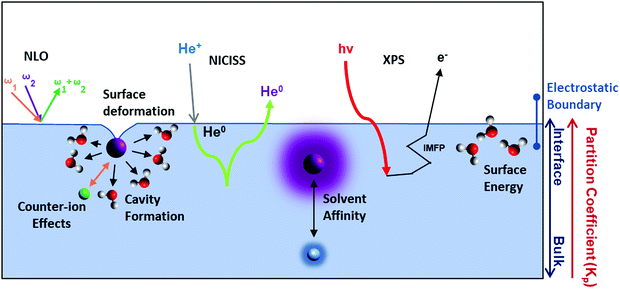
Experimentally, few techniques can quantitatively determine the presence of ions at the liquid–vapour interface and their interaction with solvent molecules. Relevant techniques include X-ray photoelectron spectroscopy209,210 (XPS) and metastable induced electron spectroscopy211–213 (MIES), X-ray reflectivity (XR),214,215 neutral impact collision ion scattering spectroscopy (NICISS),213,216–220 and non-linear optical (NLO) techniques such as vibrational sum-frequency generation (VSFG) and second-harmonic generation (SHG) spectroscopy195,221–223 (see Table S1 for descriptions in ESI†). Of these techniques however, only XPS and NICISS can directly probe concentration depth profiles of single ions at solvent surfaces. NICISS has the additional (and unique) benefit of delivering high depth resolution (down to ∼0.2 nm).
Hemminger and co-workers224–226 have applied XPS at the surfaces of aqueous electrolyte solutions to measure the ratio between ionic concentrations. They reported an aqueous specific ion order in the surface-enhanced concentration of I− > Br− > F−. In a separate investigation227 with LiI and KI salts in water, they showed higher surface concentrations of Li+ than K+. Additionally, the anion–cation ratio presented by the authors indicated that I− had a higher surface concentration in LiI solutions than KI solutions. This trend agreed with Pegram and Record's204 anion partition coefficient values for I− in LiI (1.34 ± 0.22) and KI (1.0 ± 0.14) electrolyte solutions, where a higher partition coefficient value suggests higher propensity towards the water–vapour interface.
As with surface tension, NLO techniques can only measure the net ion contribution at a solvent surface. Nevertheless, NLO-based investigations have delivered several insights regarding SIE at solvent surfaces. For instance, Allen and co-workers228 have employed VSFG extensively to study ionic interaction with solvent molecules at liquid–vapour interfaces, via the ions’ influence on the solvent hydrogen-bonding network. These investigations indicate that, for monovalent salts, the degree of the ions’ influence at the interface follows the orders I− > Br− > Cl− > F− for simple monovalent anions,221 and Li+ = NH4+> K+> Na+ for cations.229 This order agrees qualitatively with trends in ion partition coefficients (and size) for anions, but only partially for cations.230 Peterson et al.210 have reported the same order for monovalent anions using SHG spectroscopy. For divalent cations a largest-to-smallest size order of Sr2+ > Ca2+ > Mg2+ was reported by Allen and co-workers.211 Various experimental techniques show a consistent largest-to-smallest size order for monovalent anions at the water–vapour surface, in accordance with computational and theoretical works. For polyatomic and anisotropic ions less consistency exists,231 and many studies only investigate one or two salts.232–236 MD simulations related to one of these studies233 on a NaSCN salt reported an accumulation of the SCN− and depletion of Na+ at the surface, while the subsurface (between ∼5–10 Å depth) had an accumulation of Na+ and depletion of SCN−.
Liquid–vapour interfaces have also been investigated in nonaqueous solutions (more generally discussed in Section 6). In glycerol, Allen et al.237 found that NaI has a larger degree of disturbance on the surface hydrogen bonding network than NaBr. One possible explanation for this result is that the propensity of I− for the interface is larger than that of Br−. Alternatively, NICISS can been used to directly measure concentration depth profiles elementally. For instance, LiI and LiCl salts have been investigated at aqueous238–240 and formamide241 solvent surfaces, and could also be useful for exploring mixed electrolyte systems.207,242,243 For formamide,241 I− was reported to accumulate at the surface, whereas Cl− had roughly the same concentration at the outermost surface layer as the bulk. In both cases however there was a subsurface depletion of the anions. The local topology around the ions was deemed important for this analysis, as ion scattering spectroscopy revealed the surface was not flat, with structural deformations particularly near the ions. In mixed electrolytes dissolved in glycerol, NICISS concentration depth profiles showed that Br− outcompetes Cl− in interactions with the tetrahexylammonium cations at the glycerol–vapour interface.243 In water however, additional challenges arise due to its low vapour pressure, given the vacuum system. Low temperatures (e.g., −13.8 °C) and high concentrations (e.g., 7.2 m) can also enable aqueous electrolyte measurements, but this limits direct insight into standard experimental conditions. I− showed a depletion up to ∼20 Å from the surface in aqueous solutions. Nonetheless, NICISS provides a means to directly measure concentration depth profiles of each element in a solution, in contrast to indirect measurements which generally require triangulation or extra-thermodynamic assumptions from indirect measurements. NICISS is especially of use in nonaqueous electrolytes solutions (Section 6) which are gaining more attention.41,244
5. SIEs in mixed electrolytes
Specific ion effects in simple systems (i.e., single electrolytes in water) have been well studied, demonstrating the influence of ion identity on colloidal stability,245–248 structure of soft matter systems14,29 and response of polymer brushes and gels.36–38,193,249 However, the manifestation of SIEs in vivo relies on the delicate balance of myriad interactions between the solvent and multiple solutes/cosolutes. In an attempt to quantify these phenomena, industry often applies the parameterised Pitzer Method (Section 2.2). Few studies have examined this intricate and complex behaviour to explicitly resolve SIEs.To understand the behaviour between ions in a complex system, the effect of each individual ion must be considered along with their net additive or non-additive influences. In a recent investigation, Robertson et al.249 deconvolved the net response of neutral thermoresponsive polymer brushes in complex electrolytes, consisting of two anions from the same end of the Hofmeister series (Fig. 1), into the influence of the constituent ions. The authors suggest that the change in response of a system (ΔR) is the difference between the response in the presence of an electrolyte with respect to the neat solvent (ΔRi = Rsalt − Rsolv). For a responsive polymer, ΔR may be analogous to a change in LCST or swelling state. The observed net change in response (ΔRnet) results from the simple summation of the effect of each pure component salt 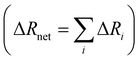 and an empirical term, δ, which accounts for deviations from pure additive behaviour (e.g., synergistic or competitive behaviour). Thus, for a binary complex electrolyte for two salts that either both salt-in or both salt-out the polymer, the net response of the system ΔRnet can be expressed as,
and an empirical term, δ, which accounts for deviations from pure additive behaviour (e.g., synergistic or competitive behaviour). Thus, for a binary complex electrolyte for two salts that either both salt-in or both salt-out the polymer, the net response of the system ΔRnet can be expressed as,
| |ΔRnet| = |ΔR1 + ΔR2| + δ | (4) |
Moghaddam and Thormann utilised DSC to investigate the stability of ungrafted poly(propylene oxide) (PPO) in aqueous solutions of binary sodium electrolytes, keeping the cation constant to decode the relative influence of different anions.250 They reported that the behaviour of PPO in the presence of two salts that salt-in PPO (NaSCN and NaI) or two salts that salt-out PPO (NaCl and NaBr) is dependent on the salt concentration. The authors reported a turnover in the manifested SIE with increasing concentration. That is, in the presence of a low concentration binary electrolyte, |ΔRnet| is greater than the |ΔRi| of PPO in the presence of either pure electrolyte, while at higher concentrations the LCST (|ΔRnet|) in the mixed salt solution lies between each of the pure composite electrolytes (Fig. 13); altering from cooperative to antagonistic behaviour. We recast the data of Moghaddam and Thormann (Fig. 13(a) and (b)), showing the net change in the LCST of PPO as a function of the concentration of a second electrolyte from the same end of the Hofmeister series. Deviations from purely additive behaviour are illustrated by δ in each inset figure. In the case of two salting-out salts (Fig. 13(a)), systematically varying the concentration of NaBr whilst maintaining a constant NaCl concentration of 0.1 M, and vice versa, yields approximately additive behaviour (δ ≈ 0). Deviations from additive behaviour occur at high NaCl concentrations as δ diverges from 0. Fig. 13(b) presents the behaviour of PPO in the presence of binary electrolytes composed of two salting-in anions. For this combination of mixed electrolytes, the behaviour is essentially additive at all concentrations.
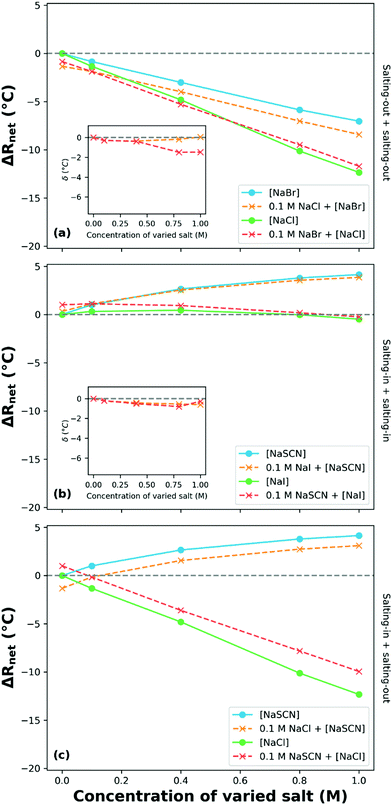 | ||
| Fig. 13 The net response in LCST (ΔRnet; change relative to the LCST of PPO in water) of ungrafted PPO as a function of the concentration of varied salt species for several binary electrolyte compositions: same end of Hofmeister series anions (a) and (b); opposite end (c). The varied salt species is denoted by square brackets. Inset plots present the δ values (deviations from purely additive behaviour) for the same effect-type binary electrolyte compositions. Data obtained and reproduced with permission from Moghaddam and Thormann,250 copyright 2015. | ||
Moghaddam and Thormann also investigated a binary electrolyte composed of two salts that salt-in and salt-out PPO, NaSCN and NaCl, Fig. 13(c).250 Here approximately additive behaviour was observed, whereby both anions impart their individual (opposite) effects onto the system. No attempt is made here to extend the definition of the δ deviation parameter to systems comprising mixtures with both salting-in and salting-out salts, owing to the non-unique range of possible relative responses for a given δ value.
Recently, Bruce et al. investigated the effects of a mixed electrolyte (composed of anions from opposite ends of the Hofmeister series) on the LCST of ungrafted pNIPAM in a combined spectroscopic and MD study.160 In the presence of a fixed concentration of Na2SO4 and systematically varied NaI concentration, a reduction in the LCST of pNIPAM was observed at low I− concentrations. This non-additive, antagonistic behaviour is contrary to the PPO-based study conducted by Moghaddam and Thormann who observed near additive behaviour for all conditions (Fig. 13).250 Bruce et al. hypothesised that the Na+ counterion preferentially interacts with the strongly hydrated SO42− anion, leaving a greater number of lone I− anions in a more hydrated state. These hydrated ions compete with the polymer for water and decrease polymer solubility. However, at all concentrations of the mixed salt the MD results indicated an increase in the number of I− ions proximal to a model oligomer compared to the pure salt, and the effects of the SO42− anion on the solvation of the I− anion was most notable in the second solvation shell. This may indicate other factors at play (for instance cation effects161) for NaI to further salt-out the polymer whilst I− itself showed an increased affinity for the polymer and increased solvation in the mixed salt system. Upon further addition of NaI, a salting-in effect was observed in comparison to the lower concentrations; this turnover in behaviour is indicative of competitive behaviour occurring between the anions (i.e., I− salting-in effects manifest instead of SO42− salting-out behaviour). Finally, in the highest iodide concentration region, it was concluded there was a depletion of ions at the surface, driving polymer collapse and thus a decrease in LCST.
Johnson et al.193 investigated the effects of mixed aqueous electrolytes composed of anions from the two extremes of the Hofmeister series. The authors probed the behaviour of a statistical copolymer brush of di(ethylene glycol)methyl ether methacrylate (MEO2MA) and ethylene glycol methyl ether methacrylate (OEGMA300) (P(MEO2MA-stat-OEGMA300)) 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mol% using QCM-D. In comparison to Moghaddam and Thormann250 and Bruce et al.,160 Johnson et al. explored the influence of temperature on the manifestation of SIEs across a wide concentration range, noting temperature-dependent SIEs (Fig. 11(d)). At low temperatures (<25 °C) and in the presence of equimolar KSCN (salting-in) and KCH3COO (salting-out) electrolytes, the impact of the ions was approximately additive, yielding a similar brush response to that in the absence of salt. However, at higher temperatures a net salting-in effect was observed in comparison to water.
20 mol% using QCM-D. In comparison to Moghaddam and Thormann250 and Bruce et al.,160 Johnson et al. explored the influence of temperature on the manifestation of SIEs across a wide concentration range, noting temperature-dependent SIEs (Fig. 11(d)). At low temperatures (<25 °C) and in the presence of equimolar KSCN (salting-in) and KCH3COO (salting-out) electrolytes, the impact of the ions was approximately additive, yielding a similar brush response to that in the absence of salt. However, at higher temperatures a net salting-in effect was observed in comparison to water.
The influence of mixed electrolyte solutions on the thermotransition of a P(MEO2MA-stat-OEGMA300) 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mol% copolymer brush has also been studied by Robertson et al.249Fig. 14 presents a subset of the data collected by Robertson et al.: ΔRnet as a function of varied salt concentration at 15 °C (most swollen state). This study reported that for binary electrolytes composed of two salts (KF and KCl) that both individually salt-out the polymer, the influence of the ions was concentration dependent. At low and intermediate concentrations of KF (containing the more charge dense of the anions), an approximately additive (δ ≈ 0) behaviour of the ions with increasing KCl concentration was observed, consistent with Moghaddam and Thormann.249,250 At high KF concentrations (500 mM), a non-monotonic impact was observed that was dependent on the KCl concentration, which was attributed to the availability of solvent molecules.249 A complementary experiment with two salting-in salts, KSCN and KI, demonstrated competitive behaviour between the salts. As shown in Fig. 14(b), all ΔRnet curves corresponding to binary electrolytes are non-monotonic with increasing salt concentration. For example, in 250 mM KSCN with varied KI concentration, antagonistic behaviour was observed at 125 mM KI, additive behaviour at 250 mM KI concentrations and again non-additive behaviour at 500 mM KI. This is similar to the three concentration regions observed by Bruce et al. for Na2SO4 and NaI mixtures.160 Robertson et al. note, however, that the non-monotonic behaviour between the ions (from antagonistic to cooperative) in Fig. 14(b) cannot be explained by the Moghaddam and Thormann competitive binding mechanism.250 Rather, it was hypothesised that the turnover is due to the reduction in salting-in behaviour driven by the inter-anion and polymer–anion interactions. Notably, when observing the 125 mM and 500 mM KSCN solutions, at high concentrations of KI the behaviour appears to converge to that observed in the pure KI salt.
20 mol% copolymer brush has also been studied by Robertson et al.249Fig. 14 presents a subset of the data collected by Robertson et al.: ΔRnet as a function of varied salt concentration at 15 °C (most swollen state). This study reported that for binary electrolytes composed of two salts (KF and KCl) that both individually salt-out the polymer, the influence of the ions was concentration dependent. At low and intermediate concentrations of KF (containing the more charge dense of the anions), an approximately additive (δ ≈ 0) behaviour of the ions with increasing KCl concentration was observed, consistent with Moghaddam and Thormann.249,250 At high KF concentrations (500 mM), a non-monotonic impact was observed that was dependent on the KCl concentration, which was attributed to the availability of solvent molecules.249 A complementary experiment with two salting-in salts, KSCN and KI, demonstrated competitive behaviour between the salts. As shown in Fig. 14(b), all ΔRnet curves corresponding to binary electrolytes are non-monotonic with increasing salt concentration. For example, in 250 mM KSCN with varied KI concentration, antagonistic behaviour was observed at 125 mM KI, additive behaviour at 250 mM KI concentrations and again non-additive behaviour at 500 mM KI. This is similar to the three concentration regions observed by Bruce et al. for Na2SO4 and NaI mixtures.160 Robertson et al. note, however, that the non-monotonic behaviour between the ions (from antagonistic to cooperative) in Fig. 14(b) cannot be explained by the Moghaddam and Thormann competitive binding mechanism.250 Rather, it was hypothesised that the turnover is due to the reduction in salting-in behaviour driven by the inter-anion and polymer–anion interactions. Notably, when observing the 125 mM and 500 mM KSCN solutions, at high concentrations of KI the behaviour appears to converge to that observed in the pure KI salt.
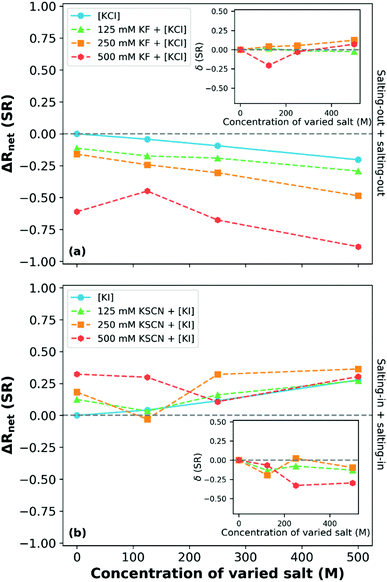 | ||
Fig. 14 The net response (ΔRnet(SR); change in swelling ratio relative to the response in water) of a P(MEO2MA-stat-OEGMA300) 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mol% copolymer brush at 15 °C in binary electrolytes composed of (a) salting-out and (b) salting-in ions where the varied species is denoted by square brackets. Inset plots present the δ values for the various binary electrolyte compositions. Adapted from ref. 249 with permission from Elsevier, copyright 2021. 20 mol% copolymer brush at 15 °C in binary electrolytes composed of (a) salting-out and (b) salting-in ions where the varied species is denoted by square brackets. Inset plots present the δ values for the various binary electrolyte compositions. Adapted from ref. 249 with permission from Elsevier, copyright 2021. | ||
6. SIEs in nonaqueous solvents
The vast majority of SIE studies have employed water as the solvent (Section 2.2). This has led to the prevalent assumption that the SIEs observed originate from the properties of water itself, or that the existence of the Hofmeister series is dependent upon water. Recent reports by Mazzini and Craig,41–44 Liu et al.,40,251–255 Gregory et al.,45,128,256 Smiatek et al.169,244,257–263 and others24,27,39,264,265 demonstrate however that SIEs and the Hofmeister series also exist in nonaqueous solvents. The origins of SIEs therefore cannot be solely attributed to an ion's ability to induce order in an aqueous environment; their origins must be more general in nature (i.e., a property of the ions themselves). Nonetheless, the role of the solvent is important in the manifestation of SIEs. Identifying the influence of the solvent on SIEs in nonaqueous environments is not only critical for SIEs to be exploited in myriad applications employing nonaqueous solvents (e.g. batteries,266 supercapacitors,267 metal electrodeposition,268 semiconductors,269 fuel cells,270 capillary electrophoresis,271etc.66,266), but also for our fundamental understanding of SIEs generally.In this respect, nonaqueous solvents pose interesting challenges. For instance, Mazzini and Craig41 have recently demonstrated that the association of anions with their solvent environment in water and methanol exhibit analogous trends; both following the Hofmeister series (measured via NMR molecular reorientation time). On the other hand, the standard molar heat capacities of the same anions exhibit no known SIE trend in water but follow a reverse Hofmeister trend in methanol. Comparable results were observed regarding the limiting molar conductivity. Similarly, while viscosity B coefficients of these anions in water were reported not to follow a known SIE trend (these are dependent on coordination number128), in methanol they followed a direct Hofmeister series. Solvent-induced SIE reversals have been observed in ion retention times in size exclusion chromatography and polymer swelling experiments.43 For instance, a direct series was found for water and MeOH in both cases, while a reverse series was seen in dimethyl sulfoxide (DMSO) and PC. In formamide (FA) electrolyte solutions, polymer-brush swelling exhibited a reverse series, despite ion retention times exhibiting no known ion specific trend. These series inversions supported prior observations of Parker272 and Pearson.273
The initial hypotheses for solvent-induced anion Hofmeister series reversal by Mazzini et al.43 were in line with the proposed polarisability origins of SIE. This suggested that a forward Hofmeister series would be followed in low polarisability solvents, such as water and methanol, whilst a reversal would occur for high polarisability solvents such as DMSO and PC. The fact that ion retention times in FA showed no known ion-specific trend whilst known ion-specific trends were observed in polymer brush swelling, suggest that FA has properties that were on the cusp of producing ion series reversal. For these protic solvents, polarisability correlates with Lewis acidity, and other work128,274 suggests that the latter is the fundamentally important property. In fact, the radial charge density of anions (ϸ, Section 2.3.3) and the solvent's Lewis acidity (quantified by the Gutmann acceptor number,275 AN) were correlated quantitatively with the magnitude of the Gibbs energy of transfer from aqueous to nonaqueous solutions (Fig. 15(a)). Similar correlations were observed for the SN2 reaction rate of nucleophilic anions with methyl iodide in nonaqueous environments (Fig. 15(b)).128 For cations, it was hypothesised that the similarity in Lewis basicity (quantified by the Gutmann donor number, DN) between water and many nonaqueous solvents (or cosolutes) allowed for non-electrostatic interactions, such as dispersion, to instead have significant influence in (partially) aqueous SIE for cations. Considerable work to address the use of donor numbers for SIE has been performed by Smiatek et al. using a conceptual density functional theory approach.257,260,263,276,277
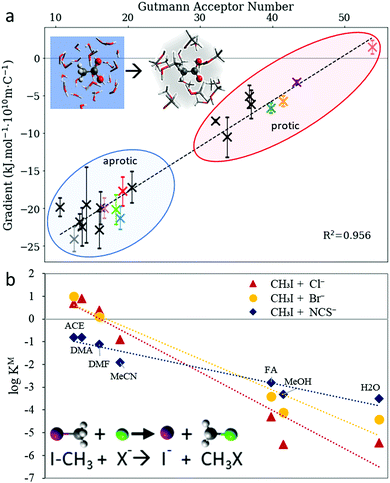 | ||
| Fig. 15 The Gutmann acceptor number approximates the effect of the solvent on anion trends (a) with the Gibbs’ free energy of transfer from aqueous to nonaqueous solvents and (b) the SN2 reaction rate with methyl iodide. Adapted from ref. 128 with permission from the Royal Society of Chemistry, copyright 2021. | ||
Whilst it appears AN quantifies the magnitude of anion SIE in nonaqueous solvents and DN has shown some success as a solvent parameter for cation solvation,278 there are two key problems that arise from their empirical origins:
1. A solvent's DN and AN are based on completely different empirical measurements, and are defined in inconsistent units. The DN is obtained by calorimetry, and is defined as the enthalpy of formation of a solvent antimony pentachloride (SbCl5) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct (in kcal mol−1). The AN is the solvent-induced 31P NMR chemical shift of triethyl phosphine oxide (Et3PO) in the solvent (in ppm). It is therefore meaningless to quantitatively compare these parameters, or simultaneously account for cation and anion effects self-consistently.
1 adduct (in kcal mol−1). The AN is the solvent-induced 31P NMR chemical shift of triethyl phosphine oxide (Et3PO) in the solvent (in ppm). It is therefore meaningless to quantitatively compare these parameters, or simultaneously account for cation and anion effects self-consistently.
2. A solvent's DN and AN are specific to the molecular probe (SbCl5 and Et3PO, respectively) from which they were each derived. This may limit their transferability for predicting solvency of Lewis acids (e.g., cations) and Lewis bases (e.g., anions) that are dissimilar to these molecular probes.
For these reasons, an ab initio unification of solvent Lewis acid and base properties is warranted. Similarly, the importance of ion solvation numbers have also been highlighted in properly understanding ion solvation in aqueous solution (Section 2.3.5),20,128,130,155,157 yet there is limited information available for nonaqueous solvents.
7. SIEs in concentrated electrolytes
To date no theory to describe the properties of highly concentrated electrolyte solutions has gained widespread acceptance, and various effects manifest in this regime (i.e., re-entrant behaviour in polyelectrolyte279–281 and colloidal systems74,282,283). DH theory describes the behaviour of dilute electrolytes successfully, however its accuracy is diminished with increasing concentration for various reasons, some of which are mentioned in Section 2. The DH equation (also called the linearised Poisson–Boltzmann (PB) equation) is the following differential equation,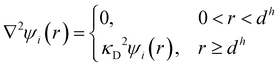 | (5) |
 | (6) |
 | (7) |
| D = ε0E + P | (8) |
| D = ε0(1 + χe)E = ε0εrE | (9) |
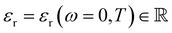 (ω is the angular frequency of the applied field). This single number is often used in understanding solvation of ions in different solvents, as solvents with higher permittivity numbers have greater capacity to screen an electric field. However, it is also a function of the composition of the mixture. The electronic and geometric nature of the solvent and solute molecules, their ability to orient toward an applied field, as well as the intermolecular interactions, all contribute. At finite frequencies, different contributions have competing effects and this can lead to phenomena such as an isopermittive point in water.287 Hence εr is also a function of concentration. Usually, high permittivity solvents will see a decrease in the value of εr with the addition of a salt while lower permittivity solvents can see the reverse. The former is thought to be due to an entropic effect of locking solvent dipoles into solvation shells of ions (salt-screening of solvent–solvent correlations), and the latter due to ion pairing and polarisation of the solvent, as proposed by Grzetic et al.288
(ω is the angular frequency of the applied field). This single number is often used in understanding solvation of ions in different solvents, as solvents with higher permittivity numbers have greater capacity to screen an electric field. However, it is also a function of the composition of the mixture. The electronic and geometric nature of the solvent and solute molecules, their ability to orient toward an applied field, as well as the intermolecular interactions, all contribute. At finite frequencies, different contributions have competing effects and this can lead to phenomena such as an isopermittive point in water.287 Hence εr is also a function of concentration. Usually, high permittivity solvents will see a decrease in the value of εr with the addition of a salt while lower permittivity solvents can see the reverse. The former is thought to be due to an entropic effect of locking solvent dipoles into solvation shells of ions (salt-screening of solvent–solvent correlations), and the latter due to ion pairing and polarisation of the solvent, as proposed by Grzetic et al.288
To illustrate the effect of adjusting the value of the static permittivity on the Debye and Bjerrum lengths, experimental values289–294 were collected and fitted to a functional form provided by Gavish and Promislow295 (detailed in the ESI†), and the correction is shown in Fig. 16. By increasing the NaCl concentration the Debye length decreases at a faster rate compared to the fixed εr form and Bjerrum length increases linearly compared to the fixed εr form.
The form of the Bjerrum length provided in eqn (7) is widely used. However, this form is derived from a simple unscreened Coulomb interaction and will therefore become increasingly inaccurate as the number of ions in solution (and therefore electrostatic screening) increases. Hence the decay will take the form of a Yukawa-like potential,296 as shown by Liu et al.,279 and results in the following transcendental equation for rij that gives the effective Bjerrum length (λeffB) in solution,
| rij = e−κDrij | (10) |
 ,
,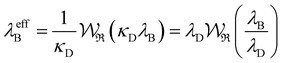 | (11) |
This effective Bjerrum length gives the length of the electrostatic-thermal interaction equivalence in the presence of ions, with a concentration dependence implicit in the calculation of λD. This is plotted in Fig. 16, showing the significant reduction in the Bjerrum length (compared to the increase by only adjusting the value of the static permittivity) if there are other ions present.
If these were the only extra corrections needed there would be nothing left to add. However surface force measurements297 by Gebbie et al.298 and Perkin's group,285,299,300 with agreement from other techniques described by Gaddam and Ducker,301 and then further critically reviewed,302 showed that there were significant deviations from the Debye length at higher concentrations, despite adjustments to the value of the permittivity. This highlights a significant breakdown of the DH picture of electrolytes. This is particularly obvious in Fig. 17(a), where there is a significant deviation at higher concentrations. Note all plots in Fig. 17 use an x-axis of 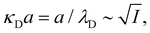 i.e., it is proportional to the ionic strength and increases with ionic concentration. In all cases a is the diameter of the particle (sometimes d is used instead of a to denote this quantity) and λD = κD−1 is the predicted Debye length (i.e., from eqn (6)). Fig. 17(a) shows that the ratio of the observed screening length divided by the Debye length (λS/λD) for 1
i.e., it is proportional to the ionic strength and increases with ionic concentration. In all cases a is the diameter of the particle (sometimes d is used instead of a to denote this quantity) and λD = κD−1 is the predicted Debye length (i.e., from eqn (6)). Fig. 17(a) shows that the ratio of the observed screening length divided by the Debye length (λS/λD) for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 aqueous electrolytes, pure room temperature ionic liquids (RTILs) and diluted ionic liquids (ILs) in PC, appear to collapse onto a single line at values of κDa ≥ 1. The authors put forward the following relationship to fit the observation,
1 aqueous electrolytes, pure room temperature ionic liquids (RTILs) and diluted ionic liquids (ILs) in PC, appear to collapse onto a single line at values of κDa ≥ 1. The authors put forward the following relationship to fit the observation,
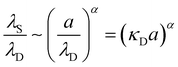 | (12) |
| λS ∼ ciona3λB | (13) |
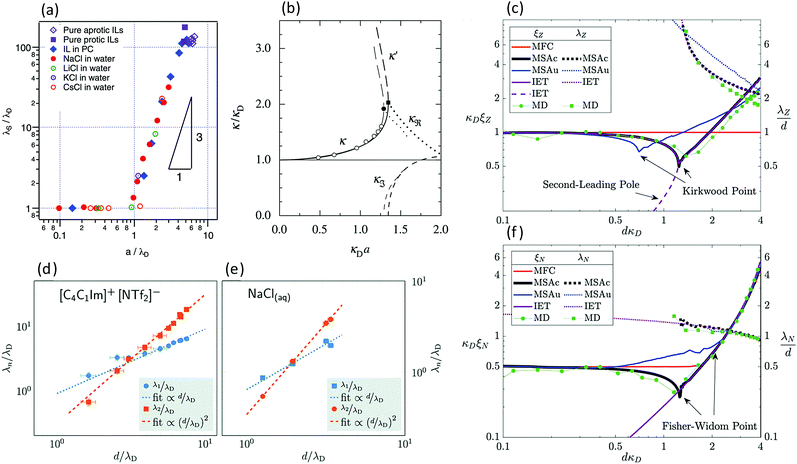 | ||
Fig. 17 Plots of various phenomena as the concentration (i.e., ionic strength) is increased. For all plots, the x-axis is given in units of 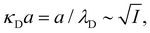 where I is the ionic strength, hence it is a measure of concentration when a is constant. (a) Experimentally measured screening of a selection of pure ILs, an IL dissolved in PC and several 1 where I is the ionic strength, hence it is a measure of concentration when a is constant. (a) Experimentally measured screening of a selection of pure ILs, an IL dissolved in PC and several 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 inorganic salts in water. (b) The behaviour of eqn (15) (thick curves) for a 1 1 inorganic salts in water. (b) The behaviour of eqn (15) (thick curves) for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 aqueous electrolyte solution at room temperature (also valid for a classical 1 1 aqueous electrolyte solution at room temperature (also valid for a classical 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 plasma in vacuum at T = 23 1 plasma in vacuum at T = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 K, showing the convergence of two solutions with decay parameters κ and κ′ to the Kirkwood point (filled symbols), at which they merge into complex conjugates. The thin curves are hypernetted-chain (HNC) results from Ennis et al.303 and open symbols are Monte Carlo (MC) simulation results from Ulander et al.304 (c) The charge decay length (ξZ, solid lines) and the wavelength (λZ, dotted lines) for several models as well as MD results, showing the rough agreement of the Kirkwood point and the scaling behaviour at higher concentrations. (d) The scaling behaviour from MD simulations indicating the presence of two decay lengths with exponents α = 1 and α = 2. (e) Similarly, but for aqueous NaCl. (f) Similar to (c) except for the number decay length (ξN) and number wavelength (λN), indicating the Fisher–Widom point. For (a), (b), (d), (e) the y-axis is in units of κ/κD = λ/λD which is the ratio of the observed screening length compared to the screening length predicted by the Debye–Hückel equation. (a) Reproduced from ref. 285 with permission from the American Physical Society, copyright 2018. (b) Reproduced from ref. 305 with permission from the Royal Society of Chemistry, copyright 2020. (c and f) Reprinted from ref. 306, with permission from AIP Publishing, copyright 2021 (d) and (e) reproduced from ref. 307 with permission from the Royal Society of Chemistry, copyright 2021 and 2020 respectively. 400 K, showing the convergence of two solutions with decay parameters κ and κ′ to the Kirkwood point (filled symbols), at which they merge into complex conjugates. The thin curves are hypernetted-chain (HNC) results from Ennis et al.303 and open symbols are Monte Carlo (MC) simulation results from Ulander et al.304 (c) The charge decay length (ξZ, solid lines) and the wavelength (λZ, dotted lines) for several models as well as MD results, showing the rough agreement of the Kirkwood point and the scaling behaviour at higher concentrations. (d) The scaling behaviour from MD simulations indicating the presence of two decay lengths with exponents α = 1 and α = 2. (e) Similarly, but for aqueous NaCl. (f) Similar to (c) except for the number decay length (ξN) and number wavelength (λN), indicating the Fisher–Widom point. For (a), (b), (d), (e) the y-axis is in units of κ/κD = λ/λD which is the ratio of the observed screening length compared to the screening length predicted by the Debye–Hückel equation. (a) Reproduced from ref. 285 with permission from the American Physical Society, copyright 2018. (b) Reproduced from ref. 305 with permission from the Royal Society of Chemistry, copyright 2020. (c and f) Reprinted from ref. 306, with permission from AIP Publishing, copyright 2021 (d) and (e) reproduced from ref. 307 with permission from the Royal Society of Chemistry, copyright 2021 and 2020 respectively. | ||
Statistical mechanics predicts a change in the screening behaviour when the Debye length is of the order of the ion size. Kirkwood308 showed that there is a crossover point where the screening behaviour would change from pure exponential decay to a damped oscillatory decay, and Lee et al.299 showed that it occurs at approximately 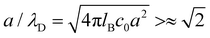 . This oscillatory decay has the functional form,
. This oscillatory decay has the functional form,
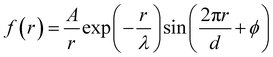 | (14) |
Subsequent theoretical and computational work has also been unable to obtain the α = 3 scaling that is observed experimentally.307,319–325 The exact contributing factors leading to the scaling behaviour are still unknown, with suggestions of the omission of polarisation306 as well as ion-pairing and/or clustering319–321 being important, with the full dissociation of “strong” 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes above 0.5 M being questionable (Section 2.3.5).326,327 However the degree and nature of such clustering and pairing is still debated. As was shown by Gebbie et al.298 and more recently by Liu et al.,279 most of the ions in the solution would need to be paired in order to get such a screening length if ion-pairing were the only explanation. Predicted electrical double-layer capacitance for such a high degree of ion pairing was also qualitatively different from experiment.328
1 electrolytes above 0.5 M being questionable (Section 2.3.5).326,327 However the degree and nature of such clustering and pairing is still debated. As was shown by Gebbie et al.298 and more recently by Liu et al.,279 most of the ions in the solution would need to be paired in order to get such a screening length if ion-pairing were the only explanation. Predicted electrical double-layer capacitance for such a high degree of ion pairing was also qualitatively different from experiment.328
Kjellander has shown that, in contrast to DH and PB theory, if all the ions are treated on the same basis, the screening decay length is different from the Debye length.284,314,329 The behaviour of the screening length can be observed by solving,
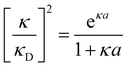 | (15) |
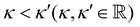 . The behaviour of these two solutions is shown in Fig. 17(b). When κDa is increased (i.e., as concentration is increased), the two solutions approach each other and merge to become complex conjugates,
. The behaviour of these two solutions is shown in Fig. 17(b). When κDa is increased (i.e., as concentration is increased), the two solutions approach each other and merge to become complex conjugates,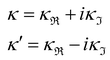 | (16) |
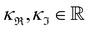 . This corresponds to the Kirkwood point and indicates the onset of an exponentially oscillating decay behaviour, where
. This corresponds to the Kirkwood point and indicates the onset of an exponentially oscillating decay behaviour, where  and
and  are related to the λ and d terms in eqn (14). Kjellander also derived an exact statistical mechanical result for the screening length, given by,
are related to the λ and d terms in eqn (14). Kjellander also derived an exact statistical mechanical result for the screening length, given by,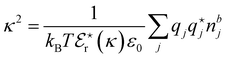 | (17) |
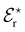 is the dielectric factor (see Kjellander284 for details), and
is the dielectric factor (see Kjellander284 for details), and 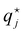 is the dressed particle charge (i.e., a renormalised charge) on ion j and nbj is the number density of j ions in the bulk phase. While this is an exact result, calculation of
is the dressed particle charge (i.e., a renormalised charge) on ion j and nbj is the number density of j ions in the bulk phase. While this is an exact result, calculation of 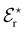 and
and 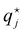 are unknown quantities. However, the modification of the charge to an effective charge is due to the presence of other ions in the solution, which will have correlated behaviour. Hence the electrostatics are highly non-local312 and points to a significant reason why the DH theory breaks down. Furthermore, this treatment also captures ion–ion correlations with the inclusion of ion-pairing (i.e. CIP, SIP, SSIP, clusters) as just highly correlated ions. The permittivity term,
are unknown quantities. However, the modification of the charge to an effective charge is due to the presence of other ions in the solution, which will have correlated behaviour. Hence the electrostatics are highly non-local312 and points to a significant reason why the DH theory breaks down. Furthermore, this treatment also captures ion–ion correlations with the inclusion of ion-pairing (i.e. CIP, SIP, SSIP, clusters) as just highly correlated ions. The permittivity term,  , is a quantity that depends on the presence of ions and also takes into account the granular nature of the solvent. Both of these terms will be specific to both the solvent and the ions that are involved.
, is a quantity that depends on the presence of ions and also takes into account the granular nature of the solvent. Both of these terms will be specific to both the solvent and the ions that are involved.
The above equations also permit more than two solutions for κ, which would lead to a linear combination of exponential and/or oscillatory exponential decays, as shown recently by Kjellander.305 This was hinted at by work by Keblinski et al.,330 and more recently Zeman et al.307 also examined this possibility and fitted simulation data of the potential of mean force with multiple functions similar to the one given by eqn (14). They found scaling relationships with α = 1 and α = 2 for two of the terms that they used to fit their simulation data for the diluted IL and for aqueous NaCl (Fig. 17(d) and (e)).
The addition of extra decay lengths increases the accuracy of the DH model (see Fig. 18).305 The term with the smallest decay parameter (largest wavelength) is the one that dominates the behaviour at long range. Recently it has been suggested that a modified Poisson–Boltzmann model may aid in explaining large experimental decay lengths.331
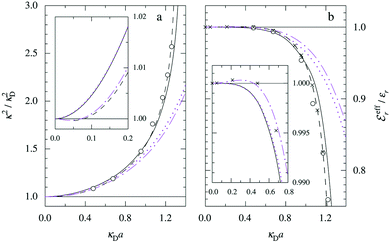 | ||
Fig. 18 The ratios (a) κ2/κD2 and (b)  plotted as functions of plotted as functions of 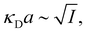 where I is the ionic strength, for monovalent electrolytes in aqueous solution at room temperature. The inset shows the behaviour at low κDa. The dot-dashed curves are from the extended exponential DH approximation (EDHX), dotted curves from the Attard's self-consistent screening length approximation (SCSL).318 The full curves are from the simple multiple-decay extended Debye–Hückel (MDE-DH) approximation, while the dashed curves and crosses show results from HNC calculations, and open circles are from MC simulations. The HNC and MC data are taken from work by Ulander304 and Ennis.303 Reproduced from ref. 305 with permission from the Royal Society of Chemistry, copyright 2020. where I is the ionic strength, for monovalent electrolytes in aqueous solution at room temperature. The inset shows the behaviour at low κDa. The dot-dashed curves are from the extended exponential DH approximation (EDHX), dotted curves from the Attard's self-consistent screening length approximation (SCSL).318 The full curves are from the simple multiple-decay extended Debye–Hückel (MDE-DH) approximation, while the dashed curves and crosses show results from HNC calculations, and open circles are from MC simulations. The HNC and MC data are taken from work by Ulander304 and Ennis.303 Reproduced from ref. 305 with permission from the Royal Society of Chemistry, copyright 2020. | ||
Salt concentration has long been recognised as a significant factor in the study of SIE. There is much more to discuss regarding SIEs at high concentration and the so-called “4th evolution of ionic liquids”332 shows there is much still to be understood about ion concentration effects in both aqueous and nonaqueous solvents. The original precipitation experiments performed by Lewith and Hofmeister required significant salt concentrations.32 Many modern studies of SIE's have also performed using high salt concentrations, leading to a prevailing assumption that SIEs are only largely relevant observed in concentrated electrolytes. In this respect it is important to highlight the study of Mazzini and Craig, who demonstrated that SIEs are observed on standard molar volumes of infinitely dilute electrolyte solutions.42 Nevertheless, in concentrated solutions, the ion size, its interaction with the other ions and the solvent and the decay lengths of the electrostatics are ion specific. There is no reason to suppose that this supplants other SIEs observed in concentrated electrolytes, and it is conceivable that ion specificity in general are the result of multiple factors (we have discussed concentration-induced SIE reversals further in Section 3.1). However, the empirical relationship of eqn (12) still lacks explanation and has mostly been explored for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes, hence the impact of ion valency on these phenomena remains to be explored. We note that the re-entrant solubility of polyelectrolytes at high salt concentrations has been attributed to the extended electrostatic decay length,279 the implication being that higher valency ions induce a departure in the electrostatic decay length from the Debye length at significantly lower concentrations than those expected from eqn (12).
1 electrolytes, hence the impact of ion valency on these phenomena remains to be explored. We note that the re-entrant solubility of polyelectrolytes at high salt concentrations has been attributed to the extended electrostatic decay length,279 the implication being that higher valency ions induce a departure in the electrostatic decay length from the Debye length at significantly lower concentrations than those expected from eqn (12).
The implications of the ion specificity of the extended electrostatic decay length at high salt are indeed broad, as they will likely influence any solution with a high ionic strength, including nonaqueous solutions (Section 6), deep eutectic solvents,333 and ionic liquids.334–339 Thus, one would expect that these SIE's are manifest in fields as diverse as crystallisation,340,341 the packing of DNA,342,343 the colloidal stability of particles,74,282,283 battery and supercapacitor technologies7,258,262,264,267,344,345 and self-assembly.72,344,346 In many cases this will result in re-entrant behaviour, that is the stability or properties of a system reverting to a state that is seen at low salt concentrations.279
8. Conclusions & outlook
There have been significant contributions to our knowledge of SIEs in recent years. The Hofmeister series itself has been quantified for anions128 based solely the ionic radial charge density (Section 2.3.3) and insight into the governing intermolecular forces in SIEs has advanced more generally.128,130,131 Mechanisms underpinning SIEs, particularly regarding the influence of cations on polymer systems, continue to be elucidated.38,45,161–163 Circumstances where SIEs either deviate from the traditional Hofmeister series or undergo complete reversals (Section 3) are becoming more extensively understood. In particular, it is now known that SIEs can be perturbed by stimuli such as solvent,43,128 temperature192,193 and UV radiation,191 in addition to the more well established changes induced by concentration,25,172,177 pH,172,174,176,194 cosolute33,178–183 and counterion.44,45,185–187 By contrast, the behaviour of ions at surfaces (Section 4) are still poorly understood, in part due to experimental techniques’ inability to delineate the individual effects of cations and anions near the interface. However, techniques such as NLO195,221,222 and NICISS213,216–220 are beginning to overcome this barrier (Table S1, ESI†), as are theoretical and computational approaches. The understanding of mixed salt SIE systems, relevant for biological and industrial applications (Section 5), has also developed recently, specifically regarding the additivity (or lack-there-of) of co-dissolved anions.160,249,250 Direct investigations of SIE in nonaqueous environments (Section 6) constitute a new frontier for the field,24,27,39–45,128,169,244,251–255,257–265 and in doing so are generalising our understanding of SIEs and their underlying mechanisms. Similarly, a new category of SIE observed in concentrated electrolytes (Section 7) has been shown to facilitate re-entrant behaviour in polyelectrolyte279–281 and colloidal systems.74,282,283Despite these advances, the ubiquity of SIEs means there is still much to be uncovered and understood. We believe the following avenues of research may help overcome the remaining challenges for understanding and predicting SIEs:
Ab initio solvent and solute properties
A multitude of factors are required for predicting an ion's behaviour in any solution (Fig. 3), given the susceptibility of SIEs to changes in the solvent or cosolute(s). Therefore, in addition to the ion's properties (Section 2.3), those of the solvent and any cosolute(s) must be considered explicitly for SIEs to be predicted. In this respect, the static relative permittivity (εr) is prevalent in established electrolyte theories (Sections 2 and 7). This parameter encompasses both positive and negative dipoles of the solution medium, and while this implies an ability to simultaneously account for cation and anion solvation, there is limited relation on relevant properties (e.g. salt solubility Fig. S2, ESI†), since it does not describe explicitly the distribution of charges in an electrolyte solution. The adjusted permittivity term,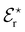 , proposed by Kjellander284 possibly overcomes these limitations, as it is an ion specific term that accounts for the bulk molecular structure of the solvent. However, it is currently an unknown quantity. Alternate solvent properties (Section 6) relating to the Lewis acidity (AN) and basicity (DN) appear relevant to the magnitude of observed SIE. It is tempting to use these to predict the potential point of reversal behaviour (Sections 3 and 6), or if salting-in or -out effects occur. However, this is generally not possible – their empirical nature limits their utility and transferability. Elucidation of solvent properties that can simultaneously account for SIE and be incorporated into generalised electrolyte theories (εr) is therefore a key requirement for a general predictive theory for SIE. Ideally, such properties would be identified in the absence of solutes, particularly considering that reliably quantifying even the most fundamental of electrolyte properties (e.g. the solubility of a salt in a solvent) remains problematic. While resolving this issue is critical for more complex SIEs to be elucidated, understanding and predicting solvent structure and properties ab initio will be a key approach in future. While modified Poisson–Boltzmann models can successfully explain ion behaviour in various surface208 and high concentration331 phenomena, we think that extending these models to include site-specific charges128 (Section 2.3.3) could also provide a basis for the elusive predictive theory of specific ion effects.
, proposed by Kjellander284 possibly overcomes these limitations, as it is an ion specific term that accounts for the bulk molecular structure of the solvent. However, it is currently an unknown quantity. Alternate solvent properties (Section 6) relating to the Lewis acidity (AN) and basicity (DN) appear relevant to the magnitude of observed SIE. It is tempting to use these to predict the potential point of reversal behaviour (Sections 3 and 6), or if salting-in or -out effects occur. However, this is generally not possible – their empirical nature limits their utility and transferability. Elucidation of solvent properties that can simultaneously account for SIE and be incorporated into generalised electrolyte theories (εr) is therefore a key requirement for a general predictive theory for SIE. Ideally, such properties would be identified in the absence of solutes, particularly considering that reliably quantifying even the most fundamental of electrolyte properties (e.g. the solubility of a salt in a solvent) remains problematic. While resolving this issue is critical for more complex SIEs to be elucidated, understanding and predicting solvent structure and properties ab initio will be a key approach in future. While modified Poisson–Boltzmann models can successfully explain ion behaviour in various surface208 and high concentration331 phenomena, we think that extending these models to include site-specific charges128 (Section 2.3.3) could also provide a basis for the elusive predictive theory of specific ion effects.
Interfacial structure
Interfacial structure and concentration in electrolyte solutions are critical for myriad chemical and biological processes, such as enzyme and protein structure and electrochemical interfaces. Next-generation electrochemical devices can more readily be realised through optimisation of the electrode interface, and in this respect the adsorption/desorption of electrolyte is the critical phenomenon. A more detailed understanding of SIEs at interfaces will also inform bulk behaviour, and the origins of non-Hofmeister ion specificity (such as those observed in bubble-bubble interactions347). In these contexts, nonaqueous solvents are of particular importance. The complete elucidation of these phenomena requires pairing elementally-resolved techniques (e.g. NICISS) and computational simulation towards answering the following questions:i. What (accumulation/depletion) trend do ions follow at aqueous and nonaqueous solvent surfaces?
ii. How does the solvent identity affect these specific ion trends?
iii. What role do counterions (Section 3.3) have on the specific ion adsorption of individual ions?
Beyond mixed salt solutions
Studying SIEs in mixed salt solutions presents challenging test cases for any prospective SIE theory. A natural extension to mixed salt systems are buffered solutions, such as those relevant to SIE in biological systems.53,175,348–350 In addition to their roles in modulating pH, buffers compete with co-existing “Hofmeister ions” to influence, both cooperatively and independently, enzyme activities, electrophoretic mobilities, antibody aggregation and protein thermal stability. The screening and competitive behaviour of buffers has recently been modelled, showing the importance of ionic strength in this respect.351 The fact that mixed salt effects have also been studied in polyelectrolytes352,353 and neutral polymer solutions (Section 5) presents alternative opportunities for studying SIEs via ionic surfactants, which are already known to influence mesophase behaviour in mixed salt-surfactant systems in an ion-specific way.354,355 Ionic surfactants also enable systematic investigation and manipulation of SIEs, for instance by using a constant charge group with increasing aliphatic tail length (i.e. in order to maintain a constant Coulombic interaction between the surfactant and the solvent, while varying non-Coulombic effects).356 Such approaches would be assisted by the fact that properties of ionic surfactant solutions (e.g., critical micelle concentration, surface tension etc.) can be readily measured to assess SIE's without requiring additional cosolutes. This also provides an additional approach to investigating specific counterion effects and SIEs in mixed salt solutions.357High salt concentrations
The ion specific re-entrant behaviour of polyelectrolyte solutions at high concentrations have recently been highlighted.279 The mechanistic understanding of such behaviour is still limited however. There remain inconsistencies between experimental observation and theory (particularly with respects to electrostatic underscreening, Section 7). Atomistic simulation of bulk structure provides the most direct means forward for elucidating the driving forces behind this non-monotonic behaviour. Notably, simulation would enable the investigation of supersaturated regimes beyond what is experimentally accessible. In this respect, SIEs in ionic liquids provide an alternate avenue for exploring SIEs at high salt concentrations (Section 7), but also one that enables counterion effects to be negated (for instance, by matching one of the ions comprising the salt with the ions in the IL).Non-Coulombic effects
Coulombic interactions between ions, cosolutes and solvents play a significant role in SIEs, particularly for charge dense anions.45,128,133 For larger, charge diffuse ions however, and/or more polarisable solvents/cosolutes, these Coulombic interactions weaken, relative to competing non-covalent interactions (viz. dispersion, induction, exchange repulsion etc.). This is most obvious in long-chain tertiary ammonium salts, tetraphenyl borates, phosphonium or arsonium (Section 2.3.2). Whilst the electrostatic contributions of “Hofmeister ions” have largely been quantified and parameterised,128 these non-Coulombic phenomena require further attention, as under certain circumstances they possibly account for SIE anomalies and reversals in general (Section 3). Indeed, compelling evidence of SIE understanding coming to maturity would be the ability to “turn off” or quench SIE by balancing these competing forces, via strategies such as surface functionalisation,184 solution composition, solvent, counterion, etc.Data science approaches
The SIE field is somewhat unusual, in that data science and machine learning approaches have made relatively few in-roads to date (compared to some other fields). This is arguably because such approaches require large, accurate and consistent data sets, for instance, describing the ion solvation structure in aqueous and non-aqueous solvents. The recent development of data resources148,256 to specifically address this issue therefore opens up exciting new opportunities for the field, relating to machine learning and deep learning approaches.Author contributions
K. P. G drafted Sections 1–3, 6, and 8 and reviewed and edited the entire manuscript. G. R. E. drafted Section 7 and reviewed the entire manuscript. H. R. drafted Section 5 and reviewed the entire manuscript. A. K. drafted Section 4. V. S. J. C. drafted Section 2.3.4. E. J. W., G. B. W., V. S. J. C and A. J. P. reviewed and edited the manuscript and acquired funding. G. G. A. reviewed Section 4 and acquired funding.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge Dr Saeed Moghaddam and Prof. Esben Thormann for providing data. A. J. P., G. B. W., E. J. W., V. S. J. C. and G. G. A. acknowledge Australian Research Council funding (ARC DP190100788). K. P. G. and H. R. acknowledge an Australian Government Research Training Program (RTP) Scholarship. H. R. would like to thank AINSE Ltd for providing financial assistance (Post Graduate Research Award). A. K. would like to acknowledge Flinders University for providing financial support through Flinders University International Tuition Fee Sponsorship and Australian Research Council (ARC DP190100788) for funding the HDR Scholarship.Notes and references
- S. Lee and M. Elimelech, Salt cleaning of organic-fouled reverse osmosis membranes, Water Res., 2007, 41, 1134–1142 CrossRef CAS PubMed.
- H. Lee, S. J. Im, H. Lee, C. M. Kim and A. Jang, Comparative analysis of salt cleaning and osmotic backwash on calcium-bridged organic fouling in nanofiltration process, Desalination, 2021, 507, 115022 CrossRef CAS.
- B. Zhang, X. Wang and X. Jia, Research on the mechanism of molten salt cleaning (MSC) for multiple contaminants in cylinder covers, J. Cleaner Prod., 2021, 302, 126990 CrossRef CAS.
- X. Wang, J. Li, L. Wang, X. Jia, M. Hong, Y. Ren and M. Ma, A novel de-rusting method with molten salt precleaning and laser cleaning for the recycling of steel parts, Clean Technol. Environ. Policy, 2021, 23, 1403–1414 CrossRef CAS.
- S. Madeswaran and S. Jayachandran, Sodium bicarbonate: a review and its uses in dentistry, Indian, J. Dent. Res., 2018, 29, 672–677 Search PubMed.
- N. K. Fageria, M. P.-B. Filho, A. Moreira and C. M. Guimarães, Foliar Fertilization of Crop Plants, J. Plant Nutr., 2009, 32, 1044–1064 CrossRef CAS.
- A. Eftekhari, Potassium secondary cell based on Prussian blue cathode, J. Power Sources, 2004, 126, 221–228 CrossRef CAS.
- K. Xu, Electrolytes and interphases in Li-ion batteries and beyond, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- D. Aurbach, Y. Talyosef, B. Markovsky, E. Markevich, E. Zinigrad, L. Asraf, J. S. Gnanaraj and H.-J. Kim, Design of electrolyte solutions for Li and Li-ion batteries: a review, Electrochim. Acta, 2004, 50, 247–254 CrossRef CAS.
- S. Li, H. Li, F. N. Hu, X. R. Huang, D. T. Xie and J. P. Ni, Effects of strong ionic polarization in the soil electric field on soil particle transport during rainfall, Eur, J. Soil Sci., 2015, 66, 921–929 CrossRef CAS.
- W. Ding, X. Liu, F. Hu, H. Zhu, Y. Luo, S. Li and H. Li, How the particle interaction forces determine soil water infiltration: specific ion effects, J. Hydrol., 2019, 568, 492–500 CrossRef CAS.
- S. Wu, C. Zhu, Z. He, H. Xue, Q. Fan, Y. Song, J. S. Francisco, X. C. Zeng and J. Wang, Ion-specific ice recrystallization provides a facile approach for the fabrication of porous materials, Nat. Commun., 2017, 8, 15154 CrossRef PubMed.
- V. S.-J. Craig, B. W. Ninham and R. M. Pashley, Effect of electrolytes on bubble coalescence, Nature, 1993, 364, 317–319 CrossRef CAS.
- C. L. Henry and V. S.-J. Craig, The Link between Ion Specific Bubble Coalescence and Hofmeister Effects Is the Partitioning of Ions within the Interface, Langmuir, 2010, 26, 6478–6483 CrossRef CAS PubMed.
- R. Tian, X. Liu, X. Gao, R. Li and H. Li, Observation of specific ion effects in humus aggregation process, Pedosphere, 2021, 31, 736–745 CrossRef.
- J. C. Warren and S. G. Cheatum, Effect of Neutral Salts on Enzyme Activity and Structure*, Biochemistry, 1966, 5, 1702–1707 CrossRef CAS PubMed.
- M. Hayashi, T. Unemoto and M. Hayashi, pH- and anion-dependent salt modifications of alkaline phosphatase from a slightly halophilic Vibrio alginolyticus, Biochim. Biophys. Acta, Enzymol., 1973, 315, 83–93 CrossRef CAS.
- V. Štěpánková, J. Paterová, J. Damborský, P. Jungwirth, R. Chaloupková and J. Heyda, Cation-Specific Effects on Enzymatic Catalysis Driven by Interactions at the Tunnel Mouth, J. Phys. Chem. B, 2013, 117, 6394 CrossRef PubMed.
- K. Garajová, A. Balogová, E. Dušeková, D. Sedláková, E. Sedlák and R. Varhač, Correlation of lysozyme activity and stability in the presence of Hofmeister series anions, Biochim. Biophys. Acta, Proteins Proteomics, 2017, 1865, 281–288 CrossRef PubMed.
- E. M. Wright and J. M. Diamond, Anion selectivity in biological systems, Physiol. Rev., 1977, 57, 109–156 CrossRef CAS PubMed.
- M. G. Cacace, E. M. Landau and J. J. Ramsden, The Hofmeister Series: Salt and Solvent Effects on Interfacial Phenomena, Q. Rev. Biophys., 1997, 30, 241 CrossRef CAS PubMed.
- Q. M. Wang and R. B. Johnson, Activation of Human Rhinovirus-14 3C Protease, Virology, 2001, 280, 80–86 CrossRef CAS PubMed.
- A. Salis, D. Bilaničová, B. W. Ninham and M. Monduzzi, Hofmeister Effects in Enzymatic Activity: Weak and Strong Electrolyte Influences on the Activity of Candida rugosa Lipase, J. Phys. Chem. B, 2007, 111, 1149 CrossRef CAS PubMed.
- D. Bilaničová, A. Salis, B. W. Ninham and M. Monduzzi, Specific Anion Effects on Enzymatic Activity in Nonaqueous Media, J. Phys. Chem. B, 2008, 112, 12066–12072 CrossRef PubMed.
- Y. Zhang and P. S. Cremer, The inverse and direct Hofmeister series for lysozyme, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15249–15253 CrossRef CAS PubMed.
- C. Carucci, F. Raccis, A. Salis and E. Magner, Specific ion effects on the enzymatic activity of alcohol dehydrogenase from Saccharomyces cerevisiae, Phys. Chem. Chem. Phys., 2020, 22, 6749–6754 RSC.
- M. Collu, C. Carucci and A. Salis, Specific Anion Effects on Lipase Adsorption and Enzymatic Synthesis of Biodiesel in Nonaqueous Media, Langmuir, 2020, 36, 9465–9471 CrossRef CAS PubMed.
- A. Somasundar, S. Ghosh, F. Mohajerani, L. N. Massenburg, T. Yang, P. S. Cremer, D. Velegol and A. Sen, Positive and negative chemotaxis of enzyme-coated liposome motors, Nat. Nanotechnol., 2019, 14, 1129–1134 CrossRef CAS PubMed.
- P. Lo Nostro and B. W. Ninham, Hofmeister phenomena: an update on ion specificity in biology, Chem. Rev., 2012, 112, 2286–2322 CrossRef CAS PubMed.
- J. Del Coso, E. Estevez, R. A. Baquero and R. Mora-Rodriguez, Anaerobic performance when rehydrating with water or commercially available sports drinks during prolonged exercise in the heat, Appl. Physiol. Nutr. Metab., 2008, 33, 290–298 CrossRef PubMed.
- F. Hofmeister, Zur Lehre Von Der Wirkung Der Salze, Naunyn-Schmiedeberg's Arch. Pharmacol., 1888, 24, 247 Search PubMed.
- W. Kunz, J. Henle and B. W. Ninham, ‘Zur Lehre von der Wirkung der Salze’ (about the science of the effect of salts): Franz Hofmeister's historical papers, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37 CrossRef CAS.
- H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, Beyond the Hofmeister Series: Ion-Specific Effects on Proteins and Their Biological Functions, J. Phys. Chem. B, 2017, 121, 1997–2014 CrossRef CAS PubMed.
- Y. J. Zhang, S. Furyk, D. E. Bergbreiter and P. S. Cremer, Specific Ion Effects on the Water Solubility of Macromolecules: PNIPAM and the Hofmeister Series, J. Am. Chem. Soc., 2005, 127, 14505 CrossRef CAS PubMed.
- T. J. Murdoch, B. A. Humphreys, J. D. Willott, K. P. Gregory, S. W. Prescott, A. Nelson, E. J. Wanless and G. B. Webber, Specific Anion Effects on the Internal Structure of a Poly(N-isopropylacrylamide) Brush, Macromolecules, 2016, 49, 6050–6060 CrossRef CAS.
- B. A. Humphreys, J. D. Willott, T. J. Murdoch, G. B. Webber and E. J. Wanless, Specific ion modulated thermoresponse of poly(N-isopropylacrylamide) brushes, Phys. Chem. Chem. Phys., 2016, 18, 6037–6046 RSC.
- T. J. Murdoch, B. A. Humphreys, E. C. Johnson, G. B. Webber and E. J. Wanless, Specific ion effects on thermoresponsive polymer brushes: comparison to other architectures, J. Colloid Interface Sci., 2018, 526, 429–450 CrossRef CAS PubMed.
- B. A. Humphreys, E. J. Wanless and G. B. Webber, Effect of ionic strength and salt identity on poly(N-isopropylacrylamide) brush modified colloidal silica particles, J. Colloid Interface Sci., 2018, 516, 153–161 CrossRef CAS PubMed.
- N. Peruzzi, B. W. Ninham, P. Lo Nostro and P. Baglioni, Hofmeister Phenomena in Nonaqueous Media: The Solubility of Electrolytes in Ethylene Carbonate, J. Phys. Chem. B, 2012, 116, 14398–14405 CrossRef CAS PubMed.
- L. Liu, T. Wang, C. Liu, K. Lin, G. Liu and G. Zhang, Specific Anion Effect in Water–Nonaqueous Solvent Mixtures: Interplay of the Interactions between Anion, Solvent, and Polymer, J. Phys. Chem. B, 2013, 117, 10936–10943 CrossRef CAS PubMed.
- V. Mazzini and V. S. J. Craig, Specific-ion effects in non-aqueous systems, Curr. Opin. Colloid Interface Sci., 2016, 23, 82–93, DOI:10.1016/j.cocis.2016.06.009.
- V. Mazzini and V. S.-J. Craig, What is the fundamental ion-specific series for anions and cations? Ion specificity in standard partial molar volumes of electrolytes and electrostriction in water and non-aqueous solvents, Chem. Sci., 2017, 8, 7052–7065 RSC.
- V. Mazzini, G. Liu and V. S.-J. Craig, Probing the Hofmeister series beyond water: specific-ion effects in non-aqueous solvents, J. Chem. Phys., 2018, 148, 222805 CrossRef PubMed.
- V. Mazzini and V. S.-J. Craig, Volcano Plots Emerge from a Sea of Nonaqueous Solvents: The Law of Matching Water Affinities Extends to All Solvents, ACS Cent. Sci., 2018, 4, 1056–1064 CrossRef CAS PubMed.
- K. P. Gregory, G. B. Webber, E. J. Wanless and A. J. Page, Lewis Strength Determines Specific-Ion Effects in Aqueous and Nonaqueous Solvents, J. Phys. Chem. A, 2019, 123, 6420–6429 CrossRef CAS PubMed.
- A. Voet, Quantative lyotropy, Chem. Rev., 1937, 20, 169 CrossRef CAS.
- V. Mazzini and V. S. J. Craig, Corrigendum to “Specific-ion Effects in Non-Aqueous Systems”, Curr. Opin. Colloid Interface Sci., 2018, 38, 214–222 CrossRef CAS.
- R. G. Pearson, Hard and soft acids and bases, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- A. Serr and R. R. Netz, Polarizabilities of hydrated and free ions derived from DFT calculations, Int. J. Quantum Chem., 2006, 106, 2960–2974 CrossRef CAS.
- T. Zemb, L. Belloni, M. Dubois, A. Aroti and E. Leontidis, Can we use area per surfactant as a quantitative test model of specific ion effects?, Curr. Opin. Colloid Interface Sci., 2004, 9, 74–80 CrossRef CAS.
- A. P. dos Santos, A. Diehl and Y. Levin, Surface Tensions, Surface Potentials, and the Hofmeister Series of Electrolyte Solutions, Langmuir, 2010, 26, 10778–10783 CrossRef CAS PubMed.
- K. Wojciechowski, A. Bitner, P. Warszyński and M. Żubrowska, The Hofmeister effect in zeta potentials of CTAB-stabilised toluene-in-water emulsions, Colloids Surf., A, 2011, 376, 122–126 CrossRef CAS.
- F. Cugia, S. Sedda, F. Pitzalis, D. F. Parsons, M. Monduzzi and A. Salis, Are specific buffer effects the new frontier of Hofmeister phenomena? Insights from lysozyme adsorption on ordered mesoporous silica, RSC Adv., 2016, 6, 94617–94621 RSC.
- J. Heyda and J. Dzubiella, Thermodynamic Description of Hofmeister Effects on the LCST of Thermosensitive Polymers, J. Phys. Chem. B, 2014, 118, 10979 CrossRef CAS PubMed.
- I. Shechter, O. Ramon, I. Portnaya, Y. Paz and Y. D. Livney, Microcalorimetric Study of the Effects of a Chaotropic Salt, Kscn, on the Lower Critical Solution Temperature (LCST) of Aqueous Poly(N-Isopropylacrylamide) (PNIPA) Solutions, Macromolecules, 2010, 43, 480 CrossRef CAS.
- Y. Zhang, S. Furyk, L. B. Sagle, Y. Cho, D. E. Bergbreiter and P. S. Cremer, Effects of Hofmeister Anions on the LCST of PNIPAM as a Function of Molecular Weight, J. Phys. Chem. C, 2007, 111, 8916 CrossRef CAS PubMed.
- K. D. Collins, Ions from the Hofmeister series and osmolytes: effects on proteins in solution and in the crystallization process, Methods, 2004, 34, 300–311 CrossRef CAS PubMed.
- M. Boström, D. R.-M. Williams, P. R. Stewart and B. W. Ninham, Hofmeister effects in membrane biology: the role of ionic dispersion potentials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 41902 CrossRef PubMed.
- A. P. Davis, D. N. Sheppard and B. D. Smith, Development of synthetic membrane transporters for anions, Chem. Soc. Rev., 2007, 36, 348–357 RSC.
- B. W. Ninham and V. Yaminsky, Ion Binding and Ion Specificity:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The Hofmeister Effect and Onsager and Lifshitz Theories, Langmuir, 1997, 13, 2097–2108 CrossRef CAS.
The Hofmeister Effect and Onsager and Lifshitz Theories, Langmuir, 1997, 13, 2097–2108 CrossRef CAS. - M. Boström, F. W. Tavares, S. Finet, F. Skouri-Panet, A. Tardieu and B. W. Ninham, Why forces between proteins follow different Hofmeister series for pH above and below pI, Biophys. Chem., 2005, 117, 217–224 CrossRef PubMed.
- L. Abezgauz, K. Kuperkar, P. A. Hassan, O. Ramon, P. Bahadur and D. Danino, Effect of Hofmeister anions on micellization and micellar growth of the surfactant cetylpyridinium chloride, J. Colloid Interface Sci., 2010, 342, 83–92 CrossRef CAS PubMed.
- W. M. Cox and J. H. Wolfenden, Viscosity of Strong Electrolytes Measured by a Differential Method, Proc. R. Soc. London, Ser. A, 1934, 145, 475 CAS.
- G. Jones and M. Dole, The Viscosity of Aqueous Solutions of Strong Electrolytes with Special Reference to Barium Chloride, J. Am. Chem. Soc., 1929, 51, 2950–2964 CrossRef CAS.
- A. A. Zavitsas, Properties of Water Solutions of Electrolytes and Nonelectrolytes, J. Phys. Chem. B, 2001, 105, 7805–7817 CrossRef CAS.
- Y. Marcus, Ions in Solution and their Solvation, 2015 Search PubMed.
- G. E. Holm and J. M. Sherman, Salt Effects in Bacterial Growth, J. Bacteriol., 1921, 6, 511–519 CrossRef CAS PubMed.
- P. Lo Nostro, L. Fratoni, B. W. Ninham and P. Baglioni, Water Absorbency by Wool Fibers:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hofmeister Effect, Biomacromolecules, 2002, 3, 1217–1224 CrossRef CAS PubMed.
Hofmeister Effect, Biomacromolecules, 2002, 3, 1217–1224 CrossRef CAS PubMed. - M. Boström, D. R.-M. Williams and B. W. Ninham, The Influence of Ionic Dispersion Potentials on Counterion Condensation on Polyelectrolytes, J. Phys. Chem. B, 2002, 106, 7908–7912 CrossRef.
- H. P. Gregor and M. Frederick, Potentiometric titration of polyacrylic and polymethacrylic acids with alkali metal and quaternary ammonium bases, J. Polym. Sci., 1957, 23, 451–465 CrossRef CAS.
- A. V. Toktarev and G. V. Echevskii, Hofmeister Anion Effect on the Formation of Zeolite Beta, Stud. Surf. Sci. Catal., 2008, 174, 167–172 CrossRef.
- E. Leontidis, Hofmeister anion effects on surfactant self-assembly and the formation of mesoporous solids, Curr. Opin. Colloid Interface Sci., 2002, 7, 81–91 CrossRef CAS.
- F. Urban, The Influence of Electrolytes on the Specific Heat of Water, J. Phys. Chem., 1931, 36, 1108–1122 CrossRef.
- T. López-León, A. B. Jódar-Reyes, J. L. Ortega-Vinuesa and D. Bastos-González, Hofmeister effects on the colloidal stability of an IgG-coated polystyrene latex, J. Colloid Interface Sci., 2005, 284, 139–148 CrossRef PubMed.
- W. Melander and C. Horváth, Salt effects on hydrophobic interactions in precipitation and chromatography of proteins: an interpretation of the lyotropic series, Arch. Biochem. Biophys., 1977, 183, 200–215 CrossRef CAS PubMed.
- G. Graziano, Salting out of methane by sodium chloride: a scaled particle theory study, J. Chem. Phys., 2008, 129, 84506 CrossRef PubMed.
- A. Pica and G. Graziano, On the effect of sodium salts on the coil-to-globule transition of poly(N-isopropylacrylamide), Phys. Chem. Chem. Phys., 2015, 17, 27750–27757 RSC.
- A. Pica and G. Graziano, Effect of sodium thiocyanate and sodium perchlorate on poly(N-isopropylacrylamide) collapse, Phys. Chem. Chem. Phys., 2020, 22, 189–195 RSC.
- R. L. Baldwin, How Hofmeister Ion Interactions Affect Protein Stability, Biophys. J., 1996, 71, 2056 CrossRef CAS PubMed.
- B. A. Rogers, H. I. Okur, C. Yan, T. Yang, J. Heyda and P. S. Cremer, Weakly hydrated anions bind to polymers but not monomers in aqueous solutions, Nat. Chem., 2022, 14, 40–45 CrossRef CAS PubMed.
- K. D. Collins, Charge Density-Dependent Strength of Hydration and Biological Structure, Biophys. J., 1997, 72, 65 CrossRef CAS PubMed.
- A. Salis and B. W. Ninham, Models and mechanisms of Hofmeister effects in electrolyte solutions, and colloid and protein systems revisited, Chem. Soc. Rev., 2014, 43, 7358–7377 RSC.
- K. D. Collins, G. W. Neilson and J. E. Enderby, Ions in Water: Characterizing the Forces That Control Chemical Processes and Biological Structure, Biophys. Chem., 2007, 128, 95 CrossRef CAS PubMed.
- J. S. Uejio, C. P. Schwartz, A. M. Duffin, W. S. Drisdell, R. C. Cohen and R. J. Saykally, Characterization of Selective Binding of Alkali Cations with Carboxylate by X-Ray Absorption Spectroscopy of Liquid Microjets, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6809 CrossRef CAS PubMed.
- E. F. Aziz, N. Ottosson, S. Eisebitt, W. Eberhardt, B. Jagoda-Cwiklik, R. Vacha, P. Jungwirth and B. Winter, Cation-Specific Interactions with Carboxylate in Amino Acid and Acetate Aqueous Solutions: X-Ray Absorption and Ab Initio Calculations, J. Phys. Chem. B, 2008, 112, 12567 CrossRef CAS PubMed.
- I. Kalcher, D. Horinek, R. R. Netz and J. Dzubiella, Ion Specific Correlations in Bulk and at Biointerfaces, J. Phys.: Condens. Matter, 2009, 21, 424108 CrossRef CAS PubMed.
- B. Hess and N. F.-A. van der Vegt, Cation Specific Binding with Protein Surface Charges, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13296 CrossRef CAS PubMed.
- J. Heyda, T. Hrobarik and P. Jungwirth, Ion-Specific Interactions between Halides and Basic Amino Acids in Water, J. Phys. Chem. A, 2009, 113, 1969 CrossRef CAS PubMed.
- J. Heyda, J. C. Vincent, D. J. Tobias, J. Dzubiella and P. Jungwirth, Ion Specificity at the Peptide Bond: Molecular Dynamics Simulations of N-Methylacetamide in Aqueous Salt Solutions, J. Phys. Chem. B, 2010, 114, 1213 CrossRef CAS PubMed.
- E. A. Algaer and N. F.-A. van der Vegt, Hofmeister Ion Interactions with Model Amide Compounds, J. Phys. Chem. B, 2011, 115, 13781 CrossRef CAS PubMed.
- K. B. Rembert, J. Paterova, J. Heyda, C. Hilty, P. Jungwirth and P. S. Cremer, Molecular Mechanisms of Ion-Specific Effects on Proteins, J. Am. Chem. Soc., 2012, 134, 10039 CrossRef CAS PubMed.
- H. I. Okur, J. Kherb and P. S. Cremer, Cations Bind Only Weakly to Amides in Aqueous Solutions, J. Am. Chem. Soc., 2013, 135, 5062 CrossRef CAS PubMed.
- P. Jungwirth and P. S. Cremer, Beyond Hofmeister, Nat. Chem., 2014, 6, 261 CrossRef CAS PubMed.
- T. O. Street, D. W. Bolen and G. D. Rose, A Molecular Mechanism for Osmolyte-Induced Protein Stability, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13997 CrossRef CAS PubMed.
- L. Vrbka, P. Jungwirth, P. Bauduin, D. Touraud and W. Kunz, Specific Ion Effects at Protein Surfaces: A Molecular Dynamics Study of Bovine Pancreatic Trypsin Inhibitor and Horseradish Peroxidase in Selected Salt Solutions, J. Phys. Chem. B, 2006, 110, 7036 CrossRef CAS PubMed.
- R. M. Leberman and A. M. Soper, Effect of high salt concentrations on water structure, Nature, 1995, 378, 364–366 CrossRef CAS PubMed.
- I. Waluyo, D. Nordlund, U. Bergmann, D. Schlesinger, L. G.-M. Pettersson and A. Nilsson, A different view of structure-making and structure-breaking in alkali halide aqueous solutions through x-ray absorption spectroscopy, J. Chem. Phys., 2014, 140, 244506 CrossRef PubMed.
- A. W. Omta, M. F. Kropman, S. Woutersen and H. J. Bakker, Negligible Effect of Ions on the Hydrogen-Bond Structure in Liquid Water, Science, 2003, 301, 347 CrossRef CAS PubMed.
- S. Funkner, G. Niehues, D. A. Schmidt, M. Heyden, G. Schwaab, K. M. Callahan, D. J. Tobias and M. Havenith, Watching the Low-Frequency Motions in Aqueous Salt Solutions: The Terahertz Vibrational Signatures of Hydrated Ions, J. Am. Chem. Soc., 2012, 134, 1030 CrossRef CAS PubMed.
- G. Stirnemann, E. Wernersson, P. Jungwirth and D. Laage, Mechanisms of Acceleration and Retardation of Water Dynamics by Ions, J. Am. Chem. Soc., 2013, 135, 11824 CrossRef CAS PubMed.
- K. J. Tielrooij, N. Garcia-Araez, M. Bonn and H. J. Bakker, Cooperativity in Ion Hydration, Science, 2010, 328, 1006–1009 CrossRef CAS PubMed.
- V. A. Parsegian, van der Waals Forces: A handbook for biologists, chemists, engineers, and physicists, 2006 Search PubMed.
- A. P. Gaiduk and G. Galli, Local and Global Effects of Dissolved Sodium Chloride on the Structure of Water, J. Phys. Chem. Lett., 2017, 8, 1496–1502 CrossRef CAS PubMed.
- M. F. Kropman and H. J. Bakker, Dynamics of water molecules in aqueous solvation shells, Science, 2001, 291, 2118–2120 CrossRef CAS PubMed.
- H. Dongshuai, L. Zeyu, Z. Peng and D. Qingjun, Molecular structure and dynamics of an aqueous sodium chloride solution in nano-pores between portlandite surfaces: a molecular dynamics study, Phys. Chem. Chem. Phys., 2016, 18, 2059–2069 RSC.
- M. Kelley, A. Donley, S. Clark and A. Clark, Structure and Dynamics of NaCl Ion Pairing in Solutions of Water and Methanol, J. Phys. Chem. B, 2015, 119, 15652–15661 CrossRef CAS PubMed.
- M. Born, Volumen und hydratationswärme der ionen, Zeitschrift für Phys., 1920, 1, 45–48 CrossRef CAS.
- U. Mayer and V. Gutmann, Phenomenological approach to cation-solvent interactions, Structure and Bonding, Springer Berlin Heidelberg, Berlin, Heidelberg, 1972, vol. 12, pp. 113–140 Search PubMed.
- P. Debye and E. Hückel, Debye–Hückel theory of electrolytes, Phys. Z., 1923, 24, 185 CAS.
- B. Derjaguin and L. Landau, Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes, Prog. Surf. Sci., 1993, 43, 30–59 CrossRef.
- E. J.-W. Verwey, Theory of the Stability of Lyophobic Colloids, J. Phys. Colloid Chem., 1947, 51, 631–636 CrossRef CAS PubMed.
- E. J.-W. Verwey and J. T.-G. Overbeek, Theory of the stability of lyophobic colloids, J. Colloid Sci., 1955, 10, 224–225 CrossRef CAS.
- B. W. Ninham, R. M. Pashley and P. Lo Nostro, Surface forces: changing concepts and complexity with dissolved gas, bubbles, salt and heat, Curr. Opin. Colloid Interface Sci., 2017, 27, 25–32 CrossRef CAS.
- G. M. Kontogeorgis, B. Maribo-Mogensen and K. Thomsen, The Debye–Hückel theory and its importance in modeling electrolyte solutions, Fluid Phase Equilib., 2018, 462, 130–152 CrossRef CAS.
- R. H. Stokes and R. A. Robinson, Ionic hydration and activity in electrolyte solutions, J. Am. Chem. Soc., 1948, 70, 1870–1878 CrossRef CAS PubMed.
- E. A. Guggenheim and J. C. Turgeon, Specific interaction of ions, Trans. Faraday Soc., 1955, 51, 747–761 RSC.
- P. Sipos, Application of the Specific Ion Interaction Theory (SIT) for the ionic products of aqueous electrolyte solutions of very high concentrations, J. Mol. Liq., 2008, 143, 13–16 CrossRef CAS.
- K. S. Pitzer, Thermodynamics of electrolytes. I. Theoretical basis and general equations, J. Phys. Chem., 1973, 77, 268–277 CrossRef CAS.
- C. Akilan, T. Chen, T. Vielma, P. M. May, G. Senanayake and G. Hefter, Volumes and Heat Capacities of Cobalt(II), Nickel(II), and Copper(II) Sulfates in Aqueous Solution, J. Chem. Eng. Data, 2020, 65, 4575–4581 CrossRef CAS.
- H. T. Kim and W. J. Frederick, Evaluation of Pitzer Ion Interaction Parameters of Aqueous Electrolytes at 25 °C. 1. Single Salt Parameters, J. Chem. Eng. Data, 1988, 33, 177–184 CrossRef CAS.
- A. Lach, L. André, S. Guignot, C. Christov, P. Henocq and A. Lassin, A Pitzer Parametrization To Predict Solution Properties and Salt Solubility in the H–Na–K–Ca–Mg–NO3–H2O System at 298.15 K, J. Chem. Eng. Data, 2018, 63, 787–800 CrossRef CAS.
- C. F. Weber, Calculation of Pitzer Parameters at High Ionic Strengths, Ind. Eng. Chem. Res., 2000, 39, 4422–4426 CrossRef CAS.
- B. W. Ninham, T. T. Duignan and D. F. Parsons, Approaches to hydration, old and new: insights through Hofmeister effects, Curr. Opin. Colloid Interface Sci., 2011, 16, 612–617 CrossRef CAS.
- W. Kunz, P. L. Nostro, B. W. Ninham, P. Lo Nostro and B. W. Ninham, The present state of affairs with Hofmeister effects, Curr. Opin. Colloid Interface Sci., 2004, 9, 1 CrossRef CAS.
- R. Heyrovska, Physical Electrochemistry of Strong Electrolytes Based on Partial Dissociation and Hydration Quantitative Interpretation of the Thermodynamic Properties of NaCl(aq) from “Zero to Saturation”, J. Electrochem. Soc., 1996, 143, 1789–1793 CrossRef CAS.
- K. D. Collins and M. W. Washabaugh, The Hofmeister Effect and the Behaviour of Water at Interfaces, Q. Rev. Biophys., 1985, 18, 323 CrossRef CAS PubMed.
- J. M. Berg, J. L. Tymoczko, G. J. Gatto. and L. Stryer, Biochemistry, W.H. Freeman & Company, a Macmillan Education Imprint, New York, Eighth edn, 1958.
- K. P. Gregory, E. J. Wanless, G. B. Webber, V. S.-J. Craig and A. J. Page, The electrostatic origins of specific ion effects: quantifying the Hofmeister series for anions, Chem. Sci., 2021, 12, 15007–15015 RSC.
- E. Leontidis, Investigations of the Hofmeister series and other specific ion effects using lipid model systems, Adv. Colloid Interface Sci., 2017, 243, 8–22 CrossRef CAS PubMed.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, Collins's rule, Hofmeister effects and ionic dispersion interactions, Chem. Phys. Lett., 2014, 608, 55–59 CrossRef CAS.
- T. P. Pollard and T. L. Beck, Toward a quantitative theory of Hofmeister phenomena: from quantum effects to thermodynamics, Curr. Opin. Colloid Interface Sci., 2016, 23, 110–118 CrossRef CAS.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, A Continuum Solvent Model of the Multipolar Dispersion Solvation Energy, J. Phys. Chem. B, 2013, 117, 9412–9420 CrossRef CAS PubMed.
- R. Prasanna Misra and D. Blankschtein, Uncovering a Universal Molecular Mechanism of Salt Ion Adsorption at Solid/Water Interfaces, Langmuir, 2021, 37, 722–733 CrossRef PubMed.
- A. Stone, The theory of intermolecular forces, oUP oxford, 2013 Search PubMed.
- D. F. Parsons and B. W. Ninham, Ab Initio Molar Volumes and Gaussian Radii, J. Phys. Chem. A, 2009, 113, 1141–1150 CrossRef CAS PubMed.
- I. Fridovich, Inhibition of Acetoacetic Decarboxylase by Anions THE HOFMEISTER LYOTROPIC SERIES, J. Biol. Chem., 1963, 238, 592–598 CrossRef CAS.
- D. A. Doyle, J. M. Cabral, R. A. Pfuetzner, A. Kuo, J. M. Gulbis, S. L. Cohen, B. T. Chait and R. MacKinnon, The Structure of the Potassium Channel: Molecular Basis of K+ Conduction and Selectivity, Science, 1998, 280, 69–77 CrossRef CAS PubMed.
- B. Hille, C. M. Armstrong and R. MacKinnon, Ion channels: from idea to reality, Nat. Med., 1999, 5, 1105–1109 CrossRef CAS PubMed.
- K. Dabrowa, F. Ulatowski, D. Lichosyt and J. Jurczak, Catching the chloride: searching for non-Hofmeister selectivity behavior in systematically varied polyamide macrocyclic receptors, Org. Biomol. Chem., 2017, 15, 5927–5943 RSC.
- Y. Marcus, The thermodynamics of solvation of ions. Part 4.—Application of the tetraphenylarsonium tetraphenylborate (TATB) extrathermodynamic assumption to the hydration of ions and to properties of hydrated ions, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 2985–2992 RSC.
- J. L.-M. Poiseuille, Experimental Investigations on the Flow of Liquids in Tubes of Very Small Diameter, Ann. Chim. Phys., 1847, 21, 76 Search PubMed.
- H. S. Frank and M. W. Evans, Free Volume and Entropy in Condensed Systems III. Entropy in Binary Liquid Mixtures; Partial Molal Entropy in Dilute Solutions; Structure and Thermodynamics in Aqueous Electrolytes, J. Chem. Phys., 1945, 13, 507–532 CrossRef CAS.
- G. A. Krestov, Thermodynamics of solvation, 1991 Search PubMed.
- R. W. Gurney, Ionic Processes in Solution, 1953 Search PubMed.
- E. R. Nightingale Jr, Phenomenological theory of ion solvation. Effective radii of hydrated ions, J. Phys. Chem, 1959, 63, 1381–1387 CrossRef.
- E. Asmus, Zur Frage des B-Koeffizienten der Jones-Dole-Gleichung, Zeitschrift für Naturforsch. A, 1949, 4, 589–594 CrossRef.
- H. D.-B. Jenkins and Y. Marcus, Viscosity B-Coefficients of Ions in Solution, Chem. Rev., 1995, 95, 2695–2724 CrossRef CAS.
-
V. Mazzini and V. S.-J. Craig, Solubility of 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes in water and non-aqueous solvents, Australian National University, 2019 DOI:10.25911/5ca429ccb08a2.
1 electrolytes in water and non-aqueous solvents, Australian National University, 2019 DOI:10.25911/5ca429ccb08a2. - S. J. Hawkes, Salts are Mostly NOT Ionized, J. Chem. Educ., 1996, 73, 421 CrossRef CAS.
- A. A. Chen and R. V. Pappu, Quantitative Characterization of Ion Pairing and Cluster Formation in Strong 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Electrolytes, J. Phys. Chem. B, 2007, 111, 6469–6478 CrossRef CAS PubMed.
1 Electrolytes, J. Phys. Chem. B, 2007, 111, 6469–6478 CrossRef CAS PubMed. - J. Gujt, M. Bešter-Rogač and B. Hribar-Lee, An investigation of ion-pairing of alkali metal halides in aqueous solutions using the electrical conductivity and the Monte Carlo computer simulation methods, J. Mol. Liq., 2014, 190, 34–41 CrossRef CAS PubMed.
- H. Ohtaki, Dissolution and nucleation phenomena of salts in water. Molecular dynamic approaches and supporting solution X-ray diffraction measurements, Pure Appl. Chem., 1993, 65, 203 CrossRef CAS.
- A. D. Pethybridge and D. J. Spiers, Conductance of some alkali metal halides in dilute aqueous solution at 25 °C, J. Chem. Soc., Faraday Trans. 1, 1977, 73, 768–775 RSC.
- G. N. Lewis, The activity of the ions and the degree of dissociation of strong electrolytes, J. Am. Chem. Soc., 1912, 34, 1631–1644 CrossRef CAS.
- R. Heyrovska, Degrees of Dissociation and Hydration Numbers of Alkali Halides in Aqueous Solutions at 25 °C (Some up to Saturation), Croat. Chem. Acta, 1997, 70, 39–54 CAS.
- R. Heyrovska, Solution phase thermodynamics of strong electrolytes based on ionic concentrations, hydration numbers and volumes of dissolved entities, Struct. Chem., 2013, 24, 1895–1901 CrossRef CAS.
- Y. Shi and T. Beck, Deconstructing Free Energies in the Law of Matching Water Affinities, J. Phys. Chem. B, 2017, 121, 2189–2201 CrossRef CAS PubMed.
- L. A. Moreira, M. Boström, B. W. Ninham, E. C. Biscaia and F. W. Tavares, Hofmeister effects: Why protein charge, pH titration and protein precipitation depend on the choice of background salt solution, Colloids Surf., A, 2006, 282–283, 457–463 CrossRef.
- E. E. Bruce and N. F.-A. van der Vegt, Does an electronic continuum correction improve effective short-range ion–ion interactions in aqueous solution?, J. Chem. Phys., 2018, 148, 222816 CrossRef PubMed.
- E. E. Bruce, P. T. Bui, B. A. Rogers, P. S. Cremer and N. F.-A. A. Van Der Vegt, Nonadditive Ion Effects Drive Both Collapse and Swelling of Thermoresponsive Polymers in Water, J. Am. Chem. Soc., 2019, 141, 6609–6616 CrossRef CAS PubMed.
- E. E. Bruce, H. I. Okur, S. Stegmaier, C. I. Drexler, B. A. Rogers, N. F.-A. van der Vegt, S. Roke and P. S. Cremer, Molecular Mechanism for the Interactions of Hofmeister Cations with Macromolecules in Aqueous Solution, J. Am. Chem. Soc., 2020, 142, 19094–19100 CrossRef CAS PubMed.
- E. E. Bruce, P. T. Bui, M. Cao, P. S. Cremer and N. F.-A. Van Der Vegt, Contact Ion Pairs in the Bulk Affect Anion Interactions with Poly(N-isopropylacrylamide), J. Phys. Chem. B, 2021, 125, 680–688 CrossRef CAS PubMed.
- P. T. Bui and P. S. Cremer, Cation Identity Affects Nonadditivity in Salt Mixtures Containing Iodide and Sulfate, J. Solution Chem., 2021, 50, 1443–1456 CrossRef CAS.
- K. D. Judd, N. M. Gonzalez, T. Yang and P. S. Cremer, Contact Ion Pair Formation Is Not Necessarily Stronger than Solvent Shared Ion Pairing, J. Phys. Chem. Lett., 2022, 13, 923–930 CrossRef CAS PubMed.
- Y. Marcus and G. Hefter, Ion pairing, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- S. Ahrland, J. Chatt and N. R. Davies, The relative affinities of ligand atoms for acceptor molecules and ions, Q. Rev., Chem. Soc., 1958, 12, 265–276 RSC.
- R. G. Pearson, Hard and soft acids and bases, HSAB, part 1: Fundamental principles, J. Chem. Educ., 1968, 45, 581 CrossRef CAS.
- Y. Marcus, Linear solvation energy relationships. Correlation and prediction of the distribution of organic solutes between water and immiscible organic solvents, J. Phys. Chem., 1991, 95, 8886–8891 CrossRef CAS.
- R. Alain Miranda-Quintana and J. Smiatek, Electronic Properties of Protein Destabilizers and Stabilizers: Implications for Preferential Binding and Exclusion Mechanisms, J. Phys. Chem. B, 2021, 125, 11857–11868 CrossRef PubMed.
- T. A. Gmür, A. Goel and M. A. Brown, Quantifying Specific Ion Effects on the Surface Potential and Charge Density at Silica Nanoparticle–Aqueous Electrolyte Interfaces, J. Phys. Chem. C, 2016, 120, 16617–16625 CrossRef.
- Q. Wen, D. Yan, F. Liu, M. Wang, Y. Ling, P. Wang, P. Kluth, D. Schauries, C. Trautmann, P. Apel, W. Guo, G. Xiao, J. Liu, J. Xue and Y. Wang, Highly Selective Ionic Transport through Subnanometer Pores in Polymer Films, Adv. Funct. Mater., 2016, 26, 5796–5803 CrossRef CAS.
- M. Boström, D. F. Parsons, A. Salis, B. W. Ninham and M. Monduzzi, Possible Origin of the Inverse and Direct Hofmeister Series for Lysozyme at Low and High Salt Concentrations, Langmuir, 2011, 27, 9504–9511 CrossRef PubMed.
- R. Prathapan, R. Thapa, G. Garnier and R. F. Tabor, Modulating the zeta potential of cellulose nanocrystals using salts and surfactants, Colloids Surf., A, 2016, 509, 11–18 CrossRef CAS.
- A. Salis, F. Cugia, D. F. Parsons, B. W. Ninham and M. Monduzzi, Hofmeister series reversal for lysozyme by change in pH and salt concentration: insights from electrophoretic mobility measurements, Phys. Chem. Chem. Phys., 2012, 14, 4343–4346 RSC.
- A. Salis and M. Monduzzi, Not only pH. Specific buffer effects in biological systems, Curr. Opin. Colloid Interface Sci., 2016, 23, 1–9 CrossRef CAS.
- E. C. Johnson, I. J. Gresham, S. W. Prescott, A. Nelson, E. J. Wanless and G. B. Webber, The direction of influence of specific ion effects on a pH and temperature responsive copolymer brush is dependent on polymer charge, Polymer, 2021, 214, 123287 CrossRef CAS.
- R. Chudoba, J. Heyda and J. Dzubiella, Tuning the collapse transition of weakly charged polymers by ion-specific screening and adsorption, Soft Matter, 2018, 14, 9631–9642 RSC.
- J. Paterova, K. B. Rembert, J. Heyda, Y. Kurra, H. I. Okur, W. S.-R. Liu, C. Hilty, P. S. Cremer and P. Jungwirth, Reversal of the Hofmeister Series: Specific Ion Effects on Peptides, J. Phys. Chem. B, 2013, 117, 8150 CrossRef CAS PubMed.
- N. Schwierz, D. Horinek and R. R. Netz, Reversed Anionic Hofmeister Series: The Interplay of Surface Charge and Surface Polarity, Langmuir, 2010, 26, 7370 CrossRef CAS PubMed.
- N. Schwierz, D. Horinek, U. Sivan and R. R. Netz, Reversed Hofmeister series—The rule rather than the exception, Curr. Opin. Colloid Interface Sci., 2016, 23, 10–18 CrossRef CAS.
- G. V. Franks, Zeta Potentials and Yield Stresses of Silica Suspensions in Concentrated Monovalent Electrolytes: Isoelectric Point Shift and Additional Attraction, J. Colloid Interface Sci., 2002, 249, 44–51 CrossRef CAS PubMed.
- S. B. Johnson, G. V. Franks, P. J. Scales and T. W. Healy, The Binding of Monovalent Electrolyte Ions on α-Alumina. II. The Shear Yield Stress of Concentrated Suspensions, Langmuir, 1999, 15, 2844–2853 CrossRef CAS.
- D. F. Parsons, M. Boström, T. J. Maceina, A. Salis and B. W. Ninham, Why Direct or Reversed Hofmeister Series? Interplay of Hydration, Non-electrostatic Potentials, and Ion Size, Langmuir, 2010, 26, 3323–3328 CrossRef CAS PubMed.
- B. Katana, D. Takács, F. D. Bobbink, P. J. Dyson, N. B. Alsharif, M. Tomšič and I. Szilagyi, Masking specific effects of ionic liquid constituents at the solid–liquid interface by surface functionalization, Phys. Chem. Chem. Phys., 2020, 22, 24764–24770 RSC.
- W. J. Xie and Y. Q. Gao, A Simple Theory for the Hofmeister Series, J. Phys. Chem. Lett., 2013, 4, 4247 CrossRef CAS PubMed.
- G. Schwarzenbach, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeleus and A. G. Sharpe, Academic Press, 1961, vol. 3, pp. 257–285 Search PubMed.
- P. Su, Z. Jiang, Z. Chen and W. Wu, Energy Decomposition Scheme Based on the Generalized Kohn–Sham Scheme, J. Phys. Chem. A, 2014, 118, 2531–2542 CrossRef CAS PubMed.
- S. Juodkazis, N. Mukai, R. Wakaki, A. Yamaguchi, S. Matsuo and H. Misawa, Reversible phase transitions in polymer gels induced by radiation forces, Nature, 2000, 408, 178–181 CrossRef CAS PubMed.
- Z. Li, X. Yuan, Y. Feng, Y. Chen, Y. Zhao, H. Wang, Q. Xu and J. Wang, A reversible conductivity modulation of azobenzene-based ionic liquids in aqueous solutions using UV/vis light, Phys. Chem. Chem. Phys., 2018, 20, 12808–12816 RSC.
- X. Chen, Z. Zhan, Q. Liu and T. Wu, Modeling the response characteristics of photo-sensitive hydrogel electrolytes in Hofmeister salt solution for the development of smart energy storage devices, Sustain, Energy Fuels, 2020, 4, 6112–6124 CAS.
- S. Wei, Z. Zhang, W. Dong, T. Liang, J. Ji, W. Tian, S. Tan, Q. Zhao, C. Wang and Y. Wu, Specific Ion Effects of Azobenzene Salts on Photoresponse of PNIPAm in Aqueous Solutions, Macromol. Rapid Commun., 2021, 42, 2100232 CrossRef CAS PubMed.
- M. Senske, D. Constantinescu-Aruxandei, M. Havenith, C. Herrmann, H. Weingärtner and S. Ebbinghaus, The temperature dependence of the Hofmeister series: thermodynamic fingerprints of cosolute–protein interactions, Phys. Chem. Chem. Phys., 2016, 18, 29698–29708 RSC.
- E. C. Johnson, T. J. Murdoch, I. J. Gresham, B. A. Humphreys, S. W. Prescott, A. Nelson, G. B. Webber and E. J. Wanless, Temperature dependent specific ion effects in mixed salt environments on a thermoresponsive poly(oligoethylene glycol methacrylate) brush, Phys. Chem. Chem. Phys., 2019, 21, 4650–4662 RSC.
- W. Yao, K. Wang, A. Wu, W. F. Reed and B. C. Gibb, Anion binding to ubiquitin and its relevance to the Hofmeister effects, Chem. Sci., 2021, 12, 320–330 RSC.
- P. B. Petersen and R. J. Saykally, On the nature of ions at the liquid water surface, Annu. Rev. Phys. Chem., 2006, 57, 333–364 CrossRef CAS PubMed.
- J. H. Hu, Q. Shi, P. Davidovits, D. R. Worsnop, M. S. Zahniser and C. E. Kolb, Reactive uptake of Cl2(g) and Br2(g) by aqueous surfaces as a function of Br-and I-ion concentration: the effect of chemical reaction at the interface, J. Phys. Chem., 1995, 99, 8768–8776 CrossRef CAS.
- P. Jungwirth and D. J. Tobias, Ions at the Air/Water Interface, J. Phys. Chem. B, 2002, 106, 6361–6373 CrossRef CAS.
- P. Jungwirth and D. J. Tobias, Specific ion effects at the air/water interface, Chem. Rev., 2006, 106, 1259–1281 CrossRef CAS PubMed.
- J. M. Herbert and S. K. Paul, Interaction Energy Analysis of Monovalent Inorganic Anions in Bulk Water Versus Air/Water Interface, Molecules, 2021, 26, 6719 CrossRef CAS PubMed.
- Y. Levin, Polarizable Ions at Interfaces, Phys. Rev. Lett., 2009, 102, 147803 CrossRef PubMed.
- C. Jie, C. D. Vecitis, M. R. Hoffmann and A. J. Colussi, Experimental anion affinities for the air/water interface, J. Phys. Chem. B, 2006, 110, 25598–25602 CrossRef PubMed.
- J. Noah-Vanhoucke and P. L. Geissler, On the fluctuations that drive small ions toward, and away from, interfaces between polar liquids and their vapors, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15125–15130 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic press, 2015 Search PubMed.
- L. M. Pegram and M. T. Record, Hofmeister salt effects on surface tension arise from partitioning of anions and cations between bulk water and the air-water interface, J. Phys. Chem. B, 2007, 111, 5411–5417 CrossRef CAS PubMed.
- L. M. Pegram and M. T. Record, Partitioning of atmospherically relevant ions between bulk water and the water/vapor interface, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14278–14281 CrossRef CAS PubMed.
- L. M. Pegram and M. T. Record, Quantifying accumulation or exclusion of H+, HO−, and Hofmeister salt ions near interfaces, Chem. Phys. Lett., 2008, 467, 1–8 CrossRef CAS PubMed.
- C. L. Henry, C. N. Dalton, L. Scruton and V. S.-J. Craig, Ion-Specific Coalescence of Bubbles in Mixed Electrolyte Solutions, J. Phys. Chem. C, 2006, 111, 1015–1023 CrossRef.
- T. T. Duignan, The surface potential explains ion specific bubble coalescence inhibition, J. Colloid Interface Sci., 2021, 600, 338–343 CrossRef CAS PubMed.
- R. Weber, B. Winter, P. M. Schmidt, W. Widdra, I. V. Hertel, M. Dittmar and M. Faubel, Photoemission from aqueous alkali-metal− iodide salt solutions using EUV synchrotron radiation, J. Phys. Chem. B, 2004, 108, 4729–4736 CrossRef CAS.
- B. Winter and M. Faubel, Photoemission from Liquid Aqueous Solutions, Chem. Rev., 2006, 106, 1176–1211 CrossRef CAS PubMed.
- O. Höfft, U. Kahnert, S. Bahr and V. Kempter, Interaction of NaI with solid water and methanol, J. Phys. Chem. B, 2006, 110, 17115–17120 CrossRef PubMed.
- O. Höfft, A. Borodin, U. Kahnert, V. Kempter, L. X. Dang and P. Jungwirth, Surface segregation of dissolved salt ions, J. Phys. Chem. B, 2006, 110, 11971–11976 CrossRef PubMed.
- G. Andersson and H. Morgner, Thermodynamics and structure of liquid surfaces investigated directly with surface analytical tools, Rev. Artic. Ann. Phys., 2017, 529, 1600230 CrossRef.
- E. Sloutskin, J. Baumert, B. Ocko, I. Kuzmenko, A. Checco, L. Tamam, E. Ofer, T. Gog, O. Gang and M. Deutsch, The surface structure of concentrated aqueous salt solutions, J. Chem. Phys., 2007, 126, 54704 CrossRef CAS PubMed.
- R. R. Kumal, S. Nayak, W. Bu and A. Uysal, Chemical Potential Driven Reorganization of Anions between Stern and Diffuse Layers at the Air/Water Interface, J. Phys. Chem. C, 2022, 126, 1140–1151 CrossRef CAS.
- H. Niehus and G. Comsa, Features of ion scattering spectroscopy in impact collision mode: focusing and neutralization effects; ordered and disordered structure determination, Nucl. Instrum. Methods Phys. Res., Sect. B, 1986, 13, 213–217 CrossRef.
- G. Andersson and H. Morgner, Impact collision ion scattering spectroscopy (ICISS) and neutral impact collision ion scattering spectroscopy (NICISS) at surfaces of organic liquids, Surf. Sci., 1998, 405, 138–151 CrossRef CAS.
- G. Andersson and H. Morgner, Investigations on solutions of tetrabutylonium salts in formamide with NICISS and ICISS: concentration depth profiles and composition of the outermost layer, Surf. Sci., 2000, 445, 89–99 CrossRef CAS.
- X. Zhao, G. M. Nathanson and G. G. Andersson, Experimental Depth Profiles of Surfactants, Ions, and Solvent at the Angstrom Scale: Studies of Cationic and Anionic Surfactants and Their Salting Out, J. Phys. Chem. B, 2020, 124, 2218–2229 CrossRef CAS PubMed.
- G. Andersson and C. Ridings, Ion scattering studies of molecular structure at liquid surfaces with applications in industrial and biological systems, Chem. Rev., 2014, 114, 8361–8387 CrossRef CAS PubMed.
- D. Liu, G. Ma, L. M. Levering and H. C. Allen, Vibrational Spectroscopy of Aqueous Sodium Halide Solutions and Air−Liquid Interfaces:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Observation of Increased Interfacial Depth, J. Phys. Chem. B, 2004, 108, 2252–2260 CrossRef CAS.
Observation of Increased Interfacial Depth, J. Phys. Chem. B, 2004, 108, 2252–2260 CrossRef CAS. - H. C. Allen, N. N. Casillas-Ituarte, M. R. Sierra-Hernández, X. Chen and C. Y. Tang, Shedding light on water structure at air-aqueous interfaces: ions, lipids, and hydration, Phys. Chem. Chem. Phys., 2009, 11, 5538–5549 RSC.
- R. R. Kumal, S. Nayak, W. Bu and A. Uysal, Chemical Potential Driven Reorganization of Anions between Stern and Diffuse Layers at the Air/Water Interface, J. Phys. Chem. C, 2022, 126, 1140–1151 CrossRef CAS.
- M. H. Cheng, K. M. Callahan, A. M. Margarella, D. J. Tobias, J. C. Hemminger, H. Bluhm and M. J. Krisch, Ambient Pressure X-ray Photoelectron Spectroscopy and Molecular Dynamics Simulation Studies of Liquid/Vapor Interfaces of Aqueous NaCl, RbCl, and RbBr Solutions, J. Phys. Chem. C, 2012, 116, 4545–4555 CrossRef CAS.
- S. Ghosal, J. C. Hemminger, H. Bluhm, B. S. Mun, E. L.-D. Hebenstreit, G. Ketteler, D. F. Ogletree, F. G. Requejo and M. Salmeron, Electron Spectroscopy of Aqueous Solution Interfaces Reveals Surface Enhancement of Halides, Science, 2005, 307, 563 LP–566 LP CrossRef PubMed.
- M. A. Brown, R. D’Auria, I. F.-W. Kuo, M. J. Krisch, D. E. Starr, H. Bluhm, D. J. Tobias and J. C. Hemminger, Ion spatial distributions at the liquid–vapor interface of aqueous potassium fluoride solutions, Phys. Chem. Chem. Phys., 2008, 10, 4778–4784 RSC.
- K. A. Perrine, K. M. Parry, A. C. Stern, M. H.-C. Van Spyk, M. J. Makowski, J. A. Freites, B. Winter, D. J. Tobias and J. C. Hemminger, Specific cation effects at aqueous solution–vapor interfaces: surfactant-like behavior of Li+ revealed by experiments and simulations, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13363–13368 CrossRef CAS PubMed.
- S. Gopalakrishnan, D. Liu, H. C. Allen, M. Kuo and M. J. Shultz, Vibrational Spectroscopic Studies of Aqueous Interfaces:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Salts, Acids, Bases, and Nanodrops, Chem. Rev., 2006, 106, 1155–1175 CrossRef CAS PubMed.
Salts, Acids, Bases, and Nanodrops, Chem. Rev., 2006, 106, 1155–1175 CrossRef CAS PubMed. - W. Hua, D. Verreault, Z. Huang, E. M. Adams and H. C. Allen, Cation effects on interfacial water organization of aqueous chloride solutions. I. Monovalent cations: Li+, Na+, K+, and NH4+, J. Phys. Chem. B, 2014, 118, 8433–8440 CrossRef CAS PubMed.
- P. B. Petersen and R. J. Saykally, Probing the Interfacial Structure of Aqueous Electrolytes with Femtosecond Second Harmonic Generation Spectroscopy, J. Phys. Chem. B, 2006, 110, 14060–14073 CrossRef CAS PubMed.
- C. Tian, S. J. Byrnes, H.-L. Han and Y. R. Shen, Surface Propensities of Atmospherically Relevant Ions in Salt Solutions Revealed by Phase-Sensitive Sum Frequency Vib, Spectrosc., 2011, 2, 1946–1949 CAS.
- P. B. Petersen, J. C. Johnson, K. P. Knutsen and R. J. Saykally, Direct experimental validation of the Jones–Ray effect, Chem. Phys. Lett., 2004, 397, 46–50 CrossRef CAS.
- P. B. Petersen, R. J. Saykally, M. Mucha and P. Jungwirth, Enhanced Concentration of Polarizable Anions at the Liquid Water Surface:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SHG Spectroscopy and MD Simulations of Sodium Thiocyanide, J. Phys. Chem. B, 2005, 109, 10915–10921 CrossRef CAS PubMed.
SHG Spectroscopy and MD Simulations of Sodium Thiocyanide, J. Phys. Chem. B, 2005, 109, 10915–10921 CrossRef CAS PubMed. - P. B. Petersen and R. J. Saykally, Adsorption of Ions to the Surface of Dilute Electrolyte Solutions:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The Jones–Ray Effect Revisited, J. Am. Chem. Soc., 2005, 127, 15446–15452 CrossRef CAS PubMed.
The Jones–Ray Effect Revisited, J. Am. Chem. Soc., 2005, 127, 15446–15452 CrossRef CAS PubMed. - P. B. Petersen and R. J. Saykally, Confirmation of enhanced anion concentration at the liquid water surface, Chem. Phys. Lett., 2004, 397, 51–55 CrossRef CAS.
- L. Piatkowski, Z. Zhang, E. H.-G. Backus, H. J. Bakker and M. Bonn, Extreme surface propensity of halide ions in water, Nat. Commun., 2014, 5, 4083 CrossRef CAS PubMed.
- Z. Huang, W. Hua, D. Verreault and H. C. Allen, Salty glycerol versus salty water surface organization: bromide and iodide surface propensities, J. Phys. Chem. A, 2013, 117, 6346–6353 CrossRef CAS PubMed.
- G. Andersson, Concentration Depth Profiles of Inorganic Ions at Liquid Surfaces, Aust. J. Chem., 2010, 63, 434–437 CrossRef CAS.
- G. Andersson, Energy-loss straggling of helium projectiles at low kinetic energies, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 032901 CrossRef.
- G. Andersson, H. Morgner and H. Pohl, Energy-loss straggling of helium projectiles at low kinetic energies: deconvolution of concentration depth profiles of inorganic salt solutes in aqueous solutions, Phys. Rev. A: At. Mol. Opt. Phys., 2008, 78, 032904 CrossRef.
- G. Andersson, H. Morgner, L. Cwiklik and P. Jungwirth, Anions of Alkali Halide Salts at Surfaces of Formamide Solutions:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Concentration Depth Profiles and Surface Topography, J. Phys. Chem. C, 2007, 111, 4379–4387 CrossRef CAS.
Concentration Depth Profiles and Surface Topography, J. Phys. Chem. C, 2007, 111, 4379–4387 CrossRef CAS. - C. Ridings, G. G. Warr and G. G. Andersson, Surface Ordering in Binary Mixtures of Protic Ionic Liquids, J. Phys. Chem. Lett., 2017, 8, 4264–4267 CrossRef CAS PubMed.
- X. Zhao, G. M. Nathanson and G. G. Andersson, Competing Segregation of Br- and Cl- to a Surface Coated with a Cationic Surfactant: Direct Measurements of Ion and Solvent Depth Profiles, J. Phys. Chem. A, 2020, 124, 11102–11110 CrossRef CAS PubMed.
- R. A. Miranda-Quintana and J. Smiatek, Specific Ion Effects in Different Media: Current Status and Future Challenges, J. Phys. Chem. B, 2021, 125, 13840–13849 CrossRef CAS PubMed.
- F. Zhang, M. W.-A. Skoda, R. M.-J. Jacobs, D. G. Dressen, R. A. Martin, C. M. Martin, G. F. Clark, T. Lamkemeyer, F. Schreiber, M. W.-A. Skoda, R. M.-J. Jacobs, D. G. Dressen, R. A. Martin, C. M. Martin, G. F. Clark, T. Lamkemeyer, F. Schreiber, M. W.-A. Skoda, R. M.-J. Jacobs, D. G. Dressen, R. A. Martin, C. M. Martin, G. F. Clark, T. Lamkemeyer and F. Schreiber, Gold Nanoparticles Decorated with Oligo(ethylene glycol) Thiols: Enhanced Hofmeister Effects in Colloid−Protein Mixtures, J. Phys. Chem. C, 2009, 113, 4839 CrossRef CAS.
- A. Dér, L. Kelemen, L. Fábián, S. G. Taneva, E. Fodor, T. Páli, A. Cupane, M. G. Cacace and J. J. Ramsden, Interfacial Water Structure Controls Protein Conformation, J. Phys. Chem. B, 2007, 111, 5344–5350 CrossRef PubMed.
- T. López-León, J. L. Ortega-Vinuesa and D. Bastos-González, Ion-Specific Aggregation of Hydrophobic Particles, ChemPhysChem, 2012, 13, 2382–2391 CrossRef PubMed.
- E. Braun, S. Mohamad Moosavi and B. Smit, Anomalous Effects of Velocity Rescaling Algorithms: The Flying Ice Cube Effect Revisited, J. Chem. Theory Comput., 2018, 14, 5262–5272 CrossRef CAS PubMed.
- H. Robertson, E. C. Johnson, I. J. Gresham, S. W. Prescott, A. Nelson, E. J. Wanless and G. B. Webber, Competitive specific ion effects in mixed salt solutions on a thermoresponsive polymer brush, J. Colloid Interface Sci., 2021, 586, 292–304 CrossRef CAS PubMed.
- S. Zajforoushan Moghaddam and E. Thormann, Hofmeister effect of salt mixtures on thermo-responsive poly(propylene oxide), Phys. Chem. Chem. Phys., 2015, 17, 6359–6366 RSC.
- T. Wang, G. Liu, G. Zhang and V. S.-J. Craig, Insights into Ion Specificity in Water–Methanol Mixtures via the Reentrant Behavior of Polymer, Langmuir, 2012, 28, 1893–1899 CrossRef CAS PubMed.
- L. Liu, T. Wang, C. Liu, K. Lin, Y. Ding, G. Liu and G. Zhang, Mechanistic Insights into Amplification of Specific Ion Effect in Water–Nonaqueous Solvent Mixtures, J. Phys. Chem. B, 2013, 117, 2535–2544 CrossRef CAS PubMed.
- T. Wang, Y. Long, L. Liu, X. Wang, V. S.-J. Craig, G. Zhang and G. Liu, Cation-Specific Conformational Behavior of Polyelectrolyte Brushes: From Aqueous to Nonaqueous Solvent, Langmuir, 2014, 30, 12850–12859 CrossRef CAS PubMed.
- Y. Xu and G. Liu, Amplification of Hofmeister Effect by Alcohols, J. Phys. Chem. B, 2014, 118, 7450–7456 CrossRef CAS PubMed.
- L. Liu, R. Kou and G. Liu, Ion specificities of artificial macromolecules, Soft Matter, 2017, 13, 68–80 RSC.
- K. P. Gregory, G. R. Elliott, E. J. Wanless, G. B. Webber and A. J. Page, Ion Solvation Repository (IonSolvR), Repository, University of Newcastle, 2022 DOI:10.25817/40r8-t633.
- A. Narayanan Krishnamoorthy, C. Holm and J. Smiatek, Specific ion effects for polyelectrolytes in aqueous and non-aqueous media: the importance of the ion solvation behavior, Soft Matter, 2018, 14, 6243–6255 RSC.
- A. Narayanan Kirshnamoorthy, K. Oldiges, M. Winter, A. Heuer, I. Cekic-Laskovic, C. Holm and J. Smiatek, Electrolyte solvents for high voltage lithium ion batteries: ion correlation and specific anion effects in adiponitrile, Phys. Chem. Chem. Phys., 2018, 20, 25701–25715 RSC.
- R. A. Miranda-Quintana and J. Smiatek, Theoretical Insights into Specific Ion Effects and Strong-Weak Acid-Base Rules for Ions in Solution: Deriving the Law of Matching Solvent Affinities from First Principles, ChemPhysChem, 2020, 21, 2605–2617 CrossRef CAS PubMed.
- J. Smiatek, Specific Ion Effects and the Law of Matching Solvent Affinities: A Conceptual Density Functional Theory Approach, J. Phys. Chem. B, 2020, 124, 2191–2197 CrossRef CAS PubMed.
- J. Smiatek, Theoretical and Computational Insight into Solvent and Specific Ion Effects for Polyelectrolytes: The Importance of Local Molecular Interactions, Molecules, 2020, 25, 1661 CrossRef CAS PubMed.
- R. A. Miranda-Quintana and J. Smiatek, Beneficial properties of solvents and ions for lithium ion and post-lithium ion batteries: implications from charge transfer models, Electrochim. Acta, 2021, 384, 138418 CrossRef CAS.
- R. A. Miranda-Quintana and J. Smiatek, Calculation of donor numbers: computational estimates for the Lewis basicity of solvents, J. Mol. Liq., 2021, 322, 114506 CrossRef CAS.
- A. E. Eisenhart and T. L. Beck, Quantum Simulations of Hydrogen Bonding Effects in Glycerol Carbonate Electrolyte Solutions, J. Phys. Chem. B, 2021, 125, 2157–2166 CrossRef CAS PubMed.
- A. E. Eisenhart and T. L. Beck, Specific Ion Solvation and Pairing Effects in Glycerol Carbonate, J. Phys. Chem. B, 2021, 125, 13635–13643 CrossRef CAS PubMed.
- K. Izutsu, Electrochemistry in nonaqueous solutions, John Wiley & Sons, 2009 Search PubMed.
- L. Fan, K. Lin, J. Wang, R. Ma and B. Lu, A Nonaqueous Potassium-Based Battery–Supercapacitor Hybrid Device, Adv. Mater., 2018, 30, 1800804 CrossRef PubMed.
- W. Simka, D. Puszczyk and G. Nawrat, Electrodeposition of metals from non-aqueous solutions, Electrochim. Acta, 2009, 54, 5307–5319 CrossRef CAS.
- J. F. Gibbons, G. W. Cogan, C. M. Gronet and N. S. Lewis, A 14% efficient nonaqueous semiconductor/liquid junction solar cell, Appl. Phys. Lett., 1984, 45, 1095–1097 CrossRef CAS.
- M. Winter and R. J. Brodd, What Are Batteries, Fuel Cells, and Supercapacitors?, Chem. Rev., 2004, 104, 4245–4270 CrossRef CAS PubMed.
- R. S. Sahota and M. G. Khaledi, Nonaqueous Capillary Electrophoresis, Anal. Chem., 1994, 66, 1141–1146 CrossRef CAS PubMed.
- A. J. Parker, The effects of solvation on the properties of anions in dipolar aprotic solvents, Q. Rev., Chem. Soc., 1962, 16, 163–187 RSC.
- R. G. Pearson and J. Songstad, Application of the principle of hard and soft acids and bases to organic chemistry, J. Am. Chem. Soc., 1967, 89, 1827–1836 CrossRef CAS.
- N. Schmelzer, J. Einfeldt and M. Grigo, Ion–solvent interactions of some ions in dipolar aprotic solvents at 25 °C, J. Chem. Soc., Faraday Trans., 1990, 86, 489–494 RSC.
- U. Mayer, V. Gutmann and W. Gerger, The acceptor number—A quantitative empirical parameter for the electrophilic properties of solvents, Monatshefte für Chemie, 1975, 106, 1235–1257 CrossRef CAS.
- J. Smiatek, A. Wohlfarth and C. Holm, The solvation and ion condensation properties for sulfonated polyelectrolytes in different solvents—a computational study, New J. Phys., 2014, 16, 025001 CrossRef CAS.
- J. Smiatek, A. Heuer and M. Winter, Properties of ion complexes and their impact on charge transport in organic solvent-based electrolyte solutions for lithium batteries: insights from a theoretical perspective, Batteries, 2018, 4, 62 CrossRef CAS.
- V. Gutmann, Empirical parameters for donor and acceptor properties of solvents, Electrochim. Acta, 1976, 21, 661–670 CrossRef CAS.
- G. Liu, D. Parsons and V. S.-J. Craig, Re-entrant swelling and redissolution of polyelectrolytes arises from an increased electrostatic decay length at high salt concentrations, J. Colloid Interface Sci., 2020, 579, 369–378 CrossRef CAS PubMed.
- P. Jia and J. Zhao, Single chain contraction and re-expansion of polystyrene sulfonate: a study on its re-entrant condensation at single molecular level, J. Chem. Phys., 2009, 131, 231103 CrossRef PubMed.
- R. Kou, J. Zhang, Z. Chen and G. Liu, Counterion Specificity of Polyelectrolyte Brushes: Role of Specific Ion-Pairing Interactions, ChemPhysChem, 2018, 19, 1404–1413 CrossRef CAS PubMed.
- T. López-León, M. J. Santander-Ortega, J. L. Ortega-Vinuesa and D. Bastos-González, Hofmeister Effects in Colloidal Systems: Influence of the Surface Nature, J. Phys. Chem. C, 2008, 112, 16060–16069 CrossRef.
- Y. Luo, H. Li, X. Gao and R. Tian, Description of colloidal particles aggregation in the presence of Hofmeister effects: on the relationship between ion adsorption energy and particle aggregation activation energy, Phys. Chem. Chem. Phys., 2018, 20, 22831–22840 RSC.
- R. Kjellander, Statistical Mechanics of Liquids and Solutions, CRC Press, 2019 Search PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Scaling Analysis of the Screening Length in Concentrated Electrolytes, Phys. Rev. Lett., 2017, 119, 1–5 Search PubMed.
- D. J. Griffiths, Introduction to Electrodynamics, Pearson, 4th edn, 2013 Search PubMed.
- T. N. Tran and T. Le, Microscopic approach for low-frequency dielectric constant of liquid water, Phys. Chem. Liq., 2021, 59, 53–61 CrossRef CAS.
- D. J. Grzetic, K. T. Delaney and G. H. Fredrickson, Contrasting Dielectric Properties of Electrolyte Solutions with Polar and Polarizable Solvents, Phys. Rev. Lett., 2019, 122, 128007 CrossRef CAS PubMed.
- J. H. Christensen, A. J. Smith, R. B. Reed and K. L. Elmore, Dielectric Properties of Phosphoric Acid Solutions at 25 °C, J. Chem. Eng. Data, 1966, 11, 60–63 CrossRef CAS.
- F. E. Harris and C. T. O’Konski, Dielectric properties of aqueous ionic solutions at microwave frequencies, J. Phys. Chem., 1957, 61, 310–319 CrossRef CAS.
- G. H. Haggis, J. B. Hasted and T. J. Buchanan, The dielectric properties of water in solutions, J. Chem. Phys., 1952, 20, 1452–1465 CrossRef CAS.
- A. De Ninno, E. Nikollari, M. Missori and F. Frezza, Dielectric permittivity of aqueous solutions of electrolytes probed by THz time-domain and FTIR spectroscopy, Phys. Lett. Sect. A: Gen. At. Solid State Phys., 2020, 384, 126865 CrossRef CAS.
- J. B. Hasted and G. W. Roderick, Dielectric properties of aqueous and alcoholic electrolytic solutions, J. Chem. Phys., 1958, 29, 17–26 CrossRef CAS.
- R. Buchner, G. T. Hefter and P. M. May, Dielectric relaxation of aqueous NaCl solutions, J. Phys. Chem. A, 1999, 103, 8–9 CrossRef.
- N. Gavish and K. Promislow, Dependence of the dielectric constant of electrolyte solutions on ionic concentration: a microfield approach, Phys. Rev. E, 2016, 94, 1–7 CrossRef PubMed.
- M. Muthukumar, 50th Anniversary Perspective: A Perspective on Polyelectrolyte Solutions, Macromolecules, 2017, 50, 9528–9560 CrossRef CAS PubMed.
- W. Lin and J. Klein, Direct measurement of surface forces: recent advances and insights, Appl. Phys. Rev., 2021, 8, 031316 CAS.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Ionic liquids behave as dilute electrolyte solutions, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Underscreening in concentrated electrolytes, Faraday Discuss., 2017, 199, 239–259 RSC.
- A. M. Smith, A. A. Lee and S. Perkin, The Electrostatic Screening Length in Concentrated Electrolytes Increases with Concentration, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- P. Gaddam and W. Ducker, Electrostatic Screening Length in Concentrated Salt Solutions, Langmuir, 2019, 35, 5719–5727 CrossRef CAS PubMed.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Long range electrostatic forces in ionic liquids, Chem. Commun., 2017, 53, 1214–1224 RSC.
- J. Ennis, R. Kjellander and D. J. Mitchell, Dressed ion theory for bulk symmetric electrolytes in the restricted primitive model, J. Chem. Phys., 1995, 102, 975–991 CrossRef CAS.
- J. Ulander and R. Kjellander, The decay of pair correlation functions in ionic fluids: a dressed ion theory analysis of Monte Carlo simulations, J. Chem. Phys., 2001, 114, 4893–4904 CrossRef CAS.
- R. Kjellander, A multiple decay-length extension of the Debye–Hückel theory: to achieve high accuracy also for concentrated solutions and explain under-screening in dilute symmetric electrolytes, Phys. Chem. Chem. Phys., 2020, 22, 23952–23985 RSC.
- P. Cats, R. Evans, A. Härtel and R. Van Roij, Primitive model electrolytes in the near and far field: decay lengths from DFT and simulations, J. Chem. Phys., 2021, 154, 124504 CrossRef CAS PubMed.
- J. Zeman, S. Kondrat and C. Holm, Bulk ionic screening lengths from extremely large-scale molecular dynamics simulations, Chem. Commun., 2020, 56, 15635–15638 RSC.
- J. G. Kirkwood, Statistical mechanics of liquid solutions, Chem. Rev., 1936, 19, 275–307 CrossRef CAS.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Double layer in ionic liquids: overscreening versus crowding, Phys. Rev. Lett., 2011, 106, 6–9 CrossRef PubMed.
- M. E. Fisher and B. Wiodm, Decay of correlations in linear systems, J. Chem. Phys., 1969, 50, 3756–3772 CrossRef CAS.
- L. Onsager, Theories of concentrated electrolytes, Chem. Rev., 1933, 13, 73–89 CrossRef CAS.
- R. Kjellander, Decay behavior of screened electrostatic surface forces in ionic liquids: the vital role of non-local electrostatics, Phys. Chem. Chem. Phys., 2016, 18, 18985–19000 RSC.
- R. Kjellander, Nonlocal electrostatics in ionic liquids: the key to an understanding of the screening decay length and screened interactions, J. Chem. Phys., 2016, 145, 124503 CrossRef PubMed.
- R. Kjellander and D. J. Mitchell, Dressed-ion theory for electrolyte solutions: a Debye–Hückel-like reformulation of the exact theory for the primitive model, J. Chem. Phys., 1994, 101, 603–626 CrossRef CAS.
- R. Kjellander, Focus Article: oscillatory and long-range monotonic exponential decays of electrostatic interactions in ionic liquids and other electrolytes: the significance of dielectric permittivity and renormalized charges, J. Chem. Phys., 2018, 148, 193701 CrossRef PubMed.
- R. J.-F. Leote De Carvalho and R. Evans, The decay of correlations in ionic fluids, Mol. Phys., 1994, 83, 619–654 Search PubMed.
- F. H. Stillinger and R. Lovett, Ion-Pair Theory of Concentrated Electrolytes, J. Chem. Phys., 1986, 48, 3858 CrossRef.
- P. Attard, Asymptotic analysis of primitive model electrolytes and the electrical double layer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3604–3621 CrossRef CAS PubMed.
- Y. Avni, R. M. Adar and D. Andelman, Charge oscillations in ionic liquids: a microscopic cluster model, Phys. Rev. E, 2020, 101, 1–6 CrossRef PubMed.
- E. Krucker-Velasquez and J. W. Swan, Underscreening and hidden ion structures in large scale simulations of concentrated electrolytes, J. Chem. Phys., 2021, 155, 134903 CrossRef CAS PubMed.
- P. Jones, F. Coupette, A. Härtel and A. A. Lee, Bayesian unsupervised learning reveals hidden structure in concentrated electrolytes, J. Chem. Phys., 2021, 154, 134902 CrossRef CAS PubMed.
- F. Coupette, A. A. Lee and A. Härtel, Screening Lengths in Ionic Fluids, Phys. Rev. Lett., 2018, 121, 75501 CrossRef CAS PubMed.
- S. W. Coles, C. Park, R. Nikam, M. Kanduč, J. Dzubiella and B. Rotenberg, Correlation Length in Concentrated Electrolytes: Insights from All-Atom Molecular Dynamics Simulations, J. Phys. Chem. B, 2020, 124, 1778–1786 CAS.
- R. M. Adar, S. A. Safran, H. Diamant and D. Andelman, Screening length for finite-size ions in concentrated electrolytes, Phys. Rev. E, 2019, 100, 42615 CrossRef CAS PubMed.
- B. Rotenberg, O. Bernard and J. P. Hansen, Underscreening in ionic liquids: a first principles analysis, J. Phys.: Condens. Matter, 2018, 30, 054005 CrossRef PubMed.
- R. Heyrovská, Equations for Densities and Dissociation Constant of NaCl(aq) at 25 °C from “Zero to Saturation” Based on Partial Dissociation, J. Electrochem. Soc., 1997, 144, 2380–2384 CrossRef.
- M. Landstorfer, On the dissociation degree of ionic solutions considering solvation effects, Electrochem. Commun., 2018, 92, 56–59 CrossRef CAS.
- Z. A.-H. Goodwin and A. A. Kornyshev, Underscreening, overscreening and double-layer capacitance, Electrochem. Commun., 2017, 82, 129–133 CrossRef CAS.
- R. Kjellander and D. J. Mitchell, An exact but linear and Poisson–Boltzmann-like theory for electrolytes and colloid dispersions in the primitive model, Chem. Phys. Lett., 1992, 200, 76–82 CrossRef CAS.
- P. Keblinski, J. Eggebrecht, D. Wolf and S. R. Phillpot, Molecular dynamics study of screening in ionic fluids, J. Chem. Phys., 2000, 113, 282–291 CrossRef CAS.
- C. W. Outhwaite and L. B. Bhuiyan, On the modified Poisson–Boltzmann closure for primitive model electrolytes at high concentration, J. Chem. Phys., 2021, 155, 14504 CrossRef CAS PubMed.
- D. R. MacFarlane, A. L. Chong, M. Forsyth, M. Kar, R. Vijayaraghavan, A. Somers and J. M. Pringle, New dimensions in salt-solvent mixtures: a 4th evolution of ionic liquids, Faraday Discuss., 2018, 206, 9–28 RSC.
- A. Sanchez-Fernandez, A. J. Jackson, S. F. Prévost, J. J. Doutch and K. J. Edler, Long-Range Electrostatic Colloidal Interactions and Specific Ion Effects in Deep Eutectic Solvents, J. Am. Chem. Soc., 2021, 143, 14158–14168 CrossRef CAS PubMed.
- D. Constantinescu, H. Weingärtner and C. Herrmann, Protein Denaturation by Ionic Liquids and the Hofmeister Series: A Case Study of Aqueous Solutions of Ribonuclease A, Angew. Chem., Int. Ed., 2007, 46, 8887–8889 CrossRef CAS PubMed.
- H. Zhao, Effect of ions and other compatible solutes on enzyme activity, and its implication for biocatalysis using ionic liquids, J. Mol. Catal. B: Enzym., 2005, 37, 16–25 CrossRef CAS.
- Z. Yang, Hofmeister effects: an explanation for the impact of ionic liquids on biocatalysis, Elsevier, 2009, vol. 144 Search PubMed.
- T. Vasantha, A. Kumar, P. Attri, P. Venkatesu and R. S. Rama Devi, The solubility and stability of amino acids in biocompatible ionic liquids, Protein Pept. Lett., 2014, 21, 15–24 CrossRef CAS PubMed.
- A. Kumar and P. Venkatesu, Does the stability of proteins in ionic liquids obey the Hofmeister series?, Int. J. Biol. Macromol., 2014, 63, 244–253 CrossRef CAS PubMed.
- H. Zhao, S. M. Campbell, L. Jackson, Z. Song and O. Olubajo, Hofmeister series of ionic liquids: kosmotropic effect of ionic liquids on the enzymatic hydrolysis of enantiomeric phenylalanine methyl ester, Tetrahedron: Asymmetry, 2006, 17, 377–383 CrossRef CAS.
- E. M. Knipping, M. J. Lakin, K. L. Foster, P. Jungwirth, D. J. Tobias, R. B. Gerber, D. Dabdub and B. J. Finlayson-Pitts, Experiments and simulations of ion-enhanced interfacial chemistry on aqueous NaCl aerosols, Science, 2000, 288(5464), 301–306 CrossRef CAS PubMed.
- Q. Han, K. M. Smith, C. Darmanin, T. M. Ryan, C. J. Drummond and T. L. Greaves, Lysozyme conformational changes with ionic liquids: spectroscopic, small angle X-ray scattering and crystallographic study, J. Colloid Interface Sci., 2021, 585, 433–443 CrossRef CAS PubMed.
- D. N. Fuller, J. P. Rickgauer, P. J. Jardine, S. Grimes, D. L. Anderson and D. E. Smith, Ionic effects on viral DNA packaging and portal motor function in bacteriophage φ29, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11245 LP–11250 LP CrossRef PubMed.
- C. Y. Zhang and N. H. Zhang, Size dependent correlation between structure and apparent stiffness of viral DNA during temperature variation, J. Mech. Phys. Solids, 2021, 154, 104501 CrossRef CAS.
- J. Wei and Q. Wang, Hofmeister Effect-Aided Assembly of Enhanced Hydrogel Supercapacitor with Excellent Interfacial Contact and Reliability, Small, Methods, 2019, 3, 1900558 CAS.
- J. R. Pinca, W. G. Duborg and R. Jorn, Ion Association and Electrolyte Structure at Surface Films in Lithium-Ion Batteries, J. Phys. Chem. C, 2021, 125, 7054–7066 CrossRef CAS.
- S. Perkin, L. Crowhurst, H. Niedermeyer, T. Welton, A. M. Smith and N. N. Gosvami, Self-assembly in the electrical double layer of ionic liquids, Chem. Commun., 2011, 47, 6572–6574 RSC.
- B. W. Ninham, R. M. Pashley and P. Lo Nostro, Surface forces: changing concepts and complexity with dissolved gas, bubbles, salt and heat, Curr. Opin. Colloid Interface Sci., 2017, 27, 25–32 CrossRef CAS.
- A. C. Rodrigo, E. Laurini, V. M.-P. Vieira, S. Pricl and D. K. Smith, Effect of buffer at nanoscale molecular recognition interfaces – electrostatic binding of biological polyanions, Chem. Commun., 2017, 53, 11580–11583 RSC.
- A. Salis, L. Cappai, C. Carucci, D. F. Parsons and M. Monduzzi, Specific Buffer Effects on the Intermolecular Interactions among Protein Molecules at Physiological pH, J. Phys. Chem. Lett., 2020, 11, 6805–6811 CrossRef CAS PubMed.
- S. Brudar and B. Hribar-Lee, Effect of Buffer on Protein Stability in Aqueous Solutions: A Simple Protein Aggregation Model, J. Phys. Chem. B, 2021, 125, 2504–2512 CrossRef CAS PubMed.
- J. H. Jordan, H. S. Ashbaugh, J. T. Mague and B. C. Gibb, Buffer and Salt Effects in Aqueous Host–Guest Systems: Screening, Competitive Binding, or Both?, J. Am. Chem. Soc., 2021, 143, 18605–18616 CrossRef CAS PubMed.
- J. D. Willott, B. A. Humphreys, G. B. Webber, E. J. Wanless and W. M. de Vos, Combined Experimental and Theoretical Study of Weak Polyelectrolyte Brushes in Salt Mixtures, Langmuir, 2019, 35, 2709–2718 CrossRef CAS PubMed.
- J. D. Willott, T. J. Murdoch, F. A.-M. Leermakers and W. M. de Vos, Behavior of Weak Polyelectrolyte Brushes in Mixed Salt Solutions, Macromolecules, 2018, 51, 1198–1206 CrossRef CAS PubMed.
- E. Yılmaz Topuzlu, H. I. Okur, B. Ulgut and Ö. Dag, Role of Water in the Lyotropic Liquid Crystalline Mesophase of Lithium Salts and Non-ionic Surfactants, Langmuir, 2021, 37, 14443–14453 CrossRef PubMed.
- D. Tatini, D. Ciardi, C. Sofroniou, B. W. Ninham and P. Lo Nostro, Physicochemical characterization of green sodium oleate-based formulations. Part 2. Effect of anions, J. Colloid Interface Sci., 2022, 617, 399–408 CrossRef CAS PubMed.
- J. Mehringer, E. Hofmann, D. Touraud, S. Koltzenburg, M. Kellermeier and W. Kunz, Salting-in and salting-out effects of short amphiphilic molecules: a balance between specific ion effects and hydrophobicity, Phys. Chem. Chem. Phys., 2021, 23, 1381–1391 RSC.
- G. Hantal, M. Sega, G. Horvai and P. Jedlovszky, Contribution of Different Molecules and Moieties to the Surface Tension in Aqueous Surfactant Solutions. II: Role of the Size and Charge Sign of the Counterions, J. Phys. Chem. B, 2021, 125, 9005–9018 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00847e |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2022 |