Physical insights from the Frumkin isotherm applied to electrolyte gated organic transistors as protein biosensors†
Pamela Allison
Manco Urbina
a,
Marcello
Berto
 a,
Pierpaolo
Greco
a,
Matteo
Sensi
a,
Pierpaolo
Greco
a,
Matteo
Sensi
 a,
Simone
Borghi
a,
Marco
Borsari
a,
Simone
Borghi
a,
Marco
Borsari
 b,
Carlo Augusto
Bortolotti
b,
Carlo Augusto
Bortolotti
 *a and
Fabio
Biscarini
*a and
Fabio
Biscarini
 *ac
*ac
aDepartment of Life Sciences, University of Modena and Reggio Emilia, via Campi 103, 41125 Modena, Italy. E-mail: carloaugusto.bortolotti@unimore.it; fabio.biscarini@unimore.it
bDepartment of Chemical and Geological Sciences, University of Modena and Reggio Emilia, via Campi 103, 41125 Modena, Italy
cCenter for Translational Neurophysiology - Italian Institute of Technology, Via Fossato di Mortara 17-19, 44121 Ferrara, Italy
First published on 12th August 2021
Abstract
Label free biosensors based on electrolyte gated organic transistors (EGOTs) are ultra-sensitive and versatile sensing devices. The dose curve represents the change of the sensor signal as a function of the concentration of the target analyte, and, under the hypothesis of dynamic equilibrium between the surface-bound probe and its target partner, can be fitted to adsorption isotherms. In this work, we show that the data obtained from both the OECT and EGOFET Interleukin-6 (IL-6) biosensors are best fitted by the Frumkin isotherm compared to the widely adopted Langmuir and Hill isotherms. Comparable values of the equilibrium association constant Ka and the Frumkin interaction parameter g′ are obtained with both OECT and EGOFET sharing the same functionalization of the gate electrode. Our study unambiguously shows that the biosensor response is, to a large extent, due to the specific binding at the gate/electrolyte interface, and that is viable to investigate the thermodynamics of biorecognition. Moreover, the electrostatic repulsions between adsorbed probe–target pairs are shown to decrease the effective equilibrium association constant as coverage increases, thus causing a loss of sensitivity for concentrations above the threshold limit 1/|g′|.
Introduction
Organic bioelectronics is emerging as a technological platform of choice for signal transduction at the biotic/abiotic interface for its outstanding amplification of small biological signals.1–5 Biosensing is among the most widely explored applications for organic electronic devices, especially involving those belonging to the Electrolyte Gated Organic Transistor (EGOT) family, that encompasses the Electrolyte Gated Organic Field Effect Transistor (EGOFET) and the Organic Electrochemical Transistor (OECT).2,4,6–8Both architectures base their operations on the response of the electrolyte ions to the potential applied between the gate and the source electrodes, the main difference between EGOFET and OECT being the permeability of the organic (semi)conducting layer to such ions.5,6,9
The examples of EGOFET-based biosensing that were proposed to date mostly consist of label-free immune-biosensors, where the analyte is quantified by monitoring the concentration-dependent changes in the current flowing between source and drain electrodes (IDS).6,10–15 Such changes can be ascribed to the binding of the analyte to a specific biorecognition unit (typically an antibody or an aptamer) immobilized either at the gate or at the organic semiconductor (OSC) channel. Since they are capacitively coupled, a shift in the electrochemical potential at the gate/electrolyte interface is transduced into an IDS modulation.6,13,16–18 EGOFETs can be therefore regarded as a potentiometric biosensors19 capable to amplify the voltage change in situ. OECTs can also be operated as potentiometric biosensors in a conceptually similar way,20 although they have been largely preferred as amperometric sensors.4,8,21,22 In the latter case, the analyte undergoes a redox reaction that either directly or via a mediator generates a faradaic current that is proportional to its concentration. The exact working mechanism of EGOTs is still debated,23 and the same holds as to whether one architecture should be preferred for biosensing purposes.19,24,25
Irrespectively of whether an EGOFET or an OECT is considered, a dose curve is constructed by plotting the change of device parameter(s) (typically the drain current intensity, but transconductance (gm), threshold voltage (Vth) or other observables can be considered) as a function of the target analyte concentration. Typically, the change in drain current normalized by the current value in the absence of analyte is obtained, yielding what is termed the signal (S) as S([c]) = [IDS([c]) − IDS(0)]/IDS(0) where IDS([c])is the drain current value at the target concentration [c], and IDS(0) is the drain current value in pure buffer [c] = 0 M.
We focus now on the EGOT-based biosensors operated as potentiometric devices. Under two assumptions, viz. the first that the observed drain current changes are linearly dependent on the target binding to the specific recognition moiety (which implies strictly that the current of the EGOT is taken in the linear regime of the transistor), and the second that the binding has attained thermal equilibrium, one can describe the corresponding dose curves in terms of equilibrium binding models (isotherms). To this end, Langmuir isotherm is by far the most used one, also in the organic bioelectronics community10,11,26–28 because of its simplicity:
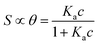 | (1a) |
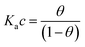 | (1b) |
Here θ is the fraction of recognition sites bound to the target analyte, thus ranges from 0 to 1, and Ka is the equilibrium association constant to be used as the only fitting parameter. We point out that, differently from the common practice especially adopted in biochemistry, being Ka dimensionless, the concentration c in eqn (1) and following, must be normalized by [c°] = 1 M, i.e. c = [c]/[c°]. Thus, the fitting of the dose curve yields a quantification of the affinity of the recognition group towards the target through the value of Ka, and hence gives an indication of the specificity of the sensing device.
The Langmuir model successfully fitted data obtained with both EGOFET10,11,28 and Graphene-based FET.27,29,30 In other cases,31 the Langmuir isotherm did not yield satisfactory fitting to the experimental data, which suggests that the assumption of independent single recognition events, upon which the Langmuir model rests, does not hold. An alternative often adopted is the Hill isotherm:11,32
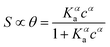 | (2a) |
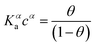 | (2b) |
The adoption of either Langmuir or Hill isotherms allows one to extract the relevant thermodynamic quantities of biorecognition from the change of Ka as a function of operational parameters,33 for instance the gate voltage VGS. One can therefore obtain the standard Gibbs energy of binding 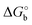 for the formation of the complex between probe and target, as well as the additional electrostatic free energy modulated by VGS. In some cases, a good agreement was found between Ka from isotherms and the value derived from kinetic studies, namely the ratio kon/koff in terms of the rate constants kon and koff.27,29
for the formation of the complex between probe and target, as well as the additional electrostatic free energy modulated by VGS. In some cases, a good agreement was found between Ka from isotherms and the value derived from kinetic studies, namely the ratio kon/koff in terms of the rate constants kon and koff.27,29
While the presence of an additional fitting parameter (the Hill exponent α) in eqn (2) yields better fitting, Hill isotherm is strictly heuristic and care should be taken when the interpretation of α values in terms of (anti)cooperative binding events is given for α (smaller) larger than 1. A more consistent justification for the adequacy of Hill model can be given by invoking multiple equilibria involving probe, target and the bound pair. Indeed, it was shown that the exponent α = 1 (corresponding to a Langmuir-like process) can decrease down to 0.5,31 or even take values α > 1.10,34 Therefore, the Hill isotherm disguises intertwined multiple equilibria that may synergically either increase or decrease the dependence on the concentration. It turns out that the understanding of the phenomena that lead to either Langmuir-type or Hill-type response may result physically ambiguous.
In this work, we propose the Frumkin isotherm as a quantitative interpretative tool for dose curves from EGOT. While Frumkin isotherm is well-known in electrochemistry, it has not yet been assessed in the context of bioelectronics. We show that Frumkin isotherm reconciles the observations of Langmuir-type response with those of the Hill-type response, while retaining an explicit, yet simple, description of the interactions (either attractive or repulsive) between adsorbed probe and target molecules. In order to assess the efficacy of the Frumkin isotherm, we compare dose curves obtained from two EGOT architectures, one based on the OECT and another on the EGOFET. Both are operated as biosensors towards the same analyte, namely the cytokine Interleukin-6 (IL-6), with the same gate, viz. a gold wire functionalized with an anti-IL-6 antibody immobilized on a mixed mercaptoundecanoic/6-mercaptohexanol self-assembled monolayer (SAM). Hence, in our experiment the gate/electrolyte interfaces where the biorecognition events occur are (effectively) identical, the only difference being ascribed to the transduction scheme of the two architectures. We use the dose curves stemming from both devices as a benchmark for the comparison of Langmuir, Hill and Frumkin isotherms. We show that, in the present case, the Langmuir isotherm fits poorly our data, while the Hill isotherm, albeit yields more satisfactory fit, provides binding constant and exponent values “unrealistically” low. The Frumkin isotherm fits well both dose curves and allows us to infer that (i) a repulsive interaction between the target molecules adsorbed on the gate effectively decreases the binding constant as θ increases, and (ii) the effective binding constants of the two architectures are comparable, thus hinting to the independence of the binding events from the transduction mechanism.
Results and discussion
Analysis of the transfer characteristics
We first assess the ability of our devices to serve as IL-6 biosensors. A gold gate electrode (G) surface is functionalized with anti-IL-6 antibodies, covalently bound to a mercaptoundecanoic/6-mercaptohexanol mixed SAM as described in the experimental section. The spin-cast source (S)-drain (D) channels consist of PEDOT:PSS film for OECTs and TIPS-Pentacene-film for EGOFETs (Fig. 1). Each device was exposed to increasing concentrations of IL-6 in the 1 pM-100 nM range in a solution buffer composed of 0.1 mg mL−1 BSA in 50 mM PBS, pH 7.4. BSA was included to mimic the albumin concentration typically found in human plasma sample undergoing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 dilution.
400 dilution.
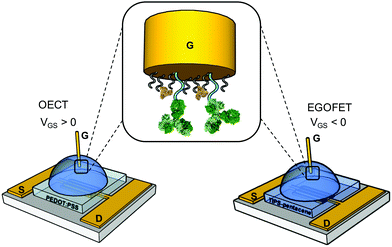 | ||
| Fig. 1 Schematics of the OECT and EGOFET IL-6 biosensors; in the zoom, the functionalized gate electrode is shown. | ||
Fig. 2 displays the typical responses of OECT (A) and EGOFET biosensor (B) to increasing concentration [IL-6]. In both device architectures the drain current increases with increasing [IL-6], as a consequence of the specific binding of IL-6 to the antibodies immobilized on the gate electrode. This behavior was consistently observed in all the five devices that were characterized for each architecture.
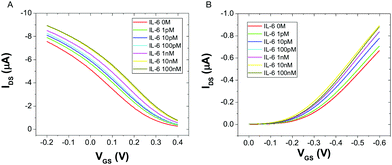 | ||
| Fig. 2 Overlay of transfer characteristics for an OECT (A) and an EGOFET (B) upon incubation with different concentrations of IL-6, at VDS = −0.2 V. | ||
The observed current increase is in line with previously reported OECT-based detection of IL-6.35 We explain the observed current shift in Fig. 2 upon IL-6 biorecognition with an intuitive physical–chemical argument based on the changes of the potential drop at the gate/electrolyte and electrolyte/channel interfaces upon IL-6 binding. We treat the mixed mercaptoundecanoic/6-mercaptohexanol SAM and the protein layer (made either of Anti-IL-6 or Anti-IL-6/IL-6) as continuous in-series dielectric layers, hence a linear decay of the potential with the distance occurs across each layer. In the diffuse layers, one outside the protein layer at the gate and the other at the electrolyte/channel interface, the potential decays exponentially following Gouy–Chapman model.
The IL-6 molecule is expected to be negatively charged at the pH under the present experimental conditions (vide infra). Therefore, binding of an IL-6 molecule to its antibody will lower the electrochemical potential of the electrolyte yielding a smaller potential drop across the electrolyte/channel interface. This is equivalent to the application of a more negative potential difference between gate and source, which would increase the charge carrier density in the channel. As a consequence, in OECT more IL-6 binds the gate electrode, more current in the channel is output as the result of less de-doping of PEDOT:PSS. The same argument, although with reverted potential at the gate electrode, holds for EGOFET as the decrease of electrochemical potential of the electrolyte due to IL-6 binding to the protein layer yields a more negative potential at the electrolyte/OSC channel and hence to a current increase due to increased “doping”. Albeit its simplicity, our explanation provides a first useful hint from the experimental observation of the change of the transfer curves upon exposure to a target analyte: the net charge (negative if current increases, else positive if current decreases) that is built at the protein layer upon adsorption.
Measurements of capacitance by non-faradaic electrochemical impedance spectroscopy on a gold surface functionalized like the gate in EGOFET/OECT show an increase in the capacitance in the presence of IL-6 with respect to the same surface not exposed to the cytokine, in accordance with an increase of negative charge induced by the binding of IL-6 to the surface (see Fig. S1, ESI†).
We point out that the net charge of the target analyte cannot be the only determinant to the shifts in the potential drop upon target binding: the nature of the biorecognition unit (e.g. its charge, electrostatic potential, solvation sphere, dipole moment) the presence of a self-assembled monolayer on the gate as well as the device channel can also play a role, albeit we disregard it here.
Analysis of the dose curve with Langmuir and Hill isotherms
We now construct the dose curves at any VGS value by calculating the signal S, corresponding to the current change normalized by the current in the absence of analyte, vs. the concentration c of the target analyte. In Fig. S2 (ESI†), we show two examples of the dose curve, one S(c, VGS = +0.3 V) for OECT (Fig. S2a, ESI†), as this VGS value lies close to the maximum transconductance region in Fig. 2a; the other S(c, VGS = −0.3 V) for EGOFET (Fig. S2b, ESI†), as VGS lies in the sub-threshold region that yields the largest signal S viz. where the sensor exhibits the highest sensitivity (see Fig. S3, ESI†).10,13,14,36 Both dose curves exhibit monotonic trends vs. c then tends to saturate for c greater than 10 nM. Thus, our biosensors respond across four orders of magnitude of c, from 1 pM to 10 nM, these values being within the significant patho-physiological range.To assess the selectivity of both EGOFET and OECT biosensors, we performed control experiments by exposing gate electrodes functionalized with anti-IL-6 antibodies to a high concentration (100 nM) of two potentially interfering cytokines, namely IL-1β and TNFα. The results displayed in Fig. S4 (ESI†), show that the signal S for non-specific targets is about ten times lower than that for 10 nM IL-6.
It is now convenient, for the sake of aligning the discussion to the isotherms introduced above, to renormalize the signal S to its plateau value, that we term Smax. For this, we assume that Smax lies 5% above the experimentally observed maximum. We chose this as plateau value to make our dataset to fall into a representative 95% of the whole statistical set. Then, we calculate the coverage θ as the ratio θ = S/Smax, thus transforming the dose curve S vs. [IL-6] into the θ vs. c curve.
We compare the different isotherm models by fitting θ vs. c data from both OECT and EGOFET with Langmuir (eqn (1a)) and Hill (eqn (2a)) models. Then, we reverse the scheme and fit c vs. θ with Langmuir (eqn (1b)), Hill (eqn (2b)) and Frumkin (eqn (3)) isotherms. We are aware that the reverse fitting strictly holds provided the relative errors on θ and c are comparable.37 We assess the models being used by means of the reduced χ2, viz. χ2 divided by the number of degrees of freedom which is the number of data minus the number of fitting parameters. The results are shown in Fig. 3 top and reported in Tables 1a and b.
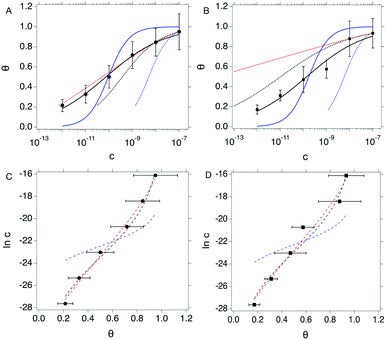 | ||
Fig. 3 Top: θ vs. c plots for OECT (A) and EGOFET (B). Continuous blue and black lines are fit to the Langmuir (eqn (1a)) and Hill (eqn (2a)) isotherms. Dotted blue, black and red lines are fit of the c vs. θ plot to the Langmuir (eqn (1b)), Hill (eqn (2b)) and Frumkin (eqn (3)) isotherms. Bottom: In![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c vs. θ plots for OECT (C) and EGOFET (D). Dashed blue, black and red lines are fit to the Langmuir, Hill and Frumkin isotherms. Error bars represent the associated standard error of the mean SEM. c vs. θ plots for OECT (C) and EGOFET (D). Dashed blue, black and red lines are fit to the Langmuir, Hill and Frumkin isotherms. Error bars represent the associated standard error of the mean SEM. | ||
| Langmuir | Hill | Reverse Langmuir | Reverse Hill | Reverse Frumkin | Reverse Langmuir logarithmic | Reverse Hill logarithmic | Reverse Frumkin logarithmic | |
|---|---|---|---|---|---|---|---|---|
| (a) | ||||||||
| K a (1012) | 1.08 (±0.70) × 10−2 | 1.35 (±0.22) × 10−2 | 2.01 (±0.21) × 10−4 | 2.70 (±0.42) × 10−3 | 3.5771 (± 0.37) | 5.7 (±6.4) × 10−3 | 1.58 (±0.39) × 10−2 | 1.44 (±0.49) |
| α | N/A | 0.344 (±0.019) | N/A | 0.523 (±0.014) | N/A | N/A | 0.368 (±0.021) | N/A |
| g′ | N/A | N/A | N/A | N/A | −10.38 (± 0.11) | N/A | N/A | −9.34 (±0.52) |
| Reduced χ2 | 0.0316 | 0.0006 | 1.0206 × 10−16 | 0.434 × 10−18 | 1.3667 × 10−20 | 7.5503 | 0.3075 | 0.1149 |
| (b) | ||||||||
| K a (1012) | 5.80 (±4.26) × 10−3 | 7.16 (±2.72) × 10−3 | 1.70 (±0.31) × 10−4 | 9.66 (±1.88) × 10−2 | 1.34 (± 1.1) × 108 | 4.75 (±5.30) × 10−3 | 9.19 (±3.34) × 10−3 | 6.09 (±1.69) × 10−1 |
| α | N/A | 0.342 (±0.045) | N/A | 0.287 (±0.006) | N/A | N/A | 0.382 (±0.034) | N/A |
| g′ | N/A | N/A | N/A | N/A | −30.0 (±0.9) | N/A | N/A | −8.71 (±0.45) |
| Reduced χ2 | 0.0393 | 0.0034 | 2.898 × 10−16 | 2.3752 × 10−19 | 2.5964 × 10−19 | 7.4581 | 0.7356 | 0.5765 |
Langmuir isotherm, either as from eqn (1a) (continuous blue line in Fig. 3a and b) and eqn (1b) (dotted blue line in Fig. 3a and b), does not yield a satisfactory fitting both with OECT (Fig. 3a) and EGOFET (Fig. 3b), which hints to the fact that the simple assumption behind this model of independent adsorption events does not hold in the present experiment. We tried to use the Hill equation instead, which turns out to fit much better our experimental data, especially for OECTs, when used in the form (2a) (continuous black line in Fig. 3a and b), whereas does not fit adequately in the form (2b) (dotted black line in Fig. 3a and b) unless one of the two fitting parameters is held constant. This implies that the χ2 function from eqn (2b) is ill-behaving, as it will disregard the residuals from the smallest concentrations. This occurrence is common to most of the fits c vs. θ because the concentration data span four orders of magnitude and the weight of the largest values is predominant. In order to overcome this numerical artifact, we perform the fitting of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c vs. θ (Fig. 3 bottom). This scheme yields a better balanced fit with Hill equation (dashed black lines in Fig. 3c and d), whereas the Langmuir fit still reveals to be inadequate (dashed blue lines in Fig. 3c and d).
c vs. θ (Fig. 3 bottom). This scheme yields a better balanced fit with Hill equation (dashed black lines in Fig. 3c and d), whereas the Langmuir fit still reveals to be inadequate (dashed blue lines in Fig. 3c and d).
A further consideration concerns the result of fitting with Hill isotherm, that yields Hill exponent α values well below 0.5. Specifically, fitting θ vs. c with eqn (2a) yields α = 0.344(±0.019) for OECT and α = 0.341(±0.045) for EGOFET; fitting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c vs. θ from the logarithm of eqn (2b) yields α = 0.368(±0.021) for OECT and α = 0.382(±0.034) for EGOFET. Such a small α value would be interpreted as the result of highly anti-cooperative binding event, and lead to extremely low KH = Kαa values (KH = 3.0 × 104 and 2.3 × 104 for OECT and EGOFET, respectively). We contend that these values hardly apply to a physically-sound description of surface-bound antibody and its antigen.
c vs. θ from the logarithm of eqn (2b) yields α = 0.368(±0.021) for OECT and α = 0.382(±0.034) for EGOFET. Such a small α value would be interpreted as the result of highly anti-cooperative binding event, and lead to extremely low KH = Kαa values (KH = 3.0 × 104 and 2.3 × 104 for OECT and EGOFET, respectively). We contend that these values hardly apply to a physically-sound description of surface-bound antibody and its antigen.
Analysis of the dose curve with Frumkin isotherm
With the aim to assign a chemical-physical rationale to the observed signal, we introduce the Frumkin isotherm, that was originally proposed for describing the adsorption of small molecular adsorbates at electrified interfaces. It is expressed as:38,39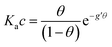 | (3) |
Here the Frumkin parameter g′ is proportional to 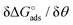 which accounts for the change of the free energy
which accounts for the change of the free energy 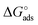 due to the interaction among the adsorbed target-probe pairs. The isotherm eqn (3) holds at the “mean field” level, where positive values of g′ indicate attractive interactions between adsorbed molecules. More precisely, g′ > 0 implies that a larger increase of surface coverage θ occurs with increasing concentration with respect to the case where lateral interactions are negligible, the latter represented by a large mean distance between adsorbed pairs. Conversely, negative g′ values are found when repulsive interactions between adsorbed pair are prevailing. Again, g′ < 0 reflects a smaller increase of surface coverage θ with increasing concentration than in the absence of solute-solute lateral interactions.
due to the interaction among the adsorbed target-probe pairs. The isotherm eqn (3) holds at the “mean field” level, where positive values of g′ indicate attractive interactions between adsorbed molecules. More precisely, g′ > 0 implies that a larger increase of surface coverage θ occurs with increasing concentration with respect to the case where lateral interactions are negligible, the latter represented by a large mean distance between adsorbed pairs. Conversely, negative g′ values are found when repulsive interactions between adsorbed pair are prevailing. Again, g′ < 0 reflects a smaller increase of surface coverage θ with increasing concentration than in the absence of solute-solute lateral interactions.
In order to assess whether one's dataset exhibits Frumkin-like behaviour, it is common practice to fit the linearized data 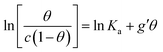 to obtain Ka and g′ from the intercept and slope of the best fit line. In the following, we perform non-linear fitting of c vs. θ directly from eqn (3) keeping both Ka and g′ free variational parameters. The best fit curves are also shown in Fig. 3a and b. We notice that the fit of the OECT data is excellent (dotted red line in Fig. 3a), whereas the fitting of EGOFET data (dotted red line in Fig. 3b) exhibits the bias towards the higher concentrations like Hill model. For EGOFET, it is necessary to perform the fitting of the ln(c) vs. θ to converge properly (dashed red lines in Fig. 3c and d).
to obtain Ka and g′ from the intercept and slope of the best fit line. In the following, we perform non-linear fitting of c vs. θ directly from eqn (3) keeping both Ka and g′ free variational parameters. The best fit curves are also shown in Fig. 3a and b. We notice that the fit of the OECT data is excellent (dotted red line in Fig. 3a), whereas the fitting of EGOFET data (dotted red line in Fig. 3b) exhibits the bias towards the higher concentrations like Hill model. For EGOFET, it is necessary to perform the fitting of the ln(c) vs. θ to converge properly (dashed red lines in Fig. 3c and d).
We now comment on the values of the fitting parameters obtained from Frumkin equation. First, we discuss the association constant Ka. For OECT at VGS = +0.3 V, we find Ka = 3.58 (±0.37) × 1012, whereas by fitting the logarithmic form of eqn (3), we obtain Ka = 1.44 (±0.49) × 1012. For EGOFET at VGS = −0.3 V, the fit converges to physically sound values of the parameters only for the logarithmic form eqn (3) for Ka = 6.09 (±1.69) × 1011. The association constant values are in line with, though slightly higher, for IL-6 binding to antibodies.40–42 From now on, we discuss only the values obtained from the logarithmic form of eqn (3) which resulted into the most stable fitting functional. Converting Ka values into free energy of binding as:
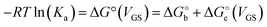 | (4) |
Since the association constant depends on VGS, we analyse its behaviour at different voltage values. In Fig. 4a we overlay the Ka values extracted from ln(c) vs. θ for OECT (VGS values from −0.1 V to 0.4 V, red squares) and those extracted for EGOFET (VGS values from −0.3 V to −0.6 V, red circles).
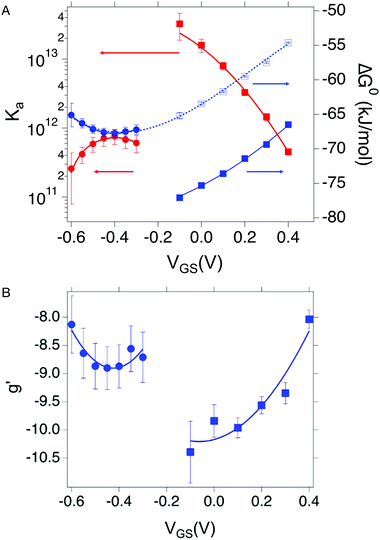 | ||
| Fig. 4 (A) Dependance of Ka (red squares and red circles for OECT and EGOFET, respectively) and its ΔG° (blue solid squares and blue circles for OECT and EGOFET, respectively) vs. VGS. Empty blue squares are ΔG° values for OECT offset by +13 kJ mol−1. (B) Dependance of g′ (blue squares and blue circles for OECT and EGOFET, respectively) vs. VGS. In both (A) and (B) the continuous lines are parabolic fits to each dataset. Dotted blue line in panel A is the best fit with eqn (5). Error bars are the estimated errors from the best fit of the ln(c) vs. θ curves at each VGS value. | ||
Remarkably, in OECTs Ka values span two decades in a VGS range as small as 0.5 V, whereas in EGOFET, Ka changes only four times in a VGS range of 0.3 V. A simple explanation is that for EGOFET in the relevant voltage range the electrode remains in a region of electroneutrality (or modest charge and/or dipole build up), while in OECT the charge/dipole build up is substantial thus making the VGS effects more sizable. In support of this argument, we notice that a vertical translation of the OECT Ka values in the logarithmic scale (hence a re-scaling by a constant factor in the linear scale) would lead to alignment of the two branches (red circles and empty squares) into a continuous variation vs. VGS.
We rationalize this by converting the Ka values into the association free energy ΔG° shown as blue markers on the right axis of Fig. 4a. The gap between the two branches (full circles and full squares) in the proximity of VGS = −0.2 V is accounted by a constant offset of the association free energy values of the OECT. We ascribe this offset to the different chemical potentials that the gate electrode takes in the EGOFET and OECT respectively. Indeed, an upward vertical displacement of the OECT data (full blue squares) by a vertical shift of +13 kJ mol−1 yields the branch with empty blue squares and makes a global polynomial fit of ΔG° (dotted blue curve in Fig. 4a) suitable for interconnecting the whole data set. The rank three of the polynomial hints to charge and dipole build up, accompanied by a dependance of the interfacial capacitance from VGS:
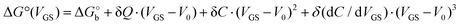 | (5) |
Here V0 is the internal voltage, characteristic of the bound antibody/antigen pair, and accounts for the electrostatic contributions to the free energy in the absence of an external applied voltage. We take it as the minimum of the fitted curve that lies in the proximity of −0.4 V. We find that the (intrinsic) binding contribution is 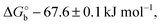 the charge build up is δQ = −2.2 ± 0.6 kC mol−1, the capacitance build up is δC = 38.7 ± 3.0 kF mol−1, and the change of capacitance δ(dC/dVGS) = −19.9 ± 3.2 kF V−1 mol−1. Simple calculations, shown in Fig. S5 (ESI†), allow us to assess that the dominant contribution to the electrostatic free energy comes from the capacitance, although around the electroneutrality point at −0.4 V the dominant contribution is the charge build up.
the charge build up is δQ = −2.2 ± 0.6 kC mol−1, the capacitance build up is δC = 38.7 ± 3.0 kF mol−1, and the change of capacitance δ(dC/dVGS) = −19.9 ± 3.2 kF V−1 mol−1. Simple calculations, shown in Fig. S5 (ESI†), allow us to assess that the dominant contribution to the electrostatic free energy comes from the capacitance, although around the electroneutrality point at −0.4 V the dominant contribution is the charge build up.
We discuss now the Frumkin factor g′, which accounts for the changes in the standard free energy of adsorption ΔG° caused by molecules getting adsorbed on the surface. From the fit of the logarithm of eqn (3) we obtain the following g′ values: −9.34(±0.19) and −8.71(±0.45) for OECT and EGOFET, respectively. In Fig. 4b we show the trend of g′ vs. VGS for OECT and EGOFET. The g′ values of OECT vary more rapidly vs. VGS between −8 and −11, whereas in EGOFET they exhibit a parabolic trend in the proximity of −8. Once again, an upward vertical offset of the OECT data will bring the experimental data onto one continuous curve (data not shown).
To the best of our knowledge, the Frumkin model has not been applied yet to elucidate the thermodynamics of antibody/antigen binding, therefore no reference values can be found in the literature. Yet, the magnitude of the g′ value found here is in line, though slightly higher, with those reported in the literature for organic molecules. Since g′ = −Δμint/RT, negative g′ values correspond to a positive Δμint where −Δμint is the interaction potential between adsorbed species. Thus, adsorption is disfavored as θ increases, due to the presence of repulsive interactions between adsorbed species, either steric or electrostatic, or both.
We stress how the Frumkin model here, despite its simplicity, successfully accounts for the emergence of intermolecular repulsions between the bound antigen/antibody pairs. The result is that the effective association free energy 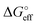 increases (becomes more positive) with respect to its standard value ΔG°:
increases (becomes more positive) with respect to its standard value ΔG°:
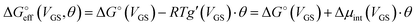 | (6) |
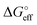 corresponds to what is typically termed the apparent standard free energy when describing adsorption on electrified interfaces.46–48
corresponds to what is typically termed the apparent standard free energy when describing adsorption on electrified interfaces.46–48
To reconciliate the apparent difference between the OECT and EGOFET datasets, we estimate the effective binding constant that we define as:
| Ka,eff(VGS,θ) = Ka(VGS)exp[g'(VGS)θ] | (7) |
Eqn (7) governs the equilibrium at a given VGS and θ. In Fig. 5 we show the top view as contour plot of log10 [Ka,eff(VGS,θ)] for the two device architectures. The values span four and six decades for EGOFET and OECT, respectively, starting from about 1011 and 1013 (almost 1014) at low surface coverage (as in Fig. 4) down to 108 in both cases when θ approaches 1. One appreciates that Ka,eff is largest at low θ (thus making the device sensitivity highest) and decreases by one order of magnitude as θ tends to 2/|g′| ∼ 0.2–0.3. This implies that the sensor, whether is OECT or EGOFET, loses sensitivity due to the electrostatic repulsions of the adsorbed IL-6 already at a few tens percent coverage. We point out that the θ = 0 values in eqn (7) tend to Ka(VGS), that is the association constant that would be predicted by the Langmuir fit in the range of the experimental dataset where the lateral interactions represented by g′ are negligible. A last observation is that the two device architectures have a different sensitivity at low θ values, while they exhibit comparable Ka,eff for large θ values. Noticeably, for large θ values the dependence of Ka,eff on VGS is damped especially for EGOFET.
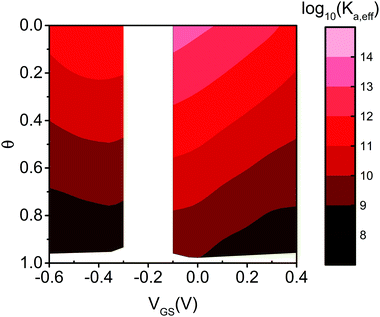 | ||
| Fig. 5 Contour plot of the effective binding constant as Log10 (Ka,eff) as a function of θ and VGS for EGOFET (left strip) and OECT (right strip). | ||
To discuss the sign of the g′ parameter, we start from the consideration that in our case the characteristic length scale of the sensing interface is much larger (several nm) of that of the classical systems treated with the Frumkin isotherm (water and small molecules, viz. a few Å). Therefore, we cannot invoke the competition between adsorbate and the water molecules forming a monolayer at the electrode/electrolyte interface. Moreover, in our gate electrode, the presence of a mixed SAM, and the further immobilization of the antibodies, moves the first hydration layer further outwards from the electrode surface. We then expect that the interaction between the charged surface and the water dipoles are much weaker here than in the case of adsorption of species at a bare electrified surface. Therefore, in our case, we propose that the charges present on the protein surface (target, probe, and their complex), and the intermolecular interactions between them are responsible for the observed sign of g′ as well as its dependence on the gate potential.
From inspection of the three-dimensional structure of IL-6 (PDB code: 1 ALU), it is apparent that several residues with charged side chains are present. By running a structure-based prediction of their protonation state using the PropKa server,49 we predict that all the Glu and Asp residues are surface exposed and likely deprotonated to yield a negative charge, while all Arg and Lys in the sequence, whose sidechains are most likely positively charged, are also exposed to the surface. Estimation of the protein isoelectric point (pI) with different web servers yields pI values around 6.2 and a predicted net protein charge at physiological pH of about −2.
We also calculated the surface electrostatic potential for IL-6 (see Fig. S6, ESI†). It is apparent that the location of the charged and polar aminoacidic side chains yields regions of markedly positive (larger than 5 kT e−1) and negative (smaller than −5 kT e−1) electrostatic potential on the protein surface rather than an even distribution. We also estimated the protein dipole moment using a dedicated web server50 and found a value of 385 Debye that is close to the average dipole moment that was estimated for more than 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 unique chains deposited in the Protein Data Bank (543(±420) Debye). Our analyses indicate that IL-6 is negatively charged at the operational pH, resulting from a constellation of charged side chains exposed to the solvent, and that it also bears a large dipole moment. These arguments support the possible relevance of electrostatic interactions between adsorbed IL-6 molecules in contributing to g′.
000 unique chains deposited in the Protein Data Bank (543(±420) Debye). Our analyses indicate that IL-6 is negatively charged at the operational pH, resulting from a constellation of charged side chains exposed to the solvent, and that it also bears a large dipole moment. These arguments support the possible relevance of electrostatic interactions between adsorbed IL-6 molecules in contributing to g′.
Conclusions
In this work, we assessed IL-6 biosensors operating with the same gate and different architectures, viz. OECT and EGOFET, for transduction of the biorecognition. We demonstrated that the Frumkin isotherm well describes the dose curves obtained by either EGOFET or OECT biosensors operating with functionalized gates. Albeit by eye the fitting result appears comparable to the Hill isotherm; a more careful analysis carried out for the IL-6/anti-IL-6 pair in this work shows that Frumkin provides better estimators of good fit than Hill, with the same number of variational parameters, and largely overcomes the performance of Langmuir.A clear advantage of Frumkin isotherm is that it provides a clear physical view of the competing or synergic phenomena that affect the biorecognition at the gate electrode of either OECT and EGOFET sensors, in terms of coverage-dependent interactions of the adsorbed pairs. In the present work, repulsions between adsorbed IL-6 molecules were identified as the main source of competing interaction that led to negative values of the Frumkin parameter g′.
An important consequence is that, differently from Hill isotherm, Frumkin isotherm yields reliable values of the association constant, in line with literature data from independent techniques, and envisions a “decrease of specificity and sensitivity” by the sensor as the effective binding constant decreases exponentially with coverage.
On the one hand, the results give us confidence for using this model in the quantitative studies of the thermodynamics of recognition. The analysis of free energy carried out with Frumkin unifies the results obtained either by OECT and EGOFET. Since the gate functionalization is the same for both architectures, this suggests that the response of the sensors, that we fit to the Frumkin model, is genuinely due to events taking place at the gate/electrolyte interface. We highlight that in the limit of low coverage the Frumkin model provides the response predicted by Langmuir's, and hence retains a consistent description of equilibria, which instead is not explicitly defined in Hill's.
On the other hand, application of Frumkin isotherm allows us to estimate the effective range of coverage viable for sensing in terms of the Frumkin parameter. Our analysis suggests that the (absolute) value of g′ can be used as a guideline for the tailoring of the gate functionalization, mainly targeting the areal density of recognition sites that keeps the effective binding constant as close as possible to the maximum value. This implies that it is neither necessary nor optimal to seek for achieving a probe coverage of the electrode close to unity, and that strategies of probe dilution” on the electrode may be effective in order to minimize |g′| when this is negative. The Frumkin parameter may indeed be a viable estimator for comparing different functionalization strategies.
Experimental
Device fabrication
The test patterns (TPs) of 1 cm2 total area were purchased from “Fondazione Bruno Kessler” (Trento, Italy). They feature four source-drain interdigitated electrodes patterned by photolithography and lift-off. EGOFET TPs have a channel width/length (W/L) = 2000, while OECT TPs have a W/L = 50. The Au electrodes are 50 nm thick with a few nm of Cr adhesive layer on a quartz substrate. TPs were cleaned before the semiconductor deposition following the standard procedure: (i) a first rinse with acetone (5 mL) to remove the photoresist layer, (ii) gently drying with nitrogen flow, (iii) washing again in hot acetone (70 °C) for 10 minutes, and (iv) gently drying with nitrogen flow; a final cleaning step (v) in piranha solution (H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2 1
H2O2 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for one minute at 150 °C, followed by (vi) abundant rinsing with water, and (vii) drying with nitrogen flow. EGOFET: 80 μL of 2% TIPS-pentacene diluted in hexane:toluene (20
1) for one minute at 150 °C, followed by (vi) abundant rinsing with water, and (vii) drying with nitrogen flow. EGOFET: 80 μL of 2% TIPS-pentacene diluted in hexane:toluene (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80) solvent was deposited on the quartz substrate by spin coating (600 rpm for 15′′) and dried in a solvent vapour rich environment at 60 °C for 30′. OECT: PEDOT:PSS solution was prepared adding 0.2% of 3-(glycidyloxypropyl)trimethoxysilane (glymo) and 5% of dimethyl sulfoxide and was deposited on the quartz substrate by spin coating (500 rpm for 3′′ and 2000 rpm for 20′′). The film was finally dried under heating conditions at 120 °C for 45′.
80) solvent was deposited on the quartz substrate by spin coating (600 rpm for 15′′) and dried in a solvent vapour rich environment at 60 °C for 30′. OECT: PEDOT:PSS solution was prepared adding 0.2% of 3-(glycidyloxypropyl)trimethoxysilane (glymo) and 5% of dimethyl sulfoxide and was deposited on the quartz substrate by spin coating (500 rpm for 3′′ and 2000 rpm for 20′′). The film was finally dried under heating conditions at 120 °C for 45′.
Gate functionalization
Polycrystalline gold wire was used as gate electrode, it was cleaned through (i) immersion in KOH at 130 °C for 4 hours, followed by abundant rinsing with water, (ii) and a final immersion in concentrated H2SO4 at 220 °C for 2 hours.Anti-IL-6 antibodies were immobilized on the gold gate surface according to the following protocol: (i) a first overnight incubation step in mixture of SAM-forming molecules (11-mercaptoundecanoic acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6-mercaptohexanol 1
6-mercaptohexanol 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in ethanol) at room temperature (RT), (ii) immersion in a solution of 200 nM N-(3-dimethylaminopropyl)-N′-ethylcarbodiimide hydrochloride (EDC) and 50 mM N-hydroxysuccinimide (NHS) in water. (iii) Incubation in phosphate buffer saline (50 mM PBS, pH 7.4) of anti-IL-6 antibody (0.1 mg mL−1) for one hour, and (iv) immersion in 0.5 M ethanolamine (ETA) in buffered solution for 30 minutes at RT. These steps were followed by a final incubation with BSA (0.1 mg mL−1 solution) for 30 minutes at RT and thoroughly rinsed with PBS. In the case of the experiments with OECT, a mixture of BSA and 0.05% Tween 20 was used as final step for the gate functionalization.
3 in ethanol) at room temperature (RT), (ii) immersion in a solution of 200 nM N-(3-dimethylaminopropyl)-N′-ethylcarbodiimide hydrochloride (EDC) and 50 mM N-hydroxysuccinimide (NHS) in water. (iii) Incubation in phosphate buffer saline (50 mM PBS, pH 7.4) of anti-IL-6 antibody (0.1 mg mL−1) for one hour, and (iv) immersion in 0.5 M ethanolamine (ETA) in buffered solution for 30 minutes at RT. These steps were followed by a final incubation with BSA (0.1 mg mL−1 solution) for 30 minutes at RT and thoroughly rinsed with PBS. In the case of the experiments with OECT, a mixture of BSA and 0.05% Tween 20 was used as final step for the gate functionalization.
Electrical characterization
Electrical measurements were acquired in 50 mM PBS, pH 7.4, containing a constant concentration of 0.1 mg mL−1 BSA (and 0.05% Tween 20 in the case of OECT-based biosensor) and increasing concentrations of IL-6 (from 1pM to 100 nM), confined in a polydimethylsiloxane (PDMS) pool under static conditions. All electrical measurements were performed at RT inside a Faraday cage with a Agilent B2912A Source Measure Unit, by applying a sweeping gate-source voltage (VGS) from −0.1 V down to −0.6 V and at a fixed drain-source (VDS) voltage of −0.2 V. EGOFETs were operated at VDS = −0.2 V and sweeping VGS from −0.1 V to −0.6 V, while OECTs were operated at VDS = −0.2 V and sweeping VGS between −0.2 V to 0.4 V VGS.Transfer curves were repeatedly acquired until stabilization was achieved, i.e., the last five transfer curves superimposed.
The experimental values in Fig. 3 are the average of the measurements performed for five (n = 5) OECT and n = 5 EGOFET devices, except for [IL-6] = 100 nM for EGOFET for which n = 4. Error bars represent the associated standard error of the mean.
Control experiments
Control experiments were performed in triplicate for both EGOFET and OECT biosensors using the same electrical parameters used for sensing experiments. Electrical responses were registered in presence of a high concentration (viz. 100 nM) of two potentially interfering cytokines, namely IL-1β and TNFα.Reagents
Acetone, BSA, glymo, DMSO, EDC, ethanol, ethanolamine, hexane, hydrogen peroxide, 6-mercaptohexanol, 11-mercaptoundecanoic acid, NHS, phosphate salts, potassium hydroxide, sulfuric acid, toluene, Tween 20 were purchased from Merk-Sigma Aldrich. TIPS-pentacene and PEDOT:PSS were purchased by Ossila ltd. Anti-IL-6 monoclonal antibody (677B 6A2) was purchased by Invitrogen, and recombinant human IL-6 (Cat.-no: 200-031) from ReliaTech GmbH.Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. B. would like to dedicate this work to Concepciò Rovira and Jaume Veciana with whom he had a long lasting, fruitful and diversified collaboration on several advanced topics of materials chemistry. This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 813863. This work was also funded by EuroNanoMed III project “AMI”. The authors thank PRIN2017-NiFTy (2017MYBTXC) for support. MS was supported by Fondazione Umberto Veronesi.References
- M. Berggren and A. Richter-Dahlfors, Adv. Mater., 2007, 19, 3201–3213 CrossRef CAS.
- L. Torsi, M. Magliulo, K. Manoli and G. Palazzo, Chem. Soc. Rev., 2013, 42, 8612 RSC.
- J. Rivnay, R. Owens and G. Malliaras, Chem. Mater., 2013, 26, 679–685 CrossRef.
- X. Strakosas, M. Bongo and R. M. Owens, J. Appl. Polym. Sci., 2015, 132, 1–14 CrossRef.
- D. T. Simon, E. O. Gabrielsson, K. Tybrandt and M. Berggren, Chem. Rev., 2016, 116, 13009–13041 CrossRef CAS PubMed.
- D. Wang, V. Noël and B. Piro, Electronics, 2016, 5, 9 CrossRef.
- P. Lin and F. Yan, Adv. Mater., 2012, 24, 34–51 CrossRef CAS PubMed.
- A.-M. Pappa, O. Parlak, G. Scheiblin, P. Mailley, A. Salleo and R. M. Owens, Trends Biotechnol., 2018, 36, 45–59 CrossRef CAS PubMed.
- J. Rivnay, S. Inal, A. Salleo, R. M. Owens, M. Berggren and G. G. Malliaras, Nat. Rev. Mater., 2018, 3, 17086 CrossRef CAS.
- M. Berto, S. Casalini, M. Di Lauro, S. L. Marasso, M. Cocuzza, D. Perrone, M. Pinti, A. Cossarizza, C. F. Pirri, D. T. Simon, M. Berggren, F. Zerbetto, C. A. Bortolotti and F. Biscarini, Anal. Chem., 2016, 88, 12330–12338 CrossRef CAS PubMed.
- M. Y. Mulla, E. Tuccori, M. Magliulo, G. Lattanzi, G. Palazzo, K. Persaud and L. Torsi, Nat. Commun., 2015, 6, 6010 CrossRef CAS PubMed.
- E. Macchia, K. Manoli, B. Holzer, C. Di Franco, M. Ghittorelli, F. Torricelli, D. Alberga, G. F. Mangiatordi, G. Palazzo, G. Scamarcio and L. Torsi, Nat. Commun., 2018, 9, 3223 CrossRef PubMed.
- C. Diacci, M. Berto, M. Di Lauro, E. Bianchini, M. Pinti, D. T. Simon, F. Biscarini and C. A. Bortolotti, Biointerphases, 05F401, 2017, 12 Search PubMed.
- M. Berto, C. Diacci, R. D’Agata, M. Pinti, E. Bianchini, M. Di Lauro, S. Casalini, A. Cossarizza, M. Berggren, D. Simon, G. Spoto, F. Biscarini, C. A. Bortolotti, M. Di Lauro, S. Casalini, A. Cossarizza, M. Berggren, D. Simon, G. Spoto, F. Biscarini and C. A. Bortolotti, Adv. Biosyst., 2018, 2, 1700072 CrossRef.
- A. Tibaldi, L. Fillaud, G. Anquetin, M. Woytasik, S. Zrig, B. Piro, G. Mattana and V. Noël, Electrochem. Commun., 2019, 98, 43–46 CrossRef CAS.
- G. Palazzo, D. De Tullio, M. Magliulo, A. Mallardi, F. Intranuovo, M. Y. Mulla, P. Favia, I. Vikholm-Lundin and L. Torsi, Adv. Mater., 2015, 27, 911–916 CrossRef CAS PubMed.
- S. P. White, K. D. Dorfman and C. D. Frisbie, J. Phys. Chem. C, 2016, 120, 108–117 CrossRef CAS.
- T. Cramer, A. Campana, F. Leonardi, S. Casalini, A. Kyndiah, M. Murgia and F. Biscarini, J. Mater. Chem. B, 2013, 1, 3728 RSC.
- E. Macchia, R. A. Picca, K. Manoli, C. Di Franco, D. Blasi, L. Sarcina, N. Ditaranto, N. Cioffi, R. Österbacka and G. Scamarcio, Mater. Horiz., 2020, 7, 999–1013 RSC.
- K. Guo, S. Wustoni, A. Koklu, E. Díaz-Galicia, M. Moser, A. Hama, A. A. Alqahtani, A. N. Ahmad, F. S. Alhamlan, M. Shuaib, A. Pain, I. McCulloch, S. T. Arold, R. Grünberg and S. Inal, Nat. Biomed. Eng., 2021, 5, 666–677 CrossRef CAS PubMed.
- C. Liao, M. Zhang, M. Y. Yao, T. Hua, L. Li, F. Yan, C. Mak, M. Zhang, H. L. W. Chan and F. Yan, Adv. Mater., 2015, 27, 676–681 CrossRef CAS PubMed.
- M. Galliani, C. Diacci, M. Berto, M. Sensi, V. Beni, M. Berggren, M. Borsari, D. T. Simon, F. Biscarini and C. A. Bortolotti, Adv. Mater. Interfaces, 2020, 7, 2001218 CrossRef CAS.
- J. Nissa, P. Janson, D. T. Simon and M. Berggren, Appl. Phys. Lett., 2021, 118, 53301 CrossRef CAS.
- R. A. Picca, K. Manoli, E. Macchia, L. Sarcina, C. Di Franco, N. Cioffi, D. Blasi, R. Österbacka, F. Torricelli, G. Scamarcio and L. Torsi, Adv. Funct. Mater., 2020, 30, 1904513 CrossRef CAS.
- M. Berggren and G. G. Malliaras, Science, 2019, 364, 233–234 CAS.
- M. Sensi, M. Berto, S. Gentile, M. Pinti, A. Conti, G. Pellacani, C. Salvarani, A. Cossarizza, C. A. Bortolotti and F. Biscarini, Chem. Commun., 2021, 57, 367–370 RSC.
- M. Larisika, C. Kotlowski, C. Steininger, R. Mastrogiacomo, P. Pelosi, S. Schütz, S. F. Peteu, C. Kleber, C. Reiner-Rozman, C. Nowak and W. Knoll, Angew. Chem., Int. Ed., 2015, 54, 13245–13248 CrossRef CAS PubMed.
- S. P. White, K. D. Dorfman and C. D. Frisbie, Anal. Chem., 2015, 87, 1861–1866 CrossRef CAS PubMed.
- C. Kotlowski, M. Larisika, P. M. Guerin, C. Kleber, T. Kröber, R. Mastrogiacomo, C. Nowak, P. Pelosi, S. Schütz, A. Schwaighofer and W. Knoll, Sens. Actuators, B, 2018, 256, 564–572 CrossRef CAS.
- C. Bonazza, J. Zhu, R. Hasler, R. Mastrogiacomo, P. Pelosi and W. Knoll, Sensors, 2021, 21 Search PubMed.
- M. Selvaraj, P. Greco, M. Sensi, G. D. Saygin, N. Bellassai, R. D’Agata, G. Spoto and F. Biscarini, Biosens. Bioelectron., 2021, 182, 113144 CrossRef CAS PubMed.
- L. Sansone, E. Macchia, C. Taddei, L. Torsi and M. Giordano, Sens. Actuators, B, 2018, 255, 1097–1104 CrossRef CAS.
- K. A. Dill, S. Bromberg and D. Stigter, Molecular driving forces: statistical thermodynamics in biology, chemistry, physics, and nanoscience, Garland Science, 2010 Search PubMed.
- S. Goutelle, M. Maurin, F. Rougier, X. Barbaut, L. Bourguignon, M. Ducher and P. Maire, Fundam. Clin. Pharmacol., 2008, 22, 633–648 CrossRef CAS PubMed.
- D. Gentili, P. D’Angelo, F. Militano, R. Mazzei, T. Poerio, M. Brucale, G. Tarabella, S. Bonetti, S. L. Marasso, M. Cocuzza, L. Giorno, S. Iannotta and M. Cavallini, J. Mater. Chem. B, 2018, 6, 5400–5406 RSC.
- X. P. A. Gao, G. Zheng and C. M. Lieber, Nano Lett., 2010, 10, 547–552 CrossRef CAS PubMed.
- W. H. Press, H. William, S. A. Teukolsky, W. T. Vetterling, A. Saul and B. P. Flannery, Numerical recipes: The art of scientific computing, Cambridge University Press, 3rd edn, 2007 Search PubMed.
- L. Bard and A. Faulkner, Electrochemical methods: fundamentals and applications, 2001 Search PubMed.
- R. Guidelli and G. Aloisi, Electrified Interfaces Phys., Chem. Biol., 1992, 337–367 CAS.
- E. Alfinito, M. Beccaria and M. Ciccarese, Biosensors, 2020, 10, 106 CrossRef CAS PubMed.
- C. Blanchetot, N. De Jonge, A. Desmyter, N. Ongenae, E. Hofman, A. Klarenbeek, A. Sadi, A. Hultberg, A. Kretz-Rommel, S. Spinelli, R. Loris, C. Cambillau and H. de Haard, J. Biol. Chem., 2016, 291, 13846–13854 CrossRef CAS PubMed.
- S. Shaw, T. Bourne, C. Meier, B. Carrington, R. Gelinas, A. Henry, A. Popplewell, R. Adams, T. Baker, S. Rapecki, D. Marshall, A. Moore, H. Neale and A. Lawson, MAbs, 2014, 6, 773–781 CrossRef PubMed.
- J. P. Landry, Y. Ke, G.-L. Yu and X. D. Zhu, J. Immunol. Methods, 2015, 417, 86–96 CrossRef CAS PubMed.
- B. C. Braden, W. Dall’Acqua, E. Eisenstein, B. A. Fields, F. A. Goldbaum, E. L. Malchiodi, R. A. Mariuzza, F. P. Schwarz, X. Ysern and R. J. Poljak, Pharm. Acta Helv., 1995, 69, 225–230 CrossRef CAS PubMed.
- H. J. Gould, B. J. Sutton, A. J. Beavil, R. L. Beavil, N. McCloskey, H. A. Coker, D. Fear and L. Smurthwaite, Annu. Rev. Immunol., 2003, 21, 579–628 CrossRef CAS PubMed.
- B. E. Conway and E. Gileadi, Can. J. Chem., 1964, 42, 90–106 CrossRef CAS.
- R. Parsons, Trans. Faraday Soc., 1958, 54, 1053–1063 RSC.
- E. Blomgren and J. O. M. Bockris, J. Phys. Chem., 1959, 63, 1475–1484 CrossRef CAS.
- M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed.
- C. E. Felder, J. Prilusky, I. Silman and J. L. Sussman, Nucleic Acids Res., 2007, 35, W512–W521 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental Data: Raw experimental data are available at Zenodo. See DOI: 10.1039/d1tc02546e |
| This journal is © The Royal Society of Chemistry 2021 |
