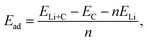Ultra-low content-induced intercalation anomaly of graphite anode enables superior capacity at sub-zero temperatures

Abstract

The rapid development of energy storage devices has driven Li-ion batteries (LIBs) to strive for higher performance, better safety, and lower cost and the ability to operate over a wide range of temperatures. However, most LIBs are used only in favorable environments rather than in extreme conditions, such as in ocean exploration, tropical areas, high altitude drones, and polar expeditions. When chronically or periodically exposed to these harsh environments, conventional LIBs fail to operate due to hindered ion conductivity, interfacial issues, and sluggish desolvation of Li-ion. Additionally, graphite has been recognized as a state-of-the-art LIB negative electrode due to its mechanical stability, electrical conductivity, cost-efficiency, and abundant availability. However, the limited Li⁺ storage capacity of 372 mA h g⁻¹ via LiC₆ coordination has become a bottleneck, hindering its further application in next-generation LIBs. Herein, we reported an intercalation anomaly under ultra-low graphite content that enables the super-lithiation stage in the electrode. The ultrahigh rate capability (2200 mA h g⁻¹ at 1C and 1100 mA h g⁻¹ at 30C) in the graphite anode was achieved by reducing its amount within the electrode and adding more conductive filler to the electrode, creating a highly conductive system. When operated at −20 °C, the ultra-low graphite anode maintained 50% capacity (1100 mA h g⁻¹) at room temperature and ranked the best among LIB anodes toward commercialization. Systematic spectroscopy analysis revealed additional capacitive behavior and distinct structural evolution that led to a Li⁺ intercalation anomaly (up to LiC₂) in the ultra-low graphite content electrode, significantly enhancing its capacity beyond 372 mA h g⁻¹. Additionally, when the battery was operated at sub-zero temperatures, this unique electrode structure with a higher conductive environment helped overcome the sluggish desolvation process at the interface and slow diffusion in the bulk electrodes. This finding sheds new light on graphite chemistry and paves the way for the development of anode-less lithium-ion batteries.

---

Introduction

Li-ion batteries (LIBs) have significantly affected modern society starting from portable energy storage devices and have been making their way towards electric vehicle applications.¹ These wide range of applications and increasing energy demand have pushed LIBs to maximize their storage capability and broaden their operation temperature. However, most LIB studies have primarily focused on the development of high specific energy materials, and the key parameters of energy efficiency regarding their commercialization are often neglected.^2,3 Thus, next-generation LIBs require novel electrode materials that are not only capable of providing high capacity and robust architectures but also able to increase energy efficiency by reducing the production cost and operating under wide range temperatures.^2,4–6 In this context, the issue related to the decayed performance of LIBs at low temperatures has become one of the main obstacles restricting their applications at high altitudes or latitudes and in certain defense and space applications.^7,8 This issue is mainly associated with several factors: low ionic conductivity of the electrolyte,^9,10 limited Li⁺ diffusivities,^11,12 and increased interfacial charge-transfer resistant.^13–15

In general, the LIB anode experiences a multi-stage process during lithiation. First, the Li-ions in the solvated form migrate from the bulk electrolyte to the surface of the electrode, which resembles the ionic conductivity of the electrolyte. Second, the Li-ions were released from the solvated form (desolvation process) at the electrode/electrolyte interface. Third, the desolvated Li-ions were further migrated through the solid electrolyte interphase (SEI) layer and then into the electrode, corresponding to the SEI resistance and solid-state diffusion process in the bulk material. Notably, these processes are significantly impacted by the temperature, especially when the operating temperature dropped to sub-zero. Various approaches have been proposed to enhance LIB performance under low-temperature operation, such as tuning electrolyte composition,^16,17 developing electrolyte additive,^18–21 and utilizing a series of nanostructure materials.^22–25 However, improvement of cycling stability associated with charge–discharge behavior at low temperatures has remained very difficult.^19,26–30

In addition, graphite has been widely used as an anode material owing to its excellent mechanical stability, electrical conductivity, abundant availability, and relatively low cost.¹ However, the limited specific capacity of 372 mA h g⁻¹ achieved by only inserting Li⁺ into the LiC₆ composition between the graphene layers severely impeded its further application as next-generation LIB electrodes.^1,3,31 Previous studies have reported that the specific capacity of graphite can be enhanced beyond LiC₆: the higher specific capacities of graphite with 900 mA h g⁻¹,³² and 1660 mA h g⁻¹,³³ can be achieved by strategies such as heat treatment (pyrolysis at 700 °C) and operation under extreme conditions (beyond 100 °C), respectively. Unfortunately, these treatments are considered costly and thus burden their practical applications. In addition, the mechanism of the relatively high specific capacity of graphite remains under debate. Several approaches have been proposed to improve the electrochemical performance of graphite under low-temperature operation, such as using mild oxidation,^34,35 adding metallic particles,^36,37 chemical doping,^38,39 and surface coating.^40,41 Nevertheless, the sluggish desolvation process at the interface and slow diffusion in the bulk electrodes again led to the failure of LIBs at low-temperature.^7,30,42,43

In light of the high specific capacity and minimal prime cost, herein, we report a Li⁺ intercalation anomaly within ultra-low graphite content that dramatically enhances the storage capacity. Reducing the graphite weight percentage while increasing the conductive filler in the electrode aims to facilitate capacitive-like behavior and enhance Li⁺ diffusivity in LIBs, which is expected to improve the desolvation Li-ion process and interfacial conductivity of the graphite anode during low-temperature operation. In brief, various anode electrodes with different graphite contents are fabricated in this study, namely, G10 (graphite 10 wt%), G20 (graphite 20 wt%), G30 (graphite 30 wt%), G40 (graphite 40 wt%), and G80 (graphite 80 wt%). An electrode without graphite, SP80, was fabricated as a control. Surprisingly, the ultra-low graphite contents (G10 and G20) exhibited a significantly different behavior from that of the high graphite content (G80). The use of low graphite content anodes, G10 and G20, leads to superior specific capacities of 2200 and 980 mA h g⁻¹, respectively, exceeding that of the commercial graphite anode (372 mA h g⁻¹) at room temperature. Furthermore, owing to the unique features, such as a high diffusion coefficient and additional pseudocapacitive contribution to the ultra-low graphite content, the G10 anode exhibited an extremely high low-temperature performance of 1100 mA h g⁻¹ (50% capacity retention than that at room temperature) when it was operated at −20 °C. Various electrochemical methods combined with comprehensive characterization techniques and simulation studies are performed to elucidate this distinct anomaly of graphite anodes.

Results and discussion

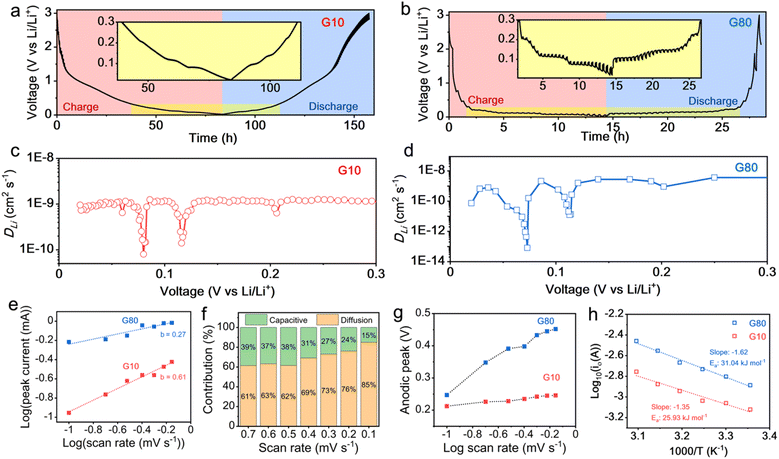
To probe the behavior of different percentages of graphite anodes during the insertion/extraction of Li⁺, a series of electrochemical measurements are first performed under room temperature conditions. First, cyclic voltammetry (CV) measurements are performed to observe the redox potentials of different percentages of graphite anodes. As shown in Fig. 1a and b, four major reduction peaks are observed in the cathodic scan of G10 (Fig. 1a), while G80 (Fig. 1b) exhibits only two major peaks. These multiple reduction peaks on the cathodic scan are represented by multi-stages of Li⁺ insertion during electrochemical processes.^44,45 The first peak at ∼0.9 V is preferential to the initial stage of the lithiation process, which begins with Li⁺ adsorption on the outermost layers of graphite owing to a higher conductive environment in the electrode. This distinct Li⁺ uptake in the graphitic carbon materials at a relatively higher voltage than 0.25 V is also observed in previous reports.^32,46–49 Furthermore, the second peak at 0.2 V can be assigned to the follow-up process from the Li⁺ adsorption process. In this phase, Li⁺ starts to be inserted into the outermost layer of the graphite, which could be signed as stage IV intercalation (30C + Li_(s) ⇌ LiC₃₀). This process is followed by continuous Li⁺ intercalation into more inner layers of graphite, as indicated by the minor peak at 0.15 V, which is an indication of stage III intercalation (LiC₃₆ + Li_(s) ⇌ 2LiC₁₈). The third and fourth peaks located at 0.1 and 0.05 V are attributed to the further Li⁺ intercalation in graphite layers presumably linked as deep intercalation stage II (1/2 LiC₁₈ + Li_(s) ⇌ 3/2 LiC₆) and stage I (6C + Li_(s) ⇌ LiC₆), respectively.

Fig. 1 Electrochemical performance of different graphite contents at room temperature. (a) and (b) Are the cyclic voltammograms of G10 and G80, respectively. The inset figure is the zoom-in on the potential of 0.02–0.3 V. (c) and (d) Are the selected charge–discharge profiles of G10 and G80, respectively, at 1C (1C: 372 mA h g⁻¹). (e) Capacity profile of half-cell LIB with electrodes containing different percentages of graphite. (f) Rate performance of G10 (black), G20 (purple), and G80 (red).

On the contrary, only two major peaks can be monitored for G80 (Fig. 1b) at 0.19 and 0.08 V during cathodic scan, which could be associated with stage IV and stage II intercalation, respectively. The missing reduction peaks of ∼0.9 and 0.05 V could indicate a minimum utilization of interlayer graphite under a high percentage in the electrode (G80). Additionally, the appearance of four major peaks in the cathodic scan can be observed in G20, G30 and G40 (Fig. S1†), indicating an excellent occurrence of Li⁺ intercalations into graphitic layers at low graphite content in the electrode. Notably, no redox peaks can be monitored on the SP80 electrode during CV measurement (Fig. S1d†), indicating that no specific redox reaction occurs in this electrode during the electrochemical process. This further implies that most electrochemical responses in the CV were caused by redox reactions within graphite particles.

In agreement with the CV results in Fig. 1a, the galvanostatic charge/discharge profile of G10 (Fig. 1c) denotes four different plateaus at 0.9, 0.2, 0.1 and 0.05 V, which correlates to their Li⁺ intercalation stages during the lithiation process. Interestingly, these four plateaus brought a significant increase in capacity for G10 up to 2200 mA h g⁻¹ after 100 cycles at 1C. This outstanding specific capacity is nearly six times higher than that of conventional graphite (372 mA h g⁻¹) via LiC₆ formation. Additionally, these four voltage plateaus can be observed on G20, G30, and G40, resulting in the Li⁺ storage capacity beyond 372 mA h g⁻¹ (Fig. S2†). However, G80 showed only two different plateaus at 0.2 and 0.1 V with a specific capacity of 230 mA h g⁻¹ at 1C (Fig. 1d). Notably, when the same charge–discharge rate of 1C was applied, G10 exhibited a significantly longer time (∼6 hours) to reach the fully lithiated stage at 0.02 V (Fig. 1c), while G80 required only 0.6 hours (Fig. 1d). This obvious time difference also suggests that reducing graphite content in the electrode could lighten graphitic layer utilization, thus having a significant impact on achieving extremely high specific capacity. Following the superior performance of G10, batteries with G20, G30, G40 and G80 exhibited capacities of ∼980 mA h g⁻¹, ∼580 mA h g⁻¹, ∼340 mA h g⁻¹ and ∼230 mA h g⁻¹, respectively (Fig. 1e). Furthermore, the extreme rate capability is demonstrated for G10 and G20 up to 30C (Fig. 1g). Moreover, G10 possessed an extremely high rate capability of ∼1430 mA h g⁻¹ at a relatively high current rate of 30C with excellent stability for up to 2000 cycles (Fig. S3†).

To verify the substantial improvement in graphite specific capacity under a low content in the electrode, we prepared G20 with the increased active material loading into the electrode up to 1.80 mg cm⁻². We also tried to reduce the loading of G80 up to 1.19 mg cm⁻². Surprisingly, the G20 electrode with a higher loading of 1.80 mg cm⁻² still has a high specific capacity of 840 mA h g⁻¹ at 1C (Fig. S4a†), while G80 can only deliver a capacity of 225 mA h g⁻¹. Moreover, a similar trend can be observed in the rate performance (Fig. S4b†), where G20 with high material loading could deliver a specific capacity of 211 mA h g⁻¹ under an extremely high current rate of 30C. Additionally, the specific capacity generated from the SP80 electrode was found to be ∼71 mA h g⁻¹ under 1C (Fig. S5†), indicating that the capacity contributed from the conductive carbon is significantly low compare with the performance of graphite performance under low percentages (G10 and G20). This low specific capacity of SP80 was consistent with the CV (Fig. S1d†), where no specific redox reaction was observed during the electrochemical process. Therefore, this suggests that graphite intercalation anomaly could occur under a lower active material content within the electrode, thus extending and enhancing graphite specific capacity beyond 372 mA h g⁻¹ (traditional LiC₆ intercalation).^1,31,32,48

To examine the effect of graphite content on the Li⁺ storage mechanism, ex situ XRD measurements of low graphite content (G20; Fig. 2a) electrode and high graphite content (G80; Fig. 2b) electrode were performed to evaluate their structural evolution during Li⁺ insertion/extraction. Surprisingly, a distinct structural evolution during Li⁺ insertion/extraction can be observed for the low graphite content of G20 compared to that of G80 (high graphite content). As shown in Fig. 2a, during the lithiation process from 3.0 to 0.14 V (namely, state A1–A3), the diffraction peak of (002) at 26.3° (A1) shifts to a lower value of 25.8° (A3), implying that the graphite interlayer-spacing (d-spacing) increases from 3.33 Å (pristine) to 3.37 Å (A1) and then 3.44 Å (A3). This increasing d-spacing is a result of the early lithiation process associated with the formation of Li⁺ intercalation stage IV (LiC₃₀) and stage III (LiC₁₈) after the Li⁺ adsorption process on the outer layer of graphite.^44,50 Furthermore, a twin diffraction peak associated with the d-spacing of 3.44 and 3.49 Å is obtained at 0.12 V (A4), indicating the transition from Li⁺ intercalation stage III to stage II during the further lithiation process (Fig. 2a). In contrast, intercalation stages III and II of the G80 electrode can only be obtained at a deeper lithiation process at 0.07 V (C6) (Fig. 2b). This suggests that a low graphite content lightens interlayer utilization more than that of a higher content. Furthermore, the G20 electrode with a d-spacing of 3.68 Å (24.1°) is obtained at 0.08 V (A5; Fig. 2a), corresponding to the deep Li⁺ intercalation of stage I (LiC₆ formation) during the lithiation process.⁵⁰ On the contrary, intercalation stage I can only be slightly observed at 0.02 V in the G80 electrode (full charge state; C8), along with the major contribution of stage II (Fig. 2b). This phenomenon further suggests that the low graphite content electrode can be fully lithiated and forms LiC₆ at a higher voltage of 0.08 V, while the higher graphite content electrode at the full charged state of 0.02 V is dominated by stage II with the minor contribution of stage I, indicating a lighten graphite interlayer utilization.^51,52 Additionally, the diffraction peak with a d-spacing of 3.68 Å on the G20 gradually becomes dominant, along with the disappearance of the diffraction peak of 25.38° (d-spacing of 3.49 Å), as the lithiation process proceeds to a deeper potential from A6 (0.07 V) to A10 (0.02 V; full charge stage). This indicates that most graphite interlayers in the G20 electrode are intensively escalated to accommodate larger Li⁺ intercalation than that in the G80 electrode. Therefore, these graphite intercalation anomalies based on the ex situ XRD studies of G20 and G80 imply that further lithiation process beyond the Li⁺ intercalation stage I (LiC₆) possibly occurred during the deep charge process of G20 from A6 (0.07 V) to A10 (0.02 V; full charge stage), thus significantly contributing to boosting the capacity of graphite under a low percentage. Moreover, the reaction process is reversible during the delithiation process.

Fig. 2 Systematic analysis of G20 and G80 at various stages. (a) Selected stages and ex situ XRD spectra of G20 at various charge–discharge stages. Charge process: A1 (0.23 V); A2 (0.17 V); A3 (0.14 V); A4 (0.12 V); A5 (0.08 V); A6 (0.07 V); A7 (0.06 V); A8 (0.05 V); A9 (0.04 V); and A10 (0.02 V). Discharge process: B1 (0.07 V); B2 (0.09 V); B3 (0.13 V); B4 (0.15 V); B5 (0.21 V); B6 (0.23 V); and B7 (0.25 V). (b) Selected stages and ex situ XRD spectra of G80 at various charge–discharge stages. Charge process: C1 (0.23 V); C2 (0.20 V); C3 (0.17 V); C4 (0.14 V); C5 (0.11 V); C6 (0.07 V); C7 (0.03 V); and C8 (0.02 V). Discharge process: D1 (0.07 V); D2 (0.13 V); D3 (0.15 V); D4 (0.18 V); D5 (0.22 V); and D6 (0.25 V). (c) Selected states of ex situ XPS analysis on G20 during the charge process, namely, Q1 (3.0 V); Q2 (0.9 V); Q3 (0.2 V); Q4 (0.15 V); Q5 (0.1 V); Q6 (0.05 V); Q7 (0.03 V); Q8 (0.02 V). (d) and (e) C1s and Li1s XPS spectra of G20 shown at various charge stages. (f) Normalized Li⁺ content in G20 at different charge stages. (g) Selected states on the 2nd charge–discharge process of G80, namely, R1 (3.0 V); R2 (0.9 V); R3 (0.2 V); R4 (0.15 V); R5 (0.1 V); R6 (0.05 V); R7 (0.03 V); and R8 (0.02 V). (h) and (i) C1s and Li1s XPS spectra of G80 shown at various charge stages. (j) Normalized Li content at different charge states of G80.

Additionally, a field emission scanning electron microscope (FESEM) analysis was performed to probe the morphological changes in graphite particles during the electrochemical process. As depicted in Fig. S6b–d,† the interlayer of graphite in G20 was significantly expanded at the full-lithiation state (0.02 V). This interlayer expansion could be ascribed to an intensive Li-ion insertion during the charge process, which is consistent with the ex situ XRD results, where d-spacing of graphite was enlarged from 3.37 (pristine) to 3.68 Å (at full-charge state of 0.02 V) (Fig. 2a). Meanwhile, at the full-discharge state (full de-lithiation at 3.0 V), the well-defined graphite interlayer can be monitored with a minimum expansion (Fig. S6f–h†). This phenomenon suggests the reversible expansion/relaxation of graphite interlayers during the electrochemical process and is consistent with the ex situ XRD results. Notably, a similar graphite interlayer expansion can also be monitored at G20 even after 100 cycles, while no significant changes can be observed for G80 (Fig. S7†). These distinct morphological changes further confirmed the intercalation anomaly of the graphite anode under ultra-low content. Furthermore, a distinct graphite morphological evolution was observed in the ex situ Raman spectroscopy of G10 and G80 before and after 100 cycles (Fig. S8†). As shown in Fig. S8,† typical graphite C–C bonding properties (sp³ (D band) and sp² (G band) carbon) can be observed for both G10 and G80. The D band showed no significant changes in G10 and G80 after 100 cycles although the G band indicated significant peak deformation for G10. As depicted in Fig. S8a,† the G band peak of G10, which was originally located at 1598 cm⁻¹ before cycles, was transformed into two overlapped peaks, namely, G⁺ (1608 cm⁻¹) and G⁻ (1576 cm⁻¹). However, the G band of G80 shifted only shifted from 1590 to 1595 cm⁻¹ after 100 cycles (Fig. S8b†). The shifting of the G band towards the higher wavenumber G⁺ (∼1600 cm⁻¹) is recognized for the intensive interlayer expansion owing to the formation of graphite intercalation compound (GIC) from insertion species, thus increasing the C=C bond length.^53,54 Meanwhile, the lower wavenumber G⁻ (1576 cm⁻¹) indicated the transformation of the sp² carbon bonding configuration or the formation of a shorter sp² chain.^55,56 This ex situ Raman analysis further implied that the graphite under low content in the electrode experienced massive interlayer expansion and structural transformation during the cycling process, which might be due to the intensive Li⁺ insertion into the interlayer of graphite. This observation was again in good agreement with the ex situ XRD and FESEM analysis.

To gain a further understanding of the chemical bonding during the electrochemical process, the ex situ XPS was also performed to evaluate chemical compositions at selected states during 2nd lithiation process, namely, states Q1–Q8 for G20 (Fig. 2c, S9 and S10†) and R1–R8 for G80 (Fig. 2g, S11 and S12†). The ex situ XPS analysis is summarized and presented in Fig. 2e–f for G20 and Fig. 2h–i for G80. As presented in Fig. 2d, the C1s spectra at the initial state, 3.0 V (Q1), showed specific binding energy (BE) of C=C, C–C, C–O, C=O, and CO₃²⁻ at 284.21, 284.76, 286.05, 287.7, and 289.05 eV, respectively. A BE associated with the π–π satellite peak can also be observed at 290.19 eV. Furthermore, an additional BE at 283.2 eV associated with C–Li binding started to appear at 0.9 V (Q2) and continued until Q8, indicating the lithiation process (Fig. 2d). Notably, the π–π satellite peak at 290.19 eV disappeared as the Li⁺ intercalation reached 0.05 V (Q6) (Fig. 2d). This indicates that the π–π interaction between basal planes of graphene was fully utilized to capture Li⁺ during intercalation, thus resulting in a weakened interlayer bonding and increased d-spacing of graphite, which is in good agreement with the ex situ XRD of G20 (Fig. 2a). In contrast, the π–π satellite peak of G80 is visible from the initial state R1 to R7, along with an additional BE at 283.2 eV for C–Li binding, which started to appear from R3 (Fig. 2h), indicating that the abundant π–π electrons in G80 are not occupied by Li⁺ during the charge process. The C1s spectra illustrate that the graphitic interlayers in low graphite content (G20) electrodes are more fully utilized during Li⁺ intercalation than those of high graphite content electrodes (G80). This unique behavior could be responsible for boosting battery performance.

In good agreement with the C1s spectra, the Li1s spectra of G20 showed the LiC₃₀ and LiC₁₈ formation with BE of 54.02 and 53.60 eV at 0.9 V (Q2) (Fig. 2e), respectively, which is recognized as Li⁺ adsorption on the graphite surface (Fig. 1a).^46,47 This phenomenon suggested that Li⁺ started to intercalate in the outer layer of graphite at 0.9 V (Q2), resulting in stage IV and stage III intercalation via the formation of LiC₃₀ and LiC₁₈ during this adsorption process. Furthermore, this process is consistent with ex situ XRD of G20 ranging from 0.23 to 0.17 V (A1 to A2), in which graphite d-spacing increased from 3.33 Å (pristine) to 3.37 and then 3.44 Å (Fig. 2a). As the applied potential is lowered to 0.2 V (Q3), the new BE at 53.40 eV for LiC₁₂ appeared along with LiC₃₀ and LiC₁₈ formation (Fig. 2e), which were no longer observable after 0.05 V (Q5). Interestingly, the BE at 53.35 eV for LiC₆ (stage I) begins to form at 0.1 V (Q5), which is in good agreement with ex situ XRD (Fig. 2a), denoting a better utilization of the graphite interlayer for the G20 electrode than that of G80 (Fig. 2b). Furthermore, an additional BE close to the LiC₂ formation appeared at 53.10 eV along with the existence of LiC₁₂ and LiC₆ when the applied potential reached 0.05 V (Q6; Fig. 2e). Importantly, when the G20 electrode was fully charged at 0.02 V (Q8), the BE of Li–Li (Li°; 52.3 eV) emerged along with LiC₆ and LiC₂ formation. This co-existing three different Li intercalation species at a fully charged state in a low graphite content electrode (G20) could be responsible for the significantly improved Li⁺ storage capability. The appearance of Li° BE could be linked to the increased Li metallic character in the state of LiC₂. In the LiC₂ configuration, it was assumed that all the benzene units from the basal plane of graphene were filled with Li ions. Therefore, the continuous insertion of Li⁺ in LiC₂ configuration further pushes the existing intercalated Li ions closer to one another, thus increasing their metallic character and forming Li–Li covalent bonds.^48,57

Additionally, the ex situ XPS was performed for G10 at different lithiation states, namely, state P1–P8, to probe the Li⁺ intercalation process. As shown in Fig. S13,† G10 behaves almost identically with G20 during the lithiation process. The BE at 283.4 eV can be monitored in the C1s spectra from P2 (0.9 V) and maintained until P8 (0.02 V), suggesting the formation of C–Li binding during the lithiation process (Fig. S13b and S14†). Notably, the π–π satellite peak at 290.10 eV for G10 disappeared when the Li⁺ intercalation process reached 0.15 V (P4) (Fig. S13b and S14†). This is slightly different from that of G20, where the π–π satellite peak disappeared at a lower voltage of 0.05 V (Q6, Fig. 2d) for G20, suggesting a better interlayer utilization of G10 than that of G20. Additionally, the L1s spectra of G10 showed that the Li–Li peak was observed when the lithiation process reached 0.03 V (P7) and 0.02 V (P8; full-lithiation stage) (Fig. S13c–d†), which is consistent with G20 (Fig. 2e–f). These findings reinforce the notion that under ultra-low content in the anode (G10 and G20), graphite could behave significantly different from that of the high-content graphite anode (G80).

The ex situ XPS study demonstrates that further Li intercalation processes beyond LiC₆ can be found in the lower graphite percentage (G10 and G20) via the formation of LiC₂, indicating a graphite intercalation anomaly under a low content electrode. In this intercalation anomaly, a large interlayer expansion of 3.68 Å at the stage of A5–A10 has opened a channel for further Li intercalation processes to form LiC₂. This is in good agreement with the previous study that the superdense Li state (LiC₂) can be formed in the graphitic layers with d-spacing of ∼3.7 Å,^58,59 which is close to the d-spacing of G20 at A10 (Fig. 2a). Moreover, another study reported that further Li⁺ insertion into the bilayer of graphitic carbon (Li_xC₆, x > 1) changes the atomic state of Li from an ionic state to nearly metallic.⁶⁰ Additionally, a recent study reported that the LiC₂ domains could co-exist during the intercalation process even at a capacity of 524 mA h g⁻¹.⁵⁷ On the contrary, Li1s spectra of G80 in Fig. 2i showed a different Li intercalation behavior than that of G20 (Fig. 2d and e). The formation of LiC₃₀ and LiC₁₈ in G80 started from 0.2 V (R3) and remained until fully charged at 0.02 V (R8), while LiC₁₂ began to emerge from R4 and dominate in the Li intercalation stage along with the additional LiC₆ formation at R8 (Fig. 2i). This behavior was consistent with the ex situ XRD spectra of G80 (Fig. 2b). More importantly, the LiC₂ and Li–Li covalent binding cannot be observed in Li1s spectra for the G80 electrode, suggesting a different Li⁺ intercalation mechanism of the G20 electrode. The Li1s spectra of G80 again confirmed that graphite particle behaves significantly different as we lowered the graphite content in the electrode.

Moreover, Fig. 2f depicts the Li–C binding evolution of G20 at different charging states (Q1–Q8) with an appropriate portion contributing to the specific charge, which clearly implies the co-existing three Li intercalation species of LiC₆, LiC₂, and Li–Li covalent bonding formation occurring during the lithiation process. However, the Li–C binding evolution of G80 in Fig. 2j reveals that LiC₁₂ species dominated Li storage, followed by LiC₆ formation at the full charge state (R8). This distinct intercalation behavior in low and high graphite content electrodes demonstrates that graphite intercalation anomalies could occur and boost the specific capacity of the graphite anode. In addition to the contribution of LiC₂ and Li–Li covalent bonding to battery capacity, another study also reported that the Li storage capacity of carbon materials could be significantly increased up to 990 mA h g⁻¹ by forming LiC₂ intercalation.⁶¹ Furthermore, an earlier study by Sato et al.⁴⁸ reported that Li–Li covalent bonding could be formed and loosely trapped upon two adjacent benzene rings in disordered carbon materials, such as graphite. This Li–Li molecule can act as a capacity reservoir for increasing capacity up to 1157 mA h g⁻¹. Furthermore, Fig. 3 shows a schematic illustration of distinct graphite intercalation behaviors under different electrode contents. As shown in Fig. 3, graphite particles experience Li⁺ intercalation anomaly, where most graphitic layers are utilized to accommodate superdense Li⁺ states under low graphite content electrodes. In this superdense Li⁺ intercalation process, three Li intercalation species of LiC₆, LiC₂, and Li–Li covalent bonding formation co-existed within the graphite particles and consequently improved storage capability. In contrast, graphite experienced a dilute Li⁺ intercalation state, where LiC₁₂ species dominated Li storage, followed by LiC₆ formation.

Fig. 3 Schematic illustration of the coexistence of two types of Li sites in graphite anodes at low and high contents. Graphitic layers are represented by hexagonals. Li ions and atoms are denoted by red and blue circles, respectively. Covalent bonds between two Li atoms are shown by blue solid lines.

A series of density functional theory (DFT) calculations were performed to examine the atomistic details of Li⁺ intercalation. Four different Li⁺ intercalation models corresponding to different intercalation stages based on the theoretical studies by Rüdorff–Hoffman (RH) were constructed and relaxed (see Fig. 4), and the respective simulated XRD spectra, intercalation energies, and capacities were computed, as displayed in Fig. S16 and Table S1.† A comparison of diffraction peaks in Fig. 2a and S16 suggests that the ∼24° peak in Fig. 2a (A6–A10) corresponds to Model I intercalation (LiC₂, Fig. 4d). The simulated diffraction peak from the Model IV intercalation (LiC₂₄, Fig. 4a) is also in agreement with the 25.8° peak (A3) in Fig. 2a. Hence, the DFT calculations confirm the presence of the LiC₂ intercalation. The adsorption energy calculations suggested that the LiC₂ is a metastable state of Li⁺ intercalation (see Table S1†). It is important to emphasize that the negative adsorption energies observed in this study result solely from the choice of reference configuration. Here, isolated Li atoms in a vacuum were used as the reference state. If an alternative reference, such as Li metal, were selected, the adsorption energy would be positive.⁵⁷ However, the primary purpose of computing adsorption energies is to gain insight into relative structural stability. Therefore, the absolute sign of the adsorption energy and the specific choice of reference state are not the most critical factors. Moreover, note that the simulated diffraction peaks from Models II and III do not match any of the peaks displayed in Fig. 2a. In particular, Model II corresponds to the LiC₆ intercalation, which also yields the lowest adsorption energy (see Table S1†). These discrepancies may stem from the limitations of DFT calculations, particularly insufficient energy minimization involving cell dimension optimization owing to the high computational cost. In our recent effort to overcome this constraint, we developed a hybrid machine learning (ML) model trained on DFT-calculated energies, particularly in high-capacity regimes, such as LiC₂. This ML model enables large-scale Monte Carlo (MC) simulations of lithium intercalation across a broad range of capacities.⁵⁷ The simulation results suggest that lithium intercalation follows a stepwise progression from higher intercalation stages (e.g., stage VI in ref. 57) toward stage I, which is consistent with the XRD experiments. Furthermore, our study identifies two new superdense GICs:LiC₄ (524 mA h g⁻¹) and LiC₂.₆ (845 mA h g⁻¹). These phases exhibit interlayer spacings comparable to LiC₆, making them difficult to distinguish from LiC₆ based on XRD data alone. From an energetic viewpoint, LiC₄ emerges as the most stable GIC, surpassing even LiC₆, while LiC₂.₆ exhibits an intercalation energy similar to that of LiC₆. These findings from extensive MC simulations suggest the feasibility of stable superdense GICs beyond LiC₆. However, it is important to note that the formation of these superdense phases may be kinetically hindered owing to sluggish lithium diffusion at higher capacities.

Fig. 4 Li⁺ intercalation models. Top/side views of (a) Model IV (LiC₂₄), (b) Model III (LiC₁₂), (c) Model II (LiC₆) and (d) Model I (LiC₂).

Considering the unique behavior of lightened interlayer utilization to a fully optimized graphitic layer and outstanding Li⁺ storage capability at room temperature, the low graphite content presumably allows a rapid Li⁺ transport in the electrodes that is beneficial to overcome the bottleneck of LIB operated at low temperature. To reveal the feasibility of low graphite content as an alternative solution for low-temperature LIB, the galvanostatic intermittent titration technique (GITT) was employed for G10 and G80 at a 0.1C rate (ESI Note 1†). Fig. 5a and b show the typical galvanostatic profiles of the G10 and G80 anodes during GITT measurement, respectively. Interestingly, G10 has a significantly faster Li⁺ diffusion coefficient (D_Li) of ∼10⁻⁹–10⁻¹⁰ cm² s⁻¹ than G80 (∼10⁻⁹–10⁻¹⁴ cm² s⁻¹) during the lithiation process (Fig. 5c and d). As shown in Fig. 5c, the D_Li of G10 decreased up to nearly 10⁻¹⁰ cm² s⁻¹ at potentials of ∼0.11 and 0.8 V owing to the formation of more compact Li–C species of LiC₁₂ and LiC₆, respectively. On the contrary, the D_Li of G80 dramatically decreased up to ∼10⁻¹¹ and ∼10⁻¹⁴ cm² s⁻¹ at potentials of ∼0.11 and 0.8 V (Fig. 5d), indicating a huge barrier for Li⁺ mobility in G80 during the lithiation process. Additionally, a small decrease in D_Li of G10 can be monitored at a potential ∼0.05 V (Fig. 5c), which could be ascribed to the formation of superdense Li intercalation (LiC₂). This further suggests that G10 could provide a significantly faster D_Li than G80 during phase transitions. This phenomenon could be attributed to the minimum resistances between graphite particles inside electrodes and electrolytes owing to a higher conductive environment that allowed a rapid electron transfer, therefore accelerating Li⁺ transport and improving LIB performance. Furthermore, it was consistent with previous studies that, the increased active material amount within the electrode could impinge the ion transport across the electrode during the charge and discharge processes.⁵ It should be noted that the solid-state Li⁺ diffusion acts as a bottleneck for insertion-type materials during the charge storage process, especially at low temperatures.^7,8,42 The increasing conducive environment by reducing the graphite content in G10 enables the fast solid-state diffusion of Li⁺ in the bulk electrode, which circumvents the limiting rate of commonly used electrode architecture.

Fig. 5 Kinetic analysis of G10 and G80. (a) and (b) GITT profiles of G10 and G80, respectively. (c) and (d) D_Li of G10 and G80 during the charge process. (e) The b value is the slope function of the log scan rate (v) vs. log peak current (i) for G10 and G80. (f) Capacitive and diffusion contribution ratios for G10 at different scan rates. (g) Anodic peak shifts of G10 and G80 at various scan rates. (h) Log i₀ vs. 1000/T plot of G10 and G80.

To further probe the ion migration kinetics, a sweep rate CV is carried out with a scan rate ranging from 0.1 to 0.7 mV s⁻¹ for both G10 and G80 (Fig. S17†). According to the power-law relation from sweep rate voltammetry (ESI Note 2†), the b values of G10 and G80 were 0.61 and 0.27 (Fig. 5e), respectively, suggesting that the ion migration in G10 was contributed by the diffusion control process and pseudocapacitive behavior simultaneously, while the G80 was contributed only by the diffusion-controlled process.^62–64 Further quantitative analysis of diffusion and capacitive contribution (ESI Note 2†) on G10 revealed that the proportion of pseudocapacitive-controlled process at the 0.7 mV s⁻¹ was 39% (Fig. 5f). This contribution gradually decreased up to 15% when the scan rate was lowered to 0.1 mV s⁻¹. This phenomenon again confirmed that the Li⁺ storage kinetics were controlled by the diffusion control process and pseudocapacitive behavior simultaneously. Furthermore, the synergic contribution of both diffusion and pseudocapacitive behavior could further explain the superior performance of low graphite content (see ESI Notes 2 and 3†). Another interesting feature is that the anodic peak of G10 was not significantly shifted at various scan rates (Fig. 5g), which was also identified as a combination of diffusion and pseudocapacitive behavior. This feature reported can help overcome the sluggish solid-diffusion process in the electrolyte/electrode interphase,⁴² which is considered one of the most impeding factors for the operation of LIBs at low temperatures. Additionally, electrochemical impedance spectroscopy (EIS) is employed to evaluate the relationship between the exchange current (i₀) and charge transfer resistance at electrode interfaces (R_ct) under different temperatures. This correlation helps to understand and estimate the activation energy of active materials using the following Arrhenius equations: i₀ = RT/nFR_ct and i₀ = A exp(−E_a/RT), where A is the temperature-independent coefficient, R represents the gas constant, T is the operating temperature (K), n represents the number of electrons being transferred, F is the Faraday constant, and E_a represents the apparent activation energy of the active materials in the electrode.^65,66 Considering these equations, the activation energy is estimated as follows: E_a = −Rk ln 10, where k is the slope of the fitting line of the Arrhenius plots (log 10i₀ as a function of 1000/T). Fig. S18† shows the Nyquist plots of the G10 and G80 electrodes at different temperature ranges. As shown in Fig. 5h, the E_a of the G10 and G80 electrodes were estimated to be 25.93 and 31.04 kJ mol⁻¹, respectively. This indicates that reducing graphite content, while increasing the conductive environment in the electrode, could minimize the graphite particle activation energy to store Li⁺.

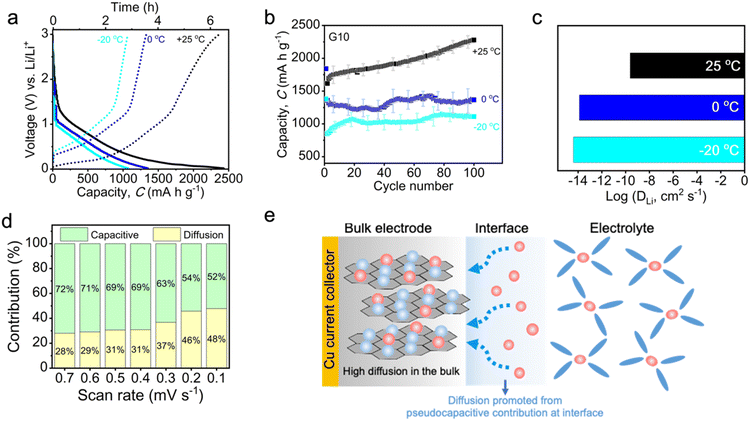
Owing to the unique features of the high diffusion coefficient and additional pseudocapacitive contribution as well as the reduction of activation energy on low graphite content, the G10 could overcome the sluggish desolvation process and slow diffusion in LIBs under low-temperature environments. To clarify this point, the electrochemical performance and kinetic study of G10 at low temperatures were performed and investigated in detail, as presented in Fig. 6. Fig. 6a shows the galvanostatic charge–discharge profile of G10 at various temperatures after 100 cycles. When the battery is operated at 0 °C, G10 can deliver a capacity of 1250 mA h g⁻¹, corresponding with a high capacity retention of 62.5% (1250 mA h g⁻¹/2200 mA h g⁻¹ = 62.5%). This capacity drop could result from sluggish Li⁺ diffusion across electrolyte–electrode at low temperatures. Surprisingly, when the battery reached an even lower temperature of −20 °C, the specific capacity of G10 was still kept at 1100 mA h g⁻¹ (50% capacity retention), indicating a superior performance at sub-zero temperatures. Furthermore, no significant changes can be observed in the galvanostatic profile of G10 at low-temperature operation, suggesting high material stability. In good agreement with the galvanostatic profile, the capacity profile indicates a reduced storage capability from 2200 mA h g⁻¹ to 1250 mA h g⁻¹ and is observed when the operation temperature is lowered from 25 °C to 0 °C (Fig. 6b) owing to limited Li diffusion at low temperature. Notably, the Li storage capacity decreased only slightly from 1250 mA h g⁻¹ to 1100 mA h g⁻¹ when the operation temperature was set at −20 °C. A capacity fluctuation was observed when the battery was operated at 0 °C and exhibited relatively steady cycling performance at −20 °C. This capacity fluctuation can be associated with the increasing electrolyte viscosity under low-temperature operation.⁶⁷ As the operating temperature is at 0 °C, the movement of EC molecules is significantly hindered owing to a higher freezing point (∼35 °C) than that of DEC at −43 °C, thus creating a binary phase condition in the electrolytes. This condition could disturb and create ion flow fluctuation in the electrolyte during the charge/discharge process across the cycles, thus resulting in a significant capacity fluctuation at 0 °C. However, this binary phase becomes a minimum at −20 °C, as the DEC molecule movement is further minimized, thereby resulting in a more steady cycling performance with a decreasing specific capacity of up to 1100 mA h g⁻¹ (Fig. 6b). In a word, the low graphite content electrode of G10 demonstrates the highest performance among the reported low-temperature LIBs in terms of operated temperature, current density and cycling performance (Table S2†).

Fig. 6 Low-temperature performance of G10. (a) and (b) Galvanostatic and capacity profiles at various temperature ranges. (c) D_Li at different temperatures. (d) Capacitive and diffusion contribution ratio at sub-zero temperature (−20 °C). (e) Schematic illustration of the lithiation process of G10 at low temperatures.

To probe the kinetic phenomena under low-temperature operation, the EIS study was again applied under different temperatures. As shown in Fig. S19a and b,† a significant increase in charge-transfer resistance can be monitored when the operation temperature is lowered from 25 °C to −20 °C, suggesting an increased interfacial charge-transfer at low temperatures. Furthermore, the D_Li of G10 shows a significant decrease from ∼10⁻¹⁰ cm² s⁻¹ to ∼10⁻¹⁴ cm² s⁻¹ as the operation temperature decreases from 25 °C to 0 °C (Fig. 6c), indicating limited Li diffusion under low temperature (see ESI Note 4†). Interestingly, the D_Li was only slightly shifted to a lower value when the operation temperature reached a sub-zero level (−20 °C; Fig. 6c). This indicates that the high conductivity on the bulk electrode is beneficial for maintaining the fast charge-transfer properties, Li⁺ diffusion ability, and battery performance at a sub-zero temperature. In addition, the sweep rate CV was again employed to determine the charge mobility at sub-zero temperatures. As shown in Fig. S19c,† the CV curve of G10 at sub-zero temperature (−20 °C) was significantly different compared to that of at 25 °C (Fig. 1a). The well-defined redox peak associated with the Li intercalation at room temperature was hardly observed at −20 °C, showing curves that are similar to pseudocapacitive intercalation behavior (Fig. S19c†). Furthermore, the corresponding b-value was found to be 0.81, an increase of 0.2 from that of 25 °C (0.61; Fig. 5f). This suggests an increased pseudocapacitive contribution during the charge–discharge process at −20 °C. The quantitative analysis of the total charge stored during the sweep rate test at −20 °C further revealed that a high 72% pseudocapacitive contribution accumulated at a higher scan rate of 0.7 mV s⁻¹, along with a significant low diffusion contribution (28%; Fig. 6d). This pseudocapacitive contribution was then gradually decreased up to 52% at a slow scan rate of 0.1 mV s⁻¹, along with an increasing diffusion contribution to 48%, indicating the simultaneous contribution of both pseudocapacitive and diffusion during the charge–discharge process. As the lithiation process illustrated in Fig. 6e, the pseudocapacitive feature of G10 at low temperatures could promote the desolvation process of Li⁺ from electrolyte/electrode at the interphase, while the fast ion diffusion on G10 accelerated the migration of Li ions in the bulk electrode. This synergistic contribution of the high diffusion coefficient in the bulk electrode and pseudocapacitive contribution turns out to be a perfect combination, which greatly facilitates G10 with excellent low-temperature performance.

Conclusions

In this work, we observed a graphite intercalation anomaly under its low content within the electrode. This intercalation anomaly turns out to be beneficial in boosting the graphite specific capacity and extending its operation range to sub-zero temperature. We believe that this method could be an efficient and effective approach to reduce the production cost of commercial graphite anodes in LIBs. Harnessing the unique feature of lightened interlayer utilization owing to fast diffusion, pseudocapacitive contribution, and lower activation energy, the low graphite content electrode demonstrated an outstanding specific capacity and ultra-high rate capability of commercial graphite. The use of low graphite content anodes, G10 and G20, leads to superior specific capacities of 2200 and 980 mA h g⁻¹, respectively, exceeding the state-of-the-art graphite anode (372 mA h g⁻¹) at room temperature. Surprisingly, the G10 anode possesses an extremely high capacity of 1100 mA h g⁻¹ as operated at sub-zero temperature (−20 °C). This by far is the highest specific capacity recorded at −20 °C. Furthermore, the G10 anode possesses an extremely high capacity of ∼1430 mA h g⁻¹ at an ultra-high current rate of 30C with excellent stability for up to 2000 cycles. The systematic spectroscopy analysis reveals that the origin of this extraordinary performance is due to the synergetic interplay of capacitive contribution and the successful formation of superdense Li⁺ intercalation between graphite interlayers. In addition, the perfect combination of a high diffusion coefficient in the bulk electrode and pseudocapacitive contribution as well as the reduced graphite activation energy in the electrode greatly enhance battery performance at low-temperature operation. These results demonstrate the simplest and cheapest attempt to optimize graphite interlayers for Li⁺ storage, advancing Li-carbon coordination beyond LiC₆ and revealing the hidden potential of graphite at low temperatures.

Experimental section

Materials

The commercially available natural graphite powder (GN-580L), conductive carbon (Super P^®; >99% (metal basis)), polyvinylidene fluoride (PVDF), and 1 M lithium hexafluorophosphate (LiPF₆) in ethylene carbonate (EC) and diethyl carbonate (DEC) (1 : 1 v/v) were purchased from UBIQ Technology Co., Ltd. N-methylpyrrolidone (NMP; >99%) was purchased from Alfa Aesar (Thermo Fisher Scientific). All the materials were used as received without further purification.

Electrode preparation

The graphite electrodes with different percentages were prepared by applying the slurry casting method. The recipe graphite electrodes are as follows: G10 (graphite 10%; super P 70%; binder (PVDF) 20%); G20 (graphite 20%; super P 60%; PVDF 20%); G30 (graphite 30%; Super P 50%; PVDF 20%); G40 (graphite 40%; Super P 40%; PVDF 20%); G80 (graphite 80%; super P 10%; PVDF 10%) and blank sample SP80 (Super P 80%; PVDF 20%). First, graphite powder, conductive carbon and binder were mixed and stirred at 450 rpm for 24 h at room temperature. Second, the slurry was then cast on the Cu current collector and dried on the hot plate at 60 °C overnight (12 h). Third, the drying process continued in the vacuum oven at 80 °C for another 8 h. Finally, the graphite electrodes were cut in a circle with a diameter of 12 mm, resulting in an electrode area of 1.13 cm². The average electrode mass loadings for the G10, G20, G30, G40, G80, and SP80 electrodes were maintained at 0.76, 0.78, 0.85, 1.00, 2.43, and 0.606 mg cm⁻², respectively. These electrodes were then transferred inside the glovebox for coin cell fabrication.

Electrochemical measurement

All electrochemical performance measurements conducted using a CR2032 coin cell assembled in the glovebox under an argon atmosphere with H₂O and O₂ concentrations were kept at <1 ppm. LIB half-cells were fabricated using graphite, at different percentages, as the working electrode and Li metal foil as the counter/reference electrode. Meanwhile, a total of 40 μL of 1 M LiPF₆ in a mixture of ethylene carbonate (EC): diethylene carbonate (DEC) (1 : 1 v/v) was used as an electrolyte. Celgard 2325 with an 18 mm diameter was used as a separator. Cyclic voltammetry was performed using a MultiPalmSens4 electrochemical analyzer with an open voltage of 0.02–3.0 V and a scan rate of 0.01 mV s⁻¹. The electrochemical impedance spectroscopy (EIS) analysis was conducted before and after the battery cycling using CHI electrochemical workstation model 760e with a frequency ranging from 10 mHz to 1 MHz and an amplitude of 10 mV. The cells were charged and discharged galvanostatically between 0.02 and 3.0 V using AcuTech battery station systems from AcuTech Systems Co., Ltd. A low-temperature reactor Eyela PSL-2500A (Tokyo Rikakikai Co., Ltd) was used to maintain the temperature for cycling performance under low-temperature conditions. Prior to the measurement at low temperature, the coincells were prelithiated at 1C rate under room temperature conditions. The prelithiated batteries were then kept inside a low-temperature reactor for 2 h at a specified temperature to reach thermal equilibrium prior to measurement. The specific capacity was calculated based on the weight of the active materials with respect to the different wt% contents in the working electrode. Unless specified, all electrochemical measurements were carried out with at least three replicates to estimate the error and were performed under room temperature conditions.

Material characterization

X-ray diffraction spectroscopy (XRD) analysis was performed using D2 phaser XRD from Bruker Co., Ltd. X-ray photoelectron spectroscopy (XPS) was performed using high-resolution XPS PHI-Quantera II, ULVAC-PHI, Inc. The scanning electron microscope (SEM) was performed using a Field-Emission Scanning Electron Microscope (FESEM), Ultra Plus–Carl Zeiss. Raman spectroscopy was performed using a home-built Raman system with a 633 nm He–Ne laser.

Computational method

In this study, the density functional theory (DFT) calculations were performed using the Vienna ab initio Simulation Package (VASP)⁶⁸ with all-electron projected augmented wave (PAW) pseudopotential.⁶⁹ The Brillouin zone was sampled by applying the Monkhorst–Pack method⁷⁰ with a grid of 2 × 2 × 4 Γ-centered k-point. For the system with twice the supercell length in the z-direction, the grid was set to 2 × 2 × 2. Electronic occupancies were described by applying the Gaussian smearing method with a smearing width of 0.05 eV. Grimme dispersion correction (DFT-D3)⁷¹ was employed to implement the van der Waals interactions, and a kinetic energy cutoff of 500 eV was used for the plane waves. All pristine and Li-intercalated graphite structures were fully optimized by DFT calculation, including the atomic position, simulation cell shapes and Å, which is consistent with the experimental value of 3.33 Å obtained from the XRD analysis. The structures for DFT calculations were constructed based on the Rüdorff–Hoffman (RH) intercalation model.^72–76 Four RH models were constructed, as depicted in Fig. 4. In Model II–IV, the Li atom packing between two adjacent graphene layers follows the conventional LiC₆ type, while the Li atom packing is set to LiC₂ in Model I. A series of DFT geometry optimization calculations were performed to investigate the cell size, stable Li adsorption configures and adsorption energies. Table S2† summarizes the adsorption energy E_ad, averaged interlayer distance d_avg and theoretical capacity of these models. Notably, the adsorption energy E_ad is defined as follows:
where E_Li+C is the energy of the Li-intercalated graphite, E_C is the energy of the pristine graphite, E_Li is the energy of one isolated Li atom, and n is the number of adsorbed Li atoms. Model II yields the lowest E_ad value of −1.867 eV, suggesting that it is the most stable configuration of the lithiated graphite. Notably, Model I (packing mode of LiC₂) is still stable after DFT relaxation with a slight increase in E_ad relative to other models, suggesting that Model I is in a metastable lithiated state.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Febri Baskoro: methodology, investigation, formal analysis, writing – original draft, writing – review & editing. Po-Yu Yang: formal analysis. Hong-Jhen Lin, Robin Chih-Hsing Wang, Hui Qi Wong and Hsinhan Tsai: investigation, formal analysis. Chun-Wei Pao: formal analysis, conceptualization, supervision, writing – review & editing. Heng-Liang Wu: resources, conceptualization, supervision, writing – review & editing. Hung-Ju Yen: conceptualization, supervision, methodology, writing – review & editing. All authors discussed the results and reviewed the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Ministry of Science and Technology in Taiwan (MOST 108-2113-M-001-023-MY3; MOST 110-2124-M-001-001) and the Innovative Materials and Analysis Technology Exploration in Academia Sinica (AS-iMATE-110-23). F. B. acknowledges the postdoctoral fellowship program supported by Academia Sinica (AS-PD-11201-M04).

Notes and references

1. J. M. Tarascon and M. Armand, Nature, 2001, 414, 359.
2. P. Meister, H. Jia, J. Li, R. Kloepsch, M. Winter and T. Placke, Chem. Mater., 2016, 28, 7203–7217.
3. S. Goriparti, E. Miele, F. De Angelis, E. Di Fabrizio, R. Proietti Zaccaria and C. Capiglia, J. Power Sources, 2014, 257, 421–443.
4. B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928.
5. J. Billaud, F. Bouville, T. Magrini, C. Villevieille and A. R. Studart, Nat. Energy, 2016, 1, 16097.
6. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264.
7. A. Gupta and A. Manthiram, Adv. Energy Mater., 2020, 10, 2001972.
8. X. Dong, Y.-G. Wang and Y. Xia, Acc. Chem. Res., 2021, 54, 3883–3894.
9. E. J. Plichta, M. Hendrickson, R. Thompson, G. Au, W. K. Behl, M. C. Smart, B. V. Ratnakumar and S. Surampudi, J. Power Sources, 2001, 94, 160–162.
10. B. V. Ratnakumar, M. C. Smart and S. Surampudi, J. Power Sources, 2001, 98, 137–139.
11. C. K. Huang, J. S. Sakamoto, J. Wolfenstine and S. Surampudi, J. Electrochem. Soc., 2000, 147, 2893.
12. Z. Syum, T. Billo, A. Sabbah, B. Venugopal, S.-Y. Yu, F.-Y. Fu, H.-L. Wu, L.-C. Chen and K.-H. Chen, ACS Sustain. Chem. Eng., 2021, 9, 8970–8979.
13. J. Zhang, J. Zhang, T. Liu, H. Wu, S. Tian, L. Zhou, B. Zhang and G. Cui, Adv. Energy Sustainability Res., 2021, 2, 2100039.
14. S. S. Zhang, K. Xu and T. R. Jow, Electrochem. Commun., 2002, 4, 928–932.
15. T. Yuan, X. Yu, R. Cai, Y. Zhou and Z. Shao, J. Power Sources, 2010, 195, 4997–5004.
16. M. C. Smart, B. V. Ratnakumar and S. Surampudi, J. Electrochem. Soc., 2002, 149, A361.
17. M. C. Smart, B. V. Ratnakumar, L. D. Whitcanack, K. B. Chin, S. Surampudi, H. Croft, D. Tice and R. Staniewicz, J. Power Sources, 2003, 119–121, 349–358.
18. A. Tron, S. Jeong, Y. D. Park and J. Mun, ACS Sustain. Chem. Eng., 2019, 7, 14531–14538.
19. Q. Li, S. Jiao, L. Luo, M. S. Ding, J. Zheng, S. S. Cartmell, C.-M. Wang, K. Xu, J.-G. Zhang and W. Xu, ACS Appl. Mater. Interfaces, 2017, 9, 18826–18835.
20. M. C. Smart, B. V. Ratnakumar, K. B. Chin and L. D. Whitcanack, J. Electrochem. Soc., 2010, 157, A1361.
21. W. Wang, T. Yang, S. Li, W. Fan, X. Zhao, C. Fan, L. Yu, S. Zhou, X. Zuo, R. Zeng and J. Nan, Electrochim. Acta, 2019, 317, 146–154.
22. Z. Sun, Z. Li, X.-L. Wu, M. Zou, D. Wang, Z. Gu, J. Xu, Y. Fan, S. Gan, D. Han and L. Niu, ACS Appl. Energy Mater., 2019, 2, 486–492.
23. J. L. Allen, T. R. Jow and J. Wolfenstine, J. Power Sources, 2006, 159, 1340–1345.
24. D. P. Abraham, J. R. Heaton, S. H. Kang, D. W. Dees and A. N. Jansen, J. Electrochem. Soc., 2008, 155, A41.
25. A. N. Jansen, D. W. Dees, D. P. Abraham, K. Amine and G. L. Henriksen, J. Power Sources, 2007, 174, 373–379.
26. X. Fan, X. Ji, L. Chen, J. Chen, T. Deng, F. Han, J. Yue, N. Piao, R. Wang, X. Zhou, X. Xiao, L. Chen and C. Wang, Nat. Energy, 2019, 4, 882–890.
27. S. Rustomji Cyrus, Y. Yang, K. Kim Tae, J. Mac, J. Kim Young, E. Caldwell, H. Chung and Y. S. Meng, Science, 2017, 356, eaal4263.
28. B. Liao, H. Li, M. Xu, L. Xing, Y. Liao, X. Ren, W. Fan, L. Yu, K. Xu and W. Li, Adv. Energy Mater., 2018, 8, 1800802.
29. K. Xu, Chem. Rev., 2014, 114, 11503–11618.
30. G. A. Collins, H. Geaney and K. M. Ryan, J. Mater. Chem. A, 2021, 9, 14172–14213.
31. H.-J. Yen, H. Tsai, M. Zhou, E. F. Holby, S. Choudhury, A. Chen, L. Adamska, S. Tretiak, T. Sanchez, S. Iyer, H. Zhang, L. Zhu, H. Lin, L. Dai, G. Wu and H.-L. Wang, Adv. Mater., 2016, 28, 10250–10256.
32. J. R. Dahn, T. Zheng, Y. Liu and J. S. Xue, Science, 1995, 270, 590.
33. M. Deschamps and R. Yazami, J. Power Sources, 1997, 68, 236–238.
34. F. Nobili, S. Dsoke, T. Mecozzi and R. Marassi, Electrochim. Acta, 2005, 51, 536–544.
35. M. Mancini, F. Nobili, S. Dsoke, F. D'Amico, R. Tossici, F. Croce and R. Marassi, J. Power Sources, 2009, 190, 141–148.
36. F. Nobili, M. Mancini, S. Dsoke, R. Tossici and R. Marassi, J. Power Sources, 2010, 195, 7090–7097.
37. Y. Yan, L. Ben, Y. Zhan and X. Huang, Electrochim. Acta, 2016, 187, 186–192.
38. F. Lu, J. Liu, J. Xia, Y. Yang and X. Wang, Ind. Eng. Chem. Res., 2020, 59, 5858–5864.
39. C. Li, Y. Xie, N. Zhang, L. Ai, Y. Liang, K. Tuo, X. Ye, G. Jia and S. Li, Ionics, 2019, 25, 927–937.
40. J. Gao, L. J. Fu, H. P. Zhang, T. Zhang, Y. P. Wu and H. Q. Wu, Electrochem. Commun., 2006, 8, 1726–1730.
41. A. Friesen, S. Hildebrand, F. Horsthemke, M. Börner, R. Klöpsch, P. Niehoff, F. M. Schappacher and M. Winter, J. Power Sources, 2017, 363, 70–77.
42. X. Dong, Y. Yang, B. Wang, Y. Cao, N. Wang, P. Li, Y. Wang and Y. Xia, Adv. Sci., 2020, 7, 2000196.
43. G. Zhu, K. Wen, W. Lv, X. Zhou, Y. Liang, F. Yang, Z. Chen, M. Zou, J. Li, Y. Zhang and W. He, J. Power Sources, 2015, 300, 29–40.
44. R. Yazami and P. Touzain, J. Power Sources, 1983, 9, 365–371.
45. D. Aurbach, M. D. Levi, E. Levi, H. Teller, B. Markovsky, G. Salitra, U. Heider and L. Heider, J. Electrochem. Soc., 1998, 145, 3024–3034.
46. M. Agostini, S. Brutti and J. Hassoun, ACS Appl. Mater. Interfaces, 2016, 8, 10850–10857.
47. L. Shi, Y. Chen, R. He, X. Chen and H. Song, Phys. Chem. Chem. Phys., 2018, 20, 16437–16443.
48. K. Sato, M. Noguchi, A. Demachi, N. Oki and M. Endo, Science, 1994, 264, 556.
49. J. Hassoun, F. Bonaccorso, M. Agostini, M. Angelucci, M. G. Betti, R. Cingolani, M. Gemmi, C. Mariani, S. Panero, V. Pellegrini and B. Scrosati, Nano Lett., 2014, 14, 4901–4906.
50. A. Missyul, I. Bolshakov and R. Shpanchenko, Powder Diffr., 2017, 32, S56–S62.
51. Y. Reynier, R. Yazami and B. Fultz, J. Power Sources, 2007, 165, 616–619.
52. N. Li and D. Su, Carbon Energy, 2019, 1, 200–218.
53. C. Sole, N. E. Drewett and L. J. Hardwick, Faraday Discuss., 2014, 172, 223–237.
54. L. J. Hardwick, H. Buqa, M. Holzapfel, W. Scheifele, F. Krumeich and P. Novák, Electrochim. Acta, 2007, 52, 4884–4891.
55. J.-B. Wu, M.-L. Lin, X. Cong, H.-N. Liu and P.-H. Tan, Chem. Soc. Rev., 2018, 47, 1822–1873.
56. A. C. Ferrari and J. Robertson, Phys. Rev. B, 2000, 61, 14095–14107.
57. P.-Y. Yang, Y.-H. Chiang, C.-W. Pao and C.-C. Chang, J. Chem. Theory Comput., 2023, 19, 4533–4545.
58. V. Z. Mordkovich, Synth. Met., 1996, 80, 243–247.
59. V. A. Nalimova, D. Guérard, M. Lelaurain and O. V. Fateev, Carbon, 1995, 33, 177–181.
60. J.-X. Huang, G. Csányi, J.-B. Zhao, J. Cheng and V. L. Deringer, J. Mater. Chem. A, 2019, 7, 19070–19080.
61. J. Kang, H.-V. Kim, S.-A. Chae and K.-H. Kim, Small, 2018, 14, 1704394.
62. V. Augustyn, J. Come, M. A. Lowe, J. W. Kim, P.-L. Taberna, S. H. Tolbert, H. D. Abruña, P. Simon and B. Dunn, Nat. Mater., 2013, 12, 518–522.
63. J. Wang, J. Polleux, J. Lim and B. Dunn, J. Phys. Chem. C, 2007, 111, 14925–14931.
64. F. Yu, Z. Liu, R. Zhou, D. Tan, H. Wang and F. Wang, Mater. Horiz., 2018, 5, 529–535.
65. I. Yamada, Y. Iriyama, T. Abe and Z. Ogumi, J. Power Sources, 2007, 172, 933–937.
66. J. Xu, I.-Y. Jeon, J.-M. Seo, S. Dou, L. Dai and J.-B. Baek, Adv. Mater., 2014, 26, 7317–7323.
67. A. Belgibayeva, A. Rakhmetova, M. Rakhatkyzy, M. Kairova, I. Mukushev, N. Issatayev, G. Kalimuldina, A. Nurpeissova, Y.-K. Sun and Z. Bakenov, J. Power Sources, 2023, 557, 232550.
68. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
69. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
70. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192.
71. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
72. W. Rüdorff and U. Hofmann, Z. Anorg. Allg. Chem., 1938, 238, 1–50.
73. E. P. M. Leiva, E. Perassi and D. Barraco, J. Electrochem. Soc., 2016, 164, A6154–A6157.
74. M. Otero, A. Sigal, E. M. Perassi, D. Barraco and E. P. M. Leiva, Electrochim. Acta, 2017, 245, 569–574.
75. E. M. Gavilán-Arriazu, J. M. Hümöller, O. A. Pinto, B. A. López de Mishima, E. P. M. Leiva and O. A. Oviedo, Phys. Chem. Chem. Phys., 2020, 22, 16174–16183.
76. E. M. Gavilán-Arriazu, O. A. Pinto, B. A. López de Mishima, D. E. Barraco, O. A. Oviedo and E. P. M. Leiva, Electrochim. Acta, 2020, 331, 135439.

---

Footnote

† Electronic supplementary information (ESI) available: Cyclic voltammograms, galvanostatic profiles, cycling performance, FESEM images, Raman spectra, ex situ XPS spectra, simulated XRD spectra, EIS spectra. See DOI: https://doi.org/10.1039/d4ta08958h

---