Accurate & cheap calculations of the lowest triplet state energy: an experimentalist's guide†
Murad J. Y.
Tayebjee‡
 *a,
Kin Long Kelvin
Lee§
b and
Timothy W.
Schmidt‡
*a,
Kin Long Kelvin
Lee§
b and
Timothy W.
Schmidt‡
 c
c
aSchool of Photovoltaic and Renewable Energy Engineering, UNSW, Sydney, NSW 2052, Australia. E-mail: m.tayebjee@unsw.edu.au
bSchool of Chemistry, UNSW, Sydney, NSW 2052, Australia
cSchool of Chemistry, ARC Centre of Excellence in Exciton Science, UNSW, Sydney, NSW 2052, Australia
First published on 22nd July 2024
Abstract
Triplet–triplet annihilation and singlet fission are bimolecular processes which can be exploited in a range of technological applications. These processes involve the first excited singlet and triplet states (S1 and T1), and have restrictions on their relative energies. While singlet–singlet energy differences are easily measured using optical spectroscopy, the singlet–triplet energy gap is less amenable to experiment. We report a computationally inexpensive method for the calculation of the energy of the lowest singlet–triplet transition for a range of extended π chromophores. Excellent correlation (mean absolute displacement ≲0.05 eV) between experiment and calculation is achieved for a wide range of molecules without requiring zero point energy calculations. This provides the experimental chemist with the necessary tools to accurately predict T1 energies for novel molecules that are candidates for triplet–triplet annihilation or singlet fission.
1. Introduction
Singlet fission (SF) and triplet–triplet annihilation (TTA) upconversion are processes with applications in efficient molecular photovoltaic devices,1–5 3D printing,6 and quantum/excitonic logic devices.7,8Both processes are bichromophoric and can occur in solution or solid phases; in SF an excited singlet generates two excited triplets, and the reverse occurs in TTA. As such, they are constricted to opposing energetic requirements on the energies of the first excited triplet (ET1) and singlet (ES1) states. For exothermic SF and TTA, ES1 ≥ 2ET1 and ES1 ≤ 2ET1, respectively. In both cases it is ideal for 2ET1 < ET2, to avoid TTA events giving rise to molecules in the T2 state (where ET2 is the energy of the second excited triplet state). Further, small spin–orbit coupling and the consequent low rate of intersystem crossing, is required for efficient SF and TTA so that loss mechanisms, S1 → T1 and T1 → S0, are unfavourable.
The energy of the first excited singlet state is easily identified by optical absorption or emission spectroscopy; the energy difference between the T1 and T2 state is also measured relatively easily using transient absorption techniques. However, the energy of the T1 state is less amenable to measurement in condensed phase systems with small spin–orbit coupling. The solvent perturbation technique has been used to enhance spin–orbit coupling and measure absorption arising from the 1ππ → 3ππ* transition.9 However, the extinction coefficient of this transition is still extremely low (<1 cm−1 M−1), necessitating the use of highly pure samples. Conversely, phosphorescence can be observed in similarly perturbed systems.10 However, this often requires a triplet sensitizer and the complete removal of triplet quenchers such as O2. Triplet energies have also been measured using engineered solid-state host matrices which allow for room-temperature phosphorescence.11 Finally, by studying the dynamics of triplet energy transfer from a number of triplet sensitizers an estimation of the T1 state energy can be made.12 All of the above techniques are cumbersome in one way or another. It would be ideal to be able to estimate the T1 energy of a candidate SF or TTA molecule using inexpensive calculations.
Much work in SF has been focused on linear polyacenes such as tetracenes13–26 and pentacenes,13,27–30 perylene diimides (PDI),31–33 benzofurans,34,35 and carotenoids.36–40 TTA-upconversion (TTA-UC) experiments have generally used aromatic hydrocarbons as emitters, but other systems have also been studied.41–43 It would be useful to be able to estimate the T1 energy through calculations in order to identify whether SF or TTA is a viable process for a given molecule. However, accurate (on the order of meV) determinations of state energies of these molecules quickly becomes too expensive for any conventional post Hartree–Fock methods since the high level wavefunction based methods such as (EOM)-CCSD and MRCI are restricted to much smaller systems. On the other hand, density functional theory (DFT) methods have proved to be an inexpensive and efficient path to ground state molecular properties. By introducing linear response methods, time-dependent DFT (TD-DFT) makes excited states of large molecules a soluble goal, which for wavefunction methods would otherwise prove intractable. TD-DFT has been used to predict excited states of molecules, with extensive systematic studies of singlet excited states,44 triplet systems,45 using collective excitations for crystalline arrays.46 The resulting vertical energies depend on the functional form used, with mean absolute errors typically on the order of 0.25 eV and 0.7 eV.47,48 We are interested in polyaromatic hydrocarbons (PAH) and other aromatic chromophores which are commonly found in systems that undergo TTA or SF. Parac and Grimme performed one of the first benchmarks on the performance of TD-DFT on PAHs.49 In their study, the singlet–triplet energy gap was calculated for a variety of unsaturated molecules, with very promising accuracy shown for both B86 and B3LYP functionals with large basis sets. However, these calculations become time-consuming in the case of large molecules.
In this work we propose a simple method of accurately estimating the lowest singlet–triplet energy difference. Using a range of molecules with known ET1, we show that a systematic error is found by performing calculations using time independent DFT. We use a systematic overestimate to adjust the calculated triplet values in a method analogous to shifting vibrational frequencies using a scalar factor.50 The remainder of this article is organized as follows. First we use a number of PAH molecules as a training set to establish the systematic error between experiment and calculation. Second, we test the efficacy of this method with two test sets: (i) PAH molecules and (ii) heteroatomic conjugated chromophores. Finally, we make predictions of the energy of ET1 using the results of the training set and both test sets in some molecules which are pertinent to SF or TTA applications.
2. Computational details
All calculations except Section 3.4 were carried out using GAMESS-US 2013 R1.51,52 Ground state geometries were optimized using HF,53 or B3LYP,54–56 or ωB97X-D57,58 functionals and STO-3G,59,60 3-21G,61,62 6-31G,63,64 6-311G,65 or 6-311+G65,66 basis sets. Where applicable, the open shell variants were used. In the case of HF geometry optimizations, subsequent single point energy calculations were carried out with B3LYP. The triplet energy, ET1, was determined by subtracting the energy of the ground singlet state (1ππ) from that of the lowest triplet state (3ππ*) without accounting for the zero point energy. Vertical transition energies, EaT1 and EpT1, were respectively calculated by using the ground singlet and triplet state geometry for comparison with the band maxima in experimental absorption and phosphorescence spectra, as shown in the inset of Fig. S1 (ESI†).Calculations in Section 3.4 were carried out using GAMESS-US 2023 R1.67 Vertical triplet energies and TD-DFT calculations are carried out using the S0 geometry optimised using B3LYP54–56 and the aug-cc-pVTZ68 basis set.
3. Results and discussion
3.1. PAH training set and first test set
Fig. 2 summarizes the calculations for the PAHs shown in Fig. 1. Due to the Jahn–Teller effect the symmetries of triphenylene (1), coronene (13) and benzene (14) were lowered in the excited 3ππ* state. Experimental values of ET1, shown in Table 1, were mostly taken from phosphorescence measurements. While this was not always possible, the highly localized nature of triplet excitons69 results in the local environment playing a minimal role in perturbing the value of ET1 (see Table 6.3 in ref. 70 for a list of results using different experimental conditions). For instance, ET1 of tetracene in ethyl iodide and in crystalline form are respectively 1.27 eV9 and 1.25 eV.71| No. | Experimental conditions | E T,exp | HF/6-311G//B3LYP/6-311+G | HF/6-31G//B3LYP/6-31G | B3LYP/6-31G | B3LYP/3-21G | B3LYP/STO-3G | B3LYP/VTZ//B3LYP/cc-pVTZh | HF/6-311G | HF/6-31G | ωb97x-D/3-21G |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Value from phosphorescence experiments results in Table 6.3 of ref. 70 unless otherwise specified. b Value taken from absorption spectra.9 c Value take the heterofission rate of pentacene-doped tetracene crystals.72 d Value taken from the lowest energy singlet–triplet absorption in single crystals at 4.2 K.73 e Value taken from singlet oxygen sensitization experiments.74 f Value taken from ref. 75. g Value taken from triplet energy transfer experiments in ref. 76. h Values of EaT1 for molecules 1–13 taken from ref. 49. | |||||||||||
| Phenanthrene 1 | Hexane 77 K | 2.70 | 3.09 | 3.10 | 2.93 | 2.97 | 3.11 | 2.77 | 2.89 | 2.89 | 3.21 |
| 1,2-Benzanthracene 2 | EPA, 77 K | 2.05 | 2.28 | 2.29 | 2.20 | 2.25 | 2.38 | 2.08 | 2.03 | 2.02 | 2.45 |
| Chrysene 3 | n-Heptane, 77 K | 2.49 | 2.73 | 2.72 | 2.66 | 2.70 | 2.81 | 2.53 | 2.71 | 2.72 | 2.93 |
| Pyrene 4 | EPA, 77 K | 2.08 | 2.25 | 2.25 | 2.25 | 2.28 | 2.37 | 2.16 | 2.49 | 2.49 | 2.47 |
| Triphenylene 5 | EPA, 77 K | 2.88 | 3.28 | 3.32 | 3.28 | 3.31 | 3.53 | 2.87 | 3.59 | 3.62 | 3.60 |
| 1,2:5,6-Dibenzanthracene 6 | EPA, 77 K | 2.26 | 2.56 | 2.58 | 2.45 | 2.50 | 2.67 | 2.26 | 2.35 | 2.35 | 2.78 |
| 3,4-Benzyrene 7 | EPA, 77 K | 1.82 | 1.95 | 1.94 | 1.90 | 1.94 | 2.00 | 1.83 | 2.01 | 2.00 | 2.12 |
| 1,2:7,8-Dibenzanthracene 8 | EPA, 77 K | 2.29 | 2.56 | 2.58 | 2.48 | 2.52 | 2.69 | 2.28 | 2.35 | 2.36 | 2.79 |
| 1:2-Benzpyrene 9 | EPA, 77 K | 2.29 | 2.53 | 2.55 | 2.50 | 2.54 | 2.68 | 2.16 | 2.89 | 2.91 | 2.82 |
| 1,2:3,4-Dibenzanthracene 10 | EPA, 77 K | 2.20 | 2.42 | 2.45 | 2.36 | 2.41 | 2.58 | 2.22 | 2.17 | 2.18 | 2.64 |
| Picene 11 | EPA, 77 K | 2.49 | 2.80 | 2.79 | 2.72 | 2.75 | 2.88 | 2.51 | 3.25 | 3.25 | 3.08 |
| Perylene 12 | Single crystal, 4.2 K | 1.53d | 1.64 | 1.67 | 1.66 | 1.70 | 1.88 | 1.54 | 2.07 | 2.09 | 1.97 |
| Coronene 13 | n-Hexane, 77 K | 2.40 | 2.77 | 2.79 | 2.76 | 2.77 | 2.96 | 2.35 | 3.41 | 3.44 | 3.17 |
| Benzene 14 | Cyclohexane, 77 K | 3.66 | 3.98 | 4.01 | 4.01 | 4.07 | 4.15 | — | 3.36 | 3.40 | 4.14 |
| Naphthalene 15 | Hexane, 298 K | 2.64 | 2.86 | 2.87 | 2.86 | 2.91 | 3.05 | 2.73 | 3.03 | 3.04 | 3.10 |
| Anthracene 16 | EPA, 77 K | 1.85 | 1.98 | 1.98 | 1.93 | 1.97 | 2.06 | — | 1.68 | 1.66 | 2.12 |
| Tetracene 17 | Ethyl iodide, 295 K | 1.27b | 1.33 | 1.33 | 1.33 | 1.37 | 1.47 | — | 1.38 | 1.36 | 1.54 |
| Pentacene 18 | Guest–host crystal | 0.86c | 0.98 | 0.97 | 0.90 | 0.94 | 1.04 | — | 0.69 | 0.67 | 1.09 |
| 1,2:5,6-Dibenzpyrene 19 | EPA, 77 K | 2.03 | 2.25 | 2.26 | 2.16 | 2.19 | 2.32 | — | 2.33 | 2.33 | 2.46 |
| Rubrene 20 | Benzene, RT | 1.14e | 1.35 | 1.34 | 1.12 | 1.18 | 1.25 | — | 0.87 | 0.85 | 1.35 |
| 9,10-Diphenylanthracene 21 | Blended polymer film | 1.77f | 1.90 | 1.90 | 1.83 | 1.89 | 1.91 | — | 1.57 | 1.57 | 2.02 |
| 5,12-Diphenyltetracene 22 | Benzene, RT | 1.20g | 1.39 | 1.38 | 1.29 | 1.33 | 1.39 | — | 1.11 | 1.11 | 1.48 |
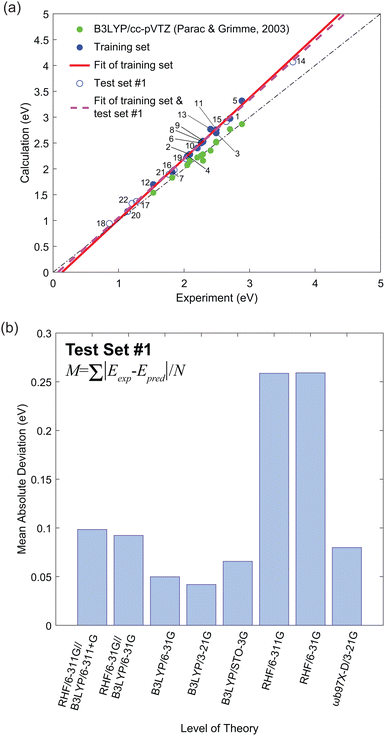
Fig. 2(a) shows the experimental versus calculated lowest singlet–triplet energy differences (Eexp and Ecalc, respectively). These plots were fit with a linear equation,
| Ecalc = mEexp + y0, | (1) |
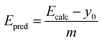 , of the molecules in the first test set. The mean absolute deviations,
, of the molecules in the first test set. The mean absolute deviations, 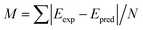 where N is the number of molecules in the test set, are plotted in Fig. 2(b) as a measure of the efficacy of a calculation method. It is clear that the use of DFT to optimize the geometry of these molecules gives excellent correlation between experiment and theory.
where N is the number of molecules in the test set, are plotted in Fig. 2(b) as a measure of the efficacy of a calculation method. It is clear that the use of DFT to optimize the geometry of these molecules gives excellent correlation between experiment and theory.
| Level of theory | m | y 0 | Pearson's r |
|---|---|---|---|
| a Parameters calculated using values reported in ref. 49 for a vertical transition from the optimized ground state geometry. b Values calculated using the results from the training set and both test sets for 1ππ–3ππ* energy differences in Jahn–Teller inactive systems. We suggest that these parameters be used for future predictive calculations. | |||
| Training set | |||
| RHF/6-311G//B3LYP/6-311+G | 1.24(3) | −0.28(7) | 0.9962 |
| RHF/6-31G//B3LYP/6-31G | 1.24(4) | −0.28(9) | 0.9947 |
| B3LYP/6-31G | 1.19(5) | −0.2(1) | 0.9912 |
| B3LYP/3-21G | 1.18(4) | −0.2(1) | 0.9929 |
| B3LYP/STO-3G | 1.22(7) | −0.1(2) | 0.9811 |
| HF/6-311G | 1.2(3) | −0.1(6) | 0.7989 |
| HF/6-31G | 1.2(3) | −0.1(6) | 0.7958 |
| ωb97x-D/3-21G | 1.24(8) | 0.0(2) | 0.9764 |
| B3LYP/cc-pVTZa | 0.99(5) | 0.0(1) | 0.9884 |
| Training set and first test set | |||
| RHF/6-311G//B3LYP/6-311+G | 1.11(2) | −0.00(5) | 0.9962 |
| RHF/6-31G//B3LYP/6-31G | 1.12(2) | −0.02(5) | 0.9962 |
| B3LYP/6-31G | 1.14(2) | −0.13(4) | 0.9974 |
| B3LYP/3-21G | 1.14(2) | −0.09(4) | 0.9980 |
| B3LYP/STO-3G | 1.17(3) | −0.03(6) | 0.9940 |
| HF/6-311G | 1.2(1) | −0.2(3) | 0.9102 |
| HF/6-31G | 1.2(1) | −0.2(3) | 0.9104 |
| ωb97x-D/3-21G | 1.17(4) | 0.08(8) | 0.9905 |
| Proposed parameters for future calculationsb | |||
| B3LYP/3-21G | 1.12(1) | −0.04(2) | 0.9985 |
Table 2 shows the gradient, m, and the y-intercept, y0, values. Clearly, the TD-DFT B3LYP/cc-pVTZ study by Parac and Grimme provides the best match between experiment and calculation.49 The Pearson's r value from the results of Parac and Grimme using B3LYP/cc-pVTZ was 0.9878.49 In contrast, our results using B3LYP/3-21G give a value of 0.9980. By exploiting the systematic error from the training set and the computationally cheaper option of using a 3-21G basis set we predict singlet–triplet energy gaps closer to the experimental value. However, it should be noted that the work of Parac and Grimme was conducted using the optimized ground state geometry to compare their results with optical absorption experiments. Since the time independent DFT calculations in Fig. 2 are of the adiabatic triplet energy, we should also compare their results with the vertical transition energies presented in Fig. S1 (ESI†).
3.2. Extension to more complex molecules
The B3LYP/3-21G level of theory was chosen for further calculations since an agreeable trade-off between computational expense and accuracy was achieved. The value of ET1 was calculated for the molecules shown in Fig. 3 to investigate whether this method can be utilized to accurately predict the lowest triplet energy of extended π chromophores which contain N or O atoms. The predicted values, Epred, are given in Table S1 (ESI†). For most of the studied molecules the value of ΔE = Eexp − Epred was ≲0.05 eV. However, the triplet energies are significantly underestimated for molecules 33–36.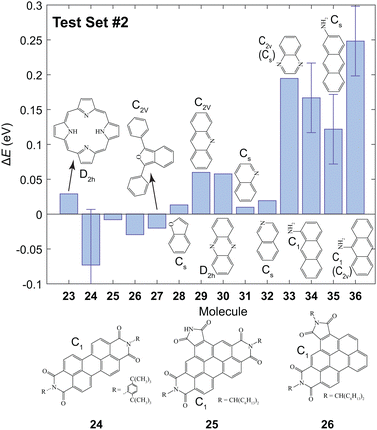 | ||
| Fig. 3 The values of ΔE for the second test set using the results from the training set and the first test set. The errors arise from the reported experimental uncertainty in ref. 12 and 77 for 24 and the amino-anthracenes (34–36), respectively. Experimental values are given in Table S1 (ESI†). | ||
In quinoxaline 33, the predicted ET1 was underestimated by 0.19 eV. In this molecule, the T1 and S1 states are (ππ*) and (nπ*), respectively.78 However, the T1 state was incorrectly calculated to be (nπ*) using B3LYP/3-21G. This incorrect assignment of the lowest triplet state means that a reasonable prediction cannot be achieved, and is a limitation of the proposed method. One should ensure that the calculated T1 is 3ππ* before implementing this method.
Poor predictions were also made for the amino-anthracenes (34–36) which contain sp2 hybridized N atoms. Moreover, experimental reports of the triplet energy of amino-anthracenes are independent of the position of the amine group. In the calculations there are significant differences between the values of ET1 of 34–36. Upon examination of the HOMO and LUMO it is clear that the 1ππ → 3ππ* transition has significant charge-transfer character since electron density is shifted from the N atom to the π system. Evidently, this is not accounted for using the proposed approach. Attempts to correct for the asymptotic nature of the wavefunction using the hybrid functional ωb97x-D did not yield more accurate results. We conclude that the predictive power using the parameters in Table 2 is limited to systems with where the 1ππ → 3ππ* transition does not have considerable charge-transfer character.
3.3. Predictions
In Table 2 we report values of y0, and gradient, m. Using the data in the final row, we predict the singlet–triplet energy gaps of the molecules shown in Fig. 4. These molecules are of interest for both SF and TTA experiments, however their lowest singlet–triplet energy difference have not been directly experimentally measured.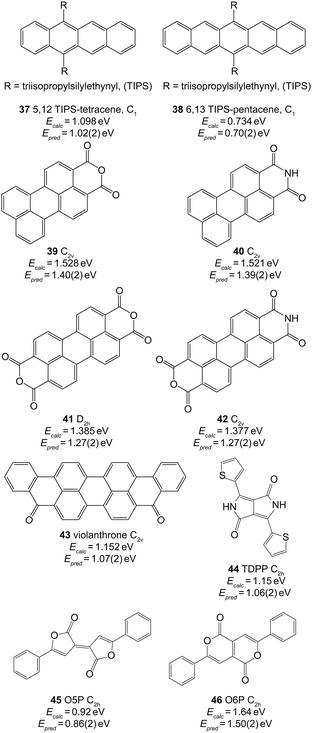 | ||
| Fig. 4 Extended π systems and predicted values of ET1 using B3LYP/3-21G and the parameters in the final row of Table 2. The symmetries used for the calculations are given next to each molecule. | ||
The triisopropylsilylethynyl moiety has been used to increase the solubility and stability of linear polyacences, as in 3779 and 38.80 SF has already been reported for both species, which have respective S1 energies of 2.25 eV69 and 1.75 eV.29 As such, we expect the T1 energies to be less than or approximately equal to 1.13 eV and 0.88 eV, respectively, in accordance with the result in Fig. 4. However, TTA has also been reported in 37, suggesting that the triplet pair state is approximately degenerate with the S1 state.69 As such, we expect the T1 energy of 37 to be approximately (withing a few kT = 0.026 eV at room temperature) 1.13 eV, and the result shown in Fig. 4 underestimates this by 0.11 eV.
The perylene moiety with attached anhydride or imide groups (molecules 39–42) has been used in both SF and TTA experiments.31–33 The predicted triplet energies of the anhydride and imide are similar. Upon examination of the HOMO and LUMO of these species it is clear that this similarity arises because there is very little electron density lying on the sp2 hybridized N or O atoms. Unfortunately there is little experimental data available to ascertain whether the values of Epred in Fig. 4 are reasonable. A recent report suggested that intramolecular SF in covalently linked perylene monoimide (PMI, 40) is unlikely to occur because the T1 energy is greater than half the vibrationally relaxed S1 energy of 2.29 eV.81 This accords with the result of Epred = 1.39 eV, however more accurate data of the T1 energy has not been reported.
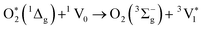 | (2) |
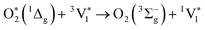 | (3) |
 | (4) |
Diketopyrrolopyrroles (DPP) are another class of materials which are promising for SF.84 Karsten et al. measured the triplet energy of a thienyl derivative of DPP to be 1.1 eV.85 This material only differed from 44 by an alkyl chain replacing the hydrogen at the pyrrole nitrogens. As we can see from Fig. 4, this agrees extremely well with our prediction of 1.06 eV.
Finally, Pechmann dyes have very recently been shown to undergo SF for the five-membered-ring isomer (45, O5P), but not for the six-membered ring isomer (46 O6P).86 While no experimental measurements of the T1 energy exist, our predictions accord with this recent work (where we have removed a methyl group as compared to the work in ref. 86). The thin-film singlet energy of O5P and O6P are approximately 2.2 eV and 2.6 eV, respectively (Fig. S17 of ref. 86). As such, our predicted triplet energies of 0.86 eV and 1.50 eV would allow for SF to occur in the former, but not the latter.
3.4. Why does this work?
We are left with an efficient and accurate way of calculating the T1 energy of a wide class of molecules. We are subtracting the energy of the geometry optimized S0 state from the geometry optimized T1 state; this yields a systematic error that increases with the energy of T1. The question remains: why does this work?The gradients and offsets listed in Table 2 do not display any significant trend with increasing the basis set level of theory. Further, the results of B3LYP are very similar to ωb97x-D, suggesting that the chosen functional has a limited effect.
However, the TD-DFT calculations of Parac and Grimme (B3LYP) were rather accurate (see Fig. 2) before applying any post-calculation empirical correction.49 This suggests that the systematic error observed in our DFT calculations are corrected for by TD-DFT.
As such, we attempt to compare the vertical transition energies from an optimized S0 ground state using both DFT and TD-DFT and a B3LYP/cc-pVTZ level of theory. Fig. 5(a) shows that TD-DFT calculates excited triplet energies which are in good agreement with the experimental values for the training set.
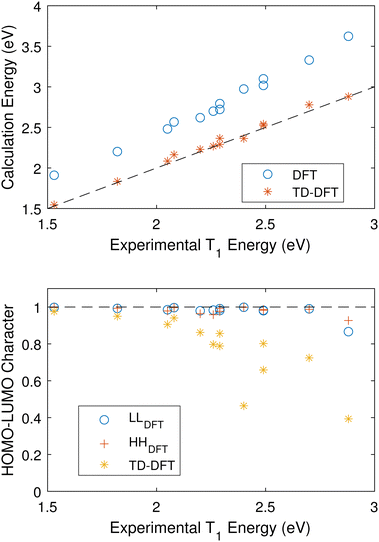 | ||
| Fig. 5 (a) Calculated vertical triplet energies as a function experimental values. Both DFT and TD-DFT were carried out at the optimized S0 geometry using B3LYP/cc-pVTZ. The DFT systematically overestimates the value of the triplet. (b) The HOMO–LUMO character of the S0 to T0 transition as output by TD-DFT and estimated using eqn (5) for DFT. | ||
Fig. 5(b) compares the S0 HOMO–LUMO character of the S0 to T1 transitions using TD-DFT and DFT. For TD-DFT this is simply generated in the calculation output. For DFT, we estimate this value by calculating the overlap of the LUMOs calculated for S0 and T1,
| LLDFT = |〈χL,S0|S|χL,T1〉|2, | (5) |
4. Conclusions
Using the data in the final row of Table 2 one can use B3LYP/3-21G to easily and accurately predict the singlet–triplet (1ππ–3ππ*) energy difference in neutral extended π chromophores. However, when either the ground singlet, first excited singlet, or ground triplet states have significant non-bonding or charge-transfer character the simple empirical model presented here is not sufficient. While this work will not replace sophisticated computations of ET1, it provides the experimental chemist with a inexpensive calculation for this difficult to measure quantity. We propose that this method may be used to rapidly screen for new singlet fission and TTA candidates. A step-by-step method is provided in the ESI.†Data availability
The code for DFT can be found at https://www.msg.chem.iastate.edu/gamess/index.html with https://aip.scitation.org/doi/10.1063/5.0005188. The versions of the code employed for this study are outlined in the Methodology section.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
MJYT acknowledges receipt of an Australian Research Council Future Fellowship (FT230100002). This work was supported by the Australian Research Council (Centre of Excellence in Exciton Science CE170100026). MJYT and KLKL acknowledge use of computing resources from the NeCTAR Research Cloud https://www.nectar.org.au. NeCTAR is an Australian Government project conducted as part of the Super Science initiative and financed by the Education Investment Fund and the National Collaborative Research Infrastructure Strategy (NCRIS). This research includes computations using the computational cluster Katana supported by Research Technology Services at UNSW Sydney. This program has been supported by the Australian Government through the Australian Renewable Energy Agency (ARENA). Responsibility for the views, information or advice expressed herein is not accepted by the Australian Government.Notes and references
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125 RSC.
- M. J. Y. Tayebjee, D. R. McCamey and T. W. Schmidt, J. Phys. Chem. Lett., 2015, 6, 2367–2378 CrossRef CAS PubMed.
- A. J. Baldacchino, M. I. Collins, M. P. Nielsen, T. W. Schmidt, D. R. McCamey and M. J. Y. Tayebjee, Chem. Phys. Rev., 2022, 3, 21304 CrossRef CAS.
- S. N. Sanders, T. H. Schloemer, M. K. Gangishetty, D. Anderson, M. Seitz, A. O. Gallegos, R. C. Stokes and D. N. Congreve, Nature, 2022, 604, 474–478 CrossRef CAS PubMed.
- R. M. Jacobberger, Y. Qiu, M. L. Williams, M. D. Krzyaniak and M. R. Wasielewski, J. Am. Chem. Soc., 2022, 144, 2276–2283 CrossRef CAS PubMed.
- R. J. Hudson, T. S. C. MacDonald, J. H. Cole, T. W. Schmidt, T. A. Smith and D. R. McCamey, Nat. Rev. Chem., 2024, 8, 136–151 CrossRef PubMed.
- S. P. Mcglynn, M. Kasha and T. Azumi, J. Chem. Phys., 1964, 40, 507–515 CrossRef CAS.
- I. J. Grahambryce and J. M. Corkill, Nature, 1960, 186, 965–966 CrossRef CAS.
- S. Reineke and M. A. Baldo, Sci. Rep., 2014, 4, 3797 CrossRef PubMed.
- W. E. Ford and P. V. Kamat, J. Phys. Chem., 1987, 91, 6373–6380 CrossRef CAS.
- P. M. Zimmerman, F. Bell, D. Casanova and M. Head-Gordon, J. Am. Chem. Soc., 2011, 133, 19944–19952 CrossRef CAS PubMed.
- J. J. Burdett, A. M. Muller, D. Gosztola and C. J. Bardeen, J. Chem. Phys., 2010, 133, 144506 CrossRef PubMed.
- J. J. Burdett, D. Gosztola and C. J. Bardeen, J. Chem. Phys., 2011, 135, 214508 CrossRef PubMed.
- J. J. Burdett and C. J. Bardeen, J. Am. Chem. Soc., 2012, 134, 8597–8607 CrossRef CAS PubMed.
- J. J. Burdett, G. B. Piland and C. J. Bardeen, Chem. Phys. Lett., 2013, 585, 1–10 CrossRef CAS.
- J. J. Burdett and C. J. Bardeen, Acc. Chem. Res., 2013, 46, 1312–1320 CrossRef CAS PubMed.
- P. J. Jadhav, A. Mohanty, J. Sussman, J. Lee and M. A. Baldo, Nano Lett., 2011, 11, 1495–1498 CrossRef CAS PubMed.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS PubMed.
- W. L. Chan, M. Ligges and X. Y. Zhu, Nat. Chem., 2012, 4, 840–845 CrossRef CAS.
- S. T. Roberts, R. E. McAnally, J. N. Mastron, D. H. Webber, M. T. Whited, R. L. Brutchey, M. E. Thompson and S. E. Bradforth, J. Am. Chem. Soc., 2012, 134, 6388–6400 CrossRef CAS.
- J. N. Mastron, S. T. Roberts, R. E. McAnally, M. E. Thompson and S. E. Bradforth, J. Phys. Chem. B, 2013, 117(49), 15519–15526 CrossRef CAS PubMed.
- M. J. Y. Tayebjee, R. G. C. R. Clady and T. W. Schmidt, Phys. Chem. Chem. Phys., 2013, 15, 14797–14805 RSC.
- M. W. B. Wilson, A. Rao, K. Johnson, S. Gélinas, R. di Pietro, J. Clark and R. H. Friend, J. Am. Chem. Soc., 2013, 135, 16680–16688 CrossRef CAS PubMed.
- G. B. Piland and C. J. Bardeen, J. Phys. Chem. Lett., 2015, 6, 1841–1846 CrossRef CAS PubMed.
- W. L. Chan, M. Ligges, A. Jailaubekov, L. Kaake, L. Miaja-Avila and X. Y. Zhu, Science, 2011, 334, 1541–1545 CrossRef CAS PubMed.
- B. Ehrler, B. J. Walker, M. L. Böhm, M. W. B. Wilson, Y. Vaynzof, R. H. Friend and N. C. Greenham, Nat. Commun., 2012, 3, 1019 CrossRef PubMed.
- B. J. Walker, A. J. Musser, D. Beljonne and R. H. Friend, Nat. Chem., 2013, 5, 1019–1024 CrossRef CAS PubMed.
- A. J. Musser, M. Liebel, C. Schnedermann, T. Wende, T. B. Kehoe, A. Rao and P. Kukura, Nat. Phys., 2015, 11, 352–357 Search PubMed.
- C. Ramanan, A. L. Smeigh, J. E. Anthony, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2011, 134, 386–397 CrossRef PubMed.
- K. M. Lefler, K. E. Brown, W. A. Salamant, S. M. Dyar, K. E. Knowles and M. R. Wasielewski, J. Phys. Chem. A, 2013, 117, 10333–10345 CrossRef CAS PubMed.
- S. W. Eaton, L. E. Shoer, S. D. Karlen, S. M. Dyar, E. A. Margulies, B. S. Veldkamp, C. Ramanan, D. A. Hartzler, S. Savikhin, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2013, 135, 14701–14712 CrossRef CAS PubMed.
- J. C. Johnson, A. J. Nozik and J. Michl, J. Am. Chem. Soc., 2010, 132, 16302–16303 CrossRef CAS PubMed.
- X. Feng, A. B. Kolomeisky and A. I. Krylov, J. Phys. Chem. C, 2014, 118, 19608–19617 CrossRef CAS.
- C. C. Gradinaru, J. T. M. Kennis, E. Papagiannakis, I. H. M. van Stokkum, R. J. Cogdell, G. R. Fleming, R. A. Niederman and R. van Grondelle, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 2364–2369 CrossRef CAS.
- C. Wang and M. J. Tauber, J. Am. Chem. Soc., 2010, 132, 13988–13991 CrossRef CAS.
- C. Wang, D. E. Schlamadinger, V. Desai and M. J. Tauber, ChemPhysChem, 2011, 12, 2891–2894 CrossRef CAS.
- C. Wang, C. J. Berg, C. C. Hsu, B. A. Merrill and M. J. Tauber, J. Phys. Chem. B, 2012, 116, 10617–10630 CrossRef CAS PubMed.
- A. J. Musser, M. Maiuri, D. Brida, G. Cerullo, R. H. Friend and J. Clark, J. Am. Chem. Soc., 2015, 137, 5130–5139 CrossRef CAS PubMed.
- S. Baluschev, T. Miteva, V. Yakutkin, G. Nelles, A. Yasuda and G. Wegner, Phys. Rev. Lett., 2006, 97, 143903 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS.
- T. W. Schmidt and F. N. Castellano, J. Phys. Chem. Lett., 2014, 5, 4062–4072 CrossRef CAS PubMed.
- D. Jacquemin, V. Wathelet, E. A. Perpète and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS.
- M. J. G. Peach and D. J. Tozer, J. Phys. Chem. A, 2012, 116, 9783–9789 CrossRef CAS.
- A. F. Morrison, Z.-Q. You and J. M. Herbert, J. Chem. Theory Comput., 2014, 10, 5366–5376 CrossRef CAS PubMed.
- D. Jacquemin, E. A. Perpète, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2010, 6, 1532–1537 CrossRef CAS PubMed.
- M. J. G. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578–3585 CrossRef CAS PubMed.
- M. Parac and S. Grimme, Chem. Phys., 2003, 292, 11–21 CrossRef CAS.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- M. S. Gordon and M. W. Schmidt, in Chapter 41 - Advances in electronic structure theory: GAMESS a decade later, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189 Search PubMed.
- C. C. J. Roothaan, Rev. Mod. Phys., 1951, 23, 69–89 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- R. H. Hertwig and W. Koch, Chem. Phys. Lett., 1997, 268, 345–351 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- W. J. Hehre, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1969, 51, 2657–2664 CrossRef CAS.
- W. J. Hehre, R. Ditchfield, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1970, 52, 2769–2773 CrossRef CAS.
- J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947 CrossRef CAS.
- M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. D. Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. G. Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- S. L. Bayliss, A. D. Chepelianskii, A. Sepe, B. J. Walker, B. Ehrler, M. J. Bruzek, J. E. Anthony and N. C. Greenham, Phys. Rev. Lett., 2014, 112, 238701 CrossRef PubMed.
- J. B. Birks, Photophysics of Aromatic Molecules, John Wiley & Sons, London, 1970 Search PubMed.
- Y. Tomkiewicz, R. P. Groff and P. Avakian, J. Chem. Phys., 1971, 54, 4504–4507 CrossRef CAS.
- J. Burgos, M. Pope, C. E. Swenberg and R. R. Alfano, Phys. Status Solidi B, 1977, 83, 249–256 CrossRef CAS.
- R. H. Clarke and R. M. Hochstrasser, J. Mol. Spectrosc., 1969, 32, 309–319 CrossRef CAS.
- W. G. Herkstroeter and P. B. Merkel, J. Photochem., 1981, 16, 331–341 CrossRef CAS.
- T. N. Singh-Rachford, J. Lott, C. Weder and F. N. Castellano, J. Am. Chem. Soc., 2009, 131, 12007–12014 CrossRef CAS PubMed.
- C. Burgdorff, T. Kircher and H. G. Lohmannsroben, Spectrochim. Acta, Part A, 1988, 44, 1137–1141 CrossRef.
- K. Rotkiewicz and Z. R. Grabowski, Trans. Faraday Soc., 1969, 65, 3263–3278 RSC.
- S. G. Hadley, J. Phys. Chem., 1971, 75, 2083–2086 CrossRef CAS.
- S. A. Odom, S. R. Parkin and J. E. Anthony, Org. Lett., 2003, 5, 4245–4248 CrossRef CAS PubMed.
- J. E. Anthony, J. S. Brooks, D. L. Eaton and S. R. Parkin, J. Am. Chem. Soc., 2001, 123, 9482–9483 CrossRef CAS PubMed.
- R. J. Lindquist, K. M. Lefler, K. E. Brown, S. M. Dyar, E. A. Margulies, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2014, 136, 14912–14923 CrossRef CAS PubMed.
- T. Wilson, J. Am. Chem. Soc., 1969, 91, 2387–2388 CrossRef CAS.
- E. M. Gholizadeh, S. K. K. Prasad, L. V. Gillan, M. P. Nielsen, N. J. Ekins-Daukes, D. R. McCamey, M. J. Y. Tayebjee and T. W. Schmidt, J. Phys. Chem. C, 2021, 125, 22464–22471 CrossRef CAS.
- P. E. Hartnett, E. A. Margulies, C. M. Mauck, S. A. Miller, Y. Wu, Y.-L. Wu, T. J. Marks and M. R. Wasielewski, J. Phys. Chem. B, 2016, 120, 1357–1366 CrossRef CAS PubMed.
- B. P. Karsten, R. K. M. Bouwer, J. C. Hummelen, R. M. Williams and R. A. J. Janssen, Photochem. Photobiol. Sci., 2010, 9, 1055–1065 CrossRef CAS PubMed.
- A. V. Girija, W. Zeng, W. K. Myers, R. C. Kilbride, D. T. W. Toolan, C. Zhong, F. Plasser, A. Rao and H. Bronstein, J. Am. Chem. Soc., 2024, 146, 18253–18261 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Vertical transition energies are included for a subset of the basis sets studied in this work. The experimental and calculated values for test set #2 are also provided. See DOI: https://doi.org/10.1039/d4tc02241f |
| ‡ These authors contributed equally to this work. |
| § Present address: Intel Corporation 2111 25th NE Ave, Hillsboro OR 97124, USA. |
| This journal is © The Royal Society of Chemistry 2024 |