Orchestration of ferro- and anti-ferromagnetic ordering in gold nanoclusters†
Nisha
Mehla
 ,
Aritra
Mukhopadhyaya
,
Aritra
Mukhopadhyaya
 ,
Shahjad
Ali
,
Shahjad
Ali
 and
Md. Ehesan
Ali
and
Md. Ehesan
Ali
 *
*
Institute of Nano Science and Technology, Sector-81, Mohali, Punjab 140306, India. E-mail: ehesan.ali@inst.ac.in
First published on 10th June 2024
Abstract
The unpaired electron in the gold clusters (Aun, n = no. of Au atoms) with an odd number of total electrons is solely responsible for the magnetic properties in the small-sized Au nano-clusters. However, no such unpaired electron is available due to pairing in the even number of atom gold clusters and behaving as a diamagnetic entity similar to bulk gold. In this work, we unveiled the spin-density distribution of odd Aun clusters with n = 1 to 19 that reveals that a single unpaired electron gets distributed non-uniformly among all Au-atoms depending on the cluster size and morphology. The delocalization of the unpaired electron leads to the spin dilution approaching a value of ∼1/n spin moments on each atom for the higher clusters. Interestingly, small odd-numbered gold clusters possess spin-magnetic moments similar to the delocalized spin moments as of organic radicals. Can cooperative magnetic properties be obtained by coupling these individual magnetic gold nanoparticles? In this work, by applying state-of-the-art computational methodologies, we have demonstrated ferromagnetic or anti-ferromagnetic couplings between such magnetic nanoclusters upon designing suitable organic spacers. These findings will open up a new avenue of nanoscale magnetic materials combining organic spacers and odd-electron nano-clusters.
1 Introduction
Ferromagnetically ordered spin systems are of great interest due to their potential applications in the field of spintronics.1–6 Such systems could be used to generate a fully spin-polarized current. Various transition metal complexes and organic magnetic materials (OMMs) have been reported in this regard.7–14Bulk gold is diamagnetic,15 but the nanoworld unfolds a contrasting scenario with the experimentally observed magnetism in nanoparticles of gold.16–25 The earliest mention of it came from the research conducted by Hori et al. in 1999 in which they focused on magnetization measurements involving gold nanoparticles (NPs) of 2.5 nm.26 Yamamoto et al. provided the initial concrete experimental confirmation of ferromagnetic spin polarization by employing the X-ray magnetic circular dichroism (XMCD) technique on gold NPs shielded with polyallyl amine hydrochloride.27
The NPs composed of Au, Ag, and Cu have been observed to exhibit permanent magnetism at room temperature using XMCD and 197Au Mössbauer spectroscopy.28 Krishna et al. have observed ferromagnetic behaviour in Au55(PPh3)12Cl6 at room temperature.29 At low temperatures, feeble ferromagnetic interactions have been detected in Au25(SCH2CH2Ph)0 using EPR and hysteresis experiments,30,31 but were not observed using the SQUID magnetometer technique.29
Since the unearthing of magnetism in nano gold, plenty of theories have been crafted to explain this phenomenon. Zhang et al. investigated the electronic behavior of Au NPs (∼2 nm) capped with dendrimer and thiol molecules which reveals that d-electron distribution in the Au NPs can be tuned by selective capping.32,33 When Au NPs are capped with strongly interacting thiols, the number of holes in the 5d band increases.34,35 The ferromagnetism in gold has also been associated with 5d localized holes generated through the Au–S bond.36 It has been shown that thiolate induced magnetism occurs in gold.37 It has been reported that the large orbital component of 5d electrons is the origin of spontaneous spin polarization in gold NPs.25,38 The gold NPs display ferromagnetic spin polarization which is found to be dependent on the size of NPs.16,39–41 In 2021, Li et al. used the electron paramagnetic resonance (EPR) technique to explore magnetism in Au25 and Au133 clusters.31 Their findings indicate that in Au NCs, magnetism isn't chiefly linked to size or ligands, but rather to the electron count.
In the experimental study by Hasan et al.,42 which provides the first experimental evidence for the adsorption of intact thiols on the gold clusters analysed by 1H NMR spectroscopy, it was found that when thiol coverage is lower (less than 2 molar equiv. of thiol), removal of hydrogen is favoured. Thus, the experimental conditions influence which of the two competing mechanisms, dissociative or undissociative, will occur. Another experimental work has also concluded that the –SH bond does not cleave during CH3SH adsorption on the Au(111) surface under ultra-high vacuum (UHV) conditions.43 It has been found that CH3SH and C3H7SH adsorb on the Au(111) surface without -SH bond scission but the -SH bond dissociates on the defective Au surface.44 One of the theoretical studies suggests that thiolates and “intact” SH species can exist together.45 It has been suggested that long alkyl chain thiols adsorb by physisorption, while thiols with a short alkyl chain adsorb by chemisorption.46 A recent study by Inkpen et al.47 demonstrates that gold–sulfur interfacial coupling in the self-assembled monolayers of dithiols is through the physisorbed interaction and thiol hydrogen is retained.
However, to comment upon which gold–thiol binding process is more favourable is out of the scope of this work and based upon the results of the above-mentioned experimental and theoretical studies we have chosen one of the possibilities of gold–thiol binding ((RS–H) remains intact,42–47 homolytic cleavage (–RṠ)48,49 and the heterolytic cleavage (–RS−)50) with thiol as the “intact” species to show how the gold nanoclusters can couple (FM/AFM) via the coupler.
Despite the knowledge of the magnetic behaviour of the gold nanoclusters, a comprehensive understanding is lacking about the delocalization of the unpaired electron i.e. the source of magnetic properties among the constituent Au-atoms. Our study aims to understand the magnetic behaviors of small gold nanoclusters. The unambiguous identification of the magnetic gold nano-clusters encourages us to ask the natural question: can magnetic ordering be induced among these tiny nano-magnets? Here we have investigated a strategy of coupling odd Aun clusters with n = 3 to 19 designing an organic spacer that sheds light on harnessing the cooperative magnetic ordering utilising gold nanoclusters.
The magnetic ordering in the gold nanoclusters using organic spacers is crucial from the device application perspective in the field of spintronics, quantum computing and various technological applications like high density memory storage, magnetic devices, nanocatalysis and biomedicine.
2 Theoretical model and computational methodology
2.1 Theoretical model
The magnetic exchange interaction between two spin centers 1 and 2 is usually expressed by the Heisenberg–Dirac–Van Vleck spin Hamiltonian,| ĤHDVV = −2JŜ1 · Ŝ2 | (1) |
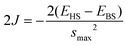 | (2) |
 | (3) |
In our analysis, we've employed the formula (3) established by Yamaguchi et al. We have noticed that smax = 1 and the difference (<S2>HS − <S2>BS) is nearly equal to 1.0 for all the systems. In the weak orbital overlap regions, the Yamaguchi formula (eqn (3)) can be reduced to the Noodleman formula (eqn (2)). Since the systems involved in our investigation have weak overlap between the magnetic orbitals, the 2J values (refer to the ESI†) obtained using eqn (2) and (3) are almost equal.
2.2 Computational methodology
The optimization of Aun clusters with n ranging from 1 to 20 and odd Aun clusters coupled via a π-conjugated molecule, thiol functionalized diethynylbenzene (t-DEB), was performed using the B3LYP hybrid functional54 and def2-TZVP55 basis set. The preference for the B3LYP functional stems from its established efficacy in accurately determining the exchange coupling constants.56–61 The gold clusters were treated using the spin-unrestricted Kohn Sham (UKS) method within the DFT framework. The RI approximation in conjunction with the auxiliary basis set def2/J was employed. In order to differentiate between the J used in the auxiliary basis set def2/J and the magnetic exchange coupling constant 2J, we have used italicized J in 2J and non-italicized J in def2/J. For the Hartree–Fock exchange calculations, a Chain of Spheres (COSX) numerical integration method was utilized to enhance the speed while preserving accuracy.62 We explored the electronic configurations of odd clusters, encompassing both doublet and quartet states, and examined even clusters, considering singlet and triplet states. The odd clusters predominantly assume a doublet ground state, while even clusters exhibit a singlet ground state. For clusters connected through the spacer, meta t-DEB, the geometry has been optimized in the triplet state, whereas when connected via para t-DEB, the geometry optimization has been conducted in the broken symmetry (BS) state which is their respective ground state.To facilitate magnetic exchange coupling analysis, we performed single-point calculations utilizing the BS-DFT method in the ORCA quantum chemical code.
3 Results and discussion
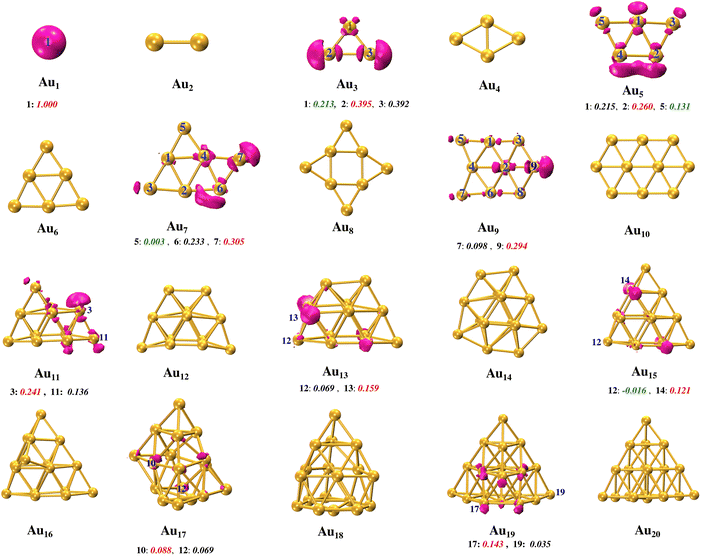
Unpaired spin-bearing odd Aun clusters can be considered atomic scale nanomagnets. The spin density distribution of the DFT-optimized geometries of the Aun (n = 1,2…20) clusters has been discussed in the following subsection. Upon designing an organic spacer, capable of effectively coupling the stable organic radicals, the magnetic ordering of the Aun clusters has been studied. The predicted ordering of magnetic ordering has been rationalized from the electronic structure.3.1 Aun clusters: geometries and spin distribution
The gold nanoclusters’ geometries used in the present work represent the global minimum geometries. We have used the global minimum geometries reported by Khatun et al.63 as the initial geometries. The authors obtained these geometries by generating several trial geometries and performing a gradient based local optimization of these trial geometries. In this work, we have further optimized these geometries at the B3LYP/def2-TZVP level. We have optimized the Aun, n = 1 to 20 clusters in the different spin states.63–66 It is observed that odd and even gold clusters have the doublet and singlet ground states, respectively (shown in section S1 of the ESI†). The optimized geometries of Aun clusters are shown in Fig. 1.It is observed that Au2 to Au10 clusters favor planar geometries67 and beyond Au10, gold clusters show a shift from 2D to 3D configurations. This is in agreement with the previously reported 2D to 3D transition of gold clusters.63–66,68,69
These structural variations in the gold clusters are due to the different nature of hybridization in frontier molecular orbitals. The singly occupied molecular orbital (SOMO) of the single Au atom is completely of s character which is quite obvious from the electronic configuration of the gold atom, with one unpaired electron in the 6s shell. Each cluster is formed by adding one more atom to the preceding cluster. The addition of one more gold atom in the vicinity of a single Au atom forms an Au–Au bond due to the overlapping of the s–s orbitals. The Au2 cluster has a Au–Au bond length of 2.53 Å, closely mirroring the experimentally observed bond length of around 2.49 Å.70 With the inclusion of a third atom to the Au2 cluster, bonding between the atoms of the Au3 cluster is no longer due to the s orbitals only but the role of hybridization of s, p, and d orbitals comes into play (see Fig. S1 and S2, ESI†). It is quite natural to assume that Au3 would have an equilateral triangle geometry but after optimization, it shows an isosceles triangular structure, characterized by two equal bond lengths of 2.66 Å and a longer length of 3.26 Å which is attributed to the antibonding s–s orbitals. The Au4 cluster is rhombus-shaped with uniform side lengths of 2.77 Å. The Au5 cluster exhibits a distinctive W shape, showcasing the bi-capped triangle geometry. The Au6 cluster assumes a planar triangular arrangement, featuring an outer equilateral triangle with dimensions measuring 5.7 Å and an inner, smaller equilateral triangle measuring 2.9 Å on each side. The Au7 cluster displays a capped triangle geometry, and Au8 and Au9 clusters embrace a tetra-crowned rhombus and bi-capped hexagon geometries respectively. Au19 is characterized by a truncated tetrahedral shape. The Au20 cluster shows a perfect tetrahedral geometry.
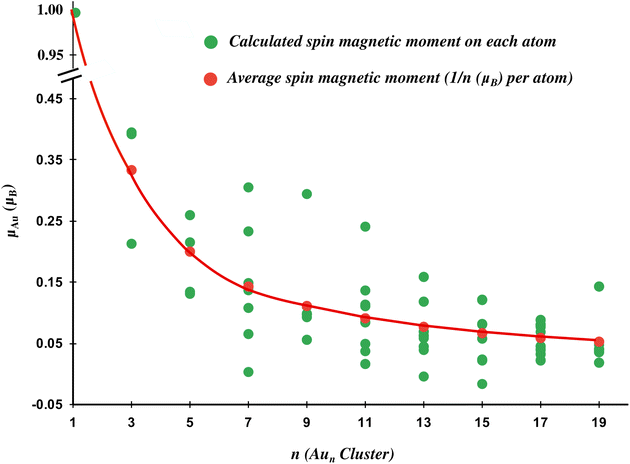
Since the even gold clusters have a singlet ground state, they do not have a spin magnetic moment, as all the electrons are paired. Unlike the even clusters, odd gold clusters always have a doublet ground state irrespective of the size of the cluster. This is due to the odd number of total electrons in the odd gold clusters which always leave one electron aloof, giving rise to the total magnetic moment of 1μB on the odd gold clusters.37 These observations are in alignment with the study performed by Zhu et al. on the magnetic properties of gold clusters.67 The spin population distribution over the atoms of odd gold clusters is shown in Fig. 2. It reveals that the spin magnetic moment is non-uniformly distributed on the different atoms of gold clusters. For example, in Au3, 0.79μB of the spin magnetic moment is distributed over two of its constituent atoms, while the remaining 0.21μB resides on the third atom. Similarly, in Au9, 0.29μB of the magnetic moment resides on one atom (marked as atoms 9 in Fig. 1), while the remaining 0.71μB is distributed among the other eight atoms.
The more fascinating fact pertains to the constant spin magnetic moment of 1μB over the odd Aun clusters, irrespective of their cluster size. But as the cluster size progresses, the spin gets diluted as 1/n μB per atom assuming the uniform distribution of the spin magnetic moment on the atoms of the gold cluster. However, it is obvious that smaller clusters have a higher average magnetic moment per atom than larger clusters. However, the smaller clusters display a larger deviation of the spin magnetic moment per atom from the average distribution curve (1/n μB per atom) in comparison to the higher-order clusters (shown in Fig. 2). Thus, the small odd gold clusters show a non-uniform distribution of the spin magnetic moment on the atoms of gold clusters which becomes uniform for the larger gold clusters.
3.2 Ordering of magnetic moment in gold clusters
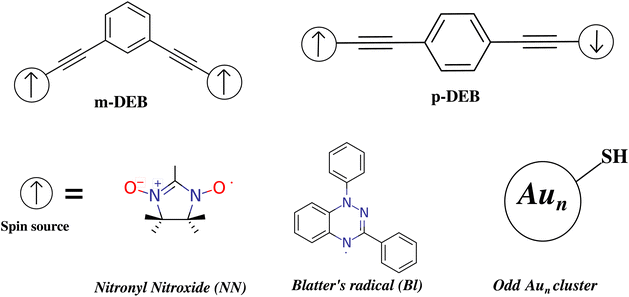
One of the key strategies to harness the magnetic ordering of the spin-bearing organic as well as inorganic moieties is to use a conjugated molecular framework as a coupler through which the magnetic exchange can be communicated between two spatially separated spin sources.9–13,71–76 The π electron-rich aromatic organic molecules, such as benzene, are an excellent choice in this context. To exhibit an efficient ordering of magnetic moments, the coupled gold clusters must retain their magnetic properties when they are connected via an organic spacer. The spatial separation of the connected Aun cluster must be sufficient to inhibit the clusters from collapsing into a single cluster. Keeping this fact in mind, diethynylbenzene (DEB) was used as the organic spacer as shown in Fig. 3. Furthermore, to connect the gold clusters and organic spacer we have functionalized the spacer with the thiol group, which is abbreviated as t-DEB. Nitronyl nitroxide (NN) and Blatter's radical (Bl) are two popular radicals that have been observed to show definite magnetic ordering when coupled via organic spacers.9,11,13,77 To test the effectiveness of the DEB molecule as a coupler, both the meta (m) and para (p) DEB have been used to couple the spin centers of the aforementioned organic radicals (Fig. 3). The nitronyl nitroxide and Blatter's radical coupled with m-DEB show a FM exchange interaction of 7.44 cm−1 and 3.60 cm−1, respectively, while an AFM exchange interaction of −225.3 cm−1 and −16.22 cm−1 is observed with the p-DEB coupler (Table 1). This is in agreement with the previously reported nature of coupling (FM/AFM) of meta/para-connected organic radicals through the benzene coupler.9,71,78 This suggests that the DEB organic spacer can effectively couple the organic radicals.| Energy (Eh) | <S2> | 2J (cm−1) | |||
|---|---|---|---|---|---|
| BS | HS | BS | HS | ||
| NN-m′-NN | −1450.665005 | −1450.665022 | 1.14 | 2.14 | 7.44 |
| NN-p′-NN | −1450.669604 | −1450.669105 | 1.17 | 2.14 | −225.30 |
| Bl-m′-Bl | −2174.975354 | −2174.977133 | 1.03 | 2.03 | 3.60 |
| Bl-p′-Bl | −2174.977170 | −2174.977133 | 1.03 | 2.03 | −16.22 |
| Au1-m-Au1 | −1452.165381 | −1452.165445 | 1.00 | 2.01 | 27.88 |
| Au1-p-Au1 | −1452.167157 | −1452.166706 | 0.99 | 2.00 | −196.34 |
| Au9-m-Au9 | −3624.244986 | −3624.244990 | 1.01 | 2.01 | 1.82 |
| Au9-p-Au9 | −3624.245767 | −3624.245670 | 1.01 | 2.01 | −42.26 |
When the single Au atom (Au1) is coupled via the m-tDEB (p-tDEB) coupler as shown in Fig. 3, a very strong ferromagnetic (antiferromagnetic) coupling with 2J values as high as 27.88 (−196) cm−1 is observed (Table 1). Henceforth, the coupling of Aun clusters through the meta and para t-DEB couplers will be designated as Aun-m-Aun and Aun-p-Aun respectively. As discussed in the previous section, the distribution of the spin moments amongst the Au atoms is not the same for the isolated clusters. Consequently, the strength of the exchange interaction is also dependent on the atomic site to which the coupler is linked. In the ESI (section S4†), we have calculated the 2J values of the Aun clusters, linked to the coupler via different atomic sites. Out of all possible combinations, the connection showing the highest 2J is further considered for understanding the variation of the strength of the magnetic coupling for the odd Aun clusters which has been shown in Fig. 6. For the meta-coupled clusters, ferromagnetic ordering is observed for Au9-m-Au9 with the 2J value of 1.82 cm−1 using the B3LYP functional (Table 1). In contrast to the clusters connected through para t-DEB, Au9-p-Au9 exhibits antiferromagnetic coupling, underscored by the 2J value of 42.26 cm−1. Thus, this is a clear indication that the magnetic moments arising out of the odd Aun clusters could be ordered by interconnecting them through an organic spacer to get the FM/AFM coupling. Table 1 indicates stronger antiferromagnetic exchange interactions than ferromagnetic interactions71,78 (refer to subsection S4.1 of the ESI†).
In order to verify the dependence of 2J on the functional, we have calculated 2J values for Au1-m/p-Au1 and Au9-m/p-Au9 using different functionals, namely local and gradient corrected functionals (BLYP, PBE), hybrid functionals (B3LYP, PBE0), meta GGA functional (TPSS), and hybrid meta GGA functional (TPSSh, M06). Local and gradient corrected functionals overestimate the 2J (refer to section S3.1 of the ESI† for variation of <S2>BS value for different functionals), but the nature of magnetic coupling through the meta and para organic spacer using every functional is found to be the same i.e., FM and AFM respectively (Fig. 4).
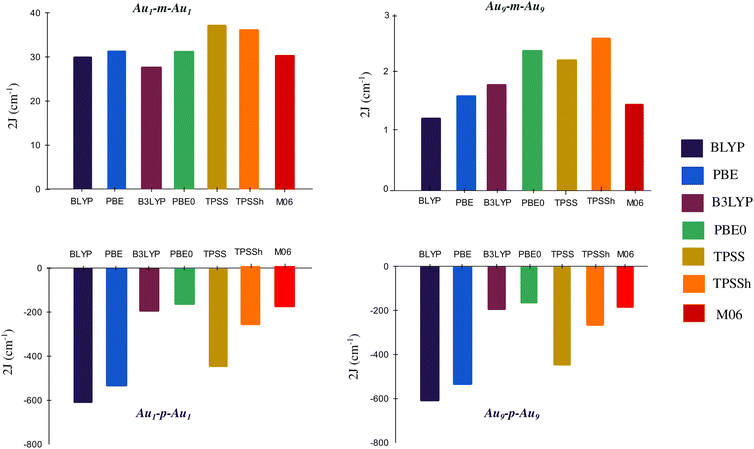 | ||
| Fig. 4 Variation in 2J with different functionals for Au1-m/p-Au1 and Au9-m/p-Au9 with def2-TZVP as the basis set. | ||
For the purpose of benchmarking, we have also done the CASSCF and CASSCF-NEVPT2 calculations whose results are provided in section 2 of the ESI† for the proto typical case of Au1-m/p-Au1. Here, our objective is only to verify the nature of coupling through the meta and para couplers. The 2J values obtained with CASSCF(6,6) and CASSCF-NEVPT2(6,6) for Au1-m-Au1 are 2.86 cm−1 and 7.28 cm−1 respectively, while for Au1-p-Au1, 2J values are −9.77 cm−1 and −36.93 cm−1. Once again, the multireference calculations for the prototypical Au1 case confirm the FM and AFM ordering with meta and para spacers respectively.
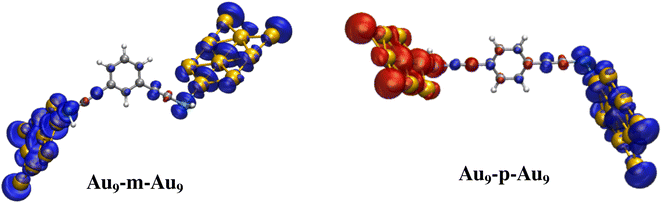
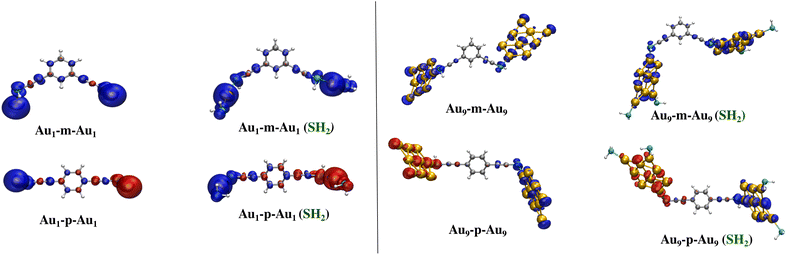
The anchoring thiol groups play a crucial role in forming the exchange pathways between the coupled Aun clusters. As shown in Fig. 5, the sulfur atoms of the –SH groups retain a significant amount of the spin density from the Au9 clusters and take part in the π conjugation with the t-DEB spacer. The ferromagnetic coupling for the meta connection and the antiferromagnetic coupling for the para connection can be rationalized by applying the simple spin alternation rule of the aromatic couplers. In the case of meta t-DEB, the spin sources from the two Au clusters are connected via 2N + 1 number of atoms, where N is the number of conjugated π-bonds and hence gives ferromagnetic coupling, whereas, in the case of para t-DEB, there are 2N atoms present in the exchange pathways between the Aun clusters which results in the antiferromagnetic ordering of the nanomagnets. However, the spin polarization of the sulfur atom is not the same for all the clusters considered here. It has been observed that higher spin polarization of organic spacers induced by the Aun cluster results in a larger magnetic exchange interaction.
When we move from a single Au atom to odd Aun clusters, the nature of magnetic ordering remains the same. However, we witnessed a substantial decrement in the magnetic coupling strength for both kinds of exchange pathways. The exchange interactions for the gold clusters using the meta coupler (m-tDEB) are shown in Fig. 6. The 2J values obtained for the coupled odd gold clusters are in the range of 0.02 to 2.32 cm−1, with the lowest and the highest 2J corresponding to Au3-m-Au3 and Au7-m-Au7, respectively. For the antiferromagnetic ordering of the magnetic moments, which has been observed using para t-DEB as a coupler (Fig. 6), the highest 2J equal to −42.26 cm−1 has been obtained for Au9-p-Au9. With Au11-p-Au11, Au7-p-Au7 and Au5-p-Au5, −30.9 cm−1, −25.6 cm−1, and −20.3 cm−1 respectively have been obtained as the 2J values, showcasing stronger antiferromagnetic coupling in these cases. Magnetic exchange interactions can also be observed when –SH is replaced with S− (anion) and Ṡ (radical). But in the case of the Ṡ radical, its free electron quenches the magnetic moment arising from odd Aun clusters, but the interesting aspect is that exchange interactions can now be observed with even Aun clusters (refer to subsection S4.2 of the ESI† for 2J values in different S–Au linkages).
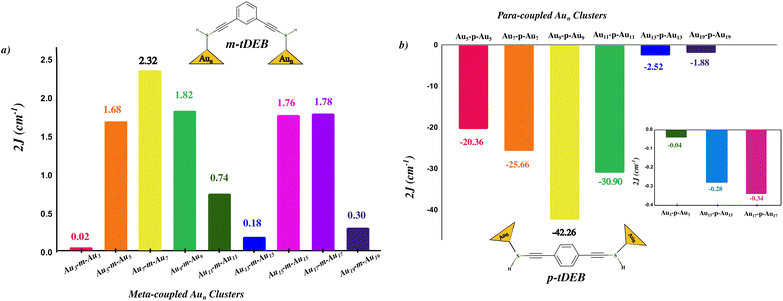 | ||
| Fig. 6 (a, b) Magnetic exchange coupling constant variation in odd Aun clusters, n = 3,…,19 coupled through the t-DEB (meta and para) organic spacer represented as Aun-m-Aun and Aun-p-Aun. The inset of (b) shows the 2J values for Au3-p-Au3, Au15-p-Au15 and Au17-p-Au17 as they have lower values in comparison to the other Aun-p-Aun geometries. Refer the ESI† for para and meta coupled Aun clusters. | ||
In the case of Au3-m/p-Au3 and Au13-m/p-Au13 to Au19-m/p-Au19 clusters, we have observed a significant reduction in magnetic interaction strength between the magnetic centers. While it's expected that the magnetic interaction strength decreases as the cluster size increases, it's notable that with just one unpaired electron present, there is a diminished spin distribution across the atoms of the Aun cluster known as the spin dilution effect. However, the case of Au3-m/p-Au3 is particularly interesting. Here, the magnetic interaction strength is unexpectedly low, despite the presence of only three atoms and the unpaired spin being distributed among them. Following this observation, we further investigated the spin population distribution in the isolated Au3 cluster and in the case where clusters are connected through benzene (refer to section S5 of the ESI† for spin density distribution). The atom of Au3 cluster attached to the SH group, whether it is 1, 2, or 3; regardless of the spin density in the isolated case that atom's spin magnetic moment reduces to 0.13μB and the spin moment redistribution leads to spin delocalization over the other two atoms of the cluster, with most of the spin moment (0.986μB) still lying with the Au3 cluster which suggests that the spin centers exhibit a propensity to avoid coupling pathways through the organic spacer. Also, it is interesting to note here the change in the geometry of the Au3 cluster from an isosceles triangle to the equilateral triangular shape when connected through the coupler.
3.3 Factors influencing exchange coupling magnitude
Magnetic exchange interactions also depend upon the shape of the magnetic orbitals, for instance the nature of orbitals in the case of AFM interactions is disjoint while FM interactions involve non-disjoint orbitals79,80(refer to subsection S4.0.3 of the ESI†).
Comparing the scenarios with and without the capping agent for Au1 and Au9 coupled through m/p-tDEB outlined in Table 2, it's evident that the incorporation of SH2 capping effectively safeguards and enhances the inherent magnetism within the gold atom as well the Au9 cluster. This is reflected in the elevated 2J-values after binding the capping agent to the gold atom and edge atoms of the Au9 cluster except in Au1-m-Au1 where the Au–S bond length is 3 Å, highest among all the cases. This enlargement of Au–S bond length moves the spin sources far away from the coupler, thereby reducing exchange interactions. Otherwise, except for Au1-m-Au1, in all the other cases spin density plots (see Fig. 7) suggest that attachment of the capping agent increases the spin magnetic moment towards the coupler pathway, thereby increasing the exchange interactions.
| Energy (Eh) | <S2> | 2J (cm−1) | |||
|---|---|---|---|---|---|
| BS | HS | BS | HS | ||
| Au1-m-Au1 | −1452.165381 | −1450.165445 | 1.01 | 2.01 | 27.88 |
| Au1-m-Au1 (SH2) | −2250.885193 | −2250.885235 | 1.01 | 2.01 | 18.48 |
| Au1-p-Au1 | −1452.167157 | −1452.166706 | 0.99 | 2.00 | −196.34 |
| Au1-p-Au1 (SH2) | −2250.887052 | −2250.886478 | 0.99 | 2.00 | −248.04 |
| Au9-m-Au9 | −3624.244986 | −3624.244990 | 1.01 | 2.01 | 1.82 |
| Au9-m-Au9 (SH2) | −5221.742238 | −5221.742254 | 1.01 | 2.01 | 6.90 |
| Au9-p-Au9 | −3624.245767 | −3624.245670 | 1.01 | 2.01 | −42.26 |
| Au9-p-Au9 (SH2) | −5221.741919 | −5221.741769 | 1.00 | 2.00 | −65.02 |
4 Conclusion
In the odd Aun (n = 1,3, … 19) clusters, one unpaired electron, responsible for the magnetism in nano-clusters, becomes distributed amongst the constituent Au atoms in an unsymmetrical manner. As the cluster size expands, this unitary spin magnetic moment becomes progressively apportioned among the increasing number of constituent atoms, thereby converging towards an approximate 1/n μB per atom. When two such one-electron paramagnetic Au-nanoclusters are coupled via an organic spacer, thiol-functionalized diethynylbenzene (t-DEB), definite magnetic ordering can be obtained. The meta and para t-DEB spacers result in the ferro and antiferromagnetic ordering of the magnetic moments. The π-conjugation in the organic spacers avail spin-altered exchange pathways to facilitate the ferro (antiferro) magnetic coupling in the meta (para)-connected Au-nanoclusters. The spin moments of the Aun clusters make the linker thiol groups spin polarised, which in turn takes part in the conjugation with the coupler and facilitates the exchange mechanisms.Author contributions
MEA conceptualized the project, supervised the work and secured funding. NM did computational data curation, data analysis and has written the initial draft. AM and SA contributed to the manuscript preparation and data analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Department of Science and Technology through SERB-CRG Project No. CRG/2022/008683 is gratefully acknowledged. S. A. thanks CSIR India for the SRF fellowship with Grant No. 09/1129(0027)/2020-EMR-I.References
- X. Li and J. Yang, First-principles design of spintronics materials, Natl. Sci. Rev., 2016, 3, 365–381 CrossRef CAS.
- C. Herrmann, G. C. Solomon and M. A. Ratner, Organic radicals as spin filters, J. Am. Chem. Soc., 2010, 132, 3682–3684 CrossRef CAS PubMed.
- W. Han, Y. Otani and S. Maekawa, Quantum materials for spin and charge conversion, npj Quantum Mater., 2018, 3, 27 CrossRef.
- A. Hirohata, K. Yamada, Y. Nakatani, I.-L. Prejbeanu, B. Diény, P. Pirro and B. Hillebrands, Review on spintronics: Principles and device applications, J. Magn. Magn. Mater., 2020, 509, 166711 CrossRef CAS.
- A. Bajaj, P. Kaur, A. Sud, M. Berritta and M. E. Ali, Anomalous effect of quantum interference in organic spin filters, J. Phys. Chem. C, 2020, 124, 24361–24371 CrossRef CAS.
- M. E. Ali, V. Staemmler, F. Illas and P. M. Oppeneer, Designing the redox-driven switching of ferro-to antiferromagnetic couplings in organic diradicals, J. Chem. Theory Comput., 2013, 9, 5216–5220 CrossRef CAS PubMed.
- T. R. Felthouse and D. N. Hendrickson, Magnetic exchange interactions in transition-metal dimers. 12. Structural and magnetic characterization of the di-. mu (1,3)-azido complex [Cu2(Me5dien)2(N3)2](BPh4)2 and similar di-.+-.(1,3)-azido copper(II) dimers. Unusual zero-field splitting in the electron paramagnetic resonance spectra, Inorg. Chem., 1978, 17, 444–456 CrossRef CAS.
- P. Gopal, R. De Gennaro, M. S. dos Santos Gusmao, R. A. R. Al Orabi, H. Wang, S. Curtarolo, M. Fornari and M. B. Nardelli, Improved electronic structure and magnetic exchange interactions in transition metal oxides, J. Phys.: Condens. Matter, 2017, 29, 444003 CrossRef PubMed.
- M. E. Ali and S. N. Datta, Broken-symmetry density functional theory investigation on bis-nitronyl nitroxide diradicals: influence of length and aromaticity of couplers, J. Phys. Chem. A, 2006, 110, 2776–2784 CrossRef CAS PubMed.
- M. E. Ali, P. M. Oppeneer and S. N. Datta, Influence of Solute- Solvent Hydrogen Bonding on Intramolecular Magnetic Exchange Interaction in Aminoxyl Diradicals: A QM/MM Broken-Symmetry DFT Study, J. Phys. Chem. B, 2009, 113, 5545–5548 CrossRef CAS PubMed.
- R. Khurana, A. Bajaj and M. E. Ali, How Plausible Is Getting Ferromagnetic Interactions by Coupling Blatter's Radical via Its Fused Benzene Ring?, J. Phys. Chem. A, 2020, 124, 6707–6713 CrossRef CAS PubMed.
- R. Khurana, A. Bajaj and M. E. Ali, Tuning the magnetic properties of a diamagnetic di-Blatter's zwitterion to antiferro-and ferromagnetically coupled diradicals, Phys. Chem. Chem. Phys., 2022, 24, 2543–2553 RSC.
- A. Bajaj and M. E. Ali, First-principle design of Blatter's diradicals with strong ferromagnetic exchange interactions, J. Phys. Chem. C, 2019, 123, 15186–15194 CrossRef CAS.
- S. Shil, D. Bhattacharya, A. Misra and D. J. Klein, A high-spin organic diradical as a spin filter, Phys. Chem. Chem. Phys., 2015, 17, 23378–23383 RSC.
- E. Vogt, in Magnetism and Metallurgy, ed. A. Berkowitz and E. Kneller, Academic Press, 1969, vol. 1, pp. 252 Search PubMed.
- R. Magyar, V. Mujica, M. Marquez and C. Gonzalez, Density-functional study of magnetism in bare Au nanoclusters: Evidence of permanent size-dependent spin polarization without geometry relaxation, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 144421 CrossRef.
- L. D. Marks, Experimental studies of small particle structures, Rep. Prog. Phys., 1994, 57, 603 CrossRef CAS.
- C. L. Cleveland, U. Landman, T. G. Schaaff, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Structural evolution of smaller gold nanocrystals: The truncated decahedral motif, Phys. Rev. Lett., 1997, 79, 1873 CrossRef CAS.
- M.-C. Daniel and D. Astruc, Gold nanoparticles: assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis, and nanotechnology, Chem. Rev., 2004, 104, 293–346 CrossRef CAS PubMed.
- V. Novotny, P. Meincke and J. Watson, Effect of size and surface on the specific heat of small lead particles, Phys. Rev. Lett., 1972, 28, 901 CrossRef CAS.
- J. Dickey and A. Paskin, Phonon spectrum changes in small particles and their implications for superconductivity, Phys. Rev. Lett., 1968, 21, 1441 CrossRef.
- R. Kubo, Electronic properties of metallic fine particles. I, J. Phys. Soc. Jpn., 1962, 17, 975–986 CrossRef CAS.
- A. Kawabata and R. Kubo, Electronic properties of fine metallic particles. II. Plasma resonance absorption, J. Phys. Soc. Jpn., 1966, 21, 1765–1772 CrossRef CAS.
- F. W. Halperin, Quantum size effects in metal particles, Rev. Mod. Phys., 1986, 58, 533 CrossRef.
- C.-Y. Li, S. K. Karna, C.-W. Wang and W.-H. Li, Spin polarization and quantum spins in Au nanoparticles, Int. J. Mol. Sci., 2013, 14, 17618–17642 CrossRef PubMed.
- H. Hori, T. Teranishi, Y. Nakae, Y. Seino, M. Miyake and S. Yamada, Anomalous magnetic polarization effect of Pd and Au nano-particles, Phys. Lett. A, 1999, 263, 406–410 CrossRef CAS.
- Y. Yamamoto, T. Miura, M. Suzuki, N. Kawamura, H. Miyagawa, T. Nakamura, K. Kobayashi, T. Teranishi and H. Hori, Direct observation of ferromagnetic spin polarization in gold nanoparticles, Phys. Rev. Lett., 2004, 93, 116801 CrossRef CAS PubMed.
- J. S. Garitaonandia, M. Insausti, E. Goikolea, M. Suzuki, J. D. Cashion, N. Kawamura, H. Ohsawa, I. Gil de Muro, K. Suzuki and F. Plazaola, et al., Chemically induced permanent magnetism in Au, Ag, and Cu nanoparticles: localization of themagnetism by element selective techniques, Nano Lett., 2008, 8, 661–667 CrossRef CAS PubMed.
- K. S. Krishna, P. Tarakeshwar, V. Mujica and C. S. Kumar, Chemically induced magnetism in atomically precise gold clusters, Small, 2014, 10, 907–911 CrossRef CAS PubMed.
- M. Agrachev, S. Antonello, T. Dainese, M. Ruzzi, A. Zoleo, E. Aprá, N. Govind, A. Fortunelli, L. Sementa and F. Maran, Magnetic ordering in gold nanoclusters, ACS Omega, 2017, 2, 2607–2617 CrossRef CAS PubMed.
- Y. Li and R. Jin, Magnetism of atomically precise gold and doped nanoclusters: delocalized spin and interparticle coupling, J. Phys. Chem. C, 2021, 125, 15773–15784 CrossRef CAS.
- P. Zhang and T. Sham, Tuning the electronic behavior of Au nanoparticles with capping molecules, Appl. Phys. Lett., 2002, 81, 736–738 CrossRef CAS.
- P. Zhang and T. Sham, X-ray studies of the structure and electronic behavior of alkanethiolate-capped gold nanoparticles: the interplay of size and surface effects, Phys. Rev. Lett., 2003, 90, 245502 CrossRef PubMed.
- J. Kübler, Theory of itinerant electron magnetism, Oxford University Press, 2017, pp. 106 Search PubMed.
- H. C. Siegmann and J. Stöhr, Magnetism: From Fundamentals to Nanoscale Dynamics, Springer Bln, 2006 Search PubMed.
- P. Crespo, R. Litrán, T. Rojas, M. Multigner, J. De la Fuente, J. Sánchez-López, M. García, A. Hernando, S. Penadés and A. Fernández, Permanent magnetism, magnetic anisotropy, and hysteresis of thiol-capped gold nanoparticles, Phys. Rev. Lett., 2004, 93, 087204 CrossRef CAS PubMed.
- A. Ayuela, P. Crespo, M. García, A. Hernando and P. M. Echenique, sp magnetism in clusters of gold thiolates, New J. Phys., 2012, 14, 013064 CrossRef.
- M. Suzuki, N. Kawamura, H. Miyagawa, J. S. Garitaonandia, Y. Yamamoto and H. Hori, Measurement of a Pauli and orbital paramagnetic state in bulk gold using X-ray magnetic circular dichroism spectroscopy, Phys. Rev. Lett., 2012, 108, 047201 CrossRef PubMed.
- V. Sahni and K.-P. Bohnen, Image charge at a metal surface, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 7651 CrossRef CAS PubMed.
- M. K. Harbola and V. Sahni, Structure of the Fermi hole at surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 745 CrossRef PubMed.
- P. Dutta, S. Pal, M. Seehra, M. Anand and C. Roberts, Magnetism in dodecanethiol-capped gold nanoparticles: Role of size and capping agent, Appl. Phys. Lett., 2007, 90, 213102 CrossRef.
- M. Hasan, D. Bethell and M. Brust, The fate of sulfur-bound hydrogen on formation of self-assembled thiol monolayers on gold: 1H NMR spectroscopic evidence from solutions of gold clusters, J. Am. Chem. Soc., 2002, 124, 1132–1133 CrossRef CAS PubMed.
- R. G. Nuzzo, B. R. Zegarski and L. H. Dubois, Fundamental studies of the chemisorption of organosulfur compounds on gold (111). Implications for molecular self-assembly on gold surfaces, J. Am. Chem. Soc., 1987, 109, 733–740 CrossRef CAS.
- I. I. Rzeźnicka, J. Lee, P. Maksymovych and J. T. Yates, Nondissociative chemisorption of short chain alkanethiols on Au (111), J. Phys. Chem. B, 2005, 109, 15992–15996 CrossRef PubMed.
- H. Grönbeck, A. Curioni and W. Andreoni, Thiols and disulfides on the Au (111) surface: the headgroup- gold interaction, J. Am. Chem. Soc., 2000, 122, 3839–3842 CrossRef.
- H. Guesmi, N. B. Luque, E. Santos and F. Tielens, Does the S- H Bond Always Break after Adsorption of an Alkylthiol on Au (111)?, Chem. – Eur. J., 2017, 23, 1402–1408 CrossRef CAS PubMed.
- M. S. Inkpen, Z.-F. Liu, H. Li, L. M. Campos, J. B. Neaton and L. Venkataraman, Non-chemisorbed gold–sulfur binding prevails in self-assembled monolayers, Nat. Chem., 2019, 11, 351–358 CrossRef CAS PubMed.
- M. Jaccob, G. Rajaraman and F. Totti, On the kinetics and thermodynamics of S–X (X = H, CH 3, SCH 3, COCH 3, and CN) cleavage in the formation of self-assembled monolayers of alkylthiols on Au (111), Theor. Chem. Acc., 2012, 131, 1–11 Search PubMed.
- G. Rajaraman, A. Caneschi, D. Gatteschi and F. Totti, A periodic mixed gaussians–plane waves DFT study on simple thiols on Au (111): adsorbate species, surface reconstruction, and thiols functionalization, Phys. Chem. Chem. Phys., 2011, 13, 3886–3895 RSC.
- H. Häkkinen, The gold–sulfur interface at the nanoscale, Nat. Chem., 2012, 4, 443–455 CrossRef PubMed.
- L. Noodleman, Valence bond description of antiferromagnetic coupling in transition metal dimers, J. Phys. Chem., 1981, 74, 5737–5743 CrossRef CAS.
- L. Noodleman, D. A. Case and A. Aizman, Broken symmetry analysis of spin coupling in iron-sulfur clusters, J. Am. Chem. Soc., 1988, 110, 1001–1005 CrossRef CAS.
- K. Yamaguchi, Y. Takahara, T. Fueno and K. Nasu, Ab initio MO calculations of effective exchange integrals between transition-metal ions via oxygen dianions: nature of the copper-oxygen bonds and superconductivity, Jpn. J. Appl. Phys., 1987, 26, L1362 CrossRef CAS.
- A. D. Becke, Densityfunctional thermochemistry. III. the role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. L. Martin and F. Illas, Antiferromagnetic exchange interactions from hybrid density functional theory, Phys. Rev. Lett., 1997, 79, 1539 CrossRef CAS.
- F. Bischoff, O. Hübner, W. Klopper, L. Schnelzer, B. Pilawa, M. Horvatić and C. Berthier, Density-functional calculation of the quadrupole splitting in the 23 Na NMR spectrum of the ferric wheel Na@ Fe 6 (tea) 6+ for various broken-symmetry states of the Heisenberg spin model, Eur. Phys. J. B, 2007, 55, 229–235 CrossRef CAS.
- O. Hübner, K. Fink and W. Klopper, The spin coupling in the diiron complex [Fe2(hpdta)(H2O)3Cl], Phys. Chem. Chem. Phys., 2007, 9, 1911–1920 RSC.
- E. Ruiz, P. Alemany, S. Alvarez and J. Cano, Toward the prediction of magnetic coupling in molecular systems: hydroxo-and alkoxo-bridged Cu(II) binuclear complexes, J. Am. Chem. Soc., 1997, 119, 1297–1303 CrossRef CAS.
- H. Nieber, K. Doll and G. Zwicknagl, Ab initio correlation approach to a ferric wheel-like molecular cluster, Eur. Phys. J. B, 2006, 51, 215–221 CrossRef CAS.
- M. Wojciechowski, B. Brzostowski and G. Kamieniarz, DFT Estimation of Exchange Coupling Constant of Cr8 Molecular Ring using the Hybrid Functional B3LYP, Acta Phys. Pol., A, 2015, 127, 407–409 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- M. Khatun, R. S. Majumdar and A. Anoop, A Global Optimizer for Nanoclusters, Front. Chem., 2019, 7, 644 CrossRef CAS PubMed.
- A. Deka and R. C. Deka, Structural and electronic properties of stable Aun (n = 2–13) clusters: A density functional study, J. Mol. Struct.: THEOCHEM, 2008, 870, 83–93 CrossRef CAS.
- S. Bulusu and X. C. Zeng, Structures and relative stability of neutral gold clusters: Aun (n = 15–19), J. Phys. Chem., 2006, 125, 154303 CrossRef PubMed.
- N. Jabr and A. Kodlaa, Dft study of small gold clusters aun (n = 2–13): The structural, electronic, thermodynamic and spectral properties, Chem. Mater. Res., 2017, 9, 17–27 Search PubMed.
- B. Zhu, D. Die, R.-C. Li, H. Lan, B.-X. Zheng and Z.-Q. Li, Insights into the structural, electronic and magnetic properties of Ni-doped gold clusters: Comparison with pure gold clusters, J. Alloys Compd., 2017, 696, 402–412 CrossRef CAS.
- P. V. Nhat, N. T. Si, J. Leszczynski and M. T. Nguyen, Another look at structure of gold clusters Aun from perspective of phenomenological shell model, Chem. Phys., 2017, 493, 140–148 CrossRef CAS.
- B. R. Goldsmith, J. Florian, J.-X. Liu, P. Gruene, J. T. Lyon, D. M. Rayner, A. Fielicke, M. Scheffler and L. M. Ghiringhelli, Two-to-three dimensional transition in neutral gold clusters: The crucial role of van der Waals interactions and temperature, Phys. Rev. Mater., 2019, 3, 016002 CrossRef CAS.
- G. A. Bishea and M. D. Morse, Spectroscopic studies of jet-cooled AgAu and Au2, J. Chem. Phys., 1991, 95, 5646–5659 CrossRef CAS.
- K. C. Ko, D. Cho and J. Y. Lee, Systematic approach to design organic magnetic molecules: strongly coupled diradicals with ethylene coupler, J. Phys. Chem. A, 2012, 116, 6837–6844 CrossRef CAS PubMed.
- I.-R. Jeon, J. G. Park, D. J. Xiao and T. D. Harris, An azophenine radical-bridged Fe2 single-molecule magnet with record magnetic exchange coupling, J. Am. Chem. Soc., 2013, 135, 16845–16848 CrossRef CAS PubMed.
- R. Khurana, A. Bajaj, K. Shamasundar and M. E. Ali, High-Spin Blatter's Triradicals, J. Phys. Chem. A, 2023, 127, 7802–7810 CrossRef CAS PubMed.
- A. K. Pal, D. R. Mañeru, I. A. Latif, I. d. P. Moreira, F. Illas and S. N. Datta, Theoretical and computational investigation of meta-phenylene as ferromagnetic coupler in nitronyl nitroxide diradicals, Theor. Chem. Acc., 2014, 133, 1–12 Search PubMed.
- D. Bhattacharya, S. Shil, A. Misra and D. Klein, Intramolecular ferromagnetic coupling in bis-oxoverdazyl and bis-thioxoverdazyl diradicals with polyacene spacers, Theor. Chem. Acc., 2010, 127, 57–67 Search PubMed.
- S. Shil, D. Bhattacharya, A. Misra and L. Bytautas, Antiaromatic Molecules as Magnetic Couplers: A Computational Quest, J. Phys. Chem. A, 2024, 128, 815–828 CrossRef CAS PubMed.
- C. Stroh, R. Ziessel, G. Raudaschl-Sieber, F. H. Köhler and P. Turek, Intramolecular exchange interactions in non-aromatic bis-nitronyl-nitroxides, J. Mater. Chem., 2005, 15, 850–858 RSC.
- D. Cho, K. C. Ko and J. Y. Lee, Organic magnetic diradicals (radical–coupler–radical): standardization of couplers for strong ferromagnetism, J. Phys. Chem. A, 2014, 118, 5112–5121 CrossRef CAS PubMed.
- M. E. Ali, A. S. Roy and S. N. Datta, Molecular tailoring and prediction of strongly ferromagnetically coupled trimethylenemethane-based nitroxide diradicals, J. Phys. Chem. A, 2007, 111, 5523–5527 CrossRef CAS PubMed.
- A. Bencini, D. Gatteschi, F. Totti, D. N. Sanz, J. A. Mc Cleverty and M. D. Ward, Density functional modeling of long range magnetic interactions in binuclear oxomolybdenum(V) complexes, J. Phys. Chem. A, 1998, 102, 10545–10551 CrossRef CAS.
- M. Cui, Y. Zhao and Q. Song, Synthesis optical properties and applications of ultra-small luminescent gold nanoclusters, TrAC, Trends Anal. Chem., 2014, 57, 73–82 CrossRef CAS.
- J. Zheng, C. Zhang and R. M. Dickson, Highly fluorescent, water-soluble, size-tunable gold quantum dots, Phys. Rev. Lett., 2004, 93, 077402 CrossRef PubMed.
- P. Dong, E. A. Fisher, M.-V. Meli and S. Trudel, Tuning the magnetism of gold nanoparticles by changing the thiol coating, Nanoscale, 2020, 12, 19797–19803 RSC.
- H. Zhang, K. Suzuki, K. Saito, J. Garitaonandia, E. Goikolea and M. Insausti, Effect of Organic Capping on the Magnetic Properties of Au Nanoparticles, Mater. Sci. Forum, 2010, 654, 1174–1177 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Energetics of isolated Aun clusters, molecular orbital plots of odd and even clusters, single point energies and the magnetic exchange coupling constant (2J) for coupled clusters using the Yamaguchi and Noodleman formula, Löwdin spin population distribution in isolated Aun clusters and when clusters are coupled via a benzene spacer, the effect of the capping agent SH2 on the spin magnetic moment of Au atoms, and variation of the overlap integral with magnetic exchange coupling. See DOI: https://doi.org/10.1039/d4nr00856a |
| This journal is © The Royal Society of Chemistry 2024 |