Manipulating ultrafast magnetization dynamics of ferromagnets using the odd–even layer dependence of two-dimensional transition metal di-chalcogenides†
Soma
Dutta
 a,
Sajid
Husain‡
*b,
Prabhat
Kumar
a,
Sajid
Husain‡
*b,
Prabhat
Kumar
 c,
Nanhe Kumar
Gupta
d,
Sujeet
Chaudhary
d,
Peter
Svedlindh
b and
Anjan
Barman
c,
Nanhe Kumar
Gupta
d,
Sujeet
Chaudhary
d,
Peter
Svedlindh
b and
Anjan
Barman
 *a
*a
aDepartment of Condensed Matter and Materials Physics, S. N. Bose National Centre for Basic Sciences, Block JD, Sector-III, Salt Lake, Kolkata 700 106, India. E-mail: abarman@bose.res.in
bDepartment of Materials Science and Engineering, Uppsala University, Box 35, SE-751 03 Uppsala, Sweden. E-mail: shusain@lbl.gov
cDepartment of Thin Films and Nanostructures, Institute of Physics of the Czech Academy of Sciences, Cukrovarnická 10/112, 162 00 Prague, Czech Republic
dThin Film Laboratory, Department of Physics, Indian Institute of Technology Delhi, New Delhi 110016, India
First published on 31st January 2024
Abstract
Two-dimensional transition metal dichalcogenides (TMDs) have drawn immense interest due to their strong spin–orbit coupling and unique layer number dependence in response to spin–valley coupling. This leads to the possibility of controlling the spin degree of freedom of the ferromagnet (FM) in thin film heterostructures and may prove to be of interest for next-generation spin-based devices. Here, we experimentally demonstrate the odd–even layer dependence of WS2 nanolayers by measurements of the ultrafast magnetization dynamics in WS2/Co3FeB thin film heterostructures by using time-resolved Kerr magnetometry. The fluence (photon energy per unit area) dependent magnetic damping (α) reveals the existence of broken symmetry and the dominance of inter- and intraband scattering for odd and even layers of WS2, respectively. The higher demagnetization time, τm, in 3 and 5 layers of WS2 is indicative of the interaction between spin–orbit and spin-valley coupling due to the broken symmetry. The lower τm in even layers as compared to the bare FM layer suggests the presence of a spin transport. By correlating τm and α, we pinpointed the dominant mechanisms of ultrafast demagnetization. The mechanism changes from spin transport to spin-flip scattering for even layers of WS2 with increasing fluence. A fundamental understanding of the two-dimensional material and its odd–even layer dependence at ultrashort timescales provides valuable information for designing next-generation spin-based devices.
Introduction
Despite countless fascinating characteristics of graphene, the lack of intrinsic spin–orbit coupling in graphene has led to the discovery of two-dimensional (2D) transition metal dichalcogenides (TMDs) MX2, where M is a transition metal and X is a chalcogen atom. Different TMDs have rapidly emerged during the last decade due to their potential for a wide range of applications and rich physics. Among them, group-VI TMDs (M = W, Mo and X = S, Se, Te) have shown unique electronic band structure properties depending on the layer number.1–4 A monolayer (ML) of a TMD corresponds to half a unit cell of the bulk crystal, implying that the mirror inversion symmetry is broken in odd numbers of layers. The top of the valence band and the bottom of the conduction band consist of two inequivalent Q valleys in addition to the splitting at K and K′ points of the hexagonal Brillouin zone2 in TMDs. Due to the lack of inversion symmetry in odd numbers of layers, the charges on the M and X atoms generate local in-plane electric fields and cause spin–orbit interaction which is strong enough to orient the spins in the bands perpendicular to the ML. Thus, this effect imitates a perpendicular magnetic field causing a giant Zeeman splitting of valleys that become fully spin polarized.5 Based on the possibility to manipulate this valley degree of freedom, the concept of valleytronics6 has emerged providing alongside the spin–orbit coupling (SOC) due to the d orbitals of the heavy metal atom, a way for spin manipulation. These effects lead to spin and valley coupled physics (spin–valleytronics), such as the valley Hall effect accompanied by the spin Hall effect,7,8 suppression of spin and valley relaxation,9etc. Rather than the widely used electrical10,11 and magnetic12 methods, joint theory–experiment reports have shown that the spin–valley polarization and intervalley coupling of excitonic states in different valleys can be accessible through optical excitation.13 Several theoretical9,14 and experimental15 reports have drawn attention to the combination of 2D TMDs with strong SOC with a 3d ferromagnet (FM) to modify the magnetic properties of the FM layer and to promote layer number dependent properties of the heterostructure.16 This layer number dependence is one of the unique characteristics of TMDs, which is however not yet been fully explored. Thus, it is essential to carry out a comprehensive study of the magnetization dynamics (via optical excitation) at ultrafast timescales of the layered TMDs as a function of the layer number. Previous reports suggest that the strong SOC promotes transfer of spin angular momentum within the spin system and plays an important role in manipulating the ultrafast demagnetization time (τm), spin switching and spin-wave propagation.16–20An all-optical study of magnetization dynamics using a pump-probe technique based on time-resolved magneto-optical Kerr effect (TR-MOKE) microscopy is one of the best methods that can provide a detailed understanding of the effect of TMD materials on a FM at the time scale of one billionth of a second20 and magnetization precession associated with damping from picoseconds to a sub-nanosecond timescale. Due to broken inversion symmetry,21 interband optical transitions will have a strong impact on magnetic damping22vis-à-vis ultrafast demagnetization. During the optical excitation in TMDs, valley dependent charge23 transfer is the mechanism underpinning all-optical switching (AOS)24 and hence ultrafast demagnetization. However, the microscopic mechanism and the role of spin–valley coupling have not been studied in detail for TMD based heterostructures.
In this work, we report the fluence dependent ultrafast demagnetization (τm) and damping (α) in WS2 (nML = 0, 1, 2, 3, 4, 5)/Co3FeB (6 nm)/Al (4 nm) thin film heterostructures by using the all-optical TR-MOKE technique. Compared to other TMDs, WS2 has high spin–orbit coupling, better thermal stability, and high field effect mobility.25 Its foremost stability with strong in-plane bonds and ability to form hybrid interfaces without any lattice matching make it a potential 2D material for magnetic information storage at an atomically thin limit. From the modulation of damping with pump laser fluence for different WS2 layer numbers, it is observed that the broken inversion symmetry for odd numbers of layers leads to interband transitions, whereas even layers are governed by intraband transitions. We have extracted the dominant contributions for ultrafast demagnetization by correlating τm and α. In the case of nML = 0 (bare FM layer), both the ultrafast demagnetization and damping are governed by the spin-flip scattering (SFS) of the 3d itinerant electrons by impurities or quasiparticles. For odd number of layers, SFS dominates for the entire fluence range, while for even number of WS2 layers, spin pumping dominates at low fluences but with the increase of laser fluence, SFS overshadows spin pumping. This study provides a detailed understanding of the magnetization dynamics and enables a non-volatile control of the ultrafast relaxation based on the layer number.
Experimental details
Controlled WS2 layers were prepared by the combined process of ion beam sputtering and subsequent plasma sulphurization of W films on thermally oxidized Si substrates. A detailed sulphurization recipe can be found in other reports.26 After the growth of the WS2 films, the samples were transferred back to the ion beam sputtering chamber for the growth of 6 nm-thick Co3FeB thin films at room temperature. The details related to the deposition of Co3FeB can be found in a previous report.22 Following that a 4 nm-thick Al layer was deposited as a capping layer to prevent the surface from degradation. Thus, the heterostructure stacks consist of the following layers from the bottom to the top: Sub//WS2 (nML = 0,1,2,3,4,5)/Co3FeB (6 nm)/Al (4 nm), where the nominal thicknesses are given in parentheses. For simplicity, the heterostructures are described as WS2 (nML)/Co3FeB throughout the manuscript. The film thickness and roughness were obtained by X-ray reflectivity (XRR) measurements and a ML of WS2 corresponding to ∼9 Å thickness and WS2 layer numbers are confirmed by Raman spectroscopy as shown in the ESI.†The static magnetic properties (see the ESI†) of the samples were measured using a vibrating sample magnetometer (VSM), whereas the magnetization dynamics were investigated using a two colour non-collinear pump-probe based TR-MOKE technique. The TR-MOKE setup consists of a femtosecond regenerative amplified laser system with a central wavelength of 800 nm, a pulse width of ∼35 fs and a repetition rate of 1 kHz. A part of this fundamental laser beam is passed through a second harmonic generator to double its frequency and generate a pump laser of wavelength 400 nm, with a pulse width of >35 fs with an identical repetition rate. The magnetization dynamics is excited by an intense pump beam (fluence between 2.5 and 15 mJ cm−2) whereas a small part of the rest of the fundamental laser beam (fluence of 1 mJ cm−2) is used as a probe beam to measure the magnetization dynamics by detecting the transient Kerr rotation signal. In our TR-MOKE experiment, the pump beam is incident at a 45° angle to the sample plane and focused on a spot having a diameter of ∼250 μm. The probe beam is tightly focused on a spot of diameter ∼100 μm and is incident normally on the sample plane located at the centre of the pump spot to detect the dynamics only from a uniformly excited region of the sample. The probe beam is polarized and chopped at a frequency of 373 Hz using an optical chopper right before reaching the sample. The transient Kerr rotation is detected in the probe beam through an analyzer and a Si detector by using a lock-in amplifier in a phase sensitive manner. The output frequency from the optical chopper is used as the reference frequency for the lock-in amplifier. An external magnetic field (tilted by ∼10° out of the sample plane) is applied to introduce a finite out-of-plane demagnetizing field, which is modulated by the pump beam to induce precessional dynamics in the samples.
Results and discussion
A schematic of the TR-MOKE setup is depicted in Fig. 1(a) along with the sample stack shown in Fig. 1(b). A typical laser induced time resolved magnetization dynamics is shown in Fig. 1(c) for the WS2 (nML = 4)/Co3FeB sample measured with a pump fluence of 10 mJ cm−2 under an in-plane bias magnetic field of 1.56 kOe. The applied magnetic field is large enough to reach saturation magnetization (Fig. S1†). The transient Kerr rotation drops within a sub-picosecond timescale followed by a recovery process. The ultrafast demagnetization20 and fast remagnetization follow the expression derived from the phenomenological three-temperature model (3TM),17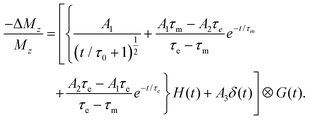 | (1) |
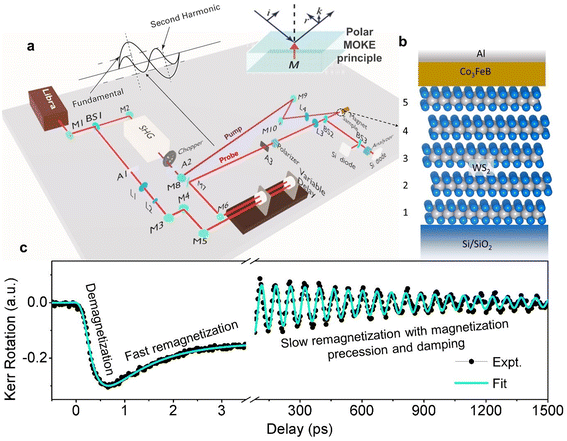 | ||
| Fig. 1 (a) TR-MOKE experimental setup. (b) Layer schematic of the WS2/Co3FeB/Al heterostructure. (c) Recorded data on the WS2 (nML = 4)/Co3FeB sample at an external bias magnetic field of 1.56 kOe and a pump fluence of 10 mJ cm−2. The three important temporal regimes are indicated in the graph. The black solid lines are fit to eqn (1) and (2). | ||
The 3TM is a thermodynamic model describing the spin fluctuations based on the energy transfer between three different subsystems: spin, electron, and lattice. Upon laser excitation, instantaneously created hot electrons are thermalized by electron–electron interactions. Shortly after that, spins also thermalize by electron–magnon interaction followed by ultrafast demagnetization. Then electron and spin start to relax by exchanging their energy with lattice via electron–phonon interaction. This is called the fast remagnetization time (τe). Here, A1 represents the restoring value of −ΔMz/Mz after equilibration of the different subsystems. A2 represents the rise of the initial electron temperature, while A3 represents the state filling effects due to the pump-probe temporal overlap, described by a Dirac delta function (δ(t)). H(t) is the Heaviside step function and G(t) is the Gaussian laser pulse. This model is useful for analyzing the experimental data and extracting quantitative information on timescales of ultrafast demagnetization and fast remagnetization. These times depend not only on the coupling parameters but also on the thermodynamic quantities such as specific heats and temperatures of three different subsystems following three different coupled differential equations (details in the ESI†).20
Fast remagnetization is followed by a slow remagnetization process that occurs within a few hundreds of ps timescale. In this timescale, heat diffuses across the temperature gradient from the ferromagnet to the substrate via the intermediate layer, i.e., WS2, called the slow remagnetization time (τ1). Exponentially decaying slow remagnetization superimposed with magnetization precession and damping can be fitted with an exponentially damped sinusoidal function,
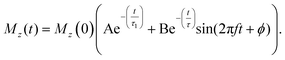 | (2) |
The precession frequency f is extracted from the fast Fourier transform (FFT), while the decay time τ and the initial phase of the precession ϕ are fitting parameters. The effective magnetization (Meff) can be extracted by fitting the bias field (H) dependent f using Kittel's formula neglecting the anisotropy energy in amorphous Co3FeB,27
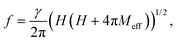 | (3) |
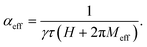 | (4) |
The magnetization precession in a magnetic field of 1.56 kOe field (Fig. 2(a)) is fitted with eqn (2) and (3) is used to fit f vs. H for different WS2 (nML)/Co3FeB samples at a pump fluence of 10 mJ cm−2; the results are shown in Fig. 2(b). The extracted Meff values for different layer numbers of WS2 (Fig. 2(c)) show a decreasing trend following previous results for TMD/FM heterostructures.22,26 Here, the 5d electrons of W are strongly hybridized with the 3d electrons of Co/Fe at the interface reducing the magnetization at the interface. A finite pd hybridization between Co/Fe and S may also contribute towards reducing the effective magnetization.26
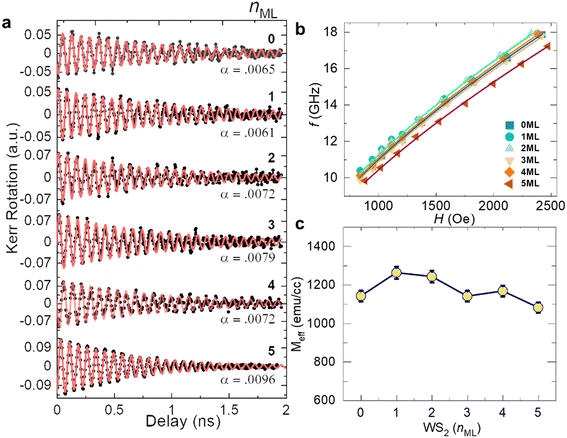 | ||
| Fig. 2 (a) Time resolved Kerr rotation showing the damped magnetization precession of WS2 (nML)/Co3FeB thin film heterostructures measured with a pump fluence of 10 mJ cm−2 at an external bias field of 1.56 kOe. The symbols are the experimental data points, and the solid lines are fits to eqn (2). (b) Corresponding precession frequency f of WS2 (nML)/Co3FeB as a function of H. Solid lines are the Kittel fits. (c) Dependence of Meff on the layer number of WS2 as extracted from Kittel fits. | ||
Using eqn (4), the effective damping parameter is calculated for the field range of ∼840 Oe to ∼2480 Oe (Fig. 3(a)). The magnetic damping includes both intrinsic and extrinsic contributions. Extrinsic contributions arise from magnetic inhomogeneities and TMS.29,30 Inhomogeneities in Co3FeB thin films may induce a variation of spin orientation via local magnetic anisotropy fields giving rise to a dephasing effect and an enhancement of the damping parameter when the applied field is not strong enough to align all spins.31 TMS occurs when two spin waves interact at an impurity or discontinuity site (k ≠ 0) in such a way that they transfer energy between the two spin waves and dissipate some of their energy at the site of the impurity. The scattering strength depends on the interfacial roughness that gives rise to an interfacial magnetic anisotropy fluctuating field leading to TMS. Thus, a strong enough applied field can suppress the extrinsic contributions.32 For all the layers of WS2, the effective damping (αeff) decreases gradually and reaches a nearly saturated value at a higher H indicating that the inhomogeneous magnetic distribution is suppressed at large external magnetic fields. The experimental data are fitted with an exponentially decaying function, αeff = α + αex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−H/H0), where α corresponds to the intrinsic damping parameter and αex
exp(−H/H0), where α corresponds to the intrinsic damping parameter and αex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−H/H0) is the extrinsic part of the damping.18,33 The variation of intrinsic damping α (as the high field suppresses the extrinsic contributions) with pump fluence for WS2 (Fig. 3(b)) shows two opposite characteristics for odd and even numbers of WS2 layers. The gradual enhancement of the background possibly emerges from the interlayer scattering for more than 2 MLs; however, the layer number dependence is remarkable in all samples.34
exp(−H/H0) is the extrinsic part of the damping.18,33 The variation of intrinsic damping α (as the high field suppresses the extrinsic contributions) with pump fluence for WS2 (Fig. 3(b)) shows two opposite characteristics for odd and even numbers of WS2 layers. The gradual enhancement of the background possibly emerges from the interlayer scattering for more than 2 MLs; however, the layer number dependence is remarkable in all samples.34
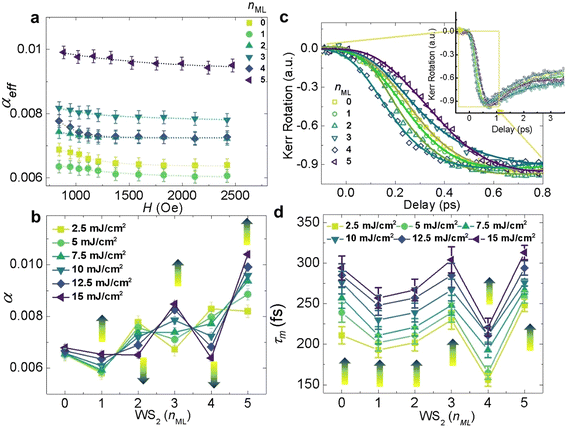 | ||
| Fig. 3 (a) Dependence of the effective damping parameter αeff on the magnetic field H for WS2 (nML)/Co3FeB at a fixed pump fluence (10 mJ cm−2). Dotted lines correspond to fits to exponentially decaying functions. (b) Variation of α with nML at various pump fluences (2.5–15 mJ cm−2) at an external bias field of 1.56 kOe. Coloured arrows indicate the increment of fluence. (c) Ultrafast demagnetization curves of WS2 (nML)/Co3FeB. The inset shows the time-resolved Kerr rotation over a longer time scale. Solid lines are fits to eqn (1). (d) Variation of τm with nML at different pump fluences (2.5–15 mJ cm−2). Coloured arrows indicate the increment of fluence. | ||
The pump fluence increases the electronic temperature (Te) up to thousands of Kelvins,35 which can be related to the absorbed laser energy per unit volume (Ea) according to the following relationship:
| Ea = Ce(Te2 − T02)/2, | (5) |
| Ea = F(1 − e)−d/ψ(1 − R)/d, | (6) |
In the absence of WS2, the damping parameter is nearly constant with pump fluence for bare Co3FeB. This is to some extent consistent with a previous study, where the damping parameter was found to be temperature independent.36 A temperature dependent damping parameter has been reported for several FM Heusler compounds,37,38 for which the temperature dependence is explained by inter- and intraband scattering of electrons. The interband scattering contribution enhances the damping with increasing temperature known as resistivity-like damping, while intraband scattering shows the opposite behaviour, referred to as conductivity-like damping.39 It should be noted that the temperature dependence of the intrinsic damping is still being debated; a theoretical model40 claims that the Gilbert damping should be independent of temperature. Thus, in a single Co3FeB layer, we have not seen any signatures of the inter- and intraband electron scattering mechanisms. However, there is significant evidence of inter- and intraband electron scattering in the damping for the WS2 (nML = 1, 2, 3, 4, 5)/Co3FeB thin film heterostructures. The damping parameter increases with the increase of pump fluence for odd numbers of WS2 layers (nML = 1, 3 and 5), indicative of interband electron scattering or resistivity-like damping, while for even numbers of WS2 layers (nML = 2, 4), intraband electron scattering dominates.22 According to Kambersky's spin flip scattering (SFS) mechanism, α depends on the spin–orbit coupling (SOC).41 Furthermore, Park et al. have shown that for 2D materials, the SOC strength is a function of temperature and the spin–orbit splitting factor (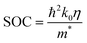 , where η is the temperature dependent spin-splitting parameter).42 Moreover, inversion symmetry breaks for 2D TMD materials with an odd number of TMD layers generating additional spin splitting. These features will provide an important implementation in spin–valleytronic devices. The layers showing higher damping would be useful for magnetic switching applications to suppress the ringing effect, while the layers with lower damping would be useful to reduce write current in STT-MRAM/SOT-MRAM devices and magnonic devices where longer propagation of spin waves is desirable. In addition to that, temperature dependent damping will provide another route to modulate damping by externally tuning the temperature of the system in place of heterostructure replacement. So, these heterostructures will be very useful to miniaturize electronic devices where temperature plays an important role.
, where η is the temperature dependent spin-splitting parameter).42 Moreover, inversion symmetry breaks for 2D TMD materials with an odd number of TMD layers generating additional spin splitting. These features will provide an important implementation in spin–valleytronic devices. The layers showing higher damping would be useful for magnetic switching applications to suppress the ringing effect, while the layers with lower damping would be useful to reduce write current in STT-MRAM/SOT-MRAM devices and magnonic devices where longer propagation of spin waves is desirable. In addition to that, temperature dependent damping will provide another route to modulate damping by externally tuning the temperature of the system in place of heterostructure replacement. So, these heterostructures will be very useful to miniaturize electronic devices where temperature plays an important role.
Several mechanisms such as cooperative effects of SOC and exchange interaction,43 SOC and applied laser field,44 phonon mediated spin-flip scattering,45–47 electron–magnon scattering,48 and electron–electron scattering49 have been suggested to explain the ultrafast demagnetization. In 2008, Malinowski et al. first showed that the laser induced spin transport can speed up the ultrafast demagnetization process and increase magnetic quenching in NM/FM heterostructures.17 Local spin-flip scattering and nonlocal spin current transport are the two key mechanisms that explain ultrafast demagnetization.50,51 An elegant method to extract the dominant contribution to ultrafast demagnetization is the simultaneous investigation and correlation of both the ultrafast demagnetization time (τm) and the damping parameter (α).18,52
The normalized ultrafast demagnetization for WS2 (nML)/Co3FeB thin film heterostructures is shown in Fig. 3(c); the experimental results were analysed by fitting to eqn (1). Here it appears that even numbers of WS2 (nML = 2, 4) layers reduce the demagnetization time (τm), indicating a spin-pumping mechanism, while odd numbers of layers enhance τm. This can be attributed to the broken inversion symmetry causing an extra spin-splitting in valleys for odd numbers of layers contributing to the relaxation of the spins and/or due to the uncompensated spins in the odd layer. However, a monolayer of WS2 shows a different behaviour from the other odd numbers of layers, i.e., a lower τm value than for the bare Co3FeB layer. This is probably due to the absence of spin splitting in the electronic band structure in monolayer WS2 (ref. 22). The τm as a function of WS2 layer number for different pump fluences ranging from 2.5 mJ cm−2 to 15 mJ cm−2 is shown in Fig. 3(d). Unlike α, for all samples, τm is increasing with pump fluence due to larger spin fluctuations at elevated temperatures.53 Variations of α and τm with pump fluence are shown in Fig. S4 of the ESI.† We have extracted specific heats and different coupling parameters between three different baths (electron, spin and lattice) numerically from the three-temperature modelling and tabulated in Table S2 of the ESI† for CoFeB (6 nm) thin films at different pump fluences.
Relationship between the ultrafast demagnetization time and the damping parameter: non-volatile control
The relationship between the ultrafast demagnetization time and the effective damping parameter can be used to extract the dominant microscopic mechanism behind these phenomena. The theoretical model by Koopmans et al.45 predicts an inverse proportionality between τm and α based on Elliot-Yafet (EY)-type spin-flip scattering. Later, based on the ‘breathing Fermi surface model’ and the ‘bubbling Fermi surface model’, Fähnle et al.54,55 derived both inverse and direct proportionalities between τm and α associated with resistivity-like and conductivity-like damping, respectively. More recently Zhang et al. proposed a model by incorporating spin transport through the interface of a FM/NM heterostructure18,52 giving rise to a direct proportionality between τm and α when the dominating mechanism is local spin-flip scattering and an inverse proportionality when the interface spin transport dominates.The correlation between τm and α is depicted in Fig. 4. In the case of odd nML (Fig. 4(a) and (b)) at the lowest and highest pump fluence used in our experiments, the results indicate a linear relationship between τm and α as prescribed by the breathing Fermi surface model and the Elliot-Yafet relationship,54
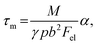 | (7) |
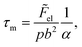 | (8) |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) el is also determined from the electronic states but is different from the Fel.
el is also determined from the electronic states but is different from the Fel. ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) el can be expressed by the matrix elements formed by the two different electronic wave functions whereas Fel contains matrix elements formed by the same electronic wavefunctions. This indicates the dominance of spin current transport. In even nML, the absence of broken inversion symmetry causes WS2 (nML = 2, 4)/Co3FeB to act like a normal NM/FM heterostructure. Due to the high SOC of WS2, it absorbs the spin angular momentum from Co3FeB and enhances the demagnetization rate through spin-pumping.56 The demagnetization rate
el can be expressed by the matrix elements formed by the two different electronic wave functions whereas Fel contains matrix elements formed by the same electronic wavefunctions. This indicates the dominance of spin current transport. In even nML, the absence of broken inversion symmetry causes WS2 (nML = 2, 4)/Co3FeB to act like a normal NM/FM heterostructure. Due to the high SOC of WS2, it absorbs the spin angular momentum from Co3FeB and enhances the demagnetization rate through spin-pumping.56 The demagnetization rate 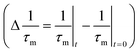 versus modulation of damping (Δα = α|t − α|t=0) at the lowest fluence for even nML has been used to find out the spin chemical potential using the relationship,18
versus modulation of damping (Δα = α|t − α|t=0) at the lowest fluence for even nML has been used to find out the spin chemical potential using the relationship,18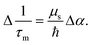 | (9) |
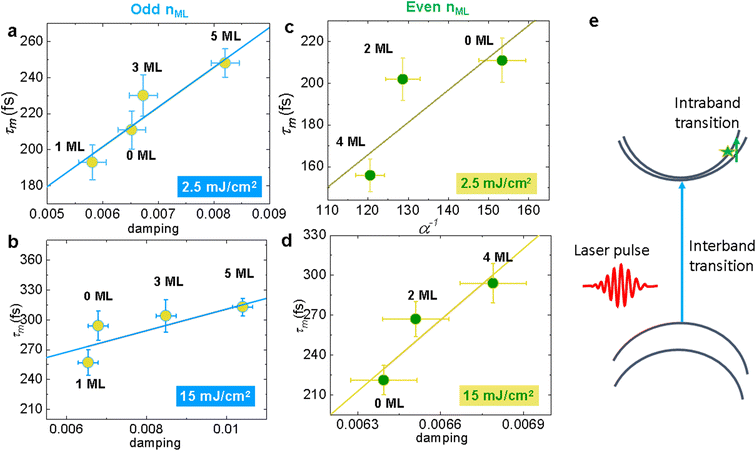 | ||
| Fig. 4 Variation of τm as a function of α for (a and c) lowest pump fluence and (b and d) highest pump fluence for odd nML and even nML, respectively. Lines in (a), (c) and (d) are fits to eqn (7), while in (b) the line is a fit to eqn (8). (e) Cartoon of laser pulse interaction resulting in inter- and intraband transitions in WS2. | ||
Here, the spin chemical potential (μs) quantifies the spin accumulation at the WS2/Co3FeB interface, which generates a spin backflow current and reduces the spin pumping. We have extracted μs to be 0.53 eV for even nML at low fluence, which enhances the demagnetization rate and the damping factor. This value is reasonable for a 2D material/FM heterostructure as it is in close proximity to the reported values for the graphene/CoFeB heterostructure.57–59 This implies that with an increase in pump laser fluence, spin-flip scattering dominates over the spin pumping contribution for an even number of layers. Unlike for NM/FM heterostructures, the direct proportionality observed for odd nML is due to the interplay between the SOC and the spin–valley splitting caused by the broken inversion symmetry, which interrupts the generation and transport of spin current via interband transitions (Fig. 4(e)). In reciprocal space, valley separation is so large that the valley index is robust against the scattering of phonons and deformation.60 So the effect of valley splitting on magnetization dynamics will make TMD/FM heterostructures a promising candidate for next-generation spintronic devices with high storage density and low power consumption.
Conclusions
In summary, we have systematically investigated the magnetization dynamics from femtosecond to nanosecond timescales in WS2(nML)/Co3FeB thin film heterostructures using time-resolved magneto-optical Kerr effect magnetometry. An odd–even WS2 layer number (nML) dependence is evidenced by measurements of the damping parameter (α). The α exhibits a laser fluence dependent characteristic due to interband electron scattering in heterostructures with odd nML because of broken inversion symmetry, while in heterostructures with even nML, intraband electron scattering explains the fluence dependence. In contrast, τm does not show any odd–even layer dependence with fluence, confirming that electron scattering plays no significant role on femtosecond timescales. Moreover, by correlating τm and α, the microscopic mechanisms involved in ultrafast demagnetization have been revealed. We have found that spin current transport is generally responsible for ultrafast demagnetization at temperatures near room temperature in heterostructures with even nML. However, with an increase of pump fluence, the spin-flip scattering (SFS) starts playing a dominating role. On the other hand, in heterostructures with odd nML, the ultrafast demagnetization is dominated by the SFS mechanism for all fluences used in this study. The understanding of how the spin–valley coupling governs the odd–even layer dependence of two-dimensional materials is an important milestone for future fundamental research and applications.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
AB gratefully acknowledges financial assistance from the S. N. Bose National Centre for Basic Sciences (SNBNCBS), India under Project No. SNB/AB/11-12/96 and SNB/AB/18-19/211 and the Department of Science and Technology (DST), Govt. of India (Grant No. DST/NM/TUE/QM-3/2019-1C-SNB). SD acknowledges UGC, Govt of India (UGC Ref. no.: 1545/(CSIR-UGC NET JUNE 2019)) for a senior research fellowship. SH and PS acknowledge the Swedish Research Council (VR, Grant no: 2017-03799) and Carl Tryggers Stiftelse főr Vetenskaplig Forskning (Grant no. CTS 17:450) for their support.References
- S. Husain, R. Gupta, A. Kumar, P. Kumar, N. Behera, R. Brucas, S. Chaudhary and P. Svedlindh, Appl. Phys. Rev., 2020, 7, 041312 CAS
.
- Z. Wu, S. Xu, H. Lu, A. Khamoshi, G.-B. Liu, T. Han, Y. Wu, J. Lin, G. Long, Y. He, Y. Cai, Y. Yao, F. Zhang and N. Wang, Nat. Commun., 2016, 7, 12955 CrossRef CAS PubMed
.
- H. Lee, S. Deshmukh, J. Wen, V. Z. Costa, J. S. Schuder, M. Sanchez, A. S. Ichimura, E. Pop, B. Wang and A. K. M. Newaz, ACS Appl. Mater. Interfaces, 2019, 11, 31543–31550 CrossRef CAS PubMed
.
- P. Sarangapani, J. Charles and T. Kubis, Phys. Rev. Appl., 2022, 17, 024005 CrossRef CAS
.
- A. F. Morpurgo, Nat. Phys., 2013, 9, 532–533 Search PubMed
.
- Y. Liu, Y. Gao, S. Zhang, J. He, J. Yu and Z. Liu, Nano Res., 2019, 12, 2695–2711 CrossRef CAS
.
- M. Yamamoto, Y. Shimazaki, I. V. Borzenets and S. Tarucha, J. Phys. Soc. Jpn., 2015, 84, 121006 CrossRef
.
- K. F. Mak, K. L. McGill, J. Park and P. L. McEuen, Science, 2014, 344, 1489–1492 CrossRef CAS PubMed
.
- D. Xiao, G.-B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802 CrossRef PubMed
.
- S. Wu, J. S. Ross, G.-B. Liu, G. Aivazian, A. Jones, Z. Fei, W. Zhu, D. Xiao, W. Yao, D. Cobden and X. Xu, Nat. Phys., 2013, 9, 149–153 Search PubMed
.
- Y. Ye, J. Xiao, H. Wang, Z. Ye, H. Zhu, M. Zhao, Y. Wang, J. Zhao, X. Yin and X. Zhang, Nat. Nanotechnol., 2016, 11, 598–602 CrossRef CAS PubMed
.
- G. Aivazian, Z. Gong, A. M. Jones, R.-L. Chu, J. Yan, D. G. Mandrus, C. Zhang, D. Cobden, W. Yao and X. Xu, Nat. Phys., 2015, 11, 148–152 Search PubMed
.
- G. Berghäuser, I. Bernal-Villamil, R. Schmidt, R. Schneider, I. Niehues, P. Erhart, S. M. de Vasconcellos, R. Bratschitsch, A. Knorr and E. Malic, Nat. Commun., 2018, 9, 971 Search PubMed
.
- D. W. Latzke, W. Zhang, A. Suslu, T.-R. Chang, H. Lin, H.-T. Jeng, S. Tongay, J. Wu, A. Bansil and A. Lanzara, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235202 CrossRef
.
- G. Wu, Y. Ren, X. He, Y. Zhang, H. Xue, Z. Ji, Q. Y. Jin and Z. Zhang, Phys. Rev. Appl., 2020, 13, 024027 CrossRef CAS
.
- S. Dutta, S. N. Panda, J. Sinha, S. Choudhury and A. Barman, ACS Appl. Nano Mater., 2022, 5, 17995–18003 CrossRef CAS
.
- G. Malinowski, F. Dalla Longa, J. H. H. Rietjens, P. V. Paluskar, R. Huijink, H. J. M. Swagten and B. Koopmans, Nat. Phys., 2008, 4, 855–858 Search PubMed
.
- W. Zhang, Q. Liu, Z. Yuan, K. Xia, W. He, Q.-F. Zhan, X.-Q. Zhang and Z.-H. Cheng, Phys. Rev. B, 2019, 100, 104412 CrossRef CAS
.
- W.-T. Lu and Z. Yuan, Phys. Rev. B, 2021, 104, 214404 CrossRef CAS
.
- E. Beaurepaire, J. C. Merle, A. Daunois and J. Y. Bigot, Phys. Rev. Lett., 1996, 76, 4250–4253 CrossRef CAS PubMed
.
- W. Yao, D. Xiao and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235406 CrossRef
.
- S. Husain, S. Pal, X. Chen, P. Kumar, A. Kumar, A. K. Mondal, N. Behera, N. K. Gupta, S. Hait, R. Gupta, R. Brucas, B. Sanyal, A. Barman, S. Chaudhary and P. Svedlindh, Phys. Rev. B, 2022, 105, 064422 CrossRef CAS
.
- Interfacial charge transfer is essential for AOS. Linearly polarized excitation should generate a coherent superposition of excitons in both K valleys. Electron hopping from a TMD to a FM is only allowed when the spin orientation of the electrons in the TMD is the same as that of the lowest-energy unoccupied conduction band. Immediately after optical excitation and before demagnetization, the transfer of electrons from the TMD with spin parallel to the FM will begin, leaving the electrons with spin opposite to that of the FM in the other K valley. However, there will be an imbalance of the remaining electrons in the K valleys. The transfer of the remaining electrons will induce remagnetization of the FM. The initial charge transfer for one of the valleys is expected to begin from a few fs to sub-hundreds of the fs timescale, before the demagnetization of the FM.
- M. D
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) browski, S. Guo, M. Strungaru, P. S. Keatley, F. Withers, E. J. G. Santos and R. J. Hicken, Nat. Commun., 2022, 13, 5976 CrossRef PubMed
browski, S. Guo, M. Strungaru, P. S. Keatley, F. Withers, E. J. G. Santos and R. J. Hicken, Nat. Commun., 2022, 13, 5976 CrossRef PubMed .
- A. S. Sethulekshmi, J. S. Jayan, A. Saritha and K. Joseph, J. Alloys Compd., 2021, 876, 160107 CrossRef CAS
.
- S. Husain, A. Kumar, P. Kumar, A. Kumar, V. Barwal, N. Behera, S. Choudhary, P. Svedlindh and S. Chaudhary, Phys. Rev. B, 2018, 98, 180404 CrossRef CAS
.
- H. C. Yuan, S. H. Nie, T. P. Ma, Z. Zhang, Z. Zheng, Z. H. Chen, Y. Z. Wu, J. H. Zhao, H. B. Zhao and L. Y. Chen, Appl. Phys. Lett., 2014, 105, 072413 CrossRef
.
- J. Walowski, M. D. Kaufmann, B. Lenk, C. Hamann, J. McCord and M. Münzenberg, J. Phys. D: Appl. Phys., 2008, 41, 164016 CrossRef
.
- A. Capua, S.-H. Yang, T. Phung and S. S. P. Parkin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 224402 CrossRef
.
- Y. Sun, H. Chang, M. Kabatek, Y.-Y. Song, Z. Wang, M. Jantz, W. Schneider, M. Wu, E. Montoya, B. Kardasz, B. Heinrich, S. G. E. te Velthuis, H. Schultheiss and A. Hoffmann, Phys. Rev. Lett., 2013, 111, 106601 CrossRef PubMed
.
- Y. Fan, X. Ma, F. Fang, J. Zhu, Q. Li, T. P. Ma, Y. Z. Wu, Z. H. Chen, H. B. Zhao and G. Lüpke, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094428 CrossRef
.
- H. Song, K.-D. Lee, C.-Y. You, S.-H. Yang, S. Parkin, B.-G. Park, J.-W. Sohn, J.-I. Hong and S.-C. Shin, Appl. Phys. Express, 2015, 8, 053002 CrossRef
.
- X. Ma, L. Ma, P. He, H. B. Zhao, S. M. Zhou and G. Lüpke, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 014438 CrossRef
.
- Y. Jiang, S. Chen, W. Zheng, B. Zheng and A. Pan, Light: Sci. Appl., 2021, 10, 72 CrossRef CAS PubMed
.
- S. Mondal and A. Barman, Phys. Rev. Appl., 2018, 10, 054037 CrossRef CAS
.
- A. Okada, S. He, B. Gu, S. Kanai, A. Soumyanarayanan, S. T. Lim, M. Tran, M. Mori, S. Maekawa, F. Matsukura, H. Ohno and C. Panagopoulos, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3815–3820 CrossRef CAS PubMed
.
- A. Kumar, F. Pan, S. Husain, S. Akansel, R. Brucas, L. Bergqvist, S. Chaudhary and P. Svedlindh, Phys. Rev. B, 2017, 96, 224425 CrossRef
.
- B. Khodadadi, A. Rai, A. Sapkota, A. Srivastava, B. Nepal, Y. Lim, D. A. Smith, C. Mewes, S. Budhathoki, A. J. Hauser, M. Gao, J.-F. Li, D. D. Viehland, Z. Jiang, J. J. Heremans, P. V. Balachandran, T. Mewes and S. Emori, Phys. Rev. Lett., 2020, 124, 157201 CrossRef CAS PubMed
.
- K. Gilmore, Y. U. Idzerda and M. D. Stiles, Phys. Rev. Lett., 2007, 99, 027204 CrossRef CAS PubMed
.
- A. T. Costa and R. B. Muniz, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 014419 CrossRef
.
- V. Kamberský, Can. J. Phys., 1970, 48, 2906–2911 CrossRef
.
- Y. H. Park, H. C. Koo, K. H. Kim, H. J. Kim, J. Chang, S. H. Han and H. Kim, IEEE Trans. Magn., 2010, 46, 1562–1564 CAS
.
- W. Hübner and G. P. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R5920–R5923 CrossRef
.
- G. P. Zhang and W. Hübner, Phys. Rev. Lett., 2000, 85, 3025–3028 CrossRef CAS PubMed
.
- B. Koopmans, J. J. M. Ruigrok, F. Dalla Longa and W. J. M. de Jonge, Phys. Rev. Lett., 2005, 95, 267207 CrossRef CAS PubMed
.
- B. Koopmans, G. Malinowski, F. Dalla Longa, D. Steiauf, M. Fähnle, T. Roth, M. Cinchetti and M. Aeschlimann, Nat. Mater., 2010, 9, 259–265 CrossRef CAS PubMed
.
- C. Illg, M. Haag and M. Fähnle, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214404 CrossRef
.
- E. Carpene, E. Mancini, C. Dallera, M. Brenna, E. Puppin and S. De Silvestri, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174422 CrossRef
.
- M. Krauß, T. Roth, S. Alebrand, D. Steil, M. Cinchetti, M. Aeschlimann and H. C. Schneider, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 180407(R) CrossRef
.
- A. J. Schellekens, W. Verhoeven, T. N. Vader and B. Koopmans, Appl. Phys. Lett., 2013, 102, 252408 CrossRef
.
- A. Eschenlohr, M. Battiato, P. Maldonado, N. Pontius, T. Kachel, K. Holldack, R. Mitzner, A. Föhlisch, P. M. Oppeneer and C. Stamm, Nat. Mater., 2013, 12, 332–336 CrossRef CAS PubMed
.
- W. Zhang, W. He, X.-Q. Zhang, Z.-H. Cheng, J. Teng and M. Fähnle, Phys. Rev. B, 2017, 96, 220415 CrossRef
.
- K. C. Kuiper, T. Roth, A. J. Schellekens, O. Schmitt, B. Koopmans, M. Cinchetti and M. Aeschlimann, Appl. Phys. Lett., 2014, 105, 202402 CrossRef
.
- M. Fähnle, J. Seib and C. Illg, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144405 CrossRef
.
- M. Fähnle and C. Illg, J. Phys.: Condens. Matter, 2011, 23, 493201 CrossRef PubMed
.
- Y. Tserkovnyak, A. Brataas and G. E. W. Bauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 224403 CrossRef
.
- S. N. Panda, S. Majumder, S. Choudhury, A. Bhattacharya, S. Sinha and A. Barman, Nanoscale, 2021, 13, 13709–13718 RSC
.
- J. C. W. Song, M. S. Rudner, C. M. Marcus and L. S. Levitov, Nano Lett., 2011, 11, 4688–4692 CrossRef CAS PubMed
.
- M. Massicotte, G. Soavi, A. Principi and K.-J. Tielrooij, Nanoscale, 2021, 13, 8376–8411 RSC
.
- Q. Cui, Y. Zhu, J. Liang, P. Cui and H. Yang, Phys. Rev. B, 2021, 103, 085421 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06197c |
| ‡ Present address: Materials Sciences Division, Lawrence Berkeley National Laboratory, CA 94720, USA. |
| This journal is © The Royal Society of Chemistry 2024 |
