Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvent-assisted self-assembly of block copolymer thin films
Przemyslaw
Pula
 ,
Arkadiusz
Leniart
and
Pawel W.
Majewski
,
Arkadiusz
Leniart
and
Pawel W.
Majewski
 *
*
Department of Chemistry, University of Warsaw, Warsaw 02089, Poland. E-mail: pmajewski@chem.uw.edu.pl
First published on 16th May 2022
Abstract
Solvent-assisted block copolymer self-assembly is a compelling method for processing and advancing practical applications of these materials due to the exceptional level of the control of BCP morphology and significant acceleration of ordering kinetics. Despite substantial experimental and theoretical efforts devoted to understanding of solvent-assisted BCP film ordering, the development of a universal BCP patterning protocol remains elusive; possibly due to a multitude of factors which dictate the self-assembly scenario. The aim of this review is to aggregate both seminal reports and the latest progress in solvent-assisted directed self-assembly and to provide the reader with theoretical background, including the outline of BCP ordering thermodynamics and kinetics phenomena. We also indicate significant BCP research areas and emerging high-tech applications where solvent-assisted processing might play a dominant role.
Scope of the review and introduction
Block copolymers (BCP) constitute an important class of self-assembling materials consisting of two or more chemically dissimilar polymeric chains called blocks. Progress in BCP science has been documented by numerous reviews focused on their synthesis,1–3 processing,4–10 and their applications.6,11–16 Arguably, the greatest advantage of BCP-mediated manufacturing of nanoscale patterns is the low-cost and high-throughput of this approach compared to the conventional methods such as photo- and e-beam lithography. Numerous applications for BCP-ordered templates have been proposed, including optical coatings,17,18 metamaterials,19–21 photonic crystals,22,23 plasmonic nanostructures,24,25 and membranes.26,27 These emerging applications have propelled research efforts aimed at understanding and harnessing the self-assembly of BCP thin films and led to the development of various directed self-assembly (DSA†) methods. DSA methods are used to accelerate the self-assembly process and to reduce patterns’ defectivity to an application enabling level and, by using directional biases, to orient (align) anisotropic BCP morphologies.4,8,10,28Polymer–solvent interactions are at the core of polymer and block copolymer science since their discovery, therefore providing a complete review of this topic exceeds the capacity of this publication. Instead, we focus on solvent-driven or solvent-assisted self-assembly of block copolymers leading to the formation of nanoscale patterns in thin films (10–1000 nm). We have also limited our discussion of BCP self-assembly in solution, thoroughly reviewed elsewhere,29,30 only to the aspects necessary to understand BCP–solvent interactions in concentrated solutions and solvent–swollen polymer films near and above the onset of the order–disorder phase transition concentration. A complete overview of BCP–solvent interactions over an entire concentration range including a thorough presentation of phase behavior can be found in the review by Alexandridis and Spontak.31 Also, we omitted solvent-mediated assembly of BCP-nanoparticle hybrid films recently reviewed by other authors.32–34 While this review focuses mainly on solvents liquid at room temperature, we would like to mention super-critical carbon dioxide (scCO2) as an attractive alternative for polymer processing, including BCPs. We would like to point the readers to the excellent review of this topic by Walker et al.35 and some more recent reports.36–39
The solution-processing compatibility of BCPs is perhaps one of their main advantages and is the reason for widespread interest in these nanomaterials. Understanding and controlling block copolymer–solvent interactions in thin films is of critical importance both for processing and practical patterning application. In this review, we focus on solvent-assisted BCP self-assembly and DSA techniques that utilize BCP–solvent interactions. Because solvent-assisted processing is probably one of the most facile DSA methods, it is frequently a method of choice for scientists who start research in these materials. At the same time, because of the intricate balance between the thermodynamics and kinetics that drives the self-assembly of BCP as well as the composition heterogeneity of the materials, it is notoriously difficult to control. These difficulties result in common pitfalls in the laboratory practice and, despite the best efforts, frequent inconsistencies in the reported results. For this reason, we first provide the reader with a theoretical overview of the topic. Then, we briefly describe popular BCP thin-film deposition techniques and present a toolbox of DSA methods, highlighting the critical practical aspects of experimental design and relate them to the major strategies of process control. As shown in Fig. 1, for the sake of clarity of presentation, we classified the reviewed DSA methods into two major categories: (i) direct casting methods in which BCP morphologies self-assemble concurrently with the material deposition step and (ii) post-casting annealing in which the BCP morphology is ordered after the casting step. We admit that in some cases, the division is rather arbitrary and we review such methods in a separate, hybrid methods category, along with more complex solvent-assisted DSA techniques, which utilize additional ordering biases such as shearing or surface-mediated interactions. Finally, we review the work dedicated to grain-coarsening kinetics and reduction of structural defects in BCP thin films.
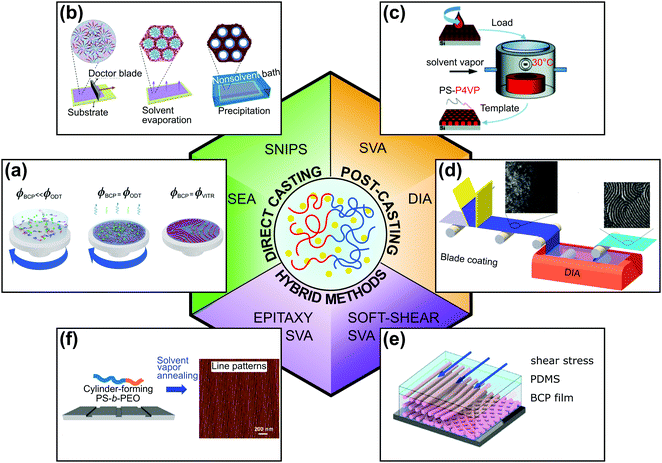 | ||
| Fig. 1 Overview of solvent-assisted directed self-assembly of BCP films. (a) Solvent evaporation annealing, (b) self-assembly and non-solvent induced phase separation, (c) solvent vapor annealing, (d) direct immersion annealing. (e) Soft-shear solvent vapor annealing, (f) epitaxy combined with solvent vapor annealing. (a) Adapted with permission from Macromolecules, 54, 11178.40 Copyright 2020 American Chemical Society, (b) adapted from Macromol. Rapid Commun., 42, 2100235.41 Copyright 2021 Macromolecular Rapid Communications published by Wiley-VCH GmbH, (c) adapted from Phys. Chem. Chem. Phys., 19, 2805.42 with permission from the Royal Society of Chemistry, (d) adapted with permission from ACS Appl. Mater. Interfaces, 7, 21639.43 Copyright 2015 American Chemical Society, (e) adapted with permission from Macromolecules, 51, 4213.44 Copyright 2018 American Chemical Society (f) adapted with permission from ACS Nano, 10, 7915.45 Copyright 2016 American Chemical Society. | ||
We center our efforts on providing the reader with a practical guide to the topic and bring their attention to a limited number of selected research reports, frequently using them as an exemplary illustration of the discussed phenomena. Where possible, we provide a reference to more comprehensive, excellent review contributions by other authors.
Overview of BCP–solvent interactions
Thermodynamic equilibrium between solvent vapor and solvent–swollen polymer
Polymer swelling induced by the sorption of solvent from a gas phase is analogous to the dissolution of the polymer in a liquid solvent. To promote solvent uptake, the thermodynamic driving force for polymer–solvent mixing, i.e., the change in the Gibbs free energy, ΔGmix must be negative:| ΔGmix = ΔHmix − TΔSmix < 0, | (1) |
For nonpolar or weakly polar polymer–solvent systems, regular solution theory defines the thermodynamic equilibrium between the activity of solvent molecules (a) in the gas phase and in polymer solution:47
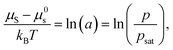 | (2) |
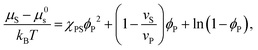 | (3) |
Equating the two equations leads to the following:
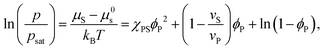 | (4) |
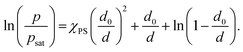 | (5) |
In addition to the chemical interactions, polymer swelling behavior is dictated by the degree of solvent vapor saturation in the gas phase, which in turn is affected by the temperature. polymer–solvent swelling equilibria are highly sensitive to changes in ambient temperature due to the exponential dependence of the vapor pressure on the temperature given by the Clausius–Clapeyron thermodynamics relation: p ∼ p0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔH/RT + const), where ΔH is the specific enthalpy of vaporization. Frequently, saturated vapor pressure at a given temperature range is calculated using the empirical Antoine equation:
exp(−ΔH/RT + const), where ΔH is the specific enthalpy of vaporization. Frequently, saturated vapor pressure at a given temperature range is calculated using the empirical Antoine equation:
| log10(psat) = A − [B/(C + T)], | (6) |
Solubility parameter and the Flory–Huggins interaction parameter
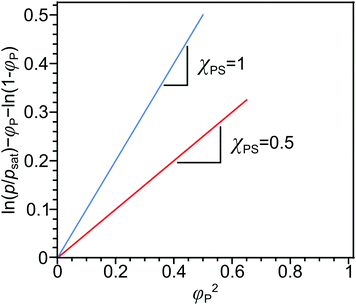
A comparison of the solubility parameters (δ) can be conveniently use to evaluate the quality of solvent towards a particular polymer instead of χPS determination. The solubility parameters theory developed by Scatchard, Hildebrand and Scott introduces square root of the cohesive energy density to be a quantitative metrics for estimating the solvency of a particular solvent: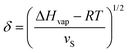 | (7) |
| ΔHmix = φPφSvM(δP − δS)2, | (8) |
Solubility analysis was subsequently developed by Hansen, who introduced partial contributions to the solubility parameter originating from hydrogen-bonding (δH), polar (δP), and nonpolar dispersive interactions (δD), which effectively map the parameter in a three-dimensional space and allow analysis of more complex solvency scenarios.59
| δ2 = δD2 + δP2 + δH2 | (9) |
Finally, the Flory–Huggins interaction parameter and solution parameters are interrelated through the Hildebrand–Scatchard regular solution theory:61
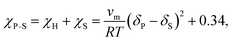 | (10) |
Dry BCP morphologies
In BCP melts, the spontaneous microphase separation begins at the order–disorder transition temperature (TODT) and, in the case of BCP solutions, above a critical polymer concentration (φODT). The transition is driven by chemical dissimilarity between the polymer chains and leads to the formation of nanoscale morphologies consisting of distinct domains. In BCP melts, the entropic term can be neglected and the chemical incompatibility between blocks is expressed as: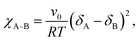 | (11) |
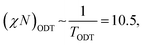 | (12) |
In the microphase-separated state, the volume ratio of the blocks and the interfacial energy minimization principles define the geometric shape of BCP domains. Typically encountered morphologies include cubically-packed spheres, hexagonally-packed cylinders, gyroidal networks, and lamellae. The interaction parameter determines the strength of the segregation and affects the degree of chain stretching at the interface between the blocks, and the width of the composition gradient, 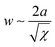 , where a is the statistical segment length.73 It is step-like in the strong-segregation limit (SSL) in high-χ systems and broadens to the width of entire domain, assuming a sinusoidal profile in the weak segregation limit (WSL).63 The characteristic repeat spacing, L (BCP periodicity) scales with the degree of BCP polymerization as: N2/3 for χN > 29 (SSL); N1/2 for χN < 5 (WSL, near the onset of chain stretching), and as N0.83 for intermediate-segregation regime.74
, where a is the statistical segment length.73 It is step-like in the strong-segregation limit (SSL) in high-χ systems and broadens to the width of entire domain, assuming a sinusoidal profile in the weak segregation limit (WSL).63 The characteristic repeat spacing, L (BCP periodicity) scales with the degree of BCP polymerization as: N2/3 for χN > 29 (SSL); N1/2 for χN < 5 (WSL, near the onset of chain stretching), and as N0.83 for intermediate-segregation regime.74
Morphologies of BCP films in the presence of solvent
The presence of neutral solvent reduces chemical incompatibility between the BCP blocks and decreases the effective interaction parameter χeff according to the dilution approximation:75,76| χeff ∼ ϕP(χAB + Δχ) = ϕP(χAB + χAS − χBS) | (13) |
| χeff ∼ ϕPχAB | (14) |
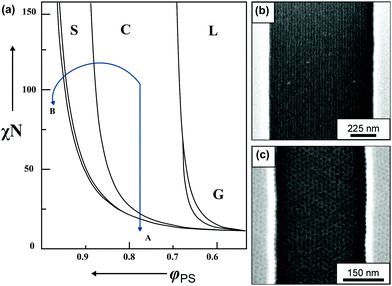 | ||
| Fig. 3 BCP morphology transitions in the presence of solvent. (a) Schematic BCP phase diagram with swelling trajectories in a non-selective solvent – A and block-A selective solvent – B. Distinct morphologies marked as L – lamellae, C – cylinders, S – spheres, G – gyroid, DIS – disordered. (b) Solvent-induced morphology transitions of cylinder-forming PαMS-b-PHOST in topographic trench pattern. Horizontally aligned cylinders after annealing in non-selective solvent – THF. (c) Hexagonally-packed spheres pattern annealed in acetone vapors (PHOST-selective solvent). (a) Adapted with permission from Macromolecules, 43, 2463.80 Copyright 2010 American Chemical Society. (b and c) Adapted with permission from ACS Nano, 2, 1396.81 Copyright 2008 American Chemical Society. | ||
For block-selective solvents the dependence of the effective Flory–Huggins parameter on BCP concentration can be more complex. The effective value of χAB in a selective solvent is given by:73,79
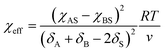 | (15) |
| ϕA = 1 − ϕAB(1 − ϕAdry) = 1 − ϕABϕBdry, | (16) |
In the presence of a strongly selective solvent, the effective interaction parameter between the polymer blocks might be increased, inducing microphase separation of an initially disordered system, or a shift from a weakly- to strongly segregated material. This opens an interesting possibility for solid-state transformations of BCP morphology by post-casting chemical processing82 which improves the structural parameters (e.g., lowers the line-edge roughness) relevant for BCP patterning applications.
In addition to the morphological transitions described above, the presence of solvent induces rearrangements of BCP chain conformation and affects the characteristic repeat-spacing, L (d-spacing, periodicity). Neutral solvent screening of unfavorable enthalpic interactions between the blocks relaxes chain conformation at the block interface. According to the mean-field theory prediction, the repeat spacing, L, in a semi-dilute BCP solution is given by the power law:83
| L ∼ ϕβ | (17) |
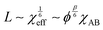 | (18) |
Kinetic effects
The presence of the solvent has a pronounced effect on chains’ mobility and reduces the glass transition temperature Tg of glass-forming polymers. The Tg of a solvent–swollen polymer can be estimated using the empirical Fox formula:94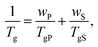 | (19) |
Polymer chains diffusion coefficient is accelerated in the presence of solvent in accordance with: 〈D〉 ∼ D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp−γNχeff, where D0 is the self-diffusion coefficient in a hypothetical phase-mixed system and γ is a constant (γ ≈ 1). In asymmetric diblocks N = NA, the number of segments of the minority block.42,95
exp−γNχeff, where D0 is the self-diffusion coefficient in a hypothetical phase-mixed system and γ is a constant (γ ≈ 1). In asymmetric diblocks N = NA, the number of segments of the minority block.42,95
The rearrangement of BCP morphology by chains’ diffusion across the domain interface is given by an activated mechanism, strongly enhanced by reduction of χeff in the presence of a neutral solvent:42,96
Dper = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−γNA(χeff − χODT)], exp[−γNA(χeff − χODT)], | (20) |
BCP thin-film casting
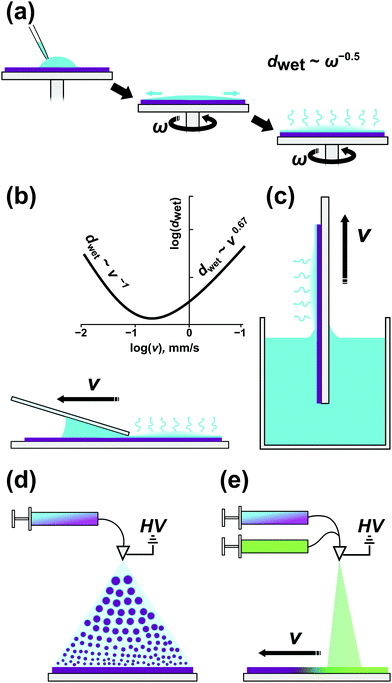
Block copolymer thin films (d < 1000 nm) are almost exclusively prepared by casting, i.e., the deposition of a polymer solution onto solid substrates followed by the evaporation of the solvent. Spin-coating (spin-casting, SC), flow-coating (blade-coating, FC), and dip-coating (DC) are popular BCP casting methods with spin-coating arguably the most widespread because of its robustness and compatibility with integrated circuits (IC) fabrication. A simple spin-coater consists of a rotary chuck to which a solid substrate is affixed, driven by a motor at a regulated rotational speed (1000–6000 RPM). The consecutive steps of a film casting are presented in Fig. 4a. After placement of a controlled volume of polymer solution on a substrate, the chuck is accelerated to a constant rotational speed and the solution is spread over the substrate with the majority of the solution volume spun off over the edges by the inertial forces. Since 95–99% of the solution volume is lost in this step, it is perhaps the most significant drawback of this method, especially when used to deposit films made of valuable materials. The spin-off step takes about a few seconds depending on the acceleration ramp profile, target spin velocity, and polymer solution parameters such as density and viscosity; the evaporation of a solvent is negligible and the thickness of the film is reduced to a few micrometers.98 During the second step, a balance of inertial and viscous forces is established, and a uniform wet film is formed on the substrate. In the last phase, the wet film thickness is reduced by solvent evaporation driven by the diffusion of the solvent towards the surface of the film until a dry film thickness is reached.99 The wet film thickness is inversely proportional to the square root of rotational speed and the same scaling is preserved in dry films.98,100 The method is highly reproducible, largely independent of polymer composition when casting is performed from the same solvent, and allows fine control of sample thickness and high coating uniformity. SC is compatible with fine topographic surface patterns used in graphoepitaxial DSA.45,101 Nonetheless, the high-material-loss drawback and SC inability to provide films of variable thickness on a single substrate make other casting methods equally attractive in research.In flow-coating (Fig. 4(b)), a polymer solution is spread over a substrate by a movable blade oriented almost horizontally with respect to the substrate surface.102,103 This blade geometry and its proximity to the substrate provide a gap (50–300 μm high) in which a polymer solution is hosted by capillary forces and which acts as an “ink” reservoir during the solution-spreading. For spreading blade velocities typically used in FC (v = 1–50 mm s−1) wet-film formation is governed by the surface-tension-modified viscous flow, i.e., the Landau–Levich flow problem,104 in which the film thickness scales as v2/3. Blade acceleration during the coating enables the formation of films with controlled thickness gradient.103 Compared to SC, the amount of material wasted is significantly smaller and depends on the size of the coated substrate and the amount of solvent which must be retained in the gap to ensure coating uniformity. The highest yield (>95%) can be achieved with blade coaters incorporated in roll-to-roll deposition systems, which provide a continuous coating on large-area flexible substrates.105,106 Consistent blade height and angle alignment, as well as edge cleanliness, affect the quality and reproducibility of the coated films.
In dip-coating, a solid substrate is immersed in a vessel filled with a BCP solution and withdrawn with a constant speed, dragging along a thin meniscus of evaporating liquid (Fig. 4(c)). The simplicity of this approach might be deceptive as several environmental factors affect the final layer thickness. In DC we distinguish two separate flow regimes – capillary and draining – that are dictated by a substrate withdrawal speed. As shown in Fig. 4b, in the Landau-Levich, viscous flow regime, dwet scales as v2/3 and as v−1 for the small-velocity, capillary regime.107 Many processing parameters influence the final film morphology apart from the withdrawal speed – solvent volatility, BCP concentration, surface tension, and viscosity are of crucial importance.108 DC, in contrast to SC, does not waste much material but at the same time requires the preparation of greater volume of the dipping solution. Simultaneous coating of both sides of a substrate can be advantageous in some applications, e.g., deposition of antireflective coatings on transparent substrates.109 It is worth noting that only dip-coating can be directly used for conformal substrate patterning of non-flat substrates including fibers and corrugated surfaces.110,111
A recently introduced BCP coating method – the electrospray deposition (ESD), relies on formation of a fine jet of BCP-containing droplets atomized by high voltage applied to a conductive nozzle (Fig. 4(d)). The ESD process exploits the microphase separation of BCP in the droplets as solvent evaporates en route to a heated substrate and can be thought of as a macromolecular CVD analog allowing epitaxial growth of ordered BCP layers.112 Despite the initial instrument construction and set-up efforts, ESD offers unique capabilities of controlling film morphology gradients in the direction normal to substrate surface and in the lateral direction. For example, such composition gradients can be realized by controlling the proportion of two BCP solutions fed into the spraying cone during the vertical growth or while moving the substrate laterally (Fig. 4(e)).112,113 Similarly, high voltage-driven flow was utilized by Onses et al. in electrohydrodynamic (EHD) near-field jet printing of BCP patterns with complex geometry and remarkable sub-500 nm lateral resolution.114 The technique can be used for precise BCP ink deposition on grapho- and chemoepitaxially patterned surfaces allowing hierarchical BCP ordering.115 In terms of material usage, both ESD and EHD jet printing are material-saving techniques. In ESD the losses are generated mostly at the periphery of the deposition zone where the coating is uneven.
While spin-coaters are readily available commercially and there are a few vendors offering dip-coaters, the other coating systems are typically home-built and their construction requires custom hardware and certain integration skills.
The selection of the casting method and the casting solvent may influence the morphology of the BCP in the subsequent annealing step. For example, casting of poly(styrene-b-dimethylsiloxane) (PS-b-PDMS) from PDMS-selective solvent resulted in horizontal cylinders and shifted to hexagonally perforated lamellae and horizontal lamellae when solvent solubility parameter was increased.116 Casting solvent can also affect the ordering kinetics; for PS-b-PDMS it has been shown that less-volatile solvents providing less free volume results in higher degree of order in the subsequent SVA annealing.117 In some cases, the magnitude of residual stresses present in the glassy BCP after the casting, could determine the final orientation of BCP morphology.118,119
Review of solvent-assisted self-assembly of BCP films
For the sake of systematic presentation, we divided the solvothermal annealing methods into three categories depending on when BCP ordering takes place, i.e., ordering simultaneous with casting (direct casting), post-casting ordering, and a separate, hybrid methods category in which two or more ordering biases are used, typically after the casting step.Simultaneous casting and annealing methods
We first review direct casting methods as, historically, slow evaporation of concentrated solutions was one of the first methods to obtain ordered bulk BCP specimens for microscopic imaging and X-ray scattering experiments.120,121 The existence of ordered morphologies in non-preferential solvents above the order–disorder transition concentration (φBCP > φODT), reflecting that of dry neat BCP material has been predicted theoretically and well-documented experimentally.83,87 Slow evaporation of a solvent from a concentrated BCP solution has been shown to yield well-ordered morphologies.122–124 Notably, a suitable selection of the casting solvent and ambient atmosphere conditions can lead to vertically ordered BCP morphologies aligned by the solvent evaporation front.125–127BCP-evaporating solvent interactions can be leveraged to control macroscopic orientation of domains in deposited thin films. Kowalewski et al. utilized the zone casting process, originally developed for obtaining large-area arrays of small molecule single-crystals128 in which BCP solution is cast from a slit-shaped nozzle onto a slowly moving substrate (Fig. 5(a)).129 By adjusting the temperature of the substrate the authors aligned cylindrical PODMA-b-PtBA-b-PODMA (poly(octadecyl methacrylate)-b-poly-(t-butyl acrylate)-b-poly(octadecyl methacrylate)) triblock parallel or perpendicular to the deposition direction indicating the role of crystalline block in the selection of alignment direction.130
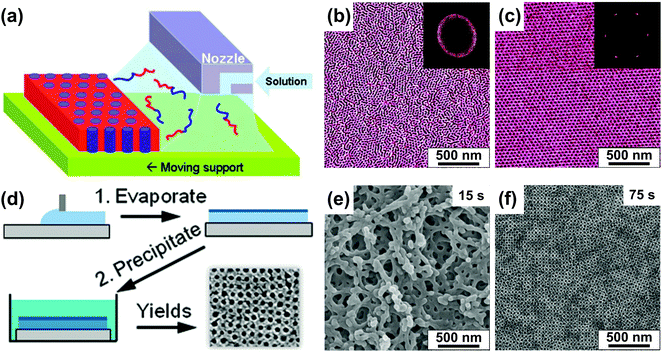 | ||
| Fig. 5 Direct casting methods. (a) Schematic representation of the zone casting technique utilizing a slit nozzle to deliver BCP solution to a moving substrate. (b and c) AFM images of PS-b-PB BCP films produced at different printing speed (b) 500 μm s−1 and (c) 2 μm s−1. (d) Schematic of preparation of a porous BCP membrane with SNIPS. (e and f) SEM images of poly(isoprene-b-styrene-b-4-vinylpyridine) films precipitated after (e) 15 s and (f) 75 s of volatile solvent evaporation. (a-c) Adapted with permission from J. Am. Chem. Soc., 133, 11802.129 Copyright 2011 American Chemical Society, (d–f) adapted with permission from Nano Lett., 11, 2892.131 Copyright 2011 American Chemical Society. | ||
Direct casting in the presence of selective solvent has also been used to obtain well-ordered vertical arrays of BCP cylinders including poly(styrene-b-ethylene oxide) (PS-b-PEO).125 It is worth noting that direct casting and controlled evaporation of solvent is a widespread method for self-assembly of bottlebrush copolymers and block copolymers with record-high molecular weight (Mn >103 kg mol−1). The processing and use of these materials as photonic crystals has been thoroughly reviewed in a recent publication by Grubbs and coworkers.23
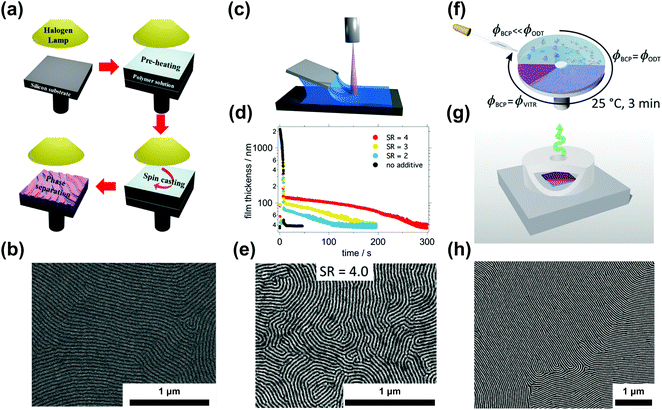 | ||
| Fig. 6 Ordering in slowly-evaporating nonvolatile solvents. (a) Schematic representation of a single-step casting assisted by halogen lamp heating and (b) the resulting ordered PS-b-PMMA film. (c) Blade coating setup used in nonvolatile additive solvent annealing (NVASA). (d) Film thickness evolution during the drying process at different swelling ratios and (e) SEM image of PS-b-P2VP ordered at SR = 4. (f) Schematic representation of solvent evaporation annealing (SEA) during spin-coating and with a convection-limiting cap (g) yielding large-grained BCP samples (h). (a and b) Adapted with permission from ACS Macro Lett., 4, 656.146 Copyright 2015 American Chemical Society, (c–e) adapted with permission from Macromolecules, 52, 5026.147 Copyright 2019 American Chemical Society, (f–h) adapted with permission from Macromolecules, 53, 11178.40 Copyright 2020 American Chemical Society. | ||
Post-casting annealing
The popularity of SVA led to the rapid development of dedicated BCP processing protocols and instruments, shown schematically in Fig. 7. Starting from static annealing in a glass desiccator or a metal dish filled with a liquid solvent (Fig. 7(a)),166,167 SVA setups progressively evolved towards more advanced systems that offer a higher degree of process control. In addition to precisely thermostated annealing chamber,88 SVA setups include a separately thermostated solvent vapor saturator (bubbler)42,168 and a set of flow regulators and gas mixers84 which control the degree of solvent vapor saturation in a stream of carrier gas introduced to the chamber. Due to the steep dependence of saturation pressure on temperature, a tight control of temperature is critical to avoid solvent condensation. For this reason, in advanced SVA experiments, the temperature of the introduced solvent vapor, and the annealing chamber, is properly adjusted with a PID-controlled heating stage.42
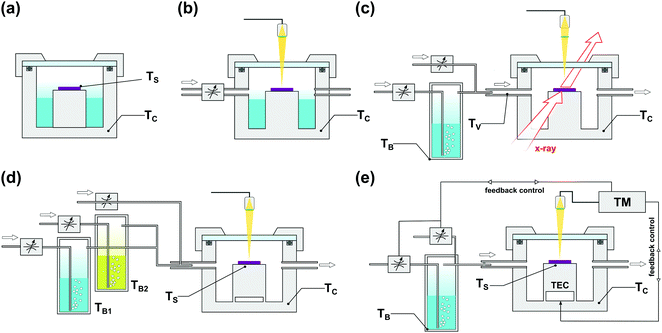 | ||
| Fig. 7 Commonly employed solvent vapor annealing apparatus. (a) Static chamber.81,158,159,169 (b) Flow setup with solvent saturation controlled by an inflow of inert gas with solvent reservoir inside the chamber and optical thickness monitor.117,124,170–174 (c) Flow setup with external solvent vapor saturator and gas mixer compatible with in situ GISAXS measurements.87,93,156,175 (d) Double bubbler setup with gas mixer for experiments with controlled composition of binary solvent vapor mixture.154 (e) High precision setup with automated closed-loop SR control by temperature differential176 or vapor composition177 adjustment. | ||
Most laboratory setups are equipped with an optical attachment for real-time monitoring of the film swelling process. Even a simple optical microscope with a color camera can be used to qualitatively assess the solvent uptake by the film, by tracking the evolution of interference color patterns and detecting usually undesirable film dewetting or surface reconstruction. Quantitative measurements of the swelling ratio, i.e., the ratio of the solvent–swollen and dry film thicknesses are realized by white light spectral reflectometry (WLSR)154,173,178 or spectral ellipsometry (SE).179–182 While both techniques are very robust, the former is more affordable and enables faster measurements and therefore is more popular. Nonetheless, precise thickness determination with WLSR is difficult when the exact value of the effective refractive index of the swollen film is unknown or difficult to compute without additional insights into its composition, e.g., annealing in a mixture of two or more solvents. In such cases, iterative approach to WLSR data analysis or SE can be employed.176 Alternatively, an in situ quartz chemical microbalance (QCM),183 or an AFM measurement184 can be used to monitor the degree of polymer swelling. In particular, in situ AFM is an exclusive technique that provides real-time and real-space insights into the evolution of the morphology of native BCPs, and can be used to track the BCP grain coarsening in SVA.184–187
The in situ grazing-incidence small angle X-ray scattering (GISAXS) is a particularly suitable tool for monitoring the progress of SVA.93,156,171,175,188 This non-invasive technique can be integrated with most SVA experiments (Fig. 7(c)) providing information on the morphological transitions in the film including the domains’ orientation and the extent of long-range order.87,163,175,180,188–190 The in-depth profiles of solvent concentration distribution in the swollen film can be inferred from X-ray175 or neutron191 reflectometry studies.
Special care must be taken when reporting and comparing the results of SVA. In particular, the reported “duration of annealing” depends whether the authors define this parameter as the overall processing duration, i.e., time spent in SVA chamber or as a time of effective exposure to a vapor at certain degree of saturation. As pointed out by Tang et al., the apparent time-scales of BCP ordering in static SVA depend on the chamber volume.127 The authors modeled the 1D transport of solvent vapor in the chamber with the second Fick's law of diffusion with appropriate initial and boundary conditions:
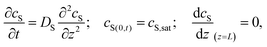 | (21) |
Long swelling ramps in the static chamber SVA extend the overall processing time and contribute to BCP ordering in a difficult-to-control manner. Similarly, the deswelling ramps frequently affect the end-point morphologies and cannot be precisely controlled.124,193 For a tight control of these ramps, more advanced SVA setups are required. In a flow chamber, modeled as continuously-stirred tank reactor, the characteristic residence time, τ, given by the volume-to-flow ratio, defines the time necessary to establish steady-state vapor saturation after the vapor delivery is started. The time needed to achieve 90% and 99% of the final saturation is 2.3τ and 4.6τ, respectively. It can be reduced by using a small-volume chamber or by increasing the flow rate, the latter associated with a potential risk of decreasing the solvent vapor saturation degree by shortening the residence of carrier gas in the bubbler. For the outlined reasons, recently reported advanced SVA setups include a separate control of the saturation degree (by adjustable temperature and flow through the bubbler) and are thermostated independently in several places including the gas mixer, vapor delivery tubing, chamber walls, and a sample post (Fig. 7(d and e)).42,168,177 Fully-automated experiments with control of solvent-uptake and desorption ramps are enabled by a closed-loop regulation of the gas flow control of vapor saturation ratio with a real-time feedback from the thickness monitor (Fig. 7(e)).153 Alternatively, this approach is also very effective in the flow setups; as proposed by Hulkkonen et al. the temperature differential between the introduced solvent vapor and BCP sample can be used to affect the swelling ratio offering very fast SR response (Fig. 8).176 The setup offers a high degree of SR setpoint accuracy through a PID control of the process and enables non-trivial swelling ramps such as sine or triangular waves suitable for testing intriguing concepts of order enhancement in BCP thin films by cyclic annealing.194
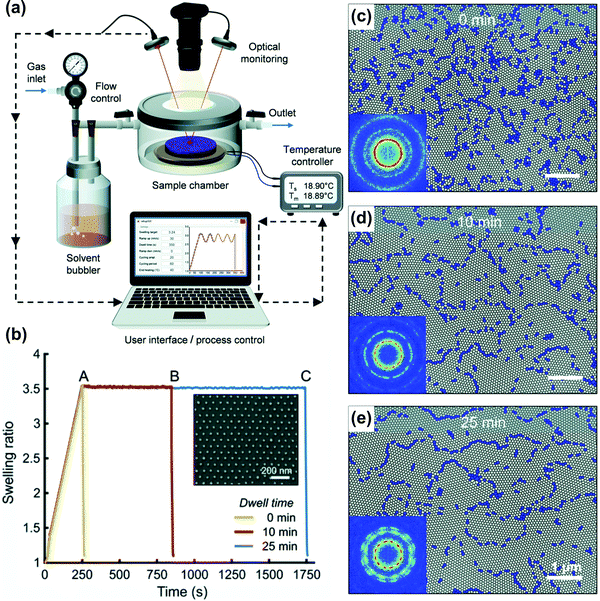 | ||
| Fig. 8 Automated solvent vapor annealing. (a) Schematic of an advanced SVA setup with closed-loop SR control. (b) Annealing pathways of cylinder-forming PS-b-P2VP 258 kg mol−1 thin films in THF vapor and corresponding morphologies after 0, 10, and 25 min (c–e). Adapted from Soft Matter, 15, 7909.176 With permission from The Royal Society of Chemistry. | ||
Due to the strong enhancement of polymer chain dynamics in the presence of a solvent, SVA emerged as a particularly potent tool for ordering ultrahigh molecular weight BCPs (Mn > 500 kg mol−1). These materials pose a great challenge for other DSA methods due to their prohibitively slow grain-coarsening kinetics. Such BCP materials can generate patterns with periods larger than 100 nm, extending the BCP applications to large-period plasmonic coatings, and photonic band-gap materials.13,18,23,195
A two-step solvothermal annealing has been first demonstrated as an efficient way to order lamellar PS-b-PMMA (256 kg mol−1, unguided self-assembly) and Mn = 733 and 1000 kg mol−1 epitaxially guided patterns by Kim et al.159 Recent reports on homologous materials include successful production of microporous ultrafiltration gyroidal membrane obtained by selective etching of PS-b-PMMA (Mn > 600 kg mol−1).196 Real-time AFM observation of highly-swollen (SR ≈ 9) 1000 kg mol−1 lamellar PS-b-PMMA grain-coarsening has been reported by Takano et al.184 Doerk et al. presented a remarkable example of SVA efficiency combined with low molecular weight homopolymer blending by ordering ultra-high Mn PS-b-PMMA (Mn = 2000 kg mol−1) and obtaining patterns with L0 > 200 nm (Fig. 9(a)).174 SVA is also effective in large Mn high segregation strength BCP systems including PS-b-PVP homologs. Cummins et al. indicated the importance of solvent neutrality and the underlayer brush for ordering vertical PS-b-P2VP lamellae (Mn = 429 kg mol−1) in the presence of PGMEA vapors.197 SVA performed at a high swelling ratio has been demonstrated by Selkirk et al. to efficiently order PS-b-P2VP lamellae of 800 kg mol−1 (Fig. 9(b)).177 The importance of high-degree of swelling in annealing of high-χ materials is corroborated by an earlier report identifying a narrow solvent saturation window (0.94 < p/psat < 1) to be effective in ordering PS-b-P4VP cylinders (Mn = 34 kg mol−1). This trend is corroborated by an in situ GISAXS-SVA study performed by Gu and coworkers who observed formation of large-grained lamellar PS-b-P2VP grains in the vicinity of the solvent-driven ODT.198
 | ||
| Fig. 9 SVA of large-periodicity block copolymer systems. (a) SEM image of a blend of 1051 kg mol−1 and 2000 kg mol−1 PS-b-PMMA with 3 kg mol−1 PS and 3 kg mol−1 PMMA homopolymers obtained after consecutive SVA in THF and hot-plate thermal annealing (L0 ∼ 211 nm). (b) SEM image of PS-b-P2VP (793 kg mol−1) annealed in THF-chloroform mixture (L0 ∼ 180 nm). (a) Adapted with permission from Macromolecules, 53, 1098.174 Copyright 2020 American Chemical Society, (b) adapted with permission from Macromolecules, 54, 1203.177 Copyright 2021 American Chemical Society. | ||
Solvent selectivity is a dominating factor determining morphology selection in SVA.117,154,167,199 Solvent vapor composition coupled with the appropriate film thickness have been demonstrated to induce the transitions of native BCP structure into a range of non-native morphologies (Fig. 10).167,200 Wu et al. reported kinetic transformations of PS-b-PLA from an initially disordered state, through cylindrical state towards native thermodynamically-defined gyroidal morphology dependent on solvent removal rate.201 Similar intricate ordering phenomena were demonstrated for other diblocks, e.g., PS-b-P2VP,202 PS-b-P4VP,86,203 PS-b-PMMA204,205 or PS-b-PDMS90,206,207 and triblocks.208
 | ||
| Fig. 10 Morphology evolution for PDMS-b-PS-b-PMPCS terpolymer of different film thickness exposed to vapors of acetone:heptane mixture of various composition. The bottom row depicts models of the above layered morphologies. Reprinted with permission from ACS Macro Lett., 8, 852.200 Copyright 2019 American Chemical Society. | ||
SVA and BCP multilayers
Fast ordering kinetics render SVA as a particularly useful high-throughput method advantageous in multi-step assembly of complex BCP architectures. Jung et al. utilized SVA-assistance for ordering of PS-b-PDMS to produce 2D and 3D silica nanomesh patterns.209 Homologous material has been used in the iterative coating-SVA-etching approach by Cheng et al. to engineer hierarchical superhydrophobic multilayered SiO2 coatings.210 Non-native multilayered ZnO structures were fabricated by templated synthesis using solvent vapor annealing as a rapid ordering method of BCP templates.211,212Combinatorial exploration of SVA
Finding suitable SVA conditions and engineering the optimal processing pathway remain a challenge and require systematic studies. Combinatorial experiments offer a great promise in this regard and have been applied to elucidate SVA phenomena, e.g., screening for optimal solvent-mixture composition in gradient-composition solvent vapor annealing178 and in recent autonomous investigations of film thickness effects.213Hybrid methods
Solvent-assisted BCP annealing can be coupled with other DSA methods to further increase the ordering efficiency and to introduce morphology-aligning biases. In this section, we discuss experimental reports which utilize such hybrid processing strategies.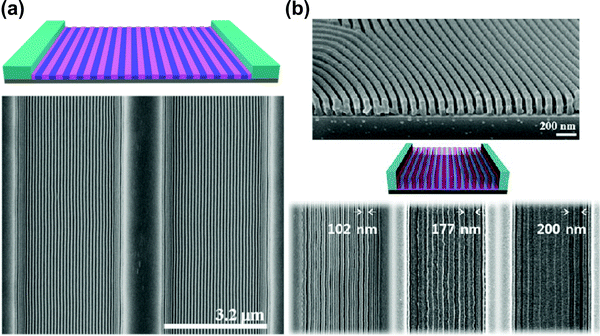 | ||
| Fig. 11 Solvent vapor-assisted graphoepitaxial ordering of high MW PS-b-PMMA lamellar patterns. SEM images of films in trench confinement. (a) 3.2 μm wide trench; (b) cross-section view and top-down images of 1.5 μm wide trench. Reprinted with permission from Macromolecules, 49, 1722,88 and ACS Nano, 7, 1952.159 Copyright 2016, 2013 American Chemical Society. | ||
As opposed to thermal annealing, solvent–vapor processing is usually performed at room temperature. This advantage is particularly important in annealing materials prone to thermal degradation such as BCP lithographic photoresists as pointed out by Bosworth et al. who combined graphoepitaxy with SVA to order PαMS-b-PHOST patterns.81 Choi et al. showed the dependence between the choice of an ordering method (SVA or TA) and the final orientation of cylinders in shallow topographic patterns.45 SVA-assisted graphoepitaxy has been extensively investigated by Ross and coworkers who demonstrated successful alignment of BCP morphologies such as line and hexagonally-packed dot patterns of high-χ PS-b-PDMS materials for use in high resolution lithography.226–228 This approach also proved successful in the self-assembly of non-native BCP motifs such as square lattices,229 mixed morphologies154 or concentric circles and spiral patterns.230 SVA-graphoepitaxy combination has also been applied to other copolymer systems including, multiblock,163,231 bottlebrush,232 and liquid crystalline BCPs.233,234
Chemical epitaxy (or chemo-epitaxy) utilizes preferential wetting interactions between chemically patterned surfaces and distinct BCP blocks. Chemo-epitaxial ordering is frequently coupled with thermal annealing,225 nevertheless, several reports of SVA-assisted chemical epitaxy have been published including studies exploiting an important BCP-lithography concept of improving patterning resolution by density multiplication,172,235 and formation of non-equilibrium morphologies.236 Aligned multilayered metallic nanomesh templated by BCPs were produced by SVA-assisted grapho- and chemoepitaxial ordering. This multistep ordering is driven by two distinct interactions – trench wall guidance of the first layer and edge nucleation of the upper layer.237
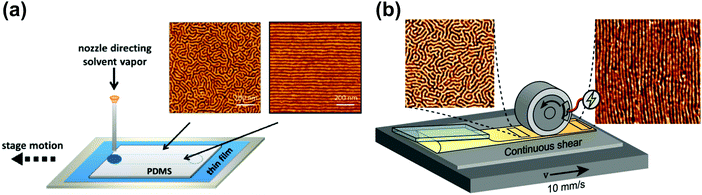 | ||
| Fig. 12 Soft-shear SVA. (a) Raster SVA soft-shearing. AFM morphologies of horizontally oriented PS-b-PI-b-PS cylinders after fast (left) and slow (right) vapor rastering; (b) scheme of an inline rolling shear alignment (IRSA) setup consisting of casting and shearing roller elements PS-b-PI-b-PS forming cylinders. AFM morphologies before (left) and after (right) the passage of the shearing roller. Reprinted with permission from ACS Macro Lett., 4, 516,248 and ACS Appl. Polym. Mater., 4, 682.255 Copyright 2015 and 2021 American Chemical Society. | ||
Residual solvent effects in thermal annealing
The presence of residual solvent, i.e., the solvent entrapped in polymer films after the casting, can be detected by spectroscopic methods, X-ray and neutron reflectometry (NR),191 and gas chromatography-mass spectrometry.257–259 The exact amounts of residual solvent reported in literature vary from less than 2 vol%260 to more than 10 vol%.261 They seem to depend on several factors including the chemical nature of polymer, its molecular weight, film thickness and the presence of underlying brush layers, and the casting method. It is certainly difficult to measure a minute loss of solvent from the film and the discrepancies in literature reports could also be a result of differences in measurement resolution, data quality, and data analysis protocols.260 It is worth noting that upon thorough drying of glassy polymers below the Tg, the solvent is replaced by voids.182 Interestingly, the presence of this rather insignificant amount of residual solvent is clearly accelerating BCP ordering kinetics. A quantitative grain-coarsening kinetic studies reported by Ferrarese-Lupi et al. have shown that the trapped solvent accelerates the early stage (<100 s) of coarsening of lamellar PS-b-PMMA domains by increasing the kinetic exponent.257,261 This quantitative assessment of the residual solvent effects was possible by applying rapid thermal processing (RTP) furnace which allows fast access to high annealing temperatures without prior removal of the solvent, whose concentration, according to Perego et al., decreases towards the substrate surface.261 Seguini with coworkers demonstrated appearance of two coexisting morphologies in RTP-treated BCP films – vertical cylinders in a solvent-rich region and periodic lamellar structures on a solvent-depleted polymer/air interface.258,259 The reservoir of solvent is provided by the random block copolymer (RCP) brush layer beneath the BCP used to promote vertical orientation of BCP domains. In general, higher amount of trapped solvent was responsible for faster grain-coarsening kinetics.258 Recently, Sparnacci et al. provided an insightful analysis of solvent distribution in RCP/BCP systems using NR.262Residual solvent clearly plays an important role in BCP self-assembly but can be obscured by more pronounced effects such as shear- and confinement ordering, therefore a consistent sample preparation protocol is of crucial importance in quantitative BCP self-assembly studies. Special care must be taken to either thoroughly remove the entrapped solvent (e.g., by vacuum desiccation), especially when its presence could be detrimental263 or to use it to one's benefit.
Grain-growth kinetics in solvent-assisted BCP self-assembly
Grain coarsening, i.e., the development of long-range orientational and positional order in block copolymer thin films under annealing is the longest stage of their morphological evolution and frequently a bottleneck of the patterning process.264 Overcoming this problem has strongly motivated research aiming at the development of DSA methods that shorten the time required to produce a BCP morphology with minimal density of structural defects or, alternatively, the largest grain-size.254,265–268 Due to the enhancement of chain mobility discussed in Section 2, solvent-assisted DSA methods are particularly efficient in terms of accelerating grain-growth kinetics and defects annihilation rate, especially when compared to conventional thermal annealing, and can shorten the annealing time by several orders of magnitude.28,42Quantitatively, the average BCP grain-size is computed from SEM or AFM images of BCP thin films or TEM section micrographs and reported as the in-plane domain orientation correlation length (ξ). This is done by a two-step process in which, first, a local domains’ orientation is mapped, and then it is used to compute the orientational correlation function g(r):269
g(r) = cos[2(φ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − φ( ) − φ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′))] ′))] | (22) |
| g(r) = e−r/ξ0 | (23) |
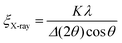 | (24) |
BCP grain coarsening process in constant-temperature thermal annealing is frequently described by an empirical kinetics power-law:185,275
| ξ = Atα | (25) |
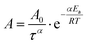 is the Arrhenius dependent term with Ea equal to the activation energy barrier for rate-limiting defect annihilation mode, and τ is the characteristic time of the order of microphase separation time-scales. The value of kinetic power-law exponent, α, depends on system dimensionality and topological constrains;269 for line patterns it is equal to 0.25 for 2D patterns,43,185,266,276–280 and ≈0.5–1 for 3D systems.265,281 Nonetheless, experimentally-reported exponents, could be much lower, especially for lamellar patterns at longer annealing times.97,257,280 Conversely, under non-stationary growth conditions, e.g., rapid thermal processing,282 presence of thermal gradients,69,283 residual solvent effects,257,261 or ordering under solvent evaporation,40 higher scaling exponents were observed.
is the Arrhenius dependent term with Ea equal to the activation energy barrier for rate-limiting defect annihilation mode, and τ is the characteristic time of the order of microphase separation time-scales. The value of kinetic power-law exponent, α, depends on system dimensionality and topological constrains;269 for line patterns it is equal to 0.25 for 2D patterns,43,185,266,276–280 and ≈0.5–1 for 3D systems.265,281 Nonetheless, experimentally-reported exponents, could be much lower, especially for lamellar patterns at longer annealing times.97,257,280 Conversely, under non-stationary growth conditions, e.g., rapid thermal processing,282 presence of thermal gradients,69,283 residual solvent effects,257,261 or ordering under solvent evaporation,40 higher scaling exponents were observed.
Eqn (25) is valid strictly under isothermal conditions and otherwise the quantitative grain-coarsening model becomes more complex. For analysis of grain-coarsening during slow heating ramps Fernandez-Regulez et al. proposed an approach, in which the non-isothermal annealing is divided into short quasi-isothermal intervals.284 For each growth interval the preexisting grain size ξ0, ξ0 = A(T)tαeq is related to the equivalent annealing time, teq, used to translate the current growth curve to a next thermal interval step (ξ = A(T)(t + teq)α). The computation is iterated until final temperature is reached. The model accounts for the linear variation of the pre-exponential factor and kinetic exponent with temperature: α = α0+ α·T.
In solvothermal annealing, both A and α may, in principle, vary with temperature and solvent concentration, as well as other factors such spatial and temporal composition and temperature gradients. For this reason the quantitative kinetics data for solvent-assisted BCP coarsening are scarce, and frequently performed by scattering experiments.84,163,198 Notably, Modi et al. presented kinetic studies of DIA process performed at a constant, moderate swelling ratio (SR = 1.6) of PS-b-PMMA,105 reporting power law exponents at optimal ordering conditions was α = 0.27, and the activation energy Ea ≈ 111 ± 63 kJ mol−1, which is lower than observed in the thermal annealing processes (270 kJ mol−1).97 Very high value of apparent kinetic exponents α = 0.5 was reported in SEA coarsening of cylindrical PS-b-P2VP in a series of controlled drying-time experiments,40 which was the result of slow transition through ODT region, in which the ordering is the most efficient. The authors have reported Ea = 26.9 ± 2.7 kJ mol−1.
Recently, a semi-empirical kinetic model of grain coarsening in solvent assisted ordering under non-constant BCP concentration was proposed.148 The kinetic exponent α has been found to exponentially decrease with the BCP concentration (φ):
α(φ) = α0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−χNφβ] exp[−χNφβ] | (26) |
Solvent-assisted grain coarsening pathways can be easily computed once the grain-coarsening rate map, i.e., dξ/dt = f(φ, t) is determined from constant BCP concentration annealing experiments.148 This approach, valid under a general assumption that instantaneous coarsening rate is only dependent on the current grain size and BCP concentration, is illustrated by Fig. 13a which shows two examples of grain-coarsening trajectories corresponding to SVA (green curve) and SEA (red curve) experiments mapped onto the φ–t space. The final grain size is calculated by numerical integration of the instantaneous rate along the distinct processing pathways (Fig. 13(b)). Equivalently, if the closed-form the grain size α(φ) and A(φ) dependences are available, the rate equation:
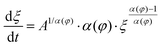 | (27) |
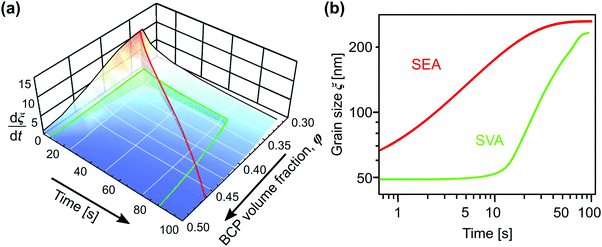 | ||
| Fig. 13 (a) Trajectories of BCP processing in solvent evaporation annealing (red) with evaporation rate of 0.45 nm s−1 and solvent vapor annealing (green) with 5 nm s−1 swelling and deswelling ramps and 60 s dwell at constant film thickness (SR = 2.8). (b) Corresponding grain-coarsening curves predicted by the empirical model incorporating contribution from swelling and deswelling ramps. Adapted with permission from ACS Macro Lett., 11, 121.148 Copyright 2022 American Chemical Society. | ||
In the case of very large-grained or aligned samples, the apparent correlation length ξ = ∞ due to the finite image-size or instrumental resolution limits. In such instances, direct defect counting methods or critical dimension analysis, e.g., line edge roughness quantification are used to assess BCP pattern quality.270,286,287 Such well-ordered BCP templates may still possess a small number of intrinsic defects, prohibitive to certain cutting-edge BCP applications such as IC patterning. A review article on the relevance of defect in BCP self-assembly has been published by Li and Muller.288 This problem has been tackled theoretically, for various BCP chemistries and morphologies.289–293
Self-consistent field theory (SCFT) is a major simulation method harnessed for SVA-assisted BCP ordering and has gained a separate review in the topic.294 In a simulation work of lamellar BCP Peters et al. calculated the defect annihilation rate for various segregation strength.295 For higher values of a χN product combined with greater film thickness the defect healing rate drop is more pronounced. Xu et al. provided a number of valuable conclusions for SVA process for lamellar BCP.296 The authors applied their model for the investigation of ordering dynamics for a non-selective solvent on substrates without chemical modification. In terms of defect removal rate they emphasized the role of initial film morphology on swelling dynamics that provides more uniform solvent distribution in the film volume which directly influences the annihilation rate. The outlined strategy for the efficient defect eradication consist of two steps – initially one makes defects labile by the excess uptake of solvent inside BCP volume which is then followed by a rapid solvent evaporation.
The kinetics of defects annihilation, as opposed to grain coarsening kinetics, can rarely be described by a simple power-law function, as it depends on the free energy of different types of defects, their relative mobility and annihilation mode.186 The measure of defects density is especially useful in long-range orientationally ordered line patterns produced by epitaxial methods, in which dislocation or bridge defects are still present. Li et al. indicated pronounced differences in annihilation kinetics between certain types of defects, e.g., the annihilation of dislocations follows power-law, annihilation of single periodicity bridges has no strong time-dependence, and annihilation of multiple periodicity bridges decreases exponentially with time.268 Moreover, the higher temperature and lower thickness affect positively the defects annihilation. The defect density metrics of kinetics ordering has also been widely used as a quantitative tool to assess the efficiency of solvothermal BCP annealing including microwave-SVA.216,218,219
Conclusions and outlook
In this review, we have presented an overview of solvent-assisted block copolymer self-assembly phenomena and related DSA methods used in BCP surface patterning. These methods are an attractive alternative to other DSA techniques in terms of processing compatibility with multiple BCP materials of a broad molecular weight range, relatively low experimental complexity, and equipment cost. Despite the lack of consensus on which solvent-assisted DSA protocol provides the most satisfactory ordering results for a given BCP material, we cross-compared film deposition and annealing methods, indicating their advantages and drawbacks. We also reviewed quantitative tools used in the characterization of BCP morphologies and in the evaluation of the efficiency of BCP annealing protocols.Although multiple solvent-assisted methods are very robust and reproducible, e.g. direct casting and solvent immersion annealing, the most widely used technique, solvent vapor annealing, and its derivatives seem to suffer from poor consistency of the reported results. We addressed this problem by analyzing the origins of experimental inconsistencies in SVA and indicated how the leading BCP research groups resolve them by properly designing their experiments. We believe that, among other factors, tighter control over swelling and deswelling ramps can greatly improve the consistency of SVA. This can be achieved by introducing a real-time monitoring of the swelling degree and a closed feedback loop to control this relevant parameter. In addition, in situ structural characterization methods such as GISAXS and AFM prove invaluable in elucidating solvent-induced BCP ordering mechanisms.
In our opinion, future advances in solvent-assisted BCP film patterning will develop in the following main directions. The first direction is dictated by the need for further research in the self-assembly of materials that cannot be treated with other DSA methods, such as ultrahigh molecular weight and temperature sensitive BCPs. The prospect of long-range ordering of the former BCP systems is particularly attractive for templating patterns with domain spacing commensurate with the wavelength of visible light exhibiting vibrantly colored Bragg diffraction. The second direction involves the development of robust methods of deposition of ordered BCP patterns on various substrates compatible with the high-throughput fabrication, e.g., the roll-to-roll deposition or fiber coating. Here, we also underscore the future role of solvent-mediated annealing methods, which utilize additional ordering biases enabling uniaxial alignment and more complex BCP ordering scenarios. These hybrid ordering methods include epitaxy-coupled SVA for very precise local control of BCP patterns required in high-fidelity IC fabrication, deposition of multilayered systems from orthogonal solvents, and continuous shear alignment suitable for large-scale fabrication of macroscopically aligned BCP films. In our opinion, the exploration of this field holds great promise for practical utilization of BCP patterns. Finally, we predict the growing importance of solvent-mediated methods, which enable BCP morphology reconfiguration. In purely-thermal methods, an alteration (e.g., reorientation of ordered lamellae) of the existing film morphology is very challenging requiring a strong reordering bias and taking a long time. On the contrary, solvent-driven phase transitions and BCP domain reorientation can be very rapid, enabling fast response to external stimuli. For numerous BCP systems, the introduction of a solvent is the only practical way of inducing the order–disorder transition since thermally driven ODT lies above their thermal damage threshold. Rapid ordering of BCP morphologies in proximity of the ODT is just one advantage of solvent-assisted DSA method, but, in our opinion, the ability of resetting, i.e., reversibly bringing the ordered morphology to the consistent starting state, can be even more important for BCP self-assembly investigations. For instance, the reversible BCP self-assembly opens a fascinating perspective for autonomous in situ investigations of BCP film ordering carried out at synchrotron beamlines including optimization of processing conditions and kinetic studies performed on a single sample.
Abbreviations
| BCP | Block copolymer |
| DSA | Directed self-assembly |
| FWHM | Full width at half-maximum |
| LC | Liquid crystal |
| ODT | Order–disorder transition |
| RCP | Random copolymer |
| RT | Room temperature |
| SCFT | Self-consistent field theory |
| SR | Swelling ratio |
| SSL | Strong segregation limit |
| WSL | Weak segregation limit |
Materials
| AAO | Aluminum anodic oxide |
| DMF | Dimethylformamide |
| P2VP | Poly(2-vinylpyridine) |
| P4VP | Poly(4-vinylpyridine) |
| PαMS | Poly(α-methylstyrene) |
| PB | Polybutadiene |
| PDMS | Polydimethylsiloxane |
| PEO | Polyethylene oxide |
| PGMEA | Propylene glycol methyl ether acetate |
| PHOST | Poly(4-hydroxystyrene) |
| PI | Polyisoprene |
| PLA | Poly(lactic acid) |
| PMMA | Poly(methyl methacrylate) |
| PODMA | Poly(octadecyl methacrylate) |
| PS | Polystyrene |
| PtBA | Poly(t-butyl acrylate) |
| THF | Tetrahydrofuran |
Methods
| AFM | Atomic force microscopy |
| BC | Blade-coating |
| CVD | Chemical vapor deposition |
| DC | Dip-coating |
| DIA | Direct immersion annealing |
| EHD | Electrohydrodynamic deposition |
| ESD | Electrospray deposition |
| FC | Flow-coating |
| FLaSK | Focused laser spike |
| GISAXS | Grazing-incidence small-angle X-ray scattering |
| IA | Immersion annealing |
| IC | Integrated circuit |
| NIPS | Non-solvent induced phase separation |
| NR | Neutron reflectivity |
| NVASA | Non-volatile solvent vapor annealing |
| QCM | Quartz chemical microbalance |
| RSVA-SS | Rapid solvent vapor annealing-soft shearing |
| RTP | Rapid thermal processing |
| SAINT | Solvent annealing induced nanowetting in templates |
| SC | Spin-coating |
| SE | Spectral ellipsometry |
| SEA | Solvent evaporation annealing |
| SEM | Scanning electron microscopy |
| SNIPS | Self-assembly non-solvent induced phase separation |
| SVA | Solvent vapor annealing |
| SVA-SS | Solvent vapor annealing-soft shearing |
| TA | Thermal annealing |
| WLSR | White light spectral reflectometry |
Author contributions
All authors contributed to the writing of the manuscript. PP and AAL contributed equally to this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AAL, PP, and PWM would like to acknowledge financial support from the First Team program (POIR.04.04.00-00-1DE6/16) of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund. PWM also acknowledges a support received from the National Science Center, Poland, under the Sonata Bis grant agreement (2020/38/E/ST5/00328).References
- K. Ishizu and S. Uchida, Prog. Polym. Sci., 1999, 24, 1439–1480 CrossRef CAS.
- M. Hillmyer, Curr. Opin. Solid State Mater. Sci., 1999, 4, 559–564 CrossRef CAS.
- H. Feng, X. Lu, W. Wang, N.-G. Kang and J. W. Mays, Polymers, 2017, 9, 494 CrossRef PubMed.
- S. B. Darling, Prog. Polym. Sci., 2007, 32, 1152–1204 CrossRef CAS.
- I. W. Hamley, Prog. Polym. Sci., 2009, 34, 1161–1210 CrossRef CAS.
- H. C. Kim, S. M. Park, W. D. Hinsberg and I. R. Division, Chem. Rev., 2010, 110, 146–177 CrossRef CAS PubMed.
- M. Luo and T. H. Epps, Macromolecules, 2013, 46, 7567–7579 CrossRef CAS.
- H. Hu, M. Gopinadhan and C. O. Osuji, Soft Matter, 2014, 10, 3867–3889 RSC.
- I. Gunkel, Small, 2018, 14, 1802872 CrossRef PubMed.
- S. R. Nowak and K. G. Yager, Adv. Mater. Interfaces, 2020, 7, 1901679 CrossRef CAS.
- I. W. Hamley, Angew. Chem., Int. Ed., 2003, 42, 1692–1712 CrossRef CAS PubMed.
- F. H. Schacher, P. A. Rupar and I. Manners, Angew. Chem., Int. Ed., 2012, 51, 7898–7921 CrossRef CAS PubMed.
- M. Stefik, S. Guldin, S. Vignolini, U. Wiesner and U. Steiner, Chem. Soc. Rev., 2015, 44, 5076–5091 RSC.
- C. Cummins, R. Lundy, J. J. Walsh, V. Ponsinet, G. Fleury and M. A. Morris, Nano Today, 2020, 35, 100936 CrossRef CAS.
- C. Pinto-Gómez, F. Pérez-Murano, J. Bausells, L. G. Villanueva and M. Fernández-Regúlez, Polymers, 2020, 12, 2432 CrossRef PubMed.
- A. Subramanian, N. Tiwale, W.-I. Lee and C.-Y. Nam, Front. Nanotechnology, 2021, 3, 766690 CrossRef.
- S. Vignolini, N. A. Yufa, P. S. Cunha, S. Guldin, I. Rushkin, M. Stefik, K. Hur, U. Wiesner, J. J. Baumberg and U. Steiner, Adv. Mater., 2012, 24, OP23–OP27 CrossRef CAS PubMed.
- H. Hulkkonen, A. Sah and T. Niemi, ACS Appl. Mater. Interfaces, 2018, 10, 42941–42947 CrossRef CAS PubMed.
- C. Kilchoer, D. Abdelrahman, S. N. Abdollahi, A. A. LaRocca, U. Steiner, M. Saba, I. Gunkel and B. D. Wilts, Adv. Photon. Res., 2020, 1, 2000037 CrossRef.
- I. Murataj, M. Channab, E. Cara, C. F. Pirri, L. Boarino, A. Angelini and F. Ferrarese Lupi, Adv. Opt. Mater., 2021, 9, 2001933 CrossRef CAS.
- A. Alvarez-Fernandez, C. Cummins, M. Saba, U. Steiner, G. Fleury, V. Ponsinet and S. Guldin, Adv. Opt. Mater., 2021, 9, 2100175 CrossRef CAS.
- A. Noro, Y. Tomita, Y. Matsushita and E. L. Thomas, Macromolecules, 2016, 49, 8971–8979 CrossRef CAS.
- A. L. Liberman-Martin, C. K. Chu and R. H. Grubbs, Macromol. Rapid Commun., 2017, 38, 1700058 CrossRef PubMed.
- P. A. Mistark, S. Park, S. E. Yalcin, D. H. Lee, O. Yavuzcetin, M. T. Tuominen, T. P. Russell and M. Achermann, ACS Nano, 2009, 3, 3987–3992 CrossRef CAS PubMed.
- A. Rahman, M. Liu and C. T. Black, J. Vac. Sci. Technol. B, 2014, 32, 06FE02 CrossRef.
- V. Abetz, Macromol. Rapid Commun., 2015, 36, 10–22 CrossRef CAS PubMed.
- S. P. Nunes, Macromolecules, 2016, 49, 2905–2916 CrossRef CAS.
- P. W. Majewski and K. G. Yager, J. Phys.: Condens. Matter, 2016, 28, 403002 CrossRef PubMed.
- J. C. Brendel and F. H. Schacher, Chem. – Asian J., 2018, 13, 230–239 CrossRef CAS PubMed.
- M. Karayianni and S. Pispas, J. Polym. Sci., 2021, 59, 1874–1898 CrossRef CAS.
- P. Alexandridis and R. J. Spontak, Curr. Opin. Colloid Interface Sci., 1999, 4, 130–139 CrossRef CAS.
- M. R. Bockstaller, R. A. Mickiewicz and E. L. Thomas, Adv. Mater., 2005, 17, 1331–1349 CrossRef CAS PubMed.
- L. Bombalski, J. Listak and M. R. Bockstaller, Annual Review of Nano Research, World Scientific, 2006, vol. 1, pp. 295–336 Search PubMed.
- B. Sarkar and P. Alexandridis, Prog. Polym. Sci., 2015, 40, 33–62 CrossRef CAS.
- T. A. Walker, D. J. Frankowski and R. J. Spontak, Adv. Mater., 2008, 20, 879–898 CrossRef CAS.
- S. Lin and P. Theato, Macromol. Rapid Commun., 2013, 34, 1118–1133 CrossRef CAS PubMed.
- A. Darabi, P. G. Jessop and M. F. Cunningham, Chem. Soc. Rev., 2016, 45, 4391–4436 RSC.
- H. Liu, S. Lin, Y. Feng and P. Theato, Polym. Chem., 2016, 8, 12–23 RSC.
- Y. Li, Y.-Y. Zhang, L.-F. Hu, X.-H. Zhang, B.-Y. Du and J.-T. Xu, Prog. Polym. Sci., 2018, 82, 120–157 CrossRef CAS.
- A. A. Leniart, P. Pula, E. H.-R. Tsai and P. W. Majewski, Macromolecules, 2020, 53, 11178–11189 CrossRef CAS PubMed.
- M. M. Rahman, Macromol. Rapid Commun., 2021, 42, 2100235 CrossRef CAS PubMed.
- R. Lundy, S. P. Flynn, C. Cummins, S. M. Kelleher, M. N. Collins, E. Dalton, S. Daniels, M. A. Morris and R. Enright, Phys. Chem. Chem. Phys., 2017, 19, 2805–2815 RSC.
- A. Modi, S. M. Bhaway, B. D. Vogt, J. F. Douglas, A. Al-Enizi, A. Elzatahry, A. Sharma and A. Karim, ACS Appl. Mater. Interfaces, 2015, 7, 21639–21645 CrossRef CAS PubMed.
- C. Zhang, K. A. Cavicchi, R. Li, K. G. Yager, M. Fukuto and B. D. Vogt, Macromolecules, 2018, 51, 4213–4219 CrossRef CAS.
- J. Choi, J. Huh, K. R. Carter and T. P. Russell, ACS Nano, 2016, 10, 7915–7925 CrossRef CAS PubMed.
- In Polymer handbook, ed. J. Brandrup, Wiley, Hoboken, NJ, 4th edn, 1999 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, New York, 1st edn, 2003 Search PubMed.
- R. F. Blanks and J. M. Prausnitz, Ind. Eng. Chem. Fund., 1964, 3, 1–8 CrossRef CAS.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, Ithaca (N.Y.) London, 1992 Search PubMed.
- J. H. Petropoulos, Polymeric gas separation membranes, CRC Press Inc., New York, 1st edn, 1994, p. 635 Search PubMed.
- J. Jaczewska, I. Raptis, A. Budkowski, D. Goustouridis, J. Raczkowska, M. Sanopoulou, E. Pamuła, A. Bernasik and J. Rysz, Synth. Met., 2007, 157, 726–732 CrossRef CAS.
- H. Elbs and G. Krausch, Polymer, 2004, 45, 7935–7942 CrossRef CAS.
- J. A. Emerson, D. T.-W. Toolan, J. R. Howse, E. M. Furst and T. H. Epps, Macromolecules, 2013, 46, 6533–6540 CrossRef CAS.
- P. Alessi, A. Cortesi, P. Sacomani and E. Valles, Macromolecules, 1993, 26, 6175–6179 CrossRef CAS.
- D. W. Tomlin and C. M. Roland, Macromolecules, 1992, 25, 2994–2996 CrossRef CAS.
- R. C. Reid, J. M. Prausnitz and T. K. Sherwood, The properties of gases and liquids, McGraw-Hill, New York, 3rd edn, 1977 Search PubMed.
- Chemical Rubber Company, CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, CRC Press, Boca Raton, 84th edn, 2003/2004, 2003 Search PubMed.
- M. L. Huggins, J. Phys. Chem., 1951, 55, 619–620 CrossRef.
- C. M. Hansen, Hansen solubility parameters: A user's handbook, CRC Press, Boca Raton, 2nd edn, 2007 Search PubMed.
- E. Stefanis and C. Panayiotou, Int. J. Thermophys., 2008, 29, 568–585 CrossRef CAS.
- T. P. Lodge and P. C. Hiemenz, Polymer Chemistry, CRC Press, Boca Raton, 3rd edn, 2020 Search PubMed.
- T. Lindvig, M. L. Michelsen and G. M. Kontogeorgis, Fluid Phase Equilib., 2002, 203, 247–260 CrossRef CAS.
- L. Leibler, Macromolecules, 1980, 13, 1602–1617 CrossRef CAS.
- M. D. Whitmore and J. Noolandi, J. Chem. Phys., 1990, 93, 2946–2955 CrossRef CAS.
- T. Xu, A. V. Zvelindovsky, G. J.-A. Sevink, K. S. Lyakhova, H. Jinnai and T. P. Russell, Macromolecules, 2005, 38, 10788–10798 CrossRef CAS.
- C. Liedel, C. W. Pester, M. Ruppel, V. S. Urban and A. Böker, Macromol. Chem. Phys., 2012, 213, 259–269 CrossRef CAS.
- M. Gopinadhan, P. W. Majewski, E. S. Beach and C. O. Osuji, ACS Macro Lett., 2012, 1, 184–189 CrossRef CAS PubMed.
- Y. Rokhlenko, M. Gopinadhan, C. O. Osuji, K. Zhang, C. S. O’Hern, S. R. Larson, P. Gopalan, P. W. Majewski and K. G. Yager, Phys. Rev. Lett., 2015, 115, 258302 CrossRef PubMed.
- B. C. Berry, A. W. Bosse, J. F. Douglas, R. L. Jones and A. Karim, Nano Lett., 2007, 7, 2789–2794 CrossRef CAS.
- G. Singh, K. G. Yager, D.-M. Smilgies, M. M. Kulkarni, D. G. Bucknall and A. Karim, Macromolecules, 2012, 45, 7107–7117 CrossRef CAS.
- D. E. Angelescu, J. H. Waller, D. H. Adamson, P. Deshpande, S. Y. Chou, R. A. Register and P. M. Chaikin, Adv. Mater., 2004, 16, 1736–1740 CrossRef CAS.
- R. L. Davis, P. M. Chaikin and R. A. Register, Macromolecules, 2014, 47, 5277–5285 CrossRef CAS.
- M. Longanecker, A. Modi, A. Dobrynin, S. Kim, G. Yuan, R. Jones, S. Satija, J. Bang and A. Karim, Macromolecules, 2016, 49, 8563–8571 CrossRef CAS.
- C. M. Papadakis, K. Almdal, K. Mortensen and D. Posselt, EPL, 1996, 36, 289 CrossRef CAS.
- E. Helfand and Y. Tagami, J. Chem. Phys., 1972, 56, 3592–3601 CrossRef CAS.
- K. J. Hanley and T. P. Lodge, J. Polym. Sci. B: Polym. Phys., 1998, 36, 3101–3113 CrossRef CAS.
- T. P. Lodge, C. Pan, X. Jin, Z. Liu, J. Zhao, W. W. Maurer and F. S. Bates, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 2289–2293 CrossRef CAS.
- T. P. Lodge, K. J. Hanley, B. Pudil and V. Alahapperuma, Macromolecules, 2003, 36, 816–822 CrossRef CAS.
- L. Zeman and D. Patterson, Macromolecules, 1972, 5, 513–516 CrossRef CAS.
- B. Nandan, M. K. Vyas, M. Böhme and M. Stamm, Macromolecules, 2010, 43, 2463–2473 CrossRef CAS.
- J. K. Bosworth, M. Y. Paik, R. Ruiz, E. L. Schwartz, J. Q. Huang, A. W. Ko, D.-M. Smilgies, C. T. Black and C. K. Ober, ACS Nano, 2008, 2, 1396–1402 CrossRef CAS PubMed.
- D. M. Yu, D. M. Smith, H. Kim, J. K.-D. Mapas, J. Rzayev and T. P. Russell, Macromolecules, 2019, 52, 3592–3600 CrossRef CAS.
- T. Hashimoto, M. Shibayama and H. Hawai, Macromolecules, 1983, 16, 1093–1101 CrossRef CAS.
- J. Zhang, D. Posselt, D.-M. Smilgies, J. Perlich, K. Kyriakos, S. Jaksch and C. M. Papadakis, Macromolecules, 2014, 47, 5711–5718 CrossRef CAS PubMed.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 1091–1098 CrossRef CAS.
- E. B. Gowd, T. Koga, M. K. Endoh, K. Kumar and M. Stamm, Soft Matter, 2014, 10, 7753–7761 RSC.
- X. Gu, I. Gunkel, A. Hexemer and T. P. Russell, Macromolecules, 2016, 49, 3373–3381 CrossRef CAS.
- K. Kim, S. Park, Y. Kim, J. Bang, C. Park and D. Y. Ryu, Macromolecules, 2016, 49, 1722–1730 CrossRef CAS.
- S. Xiong, D. Li, S.-M. Hur, G. S.-W. Craig, C. G. Arges, X.-P. Qu and P. F. Nealey, Macromolecules, 2018, 51, 7145–7151 CrossRef CAS.
- F. A. Jung, A. V. Berezkin, T. B. Tejsner, D. Posselt, D.-M. Smilgies and C. M. Papadakis, Macromol. Rapid Commun., 2020, 41, 2000150 CrossRef CAS PubMed.
- T. P. Lodge, B. Pudil and K. J. Hanley, Macromolecules, 2002, 35, 4707–4717 CrossRef CAS.
- A. Matsushita and S. Okamoto, Macromolecules, 2014, 47, 7169–7177 CrossRef CAS.
- I. Gunkel, X. Gu, Z. Sun, E. Schaible, A. Hexemer and T. P. Russell, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 331–338 CrossRef CAS.
- T. G. Fox, Bull. Am. Phys. Soc., 1956, 1, 123 CAS.
- H. Yokoyama and E. J. Kramer, Macromolecules, 1998, 31, 7871–7876 CrossRef CAS.
- H. Yokoyama, Mater. Sci. Eng. R: Rep., 2006, 53, 199–248 CrossRef.
- R. Ruiz, J. K. Bosworth and C. T. Black, Physical Review B, 2008, 77, 54204 Search PubMed.
- D. E. Bornside, C. W. Macosko and L. E. Scriven, J. Appl. Phys., 1989, 66, 5185–5193 CrossRef CAS.
- Y. Mouhamad, P. Mokarian-Tabari, N. Clarke, R. A.-L. Jones and M. Geoghegan, J. Appl. Phys., 2014, 116, 123513 CrossRef.
- L. E. Scriven, MRS Proc., 1988, 121, 717 CrossRef CAS.
- T. G. Fitzgerald, R. A. Farrell, N. Petkov, C. T. Bolger, M. T. Shaw, J. P.-F. Charpin, J. P. Gleeson, J. D. Holmes and M. A. Morris, Langmuir, 2009, 25, 13551–13560 CrossRef CAS PubMed.
- C. M. Stafford, K. E. Roskov, T. H. Epps and M. J. Fasolka, Rev. Sci. Instrum., 2006, 77, 023908 CrossRef.
- R. L. Davis, S. Jayaraman, P. M. Chaikin and R. A. Register, Langmuir, 2014, 30, 5637–5644 CrossRef CAS PubMed.
- L. Landau and B. Levich, Acta Physicochim. URSS, 1942, 17, 42–54 Search PubMed.
- A. Modi, S. M. Bhaway, B. D. Vogt, J. F. Douglas, A. Al-Enizi, A. Elzatahry, A. Sharma and A. Karim, ACS Appl. Mater. Interfaces, 2015, 7, 21639–21645 CrossRef CAS PubMed.
- T. Bucher, V. Filiz, C. Abetz and V. Abetz, Membranes, 2018, 8, 57 CrossRef PubMed.
- M. Faustini, B. Louis, P. A. Albouy, M. Kuemmel and D. Grosso, J. Phys. Chem. C, 2010, 114, 7637–7645 CrossRef CAS.
- A. Sidorenko, I. Tokarev, S. Minko and M. Stamm, J. Am. Chem. Soc., 2003, 125, 12211–12216 CrossRef CAS PubMed.
- A. Melninkaitis, K. Juškevičius, M. Maciulevičius, V. Sirutkaitis, A. Beganskienė, I. Kazadojev, A. Kareiva and D. Perednis, Laser-Induced Damage in Optical Materials: 2006, SPIE, 2007, vol. 6403, pp. 437–444 Search PubMed.
- D.-F. Lii, J.-L. Huang, L.-J. Tsui and S.-M. Lee, Surf. Coat. Technol., 2002, 150, 269–276 CrossRef CAS.
- H. Benkreira, Chem. Eng. Sci., 2004, 59, 2745–2751 CrossRef CAS.
- H. Hu, S. Rangou, M. Kim, P. Gopalan, V. Filiz, A. Avgeropoulos and C. O. Osuji, ACS Nano, 2013, 7, 2960–2970 CrossRef CAS PubMed.
- K. Toth, C. O. Osuji, K. G. Yager and G. S. Doerk, Rev. Sci. Instrum., 2020, 91, 013701 CrossRef CAS PubMed.
- M. S. Onses, C. Song, L. Williamson, E. Sutanto, P. M. Ferreira, A. G. Alleyne, P. F. Nealey, H. Ahn and J. A. Rogers, Nat. Nanotechnol., 2013, 8, 667–675 CrossRef CAS PubMed.
- M. S. Onses, A. Ramírez-Hernández, S.-M. Hur, E. Sutanto, L. Williamson, A. G. Alleyne, P. F. Nealey, J. J. de Pablo and J. A. Rogers, ACS Nano, 2014, 8, 6606–6613 CrossRef CAS PubMed.
- M. L. Wadley, I.-F. Hsieh, K. A. Cavicchi and S. Z.-D. Cheng, Macromolecules, 2012, 45, 5538–5545 CrossRef CAS.
- K. W. Gotrik and C. A. Ross, Nano Lett., 2013, 13, 5117–5122 CrossRef CAS PubMed.
- D. R. Barbero and U. Steiner, Phys. Rev. Lett., 2009, 102, 248303 CrossRef PubMed.
- X. Zhang, J. F. Douglas and R. L. Jones, Soft Matter, 2012, 8, 4980–4987 RSC.
- T. Inoue, T. Soen, T. Hashimoto and H. Kawai, J. Polym. Sci., Part A-2, 1969, 7, 1283–1301 CrossRef CAS.
- F. S. Bates, C. V. Berney and R. E. Cohen, Macromolecules, 1983, 16, 1101–1108 CrossRef CAS.
- G. Kim and M. Libera, Macromolecules, 1998, 31, 2670–2672 CrossRef CAS.
- R. Guo, H. Huang, B. Du and T. He, J. Phys. Chem. B, 2009, 113, 2712–2724 CrossRef CAS PubMed.
- J. N.-L. Albert, W.-S. Young, R. L. Lewis, T. D. Bogart, J. R. Smith and T. H. Epps, ACS Nano, 2012, 6, 459–466 CrossRef CAS PubMed.
- S. H. Kim, M. J. Misner, T. Xu, M. Kimura and T. P. Russell, Adv. Mater., 2004, 16, 226–231 CrossRef CAS.
- Y. Chen, H. Huang, Z. Hu and T. He, Langmuir, 2004, 20, 3805–3808 CrossRef CAS PubMed.
- J. Hayat, I. Mitra, Y. Qiao, G. E. Stein and C. Tang, Eur. Polym. J., 2015, 71, 476–489 CrossRef CAS.
- D. W. Breiby, O. Bunk, W. Pisula, T. I. Sølling, A. Tracz, T. Pakula, K. Müllen and M. M. Nielsen, J. Am. Chem. Soc., 2005, 127, 11288–11293 CrossRef CAS PubMed.
- C. Tang, W. Wu, D.-M. Smilgies, K. Matyjaszewski and T. Kowalewski, J. Am. Chem. Soc., 2011, 133, 11802–11809 CrossRef CAS PubMed.
- M. Kimura, M. J. Misner, T. Xu, S. H. Kim and T. P. Russell, Langmuir, 2003, 19, 9910–9913 CrossRef CAS.
- W. A. Phillip, R. M. Dorin, J. Werner, E. M.-V. Hoek, U. Wiesner and M. Elimelech, Nano Lett., 2011, 11, 2892–2900 CrossRef CAS PubMed.
- S. Sourirajan, Ind. Eng. Chem. Fund., 1963, 2, 51–55 CrossRef CAS.
- S. Rangou, K. Buhr, V. Filiz, J. I. Clodt, B. Lademann, J. Hahn, A. Jung and V. Abetz, J. Membr. Sci., 2014, 451, 266–275 CrossRef CAS.
- R. A. Mulvenna, J. L. Weidman, B. Jing, J. A. Pople, Y. Zhu, B. W. Boudouris and W. A. Phillip, J. Membr. Sci., 2014, 470, 246–256 CrossRef CAS.
- K.-V. Peinemann, V. Abetz and P. F.-W. Simon, Nat. Mater., 2007, 6, 992–996 CrossRef CAS PubMed.
- W. A. Phillip, B. O’Neill, M. Rodwogin, M. A. Hillmyer and E. L. Cussler, ACS Appl. Mater. Interfaces, 2010, 2, 847–853 CrossRef CAS PubMed.
- D. S. Marques, U. Vainio, N. M. Chaparro, V. M. Calo, A. R. Bezahd, J. W. Pitera, K. V. Peinemann and S. P. Nunes, Soft Matter, 2013, 9, 5557–5564 RSC.
- X. Qiu, H. Yu, M. Karunakaran, N. Pradeep, S. P. Nunes and K.-V. Peinemann, ACS Nano, 2013, 7, 768–776 CrossRef CAS PubMed.
- M. Radjabian and V. Abetz, Adv. Mater., 2015, 27, 352–355 CrossRef CAS PubMed.
- F. Schacher, M. Ulbricht and A. H.-E. Müller, Adv. Funct. Mater., 2009, 19, 1040–1045 CrossRef CAS.
- Y. Zhang, N. E. Almodovar-Arbelo, J. L. Weidman, D. S. Corti, B. W. Boudouris and W. A. Phillip, npj Clean Water, 2018, 1, 1–14 CrossRef CAS.
- W. A. Phillip, M. A. Hillmyer and E. L. Cussler, Macromolecules, 2010, 43, 7763–7770 CrossRef CAS.
- Y. Zhang, J. L. Sargent, B. W. Boudouris and W. A. Phillip, J. Appl. Polym. Sci., 2015, 132, 41683 Search PubMed.
- C. Yang, G. Zhu, Z. Yi, Y. Zhou and C. Gao, Chem. Eng. J., 2021, 424, 128912 CrossRef CAS.
- C. Park, C. De Rosa and E. L. Thomas, Macromolecules, 2001, 34, 2602–2606 CrossRef CAS.
- H. Jung, S. Woo, Y. Choe, D. Y. Ryu, J. Huh and J. Bang, ACS Macro Lett., 2015, 4, 656–660 CrossRef CAS PubMed.
- D. W. Weller, L. Galuska, W. Wang, D. Ehlenburg, K. Hong and X. Gu, Macromolecules, 2019, 52, 5026–5032 CrossRef CAS.
- A. A. Leniart, P. Pula, R. W. Style and P. W. Majewski, ACS Macro Lett., 2022, 11, 121–126 CrossRef CAS PubMed.
- T. Hashimoto, J. Bodycomb, Y. Funaki and K. Kimishima, Macromolecules, 1999, 32, 952–954 CrossRef CAS.
- M. Gopinadhan, P. W. Majewski, Y. Choo and C. O. Osuji, Phys. Rev. Lett., 2013, 110, 078301 CrossRef PubMed.
- W. Cao, S. Xia, M. Appold, N. Saxena, L. Bießmann, S. Grott, N. Li, M. Gallei, S. Bernstorff and P. Müller-Buschbaum, Sci. Rep., 2019, 9, 18269 CrossRef CAS PubMed.
- S. Park, Y. Kim, W. Lee, S.-M. Hur and D. Y. Ryu, Macromolecules, 2017, 50, 5033–5041 CrossRef CAS.
- G. Nelson, C. S. Drapes, M. A. Grant, R. Gnabasik, J. Wong and A. Baruth, Micromachines, 2018, 9, 271 CrossRef PubMed.
- K. W. Gotrik, A. F. Hannon, J. G. Son, B. Keller, A. Alexander-Katz and C. A. Ross, ACS Nano, 2012, 6, 8052–8059 CrossRef CAS PubMed.
- H. Elbs, C. Drummer, V. Abetz and G. Krausch, Macromolecules, 2002, 35, 5570–5577 CrossRef CAS.
- X. Gu, I. Gunkel, A. Hexemer and T. P. Russell, Colloid Polym. Sci., 2014, 292, 1795–1802 CrossRef CAS.
- C. Cummins, P. Mokarian-Tabari, P. Andreazza, C. Sinturel and M. A. Morris, ACS Appl. Mater. Interfaces, 2016, 8, 8295–8304 CrossRef CAS PubMed.
- J. Peng, D. H. Kim, W. Knoll, Y. Xuan, B. Li and Y. Han, J. Chem. Phys., 2006, 125, 064702 CrossRef PubMed.
- E. Kim, H. Ahn, S. Park, H. Lee, M. Lee, S. Lee, T. Kim, E.-A. Kwak, J. H. Lee, X. Lei, J. Huh, J. Bang, B. Lee and D. Y. Ryu, ACS Nano, 2013, 7, 1952–1960 CrossRef CAS PubMed.
- J. Xu, K. Wang, J. Li, H. Zhou, X. Xie and J. Zhu, Macromolecules, 2015, 48, 2628–2636 CrossRef CAS.
- M. Cetintas and M. Kamperman, Polymer, 2016, 107, 387–397 CrossRef CAS.
- K. Aissou, M. Mumtaz, P. Marcasuzaa, C. Brochon, E. Cloutet, G. Fleury and G. Hadziioannou, Small, 2017, 13, 1603184 CrossRef PubMed.
- S. Lee, L.-C. Cheng, K. G. Yager, M. Mumtaz, K. Aissou and C. A. Ross, Macromolecules, 2019, 52, 1853–1863 CrossRef CAS.
- C. Sinturel, M. Vayer, M. Morris and M. A. Hillmyer, Macromolecules, 2013, 46, 5399–5415 CrossRef CAS.
- C. Jin, B. C. Olsen, E. J. Luber and J. M. Buriak, Chem. Mater., 2017, 29, 176–188 CrossRef CAS.
- D. H. Lee, H. Cho, S. Yoo and S. Park, J. Colloid Interface Sci., 2012, 383, 118–123 CrossRef CAS PubMed.
- W. Bai, A. F. Hannon, K. W. Gotrik, H. K. Choi, K. Aissou, G. Liontos, K. Ntetsikas, A. Alexander-Katz, A. Avgeropoulos and C. A. Ross, Macromolecules, 2014, 47, 6000–6008 CrossRef CAS.
- A. Baruth, M. Seo, C. H. Lin, K. Walster, A. Shankar, M. A. Hillmyer and C. Leighton, ACS Appl. Mater. Interfaces, 2014, 6, 13770–13781 CrossRef CAS PubMed.
- W.-H. Huang, P.-Y. Chen and S.-H. Tung, Macromolecules, 2012, 45, 1562–1569 CrossRef CAS.
- A. Knoll, R. Magerle and G. Krausch, J. Chem. Phys., 2004, 120, 1105–1116 CrossRef CAS PubMed.
- M. Y. Paik, J. K. Bosworth, D.-M. Smilges, E. L. Schwartz, X. Andre and C. K. Ober, Macromolecules, 2010, 43, 4253–4260 CrossRef CAS PubMed.
- Y. Tada, H. Yoshida, Y. Ishida, T. Hirai, J. K. Bosworth, E. Dobisz, R. Ruiz, M. Takenaka, T. Hayakawa and H. Hasegawa, Macromolecules, 2012, 45, 292–304 CrossRef CAS.
- M. A. Chavis, D.-M. Smilgies, U. B. Wiesner and C. K. Ober, Adv. Funct. Mater., 2015, 25, 3057–3065 CrossRef CAS PubMed.
- G. S. Doerk, R. Li, M. Fukuto and K. G. Yager, Macromolecules, 2020, 53, 1098–1113 CrossRef CAS.
- A. V. Berezkin, F. Jung, D. Posselt, D.-M. Smilgies and C. M. Papadakis, Adv. Funct. Mater., 2018, 28, 1706226 CrossRef.
- H. Hulkkonen, T. Salminen and T. Niemi, Soft Matter, 2019, 15, 7909–7917 RSC.
- A. Selkirk, N. Prochukhan, R. Lundy, C. Cummins, R. Gatensby, R. Kilbride, A. Parnell, J. Baez Vasquez, M. Morris and P. Mokarian-Tabari, Macromolecules, 2021, 54, 1203–1215 CrossRef CAS PubMed.
- J. N.-L. Albert, T. D. Bogart, R. L. Lewis, K. L. Beers, M. J. Fasolka, J. B. Hutchison, B. D. Vogt and T. H. Epps, Nano Lett., 2011, 11, 1351–1357 CrossRef CAS PubMed.
- S. Hüttner, M. Sommer, A. Chiche, G. Krausch, U. Steiner and M. Thelakkat, Soft Matter, 2009, 5, 4206–4211 RSC.
- C. Sinturel, D. Grosso, M. Boudot, H. Amenitsch, M. A. Hillmyer and A. Pineau, ACS Appl. Mater. Interfaces, 2014, 7, 12146–12152 CrossRef PubMed.
- L. Xu, Z. Zou, H. Zhang and T. Shi, Chem. Res. Chin. Univ., 2017, 33, 833–838 CrossRef CAS.
- M. Y. Efremov and P. F. Nealey, Polymer, 2022, 238, 124417 CrossRef CAS.
- A. Laschitsch, C. Bouchard, J. Habicht, M. Schimmel, J. Rühe and D. Johannsmann, Macromolecules, 1999, 32, 1244–1251 CrossRef CAS.
- K. Takano, T. Nyu, T. Maekawa, T. Seki, R. Nakatani, T. Komamura, T. Hayakawa and T. Hayashi, RSC Adv., 2019, 10, 70–75 RSC.
- C. Harrison, D. H. Adamson, Z. Cheng, J. M. Sebastian, S. Sethuraman, D. A. Huse, R. A. Register and P. M. Chaikin, Science, 2000, 290, 1558–1560 CrossRef CAS PubMed.
- J. Hahm and S. J. Sibener, J. Chem. Phys., 2001, 114, 4730–4740 CrossRef CAS.
- J. G. Raybin and S. J. Sibener, Macromolecules, 2019, 52, 5985–5994 CrossRef CAS.
- D. Posselt, J. Zhang, D.-M. Smilgies, A. V. Berezkin, I. I. Potemkin and C. M. Papadakis, Prog. Polym. Sci., 2017, 66, 80–115 CrossRef CAS.
- Z. Di, D. Posselt, D.-M. Smilgies and C. M. Papadakis, Macromolecules, 2010, 43, 418–427 CrossRef CAS PubMed.
- I. Gunkel, X. Gu, Z. Sun, E. Schaible, A. Hexemer and T. P. Russell, J. Polym. Sci. Part B: Polym. Phys., 2016, 54, 331–338 CrossRef CAS.
- C. K. Shelton, R. L. Jones, J. A. Dura and T. H. Epps, Macromolecules, 2016, 49, 7525–7534 CrossRef CAS.
- J. W. Jeong, Y. H. Hur, H. Kim, J. M. Kim, W. I. Park, M. J. Kim, B. J. Kim and Y. S. Jung, ACS Nano, 2013, 7, 6747–6757 CrossRef CAS PubMed.
- B. C. Stahl, E. J. Kramer, C. J. Hawker and N. A. Lynd, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 1125–1130 CrossRef CAS.
- S. P. Paradiso, K. T. Delaney, C. J. García-Cervera, H. D. Ceniceros and G. H. Fredrickson, Macromolecules, 2016, 49, 1743–1751 CrossRef CAS.
- H. Park, S. Jo, B. Kang, K. Hur, S. S. Oh, D. Y. Ryu and S. Lee, Nanophotonics, 2022, 11, 2583–2615 CrossRef.
- S. Park, Y. Kim, H. Ahn, J. H. Kim, P. J. Yoo and D. Y. Ryu, Sci. Rep., 2016, 6, 36326 CrossRef CAS PubMed.
- C. Cummins, A. Alvarez-Fernandez, A. Bentaleb, G. Hadziioannou, V. Ponsinet and G. Fleury, Langmuir, 2020, 36, 13872–13880 CrossRef CAS PubMed.
- X. Gu, I. Gunkel, A. Hexemer, W. Gu and T. P. Russell, Adv. Mater., 2014, 26, 273–281 CrossRef CAS PubMed.
- R. Guo, H. Huang, Y. Chen, Y. Gong, B. Du and T. He, Macromolecules, 2008, 41, 890–900 CrossRef CAS.
- L.-Y. Shi, F. Liao, L.-C. Cheng, S. Lee, R. Ran, Z. Shen and C. A. Ross, ACS Macro Lett., 2019, 8, 852–858 CrossRef CAS.
- Y.-H. Wu, T.-Y. Lo, M.-S. She and R.-M. Ho, ACS Appl. Mater. Interfaces, 2015, 7, 16536–16547 CrossRef CAS PubMed.
- Y. Cong, W. Zhai and C. Wu, Soft Mater., 2021, 19, 117–128 CrossRef CAS.
- S. Kim, G. Jeon, S. W. Heo, H. J. Kim, S. B. Kim, T. Chang and J. K. Kim, Soft Matter, 2013, 9, 5550–5556 RSC.
- J. Peng, Y. Xuan, H. Wang, Y. Yang, B. Li and Y. Han, J. Chem. Phys., 2004, 120, 11163–11170 CrossRef CAS PubMed.
- Y. Li, H. Huang, T. He and Y. Gong, Appl. Surf. Sci., 2011, 257, 8093–8101 CrossRef CAS.
- Y. S. Jung and C. A. Ross, Adv. Mater., 2009, 21, 2540–2545 CrossRef CAS.
- Y. J. Choi, M. H. Byun, T. W. Park, S. Choi, J. Bang, H. Jung, J.-H. Cho, S.-H. Kwon, K. H. Kim and W. I. Park, ACS Appl. Nano Mater., 2019, 2, 1294–1301 CrossRef CAS.
- C. Luo, W. Huang and Y. Han, Macromol. Rapid Commun., 2009, 30, 515–520 CrossRef CAS PubMed.
- H. Jung, W. H. Shin, T. W. Park, Y. J. Choi, Y. J. Yoon, S. H. Park, J.-H. Lim, J.-D. Kwon, J. W. Lee, S.-H. Kwon, G. H. Seong, K. H. Kim and W. I. Park, Nanoscale, 2019, 11, 8433–8441 RSC.
- L. Cheng, J. W. Simonaitis, K. R. Gadelrab, M. Tahir, Y. Ding, A. Alexander-Katz and C. A. Ross, Small, 2020, 16, 1905509 CrossRef CAS PubMed.
- A. Subramanian, G. Doerk, K. Kisslinger, D. H. Yi, R. B. Grubbs and C.-Y. Nam, Nanoscale, 2019, 11, 9533–9546 RSC.
- L.-Y. Shi, A. Subramanian, L. Weng, S. Lee, K. Kisslinger, C.-Y. Nam and C. A. Ross, Nanoscale, 2022, 14, 1807–1813 RSC.
- G. Ginige, Y. Song, B. C. Olsen, E. J. Luber, C. T. Yavuz and J. M. Buriak, ACS Appl. Mater. Interfaces, 2021, 13, 28639–28649 CrossRef CAS.
- J. E. Seppala, R. L. Lewis and T. H. Epps, ACS Nano, 2012, 6, 9855–9862 CrossRef CAS PubMed.
- J. M. Kim, Y. J. Kim, W. I. Park, Y. H. Hur, J. W. Jeong, D. M. Sim, K. M. Baek, J. H. Lee, M. J. Kim and Y. S. Jung, Adv. Funct. Mater., 2015, 25, 306–315 CrossRef CAS.
- P. Mokarian-Tabari, C. Cummins, S. Rasappa, C. Simao, C. M. Sotomayor Torres, J. D. Holmes and M. A. Morris, Langmuir, 2014, 30, 10728–10739 CrossRef CAS PubMed.
- D. Borah, M. T. Shaw, J. D. Holmes and M. A. Morris, ACS Appl. Mater. Interfaces, 2013, 5, 2004–2012 CrossRef CAS PubMed.
- X. Zhang, K. D. Harris, N. L.-Y. Wu, J. N. Murphy and J. M. Buriak, ACS Nano, 2010, 4, 7021–7029 CrossRef CAS.
- X. Zhang, J. N. Murphy, N. L.-Y. Wu, K. D. Harris and J. M. Buriak, Macromolecules, 2011, 44, 9752–9757 CrossRef CAS.
- R. A. Segalman, H. Yokoyama and E. J. Kramer, Adv. Mater., 2001, 13, 1152–1155 CrossRef CAS.
- I. Bita, J. K.-W. Yang, S. J. Yeon, C. A. Ross, E. L. Thomas and K. K. Berggren, Science, 2008, 321, 939–943 CrossRef CAS PubMed.
- R. Ruiz, H. Kang, F. A. Detcheverry, E. Dobisz, D. S. Kercher, T. R. Albrecht, J. J. De Pablo and P. F. Nealey, Science, 2008, 321, 936–939 CrossRef CAS PubMed.
- C.-C. Liu, A. Ramírez-Hernández, E. Han, G. S.-W. Craig, Y. Tada, H. Yoshida, H. Kang, S. Ji, P. Gopalan, J. J. de Pablo and P. F. Nealey, Macromolecules, 2013, 46, 1415–1424 CrossRef CAS.
- M. J. Maher, C. T. Rettner, C. M. Bates, G. Blachut, M. C. Carlson, W. J. Durand, C. J. Ellison, D. P. Sanders, J. Y. Cheng and C. G. Willson, ACS Appl. Mater. Interfaces, 2015, 7, 3323–3328 CrossRef CAS PubMed.
- S. Ji, L. Wan, C.-C. Liu and P. F. Nealey, Prog. Polym. Sci., 2016, 54–55, 76–127 CrossRef CAS.
- Y. S. Jung and C. A. Ross, Nano Lett., 2007, 7, 2046–2050 CrossRef CAS.
- K. Lee, M. Kreider, W. Bai, L.-C. Cheng, S. S. Dinachali, K.-H. Tu, T. Huang, K. Ntetsikas, G. Liontos, A. Avgeropoulos and C. A. Ross, Nanotechnology, 2016, 27, 465301 CrossRef PubMed.
- L.-C. Cheng, W. Bai, E. F. Martin, K.-H. Tu, K. Ntetsikas, G. Liontos, A. Avgeropoulos and C. A. Ross, Nanotechnology, 2017, 28, 145301 CrossRef PubMed.
- C. Tang, J. Bang, G. E. Stein, G. H. Fredrickson, C. J. Hawker, E. J. Kramer, M. Sprung and J. Wang, Macromolecules, 2008, 41, 4328–4339 CrossRef CAS.
- H. K. Choi, J.-B. Chang, A. F. Hannon, J. K.-W. Yang, K. K. Berggren, A. Alexander-Katz and C. A. Ross, Nano Futures, 2017, 1, 015001 CrossRef.
- S. Lee, L.-C. Cheng, K. R. Gadelrab, K. Ntetsikas, D. Moschovas, K. G. Yager, A. Avgeropoulos, A. Alexander-Katz and C. A. Ross, ACS Nano, 2018, 12, 6193–6202 CrossRef CAS PubMed.
- L.-C. Cheng, K. R. Gadelrab, K. Kawamoto, K. G. Yager, J. A. Johnson, A. Alexander-Katz and C. A. Ross, Nano Lett., 2018, 18, 4360–4369 CrossRef CAS PubMed.
- L.-Y. Shi, J. Lan, S. Lee, L.-C. Cheng, K. G. Yager and C. A. Ross, ACS Nano, 2020, 14, 4289–4297 CrossRef CAS PubMed.
- L.-Y. Shi, C. Yin, B. Zhou, W. Xia, L. Weng and C. A. Ross, Macromolecules, 2021, 54, 1657–1664 CrossRef CAS.
- S. Xiong, L. Wan, Y. Ishida, Y.-A. Chapuis, G. S.-W. Craig, R. Ruiz and P. F. Nealey, ACS Nano, 2016, 10, 7855–7865 CrossRef CAS PubMed.
- L. Wan, S. Ji, C.-C. Liu, G. S.-W. Craig and P. F. Nealey, Soft Matter, 2016, 12, 2914–2922 RSC.
- R. Liu, H. Huang, Z. Sun, A. Alexander-Katz and C. A. Ross, ACS Nano, 2021, 15, 16266–16276 CrossRef CAS PubMed.
- T.-C. Wang, H.-Y. Hsueh and R.-M. Ho, Chem. Mater., 2010, 22, 4642–4651 CrossRef CAS.
- C.-J. Chu, M.-H. Cheng, P.-Y. Chung, M.-H. Chi, K.-S. Jeng and J.-T. Chen, Int. J. Polym. Mater. Polym. Biomater., 2016, 65, 695–701 CrossRef CAS.
- Y.-H. Tseng, Y.-L. Lin, J.-H. Ho, C.-T. Chang, Y.-C. Fan, M.-H. Shen and J.-T. Chen, Polymer, 2021, 228, 123859 CrossRef CAS.
- S. Ok, M. Vayer and C. Sinturel, Soft Matter, 2021, 17, 7430–7458 RSC.
- A. A. Abate, G. T. Vu, A. D. Pezzutti, N. A. García, R. L. Davis, F. Schmid, R. A. Register and D. A. Vega, Macromolecules, 2016, 49, 7588–7596 CrossRef CAS.
- G. Singh, S. Batra, R. Zhang, H. Yuan, K. G. Yager, M. Cakmak, B. Berry and A. Karim, ACS Nano, 2013, 7, 5291–5299 CrossRef CAS PubMed.
- P. W. Majewski and K. G. Yager, Macromolecules, 2015, 48, 4591–4598 CrossRef CAS.
- M. N. Basutkar, P. W. Majewski, G. S. Doerk, K. Toth, C. O. Osuji, A. Karim and K. G. Yager, Macromolecules, 2019, 52, 7224–7233 CrossRef CAS.
- Z. Qiang, L. Zhang, G. E. Stein, K. A. Cavicchi and B. D. Vogt, Macromolecules, 2014, 47, 1109–1116 CrossRef CAS.
- Z. Qiang, Y. Zhang, J. A. Groff, K. A. Cavicchi and B. D. Vogt, Soft Matter, 2014, 10, 6068–6076 RSC.
- M. Luo, D. M. Scott and T. H. Epps, ACS Macro Lett., 2015, 4, 516–520 CrossRef CAS PubMed.
- Z. Qiang, Y. Zhang, Y. Wang, S. M. Bhaway, K. A. Cavicchi and B. D. Vogt, Carbon, 2015, 82, 51–59 CrossRef CAS.
- Z. Qiang, M. L. Wadley, B. D. Vogt and K. A. Cavicchi, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 1058–1064 CrossRef CAS.
- C. K. Shelton, R. L. Jones and T. H. Epps, Macromolecules, 2017, 50, 5367–5376 CrossRef CAS.
- S. H. Sung, W. B. Farnham, H. E. Burch, Y. Brun, K. Qi and T. H. Epps III, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1663–1672 CrossRef CAS.
- H. Kang, K. Kim and B.-H. Sohn, Nanotechnology, 2020, 31, 455302 CrossRef CAS PubMed.
- Y. C. Kim, T. J. Shin, S.-M. Hur, S. J. Kwon and S. Y. Kim, Sci. Adv., 2019, 5, eaaw3974 CrossRef CAS PubMed.
- E. R. Gottlieb, P. Dimitrakellis, D. G. Vlachos and T. H. Epps, ACS Appl. Polym. Mater., 2022, 4, 682–691 CrossRef CAS.
- J. P. Singer, K. W. Gotrik, J. H. Lee, S. E. Kooi, C. A. Ross and E. L. Thomas, Polymer, 2014, 55, 1875–1882 CrossRef CAS.
- F. F. Lupi, T. J. Giammaria, M. Ceresoli, G. Seguini, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, Nanotechnology, 2013, 24, 315601 CrossRef.
- G. Seguini, F. Zanenga, T. J. Giammaria, M. Ceresoli, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, ACS Appl. Mater. Interfaces, 2016, 8, 8280–8288 CrossRef CAS PubMed.
- T. J. Giammaria, F. Ferrarese Lupi, G. Seguini, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, ACS Appl. Mater. Interfaces, 2017, 9, 31215–31223 CrossRef CAS PubMed.
- X. Zhang, K. G. Yager, S. Kang, N. J. Fredin, B. Akgun, S. Satija, J. F. Douglas, A. Karim and R. L. Jones, Macromolecules, 2010, 43, 1117–1123 CrossRef CAS.
- M. Perego, F. Ferrarese Lupi, M. Ceresoli, T. J. Giammaria, G. Seguini, E. Enrico, L. Boarino, D. Antonioli, V. Gianotti, K. Sparnacci and M. Laus, J. Mater. Chem. C, 2014, 2, 6655–6664 RSC.
- K. Sparnacci, R. Chiarcos, V. Gianotti, M. Laus, T. J. Giammaria, M. Perego, G. Munaò, G. Milano, A. De Nicola, M. Haese, L. P. Kreuzer, T. Widmann and P. Müller-Buschbaum, ACS Appl. Mater. Interfaces, 2020, 12, 7777–7787 CrossRef CAS PubMed.
- M. Fang, L. Tao, W. Wu, Q. Wei, Y. Xia, P. Li, X. Ran, Q. Zhong, G. Xing, L. Song, P. Müller-Buschbaum, H. Zhang and Y. Chen, J. Energy Chem., 2021, 61, 8–14 CrossRef.
- IEEE International Roadmap for Devices and Systems – IEEE IRDSTM, https://irds.ieee.org/ (accessed March 22, 2022).
- H. J. Dai, N. P. Balsara, B. A. Garetz and M. C. Newstein, Phys. Rev. Lett., 1996, 77, 3677–3680 CrossRef CAS.
- S. Ji, C.-C. Liu, W. Liao, A. L. Fenske, G. S.-W. Craig and P. F. Nealey, Macromolecules, 2011, 44, 4291–4300 CrossRef CAS.
- I. P. Campbell, C. He and M. P. Stoykovich, ACS Macro Lett., 2013, 2, 918–923 CrossRef CAS.
- J. Li, P. A. Rincon-Delgadillo, H. S. Suh, G. Mannaert and P. F. Nealey, JM3.1, 2019, 18, 043502 CAS.
- C. Harrison, Z. Cheng, S. Sethuraman, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, Phys. Rev. E, 2002, 66, 011706 CrossRef PubMed.
- J. N. Murphy, K. D. Harris and J. M. Buriak, PLoS One, 2015, 10, e0133088 CrossRef PubMed.
- X. Gu, J. Reinspach, B. J. Worfolk, Y. Diao, Y. Zhou, H. Yan, K. Gu, S. Mannsfeld, M. F. Toney and Z. Bao, ACS Appl. Mater. Interfaces, 2016, 8, 1687–1694 CrossRef CAS PubMed.
- Z. Sun and T. P. Russell, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 980–989 CrossRef CAS.
- J. A. Dolan, K. Korzeb, R. Dehmel, K. C. Gödel, M. Stefik, U. Wiesner, T. D. Wilkinson, J. J. Baumberg, B. D. Wilts, U. Steiner and I. Gunkel, Small, 2018, 14, 1802401 CrossRef PubMed.
- D.-M. Smilgies, J Appl Cryst, 2009, 42, 1030–1034 CrossRef CAS PubMed.
- A. M. Welander, H. Kang, K. O. Stuen, H. H. Solak, M. Müller, J. J. de Pablo and P. F. Nealey, Macromolecules, 2008, 41, 2759–2761 CrossRef CAS.
- C. Harrison, Z. Cheng, S. Sethuraman, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, Phys. Rev. E, 2002, 66, 011706 CrossRef PubMed.
- C. Harrison, D. E. Angelescu, M. Trawick, Z. Cheng, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, EPL, 2004, 67, 800 CrossRef CAS.
- C. T. Black and K. W. Guarini, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 1970–1975 CrossRef CAS.
- D. A. Vega, C. K. Harrison, D. E. Angelescu, M. L. Trawick, D. A. Huse, P. M. Chaikin and R. A. Register, Phys. Rev. E, 2005, 71, 061803 CrossRef PubMed.
- R. Ruiz, R. L. Sandstrom and C. T. Black, Adv. Mater., 2007, 19, 587–591 CrossRef CAS.
- H. J. Ryu, D. B. Fortner, S. Lee, R. Ferebee, M. De Graef, K. Misichronis, A. Avgeropoulos and M. R. Bockstaller, Macromolecules, 2013, 46, 204–215 CrossRef CAS.
- M. Ceresoli, F. G. Volpe, G. Seguini, D. Antonioli, V. Gianotti, K. Sparnacci, M. Laus and M. Perego, J. Mater. Chem. C, 2015, 3, 8618–8624 RSC.
- P. W. Majewski and K. G. Yager, ACS Nano, 2015, 9, 3896–3906 CrossRef CAS PubMed.
- M. Fernández-Regúlez, E. Solano, L. Evangelio, S. Gottlieb, C. Pinto-Gómez, G. Rius, J. Fraxedas, E. Gutiérrez-Fernández, A. Nogales, M. C. García-Gutiérrez, T. A. Ezquerra and F. Pérez-Murano, J. Synchrotron Rad., 2020, 27, 1278–1288 CrossRef PubMed.
- G. Seguini, F. Zanenga, M. Laus and M. Perego, Phys. Rev. Mater., 2018, 2, 055605 CrossRef CAS.
- N. L.-Y. Wu, X. Zhang, J. N. Murphy, J. Chai, K. D. Harris and J. M. Buriak, Nano Lett., 2012, 12, 264–268 CrossRef CAS PubMed.
- S. Pinge, Y. Qiu, V. Monreal, D. Baskaran, A. Ravirajan and Y. L. Joo, Phys. Chem. Chem. Phys., 2020, 22, 478–488 RSC.
- W. Li and M. Müller, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 187–216 CrossRef CAS PubMed.
- S.-M. Hur, V. Thapar, A. Ramírez-Hernández, P. F. Nealey and J. J. de Pablo, ACS Nano, 2018, 12, 9974–9981 CrossRef CAS PubMed.
- Y. Ren and M. Müller, Macromolecules, 2020, 53, 5337–5349 CrossRef CAS.
- W. Shi, J. Phys. Chem. Lett., 2020, 11, 2724–2730 CrossRef CAS PubMed.
- T. Hu, Y. Ren, L. Zhang and W. Li, Macromolecules, 2021, 54, 773–782 CrossRef CAS.
- T. Hu, Y. Ren and W. Li, Macromolecules, 2021, 54, 8024–8032 CrossRef CAS.
- A. F. Hannon, W. Bai, A. Alexander-Katz and C. A. Ross, Soft Matter, 2015, 11, 3794–3805 RSC.
- A. J. Peters, R. A. Lawson, B. D. Nation, P. J. Ludovice and C. L. Henderson, JM3.1, 2016, 15, 013508 Search PubMed.
- X. Xu, X. Man, M. Doi, Z. Ou-Yang and D. Andelman, Macromolecules, 2019, 52, 9321–9333 CrossRef CAS.
Footnote |
| † Here, we use the DSA term to encompass any method that directs the BCP self-assembly.7,8 More narrowly, it has been used in the context of graphoepitaxial and chemoepitaxial ordering.28–30 |
| This journal is © The Royal Society of Chemistry 2022 |