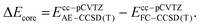The activated reaction of dichlorocarbene with triplet molecular oxygen

Abstract

The well-known dichlorocarbene (CCl₂, 1) is deemed to undergo an extremely facile addition reaction with triplet molecular oxygen (³O₂) under formation of the corresponding singlet Criegee intermediate, phosgene O-oxide. This is unexpected, because the carbene possesses a singlet ground state with a large singlet–triplet gap and, typically, only triplet carbenes react swiftly with triplet dioxygen. Hence, we deployed a careful theoretical study of this reaction and computed the oxygen addition barrier at levels of electron correlation as high as CCSD(T) and BD(TQ) and basis sets as large as cc-pV5Z. Our results firmly establish the existence of a reaction barrier, and we estimate its height to amount to 8.8 kcal mol⁻¹. Furthermore, the initially formed triplet dioxygen adduct is prone to facile O–O bond breaking rendering phosgene and triplet oxygen atoms likely products of the overall reaction. As a general conclusion, we find that carbenes are ambiphiles in oxygen additions and more electrophilic as well as that more nucleophilic carbenes show greater reactivity.

---

Introduction

Dichlorocarbene (CCl₂, 1) is the epitome of a substituted, neutral divalent carbon intermediate.¹ This fundamental halocarbene's participation in the basic hydrolysis of chloroform was suggested as early as 1862,² and Hine could corroborate this assumption in a landmark mechanistic study in 1950.³ In this regard, the initial rapid deprotonation of chloroform results in the formation of the trichloromethide anion, which subsequently eliminates a chloride ion in the rate determining step. Doering later showed that the resulting dichlorocarbene can be trapped with alkenes under formation of dichlorocyclopropanes.⁴ In this cheletropic cycloaddition, the reactivity increases with the alkene's degree of alkyl substitution establishing the electrophilicity of the reactive intermediate.⁵ Hereof, 1 serves as a reference compound for Moss’ influential ‘carbene selectivity index’, m_CXY.^6,7

While the singlet electronic ground state of dichlorocarbene is evident from the stereospecificity of its concerted cyclopropanation reactions,⁸ the actual magnitude of the singlet–triplet gap (E_S–T) was under debate for a long time.⁹ This was reflected in a fruitful competition between experimentalists and theoreticians, in which the individually applied methods were pushed towards their frontiers.¹⁰ The initially presented singlet–triplet gap of only 3(3) kcal mol⁻¹ from negative ion photoelectron spectroscopy (NIPES)¹¹ stood in stark contrast to much higher values reported in rigorous theoretical studies.^12–15 This scientific dispute incited a careful reevaluation of the experiment revealing a significant dichloromethyl carbanion contamination in the photoelectron spectra.⁹ Now, the improved experimental value after removal of the contaminant exhibits a good agreement with the best available theoretical estimate of approximately 20.1 kcal mol⁻¹.¹⁵ A similar ambiguity still exists regarding dichlorocarbene's reactivity towards triplet molecular oxygen which we subject to critical scrutiny in the underlying manuscript.

Commonly, only triplet carbenes are expected to react rapidly with triplet molecular oxygen because this process corresponds to an overall spin-allowed, twofold radical recombination reaction affording singlet carbonyl O-oxide Criegee intermediates (R₂C=O⁺–O⁻).^16–19 Yet, some singlet carbenes were still observed to react with molecular oxygen at experimentally relevant timescales in laser flash photolysis (LFP) studies, which is often explained by an initial thermal excitation of the carbene to its low-lying triplet state.^20–23 In a similar vein, some highly electrophilic singlet carbenes like difluorovinylidene^24,25 and 2H-imidazol-2-ylidene^26,27 feature swift reactions with molecular oxygen even at cryogenic temperatures under matrix isolation conditions. However, a rapid oxygen addition reaction would usually not be expected for dichlorocarbene due to its high energy triplet state precluding an initial thermal excitation mechanism. Nonetheless, reactions of dichlorocarbene with triplet molecular oxygen were repeatedly reported in the literature. For instance, it was found that the phase-transfer catalyzed reaction of chloroform with sodium hydroxide under an atmosphere of oxygen provided suitable conditions for the preparation of oxo-manganese complexes which are active in epoxidation reactions.^28,29 This was ascribed to the formation of dichlorocarbonyl O-oxide from CCl₂ and O₂ which in turn supposedly transfers an oxygen atom to the metal center. Carbonyl O-oxides are indeed potent oxygen atom transfer reagents,¹⁸ but the nature of the involved oxidant in these reactions eventually remains unclear. Under the employed hydrolysis conditions, the reaction of O₂ with the trihalomethide anion seems to present a viable mechanistic scenario as well.

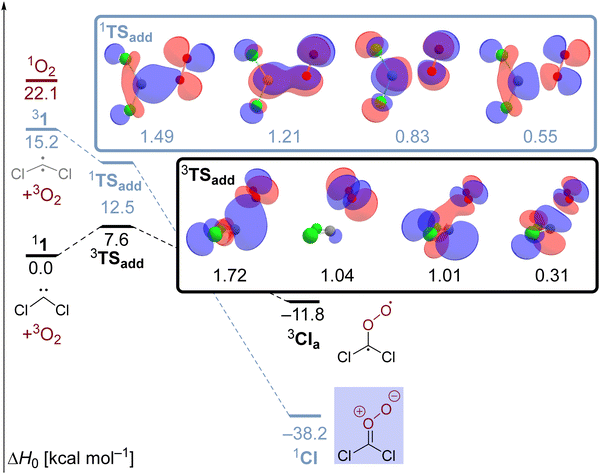
Another example is provided by the laser flash photolysis of dichlorodiazirine (2, Scheme 1) which serves as a cunningly prepared nitrogenous precursor for dichlorocarbene.^30,31 When the diazirine is irradiated at a laser wavelength of 354 nm under ambient air, a transient absorption (λ_max = 465 nm) with a lifetime of 0.5 μs is observed in the UV/visible spectrum.³¹ Since the spectral feature is absent when the reaction is performed under a nitrogen atmosphere, it is evident that the spectral carrier stems from a reaction with O₂. The authors proposed that the nascent singlet dichlorocarbene swiftly adds molecular oxygen under spin-conserving and exoergic formation of a triplet Criegee intermediate ³CI (Scheme 1) which is supported by the absence of a reaction barrier at the PBE/6-311+G(d) level. The triplet intermediate subsequently relaxes to its singlet ground state mediated by a spin-orbit coupling of 10.4 cm⁻¹ at a minimum energy crossing point (MECP) between the two involved electronic states. Utilizing Fermi's Golden Rule, the authors estimated a large intersystem crossing rate constant of 3.5 × 10⁹ s⁻¹ suggesting that the singlet Criegee intermediate ¹CI causes the absorption at 465 nm (Scheme 1). Despite the convincing computational support, this assignment had to remain tentative because the transient could not be quenched with tetramethylethylene (TME), acetaldehyde or tris(trimethylsilyl)silane which are generally expected to act as scavengers towards carbonyl oxides like ¹CI. In addition, an alternative theoretical assessment at the B3LYP/6-31G(d) level already finds an 11.8 kcal mol⁻¹ free energy barrier for the CCl₂ + O₂ reaction in an overall triplet state.³¹ The presence of a non-negligible barrier for this reaction also seems to be in better agreement with an earlier gas-phase study by Tiee and others.³² These authors monitored the reaction of ground state dichlorocarbene with dioxygen at room temperature via laser-induced fluorescence and reported a second order rate constant of ≤ 3 × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹ several orders of magnitude below the collision rate limit.

Scheme 1 Preparation of dichlorocarbene 1via laser flash photolysis of dichlorodiazirin. In the presence of oxygen, a transient assigned to Criegee intermediate ¹CI is observed.

In consideration of the inconclusive previous experimental and computational results, we aimed to establish the existence of an enthalpic barrier in the CCl₂ (X̃ ¹A₁) + O₂ (X̃³Σ⁻_g) reaction and pinpoint its magnitude at rigorous levels of theory. We additionally present an alternative reaction outcome from decomposition of the triplet Criegee intermediate ³CI and study the dependence of the ³O₂ addition reaction on carbene philicity.

Methods section

The primarily employed computational method corresponds to coupled cluster theory with single and double excitations and perturbatively included triples, CCSD(T).^33–35 Utilizing the ORCA 4 program package,³⁶ we optimized all structures involved in the CCl₂ + O₂ reaction at the CCSD(T)/cc-pVTZ level of theory with the help of numerically computed gradients. Vibrational frequencies were also obtained numerically to ensure the nature of the stationary structure and to assess the zero-point vibrational energy correction (Δ_ZPVE). Transition states were further verified with intrinsic reaction coordinate (IRC) runs with a computationally less demanding cc-pVDZ basis set. In the case of triplet states, the initially computed orbitals from the unrestricted Hartree-Fock (UHF) reference were converted to quasi-restricted orbitals to avoid problems associated with spin contamination.

In order to obtain reliable electronic energies on top of the optimized structures, we performed a focal-point analysis in which the level of electron correlation and the basis set size are systematically increased.^15,37 The convergence of the energy can then be judged from the incremental changes to the preceding, inferior level of theory. Therefore, we computed CCSD(T) single point energies with correlation consistent basis sets up to and including the sizeable cc-pV5Z basis set.^38,39 The self-consistent field energies were extrapolated from three points with a Feller-type exponential function⁴⁰ while the complete basis set (CBS) correlation energy was deduced from two points utilizing a Helgaker-type power law.^41,42 Because only valence electrons are correlated in the focal-point table, we additionally evaluated the effect of core-correlation at the all-electron AE-CCSD(T)/cc-pCVTZ level of theory^43,44 and calculated a correction according to the following equation:

Higher order correlation corrections were computed with Brueckner doubles coupled cluster theory including perturbationally estimated connected triple and quadruple excitations, BD(TQ).⁴⁵ During the CCl₂ + O₂ reaction, singlet and triplet states necessarily cross at some point and the resulting near degeneracy in the intermediate region might be associated with pronounced multireference character and a concomitantly elevated T₁ diagnostic value; the latter corresponds to the norm of the t₁ amplitudes divided by the square root of the number of correlated electrons.⁴⁶ In Brueckner theory, the orbitals are rotated in such a way that the singles amplitudes become zero resulting in a zero T₁ diagnostic value. 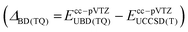It has been found that utilization of Brueckner orbitals in the coupled cluster expansion can be beneficial for the description of low-symmetry biradicals with a narrow singlet–triplet gap.⁴⁷ The necessary single points to estimate the higher order correlation correction were computed with Gaussian16⁴⁸ utilizing a cc-pVTZ basis set.

In an alternative approach, we additionally computed the oxygen addition reaction with the complete active space self-consistent field (CASSCF) method and a cc-pVTZ basis set. This made it possible to further study the chemical transformation of interest in an overall singlet state which is heavily plagued by multireference issues. The chosen active space consisted of the carbene's σ and π frontier orbitals as well as two σ- and four π-orbitals in the case of the O₂ molecule totaling to an overall CASSCF(10e, 8o) treatment. We accounted for dynamic electron correlation by computing NEVPT2/cc-pVTZ single point energies on top of the optimized structures with ORCA 4.³⁶

In order to extend our studies of triplet oxygen addition reactions to other singlet carbenes, we additionally assessed the performance of some popular pure (PBE,⁴⁹ BLYP^50–52), hybrid (PBE0,^53,54 B3LPY,^55,56 M06-2X⁵⁷), and double hybrid density functionals (B2PLYP⁵⁸ and DSD-PBEP86⁵⁹) together with a def2-TZVPP Ahlrichs basis set.⁶⁰ Moreover, we tested the rather accurate CBS-QB3⁶¹ and G4⁶² composite energy schemes. All reported energies correspond to the summed electronic and zero-point vibrational energies, ΔH₀, unless stated otherwise.

Results and discussion

We started out by assessing the barrier height of the CCl₂ (X̃ ¹A₁) + O₂ (X̃³Σ⁻_g) reaction at various levels of theory, i.e., the reaction in an overall triplet state, which corresponds to the electronic ground state near the reactants; the obtained results are summarized in Table 1. In agreement with previously reported computations and the absence of an enthalpic barrier, we were unable to localize a transition state of the oxygen addition reaction at the PBE/6-311+G(d) level of theory.³¹ However, when employing the more modern def2-TZVPP basis set, we found the O₂ addition transition state ³TS_add which is isoenergetic to the starting materials. BLYP as another pure functional already predicts a barrier height associated with ³TS_add of 2.1 kcal mol⁻¹, while all employed hybrid density functionals find even higher values. The B3LYP barrier increases by 2.7 kcal mol⁻¹ with increasing the basis set size from 6-31G(d) to def2-TZVPP, while it decreases by 1.8 kcal mol⁻¹ upon adding the D3-dispersion correction.^63,64 A barrier height of approximately 10 kcal mol⁻¹ is obtained utilizing the M06-2X hybrid and the B2PLYP double hybrid functionals, whereas DSD-PBEP86 yields the highest encountered value of 11.6 kcal mol⁻¹. The composite energy schemes CBS-QB3 and G4, which are in principle capable of achieving chemically meaningful accuracy, produce barrier heights of 6.7 and 10.1 kcal mol⁻¹, respectively. Thus, we are left with a scatter in barrier heights ranging from zero to almost 12 kcal mol⁻¹ among the employed popular levels of theory! In addition, especially the pure density functionals produce earlier transition state geometries which becomes evident in a substantially elongated distance of the forming C–O bond, whereas all more advanced methods yield values near 2 Å (cf.Table 1). Therefore, in order to remedy this situation, we tended to authoritative coupled cluster computations as described in detail in the methods section.

Table 1 Energies (in kcal mol⁻¹) and optimized C–O distances (in Å) of the ¹CCl₂ + ³O₂ addition reaction's transition state at various levels of theory

Method	ΔH^‡0 (^3TSadd)	r C–O (^3TSadd)
a A transition state could not be localized. b From a focal-point analysis targeting the BD(TQ)/CBS//CCSD(T)/cc-pVTZ energy.
PBE/6-311+G(d)	—^a	—^a
PBE/def2-TZVPP	0.0	2.63
BLYP/def2-TZVPP	2.1	2.30
PBE0/def2-TZVPP	4.7	2.07
B3LYP/6-31G(d)	3.4	2.08
B3LYP/def2-TZVPP	6.1	2.06
B3LYP(SMD:n-pentane)/def2-TZVPP	5.7	2.06
B3LYP-D3/def2-TZVPP	4.3	2.05
M06-2X/def2-TZVPP	9.8	1.96
B2PLYP/def2-TZVPP	10.0	1.99
DSD-PBEP86/def2-TZVPP	11.6	1.96
CBS-QB3	6.7	2.02
G4	10.1	2.05
Best estimate^b	8.8	2.01

---

Employing the CCSD(T)/cc-pVTZ level of theory, we were able to optimize the oxygen addition transition state ³TS_add as depicted in the potential energy diagram in Fig. 1. The transition state corresponds to a sideways attack of the dioxygen molecule indicating that dichlorocarbene reacts as an electrophile via its vacant p-orbital. The 2.01 Å distance of the forming C–O bond is still rather long and the O–O bond distance has merely increased by less than 0.02 Å from its equilibrium value in the free O₂ molecule. The associated barrier height amounts to 8.8 kcal mol⁻¹ at the targeted BD(TQ)/CBS level of theory. As confirmed with the help of an IRC computation, the transition state is connected to the C₁-symmetric triplet Criegee intermediate ³CI_a. The previously reported bisected, C_s-symmetric triplet carbonyl oxide structure obtained with the PBE/6-311+G(d) model chemistry rather corresponds to a rotational transition state at the CCSD(T)/cc-pVTZ level although there is almost no energetic penalty associated due to the shallow C–O torsional potential.³¹ Triplet Criegee intermediate ³CI_a exhibits an increased O–O bond length of 1.34 Å, while the C–O bond assumes a distance of 1.40 Å. This initial oxidation reaction step is exothermic by 11.2 kcal mol⁻¹ at our highest level of theory.

Fig. 1 Potential energy diagram of the dichlorocarbene reaction with molecular oxygen at the estimated BD(TQ)/CBS//CCSD(T)/cc-pVTZ level of theory. The black and blue surfaces correspond to overall triplet and singlet electronic states, respectively.

Since we have a particular interest in the oxygen addition barrier height and its accuracy, we present the underlying focal-point analysis in Table 2. It can be seen that the Hartree-Fock energy is nearly converged with a triple-ζ basis set and amounts to 34.7 kcal mol⁻¹ in the CBS limit. From there, the sophistication of the electron correlation treatment is systematically increased over MP2 and CCSD to CCSD(T). The incremental changes when going to higher levels of theory are all negative and decrease in absolute magnitude in each respective row of the Table. Therefore, one might use the absolute value of the best incremental δ(T) correction of 3.7 kcal mol⁻¹ as a conservative error bar to the barrier height. However, the actual accuracy is probably much higher because the higher order correlation correction Δ_BD(TQ) equals to only −0.2 kcal mol⁻¹. Adding up all corrections, we obtain the final barrier height ΔH^‡₀(³TS_add) of 8.8 kcal mol⁻¹. Such a sizeable enthalpic barrier is clearly inconsistent with a non-activated, diffusion-controlled oxygen addition reaction of dichlorocarbene.³¹ We note that the effect of solvation is unlikely to reduce the barrier height substantially, because the B3LYP barrier decreases by merely 0.4 kcal mol⁻¹ when solvation in n-pentane is implicitly accounted for with the SMD model (Table 1).⁶⁵

Table 2 Focal-point analysis of the ¹CCl₂ + ³O₂ reaction barrier height in incremental notation given in units of kcal mol⁻¹

	ΔEe(HF)	+δ MP2	+δ CCSD	+δ(T)	NET
ΔH^‡0(^3TSadd) = ECCSD(T) + ΔBD(TQ) + Δcore + ΔZPVE = (8.2 – 0.2 − 0.1 + 0.9) kcal mol^−1 = 8.8 kcal mol^−1
cc-pVDZ	+32.9	−13.5	−6.1	−2.3	11.0
cc-pVTZ	+34.4	−16.8	−4.5	−3.1	9.9
cc-pVQZ	+34.6	−17.8	−4.2	−3.4	9.1
cc-pV5Z	+34.6	−18.3	−4.2	−3.6	8.7
CBS limit	[+34.7]	[−18.7]	[−4.2]	[−3.7]	[8.2]

---

The triplet Criegee intermediate formed after traversal of transition state ³TS_add can exist in the form of two rotational isomers, ³CI_a and ³CI_b, the latter being more stable by 1.8 kcal mol⁻¹ (Fig. 1). The two conformers can be interconverted via a C–O bond rotation passing through transition state ³TS_rot with a barrier of 3.4 kcal mol⁻¹. Alternatively, the isomerization can proceed more easily through inversion of the pyramidalized radical center on the carbon atom that comes with an energetic penalty of only 0.7 kcal mol⁻¹. The IRC connects the inversion transition state ³TS_inv with the bisected triplet carbonyl oxide that was identified as a transition state earlier. Hence, there must be a bifurcation in the reaction path after ³TS_inv in the form of a valley-ridge inflection point leading to two possible enantiomeric forms of ³CI_a. Generally speaking, the triplet carbonyl oxide is rather fluxional and conformational interconversions can proceed easily.

Once formed, the triplet Criegee intermediate ³CI can relax to its singlet ground state via efficient intersystem crossing, which has previously been described in detail³¹ and is not further assessed in this work. The resulting singlet Criegee intermediate ¹CI is 37.7 kcal mol⁻¹ more stable than the starting materials and sufficiently protected from cyclization to the isomeric dioxirane by a barrier of 17.5 kcal mol⁻¹ (Fig. 1). Since it is well known that triplet Criegee intermediates exhibit low barriers towards O–O bond scission,^66,67 we reckoned that this transformation might present a viable alternative reaction outcome. We remark that this thermal reaction is different from the frequently encountered photochemical dioxygen bond breaking event in carbonyl oxides.^68–70 As expected, the attendant transition state ³TS_O–O is only 1.8 kcal mol⁻¹ higher in energy than the structurally similar triplet carbonyl oxide conformer ³CI_b and isoenergetic to the initially formed conformer ³CI_a. The bond breaking reaction is exothermic by 34.9 kcal mol⁻¹ and leads to formation of phosgene and a ground state oxygen atom O (³P). Since this low-barrier reaction is also spin-conserving, it seems likely that the oxidation of dichlorocarbene mostly leads to a splitting of molecular oxygen. In this regard, it is tempting to reassign the unknown oxidant in the manganese-catalyzed epoxidation reactions^28,29 described in the introduction to atomic oxygen in case it indeed stems from dichlorocarbene.⁷¹

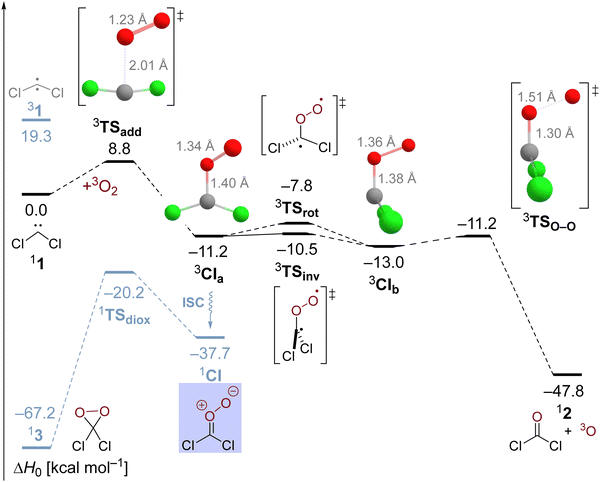
Nonetheless, the oxygen addition reaction of CCl₂ faces a considerable enthalpic barrier, which we would like to reassure once more in an alternative multireference description of the reaction. This might seem warranted because the T₁ diagnostic assumes a value of 0.048 in transition state ³TS_add indicating a slightly enhanced multireference character. Therefore, we deployed NEVPT2//CASSCF/cc-pVTZ computations and obtained the results depicted in the potential energy diagram in Fig. 2. Although the carbene's singlet–triplet gap is predicted too low at 15.2 kcal mol⁻¹, the oxygen addition reaction barrier of 7.6 and the exothermicity of 11.8 kcal mol⁻¹ are in excellent agreement with our high-level single-reference treatment supporting the reliability of the reported results. Selected natural orbitals of the employed active space are depicted in the lower inset in Fig. 2 and their respective occupation numbers suggest that the C–O bond formation is already markedly advanced in ³TS_add with emerging radical centers on the former carbenic carbon atom and the dioxygen unit. Therefore, the transition state appears to be rather late with regards to the electronic structure despite the relatively long C–O distance of 2.11 Å in the optimized CASSCF structure. The associated electronic reorganization during the reaction might be a reason for the presence of a non-negligible enthalpic barrier in the reaction of interest.

Fig. 2 Potential energy diagram of the dichlorocarbene/O₂ reaction in overall singlet (blue) and triplet states (black) at the NEVPT2//CASSCF(10e, 8o)/cc-pVTZ level of theory. The insets show selected natural orbitals of the active space and their respective occupation numbers.

Utilization of CASSCF theory also made it possible to study the oxygen addition reaction in an overall singlet state. The corresponding transition state ¹TS_add can be optimized at the CASSCF level of theory and exhibits a wide 125° Cl–C–Cl angle comparable to the triplet carbene. However, the barrier gets submerged upon inclusion of dynamic electron correlation with NEVPT2 and the relative energy of ¹TS_add with regards to the ground state reactants amounts to 12.5 kcal mol⁻¹ which is significantly higher than the triplet state activation energy. The wave function of the transition state is rather complex with five configurations exhibiting weights exceeding five percent. Selected natural orbitals of the employed active space in the upper blue inset in Fig. 2 suggest that σ- and π-bonds form simultaneously in the emerging Criegee intermediate albeit to a different extent. Most interestingly, the transition state structure ¹TS_add is not perfectly planar and an IRC computation reveals that the trajectory of the O₂ attack is also sideways in the singlet state indicating an initial interaction with the unpaired π-electron of the carbene.

The sideways approach in the triplet transition state ³TS_add discussed earlier suggests that dichlorocarbene acts as an electrophile in its reaction with ³O₂. While this is in good agreement with the previously observed enhanced reactivity of highly electrophilic singlet carbenes,^25,26 nucleophilic N-heterocyclic carbenes (NHCs) were also reported to yield monoxidation products in their reaction with triplet molecular oxygen.⁷² Thus, it seems worthwhile to study the impact of substitution on the ³O₂ addition reaction in order to develop an understanding which singlet carbenes can undergo facile oxidation reactions. We studied a set of 16 standard singlet carbenes spanning a broad range of Moss’ philicity scale and computed the triplet oxygen addition barriers and singlet–triplet gaps with the G4 method.⁷³ Although the employed theoretical model overestimated the barrier by 1.3 kcal mol⁻¹ in the case of dichlorocarbene (cf.Table 1), we deem the method more robust than other options and expect comparable errors across the studied cases. The obtained results are presented in Table 3 and Fig. 3.

Table 3 Singlet–triplet gaps and ³O₂ addition barriers of various carbenes CXY at the G4 level of theory in kcal mol⁻¹. The energies are given in reference to the carbene's philicity index m_CXY

Species	m CXY	E S–T	ΔH^‡0 (^3TSadd)
a 1,3-dimethylimidazolin-2-ylidene. b 1,3-dimethylimidazol-2-ylidene.
Cl–C–Me	0.58	10.6	3.3
Ph–C–Br	0.64	6.5	3.9
Ph–C–Cl	0.72	7.6	4.2
Br–C–Br	0.82	16.6	8.6
Cl–C–SMe	0.91	25.9	13.0
Ph–C–F	0.96	16.8	6.1
Cl–C–Cl	0.97	20.6	10.1
Cl–C–F	1.22	35.4	13.7
F–C–F	1.47	56.2	19.5
Cl–C–OMe	1.59	40.5	15.6
F–C–OMe	1.85	56.9	19.4
MeO–C–OMe	2.22	57.2	17.4
MeO–C–NMe2	2.91	57.4	15.6
Me2N–C–NMe2	3.60	44.5	10.6
SIMe2^a	—	71.5	16.9
IMe2^b	—	86.9	23.0

---

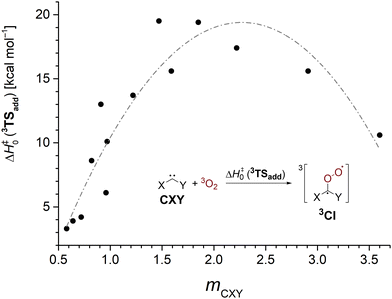Fig. 3 ³O₂ addition barriers to various carbenes CXY at the G4 level as a function of the carbene's philicity index m_CXY. The gray line is guiding the eye.

We find that carbenes with narrower singlet–triplet gaps often show an enhanced reactivity towards the addition of triplet molecular oxygen. However, there is no strong correlation and other factors governing carbenic reactivity must play a role, too (Fig. S23, ESI†). The dependence of the barrier on the philicity index plotted in Fig. 3 shows that more electrophilic carbenes indeed exhibit a higher oxygen addition reactivity. The oxidation of the electrophilic phenylchlorocarbene, Ph–C–Cl, to its corresponding Criegee intermediate has been reported to proceed within several hours at 38 K in oxygen doped argon matrices.⁷⁴ Assuming a comparable overestimation of the barrier height by the G4 method brings the computed value of 4.2 kcal mol⁻¹ into reasonable agreement with the experiment. Going to higher selectivity, ambiphilic carbenes with a philicity index m_CXY in the range of 1.5–2.2 are most reluctant to undergo oxygen addition reactions. Curiously, even more selective nucleophilic carbenes again show a decrease in barrier height indicated by the gray line in Fig. 3 which is supposed to guide the eye. We conclude that carbenes behave as ambiphiles towards molecular oxygen and electron density can be transferred both ways from the carbene to O₂ and vice versa.⁷² Hence, more electrophilic and more nucleophilic carbenes display an increased oxidation reactivity. Yet, the effect is more pronounced for electrophiles.

Conclusions and outlook

In summary, we have firmly established the presence of a considerable enthalpic barrier in the reaction of dichlorocarbene and molecular oxygen in their respective ground states by means of rigorous single- and multireference theory. According to our best estimate, the barrier height ΔH^‡₀(³TS_add) amounts to 8.8 kcal mol⁻¹. We must conclude that this result is inconsistent with the diffusion-controlled formation of a Criegee intermediate from dichlorocarbene on a nanosecond timescale.³¹ Instead, the observed 465 nm transient absorption in the LFP experiment under ambient air must come from the reaction of dichlorocarbene or its diazirine precursor in a (photo)excited state.

The triplet Criegee intermediate ³CI, that is initially formed during the ¹CCl₂ + ³O₂ reaction, can undergo a facile O–O bond breaking reaction with almost no barrier in addition to the spin-state change to its respective singlet ground state Criegee intermediate. The products of this competing reaction pathway are phosgene and triplet oxygen atom. It will present a formidable challenge to provide firm experimental evidence⁷¹ for the occurrence of this reaction step in the future. Since singlet carbenes show ambiphilic reactivity towards ³O₂, it is likely that not only more electrophilic carbenes than phenylchlorocarbene⁷⁴ will provide access to Criegee intermediates under matrix isolation conditions, but also highly nucleophilic carbenes can lead to oxidation products when exposed to molecular oxygen.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to acknowledge the generous support of this work in the form of a Liebig Fellowship provided by the Fonds der Chemischen Industrie. We are also grateful to the state of Baden-Württemberg (bwHPC) and the German Research Foundation DFG (INST 40/467-1 FUGG) for the allocation of computer time on the BwForCluster JUSTUS 2. In addition, we are obligated to Prof. Holger Bettinger for his continuous support and thank Prof. Mike Duncan for helpful discussions.

References

1. R. A. Moss, J. Org. Chem., 2010, 75, 5773–5783.
2. A. Geuther, Liebigs Ann. Chem., 1862, 123, 121–122.
3. J. Hine, J. Am. Chem. Soc., 1950, 72, 2438–2445.
4. W. von E. Doering and A. K. Hoffmann, J. Am. Chem. Soc., 1954, 76, 6162–6165.
5. W. von E. Doering and W. A. Henderson, J. Am. Chem. Soc., 1958, 80, 5274–5277.
6. R. A. Moss, C. B. Mallon and C.-T. Ho, J. Am. Chem. Soc., 1977, 99, 4105–4110.
7. R. A. Moss, Acc. Chem. Res., 1980, 13, 58–64.
8. L. D. Wescott and P. S. Skell, J. Am. Chem. Soc., 1965, 87, 1721–1724.
9. S. W. Wren, K. M. Vogelhuber, K. M. Ervin and W. C. Lineberger, Phys. Chem. Chem. Phys., 2009, 11, 4745–4753.
10. R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018.
11. R. L. Schwartz, G. E. Davico, T. M. Ramond and W. C. Lineberger, J. Phys. Chem. A, 1999, 103, 8213–8221.
12. E. A. Carter and W. A. Goddard III, J. Chem. Phys., 1988, 88, 1752–1763.
13. E. P. F. Lee, J. M. Dyke and T. G. Wright, Chem. Phys. Lett., 2000, 326, 143–150.
14. C. J. Barden and H. F. Schaefer III, J. Chem. Phys., 2000, 112, 6515–6516.
15. G. Tarczay, T. A. Miller, G. Czakó and A. G. Császár, Phys. Chem. Chem. Phys., 2005, 7, 2881–2893.
16. W. Sander, Angew. Chem., Int. Ed. Engl., 1990, 29, 344–354.
17. W. W. Sander, A. Patyk and G. Bucher, J. Mol. Struct., 1990, 222, 21–31.
18. W. H. Bunnelle, Chem. Rev., 1991, 91, 335–362.
19. W. Sander, G. Bucher and S. Wierlacher, Chem. Rev., 1993, 93, 1583–1621.
20. S. E. Condon, C. Buron, E. M. Tippmann, C. Tinner and M. S. Platz, Org. Lett., 2004, 6, 815–818.
21. M. T. H. Liu, R. Bonneau and C. W. Jefford, J. Chem. Soc., Chem. Commun., 1990, 1482–1483.
22. T. Makihara, T. Nojima, K. Ishiguro and Y. Sawaki, Tetrahedron Lett., 2003, 44, 865–868.
23. R. Bonneau, B. Hellrung, M. T. H. Liu and J. Wirz, J. Photochem. Photobiol., A, 1998, 116, 9–19.
24. C. Kötting, W. Sander, M. Senzlober and H. Bürger, Chem. – Eur. J., 1998, 4, 1611–1615.
25. W. Sander, C. Kötting and R. Hübert, J. Phys. Org. Chem., 2000, 13, 561–568.
26. J. P. Wagner, J. Am. Chem. Soc., 2022, 144, 5937–5944.
27. G. Maier and J. Endres, Chem. – Eur. J., 1999, 5, 1590–1597.
28. J. T. Groves and M. K. Stern, J. Am. Chem. Soc., 1988, 110, 8628–8638.
29. N. H. Lee, J. S. Baik and S.-B. Han, Bull. Korean Chem. Soc., 1997, 18, 796–798.
30. G. Chu, R. A. Moss and R. R. Sauers, J. Am. Chem. Soc., 2005, 127, 14206–14207.
31. R. A. Moss, J. Tian, R. R. Sauers, D. H. Ess, K. N. Houk and K. Krogh-Jespersen, J. Am. Chem. Soc., 2007, 129, 5167–5174.
32. J. J. Tiee, F. B. Wampler and W. W. Rice, Chem. Phys. Lett., 1980, 73, 519–521.
33. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
34. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
35. R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352.
36. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
37. A. G. Császár, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 1998, 108, 9751–9764.
38. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
39. D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358–1371.
40. D. Feller, J. Chem. Phys., 1993, 98, 7059–7071.
41. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
42. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
43. D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1995, 103, 4572–4585.
44. K. A. Peterson and T. H. Dunning Jr., J. Chem. Phys., 2002, 117, 10548–10560.
45. K. Raghavachari, J. A. Pople, E. S. Replogle and M. Head-Gordon, J. Phys. Chem., 1990, 94, 5579–5586.
46. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207.
47. C. J. Cramer, J. Am. Chem. Soc., 1998, 120, 6261–6269.
48. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
50. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
51. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
52. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
53. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
54. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
55. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
56. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
57. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
58. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
59. S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107.
60. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
61. J. A. Montgomery Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542.
62. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108.
63. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
64. The B3LYP/6-31G(d) pure electronic barrier is identical to the previously reported value in reference 31.
65. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
66. J. M. Anglada and J. M. Bofill, J. Org. Chem., 1997, 62, 2720–2726.
67. B. Z. Chen, J. M. Anglada, M. B. Huang and F. Kong, J. Phys. Chem. A, 2002, 106, 1877–1884.
68. J. M. Beames, F. Liu, L. Lu and M. I. Lester, J. Am. Chem. Soc., 2012, 134, 20045–20048.
69. V. J. Esposito, O. Werba, S. A. Bush, B. Marchetti and T. N. V. Karsili, Photochem. Photobiol., 2022, 98, 763–772.
70. B. Lu, Y.-y. Qin, C. Song, W.-y. Qian, L.-n. Wang and X.-q. Zeng, Chin. J. Chem. Phys., 2020, 33, 151–159.
71. S. M. Omlid, S. A. Dergunov, A. Isor, K. L. Sulkowski, J. T. Petroff, E. Pinkhassik and R. D. McCulla, Chem. Commun., 2019, 55, 1706–1709.
72. J. Tang, X. J. Gao, H. Tang and X. Zeng, Chem. Commun., 2019, 55, 1584–1587.
73. R. A. Moss and K. Krogh-Jespersen, Tetrahedron Lett., 2013, 54, 4303–4305.
74. G. A. Ganzer, R. S. Sheridan and M. T. H. Liu, J. Am. Chem. Soc., 1986, 108, 1517–1520.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03889g

---