Ultrafast photoinduced dynamics in Prussian blue analogues

Abstract

New magnetic materials and methods for controlling them are needed to improve data storage technologies. Recent progress has enabled optical detection and manipulation of spins in molecule-based magnets on the femtosecond timescale, which is promising for both increasing the read/write speed but also the data storage density. Experimental developments in femtosecond X-ray free-electron lasers (XFELs) and magneto-optics, in combination with theory advances, have opened up several new avenues to investigate molecule-based magnets. This review discusses the literature concerning ultrafast photoinduced dynamics in Prussian blue analogues (PBAs), which are molecule-based magnets. In PBAs spin–flips and lattice distortions can happen on the 100 fs timescale, which in some analogues lead to photoinduced changes in the long-range magnetic order. The literature and themes covered in this review are of relevance for ultrafast optical control of new multifunctional materials.

---

Kyle Barlow

Kyle completed his undergraduate degree in Chemical Physics at the University of Edinburgh in 2020. In his final-year project in the Johansson group, he studied ultrafast dynamics in Prussian blue analogues. Kyle is now working on the ultrafast dynamics in transition metal complexes particularly looking at single molecule magnets.

J. Olof Johansson

Olof Johansson is a lecturer in the School of Chemistry at the University of Edinburgh and is interested in ultrafast inorganic photophysics. Prior to this, he held a Royal Society of Edinburgh/BP Trust Research Fellowship (2014–2019). He received his MSc in Physics from Gothenburg University in 2007 and PhD in Chemistry from the University of Edinburgh in 2011. He was awarded the Fraser and Norma Stoddart PhD Prize in 2013 from the University of Edinburgh. In 2016 Olof became a member of the RSE Young Academy of Scotland.

---

1 Introduction

In data storage devices, information is recorded by manipulating magnetically ordered materials. Given the growing demand for faster and more efficient processing of large data sets in modern society, new materials and methods are being developed to improve the speed of the write process. In particular, the use of femtosecond (fs) laser pulses to control spins in magnetically ordered materials would allow for very fast data processing.

The problem of how fast light can change the spin state of molecules has been discussed during the last 25 years,^1–3 enabled by the development of fs lasers. In particular, inorganic complexes have been extensively studied and it is now well-known that intersystem crossing (ISC), i.e. a change in electronic state with different spin multiplicity, can happen on the order of 100 fs in [Ru(bpy)₃]²⁺ (ref. 1 and 4) and Cr(acac)₃ (ref. 5). One of the most studied systems are Fe(II) complexes. It has been shown that it is possible to change the spin quantum number from S = 0 to S = 2 in ca. 100 fs by absorbing just one photon via the metal-to-ligand charge-transfer (MLCT) transition.^6–10 This leads to a fast depopulation of the MLCT state into the ligand manifold (or metal-centred states) with different spin quantum numbers. A lot of the recent understanding of the very fast spin changes in inorganic complexes comes from the development of new techniques, such as X-ray free-electron lasers (XFELs)^8,9,11–16 (see a recent review by Chergui and Collet¹⁷), table-top X-ray sources,^18,19 and ultrafast electron diffraction.^20,21 Furthermore, developments in computational methods have been essential.^22–29 These advances have enabled chemical control of the lifetime of the excited states.^11,30 Similarly, it was recently shown that wavepackets can be controlled via synthetic design to both slow down the ISC rate to stabilise the MLCT state in Fe(II) complexes³¹ and to change the anisotropy in Mn-based single-molecule magnets.³² These advances open up possibilities to control the spin and structural evolution in the excited state of paramagnetic metal complexes. Moving towards larger systems, solvated [2×2] Fe(II) metallogrid complexes were recently studied using optical and infrared absorption spectroscopy, and X-ray emission spectroscopy.³³ In the condensed phase, sub-ps ISC has also been demonstrated in molecular crystals of Fe(III)^12,34,35 and Fe(II).^14,36 This work has led to some very exciting results, for example, that the cooperative effects of spin-crossover (SCO) in crystals and nanoparticles can lead to the possibility to control and stabilise ultrafast photoinduced phase transitions.^37–39

Spins in semiconductors can be controlled on ultrafast timescales by exciting spin-polarised carriers using circularly polarised light and where the sign of the spin polarisation depends on the helicity of the pump pulse.⁴⁰ This is detected using magneto-optical polarisation techniques, such as Faraday rotation, which are sensitive to the magnetisation of the sample and provide fs time resolution which is not possible with other techniques such as electron paramagnetic resonance. There have been several exciting breakthroughs such as the observation of coherent transfer of spin polarisation from photocarriers to localised magnetic moments on Mn²⁺ ions in magnetic heterostructures⁴¹ and even between molecularly bridged quantum dots.⁴² The field has now moved on to controlling spins of impurities in, for example diamond and silicon to create new quantum technologies.⁴³

There has also been an impressive development of ultrafast control of materials with long-range magnetic order.^44–46 This interest was initiated by the surprising discovery that fs laser pulses could affect long-range magnetic order on the 100 fs timescale by Beaurepaire et al.⁴⁷ Long-range magnetic order is key for data storage applications, because the non-volatility means that the information is stored after the laser pulse, in contrast to the work on semiconductors mentioned above. It is now possible to completely reverse the magnetisation direction using a single fs laser pulse in thin films of some metallic,⁴⁴ and, more recently, dielectric^48–50 materials. Interestingly, the magnetisation is observed to be quenched on timescales faster than the spin–phonon relaxation time, which raised the question about the conservation of angular momentum if the phonons are not engaged in the first 100 fs (spin is, of course, a form of angular momentum).^51–55 However, recently it has been shown that strain waves in magnetic Fe films can be launched on similarly fast timescales and which accommodate the conservation of angular momentum.⁵⁶ These findings highlight the complicated interaction between spins, electrons, nuclear motion, and photons. It is an important problem since fast switching of the magnetisation is needed for recording data, and the processes in hard drives are limited to the nanosecond (ns) timescale. New experimental approaches, with fs temporal resolution, are also being pursued in this field, such as XFELs,^56–60 X-ray magnetic circular dichroism (XMCD),^61,62 and spin-resolved photoemission.^63,64

Somewhere in between the detailed understanding at the molecular level and the complex multi-dimensional interactions in a magnetic solid, lies molecule-based materials. These are made from molecular building blocks and, by using the right linker, it is possible to form long-range magnetic order.⁶⁵ They open up possibilities to explore how ISC at the local scale can influence long-range magnetic order, as has been shown for the cyano-bridged Fe₂[Nb(CN)₈]·(4-pyridinealdoxime)₈·2H₂O (although not on the ultrafast timescale).⁶⁶ The approach using molecular building blocks also have the advantage of chemical flexibility, which could be used to tune and optimise materials showing, for example, photomagnetic properties.⁶⁷ Now is the time to explore these materials because of the recent developments in ultrafast experimental and computational methods mentioned above.

In this review, we discuss ultrafast dynamics taking place in molecule-based magnets of Prussian blue (PB) and its analogues.⁶⁸ Prussian blue analogues (PBAs) are cyanometalate coordination polymers and have a face-centred cubic structure with general formula M_xA_y[B(CN)₆]_z·nH₂O where M is an alkali metal and A and B are transition metal (TM) ions (Fig. 1).⁶⁸ The mixed-valence TM ions are bonded via negatively charged cyanide bridges. The B ion is coordinated to six carbon atoms and has a low spin configuration because of the large ligand-field strength in the carbon pocket. The A ion is coordinated to 6 nitrogen atoms and is either high- or low spin due to the weaker ligand-field strength in the nitrogen pocket. Of course, depending on the stoichiometry, the TM can have less than 6 neighbours and be coordinated with water. One typically encounters a 1 : 1 (x = 1) or 3 : 2 ratio (x = 0) of A and B. It is the mixed valency and superexchange interaction through the cyanide bridge that is the source of magnetic ordering in PBAs. The advantages of PBAs include room-temperature magnetic ordering (although limited to the V–Cr PBA),^69,70 tuneability of magnetic^71–74 and optical properties,^75–78 as well as multifunctional properties such as photomagnetism^79–81 and electrochromism.^82–84 There is an on-going effort into developing the quality of PBAs, as was recently reviewed.^85,86 It is also possible to form thin films^{83,84,87–93} and even heterostructures of these materials.^94–96 Magnetic heterostructures are actively explored in the ultrafast magnetism community to create fs spin-polarised currents.⁹⁷ There are already several excellent reviews on PBAs.^{67,70,77,98–100} We also note a wealth of other cyano-bridged materials with very exciting photomagnetic properties.^67,101

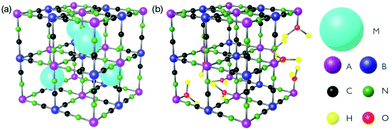Fig. 1 The general structure of PBAs with (a) 1 : 1 and (b) 3 : 2 stoichiometry of A and B. M is a cation and A and B are transition metal ions.

The primary photophysical processes in molecular materials happen on the fs timescale, and so we have attempted to collate studies concerning ultrafast dynamics in PBAs (occurring on the fs/ps timescales). For these timescales, the most used method is transient absorption (TA). This is a pump–probe technique whereby a laser pulse excites the sample and a second, delayed, laser pulse probes the photoexcited sample. The probe pulse can be quasi-monochromatic or consist of a broadband continuum spanning typically from 350–700 nm. IR probes are also possible, as has been explored for some PBAs taking advantage of the strong asymmetric cyanide stretch.¹⁰² In the data, one typically plots either the spectra of the excited species for different time delays or sometimes the decay kinetics of the signal at a particular wavelength/spectral feature. In the TA spectra, one typically observes excited-state absorption (ESA), that is absorption from the excited electronic state, or ground-state bleach (GSB), which is loss of absorbing chromophores in the ground state and results in more light reaching the detector. The GSB typically mirrors the static absorption spectrum. It is also possible to observe stimulated emission, which has the same sign as GSB in the TA spectrum because more light reaches the detector than for an un-pumped sample.

We start by giving a general introduction to the optical properties of cyano-bridged dimers, which are the building-blocks of PBAs and briefly mention work that has been done on ultrafast dynamics in these. We will then build the complexity and move on to cover the optical properties of PBAs and studies of ultrafast dynamics. We cover literature concerning the Fe–Fe, Co–Fe, Mn–Fe, and V–Cr PBAs.

A key picture that emerges is that the dynamics after photoexcitation often results in either fast back-electron transfer (BET) or trapped charge-transfer (CT) states after CT excitation. In either case, fast excitation of the cyanide stretch modes and other vibrational modes occurs. If the population of metal-centred antibonding e_g orbitals is changed, typically long-range structural distortions take place. This is to some extent determined by the ability of the solid to accommodate the changes to bond lengths after e_g population dynamics, highlighting the importance of electron–phonon coupling.

2 Cyano-bridged dimers

Cyano-bridged dimers of the type A–NC–B, where A and B are TM ions, are the building blocks of PBAs. It is therefore interesting to first survey work that has been done of these model systems. The electronic structure of mixed-valence cyanide-bridged dimers is typically classified as Class II (Robin and Day), just like PBAs.¹⁰³ In the molecules of interest, the sites are chemically different – either they are in different oxidation states or they comprise different elements. Class II implies that the 3d-electrons are not fully localised on one metal ion but some degree of delocalisation via the cyanide bridge between the two metal ions occurs. For Prussian blue, the ground state wavefunction (fully localised on one metal ion) has a ca. 1% contribution from the wavefunction corresponding to the electron localised on the other metal ion.¹⁰³ In dimers, the strongest optical transition in the visible is typically the metal-to-metal charge-transfer (MMCT) transition, which corresponds to transferring an electron from one site to another. The oscillator strength of the transition is proportional to the delocalisation between the two ions, which in turn depends on the bond length, and mixing and energy difference between the fully localised state and the transferred-electron-state.^103,104

One early study was on [(NH₃)₅Ru^III–NC–Ru^II(CN)₅]⁻ (RuRu) and [(NH₃)₅Ru^III–NC–Fe^II(CN)₅]⁻ (RuFe), where the MMCT was excited at 795 nm.¹⁰⁵ The MMCT leads to an intramolecular electron transfer, producing Ru^II in the ammonia pocket and Ru^III in the cyanide pocket (and similarly for RuFe). It was observed that back-electron-transfer (BET) occurred on 85 ± 10 fs in H₂O and 122 ± 20 fs in D₂O for both complexes. The electronic dephasing time was shorter than the instrumental temporal resolution of 20 fs. The authors observed oscillations superimposed on the decay kinetics, with frequencies corresponding to 170, 270, and 488 cm⁻¹. These modes were assigned as solvent librational degrees of freedom that are coupled to the CT process. They also observed that some degree of vibrational coherence is maintained even during the BET, with a dephasing time on the order of 300 fs (i.e. longer than the 100 fs BET). This is indicative that energy is deposited into the CN⁻ stretch modes. The energy was found to be dissipated to the solvent with a time constant of 880 ± 160 fs for RuRu in H₂O, although this time constant depends on the excitation energy since excess energy led to longer decay times (pumping at the red or blue edge of the MMCT). Several other studies have now established that the electron transfer associated with the MMCT transition in dimers is strongly coupled to the solvent and the nuclear degrees of freedom of the molecule,^106–108 which has also been confirmed by time-resolved IR studies.^109,110 Moving to extended chains, Su et al. have studied Ru^II–CN–Ru^III,III₂–CN–Ru^II,¹¹¹ who found that the lifetime of the CT state could be controlled by chemical tuning of substituent group of the metal ions. Khalil's group have studied (NC)₅Fe^II–CN–Pt^IV(NH₃)₄–NC–Fe^II(CN)₅ complexes using advanced time-resolved spectroscopies.^110,112,113 They found that intramolecular vibrational relaxation dynamics happens on the ps timescale and that the dynamics of the vibrational relaxation depends on the spatial localisation of the vibrational mode and how it couples to the solvent.¹¹⁰

Macpherson et al. have studied dimers of cyano-bridged [LCo^III–NC–Fe^II(CN)₅]⁻, where L is a pentadentate macrocyclic pentaamine or triamine-dithiaether.¹¹⁴ This dimer is an important model system for photomagnetic PBAs, since the Co–Fe PBA can be optically excited from a paramagnet to ferrimagnet,^79,115 as will be discussed below. In this process, MMCT from Fe^II to Co^III (low-spin, LS) leads to a fast reorganisation of the spin state on the Co^II site via ISC and forms Co^IIFe^III in the high-spin (HS) state. After exciting the MMCT, Macpherson et al. observed ESA below 400 nm in the dimers assigned to metal-centred transitions from Fe^III, which gives a spectral signature of the CT state. Using a combination of ns and fs TA, and at 11 and 293 K, they concluded that the LS Co^II CT state undergoes fast BET on a ps timescale, whereas the HS Co^II state lived for a longer time at low temperatures (ca. 10 ns). Recently Zimara et al. showed using both TA and time-resolved IR that in a Co^IIFe^III dimer, where Co^II is HS and Fe^III LS, photoexcitation of the MMCT band leads to a short-lived CT state (3.8 ps), followed by vibrational cooling in the hot electronic ground state.¹¹⁶ Interestingly, they also studied the square-type complex Fe₂Co₂ in both [(Co^III_LS)₂(Fe^II_LS)₂] and [(Co^II_HS)₂(Fe^III_LS)₂] states (Fig. 2). After excitation at around 800 nm, they observed a TA spectrum that did not match perfectly with the difference between the steady-state spectra of the two phases, which would have indicated a complete conversion to the HT phase. Instead, they could conclude that a one-electron transfer takes place on one of the Co–Fe pairs by comparing to calculations. They conclude that a spin-crossover to a metastable tetranuclear [Co^III_LSFe^II_LSCo^II_HSFe^III_LS] product takes place in 400 fs, which has a lifetime of over 1 ns at −30 °C. The time-resolved IR spectra in Fig. 2(b) also confirm this assignment as the intermediate peaks do not correspond to the HT phase static spectrum. We will return to the Co–Fe PBA later on in the review.

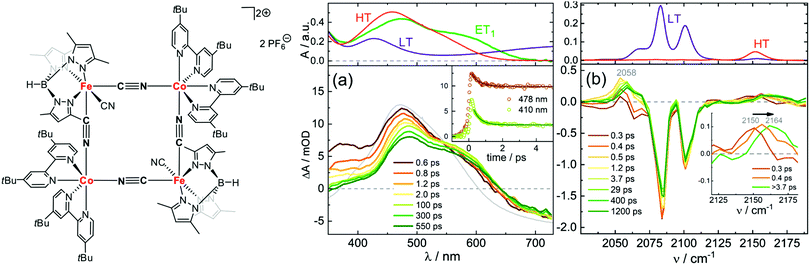Fig. 2 Structure of [(Co^III_LS)₂(Fe^II_LS)₂] together with transient absorption data in acetonitrile at −30 °C with (a) UV-visible probe and 775 nm pump wavelength and (b) IR probe and 800 nm pump. The top panels show the static absorption spectra in the LT (−30 °C) and HT (30 °C) phases. The green line (ET1) corresponds to the calculated spectrum of the one-electron transfer product [Co^III_LSFe^II_LSCo^II_HSFe^III_LS]. The bottom panels show the time-resolved spectra at selected time delays. The grey line shows the difference between the HT and LT static spectra. Reprinted with permission from Zimara et al. Inorganic Chemistry, 2021, 60, 449–459.¹¹⁶ Copyright 2021 American Chemical Society.

3 Prussian blue and its analogues

PBAs are also Class II delocalised mixed-valence compounds. The delocalisation leads to magnetic ordering via the superexchange interaction but also intense colours via MMCT transitions (which also depend on the delocalisation). Examples of colourful PBAs are Fe–Fe PB (which of course has been used as a pigment for centuries),¹¹⁷ V–Cr,^69,76 and Fe–Cr.⁷⁵ However, because of lower symmetry in the solid (vacancy sites), or simply a larger number of chromophores, other transitions compete, and it is possible to also observe d–d transitions. This makes the assignment of the optical transitions more complicated, as in the case of Cr–Cr^75,90,93,118 and Co–Fe^119–121 PBAs.

3.1 Fe–Fe PB

The ultrafast dynamics of the Prussian blue Fe₄^III[Fe^II(CN)₆]₃ (PB) was first investigated in 1995 by Arnett et al.¹²² Although the “original” PB discussed in this section is only ferromagnetic below 5 K due to the diamagnetic Fe^II ion, the early charge dynamics still lend important insight to other PBAs. Using polarisation dependent pump–probe studies, Arnett et al. investigated the optical excitation, electronic dephasing and vibrational coherences within colloidal Prussian blue particles suspended in water. The 800 nm pump excited the MMCT (Fe^II to Fe^III) band and the probe beam, of same wavelength, measured the change of transmittance through the particles at different time delays using light with parallel or perpendicular polarisation directions with respect to the pump beam polarisation direction. This type of anisotropy measurement can give information if the excited state is localised or delocalised.^123–125 The faith of the excited state within the first 50 fs can be seen from a fast decay in transmittance in the parallel probe and an increase in the transmittance of the perpendicular probe (Fig. 3). Both these signals were attributed to ground state bleach (GSB) of the MMCT band. Calculating the polarisation anisotropy of the time-resolved absorption gave a decay constant of 15 fs of the anisotropy. During optical excitation, the electron density is transferred from the Fe^II ion, with electron configuration t_2g⁶e_g⁰, to only one of the six surrounding Fe^III (t_2g³e_g²) ions in which the transition dipole moment of the MMCT is aligned with the polarisation of the pump laser. Therefore, the immediate peak in the parallel probe transmittance is due to GSB of the MMCT. No change in signal was recorded in the perpendicular probe in the very early time delays (Fig. 3a), as there is no change in the number of dipole-allowed transitions in this direction. Wavelength dependent studies were also carried out and showed a red-shift in the stimulated emission peak supporting that the 15 fs time constant is due to the rapid decay of the excited state.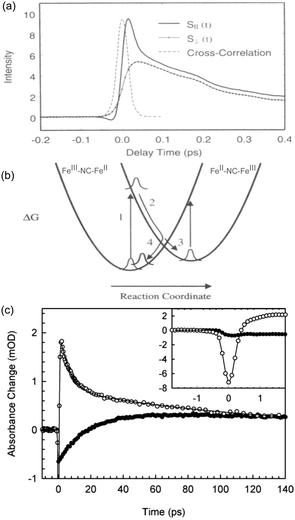

Fig. 3 Ultrafast dynamics in Fe–Fe PB. (a) The early 50 fs dynamics in the polarisation dependent transient transmission of FeFe PB shows a difference between the parallel (S_‖) and perpendicular (S_⊥) signals. (b) Model developed by Arnett et al. showing how either the excited CT state (2) can decay back to the groundstate (4 → 1) or how a long-lived CT state (3) could be formed. (a) and (b) are reprinted with permission from Arnett et al. J. Am. Chem. Soc., 1995, 117, 12262–12272.¹²² Copyright 1995 American Chemical Society. (c) In an experiment by Weidiner et al., ESA probed at 800 nm was identified after pumping at both 800 nm (open circles) and IR pulses resonant with the CN stretch mode (solid circles). After an initial bleach signal, the IR-pumped signal shows an ESA (positive signal). Figure reprinted from Weidiner et al. J. Chem. Phys., 2011, 134, 124510,¹²⁷ with the permission of AIP Publishing.

In the following 50 fs, the electron density spreads out between the remaining five Fe^III (t_2g³e_g²) ions, which now have a slight t_2g⁴e_g²-character. This delocalisation leads to a more isotropic charge distribution. There is a pronounced decrease in the transmittance in the parallel probe beam due to further absorption at the MMCT band (less GSB) that has a transition dipole moment aligned with the beam and an increase in transmission in the perpendicular probe beam (more GSB). This indicates that in the 50 fs timeframe after photoexcitation, the electron is no longer localised on a single ion and is delocalised amongst six Fe ions surrounding the Fe^III ion with electron configuration t_2g⁵e_g⁰. After around 50 fs, the parallel and perpendicular decays are identical, which the authors attribute to the localisation on the photoexcited electron to a single metal ion but with the transition dipole moment of these CT pairs randomly aligned. Fitting the deconvolved data yields a biexponential fit with time constants around 250 and 900 fs.

Recovery of the ground state can be monitored by a decrease in GSB. The authors observed ESA in the wavelength-resolved studies. This was attributed to the formation of a relaxed self-trapped CT state (Fig. 3b). The authors developed a kinetic model, which gave rate constants for the BET four times (k_BET = 3.5 ± 0.8 ps⁻¹) that of the relaxed CT state k_CT = 0.9 ± 0.2 ps⁻¹. Assuming these are the only decay mechanisms available to PB, this suggests a quantum yield of the CT state of around 20%. The residuals of the fits exhibit a damped oscillatory feature suggesting a vibrational component to the decay. A Fourier analysis of the data showed strong oscillatory components at 75 cm⁻¹ (not assigned) and 270 cm⁻¹ (heavy–light–heavy motion of Fe–CN–Fe).¹²⁶ These are on the same order of magnitude as what is found for the solvated RuRu and RuFe dimers discussed in Section 2 (170, 270, and 488 cm⁻¹). As expected, excitation of the MMCT results in excitation of vibrational modes, here manifested as a nuclear wavepacket.

The interpretation of a self-trapped state has been questioned by a more recent study by Weidinger et al., making use of time-resolved vibrational and electronic spectroscopies on colloidal PB nanoparticles.¹²⁷ Weidinger et al. performed time-resolved measurements using 800 nm both as pump and probe, and could reproduce Arnett's work. By exciting with 800 nm (electronic excitation of the MMCT) and IR probing, they found very fast BET and vibrationally excited PB nanoparticles. From probing with IR, they could conclude that other modes than the CN stretch were populated, and these were assigned to low-frequency lattice phonons. Excitation of the low-frequency modes was of course also observed by Arnett as vibrational coherences made possible with their short 20 fs temporal resolution (which Weidinger did not have access to). Interestingly, Weidinger et al. found very similar results in the 800 nm probe, when exciting the CN stretch mode directly. They observed that when probing with 800 nm after the direct IR pumping, there is an increase in the absorption at 800 nm (Fig. 3c). Arnett et al. previously assigned this increase in absorption (ESA) to an excited self-trapped CT state. However, because Weidinger had directly excited the CN stretch instead of an electronic excitation at the MMCT (800 nm), they could conclude that the ESA is a result of vibrational excitation, changing the MMCT transition oscillator strength and that there is no long-lived CT state in the FeFe PB. The anisotropy measurements by Arnett et al. do indicate that within the first 50 fs there is a delocalisation of the MMCT state but Weidingers measurements, albeit with a poorer temporal resolution, indicate that instead of a trapped CT state, a vibrationally hot ground state is formed. However, the timescales are rather different, and a broadband TA measurement might shed more light on the problem. Nevertheless, it is clear that heating of the lattice is important and similar signature of ESA due to vibrational heating has been observed in thin films of hematite (α-Fe₂O₃).¹²⁸ Clearly it is advantageous to probe the dynamics using a range of different techniques that are sensitive to different aspects of the complex photoinduced processes in PBAs.

3.2 Co–Fe PBA

One of the most fascinating PBAs is the Co–Fe PBA because it is photomagnetic. The first observation was made by Sato et al., who found that shining light on K_0.2Co_1.4[Fe(CN)₆]·6.9H₂O results in an increase in the sample magnetisation.¹¹⁵ Key material parameters were quickly identified after the initial discovery and it was shown that by inserting positive counter ions into the lattice, such as Rb⁺ and Na⁺, the Co–Fe PBA could be switched from a diamagnet to ferrimagnet using light (Fig. 4).^79,80,129 There are two phases in this PBA. In the low-temperature (LT) phase, the oxidation states are Co^III and Fe^II, both with S = 0 (Fig. 4a). The high-temperature (HT) phase comprises Co^II (S = 3/2) and Fe^III (S = 1/2) (Fig. 4b). Upon photoexcitation of the LT phase at ca. 540 nm, a CT state is formed, together with a spin-rearrangement on the Co^II site, resulting in the HT phase. The possibility to switch a diamagnet to a ferrimagnet is a very exciting prospect and is not observed in more conventional magnetic materials. The magnetic order in the photoexcited state arises because of the superexchange interaction between the spin centres, mediated via the charged bridging cyanide ligand. There is therefore a large on-going effort to understand the underlying processes and one important question that remains unsolved is how fast the magnetic long-range order arises.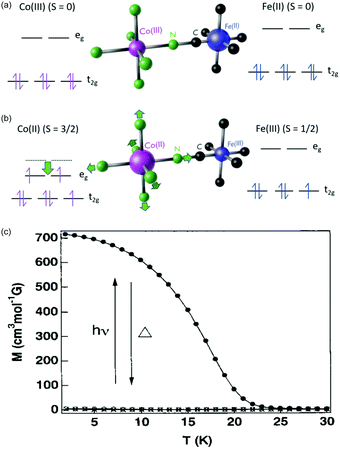

Fig. 4 Electronic structure of the Co–Fe PBA in (a) the low-temperature (LT) and (b) high-temperature (HT) phases. (c) Magnetisation curves before (open circles) and after (solid circles) illumination from a Hg–Xe lamp of Rb_0.66Co_1.25[Fe(CN)₆]·4·3H₂O. Data points marked with crosses were recorded after thermal treatment at 150 K, overlapping with the magnetisation before illumination. Figure (c) reprinted with permission from Sato et al. Inorg. Chem., 1999, 38, 4405.⁷⁹ Copyright 2021 American Chemical Society.

One of the first ultrafast studies was carried out by Kamioka et al. on Co^II[Fe^III(CN)₆]_2/3·5H₂O, which is found in the HT phase down to very low temperatures and is ferrimagnetic below 14 K.¹³⁰ The team employed transient absorption spectroscopy to observe the formation and lifetime of a CT state after excitation at the red-edge of the MMCT (800 nm) and LMCT (400 nm) bands in 10 nm diameter particles in Nafion 117 cavities. In both excitation cases, GSB and ESA were observed at wavelengths below 550 nm and above 700 nm, respectively. The results were interpreted as the formation of a CT state and they could describe the subsequent decay using a biexponential model consisting of a fast (τ_fast) and slow (τ_slow) component in each excitation condition with prefactors A_fast and A_slow (Fig. 5). The time constants for the biexponential fits were τ_fast = 20–30 ps and τ_slow = 100–300 ps. τ_fast was ascribed to the decay of the Franck–Condon CT state i.e. without local lattice relaxation. Although A_fast is roughly constant between the two excitation conditions, A_slow is enhanced dramatically by the MMCT over the LMCT and it was suggested that the slow component is due to self-trapped CT states with lattice distortion. The authors argue that LMCT is less likely to create a self-trapped CT state as two charge transfers must occur: the photoinduced LMCT then a MLCT from the Co^II to the CN⁻. The GSB is due to the decline in the number of Co^II–Fe^III pairs and the ESA is likely from excited spin states in Co^III with high spin (t_2g⁴e_g²) and intermediate (t_2g⁵e_g¹) configurations. The lifetime of the CT states increases with increasing pump fluence and they observed lifetimes from 2 ns at low fluence to 6 ns at high fluence. At low fluence, a lower density of CT pairs will be created and, therefore, the 2 ns lifetime is associated with isolated CT pairs. At high fluence, a higher density of CT pairs will be formed that manifest into a charge-ordered cluster stabilising the photoexcited state.

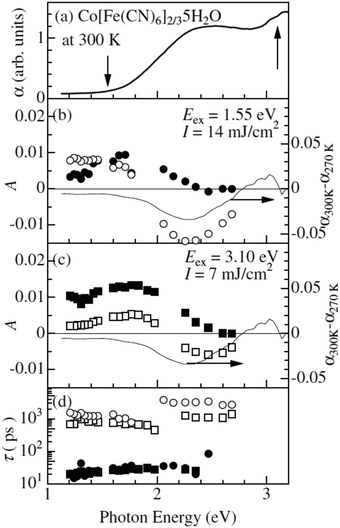Fig. 5 Ultrafast dynamics in Co^II[Fe^III(CN)₆]_2/3·5H₂O probed by TA spectroscopy. The static absorption spectrum is shown in (a) and the arrows indicate the two excitation wavelengths. The amplitudes A from biexponential fits are shown in (b) and (c), where filled symbols correspond to the fast time constant and open symbols to the slow constant. The actual time constants (fast and slow) are shown in (d). The thin lines in (b) and (c) are differential (static) absorption spectra at different temperatures. Reprinted figure with permission from Kamioka et al. Phys. Rev. B, 2008, 77, 180301(R).¹³⁰ Copyright 2021 by the American Physical Society.

Moritomo et al. used time-resolved X-ray absorption fine-structure (XAFS) spectroscopy and optical transmittance to study Na_0.8Co^III[Fe^II(CN)₆]_0.90·2.9H₂O at 300 K.^131,132 This PBA is in the LT phase up to 500 K unlike the Co^II–Fe^III PBA previously discussed. The sample was excited with 130 fs 800 nm laser pulses. The XAFS measurements showed that a CT state with high-spin Co^II is formed within the time-resolution of the measurement (100 ps). The CT state decayed with a lifetime of 32 ns at room temperature. The photoexcitation causes an expansion of the lattice parameters by 0.1% because of population of anti-bonding e_g orbitals in the high-spin Co^II state. This expansion decays on a time frame of about 40 ns correlating with the lifetime of the CT state measured by optical pump–probe measurements carried out simultaneously with the X-ray measurements. The lattice then begins to expand again after 100 ns due to heating effects.

In a different study, Zerdane et al. used X-ray absorption near edge structure (XANES) to study CsCoFe PBA (Co^III (S = 0)–Fe^II (S = 0)).¹³³ They found that starting in the low-spin configuration at room temperature and exciting with 650 nm light, the XANES data clearly showed the transfer of an electron from Fe^II to Co^III and that Co^II was formed in the high-spin state. The XANES data also indicated that the geometry around the Co site is changed as a result of the spin crossover. The dynamics was limited to the 100 ps time resolution in the experiment. Complementary optical pump–probe measurements showed that the CT state has a lifetime on the order of a few microseconds at room-temperature.

These first time-resolved measurements at synchrotrons enables studies with higher temporal resolution at XFEL facilities. This was recently done by Cammarata et al. who used both XANES and extended XAFS (EXAFS) at the LCLS XFEL with a 25 fs temporal resolution.¹²¹ The sample studied was a colloidal solution of Cs_0.7Co[Fe(CN)₆]_0.9 nanoparticles with 11 nm diameter in the LT phase at room temperature.¹³⁴ This was a ground-breaking study in many ways because it determined the nature of the transition at 540 nm, for which there was previously some debate,^119,120 and could even show the sequence of the initial states involved in the CT and spin transitions. The time-resolved data at the Co K-edge had to be fitted with three decay constants of 50, 200 and 450 fs (Fig. 6). Interestingly, the Fe edge only showed the 200 and 450 fs components, suggesting that the initial dynamics takes place on the Co site. This observation therefore determined that the 540 nm transition corresponds to a d–d transition on the Co^III site, which was also confirmed by time-dependent density functional theory (TD-DFT) calculations. The transition involves populating antibonding e_g orbitals and there is therefore a rapid expansion of the Co–N bonds. This in turn reduces the energy difference between the t_2g and e_g orbitals and the high-spin state is formed, which could be seen in the EXAFS signal. The XANES signal on the other hand, shows that the CT takes place within 200 fs, as large shifts in both the Co and Fe K-edges are observed corresponding to a change in oxidation state. The authors therefore concluded that it was the spin transition that drives the CT. Temporal oscillations are also observed in the data corresponding to a lattice torsional mode at 1.65 THz (55 cm⁻¹). The authors suggest that the breathing mode of the Co expansion, predicted to occur at 11.2 THz (374 cm⁻¹), is not observed because the lattice has no time to expand on this short timescale for which the initial expansion takes place (half the period of the breathing mode). We note that the FeFe study by Arnett mentioned above,¹²² identified oscillations in their data corresponding to 75 and 270 cm⁻¹. Presumably these are similar modes to what was observed in the CoFe PBA. Arnett did not mention any counterions and it is therefore possible that the mode at 270 cm⁻¹ was observed because of vacancies in the lattice, in contrast to the CoFe studied by Cammarata, which have fewer vacancies. Furthermore, there is no change in spin in the FeFe PB, whereas the torsional modes might be critical for the ultrafast ISC in CoFe to take place, similarly to the strain waves launched during ultrafast demagnetisation of Fe films.⁵⁶ Recent X-ray diffuse scattering studies of single-crystal of various PBAs revealed a range of different types of vacancies,¹³⁵ which could be a promising route to steer the dynamics in the excited state.

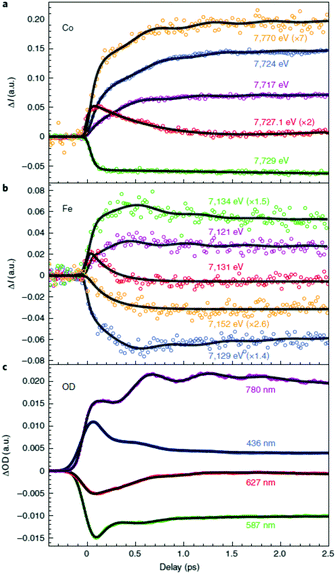Fig. 6 Time-resolved X-ray absorption data of a colloidal solution of Cs_0.7Co[Fe(CN)₆]_0.9 nanoparticles obtained using the LCLS X-ray free-electron laser (XFEL) at the (a) Co and (b) Fe K-edges.¹²¹ The data show that the initial dynamics takes place on the Co site after photoexcitation, which followed by a charge-transfer from Co to Fe. The change in e_g population leads to rapid expansion of the Co–N bonds and the launch of lattice torsional modes. This is more clearly seen as oscillations in the optical TA measurements shown in (c). Reprinted by permission from Springer Nature: Nature Chemistry Charge transfer driven by ultrafast spin transition in a CoFe Prussian blue analogue, Marco Cammarata et al. Copyright 2021.

There have also been several computational studies to understand the dynamics of the CoFe PBA. Recently, van Veenendaal employed a dissipative quantum mechanical model where the cobalt ion is coupled to the damped breathing mode of the Co^II–CN bonds.¹¹⁹ The simulation begins after photoexcitation with a Franck–Condon ²E state, centred on the Co^II with electron configuration t_2g⁶e_g¹. This assumes that a CT from Fe to Co takes place first. However, the recent XFEL measurement by Cammarata et al. show that the spin transition occurs first as discussed above. However, the work by van Veenendaal is very important and gives many insights into the interplay between electronic and nuclear degrees of freedom, as well as highlights the complex multi-electron correlation effects taking place. Within 20 fs the wavepacket undergoes ISC to the ⁴T₁ state (t_2g⁵e_g²), corresponding to a change in spin state from S = 1/2 to 90% of the expected value S = 3/2. The dynamics of the doublet to quartet transition are only weakly dependent on damping to vibrational modes. After the initial 20 fs, the conversion to the S = 3/2 state is heavily dependent on the damping due to the involvement of other quartet states, highlighting that multi-electron correlation effects and their coupling to nuclear degrees of freedom are important. It was observed that the value of the spin–orbit interaction oscillates during the first 300 fs and played a role in the ISC process. van Veenendaal predicts that time-resolved X-ray absorption measurements at XFELs should enable the direct observation of the change in spin–orbit interaction during the early dynamics,^119,136 which is a very exciting possibility.

3.3 Mn–Fe PBA

Another interesting photomagnetic system is the Rb_xMn[Fe(CN)₆]_(x+2)/3·zH₂O PBA. It has been shown that this PBA can be controlled by external stimuli and a single laser shot can cause demagnetisation.^137–140 This compound is characterised by a LT phase Fe^II (S = 0)–CN–Mn^III (S = 2) and a HT phase, where an electron has been transferred from Fe to Mn, yielding Fe^III (S = 1/2)–CN–Mn^II (S = 5/2).¹³⁸ This bistability is seen as a thermal phase transition with a wide loop (bistability characterised by thermal hysteresis in the magnetic susceptibility) and attributed to the flexibility afforded by the cyano-bridges, allowing for a Jahn-Teller distortion to take place at low temperatures (Mn^III is Jahn–Teller distorted). The RbMnFe PBA has a broad absorption around 400–600 nm, consisting of both Mn^III d–d transitions and an intervalence transition from Fe^II to Mn^III.^140,141 The photoinduced HT phase (PIHT) can be reached by optical excitation of the magnetically ordered LT phase at 3 K (ferromagnetic ordering of the Mn^III spins), which causes a demagnetisation of the sample.¹³⁷ This is because the conversion from S = 0 to S = 1/2 on the Fe ions, which leads to an overall antiferromagnetic long-range magnetic order in the PIHT phase (Fig. 7). Vibrational spectroscopy^142–144 and X-ray diffraction¹⁴⁰ demonstrate that the HT phase has formed in the photoexcited state. Tokoro et al. found that laser fluences higher than 9 mJ cm⁻² are needed to observe the photoinduced demagnetisation.¹³⁷ Just as in the case for Co–Fe, this indicates that there is a need to form the necessary number of switched sites in the crystal for a phase-transition to occur. Despite the large laser fluence, the LT is recovered after annealing at 150 K. Interestingly, the LT phase can also be recovered by further optical excitation and the magnetisation grows correspondingly. This presents an interesting way to optically switch the magnetisation in this PBA using a reversible process. Asahara et al. have studied time-resolved IR measurements and found that the charge-transfer occurs within their temporal resolution (decrease of the LT phase within < 1 ps), but that the signal is dominated by the boundaries between the LT and PIHT phases (Fig. 8).¹⁰² The authors concluded that relatively small domains and/or fjord-like domains are formed shortly after the excitation pulse. Zerdane et al. performed time-resolved XANES on the RbMnFe PBA with a 100 ps time resolution.¹³³ They found evidence that the MMCT excitation produces a change in oxidation states and complementary optical pump–probe measurements showed that this state has a lifetime on the order of 10 ms at 140 K.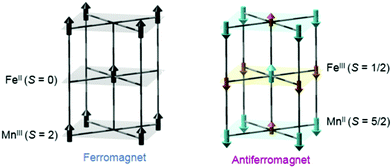

Fig. 7 Magnetic ordering of the MnFe PBA in the low-temperature (left) and photoinduced high-temperature phases (right). Reprinted with permission from Tokoro et al. Chem. Mater., 2008, 20, 423–428.¹⁴² Copyright 2021 American Chemical Society.

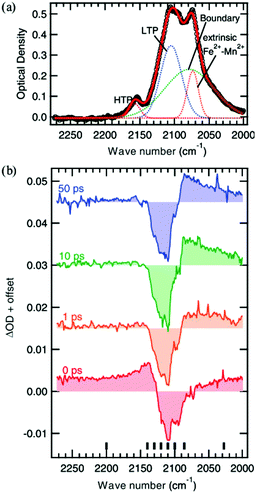Fig. 8 Vibrational spectroscopy of the Mn–Fe PBA at 4 K. The static absorption spectrum is shown in (a) where the low-temperature (LT) and photoinduced high-temperature (PIHT) phases can be seen. The sites between the two phases at the boundaries give rise to additional peaks. (b) Time-resolved IR spectra at the cyanide stretch region at selected time delays, showing the transition from the LT phase to the PIHT phase. The signal is dominated by the boundary sites at lower wavenumbers below the bleach of the LT phase (2110 cm⁻¹). Reprinted figure with permission from Asahara et al. Phys. Rev. B, 2012, 86, 195138.¹⁰² Copyright 2021 by the American Physical Society.

A computational investigation on how the delocalised molecular orbitals across the Fe–CN–Mn bond depends on the low-frequency transverse modes (around 300–500 cm⁻¹) have been carried out by Tokoro et al.^139,145 As the bond angle changes, the calculations indicate a CT from Fe^II–CN–Mn^III to Fe^III–CN–Mn^II. Clearly the coupling to vibrational modes/phonons is important for mediating the CT-induced phase-transition, as has been seen in other PBAs discussed above.

3.4 V–Cr PBA

The V^II/III–Cr^III PBA is one of the very few room-temperature molecule-based magnets.⁶⁹ It is brightly blue-coloured due to intense MMCT at 540 and 660 nm (wavelength depends on the vanadium oxidation state).^{88,118,146,147} Bozdag et al. found reversible photo-induced changes to the magnetisation of a sample of K_1.54V^II_0.77V^III_0.08[Cr^III(CN)₆](SO₄)_0.16.¹⁴⁸ The sample was placed in a magnetic field of 10 Oe and when irradiation with 350 nm CW laser light at the LMCT band, a decrease in the magnetisation of around 0.5% was observed. At a temperature of 10 K, this change in magnetisation stayed constant until irradiated with 514 nm light, when the magnetisation partially recovered. The authors also found that the magnetisation fully recovers when heating the sample above 250 K. Bozdag et al. attributed the decreasing magnetisation to the LMCT inducing structural distortions in the metal–ligand bond and/or changes in magnetic anisotropy.

The MMCT transitions in the visible spectrum give rise to a relatively large magneto-optical (MO) signal in thin films fabricated using electrodeposition on transparent substrates.^84,88 Ohkoshi et al. showed that the MO signal from the MMCT is proportional to the sample magnetisation.⁸⁸ This opens possibilities to do time-resolved Faraday rotation measurements. The first fs spin-state sensitive investigation of a PBA was carried out by Johansson et al. using ultrafast time-resolved Faraday rotation and TA on the V–Cr PBA.¹⁴⁷ The authors found a large GSB of the MMCT transitions after exciting the red edge of the LMCT band at 400 nm. The optical assignments were supported by TD-DFT calculations on the V–Cr molecular unit. The signal decayed and reached a plateau within a few ps. In a later TA study with improved time-resolution,¹⁴⁹ it was shown that the GSB decayed with ca. 200 fs and 1 ps time constants to the plateau, which stayed constant for over 2 ns.

In the femtosecond magneto-optical (fs-MO) measurements,¹⁴⁷ a white-light continuum spanning 480–690 nm was used to monitor the changes in transmission and the MO signal (Faraday rotation and ellipticity) was measured as a function of time delay between the pump and probe pulses. Measurements were carried out at 50 and 300 K and in ±0.5 T external magnetic fields in order to separate the optical and magnetic dynamical response. The fs-MO signal showed a very fast, sub-ps, response following the TA timescales, as seen in Fig. 9. This fast response is different to what is typically observed in magnetic dielectrics, where the spin–phonon interaction take place on a much longer timescale (100s of ps).^150–154 For this fast fs-MO signal, the local change in spin populations shows up at short times in the signal.

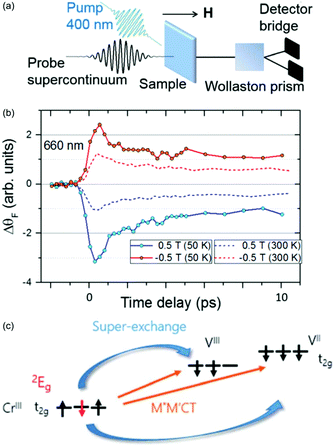Fig. 9 Ultrafast spin dynamics in the V–Cr PBA.¹⁴⁷ (a) Experimental setup used to measure the fs magneto-optical (fs-MO) signal. A small wavelength range of the white-light continuum is selected as a probe and transmitted through the sample. The change in polarisation direction (Faraday rotation, Δθ_F) is measured using a Wollaston prism and a bridged photodiode pair. (b) The signal at a probe wavelength of 660 nm measured as a function of time delay between the probe and 400 nm pump. The external magnetic field is either aligned parallel or antiparallel with the laser propagation direction. (c) The photoinduced spin–flip on the Cr sites results in a rapid change in the superexchange interaction and the fs-MO signal.

It is known that the local spin-configuration on Cr^III sites in the ground state gives S = 3/2 and that the first excited state corresponds to one of the electrons flipped, which in a local picture corresponds to S = 1/2. In molecules^5,155 and solids^156,157 this state can be populated within a few 100 fs. Johansson et al. interpreted the fast change in fs-MO signal as due to local spin–flips on the Cr sites after photoexcitation, which in turn will affect the superexchange interaction. The ps decay is due to heating of the lattice, similarly to other PBAs. The dynamics of the reaction are summarised in Fig. 9 along with the time-resolved MO signal. This work has shown the possibility of using ultrafast MO to directly measure spin dynamics and changes in the superexchange interaction. However, long-lived CT states could also play a role and future element-specific measurements, using for example XFELs, could shed more light on the problem.

4 Summary and outlook

Light-induced spin flips can happen on sub-100 fs timescales in systems ranging in size from molecules to magnetically ordered metals and dielectrics. Connecting them is that there is strong coupling between electronic, nuclear and spin degrees of freedom. We argue that molecule-based magnets, such as PBAs, bridge the limits between individual molecules and long-range ordered materials, and provide the best of both worlds with the advantage of possibilities for high-level calculations based on the dimers of the molecular building blocks.

Much can be learned from studying cyano-bridged dimers and comparing these results to PBAs. It is clear that excitation of vibrational/phonon modes take place on the sub-ps timescale in both the dimers and most of the PBAs. TA and XFEL measurements show that in some PBAs long-lived CT states are formed, which eventually can lead to a change in the long-range magnetic order, as in the Co–Fe PBA. In these measurements, one also observes a launch of coherent phonons, such as lattice bending modes, which is particularly important when the population of antibonding e_g orbitals are changed. It will be interesting to conduct experiments using a THz pump to directly excite these phonon modes. The pioneering work by Cammarata et al. highlighted the power of XFEL measurements with element-specificity, which enabled the team to demonstrate that a spin–flip occurs before the charge-transfer in the Co–Fe PBA.¹²¹ It is known that vacancies and the exact stoichiometry can have a large effect on the final photomagnetic state because these parameters influence the lattice rigidity.^79,80,129 Currently, there is a lack of systematic ultrafast studies comparing the dynamics in PBAs that only differ in their stoichiometric ratios. Work on the V–Cr PBA, using magneto-optical methods for the first time, could show that it is possible to change the magnetic exchange between sites in the lattice on a sub-picosecond timescale.¹⁴⁷ This technique is promising in combination with XFEL measurements to understand ultrafast photoinduced magnetisation dynamics. We note that steady-state illumination of the photomagnetic Co–Fe PBA results in an increase in the MO signal,⁸⁹ which would be interesting to study in a time-resolved experiment.

Until now, the electron dynamics have been explained using a localised picture of the wavepacket and focusing on direct charge-transfer between localised sites. It has been shown that optical excitation does lead to long-range structural ordering, as in the MnFe PBA, and rapid heating of the lattice. The question then is if one should also consider a delocalised conduction band in the more crystalline PBAs to see if the dynamics can be described using methods from condensed matter physics. For example, spin and charge dynamics in lead halide perovskites are described well using a band theory picture. Exciting electrons into the conduction band, Giovanni et al. were able to measure spin relaxation times of electrons and holes using time-resolved Faraday rotation,¹⁵⁸ similarly to what was previously done on Mn-doped semiconductors described in the Introduction.⁴¹ Likewise, the early 20 fs anisotropy measurements by Arnett et al. pointed to a rapid delocalisation of the charge-transfer state,¹²² which is also seen in molecular [Ru(bpy)₃]²⁺,¹²⁵ which is a problem that has been discussed for a long time. The question then arises if there is a role for free carriers but very limited amount of work on photoconductivity of PB has been done.^159,160 Such questions could potentially be answered using terahertz spectroscopy.

It will also be interesting to make use of the elemental specificity of XFELs to explore charge-transfer effects in multilayers of PBAs, such as multicore CoFe PBA.^81,161 It is possible that time-resolved IR measurements monitoring the different CN⁻ stretch modes, which provide a spectral fingerprint of the PBA oxidation state, could be used to achieve layer-specific sensitivity. Controlling magnetic (and other) properties in stimuli-responsive and multifunctional devices with fs pulses is an exciting prospect.

The fundamental understanding of manipulating spins with fs laser pulses in PBAs will set the scene to explore other magnetic materials. For example, a molecule-based magnet incorporating chromium ions and pyrazine building blocks was recently made, which displayed ordering temperatures up to 242 °C.¹⁶² New single-molecule magnets are also being developed that are magnetic around 77 K.^163–165 Understanding the fundamental photoinduced processes in magnetic molecules can lead to a change in how fast and efficient we can store digital information in the future.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support from EPSRC grant EP/S018824/1.

Notes and references

1. J. K. McCusker, Acc. Chem. Res., 2003, 36, 876–887.
2. E. A. Juban, A. L. Smeigh, J. E. Monat and J. K. McCusker, Coord. Chem. Rev., 2006, 250, 1783–1791.
3. M. Chergui, Acc. Chem. Res., 2015, 48, 801–808.
4. N. H. Damrauer, G. Cerullo, A. Yeh, T. R. Boussie, C. V. Shank and J. K. McCusker, Science, 1997, 275, 54–57.
5. E. A. Juban and J. K. McCusker, J. Am. Chem. Soc., 2005, 127, 6857–6865.
6. J. E. Monat and J. K. McCusker, J. Am. Chem. Soc., 2000, 122, 4092–4097.
7. G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633.
8. H. T. Lemke, K. S. Kjær, R. Hartsock, T. B. van Driel, M. Chollet, J. M. Glownia, S. Song, D. Zhu, E. Pace, S. F. Matar, M. M. Nielsen, M. Benfatto, K. J. Gaffney, E. Collet and M. Cammarata, Nat. Commun., 2017, 8, 15342.
9. W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348.
10. S. Zerdane, L. Wilbraham, M. Cammarata, O. Iasco, E. Rivière, M. L. Boillot, I. Ciofini and E. Collet, Chem. Sci., 2017, 8, 4978–4986.
11. W. Zhang, K. S. Kjær, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubicek, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Persson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, T. C. Weng, D. Zhu, K. Warnmark, V. Sundstrom and K. J. Gaffney, Chem. Sci., 2017, 8, 515–523.
12. M. Lorenc, J. Hébert, N. Moisan, E. Trzop, M. Servol, M. Buron-Le Cointe, H. Cailleau, M. L. Boillot, E. Pontecorvo, M. Wulff, S. Koshihara and E. Collet, Phys. Rev. Lett., 2009, 103, 028301.
13. E. Collet, N. Moisan, C. Baldé, R. Bertoni, E. Trzop, C. Laulhé, M. Lorenc, M. Servol, H. Cailleau, A. Tissot, M.-L. Boillot, T. Graber, R. Henning, P. Coppens and M. B.-L. Cointe, Phys. Chem. Chem. Phys., 2012, 14, 6192.
14. M. Cammarata, R. Bertoni, M. Lorenc, H. Cailleau, S. Di Matteo, C. Mauriac, S. F. Matar, H. Lemke, M. Chollet, S. Ravy, C. Laulhé, J.-F. Létard and E. Collet, Phys. Rev. Lett., 2014, 113, 227402.
15. K. Kunnus, M. Vacher, T. C. B. Harlang, K. S. Kjær, K. Haldrup, E. Biasin, T. B. van Driel, M. Papai, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, E. Kallman, M. Delcey, R. W. Hartsock, M. E. Reinhard, S. Koroidov, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, L. Sandberg, Z. Nemeth, D. S. Szemes, E. Bajnoczi, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, H. T. Lemke, S. E. Canton, K. B. Moller, M. M. Nielsen, G. Vanko, K. Warnmark, V. Sundstrom, P. Persson, M. Lundberg, J. Uhlig and K. J. Gaffney, Nat. Commun., 2020, 11, 634.
16. K. S. Kjær, T. B. Van Driel, T. C. B. Harlang, K. Kunnus, E. Biasin, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, A. O. Dohn, M. I. Papai, K. B. Moller, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, M. Jarenmark, J. Uhlig, V. Sundstom, K. Warnmark, P. Persson, Z. Nemeth, D. S. Szemes, E. Bajnoczi, G. Vanko, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, S. E. Canton, H. T. Lemke and K. J. Gaffney, Chem. Sci., 2019, 10, 5749–5760.
17. M. Chergui and E. Collet, Chem. Rev., 2017, 117, 11025–11065.
18. K. Zhang, R. Ash, G. S. Girolami and J. Vura-Weis, J. Am. Chem. Soc., 2019, 141, 17180–17188.
19. E. S. Ryland, K. Zhang and J. Vura-Weis, J. Phys. Chem. A, 2019, 123, 5214–5222.
20. Y. Jiang, L. C. Liu, H. M. Muller-Werkmeister, C. Lu, D. Zhang, R. L. Field, A. Sarracini, G. Moriena, E. Collet and R. J. D. Miller, Angew. Chem., Int. Ed., 2017, 56, 7130–7134.
21. Y. Jiang, L. C. Liu, A. Sarracini, K. M. Krawczyk, J. S. Wentzell, C. Lu, R. L. Field, S. F. Matar, W. Gawelda, H. M. Müller-Werkmeister and R. J. D. Miller, Nat. Commun., 2020, 11, 1530.
22. C. de Graaf and C. Sousa, Chem. – Eur. J., 2010, 16, 4550–4556.
23. L. A. Fredin, K. Wärnmark, V. Sundström and P. Persson, ChemSusChem, 2016, 9, 667–675.
24. J. Nance, D. N. Bowman, S. Mukherjee, C. T. Kelley and E. Jakubikova, Inorg. Chem., 2015, 54, 11259–11268.
25. M. Abedi, G. Levi, D. B. Zederkof, N. E. Henriksen, M. Pápai and K. B. Møller, Phys. Chem. Chem. Phys., 2019, 21, 4082–4095.
26. M. Pápai, M. Abedi, G. Levi, E. Biasin, M. M. Nielsen and K. B. Møller, J. Phys. Chem. C, 2019, 123, 2056–2065.
27. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025.
28. C. Daniel, Phys. Chem. Chem. Phys., 2021, 23, 43–58.
29. J. P. Zobel, O. S. Bokareva, P. Zimmer, C. Wolper, M. Bauer and L. Gonzalez, Inorg. Chem., 2020, 59, 14666–14678.
30. P. Chábera, Y. Liu, O. Prakash, E. Thyrhaug, A. E. Nahhas, A. Honarfar, S. Essén, L. A. Fredin, T. C. B. Harlang, K. S. Kjær, K. Handrup, F. Ericson, H. Tatsuno, K. Morgan, J. Schnadt, L. Häggström, T. Ericsson, A. Sobkowiak, S. Lidin, P. Huang, S. Styring, J. Uhlig, J. Bendix, R. Lomoth, V. Sundström, P. Persson and K. Wärnmark, Nature, 2017, 543, 695–699.
31. B. C. Paulus, S. L. Adelman, L. Jamula and J. McCusker, Nature, 2020, 582, 214–218.
32. F. Liedy, J. Eng, R. McNab, R. Inglis, T. J. Penfold, E. K. Brechin and J. O. Johansson, Nat. Chem., 2020, 12, 452–458.
33. M. A. Naumova, A. Kalinko, J. W. L. Wong, S. Alvarez Gutierrez, J. Meng, M. Liang, M. Abdellah, H. Geng, W. Lin, K. Kubicek, M. Biednov, F. Lima, A. Galler, P. Zalden, S. Checchia, P. A. Mante, J. Zimara, D. Schwarzer, S. Demeshko, V. Murzin, D. Gosztola, M. Jarenmark, J. Zhang, M. Bauer, M. L. Lawson Daku, D. Khakhulin, W. Gawelda, C. Bressler, F. Meyer, K. Zheng and S. E. Canton, J. Chem. Phys., 2020, 152, 214301.
34. R. Bertoni, M. Lorenc, A. Tissot, M. Servol, M. L. Boillot and E. Collet, Angew. Chem., Int. Ed., 2012, 51, 7485–7489.
35. M. Lorenc, C. Balde, W. Kaszub, A. Tissot, N. Moisan, M. Servol, M. Buron-Le Cointe, H. Cailleau, P. Chasle, P. Czarnecki, M. L. Boillot and E. Collet, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054302.
36. A. Marino, M. Servol, R. Bertoni, M. Lorenc, C. Mauriac, J. F. Létard and E. Collet, Polyhedron, 2013, 66, 123–128.
37. R. Bertoni, M. Lorenc, T. Graber, R. Henning, K. Moffat, J. F. Letard and E. Collet, CrystEngComm, 2016, 18, 7269–7275.
38. R. Bertoni, M. Lorenc, H. Cailleau, A. Tissot, J. Laisney, M.-L. Boillot, L. Stoleriu, A. Stancu, C. Enachescu and E. Collet, Nat. Mater., 2016, 15, 606–610.
39. A. Marino, M. Cammarata, S. F. Matar, J. F. Létard, G. Chastanet, M. Chollet, J. M. Glownia, H. T. Lemke and E. Collet, Struct. Dyn., 2016, 3, 023605.
40. S. A. Crooker, D. D. Awschalom and N. Samarth, IEEE J. Sel. Top. Quantum Electron., 1995, 1, 1082–1092.
41. S. Crooker, J. Baumberg, F. Flack, N. Samarth and D. D. Awschalom, Phys. Rev. Lett., 1996, 77, 2814–2817.
42. M. Ouyang and D. D. Awschalom, Science, 2003, 301, 1074–1078.
43. D. D. Awschalom, R. Hanson, J. Wrachtrup and B. B. Zhou, Nat. Photonics, 2018, 12, 516–527.
44. A. Kirilyuk, A. V. Kimel and T. Rasing, Rep. Prog. Phys., 2013, 76, 026501.
45. J.-Y. Bigot and M. Vomir, Ann. Phys., 2013, 525, 2–30.
46. J. Walowski and M. Münzenberg, J. Appl. Phys., 2016, 120, 140901.
47. E. Beaurepaire, J. C. Merle, A. Daunois and J.-Y. Bigot, Phys. Rev. Lett., 1996, 76, 4250–4253.
48. A. Stupakiewicz, K. Szerenos, D. Afanasiev, A. Kirilyuk and A. V. Kimel, Nature, 2017, 542, 71–74.
49. A. Stupakiewicz, K. Szerenos, M. D. Davydova, K. A. Zvezdin, A. K. Zvezdin, A. Kirilyuk and A. V. Kimel, Nat. Commun., 2019, 10, 612.
50. R. V. Mikhaylovskiy, T. J. Huisman, V. A. Gavrichkov, S. I. Polukeev, S. G. Ovchinnikov, D. Afanasiev, R. V. Pisarev, T. Rasing and A. V. Kimel, Phys. Rev. Lett., 2020, 125, 157201.
51. B. Koopmans, M. Van Kampen, J. T. Kohlhepp and W. J. M. De Jonge, Phys. Rev. Lett., 2000, 85, 844–847.
52. B. Koopmans, G. Malinowski, F. Dalla Longa, D. Steiauf, M. Fähnle, T. Roth, M. Cinchetti and M. Aeschlimann, Nat. Mater., 2010, 9, 259–265.
53. J.-Y. Bigot, M. Vomir and E. Beaurepaire, Nat. Phys., 2009, 5, 515–520.
54. G. P. Zhang, W. Hübner, G. Lefkidis, Y. Bai and T. F. George, Nat. Phys., 2009, 5, 499–502.
55. J. K. Dewhurst, S. Shallcross, P. Elliott, S. Eisebitt, C. V. K. Schmising and S. Sharma, 2020, arXiv:2012.03657 [cond-mat.mtrl-sci].
56. C. Dornes, Y. Acremann, M. Savoini, M. Kubli, M. J. Neugebauer, E. Abreu, L. Huber, G. Lantz, C. A. F. Vaz, H. Lemke, E. M. Bothschafter, M. Porer, V. Esposito, L. Rettig, M. Buzzi, A. Alberca, Y. W. Windsor, P. Beaud, U. Staub, D. Zhu, S. Song, J. M. Glownia and S. L. Johnson, Nature, 2019, 565, 209–212.
57. C. E. Graves, A. H. Reid, T. Wang, B. Wu, S. de Jong, K. Vahaplar, I. Radu, D. P. Bernstein, M. Messerschmidt, L. Müller, R. Coffee, M. Bionta, S. W. Epp, R. Hartmann, A. V. Kimel, G. Hauser, A. Hartmann, P. Holl, H. Gorke, J. H. Mentink, A. Tsukamoto, A. Fognini, J. J. Turner, W. F. Schlotter, D. Rolles, H. Soltau, L. Strüder, Y. Acremann, A. Kirilyuk, T. Rasing, J. Stöhr, A. O. Scherz and H. A. Dürr, Nat. Mater., 2013, 12, 293–298.
58. E. Iacocca, T. M. Liu, A. H. Reid, Z. Fu, S. Ruta, P. W. Granitzka, E. Jal, S. Bonetti, A. X. Gray, C. E. Graves, R. Kukreja, Z. Chen, D. J. Higley, T. Chase, L. Le Guyader, K. Hirsch, H. Ohldag, W. F. Schlotter, G. L. Dakovski, G. Coslovich, M. C. Hoffmann, S. Carron, A. Tsukamoto, A. Kirilyuk, A. V. Kimel, T. Rasing, J. Stohr, R. F. L. Evans, T. Ostler, R. W. Chantrell, M. A. Hoefer, T. J. Silva and H. A. Durr, Nat. Commun., 2019, 10, 1756.
59. B. Pfau, S. Schaffert, L. Muller, C. Gutt, A. Al-Shemmary, F. Buttner, R. Delaunay, S. Dusterer, S. Flewett, R. Fromter, J. Geilhufe, E. Guehrs, C. M. Gunther, R. Hawaldar, M. Hille, N. Jaouen, A. Kobs, K. Li, J. Mohanty, H. Redlin, W. F. Schlotter, D. Stickler, R. Treusch, B. Vodungbo, M. Klaui, H. P. Oepen, J. Luning, G. Grubel and S. Eisebitt, Nat. Commun., 2012, 3, 1100.
60. B. Vodungbo, J. Gautier, G. Lambert, A. B. Sardinha, M. Lozano, S. Sebban, M. Ducousso, W. Boutu, K. Li, B. Tudu, M. Tortarolo, R. Hawaldar, R. Delaunay, V. Lopez-Flores, J. Arabski, C. Boeglin, H. Merdji, P. Zeitoun and J. Luning, Nat. Commun., 2012, 3, 999.
61. P. Tengdin, C. Gentry, A. Blonsky, D. Zusin, M. Gerrity, L. Hellbrück, M. Hofherr, J. Shaw, Y. Kvashnin, E. K. Delczeg-Czirjak, M. Arora, H. Nembach, T. J. Silva, S. Mathias, M. Aeschlimann, H. C. Kapteyn, D. Thonig, K. Koumpouras, O. Eriksson and M. M. Murnane, Sci. Adv., 2020, 6, eaaz1100.
62. K. Yao, F. Willems, C. von Korff Schmising, C. Strüber, P. Hessing, B. Pfau, D. Schick, D. Engel, K. Gerlinger, M. Schneider and S. Eisebitt, Rev. Sci. Instrum., 2020, 91, 093001.
63. K. Bühlmann, G. Saerens, A. Vaterlaus and Y. Acremann, Sci. Rep., 2020, 10, 12632.
64. M. Plötzing, R. Adam, C. Weier, L. Plucinski, S. Eich, S. Emmerich, M. Rollinger, M. Aeschlimann, S. Mathias and C. M. Schneider, Rev. Sci. Instrum., 2016, 87, 043903.
65. J. S. Miller and A. J. Epstein, MRS Bull., 2000, 21–30.
66. S.-I. Ohkoshi, K. Imoto, Y. Tsunobuchi, S. Takano and H. Tokoro, Nat. Chem., 2011, 3, 564–569.
67. S.-I. Ohkoshi and H. Tokoro, Acc. Chem. Res., 2012, 45, 1749–1758.
68. M. Verdaguer, A. Bleuzen, V. Marvaud, J. Vaissermann, M. Seuleiman, C. Desplanches, A. Scuiller, C. Train, R. Garde, G. Gelly, C. Lomenech, I. Rosenman, P. Veillet, C. Cartier and F. Villain, Coord. Chem. Rev., 1999, 190–192, 1023–1047.
69. S. Ferlay, T. Mallah, R. Ouahès, P. Veillet and M. Verdaguer, Nature, 1995, 378, 701–703.
70. M. Verdaguer, A. Bleuzen, C. Train, R. Garde, F. Fabrizi de Biani and C. Desplanches, Philos. Trans. R. Soc., A, 1999, 357, 2959–2976.
71. O. Sato, T. Iyoda, A. Fujishima and K. Hashimoto, Science, 1996, 271, 49–51.
72. S.-I. Ohkoshi, T. Iyoda, A. Fujishima and K. Hashimoto, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 11642–11652.
73. Y. Sato, S.-I. Ohkoshi, K.-I. Arai, M. Tozawa and K. Hashimoto, J. Am. Chem. Soc., 2003, 125, 14590–14595.
74. S.-I. Ohkoshi, K. Nakagawa, K. Tomono, K. Imoto, Y. Tsunobuchi and H. Tokoro, J. Am. Chem. Soc., 2010, 132, 6620–6621.
75. S.-I. Ohkoshi, A. Fujishima and K. Hashimoto, J. Am. Chem. Soc., 1998, 120, 5349–5350.
76. M. Mizuno, S.-I. Ohkoshi and K. Hashimoto, Adv. Mater., 2000, 8904, 1955–1958.
77. M. Reczyński, K. Nakabayashi and S.-I. Ohkoshi, Eur. J. Inorg. Chem., 2020, 2669–2678.
78. S.-I. Ohkoshi, Y. Einaga, A. Fujishima and K. Hashimoto, J. Electroanal. Chem., 1999, 473, 245–249.
79. O. Sato, Y. Einaga, A. Fujishima and K. Hashimoto, Inorg. Chem., 1999, 38, 4405–4412.
80. A. Bleuzen, C. Lomenech, V. Escax, F. Villain, F. Varret, C. Cartier dit Moulin and M. Verdaguer, J. Am. Chem. Soc., 2000, 122, 6648–6652.
81. D. M. Pajerowski, M. J. Andrus, J. E. Gardner, E. S. Knowles, M. W. Meisel and D. R. Talham, J. Am. Chem. Soc., 2010, 132, 4058–4059.
82. O. Sato, J. Solid State Electrochem., 2007, 11, 773–779.
83. L. Hedley, N. Robertson and J. O. Johansson, Electrochim. Acta, 2017, 236, 97–103.
84. M. Verdaguer, M. Glavez, R. Garde and C. Desplanches, Electrochem. Soc. Interface, 2002, 11, 28.
85. Y. Huang and S. Ren, Appl. Mater. Today, 2021, 22, 100886.
86. M. B. Zakaria and T. Chikyow, Coord. Chem. Rev., 2017, 352, 328–345.
87. T. Nuida, T. Hozumi, W. Kosaka, S. Sakurai, S. Ikeda, T. Matsuda, H. Tokoro, K. Hashimoto and S.-I. Ohkoshi, Polyhedron, 2005, 24, 2901–2905.
88. S.-I. Ohkoshi, M. Mizuno, G.-J. Hung and K. Hashimoto, J. Phys. Chem. B, 2000, 104, 9365–9367.
89. Y. Sato, S.-I. Ohkoshi and K. Hashimoto, J. Appl. Phys., 2002, 92, 4834.
90. E. Coronado, M. Makarewicz, J. P. Prieto-Ruiz, H. Prima-Garcia and F. M. Romero, Adv. Mater., 2011, 23, 4323–4326.
91. E. Coronado, J. P. Prieto-Ruiz and H. Prima-Garcia, Chem. Commun., 2013, 49, 10145.
92. H. Prima-Garcia, E. Coronado, J. P. Prieto-Ruiz and F. M. Romero, Nanoscale Res. Lett., 2012, 7, 232.
93. W. E. Buschmann, S. C. Paulson, C. M. Wynn, M. A. Girtu, A. J. Epstein, H. S. White and J. S. Miller, Chem. Mater., 1998, 10, 1386–1395.
94. J. P. Prieto-Ruiz, F. M. Romero, H. Prima-García and E. Coronado, J. Mater. Chem. C, 2015, 3, 11122–11128.
95. L. Hedley, L. Porteous, D. Hutson, N. Robertson and J. O. Johansson, J. Mater. Chem. C, 2018, 6, 512–517.
96. D. R. Talham and M. W. Meisel, Chem. Soc. Rev., 2011, 40, 3356–3365.
97. A. Eschenlohr, M. Battiato, P. Maldonado, N. Pontius, T. Kachel, K. Holldack, R. Mitzner, A. Föhlisch, P. M. Oppeneer and C. Stamm, Nat. Mater., 2013, 12, 332–336.
98. A. Bleuzen, V. Marvaud, C. Mathonière, B. Sieklucka and M. Verdaguer, Inorg. Chem., 2009, 48, 3453–3466.
99. S.-I. Ohkoshi and K. Hashimoto, J. Photochem. Photobiol., C, 2001, 2, 71–88.
100. H. Tokoro and S. Ohkoshi, Dalton Trans., 2011, 40, 6825–6833.
101. O. Sato, Nat. Chem., 2016, 8, 644–656.
102. A. Asahara, M. Nakajima, R. Fukaya, H. Tokoro, S.-I. Ohkoshi and T. Suemoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195138.
103. M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1968, 10, 247–422.
104. B. Mayoh and P. Day, J. Chem. Soc., Dalton Trans., 1974, 846.
105. P. J. Reid, C. Silva, P. F. Barbara, L. Karki and J. T. Hupp, J. Phys. Chem., 1995, 99, 2609–2616.
106. P. Kambhampati, D. H. Son, T. W. Kee and P. F. Barbara, J. Phys. Chem. A, 2000, 104, 10637–10644.
107. D. H. Son, P. Kambhampati, T. W. Kee and P. F. Barbara, J. Phys. Chem. A, 2002, 106, 4591–4597.
108. M. Thoss and H. Wang, Chem. Phys. Lett., 2002, 358, 298–306.
109. C. Wang, B. K. Mohney, B. B. Akhremitchev and G. C. Walker, J. Phys. Chem. A, 2000, 104, 4314–4320.
110. K. M. Slenkamp, M. S. Lynch, J. F. Brookes, C. C. Bannan, S. L. Daifuku and M. Khalil, Struct. Dyn., 2016, 3, 023609.
111. S. D. Su, X. Q. Zhu, L. T. Zhang, Y. Y. Yang, Y. H. Wen, X. T. Wu, S. Q. Yang and T. L. Sheng, Dalton Trans., 2019, 48, 9303–9309.
112. M. S. Lynch, B. E. Van Kuiken, S. L. Daifuku and M. Khalil, J. Phys. Chem. Lett., 2011, 2, 2252–2257.
113. M. S. Lynch, K. M. Slenkamp and M. Khalil, J. Chem. Phys., 2012, 136, 241101.
114. B. P. Macpherson, P. V. Bernhardt, A. Hauser, S. Pagès and E. Vauthey, Inorg. Chem., 2005, 44, 5530–5536.
115. O. Sato, T. Iyoda, A. Fujishima and K. Hashimoto, Science, 1996, 272, 704–745.
116. J. Zimara, H. Stevens, R. Oswald, S. Demeshko, S. Dechert, R. A. Mata, F. Meyer and D. Schwarzer, Inorg. Chem., 2021, 60, 449–459.
117. M. B. Robin, Inorg. Chem., 1962, 1, 337–342.
118. D. M. Rogers and J. O. Johansson, J. Mater. Sci. Eng. B, 2018, 227, 28–38.
119. M. van Veenendaal, Sci. Rep., 2017, 7, 6672.
120. S. Watanabe, Y. Sawada, M. Nakaya, M. Yoshino, T. Nagasaki, T. Kameyama, T. Torimoto, Y. Inaba, H. Takahashi, K. Takeshita and J. Onoe, J. Appl. Phys., 2016, 119, 235102.
121. M. Cammarata, S. Zerdane, L. Balducci, G. Azzolina, S. Mazerat, C. Exertier, M. Trabuco, M. Levantino, R. Alonso-Mori, J. M. Glownia, S. Song, L. Catala, T. Mallah, S. F. Matar and E. Collet, Nat. Chem., 2021, 13, 10–14.
122. D. C. Arnett, P. Voehringer and N. F. Scherer, J. Am. Chem. Soc., 1995, 117, 12262–12272.
123. K. Wynne and R. M. Hochstrasser, Chem. Phys., 1993, 171, 179–188.
124. A. T. Yeh, C. V. Shank and J. K. McCusker, Science, 2000, 289, 935–938.
125. S. Wallin, J. Davidsson, J. Modin and L. Hammarstrom, J. Phys. Chem. A, 2005, 109, 4697–4704.
126. S. N. Ghosh, J. Inorg. Nucl. Chem., 1974, 36, 2465–2466.
127. D. Weidinger, D. J. Brown and J. C. Owrutsky, J. Chem. Phys., 2011, 134, 124510.
128. D. Hayes, R. G. Hadt, J. D. Emery, A. A. Cordones, A. B. F. Martinson, M. L. Shelby, K. A. Fransted, P. D. Dahlberg, J. Hong, X. Zhang, Q. Kong, R. W. Schoenlein and L. X. Chen, Energy Environ. Sci., 2016, 9, 3754–3769.
129. N. Shimamoto, S. I. Ohkoshi, O. Sato and K. Hashimoto, Inorg. Chem., 2002, 41, 678–684.
130. H. Kamioka, Y. Moritomo, W. Kosaka and S.-I. Ohkoshi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 180301.
131. Y. Moritomo, H. Kamioka, T. Shibata, S. Nozawa, T. Sato and S. I. Adachi, J. Phys. Soc. Jpn., 2013, 82, 033601.
132. Y. Fukuyama, N. Yasuda, H. Kamioka, J. Kim, T. Shibata, H. Osawa, T. Nakagawa, H. Murayama, K. Kato, Y. Tanaka, S. Kimura, T. Ohshima, H. Tanaka, M. Takata and Y. Moritomo, Appl. Phys. Express, 2010, 3, 016601.
133. S. Zerdane, M. Cammarata, L. Balducci, R. Bertoni, L. Catala, S. Mazerat, T. Mallah, M. N. Pedersen, M. Wulff, K. Nakagawa, H. Tokoro, S.-I. Ohkoshi and E. Collet, Eur. J. Inorg. Chem., 2018, 272–277.
134. L. Trinh, S. Zerdane, S. Mazérat, N. Dia, D. Dragoe, C. Herrero, E. Rivière, L. Catala, M. Cammarata, E. Collet and T. Mallah, Inorg. Chem., 2020, 59, 13153–13161.
135. A. Simonov, T. De Baerdemaeker, H. L. B. Bostrom, M. L. Rios Gomez, H. J. Gray, D. Chernyshov, A. Bosak, H. B. Burgi and A. L. Goodwin, Nature, 2020, 578, 256–260.
136. M. Van Veenendaal, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 125108.
137. H. Tokoro, S.-I. Ohkoshi and K. Hashimoto, Appl. Phys. Lett., 2003, 82, 1245.
138. H. Tokoro and S.-I. Ohkoshi, Bull. Chem. Soc. Jpn., 2015, 88, 227–239.
139. S.-I. Ohkoshi, H. Tokoro and E. Collet, C. R. Chim, 2019, 22, 498–507.
140. G. Azzolina, E. Collet, C. Mariette, M. Cammarata, E. Trzop, M. Sander, M. Levantino, K. Nakagawa, H. Tokoro, S.-I. Ohkoshi and R. Bertoni, Eur. J. Inorg. Chem., 2019, 3142–3147.
141. S. I. Ohkoshi, T. Nuida, T. Matsuda, H. Tokoro and K. Hashimoto, J. Mater. Chem., 2005, 15, 3291–3295.
142. H. Tokoro, T. Matsuda, T. Nuida, Y. Moritomo, K. Ohoyama, E. D. L. Dangui, K. Boukheddaden and S.-I. Ohkoshi, Chem. Mater., 2008, 20, 423–428.
143. H. Tokoro, T. Matsuda, K. Hashimoto and S.-I. Ohkoshi, J. Appl. Phys., 2005, 97, 10m508.
144. R. Fukaya, A. Asahara, S. Ishige, M. Nakajima, H. Tokoro, S.-I. Ohkoshi and T. Suemoto, J. Chem. Phys., 2013, 139, 084303.
145. H. Tokoro, K. Nakagawa, K. Imoto, F. Hakoe and S. I. Ohkoshi, Chem. Mater., 2012, 24, 1324–1330.
146. R. Garde, F. Villain and M. Verdaguer, J. Am. Chem. Soc., 2002, 124, 10531–10538.
147. J. O. Johansson, J. W. Kim, E. Allwright, D. M. Rogers, N. Robertson and J.-Y. Bigot, Chem. Sci., 2016, 7, 7061–7067.
148. K. D. Bozdag, J.-W. Yoo, N. P. Raju, A. C. McConnell, J. S. Miller and A. J. Epstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094449.
149. L. Hedley, M. D. Horbury, F. Liedy and J. O. Johansson, Chem. Phys. Lett., 2017, 687, 125–130.
150. Q. Zhang, A. V. Nurmikko, G. X. Miao, G. Xiao and A. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 064414.
151. R. D. Averitt and A. J. Taylor, J. Phys.: Condens. Matter, 2002, 14, R1357–R1390.
152. A. Kirilyuk, A. V. Kimel and T. Rasing, Rev. Mod. Phys., 2010, 82, 2731–2784.
153. T. Ogasawara, M. Matsubara, Y. Tomioka, M. Kuwata-Gonokami, H. Okamoto and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 180407(R).
154. A. V. Kimel, R. V. Pisarev, J. Hohlfeld and T. Rasing, Phys. Rev. Lett., 2002, 89, 287401.
155. S. Otto, M. Dorn, C. Förster, M. Bauer, M. Seitz and K. Heinze, Coord. Chem. Rev., 2018, 359, 102–111.
156. V. G. Sala, S. Dal Conte, T. A. Miller, D. Viola, E. Luppi, V. Véniard, G. Cerullo and S. Wall, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 014430.
157. F. Guo, N. Zhang, W. Jin and J. Chang, J. Chem. Phys., 2017, 146, 244502.
158. D. Giovanni, H. Ma, J. Chua, M. Grätzel, R. Ramesh, S. Mhaisalkar, N. Mathews and T. C. Sum, Nano Lett., 2015, 15, 1553–1558.
159. P. Somani and S. Radhakrishnan, Mater. Chem. Phys., 2002, 76, 15–19.
160. S. Ravaine, C. Lafuente and C. Mingotaud, Langmuir, 1998, 14, 6347–6349.
161. O. N. Risset, T. V. Brinzari, M. W. Meisel and D. R. Talham, Chem. Mater., 2015, 27, 6185–6188.
162. P. Perlepe, I. Oyarzabal, A. Mailman, M. Yquel, M. Platunov, I. Dovgaliuk, M. Rouzières, P. Négrier, D. Mondieig, E. A. Suturina, M.-A. Dourges, S. Bonhommeau, R. A. Musgrave, K. S. Pedersen, D. Chernyshov, F. Wilhelm, A. Rogalev, C. Mathonière and R. Clérac, Science, 2020, 370, 587–592.
163. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
164. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
165. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamaki and R. A. Layfield, Science, 2018, 362, 1400–1403.

---