Open Access Article
Open Access ArticleMagneto-structural studies of an unusual [MnIIIMnIIGdIII(OR)4]4− partial cubane from 2,2′-bis-p-tBu-calix[4]arene†‡
Marco
Coletta
 ab,
Sergio
Sanz
ab,
Sergio
Sanz
 b,
Daniel J.
Cutler
b,
Simon J.
Teat
b,
Daniel J.
Cutler
b,
Simon J.
Teat
 c,
Kevin J.
Gagnon
c,
Mukesh K.
Singh
c,
Kevin J.
Gagnon
c,
Mukesh K.
Singh
 *b,
Euan K.
Brechin
*b,
Euan K.
Brechin
 *b and
Scott J.
Dalgarno
*b and
Scott J.
Dalgarno
 *a
*a
aInstitute of Chemical Sciences, Heriot-Watt University, Riccarton, Edinburgh, Scotland EH14 4AS, UK. E-mail: S.J.Dalgarno@hw.ac.uk
bEastCHEM School of Chemistry, The University of Edinburgh, David Brewster Road, Edinburgh, Scotland EH9 3FJ, UK. E-mail: ebrechin@ed.ac.uk; mklsingh36@gmail.com
cStation 11.3.1, Advanced Light Source, Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA94720, USA
First published on 14th October 2020
Abstract
Reaction of 2,2′-bis-p-tBu-calix[4]arene (H8L) with MnCl2·4H2O, GdCl3·6H2O and 2,6-pyridinedimethanol (H2pdm) affords [MnIIIMnIIGdIII(H3L)(pdmH)(pdm)(MeOH)2(dmf)]·3MeCN·dmf (3·3MeCN·dmf) upon vapour diffusion of MeCN into the basic dmf/MeOH mother liquor. 3 crystallises in the tetragonal space group P41212 with the asymmetric unit comprising the entire cluster. The highly unusual core contains a triangular arrangement of MnIIIMnIIGdIII ions housed within a [MnIIIMnIIGdIII(OR)4]4− partial cubane. Magnetic susceptibility and magnetisation data reveal best fit parameters JMn(II)–Mn(III) = +0.415 cm−1, JMn(III)–Gd(III) = +0.221 cm−1, JMn(II)–Gd(III) = −0.258 cm−1 and DMn(III) = −4.139 cm−1. Theoretically derived magnetic exchange interactions, anisotropy parameters, and magneto-structural correlations for 3 are in excellent agreement with the experimental data.
Introduction
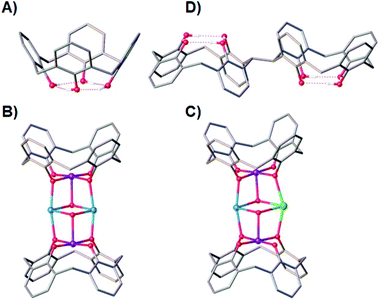
Ligand design has always been central to the evolution of molecular magnetism, whether that be in order to manipulate exchange interactions,1 direct magnetic anisotropy,2 enhance magnetocalorics,3 develop quantitative magneto-structural correlations,4 construct specific topologies,5 or self-assemble aesthetically pleasing structures – sometimes of enormous nuclearity.6 Combined with ever-improving technical capabilities and theory, progress in this diverse field continues apace.7p-tBu-calix[4]arene (TBC[4], molecular framework minus tBu groups shown in Fig. 1A) has proven to be a highly versatile ligand for the synthesis of a breadth of polymetallic transition metal (TM), lanthanide metal (LnM) and 3d–4f complexes, in which TM/LnM-TBC[4] moieties act as capping vertices.8 The TBC[4] polyphenolato pocket is particularly suited to binding the Jahn–Teller (JT) distorted MnIII ion, because it can happily accommodate four short equatorial bonds and two long axial bonds. A good illustration of this comes in the complexes [MnIII2MnII2(OH)2(TBC[4])2(dmf)6] (1, Fig. 1B) and [MnIII2MnIIGdIII(OH)2(TBC[4])2(NO3)(solvent)6] (2, Fig. 1C) whose structures can be considered as two [MnIII(TBC[4])(OH)(DMF)] metalloligands encapsulating two MnII ions (1) or one MnII ion and one GdIII ion (2).9
This general bonding motif has been exploited in the construction of a library of coordination compounds, allowing for the development of detailed empirical metal ion binding rules for TBC[4].10 Under ambient reaction conditions, TBC[4] preferentially binds TMIII ions, will bind TMII ions in the absence of TMIII ions, and will bind LnMIII ions in the absence of TMII or TMIII ions.11
One might expect that a systematic move to p-tBu-calix[8]arene would result in ready binding of two MnIII ions, however the nature of the ligand (e.g. pleated-loop) means that the polyphenolato pockets do not behave exactly as two TBC[4] equivalents. Instead, this ligand prefers to bind LnIII ions under the standard conditions we employ, though forcing conditions can be used to form Mn-based clusters.12 Although that is the case, the recent synthesis of TBC[4] molecules modified at one methylene bridge position allows this chemistry to be systematically expanded to include bis-TBC[4] molecules, an important example of which with respect to this paper is 2,2′-bis-p-tBu-calix[4]arene (H8L, Fig. 1D).13 This synthetic move to H8L presents a molecule that truly represents two TBC[4]s as opposed to TBC[8], and a perfect opportunity to translate the aforementioned empirical metal ion binding rules.
The conformational flexibility (ring inversion) of TBC[4] in solution is well known,14 and in the case of H8L, presents the possibility of having a ligand with eight phenolic O-atoms in close proximity and, importantly, all converging/oriented in the same direction. This is very attractive from the perspective of polymetallic cluster growth with paramagnetic ions. We have recently begun exploring 3d, 4f and 3d–4f cluster formation with H8L, and in doing so have reported a range of new clusters with varied nuclearity: [Mn8], [Mn10], [Mn20], [Mn6Gd2], [Mn8Gd2], [Mn4Gd4], [Fe5Gd4], [Cu13] and [Cu4Tb5].15 All of these cases show clear, systematic extension of the empirical metal ion binding rules established for TBC[4]. H8L has therefore already provided a wealth of new structural chemistry, and shows much promise for the discovery of fascinating new complexes (particularly when one considers the possibility of co-ligand addition, a common approach employed in cluster synthesis). Herein, we outline the synthesis, structure and magnetic behaviour of a new bis-TBC[4]-supported complex, [MnIIIMnIIGdIII(H3L)(pdmH)(pdm)(MeOH)2(dmf)]·3MeCN·dmf (3·3MeCN·dmf; pdmH2 = 2,6-pyridinedimethanol), together with theoretical magneto-structural studies examining the exchange interactions. The presence of the co-ligand in the resulting assembly breaks our empirical metal ion binding rules, and in doing so affords this new triangular cluster that is of interest from various perspectives.
Results and discussion
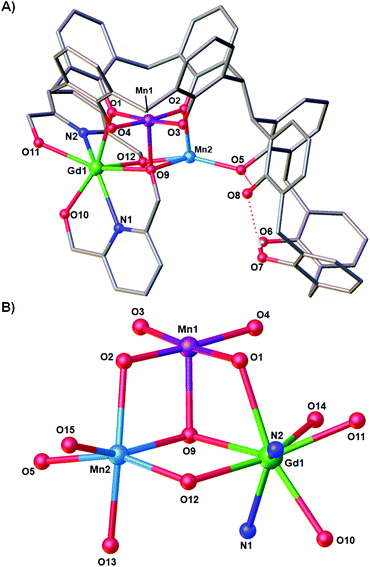
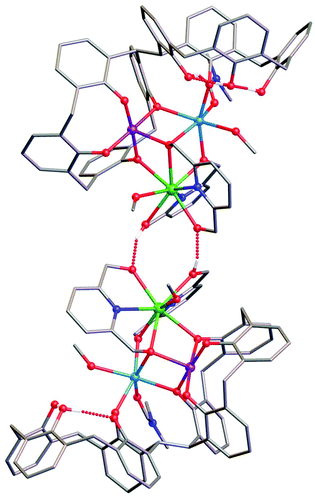
Reaction of H8L with MnCl2·4H2O, GdCl3·6H2O and H2pdm (in the presence of base, Et3N) affords single crystals of [MnIIIMnIIGdIII(H3L)(pdmH)(pdm)(MeOH)2(dmf)]·3MeCN·dmf (3·3MeCN·dmf, Fig. 2), upon vapour diffusion of MeCN into the basic dmf/MeOH mother liquor. The crystals were found to be in a tetragonal cell and structure solution was carried out in the space group P41212. The ASU comprises the entire cluster, which has a triangular arrangement of MnIIIMnIIGdIII ions housed in a [MnIIIMnIIGdIII(OR)4]4− partial cubane. The bis-TBC[4] ligand has undergone conformational change although one of the calixarene binding sites remains unoccupied. This contravenes our established binding rules for this relatively new ligand, and we hypothesise that this is due to the steric constraints enforced by the pdm/pdmH co-ligands that play an important role in directing the prevailing structure.Mn1 is in the trivalent state (Table S1‡) and is bound in a TBC[4] lower-rim tetraphenolato pocket (Mn1–O1–4, 1.873(8)–1.974(9) Å). Its coordination sphere is completed by a μ3-O atom belonging to the pdm molecule (Mn1–O9, 2.091(8) Å), which is also bonding Mn2 and Gd1 (Mn2–O9, 2.278(8) Å and Gd1–O9, 2.477(8) Å). There is a sixth, longer contact to a MeCN molecule sitting in the calixarene cavity (Mn1–C020, ∼4 Å) and thus one can consider Mn1 as being either square pyramidal or pseudo-octahedral in geometry. Mn2 is in the bivalent state, adopting a distorted octahedral geometry and is located between the two TBC[4] moieties generated through inversion of the ligand. It is bonded to two μ-phenoxides belonging to separate TBC[4] moieties (Mn2–O2, 2.224(8) Å and Mn2–O5, 2.150(8) Å), a μ-O atom of the pdmH molecule (Mn2–O12, 2.097(10) Å), a ligated dmf molecule (Mn2–O15, 2.187(11) Å) and a ligated methanol molecule (Mn2–O13, 2.225(10) Å). Gd1 is octacoordinate, is in a square antiprismatic geometry and is bonded to a phenolic oxygen (Gd1–O1, 2.393(9) Å), a ligated methanol molecule (Gd1–O14, 2.457(10) Å) and the two pdm/H ligands (Gd1–N1, 2.519(12) Å; Gd1–O10, 2.331(9) Å; Gd1–O11, 2.404(9); Gd1–N2, 2.520(12) Å and Gd1–O12, 2.296(10) Å). Structure expansion reveals that the clusters pack via H-bonding interactions along the c axis, occurring between the protonated and deprotonated OH/O groups of neighbouring H-pdm/pdm molecules (O10⋯O11′, ∼2.47 Å). The shortest metal–metal inter-cluster distance (∼5.9 Å) also occurs along the c axis, between two neighbouring Gd ions (Fig. 3).
There are several points of interest to this seemingly rather simple structure. Complex 3 is in fact the first reported example of a heterometallic [Mn2Gd] triangle containing Mn in the trivalent and bivalent states (Table S1‡). The only other such triangle in the CSD has both Mn ions in the III+ oxidation state.16 There is also a single [MnGd2] species known, with Mn in the tetravalent state.17 The triangular [MnIIIMnIIGdIII] unit in compound 3 is also found in compound 2 and as a moiety in [Mn8Gd2].9 Notably this is the first time that a TBC[4] polyphenolato pocket has ever been found to be unoccupied in our studies on 3d/4f coordination chemistry, and it is also the first example in which the bis-TBC[4] ligand is not fully deprotonated, acting here as a penta- (H3L) rather than octa-anion (L). As with all our other studies on TBC[4] and bis-TBC[4], the MnIII ion preferentially sits in the polyphenolic pocket and acts as a [MnIII(TBC[4])]− capping fragment/metalloligand.
Magnetic behaviour
The direct current (dc) molar magnetic susceptibility, χ, of a freshly prepared polycrystalline sample of 3 was measured in an applied field, B, of 0.5 T, over the 2–300 K temperature, T, range. The experimental results are showed in Fig. 4, in the form of the χMT product, where χ = M/B, and M is the magnetisation of the sample. At room temperature the χMT product of 3 has a value of 15.0 cm3 K mol−1, in good agreement with the sum of the Curie constants for non-interacting MnIII (s = 2), MnII (s = 5/2) and GdIII (s = 7/2) ions, assuming g = 2.00 (15.25 cm3 k mol−1). As temperature decreases, the χMT product remains essentially invariant to ∼50 K before increasing slightly to reach a value of ∼15.2 cm3 K mol−1 at T = 20 K, before abruptly decreasing to a value of ∼9.0 cm3 K mol−1 at T = 2.0 K. This is clearly indicative of the presence of very weak magnetic exchange interactions. In order to gain more insight into the low temperature energy spectrum of 3, low temperature variable-temperature-and-variable-field (VTVB) magnetisation data were measured in the temperature range 2–7 K, in magnetic fields from 0.5 to 7.0 T (Fig. 4 inset). At the lowest temperature and highest field, M reaches a value of ∼15.2 μB. To quantitatively interpret the magnetic properties of 3, we use the following general spin-Hamiltonian (1):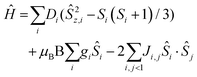 | (1) |
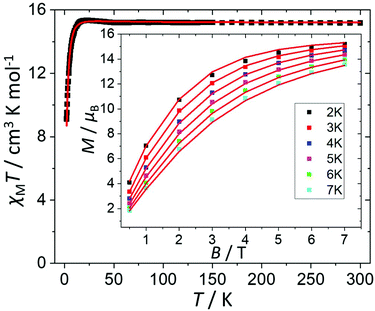 | ||
| Fig. 4 Plot of χMT vs. T in the range T = 2–300 K and B = 0.5 T. Inset: field dependence of the magnetization (M) measured in the T = 2–7 K and B = 0.5–7.0 T temperature and field ranges. The (□) symbols represent the experimental data and the solid red lines the fit of the experimental data to spin-Hamiltonian (1). See text for details. | ||
The χMT and VTVB magnetisation data were simultaneously fitted to spin-Hamiltonian (1) using the program PHI assuming three different exchange interactions in the [MnIIIMnIIGdIII] triangle.18 This results in the following best fit (error) parameters: JMn(II)–Mn(III) = +0.415 (1.4 × 10−2) cm−1, JMn(III)–Gd(III) = +0.221 (5.7 × 10−3) cm−1, JMn(II)–Gd(III) = −0.258 (3.8 × 10−3) cm−1 and DMn(III) = −4.139 (4.8 × 10−2) cm−1, with the g-factors fixed at g = 2.00 for MnII and GdIII and g = 1.98 for MnIII. Therefore, the MnIII–MnII interaction and the MnIII–GdIII interaction are very weakly ferromagnetic and the MnII–GdIII interaction is very weakly antiferromagnetic. These parameters are similar to those found for complex 2.9 With these parameters the ground spin-state of 3, when only the isotropic part of spin-Hamiltonian (1) is taken into account, is an S = 4 spin-state, lying very close to several excited spin states (Fig. 5).
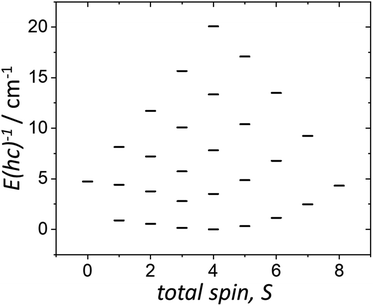 | ||
| Fig. 5 Energy spectrum of 3 at zero magnetic field, for the isotropic part of spin-Hamiltonian (1), with the determined best-fit parameters, as described in the text. | ||
Theoretical studies
To understand the origin of the magnetic exchange interactions in more detail we have performed ab initio calculations on a model complex, 3A (Fig. S1‡), using the MOLCAS 8.0 suite.19 Model 3A has the same structure as 3, but with the terminal tBu groups on the calixarene ligand replaced with Me groups to reduce computational cost.We have first performed ab initio CASSCF20/RASSI-SO21/SINGLE_ANISO22 calculations on the individual paramagnetic ions. The MnIII centre shows moderate easy-axis anisotropy (D = −3.3 cm−1, E = 0.1 cm−1, gxx/gyy/gzz = 1.99/1.99/1.96), whereas the other two paramagnetic centres, GdIII and MnII, are found to be isotropic (gxx = gyy = gzz = 2.00). These values are as expected, and in accordance with the experimental values. Next, we have performed POLY_ANISO calculations, which includes the Lines model, to estimate the magnetic coupling constants.23 The so-obtained exchange interactions are given in Table 1 and are in good agreement with the experimental values and simulate the susceptibility data well (Fig. 6a). The JMn(II)–Mn(III) and JMn(III)–Gd(III) interactions are found to be weakly ferromagnetic, whereas JMn(II)–Gd(III) is found to be weakly antiferromagnetic. It is worth noting that for both JMn(II)–Gd(III) and JMn(III)–Gd(III) the dipolar contribution is calculated to be dominant, as seen previously for other 3d–4f complexes.24
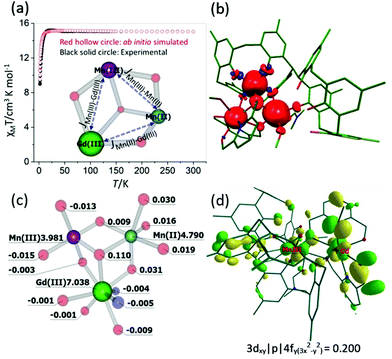 | ||
| Fig. 6 (a) Ab initio simulated, temperature dependent χMT versus T data for 3. The solid black circles are the experimental data and the hollow red circles the ab initio derived data. The core structure of 3 with magnetic coupling scheme is shown in the inset. (b) and (c) DFT computed spin density plot together with spin density values on selected atoms for model 3A. (d) Representative molecular orbital showing the 3dxy|p|4fy(3x2−y2) interaction for MnIII–GdIII pair. See Table S2‡ for the computed overlap integral values for the MnII–GdIII, MnII–GdII and MnII–MnIII pairs. | ||
| J total/cm−1 | J exchange/cm−1 | J dipolar/cm−1 | |
|---|---|---|---|
| J Mn(II)–Mn(III) | +0.50 | +0.52 (1.04/1.10) | −0.02 |
| J Mn(III)–Gd(III) | +0.10 | −0.12 (−0.08/−0.08) | +0.22 |
| J Mn(II)–Gd(III) | −0.16 | +0.08 (0.12/0.14) | −0.24 |
To further confirm the magnetic exchange values, we have performed density functional theory (DFT) calculations in the G09 suite using two different methods (see computational details section for more information).25 In the first method, we have performed calculations on model 3A. In the second method, we have performed pairwise exchange interaction calculations on model complexes containing only two paramagnetic centres, replacing the third paramagnetic centre with a diamagnetic element, i.e. GdIII/MnIII/MnII with YIII/GaIII/ZnII, respectively (Fig. S1(b)–(d)).‡ The computed magnetic exchange values from both methods are in good agreement with the ab initio calculated values (Table 1).
The spin densities for model 3A (Fig. 6(b) and (c), Fig. S2‡) reveal that while dominant spin delocalisation is observed for both the MnIII (3.981) and MnII (4.790) ions, spin polarisation is detected for GdIII (7.038). The μ3-bridging O-atom (O9, Fig. 2) has a spin density of 0.110, more than three times higher than any other bridging atoms in the molecule, and is therefore expected to play a dominant role in the magnetic superexchange. It is also worth mentioning here that the p-Me groups, which we have used in place of the tBu groups in 3A have a spin density very close to zero, suggesting the model to be reliable.
Previous studies performed on 3d–4f complexes have emphasised the importance of the 3d orbitals of the transition metals in controlling the two possible contributions (JF and JAF) to the total magnetic exchange interaction.26 The first contribution, JF, where partial electron transfer occurs from the 3d orbitals of the MnIII/MnII ions to the empty 5d/6s orbitals of GdIII ion, adds to the ferromagnetic part of the magnetic exchange interaction. The larger the charge transfer the larger the ferromagnetic contribution. The second contribution, JAF, arises from overlap between the non-orthogonal, singly occupied molecular orbitals (SOMOs) of the 3d ion with the half- filled 4f orbitals of the GdIII ions. The former contribution to the magnetic exchange interaction can be estimated using natural bonding orbital (NBO) analysis which investigates the charge transfer, whereas the latter contribution can be estimated by performing overlap integral calculations. For JexchangeMn(II)–Gd(III), all the overlap integral values are small leading to a small ferromagnetic exchange interaction (Table S2‡). For JexchangeMn(III)–Gd(III), one overlap integral value is estimated to be relatively strong (3dxy|p|4fy(3x2−y2), Fig. 6d) leading to a small anti-ferromagnetic exchange interaction. This is opposite to that obtained from the experimental fit, though we note the absolute magnitide of the difference is extremely small. Larger charge transfer from MnII(3d) → GdIII(6s/5d) compared to MnIII(3d) → GdIII(6s/5d) further supports this. For JexchangeMn(II)–Gd(III) all the overlap integral values are estimated to be small leading to a small ferromagnetic exchange interaction.
To investigate these interactions a little further, we have performed a magneto-structural correlation by varying the MnIII/MnII–O–GdIII angle, the MnIII/II/GdIII–O distance and the MnIII/II–O–GdIII–O dihedral angle on bimetallic model complexes designed from complex 3. The models 3Mn(II)–Gd(III) and 3Mn(III)–Gd(III) are shown in Fig. 7(a) and (b), respectively. The sign and magnitude of JexchangeMn(II)–Gd(III) and JexchangeMn(III)–Gd(III) are in good agreement with those in Table 1 (+0.26 cm−1 and −0.22 cm−1, respectively). Magneto-structural correlations developed for JexchangeMn(II)–Gd(III) and JexchangeMn(III)–Gd(III) suggest that the MnIII/MnII–O–GdIII angle is the most dominant structural parameter (Fig. 7(c) and (d), Fig. S3‡). At smaller angles the antiferromagnetic interaction is favoured, at the larger angles the ferromagnetic interaction is favoured. This is as expected, since at smaller angles larger overlap between the Gd(4f) and MnII/III(3d) orbitals are observed, diminishing with increasing angle (Fig. S4, Tables S3 and S4‡). These findings are in agreement with previous theoretical studies on di-, tri- and tetranuclear MnIII–GdIII cluster compounds.26
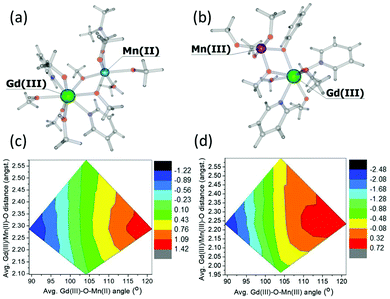 | ||
| Fig. 7 Models 3Mn(II)–Gd(III) (a) and 3(Mn(III)–Gd(III) (b) together with the magneto-structural correlation contour plots (c) and (d) performed by varying the average MnII/MnIII–O–GdIII angle and average MnIII/II/GdIII–O distance with respect to the magnetic exchange coupling constants JexchangeMn(II)–Gd(III) and JexchangeMn(III)–Gd(III). The keys represents the magntidue of the exchange, ranging from most antiferromagnetic (black) to most ferromagnetic (red). For both models, the change in the magnitude of the interaction with respect to the change in MnIII/II–O–GdIII–O dihedral angle is minimal. See Fig. S3 of the ESI for more details.‡ | ||
In search of models representing JexchangeMn(II)–Mn(III), we have developed two different models (3Mn(II)–Mn(III) − 1 and 3Mn(II)–Mn(III) − 2, Fig. S5‡). In both models the rigidity provided by the 2,2′-bis-p-tBu-calix[4]arene ligand needs to be removed in order to obtain a model whereby structural parameters can be fine-tuned. However, as soon as we remove H8L, the sign of the magnetic exchange interaction switches from ferromagnetic to antiferromagnetic (Fig. S5‡) due to presence of two strong magnetic orbital overlaps (Mn(II)dyz|p|Mn(III)dz2 and Mn(II)dx2−y2|p|Mn(III)dz2 for 3Mn(II)–Mn(III) − 1 and Mn(II)dyz|p|Mn(III)dz2 and Mn(II)dxz|p|Mn(III)dz2 for 3Mn(II)–Mn(III) − 2, Table S5, Fig. S6 and 7‡). Although this renders any further investigation moot, the above does highlight both the structural and magnetic importance of the calixarene ligand. Ligand rigidity is rarely a consideration in design criteria when contemplating the nature of magnetic exchange. Considering the bond angles and distances in 3 in tandem with previous magneto-structural studies developed for a variety of MnIII–MnII species, would infer a small ferromagnetic interaction being present in complex 3, in agreement with our calculated JexchangeMn(II)–Mn(III) value.27
Conclusions
Reaction of bis-TBC[4] with MnCl2·4H2O, GdCl3·6H2O and H2pdm results in the formation of the complex [MnIIIMnIIGdIII(H3L)(pdmH)(pdm)(MeOH)2(dmf)] (3) whose structure describes a triangular arrangement of MnIIIMnIIGdIII ions housed in a [MnIIIMnIIGdIII(OR)4]4− partial cubane. Although the bis-TBC[4] has undergone conformational change as the penta-anion (Fig. 2A), one lower-rim pocket remains unoccupied which is likely due to the steric constraints enforced by the co-ligands. Compound 3 is the first example of a heterometallic [Mn2Gd] triangle containing Mn in the trivalent and bivalent states, although this unit has previously been observed within the larger species [MnIII2MnIIGdIII] (2) and [Mn8Gd2], constructed from TBC[4] and bis-TBC[4], respectively. Susceptibility and magnetisation data reveal very weak exchange interactions between the constituent metal centres, with best fit parameters JMn(II)–Mn(III) = +0.415 (1.4 × 10−2) cm−1, JMn(III)–Gd(III) = +0.221 (5.7 × 10−3) cm−1, JMn(II)–Gd(III) = −0.258 (3.8 × 10−3) cm−1 and DMn(III) = −4.139 (4.8 × 10−2) cm−1, consistent with those seen in [MnIII2MnIIGdIII] (2). Ab initio calculated magnetic exchange interactions, anisotropy parameters, and theoretical magneto-structural correlations for 3 are found to be in excellent agreement with the experimental data, highlighting the importance of MnIII/MnII–O–GdIII angles and the rigidity of the 2,2′-bis-p-tBu-calix[4]arene (H8L) ligand in governing the sign and magnitude of the exchange interactions.Experimental section
H8L was synthesised according to literature procedure.13Synthesis of [MnIIIMnIIGdIII(H3L)(pdmH)(pdm)(MeOH)2(dmf)]·3MeCN·dmf, 3·3MeCN·dmf
H8L (150 mg, 0.116 mmol), MnCl2·4H2O (23 mg, 0.116 mmol), GdCl3·6H2O (35 mg, 0.116 mmol) and pdmH2 (32.2 mg, 0.232 mmol) were suspended in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dmf/MeOH mixture (20 mL) and stirred for 10 minutes. Et3N (0.15 mL) was added and the resulting purple solution was stirred for additional 2 hours and then filtered. The mother liquor was allowed to slowly diffuse with acetonitrile vapours, affording dark purple crystals suitable for X-ray diffraction studies. Elemental analysis (%) calculated for 1, C116H151Mn2GdN7O16 (M = 2166.6): C, 64.31%; H, 7.02%; N, 4.53%. Found: C, 64.24%; H, 6.83%; N, 4.23%. Yield 51 mg (20.3%). Crystal data for 3 (CCDC 2020261‡): C116H151Mn2GdN7O16, M = 2166.6, 0.3 × 0.03 × 0.01 mm3, tetragonal, space group P41212 (no. 92), a = 23.2275(8) Å, c = 44.2459(18) Å, V = 23
1 dmf/MeOH mixture (20 mL) and stirred for 10 minutes. Et3N (0.15 mL) was added and the resulting purple solution was stirred for additional 2 hours and then filtered. The mother liquor was allowed to slowly diffuse with acetonitrile vapours, affording dark purple crystals suitable for X-ray diffraction studies. Elemental analysis (%) calculated for 1, C116H151Mn2GdN7O16 (M = 2166.6): C, 64.31%; H, 7.02%; N, 4.53%. Found: C, 64.24%; H, 6.83%; N, 4.23%. Yield 51 mg (20.3%). Crystal data for 3 (CCDC 2020261‡): C116H151Mn2GdN7O16, M = 2166.6, 0.3 × 0.03 × 0.01 mm3, tetragonal, space group P41212 (no. 92), a = 23.2275(8) Å, c = 44.2459(18) Å, V = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 871.4(19) Å3, Z = 8, Bruker D8 diffractometer equipped with a PHOTON 100 detector, synchrotron radiation, λ = 0.7749 Å, T = 100(15) K, 2θmax = 48.852°, 151
871.4(19) Å3, Z = 8, Bruker D8 diffractometer equipped with a PHOTON 100 detector, synchrotron radiation, λ = 0.7749 Å, T = 100(15) K, 2θmax = 48.852°, 151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662 reflections collected, 15
662 reflections collected, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 095 unique (Rint = 0.0531). Final GooF = 1.037, R1 = 0.0854, wR2 = 0.1763.
095 unique (Rint = 0.0531). Final GooF = 1.037, R1 = 0.0854, wR2 = 0.1763.
Computational details
We have performed ab initio CASSCF20/RASSI-SO21/SINGLE_ANISO22 calculations on a model complex, 3A, made from the X-ray structure to estimate the magnetic coupling constants in complex 3 using the MOLCAS 8.0 suite.19 We have considered each paramagnetic ion separately by keeping the ions of interest and substituting the third paramagnetic ion with a diamagnetic ion, i.e. GdIII/MnIII/MnII with YIII/GaIII/ZnII. We have used the H.ANO-RCC…2s., C.ANO-RCC…3s2p., N.ANO-RCC…3s2p., O.ANO-RCC…3s2p1d., Mn.ANO-RCC…5s4p2d1f., Zn.ANO-RCC…5s4p2d., Ga.ANO-RCC…5s4p1d., Y.ANO-RCC…6s5p3d., Gd.ANO-RCC…7s6p4d2f1g basis sets.28 During CASSCF calculations for a single GdIII ion, we have used seven electrons in seven active 4f orbitals. For the MnIII and MnII ions we have used four and five electrons, respectively, in five active 3d orbitals. Next, in the RASSI-SO step for the GdIII ion, we have used 1, 48 and 76 roots for the octet, sextet and quartet spin multiplicities. For the MnIII ion, 5, 45 and 50 roots for quintet, triplet and singlet spin multiplicities have been used, respectively. For the MnII ion, 1, 24 and 75 roots for sextet, quartet and doublet spin multiplicities have been used, respectively.24,29 The resultant spin–orbit multiplets have been used further to estimate local magnetic properties via the SINGLE_ANISO approach.22 The magnetic exchange interactions (Js) have been computed between all paramagnetic ions for all complexes by fitting ab initio POLY_ANISO with the experimental data.23aWe have also used the G09 programme on model complex 3A to estimate the magnetic coupling constant.25 Noodlemann's broken symmetry30 together with the B3LYP functional31 is known to be a reliable approach to estimate magnetic exchange coupling constants.32 We have used the relativistically corrected effective core potential (ECP) basis set of Cundari and Stevens (CSDZ) for the GdIII ion,33 Ahlrichs-TZV basis set for the Mn ions,34 and the 6-31G** basis set for O, N, C and H atoms.35 We have computed four spin configurations to estimate three possible exchange coupling constants. The computed spin configurations include a high spin configuration with all spins up and three other configurations with one of the spin centres down. We have used the same methodology mentioned earlier for performing natural bonding orbitals (NBOs) analysis to investigate the charge transfer.32d,e
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the EPSRC for financial support under grant reference numbers EP/I03255X/1 and EP/I031421/1, and the Marie Skłodowska-Curie actions (MSCA) for grant MMQIP 832488 (to MKS). We also thank Heriot-Watt University for financial support for M. C. through the James-Watt Scholarship programme. This research used resources of the Advanced Light Source, a U.S. DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.Notes and references
- (a) O. Kahn, P. Tola, J. Galy and H. Coudanne, J. Am. Chem. Soc., 1978, 100(12), 3931 CrossRef CAS; (b) T. Mallah, A. Marvilliers and E. Rivière, Philos. Trans. R. Soc., A, 1999, 357, 3139 CrossRef CAS.
- (a) M. Murrie, Chem. Soc. Rev., 2010, 39, 1986 RSC; (b) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- (a) G. Lorusso, O. Roubeau and M. Evangelisti, Angew. Chem., Int. Ed., 2016, 55, 3360 CrossRef CAS; (b) G. Lorusso, E. Natividad, M. Evangelisti and O. Roubeau, Mater. Horiz., 2019, 6, 144 RSC.
- (a) H. Weihe and H.-U. Güdel, J. Am. Chem. Soc., 1998, 120(12), 2870 CrossRef CAS; (b) C. J. Milios, R. Inglis, A. Vinslava, R. Bagai, W. Wernsdorfer, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 12505 CrossRef CAS.
- (a) L. N. Dawe, K. V. Shuvaev and L. K. Thompson, Inorg. Chem., 2009, 48, 3329 CrossRef; (b) E. Garlatti, T. Guidi, S. Ansbro, P. Santini, G. Amoretti, J. Ollivier, H. Mutka, G. Timco, I. Vitorica-Yrezabal, G. Whitehead, R. E. P. Winpenny and S. Carretta, Nat. Commun., 2017, 8, 14543 CrossRef CAS; (c) M. S. Fataftah and D. E. Freedman, Chem. Commun., 2018, 54, 13773 RSC.
- (a) X.-Y. Zheng, Y.-H. Jiang, G.-L. Zhuang, D.-P. Liu, H.-G. Liao, X.-J. Kong, L.-S. Long and L.-S. Zheng, J. Am. Chem. Soc., 2017, 139, 18178 CrossRef CAS; (b) W.-P. Chen, P.-Q. Liao, P.-B. Jin, L. Zhang, B.-K. Ling, S.-C. Wang, Y.-T. Chan, X.-M. Chen and Y.-Z. Zheng, J. Am. Chem. Soc., 2020, 142, 4663 CrossRef CAS.
- (a) E. Garlatti, L. Tesi, A. Lunghi, M. Atzori, D. J. Voneshen, P. Santini, S. Sanvito, T. Guidi, R. Sessoli and S. Carretta, Nat. Commun., 2020, 11, 1751 CrossRef CAS; (b) T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972 RSC; (c) J. Schnack, Dalton Trans., 2010, 39, 4677 RSC.
- M. Coletta, E. K. Brechin and S. J. Dalgarno, Structural Trends in Calix[4]arene-Supported Cluster Chemistry, in Calixarenes and Beyond, ed. P. Neri, J. Sessler and M.-X. Wang, Springer International Publishing, 2016, pp. 671–689 Search PubMed.
- (a) G. Karotsis, S. J. Teat, W. Wernsdorfer, S. Piligkos, S. J. Dalgarno and E. K. Brechin, Angew. Chem., Int. Ed., 2009, 48, 8285 CrossRef CAS; (b) S. M. Taylor, G. Karotsis, R. D. McIntosh, S. Kennedy, S. J. Teat, C. M. Beavers, W. Wernsdorfer, S. Piligkos, S. J. Dalgarno and E. K. Brechin, Chem. – Eur. J., 2011, 17, 7521 CrossRef CAS; (c) M. A. Palacios, R. McLellan, C. M. Beavers, S. J. Teat, H. Weihe, S. Piligkos, S. J. Dalgarno and E. K. Brechin, Chem. – Eur. J., 2015, 21, 11212 CrossRef CAS.
- (a) C. Aronica, G. Chastanet, E. Zueva, S. A. Borshch, J. M. Clemente-Juan and D. Luneau, J. Am. Chem. Soc., 2008, 130, 2365 CrossRef CAS; (b) G. Karotsis, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, Angew. Chem., Int. Ed., 2009, 48, 9928 CrossRef CAS; (c) G. Karotsis, S. Kennedy, S. J. Teat, C. M. Beavers, D. A. Fowler, J. J. Morales, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, J. Am. Chem. Soc., 2010, 132, 12983 CrossRef CAS; (d) S. Sanz, K. Ferreira, R. D. McIntosh, S. J. Dalgarno and E. K. Brechin, Chem. Commun., 2011, 47, 9042 RSC; (e) S. Sanz, R. D. McIntosh, C. M. Beavers, S. J. Teat, M. Evangelisti, E. K. Brechin and S. J. Dalgarno, Chem. Commun., 2012, 48, 1449 RSC; (f) G. Karotsis, S. Kennedy, S. J. Dalgarno and E. K. Brechin, Chem. Commun., 2010, 46, 3884 RSC.
- (a) M. Coletta, S. Sanz, E. K. Brechin and S. J. Dalgarno, Chemistry, 2020, 2, 253 CrossRef.
- S. Du, H. Ke, Y. Bi, H. Tan, Y. Yu, J. Tang and W. Liao, Inorg. Chem. Commun., 2013, 29, 85 CrossRef CAS.
- L. T. Carroll, P. A. Hill, C. Q. Ngo, K. P. Klatta and J. L. Fantini, Tetrahedron, 2013, 69, 5002 CrossRef CAS.
- I. Thondorf, in Calixarenes 2001, Kluwer Academic, Dordrecht, 2001, ch. 15 Search PubMed.
- (a) R. McLellan, M. A. Palacios, C. M. Beavers, S. J. Teat, S. Piligkos, E. K. Brechin and S. J. Dalgarno, Chem. – Eur. J., 2015, 21, 2804 CrossRef CAS; (b) M. Coletta, R. McLellan, A. Waddington, S. Sanz, K. J. Gagnon, S. J. Teat, E. K. Brechin and S. J. Dalgarno, Chem. Commun., 2016, 52, 14246 RSC; (c) M. Coletta, R. McLellan, S. Sanz, K. J. Gagnon, S. J. Teat, E. K. Brechin and S. J. Dalgarno, Chem. – Eur. J., 2017, 23, 14073 CrossRef CAS; (d) M. Coletta, S. Sanz, L. J. McCormick, S. J. Teat, E. K. Brechin and S. J. Dalgarno, Dalton Trans., 2017, 46, 16807 RSC.
- S. Mukherjee, M. R. Daniels, R. Bagai, K. A. Abboud, G. Christou and C. Lampropoulos, Polyhedron, 2010, 29, 54 CrossRef CAS.
- C. Lampropoulos, T. C. Stamatatos, K. A. Abboud and G. Christou, Inorg. Chem., 2009, 48, 429 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS.
- (a) F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí,M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini,S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2015, 37, 506–541 CrossRef; (b) F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.-å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS; (c) J. A. Duncan, J. Am. Chem. Soc., 2009, 131, 2416–2416 CrossRef CAS; (d) V. Veryazov, P. O. Widmark, L. Serrano-Andrés, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626–635 CrossRef CAS; (e) G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef.
- B. Swerts, L. F. Chibotaru, R. Lindh, L. Seijo, Z. Barandiaran, S. Clima, K. Pierloot and M. F. A. Hendrickx, J. Chem. Theory Comput., 2008, 4, 586–594 CrossRef CAS.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- (a) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS; (b) L. F. Chibotaru, A. Ceulemans and H. Bolvin, Phys. Rev. Lett., 2008, 101, 033003 CrossRef CAS.
- (a) M. E. Lines, J. Chem. Phys., 1971, 55, 2977 CrossRef CAS; (b) L. Ungur and L. F. Chibotaru, POLY_ANISO program, 2007 Search PubMed.
- (a) Y. Peng, M. K. Singh, V. Mereacre, C. E. Anson, G. Rajaraman and A. K. Powell, Chem. Sci., 2019, 10, 5528–5538 RSC; (b) D. Basak, J. v. Leusen, T. Gupta, P. Kögerler, V. Bertolasi and D. Ray, Inorg. Chem., 2020, 59, 2387–2405 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. Austin, J. R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2013.
- (a) T. Rajeshkumar, R. Jose, P. R. Remya and G. Rajaraman, Inorg. Chem., 2019, 58, 11927–11940 CrossRef CAS; (b) M. M. Hänninen, A. J. Mota, R. Sillanpää, S. Dey, G. Velmurugan, G. Rajaraman and E. Colacio, Inorg. Chem., 2018, 57, 3683–3698 CrossRef.
- (a) J. Cirera, Y. Jiang, L. Qin, Y. Z. Zheng, G. Li, G. Wu and E. Ruiz, Inorg. Chem. Front., 2016, 3, 1272 RSC; (b) K. R. Vignesh, S. K. Langley, K. S. Murray and G. Rajaraman, Chem. – Eur. J., 2015, 21, 2881–2892 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS.
- (a) S. Realista, A. J. Fitzpatrick, G. Santos, L. P. Ferreira, S. Barroso, L. C. J. Pereira, N. A. G. Bandeira, P. Neugebauer, J. Hrubý, G. G. Morgan, J. van Slageren, M. J. Calhorda and P. N. Martinho, Dalton Trans., 2016, 45, 12301–12307 RSC; (b) J. Li, R. M. Wei, T. C. Pu, F. Cao, L. Yang, Y. Han, Y. Q. Zhang, J. L. Zuo and Y. Song, Inorg. Chem. Front., 2017, 4, 114 RSC.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef CAS.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- (a) M. K. Singh, Dalton Trans., 2020, 49, 4539–4548 RSC; (b) M. K. Singh and G. Rajaraman, Inorg. Chem., 2019, 58, 3175–3188 CrossRef CAS; (c) M. K. Singh, T. Rajeshkumar, R. Kumar, S. K. Singh and G. Rajaraman, Inorg. Chem., 2018, 57, 1846–1858 CrossRef CAS; (d) M. K. Singh, N. Yadav and G. Rajaraman, Chem. Commun., 2015, 51, 17732–17735 RSC; (e) A. Upadhyay, J. Rajpurohit, M. K. Singh, R. Dubey, A. K. Srivastava, A. Kumar, G. Rajaraman and M. Shanmugam, Chem. – Eur. J., 2014, 20, 6061–6070 CrossRef CAS; (f) C. McDonald, S. Sanz, E. K. Brechin, M. K. Singh, G. Rajaraman, D. Gaynor and L. F. Jones, RSC Adv., 2014, 4, 38182 RSC; (g) S. Hazra, S. Bhattacharya, M. K. Singh, L. Carrella, E. Rentschler, T. Weyhermueller, G. Rajaraman and S. Mohanta, Inorg. Chem., 2013, 52, 12881 CrossRef CAS.
- T. R. Cundari and W. J. Stevens, J. Chem. Phys., 1993, 98, 5555–5565 CrossRef CAS.
- (a) A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef CAS; (b) A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef CAS; (c) G. E. Scuseria and H. F. Schaefer III, J. Chem. Phys., 1989, 90, 3700 CrossRef CAS.
- V.-A. Rassolov, J.-A. Pople, M.-A. Ratner and T.-L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
Footnotes |
| † Dedicated to Prof. Alan Welch on the occasion of his retirement from Heriot-Watt University. |
| ‡ Electronic supplementary information (ESI) available: Bond valence sum calculations, experimental/theoretical figures and tables to support discussion. CCDC 2020261. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0dt02731f |
| This journal is © The Royal Society of Chemistry 2020 |