Applications of graphene and its derivatives as an adsorbent for heavy metal and dye removal: a systematic and comprehensive overview

Abstract

Because of their persistency and toxicity, dyes and heavy metal ions discharged to water bodies have become a worrisome issue. Therefore, to secure the innate beauty of our planet and to conserve our non-renewable natural resources, specifically, water, it is essential to check and/or to minimize heavy metal ion and dye concentrations before discharge. Adsorption is considered as a robust and widely acclaimed water decontamination technology. In material science research, much attention has been focused on graphene, a carbon allotrope with a two-dimensional sheet-like structure possessing unique structural properties that has been utilized in various research areas. Herein, we present recent developments, specifically focusing on the use of graphene and its derivatives as an adsorbent for dye and heavy metal ion removal from aqueous phase. A historical overview, synthesis methodologies, structural characteristics, toxicity issues, and the applications of graphene and its derivatives for dye and heavy metal ion removal along with its adsorption mechanisms are comprehensively discussed. Major challenges in graphene synthesis and future research perspectives for developing alternate synthesis methodologies are also discussed.

---

Mohammed Yusuf

Mohammed Yusuf did his Master's in Chemical Engineering at University Putra Malaysia in 2013. He is currently pursuing his Doctoral Degree (Ph.D.) in Environmental Engineering and Green Technology at Malaysian-Japan International Institute of Technology, University Technology Malaysia. His main research interest is treatment of industrial wastewater by adsorption process.

Moonis Ali Khan

Dr Khan obtained his Ph.D. in Applied Chemistry from Aligarh Muslim University. He had worked as a post-doctoral researcher at Yonsei University and University Putra Malaysia. Presently, he is working as an Assistant Professor in Chemistry Department at King Saud University. His current research is directed towards the development of composite materials and their utilization as an adsorbent for the abatement of inorganic and organic pollutants from water and wastewater.

---

1. Introduction

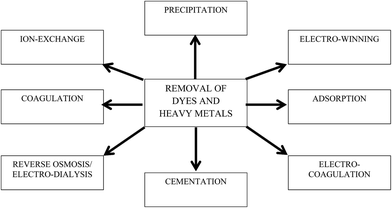
The discharge of industrial, agricultural, domestic, and municipal waste effluents into water bodies such as rivers, lakes, and ponds has inevitably resulted in an increased flux of toxic pollutants. Among water pollutants, dyes and heavy metal ions have drawn serious concern because they are non-biodegradable and tend to accumulate in living organisms. Most heavy metal ions are highly toxic, and some are reported to be suspected human carcinogens.¹ In addition, dyes add undesirable color to water resources, preventing the penetration of sunlight, retarding photosynthetic reactions, and affecting aquatic life.^2,3 Most dye molecules have an aromatic ring in their structure, which makes them highly toxic, non-biodegradable, carcinogenic, and mutagenic to both human beings and aquatic life.⁴ Hence, it is essential to remove or to minimize heavy metal ions and dyes to permissible levels before they are discharged to water bodies. Various regulatory authorities and environmental protection agencies have enforced stringent regulations to control their discharge into water resources.

A wide array of wastewater treatment techniques such as flocculation,⁵ membrane filtration,⁶ solvent extraction,⁷ biosorption,⁸ chemical precipitation,⁹ ion exchange,¹⁰ reverse osmosis,¹¹ electrocoagulation,¹² cementation,¹³ electrowinning,¹⁴ coagulation,¹⁵ and adsorption¹⁶ have been developed to reduce contaminants in potable, municipal, and wastewater as shown in Fig. 1. Among the different technologies, adsorption is considered a globally acclaimed water treatment technology due to its versatility, wide applicability, and economic feasibility. Activated carbon (AC), a carbon-based material, is considered as a conventional adsorbent for both domestic and industrial water treatment. However, high regeneration cost and column fouling are the major demerits of using AC as an adsorbent. Therefore, research to explore better alternative carbon-based adsorbents is currently ongoing. In last decade, nanocarbonaceous materials such as carbon nanotubes (CNTs) and graphene have grown as promising adsorbents to sequester dyes and heavy metal ions from aqueous phase. Compared to their counterparts, graphene has shown appreciably fast adsorption kinetics. Furthermore, the production cost of graphene is comparatively lower than CNTs and other adsorbents (i.e., resins), while their adsorption capacities are similar.¹⁷

Fig. 1 Conventional methods for the removal of dyes and heavy metal ions.

Graphene, a recently explored two-dimensional carbon allotrope, is a new addition to carbon research. High electrical conductivity, superior mechanical flexibility, unique high chemical and thermal stability, high surface functionality, and large surface area have made graphene a fascinating material for researchers. The adsorption behavior of graphene-based adsorbents has been investigated using different pollutant models.^18–21 Numerous studies have also shown the ability of graphene to adsorb different pollutants from various aqueous samples.^22–25 Moreover, graphene can treat multiple pollutants simultaneously with enhanced adsorption capacities.¹⁸ Recently, numerous works have been reported on the utilization of graphene and its composite for the removal of dyes and heavy metal ions from aqueous phase. However, to the best of our knowledge, there is no review reporting recent research on the utilization of graphene and its derivatives as an adsorbent to remove dyes and heavy metal ions. Therefore, in this review, an effort has been made to briefly describe the history, synthesis, properties, and toxicological effects of graphene. Recent developments in the use of graphene as an adsorbent for the removal of dyes and heavy metal ions over the years are comprehensively reported.

2. Graphene – an overview

2.1. History

Graphene is a parent of all graphitic forms and is a two-dimensional carbonaceous material comprising a layer of atoms arranged in six-membered ring. In 1840, the German scientist Schafhäutl reported the intercalation and exfoliation of graphite with H₂SO₄ and HNO₃ for the first time.²⁶ In an effort to characterize the molecular weight of graphite, in 1859, a British chemist named Brodie modified the Schafhaeutl method using an oxidant such as KClO₃ along with strong acids, resulting not only in intercalation of the graphite layers, but also in chemical oxidation of its surface, and finally in the formation of graphene oxide (GO).²⁷ Nearly 40 years later, Brodie's method was modified by Staudenmaier, who added chlorate salt in multiple aliquots over the course of the reaction.²⁸ These intercalation and oxidation experiments are the first examples of the delamination of graphite into its constituent lamellae. Moreover, as described below, many of these methods, or modifications thereof, are still used today for the preparation of GO and other chemically modified graphenes (CMGs). In 1962, Boehm reported that the chemical reduction of GO dispersions in dilute alkaline media with hydrazine, hydrogen sulphide, or iron(II) salts produced thin, lamellar carbon that contained only small amounts of hydrogen and oxygen.²⁹ In 1975, van Bommel and co-workers described the epitaxial sublimation of silicon from single crystals of SiC. At elevated temperatures and under ultrahigh vacuum (UHV; <10⁻¹⁰ Torr), monolayered flakes of carbon consistent with the structure of graphene were obtained.³⁰ In 1986, Boehm for the first time standardized the term “graphene” to describe a single-atom carbon sheet.³¹ This sheet has a nearly transparent, flat, single atomic sheet-like structure consisting of an individual layer of sp² hybridized carbon atoms densely packed in a honeycomb lattice with a carbon-to-carbon molecular bond length of 0.142 nm. It was considered that two-dimensional crystals such as graphene were thermodynamically unstable and presumed not to exist under ambient conditions. The breakthrough work for successful isolation and characterization of a mechanically exfoliated graphene monolayer by Nobel laureates Konstantin Novoselov and Andre Geim in 2004 at the University of Manchester opened a new dimension to graphene research.³²

2.2. Properties and structure

Theoretically, the surface area of graphene is 2630 m² g⁻¹,³³ its high-speed electron mobility is 200 000 cm² V⁻¹ s⁻¹ (ref. 34) at a carrier density of approximately 0.77 mg m⁻² (ref. 35) in magnitude, and it has the relatively highest electrical conductivity at room temperature (at a magnitude of 10⁶).³⁶ The strong mechanical properties of graphene, with a Young's modulus of approximately 1100 GPa (ref. 37) and an excellent thermal conductivity of approximately 5000 W m⁻¹ K⁻¹,^37,38 are highly favorable for various applications. Furthermore, graphene has a fracture strength of 125 GPa,³⁹ an optical transmittance of approximately 97.7%,⁴⁰ and a carrier density of 10¹² cm⁻².³⁵ Therefore, it is worth stating that graphene possesses the potential to be used in different applications across many fields.

Graphene is the basic building block for carbon allotropes, including graphite, carbon nanotubes, and fullerenes,¹ as depicted in Fig. 2. Many of these structures can be stacked together to form graphite, which is a three-dimensional (3D) structure of carbon atoms, or a “wrapper” to form fullerenes. The 3D graphene lattice structure, as illustrated in Fig. 3a, is a honeycomb net with a unit cell consisting of two triangular sub-lattices A and B. Although the honeycomb net is not itself a Bravais lattice, it can be represented as a two-dimensional triangular Bravais lattice. In the graphene lattice, two sub-lattices of carbon atoms are bonded together with σ bonds, and the π orbital of each carbon atom in the lattice contributes to a delocalized network of electrons.

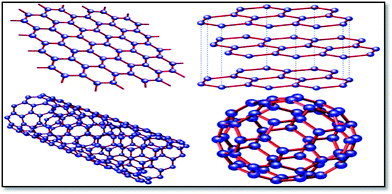Fig. 2 Graphene (top left) is a honeycomb lattice of carbon atoms that form a two-dimensional layer. Graphite (top right) can be viewed as a stack of graphene layers. Carbon nanotubes are rolled-up cylinders of graphene (bottom left). Fullerenes (C60) are cagelike, hollow molecules consisting of a wrapper of graphene composed of pentagonal and hexagonal groups of atoms.¹⁶⁵

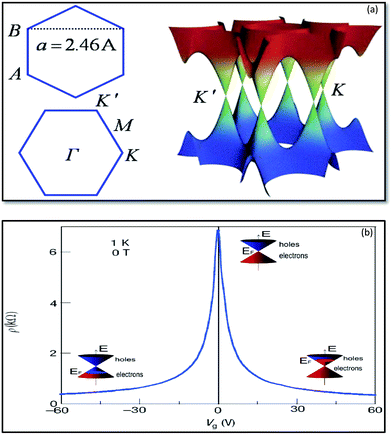Fig. 3 Band structure of graphene at low energies. The conduction and valence bands intersect at points K and K′. The dispersion relation is linear at that point (a).¹⁶⁶ Ambipolar electric field effects in monolayer graphene. The inset cones represent low-energy spectrum E(k), indicating changes in the position of the Fermi energy (EF) with increasing (inducing electron) or decreasing (inducing holes) gate voltage (V_g). The rapid decrease in resistivity ρ by adding charge carriers describes their high mobility and does not noticeably change up to room temperature (b).⁴¹

The electronic structure of graphene is different from typical 3D materials. Six double cones characterize the Fermi surface of graphene, as shown in Fig. 3b. Experimental and theoretical studies on graphene have progressed very rapidly since the experimental evidence for the 2D structure of graphite was obtained.⁴¹ The thermal instability of 2D crystals, however, prohibits the existence of graphene in its pristine form. The structure of graphene is free of defects because the same kinds of atoms are linked together by strong and flexible bonds, and this is the origin of the extraordinary properties of this material. The first graphene oxide (GO) thin films were produced in the early 1960s by Boehm et al.²⁹ A method to produce a uniform single layer of carbon was discovered in the 1970s by the sublimation of crystalline silicon carbide (SiC), which left behind a layer of monocrystalline carbon.³⁰ Unfortunately, the interaction of this layer with the underlying substrate masked the intriguing properties of isolated graphene, and the high processing cost restricted interest in this method. In the 1990s, advances in the understanding of various carbon nanostructures, namely nanotubes and fullerenes, occurred. Interest in these graphene sister structures paved the way to develop new techniques for the isolation of graphene. Finally, in 2004, researchers were able to isolate and identify graphene by using scotch tape to exfoliate single layers from graphite.³²

Fig. 4 displays chemical structures of various forms of graphene termed as graphene family nanomaterials (GFNs). GFNs comprise single-layer graphene, few-layer graphene (2–10 graphene layers), graphene oxide (GO; normally a single layer structure with various oxygen-containing functionalities and less electrical conductivity), reduced graphene oxide (rGO; normally a single layer structure with reduced oxygen-containing functionalities with high electrical conductivity), nanosheets, ultrafine graphite (more than 10 sheets but with a thickness below 100 nm), graphene ribbons, and graphene dots. With each of these forms, a variety of structures are possible, but it is extremely difficult to fully understand and interpret these structures. For example, in case of GO, it is extremely difficult to describe at the molecular level the type, the degree, and the position of the oxygenated groups introduced during the process of graphite exfoliation.⁴² Even more complicated is understanding what happens when GO is transformed under reductive condition.^43,44

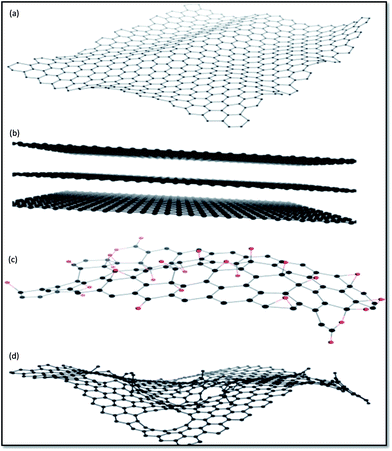Fig. 4 Representative chemical structures of some of the members of GFNs: (a) graphene, (b) few-layer graphene, (c) graphene oxide (oxygen atoms are in red), and (d) reduced graphene oxide.¹⁶⁷

2.3. Synthesis methodology

Despite the potential benefits of graphene, its widespread use has been impeded due to the challenges in synthesizing graphene from graphite or using bottom-up techniques. However, various synthesis techniques have been proposed as discussed here. The epitaxial growth method for graphene can be achieved by the heating of hexagonal crystals of silicon carbide at 2400 K.^45,46 Claire et al.⁴⁷ synthesized epitaxial graphene by vacuum graphitization during the thermal decomposition of silicon carbon at 2400 K. Decomposition of the silicon carbon crystal at 1473 K results in the formation of millimeter-size continuous graphene planes after the vaporization of silicon.^48,49

The first highly recognized method used for the preparation of graphene was mechanical exfoliation (top-down approach) carried out by Novoselov et al.³² In this method, highly-oriented pyrolytic graphite was embedded in photoresist material, and adhesive tape was used to successively peel off layers of graphene. Currently, a highly used and common technique (i.e., the Hummers' method/modified Hummers' method) is oxidation, where graphite is oxidized into graphene oxide (GO) by the use of strong acids, forming a stable solution of GO dispersed in water⁵⁰ that can subsequently be reduced by aqueous reduction agents such as hydrazine.^51,52 The chemical vapor deposition (CVD) method is another interesting technique to synthesize graphene in the presence of a metal substrate, and it is typically carried out under ultra-high vacuum and at high temperatures.⁵³ During this process, a vapor-rich hydrocarbon is heated at approximately 1073 K, allowing graphene to deposit on the surface of a metal substrate such as nickel or copper. Finally, the liquid phase exfoliation of graphite has been considered as one of the most feasible approaches for the industrial production of graphene due to its scalability and low cost. This approach typically involves sonication of graphite or graphite oxide powders in solvents. Here, it is noteworthy that there are certain advantages and disadvantages to each method that are also dependent on the end application, as summarized in Table 1.

Table 1 Graphene synthesis methodologies

Methodology	Merits	Demerits
Micromechanical exfoliation	• High quality properties	• Low yield
		• Not scalable
Epitaxial SiC growth	• Large continuous film area	• Not transferable
		• High temperature
		• Low vacuum
Reduction of GO	• Solution processed	• Poor electrical properties
	• High yield	• Small area flakes
CVD	• High quality	• High temperature
	• Large area	• Low vacuum
	• Transferable	• Difficult scalability
Solution exfoliation	• High quality	• Small area graphene flakes
	• Good scalability	• Colloidal stability
	• Low temperature

---

2.4. Toxicity

The discovery of graphene has brought a revolution to material science research. For its development, the evaluation of its safety profile and impact on human health is of primary concern. Studies conducted on graphene and its derivatives showed that they exhibit in vitro toxicity. Among derivatives, GO is considered more biocompatible, as it results in less damage and toxicity in human cells due to its greater solubility/dispensability. The most prominent route into the human body lies within the respiratory system. However, GO showed dominant accumulation in the lungs for a long period of time after being intravenously injected into rats and mice, inducing dose-dependent pulmonary toxicity.^54,55 Furthermore, it has been revealed that GO and aggregated graphene incite a severe and persistent injury in the lungs after direct injection (i.e., 50 μg per animal) in the organs of mice.⁵⁶ This is not surprising, as GO without further surface functionalization is not stable in physiological environments due to the screening of electrostatic charges and non-specific binding of protein to GO. After entering the bloodstream, the GO agglomerates are trapped in the lungs. The risk of pristine graphene nanoplatelets in the respiratory system was also reported.⁵⁷ Furthermore, it has been suggested that the biological response of graphene will vary depending on the number of layers, lateral size, stiffness, hydrophobicity, surface functionalization, and dose. Currently, it is unknown if airborne graphene flakes that are inhaled are dangerous.

3. Graphene – a potential adsorbent

3.1. Characterization

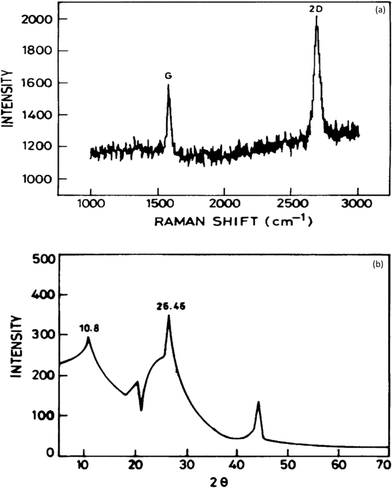
It has been established that graphene is a potential material for dye and heavy metal ion removal, and hence, various characterization probes such as Raman spectroscopy, Fourier transform infrared (FTIR) spectroscopy, X-ray diffraction (XRD), scanning electron microscopy (SEM), transmission electron microscopy (TEM), thermogravimetric analysis (TGA), and X-ray photoelectron spectroscopy (XPS) have been utilized to obtain data regarding its mechanism of action.

Raman spectroscopy is a quick and non-destructive method that uses monochromatic laser excitation to probe the structure of a material. In the Raman spectroscopy of graphene, there are three response peaks of interest corresponding to different vibrational or phonon modes in the material. These are referred to as the G peak (approximately 1580 cm⁻¹), the D peak (approximately 1350 cm⁻¹), and the 2D peak (approximately 2700 cm⁻¹).⁵⁸ The D peak appears strongly in disordered graphite, and its intensity is considered to indicate the degree of general graphene disorder. For ordered graphene, the intensity ratio of the D/G peaks should be <1%. The 2D peak is a harmonic of the D peak. Wang and co-workers showed that a clear band at 1588 cm⁻¹ assigned as the G band is associated with the vibration of sp² carbon atoms in a graphitic 2D hexagonal lattice. Another single and sharp 2D peak appearing at 2698 cm⁻¹ that corresponded to graphene with few layers⁵⁹ is shown in Fig. 5a. The interaction of X-rays with a crystalline substance (phase) resulted in the creation of a diffraction pattern. Fig. 5b shows the X-ray diffraction (XRD) signature of graphene. The analysis revealed a strong and narrow peak at 2θ = 26.46° corresponding to the (0 0 2) planes of graphene layers occurring in graphite as previously reported.⁶⁰ A peak at 2θ = 44.1 was also observed corresponding to (1 0 1). Another strong peak at 2θ = 10.8° occurred, which suggests structural expansion as oxygen-containing groups incorporated between the graphite during the course of strong oxidation.

Fig. 5 (a) Typical Raman spectra²³ and (b) XRD patterns²⁵ of graphene.

FT-IR spectroscopic analysis is a vital tool to characterize both the covalent and non-covalent functionalization of graphene and its derivatives. Characteristic bands at 3430 cm⁻¹ due to O–H stretching and at 1610 cm⁻¹ for skeletal vibration from graphitic domains of adsorbed water and aromatic domains (C=C), respectively, were observed. A peak at 1610 cm⁻¹ in graphite shifted to 1625 cm⁻¹ in GO due to the presence of electron-withdrawing oxygen functionalities. The GO showed some new peaks at 1728 cm⁻¹ for C=O stretching, 3406 cm⁻¹ for O–H stretching, and 1052 cm⁻¹ for C–O stretching. The characteristic peak of a hydroxyl group at 3430 cm⁻¹ was observed in rGO but with reduced intensity compared to GO. A characteristic epoxide group band was observed at 1052 cm⁻¹ for graphite.⁶¹

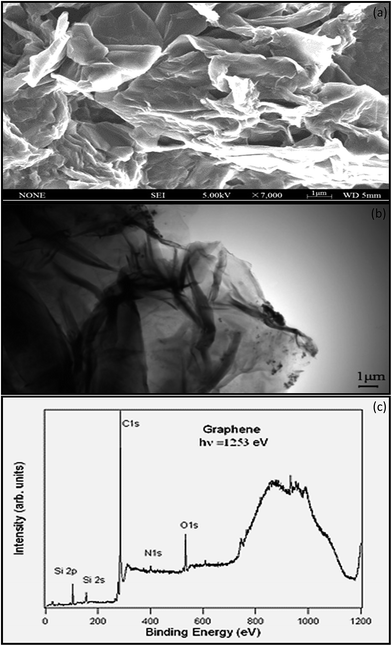
SEM is a characterization tool to examine the topography, morphology, composition, and crystallographic information of a material.⁶² Fig. 6a shows that thin-layer graphene with spontaneous stacking curls from petal-shaped aggregates was observed. The flocculate in the absence of external forces will remain stable, and it is difficult to separate them from each other. The thickness of graphene was accurately determined by taking large numbers of TEM⁶³ images to generate a series of thickness statistics. In Fig. 6b, the graphene layer stacking disorder is clearly displayed. It mainly occurs because in the oxidation process, the introduction of the hybrid carbon atoms leads to disturbances of the planar sp² carbon layer. In addition, in order to ensure thermal stability, thin layer graphene has prompted its spontaneous stacking and wrinkled features.

Fig. 6 (a) SEM image,⁸⁵ (b) TEM image,⁸⁵ and (c) wide XPS scan of cleaved UITAR²⁵ of graphene.

Stankovich provided the elemental characterization of graphene powder by XPS as shown in Fig. 6c. The Si_2p peak associated with the bonding energy of 99.9 eV represents the bond of silicon with –OH from the graphene, resulting from the partial hydrolysis of the molecule during the silylation reaction.⁶⁴ The N_1s XPS spectrum of graphene contains one peak at 400.6 eV, which is assigned to N–C³_sp. Nitrogen is introduced to the graphene surface during the synthesis and reduction process.⁶⁵ The O_1s peak at 529.4 eV is assumed to be contributed from the C=O or O=C=OH groups.⁶⁶ The C_1s (Fig. 6c) of graphene contains three components of carbon in the C–C at 284.6 eV, the carbon in the C–OH at 286.1 eV, and carbonyl carbon (C=O) at 290.6 eV.⁶⁷

The TGA analysis of GO under N₂ atmosphere showed a weight loss below 100 °C due to the degradation of the oxygen-containing group.⁶⁸ Compared to GO, rGO is thermally more stable due to the removal of large fractions of oxygen-containing moieties. The TGA analysis of exfoliated GO, initiator-modified GO, and GO/polymeric nanocomposite showed a 13% weight loss for GO in a temperature range of 100–800 °C, which was attributed to the degradation of epoxy, carboxylic, and hydroxylic groups. The observed weight losses for the modified GO and GO/polymeric nanocomposite were 32 and 56%, respectively, for the aforementioned temperature range.⁶⁵

3.2. Adsorption mechanism

Surface properties such as surface area and pore size distribution influence the adsorption on graphene. The surface area generally affects the adsorption of the adsorbate on the adsorbent, as the adsorption capacity of an adsorbent depends largely on the total surface area per unit volume of adsorbate. This includes the specific surface area that is the total internal surface area assigned by the pore size distribution of the adsorbent. When the surface becomes larger, it results in increased exposure of the area of active sites exposed to adsorbate during the adsorption. Therefore, to increase the adsorption capacity, the adsorbent should have a high porosity and small grain size distribution in order to maximize the total surface area.⁶⁹ The graphene showed an ultrahigh specific surface and no porosity. In order to improve the adsorption capacity of graphene, the introduction of porosity is an efficient and feasible method. Combining other porous materials with graphene can introduce porosity. Zhang et al.⁷⁰ combined chitosan–gelatin with GO to form ordered porous composites for Cu(II) and Pb(II) adsorption, and the composite showed an extremely high ability to adsorb both metal ions.

The introduction of different functional groups might be another possible route to enhance graphene adsorptive performance because these groups play a critical role in the binding of adsorbates. Specific functional groups have the ability to form specific bonds with metal ions. A large surface area and oxygen-containing adsorption sites on GO are chiefly responsible for the stronger adsorption of organic dyes onto GO. It has been reported that oxide-containing acidic functional groups decrease the capacity of the adsorbent to adsorb metals while hydroxyl functional groups enhance metal adsorption.⁷¹ The oxidation of graphene to GO can introduce –COOH, –C=O, and –OH functionalities over the surface, making GO hydrophilic.⁷² The mechanism of heavy metal adsorption will be discussed in the following paragraphs.

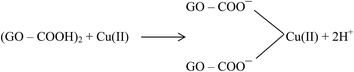
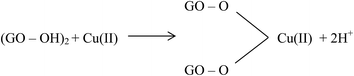
Large quantities of Pb(II) and Cd(II) were adsorbed onto GO, which was attributed to a larger surface area and oxygen functionalities on the GO.²⁰ Additionally, Wu et al.⁷³ reported the adsorption of Cu(II) on GO and fitted the experimental data to a Freundlich model with a maximum adsorption capacity of 117.5 mg g⁻¹ for Cu(II). The adsorption of Cu(II) on GO was attributed to complexation, ion-exchange, and electrostatic attraction as shown by equations below:

GO–COOH + Cu(II) → GO–COO⁻–Cu(II) + H⁺ (1)

GO–OH + Cu(II) → GO–O⁻–Cu(II) + 2H⁺ (3)

The adsorption of Cu(II) and Pb(II) on a graphite nanosheet (GNS)–MnO₂ composite was studied by Ren and coworkers.⁷⁴ The maximum adsorption capacities for Cu(II) and Pb(II) were 1637.9 and 793.65 μmol g⁻¹, respectively. FT-IR, XPS, and XRD studies showed that the adsorption of metal ions on a GNS–MnO₂ composite involved the formation of tetradendate surface complexes. The oxygen-containing surface functional groups including hydroxyl groups (C–OH or Mn–OH) were mainly involved in the adsorption process as shown in the following equations:

GNS–MnO₂–OH + M(II) → (GNS–MnO₂–O–M)⁺ + H⁺ (5)

GNS–MnO₂–O⁻ + M(II) → (GNS–MnO₂–O–M)⁺ (6)

GNS–MnO₂–OH + M(II) + H₂O → GNS–MnO₂–OMOH + 2H⁺ (7)

where M = metal ion.

Fig. 7 displays the linking of N-(trimethoxysilylpropyl)ethylenediaminetriacetic acid (EDTA–silane) with the hydroxyl groups on the GO surface.⁷⁵ A high chelation ability of EDTA together with the OH and COOH groups present on the GO surface greatly enhanced the adsorption of bivalent Pb(II) ions. The adsorption capacity of Pb(II) on EDTA–GO was 479 mg g⁻¹.

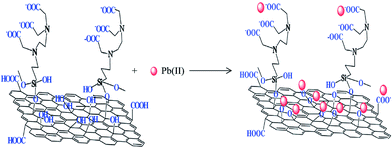Fig. 7 EDTA-modified GO and its interaction with bivalent heavy metal ions.⁷⁵

For dye removal, electrostatic attraction between positively charged amino groups and negatively charged oxygen-containing surface groups and π–π interaction between the localized π electrons in the conjugated aromatic rings of the adsorbent and adsorbate molecules are the two most common interactions that generally exist between adsorbate (dye) and adsorbent. The rGO has several active sites that interact with the dye molecules: (i) negatively charged surface-functional groups such as hydroxyl (–OH) and (–COOH) groups, (ii) delocalized π electrons within sp² carbon grains interacting with the lone electron pairs of atoms and free electrons in the aromatic rings of the dye molecule, and (iii) oxygen-containing groups available to form bonds with the dye species.^76,77 Therefore, development of functionalized graphene nanocomposites with large surface area and oxygen-containing adsorption sites is important for promising environmental applications.

The efficacy of exfoliated graphene oxide (EGO) and rGO was tested for the adsorption of methylene blue (MB), methyl violet (MV), rhodamine B (RB), and orange G (OG) from aqueous phase.⁷⁸ G band shifting in the Raman spectra (both blue- and red-shifts) was observed after dye adsorption. The interaction of cationic (MB and MV) dyes with EGO was electrostatic, while anionic dye (OG) did not show any adsorption with EGO. However, RB probably interacts with EGO through both electrostatic and van der Waals forces. Based on the variations in the G band position, the charge transferred from MV, RB, and MB to EGO whereas charge transfer from rGO to OG was observed (Fig. 8).

Fig. 8 Schematic interactions of (a) EGO/MB, (b) EGO/MV, (c) EGO/RB, and (d) rGO/OG.⁷⁸

When compared to other carbon-based adsorbents, graphene was found to be the best adsorbent for the removal of bisphenol A from water. The adsorption mechanism could be mainly a π-stacking interaction as well as hydrogen bond formation.⁷⁹ Here, the smooth surface of graphene is an additional advantage with respect to other carbonaceous materials. The interaction of delocalized π-electrons of graphene and the benzene ring of the dye, along with the weak van der Waals forces between hexagonal arrays of carbon atoms and the aromatic backbones of composite, is mainly responsible for the removal of organic dyes, especially pararosaniline from water, as compared to other adsorbent materials, as discovered by Chen et al.⁸⁰ A comparative study of MB adsorption on carbon-based adsorbents (activated carbon, GO, and CNTs) was conducted.⁸¹ The results showed that the adsorption of MB on carbon-based adsorbents was not only because of the large surface area, but also π–π electron donor–acceptor interactions and electrostatic attraction between cationic dye ions and negatively charged adsorbents, which played critical roles during adsorption. Fig. 9 and 10 illustrate the adsorption mechanism of heavy metals and dyes on graphene and its derivatives.

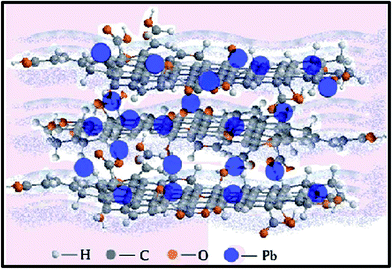Fig. 9 Illustration showing the mechanism of heavy metal ion adsorption onto graphene.¹⁶⁸

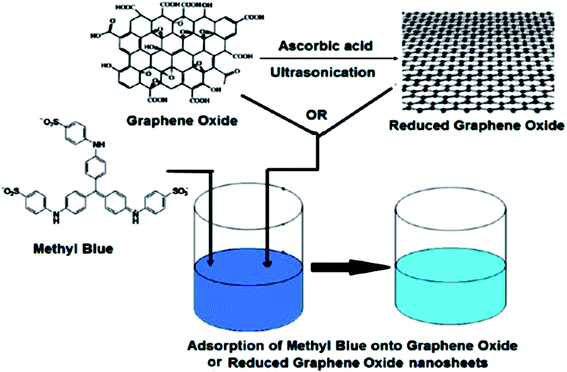Fig. 10 Schematic diagram of the mechanism of dye adsorption onto GO or rGO nanosheets.¹³⁷

4. Applications

4.1. Heavy metal adsorption on graphene and its derivatives

As mentioned in the preceding sections, numerous research reports have appeared on the utilization of graphene, GO, rGO, and their composites for the adsorption of heavy metals. These applications will be discussed in the following sections.

4.1.1. Adsorption on graphene and its composites. Leng et al.⁸² examined the possibility of using graphene as an adsorbent for the removal of Sb(III) in aqueous solutions. Batch adsorption experiments were conducted in order to study the effects of operating parameters, such as the initial concentration, pH, and temperature, on Sb(III) adsorption. The process appeared to follow the Freundlich isotherm model, rather than the Langmuir isotherm model. Under optimized conditions, the adsorption capacity of graphene for Sb(III) was found to be 10.92 mg g⁻¹. The best fit of the adsorption kinetics data was to a pseudo-second-order model, which was able to express the overall adsorption process and indicated that the rate-determining step involved chemisorption. It was observed that the adsorption capacity increased with decreasing metal ion concentrations, and decreased with decreasing temperature. Furthermore, with any increase in pH value above 3.8, an increase in the metal removal efficiency was observed. Moreover, at a pH value greater than 11, a maximum removal efficiency of 99.5% was recorded. However, Chang et al.⁸³ studied the potential to adsorb Fe(II) and Co(II) from aqueous solution using graphene through a batch adsorption technique. The maximum adsorption capacities were found to be 299.3 and 370 mg g⁻¹ for Fe(II) and Co(II), respectively. The adsorption processes were governed by the Freundlich isotherm model, while the adsorption kinetics data fitted to a pseudo-second-order model.

Huang et al.⁸⁴ synthesized graphene nanosheets (GNSs) at a low-temperature (i.e., exfoliation temperature as low as 473 K) followed by chemical exfoliation under a high vacuum condition. Furthermore, GNSs were physically modified at various temperatures, i.e., 773 K (500 °C) and 973 K (700 °C), and were denoted as GNS-500 and GNS-700, respectively. The impact of heat treatment of GNSs on surface chemistry and adsorption characteristics was studied. The results showed that GNSs have the potential to decrease the concentration of Pb(II) metal. The maximum Pb(II) adsorption capacities were 22.42 and 35.47 mg g⁻¹ for GNS-500 and GNS-700, respectively. Wu et al.⁸⁵ tested the adsorptive potential of cetyl-trimethyl ammonium bromide (CTAB)-modified graphene for the removal of Cr(VI) from aqueous solution. Introduction of CTAB to the graphene surface resulted in an increase in the adsorption capacity. The CTAB, together with the –OH and –COOH ions on the graphene surface, resulted in CTAB-infused graphene (CTAB-GN), which performed well for the removal of Cr(VI) from aqueous solutions. The adsorption equilibrium data displayed an excellent fit to the Langmuir isotherm model. The optimum adsorption of Cr(VI) on CTAB-GN was 21.57 mg g⁻¹ at pH of 2, initial concentration of 50 mg g⁻¹, temperature of 298 K, adsorbent dosage of 0.6 g, agitation speed of 150 rpm, and equilibration time of 40 minutes. The kinetics data fitted well to a pseudo-second-order kinetic model, while the thermodynamic assessment indicated that the adsorption was exothermic and a spontaneous process.

Ren et al.⁷⁴ studied the adsorption mechanism of Cu(II) and Pb(II) on a graphene δ-MnO₂ nanosheet. The adsorption data fitted well to a Langmuir isotherm model, revealing monolayer adsorption. The optimum adsorption capacities for Cu(II) and Pb(II) ions were found to be 1620 and 781 μmol g⁻¹, respectively, with an equilibration time of 3 h. The kinetics data were found to obey a pseudo-second-order kinetic model, indicating a chemisorption process.

Hao et al.⁸⁶ investigated the adsorption of Pb(II) ions using SiO₂–graphene. The optimum adsorption capacity was found to be 113.6 mg g⁻¹ at 25 °C, while the maximum percentage removal was 98.82% at pH 6 with a contact time of 30 min. The adsorption kinetics obeyed a pseudo-second-order model. The adsorption equilibrium data fitted well to the Langmuir isotherm model. The adsorption process was believed to take place by a monolayer mechanism on a homogeneous site on the surface of the SiO₂–graphene.

Chemical functionalization of graphene to improve its removal efficiency was reported by Deng and co-workers.⁸⁷ They adopted a mild, one-step electrochemical approach for the preparation of functionalized graphene sheets with the assistance of an ionic liquid and water; 1-octyl-3-methylimidazolium hexafluorophosphate (CP8) and potassium hexafluorophosphate (PF6) were used as ionic liquids. The functionalized graphene sheets thus obtained were named GNS^CP8 and GNS^PF6, respectively. They studied the adsorption of bivalent Pb(II) and Cd(II) heavy metals onto chemically functionalized GNS^CP8 and GNS^PF6. The adsorption capacities of Pb(II) and Cd(II) on GNS^CP8 were 74.18 and 30.05 mg g⁻¹, at pH 5.1 and pH 6.2, respectively. However, the adsorption capacities of Pb(II) and Cd(II) on GNS^PF6 were 406.4 and 73.42 mg g⁻¹ at pH 5.1 and pH 6.2, respectively. Both processes proved to follow the pseudo-first-order kinetics model. The isotherm studies data fitted well to both the Langmuir and Freundlich isotherm models. A desorption experiment was then considered for GNS^PF6, as it displayed a higher adsorption capacity than GNS^CP8. The experimental results showed that GNS^PF6 could be reused for five consecutive cycles without any significant loss in its initial adsorption capacity.

The adsorption of bivalent metal ions [Ag(II), Cu(II), Hg(II), and Pb(II)] in batch mode on graphene–CNT hybrid aerogels (graphene/MWCNTs and graphene/c-MWCNTs) was reported by Sui et al.⁸⁸ The experiments were conducted at room temperature with an initial concentration of 50 mg L⁻¹. The maximum adsorption capacities of Pb(II), Hg(II), Ag(II), and Cu(II) by graphene/c-MWCNTs were 104.9, 93.3, 64.0, and 33.8 mg g⁻¹, respectively, while the maximum adsorption capacities of the metal ions (in the same order) by graphene/MWCNTs were 44.5, 75.6, 46.0, and 9.8 mg g⁻¹, respectively. From these results, it could be concluded that the adsorption capacities of metal ions on graphene/c-MWCNTs were significantly higher compared to graphene/MWCNTs. This might be due to the presence of more oxygen-containing functional groups in the graphene/c-MWCNTs.

Yuan et al.⁸⁹ tested the adsorption of Cr(VI) from aqueous solutions on Mg–Al-layered graphene. A batch adsorption experiment was conducted at pH 2 with a contact time 24 h and an initial concentration range of 50–200 mg L⁻¹. The maximum adsorption capacity obtained was 183.82 mg g⁻¹. The equilibrium data fitted well with the Freundlich isotherm model, while a pseudo-second-order kinetic model well described the kinetic data.

Jabeen et al.⁹⁰ utilized a synthesized graphene sheet decorated with zero-valent iron nanoparticles (G-NZVI) for Cr(VI) removal from aqueous solutions. The Cr(VI)-containing solution had an initial concentration between 25 and 125 mg L⁻¹, pH 4.25, temperature 298 K, and contact time 4 h. The observed maximum adsorption capacity of Cr(VI) was 162 mg g⁻¹. The pore size and surface area of the iron nanoparticles embedded in the graphene sheet played very important roles in the adsorption process. The adsorption kinetic data were well described by a pseudo-second-order model, while the isotherm data were well fitted to the Langmuir isotherm model. It could be deduced that the entire adsorption process was pH-dependent.

The use of a MnO₂-synthesized graphene nanosheet/δ-MnO₂ (GNS–MnO₂) composite with a microwave assisted-method was reported by Ren et al.⁶¹ Using MnO₂ in wastewater treatment has the advantages of being environmentally friendly and cost-effective. The adsorption equilibrium, kinetics, and thermodynamics of Ni(II) ions using the composite were investigated under batch experiments. The GNS–MnO₂ provided a maximum adsorption capacity of 46.55 mg g⁻¹, which was higher than that for the MnO₂–rGO and pristine graphene nanosheets. The equilibrium adsorption data showed an excellent fit to the Langmuir isotherm model and was endothermic in nature. However, the adsorption kinetic data were best described by a pseudo-second-order rate expression. As a result, GNS–MnO₂ was proved to be a great potential substance for desorption and regeneration, with only a 9% loss from its initial adsorption capacity.

The infusion of magnetic graphene nanocomposite (MGNC) with a core @ double-shelled nanoparticle (composed of a crystalline iron core, iron oxide inner shell, and amorphous Si–S–O compound outer shell: graphene/Fe@Fe₂O₃@Si–SO) via a facile thermodecomposition process was efficient in adsorbing Cr(VI), as reported by Zhu et al.¹⁸ The composite recorded a maximum adsorption capacity of 1.03 mg g⁻¹ at an initial metal ion concentration of 1 g L⁻¹ and pH 7.0. A high adsorption rate was reported, and the adsorption kinetics were aligned to the pseudo-second-order model.

Nandi et al.⁹¹ reported the use of a manganese-incorporated iron(III) oxide–graphene magnetic nanocomposite (graphene/Mn_x²⁺Fe_2−x³⁺O₄²⁻) for the removal of As(III) from aqueous solutions. From their research, maximum As(III) adsorption (approximately 14.42 mg g⁻¹) was recorded under the following optimal experimental conditions: pH 7.0, contact time 2.5 h, temperature 300 K, and initial Fe(III) oxide concentrations 1–8 mg L⁻¹. It was reported that the equilibrium adsorption process followed the pseudo-second-order kinetics, and the equilibrium isotherm data fitted well to the Langmuir isotherm model.

4.1.2. Adsorption on GO and its composites. Apart from graphene, the efficacy of GO as an adsorbent for the removal of heavy metals from an aqueous medium was tested. Li et al.⁹² carried out research on the capability of U(VI) ions from aqueous solutions to adsorb onto GO. From the experimental results, the maximum U(VI) adsorption capacity (229 mg g⁻¹) was observed at room temperature, pH 4, and with a contact time of 4 h. In addition, the adsorption data revealed that it could be well fitted to the Langmuir isotherm model. However, a rapid decline in U(VI) uptake was observed in the alkaline region. Wu et al.⁷³ also tested the adsorption potential of GO to remove Cu(II) ions from aqueous solutions. The GO displayed a high adsorption capacity of 117.5 mg g⁻¹ for Cu(II). Regeneration studies revealed an appreciably high adsorption potential even after ten consecutive regeneration cycles.

The efficiency of GO to adsorb Zn(II) ions from aqueous solutions was tested by Wang et al.⁹³ The amounts of Zn(II) adsorbed onto GO increased with decreasing amounts of adsorbent. The kinetics data fitted well to a pseudo-second-order model. At various temperatures, the isotherm adsorption data obtained were well described by the Langmuir model, with a maximum monolayer adsorption capacity of 246 mg g⁻¹ at 293 K, pH 7.0, and initial concentrations of 10–100 mg L⁻¹. The adsorption process was strongly dependent on the pH, but weakly affected by the ionic strength and presence of foreign ions.

The potential of GO for the removal of divalent metal ions of Cu, Pb, Zn, and Cd was investigated by Sitko et al.⁹⁴ The adsorption affinity was found to follow the sequence Pb(II) > Cd(II) > Zn(II) > Cu(II) in a single metal system, but follow the sequence Pb(II) > Cu(II) ≫ Cd(II) > Zn(II) in a binary metal system. The optimum adsorption capacities for Pb(II), Cd(II), Zn(II), and Cu(II) were 1119, 530, 345, and 294 mg g⁻¹, respectively. The data were well described by the Langmuir isotherm model, proving monolayer coverage of heavy metal ions on GO, whereas pseudo-second-order model applicability was observed from the kinetics study data. Therefore, the adsorption kinetics of these ions could be controlled by chemisorption, involving strong surface interaction of the metal ions with the oxygen-containing groups on the surface of the GO.

Fang et al.²⁴ studied the removal of Co(II) from aqueous solutions by amine-modified GO (GO-NH₂). The highest Co(II) removal was 98%, and a maximum adsorption of 116.35 mg g⁻¹ was observed. The kinetics data were very well described by a pseudo-second-order model. The results showed a dependency of the adsorption mechanism on the adsorbate, adsorbent, and the rate limiting step, representing a chemisorption process involving valence forces resulting from sharing or exchanging electrons. Furthermore, the linear regression value showed that the adsorption isotherm fitted the Langmuir isotherm model, suggesting that Co(II) adsorption on the surface of the GO-NH₂ nanosheets occurred on a surface with homogeneous binding sites with the following principles: (1) equivalent adsorption energies, (2) no interaction between adsorbed species, and (3) monolayer coverage. Also, an experiment was devised by Lee and Yang⁹⁵ that used the flower-like GO–TiO₂ hybrids for the removal of Zn(II), Cd(II), and Pb(II) from water. The removal efficiency of these metal ions was significantly improved by the infusion of GO with the flower-like TiO₂ nanostructures. After a period of 6 to 12 h for hydrothermal treatment at 100 °C, the adsorption capacities at pH 5.6 were 44.8 ± 3.4 to 88.9 ± 3.3 mg g⁻¹ for Zn(II), 65.1 ± 4.4 to 72.8 ± 1.6 mg g⁻¹ for Cd(II), and 45.0 ± 3.8 to 65.6 ± 2.7 mg g⁻¹ for Pb(II). In contrast, pristine GO under identical conditions showed much lower removal capacities of 30.1 ± 2.5, 14.5 ± 1.5, and 35.6 ± 1.3 mg g⁻¹ for Zn(II), Cd(II), and Pb(II), respectively.

Recently, Musico et al.⁹⁶ studied the adsorption of Pb(II) using a GO–poly(N-vinylcarbazole) (PVK) combination to form PV–GO polymer nanocomposites. The experiment was conducted at initial Pb(II) ion concentrations of 5–300 mg L⁻¹, pH 7.0 ± 0.5, temperature 298 ± 5 K, and contact time 24 h. The results indicated that the adsorption capacity increased with the amount of GO in the nanocomposites, which likely occurred because the increase in GO concentration led to an increase in the oxygen functionalities available on the nanocomposites. The pH value of the solution played a vital role in the adsorption process, as the increase in pH resulted in an increased adsorption efficiency of the nanocomposites. From the kinetics studies data, the applicability of a pseudo-second-order kinetic model was observed. Additionally, the isotherm equilibrium data fitted well to the Langmuir isotherm model, with a maximum monolayer adsorption capacity of 887.98 mg g⁻¹.

The adsorption capacity of GO was enhanced by introducing chelating groups to its surface through a silanization reaction between (N-trimethoxysilylpropyl)ethylenediamine triacetic acid (EDTA–silane) and the hydroxyl groups of GO, as reported by Madadrang et al.⁷⁵ The experiment offered a remarkable Pb(II) adsorption capacity of 525 mg g⁻¹, which is significantly higher than pristine GO (approximately 367 mg g⁻¹) at pH 6.8, temperature 298 ± 2 K, contact time 24 h, and initial Pb(II) concentration of 5–300 mg L⁻¹. The adsorption kinetic was found to follow pseudo-second-order, and the equilibrium data were well described by the Langmuir isotherm model.

The adsorption of Cu(II) from aqueous solutions using GO aerogels was evaluated by Mi et al.⁹⁷ The initial Cu(II) ion concentration and pH value played a critical role during this experiment. The optimum adsorption capacity for Cu(II) decreased from 29.59 mg g⁻¹ (at the temperature of 313 K) to 17.73 mg g⁻¹ (at the temperature of 283 K), suggesting an endothermic adsorption process. The removal efficiency increased from 32.3 to 96.0% as the pH increased, showing that the adsorption of Cu(II) by the GO aerogel was highly pH-dependent. Also, the equilibrium data were best fitted to the Langmuir isotherm model, indicating that the active binding sites on the adsorbent surface were homogeneous for Cu(II) adsorption. The pseudo-second-order model described the adsorption process, and it was found that chemical adsorption involving electron exchanges between the adsorbent and adsorbate was dictating the adsorption of Cu(II) onto the GO aerogel.

Cheng et al.⁹⁸ conducted a study to determine the adsorption characteristics of U(VI) from aqueous solutions using sepiolite composite-supported GO. The initial U(VI) concentrations tested were 10–50 mg L⁻¹, and a maximum adsorption capacity of 161.29 mg g⁻¹ was recorded at pH 5.0 and temperature 298 K. Kinetic studies revealed that the process followed the pseudo-second-order kinetic model. Furthermore, the process was found to be exothermic in nature, and fitted well with the Langmuir isotherm model.

A study was conducted by Luo et al.⁹⁹ to compare the adsorption performances of poly 3-aminopropyltriethoxysilane GO (PAS-GO), 3-aminopropyltriethoxysilane GO (AS-GO), and pristine GO in removing Pb(II) ions from water. The entire process was conducted at pH 6.0, temperature 303 K, initial concentrations 10–400 mg L⁻¹, and contact time 7 h. The maximum Pb(II) adsorption capacities of PAS-GO, AS-GO, and pristine GO at 303 K were 312.5, 119.05, and 204.08 mg g⁻¹, respectively. In addition, an increase in temperature resulted in an increase in maximum adsorption capacity. From the adsorption isotherm data, it was revealed that the Langmuir isotherm model prevailed, while the adsorption kinetic data followed the pseudo-second-order kinetic model. This study proved that the incorporation of oligomers as cross linkers to fabricate the functional meshwork contributed towards the development of high-performance sorbents for removing heavy metal ions from wastewater.

Lei and co-workers¹⁰⁰ evaluated the adsorption capacities of heavy metals such as Zn(II), Fe(III), Pb(II), and Cd(II) on foam-infused GO (or GOF). The experiment was initialized at a concentration of 50 mg g⁻¹ for each metal ion. The adsorption isotherm obeyed the Langmuir model, and the resulting optimum adsorption capacities were 252.5, 381.3, 587.6, and 326 mg g⁻¹ for Cd(II), Pb(II), Fe(III), and Zn(II), respectively. These values were much higher compared to other conventional carbonaceous adsorbents such as AC. The adsorption capacities for all the tested heavy metal ions could be sequenced as Fe(III) > Pb(II) > Zn(II) > Cd(II). GOF indicated that a trivalent ion such as Fe(III) may provide a stronger electrostatic force of attraction to the GOF than the bivalent ions. It is also noteworthy that the variation in adsorption capacities for different heavy metals might be due to their unique characteristics as metal ion-functional groups, where some metals tend to be more attracted to certain functional groups.

A poly(amidoamine)-modified GO was prepared via a grating method by Yuan et al.¹⁰¹ for its potential application in the removal of heavy metal ions such as Fe(III), Cr(III), Zn(II), Cu(II), and Pb(II). The adsorption process was conducted at a constant concentration of 0.0193 mmol L⁻¹, contact time of 24 h, and room temperature. The maximum adsorption capacities for Fe(III), Zn(II), Cu(II), Cr(III), and Pb(II) were 0.5312, 0.2024, 0.1368, 0.0798, and 0.0513 mmol g⁻¹, respectively.

An experiment was conducted by Zhao et al.¹⁹ to explore the feasibility of few-layer graphene oxide (FGO) nanosheets as adsorbents for Co(II) and Cd(II). The adsorption capacities of Co(II) were 167.5 and 68.3 mg g⁻¹ at temperatures of 333 and 303 K, respectively, while the adsorption capacities of Cd(II) at the aforementioned temperatures were 153.6 and 106.3 mg g⁻¹, respectively. The isotherm data matched the Langmuir isotherm model. Observations from the experiment showed that the adsorption of Co(II) and Cd(II) on FGO was weakly dependent on the ionic strength and rather strongly dependent on the pH value. Consecutively, a thermodynamic study proved the endothermic nature of the process.

Hu et al.¹⁰² studied the adsorptive potential of sulfonated magnetic GO (SMGO) for the removal of Cu(II) ions from aqueous solutions. They investigated the effect of operating parameters (i.e., pH, initial Cu(II) ion concentration, and temperature) using a response surface methodology (RSM). The maximum adsorption capacity for Cu(II) was 62.73 mg g⁻¹ at pH 4.68, initial concentration 73.71 mg L⁻¹, and temperature 50 °C. The experimental isotherm data obeyed the Langmuir isotherm model, while the adsorption kinetic data followed the pseudo-second-order model. From the thermodynamic data, the adsorption reaction between Cu(II) ions and the active elements on the SMGO was endothermic and spontaneous, thus indicating that SMGO is a promising adsorbent for the effective removal of Cu(II) ions from wastewater.

Luo et al.¹⁰³ examined the potential of GO-hydrated zirconium oxide nanocomposites for As(III) and As(V) removal from wastewater. Based on the results, the adsorption capacity of As(III) was slightly higher (95.15 mg g⁻¹) than that of As(V), which was 84.89 mg g⁻¹. The pseudo-second-order kinetic model gave the best fit with the process occurring at a very fast adsorption rate, attaining equilibrium within 15 minutes. Moreover, the equilibrium data agreed with the Langmuir isotherm model. In contrast, Zhang et al.¹⁰⁴ performed an experiment to determine the adsorption performance of GO/ferric hydroxide to remove As(V) from aqueous solutions. The maximum adsorption capacity achieved was 23.78 mg g⁻¹.

Liu et al.¹⁰⁵ examined the ability of magnetite–GO (M–GO) composite to adsorb Co(II) ions from wastewater. The adsorption capacity of Co(II) was determined using varying temperatures of 303.15, 323.5, and 343.15 K, and the corresponding capacities of 12.98, 17.58, and 22.70 mg g⁻¹ were observed, respectively. The adsorption isotherm data revealed that the reaction was an endothermic and spontaneous process, and the Langmuir isotherm model and pseudo-second-order kinetic model fitted well.

To investigate the adsorption of Cr(VI) from aqueous solutions, fabrication of polypyrrole/GO (Ppy/GO) nanosheets using a sacrificial-template polymerization method was studied by the Li group.¹⁰⁶ An optimum adsorption capacity of 9.56 mmol g⁻¹ was obtained for Cr(VI) with the as-synthesized adsorbent. From this research, observations proved that the experimental data had a good fit with the Langmuir isotherm model, and the equilibrium data fit with the pseudo-second-order kinetic model.

Peng et al.¹⁰⁷ performed an experiment on GO–FeOOH composite to test its effectiveness in adsorbing As(V) from water. The adsorption process was carried out at a temperature 298 K, and the synthesized composite portrayed excellent adsorption properties. The equilibrium study could be well described by the pseudo-second-order kinetic model, and the isotherm data fit well with the Langmuir isotherm model.

The use of synthesized magnetic graphene–iron oxide composite (Fe₃O₄–GO) for the removal of U(VI) from aqueous solutions was recently reported by Zong et al.¹⁰⁸ The optimum U(VI) adsorption capacity on Fe₃O₄–GO at temperature of 293 K and pH 5.5 ± 0.1 was 69.49 mg g⁻¹. The Langmuir isotherm model and pseudo-second-order kinetic equation both governed the equilibrium and kinetic data, respectively.

Yu et al.¹⁰⁹ examined the adsorption behavior of Cu(II) ions on GO chitosan aerogel. The observed adsorption capacity was 0.254 mg g⁻¹ at a temperature of 303 K, initial concentration of 19.2 mg L⁻¹, and pH 6.0. In this experiment, the value of pH played an important role in the adsorption performance, as an increase in pH value above 6.0 would precipitate the Cu(II) ions. The adsorption kinetic followed the pseudo-second-order model, while the adsorption isotherms were slightly better fitted by the Langmuir isotherm model than the Freundlich isotherm model (with R² values of 0.993, and 0.989, respectively).

The removal capability of Pb(II) by porous GO–chitosan (PGOC) composite was studied by He et al.¹¹⁰ The recorded maximum adsorption capacity was 99 mg g⁻¹. In another variation of the study, Liu et al.²³ reported on the use of chitosan–GO (CSGO) composite as an adsorbent for the removal of Au(III) and Pb(II) from aqueous solutions in a batch system. The optimum adsorption capacity values recorded for Au(III) and Pb(II) were 1076.64 mg g⁻¹ and 216.920 mg g⁻¹, respectively. The adsorption kinetics for both ions followed the pseudo-second-order kinetic model. In addition, the chemical adsorption process was a rate-limiting step process, and the experimental data were well interpreted by the Langmuir isotherm model.

Chen et al.¹¹¹ performed an experiment to effectively remove Cu(II) and Pb(II) from aqueous solutions using a GO–chitosan hydrogen composite. The adsorption process was performed at an initial concentration range between 0 and 120 mg L⁻¹ and temperature 294 ± 1 K; however, the pH value and contact time were varied. For Cu(II), pH 5.1 and contact time of 10 h were implemented; for Pb(II), pH 4.9 and contact time of 4 h were used. The adsorption isotherm data for both metal ions agreed with the Freundlich isotherm model.

The use of magnetic chitosan–GO composite (MCGO) as a versatile adsorbent for Pb(II) oxide removal from aqueous solutions was reported by Fan et al.¹¹² The experiment was set at pH 2, contact time 1 h, initial concentration range 0–120 mg L⁻¹, and temperature 303.0 ± 0.2 K. The experiment proved that the magnetic adsorbent was stable and environmentally friendly, with a high adsorption capacity (76.94 mg g⁻¹) and extremely high desorption (90.3%).

Li et al.¹¹³ conducted an experiment using an easy chemical bonding method to synthesize magnetic cyclodextrin–chitosan–GO (CCGO). They investigated the adsorption behavior of Cr(IV) in aqueous solutions at different temperatures (303, 313, and 323 K) while maintaining constant pH 3 and initial concentration of 50 mg L⁻¹. The maximum adsorption capacities at these temperatures (303 to 323 K) were recorded as 61.31, 67.34, and 67.66 mg g⁻¹, respectively. These results proved that at higher temperatures, higher adsorption capacity values could be expected. The Langmuir isotherm model exhibited a better fit to the adsorption equilibrium data than the Freundlich isotherm model, implying that the composite surface was covered with a monolayer of Cr(VI) ions. The adsorption kinetic data followed the pseudo-second-order kinetic model.

Algothmi¹¹⁴ reported the use of calcium alginate–GO (Ca-Aig₂–GO) hybrid gel beads for effective removal of Cu(II) from aqueous solutions. A maximum Cu(II) uptake of 60.24 mg g⁻¹ was observed at room temperature and contact time of 1.5 h. The pseudo-second order rate equation provided a very good fit to the experimental kinetic data, and the Langmuir isotherm model fit well with the equilibrium isotherm data.

4.1.3. Adsorption on rGO and its composites. Yang et al.¹¹⁵ conducted research on the effect of humic acid (HA) on the Cu(II) adsorption process involving few-layered reduced GO (FrGO) and few-layered GO (FGO) using a batch equilibrium method. Two separate adsorption experiments were conducted: Experiment #1 without the HA, and Experiment #2 with the addition of the HA. For Experiment #1, the results showed that the adsorption capacities of Cu(II) on FrGO and FGO were 11.40 and 73.36 mg g⁻¹, respectively. This suggested that FGO was more effective due to its numerous oxygen-containing functional groups. Experiment #2 showed that when HA was added, the adsorption capacity of FrGO increased with increasing initial HA concentrations (from 0.0 to 30.0 mg L⁻¹). The increase in the adsorption by FrGO from 11.40 to 18.60 mg g⁻¹ suggested that the addition of HA facilitated the adsorption of Cu(II) as well as followed a pseudo-second-order kinetic model. Also, the adsorption isotherms could be simulated by the Langmuir isotherm model.

In an experiment, Li et al.¹¹⁶ explored an effective adsorbent in the form of polyaniline and rGO (PANI–rGO), which was prepared through the polymerization of aniline in the presence of GO to remove Hg(II) from aqueous solutions. The experiment was carried out at an initial concentration range of 10–40 mg L⁻¹, pH 4.0, temperature 305 K, and contact time 5 h. The maximum calculated Hg(II) adsorption capacity was 1000 mg g⁻¹. The equilibrium adsorption data were well fitted to both Langmuir and Freundlich isotherm models, and the adsorption process was well described by the pseudo-second-order kinetic model. A low adsorption capacity was recorded at a low pH, which was due to the protonation on the adsorbent surface functional groups, and also due to the decreased attachment of Hg(II) on the PANI–rGO surface.

The use of a synthesized iron–iron oxide matrix dispersed on rGO (rGO–FeO–Fe₃O₄) for As(III) adsorption from aqueous solutions was utilized by Bhunia et al.¹¹⁷ They had compared the capability of different adsorbents to remove As(III): (1) rGO–FeO, (2) rGO–Fe₃O₄, and (3) rGO–FeO/Fe₃O₄ at pH 7.0, initial concentration 2.6 mg L⁻¹, and contact time 1 h. The maximum adsorption capacities recorded were 37.3, 21.2, and 44.4 mg g⁻¹ for rGO–FeO, rGO–Fe₃O₄, and rGO–FeO–Fe₃O₄, respectively. The adsorption process appeared to follow the Langmuir isotherm model and the adsorption kinetic data to follow the pseudo-second-order model. Furthermore, because of its extremely high adsorption potential, rGO–FeO–Fe₃O₄ was further satisfactorily tested for the removal of metal ions such as Cr(III), Hg(III), Pb(II), and Cd(II). The adsorption process was conducted under the aforementioned experimental conditions. This process fitted well the Langmuir isotherm model. The maximum adsorption capacities recorded were 31.1, 22.0, 19.7, and 1.91 mg g⁻¹ for Cr(II), Hg(II), Pb(II), and Cd(II), respectively.

The removal of As(III) and As(V) from aqueous solutions using nanoscale zero-valent iron-rGO (NZVI-rGO)-modified composite was conducted by Wang et al.¹¹⁸ The experimental conditions for the adsorption were temperature 303 K and contact time 2 h. For As(III), the initial concentration was 3 mg L⁻¹, and pH ranged from 4.0 to 10.0, while for As(V), the initial concentration was 8 mg L⁻¹ and pH was 2. It was found that the solution pH played a major role in achieving the maximum adsorption. The optimum pH value for the removal of As(V) was 2, while for As(III), removal occurred at pH values ranging between 4 and 10. The adsorption capacities obtained for As(III) and As(V) were 35.83 and 29.04 mg g⁻¹, respectively. The isotherm studies indicated that the adsorption data were better fitted to the Langmuir isotherm model (R² > 0.995) than the Freundlich isotherm model (R² > 0.87). Moreover, from calculations, the pseudo-second-order kinetic model was deemed a better fit to the experimental kinetic data rather than the pseudo-first-order kinetic model.

Zhang et al.¹¹⁹ developed a magnetic cobalt ferrite–rGO nanocomposite (CoFe₂O₄–rGO) for the removal of Pb(II) and Hg(II) from aqueous solutions. A batch adsorption experiment was conducted under the following conditions: pH 5.3 and initial concentration 20 mg L⁻¹ for Pb(II), and pH 4.6 and initial concentration 5 mg L⁻¹ for Hg(II); temperature 298 K and contact time 2 h were kept constant for both analytes. The adsorption kinetics and adsorption isotherm were governed by the pseudo-second-order kinetic model and Langmuir isotherm model, respectively. In addition, the CoFe₂O₄–rGO, together with the adsorbed heavy metal ions, could be simply recovered from both the wastewater and aqueous solutions by magnetic separation at a very low magnetic field gradient, which could substantially reduce the current water treatment costs.

Sreeprasad et al.¹²⁰ performed an experiment on the adsorption of Hg(II) using two different rGO composites: rGO–MnO₂ and rGO–Ag. The adsorption experiments were conducted in batch modes at initial metal ion concentration 1 mg L⁻¹ and temperature 303 ± 2 K for both composites. The maximum adsorption capacities recorded were almost identical for rGO–MnO₂ and rGO–Ag, which were 9.50 and 9.53 mg g⁻¹, respectively.

An experiment to synthesize Fe₂O₄–rGO composites with different magnetic concentrations to remove As(III) and As(V) from water was performed by Chandra et al.¹²¹ Similar experimental conditions of initial metal ion concentration 3.7 mg L⁻¹, pH 7.0, temperature 293 K, and contact time 2 h were applied for both ions. The adsorption capacity values for the two ions were different, with As(V) having the higher capacity (13.10 mg g⁻¹) as compared to As(III) (10.20 mg g⁻¹). The adsorption kinetic studies could be described well by the pseudo-second-order kinetic model. Furthermore, the isotherm data revealed that both ions followed the Langmuir isotherm model.

Chandra and Kim¹²² conducted an experiment to determine the ability of polypyrrole–rGO (Ppy–rGO) composite to remove Hg(II) from aqueous solutions. The maximum Hg(II) adsorption capacity was 980 mg g⁻¹ at pH 3.0, temperature 298 K, contact time 3 h, and initial concentrations 50–250 mg L⁻¹. Both the Langmuir and Freundlich isotherm models prevailed in the isotherm study, as well as the pseudo-second-order kinetic model.

For the convenience of our readers, the reported results for heavy metal removal from aqueous solution and wastewater using graphene-based adsorbents are summarized in Table 2.

Table 2 Summary of reported results for heavy metal removal from aqueous solution and wastewater by graphene-based adsorbents

Adsorbent	Adsorbate	Adsorption capacity	Conc.	pH	Temp. (K)	Contact time (h)	Models applicable		Reference
							Isotherm	Kinetic
Graphene	Pb(II)	22.42 mg g^−1	40 mg L^−1	4.0	303	15	Langmuir		84
Graphene (treated at 77 K)	Pb(II)	35.21 mg g^−1	40 mg L^−1	4.0	303	15	Langmuir		84
Graphene (treated at 973 K)	Pb(II)	35.46 mg g^−1	40 mg L^−1	4.0	303	15	Langmuir		84
Graphene	Sb(II)	10.92 mg g^−1	1–10 mg L^−1	11.0	303	4	Freundlich	Pseudo-second-order	82
Graphene	Fe(II)	299.3 mg g^−1	20 mg L^−1	8.0		24			83
Graphene	Co(II)	370 mg g^−1	20 mg L^−1	8.0		24			83
Graphene	NO3	89.97 mg g^−1	500 mg L^−1	7.0	303	0.75	Langmuir	Pseudo-second-order	25
CTAB modified graphene	Cr(VI)	21.57 mg g^−1	20–100 mg L^−1	2.0	298	1	Langmuir	Pseudo-second-order	85
SiO2–graphene	Pb(II)	113.6 mg g^−1	20 mg L^−1	6.0	298	1	Langmuir	Pseudo-second-order	86
Functionalized graphene (GNS^PF6)	Pb(II)	406.4 mg g^−1		5.1		4	Langmuir, Freundlich	Pseudo-second-order	87
Functionalized graphene (GNS^PF6)	Cd(II)	73.42 mg g^−1		6.2		4	Langmuir, Freundlich	Pseudo-second-order	87
Functionalized graphene (GNS^C8P)	Pb(II)	74.18 mg g^−1		5.1		4	Langmuir, Freundlich	Pseudo-second-order	87
Functionalized graphene (GNS^C8P)	Cd(II)	30.05 mg g^−1		6.2		4	Langmuir, Freundlich	Pseudo-second-order	87
GO	Pb(II)	367 mg g^−1	5–300 mg L^−1	6.8	298 ± 2	24	Langmuir		75
GO	U(VI)	299 mg g^−1		4.0	Room temp.	4	Langmuir		92
GO	Zn(II)	30.1 ± 2.5 mg g^−1		5.6					95
GO	Cd(II)	14.9 ± 1.5 mg g^−1		5.6					95
GO	Pb(II)	35.6 ± 1.3 mg g^−1		5.6					95
GO	Cu(II)	117.5 mg g^−1	25–250 mg L^−1	5.3		2.5	Freundlich		73
GO	Pb(II)	692.66 mg g^−1	5–300 mg L^−1	7.0 ± 0.5	298 ± 5	24	Langmuir		96
GO	Cu(II)	294 mg g^−1		5.0	298	2	Langmuir	Pseudo-second-order	94
GO	Zn(II)	345 mg g^−1		5.0	298	2	Langmuir	Pseudo-second-order	94
GO	Cd(II)	530 mg g^−1		5.0	298	2	Langmuir	Pseudo-second-order	94
GO	Pb(II)	1119 mg g^−1		5.0	298	2	Langmuir	Pseudo-second-order	94
GO	Zn(II)	246 mg g^−1	10–100 mg L^−1	7.0 ± 0.1	293		Langmuir	Pseudo-second-order	93
		236 mg g^−1			303
		225 mg g^−1			318
GO aerogel	Cu(II)	17.73 mg g^−1	50–75 mg L^−1	6.3	283	0.5	Langmuir	Pseudo-second-order	97
		19.65 mg g^−1			298
		29.59 mg g^−1			313
Graphene/c-MWCNT	Pb(II)	104.9 mg g^−1	50 mg L^−1		Room temp.	120			88
Graphene/c-MWCNT	Hg(II)	93.3 mg g^−1	50 mg L^−1		Room temp.	120			88
Graphene/c-MWCNT	Ag(II)	64.0 mg g^−1	50 mg L^−1		Room temp.	120			88
Graphene/c-MWCNT	Cu(II)	33.8 mg g^−1	50 mg L^−1		Room temp.	120			88
Graphene/c-MWCNT	Pb(II)	44.5 mg g^−1	50 mg L^−1		Room temp.	120			88
Graphene/c-MWCNT	Hg(II)	75.6 mg g^−1	50 mg L^−1		Room temp.	120			88
Graphene/c-MWCNT	Ag(II)	46.0 mg g^−1	50 mg L^−1		Room temp.	120			88
Graphene/c-MWCNT	Cu(II)	9.8 mg g^−1	50 mg L^−1		Room temp	120			88
rGO–Fe(O)	As(II)	37.3 mg g^−1	2–6 mg L^−1	7.0	298	1	Langmuir	Pseudo-second-order	120
rGO–Fe3O4	As(III)	21.2 mg g^−1	2–6 mg L^−1	7.0	298	1	Langmuir	Pseudo-second-order	117
rGO–Fe(O)–Fe3O4	As(III)	44.4 mg g^−1	2–6 mg L^−1	7.0	298	1	Langmuir	Pseudo-second-order	117
rGO–Fe(O)–Fe3O4	Cr(III)	31.1 mg g^−1	2–6 mg L^−1	7.0	298	1	Langmuir		117
rGO–Fe(O)–Fe3O4	Hg(VI)	22.0 mg g^−1	2–6 mg L^−1	7.0	298	1	Langmuir		117
rGO–Fe(O)–Fe3O4	Pb(II)	19.7 mg g^−1	2–6 mg L^−1	7.0	298	1	Langmuir		117
rGO–Fe(O)–Fe3O4	Cd(II)	1.91 mg g^−1	2–6 mg L^−1	7.0	298	1	Langmuir		117
PAS-GO	Pb(II)	312.5 mg g^−1	10–400 mg L^−1	6.0	303	7	Langmuir	Pseudo-second-order	99
As-GO	Pb(II)	119.05 mg g^−1	10–400 mg L^−1	6.0	303	7	Langmuir	Pseudo-second-order	99
GO	Pb(II)	204.04 mg g^−1	10–400 mg L^−1	6.0	303	7	Langmuir	Pseudo-second-order	99
GO	Co(II)	116.35 mg g^−1	30 mg L^−1	6.0	298	12	Langmuir	Pseudo-second-order	24
GO foam	Cd(II)	252.6 mg g^−1	50 mg L^−1	10	Room temp.	1	Langmuir		100
GO foam	Zn(II)	326.4 mg g^−1	5 mg L^−1	10	Room temp.	1	Langmuir		100
GO foam	Pb(II)	381.1 mg g^−1	5 mg L^−1	10	Room temp.	1	Langmuir		100
GO foam	Fe(III)	587 mg g^−1	50 mg L^−1	10	Room temp.	1	Langmuir		100
NZVI-rGO	As(III)	35.83 mg g^−1		7.0(±0.25)	297(±0.5)	2	Langmuir	Pseudo-second-order	118
NZVI-rGO	As(V)	29.04 mg g^−1		7.0(±0.25)	297(±0.5)	2	Langmuir	Pseudo-second-order	118
Magnetic cyclodextrin–chitosan–GO	Cr(VI)	61.31 mg g^−1	50 mg L^−1	3.0	303		Langmuir	Pseudo-second-order	113
		67.34 mg g^−1			313
		67.66 mg g^−1			321
Calcium alginate–GO	Cu(II)	60.24 mg g^−1			Room temp.	1.5	Langmuir	Pseudo-second-order	114
Poly(N-vinylcarbazole)–GO	Pb(II)	887.98 mg g^−1	5–300 mg L^−1	7.0 ± 0.5	298 ± 5	24	Langmuir		96
Polypyrrole–rGO	Hg(II)	980 mg g^−1	50–250 mg L^−1	3.0	298	3	Langmuir, Freundlich	Pseudo-second-order	122
Magnetite–rGO	As(V)	13.10 mg g^−1	3–7 mg L^−1	7.0	293	2	Langmuir	Pseudo-second-order	121
Magnetite–rGO	As(III)	10.20 mg g^−1	3–7 mg L^−1	7.0	293	2	Langmuir	Pseudo-second-order	121
rGO–Ag	Hg(II)	9.50 mg g^−1	1 mg L^−1		303(±2)			Pseudo-second-order	120
rGO–MnO2	Hg(II)	9.53 mg g^−1	1 mg L^−1		303(±2)			Pseudo-second-order	120
CoFe2O4	Pb(II)	299.4 mg g^−1	20 mg L^−1	5.3	298	2	Langmuir	Pseudo-second-order	119
CoFe2O4	Hg(II)	157.9 mg g^−1	5 mg L^−1	4.6	298	2	Langmuir	Pseudo-second-order	119
Graphene/MgAl-layered double hydroxides	Cr(VI)	183.82 mg g^−1	50–250 mg L^−1	2.0		24	Freundlich	Pseudo-second-order	89
GO/ferric hydroxide	As(V)	23.78 mg g^−1	0.5–20 mg L^−1	4.0–9.0	Room temp.	24	Langmuir	Pseudo-second-order	104
Magnetite–GO	Co(II)	12.98 mg g^−1			303.2	24	Langmuir	Pseudo-second-order	105
		17.58 mg g^−1			323.2
		22.70 mg g^−1			343.2
GO–chitosan	Pb(II)	99 mg g^−1	50 mg L^−1		Room temp.		Langmuir		110
Chitosan–GO	Au(III)	1076.649 mg g^−1	80–500 mg L^−1		Room temp.	16	Langmuir	Pseudo-second-order	23
Chitosan–GO	Pb(II)	216.920 mg g^−1	80–500 mg L^−1		Room temp.	16	Langmuir	Pseudo-second-order	23
Fe304/GO	U(VI)	69.49 mg g^−1	2.25 × 10^5–2.24 × 10^−5 mol L^−1	5.5 ± 0.1	303	24	Langmuir	Pseudo-second-order	108
GO–chitosan composite hydrogen	Cu(II)	70 mg g^−1	0–120 mg L^−1	5.1	294 ± 1	10	Freundlich		157
GO–chitosan composite hydrogen	Pb(II)	90 mg g^−1	0–120 mg L^−1	4.9	294 ± 1	4	Freundlich		157
Magnetic chitosan–GO	Pb(II)	76.94 mg g^−1		5.1	303 ± (0.2)	1	Langmuir	Pseudo-second-order	112
Polypyrrole/GO	Cr(VI)	9.55 mmol g^−1					Langmuir	Pseudo-second-order	106
GO–FeOOH	As(V)	73.42 mg g^−1		7.0	298		Langmuir	Pseudo-second-order	107
GO@sepiolite	U(VI)	161.3 mg g^−1	10–50 mg L^−1	5.0	298		Langmuir		111
GO–TiO2	Zn(II)	88.9 ± 3.3 mg g^−1		5.6					95
GO–TiO2	Cd(II)	72.8 ± 1.6 mg g^−1		5.6					95
GO–TiO2	Pb(II)	65.6 ± 2.7 mg g^−1		5.6					95
GO–ZrO(OH)2	As(II)	95.15 mg g^−1	2–80 mg L^−1	7.0 ± 0.2	298.5 ± 0.2	0.25	Langmuir	Pseudo-second-order	103
GO–ZrO(OH)2	As(V)	84.89 mg g^−1	2–80 mg L^−1	7.0 ± 0.2	298.5 ± 0.2	0.25	Langmuir	Pseudo-second-order	103
Sulfonated magnetic GO composite	Cu(II)	50.68 mg g^−1	73.71 mg L^−1	5.0	283.2	6	Langmuir	Pseudo-second-order	102
		56.86 mg g^−1			303.2
		63.67 mg g^−1			323.2
EDTA modified GO	Pb(II)	525 mg g^−1	5–300 mg L^−1	6.8	298 ± 2	24	Langmuir		75
Poly(amidoamine) modified GO	Fe(III)	0.5312 mmol g^−1	0.0193 mmol L^−1		Room temp.	24			103
Poly(amidoamine) modified GO	Cr(III)	0.0798 mmol g^−1	0.0193 mmol L^−1		Room temp.	24			103
Poly(amidoamine) modified GO	Zn(II)	0.2024 mmol g^−1	0.0193 mmol L^−1		Room temp.	24			103
Poly(amidoamine) modified GO	Pb(II)	0.0513 mmol g^−1	0.0193 mmol L^−1		Room temp.	24			103
Poly(amidoamine) modified GO	Cu(II)	0.1368 mmol g^−1	0.0193 mmol L^−1		Room temp.	24			103
FrGO	Cu(II)	18.60 mg g^−1	0–30 mg L^−1	4–6	296 ± 1	24	Langmuir	Pseudo-second-order	115
FGO	Cu(II)	82.91 mg g^−1	0–30 mg L^−1	4–6	296 ± 1	24	Langmuir	Pseudo-second-order	115
FGO	Cd(II)	106.3 mg g^−1		6.0 ± 0.1	303		Langmuir		19
		153.6 mg g^−1			313
		167.5 mg g^−1			333
FGO	Co(II)	68.2 mg g^−1		6.0 ± 0.1	303		Langmuir		19
		69.4 mg g^−1			313
		79.8 mg g^−1			333
Graphene/Fe	Cr(VI)	162 mg g^−1	25–125 mg L^−1	4.25	293	4	Langmuir, Freundlich	Pseudo-second-order	90
Graphene/δ-MnO2	Ni(II)	46.55 mg g^−1	10–100 mg L^−1		298	3	Langmuir	Pseudo-second-order	61
		60.31 mg g^−1			308
		66.01 mg g^−1			318
Graphene/δ-MnO2	Cu(II)	1637.965 μmol g^−1		6.0	298 ± 2	2	Langmuir	Pseudo-second-order	61
Graphene/δ-MnO2	Pb(II)	773.65 μmol g^−1		6.0	298 ± 2	2	Langmuir	Pseudo-second-order	61
Graphene/Fe@Fe2O3@Si–S–O	Cr(VI)	1.03 mg g^−1	1 g L^−1	7.0				Pseudo-second-order	18
Graphene/Mnx^2+Fe2−x^3+O4^2−	As(III)	14.42 mg g^−1	1–8 g L^−1	7.0 ± 0.1	300 ± 1	2.5	Langmuir	Pseudo-second-order	91

---

4.2. Dye adsorption on graphene and its derivatives

Similar to heavy metals, abundant reports have appeared for dye adsorption on graphene and its derivatives. The following section will describe them in detail.

4.2.1. Adsorption on graphene and its composites. Liu et al.²³ studied the equilibrium and the dynamic adsorption of methylene blue (MB) from its aqueous solution onto graphene. The batch experiments showed that the adsorption of MB on graphene was dependent on adsorbent dosage, contact time, and temperature. The optimum dye adsorption capacity increased from 153.85 to 204.08 mg g⁻¹ with an increase in temperature from 293 to 333 K, whereas the maximum percentage removal (99.68%) was observed at pH 10. The equilibrium data followed the Langmuir isotherm model better than the Freundlich model. The adsorption kinetic of MB onto graphene fitted well with the pseudo-second-order model. Furthermore, the thermodynamic parameter revealed that the adsorption of MB onto graphene was an endothermic and spontaneous process.

An experiment was carried out by Li et al.⁹² to investigate the adsorption of cationic red X-GRL onto graphene in solution. The adsorption properties of the cationic X-GRL onto graphene were studied as a function of pH, adsorbent dosage, contact time, and temperature. The adsorption process was conducted at an initial concentration of 20–140 mg L⁻¹, contact time of 24 h, and at temperatures of 288, 313, and 333 K. The optimum adsorption capacity of 238.10 mg g⁻¹ was obtained at 333 K. The kinetic data were best described by a pseudo-second-order rate expression while the isotherm data matched the Langmuir model. The entire adsorption process was spontaneous and endothermic.

Wu et al.¹²³ performed an experiment to effectively removal methyl blue from aqueous solution using graphene. The adsorption process was carried out at an initial concentration of 5 mg L⁻¹, with temperature of 303 K, and contact time of 1 h. The thermodynamic analysis revealed a spontaneous and endothermic nature of the graphene due to π–π stacking interaction through fluorescent spectroscopy studies. The amount of dye adsorbed was found to be dependent on the initial dye concentration.

The adsorption of organic dyes (RB, MB, fuchsine) in batch experiments on fabricated graphene–CNT hybrid aerogels (graphene/c-MWCNTs and graphene/MWCNTs) by CO₂ drying of their hydrogen precursor was obtained from heating the aqueous mixture of GO and CNTs with ascorbic acid (vitamin C) without stirring as per Sui et al.⁸⁸ The adsorption process was conducted at room temperature with an initial dye concentration of 20 mg L⁻¹. The maximum adsorption capacities for RB, MB, and fuchsine by graphene/c-MWCNTs were 150.2, 191.2, and 180.8 mg g⁻¹, respectively, and 146.0, 134.9, and 123.9 mg g⁻¹, respectively, on graphene/MWCTs. A higher concentration of oxygen-containing functionalities in graphene/c-MWCNTs over graphene/MWCNTs might be a possible reason for the lower adsorption capacity values for graphene/MWCNTs.

An investigation was conducted by Zhao et al.²⁰ on a new graphene material known as “graphene sponges” (GSs) to test the adsorption of both cationic (methylene blue, rhodamine B) and anionic (methyl orange) dyes from their aqueous solution in batch adsorption mode. The adsorption was conducted at constant temperature of 298 K and initial concentration of 2 × 10⁻⁴ mol L⁻¹. The contact of the two dyes differed, with the cationic and anionic dye having a contact time of 4 and 24 h, respectively. Maximum adsorption capacities of 184, 11.5, and 72.5 mg g⁻¹ were obtained for MB, MO, and rhodamine B, respectively. Furthermore, the basic dye (MB) had the highest adsorption capacity as compared to the acidic dye (methyl orange), which may be due to the surface characteristic of the GSs and also due to the presence of the ionic charges on the dye. In addition, their studies also revealed that rhodamine B can easily be desorbed from GSs in methanol or ethanol, which suggests that GSs can repeatedly remove rhodamine B from water.

The synthesis of magnetic Fe₃O₄–graphene composite (FGC) and its application in (MB and Congo red (CR)) dye removal from aqueous media was studied by Yao et al.¹²⁴ A maximum adsorption capacity of 33.66 mg g⁻¹ was obtained at the temperature of 298 ± 0.52 K for CR, while a maximum adsorption capacity of 45.27 mg g⁻¹ was obtained at the temperature of 298 ± 0.52 K for MB. The equilibrium adsorption process was well fitted to Langmuir isotherm models for both MB and CR. Moreover, the kinetic data of MB and CR adsorption by FGC was satisfied by a pseudo-second-order kinetic model.

Ai et al.¹²⁵ illustrated a facile one-step solvothermal method for the synthesis of graphene nanosheet (GNS)/magnetic (Fe₃O₄) composite and used it for the removal of MB from aqueous solution. They studied the adsorption kinetics, isotherm, and thermodynamics in detail, and their results revealed that the kinetics and equilibrium adsorption are well described by the pseudo-second-order kinetic and Langmuir isotherm model, respectively. The observed maximum adsorption capacity at temperature of 298 K and initial concentration of 10–25 mg L⁻¹ was 43.82 mg g⁻¹.

Graphene–magnetite composite was tested for the removal of pararosaniline (Basic Red 9) by Wu et al.¹²⁶ The adsorption capacity of 198.23 mg g⁻¹ was obtained at temperature of 298 K, with an initial concentration of 20–60 mg L⁻¹ and pH 6.6 ± 0.2. In this experiment, the value of pH played an important role in the adsorption performance, as an increase in pH would precipitate the dye. The adsorption kinetic followed the pseudo-second-order model, while the adsorption isotherm was well interpreted by both the Langmuir and Freundlich isotherm model.

Wang and coworkers synthesized magnetic sulfonic graphene nanocomposite (G–SO₃H/Fe₃O₄) and used it as an adsorbent for the batch adsorption of three cationic (neutral red, safranin T, and victoria blue) and three anionic (methyl orange, brilliant yellow, and alizarin red) dyes from aqueous solution.⁹³ The adsorbent G–SO₃H/Fe₃O₄ showed an excellent adsorption capacity toward the cationic dyes compared to anionic dyes. Based on their results, the adsorption capacities of the three cationic dyes, i.e., neutral red, victoria blue, and safranin T, were 216.8 mg g⁻¹, 20.06 mg g⁻¹, and 199.3 mg g⁻¹, respectively, at an initial concentration of 20–250 mg L⁻¹, pH of 6, and at room temperature. The adsorption of cationic dyes on G–SO₃H/Fe₃O₄ followed the Langmuir isotherm and pseudo-second-order kinetics model. The adsorption capacity was found to follow a decreasing order as neutral red > victoria blue > safranin.

In another development, graphene–sand composite (GSC) was prepared using asphalt as the carbon source and was applied as an adsorbent for the removal of rhodamine 6G by Sreeprasad et al.¹²⁷ The observed adsorption capacity was 75.4 mg g⁻¹, which was obtained at a contact time of 6 h and temperature of 303 ± 2 K. The adsorption kinetics data correlated well with the pseudo-second-order kinetics model. It was also concluded that the importance of particle size of adsorbent cannot be overemphasized, as it has a strong effect on batch adsorption studies. Sen Gupta et al.¹²⁸ also tested the adsorption capability of graphene–sand composite (GSC) as an adsorbent for the removal of rhodamine 6G. The observed maximum adsorption capacity of 55 mg g⁻¹ for rhodamine 6G was obtained under the experimental conditions of initial concentration 5 mg L⁻¹, temperature of 303 ± 2 K, and contact time of 8 h. The kinetics data obeyed the pseudo-second-order kinetics model. Furthermore, a column study was also conducted, and the breakthrough curves at different bed depths were obtained. The bed depth service time (BDST) model revealed excellent agreement with dynamic flow experimental data. Finally, they were able to show that acetone can be used to regenerate GSC for multiple uses.

The capacity of the graphene–carbon nanotube hybrid (G–CNT) to efficiently adsorb MB from aqueous solution was reported by Ai and Jiang.¹²⁹ The initial dye ion concentrations tested were 10–30 mg L⁻¹, and the maximum adsorption capacity recorded for a contact time of 3 h was 81.97 mg g⁻¹. Li et al.¹³⁰ synthesized Cu₂O–graphene and Mg(OH)₂–graphene,¹³¹ and the adsorption of dyes, MB, and RB was studied. Both composites exhibited an excellent behavior for dye removal.

4.2.2. Adsorption on GO and its composites. Other than graphene, the ability of GO as an adsorbent to remove dyes from aqueous medium was also investigated. The adsorptive potential of GO to remove MB was tested by Yang et al.¹³² The process was carried out under the following experimental condition: pH 6, temperature 298 K, contact time 1 h, and initial dye concentration range 0.188–1000 g L⁻¹. It was illustrated that the amounts of MB adsorbed onto GO increased with an increase in pH and ionic strength, while the removal process was faster and more effective at lower temperature. The highest removal efficiency of 99% and the maximum adsorption capacity of 714 mg g⁻¹ were obtained. Moreover, the equilibrium data supported the Freundlich isotherm. Finally, the results demonstrated that GO can be applied in the treatment of initial effluent and contaminated natural water.

Fast and effective adsorption of MB dye from an aqueous solution onto GO was reported by Zhang et al.¹³³ The dye-containing solution had an initial concentration ranging between 0.33 and 3.3 mg L⁻¹, temperature 298 K, pH 7.0, and contact time 2 h. The maximum adsorption capacity was 1.939 mg g⁻¹. The adsorption processes became possible due to the special nanostructural properties and negatively charged surface of GO and the positively charged MB ions, which can be easily absorbed electrostatically. The equilibrium adsorption data showed an excellent fit to the Langmuir isotherm model, and the adsorption process was exothermic in nature. The adsorption was found to be more efficient at high pH value and low temperature.

An experiment to determine the feasibility of removing methyl green dye from aqueous solution using synthesized graphene nanocomposite sheets was reported by Farghali et al.¹³⁴ At an initial methyl green concentration of 50–400 mg L⁻¹, the maximum adsorption capacities of the graphene sheets were found to be 203.51, 258.39, and 312.80 mg g⁻¹ at temperature 298, 313, and 323 K, respectively. The research showed that after increasing the concentration of methyl green in the solution, the active sites on the graphene sheets are surrounded by many more methyl green ions, and the adsorption process is sufficiently carried out. The study revealed better fitting of the pseudo-second-order model to the adsorption kinetics data. From the equilibrium adsorption data, the process was best fitted to the Langmuir isotherm data. A spontaneous endothermic and physisorption process was revealed from the thermodynamic study. Li et al.¹³⁵ prepared a magnetic CoFe₃O₄-functionalized graphene sheet (CoFe₃O₄-FGS) nanocomposite via a facile hydrothermal method and used it to adsorb methyl orange. The observed maximum adsorption capacity at 10 mg L⁻¹ initial concentration was 71.54 mg g⁻¹. The pseudo-second-order model was best fitted to the kinetics data.

Ramesha et al.⁷⁸ conducted an experiment to determine the capability of GO to adsorb methylene blue, methyl violet, rhodamine B, and orange G from aqueous solutions. Experiments revealed that GO has an excellent bonding affinity for cationic dyes (i.e., methylene blue, methyl violet, and rhodamine B). The research was performed at an initial concentration of 10–50 mg L⁻¹ for both methylene blue and methyl violet at constant pH of 6 but the initial concentration of rhodamine B was varied from 1–10 mg L⁻¹ at pH 10. The obtained adsorption capacities for methylene blue, methyl violet, and rhodamine B were 17.3, 2.47, and 1.24 mg g⁻¹, respectively. The large negative charge density available in aqueous solutions supported the effective adsorption of the cationic dye. Such adsorption behavior was attributed to the fact that methylene blue and methyl violet were positively charged, whereas rhodamine B has both negative and positive charges associated with it that exist between rhodamine B and GO. The kinetics data revealed that the dye followed the pseudo-second-order kinetic, while the equilibrium data fitted well with the Langmuir isotherm.

The adsorption of MB from aqueous solution onto GO was reported by Li et al. under the following experimental conditions: temperature 298 K, pH 6.0, initial dye concentration 40–120 mg L⁻¹, and contact time 5 h (ref. 81) The results showed remarkable MB adsorption (243.90 mg g⁻¹) on GO. Moreover, the adsorption appeared to follow the Langmuir isotherm model, which revealed that the adsorption of MB on GO takes place in a monolayer adsorption manner. It is important to note that the change in the optimum MB adsorption capacity values may occur because of the different experimental conditions employed during each study. The adsorption kinetics followed the pseudo-second-order mechanism, suggesting that the adsorption might be a rate-limiting step involving valence forces through a sharing or exchange of electrons between the adsorbent and adsorbate.

Sun et al.¹³⁶ researched the use of modified GO for removing acridine orange from its aqueous solution. It was attempted to enhance the efficiency of GO as an adsorbent through in situ reduction with sodium hydrosulfide (Na₂S₂O₄) because it is less toxic, less corrosive, and extremely eco-friendly. The lateral adsorption test was performed under similar experimental conditions of initial concentration 0.1 g L⁻¹, contact time 3 h, and at room temperature. The experiment was conducted with both pristine GO and in situ rGO, and the in situ rGO had a much higher adsorption capacity (3333 mg g⁻¹) than the pristine GO (1428 mg g⁻¹). Additionally, Sharma et al.¹³⁷ examined the possibility of using GO as an adsorbent for the removal of methyl green from aqueous medium at temperature 298 K and contact time 1 h with varying pH from 4 to 9. It was observed that the adsorption capacities increased from 4.821 to 7.613 mmol g⁻¹. The Langmuir isotherm model and pseudo-second-order kinetic equation governed the equilibrium and kinetic data, respectively.

Farahani et al.¹³⁸ studied the adsorption mechanism of single and binary systems of dyes (basic blue 41 (BB41), basic red 18 (BR18)) and basic red (BR46) by GO. The adsorption equilibrium showed that the Langmuir isotherm governed the experiment well, while indicating a monolayer adsorption mechanism. The BB41, BR18, and BR46 adsorption capacities on GO were 1429, 1250, and 476 mg g⁻¹, respectively, at a contact time of 1 h, initial concentration of 5 mg L⁻¹, and temperature of 298 K. The adsorption kinetic followed the pseudo-second-order kinetic model, indicating a chemical adsorption process. In addition, the experiment revealed that dye removal with an adsorbent dosage can be attributed to the increased adsorbent surface and availability of more adsorption sites that are accessible for dyes molecules.

A GO series with different oxidation degrees was prepared using the Hummer method, and the fundamental behavior of the GO series for the removal of MB from aqueous solution was investigated and reported by Yan et al.¹³⁹ The MB contained in the solutions had an initial concentration of 600 mg dm⁻³, pH 7, temperature 298 K, and contact time 0.25 h. At varied degrees of oxidation of GO₁, GO₂, GO₃, GO₄, GO₅, and GO₆, maximum adsorption capacities of 40.6, 157.6, 334.7, 454.5, 513.9, and 570.4 mg g⁻¹, respectively, were achieved. The GO series exhibited a stronger affinity to MB in water, resulting in a fast dye removal rate and pH-independent adsorption capacity. It was concluded that by increasing the degree of oxidation, the dye uptake of GO would exponentially increase, and the isotherm adsorption behavior would change from the Freundlich to the Langmuir type of adsorption. Finally, it can be deduced that the binding feature of MB-loaded GO gradually changed from parallel stacking of the MB molecule on the graphite plane through hydrophobic π–π interaction to vertical stacking via electrostatic interaction with increased OD, resulting in a significant improvement of MB uptake.

Li et al.⁸¹ studied the adsorption of MB onto GO. From the experimental results, it was reported that the maximum adsorption capacity was 243.90 mg g⁻¹ at room temperature under the experimental conditions of pH 6.0, contact time 5 h, temperature 297 K, and initial concentration of 100 mg L⁻¹. The isotherm study revealed that the equilibrium data followed the Langmuir isotherm model. The results also revealed that the adsorption of MB by the GO adsorbent takes place in a monolayer adsorption manner. The adsorption kinetics followed the pseudo-second-order mechanism, suggesting that the adsorption might be a rate-limiting step, involving valence forces through sharing or exchange of electrons between the adsorbent and adsorbate.

The removal of cationic dyes, methyl blue (MB), and malachite green (MG) from aqueous solution using an electrostatic attraction mechanism between the dyes and GO was reported by Bradder et al.¹⁴⁰ The optimum adsorption capacities for MB and MG on GO were 351 and 248 mg g⁻¹, respectively, which were considerably higher than that of graphite and AC.

Zhang et al.¹⁴¹ researched the use of GO caged in cellulose beads (GOCB) for removing malachite green (MG) from aqueous solution. The lateral adsorption test was carried out under the experimental conditions of pH 7.0, contact time 1 h, temperature 298 K, and initial dye concentration 10 mg L⁻¹. Under optimum conditions, the adsorption capacity was calculated to be 30.091 mg g⁻¹, which was well fitted to the Langmuir isotherm model. The study also revealed that solution pH plays a very important role in the adsorption process, as there was increased electrostatic attraction between the adsorbent and MG when the pH ranged from 6.0 to 8.0. The poor adsorption when the pH was under 6 or above 8 may be attributed to the fact that the GOCB decomposes in acidic solution and dissolves in alkaline conditions.

The use of a 3D graphene oxide sponge (GO sponge) for the adsorption of cationic dyes, methylene blue (MB), and methyl violet (MV) was reported by Liu et al.²³ The 3D-GO sponge adsorbed with capacities of 397 and 467 mg g⁻¹ for MB and MV, respectively. The activation energies of the adsorption through strong π–π stacking and anion–cation interaction were 50.3 and 70.9 kJ mol⁻¹, respectively.

A covalent bonding technique to synthesize Fe₃O₄/SiO₂–GO nanocomposite, which also served as an adsorbent for the removal of MB from aqueous solution, was reported by Yao et al.¹⁴² The maximum MB adsorption capacities at temperatures 298, 318, and 333 K were 97, 102.6, and 111.1 mg g⁻¹, respectively. The equilibrium data were well fitted to the Langmuir isotherm model, while the pseudo-second-order kinetics model was well fitted to the kinetics data.

The possibility of using MgO decked multi-layered graphene (MDMLG) for the removal of safranin O (SO) dye from water was reported by Rotte et al.¹⁴³ A maximum adsorption capacity of 3.92 × 10⁻⁴ mol g⁻¹ was recorded under the following conditions: pH 12, initial dye concentration 4 × 10⁻⁴ M, and contact time 2 h. The adsorption increased with increases in pH and adsorbent dose. The removal of SO dye decreased with an increase in dye concentration. The isotherm and kinetics data fitted to the Langmuir and pseudo-second-order model, respectively. Furthermore, the MDMLG showed excellent reusability.

4.2.3. Adsorption on rGO and its composites. Kim et al.¹⁴⁴ reported the use of reduced rGO microstructure as an adsorbent for the removal of acid red 1 (AC1) and methylene blue (MB). The maximum adsorption capacity for MB was 302.11 mg g⁻¹, which was achieved at an initial concentration of 300 mg L⁻¹, while at an initial concentration 50 mg L⁻¹, the maximum adsorption capacity for AC1 was 28.51 mg g⁻¹. The equilibrium data for MB was fitted to the Langmuir isotherm model, while the Freundlich model was fitted to AC1. The adsorption rates for both dyes were found to follow the pseudo-second-order kinetic. From the results, it can be deduced that 3D rGO macrostructures were more favorable for the adsorption of cationic dye rather than anionic dye due to strong specific interactions.

Sharma et al.¹⁴⁵ conducted an experiment to study the adsorption of methyl green (MG) from aqueous solution using rGO. The experiment showed a remarkable adsorption capacity of 3.163 mmol g⁻¹ at set experimental conditions of pH 5, temperature 298 K, and contact time 1 h. The equilibrium isotherm data were well described, in the order of Toth > Sips > Dubinin–Radushkevich (D–R) > Scatchard > Langmuir > Temkin > Freundlich model at pH 4–6. However, this changed to D–R > Scatchard > Toth > Sips > Langmuir > Temkin > Freundlich model at pH 7–9. From the isotherm studies, the Langmuir isotherm was best fitted to the equilibrium data when compared to the Freundlich model. Furthermore, the experiment also revealed that the pH of the solution plays an important role in the adsorption process. Increasing the pH resulted in an increase in the adsorption capacity of MG onto rGO, which was due to the effect of pH on the electrostatic charge–charge interaction between the negatively charged rGO polar groups and the cationic dye molecule. FTIR spectrum indicates that the adsorption was due to the electrostatic interaction between the MG and the rGO nanosheets. The kinetic data showed that the process was better described by the pseudo-second-order kinetic model. Finally, the negative ΔG⁰ value of adsorption of MG onto rGO nanosheets indicated that the process was spontaneous, while the values of ΔH⁰, ΔS⁰, and activation energy values showed an increase in the adsorption capacity with temperature during the physisorption process.

Three-dimensional (3D) rGO-based hydrogels were synthesized by reduction of GO using sodium ascorbate and were used as an adsorbent for the removal of MB and rhodamine B (RB) from aqueous solution by Tiwari et al.¹⁴⁶ The experiments were conducted at an initial concentration of 0.5–10 mg L⁻¹, pH 6.4, temperature 29 K, and contact time 2 h. The results revealed an excellent removal capability of approximately 100% for MB and approximately 97% for RB when a 0.6 g L⁻¹ adsorbent dose was used. The maximum adsorption capacities for MB and RB were 7.85 and 29.44 mg g⁻¹, respectively. The high adsorption capacity of RB was due to adsorption through strong π–π stacking and anion–cation interactions. From the kinetic studies, it was revealed that the adsorption of dye followed the pseudo-second-order kinetics model. Furthermore, desorption studies were conducted using ethylene glycol that showed that the rGO-based hydrogel could be efficiently regenerated and re-used. Toxicity tests revealed that hydrogel-purified aqueous solutions were comparable to distilled water.

A one-pot solvothermal method successfully synthesized a rGO-supported ferrite (MFe₂O₄, M = Mn, Zn, Co, and Ni) hybrid adsorbent for the removal of dye pollutants, as reported by Bai et al.¹⁴⁷ After a contact time of 2 min and initial dye concentration of 5 mg L⁻¹, 92% RB and 100% MB were effectively removed. Furthermore, the hybrid also showed an enhanced photocatalytic activity for the degradation of RB and MB. In addition, the possibility of using a synthesized functional hybrid of rGO–Fe₃O₄ nanoparticles was reported by Geng et al.¹⁴⁸ The hybrid possessed excellent and versatile capacity to adsorb different dyes such as RB, rhodamine 6G (R6G), acid blue 92 (AB92), orange (II) (011), MG, and new coccine.

An investigation was conducted by Nguyen-Phan et al.¹⁴⁹ using fabricated rGO–titanate (rGO–Ti) hybrids incorporating spherical TiO₂ nanoparticles with GO layers in the presence of NaOH for the removal of MB from aqueous solution. The optimum adsorption capacity was 83.26 mg g⁻¹ at 10 mg L⁻¹ initial concentration, which was higher than the adsorption capacity obtained for pure graphene (48.7 mg g⁻¹) and tubular titanates (36.5 mg g⁻¹). Wang et al.¹⁵⁰ performed an experiment to examine the removal of RB by adsorption onto rGO/ZnO composite. The batch adsorption process was conducted for a contact time of 2 h, temperature 298 K, and at an initial dye concentration of 4–70 mg L⁻¹. The observed maximum adsorption capacity for RB was 32.6 mg g⁻¹.

A magnetic modified rGO (MrGO) nanocomposite was prepared via a one-step solvothermal method by Sun et al.¹⁵¹ and was tested for its potential as an adsorbent to remove RB and MG dyes from aqueous solutions. The adsorption process was conducted at an initial concentration of 0.5–4 mg L⁻¹, contact time of 2 h, pH 7.0 and temperature 298 K. The maximum adsorption capacities for RB and MG were 13.15 and 22.0 mg g⁻¹, respectively. The equilibrium data were well described by both the Freundlich and Langmuir models, while the kinetic study data fitted well to the pseudo-second-order kinetic model. A desorption study using ethylene glycol as the eluent revealed successful multiple rounds of recycle and reuse of MrGO without any significant change in the initial adsorption efficiency. Wang et al.¹⁵² pursued an experiment to study the adsorption of RB using core–shell structure polystyrene Fe₃O₄–GO nanocomposites. The adsorption was carried out at an initial concentration of 0–150 mg L⁻¹, contact time of 24 h, and at room temperature. The maximum adsorption capacity was 13.8 mg g⁻¹.

The use of a synthesized super paramagnetic GO–Fe₃O₄ composite as a versatile adsorbent for the removal of MB and neutral red (NR) was reported by Xie et al.¹⁵³ The equilibration times for MB and NR were 30 min and 90 min, respectively, and maximum adsorption capacities of 167.2 and 171.3 mg g⁻¹ were obtained, respectively. The use of as-fabricated magnetic cyclodextrin–GO (MCGO) as an adsorbent for the removal of MB was demonstrated by Li et al.¹⁵⁴ This work depicted a maximum adsorption capacity 261.78 mg g⁻¹ for MB, which was achieved at pH 10, initial concentration 100 mg L⁻¹, temperature 303 K, and a contact time of 5 min. The experimental isotherm data followed the Langmuir isotherm model, while the adsorption kinetic data obeyed the pseudo-second-order model. It was explained that the synergic effect of the surface properties of GO, hydrophobicity of cyclodextrin, and the magnetic properties of Fe₃O₄ in the MCGO composite provided a versatile adsorbent with good adsorption properties that is magnetically separable after the completion of the adsorption process.

Chen et al.¹¹¹ performed an experiment to effectively remove basic dye (MB) and acidic dye (eosin Y) from aqueous solutions using GO–chitosan hydrogen composite. The adsorption process was conducted at an initial concentration of 0.8 mg L⁻¹ with a temperature of 294 ± 1 K; however, the pH value and contact time were varied. For MB adsorption, pH 6.5 at a contact time of 58 h were set, while for eosin Y (acid dye), pH 7.0 and a contact time of 36 h were selected. A spectral method was used to determine the adsorption mechanism of the dyes. Electrostatic interaction was found to be the major interaction that existed between the ionic dyes and hydrogen. In another study, Fan et al.¹⁵⁵ developed a magnetic chitosan–GO (MCFO) nanocomposite through the covalent bonding of chitosan to the surface of Fe₃O₄ nanoparticles followed by covalent functionalization of GO with magnetic chitosan. From their research, maximum adsorption of 95.31 mg g⁻¹ for methyl blue was obtained at an initial concentration of 60–200 mg L⁻¹, pH 5.3, and temperature of 303 K. Pseudo-second-order and Langmuir isotherm models were fitted to kinetics and isotherm data, respectively. The thermodynamic parameter data revealed the spontaneous and exothermic nature of the adsorption process. Maximum desorption was attained with 0.5 M NaOH, and the adsorption capacity was approximately 90% of the initial saturated adsorption capacity after four adsorption–desorption cycles.

The use of magnetic chitosan–GO composite (MCGO) as a versatile adsorbent for the removal of MB from aqueous solution was reported by Fan et al.¹⁵⁶ The maximum adsorption capacity at an initial concentration of 50–100 mg L⁻¹ and temperature of 303 ± 0.2 K was 180.83 mg g⁻¹. The experiment proved that MCGO has an extraordinary adsorption capacity and fast removal rate for MB. Furthermore, the capacity of the magnetic β-cyclodextrin–chitosan GO nanocomposite to adsorb MB from aqueous solution was explored by Fan et al.¹¹² The amount of MB adsorbed onto the magnetic β-cyclodextrin–chitosan–GO increased with dose. The adsorption of MB was governed by a pseudo-second-order kinetics model. The isotherm data were well described by the Langmuir isotherm model with a maximum monolayer adsorption capacity of 84.32 mg g⁻¹ at a temperature of 293 K.

In a study carried out by Chen et al.¹⁵⁷ a hydrophilic and biocompatible three-dimensional (3D) chitosan–graphene mesostructure was prepared for the removal of reactive black 5 (RB5) from aqueous solution. From their experiment, it was revealed that at an initial RB5 concentration of 1.0 mg mL⁻¹, the RB5 removal efficiency was 97.5%. Also, the properties of Congo red (CR) as it is adsorbed onto graphene oxide (GO)–chitosan (CS)/etched (ETCH) were reported by Du et al.¹⁵⁸ The observed maximum adsorption capacity at pH 3.0, initial concentration 80 mg L⁻¹, and temperature 283 K was 294.12 mg g⁻¹. The experimental isotherm data conformed to the Langmuir isotherm model, while the adsorption kinetics data fitted well with the pseudo-first-order model. From their experimental results, it can be deduced that GO–CS/ETCH is a promising adsorbent candidate to remove dyes from wastewater.

The use of 3D graphene oxide–sodium alginate (GO–SA) gel and reduced graphene oxide–sodium alginate (rGO–SA) gel as an adsorbent for the removal of MB was investigated and reported by Ma et al.¹⁵⁹ The maximum MB adsorption capacity on GO–SA and rGO–SA at an initial concentration of 0.1 mmol L⁻¹, temperature 303 K, and contact time of 12 h was found to be 833.3 and 192.3 mg g⁻¹, respectively. The equilibrium data fitted well with both Langmuir and Freundlich isotherms, while the pseudo-second-order model and the intraparticle diffusion model well described the kinetic data. The thermodynamic parameters indicated that the adsorption of MB was a spontaneous process. Moreover, different adsorption mechanisms can be invoked due to the different types of oxygen-containing groups in the GO–SA and rGO–SA gels. Electrostatic interaction plays a leading role in the attraction between GO–SA and MB, while π–π stacking was the primary interaction between rGO–SA and MB. In addition, the adsorption of GO–SA was exothermic, while the absorption of rGO–SA was endothermic.

Yu et al.¹⁰⁹ performed an experiment to determine the adsorption capacities of GO–zeolite and carboxy-GO–zeolite powder in the removal of RB from aqueous solution. The maximum adsorption capacity values of RB on GO–zeolite and carboxy-GO–zeolite were 55.56 and 67.56 mg g⁻¹, respectively. The adsorption behavior was fitted to the Langmuir isotherm, while the kinetics data were fitted to a pseudo-second-order kinetics model. Li et al.⁸¹ conducted a study to evaluate the adsorption possibility of GO–calcium alginate (GO/CA) composite as an adsorbent for the removal of MB from aqueous solution. The adsorption studies were conducted under the following experimental conditions: initial concentration 30–80 mg L⁻¹ with pH 4.5–10.2. Temperature played a very important role in the adsorption process. A decrease in adsorption capacity from 163.93 to 140.85 mg g⁻¹ was observed when the temperature increased from 298 to 328 K, signifying the exothermic nature of the process. In addition, the maximum adsorption capacity (181.81 mg g⁻¹) was reported at 0.05 g/100 mL. The kinetics data obeyed the pseudo-second-order model, while the equilibrium data fitted to the Langmuir isotherm model.

Deng et al.¹⁶⁰ conducted an experiment on the use of synthesized magnetic GO (MGO) as an adsorbent for the removal of ionic dyes, including MB and orange G (OG), from aqueous solution. They conducted their experiment at constant experimental conditions with contact time of 6.75 h and temperature at 298 K. It was observed that the adsorption capacity values for the two dyes were different at different concentrations, with MB having a higher capacity (64.23 mg g⁻¹) at 90 mg L⁻¹ initial concentration, as compared to OG (20.85 mg g⁻¹) at an initial concentration of 60 mg L⁻¹. Furthermore, a detailed explanation was given regarding the adsorption of MB and OG onto MGO by an electrostatic attraction mechanism between MGO surface charge adsorbents, and because of the electrostatic attraction force, the MGO adsorbent with a negative surface charge at a higher pH (>3.5) favored adsorption toward the cationic dye MB with a positive charge. In contrast, for the anionic dye OG, the adsorption quality decreased with increasing pH value due to electrostatic repulsion forces. The adsorption isotherm data for the dyes were fitted well with the Langmuir model in a mono-component system, while the adsorption kinetic study followed the pseudo-second-order model.

The use of a fabricated polydopamine layer-coated GO (PD/GO) composite for the removal of MB was reported by Dong et al.¹⁶¹ When MB was adsorbed by different percentages of PD, i.e., PD5%/GO, PD15%/GO, PD35%/GO, and PD70%/GO, the maximum adsorption capacities were 1.3, 1.89, 1.7, and 0.6 g g⁻¹, respectively. From the equilibrium isotherm study, the data fitted well with the Langmuir model, showing monolayer MB coverage over the adsorbent surface. Moreover, the superior adsorption capacity of the sub-nano-thick PD layer-coated GO indicated that it is a promising adsorbent for decontaminating wastewater. Table 3 summarizes the reported results for dye removal from aqueous solution and wastewater on graphene-based adsorbents.

Table 3 Summary of reported results for dye removal from aqueous solution and wastewater by graphene-based adsorbents

Adsorbent	Adsorbate	Adsorption capacity	Conc.	pH	Temp. (K)	Contact time (h)	Models applicable		Reference
							Isotherm	Kinetic
GO/cellulose (GOCB)	Malachite green	30.091 mg g^−1	10 mg L^−1	7.0	298	5	Langmuir	Pseudo-second-order	141
Magnetic cyclodextrin–GO (MCGO)	Methylene blue	261.78 mg g^−1	100 mg L^−1	10	303	0.83	Langmuir	Pseudo-second-order	154
MgO decked multi-layered graphene (MDMLD)	Safranin O	3.92 × 10^−4 mol g^−1	4.0 × 10^−4 M	2–12	—	2	Langmuir	Pseudo-second-order	143
GO–sodium alginate (GO–SA)	Methylene blue	833.3 mg g^−1	0.1 mol L^−1	—	303	12	Langmuir and Freundlich	Pseudo-second-order and intra-particle diffusion	159
Polydopamine layer coated GO (PD5%/GO)	Methylene blue	1.3 g g^−1	—	8.5	—	—	Langmuir	—	161
Polydopamine layer coated GO (PD15%/GO)	Methylene blue	1.89 g g^−1	—	8.5	—	—	Langmuir	—	161
Polydopamine layer coated GO (PD35%/GO)	Methylene blue	1.7 g g^−1	—	8.5	—	—	Langmuir	—	161
Polydopamine layer coated GO (PD70%/GO)	Methylene blue	0.6 g g^−1	—	8.5	—	—	Langmuir	—	161
GO1	Methylene blue	40.6 mg g^−1	600 mg dm^−3	—	—	0.083	Langmuir	Pseudo-second-order	139
GO2	Methylene blue	157.6 mg g^−1	600 mg dm^−3	—	—	0.083	Langmuir	Pseudo-second-order	139
GO3	Methylene blue	334.7 mg g^−1	600 mg dm^−3	—	—	0.083	Langmuir	Pseudo-second-order	139
GO4	Methylene blue	454.5 mg g^−1	600 mg dm^−3	—	—	0.083	Langmuir	Pseudo-second-order	139
GO5	Methylene blue	513.9 mg g^−1	600 mg dm^−3	—	—	0.083	Langmuir	Pseudo-second-order	139
GO6	Methylene blue	570.4 mg g^−1	600 mg dm^−3	—		0.083	Langmuir	Pseudo-second-order	139
GO	Basic blue 41 (BB41)	1429 mg g^−1	50 mg L^−1	—	298	1	Langmuir	Pseudo-second-order	138
GO	Basic red 18 (BR18)	1250 mg g^−1	50 mg L^−1	—	298	1	Langmuir	Pseudo-second-order	138
GO	Basic red 46 (BR46)	476 mg g^−1	50 mg L^−1	—	298	1	Langmuir	Pseudo-second-order	138
GO–zeolite	Rhodamine B	55.56 mg g^−1	1–500 mg dm^−3	—	—	1	Langmuir	Pseudo-second-order	109
Carboxy-GO/zeolite	Rhodamine B	67.56 mg g^−1	1–500 mg dm^−3	—	—	1	Langmuir	Pseudo-second-order	109
Graphene oxide–chitosan/silica fibre	Congo red	294.12 mg g^−1	80 mg L^−1	3.0	293	—	Langmuir	Pseudo-first-order	158
rGO–sodium alginate (rGO–SA)	Methylene blue	192.3 mg g^−1	0.1 mol L^−1		303	12	Langmuir and Freundlich	Pseudo-second-order and intra-particle diffusion	159
rGO	Methyl green	3.163 mmol g^−1	—	5	298	1	Langmuir	Pseudo-second-order	145
rGO	Methylene blue	302.11 mg g^−1	300 mg L^−1	7	—	48	Langmuir	Pseudo-second-order	144
rGO	Acid red	28.51 mg g^−1	50 mg L^−1	7	—	48	Langmuir	Pseudo-second-order	144
GO	Methylene blue	243.65 mg g^−1	40–120 mg L^−1	6	298	5	Langmuir	Pseudo-second-order	81
GO	Methyl green	4821 mmol g^−1	—	4.0	398	1	Langmuir	Pseudo-second-order	137
		5.496 mmol g^−1		5.0
		6.167 mmol g^−1		6.0
		6.628 mmol g^−1		7.0
		7.613 mmol g^−1		9.0
Magnetic graphene oxide (MGO)	Methylene blue	64.23 mg g^−1	90 mg L^−1	—	298	6.75	Langmuir	Pseudo-second-order	160
Magnetic graphene oxide (MGO)	Orange G	20.85 mg g^−1	60 mg L^−1	—	298	6.75	Langmuir	Pseudo-second-order	160
Graphene–chitosan	Methylene blue	390 mg g^−1	0–80 mg L^−1	6.5	294 ± 1	58	—	—	111
Graphene–chitosan	Eosin Y	326 mg g^−1	0–80 mg L^−1	7.0	294 ± 1	36	—	—	111
Graphene–sand	Rhodamine 6G	75.4 mg g^−1	—	—	303 ± 2	6	—	Pseudo-second-order	127
Magnetic β-cyclodextrin–chitosan–GO	Methylene blue	84.32 mg g^−1	—	—	298	—	Langmuir	Pseudo-second-order	112
GO–calcium alginate	Methylene blue	181.81 mg g^−1	30–80 mg L^−1	—	298	5	Langmuir	Pseudo-second-order	135
Graphene–SO3H/Fe3O4	Safranin T	199.3 mg g^−1	20–250 mg L^−1	6.0	Room temp	—	Langmuir	Pseudo-second-order	93
Graphene–SO3H/Fe3O4	Neutral red	216.8 mg g^−1	20–250 mg L^−1	6.0	Room temp	—	Langmuir	Pseudo-second-order	93
Graphene–SO3H/Fe3O4	Victoria blue	200.6 mg g^−1	20–250 mg L^−1	6.0	Room temp	—	Langmuir	Pseudo-second-order	93
Graphene/CoFe2O4	Methyl green	203.51 mg g^−1	50–400 mg L^−1	—	298	—	Langmuir	Pseudo-second-order	134
		258.39 mg g^−1			313
		312.80 mg g^−1			323
Graphene–Fe3O4	Pararosaniline	1988.23 mg g^−1	20–60 mg L^−1	6.6 ± 0.2	298	1	Langmuir	Pseudo-second-order	126
rGO-based hydrogel	Methylene blue	7.85 mg g^−1	0.5–10 mg L^−1	6.4	298	2	Freundlich	Pseudo-second-order	146
rGO-based hydrogel	Rhodamine B	29.44 mg g^−1	0.5–10 mg L^−1	6.4	298	2	Freundlich	Pseudo-second-order	146
GO	Acridine orange	1428 mg g^−1	0.1 g L^−1	—	Room temp	3	Langmuir	—	136
Graphene	Methylene blue	153.85 mg g^−1	20–120 mg L^−1	10.0	293		Langmuir	Pseudo-second-order	23
		185.19 mg g^−1			313
		204 mg g^−1			333
Graphene sponge	Methylene blue	184 mg g^−1	2 × 10^−4 mol L^−1	—	298	4	—	—	20
Graphene sponge	Rhodamine B	72.5 mg g^−1	2 × 10^−4 mol L^−1	—	298	4	—	—	20
Graphene sponge	Methyl orange	11.5 mg g^−1	2 × 10^−4 mol L^−1	—	298	24	—	—	20
Magnetite@graphene	Congo red	33.66 mg g^−1	—	—	298 ± 0.52	—	Langmuir	Pseudo-second-order	124
Magnetite@graphene	Methylene blue	45.27 mg g^−1	—	—	298 ± 0.5	—	Langmuir	Pseudo-second-order	124
In situ rGO	Acridine orange	3333 mg g^−1	0.1 g L^−1	—	Room	3	Langmuir	—	136
Graphene/c-MWCNT	Rhodamine B	150.2	20 mg L^−1	—	Room temp	—		Pseudo-second-order	136
Graphene/c-MWCNT	Methylene blue	191.0	20 mg L^−1	—	Room temp	—	—	Pseudo-second-order	136
Graphene/c-MWCNT	Fuchsine	180.8	20 mg L^−1	—	Room temp	—	—	Pseudo-second-order	136
Graphene/c-MWCNT	Acid fuchsine	35.8	20 mg L^−1	—	Room temp	—	—	Pseudo-second-order	136
Graphene–CNT	Methylene blue	81.97	10–30 mg L^−1	—	—	3	Freundlich	Pseudo-second-order	129
Graphene–sand	Rhodamine 6G	55 mg g^−1	5 mg L^−1	—	303 ± 2	8	—	Pseudo-second-order	128
Fe3O4–SiO2	Methylene blue	97 mg g^−1	—	—	298	—	Langmuir	Pseudo-second-order	142
		102 mg g^−1			318
		111.1 mg g^−1			333
Polystyrene@Fe3O4@GO	Rhodamine B	13.8 mg g^−1	0–150 mg L^−1	—	Room temp	24	—	—	152
rGO@ZnO	Rhodamine B	32.6 mg g^−1	4–750 mg L^−1	—	293	—	—	—	150
rGO–titanate	Methylene blue	83.26 mg g^−1	10 mg L^−1	—	—		—	Pseudo-second-order	149
Magnetic chitosan–GO	Methyl blue	95.31 mg g^−1	60–200 mg L^−1	5.3	303	1	Langmuir	Pseudo-second-order	155
Magnetic chitosan–GO	Methylene blue	180.83 mg g^−1	50–100 mg L^−1	—	303 ± 0.2	—	Langmuir	Pseudo-second-order	156
rGO	Orange G	5.98 mg g^−1	1–60 mg L^−1	—	—	—	Langmuir	Pseudo-second-order	178
Graphene	Cationic red X-GRL	217.39 mg g^−1	20–140 mg L^−1		288	24	Langmuir	Pseudo-second-order	92
		227.39 mg g^−1			313
		238 mg g^−1			333
Graphene	Methylene blue	1.52 g g^−1	5 mg L^−1		303	96	—	—	123
GO	Methylene blue	17.3 mg g^−1	10–50 mg L^−1	10.0	—	—	Langmuir	Pseudo-second-order	78
GO	Methyl violet	2.47 mg g^−1	10–50 mg L^−1	6.0	—	—	Langmuir	Pseudo-second-order	78
GO	Rhodamine B	1.24 mg g^−1	1–10 mg L^−1	6.0	—	—	Freundlich	Pseudo-second-order	78
Graphene–Fe3O4	Fuchsine	89.4 mg g^−1	20–60 mg L^−1	6.6 ± 0.2	298	1	Langmuir	Pseudo-second-order	59
Graphene–magnetite	Methylene blue	43.82 mg g^−1	10–25 mg L^−1	—	298	—	Langmuir	Pseudo-second-order	129
CoFe2O4-functionalized graphene	Methyl orange	71.54 mg g^−1	10 mg L^−1	—	—	—	—	Pseudo-second-order	135
Magnetite–rGO	Rhodamine B	13.15 mg g^−1	0.5–4 mg L^−1	7.0	298	2	Langmuir Freundlich	Pseudo-second-order	151
Magnetite–rGO	Malachite green	22.0 mg g^−1	0.5–4 mg L^−1	7.0	298	2	Langmuir Freundlich	Pseudo-second-order	151

---

5. Graphene as adsorbent – major challenges

The science of graphene as an adsorption material is growing rapidly; however, there are many challenges and hurdles that need to be overcome. Although the raw materials required for graphene synthesis are naturally abundant, it is still a challenge for graphene scientists to modify and/or to develop methods that will create adsorbents that are highly selective and have high adsorption potential. Graphene-based materials with low aggregation and highly specific surface areas show a high adsorption capacity for organic pollutants, especially benzene-containing compounds, where the π–π interaction between graphene and the adsorbate plays a dominant role.^19,162–164 Therefore, one of the major problems faced in using graphene as an adsorbent is the aggregation of the graphene sheets. It is important to prevent this aggregation between the graphene layers because the aggregations reduce accessibility and thereby limit the available adsorption sites to which pollutants will bind. The aggregation can be avoided by the introduction of oxygen groups, which improve the dispersion properties of graphene in solution and thus greatly increase the ability of graphene to remove pollutants. In another development for convenient separation, magnetic particles are introduced to the adsorbent to form a magnetic graphene composite. The added magnetic particles will also play an important role in preventing aggregation of the graphene.

Currently, the technique used for large-scale synthesis of graphene is Hummer's method, which involves an oxidation and reduction process. Some of the major drawbacks of this method are that the oxidation process consumes a large quantity of strong acids and oxidants, and produces large amounts of acidic waste that require a high cost for treatment and safe disposal. Hence, it may be an environmentally unfriendly and expensive method. Furthermore, the hydrazine used in this method is a suspected carcinogen and hazardous to the environment. In addition, a strong oxidation process may give rise to unwanted defects in graphene, which will significantly compromise the superior properties of graphene. Hummers' method cannot produce graphene sheets with controlled sizes and desired geometrical shapes. Therefore, exploration of other methodologies to tackle the aforementioned issues is extremely urgent.

Scientists have put forward few solutions for solving some of the aforementioned problems. Many different oxidation processes of graphene in the categories of chemical/thermal oxidation have been introduced and established for desired results. In addition, the use of the hydrazine can be avoided by substituting it with ascorbic acid (vitamin C), which is non-toxic and environmentally friendly. A milder exfoliation process can be utilized with the assistance of additional species such as multi-pyrene tethered amphiphiles. Lee et al.⁷⁷ may present the featured synthetic direction, as it will produce graphene sheets with a controllable size and internal conjugated structure.

Although it is well known that a single graphene sheet has superior mechanical properties, the mechanical properties of pure collective graphene products or graphene composites are usually significantly compromised by weak inter-sheet interactions. Therefore, at present, there remains a major challenge regarding how to strengthen the interaction between the adjacent graphene sheets or the interaction between the graphene sheets and its modifier functionalities. As graphene can be modified via either covalent or non-covalent bonding, e.g., π–π stacking, hydrogen bonding, etc., a multifunctional inter-graphene “welding” molecule or metallic nanoparticles might be a good alternative to improve the inter-layer electrical communication.

The synthesis of GO and rGO is challenging, as there is always a need to look into more facile, robust, and efficient preparation methods for GO, graphene, and their composites. Based on other reports and our own experience, it has been realized that exhaustive studies are still required for a complete understanding of graphene structure, although research studies exploring the chemistry of GO and graphene are currently expanding at a rapid rate. Another important aspect that needs to be addressed is the lack of synthetic approaches that demonstrate reproducible and controlled methods; currently, there is an urgent need for research in this area.

6. Conclusions and future research perspectives

In this review, applications of graphene and its derivatives for heavy metal and dye removal have been presented. The large-scale, cost-effective, and ecofriendly preparation of high-quality graphene and its derivatives is essential for many applications. In case of electrostatic interaction, anionic pollutants are usually favored by low pH value. Anions have been proposed to be adsorbed through specific and non-specific adsorption. Nevertheless, the adsorption of cations and anions is based on three adsorption mechanisms consisting of electrostatic interaction, ion exchange, and complex formation. The adsorption isotherm and kinetics can be described by the Langmuir isotherm and the pseudo-second-order model. The adsorption process for graphene-based materials is spontaneous, endothermic, and feasible.

A comprehensive application of graphene nanocomposites for removing organic and inorganic pollutants in the environment shows great potential. Due to the outstanding physicochemical properties of graphene, it will play a very important role in environmental pollution management in the future. Firstly, in the detection of organic and inorganic pollutants, graphene nanocomposite revealed its great potentiality for environmental application. However, it is still too early to implement large-scale applications of these nanocomposites in environmental monitoring and remediation due to the essential question regarding toxicity that arises for both short- and long-term exposure of graphene to ecosystems and the human body, which remains largely unaddressed. Despite these challenges, graphene nanocomposite is still one of the most exciting platforms for energy and environmental studies. Secondly, the preparation of graphene material via “chemical” processing routes, for example, the oxidation of graphene followed by reduction of the GO platelet obtained by exfoliation, may be able to produce fairly large amounts of cost-effective “graphene.” However, the chemical details, for example, the oxidation/reduction mechanism and detailed chemical structure, are currently lacking. Very few graphene-based materials have been produced and analyzed when compared to other well-known nanomaterials, and thus, it is recommended that future studies evaluate the feasibility of producing more graphene-based materials, with further developments in nanomaterial manufacturing.

Moreover, advances in both fundamental physics and chemistry and practical techniques will enable revolutionary applications based on graphene and its composites to expand the horizons of graphene nanocomposites and open up new windows in environmental remediation and restoration.

Acknowledgements

The authors would like to thank the Malaysia-Japan International Institute of Technology (MJIIT) for providing the grant to conduct this research. One of the authors (SAZ) is grateful for research funding from Kwangwoon University in 2015.

References

1. F. Fu and Q. Wang, J. Environ. Manage., 2011, 92, 407–418.
2. F. Marahel, M. A. Khan, M. Ehsan, B. Iman and H. Soraya, Desalin. Water Treat., 2015, 53, 826–835.
3. N. M. Julkapli, S. Bagheri and S. B. Abd Hamid, Sci. World J., 2014, 25, 692307.
4. H. Hou, R. Zhou, P. Wu and L. Wu, Chem. Eng. J., 2012, 211–212, 336–342.
5. A. R. Karbassi and S. Nadjafpour, Environ. Pollut., 1996, 93, 257–260.
6. M. Soylak, Y. E. Unsal, N. Kizil and A. Aydin, Food Chem. Toxicol., 2010, 2, 517–521.
7. E. Makrlik and P. Vanura, J. Radioanal. Nucl. Chem., 2005, 267, 233–235.
8. A. E. Ofomaja, E. B. Naidoo and S. J. Modise, J. Environ. Manage., 2010, 91, 1674–1685.
9. M. M. Matlock, B. S. Howerton and D. A. Atwood, Ind. Eng. Chem. Res., 2002, 41, 1579–1582.
10. A. Dabrowski, Z. Hubicki, P. Podkościelny and E. Robens, Chemosphere, 2004, 56, 91–106.
11. M. M. Rao, D. K. Ramana, K. Seshaiah, M. C. Wang and S. W. C. Chien, J. Hazard. Mater., 2009, 2, 1006–1013.
12. J. R. C. Parga, D. L. Cocke, J. L. Valenzuela, J. A. Gomes, M. Kesmez, G. Irwin, H. Moreno and M. Weir, J. Hazard. Mater., 2005, 124, 247–254.
13. S. A. Nasier, Chem. Biochem. Eng. Q., 2013, 17, 219–224.
14. A. J. B. Dutra, A. Espinola and P. P. Borges, Miner. Eng., 2000, 13, 1139–1148.
15. G. Ayoub, L. Semerjian, A. Acra, M. Fadel and B. Koopman, J. Environ. Eng., 2001, 127, 196–207.
16. M. Imamoglu and O. Tekir, Desalination, 2008, 228, 108–113.
17. J. Xu, S. T. Yang and J. Lao, Rev. Inorg. Chem., 2013, 33, 139–169.
18. J. Zhu, S. Wei, H. Gu, S. B. Rapole, Q. Wang, Z. Luo, N. Haldolaarachchige, D. P. Young and Z. Guo, Environ. Sci. Technol., 2012, 46, 977–985.
19. G. L. J. Zhao, X. Ren, C. Chen and X. Wang, Environ. Sci. Technol., 2011, 45, 10454–10462.
20. G. Zhao, W. T. C. Chen and X. Wang, RSC Adv., 2012, 2, 9286–9303.
21. L. W. Xiao, S. L. Yu and Y. L. Tang, Prog. Chem., 2013, 25, 419–430.
22. Y. Len, W. Guo, S. Su, C. Yi and L. Xing, Chem. Eng. J., 2012, 211–212.
23. L. Liu, C. Li, C. Bao, Q. Jia, P. Xiao, X. Liu and Q. Zhang, Talanta, 2012, 93, 350–357.
24. F. Fang, L. Kong, J. Huang, S. Wu, K. Zhang, X. Wang, B. Sun, Z. Jin, J. Wang, X.-J. Huang and J. Liu, J. Hazard. Mater., 2014, 270, 1–10.
25. P. Gansan and R. S. Vasudevan, J. Taiwan Inst. Chem. Eng., 2013, 44, 808–814.
26. C. Schafhäutl, U. d-V. d-Kohlenstoffes mit Silicium, Eisen and anderen Metallen, welche die verschiedenen Gattungen von Roheisen, Stahl und Schmiedeeisen bilden, J. Prakt. Chem., 1840, 21, 129–157.
27. B. C. Brodie, Trans. R. Soc., 1859, 149, 249.
28. L. Staudenmaier, Verfahren zur Darsatellung der Graphitsaure, Ber. Dtsch. Chem. Ges., 1898, 31, 1481–1487.
29. H. P. Boehm, A. Clauss, U. Hofmann and G. O. Fishcher, Proceedings of the fifth conference of carbon, 1962.
30. A. J. Van Bommel, J. E. Crombeen and A. Van Tooren, Surf. Sci., 1975, 48, 463–472.
31. H. P. Boehm, R. Setton and E. Stumpp, Carbon, 1986, 24, 241–245.
32. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dobonos and I. V. Griorieva, Science, 2004, 306, 666–669.
33. M. D. Stoller, S. Park, Y. Zhu, J. An and R. S. Ruoff, Nano Lett., 2008, 8, 3498–3502.
34. K. L. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Funderberg, J. Hones, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351–355.
35. S. Basu and P. Bhattacharyya, Sens. Actuators, B, 2012, 173, 1–21.
36. W. L. I. Choi, R. Seelaboyina and Y. S. Kang, Crit. Rev. Solid State Mater. Sci., 2010, 35, 52–71.
37. C. Lee, X. Wei, J. W. Kysar and J. Hones, Science, 2008, 321, 385–388.
38. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. C. N. Lau, Nano Lett., 2008, 8, 902–907.
39. L. Kui, Z. GuiXia and W. Xiangke, Chin. Sci. Bull., 2012, 57, 1223–1234.
40. Y. Zhu, S. Murali, W. Cai, X. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906–3924.
41. A. K. Geim and K. S. Novosolov, Nat. Mater., 2007, 3, 183–191.
42. W. S. Hummers Jr and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339.
43. A. M. Dimiev, S. M. Bachilo, R. Saito and J. M. Tour, ACS Nano, 2012, 6, 7842–7849.
44. K. P. Loh, Q. Bao, P. K. Ang and J. Yang, J. Mater. Chem., 2010, 20, 2277–2289.
45. M. J. McAllister, J.-L. Li, D. H. Adamson, H. C. Schniepp, A. A. Abdala, J. Liu, M. H. Herrera-Alonso, D. L. Milius, R. Car, R. K. Prud'homme and I. A. Aksay, Chem. Mater., 2007, 19, 4396–4404.
46. C. Junghun, L. Hangil, K. Ki-jeong, K. Bongsoo and K. Sehun, J. Phys. Chem. Lett., 2010, 1, 505–509.
47. C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, Science, 2006, 312, 1191–1196.
48. W. A. de Heer, C. Berger, X. Wu, P. N. First, E. H. Conrad, X. Li, T. Li, M. Sprinkle, J. Hass, M. L. Sadowski, M. Potemski and G. Martinez, Solid State Commun., 2007, 143, 92–100.
49. T. Seyller, A. Bostwick, K. V. Emtsev, K. Horn, L. Ley, J. L. McChesney, T. Ohta, J. D. Riley and E. Rotenberg, Phys. Status Solidi, 2008, 245, 1436–1446.
50. S. K. Y. Some, E. Hwang, H. Yoo and H. Lee, Chem. Commun., 2012, 48, 7732–7734.
51. D. Li, M. B. Müller, S. Gilje, R. B. Kaner and G. G. Wallace, Nat. Nanotechnol., 2008, 3, 101–105.
52. V. C. Tung, M. J. Allen, Y. Yang and R. B. Kaner, Nat. Nanotechnol., 2009, 4, 25–29.
53. C. Lahiri and S. Kang, Crit. Rev. Solid State Mater. Sci., 2010, 35, 52–71.
54. K. Wang, J. Ruan, H. Song, J. Zhang, Y. Wo, S. Guo and D. Cui, Nanoscale Res. Lett., 2011, 6, 8,  DOI:10.1007/s11671-010-9751-6.
55. W. Zhang, C. Zhou, W. Zhou, A. Lei, Q. Zhang, Q. Wan and B. Zou, Bull. Environ. Contam. Toxicol., 2011, 87, 86–90.
56. M. C. Duch, G. R. Budinger, Y. T. Liang, S. Soberanes, D. Urich, S. E. Chiarella, L. A. Campochiaro, A. Gonzalez, N. S. Chandel, M. C. Hersam and G. M. Mutlu, Nano Lett., 2011, 11, 5201–5207.
57. A. Schinwald, F. A. Murphy, A. Jones, W. MacNee and K. Donaldson, ACS Nano, 2012, 6, 736–746.
58. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
59. C. Wang, L. Zhan, W. M. Qiano and L. C. ling, New Carbon Mater., 2011, 26, 21.
60. G. Titelman, V. Gelman, S. Bron, R. L. Khalfin, Y. Cohen and H. Bianco-Peled, Carbon, 2005, 43, 641–649.
61. Y. M. Ren, N. Yan, Q. Wen, Z. J. Fan, T. Wei, M. L. Zhang and J. Ma, Chem. Eng. J., 2011, 175, 1–7.
62. J. I. Goldstein, D. E. Newbury, P. Echlin, D. C. Joy, A. Roming, C. E. Lyman, C. FIori and E. lifshin, New York. 1992.
63. Y. Hernande, V. Nicolosi, M. Lotya, F. M. Bligh, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gunko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568.
64. P. C. Ma, J. K. Kim and B. Z. Tang, Carbon, 2006, 44, 3232–3238.
65. D. Yang, A. Valamakanni, P. S. Bozoklu, M. Stoller and R. D. Piner, Carbon, 2009, 47, 145–152.
66. D. Li, M. R. Muller, R. B. Gilje Kaner and G. G. Wallace, Nat. Nanotechnol., 2008, 3, 101–103.
67. S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlheaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565.
68. J. Shen, Y. Hu, M. Shi, X. Lu, C. Qin, C. Li and M. Ye, Chem. Mater., 2009, 21, 3514–3520.
69. M. Kaustubha, D. Dababrata and N. B. Manindra, Sep. Purif. Technol., 2008, 58, 311–319.
70. N. Zhang, H. Qiu, Y. Si, W. Wang and J. Gao, Carbon, 2011, 49, 827–837.
71. A. H. Norizilah, A. Fakhrul-Razi, T. S. Y. Choong and A. L. Chuah, J. Nanomater., 2011, 495676,  DOI:10.1155/2011/495676.
72. Z. J. Fan, W. Kai, J. Y. Yan, T. W. Wei, L. J. Zhi, J. Feng, Y. M. Ren, L. P. Song and F. Wei, ACS Nano, 2011, 5, 191–198.
73. W. Wu, Y. Yang, H. Zhou, T. Ye, Z. Huang, R. Liu and Y. Kuang, Water, Air, Soil Pollut., 2013, 224, 1372.
74. Y. Ren, N. Yan, J. Feng, J. Ma, Q. Wen, L. Nan and D. Qing, Mater. Chem. Phys., 2012, 136, 538–544.
75. C. J. Madadrang, H. Y. Kim, G. Gao, N. Wang, J. Zhu, H. Fen, M. Gorrring, M. L. Kasner and S. Hou, ACS Appl. Mater. Interfaces, 2012, 4, 1186–1193.
76. S. Pei and H.-M. Cheng, Carbon, 2012, 50, 3210–3228.
77. D.-W. Lee, T. Kim and M. Lee, Chem. Commun., 2011, 47, 8259–8261.
78. G. K. Ramesha, A. V. Kumara, H. B. Muralidhara and S. Sampath, J. Colloid Interface Sci., 2011, 361, 270–277.
79. A. Hu and A. Apblett, Lecture Notes in Nanoscale Science and Technology, 2014, p. 22, ISBN: 978-3-319-06577-9.
80. D. Chen, L. Tang and J. Li, Chem. Soc. Rev., 2010, 39, 3157–3180.
81. Y. Li, Q. Du, T. Liu, X. Peng, J. Wang, J. Sun, Y. Wang, S. Wu, Z. Wang, Y. Xia and L. Xia, Chem. Eng. Res. Des., 2013, 91, 361–368.
82. Y. Leng, W. Guo, S. Su, C. Yi and L. Xing, Chem. Eng. J., 2012, 212, 406–411.
83. C.-F. Chang, T. Q. Duc and J.-R. Chen, Appl. Surf. Sci., 2013, 264, 329–334.
84. Z.-H. Huang, X. Zheng, W. Lv, M. Wang, Q.-H. Yang and F. Kang, Langmuir, 2011, 27, 7558–7562.
85. Y. Wu, H. Luo, H. Wang, C. Wang, J. Zhang and Z. Zhang, J. Colloid Interface Sci., 2013, 394, 183–191.
86. L. Hao, H. Song, L. Zhang, X. Wan, Y. Tang and Y. Lv, J. Colloid Interface Sci., 2012, 369, 381–387.
87. X. Deng, L. Lu, H. Li and F. Luo, J. Hazard. Mater., 2010, 183, 923–930.
88. Z. Sui, Q. Meng, X. Zhang, R. Ma and B. Cao, J. Mater. Chem., 2012, 22, 8767–8771.
89. Y. Yuan, G. Zhang, Y. Li, G. Zhang, F. Zhang and X. Fan, Polym. Chem., 2013, 4, 2164–2167.
90. H. Jabeen, V. Chandra, S. Jung, J. W. Lee, K. S. Kim and S. B. Kim, Nanoscale, 2011, 3, 3583–3585.
91. D. Nandi, K. Gupta, A. K. Ghosh, A. De, S. Banerjee and U. C. Ghosh, J. Nanopart. Res., 2012, 14, 1272.
92. Z. J. Li, F. Chen, L. Y. Yuan, Y. L. Liu, Y. L. Zhao, Z. F. Chai and W. Q. Shi, Chem. Eng. J., 2012, 210, 539–546.
93. H. Wang, X. Yuan, Y. Wu, H. Huang, G. Zeng, Y. Liu, X. Wang, N. Lin and Y. Qi, Appl. Surf. Sci., 2013, 279, 432–440.
94. R. Sitko, E. Turek, B. Zawisza, E. Malicka, E. Talik, J. Heimann, A. Gagor, B. Feist and R. Wrzali, Dalton Trans., 2013, 5682–5689.
95. Y.-C. Lee and J.-W. Yang, Ind. Eng. Chem., 2012, 18, 1178–1185.
96. Y. L. F. Musico, C. M. Santos, M. L. P. Dalida and D. F. Rodrigues, J. Mater. Chem., 2013, 1, 3789–3796.
97. X. Mi, G. Huang, W. Xie, W. Wang, Y. Liu and J. Gao, Carbon, 2012, 50, 4856–4864.
98. H. Cheng, K. Zeng and J. Yu, J. Radioanal. Nucl. Chem., 2013, 298, 599–603.
99. S. Luo, X. Xu, G. Zhou, C. Liu, Y. Tang and Y. Liu, J. Hazard. Mater., 2014, 274, 145–155.
100. Y. Lei, Y. Luo and L. Zhang, Chem. Phys. Lett., 2014, 593, 122–127.
101. X. Yuan, Y. Wang, J. Wang, C. Zhou, Q. Tang and X. Rao, Chem. Eng. J., 2013, 221, 204–213.
102. X.-J. Hu, Y. Liu, H. Wang, A. Chen, G. Zeng, S. Liu, Y. Guo, X. Hu, T. Li, Y. Wang, L. Zhou and S. Liu, Sep. Purif. Technol., 2013, 108, 189–195.
103. X. Luo, C. Wang, L. Wang, F. Deng, S. Luo, X. Tu and C. Au, Chem. Eng. J., 2013, 220, 98–106.
104. K. Zhang, V. Dwivedi, C. Chi and J. Wu, J. Hazard. Mater., 2010, 182, 162–168.
105. M. Liu, C. Chen, J. Hu, X. Wu and X. Wang, J. Phys. Chem. C, 2011, 115, 25234–25240.
106. S. Li, X. Lu, Y. Xue, J. Lei, T. Zheng and C. Wang, PLoS One, 2012, 7, e43328.
107. F. Peng, T. Luo, L. Qiu and Y. Yuan, Mater. Res. Bull., 2013, 48, 2180–2185.
108. P. Zong, S. Wang, Y. Zhao, H. Wang, H. Pan and C. He, Chem. Eng. J., 2013, 220, 45–52.
109. B. Yu, J. Xu, J.-H. Liu, S.-T. Yang, J. Luo, Q. Zhou, J. Wan, R. Liao, H. Wang and Y. Liu, J. Environ. Chem. Eng., 2013, 1, 1044–1050.
110. Y. Q. He, N. N. Zhan and X. D. Wang, Chin. Chem. Lett., 2011, 22, 859–862.
111. Y. Chen, L. Chen, H. Bai and L. Li, J. Mater. Chem. A, 2013, 1, 1992–2001.
112. L. Fan, C. Luo, S. Min, L. Xiangjuan and Q. Huamin, Colloids Surf., B, 2013, 103, 523–529.
113. L. Li, S. L. Fan, M. Sun, H. Qiu, X. Li, H. Duan and C. Luo, Colloids Surf., B, 2013, 107, 76–83.
114. W. M. Algothmi, N. M. Babdaru, Y. Yu, J. G. Shapter and A. V. Ellis, J. Colloid Interface Sci., 2013, 397, 32–38.
115. S. Yang, L. Li, Z. Pei, C. Li, X. Shan, B. Wen, S. Zhang, L. Zheng, J. Zhang, Y. Xie and R. Huang, Carbon, 2014, 75, 227–235.
116. R. Li, L. Liu and F. Yang, Chem. Eng. J., 2013, 229, 460–468.
117. P. Bhunia, G. Kim, C. Baik and H. Lee, Chem. Commun., 2012, 48, 9888–9890.
118. C. Wang, H. Luo, Z. Zhang, Y. Wu, J. Zhang and S. Chen, J. Hazard. Mater., 2014, 268, 124–131.
119. Y. Zhang, L. Yan, W. Xu, X. Guo, L. Cui, L. Gao, Q. Wei and B. Du, J. Mol. Liq., 2014, 191, 177–182.
120. T. S. Sreeprasad, S. M. Maliyekkal, K. P. Lisha and T. Pradeep, J. Hazard. Mater., 2011, 18, 921–931.
121. V. Chandra, J. Park, Y. Chun, J. W. Lee and I. C. Hwang, ACS Nano, 2010, 4, 3979–3986.
122. C. Chandra and K. S. Kim, Chem. Commun., 2011, 47, 3942–3944.
123. T. Wu, X. Cai, S. Tan, H. Li, J. Liu and W. Yang, Chem. Eng. J., 2011, 173, 144–149.
124. Y. Yao, S. Miao, S. Liu, L.-P. Ma, H. Sun and S. Wang, Chem. Eng. J., 2012, 184, 332.
125. L. Ai, C. Zhang and Z. Chen, J. Hazard. Mater., 2011, 192, 1515–1524.
126. Q. Wu, C. Feng, C. Wang and Z. Wang, Colloids Surf., B, 2013, 101, 210–214.
127. T. S. Sreeprasad, S. S. Gupta, Sen, S. Gupta, S. M. Maliyekkal and T. Pradeep, J. Hazard. Mater., 2013, 246–247, 213–220.
128. S. Sen Gupta, T. S. Sreeprasad, S. M. Maliyekkal, S. K. Das and T. Pradeep, ACS Appl. Mater. Interfaces, 2012, 4, 4156–4163.
129. L. Ai and J. Jiang, Chem. Eng. J., 2012, 192, 156–163.
130. B. Li, H. Cao and G. Yin, J. Mater. Chem., 2011, 21, 10645–10648.
131. B. C. H. Li and G. Yin, J. Mater. Chem., 2011, 21, 13765–13768.
132. S.-T. Yang, S. Chen, Y. Chang, A. Cao, Y. Liu and H. Wang, J. Colloid Interface Sci., 2011, 359, 24–29.
133. W. Zhang, C. Zhou, W. Zhou, A. Lei, Q. Zhang, Q. Wan and B. Zou, Bull. Environ. Contam. Toxicol., 2011, 87, 86–90.
134. A. A. Farghali, M. Bahgat, W. M. A. El-Rouby and M. H. Kherdr, J. Alloys Compd., 2013, 555, 193–200.
135. N. Li, M. Zheng, X. Chang, G. Ji, H. Lu, L. Xue, P. Lija and C. Jieming, J. Solid State Chem., 2011, 184, 953–958.
136. L. Sun and H. B. Yu, J. Hazard. Mater., 2012, 203–204, 101–110.
137. P. Sharma and M. R. Das, J. Chem. Eng. Data, 2013, 58(1), 151–158.
138. H. Z. Farahani, H. H. Monfared and N. M. Mohmoodi, Desalin. Water Treat., 2014, 1–13,  DOI:10.1080/19443994.2014.960462.
139. H. Yan, X. Tao, Z. Yang, K. Li, H. Yang, A. Li and R. Cheng, J. Hazard. Mater., 2014, 268, 191–198.
140. P. Bradder, S. K. Ling, S. Wang and Liu, J. Chem. Eng. Data, 2011, 56, 138–141.
141. X. Zhang, H. Yu, H. Yang, Y. Wan, H. Hu and Z. Zhai, J. Colloid Interface Sci., 2015, 437, 277–282.
142. Y. Yao, S. Miao, S. Yu, L. P. Ma, H. Sun and S. Wang, J. Colloid Interface Sci., 2012, 379, 20–26.
143. N. R. Rotte, S. Yerramala, J. Bonoface and V. V. S. Srikanth, Chem. Eng. J., 2014, 258, 412–419.
144. H. Kim, S.-O. Kang, S. Park and S. H. Park, J. Ind. Eng. Chem., 2014, 2060, 6.
145. P. Sharma, B. K. Saikia and M. R. Das, Colloids Surf., A, 2014, 457, 125–133.
146. J. N. Tiwari, K. Mahesh, N. H. Le, K. C. Kemp, R. Timilsina, R. N. Tiwari and K. S. Kim, Carbon, 2013, 56, 173–182.
147. S. Bai, Z. X. Shen, Y. Liu, G. Zhu, X. Xu and K. Chen, Carbon, 2012, 50, 2337–2346.
148. Z. Geng, Y. Lin, X. Yu, Q. Shen, L. Ma, Z. Li, N. Pan and X. Wang, J. Mater. Chem., 2012, 22, 3527–3535.
149. T.-D. Nguyen-Phan, V. H. Pham, E. J. Kim, E.-S. Oh, S. H. Hur, J. S. Chung, B. Lee and E. W. Shin, Appl. Surf. Sci., 2012, 258, 4551–4557.
150. J. T. T. Wang, B. Tang, X. Hou, L. Sun and X. Wang, ACS Appl. Mater. Interfaces, 2012, 4, 3084–3090.
151. H. C. L. Sun and L. Lu, Nano Res., 2011, 4, 550–562.
152. J. Wang, B. Tang, T. Tsuzuki, Q. Liu, X. Hou and L. Sun, Chem. Eng. J., 2012, 204/206, 258–263.
153. G. Xie, P. Xi, F. Liu, L. Huang, Y. Shi, F. Hou, Z. Zeng, C. Shao and J. Wang, J. Mater. Chem., 2012, 22, 1033–1039.
154. L. Li, L. Fan, H. Duan, X. Wang and C. Luo, RSC Adv., 2014, 4, 37114–37121.
155. L. Fan, C. Luo, X. Li, F. Lu, H. Qiu and M. Sun, J. Hazard. Mater., 2012, 272279, 215–216.
156. L. Fan, C. Luo, M. Sun, X. Li, F. Lu and H. Qiu, Bioresour. Technol., 2012, 114, 703–706.
157. Z. X. Chen, Z. M. Zhao, Y. L. Cao, X. P. Ai, H. X. Yang and J. Liu, Adv. Energy Mater., 2011, 2, 95–102.
158. Q. Du, J. Sun, Y. Li, X. Yang, X. Wang, Z. Wang and L. Xia, Chem. Eng. J., 2014, 245, 99–106.
159. T. Ma, P. R. Chang, P. Zheng, F. Zhao and X. Ma, Chem. Eng. J., 2014, 240, 595–600.
160. J.-H. Deng, X.-R. Zhang, G.-M. Zeng, J.-L. Gong, Q.-Y. Niu and J. Liang, Chem. Eng. J., 2013, 226, 189–200.
161. Z. W. D. Dong, X. Liu, X. Pei, L. Chen and J. Jin, J. Mater. Chem. A., 2014, 2, 5034–5040.
162. S. B. Yang, J. Hu, C. L. Chen, D. Shao and X. Wang, Environ. Sci. Technol., 2011, 45, 3621–3627.
163. D. D. Shao, Z. Q. Jiang and X. Wang, Chemosphere, 2011, 82, 751–758.
164. D. D. Shao, G. D. Sheng and C. L. Chen, Chemosphere, 2010, 79, 79–685.
165. A. C. G. A. Neto and N. M. R. Peres, Phys. World, 2006, 19, 33–37.
166. M. I. Katsnelson, Eur. J. Phys., 2006, 51, 157–160.
167. A. Bianco, Angew. Chem., Int. Ed., 2013, 52, 4986–4997.
168. G. Zhao, X. Ren, X. Gao, X. Tan, J. Li, C. Chen, Y. Huang and X. Wang, Dalton Trans., 2011, 10945.

---