Time–strain inseparability in multiaxial stress relaxation of supramolecular gels formed via host–guest interactions†
Takuro
Kimura
a,
Takuma
Aoyama
a,
Masaki
Nakahata
 b,
Yoshinori
Takashima
b,
Yoshinori
Takashima
 c,
Motomu
Tanaka
c,
Motomu
Tanaka
 de,
Akira
Harada
de,
Akira
Harada
 f and
Kenji
Urayama
f and
Kenji
Urayama
 *ag
*ag
aDepartment of Macromolecular Science and Engineering, Kyoto Institute of Technology, Sakyo-ku, Kyoto 606-8585, Japan
bDepartment of Materials Engineering Science, Graduate School of Engineering Science, Osaka University, 560-8531 Osaka, Japan
cInstitute for Advanced Co-Creation Studies, Osaka University, Suita, Osaka 565-0871, Japan
dCenter for Integrative Medicine and Physics, Institute for Advanced Study, Kyoto University, 606-8501 Kyoto, Japan
ePhysical Chemistry of Biosystems, Institute of Physical Chemistry, Heidelberg University, D69120 Heidelberg, Germany
fThe Institute of Scientific and Industrial Research, Osaka University, Ibaraki, Osaka 567-0047, Japan
gDepartment of Material Chemistry, Graduate School of Engineering, Kyoto University, 615-8510 Kyoto, Japan. E-mail: urayama.kenji.2s@kyoto-u.ac.jp
First published on 24th June 2022
Abstract
Supramolecular hydrogels utilizing host–guest interactions (HG gels) exhibit large deformability and pronounced viscoelasticity. The inclusion complexes between β-cyclodextrin (host) and adamantane (guest) units on the water-soluble polymers form transient bonds. The HG gels show significant stress relaxation with finite equilibrium stress following the step strain. The stress relaxation process reflects the detachment dynamics of the transient bonds which sustain the initial stress, while the finite equilibrium stress is preserved by the permanent topological cross-links with a rotaxane structure. Nonlinear stress relaxation experiments in biaxial stretching with various combinations of two orthogonal strains unambiguously reveal that time and strain effects on stress are not separable. The relaxation is accelerated for a short time frame (<102 s) with an increase in the magnitude of strain, whereas it is retarded for a longer time window with an increase in the anisotropy of the imposed biaxial strain. The time–strain inseparability in the HG gels is in contrast to the simple nonlinear viscoelasticity of a dual cross-link gel with covalent and transient cross-links in which the separability was previously validated by the same assessment. We currently interpret that the significant susceptibility of the detachment dynamics to the deformation type results from the structural characteristics of the HG gels, i.e., the host and guest moieties covalently connected to the network chains, the considerably low concentrations (<0.1 M) of these moieties, and the slidability of the permanent rotaxane cross-links.
Introduction
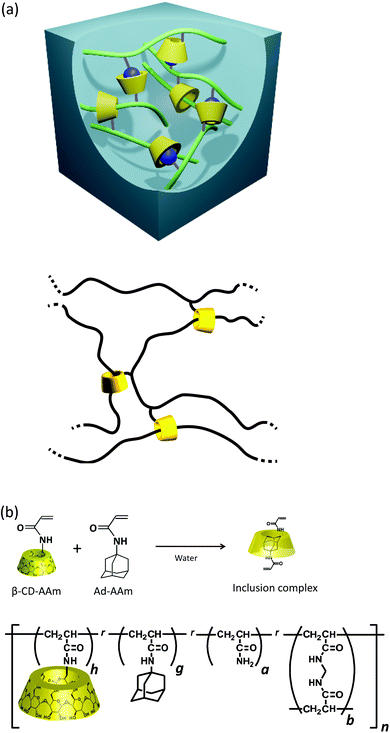
Polymer gels are unique soft solids which possess reversible deformability and the capacity to retain a solvent of several times their own weight. These unparalleled features enable a wide range of possibilities for their utilization in food, cosmetics, and biomedical applications, and tissue engineering;1,2 however, a major application issue to be overcome is the enhancement of their mechanical toughness.3 A promising approach for this issue is to utilize temporary bonds (cross-links) which repeat the attachment and detachment processes within a characteristic time for a mechanism of energy dissipation. Several studies4–7 have demonstrated that polymer gels become pronouncedly tough and viscoelastic by introducing various types of transient bonds. For example, dual cross-linked (DC) poly(vinyl alcohol) (PVA) hydrogels7 utilize the coordination of free borate ions on hydroxy groups in the network strands as transient bonds, and the polyampholyte physical hydrogels have ionic bonds with a wide distribution of strength.6Harada et al. reported a new class of supramolecular gels with high flexibility, toughness, and self-healing capacities utilizing host–guest (HG) interactions between the side chains as transient bonds.8–10 For example, linear, water-soluble polymer chains possessing few units of β-cyclodextrin (β-CD; host) and adamantane (Ad; guest) can form hydrogels cross-linked by inclusion complexes (Fig. 1a). The HG hydrogels are reversibly extensible while remaining insoluble even in good solvents. In the HG gels, a small part of rotaxane structure acts as permanent and movable topological cross-links.11–15 The rotaxane structure is formed by penetration of the main chain polymer constituting the network into the cavities of the β-CDs at the side chains (Fig. 1a and b). The excellent mechanical and self-healing properties of HG gels make them potentially valuable for practical uses such as scratch curable coatings. Several physical properties of HG gels have been investigated including extensibility,9 swelling,12 linear viscoelasticity,11 and the dynamic regulation of cell–substrate interactions.16 The analysis of linear viscoelasticity under small strain amplitudes showed that the HG cross-links act as a sticker in the network, retarding the Rouse molecular motion of the network strands.11
Since HG gels possess both pronounced viscoelasticity and high extensibility, the nonlinear stress–strain relationship will be significantly dependent on the strain rate. The time effect on the nonlinear stress–strain relationship of the HG hydrogels, however, is largely unknown. Whether the time and strain effects on stress are separable or not is crucial for the understanding of nonlinear viscoelasticity. The time–strain separability facilitates in establishing the constitutive equations for the time-dependent stress–strain behavior of viscoelastic materials.17,18 When viscoelastic gels are subjected to an instantaneous strain γ at time t = 0, kept constant at t > 0, the resultant stress (σ) depends on γ and decays with elapsed time. The stress relaxation is expressed as
| σ(γ, t) = Δσ(γ, t) + σ∞(γ) | (1) |
| Δσ(γ, t) = H(γ)ϕ(t) | (2) |
Since the time–strain separability is not a rule derived from fundamental laws, it must be assessed via experiments for the materials of interest.19 In particular, the separability was intensively investigated for the nonlinear stress relaxation of entangled polymer melts with various architectures, such as linear-, star-, and comb-shaped polymers, subjected to single- or double-step large shear strains.20–27 The previous accounts showed that the two effects are separable in a relatively long time frame, which is several times longer than the Rouse relaxation time of the chain segments between entanglement points while inseparable within a shorter time frame. Several studies validated the time–strain separability in uniaxial extension excepting high strain regime for the viscoelastic gels such as the DC-PVA hydrogels28 and the polyampholyte hydrogels29 with transient bonds. Whether the strain and time effects on stress are separable or not is a key to model the pronouncedly time dependent stress–strain behavior of the polymer gels with transient bonds.
We investigate here the nonlinear stress relaxation for the HG gels using biaxial stretching with various combinations of two orthogonal strains as an imposed strain. Such general biaxial strain covers a wide range of physically accessible deformations for incompressible hyperelastic materials such as gel and rubber,30–33 while conventional uniaxial stretching is only a particular deformation among them. The biaxial data provide a definite basis to strictly discuss the nonlinear viscoelasticity of elastomeric materials. Using the biaxial stress relaxation data, we unambiguously validated the time–strain separability for the DC-PVA hydrogels.34 The present paper reveals that the time and strain effects are not separable in the HG gels, although the HG gels show significant stress relaxation similar to the DC-PVA gels. The results also provide a basis not only for the understanding of the interplay between the HG interaction and mechanical properties, but also for the materials design utilizing supramolecular chemistry.
Experimental section
Sample preparation
The HG gels were prepared by employing 6-acrylamido-β-cyclodextrin (β-CD-AAm) as host monomers and adamantane acrylamide (Ad-AAm) as guest monomers in two steps.9 The mixtures of water, β-CD-AAm and Ad-AAm were heated to and maintained at 90 °C for 2 hours to form the solutions of inclusion complexes. After filtration, the inclusion complexes were copolymerized with the acrylamide (AAm) monomer using ammonium persulfate and N,N,N′,N′-tetramethylenediamine as an initiator at 25 °C. The HG gels containing covalent cross-links were made by also adding N,N′-methylenebisacrylamide (BIS) to the monomer mixtures. The total monomer concentration was 1.8 M. The molar fractions of the β-CD-AAm and Ad-AAm units (denoted as h and g in Fig. 1b and Table 1) in the total monomers were varied so that the sum could be 5.2 mol%, in order to compare the properties of the HG gels with the excessive amounts of host or guest units, and the stoichiometric balance of them. The values of h and g of the monomer solutions after filtration were evaluated by a method11 using NMR. The evaluated molar fractions of β-CD-AAm in the sum of β-CD-AAm and Ad-AAm [XCD; XCD = h/(h + g)] were 0.33, 0.50 and 0.63. The resultant HG gels were repeatedly washed with water and left to swell for 3 days until equilibrium was attained. Table 1 lists the characteristics of each specimen. The numerals in the sample code denote the XCD value and the molar fraction of BIS. The volume ratio Q in Table 1 (Q = Vs/Vp) is the ratio of the as-prepared and swollen state volumes (Vp and Vs, respectively). The HG gels underwent no significant volume change before and after the immersion. These gel sheets in the equilibrium swollen state were employed for the mechanical measurements.| h (mol%) | g (mol%) | a (mol%) | b (mol%) | X CD | E 0 (kPa) | Q | |
|---|---|---|---|---|---|---|---|
| a X CD = h/(h + g). b Not measured. | |||||||
| HGG33-0 | 1.7 | 3.5 | 94.8 | 0 | 0.33 | 11.2 | 0.83 |
| HGG50-0 | 2.6 | 2.6 | 94.8 | 0 | 0.50 | 23.3 | 0.82 |
| HGG63-0 | 3.3 | 1.9 | 94.8 | 0 | 0.63 | 14.0 | 1.06 |
| HGG63-2 | 3.3 | 1.9 | 94.6 | 0.2 | 0.63 | 18.8 | 0.99 |
| HGG63-4 | 3.3 | 1.9 | 94.4 | 0.4 | 0.63 | 25.5 | 1.00 |
| CDG-0 | 3.3 | 0 | 96.7 | 0 | 1 | 13.5 | —b |
| AG-2 | 0 | 0 | 100 | 0.2 | 0 | 13.8 | —b |
| AG-4 | 0 | 0 | 100 | 0.4 | 0 | 16.5 | —b |
A gel specimen with topological rotaxane cross-links containing no inclusion complex, i.e., XCD = 1, (designated as CDG-0; Fig. 1a) was also prepared by copolymerizing the β-CD-AAm and AAm monomers. For comparison, poly(acrylamide) gels (AG) with covalent cross-links containing no inclusion complex were made by the copolymerization of the AAm monomer and BIS. The as-prepared CDG and PG sheets were used for the tensile tests, because they swell largely in water unlike the HG gels.
Mechanical experiments
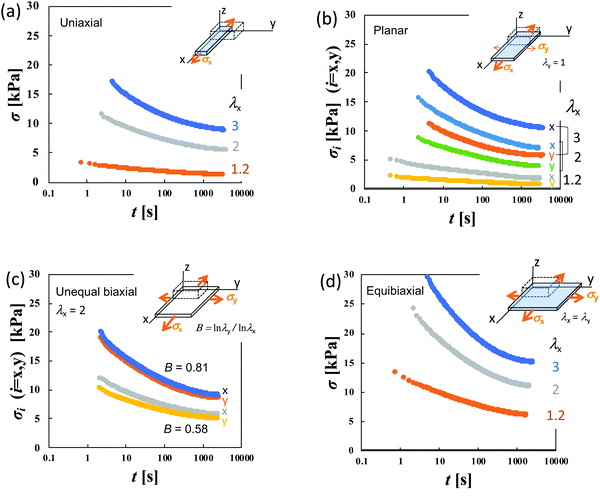
Stress relaxation measurements for sheet specimens with dimensions of 65 × 65 × 2 mm were performed with a custom-made biaxial tensile tester35 designed for soft elastomeric materials using five types of extensions—uniaxial (U), planar (PE), equibiaxial (EB), and unequal biaxial with two different strain ratios (UB)—as imposed deformations. The corresponding uniaxial tests were conducted using specimens with dimensions of 40 × 5 × 2 mm using an AC-500N-CMT (TSE, Japan). The specimen surfaces were coated with silicone oil to avoid water vaporization. For the planar extension (PE), the sheets are stretched along the x-axis while keeping the dimension in the y-axis unchanged (λy = 1 where λi is the dimensional ratio in the i-direction). The magnitudes of λx utilized were 1.2, 2.0, and 3.0 for the uniaxial, planar and equibiaxial extension. In unequal biaxial tension (UB), the degrees of λy used were 1.75 and 1.5 at λx = 2.0. The anisotropy B of the imposed strain is represented by the ratio of the true strains (loge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ) in two directions, and defined as B ≡ loge
λ) in two directions, and defined as B ≡ loge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λy/loge
λy/loge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λx. The B values are 1, 0.81, 0.58, 0, and −0.5 for EB, the two types of UB, PE, and U, respectively. After the target strains were imposed with an initial strain rate of 0.21 s−1, the reduction of the forces at each constant strain was measured as a function of time. The elapsed time, t, after the strain imposition was corrected using the Zapas–Craft method36,37 to consider the difference between an ideal (instantaneous) step strain and the strain imposition which requires a finite time. This is calculated by t = t′ − t1/2, where t′ and t1 denote the experimental time and the time required for the strain imposition, respectively.
λx. The B values are 1, 0.81, 0.58, 0, and −0.5 for EB, the two types of UB, PE, and U, respectively. After the target strains were imposed with an initial strain rate of 0.21 s−1, the reduction of the forces at each constant strain was measured as a function of time. The elapsed time, t, after the strain imposition was corrected using the Zapas–Craft method36,37 to consider the difference between an ideal (instantaneous) step strain and the strain imposition which requires a finite time. This is calculated by t = t′ − t1/2, where t′ and t1 denote the experimental time and the time required for the strain imposition, respectively.
The data reproducibility was confirmed by doing each test more than twice and by using the multiple specimens.
Results and discussion
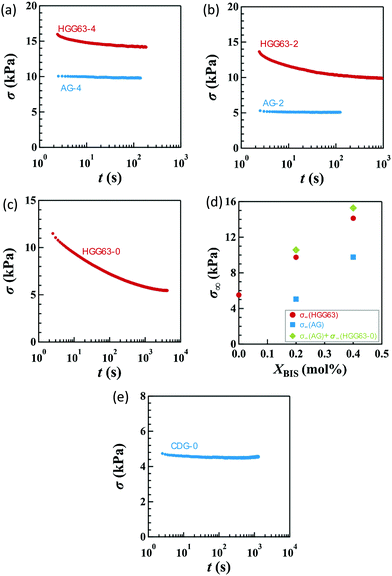
Fig. 2a–c display the stress relaxation after the imposition of 100% nominal uniaxial strain (λx = 2) for HGG63-4, HGG-63-2 and HGG63-0, respectively. For comparison, the data of AG with the same covalent cross-link concentrations (AG-4 and AG-2) are shown in each panel. The stress of each HG gel shows pronounced relaxation, and it reaches a finite equilibrium value (σ∞) after sufficiently long time. As the covalent cross-link concentration increases in the HG gels, the σ∞ value increases (Fig. 2d) and the equilibration time for stress decreases. In contrast, each AG gel exhibits finite stress without stress relaxation. These results obviously indicate that the stress relaxation in the HG gels is predominantly caused by the dissociation of the inclusion complexes, and that the finite σ∞ values for HGG63-0 are preserved by the permanent topological rotaxane cross-links whereas those for HGG63-4 and HGG63-2 are sustained by the covalent cross-links and the rotaxane cross-links. Interestingly, the summation of the σ∞ values of each AG and HGG63-0 agrees with that of the corresponding HG gel, which is shown in Fig. 2d. This agreement indicates that σ∞ of the HG gels with covalent cross-links is well approximated by the simple sum of the contributions of topological rotaxane cross-links and covalent cross-links. CDG-0 without the inclusion complex shows finite equilibrium stress but without stress relaxation (Fig. 2e), thereby confirming that the presence of permanent rotaxane cross-links and no contribution of their slidability along the network strands to the stress relaxation in the time window under consideration.Fig. 3a–d show the stress relaxation in uniaxial (U), planar (PE), unequal biaxial (UB), and equibiaxial (EB) extensions with various degrees of λx for HGG63-0 without covalent cross-links. The elapsed time (t) in the figures is obtained by the Zapas–Craft approach36,37 to rectify the difference between the strain application by a constant crosshead-speed ramp and ideal instantaneous step strain (See the Experimental section). The ideal step strain is assumed to be applied at t = 0. The stress relaxation in general stretching is expressed as follows:
| σi(λx, λy, t) = Δσi(λx, λy, t) + σ∞i(λx, λy) (i = x, y), | (3) |
| Δσi(λx, λy, t) = H(λx, λy)ϕ(t) | (4) |
The separability is validated by the collapse of the data into a single curve after the vertical shifts of the relaxation curves of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δσ in various deformations.38 Note that the shift factor is proportional to H. Fig. 4a show the failure of the corresponding superposition of log
Δσ in various deformations.38 Note that the shift factor is proportional to H. Fig. 4a show the failure of the corresponding superposition of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δσ–logt curves for three different types of stretching with various values of λx using the vertical shift factors (a). The global shapes of curves are obviously different from each other in the short and long time regions, indicating that the time–strain separability defined eqn (4) is no longer valid.
Δσ–logt curves for three different types of stretching with various values of λx using the vertical shift factors (a). The global shapes of curves are obviously different from each other in the short and long time regions, indicating that the time–strain separability defined eqn (4) is no longer valid.
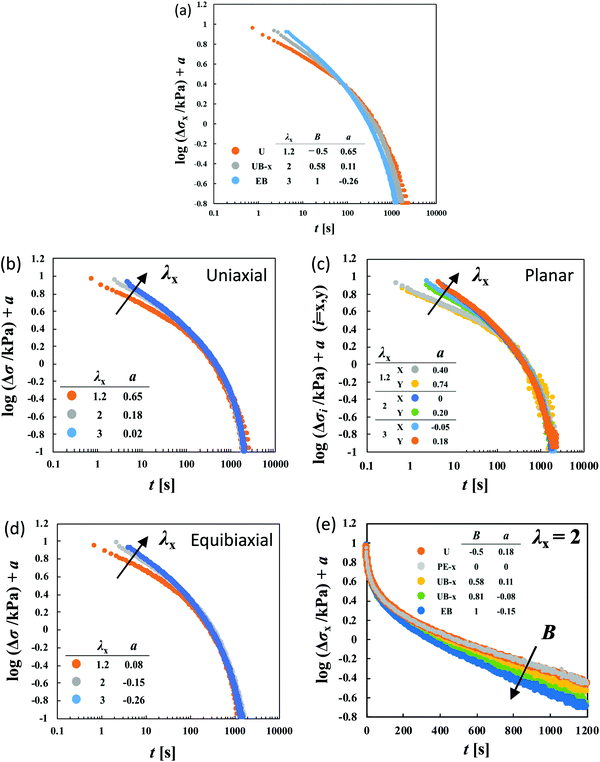 | ||
Fig. 4 (a) Failure of the superposition of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δσ–log Δσ–log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t curves for different types of deformation at various values of λx by vertical shift with a factor of a for HGG63-0. The failure at short times is appreciable in the superposition of the curves for the same type of deformation with various values of λx: (b) uniaxial, (c) planar, and (d) equibiaxial extension. (e) The failure at long times is appreciable in the superposition of the curves with the same value of λx (λx = 2) for various types of stretching. The planar extension (PE) data in the x-direction at λx = 2 are chosen as the reference for the shifts (a = 0). The original curves before the vertical shifts are shown in Fig. S1 of the ESI.† t curves for different types of deformation at various values of λx by vertical shift with a factor of a for HGG63-0. The failure at short times is appreciable in the superposition of the curves for the same type of deformation with various values of λx: (b) uniaxial, (c) planar, and (d) equibiaxial extension. (e) The failure at long times is appreciable in the superposition of the curves with the same value of λx (λx = 2) for various types of stretching. The planar extension (PE) data in the x-direction at λx = 2 are chosen as the reference for the shifts (a = 0). The original curves before the vertical shifts are shown in Fig. S1 of the ESI.† | ||
To elucidate the details of the inseparability, Fig. 4b–d represent the superpositions of the curves in the same stretching type but with different values of λx; uniaxial, planar, and equibiaxial extension, respectively. The planar stretching data in the x-direction are chosen as a reference for the shifts (a = 0). For every type of extension, the superposition is successful in a long t window of t > 100 s, while it is not valid any longer within t < 100 s. Another common observation for each deformation in a short t region is that the gradients of the curves tend to increase with an increase in λx. The Δσx(t) and Δσy(t) data in planar stretching are well superposed on each other in the full range of t, showing no anisotropy in stress relaxation dynamics. Fig. 4e shows the superpositions of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δσ–t curves at λx = 2 with different degrees of anisotropy in the imposed strain field (B), i.e., B ≡ loge
Δσ–t curves at λx = 2 with different degrees of anisotropy in the imposed strain field (B), i.e., B ≡ loge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λy/loge
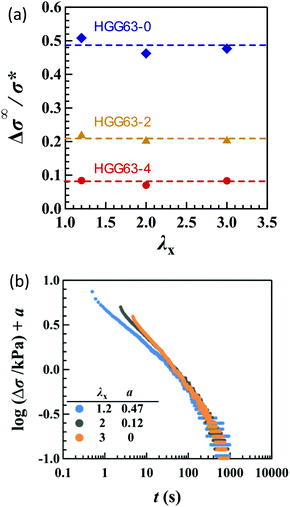
λy/loge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λx. At t < 100 s, the curves merge into a single curve but their slopes at t > 100 s depend on B. The slopes increase as the strain field becomes isotropic (i.e., B increases). The specimens HGG33-0 and HGG50-0 show inseparability similar to HGG63-0 (Fig. 5), indicating that the separability is invalid independent of the molar ratio of the host and guest units. The relaxation component Δσ is influenced by the σ∞ value, but the present conclusion, i.e., the failures of the superposition of the curves, is unchanged by small errors in the σ∞ values. Indeed, the Δσ–t curves for the same deformation obtained by the two independent tests were almost identical, indicating good reproducibility of the data, which is shown in Fig. S2 in the ESI.† It should also be noted that the separability was validated for the stress relaxation behavior of DC-PVA hydrogels in the entire t region along the same procedure including the Zapas–Craft approach for the time correction in the short t region.34 These facts ensure the time–strain inseparability for the stress relaxation of the HG gels observed here.
λx. At t < 100 s, the curves merge into a single curve but their slopes at t > 100 s depend on B. The slopes increase as the strain field becomes isotropic (i.e., B increases). The specimens HGG33-0 and HGG50-0 show inseparability similar to HGG63-0 (Fig. 5), indicating that the separability is invalid independent of the molar ratio of the host and guest units. The relaxation component Δσ is influenced by the σ∞ value, but the present conclusion, i.e., the failures of the superposition of the curves, is unchanged by small errors in the σ∞ values. Indeed, the Δσ–t curves for the same deformation obtained by the two independent tests were almost identical, indicating good reproducibility of the data, which is shown in Fig. S2 in the ESI.† It should also be noted that the separability was validated for the stress relaxation behavior of DC-PVA hydrogels in the entire t region along the same procedure including the Zapas–Craft approach for the time correction in the short t region.34 These facts ensure the time–strain inseparability for the stress relaxation of the HG gels observed here.
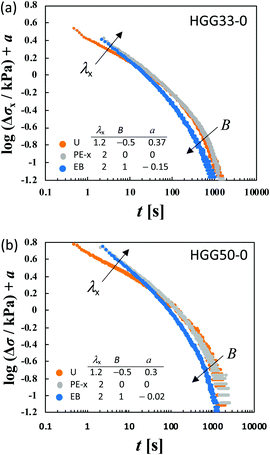 | ||
Fig. 5 Failure of the superposition of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δσ–log Δσ–log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t curves for different types of deformation with various values of λx by vertical shift with a factor of a for (a) HGG33-0 and (b) HGG50-0. Qualitative features of the failure of the superposition are common to HGG33-0, HGG50-0 and HGG64-0 (Fig. 4). t curves for different types of deformation with various values of λx by vertical shift with a factor of a for (a) HGG33-0 and (b) HGG50-0. Qualitative features of the failure of the superposition are common to HGG33-0, HGG50-0 and HGG64-0 (Fig. 4). | ||
To characterize the relaxation modes of Δσ(λx, λy, t), the generalized Maxwell model expressed by the Prony series39 was fitted to the normalized relaxation data f(t) as follows:
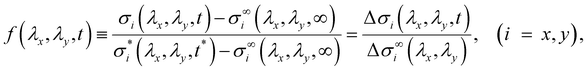 | (5) |
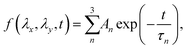 | (6) |
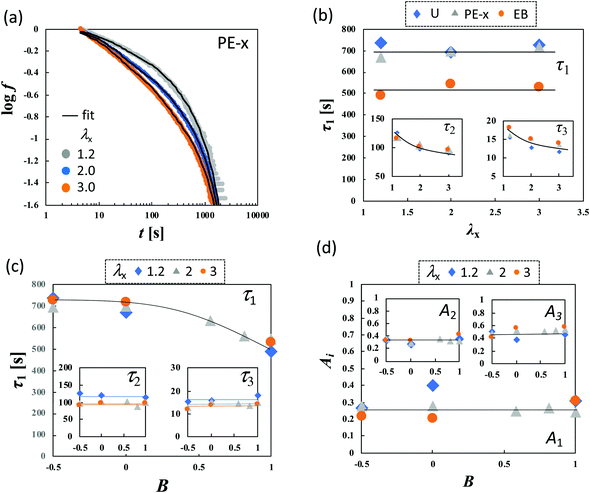 | ||
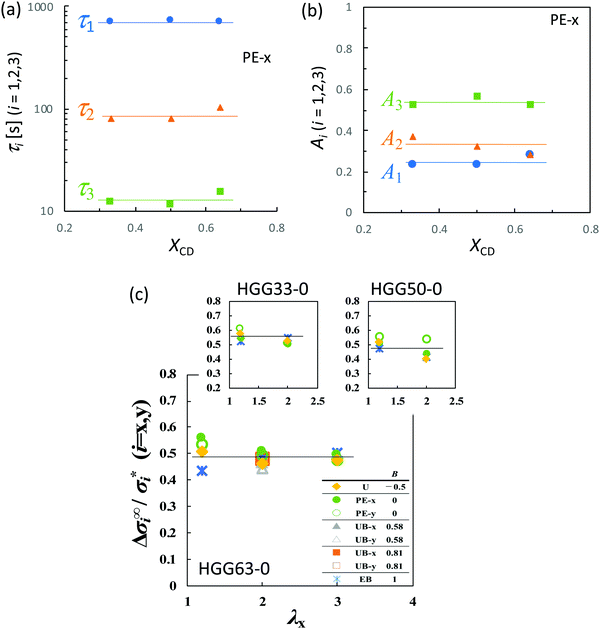
Fig. 6 (a) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f–log f–log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t curves for planar extension in x-direction with various values of λx for HGG63-0. The black solid lines represent the fitted curves of eqn (2). (b) Dependence of τi (i = 1, 2, and 3) on λx in various types of stretching, (c) Dependence of τi (i = 1, 2, and 3), and (d) Ai (i = 1, 2, and 3) on the anisotropy of the imposed strain field (B) for various values of λx for HGG63-0. t curves for planar extension in x-direction with various values of λx for HGG63-0. The black solid lines represent the fitted curves of eqn (2). (b) Dependence of τi (i = 1, 2, and 3) on λx in various types of stretching, (c) Dependence of τi (i = 1, 2, and 3), and (d) Ai (i = 1, 2, and 3) on the anisotropy of the imposed strain field (B) for various values of λx for HGG63-0. | ||
As presented in Fig. 6b, all types of stretching examined here share a common feature for each parameter. The longest relaxation time τ1 is independent of λx, while both τ2 and τ3 become smaller with increasing λx in the short t region. This tendency represents the failure of the superposition of the curves in the short time region in Fig. 4. The longest relaxation time, τ1, becomes smaller with increasing B, whereas τ2 and τ3 are independent of B regardless of the values of λx (Fig. 6c). This result is in concurrence with the feature in the long time region in Fig. 4e, since the inverse of the slope in the figure is proportional to τ1. The relaxation strength An (n = 1, 2, and 3) is unaffected by λx and B (Fig. 6d).
The compositions XCD influence the initial Young's modulus E0, and E0 tends to be maximum at the stoichiometric ratio (XCD = 0.50) (Table 1). Importantly, XCD has no appreciable effect on τn or An (n = 1, 2, and 3) (Fig. 7a and b). The relative magnitudes of the total stress relaxation to the initial stress, Δσ∞/σ*, are compared among the different types of stretching and various values of λx in Fig. 7c. The magnitude for HGG63-0 is approximately 50%, and is independent of the type, degree, and direction of imposed strain. Moreover, the values are mostly unaffected by XCD.
The introduction of covalent cross-links into the HG gels reduces the total magnitude of stress relaxation. Fig. 8a compares the Δσ∞/σ* values in uniaxial stretching among HGG63-0, -2 and -4. HGG63-4 exhibits almost no stress relaxation, while the stress relaxation magnitude of HGG63-2 is nearly a half of that of HGG63-0. Introducing the covalent cross-links reduces the number and the length of the network chains which can relax via the detachment of transient bonds, resulting in a decrease in the relaxation magnitude. Importantly, the time–strain effects in HGG63-2 are inseparable similar to those in HGG63-0 (Fig. 8b), indicating that the time–strain inseparability still remains invalid in the presence of covalent cross-links.
As mentioned before, the same assessment validates the time–strain separability for the DC-PVA gels containing both covalent and transient cross-links.34 What distinguishes the relaxation dynamics of DC-PVA and HG gels? These two gels have the following differences: (i) the mobility of association sites, (ii) the number density of the sites available for association, and (iii) the type of permanent cross-links. With respect to (i), the counterpart for the association (borate ion) in DC-PVA gels is chemically unbound to the network chains,7 whereas both association sites in HG gels are covalently connected to them. With respect to (ii), the DC-PVA gels have an association site (hydroxyl group) in nearly every repeating unit (99.0%), while the number fractions of β-CD and Ad units in all the repeating units for HGG-64 are only 3%. The concentration of the associative sites on the network chains in DC-PVA gels (with a PVA concentration of 14 wt%) is 1.6 M, while that in the HG gels is only about 0.03 M. The corresponding upper limit concentration for the HG gels was as large as 0.1 M due to the occurrence of the phase separation,9 precluding the comparison of these two gels at the same concentration. The features (i) and (ii) of the HG gels are expected to make the dissociation dynamics susceptible to the orientation and distortion of network chains, that is, the type and degree of imposed deformation, because both association sites are covalently bound to the network chains and their concentrations are considerably low.
With respect to (iii), DC-PVA gels have covalent fixed cross-links,7 while the HG gels have permanent and movable topological cross-links with the rotaxane structure.11–13,15 The sliding nature of the rotaxane cross-links enables variations in the chain lengths between neighboring rotaxane cross-links in response to the imposed deformation,40 resulting in various peculiar physical properties reported for the polyrotaxane gels with figure-of-eight cross-links.41–44 Recently, we reported that the ultimate elongation (λmax) in biaxial loading for the polyrotaxane gels is unusually lower than that in uniaxial loading.45 This marked sensitivity of λmax to loading conditions indicates that the chain supply mechanism considerably depends on the loading axiality. In uniaxial loading, the extra chain portions are supplied from the two stress-free directions to the loading direction through the rotaxane cross-links, resulting in high λmax. In contrast, in biaxial loading, the chains are supplied from only one stress-free direction, and furthermore, the supplied chain portions are shared among the two loading directions, leading to considerably less λmax. It is plausible to expect that the chain supply function via rotaxane cross-links should affect the detachment dynamics between the host and guest units depending on the type and degree of deformations.
Therefore, all three features (i)–(iii) can be considered to make the dissociation dynamics susceptible to the orientation and distortion of network chains. To elucidate the origin of relaxation spectra sensitive to the type and degree of deformation requires varying systematically the fixation and concentration of the associative sites, and the type of permanent cross-links. A recent study46 revealed that the mechanical properties of the HG gels were influenced by the chemical structures of the host and guest units which affect the HG interaction via an electric barrier, CD cavity size, and size of the guest unit. The effects of these factors on the relaxation dynamics will be addressed in our future work.
Conclusions
The HG gels exhibit pronounced stress relaxation with finite equilibrium stress following the step strain. The dissociation dynamics of the transient cross-links which sustain the initial stress governs the stress relaxation process, and the permanent topological cross-links with the rotaxane structure preserve the finite equilibrium stress. We have demonstrated the time–strain inseparability for the HG gels based on the nonlinear stress relaxation behavior in various types and magnitudes of stretching, while the same assessment validated the separability for the viscoelastic DC-PVA gels possessing both permanent covalent and transient bonds. In the HG gels, the relaxation in a short time region (<102 s) is faster by increasing the degree of imposed strain, while that in a longer time region is slower with the increase in the anisotropy of the imposed biaxial strain. The time–strain inseparability in the HG gels signifies that the dissociation dynamics of the transient cross-links depends on the types and degrees of imposed deformation. The inseparability is also verified in the HG gels to which the covalent cross-links are introduced. The significant susceptibility of the dissociation dynamics to the imposed deformation is expected to result from the structural characteristics of the HG gels, i.e., the host and guest units covalently bound to the network chains, their considerably low concentrations (<0.1 M), and the chain supply mechanism via the permanent rotaxane cross-links significantly depending on the types of imposed deformation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the ImPACT Program of the Council for Science, Technology and Innovation (Cabinet Office, Government of Japan) (K. U.), the JSPS Grant-in-Aid for Scientific Research on Innovative Areas “Discrete Geometric Analysis for Materials Design” (grant no. JP20H04638) (K. U.) and JSPS KAKENHI Grant No. 19H05719 (M. N., Y. T., and M. T.). M. T. thanks the Nakatani Foundation for support. The authors acknowledge Dr Junsu Park at Osaka University for the assistance in drawing the schematics.References
- S. Van Vlierberghe, P. Dubruel and E. Schacht, Biomacromolecules, 2011, 12, 1387–1408 CrossRef CAS PubMed.
- H. W. Ooi, S. Hafeez, C. A. van Blitterswijk, L. Moroni and M. B. Baker, Mater. Horiz., 2017, 4, 1020–1040 RSC.
- C. Creton, Macromolecules, 2017, 50, 8297–8316 CrossRef CAS.
- K. J. Henderson, T. C. Zhou, K. J. Otim and K. R. Shull, Macromolecules, 2010, 43, 6193–6201 CrossRef CAS.
- J. Y. Sun, X. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. A. Haque, T. Nakajima and J. P. Gong, Nat. Mater., 2013, 12, 932–937 CrossRef CAS PubMed.
- T. Narita, K. Mayumi, G. Ducouret and P. Hébraud, Macromolecules, 2013, 46, 4174–4183 CrossRef CAS.
- M. Nakahata, Y. Takashima, H. Yamaguchi and A. Harada, Nat. Commun., 2011, 2, 511 CrossRef PubMed.
- M. Nakahata, Y. Takashima and A. Harada, Macromol. Rapid Commun., 2016, 37, 86–92 CrossRef CAS PubMed.
- T. Kakuta, Y. Takashima, M. Nakahata, M. Otsubo, H. Yamaguchi and A. Harada, Adv. Mater., 2013, 25, 2849–2853 CrossRef CAS PubMed.
- Y. Kashiwagi, T. Katashima, M. Nakahata, Y. Takashima, A. Harada and T. Inoue, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 1109–1117 CrossRef CAS.
- Y. Kashiwagi, T. Katashima, Y. Takashima, A. Harada and T. Inoue, Nihon Reoroji Gakkaishi, 2019, 47, 99–104 CrossRef CAS.
- R. Ikura, J. Park, M. Osaki, H. Yamaguchi, A. Harada and Y. Takashima, Macromolecules, 2019, 52, 6953–6962 CrossRef CAS.
- R. Ikura, Y. Ikemoto, M. Osaki, H. Yamaguchi, A. Harada and Y. Takashima, Polymer, 2020, 196, 122465 CrossRef CAS.
- Y. Kashiwagi, O. Urakawa, S. Zhao, Y. Takashima, A. Harada and T. Inoue, Macromolecules, 2021, 54, 3321–3333 CrossRef CAS.
- M. Hörning, M. Nakahata, P. Linke, A. Yamamoto, M. Veschgini, S. Kaufmann, Y. Takashima, A. Harada and M. Tanaka, Sci. Rep., 2017, 7, 7660 CrossRef PubMed.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, Oxford, 1999 Search PubMed.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, John Wiley & Sons, 2nd edn, 1987 Search PubMed.
- Y. Kwon and K. S. Cho, J. Rheol., 2001, 45, 1441–1452 CrossRef CAS.
- K. Osaki and M. Kurata, Macromolecules, 1980, 13, 671–676 CrossRef CAS.
- K. Osaki, K. Nishizawa and M. Kurata, Macromolecules, 1982, 15, 1068–1071 CrossRef CAS.
- C. M. Vrentas and W. W. Graessley, J. Rheol., 1982, 26, 359–371 CrossRef CAS.
- D. C. Venerus, C. M. Vrentas and J. S. Vrentas, J. Rheol., 1990, 34, 657–684 CrossRef.
- G. Marrucci and N. Grizzuti, J. Rheol., 1983, 27, 433–450 CrossRef CAS.
- L. A. Archer and S. K. Varshney, Macromolecules, 1998, 31, 6348–6355 CrossRef CAS.
- J. H. Lee, K. Orfanou, P. Driva, H. Iatrou, N. Hadjichristidis and D. J. Lohse, Macromolecules, 2008, 41, 9165–9178 CrossRef CAS.
- K. M. Kirkwood, L. G. Leal, D. Vlassopoulos, P. Driva and N. Hadjichristidis, Macromolecules, 2009, 42, 9592–9608 CrossRef CAS.
- K. Mayumi, A. Marcellan, G. Ducouret, C. Creton and T. Narita, ACS Macro Lett., 2013, 2, 1065–1068 CrossRef CAS PubMed.
- F. Luo, T. L. Sun, T. Nakajima, T. Kurokawa, Y. Zhao, A. Bin Ihsan, H. L. Guo, X. F. Li and J. P. Gong, Macromolecules, 2014, 47, 6037–6046 CrossRef CAS.
- L. R. G. Treloar, The Physics of Rubber Elasticity, Clarendon Press, Oxford, 3rd edn, 1975 Search PubMed.
- N. W. Tschoegl and C. Gurer, Macromolecules, 1985, 18, 680–687 CrossRef CAS.
- K. Urayama, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 3440–3444 CrossRef CAS.
- K. Urayama, Polym. Int., 2017, 66, 195–206 CrossRef CAS.
- T. Kimura and K. Urayama, ACS Macro Lett., 2020, 9, 1–6 CrossRef CAS PubMed.
- B. Yohsuke, K. Urayama, T. Takigawa and K. Ito, Soft Matter, 2011, 7, 2632–2638 RSC.
- L. J. Zapas and T. Craft, Rubber Chem. Technol., 1967, 40, 506–516 CrossRef.
- A. Flory and G. B. McKenna, Mech. Time-Depend. Mater., 2004, 8, 17–37 CrossRef.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford Unv. Press, Oxford, 1986 Search PubMed.
- J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley & Sons, New York, 3rd edn, 1980 Search PubMed.
- K. Mayumi, K. Ito and K. Kato, Polyrotaxane and Slide-Ring Materials, The Royal Society of Chemistry, 2016 Search PubMed.
- Y. Bitoh, N. Akuzawa, K. Urayama, T. Takigawa, M. Kidowaki and K. Ito, Macromolecules, 2011, 44, 8661–8667 CrossRef CAS.
- C. Katsuno, A. Konda, K. Urayama, T. Takigawa, M. Kidowaki and K. Ito, Adv. Mater., 2013, 25, 4636–4640 CrossRef CAS PubMed.
- C. Liu, H. Kadono, K. Mayumi, K. Kato, H. Yokoyama and K. Ito, ACS Macro Lett., 2017, 6, 1409–1413 CrossRef CAS PubMed.
- A. Tanaka, K. Kato, K. Ito and K. Urayama, Soft Matter, 2018, 14, 2808–2815 RSC.
- T. Aoyama, K. Kato and K. Urayama, ACS Macro Lett., 2022, 11, 362–367 CrossRef CAS PubMed.
- Y. Takashima, K. Otani, Y. Kobayashi, H. Aramoto, M. Nakahata, H. Yamaguchi and A. Harada, Macromolecules, 2018, 51, 6318–6326 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Double logarithmic plots of Δσ versus t for different types of stretching at various degrees of imposed strain for HGG63-0, the reproducibility of the stress relaxation behavior for HGG63-2, and the fitted results of eqn (4) to the t dependence of f for several types of stretching for HGG63-0. See DOI: https://doi.org/10.1039/d2sm00285j |
| This journal is © The Royal Society of Chemistry 2022 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif)