Open Access Article
Open Access ArticleA multiple model approach for evaluating the performance of time-lapse capsules in trapping heavy metals from water bodies†
Shu-Yuan Pan *,
Wei-Jhan Syu,
Tsun-Kuo Chang and
Cheng-Hsun Lee
*,
Wei-Jhan Syu,
Tsun-Kuo Chang and
Cheng-Hsun Lee
Department of Bioenvironmental Systems Engineering, National Taiwan University, Taipei City, 10617 Taiwan, Republic of China. E-mail: sypan@ntu.edu.tw
First published on 25th April 2020
Abstract
Adsorption by ion-exchange resins has been widely used as a cost-effective method for removing numerous hazardous materials, particularly heavy metals, from aqueous solutions. For effectively detecting the illegal discharge of industrial wastewater containing heavy metals, we developed “time-lapse capsules” to trap metallic ions from water bodies. Despite recent progress in the development of time-lapse capsules, a fundamental understanding was still needed to unravel the adsorption behavior of different heavy metals for further improvement of the design and scale-up of the capsule. In this study, three different approaches, viz., response surfaces (from the statistical point of view), time-dependent diffusion-controlled models (from the kinetic point of view), and adsorption isotherms (from the equilibrium point of view), were utilized to evaluate the effect of operating factors on the adsorption of heavy metals from watershed using time-lapse capsules. The obtained results indicated that the key parameters, such as adsorption rate constant, diffusivity, and maximum adsorption capacity, could provide insights into the basis of design criteria.
1. Introduction
A water body is generally defined as a body of accumulated water forming a physiographical feature on a planet's surface, such as oceans, watersheds, lakes, wetlands, and reservoirs (even phytotelma). Illegal discharges of industrial wastewater containing heavy metals into water bodies, particularly rivers and streams, have been a critical issue in sustainable watershed management and source water protection around the world.1,2 A polluted water body deteriorates the quality of irrigation water and thus, causes risk to the safety of crops and foods. Events of illegal discharges (wastewater) from industries, however, are usually intentional at a random time. In other words, this type of water pollution is difficult to identify because the sources of illegal discharges are hard to find out. On the other hand, the conventional analysis of heavy metals in water samples is relatively time-consuming and expensive, which makes the monitoring of heavy metal pollution in rivers unpractical. Therefore, the development of rapid and effective approaches for monitoring, sampling, and analysis of heavy metal pollution in water bodies are necessary.For detecting illegal discharges of wastewater, Huang et al.3 developed ion-exchange resin sachets (referred to as “time-lapse capsules” in this work) to trap metallic ions from the watershed, such as irrigation and drainage channels, throughout a certain period of time (usually >seven days). The time-lapse capsules were manufactured by packing a certain amount of ion-exchange resins into a non-woven fabric sachet. The time-lapse capsules were surrounded by a cylindrical polyethylene mesh to increase the mechanical durability. It is noted that the adsorption by ion-exchange resins has been used for various applications, such as removal of heavy metals,4,5 removal of perfluoroalkyl substances,6 removal of metal complexed azo dyes,7 nutrient recovery from urine,8 and precious metal recovery from electrical and electronic wastes.9,10 The developed time-lapse capsules could be readily deployed in monitoring works and could serve as concentrators of heavy metals from a water body. Therefore, once there is an illegal discharge of wastewater at any time, the deployed time-lapse capsules in the watershed could trap the heavy metals from the wastewater. The concentration of the adsorbed heavy metals on the time-lapse capsules could also be rapidly determined by the non-destructive X-ray fluorescence core-scanning (XRF-CS) technique.3,11 According to the results reported by Huang et al.,3 the concentrations of heavy metals determined by the XRF-CS (the increase on the resin) and the conventional analytical method (the reduction in water) exhibited excellent correlations (R2 > 0.97) even at a short scanning time (<1 s). By doing so, one could identify the potential hot spots of illegal discharge in situ and then keep deploying more time-lapse capsules upstream until the discharge point of the industry is located.
The efficiency of time-lapse capsules for the adsorption of metals from water bodies can be attributed to a number of factors, such as the water flow rate in the channels, the chemistry between the metallic ions and the adsorbent, and the physico-chemical properties of ion exchange resins. From the theoretical point of view, the removal kinetics and equilibrium isotherms are essential for the effective design of the adsorption system. In general, the kinetics of adsorption by ion-exchange resins are governed by the extent of agitation, the initial concentration of the ions in the solution, the ionic size and mobility, the type of counter ions, and the nature of exchangers. The analysis of adsorption kinetics can provide information about the adsorption mechanism of heavy metals and the time required to reach equilibrium. Likewise, the adsorption isotherms can elucidate the interactions of the metal ions with the resins and estimate the adsorption capacity.12,13 Extensive studies have been reported on the application of various ion-exchange resins for the removal of heavy metals from aqueous solutions. However, to the best of our knowledge, scarcely any study has been focused on the fundamental research of adsorption of heavy metals, such as kinetics and isotherms, especially using time-lapse capsules.
Despite recent progress in the development of time-lapse capsules, a fundamental understanding is still needed to unravel the adsorption behaviors of different heavy metals for further improvement of the design and scale-up of the capsules. In this study, multiple model approaches were utilized to evaluate the effect of the operating factors on the heavy metal trapping performance from water using time-lapse capsules. By using the experimental data, the response surfaces of key operating parameters (including initial concentration, stirring speed, and adsorption time) with respect to the performance of adsorption were established from the statistical point of view. Apart from this, the kinetics of adsorption of different metal ions were evaluated using classical heterogeneous models, such as pseudo-first-order, pseudo-second-order, and diffusion-controlled models. The adsorption isotherms (from the equilibrium point of view) were also determined at the equilibrium of the heterogeneous system. Therefore, by doing so, we could systematically understand the adsorption behaviors of different heavy metals using time-lapse capsules from different angles, which would be beneficial for the scale-up of operation and the improvement of design in the future.
2. Materials and methods
2.1 Materials
In this study, a sodium-type cation exchange resin (Amberlite™ IR120) was used to prepare the time-lapse capsule. Table S1 (see ESI†) presents the physico-chemical characteristics of the IR120 resin. The matrix of the resin was the styrene divinylbenzene copolymer with a sulfonate-based functional group, possessing a total exchange capacity of 2.00 eq L−1. The detailed procedure for the preparation of time-lapse capsules can be found in our previous studies.3,112.2 Batch adsorption experiments
The adsorption of different metal ions (i.e., Zn, Cu, Cr, Pb, Ni, Ca, Mn, and Ti) by the time-lapse capsules was evaluated in a batch system. For each metal ion, four different levels of concentrations (see Table S2†) were prepared in accordance with the Effluent Standards in Taiwan.14 In order to study the effect of mixing, the adsorption experiments were performed using the Jar-Tester machine (JT-6, Shin-Kwang Precision Industry Ltd., Taiwan) at different stirring speeds, i.e., 50, 100, 150, and 200 rpm at 20 °C for 2 h. The type of stirrer used in the Jar-Tester machine was a single straight blade with a length of 8 cm and a width of 2 cm (SAE 304 stainless steel). The volume of solution for each batch test was one liter and 20 g of the ion exchange resin was used in each time-lapse capsule. After the experiment was finished, the time-lapse capsule was removed from the solution and the residual amounts of metal ions in the solution were analyzed by ICP-OES (Agilent 5110, USA).The removal efficiency of the metal ions (R) was calculated using eqn (1):
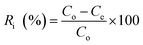 | (1) |
The amount of metal ion adsorbed onto a unit dry mass of the resin (qe) can be determined by mass balance using eqn (2):
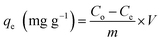 | (2) |
2.3 Kinetic adsorption models
The contact time between the adsorbate and the adsorbent is an important factor as ion removal through adsorption could occur on the solid–liquid interface. Adsorption kinetics can provide information regarding the rate of removal of ions using the time-lapse capsules as well as the controlling mechanisms of adsorption processes such as chemical reactions and/or mass transfer. The kinetic parameters play a vital role in the design and scale-up of the adsorption process. In order to evaluate the reaction kinetics of ion (adsorbate) removal using the time-lapse capsules, different types of models, including pseudo-first-order, pseudo-second-order, and diffusion-controlled mechanism, were applied in this study.
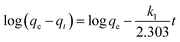 | (3) |
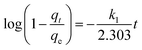 | (4) |
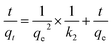 | (5) |
If external diffusion of metal ions (within the diffuse layers outside the sorbent) is the rate limiting factor, the adsorption data can be described by eqn (6):
| ln(Ct/Co) = −kf(A/V) × t | (6) |
If the intraparticle diffusion model is the rate limiting step, the experimental data could be described by the following model:18
| qt = kpt1/2 + I | (7) |
2.4 Adsorption isotherms
The adsorption isotherms can provide insights on the equilibrium between the metal ions presented in the solution and on the adsorbent at a certain temperature. The extent of the adsorption capacity depends on several factors, such as the theoretical capacity of the ion exchange resin, the selectivity of the adsorbent over other ions present in the solution, and the approximation rate to the equilibrium load. In this study, the Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich isotherm models were used to describe the equilibrium data and to evaluate the surface properties of the adsorbent and its adsorption behaviors.
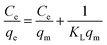 | (8) |
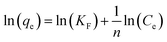 | (9) |
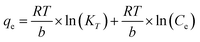 | (10) |
| ln(qe) = ln(qm) − βε2 | (11) |
ε = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 + 1/Ce) ln(1 + 1/Ce)
| (12) |
By assuming that the adsorbate was transferred from infinity in the solution to the surface of the resin,19 the mean free energy of adsorption per molecule of the adsorbate (E, kJ mol−1) can be determined by eqn (13).
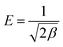 | (13) |
This parameter can provide information about the mechanism of adsorption:20–22 (i) the adsorption process was followed by ion-exchange if E was between 8–16 kJ mol−1, or (ii) by physical adsorption if E was less than 8 kJ mol−1. It was noted that E value less than 8 kJ mol−1 indicated a weak sorbent–sorbate interaction, which might lead to subsequent release of the adsorbed metal ions back into the solution from the surface of the adsorbent after sorption equilibrium.
3. Results and discussion
3.1 Effect of initial concentration, stirring speed, and adsorption time on metal trapping
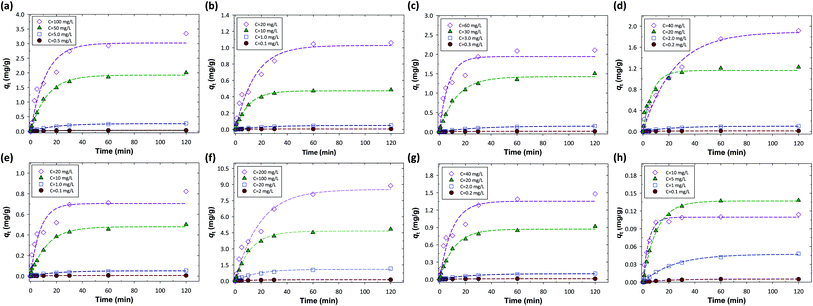
In this study, the performance of time-lapse capsules for heavy metal adsorption from water bodies was evaluated by using the batch adsorption experiments. The variable parameters include initial concentration (four levels for each metal, see Table S2†), stirring speed (50, 100, 150, and 200 rpm), and adsorption time (0, 0.5, 1, 3, 5, 10, 20, 30, 60, and 120 min), thereby resulting in a total of 144 experimental data for each metal. Fig. 1 shows the effect of different adsorption (contact) times and initial concentrations on the removal of metal ions in terms of the amounts of metal ions adsorbed on the resins (qt, mg g−1) at a stirring speed of 200 rpm. We found that the adsorption of metal ions on the resins could proceed via two stages in the period of contact as follows: (i) rapid uptake and (ii) slow adsorption. For the first stage, the value of qt increased rapidly as the adsorption (contact) time increased from 0 to 40 min, especially within the first 20 min. After 40 min, the value of qt became relatively constant (the second stage), indicating that equilibrium was reached. The phenomena of this two-stage adsorption might be attributed to the available active sites on the ion-exchange resins. Rapid uptake of metal ions occurred due to a great number of active sites on the surface of the resins that were readily accessible at the beginning of the adsorption experiments. The rate of adsorption decreased thereafter as the active sites on the resins were gradually occupied by metal ions.Similarly, with the increase in the initial concentrations of the metal ions, the value of qt increased accordingly. Different initial concentrations would thus correspond to different levels of the final equilibrium saturation adsorption capacity (qe). Aside from the active sites on the resins, for the first stage, the slope of the adsorption curve (i.e., Zn, Cu, Cr, Ni, Ca, and Mn) at higher initial concentration was steeper due to the higher concentration gradient. The higher concentration gradient could provide a greater driving force to overcome resistance to external mass transfer (i.e., film diffusion) between the solution and the resin phases. It is noteworthy that the adsorption kinetics and capacities could be affected by the design of the time-lapse capsules, such as the particle size and packing density of the resins. The adsorption kinetics generally increased as the particle size of the resins decreased. For adsorption capacities, the packing density of the resins in a time-lapse capsule should be determined based on the expected concentrations of heavy metals in water bodies to avoid over-saturated adsorption.
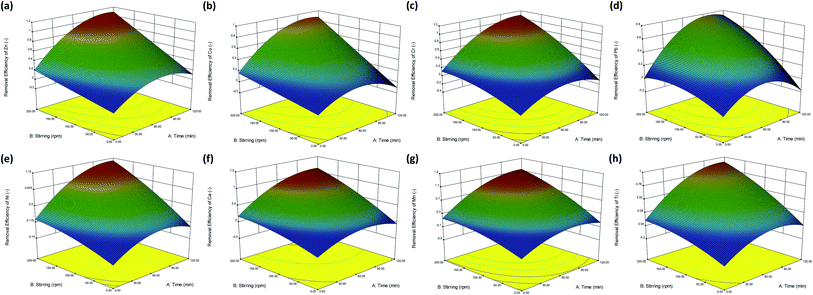
Based on these experimental data, we formulated non-linear programs to evaluate the effect of the initial concentration, stirring speed, and adsorption time on the efficiency of adsorption of the metals. Table 1 presents the results of non-linear programs for describing the adsorption behaviors of metals in terms of different operating parameters. Based on the experimental data, the non-linear programs were developed to predict the response of system performance from the statistical point of view. In the non-linear programs, A, B, and C were coded parameters and denoted as the adsorption time (min), stirring speed (rpm), and concentration in water (mg L−1), respectively. For the adsorption behavior of all the metals, we found that the modified quadratic programs were the best fitting models as the p-value of all the models was less than 0.0001 (CI: 95%). The coefficients of determination (R2) for all the developed models were in the range between 0.848 and 0.876. The analysis of variance (ANOVA) results of the developed models for different metals are summarized in the ESI (Tables S1–S8†), indicating that the adsorption of metals, especially Zn, Cu, Cr, Ca, and Mn, could be well described by the developed models. Based on these developed models, we could easily visualize the performance of metal trapping under different operating conditions, identify the effect of operating parameters on the removal efficiency, and determine the maximum efficiency at certain constraint conditions.
| Metal | Response surface model (in terms of removal efficiency)a | Eqn. | R2 |
|---|---|---|---|
| a A, B, and C are coded and denoted as the adsorption time (min), stirring speed (rpm), and concentration in water (mg L−1), respectively. | |||
| Zn | Zn = 0.54 + 0.24A + 0.29B − 0.10C + 0.16AB − 0.08AC − 0.07BC − 0.27A2 | (14) | 0.864 |
| Cu | Cu = 0.46 + 0.18A + 0.31B − 0.28C + 0.18AB − 0.14AC − 0.25A2 − 0.17C2 | (15) | 0.848 |
| Cr | Cr = 0.58 + 0.29A + 0.40B − 0.28C + 0.19AB − 0.27A2 − 0.11B2 − 0.23C2 | (16) | 0.876 |
| Pb | Pb = 0.51 + 0.17A + 0.27B − 0.15C + 0.18AB − 0.12AC − 0.16BC − 0.29A2 − 0.11B2 | (17) | 0.862 |
| Ni | Ni = −0.38 − 0.08A + 0.07B − 2.11C + 0.16AB − 0.39AC − 0.30BC − 0.23A2 − 0.07B2 − 1.11C2 | (18) | 0.869 |
| Ca | Ca = 0.63 + 0.29A + 0.40B − 0.03C + 0.19AB − 0.03AC − 0.03BC − 0.27A2 − 0.10B2 | (19) | 0.872 |
| Mn | Mn = 0.43 + 0.11A + 0.38B − 0.23C + 0.17AB − 0.21AC − 0.26A2 − 0.12B2 | (20) | 0.856 |
| Ti | Ti = −0.30 − 0.49A − 0.13B − 0.91C + 0.13AB − 0.82AC − 0.47BC − 0.22A2 − 0.08B2 | (21) | 0.857 |
Fig. 2 shows the response surfaces of the developed models for the removal (adsorption) efficiency of different metals, in terms of adsorption time and stirring speed. The results indicated that for all the metals, the removal efficiency increased as both the adsorption time and stirring speed increased. According to the coefficients of each term in the equations (Table 1), the stirring speed (denoted as B) exhibited the most positive influence on the removal efficiency. In other words, compared to the adjustment of other parameters, it was more effective to enhance the removal efficiency by increasing the stirring speed from 50 to 200 rpm. The sequence of metal removal efficiency on increasing one unit of stirring speed was in the order: Cr ∼ Ca > Mn > Cu > Zn > Pb > Ni > Ti. The extent of mixing (stirring) could be attributed to the rate of the diffusion-controlled step for surface sorption from the liquid phase onto the surface of the solid resin. It was noted that the mass transfer considerations for adsorption included (i) convection and diffusion through the liquid film surrounding the resin (so-called film diffusion), (ii) diffusion along the length of a pore (so-called pore diffusion), and (iii) adsorption onto the vacant site of the solid surface.23 Sufficient mixing between the water samples and the time-lapse capsules could effectively promote the rate of film diffusion, thereby shortening the time required to reach equilibrium. Thus, in the following analyses, including kinetics and adsorption isotherm, the stirring speed was fixed at 200 rpm to ensure rapid mass transfer in the bulk solution.
The removal efficiency of the metals could also be enhanced by prolonging the adsorption time, especially for the first 40 min. According to the coefficient of term A in the equations (Table 1), a similar trend of metal removal efficiency on increasing one unit of adsorption time was noticed: Cr ∼ Ca > Zn > Cu ∼ Pb > Mn > Ni > Ti. However, once the maximum adsorption capacity of the resins (the saturation point, or sometimes called as the equilibrium distribution) was reached, the removal efficiency remained almost unchanged, even when the adsorption time was further prolonged. It was noted that the adsorption of metals could be considered as a partitioning of the adsorbate (ions) between the liquid phase and the resin adsorbent.23 In the following analyses, we studied several adsorption isotherm and kinetic models to elucidate the equilibrium behaviors and adsorption rates.
3.2 Adsorption kinetics
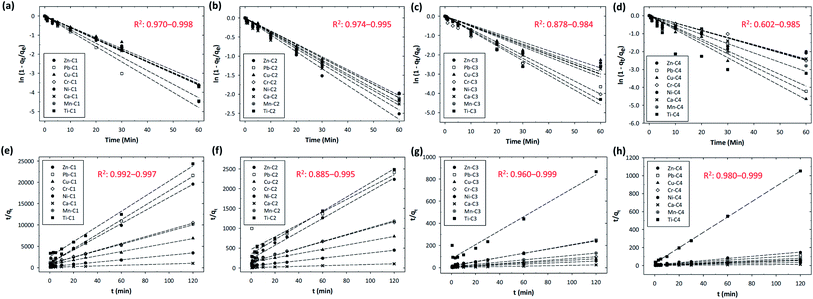
Among the operating factors (adsorption time, stirring speed, and concentration) used in this study, the stirring speed was the most dominant factor affecting the adsorption efficiency of all the metals. In a real watershed, the water flow rate is usually high enough to ensure complete mixing, i.e., the concentration difference of the metals within the liquid film surrounding the resin might not be significant. Therefore, to evaluate the adsorption kinetics of different metals using time-lapse capsules, we neglected the limiting step of film diffusion by analyzing the experimental data with the highest designated stirring speed (i.e., 200 rpm). In this study, the adsorption kinetic models were established using two different approaches based on (i) the adsorption capacity of the solid adsorbent and (ii) the type of diffusion-controlled mechanism.Table 2 summarizes the kinetic data extracted from the pseudo-first and pseudo-second order models for the adsorption of metal ions using time-lapse capsules at 20 °C. Based on the obtained pseudo-second-order rate constant, the half-adsorption time (t1/2) for different metals was determined. The half-adsorption time was defined as the time required to reach half the amount of the maximum adsorption capacity by the ion-exchange resins. The half-adsorption time could be used as a measure of the adsorption rate, as described by eqn (22).27
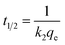 | (22) |
| Metal | Concn. | Pseudo-first order | Pseudo-second order | t1/2 (min) | ||||
|---|---|---|---|---|---|---|---|---|
| k1 (min−1) | k1tref (−) | R2 | k2 (g mg−1 min−1) | qmax (mg g−1) | R2 | |||
| Zn | C1 | 0.060 ± 0.002 | 3.612 | 0.987 | 3.205 | 0.037 | 0.995 | 8.4 |
| C2 | 0.044 ± 0.001 | 2.658 | 0.985 | 0.213 | 0.304 | 0.995 | 15.4 | |
| C3 | 0.050 ± 0.004 | 2.988 | 0.923 | 0.042 | 2.200 | 0.999 | 10.8 | |
| C4 | 0.041 ± 0.004 | 2.454 | 0.851 | 0.026 | 3.587 | 0.995 | 10.7 | |
| Pb | C1 | 0.080 ± 0.004 | 4.794 | 0.970 | 28.66 | 0.006 | 0.997 | 5.8 |
| C2 | 0.037 ± 0.001 | 2.238 | 0.994 | 0.525 | 0.064 | 0.885 | 29.8 | |
| C3 | 0.067 ± 0.004 | 4.038 | 0.956 | 0.289 | 0.515 | 0.997 | 6.7 | |
| C4 | 0.066 ± 0.003 | 3.930 | 0.970 | 0.089 | 1.151 | 0.993 | 9.8 | |
| Cu | C1 | 0.057 ± 0.002 | 3.408 | 0.984 | 3.513 | 0.020 | 0.992 | 14.2 |
| C2 | 0.034 ± 0.001 | 2.034 | 0.995 | 0.203 | 0.185 | 0.958 | 26.6 | |
| C3 | 0.045 ± 0.004 | 2.676 | 0.888 | 0.054 | 1.643 | 0.997 | 11.3 | |
| C4 | 0.078 ± 0.003 | 4.686 | 0.975 | 0.070 | 2.232 | 0.996 | 6.4 | |
| Cr | C1 | 0.059 ± 0.001 | 3.552 | 0.995 | 7.138 | 0.013 | 0.997 | 10.8 |
| C2 | 0.035 ± 0.001 | 2.088 | 0.980 | 0.486 | 0.118 | 0.992 | 17.4 | |
| C3 | 0.073 ± 0.004 | 4.368 | 0.960 | 0.155 | 1.282 | 0.999 | 5.0 | |
| C4 | 0.040 ± 0.001 | 2.412 | 0.985 | 0.030 | 2.139 | 0.980 | 15.6 | |
| Ni | C1 | 0.071 ± 0.003 | 4.284 | 0.982 | 22.42 | 0.007 | 0.995 | 6.4 |
| C2 | 0.038 ± 0.002 | 2.286 | 0.974 | 1.251 | 0.059 | 0.990 | 13.5 | |
| C3 | 0.048 ± 0.004 | 2.874 | 0.878 | 0.200 | 0.538 | 0.996 | 9.3 | |
| C4 | 0.041 ± 0.005 | 2.484 | 0.718 | 0.173 | 0.847 | 0.991 | 6.8 | |
| Ca | C1 | 0.062 ± 0.001 | 3.696 | 0.994 | 0.662 | 0.130 | 0.995 | 11.6 |
| C2 | 0.040 ± 0.002 | 2.400 | 0.963 | 0.073 | 1.241 | 0.990 | 11.0 | |
| C3 | 0.053 ± 0.004 | 3.162 | 0.912 | 0.018 | 5.294 | 0.998 | 10.5 | |
| C4 | 0.042 ± 0.002 | 2.502 | 0.975 | 0.006 | 10.02 | 0.989 | 16.6 | |
| Mn | C1 | 0.060 ± 0.001 | 3.588 | 0.995 | 6.543 | 0.013 | 0.995 | 11.8 |
| C2 | 0.037 ± 0.001 | 2.214 | 0.984 | 0.521 | 0.115 | 0.989 | 16.7 | |
| C3 | 0.050 ± 0.004 | 3.012 | 0.889 | 0.112 | 0.987 | 0.999 | 9.0 | |
| C4 | 0.052 ± 0.004 | 3.120 | 0.910 | 0.078 | 1.575 | 0.996 | 8.1 | |
| Ti | C1 | 0.061 ± 0.001 | 3.624 | 0.998 | 12.52 | 0.006 | 0.994 | 13.3 |
| C2 | 0.035 ± 0.001 | 2.094 | 0.985 | 0.902 | 0.056 | 0.993 | 19.8 | |
| C3 | 0.077 ± 0.003 | 4.590 | 0.984 | 0.493 | 0.158 | 0.960 | 12.8 | |
| C4 | 0.071 ± 0.011 | 4.254 | 0.602 | 2.691 | 0.117 | 0.999 | 3.2 | |
The results indicated that the half-adsorption time was not necessarily proportional to the initial concentration of the metals in the water bodies. In most cases, the half-adsorption time firstly increased as the initial concentration increased from C1 to C2 (e.g., Zn, Pb, Ni, and Mn) or from C1 to C3 (e.g., Cu), and then rapidly decreased if the initial concentration further increased to C4.
| Metal | Concn. | External diffusion | Intraparticle diffusion | ||||
|---|---|---|---|---|---|---|---|
| kf (mm min−1) | R2 | kp,1 (mg g−1 min−1/2) × 103 | R2 | kp,2 (mg g−1 min−1/2) × 103 | R2 | ||
| Zn | C1 | 0.097 ± 0.007 | 0.933 | 5.2 ± 0.2 | 0.995 | 1.2 ± 0.6 | 0.779 |
| C2 | 0.096 ± 0.002 | 0.994 | 41.3 ± 1.2 | 0.996 | 10.5 ± 2.8 | 0.932 | |
| C3 | 0.059 ± 0.007 | 0.763 | 354.4 ± 18.1 | 0.987 | 55.6 ± 6.8 | 0.985 | |
| C4 | 0.021 ± 0.004 | 0.474 | 502.8 ± 53.0 | 0.947 | 111.4 ± 13.1 | 0.986 | |
| Pb | C1 | 0.083 ± 0.012 | 0.672 | 0.8 ± 0.0 | 0.990 | 0.2 ± 0.1 | 0.830 |
| C2 | 0.116 ± 0.006 | 0.969 | 7.1 ± 0.3 | 0.991 | 2.7 ± 0.6 | 0.955 | |
| C3 | 0.086 ± 0.011 | 0.767 | 86.4 ± 5.2 | 0.983 | 7.6 ± 2.5 | 0.899 | |
| C4 | 0.041 ± 0.006 | 0.672 | 151.8 ± 11.3 | 0.973 | 38.2 ± 2.4 | 0.716 | |
| Cu | C1 | 0.097 ± 0.005 | 0.957 | 2.5 ± 0.1 | 0.996 | 0.7 ± 0.5 | 0.660 |
| C2 | 0.107 ± 0.006 | 0.967 | 20.2 ± 1.6 | 0.968 | 9.3 ± 2.0 | 0.957 | |
| C3 | 0.072 ± 0.006 | 0.891 | 258.1 ± 14.0 | 0.986 | 47.4 ± 0.9 | 0.999 | |
| C4 | 0.021 ± 0.004 | 0.144 | 331.6 ± 44.5 | 0.917 | 29.2 ± 16.5 | 0.758 | |
| Cr | C1 | 0.140 ± 0.001 | 0.999 | 1.8 ± 0.1 | 0.985 | 0.3 ± 0.2 | 0.660 |
| C2 | 0.092 ± 0.003 | 0.988 | 14.1 ± 0.4 | 0.997 | 5.9 ± 1.1 | 0.966 | |
| C3 | 0.122 ± 0.009 | 0.905 | 199.6 ± 19.1 | 0.956 | 18.2 ± 8.3 | 0.826 | |
| C4 | 0.062 ± 0.004 | 0.955 | 230.0 ± 5.9 | 0.997 | 121.2 ± 51.9 | 0.845 | |
| Ni | C1 | 0.052 ± 0.003 | 0.939 | 0.8 ± 0.0 | 0.990 | 0.2 ± 0.1 | 0.660 |
| C2 | 0.097 ± 0.003 | 0.990 | 7.4 ± 0.2 | 0.994 | 2.9 ± 0.5 | 0.971 | |
| C3 | 0.074 ± 0.007 | 0.860 | 85.2 ± 4.2 | 0.988 | 13.4 ± 0.5 | 0.999 | |
| C4 | 0.025 ± 0.004 | 0.314 | 107.3 ± 12.4 | 0.937 | 24.3 ± 7.4 | 0.915 | |
| Ca | C1 | 0.168 ± 0.017 | 0.876 | 19.7 ± 0.6 | 0.995 | 3.5 ± 0.0 | 1.000 |
| C2 | 0.127 ± 0.007 | 0.963 | 153.9 ± 4.0 | 0.997 | 55.0 ± 12.4 | 0.952 | |
| C3 | 0.081 ± 0.007 | 0.862 | 883.4 ± 54.8 | 0.981 | 116.1 ± 12.9 | 0.988 | |
| C4 | 0.031 ± 0.004 | 0.734 | 1246 ± 107 | 0.964 | 387.2 ± 99.8 | 0.938 | |
| Mn | C1 | 0.107 ± 0.005 | 0.965 | 1.9 ± 0.1 | 0.982 | 0.3 ± 0.2 | 0.660 |
| C2 | 0.093 ± 0.002 | 0.993 | 14.0 ± 0.6 | 0.992 | 5.6 ± 1.1 | 0.964 | |
| C3 | 0.067 ± 0.008 | 0.787 | 160.3 ± 9.3 | 0.983 | 23.8 ± 1.4 | 0.997 | |
| C4 | 0.023 ± 0.004 | 0.359 | 225.1 ± 29.1 | 0.923 | 34.9 ± 5.1 | 0.979 | |
| Ti | C1 | 0.078 ± 0.007 | 0.874 | 0.8 ± 0.0 | 0.990 | 0.2 ± 0.1 | 0.660 |
| C2 | 0.063 ± 0.002 | 0.979 | 6.7 ± 0.4 | 0.990 | 2.7 ± 0.6 | 0.955 | |
| C3 | 0.025 ± 0.005 | 0.324 | 27.5 ± 1.9 | 0.978 | 1.7 ± 1.0 | 0.743 | |
| C4 | 0.006 ± 0.002 | 0.532 | 20.0 ± 3.5 | 0.868 | 0.9 ± 0.2 | 0.946 | |
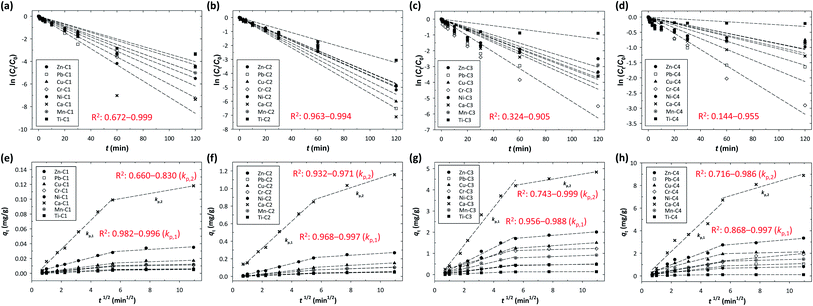
Fig. 4 shows the fitting curves at different initial concentrations accompanied by the least-square regression analysis of the models. It was found that the intraparticle diffusion coefficient (kp) increased significantly with the increase in the initial concentration of the metals. The best-fit lines for the intraparticle-diffusion model did not pass through the origin, indicating that there was an initial boundary layer resistance. For the intraparticle-diffusion model, the boundary layer effect became more significant as the intercept of the fitting curves increased. As shown in Fig. 4(e–h), a multilinearity for intraparticle-diffusion models was observed, indicating that multiple steps of mechanism occurred during the adsorption process: the rapid diffusion (phase I) and the slow diffusion (phase II). In phase I (the first linear segment, corresponding to kp,1), macro-pore diffusion was dominant with instantaneous occupation of the available adsorbing sites on the surface of the resins. In contrast, in phase II (the second linear segment, corresponding to kp,2), micro-pore diffusion was dominant with slow diffusion of metals from the surface film into the micro-pores, as well as slow migration of metals from the liquid phase onto the surface of the resins.
3.3 Adsorption equilibrium and isotherm
Adsorption isotherms are essential for the design of adsorption systems as they describe the relationship between the equilibrium concentration of metal ions in the solution (Ce) and the amount of metal ions adsorbed onto the adsorbent (qe) at a constant temperature. The data from adsorption isotherm models can provide information about the adsorption capacity of the adsorbent, as well as the prediction of adsorption parameters. Table 4 presents the adsorption isotherm parameters for different metal ions using time-lapse capsules at 20 °C. The results indicated that three isotherm models, viz., the Langmuir, Temkin, and D–R models, fitted very well for most of the metal ions. The coefficients of determination for the Langmuir, Temkin, and D–R models were in the range of 0.973–1.000 (except for Ti), 0.824–0.987 (except for Cr), and 0.811–0.995 (except for Pb), respectively.| Metals | (1) Langmuir | (2) Freundlich | (3) Temkin | (4) Dubinin–Radushkevich | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KL (L mg−1) | qm (mg g−1) | R2 | RLa | KF | n (−) | R2 | KT (L mg−1) | b (kJ mol−1) | R2 | qm (mg g−1) | E (kJ mol−1) | R2 | |
| a RL values were determined at the concentration in accordance with Taiwan EPA's effluent standards (i.e., C2).b The obtained values were meaningless. | |||||||||||||
| Zn | 1.24 | 2.75 | 0.998 | 0.13 | 0.70 | 2.01 | 0.872 | 0.08 | 6.3 | 0.975 | 0.0024 | 27.5 | 0.977 |
| Pb | 0.42 | 2.71 | 0.973 | 0.70 | 0.53 | 1.84 | 0.617 | 0.44 | 19.3 | 0.921 | 0.0006 | 31.8 | 0.464 |
| Cu | 0.34 | 6.30 | 1.000 | 0.50 | 0.66 | 2.15 | 0.738 | 0.30 | 10.4 | 0.987 | 0.0020 | 29.4 | 0.919 |
| Cr | 0.12 | 16.3 | 0.985 | 0.79 | 1.82 | 1.75 | 0.891 | 1.87 | 11.7 | 0.722 | 0.0011 | 34.2 | 0.811 |
| Ni | 0.13 | 6.37 | 1.000 | 0.88 | 0.44 | 2.02 | 0.892 | 0.92 | 27.9 | 0.949 | 0.0006 | 32.4 | 0.981 |
| Ca | 0.83 | 10.9 | 0.999 | 0.05 | 2.56 | 2.64 | 0.854 | 0.38 | 3.0 | 0.951 | 0.0063 | 31.5 | 0.971 |
| Mn | 0.36 | 4.23 | 0.999 | 0.58 | 0.52 | 1.98 | 0.895 | 0.31 | 15.0 | 0.957 | 0.0011 | 30.5 | 0.971 |
| Ti | —b | —b | —b | —b | 0.08 | 2.56 | 0.749 | 0.50 | 152.3 | 0.824 | 0.0001 | 31.1 | 0.995 |
From the Langmuir model, the maximum adsorption capacities (qm) for Zn, Pb, Cu, Cr, Ni, Ca, and Mn were found to be 2.8, 2.7, 6.3, 16.3, 6.4, 10.9, and 4.2 mg g−1, respectively. The adsorption energy constants (KL) for Zn, Pb, Cu, Cr, Ni, Ca, and Mn were 1.24, 0.42, 0.34, 0.12, 0.13, 0.83, and 0.36 L mg−1, respectively. To describe the affinity between the adsorbents and the metal ions, the concept of separation factor (RL, dimensionless) was applied as determined by eqn (23):
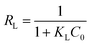 | (23) |
The Temkin model could also well predict the adsorption behavior of most of the metal ions, except for Cr and Ti. The obtained KT values for Zn, Pb, Cu, Ni, Ca, and Mn were 0.08, 0.44, 0.30, 0.92, 0.38, and 0.51 L mg−1, respectively. The equilibrium binding constant was related to the maximum binding energy. The heat of adsorption (b) for Zn, Pb, Cu, Ni, Ca, and Mn was 6.3, 19.3, 10.4, 27.9, 3.0, and 15.0 J mol−1, respectively.
The adsorption of Ti could be well described only by the D–R model, with a high R2 value of 0.995. The D–R model could also be used to predict the adsorption of most of the metal ions, except for Pb and Cr. The determined E values for Zn, Cu, Ni, Ca, Mn, and Ti were 27.5, 29.4, 32.4, 31.5, 30.5, and 31.1 kJ mol−1, respectively. E values higher than 8 kJ mol−1 indicated chemisorption,29 which would follow the ion-exchange mechanism. The obtained results from the isotherm models were consistent with that from the kinetic models. The obtained qm values for Zn, Cu, Ni, Ca, Mn, and Ti were 0.002, 0.002, 0.001, 0.001, 0.006, and 0.001 mg g−1, respectively.
3.4 Insights into the fundamentals and practical applications
In this study, three different approaches, i.e., response surfaces (from the statistical point of view, see Table 1), time-related and/or diffusion-controlled models (from the kinetic point of view, see Table 2), and adsorption isotherm (from the equilibrium point of view, see Table 3), were utilized to evaluate the effect of operating factors on the entrapment of heavy metals from water using time-lapse capsules. The response surface models were established based on the experimental design to describe the adsorption behaviors of different metal ions with respect to various operating parameters. Since they were developed from the statistical point of view, the obtained coefficients usually have no physical meanings. However, based on these empirical response surfaces, one could easily identify the operating conditions for achieving the maximum adsorption ratio. One way to enhance the fundamental basis (physically meaningful) of the response surface models was to combine it with the unit-factor method, i.e., using dimensionless groups as the equation inputs. The concept of dimensional homogeneity could be utilized in the design of process scale-up.Conversely, the kinetic models (such as diffusion-controlled kinetics) were applied to determine the rate-limiting step in a heterogeneous system based on the fundamental mechanisms and theories. These classical kinetic models have been widely used because of their conceptual and mathematical simplicity, compared to the models based on numerical analysis. The key design parameters of the time-lapse capsules, for e.g., the adsorption rate constant and diffusion coefficient, could be obtained with these kinetic models. The obtained constants and/or coefficients could provide information about the adsorption behaviors at the liquid–solid interface. Hence, it was assumed that these models could be applied for future scale-up and optimization. Likewise, the adsorption isotherm models were developed based on the fundamentals of equilibrium adsorption with respect to different initial concentrations at a constant temperature. The obtained isotherm data described the equilibrium relationship between the time-lapse capsules (adsorbent) and the heavy metals (adsorbate). The distributions of different heavy metals between the time-lapse capsules and the water solution at equilibrium were useful for estimating the maximum adsorption capacity of the designed systems.
This research should be considered as the pioneering study reporting the adsorption kinetics and capacities of different heavy metals using time-lapse capsules, which could be used as the design criteria for future improvement. The concept of developing low-cost materials (i.e., time-lapse capsules) provides an insight into the in situ and simple monitoring of heavy metals in water bodies. In practice, the deployment of time-lapse capsules can easily identify the potential sources and patterns of illegal or accidental discharges containing heavy metals from industries into natural water bodies without intensive labor. In addition, the time-lapse capsules can be possibly used to capture trace emerging contaminants, such as perfluorooctanoic and perfluorooctanesulfonic acids, from an aqueous environment by concentrating them onto the ion-exchange resins over a period of time. This technique exhibits a great potential of wide applications in tracking or extracting various types of pollutants (even at the sub-ppm level) from water bodies and/or paddy soils at low cost. In our previous study,30 we successfully utilized the XRF technique to rapidly determine the concentrations of heavy metals adsorbed on the time-lapse capsules. For the sake of heavy metal monitoring, the regeneration of the used ion-exchange resins was not necessary as the time-lapse capsules were designed for one-time use.
3.5 Priority research directions: adsorption behaviors and interactions
In this study, we have provided an insight into the adsorption behaviors of different heavy metals using time-lapse capsules from different angles by using a multiple model approach. The obtained kinetic and isotherm parameters could be used to improve the design of time-lapse capsules. In this section, we have proposed several priority research directions for future studies, including (1) sorption kinetics adapted to field operations, (2) interactions and competitive sorption of different heavy metals, and (3) contribution of electrostatic sorption and complexation.4. Conclusion
In this study, multiple model approaches including response surfaces, kinetics, and isotherms were utilized to evaluate the effect of operating factors on the performance of trapping heavy metals from water using time-lapse capsules. The results indicated that the adsorption of metal ions on the time-lapse capsules proceeded in two stages in the period of contact time, viz., (i) rapid uptake, especially within the beginning 20 min and (ii) slow adsorption after 40 min. This could be attributed to the available active sites on the ion-exchange resins. According to the kinetic analyses, it was suggested that adsorption was due to chemisorption and the adsorption mechanism was adsorbate diffusion rather than surface control. The rate-limiting step would be external diffusion control at low initial concentrations, which gradually switched to intraparticle diffusion control as the initial concentration of metals increased. The results from the intraparticle-diffusion models also indicated that there was an initial boundary layer resistance. The obtained external diffusion coefficients for Zn, Pb, Cu, Cr, Ni, Ca, Mn, and Ti were 0.10, 0.12, 0.11, 0.09, 0.10, 0.13, 0.09, and 0.06 mm min−1, respectively. Similarly, the results of the isotherm models indicated favorable adsorption of the metal ions using time-lapse capsules. Both the Langmuir and Temkin isotherm models fitted well for the adsorption behavior of most of the metal ions, while the adsorption of Ti could be well described only by the D–R isotherm model. In order to enhance the fundamental knowledge of heavy metal adsorption using time-lapse capsules, our future work will be focused on the contribution of electrostatic adsorption and complexation to adsorption, as well as the competitive adsorption of different heavy metals.Conflicts of interest
There are no conflicts to declare.Acknowledgements
High appreciation goes to the Council of Agriculture, Executive Yuan, Taiwan (ROC) for the financial support under Grant number 106AS-15.2.2-IE-b1 and 1082101021901-110201b1. Shu-Yuan Pan also thanks the financial support from National Taiwan University under the Grant Number 109L7303 and from Ministry of Science and Technology (MOST) under the Grant Number 108-2636-M-002-012.References
- Y. Owusu-Asante, Analysis and determination of optimum risk factors to prioritize illegal discharge potential in urban catchments, Phys. Chem. Earth, 2019, 111, 86–99 CrossRef.
- F. Xia, L. Qu, T. Wang, L. Luo, H. Chen, R. A. Dahlgren, M. Zhang, K. Mei and H. Huang, Distribution and source analysis of heavy metal pollutants in sediments of a rapid developing urban river system, Chemosphere, 2018, 207, 218–228 CrossRef PubMed.
- J. S. Huang, S. C. Lin, L. Lowemark, S. Y. H. Liou, Q. Chang, T. K. Chang, K. Y. Wei and I. W. Croudace, Rapid assessment of heavy metal pollution using ion-exchange resin sachets and micro-XRF core-scanning, Sci. Rep., 2019, 9, 6601 CrossRef PubMed.
- F.-Q. An, Y. Wang, X.-Y. Xue, T.-P. Hu, J.-F. Gao and B.-J. Gao, Design and application of thiourea modified D301 resin for the effective removal of toxic heavy metal ions, Chem. Eng. Res. Des., 2018, 130, 78–86 CrossRef.
- K. Xiao, F. Xu, L. Jiang, Z. Dan and N. Duan, The oxidative degradation of polystyrene resins on the removal of Cr(VI) from wastewater by anion exchange, Chemosphere, 2016, 156, 326–333 CrossRef PubMed.
- F. Dixit, B. Barbeau, S. G. Mostafavi and M. Mohseni, PFOA and PFOS removal by ion exchange for water reuse and drinking applications: role of organic matter characteristics, Environ. Sci.: Water Res. Technol., 2019, 5, 1782–1795 RSC.
- G. Bayramoglu, A. Akbulut, G. Liman and M. Y. Arica, Removal of metal complexed azo dyes from aqueous solution using tris(2-aminoethyl)amine ligand modified magnetic p(GMA-EGDMA) cationic resin: Adsorption, isotherm and kinetic studies, Chem. Eng. Res. Des., 2017, 124, 85–97 CrossRef.
- W. A. Tarpeh, I. Wald, M. Wiprächtiger and K. L. Nelson, Effects of operating and design parameters on ion exchange columns for nutrient recovery from urine, Environ. Sci.: Water Res. Technol., 2018, 4, 828–838 RSC.
- S. Gámez, K. Garcés, E. de la Torre and A. Guevara, Precious metals recovery from waste printed circuit boards using thiosulfate leaching and ion exchange resin, Hydrometallurgy, 2019, 186, 1–11 CrossRef.
- R. K. Nekouei, F. Pahlevani, M. Assefi, S. Maroufi and V. Sahajwalla, Selective isolation of heavy metals from spent electronic waste solution by macroporous ion-exchange resins, J. Hazard. Mater., 2019, 371, 389–396 CrossRef CAS.
- P.-K. Shih, L.-C. Chiang, S.-C. Lin, T.-K. Chang and W.-C. Hsu, Application of Time-Lapse Ion Exchange Resin Sachets (TIERS) for Detecting Illegal Effluent Discharge in Mixed Industrial and Agricultural Areas, Sustainability, 2019, 11, 3129 CrossRef CAS.
- J. Ma, J. Shen, C. Wang and Y. Wei, Preparation of dual-function chelating resin with high capacity and adjustable adsorption selectivity to variety of heavy metal ions, J. Taiwan Inst. Chem. Eng., 2018, 91, 532–538 CrossRef CAS.
- B. J. Ni, Q. S. Huang, C. Wang, T. Y. Ni, J. Sun and W. Wei, Competitive adsorption of heavy metals in aqueous solution onto biochar derived from anaerobically digested sludge, Chemosphere, 2019, 219, 351–357 CrossRef CAS PubMed.
- EPA Taiwan, Database: Clearance of Municipal Solid Waste by Implementing Agencies, 2018, Data Period: 1998/01/01 to 2018/05/31.
- S. Lagergren, About the theory of so-called adsorption of soluble substances, K. Sven. Vetenskapsakad. Handl., 1898, 24, 1–39 Search PubMed.
- Y. S. Ho and G. McKay, Pseudo-second order model for sorption processes, Process Biochem., 1999, 34, 451–465 CrossRef CAS.
- E.-A. Kwak, S.-J. Kim and J.-H. Kim, Effect of ion exchange resin on increased surface area crystallization process for purification of vancomycin, Korean J. Chem. Eng., 2012, 29, 1487–1492 CrossRef CAS.
- W. J. Weber and J. C. Morris, presented in part at the Proceedings of International Conference on Water Pollution Symposium, 1962 Search PubMed.
- S. S. Dubey and R. K. Gupta, Removal behavior of Babool bark (Acacia nilotica) for submicro concentrations of Hg2+ from aqueous solutions: a radiotracer study, Sep. Purif. Technol., 2005, 41, 21–28 CrossRef CAS.
- A. S. Özcan, B. Erdem and A. Özcan, Adsorption of Acid Blue 193 from aqueous solutions onto BTMA-bentonite, Colloids Surf., A, 2005, 266, 73–81 CrossRef.
- M. H. El-Naas, S. Al-Zuhair and M. A. Alhaija, Removal of phenol from petroleum refinery wastewater through adsorption on date-pit activated carbon, Chem. Eng. J., 2010, 162, 997–1005 CrossRef CAS.
- M. S. Onyango, Y. Kojima, O. Aoyi, E. C. Bernardo and H. Matsuda, Adsorption equilibrium modeling and solution chemistry dependence of fluoride removal from water by trivalent-cation-exchanged zeolite F-9, J. Colloid Interface Sci., 2004, 279, 341–350 CrossRef CAS.
- A. Gabelman, Adsorption Basics: Part 1, American Institute of Chemical Engineering, 2017, pp. 48–53 Search PubMed.
- L. Li, F. Liu, X. Jing, P. Ling and A. Li, Displacement mechanism of binary competitive adsorption for aqueous divalent metal ions onto a novel IDA-chelating resin: isotherm and kinetic modeling, Water Res., 2011, 45, 1177–1188 CrossRef CAS PubMed.
- M. Assefi, S. Maroufi, R. K. Nekouei and V. Sahajwalla, Selective recovery of indium from scrap LCD panels using macroporous resins, J. Cleaner Prod., 2018, 180, 814–822 CrossRef CAS.
- Y. N. Thakare and A. K. Jana, Performance of high density ion exchange resin (INDION225H) for removal of Cu(II) from waste water, J. Environ. Chem. Eng., 2015, 3, 1393–1398 CrossRef CAS.
- M. Doğan, Y. Özdemir and M. Alkan, Adsorption kinetics and mechanism of cationic methyl violet and methylene blue dyes onto sepiolite, Dyes Pigm., 2007, 75, 701–713 CrossRef.
- M. M. Rao, A. Ramesh, G. P. C. Rao and K. Seshaiah, Removal of copper and cadmium from the aqueous solutions by activated carbon derived from Ceiba pentandra hulls, J. Hazard. Mater., 2006, 129, 123–129 CrossRef.
- F.-Q. An, R.-Y. Wu, M. Li, T.-P. Hu, J.-F. Gao and Z.-G. Yuan, Adsorption of heavy metal ions by iminodiacetic acid functionalized D301 resin: Kinetics, isotherms and thermodynamics, React. Funct. Polym., 2017, 118, 42–50 CrossRef CAS.
- W. J. Syu, T. K. Chang and S. Y. Pan, Establishment of an Automatic Real-Time Monitoring System for Irrigation Water Quality Management, Int. J. Environ. Res. Public Health, 2020, 17(3), 737 CrossRef PubMed.
- X.-P. Zhang, F.-Q. Liu, C.-Q. Zhu, C. Xu, D. Chen, M.-M. Wei, J. Liu, C.-H. Li, C. Ling, A.-M. Li and X.-Z. You, A novel tetraethylenepentamine functionalized polymeric adsorbent for enhanced removal and selective recovery of heavy metal ions from saline solutions, RSC Adv., 2015, 5, 75985–75997 RSC.
- S. Khalili, B. Khoshandam and M. Jahanshahi, Synthesis of activated carbon/polyaniline nanocomposites for enhanced CO2 adsorption, RSC Adv., 2016, 6, 35692–35704 RSC.
- Z. Wu, Z. Sun, P. Liu, Q. Li, R. Yang and X. Yang, Competitive adsorption of naphthalene and phenanthrene on walnut shell based activated carbon and the verification via theoretical calculation, RSC Adv., 2020, 10, 10703–10714 RSC.
- O. Kazak, A. Tor, I. Akin and G. Arslan, Preparation and characterization of novel polysulfone-red mud composite capsules for the removal of fluoride from aqueous solutions, RSC Adv., 2016, 6, 86673–86681 RSC.
- E. Pehlivan and T. Altun, Ion-exchange of Pb2+, Cu2+, Zn2+, Cd2+, and Ni2+ ions from aqueous solution by Lewatit CNP 80, J. Hazard. Mater., 2007, 140, 299–307 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra03017a |
| This journal is © The Royal Society of Chemistry 2020 |