Open Access Article
Open Access ArticleThermodynamic and kinetic studies of H2 and N2 binding to bimetallic nickel-group 13 complexes and neutron structure of a Ni(η2-H2) adduct†
Ryan C.
Cammarota‡
a,
Jing
Xie‡
 abe,
Samantha A.
Burgess
abe,
Samantha A.
Burgess
 c,
Matthew V.
Vollmer
a,
Konstantinos D.
Vogiatzis
c,
Matthew V.
Vollmer
a,
Konstantinos D.
Vogiatzis
 abf,
Jingyun
Ye
abf,
Jingyun
Ye
 ab,
John C.
Linehan
ab,
John C.
Linehan
 c,
Aaron M.
Appel
c,
Aaron M.
Appel
 c,
Christina
Hoffmann
c,
Christina
Hoffmann
 d,
Xiaoping
Wang
d,
Xiaoping
Wang
 d,
Victor G.
Young
Jr.
a and
Connie C.
Lu
d,
Victor G.
Young
Jr.
a and
Connie C.
Lu
 *a
*a
aDepartment of Chemistry, University of Minnesota-Twin Cities, 207 Pleasant Street SE, Minneapolis, Minnesota 55455, USA. E-mail: clu@umn.edu
bSupercomputing Institute, Chemical Theory Center, University of Minnesota-Twin Cities, 207 Pleasant Street SE, Minneapolis, Minnesota 55455, USA
cCatalysis Science Group, Pacific Northwest National Laboratory, P. O. Box 999, MS K2-57, Richland, Washington 99352, USA
dNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
eKey Laboratory of Cluster Science of Ministry of Education, School of Chemistry and Chemical Engineering, Beijing Institute of Technology, Beijing 100081, China
fDepartment of Chemistry, University of Tennessee, Knoxville, Tennessee 37996, USA
First published on 10th June 2019
Abstract
Understanding H2 binding and activation is important in the context of designing transition metal catalysts for many processes, including hydrogenation and the interconversion of H2 with protons and electrons. This work reports the first thermodynamic and kinetic H2 binding studies for an isostructural series of first-row metal complexes: NiML, where M = Al (1), Ga (2), and In (3), and L = [N(o-(NCH2PiPr2)C6H4)3]3−. Thermodynamic free energies (ΔG°) and free energies of activation (ΔG‡) for binding equilibria were obtained via variable-temperature 31P NMR studies and lineshape analysis. The supporting metal exerts a large influence on the thermodynamic favorability of both H2 and N2 binding to Ni, with ΔG° values for H2 binding found to span nearly the entire range of previous reports. The non-classical H2 adduct, (η2-H2)NiInL (3-H2), was structurally characterized by single-crystal neutron diffraction—the first such study for a Ni(η2-H2) complex or any d10 M(η2-H2) complex. UV-Vis studies and TD-DFT calculations identified specific electronic structure perturbations of the supporting metal which poise NiML complexes for small-molecule binding. ETS-NOCV calculations indicate that H2 binding primarily occurs via H–H σ-donation to the Ni 4pz-based LUMO, which is proposed to become energetically accessible as the Ni(0)→M(III) dative interaction increases for the larger M(III) ions. Linear free-energy relationships are discussed, with the activation barrier for H2 binding (ΔG‡) found to decrease proportionally for more thermodynamically favorable equilibria. The ΔG° values for H2 and N2 binding to NiML complexes were also found to be more exergonic for the larger M(III) ions.
Introduction
Developing homogeneous base metal catalysts which can activate H2 and selectively mediate catalytic hydrogenation, H2 oxidation, and proton reduction have been active areas of research in recent years.1–5 In such processes, the strength of H2 binding, the interplay between σ-donation (H2 σ → M) and π-back-donation (M → H2 σ*), the resulting extent of H–H activation, and the ease of generating reactive M–H species all can play a critical role in determining catalytic activity and selectivity. H2 activation is typically initiated by side-on binding of H2 to form a M(η2-H2) adduct, which precedes the generation of reactive M–H species via subsequent oxidative addition or deprotonation events.6–8 Despite the ubiquity of H2 binding as a key fundamental reaction step in catalysis,9 limited experimental data has been reported regarding the thermodynamic and kinetic favorability of H2 binding to transition metals, especially for the first-row transition metals.6–8 To the best of our knowledge, thermodynamic H2-binding data have only been reported for a handful of first-row metal complexes: Cr(PCy3)2(CO)3,10,11 [Mn(CO)(dppe)2]+,12 [Fe(P4N2)]+,13 and Co(TPB),14 where dppe is bis(diphenylphosphino)ethane, P4N2 is a tetraphosphine with two pendant amines, and TPB is tris(o-diisopropylphosphinophenyl)borane. Moreover, without a series of similar M(η2-H2) adducts with which to compare thermodynamic data, the understanding gained by quantifying H2 binding to a single metal complex are relatively limited.Recently, the double-decker ligand, [N(o-(NCH2PiPr2)C6H4)3]3− (abbreviated as L), was used to prepare bimetallic (η2-H2)MAMBL complexes in which group 13 Lewis acidic supporting metal ions (MB) induce H2 binding at Ni(0) and Co(−I) metal centers (MA).15,16 Figueroa and Gabbaï have independently shown that appending a Lewis acidic σ-acceptor to a d10 transition metal induces binding of a Lewis base donor trans to the σ-acceptor.17–19 We and others have used a tethered σ-acceptor to promote activity at the transition metal for catalytic CO2 functionalization.20–22 Here, we report the first thermodynamic and kinetic studies of H2 binding to a Ni center in an isostructural series, where MB = Al, Ga, and In. In the case of the In(III) supporting ion, strong H2 binding allowed for structural elucidation via single-crystal neutron diffraction. Significant modulation of the thermodynamic favorability of both H2 and N2 binding to Ni was enabled by introducing and varying the group 13 supporting metal ion, with H2 binding free energies (ΔG°) found to span nearly the entire range of previously reported values. The (η2-H2)NiML complexes also exhibit different extents of H–H activation and kinetic rates of H2 binding and loss. Through a combination of experimental and theoretical studies on binding and electronic structure, we present a comprehensive understanding of how a supporting group 13 metal ion poises a proximal transition metal for small-molecule binding and influences both the thermodynamics and kinetics of binding equilibria.
Results & discussion
Part I. Neutron diffraction study of (η2-H2)NiInL and NMR characterization of (η2-H2)NiAlL
We have previously reported a series of bimetallic NiML complexes featuring Ni(0)→M(III) dative bonds (M = Al (1), Ga (2), and In (3)), where larger group 13 ions, Ga and In, promote H2 binding to formally d10 Ni centers.16 The resulting non-classical H2 adducts, (η2-H2)NiGaL (2-H2) and (η2-H2)NiInL (3-H2), were characterized by 1H NMR spectroscopy techniques. In addition, the remarkable stability of 3-H2 allowed for its molecular structure to be determined by single-crystal X-ray diffraction at 123 K.16 We currently report a single-crystal neutron diffraction study of 3-H2 at 100 K (Fig. 1) and the corresponding X-ray structure at 100 K. To our knowledge, 3-H2 is the first H2 adduct of Ni, or of any d10 metal, to be structurally characterized by neutron diffraction. To date, only two other Ni(0) H2-adducts have been reported, [O(SiH(o-iPr2PC6H4)2)2]Ni2(η2-H2)2 and [PhB(o-iPr2PC6H4)2]Ni(η2-H2), both of which were characterized in situ at low T.23,24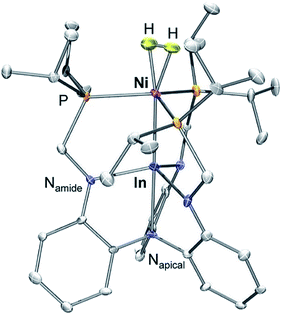 | ||
| Fig. 1 Neutron structure of 3-H2. Ellipsoids are shown at the 50% probability level, and H atoms (with the exception of H2) have been omitted for clarity. | ||
Table 1 displays selected structural parameters for 3-H2. Of note, the bond distances for non-hydrogen atoms in the X-ray and neutron structures of 3-H2 are essentially identical within experimental error (Table S4†). The Ni–H distances between the two structures are also within error, though the H–H bond length differs by 0.12 Å. The neutron structure, which is more reliable for placement of H atoms, validates an intact H2 molecule that is bound in side-on fashion to the Ni center. Upon H2 coordination, the Ni–In bond distance increases slightly from 2.457(1) Å in 3 to 2.4789(2) Å in 3-H2. The H–H bond length of 0.80(2) Å is slightly elongated relative to that in free H2 (0.74 Å), but shorter than the solution-state distance of 0.91 Å that was determined based on the JHD coupling constant of 3-HD.16 This discrepancy can be attributed to rapid librational motion of H2 in 3-H2, a phenomenon which typically leads to an average contraction of ∼0.07 Å in the apparent solid-state H–H bond distance relative to the solution-state distance determined by NMR studies.7,25–27 Consistent with this attribution, fast H2 rotation in solution relative to molecular tumbling is also supported by the previously reported T1 (min) value for the coordinated H2 ligand of 3-H2.16
| 3-H2 (neutron) | 3-H2 (X-ray) | |
|---|---|---|
| a Values in Å (estimated standard deviations in parentheses). See Table 6 for crystallographic details. See Table S4 for a detailed comparison of the X-ray and neutron structures. | ||
| H–H | 0.80(2) | 0.92(3) |
| Ni–H | 1.61(2) | 1.58(2) |
| 1.61(2) | 1.65(2) | |
| Ni–In | 2.39(2) | 2.4789(2) |
| Ni–P (avg.) | 2.26(1) | 2.2618(4) |
| In–Namide (avg.) | 2.13(1) | 2.115(1) |
| In–Napical | 2.40(2) | 2.366(1) |
| Ni to P3-plane | 0.31 | 0.29 |
| In to N3-plane | 0.52 | 0.50 |
Notably, the Ni–H bond distance is a parameter that neutron diffraction is uniquely able to experimentally evaluate. The two equivalent Ni–H bond lengths of 1.61(2) Å fall on the longer end of the wide range of the Ni–H distances reported for terminal Ni hydrides (cf. 1.32 to 1.65 Å).28 Although direct comparisons are sparse due to the rarity of structurally characterized M(η2-H2) complexes, the M–H and H–H distances in 3-H2 are both similar to those for (η2-H2)Co(TPB), which has M–H and H–H distances of 1.66/1.67 Å and 0.83(2) Å, respectively.29 Short contact distances between the H2 unit and the hydrogen atoms of the ligand isopropyl phosphine groups were observed in both 3-H2 and (η2-H2)Co(TPB), the closest of which were 2.24 Å and 2.10 Å, respectively. These distances are, within error, close to the intermolecular H⋯H van der Waals distance (2.2 Å).30
Previously, no reaction was observed between NiAlL (1) and H2 (1 atm) at room temperature. Subsequent studies have found that either high H2 pressure or low T is needed to observe H2 binding to 1. At 34 atm H2 and 232 K, a new species was observed by 1H NMR spectroscopy that is assigned as (η2-H2)NiAlL (1-H2) based on a diagnostic resonance for bound H2 at −1.5 ppm (Fig. S8 and S9†) and a short T1 (min) value of ≤49(5) ms (500 MHz, THF-d8; Fig. S10†).31,32 The 1H NMR spectrum of the HD isotopomer, (η2-HD)NiAlL (1-HD), which was formed at 213 K under 3.8 atm HD, displayed a characteristic 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 triplet for the bound HD ligand, with JHD = 34.4 Hz (Fig. S11†).
1 triplet for the bound HD ligand, with JHD = 34.4 Hz (Fig. S11†).
With the addition of 1-H2 to complete the isostructural trio of Ni(η2-H2) complexes, it is apparent that H2 activation increases as the supporting metal is varied down group 13 from Al to Ga to In, as reflected by the decreasing JHD values (in Hz): 34.4 for 1-HD > 33.2 for 2-HD > 31.7 for 3-HD (at 213 K; Fig. S11†). Thus, the corresponding estimated solution-state H–H bond distances increase as the supporting metal is varied down group 13, from 0.86 Å for 1-H2, to 0.88 Å for 2-H2, to 0.91 Å for 3-H2.33 The relative extents of H–H bond activation for the (η2-H2)NiML complexes are also in accord with those predicted by DFT calculations (Tables S13, S19 and S20†). That 1-H2 would have the shortest H–H distance of the trio, and the closest to that of free H2, is suggestive of the weak and labile nature of H2 binding to 1 relative to H2 binding to 2 and 3.6,7 We further note that the isostructural mononuclear Ni complex, NiLH3 (4),34 does not bind H2 even under forcing conditions (193 K, 34 atm H2),20 which suggests that the supporting metal plays a pivotal role in inducing H2 binding and controlling the extent of H2 activation. Lastly, both 2-H2 and 3-H2 exhibit a greater extent of H2 activation compared to the two other Ni(0) H2-adducts: [O(SiH(o-iPr2PC6H4)2)2]Ni2(η2-H2)2 (JHD = 34.2 Hz) and [PhB(o-iPr2PC6H4)2]Ni(η2-H2) (JHD = 36.5 Hz).23,24
Part II. H2 and N2 binding energies for the NiML triad
Intrigued by the varied propensities for binding and activating H2 enabled by changing a single atom, we set out to understand how the group 13 supporting metal influences the thermodynamics and kinetics of Ni–H2 binding equilibria. Previously, (η2-H2)NiGaL (2-H2) was generated in situ under 1 atm H2, but reverted to 2 upon exposure to vacuum or Ar.16 Because of its reversible H2 binding at ambient conditions, 2 was an ideal candidate for initiating binding equilibrium studies. Variable-temperature (VT) 31P NMR spectra of 2 in toluene-d8 under 6.8 atm H2 displayed a single resonance, which shifted downfield from 42.7 to 56.4 ppm as the temperature was decreased from 368 K to 221 K (Fig. 2a). As a control experiment, the VT NMR profile of 2 under Ar showed a minimal change in the 31P shift (Δδ < 0.5 ppm) over a similar T range (Fig. S12 and S13†). Hence, the VT NMR behavior of 2 under an H2 atmosphere is consistent with an equilibrium between 2 and 2-H2 that is governed by fast chemical exchange relative to the 31P NMR timescale (202.4 MHz), where the latter is favored at low T and both species are three-fold symmetric in solution.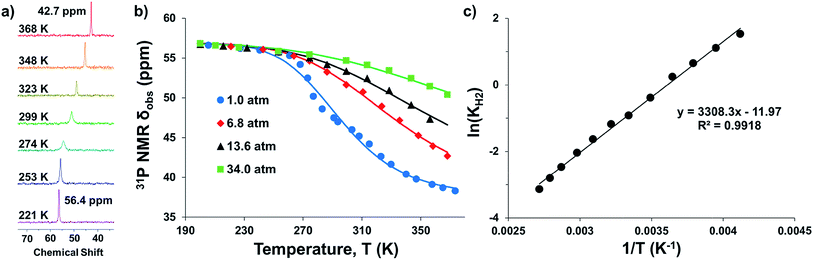 | ||
| Fig. 2 (a) VT 31P NMR spectra of 2 under 6.8 atm H2 in toluene-d8 from 368 to 221 K. (b) Plots of 31P δ vs. T obtained for various H2 pressures. Data are shown as points, and solid traces represent the best–fit curves obtained by varying ΔH° and ΔS° as parameters (see ESI†). (c) Representative van't Hoff plot of ln(KH2) vs. 1/T at 6.8 atm H2. The thermodynamic binding parameters shown in Table 2 were determined from van't Hoff plots for data sets collected at 6.8 and 13.6 atm H2, which exhibit fast chemical exchange. | ||
Analogous VT 31P NMR experiments were also performed for 2 under various H2 pressures of 1.0, 13.6, and 34 atm (Fig. S1, S14 and S15†). Of note, for all H2 pressures examined, the same low T convergence of the 31P resonance to ∼56.9 ppm was observed at 193 K, which corresponds to the 31P chemical shift of 2-H2 (Fig. 2b). At high T, the observed 31P chemical shift approaches that of 2, with closer convergence observed at lower H2 pressures. These observations are consistent with rapid interconversion between 2 and 2-H2, such that the observed chemical shift (31P δ) is the population-weighted average of the chemical shifts of these exchanging species.35 Thus, the observed 31P δ can be converted into the equilibrium concentration ratio of 2 and 2-H2 (see ESI†). The equilibrium constant for H2 binding, KH2, was determined according to eqn (1), where PH2 is the H2 pressure:
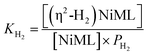 | (1) |
Next, the thermodynamic parameters for H2 binding, ΔH°, ΔS°, and ΔG°, were determined using two complementary methods: (1) non-linear fitting of the 31P δ vs. T plot in Fig. 2b; and (2) linear regression of the van't Hoff plot of ln(KH2) vs. 1/T, as shown in Fig. 2c. The analyses were performed using the 6.8 and 13.6 atm datasets, where chemical exchange was rigorously fast relative to the 31P NMR timescale and the variability of 31P δ with T was significant enough to reflect the sampling of an adequate portion of the binding equilibrium. The van't Hoff plot gives ΔH° = −6.3(2) kcal mol−1, ΔS° = −23.0(7) cal (mol K)−1, and ΔG° = +0.6(3) kcal mol−1 for H2 binding to 2, where the standard state conditions are defined as 298 K, 1 atm H2, and 1 M concentrations of all other species in toluene-d8. Non-linear fitting of the 31P δ vs. T plot yields the same thermodynamic values within experimental error (Fig. S16, S17 and Table S2†).
The H2 binding equilibria for the other NiML complexes, 1 (M = Al) and 3 (M = In), were also investigated by VT 31P NMR spectroscopy. For H2 binding to 1, the VT 31P NMR spectra in toluene-d8 (363 to 210 K, 34 atm H2) show a single 31P resonance shifting downfield relative to that of 1 (30.7 ppm) with decreasing T, and ultimately converging to a chemical shift of ∼44.3 ppm for 1-H2 (Fig. S18†). The corresponding van't Hoff analysis for H2 binding to 1 gives ΔH° = −6.3(1) kcal mol−1, ΔS° = −26.4(4) cal (mol K)−1, and ΔG° = +1.6(2) kcal mol−1 (Fig. S19†). Since 3 binds H2 strongly, sub-ambient H2 pressure was necessary to establish a measurable equilibrium between 3 and 3-H2 (Fig. S20–S22†). Under 1 atm of 10% H2 in Ar, where PH2 = 0.1 atm, a single 31P peak was observed from 299 to 357 K (Fig. S20†). However, the lineshapes of the observed 31P peaks are noticeably broadened, which indicates that chemical exchange between 3 and 3-H2 falls into the fast-intermediate regime relative to the 31P NMR timescale.36 This is problematic because non-Lorentzian lineshapes and exchange broadening may diminish the reliability of the thermodynamic parameters determined under fast-intermediate exchange conditions.37 Hence, we caution that the thermodynamic values for H2 binding to 3, ΔH° = −14.8(6) kcal mol−1, ΔS° = −37(2) cal mol−1 K−1, and ΔG° = −3.7(7) kcal mol−1 (Fig. S23† and Table 2), should be treated as estimates.
| 1 | 2 | 3 | |
|---|---|---|---|
| a Standard deviations obtained from van't Hoff linear regression analyses are given in parentheses. Standard state is defined as 298 K, 1 atm H2 (or N2), and 1 M of all other species in toluene-d8. b H2 binding studies have also been conducted for 2 in THF (Fig. S27–S29): ΔG° = +0.1(1) kcal mol−1, ΔH° = −7.5(1) kcal mol−1, and ΔS° = −25.4(1) cal mol−1 K−1. c Units of kcal mol−1, see Computational methods in Experimental section for details. d Estimated values extracted from fast-intermediate exchange regime data (Fig. S20–S23). e Corrected ΔG° value of −3.0(7) kcal mol−1 is likely a better estimate. See text for explanation of the +0.7 kcal mol−1 correction term. | |||
| ΔH° (kcal mol−1) | −6.3(1) | −6.3(2) | −14.8(6)d |
| ΔS° (cal mol−1 K−1) | −26.4(4) | −23.0(7) | −37(2)d |
| ΔG° (kcal mol−1) | 1.6(2) | 0.6(3) | −3.7(7)d |
| −3.0(7)e | |||
| ΔG° (DFT)c | 2.8 | 0.9 | −1.9 |
To assess the reliability of this estimated ΔG° value, a control experiment was performed on 2 under identical conditions with 0.1 atm H2, which showed similarly broad 31P peaks due to fast-intermediate chemical exchange (Fig. S24 and S25†). Comparing the binding parameters obtained for 2 under 0.1 atm H2 to those obtained under rigorously fast exchange conditions (6.8 and 13.6 atm H2), we find that the thermodynamic favorability of H2 binding was overestimated by 0.7 kcal mol−1 using the 0.1 atm H2 dataset. Thus, by applying this 0.7 kcal mol−1 empirical correction, we propose that a better ΔG° estimate for H2 binding to 3 is −3.0(7) kcal mol−1. In support, lineshape simulations of VT 31P NMR spectra of 3 under 1 atm H2 independently gives ΔG° = −2.3(2) kcal mol−1, which is within experimental error of the corrected value of −3.0(7) kcal mol−1 (Fig. S26†).
Next, we sought to investigate the related equilibria of N2 binding to the NiML complexes using VT 31P NMR experiments. The equilibrium between 2 and 2-N2 was monitored at 1 atm N2 and low T (226 to 193 K). Distinct 31P resonances were observed for both 2 and 2-N2 (Fig. S30†), which is characteristic of slow chemical exchange relative to the 31P NMR timescale (161.9 MHz). Quantitative integration of the 31P NMR peaks for 2 and 2-N2 allowed for a straightforward determination of KN2 using eqn (2), where PN2 is the N2 pressure:
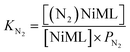 | (2) |
Conversely, the interconversion of 3 and 3-N2 is fast relative to the 31P NMR timescale (161.9 MHz) at 1 atm N2 and T > 288 K (Fig. S6 and S31†). As such, the observed chemical shift of the single 31P NMR resonance represents the population-weighted average of the chemical shifts of 3 and 3-N2, and the VT NMR data were analyzed as previously described for H2 binding to 2 (Fig. S31 and S32†). Lastly, the observed equilibrium between 1 and 1-N2 at 51 atm N2 switches from slow exchange at low T (≤210 K) to fast exchange at higher T (≥243 K) (Fig. S33†). Thus, KN2 was evaluated based on the distinct 31P NMR peak integrations for 1 and 1-N2 at low T, and based on the observed 31P chemical shift at high T. The thermodynamic binding parameters for the H2 and N2 binding equilibria of the NiML complexes are compiled in Tables 2 and 3. Additionally, DFT calculations using the M06-L38/bs1 method correctly predict the experimental trends in both the H2 and N2 binding free energies for the trio of NiML complexes (Tables 2 and 3).
Across the NiML series, ΔG° for both H2 and N2 binding was modulated by ∼5 kcal mol−1, with increasing thermodynamic favorability for both H2 and N2 binding observed as the supporting metal was varied down group 13 (Tables 2 and 3). Notably, ΔG° values for H2 binding to the NiML complexes nearly span the entire range of previously reported values (from −2 to +3 kcal mol; Tables S6 and S7†). This is remarkable considering that the full range of literature ΔG° values encompasses H2 binding to various transition metals (e.g. Cr, Mo, W, Re, Fe, Ru, Co, and Ir) in diverse ligand environments.10,11,13,14,39–45 In contrast, the NiML trio features an isostructural Ni site within the same ligand framework, where the primary difference is the identity of the group 13 metal. We hypothesize that the strength of the Ni(0)→M(III) dative interaction directly tunes the binding at Ni in the position trans to M(III), where greater Ni(0)→M(III) interactions lead to stronger small-molecule binding. This hypothesis is generally consistent with other literature examples wherein the interaction of a σ-acceptor with a d10 transition metal enhances donor-binding at the trans position.17–19 DFT calculations predict that supporting Ni with In(III) in 3 increases the favorability of H2 binding by ∼8 kcal mol−1 relative to NiLH3 (4), which are the two limiting extremes in this series (Table S16†).
To the best of our knowledge, (η2-H2)Co(TPB) and [(η2-H2)Re(CNtBu)3(PCy3)2]+ were previously reported to have the most favorable H2 binding free energies, with 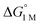 = −4.8(9) and −4.8(1.3) kcal mol−1, respectively (Table S7†).14,39 Notably, 3 binds H2 even more favorably, with
= −4.8(9) and −4.8(1.3) kcal mol−1, respectively (Table S7†).14,39 Notably, 3 binds H2 even more favorably, with 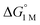 ∼ −6.5(7) kcal mol−1, which was obtained by converting ΔG° at PH2 = 1 atm to ΔG° for [H2] = 1 M. In addition, the determination of both H2 and N2 binding energies for first-row transition metal complexes is rare.10,11,13,14,46 Across the NiML series, the binding free energies for H2 are more favorable than those for N2 by 1.9(4), 1.5(5), and ∼1.8(8) kcal mol−1 for 1, 2, and 3, respectively (Tables 2 and 3). A similar trend was reported for [Fe(P4N2)]+ and Cr(CO)3(PCy3)2, whereas
∼ −6.5(7) kcal mol−1, which was obtained by converting ΔG° at PH2 = 1 atm to ΔG° for [H2] = 1 M. In addition, the determination of both H2 and N2 binding energies for first-row transition metal complexes is rare.10,11,13,14,46 Across the NiML series, the binding free energies for H2 are more favorable than those for N2 by 1.9(4), 1.5(5), and ∼1.8(8) kcal mol−1 for 1, 2, and 3, respectively (Tables 2 and 3). A similar trend was reported for [Fe(P4N2)]+ and Cr(CO)3(PCy3)2, whereas 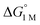 energies for H2 and N2 binding to Co(TPB) are identical within error (Tables S6–S9†). The finding that N2 binding is more competitive with H2 binding for Co(TPB) than it is for NiML complexes is consistent with the greater π-basicity of low-valent Co toward N2.47,48
energies for H2 and N2 binding to Co(TPB) are identical within error (Tables S6–S9†). The finding that N2 binding is more competitive with H2 binding for Co(TPB) than it is for NiML complexes is consistent with the greater π-basicity of low-valent Co toward N2.47,48
In further examining the ΔH° and ΔS° contributions for binding to NiML (1–3), the large negative ΔS° values for H2 and N2 binding reflect the entropic cost of binding a gas molecule (Tables 2 and 3). In general, a greater entropic cost was observed for N2 binding than for H2 binding; this trend can be explained in part by the larger absolute entropy of N2 relative to H2.11 It is also striking that both H2 and N2 binding to 3 are considerably more exothermic (ΔΔH° ≈ −9 kcal mol−1) and entropically costly (ΔΔS° ≈ −13 and −20 cal mol−1 K−1, respectively) compared with binding to 1 and 2 (Tables 2 and 3). The fact that binding to 3 has the most favorable enthalpic and most unfavorable entropic terms is consistent with tighter and more rigid binding of both H2 and N2. Intriguingly, because 1 and 2 have identical ΔH° values for both H2 and N2 binding, the differences in their observed binding propensities originate from the differences in ΔS° values.
Part III. Kinetics of self-exchange for NiML and (η2-H2)NiML complexes
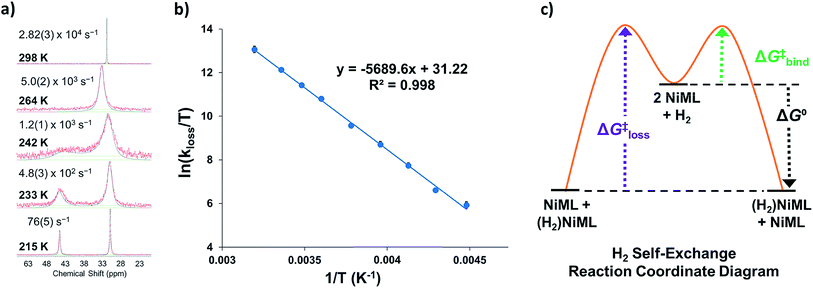
To understand the dependence of the kinetics of the H2 binding process on the supporting metal, VT 31P NMR lineshape simulations of NiML under 1 atm H2 were performed to extract self-exchange rates for the interconversion between NiML and (η2-H2)NiML. Exchange rates were determined via least-squares fitting of the VT 31P NMR spectra using a two-site, non-mutual exchange model (see Experimental section and ESI† for details).49,50 Good agreement was generally achieved between the experimental and simulated spectra, as illustrated in Fig. 3a for the VT 31P NMR study of 1 under 1 atm H2. Similar lineshape analyses were performed for each NiML complex, which allowed exchange rates to be determined at seven or more different temperatures between 213 K and 344 K (Fig. S42–S44†). Notably, the exchange rate decreases by a factor of ∼6 at 298 K upon varying the supporting metal from Al to In (Table 4). Exchange rates at 298 K were found to correlate strongly with both H2 binding free energies (R2 = 0.996, Fig. S47†) and H–H bond distances in (η2-H2)NiML complexes (R2 = 0.958, Fig. S48†), with slower kinetic rates of H2 exchange for more thermodynamically favorable binding equilibria where H2 is more activated. The H2 binding equilibrium for complex 1 is especially dynamic, with interconversion between 1 and 1-H2 occurring over 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times per second at 298 K and 1 atm H2 (Fig. 3a and Table 4).
000 times per second at 298 K and 1 atm H2 (Fig. 3a and Table 4).
| Complex | 1 | 2 | 3 | |
|---|---|---|---|---|
a All values determined for a standard state of 1 M H2, 1 M for all other species in toluene-d8, and 298 K. 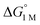 , ΔG‡, and ΔH‡ values are in units of kcal mol−1, and ΔS‡ values are in units of cal (mol K)−1. Rateex and kloss are in s−1, and raterel is the relative rate.
b [Ni]total = 7.5 mM.
c ΔG‡loss ≈ ΔG‡exchange for unimolecular H2 loss.
d , ΔG‡, and ΔH‡ values are in units of kcal mol−1, and ΔS‡ values are in units of cal (mol K)−1. Rateex and kloss are in s−1, and raterel is the relative rate.
b [Ni]total = 7.5 mM.
c ΔG‡loss ≈ ΔG‡exchange for unimolecular H2 loss.
d
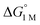 are directly derived from values in Table 2 by converting the standard state for H2 from 1 atm H2 to 1 M. See ESI for details. are directly derived from values in Table 2 by converting the standard state for H2 from 1 atm H2 to 1 M. See ESI for details.
|
||||
| Self-exchangeb | Rateex (×104) | 2.82(3) | 2.2(2) | 0.437(5) |
| Raterel | 6.4 | 4.9 | 1.0 | |
| H2 lossc | k loss (×106) | 55(3) | 6.5(5) | 0.60(3) |
| ΔH‡loss | 11.3(2) | 10.1(4) | 9.3(4) | |
| ΔS‡loss | 7.5(1) | 3.5(1) | −0.3(1) | |
| ΔG‡loss | 9.1(2) | 9.1(4) | 9.4(4) | |
| H2 binding |
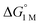
|
−1.9(2) | −2.9(2) | −6.5(7) |
| ΔG‡bind | 7.2(3) | 6.2(5) | 2.9(8) | |
We propose a self-exchange mechanism comprised of H2 loss from (η2-H2)NiML to generate NiML and free H2, and H2 binding to another NiML complex to form (η2-H2)NiML (Fig. 3c). The rate constants for H2 loss from (η2-H2)NiML, kloss, were determined at each T based on the exchange rates and the known equilibrium concentrations of (η2-H2)NiML (see ESI†). Eyring analyses for kloss allowed for the determination of activation barriers for H2 loss from (η2-H2)NiML complexes, as shown in Fig. 3b for 1-H2. Eyring plots for H2 loss from 2-H2 and 3-H2 are shown in Fig. S49 and S50,† respectively. The free energy barriers for H2 loss (ΔG‡loss) were found to be similar for all complexes (9.1 to 9.4 kcal mol−1), with ΔH‡ and ΔS‡ values ranging from 9.3 to 11.3 kcal mol−1 and from −0.3 to +7.5 cal (mol K)−1, respectively (Table 4). The fact that ΔS‡loss values are positive or close to zero in all cases is consistent with the expected gain in H2 freedom of motion, while positive ΔH‡loss values suggest that partial Ni–H2 bond breaking is the dominant process involved in reaching the transition state for H2 loss. Interestingly, both ΔH‡loss and ΔS‡loss values for the (η2-H2)NiML complexes decrease as the supporting metal is varied down group 13 (Al > Ga > In; Table 4).
Furthermore, ΔS‡loss values (∼0 or >0) are consistent with unimolecular H2 loss from (η2-H2)NiML, as opposed to H2 self-exchange via an intermolecular LMNi⋯H2⋯NiML transition state. Such a transition state also seems unlikely because of the steric clash between the diisopropyl ligand groups surrounding each Ni site. Using the proposed reaction coordinate diagram, one can further extract the free energy barrier for H2 binding (ΔG‡bind) by using the thermodynamic relationship: ΔG‡loss = ΔG‡bind − 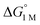 . Of note,
. Of note, 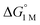 is the free energy of H2 binding after converting the H2 standard state from 1 atm (as given in Table 2) to 1 M. Hence, the ΔG‡bind values for 1, 2, and 3 are 7.2(3), 6.2(5), and ∼2.9(8) kcal mol−1, respectively, where the activation barriers for H2 binding are lower for more thermodynamically favorable binding equilibria (Table 4).
is the free energy of H2 binding after converting the H2 standard state from 1 atm (as given in Table 2) to 1 M. Hence, the ΔG‡bind values for 1, 2, and 3 are 7.2(3), 6.2(5), and ∼2.9(8) kcal mol−1, respectively, where the activation barriers for H2 binding are lower for more thermodynamically favorable binding equilibria (Table 4).
Activation barriers and rate constants for H2 binding and loss have seldom been reported despite their relevance for many catalytic processes. ΔH‡loss values for (η2-H2)NiML (9.3 to 11.3 kcal mol−1) are comparable to those reported (in kcal mol−1) for [Ru(η2-H2)H3(PPh3)3]+ (8.8),31 Cr(η2-H2)(CO)3(PCy3)2 (12.1),10 Ir(η2-H2)(H)2X(PtBu2Me)2 (9.4 to 11.3 for X = Cl, Br, I),40 and Ir(η2-H2)(H)2X(PiPr3)2 (10.1 to 11.4 for X = Cl, Br, I),51 and are significantly lower than those reported for W(η2-H2)(CO)3(PCy3)2 (16.9)44 and Ru(η2-H2)(H)2(PPh3)3 (17.9).31 Perhaps the most thoroughly studied H2 binding equilibrium is that of W(η2-H2)(CO)3(PCy3)2, for which rate constants for both H2 binding (kbind) and loss (kloss) have been directly measured to be ∼2 × 106 M−1 s−1 and 469 s−1 at 298 K, respectively.44,52 In comparison, the kloss values for (η2-H2)NiML complexes are 3 to 5 orders of magnitude greater than that for W(η2-H2)(CO)3(PCy3)2 (Table 4). This can be rationalized by the fact that H2 is much more activated in W(η2-H2)(CO)3(PCy3)2, which co-exists with its dihydride species at 298 K (K ∼0.25).7,44,45 In contrast, HNi(μ-H)ML dihydride species, which have some precedent in the literature,24,53,54 have not been observed.16,55 DFT calculations predict such a species to be unstable relative to (η2-H2)NiML by 12 to 19 kcal mol−1 under 1 atm H2 (Table S25, S26 and Fig. S55†).
Part IV. Insights from quantum chemical calculations and UV-Vis spectra
Complexes 1–3 and NiLH3 (4), as well as their H2 and N2 adducts, were investigated by density functional theory (DFT) calculations using several different functionals and basis sets (see Experimental section and Table S3†). The M06-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56,57/bs4 method gave the best agreement between the optimized and experimental geometries for the three Ni–In complexes: 3, 3-N2, and 3-H2 (Tables S13–S15†).16 On the other hand, the relative free energies (ΔG°) for H2 and N2 binding to 1–3 were best matched by M06-L38/bs1 (Tables S16 and S17†), which correctly predicted the trends of stronger H2 binding than N2 and increasing binding favorability for M = In > Ga > Al (Tables 2 and 3).
56,57/bs4 method gave the best agreement between the optimized and experimental geometries for the three Ni–In complexes: 3, 3-N2, and 3-H2 (Tables S13–S15†).16 On the other hand, the relative free energies (ΔG°) for H2 and N2 binding to 1–3 were best matched by M06-L38/bs1 (Tables S16 and S17†), which correctly predicted the trends of stronger H2 binding than N2 and increasing binding favorability for M = In > Ga > Al (Tables 2 and 3).
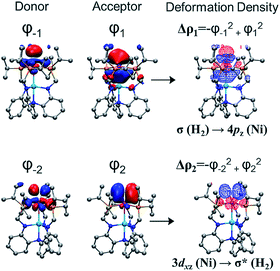
To better understand chemical bonding between H2 and Ni in the (η2-H2)NiML complexes, we conducted energy decomposition analysis (EDA).58 EDA allows for the total interaction energy (ΔEint) between the H2 and NiML fragments to be partitioned into the following terms: electrostatic energy (ΔEelstat), Pauli repulsive interaction (ΔEPauli), dispersion (ΔEdisp), and covalent interaction (ΔEorb).58 The ΔEorb term can be further divided into individual energy contributions associated with specific orbital interactions, and thereby allows for differentiation of σ, π, and δ bonding interactions. The extended transition-state method coupled with natural orbitals for chemical valence theory (ETS-NOCV59) was then utilized to analyze the bonding interactions between Ni and H2. Fig. 4 illustrates the two most important NOCV pairs for the Ni–H2 interaction in 3-H2, in which chemical bonding is indicated by deformation in the electron densities (Δρ). Overall, two orbital interactions are important: (1) σ-donation from the H2 σ-bond to the empty Ni 4pz orbital, which accounts for 56% of ΔEorb and is comprised of Δρ1 (38%; Fig. 4) and Δρ3 (18%; Fig. S53†); and (2) π-back-donation from a Ni 3dπ orbital to the empty H2 σ* orbital, which accounts for 35% of ΔEorb. Similarly, greater contributions of σ-donation (57–59% of ΔEorb) compared to π-back-donation (34–35% of ΔEorb) were also observed for Ni–H2 orbital interactions in 1-H2 and 2-H2 (Table S22†).
The total interaction energy (ΔEint) between the H2 and Ni fragments becomes increasingly favorable in the order, (η2-H2)NiLH3 < 1-H2 < 2-H2 < 3-H2 (Table S21†). Of interest, the less favorable ΔEint predicted for (η2-H2)NiLH3 arises from a large, unfavorable ΔEPauli term, which is the repulsive interaction energy between like spins in the H2 and NiLH3 fragments. This makes sense as NiLH3 lacks a Ni→M interaction that would result in attenuation of Ni electron density. Within the (η2-H2)NiML series, both the ΔEelstat and ΔEorb terms become more favorable as M is varied down the group 13 triad (Table S21†). Furthermore, the greater relative importance of σ-donation to H2 binding than π-back-donation is consistent with the trend that H2 binding favorability increases as the Ni center becomes more electron-deficient, as judged by the Ni(I/0) redox potentials (Fig. S71 and Table S39†).16 Hence, we propose that increased electron-withdrawal via Ni→M dative bonding as M is varied down group 13 induces stronger electrostatic and covalent interactions between H2 and NiML, with a concomitant decrease in unfavorable Pauli repulsion between the two fragments.
Given the rarity of H2 and N2 binding to a Ni(0) metal center, we next sought to understand the specific electronic perturbations of the supporting group 13 metal ion that poise NiML to bind small molecules. To lend insight, UV-Vis spectroscopy studies in conjunction with time-dependent density functional theory (TD-DFT) calculations were conducted to investigate the electronic structure of complexes 1–4 and their H2 and N2 adducts. The UV-Vis spectra of NiLH3 and 1–3 are shown in Fig. 5a (THF, 298 K), along with the corresponding TD-DFT predicted spectra, where M06-D3/bs4 showed the best agreement with experiment (Fig. 5b and Table S29†). We also sought to understand how the binding of H2 and N2 to the NiML complexes further impacts electronic structure. In this regard, it is notable that small-molecule binding to NiML often manifests in vibrant color changes. For example, exposure of a THF solution of 3 under Ar to an N2 or H2 atmosphere resulted in a color change from a deep red-purple color to a lighter red (3-N2) or yellow-brown (3-H2), respectively (Fig. 5c).
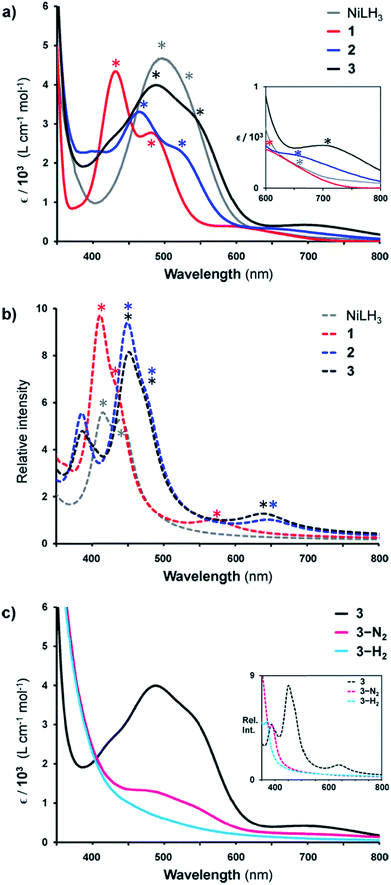 | ||
| Fig. 5 (a) UV-Vis spectra of NiLH3 (grey), 1 (red), 2 (blue), and 3 (black) obtained in THF at room temperature. Inset is a close-up of the 600–800 nm range. (b) TD-DFT predicted spectra of NiLH3 and 1–3 (M06-D3/bs4, SMD/THF) shown as dotted lines. (c) UV-Vis spectra of 3 (under Ar, black), 3-N2 (under 1 atm N2, pink), and 3-H2 (under 1 atm H2, cyan) in THF at 298 K, with TD-DFT plots shown in the inset. Note that small features corresponding to 3 can be seen in the UV-Vis spectrum of 3-N2 due to the equilibrium binding of N2 under these conditions. Asterisks in spectra correspond to bands I, II, or III, as listed in Table 5. | ||
The UV-Vis spectra of 1–3 share the same pattern of three peaks between 400 and 800 nm, which are marked with asterisks in Fig. 5a and listed in Table 5 as peaks I, II, and III. These peaks all red-shift upon varying the supporting metal from Al to Ga to In. The TD-DFT calculated transition energies for 1–3 agree reasonably well with experiment, with the predicted excitations generally blue-shifted by 0.04 to 0.3 eV for peaks I to III (Table 5). The TD-DFT results also correctly predicted the red-shift of all peaks for 2 relative to 1, but the subtle spectral differences between 2 and 3 were not discerned by TD-DFT despite testing several methods (Table S29, Fig. S57 and S58†). For NiLH3, a broad absorption feature is observed at ∼500 nm, which was fit with two overlapping peaks with maxima at 491 and 533 nm, along with a low-intensity shoulder at 663 nm (Table S27, Fig. S56†).
UV-Vis peaks I–III for NiLH3 and 1–3 were assigned based on the TD-DFT results (Table 5). Each peak corresponds to an electronic excitation from either a Ni 3d orbital or a ligand-based molecular orbital (MO) to the lowest unoccupied molecular orbital (LUMO), the latter of which is highly similar for all complexes. For NiLH3, the LUMO has both Ni 4pz and P 4p character, whereas the LUMO for complexes 1–3 also has additional contributions from Ni (3d, 4s) and M (s, pz) atomic orbitals (Fig. S59 and Table S31†). For all complexes, peaks I and II arise from electronic excitations to the LUMO from the Ni dxy/dx2−y2 and dxz/dyz orbitals, respectively. Peak III for NiLH3 is a transition from a pure dz2 orbital to the LUMO, while peak III for 1–3 is a more complex transition from a mixed ligand-based arene π* MO with partial Ni dz2 character to the LUMO (Table S28†).
Based on these transition assignments, semi-quantitative MO diagrams for NiLH3 and 1–3 can be constructed (Fig. 6). For NiLH3, the d-orbital manifold is consistent with that expected for a trigonal-planar metal center with three σ-donors: the degenerate dxy/dx2−y2 orbitals are the most destabilized, followed by dz2, and then the dxz/dyz set. For 1–3, the presence of the supporting group 13 metal ion results in the stabilization of the Ni 3dz2 orbital via Ni→M(pz/s) dative bonding, which is consistent with the blue shift in the predicted pure 3dz2 → LUMO transitions in the bimetallic NiML complexes (363 to 385 nm; Table S30†) relative to NiLH3 (443 nm). The Ni dxz/dyz orbitals, on the other hand, are destabilized upon the introduction of the supporting metal and its variation down group 13. Presumably, the π-back-bonding interaction, Ni dxz/dyz → P–C σ*, becomes weaker as the Ni center becomes more electron-deficient due to stronger electron withdrawal by the supporting metal (In > Ga > Al > no support).16 In support, both the Ni–P bonds elongate and the 31P NMR signal shifts downfield from NiLH3 to 1 to 2 to 3.
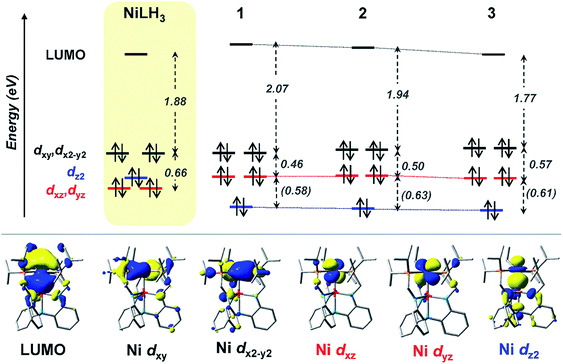 | ||
| Fig. 6 (Top) MO diagrams of NiLH3 and complexes 1–3. The ligand field energies (in eV) are based on UV-Vis data (Table 5). TD-DFT calculated energies are shown (in eV, italicized within parentheses) when experimental values were not obtainable. (Bottom) MOs for complex 2, which are representative of those for the series. Note that MO energies are drawn to scale, but energy comparisons across the complexes are qualitative. | ||
Another notable MO trend involves the energy difference between the Ni dxz/dyz orbitals and the LUMO, as reflected in the peak II energies, which decrease upon the introduction and variation of the supporting metal down group 13. This particular energy gap is important because the LUMO and the Ni dxz/dyz orbitals are the frontier Ni-based MOs that participate in small-molecule binding, with the Ni-based LUMO accepting σ-donation from either the H2 σ-bond or the N2 lone pair, and the Ni dxz/dyz orbitals participating in π-back-bonding to either the H2 σ* or N2 π* LUMOs. Overall, the Ni dxz/dyz → LUMO excitation energy decreases by ∼0.2 eV across the NiML complexes, from 2.53 eV in 1 to 2.44 eV in 2 to 2.34 eV in 3 (Table S28†). Thus, it is reasonable to propose that varying the supporting metal from Al to Ga to In results in the destabilization of the Ni dxz/dyz orbital set and the stabilization of the Ni-based LUMO, such that both become more energetically accessible to interact with small-molecule substrates.
The involvement of the LUMO in small-molecule binding is further supported by examining the changes in the UV-Vis spectra for 3 upon binding H2 and N2 (Fig. 5c). Notably, both the experimental and theoretical spectra of 3-H2 and 3-N2 lack any intense features between 400 and 700 nm. Instead, the lowest energy transitions for 3-H2 and 3-N2 are predicted at 375 and 391 nm, respectively. The shift to higher energy excitations for the H2 and N2 adducts can be qualitatively explained by the nature of their acceptor MOs, which we define as the lowest-energy unoccupied MO with significant Ni character, rather than those that are ligand based (Fig. S60–S63 and Tables S33–S38†). For both 3-H2 and 3-N2, the acceptor MO appears to be an anti-bonding combination of the LUMO in 3 and the donor MO of the small molecule (Fig. S64†). Thus, upon small-molecule binding via the dominant σ-donation interaction with the LUMO of NiML, the resulting acceptor orbitals in (L′)NiML adducts (L′ = H2, N2) to which electrons can be excited are of higher energy relative to the Ni 3d manifold, and thereby give rise to higher energy electronic transitions.
Part V. Linear free-energy relationships
We examined linear free-energy relationships across the NiML series to quantify the effect of the supporting group 13 metal on the thermodynamics and kinetics of small-molecule binding. For H2 binding, an excellent correlation was observed between the thermodynamic free energies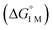 and the free energies of activation (ΔG‡bind), where more exergonic binding equilibria have smaller activation barriers (R2 = 0.999, Fig. 7a). The slope of +0.93 in the ΔG‡bindversus
and the free energies of activation (ΔG‡bind), where more exergonic binding equilibria have smaller activation barriers (R2 = 0.999, Fig. 7a). The slope of +0.93 in the ΔG‡bindversus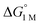 plot indicates that a decrease of ∼1 kcal mol−1 in
plot indicates that a decrease of ∼1 kcal mol−1 in 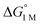 for H2 binding corresponds to a commensurate lowering of the free energy barrier. Reasonably strong correlations were also found between the Ni 3dxz/dyz → LUMO excitation energy and ΔG° for H2 (R2 = 0.924) and N2 (R2 = 0.963) binding (Fig. 7b). This correlation makes sense since the Ni 3dxz/dyz orbitals and the LUMO are the Ni-based frontier orbitals that participate in small-molecule binding (vide supra). The slopes of the plots of ΔG° for H2 and N2 binding versus the Ni 3dxz/dyz → LUMO excitation energy (in kcal mol−1) are close to unity, where a decrease of 1 kcal mol−1 in the Ni 3dxz/dyz → LUMO excitation energy is associated with a nearly equivalent increase in the favorability of H2/N2 binding.
for H2 binding corresponds to a commensurate lowering of the free energy barrier. Reasonably strong correlations were also found between the Ni 3dxz/dyz → LUMO excitation energy and ΔG° for H2 (R2 = 0.924) and N2 (R2 = 0.963) binding (Fig. 7b). This correlation makes sense since the Ni 3dxz/dyz orbitals and the LUMO are the Ni-based frontier orbitals that participate in small-molecule binding (vide supra). The slopes of the plots of ΔG° for H2 and N2 binding versus the Ni 3dxz/dyz → LUMO excitation energy (in kcal mol−1) are close to unity, where a decrease of 1 kcal mol−1 in the Ni 3dxz/dyz → LUMO excitation energy is associated with a nearly equivalent increase in the favorability of H2/N2 binding.
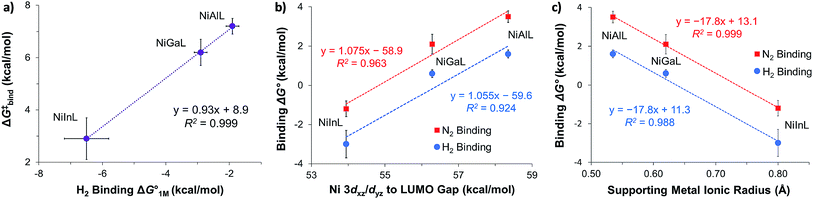 | ||
Fig. 7 (a) Plot of free energy barrier for H2 binding (ΔG‡bind) vs. thermodynamic free energy for H2 binding 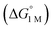 , with the standard deviation in all values shown by error bars and all standard states defined to be [H2] = 1 M in toluene-d8. (b–c) Plots of ΔG° for H2 (blue circles) and N2 binding (red squares) vs. Ni 3dxz/dyz to LUMO energy gap (b) and vs. supporting metal Shannon ionic radii (c). Ni 3dxz/dyz to LUMO energy gaps were measured experimentally by UV-Vis spectroscopy with transition assignments from TD-DFT calculations (see ESI† and Table 5). , with the standard deviation in all values shown by error bars and all standard states defined to be [H2] = 1 M in toluene-d8. (b–c) Plots of ΔG° for H2 (blue circles) and N2 binding (red squares) vs. Ni 3dxz/dyz to LUMO energy gap (b) and vs. supporting metal Shannon ionic radii (c). Ni 3dxz/dyz to LUMO energy gaps were measured experimentally by UV-Vis spectroscopy with transition assignments from TD-DFT calculations (see ESI† and Table 5). | ||
The isostructural nature of the (η2-H2)NiML series allows us to further interrogate which intrinsic properties of the group 13 support (M) dictate the favorability of H2 and N2 binding. A strong negative correlation was found between the size of the supporting metal, as represented by Shannon's M(III) ionic radii,60 and ΔG° for both H2 (R2 = 0.988) and N2 (R2 = 0.999) binding (Fig. 7c), where larger supporting ions induce more exergonic binding. The finding that larger supporting metals better poise Ni for small-molecule binding is likely a composite effect of both electronic and steric factors. Larger group 13 supporting metals show stronger Ni→M bonding interactions (Table S24b†) and shift the Ni(0/I) oxidation to more positive potentials,16 both of which should lower the Pauli repulsion associated with binding a donor (Fig. S71†). Also, larger group 13 ions force Ni to move further above the P3-plane which should minimize the structural reorganization energy associated with small-molecule binding (Fig. S72†).
The confluence of steric and electronic effects is also supported by the fact that neither effect can solely account for the observed trends. For example, the position of Ni above the P3-plane is identical for both Al and Ga (0.13 Å), despite their distinct differences in ΔG° for H2/N2 binding. Also, correlations between ΔG° for H2/N2 binding and Ni redox potentials are comparatively poor, whether one considers the Ni(0/I) oxidation or the Ni(−I/0) reduction potentials (R2 = 0.726 to 0.891, Fig. S68 and S69†).16,61 Typically Lewis acidity is expected to correlate with σ-accepting ability, yet no linear relationship exists between ΔG° for H2/N2 binding and the relative Lewis acidities of group 13 metals, as given by the pKa values of the corresponding M(H2O)63+ complexes (R2 = 0.02–0.05, Fig. S66†).62,63 It is plausible that the Lewis acidity scale based on M–OH2 bonds, where H2O is the Lewis base, is an inappropriate benchmark for a Ni(0) Lewis base. You and Gabbaï have recently proposed that the double-decker ligand framework, which imposes spatial constraints, may “accentuate” the influence of the group 13 ion's size.64 It is noteworthy that ΔG° values for H2 (R2 = 0.945) and N2 (R2 = 0.977) binding correlate reasonably well with the degree of Ni→M dative bonding, as quantified by the ratio of the solid-state Ni–M bond distance to the sum of the covalent radii of Ni and M (Fig. S67†).65,66 This finding is consistent with the hypothesis that group 13 metals can significantly tune the reactivity of a proximal Ni center via a direct Ni(0)→M(III) dative interaction.
Conclusion
H2 and N2 binding is atypical for Ni complexes and facilitating H2 activation to form reactive Ni(η2-H2) and/or Ni–H species poses a difficult hurdle for developing homogeneous Ni catalysts for H2 oxidation, proton reduction, and related processes. Excitingly, we find that supporting Ni with group 13 metals induces the binding of H2 and N2 to Ni, with H2 binding found to be ∼2 kcal mol−1 more favorable than N2 binding in each case. The pivotal role of the supporting metal in promoting binding to the NiML complexes is highlighted by the inability of NiLH3, a similarly ligated mononuclear Ni center, to bind H2 or N2 under any conditions examined. The dramatic tuning effect of the supporting group 13 metal is illustrated by the wide range of ΔG° values for H2 binding, which span ∼8 kcal mol−1 (including NiLH3) and nearly cover the entire range of previously reported values. H2 binding to NiInL (3) is more exergonic than any such equilibrium reported, allowing for solid-state characterization of (η2-H2)NiInL (3-H2) via neutron diffraction, which is unprecedented for an H2 adduct of Ni or any d10 metal.Theoretical calculations have provided important insights into the role of the supporting metal in promoting small-molecule binding. Specifically, complementary σ-interactions are proposed based on ETS-NOCV calculations, where H2 → Ni σ-donation to the energetically-accessible Ni(4pz)-based LUMO is the dominant binding interaction, which is likely induced by electron withdrawal from Ni via the dative Ni(0)→M(III) bond. The involvement of the LUMO in small-molecule binding is supported by TD-DFT and UV-Vis studies, along with the strong correlation between ΔG° values for H2/N2 binding and the Ni 3dxz/dyz → LUMO excitation energy. Notably, the size of the supporting M(III) ion correlates best with ΔG° values for H2 and N2 binding, with larger group 13 supporting metals inducing more favorable binding by: rendering Ni more electron-deficient, favoring stronger Ni→M interaction, and minimizing the structural reorganization energy. Moreover, thermodynamically favorable H2 binding equilibria (In > Ga > Al) have proportionally smaller free energies of activation.
Overall, a thorough understanding of H2 and N2 binding to NiML complexes, and the integral role of the supporting metal therein, has been presented. Future work will explore the impact of the thermodynamics and kinetics of H2 binding equilibria on catalytic CO2 hydrogenation reactivity, where H2 binding to displace formate has been found to be the rate-determining step in catalysis.20,67 Additionally, the generalizability of the strategy of favorably altering base-metal reactivity via interactions with group 13 supporting metals will be assessed, and efforts are currently underway to extend our studies to other ligand frameworks and transition metals.
Experimental section
Additional information is provided in the ESI.†General considerations
Unless otherwise stated, all manipulations were performed under an Ar or N2 atmosphere inside a glovebox or using standard Schlenk techniques. Standard solvents were deoxygenated by sparging with N2 and dried by passing through activated alumina columns of a SG water solvent purification system. Deuterated solvents and HD gas (97% D content) were purchased from Cambridge Isotope Laboratories, Inc. Deuterated solvents were degassed via freeze–pump–thaw cycles, and either stored over activated 4 Å molecular sieves or stirred with Na–K alloy and distilled. N2 and H2 gases were purchased from Matheson Trigas, Inc., and a gas mixture of 10% H2/90% Ar was purchased from Praxair, Inc. All other reagents were purchased from commercial vendors and used without purification unless otherwise noted. The ligand N(o-(NHCH2PiPr2)C6H4)3 (abbreviated as LH3), NiAlL (1), NiGaL (2), NiInL (3), (η2-H2)NiGaL (2-H2), (N2)NiInL (3-N2), (η2-H2)NiInL (3-H2), and NiLH3 (4) were synthesized according to the literature.16,34,681H and 31P NMR spectra were recorded on Bruker (400 or 500 MHz) or Varian (500 MHz) spectrometers and referenced to internal residual solvent (or H3PO4 for 31P NMR spectra). For VT NMR experiments, the temperature was calibrated using a methanol (≤298 K) or an ethylene glycol (>298 K) standard. UV-Vis spectra were collected on a Cary-14 instrument. Cyclic voltammetry experiments were performed using a CHI Instruments 620D potentiostat. The one-cell setup utilized a glassy carbon working electrode, platinum wire counter electrode, and Ag/AgNO3 reference electrode in CH3CN.In situ generation of (η2-H2)NiAlL (abbreviated as 1-H2)
A solution of 1 (15 mg, 19.6 μmol) in THF-d8 (∼0.30 mL) was added to a PEEK NMR cell and pressurized to 34 atm H2. The following NMR data are reported at 34 atm H2; an equilibrium between 1 and 1-H2 can also be observed under 1 atm H2 at low T. 1H{31P} NMR (ppm, THF-d8, 232 K, 500 MHz): 7.34 (br, 3H, ArH), 6.87 (br, 3H, ArH), 6.34 (br, 6H, ArH), 3.00 (br, 3H, CHH′), 2.87 (br, 3H, CHH′), 2.10 (m, 6H, CH(CH3)2), 1.27 to 0.90 (36H, CH(CH3)2), −1.5 (br, 2H, (H2)Ni, T1 (min) ≤ 0.49(5) s at 200 K). 31P NMR (ppm, 200 K, 202.4 MHz): 44.9 (in THF-d8), or ∼44.3 (in toluene-d8). The lability of H2 precluded elemental analysis from being obtained.In situ observation of (N2)NiAlL (1-N2) and (N2)NiGaL (2-N2)
A solution of 1 (3.7 mg, 4.8 μmol) in toluene-d8 (0.30 mL) was added to a PEEK NMR cell and pressurized to 51 atm N2. Similarly, a solution of 2 (5.0 mg, 6.2 μmol) in toluene-d8 (0.41 mL) was added to a J. Young NMR tube under 1 atm N2. Neither 1-N2 nor 2-N2 was isolable due to lability of the N2 ligand. Both 1-N2 and 2-N2 were observed in the presence of 1 and 2, respectively, which limited 1H NMR characterization due to overlapping resonances. For 1-N2: 31P NMR (ppm, toluene-d8, 190 K, 51 atm N2, 202.4 MHz): ∼32.2. For 2-N2: 31P NMR (ppm, toluene-d8, 193 K, 1 atm N2, 162 MHz): ∼43.5.X-ray and neutron diffraction crystallographic and structure refinement details
| Radiation type | X-ray | Neutron |
| Chemical formula | C39H62N4P3InNi | C39H62N4P3InNi |
| F w | 853.36 | 853.36 |
| Cryst syst | Orthorhombic | Orthorhombic |
| Space group | P212121 | P212121 |
| a (Å) | 12.2127(4) | 12.2010(10) |
| b (Å) | 14.5402(5) | 14.5638(12) |
| c (Å) | 22.5601(8) | 22.547(2) |
| α (deg) | 90 | 90 |
| β (deg) | 90 | 90 |
| γ (deg) | 90 | 90 |
| V (Å3) | 4006.1(2) | 4006.4(6) |
| Z | 4 | 4 |
| λ (Å), μ (mm−1) | 0.71073, 1.198 | 0.60–3.36, 0.1570 + 0.1306λ |
| T (K) | 100(2) | 100(2) |
| Θ | 2.285 to 36.348 | 7.352 to 78.740 |
| Reflns collected | 237![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 431 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 303 303 |
| Unique reflns | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473 473 |
4718 |
| Data/restraint/parameters | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473/0/451 473/0/451 |
4718/1068/991 |
| R1, wR2 (I > 2σ(I)) | 0.0181, 0.0392 | 0.0620, 0.1262 |
General procedure for H2/N2 binding studies
A toluene-d8 solution of NiML (15 mM) was filtered and transferred to either a J. Young NMR tube (≤3.8 atm) or a PEEK NMR cell (≥6.8 atm).78,79 For high-pressure studies, the PEEK cell was sealed and connected to a high-pressure line equipped with a vacuum pump and an ISCO syringe pump. The line was purged with H2 or N2 gas three times. Next, the headspace was degassed by opening the PEEK cell to static vacuum (3 × 30 s), and H2 or N2 gas was then delivered to the cell from an ISCO syringe pump running constantly at the desired pressure (i.e. continuous gas feed). The contents of the PEEK cell were mixed using a vortex mixer for ∼15 min prior to NMR data collection to allow for pressure stabilization and equilibration. For low-pressure studies, J. Young NMR tubes were pressurized after freeze–pump–thaw cycles. VT 31P NMR spectra were acquired at several different T (193 to 368 K) in all studies, with an adequate number of scans collected (typically 64 to 160 scans) to quantify the observed peak position (for fast chemical exchange) and/or the relative peak integrations (for slow chemical exchange). 31P spectra were typically collected with a recycle delay time of 2 s and an acquisition time of 1.68 s. In cases where quantitative integration of multiple peaks was desired, a longer delay time of 10 s was used.CAUTION: H2 is a highly flammable gas. Pressurized vessels must be handled with care using proper personal protective equipment. PEEK cells were employed for the high-pressure NMR studies, as described previously.78,79
General procedure for kinetic studies of H2 self-exchange
A solution of NiML (7.5 mM in 0.70 mL) was prepared in toluene-d8 and transferred to a J. Young NMR tube. VT 31P NMR spectra were obtained at various T (≥7 data points, 214 K to 344 K) for samples under 1 atm Ar to determine intrinsic linewidths and chemical shifts for NiML complexes. Subsequently, after freeze–pump–thaw cycles, the VT 31P NMR profile was obtained under 1 atm H2. NMR lineshape analysis was performed using the gNMR (version 5.0) program80 to extract H2 self-exchange rates at each T (see ESI for details†). 31P NMR spectra were typically collected with a delay time of 2 s, an acquisition time of 1.68 s, and with 160 scans.Computational methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56,82) and five basis sets (denoted as bs0 to bs4, Table S3†) were evaluated. The M06-L/bs1 method (def2-TZVPP for H2, N2, Ni, Al, Ga, and In, with the SDD effective core potential83 for In; def2-TZVP basis set for N, P; and def2-SVP for C and H atoms)84 gave the best match to the experimental binding energies, and had been used in related prior studies.67 Geometric structures were optimized in the gas phase at 0 K, using the crystal structure atomic coordinates as the initial geometries when available (1–3, 3-H2, and 3-N2). Vibrational frequency analyses were performed with the harmonic approximation to confirm the nature of all species (0 and 1 imaginary frequency for ground-state and transition-state structures, respectively). Unless otherwise noted, Gibbs free energies at 298.15 K and 1 atm were computed by adding zero-point vibrational energies and thermal corrections. Solvation effects were considered by performing single-point calculations for all stationary points using the SMD solvation model.85 The H2 and N2 binding energies for NiML were calculated according to the following equation:
56,82) and five basis sets (denoted as bs0 to bs4, Table S3†) were evaluated. The M06-L/bs1 method (def2-TZVPP for H2, N2, Ni, Al, Ga, and In, with the SDD effective core potential83 for In; def2-TZVP basis set for N, P; and def2-SVP for C and H atoms)84 gave the best match to the experimental binding energies, and had been used in related prior studies.67 Geometric structures were optimized in the gas phase at 0 K, using the crystal structure atomic coordinates as the initial geometries when available (1–3, 3-H2, and 3-N2). Vibrational frequency analyses were performed with the harmonic approximation to confirm the nature of all species (0 and 1 imaginary frequency for ground-state and transition-state structures, respectively). Unless otherwise noted, Gibbs free energies at 298.15 K and 1 atm were computed by adding zero-point vibrational energies and thermal corrections. Solvation effects were considered by performing single-point calculations for all stationary points using the SMD solvation model.85 The H2 and N2 binding energies for NiML were calculated according to the following equation:| X(g) + NiML(solv) → X-NiML(solv) | (3) |
In eqn (3), X(g) is H2 or N2, and the standard state is defined as 1 atm for X(g). The overall energy for eqn (3) was determined based on the gas-phase free energies for H2 or N2 and the Gibbs free energies with solvation (in toluene) for NiML(solv) and X-NiML(solv).
EDA breaks the total interaction energy (ΔEint) between the H2 and NiML fragments into four components, as shown in eqn (4):
| ΔEint (EDA) = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp | (4) |
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors thank Prof. Laura Gagliardi, Prof. Chris Cramer, Dr Molly O'Hagan, Dr Adrian Houghton, and Dr Tom Autrey for helpful discussions. James Moore is acknowledged for assistance with X-ray diffraction. R. C. C. was supported by the DOE Office of Science Graduate Student Research and the UMN Doctoral Dissertation Fellowship programs. M. V. V. was supported by the NSF Graduate Research Fellowship. C. C. L. acknowledges NSF (CHE-1665010) for support of the experimental work. J. X., J. Y., and K. D. V. were supported as part of the Inorganometallic Catalyst Design Center, an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences under Award DE-SC0012702. S. A. B., J. C. L., and A. M. A. were supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences & Biosciences. Single crystal neutron diffraction experiment performed on TOPAZ used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory, under Contract No. DE-AC05-00OR22725 with UT-Battelle, LLC. X-ray diffraction experiments were performed using a crystal diffractometer acquired through an NSF-MRI award (CHE-1229400).References
- L. Alig, M. Fritz and S. Schneider, Chem. Rev., 2019, 119, 2681–2751 CrossRef CAS PubMed.
- S. J. C. Robinson and D. M. Heinekey, Chem. Commun., 2017, 53, 669–676 RSC.
- R. H. Morris, Acc. Chem. Res., 2015, 48, 1494–1502 CrossRef CAS PubMed.
- P. J. Chirik, Acc. Chem. Res., 2015, 48, 1687–1695 CrossRef CAS PubMed.
- R. M. Bullock and M. L. Helm, Acc. Chem. Res., 2015, 48, 2017–2026 CrossRef CAS PubMed.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769 CrossRef CAS PubMed.
- G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205 CrossRef CAS PubMed.
- P. G. Jessop and R. H. Morris, Coord. Chem. Rev., 1992, 121, 155–284 CrossRef CAS.
- G. J. Kubas, Catal. Lett., 2005, 104, 79–101 CrossRef CAS.
- J. M. Millar, R. V. Kastrup, M. T. Melchior, I. T. Horvath, C. D. Hoff and R. H. Crabtree, J. Am. Chem. Soc., 1990, 112, 9643–9645 CrossRef CAS.
- A. A. Gonzalez and C. D. Hoff, Inorg. Chem., 1989, 28, 4295–4297 CrossRef CAS.
- D. G. Abrecht and B. Fultz, J. Phys. Chem. C, 2012, 116, 22245–22252 CrossRef CAS PubMed.
- D. E. Prokopchuk, G. M. Chambers, E. D. Walter, M. T. Mock and R. M. Bullock, J. Am. Chem. Soc., 2019, 141, 1871–1876 CrossRef CAS PubMed.
- D. L. M. Suess, C. Tsay and J. C. Peters, J. Am. Chem. Soc., 2012, 134, 14158–14164 CrossRef CAS PubMed.
- M. V. Vollmer, J. Xie and C. C. Lu, J. Am. Chem. Soc., 2017, 139, 6570–6573 CrossRef CAS PubMed.
- R. C. Cammarota and C. C. Lu, J. Am. Chem. Soc., 2015, 137, 12486–12489 CrossRef CAS PubMed.
- B. R. Barnett, C. E. Moore, P. Chandrasekaran, S. Sproules, A. L. Rheingold, S. DeBeer and J. S. Figueroa, Chem. Sci., 2015, 6, 7169–7178 RSC.
- T.-P. Lin, C. R. Wade, L. M. Pérez and F. P. Gabbaï, Angew. Chem., Int. Ed., 2010, 49, 6357–6360 CrossRef CAS PubMed.
- T.-P. Lin, R. C. Nelson, T. Wu, J. T. Miller and F. P. Gabbaï, Chem. Sci., 2012, 3, 1128–1136 RSC.
- R. C. Cammarota, M. V. Vollmer, J. Xie, J. Ye, J. C. Linehan, S. A. Burgess, A. M. Appel, L. Gagliardi and C. C. Lu, J. Am. Chem. Soc., 2017, 139, 14244–14250 CrossRef CAS PubMed.
- J. Takaya and N. Iwasawa, J. Am. Chem. Soc., 2017, 139, 6074–6077 CrossRef CAS PubMed.
- P. Steinhoff, M. Paul, J. P. Schroers and M. E. Tauchert, Dalton Trans., 2019, 48, 1017–1022 RSC.
- B. A. Connor, J. Rittle, D. VanderVelde and J. C. Peters, Organometallics, 2016, 35, 686–690 CrossRef CAS.
- W. H. Harman, T. P. Lin and J. C. Peters, Angew. Chem., Int. Ed., 2014, 53, 1081–1086 CrossRef CAS PubMed.
- R. H. Morris and R. J. Wittebort, Magn. Reson. Chem., 1997, 35, 243–250 CrossRef CAS.
- P. A. Maltby, M. Schlaf, M. Steinbeck, A. J. Lough, R. H. Morris, W. T. Klooster, T. F. Koetzle and R. C. Srivastava, J. Am. Chem. Soc., 1996, 118, 5396–5407 CrossRef CAS.
- G. J. Kubas, C. J. Burns, J. Eckert, S. W. Johnson, A. C. Larson, P. J. Vergamini, C. J. Unkefer, G. R. K. Khalsa, S. A. Jackson and O. Eisenstein, J. Am. Chem. Soc., 1993, 115, 569–581 CrossRef CAS.
- N. A. Eberhardt and H. Guan, Chem. Rev., 2016, 116, 8373–8426 CrossRef CAS PubMed.
- W. A. Gunderson, D. L. M. Suess, H. Fong, X. Wang, C. M. Hoffmann, G. E. Cutsail, J. C. Peters and B. M. Hoffman, J. Am. Chem. Soc., 2014, 136, 14998–15009 CrossRef CAS PubMed.
- R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391 CrossRef CAS.
- J. Halpern, L. Cai, P. J. Desrosiers and Z. Lin, J. Chem. Soc., Dalton Trans., 1991, 717–723 RSC.
- R. H. Crabtree and D. G. Hamilton, J. Am. Chem. Soc., 1986, 108, 3124–3125 CrossRef CAS.
- T. A. Luther and D. M. Heinekey, Inorg. Chem., 1998, 37, 127–132 CrossRef CAS PubMed.
- L. J. Clouston, R. B. Siedschlag, P. A. Rudd, N. Planas, S. Hu, A. D. Miller, L. Gagliardi and C. C. Lu, J. Am. Chem. Soc., 2013, 135, 13142–13148 CrossRef CAS PubMed.
- M. P. Williamson, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 73, 1–16 CrossRef CAS PubMed.
- R. G. Bryant, J. Chem. Educ., 1983, 60, 933–935 CrossRef CAS.
- J. Feeney, J. G. Batchelor, J. P. Albrand and G. C. K. Roberts, J. Magn. Reson., 1979, 33, 519–529 CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- D. M. Heinekey, M. H. Voges and D. M. Barnhart, J. Am. Chem. Soc., 1996, 118, 10792–10802 CrossRef CAS.
- B. E. Hauger, D. Gusev and K. G. Caulton, J. Am. Chem. Soc., 1994, 116, 208–214 CrossRef CAS.
- D. G. Gusev, A. B. Vymenits and V. I. Bakhmutov, Inorg. Chem., 1992, 31, 1–2 CrossRef CAS.
- M. Mediati, G. N. Tachibana and C. M. Jensen, Inorg. Chem., 1990, 29, 3–5 CrossRef CAS.
- D. G. Gusev, V. I. Bakhmutov, V. V. Grushin and M. E. Vol'pin, Inorg. Chim. Acta, 1990, 177, 115–120 CrossRef CAS.
- K. Zhang, A. A. Gonzalez and C. D. Hoff, J. Am. Chem. Soc., 1989, 111, 3627–3632 CrossRef CAS.
- A. A. Gonzalez, K. Zhang, S. P. Nolan, R. Lopez de la Vega, S. L. Mukerjee, C. D. Hoff and G. J. Kubas, Organometallics, 1988, 7, 2429–2435 CrossRef CAS.
- D. E. Prokopchuk, E. S. Wiedner, E. D. Walter, C. V. Popescu, N. A. Piro, W. S. Kassel, R. M. Bullock and M. T. Mock, J. Am. Chem. Soc., 2017, 139, 9291–9301 CrossRef CAS PubMed.
- P. L. Holland, Dalton Trans., 2010, 39, 5415–5425 RSC.
- C. Tsay and J. C. Peters, Chem. Sci., 2012, 3, 1313–1318 RSC.
- J. L. Sudmeier, J. L. Evelhoch and N. B. H. Jonsson, J. Magn. Reson., 1980, 40, 377–390 CAS.
- D. S. Stephenson and G. Binsch, J. Magn. Reson., 1978, 32, 145–152 CAS.
- T. Le-Husebo and C. M. Jensen, Inorg. Chem., 1993, 32, 3797–3798 CrossRef CAS.
- D. C. Grills, R. van Eldik, J. T. Muckerman and E. Fujita, J. Am. Chem. Soc., 2006, 128, 15728–15741 CrossRef CAS PubMed.
- K. M. Gramigna, D. A. Dickie, B. M. Foxman and C. M. Thomas, ACS Catal., 2019, 9, 3153–3164 CrossRef CAS.
- W. H. Harman and J. C. Peters, J. Am. Chem. Soc., 2012, 134, 5080–5082 CrossRef CAS PubMed.
- R. C. Cammarota, L. J. Clouston and C. C. Lu, Coord. Chem. Rev., 2017, 334, 100–111 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154122 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. V. Vollmer, J. Xie, R. C. Cammarota, V. G. Young, E. Bill, L. Gagliardi and C. C. Lu, Angew. Chem., Int. Ed., 2018, 57, 7815–7819 CrossRef CAS PubMed.
- D. D. Perrin, Ionisation Constants of Inorganic Acids and Bases in Aqueous Solution, Pergamon Press, Elmsford, NY, 2nd edn, 1982 Search PubMed.
- E. Y. Tsui, R. Tran, J. Yano and T. Agapie, Nat. Chem., 2013, 5, 293–299 CrossRef CAS PubMed.
- D. You and F. P. Gabbaï, Trends in Chemistry, 2019 DOI:10.1016/j.trechm.2019.03.011.
- A. Amgoune and D. Bourissou, Chem. Commun., 2011, 47, 859–871 RSC.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 21, 2832–2838 RSC.
- J. Ye, R. C. Cammarota, J. Xie, M. V. Vollmer, D. G. Truhlar, C. J. Cramer, C. C. Lu and L. Gagliardi, ACS Catal., 2018, 8, 4955–4968 CrossRef CAS.
- P. A. Rudd, S. Liu, L. Gagliardi, V. G. Young and C. C. Lu, J. Am. Chem. Soc., 2011, 133, 20724–20727 CrossRef CAS PubMed.
- L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, J. Appl. Crystallogr., 2015, 48, 3–10 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- Persistence of Vision (TM) Raytracer, Persistence of Vision Pty. Ltd., Williamstown, Victoria, Australia, 2004 Search PubMed.
- Z.-L. Xue, A. J. Ramirez-Cuesta, C. M. Brown, S. Calder, H. Cao, B. C. Chakoumakos, L. L. Daemen, A. Huq, A. I. Kolesnikov, E. Mamontov, A. A. Podlesnyak and X. Wang, Eur. J. Inorg. Chem., 2019, 1065–1089 CrossRef CAS.
- J. Zikovsky, P. F. Peterson, X. P. P. Wang, M. Frost and C. Hoffmann, J. Appl. Crystallogr., 2011, 44, 418–423 CrossRef CAS.
- A. J. Schultz, M. R. V. Jorgensen, X. Wang, R. L. Mikkelson, D. J. Mikkelson, V. E. Lynch, P. F. Peterson, M. L. Green and C. M. Hoffmann, J. Appl. Crystallogr., 2014, 47, 915–921 CrossRef CAS.
- A. J. Schultz, K. Srinivasan, R. G. Teller, J. M. Williams and C. M. Lukehart, J. Am. Chem. Soc., 1984, 106, 999–1003 CrossRef CAS.
- A. Thorn, B. Dittrich and G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 448–451 CrossRef CAS.
- C. R. Yonker and J. C. Linehan, Prog. Nucl. Magn. Reson. Spectrosc., 2005, 47, 95–109 CrossRef CAS.
- C. R. Yonker and J. C. Linehan, J. Organomet. Chem., 2002, 650, 249–257 CrossRef CAS.
- P. H. M. Budzelaar, gNMR User Manual, 5.0, IvorySoft, 2006 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. MennucciG. A. Petersson, Gaussian 09, Revision E. 01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- ADF2016, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. Van Lenthe, J. Snijders and E. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional data for crystallographic, thermodynamic, kinetic, and computational studies (PDF), DFT-optimized geometries (XYZ), X-ray and neutron crystallographic data for 3-H2 (CIF). CCDC 1889774 and 1889775. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc02018g |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |