Open Access Article
Open Access ArticleMicrophase separation of highly amphiphilic, low N polymers by photoinduced copper-mediated polymerization, achieving sub-2 nm domains at half-pitch†
Ellis
Hancox
a,
Evelina
Liarou
 a,
James S.
Town
a,
James S.
Town
 a,
Glen R.
Jones
a,
Glen R.
Jones
 a,
Siân A.
Layton
b,
Steven
Huband
a,
Siân A.
Layton
b,
Steven
Huband
 c,
Martin J.
Greenall
c,
Martin J.
Greenall
 d,
Paul D.
Topham
d,
Paul D.
Topham
 b and
David M.
Haddleton
b and
David M.
Haddleton
 *a
*a
aDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK. E-mail: d.m.haddleton@warwick.ac.uk
bAston Institute of Materials Research, Aston University, Birmingham, B4 7ET, UK
cDepartment of Physics, University of Warwick, Coventry, CV4 7AL, UK
dDepartment of Mathematics and Physics, University of Lincoln, Brayford Pool, Lincoln, LN6 7TS, UK
First published on 13th November 2019
Abstract
The lower limit of domain size resolution using microphase separation of short poly(acrylic acid) homopolymers equipped with a short fluorinated tail, posing as an antagonist ‘A block’ in pseudo AB block copolymers has been investigated. An alkyl halide initiator with a fluorocarbon chain was utilized as a first ‘A block’ in the synthesis of low molecular weight polymers (1400–4300 g mol−1) using photoinduced Cu(II)-mediated polymerization allowing for very narrow dispersity. Poly(tert-butyl acrylate) was synthesized and subsequently deprotected to give very low degrees of polymerization (N), amphiphilic polymers with low dispersity (Đ = 1.06–1.13). By exploiting the high driving force for demixing and the well-defined ‘block’ sizes, we are able to control the nanostructure in terms of domain size (down to 3.4 nm full-pitch) and morphology. This work demonstrates the simple and highly controlled synthesis of polymers to push the boundaries of the smallest achievable domain sizes obtained from polymer self-assembly.
Introduction
The remarkable properties and tunability of block copolymers (BCPs) offer themselves to a wide range of applications, such as nanoporous membranes for drug delivery,1 nanolithography and microelectronics.2–4 These applications have driven the need for smaller domain sizes by feasible synthesis, rendering BCPs a plausible candidate. The thermodynamic driving force of BCP self-assembly (phase separation) is directly related to a balance between the incompatibility of blocks (the Flory–Huggins interaction parameter, chi, χ) and the total degree of polymerization of the polymer (N), therefore, reaching the limits of ultrasmall domain spacings requires high χ-low N BCPs.5 One of the most widely studied block copolymers for microphase separation in the bulk (solid state) is polystyrene-b-poly(methyl methacrylate),6–9 although the smallest achievable lamellar domain spacing is limited to 17.5 nm full-pitch, as a result of relatively low χ.10 Self-consistent mean-field theory (SCFT) predicts that the order–disorder transition (ODT) of a perfectly symmetrical diblock copolymer occurs when χN > 10.5, and materials are typically disordered below this value.11 Dispersity (Đ) is a further important factor affecting bulk microphase separation, in which an increase in Đ has been shown to change morphology, increase domain spacing and decrease overall degree of order.12–14 There have been several recent reports of sub-10 nm domain sizes.4,15–18 In order to push the lower size limit even further, SCFT suggests that the combination of a fluorinated block with a block comprising of highly polar repeat units could lead to domain spacings as small as 2 nm.19The nature of the C–F bond presents an extreme in resistance to external stimuli, low flammability and high hydrophobicity to polymers with high fluorine content.20 Fluoropolymers can give a wide variety of materials with potential structures and morphologies from semi-crystalline to fully amorphous, and applications across coatings and electronics.21 The distinctive properties of fluorine contributes to a high degree of incompatibility of blocks in many BCP combinations, with the potential to achieve nanoscale domain spacings in microphase separation.16 Such polymers have been previously synthesized by reversible-deactivation radical polymerization (RDRP) techniques, which is an optimum choice due to the ability to control molecular weight, dispersity and architecture.22,23 Photoinduced Cu(II)-mediated controlled radical polymerization has proven to be a versatile approach to BCP synthesis, allowing the use of various activated monomers in both aqueous and organic solvents, with reduced side reactions,24 and without the need for rigorous deoxygenation.25 Photoinduced Cu(II)-polymerisation in conjunction with aliphatic tertiary amines26,27 provides spatiotemporal control, very low dispersity and high end-group fidelity via simple implementation.
Reversible addition–fragmentation polymerization (RAFT) has also been frequently used to synthesize high χ BCPs.5,28 Atom-transfer radical polymerization (ATRP) with Cu(I) has been used previously, but in combination with anionic polymerization.4,16 A feature of ATRP is that the ester bond of the alkyl halide may be susceptible to post-polymerization modification conditions and promote unwanted hydrolysis. Herein, we hypothesise the combination of highly hydrophobic fluorine and highly hydrophilic acid units will result in high incompatibility between blocks, and we exploit photoinduced Cu-mediated polymerization for the synthesis of low molecular weight poly(acrylic acid)-fluoro block co-oligomers (BCOs) with very low dispersity (Đ = 1.06–1.13), allowing for very low N, which results in, to the best of our knowledge, the smallest domain sizes from polymer aggregation to date.
Results and discussion
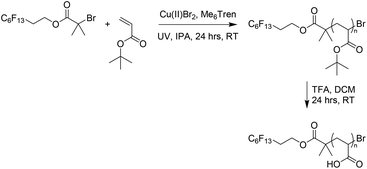
An alternative approach to the synthesis and subsequent self-assembly of BCOs is reported herein. The organic synthesis of an alkyl halide initiator with a PTFE-like side chain serves as a truly discrete first oligomeric ‘block’ (with effectively three repeat units) for a series of polymers with incredibly low N. Esterification of a fluorinated alcohol resulted in an alkyl halide initiator, PFOBiB (perfluorooctyl bromoisobutyrate), with a fluorocarbon moiety of 13 fluorine atoms (Scheme 1). This polymerization allows for very low dispersity (Đ < 1.10), very high initiator efficiency and very low degree of polymerization (DP) materials such that it is possible to distinguish between polymers with small incremental differences such as DP = 5, 10, 15, etc. This is not the case when dispersity is much broader or initiator efficiency is not close to 100% as with much of the controlled radical polymerization chemistry reported, yet is key to our strategy.Our rationale was that PFOBiB would itself be a block (F13) with discrete dispersity, and possess a high χ interaction parameter with a polar homopolymer, which maintains a low N. PFOBiB was characterized by 1H, 13C and 19F NMR spectroscopy (Fig. S1–3†), the excessive splitting observed in the 13C spectrum is a result of carbon–fluorine coupling. 1, 2 and 3-bond J values range from 160–300, 15–50 and 5–20 Hz, respectively,29 producing clear splitting of a qt and tt for terminal fluorine environments. The Cu(II)-photo mediated polymerizations of methyl acrylate in DMSO were carried out to test efficacy as an effective initiator. Successful polymerizations showed excellent end group fidelity and very low dispersity polymers at low N (Table S1†). Similar reactions were carried out alongside these, utilizing ethyl α-bromoisobutyrate (EBiB) initiator as a control, revealing that the presence of fluorine in the initiator had little effect on the initiator efficiency.
The second block was synthesized by polymerization of tert-butyl acrylate (t-BA) with subsequent deprotection to give poly(acrylic acid) (PAA) (Scheme 2), which has been previously reported in BCP self-assembly.30–32 Polymerization of a protected monomer was chosen as it better matches the solubility profile of PFOBiB. Furthermore, the direct polymerization of AA can be problematic.33 Reactions were carried out in IPA rather than DMSO to prevent a biphasic system occurring due to the insolubility of Pt-BA in DMSO.34 Polymers of varying N were synthesized (N = 10 to 30) with 8 CF2/CH2 repeat units in the initiator to give a range of different PAA volume fractions (fPAA) due to the constant F13 block, thus covering a controlled range across the phase diagram to induce a change in nanostructure at higher PAA contents. These polymers were obtained in high conversion (>99%) and low dispersity (Table 1, Fig. S4†), which is inherently minimized by the lack of a need for sequential monomer addition. F13-Pt-BAn polymers were subsequently deprotected using trifluoroacetic acid (TFA) to afford the F13-PAAn white powders. The loss of the t-butyl peak in the 1H NMR spectra indicates a successful deprotection (Fig. S5†). F13-PAAnN values were calculated by comparing the methyl groups of the F13-group to the polymer t-butyl peak from 1H NMR spectra of the equivalent F13-Pt-BAn, as recognizable protons were lost after deprotection. Similarly, the dispersities were taken from F13-Pt-BAn as F13-PAAn failed to elute properly in both THF and DMF GPC-SEC solvents. This was attributed to the highly amphiphilic nature combined with very low molecular weight. F13-Pt-BAn has a significantly higher mass therefore and drastically different solubility to F13-PAAn, retention times could be obtained. The F13-block has a more negative refractive index than the GPC solvents, which also contributed to abnormalities in the molecular weight distributions for F13-PAAn.
| Sample | N AA | M n, GPC-SEC | Đ GPC-SEC | M n, theo. (g mol−1) | M n, MALDI (g mol−1) |
|---|---|---|---|---|---|
| a Degree of polymerization calculated from F13-Pt-BAn (1H NMR). b M n, GPC-SEC taken from GPC-SEC of F13-Pt-BAn in THF. c Dispersity calculated from GPC-SEC of F13-Pt-BAn in THF. d M n, theo predicted from NNMR values. | |||||
| F13-PAA4 | 4 | 1400 | 1.08 | 801 | 741 |
| F13-PAA5 | 5 | 1450 | 1.06 | 873 | N/A |
| F13-PAA6 | 6 | 1400 | 1.09 | 945 | 848 |
| F13-PAA9 | 9 | 1900 | 1.11 | 1162 | 978 |
| F13-PAA11 | 11 | 1950 | 1.10 | 1306 | 1317 |
| F13-PAA15 | 15 | 2650 | 1.08 | 1594 | N/A |
| F13-PAA18 | 18 | 3400 | 1.10 | 1810 | 1744 |
| F13-PAA25 | 25 | 4300 | 1.13 | 2515 | 2097 |
MALDI-ToF-MS further supported the characterization of F13-PAAn, (Fig. 1 and Fig. S6–12†). Profiles show an increasing mass unit of 72 g mol−1, consistent with the AA repeat unit. However, multiple end group distributions including H- and Br-termination suggests a loss of end group during hydrolysis. Br-Termination is not expected to be dominant as strongly acidic conditions are expected to reduce it. For all F13-PAAn polymers, the main distribution showed consistency with vinyl termination, however, this is also consistent with cyclization of the terminal AA unit due to the presence of carboxylate anions.33 It is likely that during hydrolysis, residual TFA continues to deprotonate AA units, thus promoting the cyclization of a lactone and elimination of HBr. The structure of the end group becomes important at low N as the loss of Br and concomitant rearrangement (Scheme 3) is substantial. The replacement of the carboxylic acid group with a rigid lactone ring would likely influence χ at such low N, however, the effect of end group is beyond the scope of this study. MALDI-ToF-MS data were also used to calculate Mn and Đ using the highest intensity peaks (Table 1), purely for confirmation of synthesis, as GPC-SEC (and 1H NMR) was found unreliable for PAA and it is known that MALDI-ToF-MS can underestimate molecular weight. Despite being a less robust method due to varying ionization efficiencies of different molecular weights, MALDI-ToF-MS has been shown to be valid for low dispersity and low N polymers.35
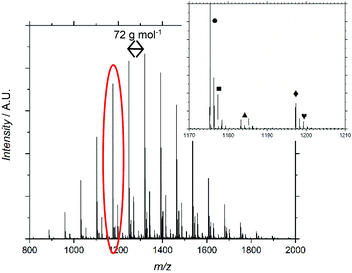 | ||
| Fig. 1 MALDI-ToF-MS spectrum for F13-PAA11. Inset shows which terminal group represents each distribution. | ||
Glass transition temperatures (Tg) obtained from differential scanning calorimetry (DSC) showed an increase in Tg with N, which plateaus at ∼110 °C (Fig. S13a and b†), therefore, microphase separation was achieved by thermal annealing (TA) the polymers in a PTFE cap at 120 °C overnight. As a result, variables associated with solvent vapour annealing (SVA) are avoided, such as evaporation rate, solvent concentration and solvent type/selectivity, which all have the potential to influence domain size and nanostructure.36
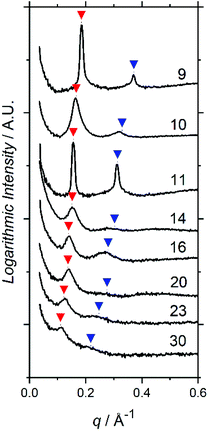
SAXS profiles show principal structure-factor peaks for all TA films (Fig. 2), which are not present in either the profiles for the PFOBiB liquid initiator (Fig. S14†) or the EBiB-PAAn non-fluorinated polymers (Fig. S15†). This indicates the formation of domains and corroborates the strong incompatibility present in F13-PAAn. It should also be noted that SAXS studies of F13-Pt-BAn polymers are not possible for direct comparison, as these are viscous liquids at room temperature and F13-PAAn are solids.
First order peaks were converted into domain spacings (d) viaeqn (1), whereby q* is the principal peak.
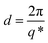 | (1) |
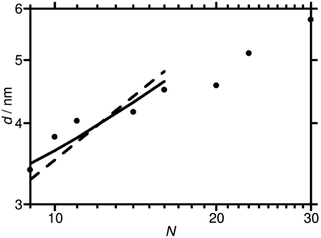
Domain spacings were found to increase with increasing N (Fig. 3) where the longer PAA length forces the common F13 domains further apart. Domains ranged from 3.4–5.8 nm reported at full-pitch (which represents the average total distance between like domains), which to the best of our knowledge are the smallest reported for polymer self-assembly to date.15,16,37 Presence of higher order peaks allows the morphology (nanostructures) to be ascertained. Second order peaks occurring at q/q* = 2 and q/q* = √3 represent lamellar (LAM) and hexagonally packed cylinders (HEX), respectively (Table 2). Strong Bragg peaks with narrow widths (N ≤ 11) imply a well-ordered material with good agreement with LAM nanostructure. Polymers where N ≥ 14 show weak intensity higher order peaks, indicating a weakly phase separated structure (W) with more ‘liquid-like’ order. Broadening of SAXS peaks arise for various reasons, the Williamson–Hall plot combines the Scherrer equation, which recognizes that line broadening increases as mean size of ordered domains decreases, with the Stokes and Wilson expression for strain broadening.38 This explains that N = 10 is likely kinetically trapped in a strained state, and proposes future in situ SAXS temperature studies to further investigate the ODT and χ values of these polymers.39 At N ≥ 20, the weak second order reflection appears to shift closer to q/q* = √3, which would suggest a shift from lamellae morphology to hexagonally packed cylinders, although the SAXS features for these polymers are too weak to confirm such a transition.
| Sample | N | d (nm) | f PAA | Nanostructure |
|---|---|---|---|---|
| a Total degree of polymerization calculated from volume fraction of both blocks, see S17† for volume fraction calculation. b Reported at full-pitch. LAM = lamellae, HEX = hexagonally packed cylinders and W = weak, liquid-like order. | ||||
| F13-PAA4 | 9 | 3.4 | 0.58 | LAM |
| F13-PAA5 | 10 | 3.8 | 0.63 | LAM |
| F13-PAA6 | 11 | 4.0 | 0.66 | LAM |
| F13-PAA9 | 14 | 4.2 | 0.74 | W/LAM |
| F13-PAA11 | 16 | 4.5 | 0.77 | W/LAM |
| F13-PAA15 | 20 | 4.6 | 0.82 | W/HEX |
| F13-PAA18 | 23 | 5.1 | 0.84 | W/HEX |
| F13-PAA25 | 30 | 5.8 | 0.88 | W/HEX |
The extremely short length of the molecules leads to some differences from the standard behaviour of high χ block copolymers. As a preliminary, rough illustration of this, we have performed some simple theoretical modelling with a view to gaining insight into these new materials to pave the way for future studies in this area. Accordingly, we compare fits to the plot of d against N for the lamellar phase obtained using three simple models, each based on different assumptions about the nature of the molecules. We use the values of N listed in Table 2, and have checked that using a definition of N that takes the volume of the repeat unit of one of the blocks as a reference volume (as is often done in fits to domain spacing data40) does not significantly change our results.
Firstly, we fit the plot of d against N for the lamellar phase with the standard strong segregation formula d = cN2/3, where c is an adjustable parameter.41 This formula is valid for high values of χN, and leads to a fit, shown with a dashed line in Fig. 3, that has a steeper slope than our data. Having noted this, there are two main ways in which the shortness of the molecules can be taken into account. The first is to suppose that the F13 block is so short that it should be treated as a rod. Support for this assumption is provided by simulations of PTFE,42 which find that these polymers have a Kuhn length of 2.3 nm, longer than the molecular length of the F13 block itself. We therefore fit the data with a formula derived43 for high χ rod-coil block copolymers in the lamellar phase, d = cN2/3fPAA−1/3 (solid line in Fig. 3). This gives improved agreement. Alternatively, it can be supposed that the value of χN is low enough for the sample to be in the weak segregation regime,41 where d = cN1/2. The fit obtained using this formula is very similar to that obtained using the formula for rod-coil polymers (although it would give a straight line on the log–log plot above without the slight curvature of the rod-coil graph) and is not plotted separately.
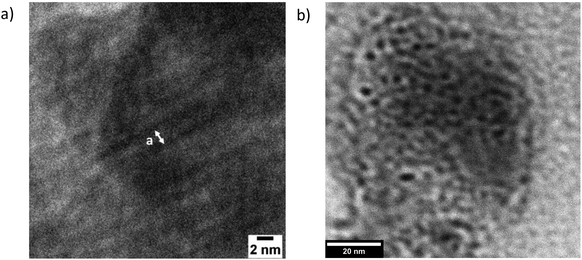
In short, further investigations are needed to determine which of the final two models is more applicable here. Specifically, more data on the temperature- and N-dependence of the morphologies, together with a model with more microscopic detail, are needed. This more complete model would also take into account the possibility of some molecular alignment within the PAA blocks, which is suggested by the occurrence of high q peaks in the equivalent EBiB-PAAn polymers (i.e. non-fluorinated, Fig. S15†), and their absence in the liquid initiator precursors (EBiB or PFOBiB, Fig. S14†). Transmission electron microscopy (TEM) of F13-PAA6, and F13-PAA18 showed morphologies which support the nanostructures revealed from SAXS. Many difficultites are associated with performing electron microscopy on these polymers. Charging effects prevented nanometer scale resolution as the film would burn, despite using low voltage (200 kV). The samples have an inherent lack of electron density, whereas polymers with aromatic moiety (e.g. poly(styrene)), overcome this problem.37,44 Usually, samples would be stained with an electron rich substance to create constrast, however these are often of a larger particle size than the nanometer scale desired for F13-PAAn polymers (i.e. Au nanoparticles ∼20 nm). Despite these difficulties, TEM of TA F13-PAA6 (Fig. 4a) showed the linear pattern of LAM with a domain spacing calculated from TEM of d = ∼2.6 nm. The ‘liquid-like’ order of W/HEX can be seen in the TEM image of F13-PAA18 (Fig. 4b). The domain spacing was found to be ∼5.4 nm for F13-PAA18, from an average of 12 measurements (Fig. S18†). The TEM-calculated domain spacings differ slightly from those obtained from SAXS, because unlike X-ray techniques, microscopy is not necessarily representative of the whole sample and it is not unusual for the surface structure to differ from the bulk, due to migration of groups to the hydrophobic air interface. It should also be noted that sizes could differ due to the different sample preparation methods for TEM and SAXS. SAXS films were prepared as thick films (∼1 mm) on a PTFE surface, compared to dropcasted solutions (1 mg ml−1) onto copper grids for TEM.
Conclusions
In summary, we have synthesized polymers of low molecular weight with high block incompatibility and studied the self-assembling properties in the solid state. We have used thermal annealing to induce microphase separation, achieving a domain spacing as small as 3.4 nm reported full-pitch, which is, as far as we are aware, the lowest reported to date for this type of polymer assembly. SAXS studies indicated an increase in domain spacing with increasing PAA degree of polymerization and eventually a change in morphology (tentatively assigned to a shift from weakly ordered lamellae to weakly ordered hexagonally packed features) above PAA volume fractions of 0.82. In-depth study behind the theory and construction of the phase diagram of these novel polymers is currently in progress and will follow. TEM indicated the same nanostructures given by SAXS on representative samples, albeit showing smaller domain spacings, particularly for our smallest polymer (2.6 nm versus 4.0 nm). This approach to high χ polymers has proven to be a successful concept in polymer self-assembly for potential future use in the microelectronics industry's ever-growing need for smaller domain sizes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Warwick-Monash Alliance (E. H.) and the University of Warwick for funding (E. L., G. R. J.) and the Warwick Polymer Characterisation RTP (Dr Daniel Lester) and X-Ray RTP (Dr Steven Huband) for access to equipment and the EPSRC Doctoral Training Centre in Analytical Science (J. S. T.). Raw data files for data described are available for download free of charge at https://wrap.warwick.ac.uk/128511.Notes and references
- E. A. Jackson and M. A. Hillmyer, ACS Nano, 2010, 4, 3548–3553 CrossRef CAS PubMed.
- T. J. Giammaria, M. Laus and M. Perego, Adv. Phys.: X, 2018, 3, 1445558 Search PubMed.
- M. C. García-Gutiérrez, M. Fernández-Regúlez, A. Nogales, L. Evangelio, T. F. Keller, J. Fraxedas, B. Rösner, F. Perez-Murano, C. David, S. Gottlieb and T. A. Ezquerra, Mol. Syst. Des. Eng., 2018, 4, 175 Search PubMed.
- J. G. Kennemur, L. Yao, F. S. Bates and M. A. Hillmyer, Macromolecules, 2014, 47, 1411–1418 CrossRef CAS.
- W. Zhang, M. Huang, S. Al Abdullatif, M. Chen, Y. Shao-Horn and J. A. Johnson, Macromolecules, 2018, 51, 6757–6763 CrossRef CAS.
- P. Mansky, T. P. Russell, C. J. Hawker, M. Pitsikalis and J. Mays, Macromolecules, 1997, 30, 6810–6813 CrossRef CAS.
- C. J. Hawker, P. M. Chaikin, E. Huang, R. A. Register, C. Harrison, J. Mays and T. P. Russell, Macromolecules, 1998, 31, 7641–7650 CrossRef.
- S. Woo, S. Jo, D. Y. Ryu, S. H. Choi, Y. Choe, A. Khan, J. Huh and J. Bang, ACS Macro Lett., 2017, 6, 1386–1391 CrossRef CAS.
- S. Ham, C. Shin, E. Kim, D. Y. Ryu, U. Jeong, T. P. Russell and C. J. Hawker, Macromolecules, 2008, 41, 6431–6437 CrossRef CAS.
- S. H. Anastasiadis, T. P. Russell, S. K. Satija and C. F. Majkrzak, Phys. Rev. Lett., 1989, 62, 1852–1855 CrossRef CAS PubMed.
- L. Leibler, Macromolecules, 1980, 13, 1602–1617 CrossRef CAS.
- B. Oschmann, J. Lawrence, M. W. Schulze, J. M. Ren, A. Anastasaki, Y. Luo, M. D. Nothling, C. W. Pester, K. T. Delaney, L. A. Connal, A. J. McGrath, P. G. Clark, C. M. Bates and C. J. Hawker, ACS Macro Lett., 2017, 6, 668–673 CrossRef CAS.
- B. Van Genabeek, B. F. M. De Waal, B. Ligt, A. R. A. Palmans and E. W. Meijer, ACS Macro Lett., 2017, 6, 674–678 CrossRef CAS PubMed.
- N. A. Lynd and M. A. Hillmyer, Macromolecules, 2005, 38, 8803–8810 CrossRef CAS.
- J. Kwak, A. K. Mishra, J. Lee, K. S. Lee, C. Choi, S. Maiti, M. Kim and J. K. Kim, Macromolecules, 2017, 50, 6813–6818 CrossRef CAS.
- S. Jo, S. Jeon, T. Jun, C. Park and D. Y. Ryu, Macromolecules, 2018, 51, 7152–7159 CrossRef CAS.
- S. M. Park, O. H. Park, J. Y. Cheng, C. T. Rettner and H. C. Kim, Nanotechnology, 2008, 19, 455304 CrossRef PubMed.
- A. P. Lane, X. Yang, M. J. Maher, G. Blachut, Y. Asano, Y. Someya, A. Mallavarapu, S. M. Sirard, C. J. Ellison and C. G. Willson, ACS Nano, 2017, 11, 7656–7665 CrossRef CAS PubMed.
- C. Sinturel, F. S. Bates and M. A. Hillmyer, ACS Macro Lett., 2015, 4, 1044–1050 CrossRef CAS.
- B. Ameduri, Chem. Rev., 2009, 109, 6632–6686 CrossRef CAS PubMed.
- A. Vitale, R. Bongiovanni and B. Ameduri, Chem. Rev., 2015, 115, 8835–8866 CrossRef CAS PubMed.
- J.-S. Wang and K. Matyjaszewski, J. Am. Chem. Soc., 1995, 117, 5614–5615 CrossRef CAS.
- M. Kato, M. Kamigaito, M. Sawamoto and T. Higashimura, Macromolecules, 1995, 28, 1721–1723 CrossRef CAS.
- A. Anastasaki, C. Waldron, P. Wilson, R. McHale and D. M. Haddleton, Polym. Chem., 2013, 4, 2672–2675 RSC.
- A. Anastasaki, G. R. Jones, N. G. Engelis, D. M. Haddleton, E. Liarou, K. Velonia and R. Whitfield, Angew. Chem., Int. Ed., 2018, 57, 8998–9002 CrossRef PubMed.
- A. Anastasaki, V. Nikolaou, Q. Zhang, J. Burns, S. R. Samanta, C. Waldron, A. J. Haddleton, R. McHale, D. Fox, V. Percec, P. Wilson and D. M. Haddleton, J. Am. Chem. Soc., 2014, 136, 1141–1149 CrossRef CAS PubMed.
- A. Anastasaki, V. Nikolaou, G. S. Pappas, Q. Zhang, C. Wan, P. Wilson, T. P. Davis, M. R. Whittaker and D. M. Haddleton, Chem. Sci., 2014, 5, 3536–3542 RSC.
- G. Jeong, D. M. Yu, J. K. D. Mapas, Z. Sun, J. Rzayev and T. P. Russell, Macromolecules, 2017, 50, 7148–7154 CrossRef CAS.
- E. W. Della, E. Cotsaris and P. T. Hine, J. Am. Chem. Soc., 1981, 103, 4131–4135 CrossRef CAS.
- M. Zhang, T. Breiner, H. Mori and A. H. E. Müller, Polymer, 2003, 44, 1449–1458 CrossRef CAS.
- O. Colombani, M. Ruppel, F. Schubert, H. Zettl, D. V. Pergushov and A. H. E. Müller, Macromolecules, 2007, 40, 4338–4350 CrossRef CAS.
- A. J. Ryan, C. J. Crook, J. R. Howse, P. Topham, R. A. L. Jones, M. Geoghegan, A. J. Parnell, L. Ruiz-Pérez, S. J. Martin, A. Cadby, A. Menelle, J. R. P. Webster, A. J. Gleeson and W. Bras, Faraday Discuss., 2005, 128, 55–74 RSC.
- M. Fantin, A. A. Isse, A. Venzo, A. Gennaro and K. Matyjaszewski, J. Am. Chem. Soc., 2016, 138, 7216–7219 CrossRef CAS PubMed.
- C. Boyer, A. Atme, C. Waldron, A. Anastasaki, P. Wilson, P. B. Zetterlund, D. Haddleton and M. R. Whittaker, Polym. Chem., 2013, 4, 106–112 RSC.
- C. E. Kassis, J. M. DeSimone, R. W. Linton, E. E. Remsen, G. W. Lange and R. M. Friedman, Rapid Commun. Mass Spectrom., 1997, 11, 1134–1138 CrossRef CAS.
- S. H. Kim, M. J. Misner, T. Xu, M. Kimura and T. P. Russell, Adv. Mater., 2004, 16, 226–231 CrossRef CAS.
- Y. Pang, X. Jin, G. Huang, L. Wan and S. Ji, Macromolecules, 2019, 52(8), 2987–2994 CrossRef CAS.
- R. Delhez, P. Scardi and M. Leoni, J. Appl. Crystallogr., 2004, 37, 381–390 CrossRef.
- W. J. Durand, G. Blachut, M. J. Maher, S. Sirard, S. Tein, M. C. Carlson, Y. Asano, S. X. Zhou, A. P. Lane, C. M. Bates, C. J. Ellison and C. G. Willson, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 344–352 CrossRef CAS.
- S. M. Mai, J. P. A. Fairclough, I. W. Hamley, M. W. Matsen, R. C. Denny, B. X. Liao, C. Booth and A. J. Ryan, Macromolecules, 1996, 29, 6212–6221 CrossRef CAS.
- F. Bates, Annu. Rev. Phys. Chem., 1990, 41, 525–557 CrossRef CAS PubMed.
- K. M. Salerno and N. Bernstein, J. Chem. Theory Comput., 2018, 14, 2219–2229 CrossRef CAS PubMed.
- M. Müller and M. Schick, Macromolecules, 1996, 29, 8900–8903 CrossRef.
- Y. Yoshimura, A. Chandra, Y. Nabae and T. Hayakawa, Soft Matter, 2019, 15, 3463–3632 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9py01312a |
| This journal is © The Royal Society of Chemistry 2019 |