Open Access Article
Open Access ArticlePerspectives on systematic optimization of ultrasensitive biosensors through experimental design
Mariapia
Caputo
 a,
Angelo
Tricase
a,
Verdiana
Marchianò
a,
Cecilia
Scandurra
a,
Angelo
Tricase
a,
Verdiana
Marchianò
a,
Cecilia
Scandurra
 b,
Matteo
Piscitelli
c,
Lucia
Sarcina
b,
Matteo
Piscitelli
c,
Lucia
Sarcina
 b,
Michele
Catacchio
a,
Cinzia
Di Franco
d,
Paolo
Bollella
b,
Michele
Catacchio
a,
Cinzia
Di Franco
d,
Paolo
Bollella
 be,
Luisa
Torsi
be,
Luisa
Torsi
 be and
Eleonora
Macchia
be and
Eleonora
Macchia
 *aef
*aef
aDipartimento di Farmacia-Scienze del Farmaco, Università degli Studi di Bari, Italy. E-mail: eleonora.macchia@uniba.it
bDipartimento di Chimica, Università degli Studi di Bari, Italy
cDipartimento Interateneo di Fisica, Università degli Studi di Bari, Italy
dCNR IFN, Bari, Italy
eCenter for Colloid and Surface Science, Bari, Italy
fFaculty of Science and Engineering, Åbo Akademi University, Turku, Finland
First published on 16th September 2024
Abstract
Biosensors have demonstrated versatility across numerous applications; however, their systematic optimization remains a primary obstacle, limiting their widespread adoption as dependable point-of-care tests. Experimental design, a powerful chemometric tool, offers a solution by effectively guiding the development and optimization of ultrasensitive biosensors. This perspective review provides an overview of recent applications of experimental design in the deployment of optical and electrical ultrasensitive biosensors. Various experimental designs, including full factorial, central composite, and mixture designs, are examined as systematic methodologies for optimizing biosensor fabrication, accounting for both individual variable effects and their interactions. Illustrative examples showcasing the optimization of optical and electronic biosensors through design of experiments are presented and critically analyzed. Finally, the future prospects of experimental design in the biosensor community are outlined, highlighting its potential to expedite development and bolster the performance of biosensing devices for point-of-care diagnostics, thereby facilitating their sustainable and reliable integration.
Introduction
Over the past decade, substantial efforts have been directed toward advancing rapid, dependable, highly sensitive, and selective biosensing aimed at identifying specific biomarkers.1,2 The ultrasensitive recognition of proteins, peptides, and genomic markers, namely with a limit of detection (LOD) lower than femtomolar, is increasingly regarded as essential for facilitating early diagnosis of diseases that are progressive, life-threatening, and detrimental to quality-of-life.3,4 Undoubtedly, the progression of biomedical research and clinical practices hinges largely on the development of robust methodologies for accurately and sensitively detecting biomolecules. Such technologies provide clinicians with a crucial tool for combating diseases by allowing for early interventions, which significantly improve the chances of successful treatment.5,6 To accomplish this, it is crucial to include a biolayer which allows the biosensor to specifically recognize target molecules. Thus, optimizing the biosensor's design is essential for improving biochemical transduction and amplification. Typically, this encompasses optimizing the formulation of the detection interface, the immobilization strategy of the biorecognition elements, and the detection conditions, which are crucial parameters for maximizing sensor performance. Nonetheless, many studies tend to optimize individual variables independently, a straightforward yet problematic approach, particularly when dealing with interacting variables. The conditions established for sensor preparation and operation may not truly represent the optimum, hindering the practical applications of these biosensors in point-of-care diagnostic settings.A chemometric method, known as experimental design or design of experiment (DoE), has facilitated the systematic and statistically reliable optimization of parameters.7 DoE approach foresees a model-based optimization, resulting in the development of a data-driven model that connects variations in the variables of input, such as properties of the materials engaged in the biosensor development and production parameters, to the sensor outputs.8,9 While deterministic models rooted in first principles are inherently preferable for this aim, their practical implementation is often hindered by inadequate knowledge or resources necessary for their construction. Consequently, empirical models, specifically those driven by data, are frequently employed as viable alternatives. However, for optimization purposes, it is imperative that the data utilized in constructing these models are suitable to ensure causality and necessitate independent variation in the input variables.10,11 As a result, retrospective analysis performed using happenstance data, originating from standard protocols, is inherently unsuitable for constructing data-driven models due to the intrinsic non-causal nature of the data.12 To surmount the challenges associated with deriving meaningful conclusions from such happenstance data, the DoE workflow should be undertaken. Therefore, DoE is applied before data acquisition to optimize the process of interest, while multivariate data analysis techniques, which are suitable for extracting embedded information from the dataset, are not directly applicable for optimization purposes. It initiates by identifying all factors that may exhibit a causality relationship with the targeted output signal, referred to as the response. Subsequently, after the selection of these factors, the next crucial step is to establish their experimental ranges and the distribution of experiments to be conducted within the experimental domain. The responses gathered from these predetermined points within the experimental domain are then utilized to construct a mathematical model through linear regression, elucidating the relationship between the outcomes and the experimental conditions. Notably, the set of experiments is predetermined, signifying a shift from the conventional univariate approaches wherein each experiment is defined based on the outcomes of previous ones, resulting in localized knowledge of the optimization process. Conversely, in DoE approaches, the experimental plan is established a priori, enabling the response's prediction at any point within the experimental domain. This approach provides comprehensive, global knowledge, offering the maximum possible information for optimization purposes. Furthermore, DoE approaches consider potential interactions among variables. This occurs when an independent variable exerts varying effects on the response based on the values of another independent variable. Such interactions consistently elude detection in customary one-variable-at-a-time approaches. Hence, DoE emerges as an exceptionally potent tool for steering the optimization of ultrasensitive biosensing platforms, requiring a diminished experimental effort compared to univariate strategies. Importantly, this approach not only holds significant empirical value but also yields a data-driven model that can offer insights into the physical rationalization of the observed effects. This frequently proves advantageous in offering valuable and unforeseen insights into elucidating the fundamental mechanisms underlying the transduction and amplification processes.
In this perspective review, an in-depth exploration of the fundamental concepts and applications of DoE in the context of optimizing ultrasensitive biosensors is presented. Experimental design is widely applicable for optimizing various types of biosensors. However, it is especially crucial for ultrasensitive platforms with sub-femtomolar detection limits, where challenges like enhancing the signal-to-noise ratio, improving selectivity, and ensuring reproducibility are particularly pronounced. For these highly sensitive assays, optimization is vital and can be significantly enhanced through the application of design of experiments (DoE) methodologies. Specifically, a comprehensive overview of the key theoretical models utilized within the DoE framework is provided. The primary objective of this perspective is to underscore the notable advantages, namely the reduction in experimental effort and the enhancement of information quality. To achieve this objective, several instances of DoE application in the optimization of biosensing platforms are critically examined, encompassing both electronic and optical transduction methodologies. Consequently, this review intends to provide a thorough analysis of the utilization of the DoE statistical toolbox, accentuating its inherent capacity to foster innovation, drive discovery, and facilitate the application of ultrasensitive biosensors in a clinically relevant environment.
Experimental design
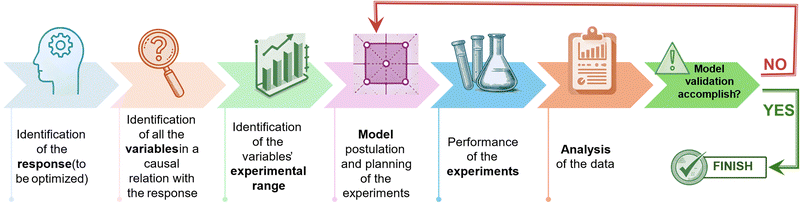
The experimental design hinges on the development of a data-driven model constructed using causal data collected across a comprehensive grid of experiments covering the entire experimental domain. The arrangement of experimental points used to explore the spectrum of factors is determined based on the hypothesized mathematical model, which establishes a relationship between the response and the experimental conditions. The model's coefficients are computed using the least squares method, enabling the prediction of the response across the whole experimental domain, including points where experiments have not been directly carried out. It is crucial to note that the resulting model represents an approximation of the true response, necessitating validation to ensure its adequacy in representing the actual response. One approach to address this aspect is to inspect the residuals of the model, which denote the discrepancy between the measured and predicted responses.13 Should the data exhibit inadequate fitting by the provisional model chosen, consideration should be given to devising a new design to accurately approximate the system. In this context, it is noteworthy that a singular experimental design often fails to culminate in the optimization of the final process, as schematically summarized in the diagram in Fig. 1. Nevertheless, the data gathered from this initial design typically serves as a foundation for refining the problem by eliminating variables that are not significant, redefining the experimental domain, or adjusting the hypothesized model, preceding the execution of a new DoE. For instance, in cases where the response function to be optimized demonstrates approximate linearity with respect to the independent variables, a first-order orthogonal design can yield substantial information with minimal experimental effort. Specifically, such designs are exemplified by full factorial designs, which serve as effective tools for fitting first-order approximating models, albeit they may fail to account for curvature in certain responses.14 To overcome this limitation, second-order models become essential when the response follows a quadratic function with respect to the experimental variables. Central composite designs can be employed to augment initial factorial designs for the estimation of quadratic terms, thereby enhancing the predictive capacity of the model. As it is often necessary to conduct multiple DoE iterations, it is advisable not to allocate more than 40% of the available resources to the initial set of experiments. The subsequent section will provide an overview of the primary experimental designs for independent variables along with the corresponding grid of experiments to be conducted. In these designs, each variable is adjustable within the selected range, irrespective of the values assigned to other variables. Furthermore, the mixture design will be briefly discussed towards the conclusion of this section. These designs follow the inherent rule that the combined total of all components must equal 100%.15 Consequently, the mixture's components cannot be altered independently, as changing the proportion of one component necessitates proportional changes of the others.Factorial designs
The 2k factorial designs are first-order orthogonal designs, necessitating 2k experiments, where k represents the number of the variables being studied.7 In these models, which incorporate both quantitative and qualitative variables, each factor is assigned two levels coded as −1 and +1. These coded levels correspond to the variable's range selected based on the specific application, defining the experimental plan. The experimental matrix, defining the grid of experiments used to compute the coefficient of the model, has 2k rows each one representing an individual experiment, and k columns, with each column representing a specific variable. As an illustration, the experimental matrix of a 22 factorial design is depicted in Table 1. Here, the matrix comprises four rows and two columns, corresponding to variables X1, and X2. In the first column, the values alternate between −1 and +1 for each row, while in the second column, they switch every two rows. This method can be applied to construct the experimental matrix for factorial designs involving any number of variables.| Test number | X 1 | X 2 |
|---|---|---|
| 1 | −1 | −1 |
| 2 | +1 | −1 |
| 3 | −1 | +1 |
| 4 | +1 | +1 |
From a geometric perspective, the experimental domain is illustrated in Fig. 2a as a square. If 3 variables are involved in the factorial design the experimental domain will be a cube, while if the variables exceed three, the experimental domain will correspond to a hypercube. The responses will be recorded at each corner of the square, which represents one of the rows of the experimental matrix. The postulated mathematical model is thus defined according to the subsequent equation:
| Y = b0 + b1X1 + b2X2 + b12X1X2 | (1) |
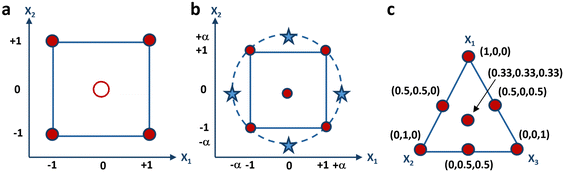 | ||
| Fig. 2 Graphical representation of the experimental domain of (a) 22 factorial-design, (b) central- composite design, and (c) 3-component mixture. | ||
Furthermore, to confirm the model's validity, it is advisable to conduct the response assessment at the central point of the experimental domain. The recorded response will not be utilized for constructing the data-driven model; rather, it will solely serve to assess the predictive capability of the hypothesized model. Specifically, the anticipated response at the central point, denoted as the computed value for the b0 coefficient, should be compared with the experimental value. If the approximation of the outcome at the central point concurs with the experimental result, then the model is deemed verified and it is applicable across the entire range of experiments. Conversely, should the approximation diverge from the experimental value, it necessitates modification of the hypothesized model, followed by the execution of a new experimental design.
Central composite designs
Full factorial designs are valuable for fitting first-order approximating models but are not suitable for capturing the quadratic dependence of the response on the variables. Therefore, a model of second order is required to provide a sufficient approximation for this purpose and estimate the quadratic terms. The experimental matrix in this instance, presuming the presence of two independent variables, is illustrated in Table 2, and can be viewed as an extension of the 2k factorial design.| Test number | X 1 | X 2 |
|---|---|---|
| 1 | −1 | −1 |
| 2 | −1 | +1 |
| 3 | +1 | +1 |
| 4 | +1 | −1 |
| 5 | 0 | −α |
| 6 | 0 | +α |
| 7 | −α | 0 |
| 8 | +α | 0 |
| 9 | 0 | 0 |
With k variables at play, the initial 2k experiments mirror those defined for a factorial design. Subsequently, the following 2k experiments are derived by maintaining all variables at their central level, while varying one variable to either −α or +α, where α denotes how far the additional axial points are from the center of the domain. The final experiment is conducted at the center point of the experimental domain, possibly in triplicate to enhance prediction accuracy within the vicinity of the center. It has indeed been demonstrated that increasing replicates’ number of the center point results in reduced leverage. When multiplied by the experimental domain's variance, this leverage yields the estimated response's variance, which can be evaluated at each point within the domain. If the leverage value equals 1, it suggests that the response can be predicted with an equivalent accuracy to the experimental value. However, if the leverage is less than 1, it suggests that the prediction of the response has greater precision than the experimental measurement. A visual depiction of the experimental grid is presented in Fig. 2b, encompassing a square domain when two variables are considered. This grid comprises a factorial design, represented by the corners of the square, and a star design, represented by the axial points, marked as stars. The star points in the experimental domain encompass all points at the same distance from the central point, resulting in a design that covers a spherical domain. In such cases, the central composite design is referred to as a circumscribed central composite design. Moreover, the face-centered model is a specific instance of a central-composite model, wherein the stars are positioned at the midpoint of each side of the square, implying that α is equal to 1.
Central composite designs enable the estimation of the linear terms, constant term, quadratic terms and variable interactions, based on the model below, when considering two independent variables, X1 and X2:
| Y = b0 + b1X1 + b2X2 + b12X1X2 + b11X12 + b22X22 | (2) |
Given that the experimental matrix plans for 9 experiments to calculate six coefficients, three degrees of freedom remains to evaluate the coefficients’ variance. The significance levels of each coefficient are customarily delineated in the model equation utilizing the subsequent convention: * = p < 0.05, ** = p < 0.01, *** = p < 0.001. These p-values are used to assess the significance of each coefficient, defining the confidence intervals in the Student's t-test.
Mixture designs
All experimental designs previously discussed entail independent variables, signifying that each variable can be adjusted to any value within the experimental range autonomously from the values of the others. Conversely, in mixture designs, there exists an inherent constraint mandating that the summation of all components within a formulation to be optimized must equal 1, or 100%. Consequently, the mixture's components cannot be changed independently, as modifying the proportion of one induces a corresponding alteration in the percentages of the other components. Therefore, mixture design aims to explore how altering the ratios among the variables affects the response to be optimized. Fig. 2c illustrates the graphical representation of the experimental domain of a three-component mixture consisting of X1, X2, and X3. The representation is an equilateral triangle, with its vertices the vertices symbolize the pure components, the edges depict the binary mixtures, and the internal points correspond to the ternary mixtures. The experimental domain of a mixture comprising more than three components manifests as a regular polyhedron, featuring a quantity of vertices equivalent to the number of components, and residing within a space whose dimensionality aligns with one less than the number of components. For instance, the experimental domain of a mixture model containing four components adopts the form of a tetrahedron. Conversely, mixtures encompassing more than four components occupy spaces exceeding three dimensions. The experimental matrix of a mixture design for a formulation comprising three components is depicted in Table 3, detailing the seven experiments required for computing the model coefficients.| Test number | X 1 | X 2 | X 3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | 0.50 | 0.50 | 0 |
| 5 | 0.50 | 0 | 0.50 |
| 6 | 0 | 0.50 | 0.50 |
| 7 | 0.33 | 0.33 | 0.33 |
The model derived from the aforementioned mixture design yields the equation described below:
| Y = b1X1 + b2X2 + b3X3 + b12X1X2 + b13X1X3 + b23X2X3 + b123X1X2X3 | (3) |
This equation includes three linear terms, two-term interactions that represent the synergistic effects between two components, and a three-term interaction, with its coefficient indicating the combined synergistic impact of all three components. The latter is typically one order of magnitude greater than the others. Importantly, eqn (3) does not incorporate the constant term, as it ought to reflect the value assumed by the response when level 0 is set for all variables. For independent variables, this entails assessing the response at the center of the domain. However, in the case of mixtures, it is essential to acknowledge that the sum of all components always equals 1. Consequently, it is impossible to encounter a scenario where all variables assume level 0.
Biosensors optimization via experimental design
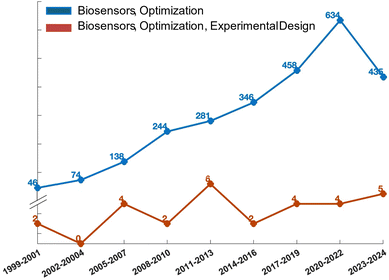
A biosensor is defined, according to the guidelines established by the international union of pure and applied chemistry (IUPAC), as an analytical system that incorporates biological recognition elements whose interaction with an analyte is transformed into a measurable signal by a transducer.16 The transducer may rely on piezoelectric, electrical, mechanical, or optical mechanisms.17–19 Optical and electrical biosensors are of particular interest due to their excellent signal-to-noise ratio, sensitivity, stability, and ease of miniaturization.2,20 Optical detection is achieved through the exploitation of the interaction between the biorecognition element and an optical field. When the optical signal results from a luminescent, fluorescent, or colorimetric secondary probe coupled to the target analyte, the optical biosensor is classified as label-needing. This classification encompasses techniques like the enzyme-linked immunosorbent assay (ELISA), which remains a cornerstone in immunoassays, and which has evolved into the “digital” single-molecule assay (SIMOA) technology developed by Quanterix.6 In these assays, the target analyte is typically immobilized in a microplate well using a specific antibody referred to as a capture antibody. Subsequently, a detection antibody is introduced, thereby creating a sandwich configuration with the antigen positioned between the two antibodies.21,22 The detection antibody is enzymatically labelled. The breakdown of a chromogenic substrate by the enzyme generates an amplified optical signal, facilitating precise and sensitive identification of the enzyme's presence and, consequently, the analyte in question.23 On the contrary, when the analyte-transducer interaction generates the detected signal, the sensor is categorized as label-free. This classification encompasses biosensors utilizing surface plasmon resonance (SPR), which measures the variations at the sensor surface of the mass density, facilitating the direct monitoring of molecular affinity bindings.24 The metallic layer covering the optical element's surface is covered with the biofunctionalized active interface of the SPR biosensor. The probing mechanism of the device is based on the optical field of surface plasmons, confined to the surface of the active device.25,26 When the biochemical interactions on the sensor's surface occur, variations in the local refractive index will be registered. Optical biosensors have long been regarded as the gold standard in clinical diagnostics and drug discovery. However, the sophisticated nature of the detection apparatus, coupled with the substantial fabrication expenses and extended time-to-results often spanning hours, has spurred investigations into simpler and more economical methods. As a result, technologies leveraging electrical transduction mechanisms have been devised.17,19 These typically include transistor-based bioelectronic sensors, which function either as amperometric or potentiometric devices.27 In potentiometry, the voltage difference between a reference electrode and a working electrode is measured without the passage of current.28–30 Conversely, amperometric techniques utilize a potential difference across two electrodes and quantify the resulting current produced by the analyte's electrolysis.31 The latter, namely the faradaic current, is what helps the electrode/electrolyte interface balance to be established through electron transfer. Potentiometric assessments are conducted at equilibrium, whereas amperometric evaluations are performed within a system inherently lacking equilibrium. Extensive research has been conducted on amperometric sensors, such as the organic electrochemical transistor (OECT), and potentiometric sensors, like the electrolyte gated organic field effect transistor (EGOFET).In all of these instances, low limit of detection (LOD), and high selectivity and sensitivity, alongside high reproducibility and repeatability, are highly desirable.3 To fulfil these specifications, DoE proves to be extremely useful. Despite the long-standing existence of DoE models, their extensive utilization in optimizing biosensors has been limited, as apparent by the analysis of the development trend diagram in Fig. 3. The development trend illustrates a comparison of research articles focused on biosensor optimization using DoE (red curve) versus the traditional one-variable-at-a-time approach (blue curve) from 1999 to the present. Data from the web of science (WoS) database indicate that the prevailing practice in the field remains the traditional approach of altering one variable at a time. Specifically, out of 2685 research articles on the optimization of biosensing technologies since 1999, only 29 employ a DoE approach. Instead, the prevailing practice in the field remains the traditional approach of altering one variable at a time.32 Rather, DoE can be considered a fundamental instrument for comprehending the influence of individual sensor components, detection conditions, and their combined effects. Moreover, a primary objective of DoE is to minimize the quantity of optimization experiments selecting the independent variables’ values to be tested. This reduction in experimental trials leads to decreased consumption of chemicals and reagents, improved operational efficiency, and a decrease in waste generated from experiments. Therefore, incorporating DoE into the development of sensors aligns with the grounds of green chemistry, which strive to enhance the efficiency and sustainability of thoughtfully designed chemical processes. In the following sections, examples of optical and electronic biosensors' optimization guided by the DoE approach are presented and summarized in Table 4.
| Technology | Transduction mechanism | Target molecule | # Variables | Response | DOE model |
|---|---|---|---|---|---|
| SIMOA33 | Optical | Immunoglobulins | 2 | LOD | Factorial design |
| SIMOA34 | Optical | Cytokine IL-6 d | 2 | LOD | Factorial design |
| SIMOA6 | Optical | CD55, MUC1 | 2 | LOI | Factorial design |
| Bacterial bioluminescent biosensor35 | Optical | Escherichia coli | 6 | Induction ratio, response time, recovery time | Factorial design |
| SPR36 | Optical | 18 predefined regeneration cocktails | 3 | Regeneration effect value | Mixture design |
| Stencil-printed OECT37 | Electrical | — | 3 | On/off ratio, transconductance and threshold voltage | Factorial design |
| pH-responsive hydrogel sensor38 | Electrical | Tissue acidosis | 4 | pH sensitivity | Factorial design |
| Microfluidic biosensor39 | Electrical | Sars-CoV-2 | 7 | Response time of the integrated flow confinement microfluidic biosensor | Factorial design |
| Amperometric glucose biosensor40 | Electrical | Glucose | 2 | Biosensor sensitivity | Factorial design |
| Disposable amperometric DNA biosensor41 | Electrical | Hepatitis C virus genotype 1 DNA | 6 | Current intensity | Factorial design |
| Genosensor42 | Electrical | 86-mer DNA peanut sequence | 2 | Current intensity of signal and blank | Factorial design |
| Amperometric immunoassay43 | Electrical | Clostridium tetani antibody | 4 | Current intensity | Central composite design |
| Biosensor for detection of Salmonella typhimurium44 | Electrical | Salmonella typhimurium | 2 | Current intensity | Central composite design |
| MWCNTs/graphene oxide/pyrogallol composite for sensitive biosensor45 | Electrical | Omeprazole | 3 | Current intensity | Central composite design |
| Electrode surface composition for glucose biosensor fabrication46 | Electrical | Glucose | 3 | Current intensity | Central composite design |
| Glucose biosensor47 | Electrical | Glucose | 2 | Microbial fuel cell sensitivity | Central composite design |
| Multienzyme system48 | Electrical | Sucrose | 3 | Response time | Central composite design |
| Molecularly imprinted biosensor49 | Electrical | Thyroglobulin | 5 | Current intensity | Central composite design |
| Electrochemical biosensor50 | Electrical | Folic acid | 4 | Current intensity | Central composite design |
| Screen-printed biosensors51 | Electrical | Glucose | 3 | Current intensity | Central composite design |
| Biosensors based on acrylic microgels52 | Electrical | Glucose and cathecol | 2 | Current intensity | Central composite design |
| Label free electrochemical nucleic acid biosensors53 | Electrical | Listeria monocytogenes | 3 | Biosensor selectivity | Central composite design |
| Monoamine oxidase (MAO)/horseradish peroxidase (HRP) and diamine oxidase (DAO)/horseradish peroxidase (HRP) based biosensors54 | Electrical | Biogenic amines | 3 | Current intensity | Central composite design |
| Cholesterol biosensor based on nanocellulose55 | Electrical | Cholesterol | 4 | Current intensity | Central composite design |
| Disposable sensors and biosensors for detection of formaldehyde56 | Electrical | Formaldehyde | 2 | Oxidation current | Central composite design |
| Urea based amperometric biosensor57 | Electrical | Hg(II) | 3 | Delta current | Central composite design |
| Acid phosphatase based amperometric biosensors58 | Electrical | As(V) – arsenic | 3 | Delta current | Central composite design |
| CYP450 biosensors based on screen-printed carbon electrodes59 | Electrical | Cocaine | 2 | Current intensity | Central composite design |
| Enzyme stencil-printing for wearable biosensor60 | Electrical | Lactate and glucose | 2 | Electron transfer rate constant and rheological parameter | Central composite design |
Optical biosensors
Among the label-needing bioassays, ELISA continues to be the preferred method for protein detection, boasting a LOD that spans from the 10−9 M to 10−12 M concentrations. Notable progress in this domain involves the evolution of ELISA into the digital sphere. Regarding this, Quanterix has developed a single-molecule assay (SIMOA) technology. The SR-X™ SIMOA has introduced a methodology to simultaneously detect thousands of individual protein molecules, employing reagents similar to those utilized in ELISA.61 This single-molecule immunoassay entails the formation of a sandwich antibody complex into a microscopic beads measuring 2.7 μm in diameter, which are subsequently tagged with an enzyme, similar to the process in a conventional ELISA. These beads are then distributed into femtoliter-sized reaction chambers arrays that are capable of isolating and sensing individual molecules. This enables the conduct of multiplexed protein assays with detection limits below the femtomolar (10−15 M) level. The SP-X planar technology, a more straightforward and practical variation of the SIMOA platform, has recently been introduced. It achieves detection limits in the femtomolar range at its best performance.21Multiple commercially accessible Homebrew SIMOA kits have been developed for customizable assays, aiming to simplify the identification of different proteins in oncology, neurology, and immunology. These kits are used applying dense capturing antibody layers onto the bottom of microplate wells and then using a conventional sandwich-type immunometric chemiluminescent detection technique. The chemiluminescent signal from the arrays is then captured using a CCD camera. Protein concentrations in unknown samples are determined by comparing the intensity of collected signals with those from calibrator solutions. While commercially available ready-to-use SIMOA kits have been developed for numerous clinical applications, Homebrew SIMOA kits must be developed when customizable assays are required. Scandurra et al.33 introduced, for the first time, the development and the enhancement of a SIMOA SP-X Homebrew assay using the DoE approach. This assay was specifically tailored for identifying and measuring a marker of inflammation, the immunoglobulin M (IgM). The biosensor for IgM detection is delineated in Fig. 4a, comprising four fundamental steps. At first, a peptide tag is designed to attach the anti-IgM capture antibodies (CA) to the anchor antibodies, densely printed in circular spots of 600 μm in diameter located at the bottom of the 96-well ELISA plate.
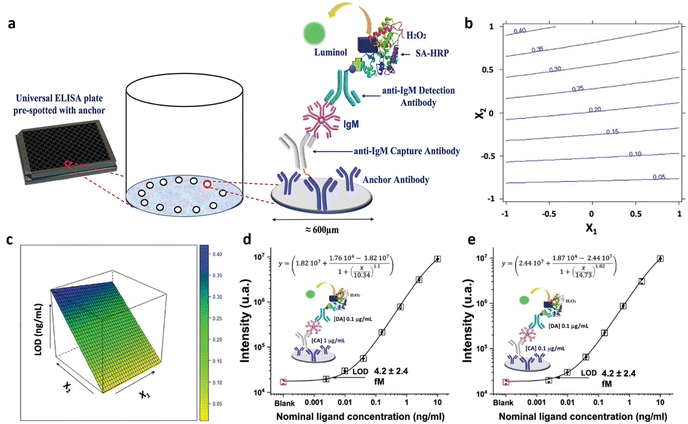 | ||
| Fig. 4 (a) Scheme of the biosensor development; (b) isoresponse contour plot and (c) the response surface for LOD response. IgM calibration curve recorded using (d) 1 μg mL−1 0.1 μg mL−1 and (e) 0.1 μg mL−1 and 0.1 μg mL−1 of CA and DA anti-IgM antibodies respectively. Adapted and reproduced with permission from ref. 35. Copyright 2022, Wiley-VCH under Creative Commons Attribution 4.0 License (CC BY 4.0). | ||
Subsequently, the assay proceeds in a conventional sandwich immunoassay configuration, with the analyte situated between the capture antibody labelled with the peptide and the detector antibodies (DA) holding a biotin functionality. The immunocomplexes are labelled with the streptavidin-horseradish peroxidase enzyme. Finally, into each well luminol and H2O2 are introduced, triggering an interaction between the enzyme and the substrate that causes light to be emitted locally from the immunocomplexes.
The assay includes IgM standard solutions covering a concentration range from 2.5 fM (2.5 × 10−15 M) to 10 pM (10−11 M). A 22 full factorial design was applied to improve the analytical performance of the SIMOA SP-X custom test, encompassing two variables: anti-IgM CA concentration (X1) and the concentration of the DA (X2). Specifically, the assays were executed in triplicate, exploring an experimental domain from 1 to 50 μg mL−1 for both CA and DA concentrations. The proposed model aims to minimize the LOD of SIMOA. The coefficients significance were evaluated to discern the impact of the capture and detection antibody concentrations. Notably, all terms of the model exhibit significance, with the linear terms of X2 demonstrating a larger absolute value compared to others, indicating that an increase in the assay's LOD is observed with elevated detection antibody concentration. Therefore, superior results can be achieved by reducing the concentration of detection antibodies. Furthermore, the linear term for X1 has negative coefficient. The higher CA concentration, the higher the assay sensitivity, as the LOD level is minimized. Additionally, the interaction term between X1 and X2 has been determined to be statistically significant. The response at each point within the experimental range can be visually depicted using an isoresponse contour plot, as shown in Fig. 4b. The isoresponse plot demonstrates that with higher concentrations of the DA, the influence of the CA on the LOD becomes more prominent. Conversely, lowering the concentrations of the DA produces no discernible effect on the concentration of the CA. Moreover, Fig. 4c shows the response surface, which indicates that a lower concentration of the DA corresponds to the optimal condition within the experimental domain. Conversely, increasing the concentration of the CA does not significantly enhance sensitivity but notably impacts the reagent costs of the assay. The demonstrated behavior was confined to the experimental setting, yet exploring its consistency beyond these boundaries was deemed valuable. As a subsequent step, CA and DA concentrations were further reduced beyond the experimental boundaries to optimize assay sensitivity while managing costs. Fig. 4d presents the calibration curve with a LOD of (4.2 ± 2.4) fM, obtained using 1 and 0.1 μg mL−1 of CA and DA respectively. This LOD is 70% lower than that obtained using a standard concentration of 1 μg mL−1 for both CA and DA. The signal-to-background ratio has been enhanced reducing the DA concentration by one order of magnitude, thereby substantially boosting assay sensitivity. Similarly, the impact of lowering capture antibody concentration was investigated. The assay employing the same concentration for both antibodies, that is 0.1 μg mL−1 (Fig. 4e), yielded comparable results in LOD and signal-to-background ratio to that shown in Fig. 4d. Notably, reducing CA concentration by an order of magnitude had a negligible effect on the SIMOA SP-X assay performance but substantially reduced assay costs. Consequently, the authors applied DoE method to achieve an IgM LOD of approximately 4 fM, a competitive result compared to commercially available kits for SIMOA Planar Array. Additionally, the authors demonstrated that using a solution with one order of magnitude less concentrated polyclonal capturing and detecting layers can achieve improved LOD, significantly reducing test costs.
Additionally, a similar approach has been adopted to create a Simoa SP-X assay to measure human Interleukin 6 (IL-6) in blood serum,34 as depicted in Fig. 5a, which outlines the procedure of the biosensor development. Its sensitivity was enhanced using a DoE involving the concentrations of the anti-IL6 capture and detection antibody. A 22 factorial design was used to investigate the experimental domain, shown in Fig. 5b, with the CA and DA concentrations at both lower and higher levels (−1 and +1, respectively), ranging from 0.1 to 5 μg mL−1. Data from experiments carried out at the edges of the experimental field, were utilized to establish a linear model linking the limit of detection with the two variables. Additionally, to calculate the model's coefficients, four separate tests were performed twice. The model's statistical relevance was assessed using the remaining four degrees of freedom. Furthermore, to verify the predictive ability of the model, two extra measures were conducted at the central point, where both the CA and DA concentrations were maintained at 2.5 μg mL−1. The central point showed a predicted LOD of 218 aM, compared with the experimental value of (238 ± 64) aM, where the error is the pooled standard deviation over four degrees of freedom. The predicted and experimental LOD values are statistically comparable, suggesting the model's validity across the full experimental domain. Therefore, the model proved to be robust and acceptable. The developed IL-6 assay achieved a LOD of (57 ± 26) aM. Fig. 5c displays the calibration curve for the IL-6 assay under these optimal conditions. The standard commercial SIMOA kits have a LOD of (1.5 ± 0.8) fM, which is one order of magnitude higher compared to the LOD achieved by the authors using the DoE method. An identical methodology was employed in formulating the SIMOA assay for quantifying MUC1 and CD55 levels among pancreatic cancer patients.6 A 22 factorial design was employed to enhance the limit of identification (LOI), using the concentrations of the CA and DA as variables.2,5 Consequently, the MUC1 assay yielded a LOI of 20 fM, whereas the LOI for CD55 reached a maximum of 5 pM. Furthermore, Horry et al.35 explored the effectiveness of DoE in optimizing a liquid-phase bacterial bioluminescent biosensor. Their objective was to analyze the impact of six growth factors on biosensor's performance metrics. These factors were the concentration of the glucose, the rate of dilution, the levels of oxygen, the decanal concentration, the capacity of the buffer and the temperature. The performance metrics included recovery, response time, and induction ratio. In summary, the study revealed that the identified growth factors were key drivers of the biosensor's performance variations. Utilizing linear regression models derived from statistical analysis, three distinct zones were defined within the experimental domain. While two zones encompassed combinations of growth factors resulting in low induction ratios, the third zone featured local optimum associated with simultaneous increases in induction ratio, response time, and recovery time. Through simultaneous optimization of the three main performance criteria using experimental data, specific combinations of growth factor values were identified. This modeling process underscored the possibility of isolating multiple sets of growth factor values to enhance biosensor performance.
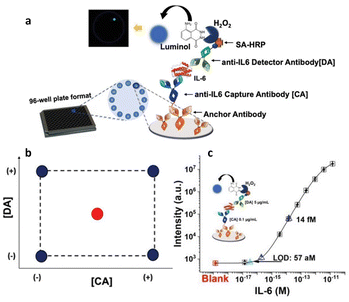 | ||
| Fig. 5 (a) Workflow of the biosensor development; (b) experimental domain; (c) calibration curve with optimal CA and DA concentrations, such as 0.1 μg mL−1 and 5 μg mL−1, respectively. Adapted and reproduced with permission from ref. 34. Copyright 2023, Wiley-VCH under Creative Commons Attribution 4.0 License (CC BY 4.0). | ||
Andersson et al.36 devised an additional pioneering method, employing a mixture design, aiming to optimize an SPR assay targeting the p24 HIV-1 antigen. In pursuit of this objective, the gold detecting interface of an SPR Biacore apparatus was functionalized with monoclonal anti-p24 antibodies utilizing conventional self-assembled monolayer chemistry.3,26,62 The assay for the p24 antigen was conducted employing a regenerative protocol. Such an approach is frequently employed in the majority of SPR assays,63,64 although one of the primary limitations lies in incomplete surface regeneration, resulting in a relatively high and unstable baseline, rendering it unsuitable for analyzing low analyte concentrations.65 Therefore, the optimization of regeneration conditions holds significant importance. This study aims to optimize the regeneration of assay systems that employ antibodies as biorecognition elements. The aim was to disrupt the non-covalent bonds between antigen epitope and antibody paratope ensuring there were no permanent alterations to the antibody–antigen binding properties. A comprehensive regeneration optimization (RO) protocol has been devised, relying on a chemical library encompassing 6 components, each representing different chemical properties of most of the regeneration agents. These components were chaotropic activity/ionic strength (I), acid (A), detergent (D), base (B), chelating agent (C) and nonpolar solvent (U). The regeneration capabilities of 18 predetermined regeneration cocktails (combinations of those 6 components) were initially evaluated during the screening phase. For the subsequent optimization phase, two different designs were utilized. When optimization required focusing on two components, a two-dimensional mixture design was utilized. Conversely, if three components were involved in the optimization, a three-component mixture design was implemented. The definition of the cocktails in the two-component mixture design is shown in Fig. 6a, where the cocktails’ compositions are indicated in the diagram and in the inset of the table. The number shown in superscript on the diagram corresponds, in the table, to the cocktail number. For each cocktail, the value of the regeneration effect (Re) was recorded and used as the response for the mixture design. The response was calculated based on the percentage of analyte that was eliminated following the injection of the cocktail. The response plot depicted in Fig. 6b revealed that combining one volume of component A at pH 4 with one volume of component I, specifically a 0.5 M EDTA solution (v/v 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), achieved complete surface regeneration. Furthermore, Fig. 6c illustrates the composition of the cocktails in the three-component design, with each box representing the composition of a single cocktail comprising the three components. In the context of a three-component mixture design, the chelating agent was introduced to the previous two-component mixture comprising components A and I. The optimized mixture comprises 33% of each component, as reported in Fig. 6d, allowing achieving a complete regeneration of the SPR detecting surface. The experiment led to the identification of a regeneration cocktail that successfully achieved complete regeneration. The cocktail AIC resulted in a Re value as high as 100%. So, the authors proposed an innovative optimization protocol based on mixture design, presents numerous benefits compared to conventional regeneration optimization methods. This protocol is widely applicable as it can be employed with the majority of affinity-based biosensors.
1), achieved complete surface regeneration. Furthermore, Fig. 6c illustrates the composition of the cocktails in the three-component design, with each box representing the composition of a single cocktail comprising the three components. In the context of a three-component mixture design, the chelating agent was introduced to the previous two-component mixture comprising components A and I. The optimized mixture comprises 33% of each component, as reported in Fig. 6d, allowing achieving a complete regeneration of the SPR detecting surface. The experiment led to the identification of a regeneration cocktail that successfully achieved complete regeneration. The cocktail AIC resulted in a Re value as high as 100%. So, the authors proposed an innovative optimization protocol based on mixture design, presents numerous benefits compared to conventional regeneration optimization methods. This protocol is widely applicable as it can be employed with the majority of affinity-based biosensors.
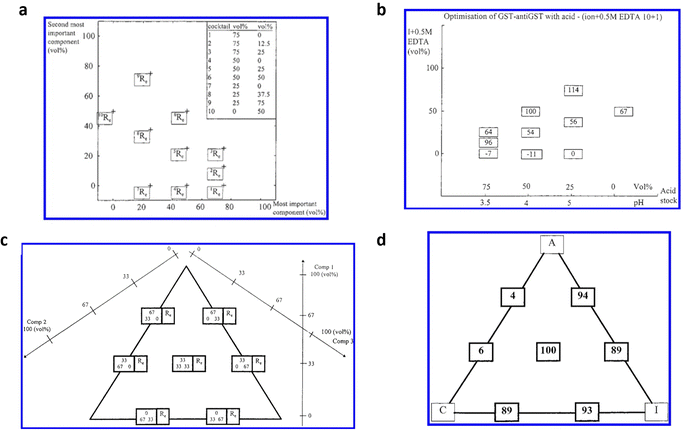 | ||
| Fig. 6 (a) Description of the mixtures in the two-components optimization experiment; the composition of the mixture is reported both in the diagram, and in the table in the inset. Each mixture number in the table is reported as superscript in the diagram. (b) Optimization of regeneration effect value Re; for each mixture, the measured regeneration effect (Re) is plotted in a box at the position corresponding to the mixture composition. (c) Definitions of the experimental domain of the three-components mixture design; the compositions of the three-component mixtures are denoted in the left boxes in the diagram. The mixtures defined at the lower right-hand position in the graph consists of 0 vol% of component 1, 33 vol% of component 2, and 67 vol% of component 3. The right boxes report the calculated Re values for each mixture composition. (d) Response plot from the three components mixture design. The measured Re values are plotted in boxes at positions corresponding to the mixture compositions. Adapted and reproduced with permission from ref. 36. Copyright 2019 American Chemical Society. | ||
Electrical biosensors
Electrical biosensors utilize the interaction between the appropriate biorecognition element, which is attached to the active surface of an electronic transducer, and the target analyte. The transducer is tasked with converting the biochemical signals produced by the biorecognition element/analyte interaction into measurable electrical signals. Therefore, to maximize the analytical performance of such biosensors, it is essential to account for a series of crucial parameters such as the choice of active materials, the experimental conditions for biomolecule's immobilization, and detection protocols. To this aim, different DoE approaches have been devised to maximize the sensitivity, selectivity, and stability of the biosensing devices. Recently, Ghafari et al.37 proposed a procedure for fabricating a stencil-printed organic electrochemical transistor (OECTs), wherein the electrical characteristics can be managed by modifying the manufacturing conditions of the electronic channel. The construction of the OECTs on a glass substrate underwent several stages, illustrated in Fig. 7a. The first step involved gold evaporation onto glass using the shadow masking technique, where the width of the wire attached to the mask determines the gap between the source and drain electrodes. Next, the gold electrodes were cleaned, and a vinyl adhesive mask was applied to define the PEDOT region. Following this, the PEDOT solution was deposited, and the annealing procedure was carried out. The setup then included placing the glass slide into a slide container, with the Ag/AgCl wire acting as the gate of the OECT. The electrolyte used in this setup was a 0.1 M NaCl solution. To enhance the OECT figures of merit, a full factorial design, encompassing three factors each at two levels, has been implemented.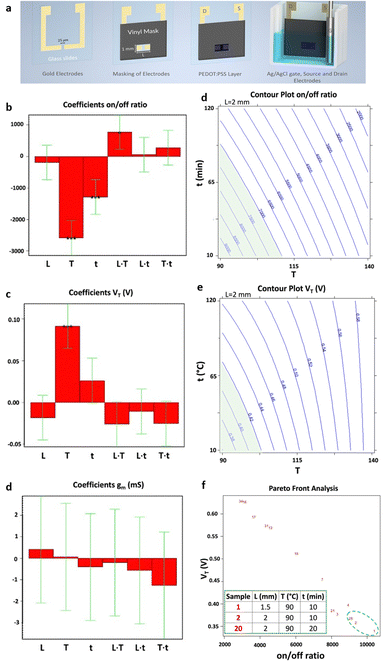 | ||
| Fig. 7 (a) Representation of device fabrication. Bar graph of the coefficients of the models of the three responses: (b) on–off ratio, (c) threshold voltage (VT) and (d) transconductance (gm). Each bar graph displays the coefficients associated with the three factors analysed (L = channel length, T = annealing temperature, and t = annealing time) as well as their interactions. Isoresponse contour plot of (e) on–off ratio and (f) VT. For each of them, the region of acceptability is highlighted in green. (g) Pareto-front analysis for VT and on–off ratio. The table presents the best conditions, highlighted with a green dashed circle in the figure, aiming to maximize and minimizing the on–off ratio and the VT, respectively. Reproduced from ref. 37 with permission from the Royal Society of Chemistry, distribuited under CC BY-NC. | ||
The key parameters included the temperature applied for annealing (T), the time of the annealing step (t) and the length (L) of the stencil-printed active channel, based on an organic semiconductor PEDOT:PSS (poly(3,4-ethylenedioxythiophene) polystyrene sulfonate). The 23 full factorial design included the on–off ratio, the transconductance (gm) and the threshold voltage (VT), as responses. In the experimental design, each condition's response was analyzed twice in a random order, allowing for the estimation of the significance of each coefficient with eight degrees of freedom.
Repeated measurements were conducted at the central point, where the active channel length was 2 mm and subjected to annealing for 65 minutes at 115 °C. This was done to confirm the validity of the linear model. Fig. 7b and c displays the model coefficients for the threshold voltage and the on–off ratio. Their significance levels are denoted by the asterisks (*p < 0.05, **p < 0.01, and ***p < 0.001). For both designs, the highest leverage achieved was as low as 0.43, indicating that the response predictions are more accurate than the experimental data measured under the identical conditions. The initial observation pertains to the on–off ratio, with its coefficients depicted in Fig. 7b, aiming for maximization. Notably, the linear term of X2 exhibits a notably higher absolute value compared to others, implying a decrease in response with increasing annealing temperature. Additionally, the linear factors associated with X3, which represents annealing time, have a notable impact on the on–off ratio, decreasing as the annealing time increases. The interaction between temperature of annealing and active channel length is notable, indicating a stronger impact of annealing temperature at shorter lengths. The subsequent focus is on the threshold voltage, whose coefficients are shown in Fig. 7c as bar plot, necessitating minimization to achieve the smallest possible subthreshold swing. In this context, the linear term of X2 emerges as the sole significant factor affecting the threshold voltage. A 25 °C increase in annealing temperature corresponds to a 100 mV rise in threshold voltage, indicating a roughly 20% variation. As X2 does not participate in interaction with other variables, the impact of the temperature of annealing remains consistent regardless of the values of active channel length and time of annealing. Furthermore, as illustrated in Fig. 7d, the transconductance shows no significant dependency on the other factors analyzed across the entire range of experiments, indicating that its average value remains (28.0 ± 3.4) mS, independently of the other variable values. Isoresponse curves for the on–off ratio and VT, depicted in Fig. 7e and f, investigate the entire spectrum of annealing time and temperature while maintaining a fixed stencil length of 2 mm. These curves clearly illustrate that reducing both the temperature and the time of annealing decreases VT and increases the on–off ratio. A multicriteria-based decision-making procedure using Pareto-front analysis was performed to find the best experimental conditions that would simultaneously meet the acceptability criteria for threshold voltage and on–off ratio in the further development of a biosensing platform. In Fig. 7g, the green dashed circle indicates the optimal conditions. The group includes 3 samples: one measuring 1.5 mm in stencil length annealed at 90 °C for 10 minutes, and two with 2 mm of length, annealed at 90 °C one for 10 minutes and another for 20 minutes. Among these conditions, the authors selected the sample with a length of the stencil of 2 mm annealed for 10 minutes at 90 °C as the best condition due to its more manageable geometrical parameter. The OECT devices obtained through the stencil printing technique, known for their efficiency, affordability, and rapidity, demonstrate substantial transconductance at minimal operating voltages. Utilizing the DoE, the threshold voltage, with a value of 260 mV, was minimized while maintaining a high on–off ratio of 7 × 103. Significantly, a signal/noise ratio of up to 40 dB was achieved, marking one of the highest reported values for this kind of devices functioning in an aqueous electrolyte under direct current mode. Following the DoE methodology, the morphology of the OECTs was assessed using atomic force microscopy (AFM). The evaluation of structural characteristics and electric performance formed the basis for establishing a connection between the microstructure of PEDOT:PSS and the annealing condition. The DoE approach has thus yielded valuable insights into the influence of fabrication parameters on the electrical conduction characteristics of PEDOT-PSS films. One of the most commonly adopted responses in the biosensor's optimization is the device sensitivity. In this regard, a full factorial design was employed by Mignani et al.40 to detect the optimal conditions to fabricate the biofunctionalized working electrode of an amperometric glucose biosensor. Specifically, a glucose biosensor was devised by employing a clay matrix (Ni/Al–NO3 HT) as a substrate for embedding the enzyme glucose oxidase (GOx). The clay matrix was synthesized electrochemically to ensure consistency, and GOx was immobilized during this process. To prevent enzyme detachment, glutaraldehyde vapors were utilized for cross-linking. The biosensor sensitivity to glucose, crucial for its effectiveness, was influenced by parameters associated with the electrochemical synthesis. In this study, the authors used a full-factorial design to establish the best parameters for electrochemical synthesis, aiming to enhance biosensor performance. The concentration of the enzyme and the molar ratio of nickel to aluminum, emerged as the pivotal factors. These two variables are used to uncover linear interactions and underscore the importance of enzyme concentration and its interplay with Ni/Al molar ratio. Three additional replicates were conducted at the minimum setting for both factors, supplementing the original nine DoE experiments. Furthermore, for the validation of the model, three independent experiments were performed. A custom-made electrode was utilized for each experiment, with the sensitivity of the biosensor calculated individually for every trial. According to the experimental setup, the preferred Ni/Al ratio falls between 3 and 4, while the ideal GOx concentration is 3 mg mL−1. The biosensor, manufactured with a Ni/Al ratio equal to 3 and an enzyme concentration of 3 mg mL−1, exhibited a glucose sensitivity of (6.2 ± 0.2) × 10−6 A mM−1 cm−2, measured in electrode area units. Initially, this figure may appear relatively modest when juxtaposed with values documented in existing literature. As an example, Shan et al.66 immobilized in a similar matrix the GOx, achieving a sensitivity value of (34.8 ± 0.7) × 10−6 A mM−1 cm−1 in the development of a biosensor for glucose sensing. However, the quantity of GOx distributed on their electrode surfaces was approximately 1400 μg cm−2. Differently, in their study the authors achieved a higher sensitivity by using a concentration of GOx as low as 46 μg cm−2. Moreover, the refined experimental parameters for electrodeposition ensure excellent reproducibility in biosensor production. The relative standard deviation linked to the sensitivity of five distinct electrodes, derived from a Ni/Al ratio of 3 and a concentration of the enzyme of 3 mg mL−1, was at most of 5%. This outcome exceeds the sensitivity of similar sensors using a comparable enzyme concentration by a factor of ten, surpassing the current state of the art.66 Bhat et al.38 used a full factorial design to optimize a pH-responsive hydrogel sensor, to monitor tissue acidosis in real time, which may occur as a result of traumatic hemorrhaging. This approach enables the rapid identification of optimal process conditions while minimizing the required number of experiments. The effects of a hydrophilic/hydrophobic mixture was investigated using a full factorial design. A sensitive hydrogel based on poly(HEMA) was developed for detecting pathophysiological pH levels within the range of 7.35–7.45, enabling the measurement of small fluctuations linked to tissue acidosis. Kaziz et al.39 utilized DoE approach to enhance the performance of a microfluidic device for SARS-COV-2 detection. The aim was to minimize detection time by optimizing seven variables: Reynolds, Damkohler and Schmidt number, equilibrium dissociation constant, confinement position, relative adsorption capacity and confinement coefficient. Through the application of DoE, the optimal combination of the variables was determined to achieve the shortest response time. Furthermore, it was illustrated that among all the optimization factors, the relative adsorption capacity, measuring the difference of the density of analytes between the biofunctionalized surfaces and the bulk, contributed the most (37%) to reducing the time of the response. Moreover, the Schmidt number, which varies inversely with the antigen diffusion coefficient, had the least contribution (7%). A full factorial design has been proposed by López et al.42 to optimize the LOD of the proposed device for the ultrasensitive DNA sequence detection, comprising 86 bases, encoding the allergenic conglutin-homolog protein from peanut. The working electrode comprises a screen-printed gold electrode modified with the capture probe. This probe is attached using a mixed self-assembled monolayer, as illustrated in step 1 of Fig. 8a. The DNA target binds in solution a biotinylated-detecting complementary probe (Fig. 8a step 2), and subsequently is immobilized on the modified electrode through the capture probe in a sandwich assay (Fig. 8a step 3). Then, the conjugation with streptavidin-alkaline phosphatase occurs to accomplish the electrochemical detection (Fig. 8a step 4). The optimization of the detecting interface composition has been carried out using a DoE approach aiming at maximizing the signal-to-noise ratio of the assay. Remarkably, the initial design involving 13 process variables was conducted to determine the factors yielding the most substantial influence on the response. Based on this screening, a further full factorial design was performed, investigating the influence of the concentrations of capture probe (cCP) and 6-mercapto-1-hexanol molecule (cMCH), acting as a spacer in the self-assembled monolayer structure, on the sensor analytical performance. Two factorial designs were evaluated taking the relative current change registered with the blank (blank) and after exposure to increasing concentration of the target DNA strand (signal). multiple response optimization was then employed to simultaneously maximize the signal while minimizing the blank, namely the noise. The overlay contour plots and the response surface for each response are illustrated in Fig. 8b and c. These plots highlight the range for cCP and cMCH that meet both response criteria. The upper table in Fig. 8d presents the combinations of the levels of the variables that allow achieving the best value of the desirability function within the defined range, while the other table indicates the best values reached. The optimal concentrations were determined to be 3.15 mM for the mercaptohexanol and 1.34 μM for the capture probe. The biosensor performance was enhanced by implementation under optimum conditions to reach the low LOD of 10 pM, which is two orders of magnitude below what similar amperometric sensors achieved.67 Uliana et al.41 also employed a 23 full factorial design to optimize a DNA-based device for early detection of hepatitis C infections. The proposed approach aimed to optimize the assay sensitivity as a function of the process parameters involved in the biotinylated DNA probe immobilization. The optimized amperometric sensor was employed in ten HCV-infected patients for detecting HCV genotype 1, while 20 healthy volunteers are taken as control group. The sensor was benchmarked against the standard qualitative test, namely Amplicor Hepatitis C Virus, demonstrating a LOD of 600 viral copies per mL.68
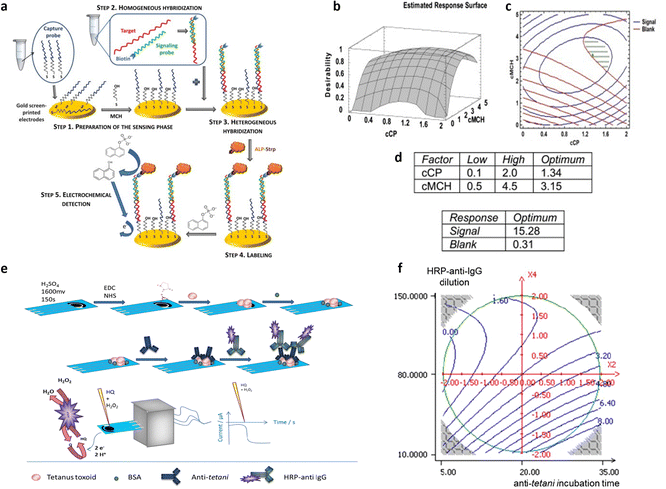 | ||
| Fig. 8 (a) Genosensor scheme; (b) response surface for desirability function, (c) contour plots for blank and signal; (d) best values (upper table) and responses (bottom table) for cCP and cMCH Adapted and reproduced with permission from ref. 42. Copyright 2014 Elsevier B.V. All rights reserved. (e) Representation of the amperometric immunoassay for Clostridium tetani antibody detection; (f) 2D contour plot of anti-tetani incubation time and HRP-anti-IgG dilution. The other two variables were fixed at their optimal values (concentration of BSA of 1.375% (m/v) and time of the HRP-anti-IgG incubation of 20 min). Adapted and reproduced with permission from ref. 43. Copyright 2015 Elsevier B.V. All rights reserved. | ||
Furthermore, the DoE approach proved well-suited to facilitate the optimization of biosensors for bacterial detection. Patris et al.43 utilized a central-composite design, aiming to maximize the response current signal of an amperometric immunosensor enabling the ultrasensitive and rapid detection of the Gram-positive bacterium Clostridium tetani. The proposed immunosensor features the covalent immobilization of the anti-tetani biorecognition element through self-assembled monolayer chemistry on a screen-printed electrode, as illustrated in Fig. 8e. The DoE was utilized to optimize the immunoassay response, focusing on four biofunctionalization process variables: the incubation time of the anti-tetani biorecognition element, the bovine serum albumin blocking agent concentration and the concentration of the detector antibody marked with horseradish peroxidase enzymatic. The model's response was defined by the amperometric signal measured when the bacterium was present at a concentration 2 × 107 CFU mL−1. Specifically, a circumscribed central composite design (CCCD) was formulated. Twenty-five experiments were conducted in random order, while 7 replicates of the center point were acquired to assess model variability. Additionally, five test points were included to validate the constructed model. Residual analysis was implemented to assess the predictive capacity of the model by comparing the experimental and predicted outcomes for each experiment. The latter indicates the acceptability of the model in the whole experimental domain. The investigation of the optimal experimental conditions was conducted to obtain the biofunctionalization settings providing the highest current signal, and the outputs are shown in the 2D isoresponse contour plot in Fig. 8f. The figure highlights that the most significant variables affecting the response are the labeled antibody dilution factor and the incubation time of the anti-tetani antibody. Specifically, to optimize the response, the concentration of the detector antibody marked with the enzymatic label should be reduced, while increasing the incubation time for the capturing anti-tetani antibody. Conversely, the concentration of the BSA and the incubation time for HRP-anti-IgG exerted minimal influence. Upon optimization, the immunoassay achieved a limit of detection and a limit of quantification of 4 × 105 CFU mL−1 and 5 × 105 CFU mL−1 respectively, both surpassing the bacterium assay carried out with ELISA state-of-the-art immunometric test. Additional research has reported on the application of DoE models to enhance the sensitivity of biosensors targeting foodborne bacterial pathogens. For instance, Melo et al.44 explored the application of a central-composite design to optimize the biosensor performance for Salmonella typhimurium. To this end, the working gold electrode of an amperometric sensor was modified using the self-assembled monolayer, immobilizing the anti-Salmonella antibodies using cysteamine thiol and protein A. The analytical response of the biosensor was elicited via a secondary antibody labelled with a peroxidase enzyme, and the signal was assessed using chronoamperometry. The two independent variables incorporated into the DoE model were the concentrations of hydrogen peroxide and hydroquinone, utilized as electrolytes in the electrochemical cell. The optimized biosensor exhibited a time-to-result of 125 minutes and a LOD of 10 CFU mL−1, thereby underscoring the device's potential for applications in food safety and emergency response. Another foodborne pathogen is Listeria monocytogenes, commonly found in domestic and food processing environments. Urkut et al.53 introduced a label-free electrochemical-nucleic-acid biosensor for detecting Listeria monocytogenes amplicons. They utilized a three-factor central composite design to explore the impact of different hybridization parameters, such as salt and target concentrations, and the time of hybridization, on biosensor selectivity. The selectivity ratio, calculated as the ratio between the electrochemical signals recorded during hybridization with the complementary probe and those from the negative control experiment, served as the model's response. The optimized sensor was proven capable of detecting Listeria monocytogenes amplicons obtained from 12 food samples and benchmarked against state-of-the-art polymerase chain reaction (PCR). The results obtained with the optimized electrochemical sensors are all confirmed by PCR. Abdi et al.55 proposed central composite design to find the best experimental conditions to fabricate an ultrasensitive biosensor to detect cholesterol. As depicted in Fig. 9a, the electrochemical biosensor was developed starting from the immobilization of cholesterol oxidase (ChOx) onto screen-printed working electrode (SPE) modified with polyaniline/crystalline nanocellulose/ionic liquid (PANi/CNC/IL). Based on the data obtained from a first screening DoE, significant experimental parameters were determined, namely the enzyme concentration, the electrolyte ionic strength, the concentration of glutaraldehyde (GLU) crosslinking agent, and the concentration of PANi/CNC nanocomposite. The objective was to maximize the peak current obtained from differential pulse voltammetry when exposed to a cholesterol solution with a concentration of 1.0 M. Fig. 9b shows the residual analysis, illustrating the residuals between predicted and experimental responses taken according to the DoE experimental matrix. The authors obtained a coefficient of determination (R2) for the model of 0.86, signifying that the model accounts for 86% of the response variability. For a more comprehensive understanding of how individual variables influence the current response, response surfaces were visualized as 3D isoresponse contour plots, as shown in Fig. 9c–f. Each plotted surface represents the interaction of two variables while holding the others at their central point values. As shown in Fig. 9c, a higher ionic strength combined with a reduced enzyme quantity improves the current signal. Fig. 9d shows the impact of PANi/CNC nanocomposite and enzyme concentration on the current, illustrating that increasing the PANi/CNC amount drastically boosts the current response while decreasing the enzyme quantity. From Fig. 9e, it is clear that an increase in the ionic straight enlarges the response, with an optimal GLU amount observed at 4.7 μL. Finally, Fig. 9f demonstrates that both the nanocomposite sample and GLU amounts contribute to an increase in the amperometric response, though beyond 8.3 μL of GLU, a decrease in the current is observed with increasing the nanocomposite concentration. In summary, both GLU and nanocomposite concentration have a significant interaction. The optimized biosensor, fabricated according to the finding collected with the DoE, was validated for cholesterol detection, demonstrating a dynamic linear range covering five orders of magnitude of analyte concentrations, with a LOD of 48 pM. Moreover, the suggested biosensor demonstrated satisfactory repeatability and reproducibility, even though coexisting electroactive compounds, such as glucose and ascorbic acid, showed minimal interference.
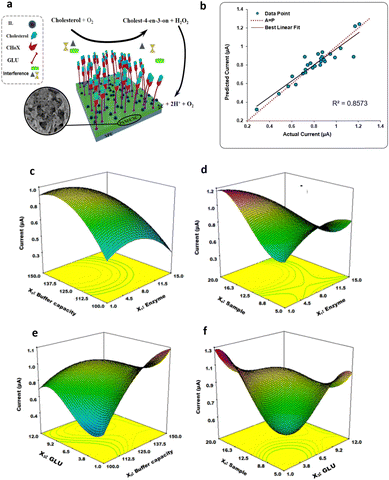 | ||
| Fig. 9 (a) Depiction of the electrode modification process; (b) predicted versus actual current values; response surface plot of the combination of (c) enzyme concentration and buffer capacity, (d) nanocomposite sample and enzyme concentration, (e) GLU and ionic strength, (f) GLU quantity and sample concentration on the current response. Adapted and reproduced with permission from ref. 55 Copyright 2019 Elsevier B.V. All rights reserved. | ||
Central composite design has also guided the optimization of many electronic biosensors detecting small molecules, drugs, biogenic amines, toxic elements like mercury oxide or arsenic, and metabolites.49,50,54,56–59 Sensor-detecting interface composition, pH of the electrolyte solution, deposition times, enzymatic mediators’ concentration or applied potential are just some of the variables considered in these studies to obtain a LOD in the sub-picomolar range. Special consideration has been given to the optimization of amperometric sensors tailored for glucose detection, through the application of central composite designs.
For instance, Kocoglu et al.46 utilized this method to optimize the working electrode surface composition, analysing three variables, namely the concentrations of titanium dioxide nanoparticle, carboxylated multiwall carbon nanotube, and glucose oxidase, aiming to maximize the biosensor selectivity. The sensor, fabricated in accordance with the findings of the DoE was used in human serum samples, to detect glucose. Subsequently, the obtained results were compared with those derived from the state-of-the-art spectrophotometric method, showing no statistical disparity, at a confidence level of 95%, between the outcomes of the two methods. Similarly, Gonzalo-Ruiz et al.51 employed the same approach for glucose determination in white wine samples, using applied potential, mediator concentration in solution, and enzymatic activity as variables to minimize the device-to-device fluctuation, thus improving the biosensor reproducibility. Utilizing a central composite design, they improved the chronoamperometric signal, achieving a maximum device-to-device fluctuation of 6.5%, measured on 5 different biosensors in the optimized configuration. Furthermore, in their investigation, Retama et al.52 fabricated a biosensor for glucose and catechol detection, applying an experimental design methodology to probe the biosensor behaviour by varying the pH and temperature of the electrolyte solution at both low and high substrate concentrations. This facilitated the authors in distinguishing between the irreversible or reversible influence of those factors on enzymatic activity, and thus on biosensor response. Specifically, 14 experiments were conducted, encompassing all potential combinations of pH and, in a random sequence, with eight replicates at the central point. The relative current changes upon exposure to glucose and catechol analytes correspond to the response of the central composite design. The experimental design demonstrated a reversible impact of pH on enzyme activity, while the optimal temperature value determined through experimental design was 10 °C lower than that of state-of-the-art characterization, attributable to enzyme activity degradation caused by irreversible thermal denaturation. Dessie et al.47 proposed the DoE approach to optimize the sensitivity of a biosensor with a microbial-fuel-cell for detection of the glucose. They proposed an economical and eco-friendly approach using polyvinyl alcohol (PVOH) as a binder to creatine a polyaniline/pencil graphite (PANI/PG) electrode. Through a two-factor central-composite design, the influence of PVOH immobilization on a PANI/PG anode on the analytical performance of a glucose microbial-fuel-cell was assessed. Key parameters, such as initial glucose concentrations and the mass ratios of PVOH binder, were analyzed to evaluate the performance of the biosensor. The peak sensitivity for glucose was observed at a PVOH mass of approximately 15.3 wt% and an initial glucose concentration of 0.72 mM, resulting in enhanced sensitivity compared to commercially available electrodes. Gouda et al.48 proposed a multienzyme system for a sucrose biosensor, aiming to optimize the assay time-to-result while minimizing enzyme consumption, using a quadratic model. The latter involved investigating the linear, quadratic, and cross-product effects of three factors (three-enzyme concentrations). Three replicates of the center point were assessed to increase prediction accuracy. To optimize multienzyme concentrations for minimizing biosensor response time, a central composite design was applied, focusing on glucose oxidase concentration, invertase and mutarotase. Under optimal conditions the predicted and actual response times showed perfect alignment, with values of 2.26 and 2.35 minutes, respectively.
Experimental design methods have been proposed also to optimize biosensor manufacturing processes. For instance, Marchianò et al.60 employed a DoE methodology to formulate graphite-conductive-ink, comprising chitosan, glycerol and graphite as constituents, for the development of fully printed wearable biosensors aimed at monitoring glucose and lactate levels. The study aimed to achieve fully printed enzyme-based amperometric biosensors on flexible substrates. The experimental design encompassed rheological and electrochemical parameters, as illustrated in Fig. 10a. A two-factor face-centered design was employed to analyze the interaction between these variables and their influence on ink formulation. The variables investigated were the percentage of chitosan and ratio of graphite to glycerol, chosen to explore standard experimental ranges for formulating water-based conductive ink, ranging from 1.5% to 2.1% chitosan and 85% to 95% graphite, with 15% and 5% of glycerol, respectively. The evaluated responses included the electron transfer rate (k0), the electroactive area (AEA), and the rheological parameter tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = G′′/G′, all of which were targeted for maximization. Fig. 10b–d present bar plots illustrating the coefficients for each response with the confidence interval at p = 0.05. The significance is indicated by the stars in the figure (* = p < 0.05; ** = p < 0.01). Fig. 10e–l depict the uncertainty of prediction, showing the contour plots for both responses and semi-amplitude of the confidential interval of the response. Regarding the first response, AEA, the importance of the linear terms implies that it decreases with lower chitosan level and increases with higher graphite content. Additionally, the quadratic term for chitosan indicates non-linear behavior. However, for the second response, k0, the variance is explained by the model only for 13% and does not present coefficients with high significance, offering no insights on the variables’ effects. In the model for the tan
δ = G′′/G′, all of which were targeted for maximization. Fig. 10b–d present bar plots illustrating the coefficients for each response with the confidence interval at p = 0.05. The significance is indicated by the stars in the figure (* = p < 0.05; ** = p < 0.01). Fig. 10e–l depict the uncertainty of prediction, showing the contour plots for both responses and semi-amplitude of the confidential interval of the response. Regarding the first response, AEA, the importance of the linear terms implies that it decreases with lower chitosan level and increases with higher graphite content. Additionally, the quadratic term for chitosan indicates non-linear behavior. However, for the second response, k0, the variance is explained by the model only for 13% and does not present coefficients with high significance, offering no insights on the variables’ effects. In the model for the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ response, the only significant coefficient id the interaction between the variables X1 and X2. The response surface plot, depicted in Fig. 10g, illustrates that the maximum response is achieved when both variables are either at their highest or lowest levels. The highest predicted values for the AEA response were obtained with the latter condition, resulting in the preferred condition. Therefore, after analyzing the response surfaces, the optimal condition involves 95%, 5% and 1.5% of graphite, glycerol and chitosan, respectively. This optimal condition resulted in the highest predicted value for all responses. Additionally, the authors incorporated glucose oxidase and lactate oxidase into the graphite conductive ink. The biosensors produced from these inks exhibited a low LOD and an exceptional sensitivity, recording values of 4.3 μA mM−1 and 3.3 μA mM−1, respectively, with ferricyanide serving as the electron mediator.
δ response, the only significant coefficient id the interaction between the variables X1 and X2. The response surface plot, depicted in Fig. 10g, illustrates that the maximum response is achieved when both variables are either at their highest or lowest levels. The highest predicted values for the AEA response were obtained with the latter condition, resulting in the preferred condition. Therefore, after analyzing the response surfaces, the optimal condition involves 95%, 5% and 1.5% of graphite, glycerol and chitosan, respectively. This optimal condition resulted in the highest predicted value for all responses. Additionally, the authors incorporated glucose oxidase and lactate oxidase into the graphite conductive ink. The biosensors produced from these inks exhibited a low LOD and an exceptional sensitivity, recording values of 4.3 μA mM−1 and 3.3 μA mM−1, respectively, with ferricyanide serving as the electron mediator.
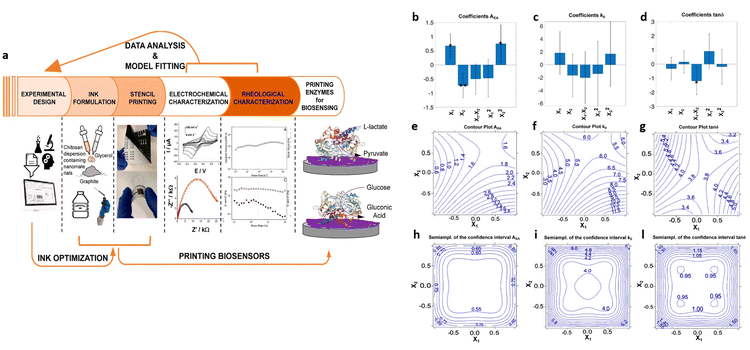 | ||
| Fig. 10 (a) Illustration of the biosensor development; (b)–(d) bar plot of the coefficients at p = 0.05; asterisks denote coefficient significance (* = p < 0.05, ** = p < 0.01).; contour plots of (e)–(g) the three responses and (h)–(l) semi-amplitude of the confidential interval of the responses. Adapted and reproduced with permission from ref. 60. Copyright 2023, published by American Chemical Society under CC-BY 4.0. | ||
Conclusions and future perspectives
The preceding examples have demonstrated the efficacy of DoE as a method for optimizing the analytical performance of biosensors, encompassing both optical and electronic transduction mechanisms. The primary experimental design models and their typical workflow have been discussed, along with several instances of optimized optical and electronic biosensors, emphasizing the advantages of employing DoE over univariate approaches. The quality of data obtained through data-driven models has been highlighted. Despite the evident benefits of DoE, its adoption within the biosensors’ community remains limited, with traditional one-variable-at-time approaches prevailing. However, DoE offers comprehensive insights, providing maximum information for optimization while typically requiring a minimal number of predetermined experiments. This reduction in experimental iterations minimizes chemical and reagent consumption, enhances operational efficiency, and reduces waste generation. Therefore, integrating DoE into biosensor development aligns with the principles of green chemistry, thereby enhancing the efficacy and sustainability of chemical processes. However, solely emphasizing DoE without considering the chemical aspects of the work may obscure genuine innovation and hinder discussions on how sensor components improve analytical capabilities. Instead, DoE should be utilized to understand the impact of individual sensor components, detection conditions, and their synergistic interactions. DoE presents a valuable tool for advancing point-of-care diagnostics while promoting the principles of green chemistry and sustainability. Encouraging wider adoption of DoE within the biosensor's community requires equipping researchers with knowledge of chemometrics, enabling effective utilization of these tools in research. Ultimately, the successful implementation of DoE promises to enhance chemical sustainability, improve sensor performance, and expedite the deployment of advanced biosensors across various fields.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Prof. Riccardo Leardi and Dr Emanuele Farinini are acknowledge for useful discussions. Centro di Innovazione Regionale Digital Assay, Regione PUGLIA Delibera Regionale n 702 del 08/11/2022 CUP B93C22000840001; NoOne-A binary sensor with single-molecule digit to discriminate biofluids enclosing zero or at least one biomarker, ERC Stg2021, GA:101040383; PRIN project prot.2017RHX2E4 “At the forefront of Analytical ChemisTry: disrUptive detection technoLogies to improve; Italian network of excellence for advanced diagnosis (INNOVA), Ministero della Salute -code PNC-E3-2022-23683266 PNC-HLS-DA, CUP: C43C22001630001; Complementary National Plan PNC-I.1 “Research initiatives for innovative technologies and pathways in the health and welfare sector” D.D. 931 of 06/06/2022, DARE – DigitAl lifelong pRevEntion initiative, code PNC0000002, CUP: B53C22006420001; Tecnologie portatili e protocolli innovativi per la diagnosi ultrasensibile di Xylella fastidiosa direttamente in piante e vettori (1LIVEXYLELLA) Ministero dell’agricoltura, della sovranità alimentare e delle foreste – MIPAAF D.M. n.419161 del 13/09/2022; Research actions for reducing the impact on agricultural and natural ecosystems of the harmful plant pathogen Xylella fastidiosa (REACH-XY) – CUP B93C22001920001. PNRR MUR project PE0000023-NQSTI – National Quantum Science and Technolgy Institute; MUR – Dipartimenti di Eccellenza 2023-2027 – Quantum Sensing and Modelling for One-Health (QuaSiModO) are acknowledged for partial financial support.Notes and references
- E. Macchia, K. Manoli, C. Di Franco, G. Scamarcio and L. Torsi, New trends in single-molecule bioanalytical detection, Anal. Bioanal. Chem., 2020, 412, 5005–5014 CrossRef CAS.
- E. Macchia, F. Torricelli, M. Caputo, L. Sarcina, C. Scandurra, P. Bollella, M. Catacchio, M. Piscitelli, C. Di Franco, G. Scamarcio and L. Torsi, Point-Of-Care Ultra-Portable Single-Molecule Bioassays for One-Health, Adv. Mater., 2023, 36, 2309705 CrossRef.
- E. Macchia, F. Torricelli, P. Bollella, L. Sarcina, A. Tricase, C. Di Franco, R. Österbacka, Z. M. Kovács-Vajna, G. Scamarcio and L. Torsi, Large-Area Interfaces for Single-Molecule Label-free Bioelectronic Detection, Chem. Rev., 2022, 122, 4636–4699 CrossRef CAS PubMed.
- S. K. Sailapu, E. Macchia, I. Merino-Jimenez, J. P. Esquivel, L. Sarcina, G. Scamarcio, S. D. Minteer, L. Torsi and N. Sabaté, Standalone operation of an EGOFET for ultra-sensitive detection of HIV, Biosens. Bioelectron., 2020, 15, 112103 CrossRef PubMed.
- E. Genco, F. Modena, L. Sarcina, K. Björkström, C. Brunetti, M. Caironi, M. Caputo, V. M. Demartis, C. Di Franco, G. Frusconi, L. Haeberle, P. Larizza, M. T. Mancini, R. Österbacka, W. Reeves, G. Scamarcio, C. Scandurra, M. Wheeler, E. Cantatore, I. Esposito, E. Macchia, F. Torricelli, F. A. Viola and L. Torsi, A Single-Molecule Bioelectronic Portable Array for Early Diagnosis of Pancreatic Cancer Precursors, Adv. Mater., 2023, 35, 2304102 CrossRef CAS PubMed.
- C. Scandurra, K. Björkström, M. Caputo, L. Sarcina, E. Genco, F. Modena, F. A. Viola, C. Brunetti, Z. M. Kovács-Vajna, C. Di Franco, L. Haeberle, P. Larizza, M. T. Mancini, R. Österbacka, W. Reeves, G. Scamarcio, M. Wheeler, M. Caironi, E. Cantatore, F. Torricelli, I. Esposito, E. Macchia and L. Torsi, Analysis of Clinical Samples of Pancreatic Cyst's Lesions with A Multi-Analyte Bioelectronic Simot Array Benchmarked Against Ultrasensitive Chemiluminescent Immunoassay, Adv. Sci., 2024, 2308141, 1–14 Search PubMed.
- R. Leardi, Experimental design in chemistry: A tutorial, Anal. Chim. Acta, 2009, 652, 161–172 CrossRef CAS PubMed.
- D. Palací-López, P. Villalba, P. Facco, M. Barolo and A. Ferrer, Improved formulation of the latent variable model inversion–based optimization problem for quality by design applications, J. Chemom., 2020, 34, 1–18 CrossRef.
- E. Tomba, M. Barolo and S. García-Muñoz, General framework for latent variable model inversion for the design and manufacturing of new products, Ind. Eng. Chem. Res., 2012, 51, 12886–12900 CrossRef CAS.
- S. Addelman, Statistic of Experiments, Technometrics, 1979, 21, 387–388 CrossRef.
- D. Bonvin, C. Georgakis, C. C. Pantelides, M. Barolo, M. A. Grover, D. Rodrigues, R. Schneider and D. Dochain, Linking Models and Experiments, Ind. Eng. Chem. Res., 2016, 55, 6891–6903 CrossRef CAS.
- C. M. Jaeckle and J. F. MacGregor, Industrial applications of product design through the inversion of latent variable models, Chemom. Intell. Lab. Syst., 2000, 50, 199–210 CrossRef CAS.
- J. G. Pigeon, Statistics for Experimenters: Design, Innovation and Discovery, Technometrics, 2006, 48, 303–304 CrossRef.
- R. E. Kempson and R. Mead, The design of Experiments, Statistician, 1990, 39, 91 CrossRef.
- J. A. Cornell, The Original Mixture Problem: Designs and Models for Exploring the Entire Simplex Factor Space, Experiments with Mixtures, 2002, pp. 22–95 CAS.
- A. Hulanicki, S. Glab and F. Ingman, Chemical sensors definitions and classification, Pure Appl. Chem., 1991, 63, 1247–1250 CrossRef.
- L. Torsi, M. Magliulo, K. Manoli and G. Palazzo, Organic field-effect transistor sensors: A tutorial review, Chem. Soc. Rev., 2013, 42, 8612–8628 RSC.
- Y. Park, T. V. Dang, U. Jeong, M. Il Kim and J. Kim, Comparison of Optical and Electrical Sensor Characteristics for Efficient Analysis of Attachment and Detachment of Aptamer, Biosensors, 2022, 12, 979 CrossRef CAS.
- O. Smutok and E. Katz, Biosensors: Electrochemical Devices—General Concepts and Performance, Biosensors, 2023, 13, 44 CrossRef CAS.
- C. Chen and J. Wang, Optical biosensors: An exhaustive and comprehensive review, Analyst, 2020, 145, 1605–1628 RSC.
- C. I. Tobos, S. Kim, D. M. Rissin, J. M. Johnson, S. Douglas, S. Yan, S. Nie, B. Rice, K. J. Sung, H. D. Sikes and D. C. Duffy, Sensitivity and binding kinetics of an ultra-sensitive chemiluminescent enzyme-linked immunosorbent assay at arrays of antibodies, J. Immunol. Methods, 2019, 474, 112643 CrossRef CAS.
- R. De La Rica and M. M. Stevens, Plasmonic ELISA for the ultrasensitive detection of disease biomarkers with the naked eye, Nat. Nanotechnol., 2012, 7, 821–824 CrossRef CAS.
- M. Rao, K. Kapila and R. Gupta, Enzyme Linked Immunosorbent Assay Revisited, Med. J. Armed Forces, 1997, 53, 45–51 CrossRef.
- L. Sarcina, E. Macchia, G. Loconsole, G. D’Attoma, P. Saldarelli, V. Elicio, G. Palazzo and L. Torsi, Surface Plasmon Resonance Assay for Label-Free and Selective Detection of Xylella Fastidiosa, Adv. NanoBiomed Res., 2021, 1, 2100043 CrossRef CAS.
- L. Sarcina, C. Scandurra, C. Di Franco, M. Caputo, M. Catacchio, P. Bollella, G. Scamarcio, E. Macchia and L. Torsi, A stable physisorbed layer of packed capture antibodies for high-performance sensing applications, J. Mater. Chem. C, 2023, 11, 9093–9106 RSC.
- L. Sarcina, P. Delre, G. Graziano, A. Stefanachi, D. Blasi, R. A. Picca, C. Di Franco, F. Leonetti, G. Scamarcio, P. Bollella, G. F. Mangiatordi, E. Macchia and L. Torsi, Controlling the Binding Efficiency of Surface Confined Antibodies through the Design of Mixed Self-Assembled Monolayers, Adv. Mater. Interfaces, 2023, 10, 2300017 CrossRef CAS.
- E. Macchia, R. A. Picca, K. Manoli, C. Di Franco, D. Blasi, L. Sarcina, N. Ditaranto, N. Cioffi, R. Österbacka, G. Scamarcio, F. Torricelli and L. Torsi, About the amplification factors in organic bioelectronic sensors, Mater. Horiz., 2020, 7, 999–1013 RSC.
- E. Macchia, K. Manoli, B. Holzer, C. Di Franco, M. Ghittorelli, F. Torricelli, D. Alberga, G. F. Mangiatordi, G. Palazzo, G. Scamarcio and L. Torsi, Single-molecule detection with a millimetre-sized transistor, Nat. Commun., 2018, 9, 3223 CrossRef PubMed.
- E. MacChia, A. Tiwari, K. Manoli, B. Holzer, N. Ditaranto, R. A. Picca, N. Cioffi, C. Di Franco, G. Scamarcio, G. Palazzo and L. Torsi, Label-Free and Selective Single-Molecule Bioelectronic Sensing with a Millimeter-Wide Self-Assembled Monolayer of Anti-Immunoglobulins, Chem. Mater., 2019, 31, 6476–6483 CrossRef CAS.
- R. A. Picca, K. Manoli, E. Macchia, L. Sarcina, C. Di Franco, N. Cioffi, D. Blasi, R. Österbacka, F. Torricelli, G. Scamarcio and L. Torsi, Adv. Funct. Mater., 2020, 30, 1904513 CrossRef CAS.
- A. Tricase, A. Imbriano, E. Macchia, L. Sarcina, C. Scandurra, F. Torricelli, N. Cioffi, L. Torsi and P. Bollella, Electrochem. Sci. Adv., 2023, 3, e2100215 CrossRef CAS.
- P. Puthongkham, S. Wirojsaengthong and A. Suea-Ngam, Machine learning and chemometrics for electrochemical sensors: Moving forward to the future of analytical chemistry, Analyst, 2021, 146, 6351–6364 RSC.
- C. Scandurra, P. Bollella, R. Österbacka, F. Leonetti, E. Macchia and L. Torsi, Implementation of Experimental Design Techniques to Optimize Immunoglobulins detection with ultrasensitive sandwich immunoassays, Adv. Sens. Res., 2022, 1, 2200009 CrossRef.
- C. Scandurra, K. Björkström, L. Sarcina, A. Imbriano, C. Di Franco, R. Österbacka, P. Bolella, G. Scamarcio, L. Torsi and E. Macchia, Single Molecule with a Large Transistor – SiMoT cytokine IL-6 Detection Benchmarked against a Chemiluminescent Ultrasensitive Immunoassay Array, Adv. Mater. Technol., 2023, 8, 2201910 CrossRef CAS.
- H. Horry, A. Maul and G. Thouand, Optimization of a bacterial bioluminescent biosensor through experimental design, Sens. Actuators, B, 2007, 127, 649–657 CrossRef CAS.
- K. Andersson, M. Hämäläinen and M. Malmqvist, Identification and optimization of regeneration conditions for affinity- based biosensor assays. A multivariate cocktail approach, Anal. Chem., 1999, 71, 2475–2481 CrossRef PubMed.
- A. M. Ghafari, M. Catacchio, E. Rosqvist, A. Luukkonen, A. Eklund, K. Björkström, P. Bollella, L. Torsi, E. Macchia and R. Österbacka, Experimental design of stencil-printed high-performance organic electrochemical transistors, Mater. Adv., 2023, 4, 6718–6729 RSC.
- A. Bhat, J. M. Amanor-Boadu and A. Guiseppi-Elie, Toward Impedimetric Measurement of Acidosis with a pH-Responsive Hydrogel Sensor, ACS Sens., 2020, 5, 500–509 CrossRef CAS PubMed.
- S. Kaziz, I. Ben Mariem, F. Echouchene, M. Belkhiria and H. Belmabrouk, Taguchi optimization of integrated flow microfluidic biosensor for COVID-19 detection, Eur. Phys. J. Plus, 2022, 137, 1–12 Search PubMed.
- A. Mignani, G. Luciano, S. Lanteri, R. Leardi, E. Scavetta and D. Tonelli, Optimization of a glucose biosensor setup based on a Ni/Al HT matrix, Anal. Chim. Acta, 2007, 599, 36–40 CrossRef CAS PubMed.
- C. V. Uliana, J. O. Tognolli and H. Yamanaka, Application of factorial design experiments to the development of a disposable amperometric DNA biosensor, Electroanalysis, 2011, 23, 2607–2615 CrossRef CAS.
- M. S. P. López, G. F. Cabanillas, M. J. L. Castañón and B. López-Ruiz, Development of a genosensor for peanut allergen ARA h 2 detection and its optimization by surface response methodology, Biosens. Bioelectron., 2014, 62, 350–356 CrossRef.
- S. Patris, M. Vandeput, G. M. Kenfack, D. Mertens, B. Dejaegher and J. M. Kauffmann, An experimental design approach to optimize an amperometric immunoassay on a screen printed electrode for Clostridium tetani antibody determination, Biosens. Bioelectron., 2016, 77, 457–463 CrossRef CAS PubMed.
- A. M. A. Melo, D. L. Alexandre, M. R. F. Oliveira, R. F. Furtado, M. F. Borges, P. R. V. Ribeiro, A. Biswas, H. N. Cheng, C. R. Alves and E. A. T. Figueiredo, Optimization and characterization of a biosensor assembly for detection of Salmonella typhimurium, J. Solid State Electrochem., 2018, 22, 1321–1330 CrossRef CAS.
- M. A. Mohamed, A. M. Yehia, C. E. Banks and N. K. Allam, Novel MWCNTs/graphene oxide/pyrogallol composite with enhanced sensitivity for biosensing applications, Biosens. Bioelectron., 2017, 89, 1034–1041 CrossRef CAS.
- İ. O. Koçoğlu, P. E. Erden, A. Kenar and E. Kılıç, Application of central composite design for the optimization of electrode surface composition for glucose biosensor fabrication, Anal. Bioanal. Chem., 2019, 411, 413–425 CrossRef PubMed.
- Y. Dessie and S. Tadesse, Optimization of polyvinyl alcohol binder on PANI coated pencil graphite electrode in doubled chamber microbial fuel cell for glucose biosensor, Sens. Biosens. Res., 2022, 36, 100484 Search PubMed.
- M. D. Gouda, M. S. Thakur and N. G. Karanth, Optimization of the multienzyme system for sucrose biosensor by response surface methodology, World J. Microbiol. Biotechnol., 2001, 17, 595–600 CrossRef CAS.
- A. R. Jalalvand, S. Mohammadi and F. Majidi, Fabrication of a novel molecularly imprinted biosensor assisted by higher-order calibration methods and a computer-generated experimental design for determination of thyroglobulin in the presence of thyroxine and triiodothyronine as uncalibrated interfere, Chemom. Intell. Lab. Syst., 2023, 243, 105006 CrossRef CAS.
- L. Mirmoghtadaie, A. A. Ensafi, M. Kadivar and P. Norouzi, Highly selective electrochemical biosensor for the determination of folic acid based on DNA modified-pencil graphite electrode using response surface methodology, Mater. Sci. Eng., C, 2013, 33, 1753–1758 CrossRef CAS.
- J. Gonzalo-Ruiz, M. Asunción Alonso-Lomillo and F. Javier Muñoz, Screen-printed biosensors for glucose determination in grape juice, Biosens. Bioelectron., 2007, 22, 1517–1521 CrossRef CAS PubMed.
- J. Rubio Retama, M. Sánchez-Paniagua López, J. P. Hervás Pérez, G. Frutos Cabanillas, E. López-Cabarcos and B. López-Ruiz, Biosensors based on acrylic microgels: A comparative study of immobilized glucose oxidase and tyrosinase, Biosens. Bioelectron., 2005, 20, 2268–2275 CrossRef CAS PubMed.
- Z. Urkut, P. Kara, Y. Goksungur and M. Ozsoz, Response surface methodology for optimization of food borne pathogen detection in real samples based on label free electrochemical nucleic acid biosensors, Electroanalysis, 2011, 23, 2668–2676 CrossRef CAS.
- M. A. Alonso-Lomillo, O. Domínguez-Renedo, P. Matos and M. J. Arcos-Martínez, Disposable biosensors for determination of biogenic amines, Anal. Chim. Acta, 2010, 665, 26–31 CrossRef CAS PubMed.
- M. M. Abdi, R. L. Razalli, P. M. Tahir, N. Chaibakhsh, M. Hassani and M. Mir, Optimized fabrication of newly cholesterol biosensor based on nanocellulose, Int. J. Biol. Macromol., 2019, 126, 1213–1222 CrossRef CAS.
- L. Del Torno-De Román, M. A. Alonso-Lomillo, O. Domínguez-Renedo, C. Merino-Sánchez, M. P. Merino-Amayuelas and M. J. Arcos-Martínez, Fabrication and characterization of disposable sensors and biosensors for detection of formaldehyde, Talanta, 2011, 86, 324–328 CrossRef.
- O. Domínguez-Renedo, M. A. Alonso-Lomillo, L. Ferreira-Gonçalves and M. J. Arcos-Martínez, Development of urease based amperometric biosensors for the inhibitive determination of Hg (II), Talanta, 2009, 79, 1306–1310 CrossRef.
- S. Sanllorente-Méndez, O. Domínguez-Renedo and M. J. Arcos-Martínez, Development of acid phosphatase based amperometric biosensors for the inhibitive determination of As(V), Talanta, 2012, 93, 301–306 CrossRef PubMed.
- L. Asturias-Arribas, M. A. Alonso-Lomillo, O. Domínguez-Renedo and M. J. Arcos-Martínez, CYP450 biosensors based on screen-printed carbon electrodes for the determination of cocaine, Anal. Chim. Acta, 2011, 685, 15–20 CrossRef CAS PubMed.
- V. Marchianò, A. Tricase, M. Caputo, E. Farinini, R. Leardi, A. Imbriano, D. Leech, R. Kidayaveettil, L. Gentile, L. Torsi, E. Macchia and P. Bollella, Tailoring Water-Based Graphite Conductive Ink Formulation for Enzyme Stencil-Printing: Experimental Design to Enhance Wearable Biosensor Performance, Chem. Mater., 2024, 36, 358–370 CrossRef.
- D. M. Rissin, C. W. Kan, T. G. Campbell, S. C. Howes, D. R. Fournier, L. Song, T. Piech, P. P. Patel, L. Chang, A. J. Rivnak, E. P. Ferrell, J. D. Randall, G. K. Provuncher, D. R. Walt and D. C. Duffy, Single-molecule enzyme-linked immunosorbent assay detects serum proteins at subfemtomolar concentrations, Nat. Biotechnol., 2010, 28, 595–599 CrossRef CAS.
- B. Holzer, K. Manoli, N. Ditaranto, E. Macchia, A. Tiwari, C. Di Franco, G. Scamarcio, G. Palazzo and L. Torsi, Characterization of Covalently Bound Anti-Human Immunoglobulins on Self-Assembled Monolayer Modified Gold Electrodes, Adv. Biosyst., 2017, 1, 1700055 CrossRef.
- R. B. M. Schasfoort, Handbook of Surface Plasmon Resonance, Royal Society of Chemistry, 2017 Search PubMed.
- K. Bonroy, F. Frederix, G. Reekmans, E. Dewolf, R. De Palma, G. Borghs, P. Declerck and B. Goddeeris, Comparison of random and oriented immobilisation of antibody fragments on mixed self-assembled monolayers, J. Immunol. Methods, 2006, 312, 167–181 CrossRef CAS PubMed.
- Y. Fang, P. Björn, L. Stefan and K. Wolfgang, Surface Plasmon Fluorescence Spectroscopy for Protein Binding Studies, Protein Microaaray Technology, 2004 Search PubMed.
- D. Shan, W. Yao and H. Xue, Amperometric detection of glucose with glucose oxidase immobilized in layered double hydroxides, Electroanalysis, 2006, 18, 1485–1491 CrossRef CAS.
- B. Martín-Fernández, A. J. Miranda-Ordieres, M. J. Lobo-Castañón, G. Frutos-Cabanillas, N. De-los-Santos-Álvarez and B. López-Ruiz, Strongly structured DNA sequences as targets for genosensing: Sensing phase design and coupling to PCR amplification for a highly specific 33-mer gliadin DNA fragment, Biosens. Bioelectron., 2014, 60, 244–251 CrossRef PubMed.
- C. L. Sung, A. Anisha, L. Nitta, L. Jeff, Q. Y. Jian, S. Stephen, K. Gutekunst and R. Maurice, Improved Version 2.0 Qualitative and Quantitative AMPLICOR Reverse Transcription-PCR Tests for Hepatitis C Virus RNA: Calibration to International Units, Enhanced Genotype Reactivity, and Performance Characteristics, J. Clin. Microbiol., 2000, 4171–4179 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |