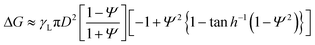Open Access Article
Open Access ArticleParticulate gel liquid marbles†
Mizuki
Tenjimbayashi
 *ab and
Ryota
Tamate
*ab and
Ryota
Tamate
 c
c
aResearch Center for Materials Nanoarchitectonics (MANA), National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan. E-mail: TENJIMBAYASHI.Mizuki@nims.go.jp
bFOREST, Japan Science and Technology Agency, Saitama 332-0012, Japan
cResearch Center for Macromolecules & Biomaterials, NIMS, 1-2-1 Sengen, Tsukuba, 305-0047, Japan
First published on 19th June 2024
Abstract
Non-sticking water droplets stabilized by a particulate polydimethylsiloxane (PDMS) organogel, namely “particulate gel liquid marbles (PGLMs)” are prepared via mechanochemistry. PGLMs exhibited superior compression/impact stability to conventional particle-stabilized LMs owing to the rheological features of the organogel. Moreover, the shape reconfigurability of the PG enabled the plastic deformation of PGLMs.
The design of liquid non-sticking surfaces/interfaces is of great interest owing to their anti-fouling and self-cleaning functions.1 Hydrophobic nano/micro textures prevent the sticking of water droplets to a contacting substrate by forming the Cassie–Baxter interface,2 which entraps the air layer beneath the droplet and minimizes the droplet contact area. On one hand, the structure is fixed on the substrate, and the surface exhibits superhydrophobicity. On the other hand, when the hydrophobic texture is formed on the droplet by adsorption of hydrophobic fine particles, the non-sticking droplet is recognized as a liquid marble (LM).3
LMs have been intensively studied due to their unique properties since the first report in 2001.4 LMs behave like a soft solid but are reconfigurable (e.g., splitting and coalescing) like liquid. Moreover, LMs roll off the tilted substrate or float on the water pool. These properties enabled loss-less inner liquid transportation and easy recyclability of outer particles. Thus, LMs are expected to use sustainable materials for transportation. Various lab-in-a-marble applications have been considered by replacing the inner liquid with a responsive one with chemicals, sensing molecules, and cells.3 Moreover, functional/responsive particles covering the droplet make the applications more convenient.5
However, LMs are mechanically weak because the hydrophobic particle texture on the droplet is discontinuous, and mechanical stimuli induce cracking or inner liquid penetration.6 Thus, various studies focused on the mechanical durability of LMs. Compression and/or impact stability of LMs upon changing the possible parameters: particle size or shape, droplet size, viscosity, or surface tension, contacting substrate wettability, on/under water conditions, have been investigated.7–13 However, LMs still suffer from fragility. Ideas to polymerize the hydrophobic texture of LMs have also been reported; however, interfacial polymerization leads to the loss of the reconfigurability of LMs.14
Recently, various new concepts of LMs have been reported. Roy et al. reported LMs, whose particle layer was impregnated with a lubricant.15 Aono et al. reported that the LM was made of droplet-shaped foam.16 Takei et al. reported LMs, whose particles were made of hydrophobic gelatine.17 These researchers succeeded in tethering a sister fluid phase (infusing liquid, bubble, or gel) in the LM system. We hypothesize that the sister fluid can dissipate the mechanical stimuli owing to its viscous effect, potentially modulating the mechanical stability of LMs.
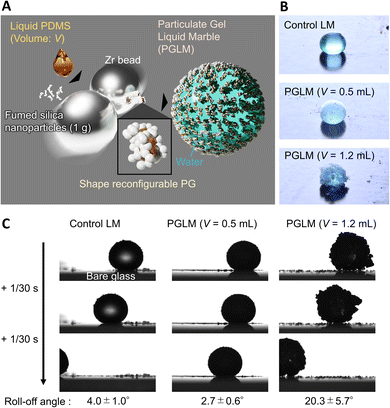
Here, we designed LMs made of water droplets covered with a PG, namely PGLMs (Fig. 1A and B). The PGLMs exhibit non-sticking rolling-off behaviors on tilted glass substrates like classical LMs (Fig. 1C). The PG consists of a percolated network of fumed silica nanoparticles whose primary diameter is ∼7 nm (AEROSIL® 300, Evonik Industries, Germany) in liquid PDMS with a viscosity of 105 mPa s (Fig. S1†). It is known that the mechano-chemical process enables the modification of silica nanoparticles with PDMS.18 We added an excess amount of liquid PDMS in mechano-chemical processes and succeeded in forming PG particles. In this work, we study the effect of PDMS volume fraction on the PG structure and PGLM mechanical properties. As a result, the PGLM exhibits higher resilience and mechanical stability than the LM covered with commercial PDMS-modified fumed silica nanoparticles (AEROSIL® RY300, Evonik Industries, Germany) as the control, opening a new door to a robust LM design strategy.
Moreover, the PG exhibits shape reconfiguration properties and provides mechano-adaptivity to PGLMs. We expect the PGLMs to evolve from classical “responsive” to “adaptive” LMs. The PG process is universal to various viscous liquids and thus potentially diversifies the sister liquid-based LM system.
Fig. 2A explains the effect of liquid PDMS volume on the PG structure. While AEROSIL® 300 weight is kept at 1 g, liquid PDMS volume V varies from 0 to 1.5 mL. PG grows with the increase in PDMS volume. Because the fumed silica nanoparticles are wet by liquid PDMS, the capillarity of liquid PDMS isotopically wets the nanoparticles. However, the bulk elasticity limits the spill of PDMS from nanoparticle networks. Fig. 2B visualizes the PG structure and AEROSIL® 300 as a comparison using digital microscopy. Due to the electrostatic force, AEROSIL® 300 is in a semi-transparent micrometer aggregate state. However, PDMS-added grains are white-colored ones. The differences in transparency depend on whether or not PDMS is infused in the nanoparticle network. The tendency is observed for comparison between the control LM and PGLMs (Fig. 1B). We measured the short (long) diameters a (b) of grains from these images. Then, the grain diameter D = (a + b)/2 and the sphericity Ψ = a/b are obtained (Fig. 2C). As shown in Fig. 2D, while the diameter is nearly constant up to V = 1 mL, it exponentially increases from tens of μm to mm with varying V from 1 to 1.5 mL. The D increase can be explained by the PDMS sticking to the nanoparticles. We assume that the constant diameter at V < 1 mL is owing to the competition between the mechanical cracking of particles, leading to the decrease of size, and PDMS sticking, leading to the increase of size. The diameter error is negligible since the ball milling makes the grains uniform (see the histograms in Fig. S2†). Fig. 2E shows that the sphericity remains constant at ∼0.7 except for V = 1.5 mL. The high sphericity at V = 1.5 mL can be explained by the surface tension effect which strengthens with the liquid PDMS amount. Unlike the classical LMs that use (elastic) solid particles, the PG plastically deforms due to the unfixed particulate network. Thus, the PG can transform its shape through mechanical compression. Such reconfigurable particles have not been applied in LMs. In Fig. 2F, simple compression transforms the PG from sphere to plate.
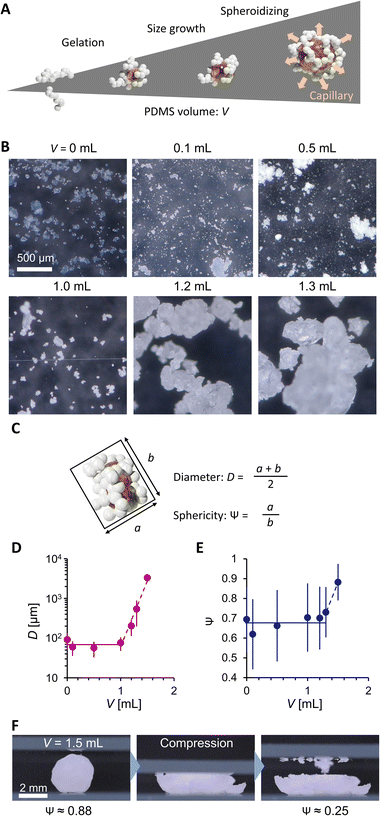 | ||
| Fig. 2 (A) PDMS volume effect on PG. (B) Digital microscopic images. (C) Scheme explaining PG geometry analysis. (D) Diameter and (E) sphericity of PG. (F) Mechanical shape reconfiguration of PG. | ||
We then evaluated the wettability and powder fluidity of PGs, as shown in Fig. 3. Fig. 3A shows the photo images of the water droplets on grain beds. While water spread on a hydrophilic AEROSIL® 300 (V = 0) bed, the bed formed by PDMS-added grains (V = 0.1 to 1.2 mL) exhibits superhydrophobic negligibly small sticking behaviors against 20 μL water droplets. The droplet on PG with V = 1.5 mL exhibited a high contact angle but stuck to the PG surface (see Fig. S3†). Such wettability variation is due to the different wetting states (Fig. 3B). Although the measurement of the accurate water contact angle on the powder bed is difficult, the wetting states are easily judged from the water adhesion behavior.6 In V = 0, water is entrapped between the nanoparticles owing to the intrinsic hydrophilicity of AEROSIL® 300. At V ranging from 0.1 to 1.2 mL, the water cannot invade between the nanoparticles owing to the hydrophobicity from PDMS modification; instead, the air is entrapped beneath the water droplet, forming the Cassie–Baxter interface. Notably, 0.1 mL of PDMS is enough to hydrophobize AEROSIL® 300. For V = 0.5 to 1.2 mL, liquid PDMS is entrapped in the nanoparticles while forming a Cassie–Baxter interface with water. This means that the liquid PDMS is insufficient to cover the surface nanoparticles of the grains.19 At V = 1.5 mL, the water in the Wenzel state sticks to the PG mediated by partially surface-exposed liquid PDMS.
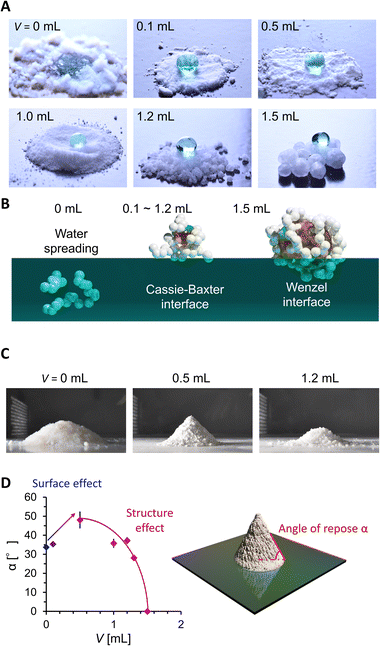 | ||
| Fig. 3 (A) 20 μL water droplets on PG. (B) Water adhesion states on PG estimated from water contact behaviors. (C) Shape of particles or the PG powder mountain. (D) Angle of repose evolution. | ||
We then evaluated the powder fluidity of PGs via the angle of repose α measurement (Fig. 3C and D). In general, α increases with the friction between grains (i.e., surface effect) or decreases with D and Ψ (i.e., structure effect). We observed α increases with V from 0, 0.1, to 0.5 mL while D being constant and Ψ increasing (Fig. 2D and E). It means that the surface friction increases with V from 0 to 0.1 mL and 0.1 to 0.5 mL. The increased surface friction from 0 to 0.1 mL means PDMS modification on the nanoparticle surface. The significant α jump between V = 0.1 and 0.5 mL means a drastic change in grain surface properties, depending on whether the liquid PDMS sticks to the grains. At V > 0.5 mL, α exponentially decreases with V, while the sticky liquid PDMS fraction on the grain is expected to increase. The decrease in α is because the structural change (D and Ψ) with V dominates over α rather than the surface friction. The α of PGs did not increase even after two months in a glass bottle (Fig. S4†), which indicated that the spill of the PDMS in PG did not occur, at least on a monthly scale.
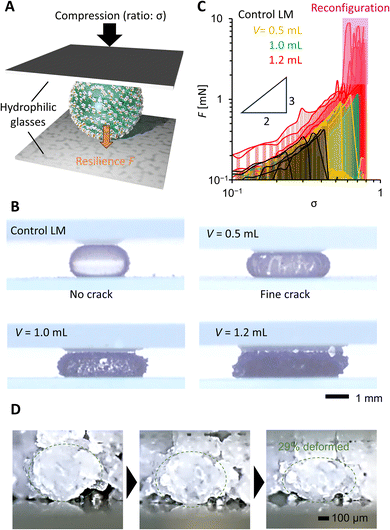
In Fig. 4, we evaluated the compression stability of PGLMs. PGLMs were prepared by covering a 10 μL water droplet with PG and compared with the control LM using AEROSIL® RY300. PG densely covered the water droplet surface and worked to delay the water evaporation (Fig. S5†). The PGLM or LM was compressed at a speed of 0.1 mm s−1 between two hydrophilic glass plates and the compression ratio σ was measured versus resilience F using a microbalance (Fig. 4A). The side-view compression behaviors are shown in Movie S1† and Fig. 4B captured just before the breakage. We find that PGLMs had superior compression stability to the control LM as their critical compression ratio is higher than that of the control. However, the critical compression ratio was not significantly different between PGLMs despite the change in the roughness. The PGLMs break down with cracks on their surface (Fig. 4B), while the control LM has no crack throughout the compression. The cracking suggests the fracture of the PG network at the surface, which might increase the rupture energy of the PGLM compared to the control LM. The networked shell feature may arise from the capillary bridging of nanoparticles via liquid PDMS.20Fig. 4C plots the σ–F curve in the log–log scale obtained from Fig. S6.† We obtained the power law F–σ3/2 from the slope of the LM and PGLMs with V = 0.5 and 1.0 mL. This power law explains the elastic sphere compression force, known as the Hertz model.21 Thus, the resilience mainly comes from the quasi-elasticity of the water,22 not the variation in the shell elasticity. In contrast, PGLMs with V = 1.2 mL exhibited a non-monotonic σ–F curve. Classically, when the LMs break down, their resilience drastically decreases. A similar tendency is observed for PGLMs with V = 0.5 and 1.0 mL, but not with V = 1.2 mL when comparing Fig. 4B with Fig. 4C. Instead, the resilience drastically increased after breakage, resulting from the PGs' viscous energy dissipation in shape rearrangement (disconnecting/reconnecting the liquid PDMS capillary bridge), which is confirmed by the side-view microscopic observation (Fig. 4D) and the non-monotonic resilience curve of PG compression (Fig. S7†). For V = 1.2 mL, unlike the cases of V = 0.5 and 1.0 mL, the size of the PG particles comprising the PGLM is not negligibly small compared with that of the PGLM. Therefore, we assume that the large fluctuation in resilience at the high compression area (the pink highlighted region in Fig. 4C) is attributed to the contribution from the compression stress for reconfiguration of the PG network (Fig. 2F). Specifically, the PGs' reconfiguration mainly occurred on the side of the PGLM as seen in Movie S1.† This is because the force chain connecting PGs and the glass plate is formed on the side of the PGLMs, and transmits compression force to PGs.
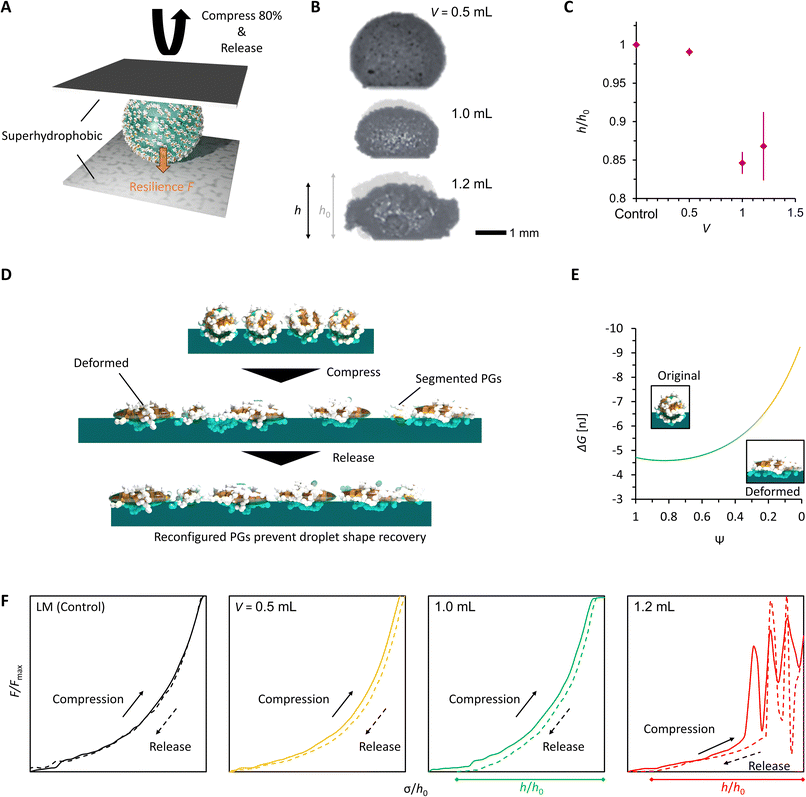
To confirm the reconfiguration effect of PGLMs, we investigated the hysteresis during the compression and release of the PGLMs, as shown in Fig. 5. In this experiment, PGLMs were sandwiched between superhydrophobically coated glass plates, experiencing 80% compression and release, and resilience was monitored (Fig. 5A). On superhydrophobic surfaces, LMs are free from breakage owing to the reversible transition between particle adsorbed and water surface exposed states,23 which enables the monitoring of compression hysteresis without breakage. The side-view of the compression/releasing behavior is shown in Movie S2†,and Fig. 5B highlights the shape change through the compression/releasing process, indicating the V-dependent distortion of PGLMs. The distortion was quantified by the height ratio of PGLMs before and after the compression (h/h0), as shown in Fig. 5C. The PGLMs with V = 1.0 and 1.2 mL were distorted through compression (h/h0 ≈ 0.85), while the control LM and PGLM with V = 0.5 mL kept their original shapes, i.e., h/h0 ≈ 1. Since the liquid surface tension is not changed by compression, the PGLM distortion is due to the structural change in the PG shell. As shown in Fig. 5D, the surface area of the LM increases when it is compressed. In the case of a classical LM, the gap between the particles increases as it deforms. When the LM is released, the gap disappears and returns to its original shape. In contrast, when the PGLM is compressed, the PG layer is reconfigured on the water surface, and the contact area between PG and water changes dynamically. The space between particles becomes smaller than between non-deformed particles, and the PGLM cannot return to its original shape when released. The reconfiguration is owing to the shape deformation, rearrangement, and/or segmentation of the PG shell (Fig. 2F). The rearrangement decreases the PG absorption energy with increasing water–PG contact area. For example, Fig. 5E numerically studies the effect of PG shape deformation on absorption energy. Simple modeling of PG to be a prolate spheroid with its Young's water contact angle being 90° (see Fig. S8 and Note S1† for details), Gibbs energy change ΔG through PG adsorption to the water surface from the air side can be estimated as:
Fig. 5F plots normalized resilience during the compression and release. The hysteresis of PGLMs looks more significant than that of the control LM, depending on the shell reconfiguration degree. The fluctuation in resilience at V = 1.2 mL corresponds to the energy dissipation of PG. The resilience becomes zero for PGLMs with V = 1.0 and 1.2 mL before the plates reach the initial compression height (σ < h0). The mechanical properties of PGLMs shown in Fig. 4 and 5 do not appear in classical (soft) solid particle-based LMs.
Finally, we studied the impact stability of the PGLMs (Fig. 6A). We dropped the PGLM with 10 μL water onto a hydrophilic glass surface from the impact height h, the distance between the glass surface and the bottom of the PGLM. Assuming that the potential energy of PGLMs is fully converted to kinetic energy, the impact energy is given by Eimpact ≈ mgh, where m is the weight of the PGLM and g is the gravitational acceleration constant. We judged the PGLMs' breakage depending on whether they kept spherical or adhered to the glass surface. The result is summarized in Fig. 6B. We find that the PGLMs exhibited significantly superior impact resistance to the control LM, and their critical impact energy increased with V. Since the powder size between PG (V = 0.5 and 1.0 mL) and control is not significantly different, the increased impact stability is mainly contributed by the viscous dissipation of the liquid PDMS. In the case of PGLMs (V = 1.2 mL), the grain size is significantly greater than the compared samples. With the increase of the powder size, the substrate–inner water gap length and particle attraction can be increased.25 The highest impact stability for the PGLM (V = 1.2 mL) may be owing to the synergetic effect of viscous dissipation and size growth. Fig. 6C and Movie S3† display the bouncing behaviors of the impacting LM and PGLMs. Due to the viscous dissipation of impact energy, impacting PGLMs with V = 1.0 or 1.2 mL exhibited low or no bouncing, while those with V = 0.5 mL or control LM apparently bounced off at lower Eimpact. Moreover, we have summarized the compression/impact stability between classical LMs and PGLMs in Table S1,† which supports the effectiveness of the viscous dissipation approach in improving the LM robustness.
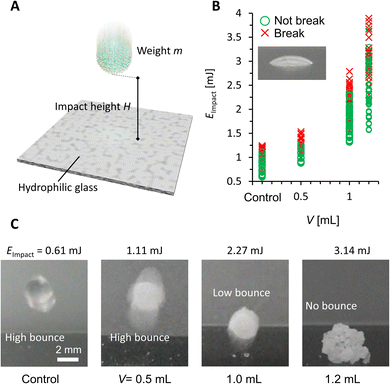 | ||
| Fig. 6 (A) Scheme of the impact test. (B) Impact stability under different impact energy conditions. (C) Bouncing behavior of impacting LMs and PGLMs. | ||
In summary, PGLMs exhibited superior compression/impact stability to classical LMs and shape reconfigurability caused by the viscoelastic features of PG. While LM design parameters are reaching a limit, this study establishes new design guidelines, including introducing sister fluid as a gel component. In our PGLMs, the sister liquid PDMS improved mechanical functions through viscoelastic effects and adaptive morphological changes of shells.26 Sister fluids are not only limited to PDMS, but functional fluids like ionic liquids, liquid metals, ferrofluids, liquid crystals, biofluids, phase change liquids, non-Newtonian liquids, and other responsive fluids.27–30 The synergetic effect of functional particles and liquids of PGs makes the PGLMs highly functional.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
M. T.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, validation, visualization, writing – original draft, review and editing. R. T.: data curation, formal analysis, investigation, methodology, validation, writing – original draft, review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors appreciate support from WPI-MANA. We thank Ms. Makiko Yabune and Ms. Michie Saito who supported this work. This work is supported by JST FOREST (JPMJFR223V), and partially by JSPS KAKENHI (21H01643 and 23K18567) .Notes and references
- M. Tenjimbayashi and K. Manabe, Sci. Technol. Adv. Mater., 2022, 23, 473–497 CrossRef PubMed.
- A. Lafuma and D. Quéré, Nat. Mater., 2003, 2, 457–460 CrossRef CAS PubMed.
- M. Tenjimbayashi, T. Mouterde, P. K. Roy and K. Uto, Nanoscale, 2023, 15, 18980–18998 RSC.
- P. Aussillous and D. Quéré, Nature, 2001, 411, 924–927 CrossRef CAS PubMed.
- S. Fujii, S. Yusa and Y. Nakamura, Adv. Funct. Mater., 2016, 26, 7206–7223 CrossRef CAS.
- M. Tenjimbayashi and S. Fujii, Small, 2021, 17, 2102438 CrossRef CAS PubMed.
- Y. Asaumi, M. Rey, K. Oyama, N. Vogel, T. Hirai, Y. Nakamura and S. Fujii, Langmuir, 2020, 36, 13274–13284 CrossRef CAS PubMed.
- Z. Liu, X. Fu, B. P. Binks and H. C. Shum, Langmuir, 2015, 31, 11236–11242 CrossRef CAS PubMed.
- M. Tenjimbayashi, Y. Watanabe, Y. Nakamura and M. Naito, Adv. Mater. Interfaces, 2020, 7, 183–195 Search PubMed.
- Z. Zhao, C. Ling, D. Wang, J. Wang, J. Saczek, S. Pramana, S. Sridhar, J. Shang, B. B. Xu, D. C. W. Tsang, J. Chen and S. Wang, Small, 2020, 16, 2002802 CrossRef CAS PubMed.
- Y. Timounay, O. Pitois and F. Rouyer, Phys. Rev. Lett., 2017, 118, 1–5 CrossRef PubMed.
- J. Saczek, X. Yao, V. Zivkovic, M. Mamlouk, D. Wang, S. S. Pramana and S. Wang, Adv. Funct. Mater., 2023, 33, 2214840 CrossRef.
- N. Barman, A. Shome, S. Kumar, P. Mondal, K. Jain, M. Tenjimbayashi and U. Manna, Adv. Funct. Mater., 2021, 31, 2011198 CrossRef.
- K. L. Thompson, M. Williams and S. P. Armes, J. Colloid Interface Sci., 2015, 447, 217–228 CrossRef CAS PubMed.
- P. K. Roy, B. P. Binks, E. Bormashenko, I. Legchenkova, S. Fujii and S. Shoval, J. Colloid Interface Sci., 2020, 575, 35–41 CrossRef CAS PubMed.
- K. Aono, K. Ueno, S. Hamasaki, Y. Sakurai, S. Yusa, Y. Nakamura and S. Fujii, Langmuir, 2022, 38, 7603–7610 CrossRef CAS PubMed.
- T. Takei, R. Tomimatsu, T. Matsumoto, K. R. Sreejith, N.-T. Nguyen and M. Yoshida, Polymers, 2022, 14, 4849 CrossRef CAS PubMed.
- N. Celik, S. Akay, F. Sahin, G. Sezer, E. Dagasan Bulucu, M. Ruzi, H. Butt and M. S. Onses, Adv. Mater. Interfaces, 2023, 10, 1–12 Search PubMed.
- E. Jenner and B. D'Urso, Appl. Phys. Lett., 2013, 103, 251606 CrossRef.
- E. Koos and N. Willenbacher, Science, 2011, 331, 897–900 CrossRef CAS PubMed.
- H. Butt, K. Graf and M. Kappl, Physics and Chemistry of Interfaces, Wiley, 2003 Search PubMed.
- S. Asare-Asher, J. N. Connor and R. Sedev, J. Colloid Interface Sci., 2015, 449, 341–346 CrossRef CAS PubMed.
- M. Tenjimbayashi, S. Samitsu, Y. Watanabe, Y. Nakamura and M. Naito, Adv. Funct. Mater., 2021, 31, 1–8 Search PubMed.
- T. Matsuda, R. Kawakami, R. Namba, T. Nakajima and J. P. Gong, Science, 2019, 363, 504–508 CrossRef CAS PubMed.
- Y. Asaumi, M. Rey, K. Oyama, N. Vogel, T. Hirai, Y. Nakamura and S. Fujii, Langmuir, 2020, 36, 13274–13284 CrossRef CAS PubMed.
- J. Zhang, B. Chen, X. Chen and X. Hou, Adv. Mater., 2021, 33, 2005664 CrossRef CAS PubMed.
- M. Kole and S. Khandekar, J. Magn. Magn. Mater., 2021, 537, 168222 CrossRef CAS.
- T. Daeneke, K. Khoshmanesh, N. Mahmood, I. A. de Castro, D. Esrafilzadeh, S. J. Barrow, M. D. Dickey and K. Kalantar-zadeh, Chem. Soc. Rev., 2018, 47, 4073–4111 RSC.
- T. Nakanishi, Functional Organic Liquids, Wiley, 2019 Search PubMed.
- G. Kaur, H. Kumar and M. Singla, J. Mol. Liq., 2022, 351, 118556 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02203c |
| This journal is © The Royal Society of Chemistry 2024 |