Open Access Article
Open Access ArticleShape anisotropy induced jamming of nanoparticles at liquid interfaces: a tensiometric study†
Chandan
Kumar‡§
a,
Suman
Bhattacharjee‡
 b and
Sunita
Srivastava
b and
Sunita
Srivastava
 *a
*a
aSoft Matter and Nanomaterials Laboratory, Department of Physics, Indian Institute of Technology Bombay, Mumbai, 400 076, India. E-mail: sunita.srivastava@phy.iitb.ac.in; Tel: +91-22-2576-7572
bCentre for Research in Nanotechnology & Science (CRNTS), Indian Institute of Technology Bombay, Mumbai, 400 076, India
First published on 24th July 2024
Abstract
The intersection of nanotechnology and interfacial science has opened up new avenues for understanding complex phenomena occurring at liquid interfaces. The assembly of nanoparticles at liquid/liquid interfaces provides valuable insights into their interactions with fluid interfaces, essential for various applications, including drug delivery. In this study, we focus on the shape and concentration effects of nanoscale particles on interfacial affinity. Using pendant drop tensiometry, we monitor the real-time interfacial tension between an oil droplet and an aqueous solution containing nanoparticles. We measure two different types of nanoparticles: spherical gold nanoparticles (AuNPs) and anisotropic gold nanorods (AuNRs), each functionalized with surfactants to facilitate interaction at the interface. We observe that the interface equilibrium behaviour is mediated by kinetic processes, namely, diffusion, adsorption and rearrangement of particles. For anisotropic AuNRs, we observe shape-induced jamming of particles at the interface, as evidenced by their slower diffusivity and invariant rearrangement rate. In contrast, the adsorption of spherical AuNPs is dynamic and requires more time to reach equilibrium, indicating weaker interface affinity. By detailed analysis of the interfacial tension data and interaction energy calculations, we show that the anisotropic particle shape achieves stable equilibrium inter-particle separation compared to the isotropic particles. Our findings demonstrate that anisotropic particles are a better design choice for drug delivery applications as they provide better affinity for fluid interface attachment, a crucial requirement for efficient drug transport across cell membranes. Additionally, anisotropic shapes can stabilize interfaces at low particle concentrations compared to isotropic particles, thus minimizing side effects associated with biocompatibility and toxicity.
Introduction
The self-assembly of molecules at liquid interfaces drives an interesting range of phenomena observed in complex fluid systems. The properties of liquid interfaces, particularly their tunable surface tension, self-assembly capabilities, and controlled confinement, have enabled surface engineering for optimal interfacial behavior. These advantageous features enable the formation of precisely shaped microfluidic droplets, tailored for delicate fluid manipulation within microfluidic devices and lab-on-a-chip technologies,1 and plasmonic nanocrystalline films with enhanced light–matter interactions for improved sensing and optoelectronic applications.2,3 Understanding the mechanisms behind interfacial processes drives both fundamental and applied research on the assembly of solids at liquid interfaces. The success of many scientific and technological applications, such as water filtration and biomolecular separation,4,5 revolves around the phenomena occurring at the interface between two immiscible liquids, such as oil and water.6 Further, fluid interfaces formed by mixing two immiscible liquids are of great interest because of their resemblance to living cell membranes and because they provide model systems for the study of protein-biomolecule adsorption at such interfaces.7 In biomedical applications, many natural delivery systems, such as viruses and blood cells, possess anisotropic shapes, and thus understanding the nanoscale interaction mechanisms of anisotropic structures with model biological fluid interfaces is crucial. Studies reveal that anisotropic particles are more effective than spherical nanocarriers in terms of membrane binding and drug efficacy, although the nanoscale interaction mechanisms require further investigation,8,9 which is the focus of this work.The adsorption of nanostructures at an interface advances through several stages, including diffusion-limited adsorption, cooperative displacement of particles, and rearrangement to attain an equilibrium position and optimal density.1,10,11 These interfacial processes can induce structural changes at the interface, impacting particle adsorption and liquid/liquid interactions, which emanate from a diverse array of self-assembled microstructures.12–14 The dynamics of this process are significantly influenced by the particle shape and size,15 mass loading,16 and surfactant concentration at the interface.17 In the nano-regime, the interface binding energy is comparable to thermal energy, resulting in a dynamic adsorption and desorption process occurring at the same time. This creates instability at the interface, leading to non-equilibrium states with different mechanisms for nanoparticle adsorption. However, it is possible to increase particle binding affinity to the interface through design manipulation. The size, shape, and concentration of nanoparticles significantly influence the adsorption mechanism due to their impact on binding energy.18
Upon adsorption, isotropic nanoparticles tend to form uniform, closely packed monolayers due to their symmetrical shape. In contrast, anisotropic particles exhibit more complex adsorption behaviors influenced by their shape anisotropy. For instance, rod-shaped particles may align parallel to the interface,19 while disk-shaped particles may orient themselves to maximize interfacial contact.20 The initial nanoparticle positional configuration at the interfaces significantly impacts subsequent processes such as rearrangement and jamming, which may arise due to restricted degrees of freedom in densely packed systems. The jamming threshold and the resulting structure are highly reliant on particle shape anisotropy and size. Isotropic particles rearrange in a relatively straightforward manner, whereas anisotropic particles can form more intricate and varied structures due to their directional interactions and orientations.21 It is evident that size and shape-dependent adsorption significantly impact the overall thermodynamic, mechanical, and interactive properties of liquid–liquid interfaces.22–24
Fluid interface geometry has been crucial in exploring the regime of tunable solidification, attracting interest for elucidating assembly principles in jammed and liquid states.25 The Langmuir–Blodgett (LB) technique allows precise control over surface pressure, enabling the formation of uniform and densely packed monolayers.26 This method, while advantageous at air–water interfaces, has limitations for studies focused on liquid–liquid interfaces. Fluctuations due to the dynamic nature of both liquids hinder the formation of uniform monolayers. These challenges necessitate alternative methods for manipulating monolayers at the water–oil interface.27,28 Several techniques for measuring interfacial tension have been proposed,29 with pendant drop tensiometry emerging as one of the most simple, robust, and versatile methods for unraveling the complex nature of particle-laden liquid–liquid interfaces.27,30–32 This method allows researchers to control the interfacial area and surrounding environment, enabling them to investigate nanostructure adsorption behavior at liquid–liquid interfaces, advancing material design, targeted drug delivery, and microfluidics.
We utilize the pendant drop method to investigate how the shape anisotropy of nanoscale particles affects interfacial tension at the oil–water interface. Further, we explore the interplay between nanoparticle morphology and concentration and their interaction mechanisms at the liquid–liquid interface. The analysis reveals a novel kinetic effect induced by the jamming of anisotropic nanoparticles. Compared to anisotropic particles, isotropic nanoparticles exhibit weaker interfacial affinity, requiring longer adsorption times and higher concentrations for effective binding at the interface. A detailed analysis of interfacial tension data and interaction energy calculations demonstrates that the anisotropic particle shape provides a superior driving force for interfacial attachment compared to isotropic particles. Our findings suggest that anisotropic particles are a better design choice for drug delivery applications due to their superior affinity for fluid interface attachment, which is crucial for efficient drug transport across cell membranes.
Experimental section
Chemicals
Gold(III) chloride trihydrate (HAuCl4·3H2O, ≥99.9%), dodecane (C12H26, ≥99%), trisodium citrate dihydrate (C6H5Na3O7·2H2O, ≥99.0%), and silver nitrate (AgNO3, ≥99.0%) are obtained from Sigma Aldrich. Hexadecyltrimethylammonium bromide/CTAB (C19H42BrN, >98%), sodium borohydride (NaBH4, >96%) and L-ascorbic acid (C6H8O6, >99%) were purchased from Spectrochem Pvt Ltd (India). 5-Bromosalicylic acid (C7H5BrO3, >98.0%) was obtained from TCI. Nitric acid (HNO3) and hydrochloric acid (HCl) of EMAPRTA grade (Merck) were used for the preparation of aqua regia. Deionized (DI) water (resistivity 18.2 MΩ cm) is used for all experiments.Nanoparticle synthesis in different shapes
The interfacial studies are performed with particles of two different shapes: isotropic spherical gold nanoparticles (AuNPs) and anisotropic gold nanorods (AuNRs). The nanoscale particles are synthesized using an improvised protocol developed earlier based on a seed-mediated growth process.21,33,34For AuNRs, firstly a seed solution of spherical gold nanoparticles was prepared using 5 mL of 0.2 M CTAB solution mixed with HAuCl4 (0.5 mM, 5 mL). Freshly prepared 600 μL of 0.1 M ice cold NaBH4 is added to the solution under vigorous stirring. For growth solution, 45 mL of 0.2 M CTAB and HAuCl4 (5 mM, 9 mL) are mixed with 112.5 μL of both 0.1 M AgNO3 and 1.22 M HCl, in that order. The temperature is kept at 30 °C for the growth. Freshly made ascorbic acid (10 mM, 5.5 mL) is added to the growth solution under vigorous stirring, followed by 75 μL of seed solution (aged for 30 minutes after preparation). The growth solution is incubated overnight at 30 °C, which leads to the formation of highly monodisperse AuNRs.
For AuNPs, citrate capped seeds are prepared first, which in turn produces CTAB capped larger nanoparticles by ligand exchange. First, freshly prepared 300 μL of ice cold NaBH4 (0.1 M) is added to a 10 mL solution of 0.25 mM HAuCl4 and sodium citrate. This seed solution is incubated for 2 hours at room temperature. Meanwhile, a growth solution containing 80 mM CTAB and 0.25 mM gold is prepared. The temperature can be raised up to 50 °C to dissolve the CTAB faster, but it must be cooled down to room temperature before further use. 0.25 mL of 100 mM freshly prepared ascorbic acid is added to 45 mL of growth solution under vigorous stirring, followed by addition of 5 mL of the seed. Stirring is continued for 10 minutes until the solution turns dark red. The solution is incubated overnight at room temperature. In both cases, the growth solutions are centrifuged twice at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 15 minutes to remove excess CTAB and other contaminants.
000 rpm for 15 minutes to remove excess CTAB and other contaminants.
All the glassware used for the synthesis is washed with aqua regia (HNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl = 1
HCl = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) and thoroughly rinsed with DI water and oven-dried. Surfactant, CTAB, is used for surface coating of both the spherical and rod shaped particles for the stability of colloidal suspensions, giving them a net positive surface charge. The particle's size and shape characterization is illustrated in detail in Fig. S1 in the ESI.†
3) and thoroughly rinsed with DI water and oven-dried. Surfactant, CTAB, is used for surface coating of both the spherical and rod shaped particles for the stability of colloidal suspensions, giving them a net positive surface charge. The particle's size and shape characterization is illustrated in detail in Fig. S1 in the ESI.†
Measurement of interfacial tension
A pendant drop at equilibrium is defined by the Young–Laplace equation, establishing a connection between the Laplace pressure across an interface, the curvature of the interface, and the interfacial tension, γ:27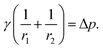 | (1) |
The estimate of the surface/interface tension value in an experiment is obtained through a geometrical fit of the drop. While the theoretical formalism for the pendant drop is relatively simple, its application to experimental data involves a sophisticated computational workflow to achieve precise alignment between experimental images and the Young–Laplace equation. This workflow comprises two distinct stages: primary image analysis to extract the drop profile, followed by iterative optimization to determine the optimal physical parameters that accurately model the extracted profile. OneAttension (Biolin Scientific) software is utilized for both image processing and numerical optimization to estimate the interface tension profile for the pendant drop in our experiments, given in eqn (1). One of the most critical steps to obtaining an accurate estimate of interface tension is the optimization of the droplet's volume. The ratio between the gravitational force and the surface tension force acting on a drop is given by the bond number, B = ΔρgL/γ, where Δρ is the density difference for the two fluids, g is the gravitational acceleration, L is a characteristic dimension for the drop and γ is the interfacial tension. For low bond number systems, this method has well-known limitations. Hence, optimization has been done to adjust the volume of the pendant drop using water such that a stable γ ∼ 72 mN m−1 is obtained. In a system involving two fluids, the primary criterion is that the fluids are not miscible. It is also beneficial to have a high initial interfacial tension because this generates a large driving force at the interface, which promotes the nanoparticle assembly. In pendent drop experiments, a J-shaped needle is used to form a suspended droplet. The density of the liquid forming the droplet is lower than the density of the surrounding dispersion liquid, which ensures that a stable suspended droplet is formed at the end of the needle. The interfacial surface tension profile of the suspended drop at the oil–water interface is monitored using a Biolin Theta Flex optical tensiometer. In a typical experiment, an inverted drop of dodecane (15 ± 1 μL) is created inside a glass cuvette filled with 6 mL of DI water (subphase). The estimation of the number of nanoparticles required to form a complete layer on the droplet's surface (before overcrowding occurs at the oil/water interface) has been done to identify the minimum experimental concentration of the nanoparticles. The subphase phase is exchanged with the desired nanoparticle (AuNR/AuNP) solution for the respective experiments.
Results and discussion
Size and shape of colloids in suspension
The size estimate and shape determination of the freshly synthesized colloidal particles, AuNRs and AuNPs, are obtained from high-resolution TEM images [Fig. S1†]. The length (L) and diameter (D) of colloidal AuNRs are ∼63.5 ± 4.0 nm and ∼15.4 ± 1.6 nm, respectively, resulting in an anisotropic rod with an aspect ratio, (L/D) of ∼4. The average size of spherical particles is calculated to be 16.1 ± 1.5 nm, suggesting the formation of highly monodisperse particles.The UV-vis absorption spectroscopy data of anisotropic AuNRs exhibit two distinct plasmon resonance bands [Fig. S2(a)†] at 508 nm and 819 nm, corresponding to the surface plasmon oscillations along transverse and longitudinal axes, respectively. As gold nanoparticles grow and change their morphology, their surface plasmon absorption peaks also change. The plasmon absorption band for CTAB capped AuNPs is 525 nm [Fig. S2(b)†].
Fig. S3 and S4† depict the hydrodynamic size distribution and surface potential estimates of the colloids as determined by dynamic light scattering (DLS) and zeta potential measurements. The zeta potential estimates for AuNRs and AuNPs were obtained as ∼+49 mV and ∼+38 mV, respectively. The positively charged surfactant (CTA+Br−) adsorbs on the colloid's surface providing stability via repulsive forces. In DLS measurements, the hydrodynamic size is estimated using the Stokes–Einstein equation, which assumes spherical particles. For anisotropic AuNRs, two peaks in the DLS data are observed experimentally, due to diffusion corresponding to the long and short axes of the rods. For non-spherical particles, DLS can only approximate one dimension (a peak at ∼61 nm), and the rotational degree of freedom of the particles can lead to unwanted peaks in the DLS data,35 as shown in Fig. S3(a).† It can be seen in Fig. S4† that the hydrodynamic size of CTAB capped AuNPs is ∼31 nm, which is nearly twice the size determined by TEM. This confirms that CTAB ligands are grafted on the surface of the nanoparticle, resulting in an effective increase in the size of AuNPs.
Nanoparticles at the oil–water interface
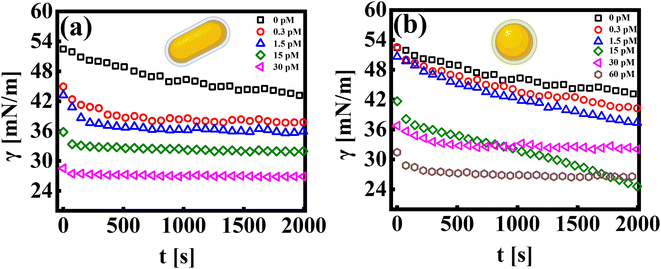
The pendant drop method is an effective way to measure the tension of colloidal suspensions at surfaces and interfaces.27 It uses an automated methodology to capture the drop's image, detect edges, fit data to the Young–Laplace equation, and determine the interfacial tension profile as a function of time.36,37 The interfacial tension profile for systems consisting of a colloidal suspension of rods and spherical particles is shown in Fig. 1(a and b), respectively. The bare dodecane and water interface exhibits interfacial tension, γ0 ∼ 50 mN m−1, and is stable over time.Let us first discuss the experimental data from the pendant drop measurements, which investigate the influence of the nanoparticle shape (rod and sphere) on the dynamic interfacial tension profile as a function of time (γ = γ(t)). The addition of nanoparticles into the sub-phase results in an exponential decay of the interfacial tension profile at short times, followed by a quasi-equilibrium state, wherein the interfacial tension value reaches a plateau at long times. This constant value in the γ vs. t profile signifies that the interface has attained a maximum nanoparticle coverage at a given concentration. All experiments are recorded for a measurement time of ∼2000 seconds. The measurement time was carefully chosen to avoid errors in data due to mechanical stability at longer times. It is observed that the time taken by the interface to reach an equilibrium value in γ decreases with an increase in particle concentration. As can be seen in Fig. 1(a), at the lowest concentration of AuNRs (CR ∼ 0.3 pM), γ reaches a saturation value after a period of ∼300–400 seconds, whereas at CR ∼ 30 pM, the γ vs. t profile exhibits saturation almost instantaneously.
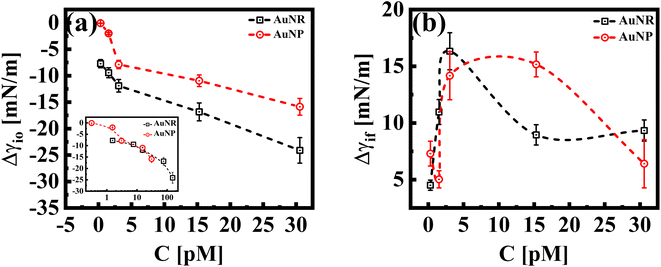
While both the nanoparticle systems, AuNPs and AuNRs, exhibit a qualitatively similar γ vs. t profile, they reach a plateau in γ (indicating a saturated interface), at different concentrations, as shown in Fig. 1(b). For the AuNP system at all concentrations, CS < 30 pM, the interface tension continuously decreases, suggesting that the nanoparticles have not fully covered the interface, within the measured time frame. For CS ≥ 30 pM, we obtain the γ vs. t profile, where the interfacial tension reaches a plateau similar to that of the AuNR system observed at a lower concentration CR ≃ 15 nM. We further performed measurements at an even higher concentration (CS ≃ 60 pM) and found that the saturation observations are consistent, with the γ vs. t profile showing a plateau. This reinforces the observation that AuNRs are significantly more efficient at lowering and stabilizing the interfacial tension at comparatively lower concentrations than AuNPs. Nanoparticle adsorption at an interface reduces interfacial tension, with the magnitude of this decrease proportional to the extent of nanoparticle coverage.38 To determine the nanoparticle coverage at different nanoparticle concentrations, we calculate the change in interfacial tension, Δγio (=γi − γ0), which is the difference between the initial interfacial tension of the dodecane-AuNR/NP system at t = 0 s (γi) and the bare dodecane–water interface (γ0) [Fig. 2(a)]. For both AuNR and AuNP systems, we measure a negative value of interface tension with respect to the oil–water interface, indicating nanoparticle adsorption. Further, the estimate of |Δγio| increases with concentration, suggesting that a higher concentration of nanoparticles leads to more particles going to the interface.
Our results reveal insights into the geometric effect of the nanoparticle shape, with rods being more effective at lowering the interfacial tension compared to spheres at similar molar concentrations. To explain this, we show, in the inset of Fig. 2(a), a Δγiovs. C plot, where the concentrations of AuNRs were adjusted to account for their larger surface area compared to AuNPs (approximately five times larger; AuNR/AuNP ∼5). Interestingly, the Δγio values for both AuNRs and AuNPs (adjusted for the surface area) almost perfectly overlap. This suggests that, since the AuNRs occupy a larger area at the interface compared to AuNPs, an equivalent number of AuNPs will result in a similar adsorption trend to that of the AuNRs.
In Fig. 2(b), we show Δγif, the difference between the initial interface tension, γi, (t = 0 s), and the final/equilibrium value, γf, (at t = 2000 s), obtained from the interfacial tension profiles in Fig. 1. The estimates of Δγif reflect the interface saturation and its equilibrium behavior at varying nanoparticle concentrations in the continuous medium. We find that with an increase in concentration, the estimate of Δγif increases for both particle systems, followed by a cross-over behavior where Δγif decreases and exhibits constancy, with a further increase in concentration. The saturated interface with maximum coverage would correspond to smaller estimates of Δγif, as such an interface is expected to reach an equilibrium value faster than an unsaturated interface. Thus, we can identify the cross-over concentration in Fig. 2(b), as the concentration at which the interface reaches maximum coverage. Interestingly this cross over for the AuNR system occurs at CR ≈ 3 pM, whereas the same is observed for AuNPs at CS > 15 pM. We conclude that in the case of AuNRs, the maximum coverage is reached at a 5-fold smaller concentration compared to AuNPs. At concentrations below the cross-over concentration, when the interface is not fully saturated, the estimates of Δγif increase with concentration and saturate at an estimate of ≈15 mN m−1 for both systems. At a concentration ∼30 pM, we measure a similar value of Δγif for both shapes of particles. This suggests that both systems have reached a maximum particle coverage, where no more particles can bind at the interface.
Adsorption kinetics of AuNRs and AuNPs
Nanoparticles adsorb at the liquid/liquid interfaces when they are introduced into a system containing two different liquids. The differences in interfacial energy between the nanoparticles and the liquids cause the nanoparticles to attach to the interface. The energy associated with a particle getting trapped in an interface is dependent on the size of the particle, the orientation of the attachment, and the interfacial tension between the two media. This energy is termed the detachment energy, ΔE, of the particle-interface system and is given by:ΔE = πr2γ0(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 θ)2 | (2) |
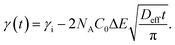 | (3) |
| Particle | C (pM) | ΔE/KBT | U/KBT | D 0 (m2 s−1) | D eff (m2 s−1) |
|---|---|---|---|---|---|
| AuNP | 0.3 | 2211.07 | −34.11 | 3.53 × 10−11 | 2.29 × 104 |
| AuNR | 0.3 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688.53 688.53 |
−30.95 | 1.35 × 10−11 | 3.72 × 102 |
| AuNP | 30 | 2211.07 | −24.09 | 3.53 × 10−11 | 1.02 |
| AuNR | 30 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688.53 688.53 |
−20.86 | 1.35 × 10−11 | 0.02 |
The study of the diffusion coefficient is important for understanding the transport of molecules or particles across the interface. It has been demonstrated that the adsorption of particles consists of three main kinetic processes: (i) diffusion from the bulk to the interface, (ii) adsorption (penetration) and interfacial unfolding, and (iii) aggregation within the interfacial layer, as well as the formation of multilayers.44 In a specific diffusion process occurring on short time scales (Fickian diffusion), the change in interfacial tension over time follows a square root relationship, 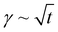 . In the subphase, the nanoparticles are under constant Brownian motion, where the movement of the particles is stochastic. The presence of the interface creates a flux, as the particle assumes it to be a sink and tends to diffuse towards it. At t → 0, the nanoparticles moving towards the interface experience only a bare interface. Once, the interface gets crowded with particles, the diffusive nature also changes.45 A typical interfacial tension profile for the AuNR system at 0.3 pM, revealing Fickian diffusion, is shown in Fig. 3(a). The linear portion of the data, extending up to the first change in the slope (indicated by the blue dotted line), is used to estimate the effective diffusion coefficient (Deff) using eqn (3). This confirms that at a short time, the nanoparticle's diffusion process is the dominant factor controlling their adsorption at the interface, as also observed in previous research.43,46,47 Similar behavior was observed in the
. In the subphase, the nanoparticles are under constant Brownian motion, where the movement of the particles is stochastic. The presence of the interface creates a flux, as the particle assumes it to be a sink and tends to diffuse towards it. At t → 0, the nanoparticles moving towards the interface experience only a bare interface. Once, the interface gets crowded with particles, the diffusive nature also changes.45 A typical interfacial tension profile for the AuNR system at 0.3 pM, revealing Fickian diffusion, is shown in Fig. 3(a). The linear portion of the data, extending up to the first change in the slope (indicated by the blue dotted line), is used to estimate the effective diffusion coefficient (Deff) using eqn (3). This confirms that at a short time, the nanoparticle's diffusion process is the dominant factor controlling their adsorption at the interface, as also observed in previous research.43,46,47 Similar behavior was observed in the 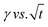 profile for both the AuNP and AuNR particles at all the different concentrations.
profile for both the AuNP and AuNR particles at all the different concentrations.
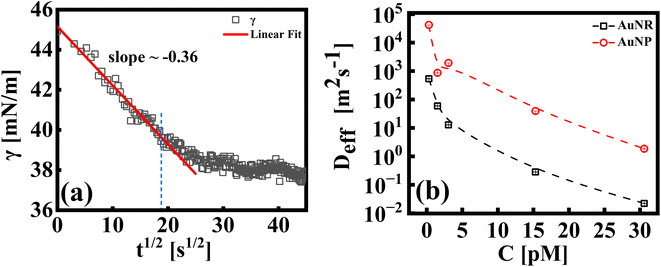 | ||
| Fig. 3 (a) A typical representative plot for γ vs. t1/2, for an AuNR suspension at 0.3 pM. A linear fit to the data using eqn (3) is shown by the extrapolated solid line (up to t ∼ 400 s). The extent of the fitting range is shown via the blue dotted line. (b) Effective diffusion coefficients, (Deff), for AuNP and AuNR systems as indicated in the respective legends. | ||
In Fig. 3(b), we compare the estimates of Deff, which is the diffusion behavior of AuNR and AuNP particles towards the interface, calculated by fitting eqn (3) to the measured interfacial tension profiles as explained above. At any given concentration, it has been found that the Deff of AuNPs is at least two orders of magnitude higher than that of AuNRs. This difference can be explained by the size and shape of the particles, which play a crucial role in how easily they move through the liquid. Even though the diameter of the rods is similar to the diameter of the nanoparticles, the rods are about four times longer. This larger size and elongated shape make AuNRs experience more drag from the surrounding liquid as they move, obstructing their diffusion compared to the smaller, spherical AuNPs. Additionally, the larger surface area of AuNRs (around five times that of AuNPs) means that they collide with each other more frequently, further slowing them down. Additionally, it is worth noting that factors such as the shape of the nanoparticles can also influence the effective diffusion coefficient. The AuNRs, owing to their longer axis (4× longer compared to the AuNP size), adsorb to the interface occupying a larger area even for equal particle concentrations. This faster coverage of the interface by AuNRs also hinders their diffusion towards the interface.
Using the Stoke–Einstein relationship 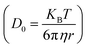 in solution, we have calculated the free diffusion coefficient, (D0), to obtain an approximate estimate of nanoparticle diffusivity at the dodecane/water interface. Here KB, T and η represent the Boltzmann constant, temperature of the aqueous suspension, and solvent viscosity (η = 0.83 cP for water), respectively. We estimate D0 values ≈ 3.53 × 10−11 m2 s−1 and 1.35 × 10−11 m2 s−1, respectively, for AuNPs and AuNRs. For AuNRs, the effective radius, reff, is used for the calculation of D0. It is worth noting that the free diffusivity of AuNPs is about 2.7× higher than that of AuNRs.The nanoparticle adsorption at the interface rapidly forms an energy barrier due to collisions between particles that have detached from the interface and those approaching from the bulk. Particles adsorbing at the interface face an energy barrier, U, that determines the effective diffusivity (Deff). Under the influence of U, Deff can be related to D0 as follows:
in solution, we have calculated the free diffusion coefficient, (D0), to obtain an approximate estimate of nanoparticle diffusivity at the dodecane/water interface. Here KB, T and η represent the Boltzmann constant, temperature of the aqueous suspension, and solvent viscosity (η = 0.83 cP for water), respectively. We estimate D0 values ≈ 3.53 × 10−11 m2 s−1 and 1.35 × 10−11 m2 s−1, respectively, for AuNPs and AuNRs. For AuNRs, the effective radius, reff, is used for the calculation of D0. It is worth noting that the free diffusivity of AuNPs is about 2.7× higher than that of AuNRs.The nanoparticle adsorption at the interface rapidly forms an energy barrier due to collisions between particles that have detached from the interface and those approaching from the bulk. Particles adsorbing at the interface face an energy barrier, U, that determines the effective diffusivity (Deff). Under the influence of U, Deff can be related to D0 as follows:
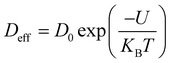 | (4) |
By using eqn (4), U was calculated from the Deff values and is presented in Table 1. Deff ≫ D0 typically suggests that the nanoparticle experiences less hindrance or resistance while moving through the medium than predicted using the Stokes–Einstein equation. This can occur due to various factors, such as particle–particle interactions, non-uniform flow fields, and anomalous diffusion behavior.
To gain deeper insights into these interfacial dynamics that are crucial for understanding the interaction of nanoparticles with the interface, we utilized the established mathematical framework proposed by Graham and Phillips. The temporal evolution of this complex behavior can be captured by a first-order equation, allowing for quantitative analysis of their rates,48 given by:
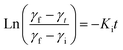 | (5) |
The dynamic surface tension, γt, at times t = 0 and t = 2000 is denoted as γi and γf, respectively. Ki is the first order rate constant and calculated by fitting the interfacial tension data to eqn (5). Typically, there are two different slopes (Fig. S5†); the initial slope (Ki ≡ Kads) represents the rate at which molecules adsorb to the liquid/liquid interface, while the second slope (Ki ≡ Karr) corresponds to the rate constant for rearrangement at the interface. In Fig. 4, we show the estimates of Kads and Karr, for both the AuNP and AuNR systems, the inverse of which is proportional to time for nanoparticle adsorption and rearrangement at the interface, respectively. Interestingly, the data unravel a fascinating difference in the adsorption and rearrangement time scales of AuNPs and AuNRs, at the interface.
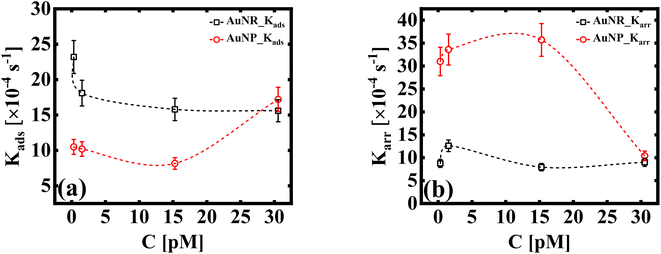 | ||
| Fig. 4 (a) First order adsorption rate, Kads, and (b) molecular rearrangement rate, Karr, of adsorbed particles at the liquid/liquid interface (dashed lines as a guide to the eye). The estimates in (a and b) are obtained using the linear regression model given by eqn (5). | ||
For the AuNP system at particle concentration ≤15 pM, the estimate of Kads, which quantifies the tendency of the nanoparticles to bind to the interface, does not change much [Fig. 4(a)] and stays fairly steady. This suggests that in this concentration regime, particles constantly bind and detach from the interface. This continuous exchange keeps the Kads value relatively constant because the rate of attachment is balanced by the rate of detachment. When the concentration of the solution CS ≥ 30 pM, we measure an increase in the value of Kads. This suggests that AuNPs attach to the interface in a stable way at high concentrations. Conversely, the AuNR system shows a slight decrease in Kads initially (up to ∼3 pM), suggesting slow adsorption. As the anisotropic particles absorb at the interface, the local particle density increases, thus creating a barrier for the incoming particles, with increasing concentration. This can be attributed to shape induced jamming at the interface, which prevents particle exchange with the medium, a phenomenon observed in the case of isotropic particles. As the AuNRs occupy approximately five times more area at the interface compared to a spherical AuNP, it is intuitive to assume that the interface becomes saturated with AuNRs, even at the lowest concentration. This reduces the effective concentration of the incoming particles at the interface, leading to a decrease in the adsorption coefficient. A constant estimate of Kads with a further increase in particle concentration (CR ≥ 3 pM) indicates that their interface binding rate remains relatively unchanged regardless of the particle concentration in the subphase. This invariant Kads with increasing AuNR concentration can be attributed to the jamming effect. Jamming occurs when adsorbed particles surround and cage the incoming particles, preventing them from accessing the adsorption sites at the interface.
These observations suggest that the spherical shape of the AuNP system results in a more dynamic exchange of particles with the medium, until a very high concentration is reached, at which point interface saturation and equilibrium are achieved. The rate constant corresponding to nanoparticle's rearrangement at the interface is shown in Fig. 4(b). We found that Karr for AuNRs remains invariant under all experimental conditions, which corroborates the idea of a jammed interface due to shape anisotropy, even at small nanoparticle concentrations, where we observe no scope for any dynamic behaviour. In the case of AuNPs, Karr initially shows a high value owing to the dynamic nature of the nanoparticle layer at the interface. Karr falls sharply at CS ≥ 30 pM, when the interface finally reaches the quasi-equilibrium state.
Calculation of total interactions between AuNPs and AuNRs near the interface
Beyond the diffusion-limited regime, the adsorption or rearrangement of the nanoparticles at the interface involves interactions at the nanoscale. The nanoparticles have a positively charged surfactant coating around them and the dodecane interface is negatively charged, as reported in the literature.49 To understand the interaction between the particle and the interface, it is helpful to conceptualize it as an inter-particle interaction occurring in the presence of an interface. These interactions involve the inter-particle van der Waals forces at the interface, as well as the electric double–layer interaction originating from the surface charge of the particles in the vicinity of an oppositely charged interface. Following the DLVO (Derjaguin, Landau, Verwey, and Overbeek) theory of colloidal stability,38 we examined the interaction between two identical spherical particles carrying a fixed surface potential. The total interaction energy, UT(h), between two spherical particles of radius, r, separated by a distance, h, from each other at the interface, is the sum of the repulsive electrostatic interaction energy, Uel, and the attractive van der Waals interaction energy, UvdW. Thus, we have UT = Uel + UvdW. The van der Waals interaction between two spherical particles with a flat plate can be written as: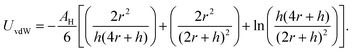 | (6) |
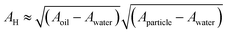 . Here, Aoil is the Hamaker constant for dodecane (5 × 10−20 J), Awater is the Hamaker constant for water (3.7 × 10−20 J), and Aparticle is the Hamaker constant for gold (47 × 10−20 J).38 Using this equation, we calculate the effective Hamaker constant to be AH = 7.5 × 10−20 J, which enables us to determine the van der Waals interaction between the particles at the interface based on the particle radius (r) and the surface-to-surface distance (h). We have considered h values from 0.025 to 15 nm. The electrostatic interaction energy between nanoparticles at the interface is estimated using the formulation given by:
. Here, Aoil is the Hamaker constant for dodecane (5 × 10−20 J), Awater is the Hamaker constant for water (3.7 × 10−20 J), and Aparticle is the Hamaker constant for gold (47 × 10−20 J).38 Using this equation, we calculate the effective Hamaker constant to be AH = 7.5 × 10−20 J, which enables us to determine the van der Waals interaction between the particles at the interface based on the particle radius (r) and the surface-to-surface distance (h). We have considered h values from 0.025 to 15 nm. The electrostatic interaction energy between nanoparticles at the interface is estimated using the formulation given by: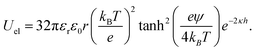 | (7) |
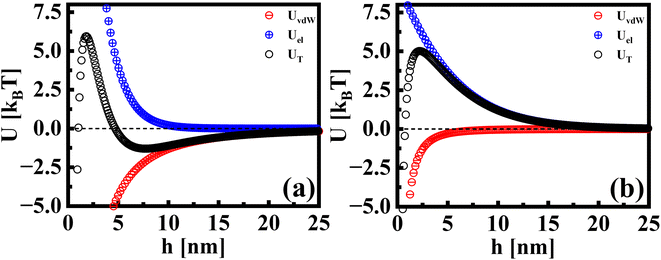 | ||
| Fig. 5 The interaction potentials between particles in the presence of a flat interface. The attractive, repulsive, and total interaction energies are shown for (a) AuNRs and (b) AuNPs. | ||
Conclusion
In this study, we investigate shape and concentration effects on the self-assembly mechanism of surfactant coated nanoparticles at a liquid/liquid interface. Using pendant drop tensiometry, we monitor the dynamic interfacial tension, as spherical AuNPs and anisotropic AuNRs diffuse towards the interface of a dodecane micro-droplet. We observed that AuNRs adsorb and create a stable interface layer at all particle concentrations, whereas the adsorption of AuNPs is dynamic, with particle exchange from the continuous phase. The interface establishes a stable AuNP layer at a concentration approximately 100× higher than that required for the AuNRs. The estimates of adsorption and rearrangement coefficients provide insights into the nanoparticles' adsorption kinetics at the interface. We find that AuNRs possess ∼3× higher adsorption coefficients than AuNPs, suggesting better affinity of the anisotropic particles towards the interface. Further, the rearrangement coefficient for AuNRs does not change with concentration. This difference is attributed to the influence of the particle's shape and size on their adsorption behavior. Due to the larger surface area, AuNRs effectively cover the interface with a smaller number of particles compared to the smaller, spherical AuNPs. For anisotropic AuNRs, we observe shape-induced jamming of particles at the interface, as evidenced by their slower diffusivity and invariant rearrangement rate. The estimates of the interaction energies between the particles near the interface indicate that the anisotropic particle shape achieve stable equilibrium inter-particle separation compared to isotropic particles.To summarize, the findings from the current work highlight the impact of shape and concentration on nanoparticle interactions at the liquid/liquid interface, contributing to advancements in understanding the dynamic behavior of nanoparticles at fluid interfaces. We demonstrate that anisotropic particles exhibit enhanced interfacial binding and stable equilibrium inter-particle separation at the interface. This study holds significant importance for optimizing the design of nanoscale carriers in drug delivery applications. Our results indicate that anisotropic nanocarriers offer advantages in fluid interface attachment, a pivotal factor in improving drug transport across cellular membranes. The choice of anisotropic particle design may offer additional advantages of bio-imaging and controlled and targeted delivery. Additionally, their ability to stabilize interfaces at lower particle concentrations compared to isotropic particles can help minimize concerns regarding biocompatibility and toxicity related side effects.
Data availability
This manuscript presents both the raw data and the analysis derived from processing the data. The raw data can be found in the Fig. 1 of main manuscript. Fig. 2–4 present the derived analysis from the raw data. Details on the processing steps used to generate this analysis are provided in the ESI.†Author contributions
CK – conceptualization, investigation, methodology, data curation, and writing – original draft. SB – investigation, methodology, data curation, formal analysis, writing – original draft, and review & editing. SS – conceptualization, investigation, supervision, funding acquisition, resources, validation, and writing – review & editing. CK and SB contributed equally to the manuscript. All authors have approved the final version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank SAIF IITB [FEG-SEM, FEG-TEM (200 kV/300 kV)] instrument facilities. CK acknowledges Dept. of Physics, IITB for funding. SB acknowledges the financial support from CRNTS, IIT Bombay. SS acknowledges support from CRS-UGC-DAE, India.References
- M. Cui, T. Emrick and T. P. Russell, Stabilizing liquid drops in nonequilibrium shapes by the interfacial jamming of nanoparticles, Science, 2013, 342, 460–463 CrossRef CAS PubMed.
- Y. Lin, H. Skaff, T. Emrick, A. Dinsmore and T. P. Russell, Nanoparticle assembly and transport at liquid-liquid interfaces, Science, 2003, 299, 226–229 CrossRef CAS PubMed.
- Y. Lin, A. Böker, H. Skaff, D. Cookson, A. Dinsmore, T. Emrick and T. P. Russell, Nanoparticle assembly at fluid interfaces: structure and dynamics, Langmuir, 2005, 21, 191–194 CrossRef CAS PubMed.
- J. He, P. Kanjanaboos, N. L. Frazer, A. Weis, X.-M. Lin and H. M. Jaeger, Fabrication and Mechanical Properties of Large-Scale Freestanding Nanoparticle Membranes, Small, 2010, 6, 1449–1456 CrossRef CAS PubMed.
- J. He, X.-M. Lin, H. Chan, L. Vukovic, P. Král and H. M. Jaeger, Diffusion and filtration properties of self-assembled gold nanocrystal membranes, Nano Lett., 2011, 11, 2430–2435 CrossRef CAS PubMed.
- X. Hua, M. A. Bevan and J. Frechette, Competitive adsorption between nanoparticles and surface active ions for the oil–water interface, Langmuir, 2018, 34, 4830–4842 CrossRef CAS PubMed.
- X. Huang, M. Li, D. C. Green, D. S. Williams, A. J. Patil and S. Mann, Interfacial assembly of protein–polymer nano-conjugates into stimulus-responsive biomimetic protocells, Nat. Commun., 2013, 4, 2239 CrossRef PubMed.
- J. Chen, N. E. Clay, N.-H. Park and H. Kong, Non-spherical particles for targeted drug delivery, Chem. Eng. Sci., 2015, 125, 20–24 CrossRef CAS PubMed.
- C. Uhl, Y. Gao, S. Zhou and Y. Liu, The shape effect on polymer nanoparticle transport in a blood vessel, RSC Adv., 2018, 8, 8089–8100 RSC.
- X. Hua, J. Frechette and M. A. Bevan, Nanoparticle adsorption dynamics at fluid interfaces, Soft Matter, 2018, 14, 3818–3828 RSC.
- X. Ji, X. Wang, Y. Zhang and D. Zang, Interfacial viscoelasticity and jamming of colloidal particles at fluid–fluid interfaces: a review, Rep. Prog. Phys., 2020, 83, 126601 CrossRef CAS PubMed.
- A. J. Mendoza, E. Guzmán, F. Martínez-Pedrero, H. Ritacco, R. G. Rubio, F. Ortega, V. M. Starov and R. Miller, Particle laden fluid interfaces: Dynamics and interfacial rheology, Adv. Colloid Interface Sci., 2014, 206, 303–319 CrossRef CAS PubMed.
- J. Krägel and S. R. Derkatch, Interfacial shear rheology, Curr. Opin. Colloid Interface Sci., 2010, 15, 246–255 CrossRef.
- S. Srivastava, D. Nykypanchuk, M. Fukuto, J. D. Halverson, A. V. Tkachenko, K. G. Yager and O. Gang, Two-dimensional DNA-programmable assembly of nanoparticles at liquid interfaces, J. Am. Chem. Soc., 2014, 136, 8323–8332 CrossRef CAS PubMed.
- H.-L. Cheng and S. S. Velankar, Film climbing of particle-laden interfaces, Colloids Surf., A, 2008, 315, 275–284 CrossRef CAS.
- L. Dong and D. Johnson, Surface tension of charge-stabilized colloidal suspensions at the water- air interface, Langmuir, 2003, 19, 10205–10209 CrossRef CAS.
- K. Hadler and J. Cilliers, The effect of particles on surface tension and flotation froth stability, Min. Metall. Explor., 2019, 36, 63–69 Search PubMed.
- Y. Chai, J. Hasnain, K. Bahl, M. Wong, D. Li, P. Geissler, P. Y. Kim, Y. Jiang, P. Gu and S. Li, et al, Direct observation of nanoparticle-surfactant assembly and jamming at the water-oil interface, Sci. Adv., 2020, 6, eabb8675 CrossRef CAS PubMed.
- J. L. Eatson, J. R. Gordon, P. Cegielski, A. L. Giesecke, S. Suckow, A. Rao, O. F. Silvestre, L. M. Liz-Marzán, T. S. Horozov and D. M. A. Buzza, Capillary Assembly of Anisotropic Particles at Cylindrical Fluid–Fluid Interfaces, Langmuir, 2023, 39, 6006–6017 CrossRef CAS PubMed.
- C. Kumar and S. Srivastava, Structural and Dynamical Studies of a Lipid–Nanoclay Composite Layer at the Air–Water Interface, Langmuir, 2022, 38, 10400–10411 CrossRef CAS PubMed.
- S. Khawas, S. Bhattacharjee, S. Mukherjee, A. Sain and S. Srivastava, Directing the formation of tunable superlattice crystalline phases from anisotropic nanoparticles, Colloids Surf., A, 2024, 133762 CrossRef CAS.
- G. Li and Y. Y. Zuo, Molecular and colloidal self-assembly at the oil-water interface, Curr. Opin. Colloid Interface Sci., 2022, 101639 CrossRef CAS.
- L. Helden, K. Dietrich and C. Bechinger, Interactions of colloidal particles and droplets with water–oil interfaces measured by total internal reflection microscopy, Langmuir, 2016, 32, 13752–13758 CrossRef CAS PubMed.
- C. Anzivino, F. Chang, G. Soligno, R. Van Roij, W. K. Kegel and M. Dijkstra, Equilibrium configurations and capillary interactions of Janus dumbbells and spherocylinders at fluid–fluid interfaces, Soft Matter, 2019, 15, 2638–2647 RSC.
- Z. Zhang, Y. Jiang, C. Huang, Y. Chai, E. Goldfine, F. Liu, W. Feng, J. Forth, T. E. Williams and P. D. Ashby, et al, et al. Guiding kinetic trajectories between jammed and unjammed states in 2D colloidal nanocrystal-polymer assemblies with zwitterionic ligands, Sci. Adv., 2018, 4, eaap8045 CrossRef CAS PubMed.
- S. Srivastava, D. Nykypanchuk, M. Fukuto and O. Gang, Tunable nanoparticle arrays at charged interfaces, ACS Nano, 2014, 8, 9857–9866 CrossRef CAS PubMed.
- J. D. Berry, M. J. Neeson, R. R. Dagastine, D. Y. Chan and R. F. Tabor, Measurement of surface and interfacial tension using pendant drop tensiometry, J. Colloid Interface Sci., 2015, 454, 226–237 CrossRef CAS PubMed.
- J. Eggers and E. Villermaux, Physics of liquid jets, Rep. Prog. Phys., 2008, 71, 036601 CrossRef.
- J. Drelich, C. Fang and C. White, Measurement of interfacial tension in fluid-fluid systems, Encycl. Surf. Colloid Sci., 2002, 3, 3158–3163 Search PubMed.
- A. M. Worthington II, On pendent drops, Proc. R. Soc. London, 1881, 32, 362–377 CrossRef.
- A. Toor, J. Forth, S. Bochner de Araujo, M. C. Merola, Y. Jiang, X. Liu, Y. Chai, H. Hou, P. D. Ashby and G. G. Fuller, et al, Mechanical properties of solidifying assemblies of nanoparticle surfactants at the oil–water interface, Langmuir, 2019, 35, 13340–13350 CrossRef CAS PubMed.
- A. Huerre, F. Cacho-Nerin, V. Poulichet, C. E. Udoh, M. De Corato and V. Garbin, Dynamic organization of ligand-grafted nanoparticles during adsorption and surface compression at fluid–fluid interfaces, Langmuir, 2018, 34, 1020–1028 CrossRef CAS PubMed.
- S. Tang, Y. Li, H. Huang, P. Li, Z. Guo, Q. Luo, Z. Wang, P. K. Chu, J. Li and X.-F. Yu, Efficient enrichment and self-assembly of hybrid nanoparticles into removable and magnetic SERS substrates for sensitive detection of environmental pollutants, ACS Appl. Mater. Interfaces, 2017, 9, 7472–7480 CrossRef CAS PubMed.
- R. Fenger, E. Fertitta, H. Kirmse, A. F. Thünemann and K. Rademann, Size dependent catalysis with CTAB-stabilized gold nanoparticles, Phys. Chem. Chem. Phys., 2012, 14, 9343–9349 RSC.
- R. Pecora, Dynamic light scattering measurement of nanometer particles in liquids, J. Nanopart. Res., 2000, 2, 123–131 CrossRef CAS.
- F. Hansen and G. Rødsrud, Surface tension by pendant drop: I. A fast standard instrument using computer image analysis, J. Colloid Interface Sci., 1991, 141, 1–9 CrossRef CAS.
- A. Z. Stetten, F. S. Kratz, N. Schilderink, S. Ayirala, M. H. Duits, J. Kierfeld and F. Mugele, Elastometry of Complex Fluid Pendant Capsules, Langmuir, 2023, 39, 16303–16314 CrossRef CAS PubMed.
- J. N. Israelachvili. Intermolecular and Surface Forces, Academic press, 2011 Search PubMed.
- G. Yang and D. T. Hallinan, Gold nanoparticle monolayers from sequential interfacial ligand exchange and migration in a three-phase system, Sci. Rep., 2016, 6, 35339 CrossRef CAS PubMed.
- E. Guzmán, F. Ortega and R. G. Rubio, Forces controlling the assembly of particles at fluid interfaces, Langmuir, 2022, 38, 13313–13321 CrossRef PubMed.
- W. H. Qi, M. P. Wang and Q. Liu, Shape factor of nonspherical nanoparticles, J. Mater. Sci., 2005, 40, 2737–2739 CrossRef CAS.
- A. Ward and L. Tordai, Time-dependence of boundary tensions of solutions I. The role of diffusion in time-effects, J. Chem. Phys., 1946, 14, 453–461 CrossRef CAS.
- N. Bizmark, M. A. Ioannidis and D. E. Henneke, Irreversible adsorption-driven assembly of nanoparticles at fluid interfaces revealed by a dynamic surface tension probe, Langmuir, 2014, 30, 710–717 CrossRef CAS PubMed.
- O. E. Pérez, C. C. Sánchez, A. M. Pilosof and J. M. R. Patino, Dynamics of adsorption of hydroxypropyl methylcellulose at the air–water interface, Food Hydrocolloids, 2008, 22, 387–402 CrossRef.
- A. Nelson, D. Wang, K. Koynov and L. Isa, A multiscale approach to the adsorption of core–shell nanoparticles at fluid interfaces, Soft Matter, 2015, 11, 118–129 RSC.
- G. Gyulai and É. Kiss, Interaction of poly (lactic-co-glycolic acid) nanoparticles at fluid interfaces, J. Colloid Interface Sci., 2017, 500, 9–19 CrossRef CAS.
- S. Ferdous, M. A. Ioannidis and D. Henneke, Adsorption kinetics of alkanethiol-capped gold nanoparticles at the hexane–water interface, J. Nanopart. Res., 2011, 13, 6579–6589 CrossRef CAS.
- D. Graham and M. Phillips, Proteins at liquid interfaces: I. Kinetics of adsorption and surface denaturation, J. Colloid Interface Sci., 1979, 70, 403–414 CrossRef CAS.
- I. Muntz, F. Waggett, M. Hunter, A. B. Schofield, P. Bartlett, D. Marenduzzo and J. H. Thijssen, Interaction between nearly hard colloidal spheres at an oil-water interface, Phys. Rev. Res., 2020, 2, 023388 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00280f |
| ‡ Contributed equally to this work. |
| § Current address: Department of Materials Science and Engineering, Nagoya University, Nagoya, 464-8603, Aichi, Japan. |
| This journal is © The Royal Society of Chemistry 2024 |