Open Access Article
Open Access ArticleA computational investigation of eumelanin–drug binding in aqueous solutions†
Sepideh
Soltani
 a,
Anupom
Roy
a,
Anupom
Roy
 b,
Arto
Urtti
cd and
Mikko
Karttunen
b,
Arto
Urtti
cd and
Mikko
Karttunen
 *ab
*ab
aDepartment of Physics and Astronomy, The University of Western Ontario, 1151 Richmond Street, London, Ontario N6A 3K7, Canada. E-mail: mkarttu@uwo.ca
bDepartment of Chemistry, The University of Western Ontario, 1151 Richmond Street, London, Ontario N6A 5B7, Canada
cSchool of Pharmacy, University of Eastern Finland, Yliopistonranta 1 C, FI-70210 Kuopio, Finland
dFaculty of Pharmacy, University of Helsinki, Viikinkaari 5 E, FI-00790 Helsinki, Finland
First published on 17th May 2024
Abstract
Melanin is a widely found natural pigment serving multiple physiological functions and having numerous applications in industries and pharmaceuticals. Due to the diverse structural properties of melanin, drug molecules exhibit varying degrees of affinity towards it. Consequently, drug molecules binding to melanin, including eumelanin, possess significant implications for drug delivery, biodistribution, and the treatment of various diseases. Here, we investigate allosteric binding between drugs and eumelanin using computational techniques such as molecular dynamics (MD) simulations, density functional theory (DFT) calculations, and free energy calculations. Eumelanin, composed of DHI and DHICA molecules, was utilized in different systems, including aggregated and random arrangements, with the addition of neutral or charged eumelanin and selected drug molecules (chloroquine, levofloxacin, timolol, methotrexate, and diclofenac). The MD simulations revealed conformational changes in both eumelanin and drug molecules upon interaction along with the creation of binding sites or cavities. Evaluation of binding free energy through molecular mechanics Poisson–Boltzmann surface area (MM-PBSA) calculations indicated that neutral timolol and charged diclofenac exhibited the strongest binding to DHI aggregated bundles, while both neutral and charged methotrexate showed the strongest binding in random DHI systems. In contrast, neutral and charged chloroquine displayed the strongest binding in random systems with DHICA (neutral and charged) respectively. Following MD simulations, DFT calculations were employed to further investigate the strength of drug–eumelanin binding. By utilizing the drug–eumelanin poses obtained from MD simulations, DFT calculations demonstrated that the binding strength is influenced by the structural orientation and conformation of both the drug and eumelanin molecules. Overall, drug–eumelanin binding depends on various factors, including conformational changes in both the drug and eumelanin, the charges of the molecules, the presence of binding sites (especially in DHI eumelanin), the occurrence of π–π and hydrogen bond interactions, and the surrounding solvent environment.
1 Introduction
Melanin is a widespread natural pigment consisting of indoles and phenols, and it is commonly present in various organisms such as plants, microorganisms, marine cephalopods, animals, and humans.1 It has even be detected in well-preserved dinosaur fossils and ancient bird feathers.2 Given its broad occurrence across diverse life forms, and structures resulting from the oxidation of phenols and the subsequent polymerization of intermediate phenols and their resulting quinones, melanin is generally referred to as a heterogeneous polymer.3Melanin is typically divided into three main categories, eumelanin, pheomelanin, and allomelanin based on the chemical structure of the pigment's monomeric subunit.1 However, a broader classification recognizes five major categories: eumelanin, the focus of this study, pheomelanin, allomelanin, neuromelanin, and pyomelanin.4 Eumelanin, which appears primarily black-brown, is prevalent in human hair and skin, and it is also produced by certain bacteria, fungi, and myxomycetes.5 Pheomelanin, on the other hand, is predominantly yellowish or reddish and is found in high concentrations in poultry feathers, red hair in humans, insects, amphibians, and reptiles.6 Allomelanin encompasses a heterogeneous polymer that can exhibit various colors and is commonly found in numerous fungi and plants, lacking nitrogen content.7 Neuromelanin is a dark insoluble pigment that has a pheomelanin core and eumelanin shell. It is, however, not produced by melanocytes but rather in catecholaminergic neurons located in the substantia nigra region of the brain.8–10 Lastly, pyomelanin is a water-soluble pigment that does not possess a biosynthetic pathway. It is associated with the activation of the L-tyrosine/L-phenylalanine degradation pathway and is widely present in bacteria and fungi.11
Eumelanin exists in the form of a complex macromolecule composed of 5,6-dihydroxyindole (DHI) and its 2-carboxylated form, 5,6-dihydroxyindole-2-carboxylic acid (DHICA).1 Although eumelanins consist of DHI and DHICA at the fundamental level, the precise structure remains unknown and, consequently, the natural aggregation or stacking behaviors of eumelanin are still subjects of ongoing discussion.12–15 However, this defining characteristic relies on factors such as the abundance of carboxylic acid groups with negative charges, the presence of aromatic rings facilitating π-interactions, hydrogen bonds, and van der Waals interactions.12 In the human body, eumelanin functions as a natural sunscreen by absorbing UV radiation, safeguarding the skin from harm, and reducing the risk of skin cancer.16 Moreover, eumelanin in the eye acts as a protector for photoreceptor cells, preserving retinal health by shielding them from UV light.17 Eumelanin also plays a role in regulating body temperature by absorbing and dissipating heat.18 Additionally, eumelanin exhibits antioxidant properties by counteracting harmful free radicals within the body.12
Melanin has also demonstrated a wide range of applications in biotechnology, medicine, and the environment.19 Studies have revealed that it possesses potent anti-inflammatory properties due to its ability to inhibit cyclooxygenase (COX) and lipoxygenase (LOX) enzymes.20 Furthermore, melanin can provide protection for the digestive system by reducing the secretion of gastric juice.19 Its ability to remain in pigmented tissues for extended periods of time makes it suitable for use as a vehicle or conduit for drug delivery, facilitating the transportation of drugs to their target locations, particularly when administered orally.21 For instance, a melanin–iron complex can effectively treat iron-deficiency anemia by alleviating symptoms, enhancing the availability of iron, and reducing side effects compared to conventional drug treatments.22 Additionally, melanin has been recognized as a highly efficient and rapid ion exchange agent capable of binding toxins, chemicals, and heavy metals, effectively acting as a scavenger for free radicals.23
In medicinal chemistry, the focus has been on its capacity to bind and interact with drugs. A specific experimental investigation highlighted the substantial impact of ocular melanin on ocular pharmacokinetics by binding small-molecule drugs, offering a potential approach for prolonging drug retention in the eye.24 A combined experimental and computational study explored the influence of cellular factors on the release and retention of drugs in melanin-containing cells, aiding the development of drugs that bind to melanin for extended ocular effects.25In vivo and in vitro research has demonstrated that melanin–drug binding can affect the distribution and elimination of ocular medications.26 Another in vitro study indicated that melanin can be utilized for analyzing drug incorporation into hair, enabling the determination of drug use in both clinical and forensic toxicology.27 Lastly, an experimental study proposed the use of melanin as a novel nanocarrier for pH-responsive drug release in formulations targeting the colon and intestines in drug delivery systems.28
Computational techniques such as MD simulations, DFT calculations, and molecular docking have already demonstrated their utility and efficiency in drug discovery, as well as in the identification of different molecular characteristics, including binding properties.29 For example, MD simulations30 can offer insights into the system's dynamic behavior, including the drug and eumelanin's conformational changes and movements. Additionally, it can identify potential binding sites and provide binding affinities. Meanwhile, DFT31 calculations can provide more detailed information on the electronic structure and energetics of the system, such as how drugs and eumelanin interact and thermodynamic information such as free binding energy. Combining the information obtained from both MD simulations and DFT calculations can provide a comprehensive understanding of the drug–eumelanin interactions, including information about energy, dynamic behavior, and thermodynamics of the system. Conversely, molecular docking32 is an approach that examines the arrangement and positioning of molecules within the binding site of a macromolecular target, such as eumelanin.
The objective of this study is to examine how drugs bind to different forms of eumelanin (DHI and DHICA), which can be either aggregated or random. To investigate the behavior and interaction of these various eumelanin forms with one or more drug molecules, we employed MD simulations, DFT calculations, and molecular docking.
2 Computational methods
We combined three different computational methods, namely MD simulations, DFT calculations, and molecular docking to study the binding properties of eumelanin (DHI and DHICA) with five different drugs (chloroquine, levofloxacin, timolol, methotrexate, and diclofenac). The selection of drug molecules was based on previous experiments conducted on melanin binding with these drugs.24,34 The MD simulations allowed us to study eumelanins’ (DHI and DHICA) conformational changes in the presence of drugs possessing neutral or charged states. This also included examining the behavior of charged eumelanin (DHICA) when exposed to drugs of both neutral and charged states.The information from MD simulations was further used to identify stable drug–eumelanin interactions, to determine binding sites, and to calculate binding energies. In addition, the stable conformations of drug–eumelanin complexes were used in DFT calculations to assess the strength of binding and structural orientations. Due to the computational costs associated with DFT, we limited our analysis to systems of a single drug molecule and a single eumelanin molecule, enabling us to obtain binding energies.
As the third approach, we utilized molecular docking to investigate the binding affinities of neutral and charged drugs to the eumelanin systems that had already undergone conformational changes in the presence of drug molecules during the MD simulations. The equilibrated structures from the MD simulations were used as the starting point. To perform the MD simulations, we created two types of eumelanin systems, namely aggregated and random, based on our prior studies.35,36 The structures of DHI and DHICA eumelanin used in this study are shown in Fig. 1. The figure illustrates the units in the DHI- and DHICA-eumelanin models employed in this study. However, it is important to note that our models represent specific structural configurations. Eumelanin structure and monomer units may vary in different cases, see for example ref. 37–45. We would also like to mention that the model for the DHICA molecule consists of three units. Experimental results using X-ray and neutron scattering indicate longer oligomers, in particular those consisting of 4–5 units.12,46–49 Here, the length of three units was chosen for computational efficiency and to be able compare directly with previous MD simulations.36
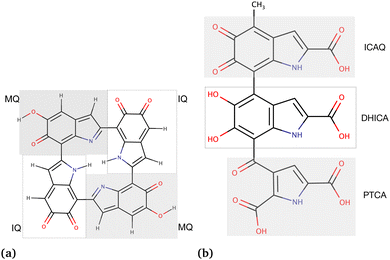 | ||
| Fig. 1 Chemical structures of the eumelanin models used in this study: (a) DHI-eumelanin protomolecule, DHI-based tetrameric model introduced by Kaxiras et al.33 (monomer units are IQ moiety: indole-5,6-quinone and MQ moiety: IQ tautomer including quinone-methide). (b) DHICA-eumelanin: the monomer units of the model are the ICAQ moiety: indole-2-carboxylic acid-5,6-quinone; the DHICA moiety, and the PTCA moiety: (pyrrole-2,3,5-tricarboxylic acid). | ||
The rationale for the aggregated and random structures was the following: eumelanin can exhibit different structural arrangements depending on conditions and charges. For instance, at physiological pH (7.4), DHICA-eumelanin carries a net negative charge (−4) as all of its four carboxyl groups become ionized50,51 (Fig. 1b; the DHICA and ICAQ moities have one, and the PTCA moiety has two carboxyl groups), and it may exist in a random form. DHI-eumelanin is neutral51 and can be found in both aggregated and random forms. In industrial applications,52 both of them can be neutral or charged and can adopt aggregated or random forms.
2.1 Molecular dynamics simulations
| System composition | Drug | No. of water molecules | Counterions (K+/Cl−) | Duration (μs) |
|---|---|---|---|---|
| 27 neutral DHICA (aggregated) + 7 neutral drugs | Chloroquine | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 232 |
0 | 3.00 |
| Levofloxacin | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249 249 |
0 | 3.00 | |
| Timolol | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268 268 |
0 | 3.00 | |
| Methotrexate | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222 |
0 | 3.00 | |
| Diclofenac | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052 052 |
0 | 3.00 | |
| 27 neutral DHICA (random) + 7 neutral drugs | Chloroquine | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 464 |
0 | 3.00 |
| Levofloxacin | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
0 | 3.10 | |
| Timolol | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
0 | 3.00 | |
| Methotrexate | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211 211 |
0 | 3.00 | |
| Diclofenac | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 804 |
0 | 3.00 | |
| 27 charged DHICA (random) + 7 charged drugs | Chloroquine | 6165 | 94 (K+) | 3.00 |
| Levofloxacin | 6160 | 108 (K+) | 3.00 | |
| Timolol | 6156 | 101 (K+) | 3.10 | |
| Methotrexate | 6122 | 122 (K+) | 3.50 | |
| Diclofenac | 6182 | 114 (K+) | 2.00 | |
| 27 neutral DHI (aggregated) + 7 neutral drugs | Chloroquine | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235 235 |
0 | 3.00 |
| Levofloxacin | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
0 | 3.00 | |
| Timolol | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 433 433 |
0 | 3.00 | |
| Methotrexate | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395 395 |
0 | 3.00 | |
| Diclofenac | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 492 492 |
0 | 2.00 | |
| 27 neutral DHI (random) + 7 neutral drugs | Chloroquine | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281 281 |
0 | 3.00 |
| Levofloxacin | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856 856 |
0 | 3.00 | |
| Timolol | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 873 |
0 | 3.00 | |
| Methotrexate | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276 276 |
0 | 3.00 | |
| Diclofenac | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 880 |
0 | 2.00 | |
| 27 neutral DHI (aggregated) + 7 charged drugs | Chloroquine | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403 403 |
14 (Cl−) | 3.00 |
| Levofloxacin | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
0 | 3.00 | |
| Timolol | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
7 (Cl−) | 3.00 | |
| Methotrexate | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374 374 |
14 (K+) | 3.00 | |
| Diclofenac | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
7 (K+) | 2.00 | |
| 27 neutral DHI (random) + 7 charged drugs | Chloroquine | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 093 093 |
14 (Cl−) | 3.00 |
| Levofloxacin | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
0 | 3.00 | |
| Timolol | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
7 (Cl−) | 3.00 | |
| Methotrexate | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 986 986 |
14 (K+) | 3.00 | |
| Diclofenac | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 881 881 |
7 (K+) | 2.00 | |
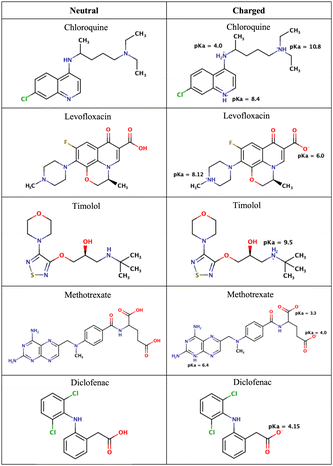 | ||
| Fig. 2 Chemical structures of the drugs used in this study. The figure shows their neutral states and their potential ionization with the corresponding pKa values. | ||
Each of the above systems consisted of a combination of 27 eumelanins and 7 drug molecules in total. The concentrations of eumelanin ranged from 50 to 210 mg ml−1. The eumelanin concentrations were determined using c = n/V, where c is the concentration, n is the amount of the solute (in mol) calculated as n = N/NA, where NA is Avogadros number, and V is the volume of the solution.
The systems underwent an initial pre-equilibration in the NVT ensemble for 2 ns (constant particle number, volume, and temperature). This was followed by a second pre-equilibration step in the NPT ensemble for 2.0 ns (constant particle number, pressure, and temperature) using the Parrinello–Rahman barostat67 at 1 bar, a compressibility of 4.5 × 10−5 bar−1, and a time constant of 2.0 ps. Temperature was set to 300 K. The production runs were then carried out for 2–3 μs in the NPT ensemble. Visualizations were performed using visual molecular dynamics (VMD)68 and PyMol.69
In this study we rigorously uphold the established standards governing molecular dynamics (MD) simulations by employing a thorough approach that utilizes three replica copies to greatly investigate the system under examination. The initial simulation, as detailed in Table 1, forms the foundational basis, providing essential insights into the system's behavior and dynamics. Following this primary exploration, the second and third replicas are initialized from the concluding state of the initial simulation, ensuring a seamless continuation of the investigative process. These subsequent replicas are subjected to a series of meticulous procedures, including energy minimization, NVT, and NPT runs as mentioned above, each tracked over a duration of 150 nanoseconds. This iterative methodology allows for the achievement of diverse starting conditions and trajectories, facilitating a comprehensive examination of the system's dynamic behavior and enabling thorough exploration of potential variations. Furthermore, a comprehensive analysis of the statistical variance observed among the replicas is presented, enriching the understanding of the reliability and reproducibility of the computational findings. Such a thorough approach underscores the study's commitment to methodological rigor. This approach also is essential for establishing trustworthiness and credibility within the domain of molecular modeling and simulation research. Overall, by following these strict guidelines, we can draw more solid and meaningful conclusions of drug-binding eumelanin with MD simulations in result section.
2.2 Binding free energy calculations
The dissociation binding constant (Kd) is commonly utilized in experiments to determine the binding energy since it is related to the standard free energy. This relationship is expressed by the equation34ΔGbind = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd, Kd, | (1) |
Eqn (1) provides a theoretical estimate of the binding free energy, which is often utilized to analyze experimental data through the dissociation binding constant. This equation, however, cannot be directly applied to MD simulations. Nevertheless, by considering the free energies of the receptor, ligand, and receptor–ligand complex, the MM-PBSA approach allows for the calculation of binding free energy (ΔGbind) in MD simulations. Moreover, the MM-PBSA approach considers the intricate molecular interactions and solvation effects.70 The MM-PBSA method is employed for small molecule binding as an endpoint approach to estimate the difference in binding free energy between the ligand–receptor complex and the separate unbound components (ligand, receptor).70 Consequently, the binding free energy between the ligand and receptor can be defined as
| ΔGbind = ΔGreceptor–ligand − ΔGreceptor − ΔGligand. | (2) |
The disparity in free energy between the complex and individual components can be further broken down into enthalpic (ΔH) and entropic (−TΔS) terms, which assess changes in bonding interactions and conformational disorder upon binding. The enthalpic energy term is approximated by the gas-phase molecular mechanics energy (ΔEMM) and the solvation free energy (ΔGsolv). Estimating the configurational entropy (−TΔS) typically involves techniques such as normal mode or quasi-harmonic analysis, but it is often disregarded due to its high computational cost and the challenge of achieving convergence.70 With the above, eqn (2) can be written as
| ΔGbind = ΔH − TΔS = ΔEMM + ΔGsolv − TΔS. | (3) |
The calculation of ΔEMM involves utilizing the molecular mechanics force field (i.e., the OPLS-AA force field in this study), which encompasses the covalent (ΔEcovalent), electrostatic (ΔEelec), and van der Waals dispersion and repulsion (ΔEvdW) energies. Within the covalent term, there are variations in bond energies (ΔEbond), angle energies (ΔEangle), and torsion energies (ΔEtorsion), that is, ΔEMM = ΔEcovalent + ΔEelec + ΔEvdW, where ΔEcovalent = ΔEbond + ΔEangle + ΔEtorsion.
The term ΔGsolv in eqn (3) characterizes the impact of polar and non-polar interactions during the transfer of the ligand from a gas phase to a solvent. The polar solvation component (ΔGpolar) quantifies the energy associated with the solute's charge distribution in the continuous solvent and is determined by solving the Poisson–Boltzmann equation (PBE). The non-polar solvation term (ΔGnon-polar) measures the energy resulting from the solute creating a cavity within the solvent and the van der Waals interactions at the interface between the solute and the cavity.70 Therefore, the overall solvation free energy can be expressed as
| ΔGsolv = ΔGpolar + ΔGnon-polar, | (4) |
Both MMPBSA and MMGBSA methodologies offer avenues for computing binding free energies. However, MMPBSA relies on the Poisson–Boltzmann (PB) equation to evaluate the electrostatic contribution to solvation, which, with the price of computational intensity, provides higher accuracy.70 This electrostatic component assumes significance in this study owing to the intricate interactions among drug molecules, eumelanin molecules, and the surrounding solutions. Conversely, MMGBSA employs the generalized Born model, an approximation of the PB equation, which, while computationally less demanding, is also less precise compared to MMPBSA.72
2.3 DFT calculations
The final structures from the first replica of the MD simulations were used for obtaining the poses of drugs bound to DHI and DHICA for DFT calculations; the structures are available online, see Section Data availability. Each model consisted of one eumelanin (DHI or DHICA) and one drug molecule, either neutral or charged. The Gaussian 16 program73 was used for the calculations. The M06-2X/6-31G(d,p) level of theory was used for optimization and harmonic frequency calculations, while the eumelanin–drug structure and solvent environment were modeled using the IEFPCM (integral equation formalism of the polarizable continuum model) method (ε = 78.35 for water). We selected the M06-2X functional for its purported greater reliability and accuracy in describing non-covalent long-range interactions, van der Waals interactions and main group thermochemistry.74,75 To obtain single-point energies, the M06-2X/6-311+G(2df,p) level of theory was used, and Gibbs free energy corrections were obtained from the M06-2X/6-31G(d,p) level of theory. Then, the binding Gibbs free energies were obtained using IEFPCM(water)-M06-2X/6-311+G(2df,p)//IEFPCM(water)-M06-2X/6-31G(d,p) levels of theory. Finally, the drug binding free energies were calculated using| EΔG(binding) = E(eumelanin–drugcomplex) − E(eumelanin) − E(drug). | (5) |
2.4 Molecular docking
We employed the induced-fit ligand–protein binding docking method76 for molecular docking. The DHI and DHICA eumelanin were obtained from the MD simulations, considering both aggregated and random systems. For the docking calculation, we utilized DHI and DHICA eumelanin bundles as the receptors, while the drug molecules served as the ligands. The minimized ligand molecules were also acquired from the MD simulations. To prepare receptors, all the water molecules, drug molecules, and ions were removed from all the DHI and DHICA eumelanin systems. To prepare AutoDock readable receptor and ligand structures, we utilized the UCSF Chimera program.77 The induced-fit ligand–protein binding molecular docking was performed using the AutoDock Vina program.78 The specific parameters for the grid boxes used in each system, are provided in Table S1 (ESI†).The eumelanin bundle lacks a clearly defined active site, leading drug molecules to bind to its allosteric site. These allosteric sites exhibit dynamic behavior, undergoing various conformational changes in response to drug molecules during MD simulation. Consequently, to investigate eumelanin–drug binding, we initially prepared a mixture of drug molecules and eumelanin. After the equilibration of the systems during MD simulation, we utilized the appropriate structures obtained from the MD (specifically, the last snapshot structure) for docking studies. It has been observed that the allosteric sites stabilize with the presence of drug molecules due to MD simulation equilibration. Therefore, these stabilized eumelanin structures are deemed suitable for docking studies, leading to the sequence of calculations in this study being MD simulations followed by docking simulations. The approach is is similar in spirit to that of Firouzi et al.79
3 Results and discussion
Experimental studies80 have shown that eumelanin does not possess a well-defined structure, and its molecular weight can range from somewhat under 1000 to over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1.34,81 In this study, the estimated molecular weights of DHI and DHICA eumelanin are 583.72 g mol−1 and 993.44 g mol−1, respectively. Furthermore, the concentration of eumelanin in the human retinal pigment epithelium (RPE) can vary from 11 to 22 mg ml−1, while in RPE choroid cells, it can reach concentrations as high as 750 mg ml−1.80 Eumelanin concentrations in our prepared systems, as described in the Computational methods range from 50 to 210 mg ml−1, which is considerably higher than the concentrations found in biological systems. Conversely, many experiments82 typically employ lower concentrations of eumelanin (e.g., 1 mg ml−1) along with low drug concentrations (0.5–500 μM). Compared to experimental conditions, the drug concentrations used in MD simulations are much higher, ranging from 23 to 54 mM, involving 7 drugs and 27 eumelanin molecules (DHI and DHICA) in a 1
000 g mol−1.34,81 In this study, the estimated molecular weights of DHI and DHICA eumelanin are 583.72 g mol−1 and 993.44 g mol−1, respectively. Furthermore, the concentration of eumelanin in the human retinal pigment epithelium (RPE) can vary from 11 to 22 mg ml−1, while in RPE choroid cells, it can reach concentrations as high as 750 mg ml−1.80 Eumelanin concentrations in our prepared systems, as described in the Computational methods range from 50 to 210 mg ml−1, which is considerably higher than the concentrations found in biological systems. Conversely, many experiments82 typically employ lower concentrations of eumelanin (e.g., 1 mg ml−1) along with low drug concentrations (0.5–500 μM). Compared to experimental conditions, the drug concentrations used in MD simulations are much higher, ranging from 23 to 54 mM, involving 7 drugs and 27 eumelanin molecules (DHI and DHICA) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 ratio. This is because concentrations ranging from 0.25 μM to 500 μM are too low for MD simulations.
4 ratio. This is because concentrations ranging from 0.25 μM to 500 μM are too low for MD simulations.
As mentioned in the Methods section, we chose drug molecules based on previous experimental studies.24,34 Consequently, we considered their neutral state and the charge state corresponding to physiological pH, see Fig. 2.
At pH 4.7 chloroquine can acquire three positive charges, but at pH 7.4, it only has two positive charges.51 The latter was used in the simulations. Levofloxacin is a compound with both positive and negative charges. At pH 7.4, levofloxacin predominantly exists in its zwitterionic form without any net charge.83 Timolol is categorized as a weak base and can undergo protonation in an aqueous solution. At pH 7.4, it is primarily found in its protonated form, carrying a positive charge.84 Methotrexate, on the other hand, is considered a weak acid and can undergo deprotonation in an aqueous solution. At pH 7.4, it mainly exists in its deprotonated form.85 Similar to methotrexate, diclofenac is also classified as a weak acid and can undergo deprotonation in an aqueous solution. At pH 7.4, diclofenac is primarily present in its deprotonated form.86
3.1 Conformational changes of drug–eumelanin complexes
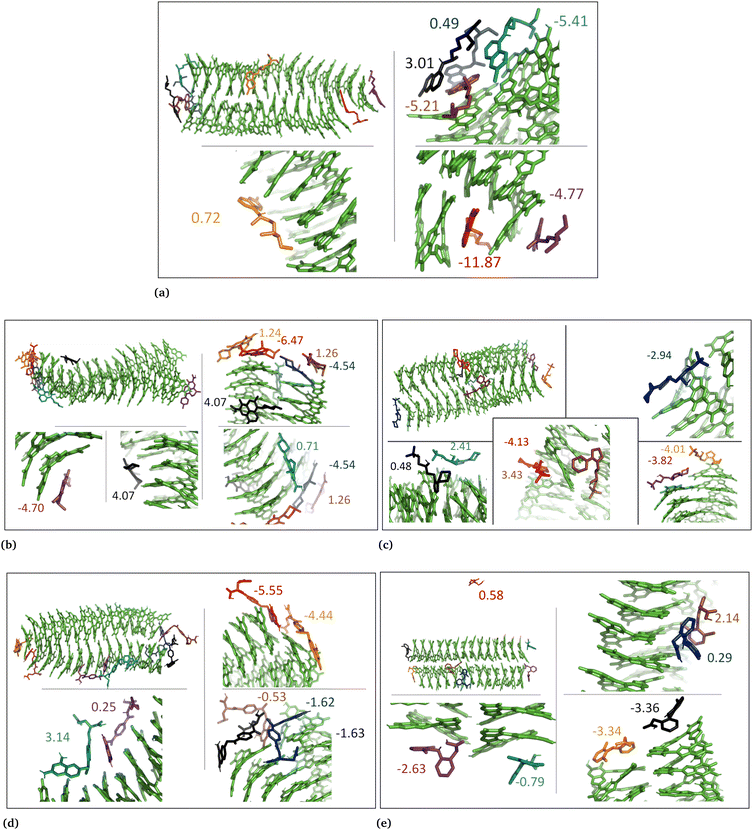
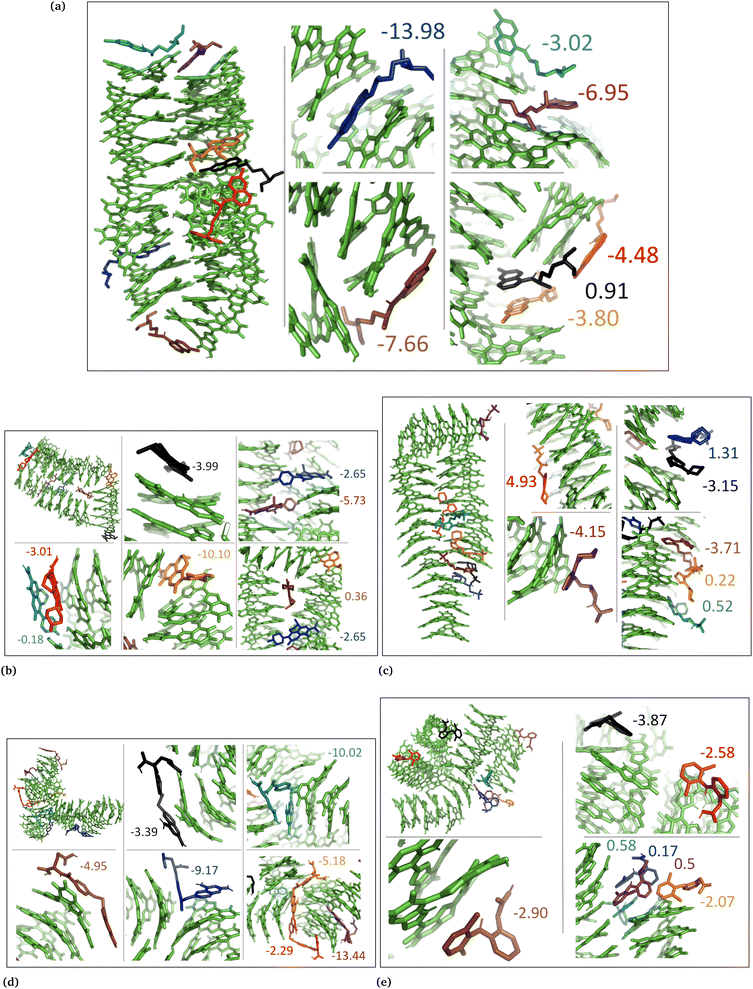
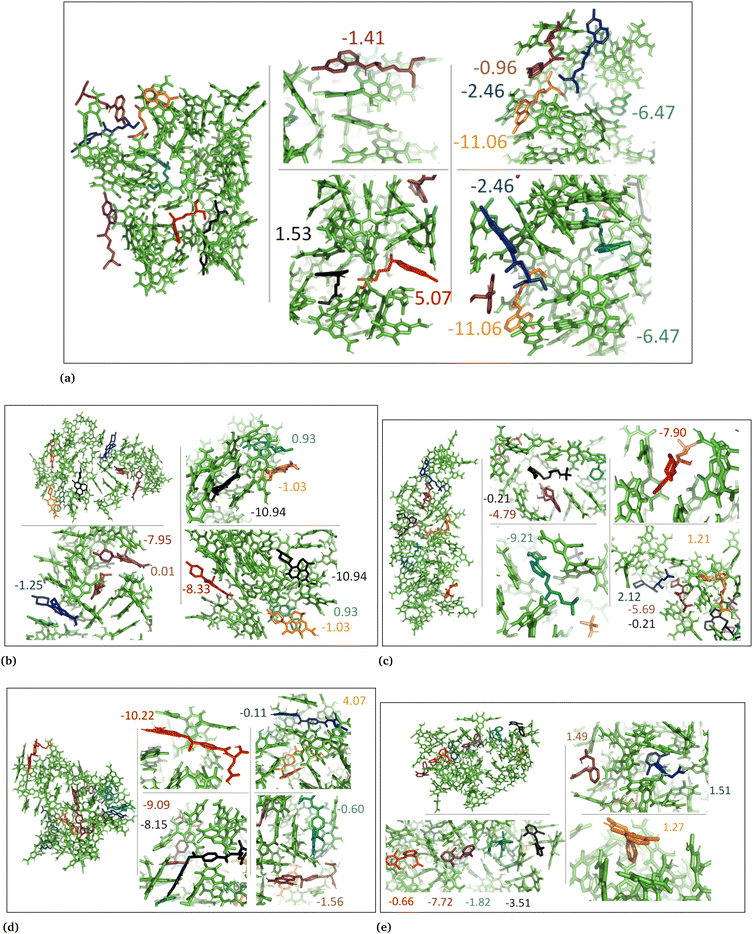
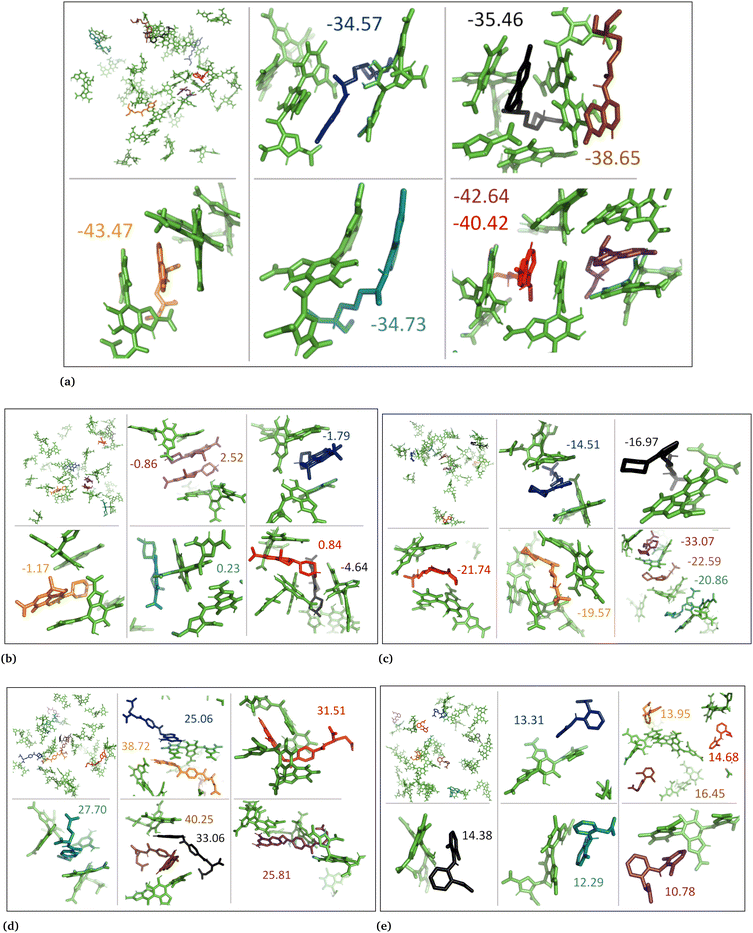
The drug–eumelanin MD simulations revealed that all systems underwent conformational changes, enabling drug molecules to interact with eumelanin. Fig. 3–9 and Fig. S1–S7 (ESI†) show illustrations of conformational changes that occurred in eumelanin (DHI and DHICA) aggregated and random systems in the presence of drug molecules. The figures are from first simulations and the replica copies are not shown.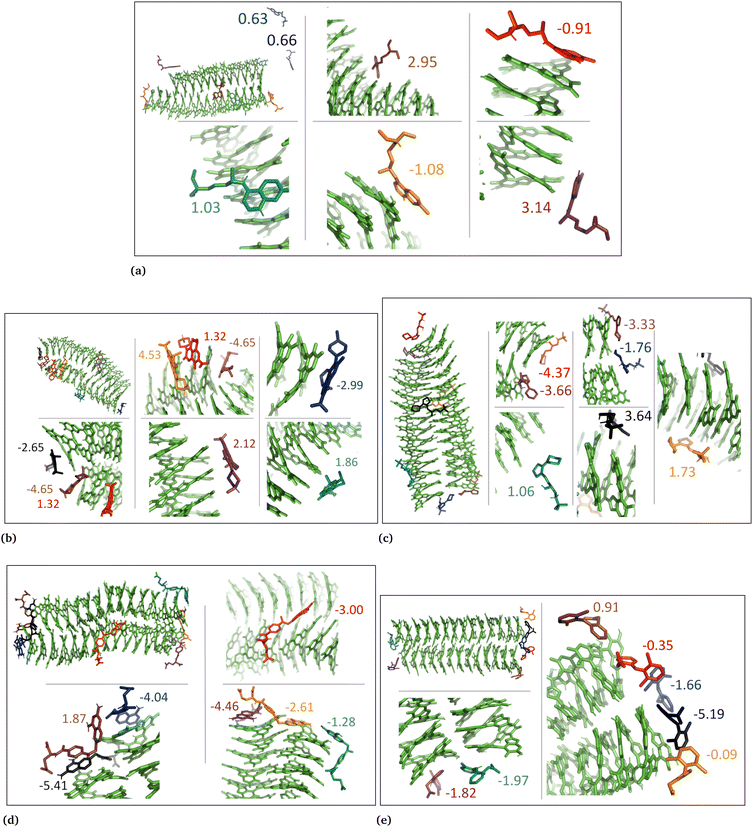 | ||
| Fig. 5 Illustration shows aggregated DHI with charged drug molecules. (a) Chloroquine, (b) levofloxacin, (c) timolol, (d) methotrexate, and (e) diclofenac. Binding energies are shown in kcal mol−1. | ||
 | ||
| Fig. 6 DHI random system with charged drug molecules. (a) Chloroquine, (b) levofloxacin, (c) timolol, (d) methotrexate, and (e) diclofenac. Binding energies are shown in kcal mol−1. | ||
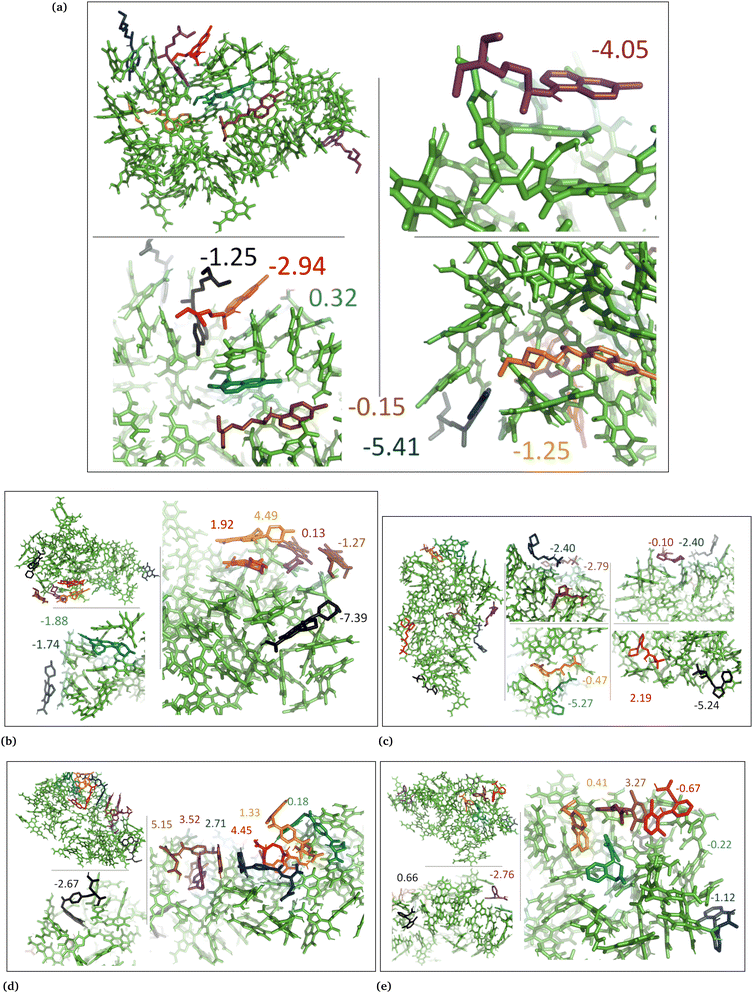 | ||
| Fig. 7 DHICA aggregated system with uncharged drug molecules. (a) Chloroquine, (b) levofloxacin, (c) timolol, (d) methotrexate, and (e) diclofenac. Binding energies are shown in kcal mol−1. | ||
In the case of DHI aggregated systems (Fig. 3 and Fig. S1 and S2, ESI†), it was observed that all neutral drug molecules interacted with DHI without disturbing the stacking. Additionally, a large number of drug molecules demonstrated a greater tendency to interact with DHI via π–π interactions, forming small drug clusters at the planar sides of the DHI stacks. However, a few drug molecules also exhibited a tendency to interact with the DHI stacks through the tops of their hydroxyl sides, forming hydrogen bonds and π–π interactions. Interestingly, the DHI-aggregated stacks remained intact even when charged drug molecules interacted with it.
In the DHI random systems (Fig. 4 and Fig. S3 and S4, ESI†), the DHI and the drug molecules were initially placed randomly in the simulation box. During the simulation, the DHI molecules aggregated and formed multiple stackings, creating cavities for drug molecules to interact. In these random systems, drug molecules were more evenly distributed over the DHI stacking compared to the DHI aggregated systems, regardless of their charge. Furthermore, drug molecules in these random systems showed only low tendency to form clusters. When charged drug molecules interacted with the DHI stacks, they also occupied the cavities in the stacks and were widely distributed throughout the DHI stackings.
In the cases of the DHICA aggregated systems (Fig. 7 and Fig. S5, ESI†), chloroquine, timolol, and diclofenac were widely distributed throughout the DHICA aggregation. On the other hand, levofloxacin and methotrexate formed clusters with multiple levofloxacin and methotrexate molecules accumulating during the simulations.
In the DHICA random systems (Fig. 8 and Fig. S6, ESI†), the neutral DHICA molecules accumulated and interacted with neutral drug molecules during the simulations. Since DHICA molecules were randomly placed at the beginning of each simulation, the drug molecules had a better opportunity to occupy the regions inside the accumulated bundles of DHICA. Consequently, the drug molecules were more evenly distributed within the accumulation compared to the DHICA aggregated systems.
In the case of DHICA random systems with charged drugs (Fig. 6 and Fig. S7, ESI†), it is important to note that DHICA molecules were negatively charged when placed with charged drugs prior to the simulations. The charged DHICA molecules did not accumulate during the simulations due to their negative charges as also shown in our prior study.36 Since DHICA molecules did not accumulate, the charged drug molecules were widely dispersed throughout the systems. However, in these situations, the charged drug molecules engaged in interactions with one or two negatively charged DHICA molecules at a time through π–π interactions and Coulombic interactions.
3.2 Drug–eumelanin binding free energy
The MM-PBSA free energy calculations are derived from the data obtained from the three mentioned replica copies, and the resulting outcomes are documented in Table 2. The methodology employed for calculating these results involves considering the presence of seven distinct drugs within each replica and are shown in Table S1 (ESI†). Consequently, both the free energy values and their associated variances are computed for each simulation (Tables S2–S4, ESI†). To ensure the reliability and robustness of the final results, a weighted average free energy approach is utilized, along with a combination of variances in Table 2. The figures display the free energy results for the initial simulations, as they originate from the data of the first replica simulation.| Drug name | State | DHI (aggregated) | DHI (random) | DHICA (aggregated) | DHICA (random) |
|---|---|---|---|---|---|
| Chloroquine | Neutral | −3.03 ± 0.7 | −5.42 ± 2.9 | −1.52 ± 1.2 | −1.94 ± 2.6 |
| Levofloxacin | −0.43 ± 1.8 | −3.72 ± 2.2 | +0.19 ± 1.6 | −4.18 ± 2.0 | |
| Timolol | −1.45 ± 1.2 | −0.78 ± 1.8 | −2.36 ± 1.2 | −2.76 ± 1.9 | |
| Methotrexate | −2.19 ± 1.4 | −6.68 ± 2.2 | +2.76 ± 1.4 | −4.18 ± 2.1 | |
| Diclofenac | −0.79 ± 1.0 | −1.57 ± 0.9 | +0.01 ± 0.5 | −1.45 ± 2.5 | |
| Chloroquine | Charged | +1.02 ± 1.1 | −0.20 ± 0.7 | NA | −37.35 ± 2.5 |
| Levofloxacin | −0.77 ± 2.4 | −0.63 ± 1.3 | NA | +0.05 ± 1.4 | |
| Timolol | −0.97 ± 1.1 | −1.61 ± 0.7 | NA | −21.14 ± 3.1 | |
| Methotrexate | −3.28 ± 1.0 | −4.97 ± 1.2 | NA | 27.24 ± 1.3 | |
| Diclofenac | −2.40 ± 1.5 | −4.86 ± 0.6 | NA | 13.76 ± 1.1 | |
In aggregated DHI systems with neutral drugs, chloroquine exhibited the strongest average binding with the lowest binding energy of −3.03 ± 0.7 kcal mol−1 (Table 2, column 3). It was also observed that among the seven drug molecules in each system, those that interacted with the planar side or the flat surface of DHI (Fig. 1a) demonstrated the strongest binding, as depicted in Fig. 3. This pattern held true for all neutral drug molecules interacting with the DHI aggregated bundle. The ranking of drug molecules based on their average binding strength to the DHI aggregated bundle was: chloroquine (−3.03) > methotrexate (−2.19) > timolol (−1.45) > diclofenac (−0.79) > levofloxacin (−0.43).
In the case of DHI random systems with neutral drugs, both the neutral drug molecules and DHI were randomly positioned at the start of the simulation. Over time, the DHI molecules aggregated and formed multiple stacks while interacting with the drug molecules, as illustrated in Fig. 4. Unlike in the DHI aggregated systems, in this scenario, the drug molecules had a greater opportunity to occupy the cavities created by the stacking of DHI molecules. Nevertheless, similar to the DHI aggregated systems, the interactions between drug molecules and the planar side of DHI remained crucial for stronger binding. Methotrexate exhibited the strongest average binding, with the lowest average binding free energy of −6.68 ± 2.2 kcal mol−1 (Table 2, column 4). This can be attributed to the planar surface of methotrexate interacting with the planar side of DHI and being positioned between the DHI stack, facilitating strong π–π interactions between DHI and methotrexate molecules (Fig. 4d). A similar trend was observed for other drug molecules, indicating a stronger binding affinity when interacting with random DHI molecules. Therefore, the ranking of drug molecules based on their binding strength to the DHI random bundle was determined to be methotrexate (−6.68) > chloroquine (−5.42) > levofloxacin (−3.72) > diclofenac (−1.57) > timolol (−0.78).
In the case of DHI aggregated systems with charged drugs, Fig. 5, methotrexate exhibited the strongest average binding with the lowest average binding energy of −3.28 ± 1.0 kcal mol−1 (Table 2, column 3). The planar L-shapes surfaces of methotrexate molecules (see Fig. 5d) are engaged in simultaneous interactions with multiple DHI-eumelanin entities in this scenario. The second strongest average binding belongs to diclofenac with −2.40 ± 1.5 kcal mol−1. It is notable that out of the seven diclofenac molecules, five of them accumulated together while interacting with the planar side of the DHI aggregated stack, indicating a high tendency for diclofenac molecules to interact with each other in their charged form. Similarly, for other drug molecules, those that interacted through the planar side of DHI by forming robust π–π interactions displayed stronger binding. Consequently, the ranking of the charged drug molecules based on their binding strength to the DHI aggregated bundle was determined to be methotrexate (−3.28) > diclofenac (−2.40) > timolol (−0.97) > levofloxacin (−0.77) > chloroquine (+1.02).
In the case of DHI random systems with charged drugs, where the charged drug molecules and the neutral DHI molecules are randomly positioned at the start of the simulation, the DHI molecules aggregate and form multiple stacks while interacting with the charged drugs, as illustrated in Fig. 6. Similarly to the DHI random systems with neutral drug molecules, the average strongest binding was observed for methotrexate, with the lowest average binding energy of −4.97 ± 4.5 kcal mol−1 (Table 2, column 4). As seen in previous DHI systems, all charged drug molecules exhibited a similar interaction pattern with the DHI random system. Therefore, the ranking of the charged drug molecules based on their binding strength to the DHI random bundle was determined to be methotrexate (−4.97) > diclofenac (−4.86) > timolol (−1.61) > levofloxacin (−0.63) > chloroquine (−0.20).
In the DHICA aggregated systems with neutral drugs, where the neutral drug molecules interacted with the neutral aggregated DHICA bundle (Fig. 7), the strongest average binding was observed for timolol, with the lowest average binding energy of −2.36 ± 1.2 kcal mol−1 (Table 2, column 5) followed by chloroquine (−1.52 ± 1.2). The ranking of the neutral drug molecules based on their binding strength was determined to be timolol (−2.36) > chloroquine (−1.52) > levofloxacin (+0.19) > diclofenac (+0.01) > methotrexate (+2.76).
In the case of DHICA random systems with neutral drugs, where both the neutral drug molecules and neutral DHICA molecules were randomly positioned at the start of the simulation. The neutral DHICA molecules aggregated and formed a bundle while interacting with the drug molecules, Fig. 8. It is important to note that in this scenario, the drug molecules had a greater opportunity to be positioned within the middle of the bundle during the interactions and bundle formation. The strongest average binding was determined for levofloxacin, with the lowest binding energy of −4.08 ± 6.8 kcal mol−1 (Table 2, column 6). Additionally, the ranking of the neutral drug molecules based on their binding strength to the DHICA random bundle was found to be levofloxacin (−4.18) ≈ methotrexate (−4.18) > timolol (−2.76) > chloroquine (−1.94) > diclofenac (−1.45).
In the case of DHICA random systems with charged drugs, where both the charged drug molecules and the charged DHICA molecules were randomly positioned at the start of the simulation, the charged DHICA molecules did not aggregate due to their negative charges while interacting with the charged drugs, Fig. 9. It was observed that most of the drug molecules interacted with either one or two DHICA molecules simultaneously, as the negative charges of DHICA prevented their accumulation. The ranking of the charged drug molecules based on their average binding strength to the DHICA random molecules was found to be chloroquine (−37/35) > timolol (−21.14) > levofloxacin (+0.05) > diclofenac (+13.76) > methotrexate (+27.24). The ranking is consistent with findings from experimental studies,25,34 except for levofloxacin. Overall, the calculations using MM-PBSA for drug–eumelanin binding free energies demonstrate that drug molecules, whether neutral or charged, bind to various sites of different eumelanin systems with varying degrees of binding strength.
3.3 DFT calculations
The MD simulations revealed that both the aggregated and random DHI and DHICA systems experienced conformational changes when interacting with the drug molecules. These conformational changes and drug binding at different eumelanin sites demonstrate that drug molecules bind to the various eumelanin sites with different binding strengths. To investigate the binding energies on a single eumelanin molecule, DFT calculations were conducted using a single eumelanin molecule (DHI or DHICA) and a single drug molecule. As described in Computational methods, single eumelanin–drug complexes were obtained from each of the MD simulation systems. Their binding energies using DFT calculations are presented in Table 3 and Fig. S8–S17 (ESI†).| Drug name | State | DHI (aggregated) | DHI (random) | DHICA (aggregated) | DHICA (random) |
|---|---|---|---|---|---|
| Chloroquine | Neutral | −1.2 | −4.4 | −6.0 | +3.1 |
| Levofloxacin | −0.8 | +1.2 | +0.9 | +2.9 | |
| Timolol | +1.4 | −2.9 | +10.2 | +2.8 | |
| Methotrexate | −1.7 | −0.8 | +7.6 | +9.5 | |
| Diclofenac | +0.8 | +2.0 | +6.0 | −0.3 | |
| Chloroquine | Charged | −2.3 | −0.6 | NA | −16.6 |
| Levofloxacin | −1.2 | −11.0 | NA | +6.2 | |
| Timolol | +1.8 | +3.7 | NA | −7.1 | |
| Methotrexate | +2.0 | −5.2 | NA | +4.8 | |
| Diclofenac | +1.6 | +2.6 | NA | +20.9 | |
In the aggregated DHI systems (column ‘aggregated’ in Table 3), the binding Gibbs free energies of neutral drugs suggest that single neutral methotrexate and chloroquine compounds have a higher binding affinity towards single (neutral) DHI eumelanin compared to other drug compounds. The ranking from the strongest to the weakest binding was found to be methotrexate (−1.7) > chloroquine (−1.2) > levofloxacin (−0.8) > diclofenac (+0.8) > timolol (+1.4).
For a single charged drug molecule bound to a single neutral DHI molecule, the results in Table 3 indicate that the charged chloroquine and levofloxacin molecules have the highest binding affinities. The ranking from the strongest to the weakest binding is chloroquine (−2.3) > levofloxacin (−1.2) > diclofenac (+1.6) > timolol (+1.8) > methotrexate (+2.0).
For DHI random systems (column ‘random’ in Table 3), the results indicate that chloroquine and timolol have the highest binding affinities towards single neutral DHI eumelanin. The order of binding strengths was chloroquine (−4.4) > timolol (−2.9) > methotrexate (−0.8) > levofloxacin (+1.2) > diclofenac (+2.0). We also calculated the eumelanin–drug binding energies for charged drug compounds, and the results show that charged levofloxacin and methotrexate compounds have the highest binding affinities towards DHI eumelanin. The order of binding strengths was levofloxacin (−11.0) > methotrexate (−5.2) > chloroquine (−0.6) > diclofenac (+2.6) > timolol (+3.7).
For the DHICA aggregated systems, (column ‘aggregated’ in Table 3) the binding free energies for single neutral drugs were also calculated and the results indicate that only chloroquine has binding affinity. The order of binding strengths was chloroquine (−6.0) (the only binding one) > levofloxacin (+0.9) > diclofenac (+6.0) > methotrexate (+7.6) > timolol (+10.2).
For DHICA random systems, (column ‘random’ in Table 3) the binding free energies of single neutral drugs and single charged DHICA eumelanin were calculated and the results suggest that of the neutral drugs, only diclofenac has binding affinity. The order of binding strengths was diclofenac (−0.3) > timolol (+2.8) > levofloxacin (+2.9) > chloroquine (+3.1) > methotrexate (+9.5). For the charged drugs chloroquine and timolol had binding affinity. The ranking was chloroquine (−16.6) > timolol (−7.1) > methotrexate (+4.8) > levofloxacin (+6.2) > diclofenac (+20.9).
In general, the strength of binding is influenced by the structural orientation and conformation of both the drug and eumelanin. In systems involving DHI, both neutral and charged drug compounds exhibited varying degrees of binding affinity to single DHI eumelanin molecule. Interestingly, this occurred even though the charge of the DHI eumelanin was neutral in both aggregated and random systems (Fig. S8, S10, S12, S14 and S16, ESI†). In the DHI systems, charged chloroquine exhibited the strongest binding to DHI eumelanin with the lowest binding energy of −2.3 kcal mol−1, whereas charged methotrexate was the weakest binder with the highest binding energy of +2.0 kcal mol−1. However, in DHI random systems, charged levofloxacin showed the strongest binding to DHI eumelanin with the lowest binding energy of −11.0 kcal mol−1, and charged timolol showed the weakest binding with the highest binding energy of +3.7 kcal mol−1.
In neutral DHICA eumelanin systems, chloroquine exhibited the strongest binding affinity with the lowest binding energy of −6.0 kcal mol−1, and timolol exhibited the weakest binding affinity with the highest binding energy of +10.0 kcal mol−1. In charged DHICA eumelanin systems, chloroquine exhibited the strongest binding affinity with the lowest binding energy of −16.6 kcal mol−1, while diclofenac exhibited the weakest binding affinity with the highest binding energy of +20.9 kcal mol−1. In all systems (Fig. S8–S17, ESI†), it was further observed that slight changes in conformation and charge of drugs and eumelanin can affect binding energy, as well as the number of π–π and hydrogen bond interactions. It is worth noting that DFT calculations were performed on a single drug and single eumelanin compounds with implicit water, whereas biological conditions involve multiple eumelanin compounds interacting with one or more drugs with explicit water molecules, which could impact the binding affinity and energy. Therefore, larger models with multiple eumelanin compounds and drugs are required to investigate this further, and QM/MM calculations may also be useful. Additionally, the structure of eumelanin should also be considered as a crucial factor for investigating drug–eumelanin binding because the complete structure of eumelanin is still unknown.
3.4 Molecular docking
Additionally, we conducted molecular docking calculations on eumelanin systems obtained from the MD simulations. The MD simulations revealed that eumelanin (DHI or DHICA) undergoes conformational changes, and formation of cavities or binding sites in the presence of drug molecules. To explore the binding affinities, we employed molecular docking. The AutoDock Vina molecular docking program was used to calculate the drugs’ binding affinities, Table 4.| Drug name | State | DHI (aggregated) | DHI (random) | DHICA (aggregated) | DHICA (random) |
|---|---|---|---|---|---|
| Chloroquine | Neutral | −5.3 | −9.4 | −5.9 | −5.2 |
| Levofloxacin | −7.6 | −10.5 | −8.9 | −5.3 | |
| Timolol | −5.9 | −7.9 | −7.3 | −4.3 | |
| Methotrexate | −7.9 | −12.1 | −9.8 | −7.6 | |
| Diclofenac | −6.5 | −8.5 | −7.4 | −5.0 | |
| Chloroquine | Charged | −5.7 | −9.4 | NA | −5.2 |
| Levofloxacin | −7.6 | −10.1 | NA | −5.2 | |
| Timolol | −5.9 | −8.1 | NA | −4.8 | |
| Methotrexate | −8.0 | −12.5 | NA | −6.9 | |
| Diclofenac | −6.6 | −9.7 | NA | −5.1 | |
In the case of the DHI aggregated systems with neutral drug molecules, methotrexate exhibited the strongest binding affinity, with the lowest binding energy of −7.9 kcal mol−1. The ranking of binding strengths, from strongest to weakest, was as follows: methotrexate (−7.9) > levofloxacin (−7.6) > diclofenac (−6.5) > timolol (−5.9) > chloroquine (−5.3). Similarly, in DHI random systems with neutral drug molecules, methotrexate again displayed the strongest binding affinity, with a binding energy of −12.1 kcal mol−1. The ranking of binding strengths, from strongest to weakest, was as follows: methotrexate (−12.1) > levofloxacin (−10.5) > chloroquine (−9.4) > diclofenac (−8.5) > timolol (−7.9).
In the case of the DHI aggregated systems with charged drug molecules, methotrexate exhibited the strongest binding affinity, with the lowest binding energy of −8.0 kcal mol−1. The ranking of binding strengths, from strongest to weakest, was as follows: methotrexate (−8.0) > levofloxacin (−7.6) > diclofenac (−6.6) > timolol (−5.9) > chloroquine (−5.7). Similarly, in DHI random systems with charged drug molecules, methotrexate showed the strongest binding affinity, with a binding energy of −12.5 kcal mol−1. The ranking of binding strengths, from strongest to weakest, was as follows: methotrexate (−12.5) > levofloxacin (−10.1) > diclofenac (−9.7) > chloroquine (−9.4) > timolol (−8.1).
On the other hand, for the DHICA aggregated systems with neutral drug molecules, methotrexate displayed the strongest binding affinity, with the lowest binding energy of −9.8 kcal mol−1. The ranking of binding strengths, from strongest to weakest, was as follows: methotrexate (−9.8) > levofloxacin (−8.9) > diclofenac (−7.4) > timolol (−7.3) > chloroquine (−5.9).
Regarding DHICA random systems with neutral drug molecules, methotrexate again exhibited the strongest binding affinity, with the lowest binding energy of −7.6 kcal mol−1. The ranking of binding strengths, from strongest to weakest, was as follows: methotrexate (−7.6) > levofloxacin (−5.3) > chloroquine (−5.2) > diclofenac (−5.0) > timolol (−4.3). In DHICA random systems with charged drug molecules, once again, methotrexate demonstrated the strongest binding affinity, with a binding energy of −6.9 kcal mol−1. The ranking of binding strengths, from strongest to weakest, was as follows: methotrexate (−6.9) > chloroquine (−5.2) and levofloxacin (−5.2) > diclofenac (−5.1) > timolol (−4.8).
Overall, methotrexate, whether in a neutral or charged state, displayed the strongest binding affinity towards all eumelanin (DHI and DHICA) systems. It is important to note that no aqueous solution was used during the molecular docking process, which could potentially affect the calculation of binding affinity. As a result, the molecular docking results for binding affinities did not align consistently with the MD and DFT calculations.
3.5 Experimental vs. computational
Our computational analyses at multiple scales, including molecular dynamics (MD), density functional theory (DFT) calculations, and docking, yielded varied binding outcomes attributable to differences in calculation methods and parameters such as pH, ionization state of compounds, and eumelanin condition. Consequently, the ranking of melanin binding was not consistently maintained, a discrepancy attributed to both computational method disparities and nuances in experimental characteristics.Pigmented tissues encompass diverse melanin types, and melanin extracted from various sources may not exhibit a ‘clean’ state, as is the case in computational simulations, due to deviations in physical 3D structure and impurities in particles. This discrepancy between experimental studies and computational results is evident in the heterogeneous nature of melanin binding, as revealed in vitro experiments.87 The current computational findings suggest that melanin binding lacks specific high affinity, instead demonstrating relatively low affinity characterized by diverse interactions with melanin.
In-depth analysis of drug binding data, including substances like chloroquine and methotrexate, disclosed multiple binding energies resulting from various types of binding for each drug. Consequently, defining one or two binding sites appears inadequate, prompting a preference for the Sips isotherm to describe heterogeneous binding.87 The study anticipates that even slight alterations in melanin particle structures may impact binding properties, with particle size also influencing results.24
Various methodologies, including equilibrium binding studies in simple vials,24 two-compartmental systems with dialysis membranes,88 and microscale thermophoresis,34 have been employed in experiments investigating the binding of drugs to melanin. However, most studies on melanin binding report binding percentages under specific experimental conditions, typically utilizing a single drug concentration and a fixed amount of melanin particles.89 Unfortunately, such experimental data do not facilitate the calculation of dissociation constants (Kd) or binding capacity (Bmax). Determining Kd values, crucial for comparisons with molecular modeling simulations, is challenging due to the necessity of using various drug concentrations.26 Additionally, the high binding capacity of melanin poses difficulties in reliably determining Kd values, especially in the cases of drugs with high melanin affinity and low water-solubility, where achieving high drug concentrations is often problematic. Consequently, there is limited available Kd data, and values can vary across different methods, sometimes leading to disparities in Kd values obtained through distinct approaches.34
External factors play a role in modifying binding levels within cells and the living body. For instance, the drug permeability of melanosome and plasma membranes acts as a constraint on drug escape from cells, leading to prolonged drug retention.90 The pH of melanosomes, a crucial factor, may be influenced by basic drugs such as chloroquine, which elevate the pH of other cell organelles like endosomes and lysosomes. The actual pH within melanosomes during drug accumulation remains unknown. In vitro melanin binding studies, coupled with predictive simulations, prove valuable in drug development, as evidenced by the correlation between drug retention in pigmented rat eyes after intravenous injections and in vitro binding results.91
Overall, the comparison of computational and experimental results requires careful consideration to ensure optimal alignment between the two.
4 Conclusion
We conducted a study to examine the binding of drugs to eumelanin (DHI and DHICA) using three computational techniques: MD, DFT calculations, and molecular docking. Various eumelanin systems were utilized, including aggregated systems of DHI and DHICA (where neutral aggregated eumelanin molecules were used at the start of the simulations), random systems of DHI and DHICA (where neutral eumelanin molecules were randomly placed at the start of the simulations), and random systems of DHICA (where charged DHICA molecules were randomly placed at the start of the simulations). Based on experimental studies, we selected drug molecules such as chloroquine, levofloxacin, timolol, methotrexate, and diclofenac with their neutral and charged form at physiological pH 7.4. Our computational investigations yielded the following findings:• MD simulations showed that drug molecules (neutral or charged) and eumelanin (DHI and DHICA) undergo conformational changes when they interact, resulting in the formation of different shapes of eumelanin in the presence of drug molecules, which create cavities or binding sites.
• When drug molecules (neutral or charged) interacted with aggregated eumelanin (DHI or DHICA), they did not penetrate into the eumelanin bundle; instead, they positioned themselves on the surface. However, when drug molecules and eumelanin were randomly placed at the beginning of the simulations, drug molecules had a higher likelihood of being situated in the middle of the eumelanin bundle.
• Based on calculations of drug–eumelanin binding free energies using MM-PBSA, neutral chloroquine exhibited the strongest average binding with the lowest average binding energy (−3.02 ± 0.7 kcal mol−1) when interacting with DHI aggregated bundle. On the other hand, charged methotrexate showed the strongest average binding with the lowest average binding energy (−3.28 ± 1.0 kcal mol−1) when interacting with DHI aggregated bundle. In the case of randomly placed neutral DHI eumelanin molecules, both neutral and charged methotrexate exhibited the strongest average binding, with the lowest average binding energies of −6.68 ± 2.2 kcal mol−1 and −4.97 ± 1.2 kcal mol−1, respectively. For DHICA aggregated systems, neutral timolol showed the strongest average binding with the lowest average binding energy of −2.36 ± 1.2 kcal mol−1. However, when neutral DHICA and neutral drug molecules were randomly placed, neutral levofloxacin and methotrexate exhibited the strongest average binding with the lowest average binding energy of −4.18 ± 2.0 kcal mol−1 and −4.18 ± 2.1 kcal mol−1 respectively. Finally, when charged DHICA eumelanin and charged drug molecules were randomly placed, charged chloroquine exhibited the strongest average binding with the lowest average binding energy of −37.35 ± 2.5 kcal mol−1 which has Coulombic interactions as well as planar interactions with DHICA-eumelanin. The charged DHICA-eumelanin and drug binding results are in agreement with experiment but levofloxacin.
• DFT calculations were performed to investigate the binding energy between a single eumelanin molecule and a single drug molecule, using poses obtained from MD simulations. These calculations revealed that the strength of binding is influenced by the structural orientation and conformation of both the drug and eumelanin molecules. In DHI aggregated systems, charged chloroquine demonstrated the strongest binding to DHI eumelanin, with the lowest binding energy of −2.3 kcal mol−1. However, in DHI random systems, charged levofloxacin exhibited the strongest binding to DHI eumelanin, with the lowest binding energy of −11.0 kcal mol−1. In neutral DHICA eumelanin systems, chloroquine exhibited the strongest binding affinity, with the lowest binding energy of −6.0 kcal mol−1. In charged DHICA eumelanin systems, chloroquine exhibited the strongest binding affinity, with the lowest binding energy of −16.6 kcal mol−1.
• Molecular docking calculations revealed that methotrexate, in both neutral and charged states, displayed the strongest binding affinity to all eumelanin systems.
Overall, our study indicates that drug–eumelanin binding depends on various factors, including conformational changes of both the drug and eumelanin, the charges of both molecules, binding sites (particularly for DHI eumelanin), the number of π–π and hydrogen bond interactions, and the solvent environment. Therefore, further investigation using larger models with multiple combinations of eumelanin molecules and drug molecules is necessary. Additionally, it is important to consider the eumelanin structure as a critical factor in studying drug–eumelanin binding, as the precise structure of eumelanin remains unknown.
In addition, comparing computational and experimental results in drug–melanin binding poses challenges due to diverse factors. The multiscale computational analyses, involving MD, DFT calculations, and docking, demonstrate varying outcomes in melanin binding due to differences in calculation methods and parameters, including pH and ionization state. Discrepancies between experimental and computational results arise from the diverse melanin types in pigmented tissues and impurities in particles. Computational findings indicate a lack of specific high affinity in melanin binding, displaying relatively low affinity with heterogeneous interactions. Most experimental studies on melanin binding report percentages under specific conditions, often using a single drug concentration and a fixed quantity of melanin particles, making the calculation of dissociation constants (Kd) challenging. Determining Kd values for comparison with molecular modeling simulation results is demanding, requiring the use of various drug concentrations. Furthermore, external factors such as drug permeability of melanosome and plasma membranes impede drug escape from cells, prolonging drug retention. Hence, caution is essential when comparing computational and experimental results for optimal alignment.
Data availability
Parameters for DHI, DHICA and all the drug molecules used in this study are available as open source at https://github.com/SoftSimu/melanin.Author contributions
Conceptualization, M. K.; methodology, validation, formal analysis, investigation, and data curation, S. S., A. R. and M. K.; resources, M. K.; writing – original draft preparation, S. S.; writing – review and editing, all authors; visualization, S. S. and A. R.; supervision, M. K.; funding acquisition, M. K. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no competing interests. There are no conflicts to declare.Acknowledgements
MK acknowledges financial support by the Natural Sciences and Engineering Research Council of Canada (NSERC) and Canada Research Chairs Program. Computational resources were provided by the Digital Research Alliance of Canada.Notes and references
- L. Guo, W. Li, Z. Gu, L. Wang, L. Guo, S. Ma, C. Li, J. Sun, B. Han and J. Chang, Int. J. Mol. Sci., 2023, 24, 4360 CrossRef CAS PubMed
.
- I.-E. Pralea, R.-C. Moldovan, A.-M. Petrache, M. Ilieş, S.-C. Hegheş, I. Ielciu, R. Nicoară, M. Moldovan, M. Ene, M. Radu, A. Uifălean and C.-A. Iuga, Int. J. Mol. Sci., 2019, 20, 3943 CrossRef CAS PubMed
.
- F. Solano, New J. Sci., 2014, 2014, 1–28 CrossRef
.
- M. d'Ischia, K. Wakamatsu, A. Napolitano, S. Briganti, J.-C. Garcia-Borron, D. Kovacs, P. Meredith, A. Pezzella, M. Picardo, T. Sarna, J. D. Simon and S. Ito, Pigm. Cell Melanoma Res., 2013, 26, 616–633 CrossRef PubMed
.
- K. Tarangini and S. Mishra, Biotechnol. Rep., 2014, 4, 139–146 CrossRef PubMed
.
- J. Schmaler-Ripcke, V. Sugareva, P. Gebhardt, R. Winkler, O. Kniemeyer, T. Heinekamp and A. A. Brakhage, Appl. Environ. Microbiol., 2009, 75, 493–503 CrossRef CAS PubMed
.
- P. Płonka and M. Grabacka, Acta Biochim. Pol., 2006, 53, 429–443 CrossRef
.
- W. D. Bush, J. Garguilo, F. A. Zucca, A. Albertini, L. Zecca, G. S. Edwards, R. J. Nemanich and J. D. Simon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14785–14789 CrossRef CAS PubMed
.
- M. dIschia, A. Napolitano, V. Ball, C.-T. Chen and M. J. Buehler, Acc. Chem. Res., 2014, 47, 3541–3550 CrossRef CAS PubMed
.
- W. Cao, X. Zhou, N. C. McCallum, Z. Hu, Q. Z. Ni, U. Kapoor, C. M. Heil, K. S. Cay, T. Zand, A. J. Mantanona, A. Jayaraman, A. Dhinojwala, D. D. Deheyn, M. D. Shawkey, M. D. Burkart, J. D. Rinehart and N. C. Gianneschi, J. Am. Chem. Soc., 2021, 143, 2622–2637 CrossRef CAS PubMed
.
- A. Vasanthakumar, A. DeAraujo, J. Mazurek, M. Schilling and R. Mitchell, Microbiology, 2015, 161, 1211–1218 CrossRef CAS PubMed
.
- P. Meredith and T. Sarna, Pigm. Cell Res., 2006, 19, 572–594 CrossRef CAS PubMed
.
- C. Grieco, F. R. Kohl, A. T. Hanes and B. Kohler, Nat. Commun., 2020, 11, 4569 CrossRef CAS PubMed
.
- X. Wang, L. Kinziabulatova, M. Bortoli, A. Manickoth, M. A. Barilla, H. Huang, L. Blancafort, B. Kohler and J.-P. Lumb, Nat. Chem., 2023, 787–793 CrossRef CAS PubMed
.
- P. A. Abramov, O. I. Ivankov, A. B. Mostert and K. A. Motovilov, Phys. Chem. Chem. Phys., 2023, 25, 16212–16216 RSC
.
- J. DOrazio, S. Jarrett, A. Amaro-Ortiz and T. Scott, Int. J. Mol. Sci., 2013, 14, 12222–12248 CrossRef PubMed
.
- M. Istrate, B. Vlaicu, M. Poenaru, M. Hasbei-Popa, M. C. Salavat and D. A. Iliescu, Rom. J. Ophthalmol., 2020, 64, 100 CrossRef PubMed
.
- M. Brenner and V. J. Hearing, Photochem. Photobiol., 2008, 84, 539–549 CrossRef CAS PubMed
.
- N. E.-A. El-Naggar and W. I. Saber, Polymers, 2022, 14, 1339 CrossRef CAS PubMed
.
- N. K. Kurian, H. P. Nair and S. G. Bhat, Asian J. Pharm. Clin. Res., 2015, 8, 251–255 Search PubMed
.
- A. S. ElObeid, A. Kamal-Eldin, M. A. K. Abdelhalim and A. M. Haseeb, Basic Clin. Pharmacol. Toxicol., 2017, 120, 515–522 CrossRef CAS PubMed
.
- M. Lei, C.-H. Xue, Y.-M. Wang, Z.-J. Li, Y. Xue and J.-F. Wang, J. Food Sci., 2008, 73, H207–H211 CAS
.
- E. S. Jacobson, Clin. Microbiol. Rev., 2000, 13, 708–717 CrossRef CAS PubMed
.
- P. Jakubiak, F. Lack, J. Thun, A. Urtti and R. Alvarez-Sánchez, Mol. Pharmaceutics, 2019, 16, 2549–2556 CrossRef CAS PubMed
.
- S. Bahrpeyma, M. Reinisalo, L. Hellinen, S. Auriola, E. M. Del Amo and A. Urtti, J. Controlled Release, 2022, 348, 760–770 CrossRef CAS PubMed
.
- A.-K. Rimpela, M. Schmitt, S. Latonen, M. Hagstrom, M. Antopolsky, J. A. Manzanares, H. Kidron and A. Urtti, Mol. Pharmaceutics, 2016, 13, 2977–2986 CrossRef CAS PubMed
.
- M. F. Testorf, R. Kronstrand, S. P. Svensson, I. Lundström and J. Ahlner, Anal. Biochem., 2001, 298, 259–264 CrossRef CAS PubMed
.
- M. Araújo, R. Viveiros, T. R. Correia, I. J. Correia, V. D. Bonifácio, T. Casimiro and A. Aguiar-Ricardo, Int. J. Pharm., 2014, 469, 140–145 CrossRef PubMed
.
- G. Sliwoski, S. Kothiwale, J. Meiler and E. W. Lowe, Pharmacol. Rev., 2014, 66, 334–395 CrossRef PubMed
.
- A. Hospital, J. R. Goñi, M. Orozco and J. L. Gelp, Adv. Appl. Bioinf. Chem., 2015, 8, 37–47 Search PubMed
.
- M. Orio, D. A. Pantazis and F. Neese, Photosynth. Res., 2009, 102, 443–453 CrossRef CAS PubMed
.
- P. H. Torres, A. C. Sodero, P. Jofily and F. P. Silva-Jr, Int. J. Mol. Sci., 2019, 20, 4574 CrossRef CAS PubMed
.
- E. Kaxiras, A. Tsolakidis, G. Zonios and S. Meng, Phys. Rev. Lett., 2006, 97, 218102 CrossRef PubMed
.
- L. Hellinen, S. Bahrpeyma, A.-K. Rimpelä, M. Hagström, M. Reinisalo and A. Urtti, Pharmaceutics, 2020, 12, 554 CrossRef CAS PubMed
.
- S. Soltani, S. Sowlati-Hashjin, C. G. Tetsassi Feugmo and M. Karttunen, J. Phys. Chem. B, 2022, 126, 1805–1818 CrossRef CAS PubMed
.
- S. Soltani, S. Sowlati-Hashjin, C. G. Tetsassi Feugmo and M. Karttunen, Molecules, 2022, 27, 8417 CrossRef CAS PubMed
.
- A. Corani, A. Huijser, T. Gustavsson, D. Markovitsi, P.-Å. Malmqvist, A. Pezzella, M. d'Ischia and V. Sundström, J. Am. Chem. Soc., 2014, 136, 11626–11635 CrossRef CAS PubMed
.
- M. d'Ischia, K. Wakamatsu, A. Napolitano, S. Briganti, J.-C. Garcia-Borron, D. Kovacs, P. Meredith, A. Pezzella, M. Picardo, T. Sarna, J. D. Simon and S. Ito, Pigm. Cell Melanoma Res., 2013, 26, 616–633 CrossRef PubMed
.
- M. d'Ischia, A. Napolitano, A. Pezzella, P. Meredith and M. Buehler, Angew. Chem., Int. Ed., 2020, 59, 11196–11205 CrossRef PubMed
.
- C. T. Chen, F. J. Martin-Martinez, G. S. Jung and M. J. Buehler, Chem. Sci., 2017, 8, 1631–1641 RSC
.
- C. T. Chen, C. Chuang, J. Cao, V. Ball, D. Ruch and M. J. Buehler, Nat. Commun., 2014, 5, 1 RSC
.
- C. T. Chen, V. Ball, J. J. de Almeida Gracio, M. K. Singh, V. Toniazzo, D. Ruch and M. J. Buehler, ACS Nano, 2013, 7, 1524–1532 CrossRef CAS PubMed
.
- U. Kapoor and A. Jayaraman, J. Phys. Chem. B, 2020, 124, 2702–2714 CrossRef CAS PubMed
.
- J. Träg, P. Duchstein, M. Hennemann, T. Clark, D. M. Guldi and D. Zahn, J. Phys. Chem. A, 2019, 123, 9403–9412 CrossRef PubMed
.
- D. Tuna, A. Udvarhelyi, A. L. Sobolewski, W. Domcke and T. Domratcheva, J. Phys. Chem. B, 2016, 120, 3493–3502 CrossRef CAS PubMed
.
- J. Cheng, S. C. Moss, M. Eisner and P. Zschack, Pigm. Cell Res., 1994, 7, 255–262 CrossRef CAS PubMed
.
- J. Cheng, S. C. Moss and M. Eisner, Pigm. Cell Res., 1994, 7, 263–273 CrossRef CAS PubMed
.
- G. W. Zajac, J. M. Gallas, J. Cheng, M. Eisner, S. C. Moss and A. E. Alvarado-Swaisgood, Biochim. Biophys. Acta, 1994, 1199, 271–278 CrossRef CAS PubMed
.
- J. M. Gallas, K. C. Littrell, S. Seifert, G. W. Zajac and P. Thiyagarajan, Biophys. J., 1999, 77, 1135–1142 CrossRef CAS PubMed
.
- K. Kirla, K. Groh, M. Poetzsch, R. Banote, J. Stadnicka-Michalak, R. Eggen, K. Schirmer and T. Kraemer, Front. Pharmacol., 2018, 9, 414 CrossRef PubMed
.
- R. Schroeder, P. Pendleton and J. Gerber, Colloids Surf., B, 2015, 134, 8–16 CrossRef CAS PubMed
.
- M. Ye, G.-y Guo, Y. Lu, S. Song, H.-y Wang and L. Yang, Int. J. Biol. Macromol., 2014, 63, 170–176 CrossRef CAS PubMed
.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, Nucleic Acids Res., 2023, 51, D1373–D1380 CrossRef PubMed
.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS
.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed
.
- C. Kutzner, S. Páll, M. Fechner, A. Esztermann, B. L. de Groot and H. Grubmüller, J. Comput. Chem., 2019, 40, 2418–2431 CrossRef CAS PubMed
.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS
.
-
H. Berendsen, J. Postma, W. van Gunsteren and J. Hermans, ch. Interaction models for water in relation to protein hydration, in Intermolecular Forces, ed. Pullman B., Springer, Dordrecht, 1981 Search PubMed
.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS
.
- G. A. Cisneros, M. Karttunen, P. Ren and C. Sagui, Chem. Rev., 2013, 114, 779–814 CrossRef PubMed
.
- D. A. C. Beck, R. S. Armen and V. Daggett, Biochemistry, 2005, 44, 609–616 CrossRef CAS PubMed
.
- S. Piana, K. Lindorff-Larsen, R. M. Dirks, J. K. Salmon, R. O. Dror and D. E. Shaw, PLoS One, 2012, 7, e39918 CrossRef CAS PubMed
.
- J. Wong-Ekkabut and M. Karttunen, J. Chem. Theory Comput., 2012, 8, 2905–2911 CrossRef CAS PubMed
.
- J. Wong-ekkabut and M. Karttunen, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2529–2538 CrossRef CAS PubMed
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef CAS PubMed
.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
- L. Schrödinger and W. DeLano, PyMOL, https://www.pymol.org/pymol.
- E. King, E. Aitchison, H. Li and R. Luo, Front. Mol. Biosci., 2021, 8, 712085 CrossRef CAS PubMed
.
- M. S. Valdés-Tresanco, M. E. Valdés-Tresanco, P. A. Valiente and E. Moreno, J. Chem. Theory Comput., 2021, 17, 6281–6291 CrossRef PubMed
.
- E. Wang, H. Sun, J. Wang, Z. Wang, H. Liu, J. Z. Zhang and T. Hou, Chem. Rev., 2019, 119, 9478–9508 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed
.
- M. Walker, A. J. Harvey, A. Sen and C. E. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600 CrossRef CAS PubMed
.
- E. G. Hohenstein, S. T. Chill and C. D. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996–2000 CrossRef CAS PubMed
.
- E. B. Miller, R. B. Murphy, D. Sindhikara, K. W. Borrelli, M. J. Grisewood, F. Ranalli, S. L. Dixon, S. Jerome, N. A. Boyles, T. Day, P. Ghanakota, S. Mondal, S. B. Rafi, D. M. Troast, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2021, 17, 2630–2639 CrossRef CAS PubMed
.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed
.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461 CrossRef CAS PubMed
.
- R. Firouzi, S. Sowlati-Hashjin, C. Chávez-Garca, M. Ashouri, M. H. Karimi-Jafari and M. Karttunen, Int. J. Mol. Sci., 2023, 24, 8161 CrossRef CAS PubMed
.
- X. Shu, H. Li, B. Dong, C. Sun and H. F. Zhang, Biomed. Opt. Express, 2017, 8, 2851–2865 CrossRef CAS PubMed
.
- S. Meng and E. Kaxiras, Biophys. J., 2008, 94, 2095–2105 CrossRef CAS PubMed
.
- A.-K. Rimpelä, M. Hagström, H. Kidron and A. Urtti, J. Controlled Release, 2018, 283, 261–268 CrossRef PubMed
.
- T. Hirano, S. Yasuda, Y. Osaka, M. Kobayashi, S. Itagaki and K. Iseki, Biochim. Biophys. Acta, Biomembr., 2006, 1758, 1743–1750 CrossRef CAS PubMed
.
- L. Settimo, K. Bellman and R. M. Knegtel, Pharm. Res., 2014, 31, 1082–1095 CrossRef CAS PubMed
.
- A. O. Hay, R. Trones, L. Herfindal, S. Skrede and F. A. Hansen, Adv. Sample Prep., 2022, 2, 100011 CrossRef
.
- M. Lahti and A. Oikari, Arch. Environ. Contam. Toxicol., 2011, 61, 202–210 CrossRef CAS PubMed
.
- J. A. Manzanares, A.-K. Rimpela and A. Urtti, Mol. Pharmaceutics, 2016, 13, 1251–1257 CrossRef CAS PubMed
.
- L. Pelkonen, U. Tengvall-Unadike, M. Ruponen, H. Kidron, E. M. Del Amo, M. Reinisalo and A. Urtti, Eur. J. Pharm. Sci., 2017, 109, 162–168 CrossRef CAS PubMed
.
- P. Jakubiak, M. Reutlinger, P. Mattei, F. Schuler, A. Urtti and R. Alvarez-Sánchez, J. Med. Chem., 2018, 61, 10106–10115 CrossRef CAS PubMed
.
- A.-K. Rimpelä, M. Reinisalo, L. Hellinen, E. Grazhdankin, H. Kidron, A. Urtti and E. M. Del Amo, Adv. Drug Delivery Rev., 2018, 126, 23–43 CrossRef PubMed
.
- P. Jakubiak, C. Cantrill, A. Urtti and R. Alvarez-Sánchez, Mol. Pharmaceutics, 2019, 16, 4890–4901 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S7: the conformational changes of eumelanin (DHI and DHICA) and drugs which were obtained from MD simulations. Fig. S8–S17: DFT optimized single eumelanin (DHI and DHICA) molecule and single drug molecule binding with energy. Table S1: binding free energy of eumelanin–drug systems in the MD simulations, second and third replica copy results. Table S2: the average drug–eumelanin binding free energies (kcal mol−1) calculated by using the MM-PBSA approach. Each system contains 27 eumelanin and 7 drug molecules. Results from first simulations. Table S3: average drug–eumelanin binding free energies (kcal mol−1) from MM-PBSA analysis: results from the second replica simulations. Table S4: average drug–eumelanin binding free energies (kcal mol−1) from MM-PBSA analysis: results from the third replica. Table S5: AutoDock Vina grid box parameters used in molecular docking. See DOI: https://doi.org/10.1039/d4ma00246f |
| This journal is © The Royal Society of Chemistry 2024 |