Open Access Article
Open Access ArticleOptimization of safe doping level for enhanced CO2 flux in composite membrane†
Atul P.
Jamale
 * and
Gonçalo
Henriques
* and
Gonçalo
Henriques
Department of Materials and Ceramic Engineering, CICECO, Aveiro Institute of Materials, University of Aveiro, 3810-193, Aveiro, Portugal. E-mail: jamaleatul@gmail.com; atuljamale@ua.pt
First published on 19th January 2024
Abstract
Rare earth doped oxides have been intensively promoted for the last two decades to embrace the high-performance target of a ceramic–carbonate composite CO2-separation membrane, with countless incidents of exsolution. Unfortunately, information about securing a safe doping limit in the above case is unavailable in the public domain. Herein we provide a first report, where an answer to this question is rigorously attempted. Thus, the study demonstrates a maximum safe level of doping in a Ce1−XGdXO2−δ–LiNaCO3 (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 vol%) composite, where X = 0.10, 0.15 or 0.20. The required sets of ceramic matrix powders were prepared using the Pechini method and consolidated at 1500 °C, with intermediate powder coarsening. The composite membranes were obtained by impregnating these matrices with LiNaCO3 at 700 °C. The impedance measurement illustrated the highest bulk and total conductivity, at 250 °C, in composites with 10 mol% and 15 mol% of Gd doping, respectively. CO2-separation followed the trend in total conductivity, with highest flux of 0.14 cm3 min−1 cm−2 at 650 °C for 15 mol% Gd. Post-mortem analysis showed the precipitation of Gd and evaporation of the melt with retention of carbon allotropes on the sweep face of the membrane of 20 mol% Gd. In short, this work gives some insight into optimizing rare earth Gd-doping for improved the performance of a composite CO2-separation membrane.
20 vol%) composite, where X = 0.10, 0.15 or 0.20. The required sets of ceramic matrix powders were prepared using the Pechini method and consolidated at 1500 °C, with intermediate powder coarsening. The composite membranes were obtained by impregnating these matrices with LiNaCO3 at 700 °C. The impedance measurement illustrated the highest bulk and total conductivity, at 250 °C, in composites with 10 mol% and 15 mol% of Gd doping, respectively. CO2-separation followed the trend in total conductivity, with highest flux of 0.14 cm3 min−1 cm−2 at 650 °C for 15 mol% Gd. Post-mortem analysis showed the precipitation of Gd and evaporation of the melt with retention of carbon allotropes on the sweep face of the membrane of 20 mol% Gd. In short, this work gives some insight into optimizing rare earth Gd-doping for improved the performance of a composite CO2-separation membrane.
1 Introduction
The side effects of carbon emissions are rated as climatic change and global warming.1,2 To lessen their severity, other alternatives are being developed with hydrogen-based technologies in particular reflecting a reliable solution. Despite all efforts aimed at reducing carbon footprints, 96% of today's hydrogen is produced using oxy, dry, and steam reforming of methane and other hydrocarbons. Thus, the problem remains the same; only the definition of how to look at the problem has been slightly modified with respect to scientific interest. This means that all recent advances, including green energy technologies, are deficient for meeting the goal of net zero-carbon emission without the help of carbon capture and recycling technologies.3–8 In fact, carbon is being continuously released in various natural processes and is not categorized as a pollutant class up to the scale of the earth's natural capacity to neutralize its impact. In imitation of this auto-neutralization by nature, some carbon dioxide recycling industries are being developed in parallel to incorporate its benefits in carbonated beverages, fire extinction, refrigerants, inert blankets for food items, decaffeination of coffee, and the production of urea, calcium carbonate, etc. Thus, the correct management (separation, condensation, and recycling) of CO2 released in steam reforming processes could indirectly provide the advantage of shifting the hydrogen production cycle from grey to green on the environmental spectrum.| CH4 + H2O ↔ CO + 3H2 ΔH298 = 206 kJ mol−1 | (1) |
| CO + H2O ↔ CO2 + H2 ΔH298 = −41 kJ mol−1 | (2) |
| CH4 + 2H2O ↔ CO2 + 4H2 ΔH298 = 165 kJ mol−1 | (3) |
As shown in eqn (1), the steam reforming of methane (SRM) occurs at 800–1000 °C and 14–30 atm pressure.9 The in situ exothermic water–gas shift (WGS) reaction further elevates the production capacity at a negative energy cost (eqn (2)). The positive slope of population growth and food requirements is mostly dictated by agriculture and animal farming piling up tons of manure every day. These bio-wastes could be positively credited to biogas, which is a mixture of methane (50–80%) and CO2 (15–50%).10 Because of the abundance of bio-waste, the feasibility of direct steam reforming of biogas is also being sought with no additional modifications to the SRM reactor. Rationalizing the ground-level situation, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202 bio-gas plants are currently running across Europe (data from 2018), with a likely expected growth of 2% per year.11 With this data H2-production from biogas could be realistic, avoiding the constant injection of CO2 into the earth's atmosphere. Because of the hot nature of exhausted H2, CO2, and other gases at trace to ultra-trace level at SRM reactor sites, several high-temperature CO2-separation techniques have been suggested.
202 bio-gas plants are currently running across Europe (data from 2018), with a likely expected growth of 2% per year.11 With this data H2-production from biogas could be realistic, avoiding the constant injection of CO2 into the earth's atmosphere. Because of the hot nature of exhausted H2, CO2, and other gases at trace to ultra-trace level at SRM reactor sites, several high-temperature CO2-separation techniques have been suggested.
High-temperature inorganic membranes have recently been discussed for their high selectivity, endurance, and permeance of CO2 gas under various conditions. These dense membranes are typically made of dual-phase ceramic–carbonate composites and have shown their capability of working without interruption, until a leak appears in the system. The driving forces for CO2-permeation through membranes are assumed to be the logarithmic gradient of CO2 partial pressure across the feed and sweep sides of the membrane, and the ambipolar conductivity of the compositing phases.12,13 For instance, the membranes of an insulating matrix extract CO2via a partial pressure gradient mechanism (eqn (4)), and depend on the length of the two-phase boundary.14 The extremely low CO2-retraction in this case is due to the involvement of the slow diffusion kinetics of bulky bicarbonate ions. The use of an oxide ionic conducting matrix adds other surface exchange kinetics and lighter species (eqn (6)). However, electronic and/or mixed oxide ionic electronic conducting (MIEC) matrices need a small but mandatory flux of oxygen in the feed to convert CO2 to carbonate ions viaeqn (5), with scarce CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 selectivity ≤2.15 Ideally, a specific matrix is vital in respect of the composition of input gases and the required purity of CO2 on the sweep side, if it is to have further commercial applications, where purity does matter. Since SRM involves H2O, CO, CO2, and H2 gases, electronic and MIEC matrices are less useful. Although the oxide ionic conductivity of MIEC partially removes CO2 from such a mixture of gases, the larger A-site cation of the often used perovskite reacts heavily reacts with the carbonate melt.16,17
O2 selectivity ≤2.15 Ideally, a specific matrix is vital in respect of the composition of input gases and the required purity of CO2 on the sweep side, if it is to have further commercial applications, where purity does matter. Since SRM involves H2O, CO, CO2, and H2 gases, electronic and MIEC matrices are less useful. Although the oxide ionic conductivity of MIEC partially removes CO2 from such a mixture of gases, the larger A-site cation of the often used perovskite reacts heavily reacts with the carbonate melt.16,17
| CO2 (G) + CO3=(MC) ↔ C2O5=(MC) | (4) |
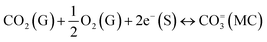 | (5) |
| CO2 (G) + O=(S) ↔ CO3=(MC) | (6) |
Dry reforming of methane using a composite CO2-separation membrane was proposed for the first time by Anderson et al.,18 in 2013, where a methane reforming 10% Ni/γ-alumina catalyst was mounted on the sweep side. Due to the inadequate CO2-permeability of the LSCF supported composite, i.e. only 0.17 ml min−1 at 850 °C, the H2 production rate was just 0.29 ml min−1. A stability study of the membrane under similar feed conditions by Norton et al.19 reports that the instability of LSCF is the main cause of the sharply decreasing performance. They found SrCO3 impurity on the feed surface of the membrane. Thus, oxide ion conducting Sm/Gd-doped ceria matrix-based composites were pursued in later studies under simulated WGS,20 oxy21 and dry CO2, and steam22 reforming conditions of hydrocarbons. Recent reports also include the H2S tolerance of the membrane resembling the possible interaction of ceramic and molten salt via S loan pair driven chemisorption,23 as sulfur exists in fuels and has effects at as low as 50 ppm.
Sm-doped ceria (SDC) has been extensively studied as a matrix for CO2-separation. Recalling the system used at hydrocarbon reforming sites, various feed and sweep conditions were independently tested by different groups. For example, feed containing ∼5% H2 was examined by Zhang et al.,24 with membrane degradation observed after 1015 h of operation. Shortly after, in 2014, a prolonged 30-day period of stability was observed in 50% CO, 35% CO2, 10% H2, and 5% N2 feed by Norton.25 Initially, there seemed to be a slight fluctuation in permeation of about 0.35 ml min−1 cm−2, with a reasonably stable flow of 0.26 ml min−1 cm−2 achieved after 20 days. The transient stability was described as being the result of the decomposition of SDC into incipient phases. A catalyst-free ceramic–carbonate membrane for the high-temperature WGS reaction was simulated in 2021 by Meng et al.26 However, a practical demonstration of the concept had already been delivered by the same group in 2016,20 with final CO2 recovery of 18.4–23% for the ratio of H2O to CO2 in the range of 3 to 1. H2-generation using combined steam reforming of methane and a dual-phase composite membrane system was reported in late 2020 by Wu.22 The results were also compared with a standard bed reactor. Data assessment confirmed 90% H2 yield for a membrane reactor, which is far better than that for a conventional reactor, where the H2 yield was recorded as around 81%. Oscar Ovalle-Encinia et al.27 later modelled the in situ operation of an SRM reactor and CO2-separation membrane under high pressure, revealing the challenges associated with the operation of the membrane under high pressure. The reliability of the model was also confirmed with available experimental data at 1 atm.
The most common and interesting fact is that all the membranes studied for an H2-containing atmosphere or syngas exclusively involved a 20 mol% Sm-doped ceria matrix. Probably, the high oxide ionic conductivity makes it the first choice.28 Post-mortem analysis was also reported in a few studies. These analyses reflect a lack of uniqueness, and new speculations were urged about the scope of species sighted across the membrane surfaces.23,29–31 Thus, the real cause of the improvement or degradation remained a mystery. Secondly, screening for system susceptibility has scarcely been discussed in the circumstances of other dopants and/or at varying contents, despite the effective ionic size of Gd3+ (1.053 Å) being smaller than that of Sm3+ (1.079 Å) and closer to the Ce4+ (0.97 Å) of the host lattice. Furthermore, it is the second-most studied dopant after Sm3+ in an SOFC electrolyte and composite membrane for CO2-separation, with the key emphasis only on the feed gas mixture of N2 and CO2.
In a previous attempt, we took some initiatives to address the driving force for degradation in a long-term composite stability study of 10 mol% Gd-doped ceria and a eutectic mixture of Li–Na carbonate, in a feed and sweep atmosphere of CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 (50
N2 (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 vol%) and Ar (100 vol%), respectively.32 In this work, we emphasize an understanding of the impact of the oxide ionic domain on CO2-separation and possible physiochemical changes, in a feed gas of 5% H2. The quantity of H2 used herein is relatively lower than under SRM conditions. But it is the first kind of study where the motive is to find a maximum level of safe doping. Furthermore, as detailed in the previous study, Gd3+ defused under a CO2 gradient, so investigating suitable ceramic doping becomes of paramount importance. Therefore, the ceramic phase of the composite membranes was altered for Gd-doping in the 10 to 20 mol% range. Pre- and post-mortem analyses were also performed to support the claimed hypothesis and deviation from ideal behaviour.
50 vol%) and Ar (100 vol%), respectively.32 In this work, we emphasize an understanding of the impact of the oxide ionic domain on CO2-separation and possible physiochemical changes, in a feed gas of 5% H2. The quantity of H2 used herein is relatively lower than under SRM conditions. But it is the first kind of study where the motive is to find a maximum level of safe doping. Furthermore, as detailed in the previous study, Gd3+ defused under a CO2 gradient, so investigating suitable ceramic doping becomes of paramount importance. Therefore, the ceramic phase of the composite membranes was altered for Gd-doping in the 10 to 20 mol% range. Pre- and post-mortem analyses were also performed to support the claimed hypothesis and deviation from ideal behaviour.
2 Experimental section
2.1 Synthesis of ceramic powder and porous matrix
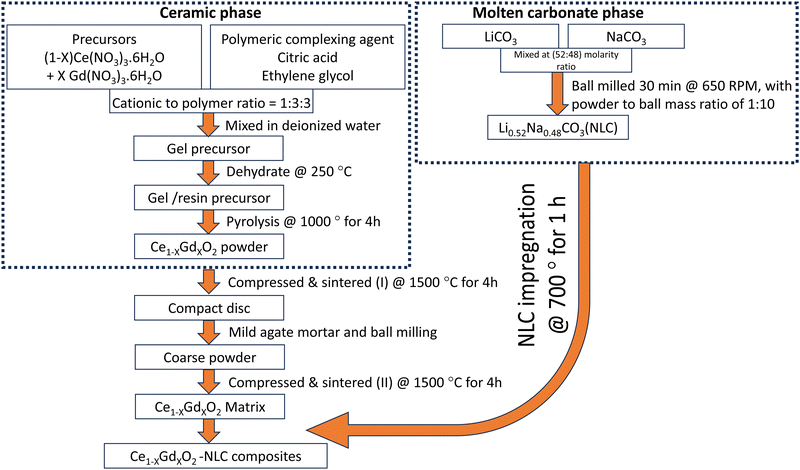
Ce1−XGdXO2−δ (X = 0.10, 0.15, 0.20) ceramic powders were used in the fabrication of the matrix phase of the composite membranes. The powders were synthesized using the low-temperature Pechini method, where cationic reagents Ce(NO3)3·6H2O (Acros Organics, 99.5%) and Gd(NO3)3·6H2O (Acros Organics, 99.9%) were weighed in the required final stoichiometry of the powder. These precursors were dissolved in deionized water under constant magnetic stirring. Thereafter, the free cations of the solution were complexed using citric acid (PanReac AppliChem, 99.5%) and ethylene glycol (PanReac AppliChem, 99%) in a respective molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. The solution containing cationic precursor and organic chelates was dehydrated at 250 °C to transform it to polymeric resin, with retention of weakly matured grains of the CGO and some organics. The organic residue was then burnt at 1000 °C for 4 hours. The yield of the powders was also evaluated from a weight ratio of powder obtained after calcination to the calculation made for 15 g of final power. The yield was over 95% for all powders. These powders were mixed independently in ethanol medium for a high degree of homogeneity, oven-dried, and pressed to 25 mm discs for initial coarsening at 1500 °C for 4 h. To recover the coarse structure of the powder, the rigid ceramics were gently crushed using an agate mortar and then ball milled for 30 minutes. The coarsened powders, with a polyvinyl alcohol (PVA) binder, were compressed uniaxially and isostatically at 10 MPa and 196 Mpa, respectively, to diameters of 8 mm and 25 mm. These green bodies were subjected to high-temperature sintering at 1500 °C for 4 h to percolate roughly 20 vol% of bulk porosity. The obtained matrices of Ce1−XGdXO2−δ, with X = 0.10, 0.15, 0.20, are hereafter abbreviated to CGO10, CGO15, and CGO20, respectively.
3. The solution containing cationic precursor and organic chelates was dehydrated at 250 °C to transform it to polymeric resin, with retention of weakly matured grains of the CGO and some organics. The organic residue was then burnt at 1000 °C for 4 hours. The yield of the powders was also evaluated from a weight ratio of powder obtained after calcination to the calculation made for 15 g of final power. The yield was over 95% for all powders. These powders were mixed independently in ethanol medium for a high degree of homogeneity, oven-dried, and pressed to 25 mm discs for initial coarsening at 1500 °C for 4 h. To recover the coarse structure of the powder, the rigid ceramics were gently crushed using an agate mortar and then ball milled for 30 minutes. The coarsened powders, with a polyvinyl alcohol (PVA) binder, were compressed uniaxially and isostatically at 10 MPa and 196 Mpa, respectively, to diameters of 8 mm and 25 mm. These green bodies were subjected to high-temperature sintering at 1500 °C for 4 h to percolate roughly 20 vol% of bulk porosity. The obtained matrices of Ce1−XGdXO2−δ, with X = 0.10, 0.15, 0.20, are hereafter abbreviated to CGO10, CGO15, and CGO20, respectively.
2.2 Synthesis of molten carbonate
The molten salt phase of the ceramic–carbonate composite was mechanochemically synthesized. For the eutectic mixture of LiNaCO3 (NLC), high-purity Li2CO3 (Sigma-Aldrich, 99%) and Na2CO3 (Sigma-Aldrich, 99%) reagents were mixed in a molar ratio of 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48. The mixture was ball milled at 650 rpm for 30 min. to ensure suitable conditions for a mechanochemical reaction. This reaction was carried out in a nylon jar with a powder to 3% tetragonal zirconia polycrystalline (TZP) balls mass ratio of 1
48. The mixture was ball milled at 650 rpm for 30 min. to ensure suitable conditions for a mechanochemical reaction. This reaction was carried out in a nylon jar with a powder to 3% tetragonal zirconia polycrystalline (TZP) balls mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. Powders of fixed 5 g mass were considered each time for such a reaction.
10. Powders of fixed 5 g mass were considered each time for such a reaction.
2.3 Processing of dual-phase CGO–NLC composites
The composites of size 8 mm and 25 mm were referred for respective electrical and CO2-separation experiments. However, the common preparation protocols were restricted to avoid the possibility of alteration of results. NLC of 0.1 g and 0.6 g weight were compressed into cylindrical discs and mounted onto ceramic matrices of sizes 8 mm and 25 mm, respectively, for impregnation at 700 °C for 1 h. Heating and cooling both were controlled at 5 °C per min. After cooling the furnace to room temperature, excessive leftover carbonate was gently removed from the top and bottom surfaces of the samples using fine-grained SiC paper. For simplicity, the overall procedure followed during the synthesis of the ceramic–carbonate composite is also illustrated in a flow chart (Fig. 1). The impregnated matrices of CGO10, CGO15, and CGO20 are hereafter abbreviated to CGO10C, CGO15C, and CGO20C composites, respectively. The details of composite abbreviations, phase composition, and type of experiment performed are all given in Table 1.| Composite abbreviations | Phase composition (vol%) | Experiments performed | |
|---|---|---|---|
| CGO | NLC | ||
| CGO10C | 75.5 | 19.2 | Impedance |
| 79.4 | 17.1 | CO2-separation | |
| CGO15C | 76.1 | 17.3 | Impedance |
| 76.8 | 16.8 | CO2-separation | |
| CGO20C | 78.9 | 17.5 | Impedance |
| 77.2 | 18.4 | CO2-separation | |
2.4 Characterization of membrane
The relative vol% of infiltrated salt, density of the ceramic matrix, and composites were all determined from the physical dimensions, mass of samples (obviously before and after infiltration), and known theoretical densities of the individual phases from the available literature. The membranes were also put through a manual leak-free test, where the sample was glued on one end of a hollow metallic tube and immersed in an ethanol bath, while high-pressure air was pumped through the other end of the tube to observe any bubbles. Visual observation that no bubbles were leaving through the sealed end ensured the membrane was free of minor cracks and internal damage. Since CO2-separation is vulnerable even with an unprecedentedly small amount of impurity, the matrix and composite were both tested at all stages of processing and CO2-separation. The crushed powders of the matrices and composites, and the feed and sweep faces of one of the analyzed composite membranes were scanned using an X-ray diffractometer (XRD, PANalytical, X'Pert-pro), irradiated with Cu-Kα radiation of 1.54 Å wavelength. The scanning speed was normal and carried out within angular 2θ range of 10° to 80°. The powders and solid samples were X-ray scanned using two different machines, depending on their earliest availability. The machines were procured from different manufacturers. A scanning electron microscope (SEM, Hitachi SU-70) equipped with an EDS (Bruker) attachment was also used to display the microstructural features of the ceramic (voids, grain sizes, and connectivity), the distribution of MC, and elemental uniformity. The samples considered in the present study included initial ceramic matrices, fresh composites, and one composite tested under CO2-separation.Electrochemical impedance spectroscopy (EIS, HP 4284A LCR meter instrument) was used to study the temperature-dependent electrical properties of the ceramic–carbonate composites. The measurements were performed within a temperature range of 200 °C to 700 °C, and at intervals of 25 °C, using an asymmetrical cell configuration. The electrical response was recorded for a frequency sweep from 20 Hz to 1 MHz, and at a constant root means square (RMS) signal amplitude of 0.5 V. Prior to beginning the measurements, the composites were polished to provide parallel and plane surfaces, then coated with an Au current collector, and fired at 650 °C for 20 min. The computer-generated EIS files were then analysed with the help of Z-view software (Scribner Associates Inc.). A description of the typical data fitting solution, circuit elements, and limitations can be found elsewhere.33
2.5 High-temperature CO2-permeation test
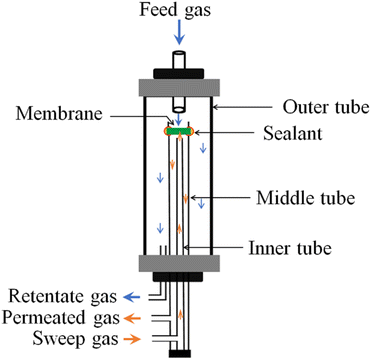
High-temperature CO2 permeation experiments were carried out using a laboratory-built setup. As shown schematically (Fig. 2), three alumina tubes were co-axially mounted, with an outer alumina chamber feeding the mixture of gases to the middle chamber, where the already-sealed dense membrane sweeps CO2 to the permeated side, and then flushes out those traces to a gas chromatograph (GC, Agilent 6890 N) for detection and analysis using a steady flow of argon through the third, inner, tube. Plot U (8 m × 0.32 mm) and Molsieve 5 A (10 m × 0.32 mm) columns of the GC separate the components of the swept gas and read the signal in a thermal conducting detector (TCD) based on different retention times. Owing to the high reactivity of alumina and glass sealants with carbonates,31 special care was taken to seal the composite membrane, where only a paste prepared from a nominal mixture of CGO (ball milled at 600 rpm for 1 h), NLC, and ethylene glycol was used and applied at the interface of the membrane and alumina tube. The entire assembly was then fixed in a vertical tube furnace. Thereafter, the temperature of the system was slowly raised at a heating rate of 0.3 °C per min. to a first measurement temperature of 550 °C. The feed and sweep gas atmospheres were also resumed simultaneously to avoid the possibility of evaporation of the eutectic during heating.With the assumption that the membrane will be used at SRM reactor sites and the safety protocol enforced by the educational institute, a gas stream of CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2
N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 (50%
H2 (50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45%
45%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5%) composition was introduced at the feed side, while a constant flow of argon was set on the permeated side of the membrane. Inlet and outlet gas flows were regulated at 20 standard cubic centimetre per minute (SCCM) and at atmospheric pressure using a gas flowmeter (Alicat Scientific). The gases considered for the proposed sets of experiments were all purchased from a liquid air agency, with purity greater than 99%. Since N2 is inert and does not belong to the ionic species of the membrane, the detection of N2 on sweeping helped us to determine CO2 leaks through the membrane and/or sealant. The equivalent value of N2 was deducted from the total CO2% to correct for the membrane permeability. The experiments were performed from 550 °C to 700 °C, at intervals of 25 °C. At each step, the system was allocated a waiting time of 30 minutes to reach the steady state before recording the GC reading. After executing the required number of readings, the membranes were safely detached and stored in a desiccator for post-mortem analysis. One of the samples, CGO20C, was selected for such analysis using XRD, SEM, and a combined Raman-AFM-SNOM confocal microscope (WITec alpha300 RAS+, WITec, Ulm, Germany) techniques.
5%) composition was introduced at the feed side, while a constant flow of argon was set on the permeated side of the membrane. Inlet and outlet gas flows were regulated at 20 standard cubic centimetre per minute (SCCM) and at atmospheric pressure using a gas flowmeter (Alicat Scientific). The gases considered for the proposed sets of experiments were all purchased from a liquid air agency, with purity greater than 99%. Since N2 is inert and does not belong to the ionic species of the membrane, the detection of N2 on sweeping helped us to determine CO2 leaks through the membrane and/or sealant. The equivalent value of N2 was deducted from the total CO2% to correct for the membrane permeability. The experiments were performed from 550 °C to 700 °C, at intervals of 25 °C. At each step, the system was allocated a waiting time of 30 minutes to reach the steady state before recording the GC reading. After executing the required number of readings, the membranes were safely detached and stored in a desiccator for post-mortem analysis. One of the samples, CGO20C, was selected for such analysis using XRD, SEM, and a combined Raman-AFM-SNOM confocal microscope (WITec alpha300 RAS+, WITec, Ulm, Germany) techniques.
3 Results and discussion
3.1 Structural assessment of matrix and fresh composites
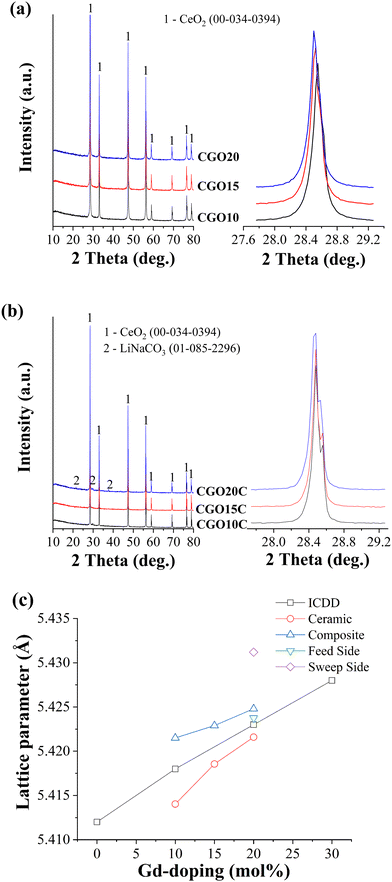
High purity of the ceramic is critically important in high-performance CO2-separation by a composite. The phase purity and other crystallographic information for all the ceramics were obtained at various stages, including the initially fabricated matrix, after impregnation with NLC, and immediately after high-temperature gas separation (described in Section 3.3).Normalized powder X-ray diffraction patterns of Ce1−XGdXO2−δ matrices, with X = 0.10, 0.15, and 0.20, and composites obtained after NLC impregnation at 700 °C for 1 h are depicted in Fig. 3. An enlarged view of the principal (111) orientation is also shown on the right-hand side of the main patterns. The patterns of the ceramic matrices (Fig. 3a) were compared with a primitive cubic fluorite structure of CeO2 of space group FM3M (ICDD 00-0340394). All reflections were found to be concurrent with the reference pattern, with small low angle shifts. These shifts, which consistently increased for elevated mol% of Gd, are in line with the description of lattice expansion due to the substitution of tiny Ce4+ with the larger Gd3+ and the improved solid solubility of Gd3+.34 The lattice parameters for CGO10, CGO15, and CGO20 were calculated as 5.414 Å, 5.4186 Å, and 5.4216 Å, respectively. The changes in lattice parameters are small and could be understood from the second and third digits after the decimal point.
Subsequent analysis of crushed powders of freshly prepared composite, as shown in Fig. 3b, showed low-intensity carbonate peaks. Shoulder spikes are also observed on the individual main peaks of the composite. However, these spikes are distinct compared to ceramic powders. For simplicity, the zoom-in feature of the (111) principal orientation is shown, as was done before for the ceramic matrices. The difference in these spectra is most likely due to different X-ray scanning machines used according to their earliest availability and the conclusion of the respective sets of experiments. The small kink on the main peaks originated from the mixed Kα1 and Kα2 irradiation of the copper target. The intensity ratio of 2 between those reflections gives a strong indication of mixed radiation of nearly the same wavelength. However, within the detection limit of the instrument, no traces were recognized, evidencing chemical stability among the constituent phases of the composites.
The lattice parameters evaluated from these patterns and directly obtained from standard ICDD cards are plotted together as a function of Gd-doping. As shown in Fig. 3c, the lattice parameter of sintered ceramic matrices is smaller than expected for the corresponding mol% of Gd-doping. This deviation indicates that the ceramics may include a low amount of Gd in a fluorite lattice of CeO2 or that some unreacted Gd may be retained as micro-phases across the grain boundaries. However, a presence below 2%, which may also vary up to 5% depending on the type of composition of the constituents, is hard to detect in regular XRD.35 Quantitative elemental analysis was carried out on these matrices (Table 2) and the corresponding spectra are presented separately in supplementary Fig. S1 (ESI†). This showed that the actual mol% of Gd in CGO10, CGO15, and CGO20 were 8.7 mol%, 14.1 mol%, and 19.5 mol%, respectively. The Ce to Gd ratio evaluated from the second and third columns of Table 2 is also compared with the standard value. The higher values show that the mol% of Gd deviates from the standard value and is below the assumed figure. Thus, due to the lower Gd mol% than expected for the relevant ceramics, although the difference is insignificant, the difference between the lattice parameter of the ceramic and that on the standard ICDD card is obvious.
| Matrix | Ce (at%) | Gd (at%) | Ce/Gd ratio | |
|---|---|---|---|---|
| Estimated | Standard | |||
| CGO10 | 91.26 | 8.73 | 10.41 | 10 |
| CGO15 | 85.91 | 14.09 | 6.10 | 5.6 |
| CGO20 | 80.46 | 19.54 | 4.12 | 4 |
The behaviour of the lattice parameter of the ceramic after NLC impregnation is a bit confusing, increasing above the ICDD values. It is possible the molten salt facilitated the diffusion of unreacted Gd to the ceramic lattice, but such an allowed increment is expected to increase the lattice parameter to a value below the standard ICDD value. The possibility of doping and co-doping of Ce4+ (97 p.m.) and Gd3+ (105.3 p.m.) sites with Li+ (92 p.m.) and Na+ (118 p.m.) cations from the melt is hard to accept due to the huge disparity between the charges and ionic sizes.36 If a smaller but close matching Li+ cation of the melt substitutes for ceramic cations, then the unit cell should shrink instead of increasing. Since oxide vacancies are relatively larger than oxide ions, the incubation of bulk and/or surface vacancies could be another possible reason for the increasing lattice parameter. Quenching of such thermally induced vacancies during the process of high-temperature impregnation of the melt is indeed hard to believe. The exact reason for the increased lattice parameter of the ceramic phase of the composite is unclear. But, as NLC impregnation incorporates the crystallographic new ceramic/carbonate interface into a system, it could perturb the lattice strain, and hence the lattice constant. A sort of perturbation was reported in a polarized Raman spectroscopy study of a ceramic–carbonate system by Mizuhata et al.37 Such a strained region, including surface and/or interfaces, was referenced by J.A. Kilner to a driving force for the segregation of impurities.38 Thus, the higher the tensile strain, the higher will be the surface or interface impurity.
3.2 SEM/EDS analysis
The SEM morphologies of CGO10, CGO15, and CGO20 matrices, and respective NLC-based composites, are shown in Fig. 4. The ceramic grains of the matrices (Fig. 4A1–A3) seem to be separated by narrow pores, which appear as darker regions in the SEM. The pore sizes were evaluated over 65 different places on the matrices and were found to be 0.95, 1.79, and 1.2 microns, respectively. The irregular shapes and sizes of the ceramic grains elucidate the degree of matrix inhomogeneity. Besides these observations, CGO15 grains are rounded and larger compared to those of CGO10 and CGO15. Whereas CGO10 and CGO15 grains are elongated and joined by a narrow neck. Since all ceramics were coarsened at 1500 °C, the different sizes of the grains may be due to different amounts of time spent in initial agate-mortar grinding. Ceramics with lower agate-mortar grinding time may have leftover larger particles, which are hard to reduce in size during their subsequent ball milling. Some such larger particles can be seen in the low-magnification SEM image of Fig. S2 (ESI†), indicated by yellow marks. This indicates that powder coarsening retains the mixed sizes of the ceramic grains in the matrix.High-temperature filling with MC changes the microstructure of the initial ceramic matrices. The gaps between successive ceramic grains, which previously seemed dark, now appear light grey in the composites (Fig. 4B1–B3). This change partly hides some topographic features of the ceramic. For example, the narrow neck (the region joining two ceramic grains) is now invisible with preservation of only the hilly ceramic structure. Thus, the microstructure of the composite appears very different from that of the matrix. The above composite microstructure gives a rough idea of compactness, with an estimated apparent density of ≥95% with respect to the theoretical density of a composite.
Complementary elemental atomic number mapping is presented in Fig. 4C1–C3. It provides the semi-qualitative distribution of elements cum phases. With the limitation of energy detection capability, Li is outside the analysis range. Ce (red), Gd (blue), and Na (green) are the only elements addressed here. The detection of Na could be read as a sign of the signal originating from the carbonate. From mapping it is clear the carbonate occupies the empty space of the ceramic. In the composite this region appears as green pools on a red/violet carpet of ceramic. Careful examination provided further detail of the variation in carpet colour from red (10 mol%) to faint violet (15 mol%), and then bright violet (20 mol%), revealing composite matrices with increasing mol% of Gd dopant. However, the XRD and EDS do not provide any direct evidence for the precipitation of Gd and/or Ce in the territory of the carbonate, although the measurable reactivity of Gd2O3 with alkaline carbonate has been documented at 650 °C.32,39
3.3 Electrical conductivity
The rationalization is simple: physical techniques that are less effective at acknowledging the presence of minor impurities, which could be suspended in the bulk of the NLC melt, and sometimes even stuck at the interface of the melt/ceramic and/or periphery of ceramic grain-boundaries, can give only a rough estimation of the effect of doping on CO2 permeability. It is well understood in solid-state electrochemistry that doping above the threshold limit has a negative impact on the properties of oxide ion conducting electrolytes, in both single phase and composites.40,41 Thus, delivering accurate doping is important. Furthermore, in an effort to assess system vulnerability, which is particularly essential in a situation where a harsh MC is present as one of the constituent phases, the electrochemical impedance of the composites was studied in the range 200 °C to 700 °C. The analysed data were then presented in temperature-dependent electrical conductivity form (Fig. 5a). Low (250 °C) and high (650 °C) temperature conductivities are also given in Table 3.| Composites | Conductivity, S cm−1 | |
|---|---|---|
| 250 °C | 650 °C | |
| CGO10C | 6.3 × 10−6 | 1.8 × 10−1 |
| CGO15C | 9.3 × 10−6 | 1.5 × 10−1 |
| CGO20C | 2.5 × 10−6 | 1.2 × 10−1 |
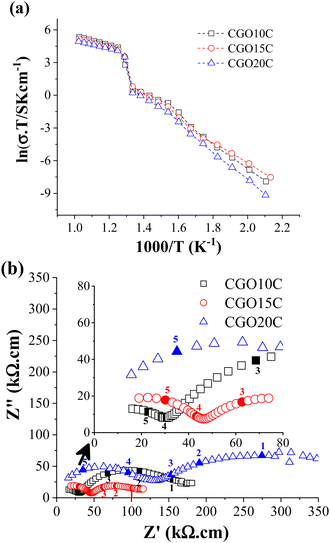
A jump in ionic conductivity is observed around the solid to molten phase transition temperature, and then the system achieves saturation. Such a transition is normal, and is symbolized in the literature by the inverted S- or Z-shapes of the Arrhenius plots.42 Carbonates are pure ionic conductors, with conductivities in the range of 1 S cm−1 to 5 S cm−1 at 900 °C.43 The highest conductivity is achieved only above the melting point due to the free and fast diffusion of ionic species. Below this level, cations and anions are tightly bonded and behave as an insulator. In contrast, an oxide ion conductor conducts electric current due to the diffusion of oxide ions through existing intrinsic and extrinsic oxide vacancies, even far below the melting point, which increases as a function of temperature. Thus, EIS below the melting point of the salt gives the characteristic property of a ceramic matrix, while above the melting point NLC dominates the property, with only a slight contribution from the ceramic. From the Arrhenius plots in Fig. 5a and Table 3, it is clear that CGO10C possesses the highest conductivity at 650 °C. So, by definition, composite CGO10C must acquire a higher amount of highly conducting NLC phase than the other two composites.
The extension of measurement to the low-temperature region shows a small deviation at about 350 °C. That is not surprising, as condensation of water on the carbonate surface partly induces conductivity owing to hydroxide species.44 This feature is displayed in the intermediate-frequency branch of EIS (Fig. S3, ESI†), carried out at various RMS voltages. Besides extrinsic influence, total conductivity measured at 250 °C (Table 3) decreased in composites for matrices with Gd-doping above 15 mol%.
In detailing the electrical conductivity of the ceramic phase, the impedance spectra of the composites at 250 °C are presented in Fig. 5b. Following the extremely low conductivity of MC below the eutectic point and a typical explanation of the electrochemical impedance of ceramics, the high and intermediate frequency (HF & IF) curves recognize the responses of grain and grain-boundary plus voids (filled with MC in the composite), respectively. As shown in Fig. 5b, continuously increasing grain/bulk resistance from 10 mol% to 20 mol% of doping clears the heavy doping recombines the free vacancies of the bulk by vacancy–dopant interaction, and hence reduces the number of sites for the diffusion of oxide ions. An optimum Gd-doping of 10 mol% is confirmed in independent studies by Gandolini et al.45 and Steele et al.40 However, the microstructure overshadows this limit (determined from total conductivity alone in Fig. 5a).
From the SEM, it is very clear that the grains of CGO15 are larger than those of the other matrices. A relatively larger grain reduces the grain boundary (GB) fraction and the resistance offered by it. The voids of the matrices, filled with NLC in the composites, also add a resistive contribution, and the effects can be read in terms of size, shape, and orientation with respect to the direction of charge carrier diffusion.46 The overlapping frequency responses of GB and void make it hard to distinguish them in EIS and they are counted here as a global contribution. This information is directly extracted from the IF curve, where the diameter of CGO15C is the smallest. The larger magnitude of the IF curve of CGO20C due to higher precipitation of Gd in the GB region is also desirable (see the description of XRD in Section 3.3).47 Thus, larger ceramic grains and the absence of a neck-like microstructure in CGO15 partly compensate for the adverse impact of over-doping (HF curve) with reduced total resistance (LF + HF curve) in EIS. In other words, the pore phase of CGO15 percolates in such a way as to minimize the length of oxide ionic diffusion in the ceramic phase of the composite.
3.4 CO2-separation
Fig. 6a shows CO2-separation through CGO–NLC (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 vol%) composite membranes, where Gd doping of the ceramic phase varied from 10 mol% to 20 mol%. The graph represents the temperature dependence of CO2 flux at a fixed CO2
20 vol%) composite membranes, where Gd doping of the ceramic phase varied from 10 mol% to 20 mol%. The graph represents the temperature dependence of CO2 flux at a fixed CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2
N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 feed input of 50
H2 feed input of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 vol% and at a monitored gas flow of 20 SCCM. Within 550 °C to 700 °C, a monotonous increment of CO2 flux is observed. The dispersive nature of the plots indicates that the process is thermally activated, which could be due to vacancy formation, acceleration of the diffusion of active ionic species, or surface kinetics across the feed and sweep faces of the membrane, and all are relaxed at increasingly higher temperature.
5 vol% and at a monitored gas flow of 20 SCCM. Within 550 °C to 700 °C, a monotonous increment of CO2 flux is observed. The dispersive nature of the plots indicates that the process is thermally activated, which could be due to vacancy formation, acceleration of the diffusion of active ionic species, or surface kinetics across the feed and sweep faces of the membrane, and all are relaxed at increasingly higher temperature.
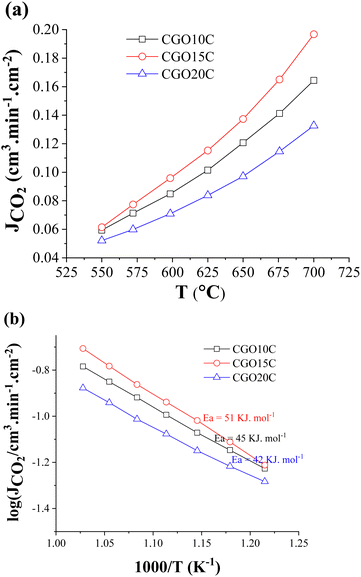 | ||
| Fig. 6 Temperature-dependent (a) CO2-separation flux, and (b) Arrhenius behaviour of CGO10C, CGO15C, and CGO20C composite membranes. | ||
Data comparison among the presumed composites shows a maximum permeation of 0.2 cm3 min cm−2 at 700 °C. From Fig. 6a it is clear the maxima go through 15 mol%, and then reverse with further doping. The evaluated values of composite CO2-separation for ceramics of 10 to 20 mol% Gd are comparable to previously published reports on composites (Table 4) of similar dopant and/or doping content, and of nearly equal active thicknesses. The reasonable difference between our CGO20C result (0.1 cm3.min cm−2) and that of S.G.M. Carvalho et al.31 (0.4 cm3.min cm−2) is also noted, where it is recalled that directional microstructure is an important factor.
| Oxide phase | Vol% | T (°C) | Feed gas | Membrane type | CO2 flux | Ref. | |
|---|---|---|---|---|---|---|---|
| Vol% CO2 (other) | Geometry | Thickness (mm) | cm−3 cm−2 min−1 | ||||
| Bi1.5Y0.3Sm0.2O3 | ? | 650 | 50 (Ar) | Flat | Thin | 0.066 | 48 |
| Zr0.92Y0.08O2 | 66 | 650 | 50 (He) | Flat | 0.2–0.4 | 0.013 | 49 |
| CeO2 | 60–70 | 650 | 20 (He, N2) | Flat | 1.0 | 0.007 | 50 |
| Ce0.85Sm0.15O2 | ? | 700 | 50 (20%O2, 20%He) | Tubular | 1.0 | 0.15 | 51 |
| Ce0.8Sm0.2O2 | 70 | 650 | 50 (4.8H2, 45.2N2) | Flat | 1.2 | 0.1 | 52 |
| Ce0.9Gd0.1O2 | ? | 650 | 50 (N2) | Tubular | 0.58 | 0.13 | 53 |
| Ce0.8Gd0.2O2 | 70 | 600 | 20 (Ar) | Flat | 0.8 | 0.4 | 31 |
| Ce0.9Gd0.1O2 | 79 | 650 | 50 (5%H2, 45%N2) | Flat | 1.0 | 0.12 | This work |
| Ce0.85Gd0.15O2 | 77 | 650 | 50 (5%H2, 45%N2) | Flat | 1.0 | 0.14 | |
| Ce0.8Gd0.2O2 | 77 | 650 | 50 (5%H2, 45%N2) | Flat | 1.0 | 0.10 | |
To gain insight into the process promoting CO2-permeation, the activation energies were calculated from the Arrhenius plots. As depicted in Fig. 6b, the activation energies of CGO10C, CGO15C, and CGO20C lie in a shorter range of 42–51 kJ mol−1, with the actual values decreasing with higher doping. In fact, these values match neither the activation energies of the ceramic matrix (70–96 kJ mol−1) nor that of MC (∼19 kJ mol−1,43). This is not the first time that we have cited a low value. We delivered an activation energy of 52 kJ mol−1 in a previous study of the CGO10C composite, with just the difference of cobalt being used as a sintering additive in the consolidation of the matrix.32 S.G.M. Carvalho et al.31 noted an even much lower activation energy of 30 kJ mol−1, when the matrices were processed using tape and freeze casting. The authors said that the gas separation is controlled by kinetics through both matrix and molten phases. The reduction in Ea to 34–39 kJ mol−1 in a study of a BZY-LNC membrane led to other hypotheses for the transport mechanism. K. Zhang et al.54 respond in their study that the presence of carbonate suppresses the grain boundary effect of the ceramic. It is, however, interesting to realize that the sweep side of Zhang's membrane was continuously exposed to a partially hydrated atmosphere.
A higher activation energy means the process is predominantly controlled by a high activation energy mechanism, i.e., oxide ion transport of the ceramic phase of the composite (70–80 kJ). If the process is rate limited by ionic species from the MC phase of the composite, then a typical value is expected to be in the 20–30 kJ range. The difference in activation energy between those ranges for ceramic and MC is not well understood. Different explanations are involved in the literature according to the most favourable situation, e.g., experimental conditions (dry vs humid), or ceramic and composite processing (microstructure). No doubt, those conditions essentially affect the type of charge carrier, grain to grain boundary fraction (particle size effect), and diffusion length (tortuosity effect) of active species. Remembering the critical importance of the above parameters, we employed identical testing conditions (dry atmosphere), membrane thickness (1 mm), and powder, matrix, and composite processing. Despite identical protocols being followed in the synthesis of twin samples by S.G. Patricio et al.,55 the effect of tortuosity seems impossible to discard. Secondly, unrecognizable changes in the surface for extrinsic hydroxide inclusions, due to the humidity of the commercial feed and sweep gases, and changing seasonal and regional (territorial location) humidity level, limit the depth of understanding.
The effect of secondary hydroxide species has already been observed in the low-temperature electrical conductivity of composites (Fig. 5a), though an external hydration condition was absent. That means the hydration of the carbonate surface and/or composite, during sample handling or due to the sensitivity of the carbonates, automatically triggers the effect in experiments. Hydroxide to carbonate conversion is rapid in a CO2-rich atmosphere (feed condition), and happens far below 500 °C.56 Constant exposure to inert gas (on the sweep side) reasonably suppresses this kinetic. Thus, water might be negligible, but visual observation of post CO2-separation showed the condensation of some droplets on the metallic part of the sweep side. Since in our experiments the feed gas contains 5% H2, the consumption of hydrogen, due to partial reduction of the ceramic surface for Ce4+ + e− ↔ Ce3+ or an in situ initiated CO2 + H2 ↔ CO + H2O reaction, may introduce water, where CO might be further reduced on ceramic surface to carbon. Thus, sliding of the activation energy between the region of oxide ion conductor and MC is due to transport of mixed (H+/OH−/O2−) species, and all are rate determining for CO2-separation.
Composite CO2-separation over membranes of increasing Gd doping from 10 to 20 mol% shows the highest value around 15 mol% (Fig. 6a). Ideally, increased doping hosts more vacancies and the fast diffusion of oxide ions. However, the results are contradictory, illustrating a maximum at 15 mol% and degrading thereafter. The solid solubility of Gd2O3–CeO2 was well investigated using the crystal structure and lattice thermal expansion. All studies show that the unit cell stabilizes to a fluorite structure with a maximum of 40 mol% rare earth doping, and then starts the accommodation of complex inclusions for further addition.34,57 The electrical conductivity measurement is in fact not fully convenience to structural and thermal expansion giving totally different solid solubility range between 10 mol% and 20 mol%.45,58,59 The sharp demarcation has indeed been criticized in the context of the lack of knowledge about siliceous impurities in the starting materials,60 the presentation of low (∼500 °C) vs high (∼800 °C) temperature conductivity references, as the dissociation of vacancy clusters at higher temperature shifts this limit to a higher level,61 and the researcher's preferences with regard to bulk62 vs grain boundary and total conductivity. Nonetheless, the sharp decline in CO2-separation in a membrane with 20 mol% Gd is a question of interest, and thus the tested sample was readied for post-analysis to disclose the reasons behind the decline. The grey spots observed across the sweep side are another reason, increasing curiosity about the phenomenon of condensation of foreign species, and their possible contribution.
3.5 Post-mortem analysis
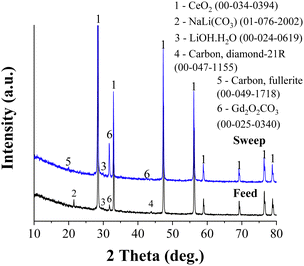
Fig. 7 shows the XRD patterns of the feed and sweep faces of CGO20C after CO2-separation. The patterns are mounted one above the other to distinguish the changes in peak orientation. It is clear from the figure that the patterns are dissimilar, with respect to their quirky orientations and the difference in their intensity. The characteristic peaks of the matrix phase (indicated by 1) remain at the same diffraction angles, with a small low angle shift observed for the sweep side. The NLC peak is observed only for the feed side. Whereas no NLC is detected on scanning the sweep side, which was all the time exposed to pure argon with a small amount of permeated CO2 gas. That means a higher amount of CO2 reduces the rate of evaporation of NLC at the feed side while the exact opposite process might happen at the sweep side. An observation consistent with this was reported by Tong et al.29 in a post-mortem SEM analysis of a membrane, where the sweep side was shown to be porous compared to freshly prepared samples. The formation of hydroxide and hydrated species, visible in the pattern, also supports the above discussion on the possible promotion effect due to the counter transportation of hydroxide ions.Irrespective of the already detailed common observations in previous publications, the formation of rare earth oxycarbonate and some allotropes of carbon are traced herein. Gd2O2CO3 peaks appear on both feed and sweep sides. However, the higher peak intensity for the sweep side reflects the significant amount of Gd2O2CO3 stacked on the sweep side. The gradient of CO2, the decreasing CO2 partial pressure from the feed to the sweep side, may drive and deposit such species preferentially on the counter surface. In other words, Gd2O2CO3 forms at a tri-junction of CO2, MC, and CGO phases and then gradually diffuses through MC under the gradient of CO2 to the sweep side. An analogous principle was dealt with recently in our previous report.32 A similar observation was made in a study of an La1.5Sr0.5NiO4±δ membrane,15 where intense SrCO3 reflections are exclusively found across the sweep side. Also, Fig. 3C demonstrates that the lattice parameter of the sweep side is much higher than that on the feed side. The full width at half maxima (FWHM) calculated for the feed and sweep sides were 0.15 and 0.17 deg., respectively. Such larger lattice parameter and peak broadening shed light on the changes in Gd composition from the surface to core of the grain (core–shell structure) on the sweep side of the membrane.
The formation of Gd2O2CO3, which decomposes only above 900 °C, partly consumes the melt phase. This reduced melt phase or changes in the eutectic composition negatively affect performance. Recalling the higher precipitation of Gd at the grain boundaries of CGO20, the dissolution and diffusion of Gd through the NLC phase of CGO20C are significant. Furthermore, 5 vol% of H2 in the feed gas accelerates the dissociation of CGO and the decay rate of the membrane.
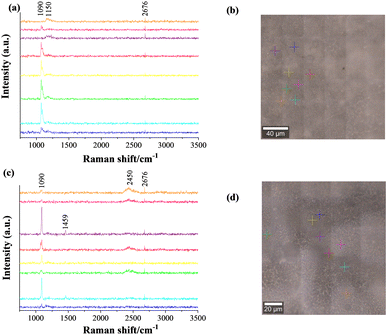
Diamond and fullerite carbons were observed in X-ray studies of the flip sides of the membrane. The intensity of the response of those phases was, however, weak. The feed and sweep faces were reassessed using FT-Raman spectroscopy at an excitation laser wavelength of 530 nm. The FT-Raman spectra along with optical images of the scanned areas are shown in Fig. 8. The coloured crosses in Fig. 8b and d indicate the area of analysis, and the respective pattern is indicated by identical colours in Fig. 8a and c. The selection of sites was done according to the grey and white shades observed on both faces of the membrane. 1073 cm−1 and 1096 cm−1 bands, as displayed in Fig. 8a and c, correspond to the symmetric C–O vibration (ν1) of double carbonates.63 These two bands are observed in all the spectra with different intensities. In some cases, e.g., the purple and orange spectra of the feed side, these bands are absent. This indicates the scanning might have fallen in a region of ceramic grains, with no or few carbonate signals.
Another common 2d band at about 2676 cm−1 is due to the double resonance of graphene and/or graphite.64 The additional vibration around 1459 cm−1 (sharp) and 2450 cm−1 (broad), for a particular sweep side, respectively illustrate the presence of C6065 and single or double walled carbon nanotubes species.66 While the extra band at 1150 cm−1 in the feed side spectrum of the membrane was identified as nanocrystalline diamond.67 Because of the higher excitation wavelength of 532 nm used in the Raman spectrometer, all bands are observed at lower wavenumbers, compared to standard data, which normally uses a laser source of 514 nm wavelength. However, the mechanism of formation of different allotropes of carbon is a mystery. It is most likely due to the 5% H2 in the feed gas reducing the ceramic surface by a Ce4+ to Ce3+ reaction. Such a transformation is dependent on the atmosphere and induces a localized catalytic reaction to reduce CO2 (gas phase) and/or CO3= (through the molten phase) to carbon.
Scanning of the sweep surface for SEM morphology in Fig. 9 gives more details. Two distinct microstructures are observed in the low-magnification SEM, while high magnification was only used to discover new morphological information. The bright and irregular shapes of the ceramic grains agree well with freshly prepared matrices and the conventional description of a ceramic body. The in situ grown flake-like structure on the sweep face of the CGO20C membrane might involve graphitic or other forms of carbon structure. The comparatively high brightness of the new morphology compared to the carbonate phase (Fig. 4B1–B3) also sheds some light on the nature of the conductivity of the new phases.
 | ||
| Fig. 9 SEM images of the sweep side of the CGO20C membrane captured after a CO2-separation test at different magnifications. | ||
3.6 Final remarks
Doping with an aliovalent element at the host site of fluorite structure CeO2 usually increases conductivity due to the formation of an oxide vacancy. Thus, by increasing the doping from 10 mol% to 20 mol% in CeO2 we should expect a positive trend in conductivity and CO2-separation. Testing the ground reality using the low-temperature electrochemical impedance of the CGO–NLC (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 vol%) composite, where Gd doping of CGO varied from 10 to 20 mol%, showed the grain-interior conductivity to be higher only for 10 mol% Gd doping. Over-doping has an adverse impact on the bulk mobility, following the bulk conductivity trend of CGO10C > CGO15C > CGO20C. However, the opposite is noted in total conductivity, where the previous trend is slightly modified to CGO15C > CGO10C > CGO20C. This trend is also repeated in the IF arc of EIS and SEM micrographs, which relate to tortuosity. That is, material tortuosity, which emerges automatically due to the different microstructures of the ceramic, is forced to follow the trend of total conductivity in CO2-permeation. If the ceramic microstructure of composite membranes is the same, then the picture of CO2-permeation could be different and will follow the analogue of the first trend.
20 vol%) composite, where Gd doping of CGO varied from 10 to 20 mol%, showed the grain-interior conductivity to be higher only for 10 mol% Gd doping. Over-doping has an adverse impact on the bulk mobility, following the bulk conductivity trend of CGO10C > CGO15C > CGO20C. However, the opposite is noted in total conductivity, where the previous trend is slightly modified to CGO15C > CGO10C > CGO20C. This trend is also repeated in the IF arc of EIS and SEM micrographs, which relate to tortuosity. That is, material tortuosity, which emerges automatically due to the different microstructures of the ceramic, is forced to follow the trend of total conductivity in CO2-permeation. If the ceramic microstructure of composite membranes is the same, then the picture of CO2-permeation could be different and will follow the analogue of the first trend.
Post-mortem assessment of CGO20C details the process involved in degradation. Gd-dislocation under the gradient of CO2 partial pressure and constant stacking on the ceramic grains of the sweep side affect the current due to the diffusion of oxide ions through the ceramic phase and CO2-permeation. Partial degradation of the melt could be another reason, as decomposed carbon species are observed across the sweep and feed sides. These species involve different allotropes of carbon, including graphite, graphene, nanocrystalline diamond, and single or multi-walled carbon nanotubes. It is essential to note that the experiments were performed in feed containing 5% H2 (with unknown traces of impurities) and the sealants used herein are composed of organic ethylene glycol. The partial hydration of the composite surface may also affect the observations on a case-to-case basis.
4 Conclusions
With respect to the lack of findings on the required safe doping of the ceramic phase of a ceria–carbonate composite, the present research gives some insight into Gd doping in the range 10–20 mol%. The initial XRD and complementary SEM/EDS mapping show no anomalies before or after impregnation of NLC into ceramic matrices. The low-temperature impedance of the composites was surprising. Doping above 10 mol% reduced the bulk conductivity in inverse proportion, following the trend CGO10C > CGO15C > CGO20C, indicating that the concentration of vacancies falls through vacancy–dopant interaction. However, the trend in total conductivity of CGO15 > CGO10C > CGO20C reflects the addition of a tortuosity (microstructural) effect, which is least for CGO15C compared to the other two. CO2-separation followed the trend in total conductivity. If all ceramic matrices possess equal tortuosity, then the trends in bulk and total conductivity, and CO2-separation could be identical, decreasing in the sequence CGO10C, CGO15C, and CGO20C. The segregation of Gd at the GB for heavily doped ceria (20 mol% of Gd), later dissolved as oxycarbonate and diffused to the sweep side via NLC channels, cause the underperformance and fast decay of CO2-separation. The decomposition of carbonate and/or CO2 to carbon in an H2-containing atmosphere is also pronounced due to the surface reduction reaction of Ce4+ to Ce3+. Thus, the highest level of safe Gd-doping for greater performance is 10–15 mol%, which could be improved further by controlling the tortuosity.Author contributions
Atul Jamale – conceptualization, led the investigation, visualization, and wrote, reviewed & edited the original draft. Goncalo – data curation, visualization, and formal analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was developed within the scope of the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020, UIDP/50011/2020 & LA/P/0006/2020, financed by national funds through the FCT/MCTES (PIDDAC). Specific support (AJ) provided by national funds (OE), through FCT, IP, in the scope of the framework contract foreseen in the numbers 4, 5, and 6 of the article 23 of the Decree-Law 57/2016, of August 29, changed by Law 57/2017, of July 19. GH is thankful for financial assistance through a starting research grant, Verão com ciência (UID 50011-CICECO).References
- G. P. Peters, R. M. Andrew, T. Boden, J. G. Canadell, P. Ciais, C. Le Quéré, G. Marland, M. R. Raupach and C. Wilson, Nclimate, 2012, 1783, 2–4 Search PubMed.
- S. Fawzy, A. I. Osman, J. Doran and D. W. Rooney, Environ. Chem. Lett., 2020, 18, 2069–2094 CrossRef CAS.
- C. Y. Park, C. I. Kong, E. Y. Kim, C. H. Lee, K. S. Kim, J. H. Lee, J. Lee and S. Y. Moon, Chem. Eng. J., 2023, 455, 140883 CrossRef CAS.
- S. Vinoth, W. J. Ong and A. Pandikumar, Coord. Chem. Rev., 2022, 464, 214541 CrossRef CAS.
- S. Vinoth, K. S. Shalini Devi and A. Pandikumar, TrAC, Trends Anal. Chem., 2021, 140, 116274 CrossRef CAS.
- M. Liu, K. Xie, M. D. Nothling, L. Zu, S. Zhao, D. J. E. Harvie, Q. Fu, P. A. Webley and G. G. Qiao, ACS Cent. Sci., 2021, 7, 671–680 CrossRef CAS PubMed.
- S. Kim, C. A. Scholes, D. E. Heath and S. E. Kentish, Chem. Eng. J., 2021, 411, 128468 CrossRef CAS.
- S. G. M. Carvalho, E. N. S. Muccillo and R. Muccillo, Membranes, 2023, 13, 1–12 CrossRef PubMed.
- L. Barelli, G. Bidini, F. Gallorini and S. Servili, Energy., 2008, 33, 554–570 CrossRef CAS.
- R. Dimitrov, Z. Ivanov, P. Zlateva and V. Mihaylov, Optimization of biogas composition in experimental studies, E3S Web Conf., 2019, 112, 1–6 CrossRef.
- European Biogas Association Statistical Report 2019: European Overview (2020) https://uabio.org/en/materials/7524/, Accessed 04th April 2023.
- J. L. Wade, K. S. Lackner and A. C. West, Solid State Ionics, 2007, 178, 1530–1540 CrossRef CAS.
- S. G. Patrício and F. M. B. Marques, Int. J. Energy Res., 2016, 40, 2150–2161 CrossRef.
- M. Kazakli, G. A. Mutch, G. Triantafyllou, A. G. Gil, T. Li, B. Wang, J. J. Bailey, D. J. L. Brett, P. R. Shearing, K. Li and I. Metcalfe, J. Membr. Sci., 2021, 617, 118640 CrossRef CAS.
- S. Wang, J. Tong, L. Cui, P. Zhang and F. Zhou, J. Membr. Sci., 2022, 647, 120278 CrossRef CAS.
- A. P. Jamale and F. M. B. Marques, Int. J. Energy Res., 2018, 42, 4805–4816 CrossRef CAS.
- A. Jamale, M. Starykevich and F. M. B. Marques, Int. J. Energy Res., 2021, 45, 2945–2958 CrossRef CAS.
- M. Anderson and Y. S. Lin, AIChE J., 2013, 59, 2207–2218 CrossRef CAS.
- T. T. Norton, J. Ortiz-Landeros and Y. S. Lin, Ind. Eng. Chem. Res., 2014, 53, 2432–2440 CrossRef CAS.
- X. Dong and Y. S. Lin, J. Membr. Sci., 2016, 520, 907–913 CrossRef CAS.
- J. A. Fabián-Anguiano, C. G. Mendoza-Serrato, C. Gómez-Yáñez, B. Zeifert, X. Ma and J. Ortiz-Landeros, Chem. Eng. Sci., 2019, 210, 115250 CrossRef.
- H. C. Wu, Z. Rui and J. Y. S. Lin, J. Membr. Sci., 2020, 598, 117780 CrossRef CAS.
- T. Chen, H. C. Wu, Y. Li and Y. S. Lin, Ind. Eng. Chem. Res., 2017, 56, 14662–14669 CrossRef CAS.
- L. Zhang, N. Xu, X. Li, S. Wang, K. Huang, W. H. Harris and W. K. S. Chiu, Energy Environ. Sci., 2012, 5, 8310–8317 RSC.
- T. T. Norton, B. Lu and Y. S. Lin, J. Membr. Sci., 2014, 467, 244–252 CrossRef CAS.
- J. Y. S. Lin, L. Meng and O. Ovalle-Encinia, Ind. Eng. Chem. Res., 2021, 60, 3581–3588 CrossRef.
- O. Ovalle-Encinia, H. C. Wu, T. Chen and J. Y. S. Lin, J. Membr. Sci., 2022, 641, 119914 CrossRef CAS.
- H. Inaba, Solid State Ionics, 1996, 83, 1–16 CrossRef CAS.
- J. Tong, L. Zhang, M. Han and K. Huang, J. Membr. Sci., 2015, 477, 1–6 CrossRef CAS.
- T. T. Norton and Y. S. Lin, Solid State Ionics, 2014, 263, 172–179 CrossRef CAS.
- S. G. M. Carvalho, E. N. S. Muccillo, F. C. Fonseca, M. Müller, F. Schulze-Küppers, S. Baumann, W. A. Meulenberg, O. Guillon and R. Muccillo, J. Membr. Sci., 2022, 648, 120355 CrossRef CAS.
- A. Jamale, M. Starykevich and F. M. B. Marques, J. Membr. Sci., 2022, 662, 120968 CrossRef CAS.
- A. I. B. Rondão, S. G. Patrício, F. M. L. Figueiredo and F. M. B. Marques, Electrochim. Acta, 2013, 109, 701–709 CrossRef.
- V. Grover and A. K. Tyagi, Mater. Res. Bull., 2004, 39, 859–866 CrossRef CAS.
- H. Khan, A. S. Yerramilli, A. D’Oliveira, T. L. Alford, D. C. Boffito and G. S. Patience, Can. J. Chem. Eng., 2020, 98, 1255–1266 CrossRef CAS.
- B. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- M. Mizuhata, T. Ohashi and A. B. Béléké, Int. J. Hydrogen Energy, 2012, 37, 19407–19416 CrossRef CAS.
- G. F. Harrington, S. J. Skinner and J. A. Kilner, J. Am. Ceram. Soc., 2018, 101, 1310–1322 CrossRef CAS.
- M. Yamauchi, Y. Itagaki, H. Aono and Y. Sadaoka, J. Eur. Ceram. Soc., 2008, 28, 27–34 CrossRef CAS.
- B. C. H. Steele, Solid State Ionics, 2000, 129, 59–66 CrossRef.
- V. Lair, V. Albin, A. Ringuedé and M. Cassir, Int. J. Hydrogen Energy, 2012, 37, 19357–19364 CrossRef CAS.
- I. Khan, M. I. Asghar, P. D. Lund and S. Basu, Int. J. Hydrogen Energy, 2017, 42, 20904–20909 CrossRef CAS.
- T. Kojima, Y. Miyazaki, K. Nomura and K. Tanimoto, J. Electrochem. Soc., 2007, 154, F222–F230 CrossRef CAS.
- A. Grishin, M. Ben Osman, H. Meskine, V. Albin, V. Lair, M. Cassir and A. Ringuedé, Energies, 2022, 15, 20–29 CrossRef.
- A. Gondolini, E. Mercadelli, A. Sanson, S. Albonetti, L. Doubova and S. Boldrini, J. Eur. Ceram. Soc., 2013, 33, 67–77 CrossRef CAS.
- M. Kleitz and M. C. Steil, J. Eur. Ceram. Soc., 1997, 17, 819–829 CrossRef CAS.
- D. Pérez-Coll, P. Núñez, J. C. Ruiz-Morales, J. Peña-Martínez and J. R. Frade, Electrochim. Acta, 2007, 52, 2001–2008 CrossRef.
- Y. Li, Z. Rui, C. Xia, M. Anderson and Y. S. Lin, Catal. Today, 2009, 148, 303–309 CrossRef CAS.
- J. L. Wade, C. Lee, A. C. West and K. S. Lackner, J. Membr. Sci., 2011, 369, 20–29 CrossRef CAS.
- W. Xing, T. Peters, M. L. Fontaine, A. Evans, P. P. Henriksen, T. Norby and R. Bredesen, J. Membr. Sci., 2015, 482, 115–119 CrossRef CAS.
- M. L. Fontaine, T. A. Peters, M. T. P. McCann, I. Kumakiri and R. Bredesen, Energy Procedia, 2013, 37, 941–951 CrossRef CAS.
- L. Zhang, N. Xu, X. Li, S. Wang, K. Huang, W. H. Harris and W. K. S. Chiu, Energy Environ. Sci., 2012, 5, 8310–8317 RSC.
- Z. Yang, Y. Zhu and M. Han, J. Alloys Compd., 2017, 723, 70–74 CrossRef CAS.
- K. Zhang, S. Sun, N. Xu and K. Huang, J. Membr. Sci., 2022, 650, 120421 CrossRef CAS.
- S. G. Patrício, E. I. Papaioannou, B. M. Ray, I. S. Metcalfe and F. M. B. Marques, J. Membr. Sci., 2017, 541, 253–261 CrossRef.
- M. R. Cerón, L. S. Lai, A. Amiri, M. Monte, S. Katta, J. C. Kelly, M. A. Worsley, M. D. Merrill, S. Kim and P. G. Campbell, J. Membr. Sci., 2018, 567, 191–198 CrossRef.
- J. Zhang, C. Ke, H. Wu, J. Yu, J. Wang and Y. Wang, J. Alloys Compd., 2017, 718, 85–91 CrossRef CAS.
- S. A. Acharya, V. M. Gaikwad, V. Sathe and S. K. Kulkarni, Appl. Phys. Lett., 2014, 104, 113508 CrossRef.
- S. A. Acharya, V. M. Gaikwad, S. W. D’Souza and S. R. Barman, Solid State Ionics, 2014, 260, 21–29 CrossRef CAS.
- T. S. Zhang, J. Ma, Y. J. Leng, S. H. Chan, P. Hing and J. A. Kilner, Solid State Ionics, 2004, 168, 187–195 CrossRef CAS.
- S. Shirbhate, R. N. Nayyar, P. K. Ojha, A. K. Yadav and S. Acharya, J. Electrochem. Soc., 2019, 166, F544–F554 CrossRef CAS.
- S. Omar, E. D. Wachsman, J. L. Jones and J. C. Nino, J. Am. Ceram. Soc., 2009, 92, 2674–2681 CrossRef CAS.
- S. Kim, S. H. Ku, S. Y. Lim, J. H. Kim and C. B. Park, Adv. Mater., 2011, 23, 2009–2014 CrossRef CAS PubMed.
- V. Zólyomi, J. Koltai and J. Kürti, Phys. Status Solidi B, 2011, 248, 2435–2444 CrossRef.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds: Part A: Theory and Applications in Inorganic Chemistry, 6th edn, 2008 Search PubMed.
- T. Shimada, T. Sugai, C. Fantini, M. Souza, L. G. Cançado, A. Jorio, M. A. Pimenta, R. Saito, A. Grüneis, G. Dresselhaus, M. S. Dresselhaus, Y. Ohno, T. Mizutani and H. Shinohara, Carbon, 2005, 43, 1049–1054 CrossRef CAS.
- A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 2–5 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00846k |
| This journal is © The Royal Society of Chemistry 2024 |