Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Review on the use of impedance spectroscopy for IPMC-like devices: application, models, and a new approach to data treatment
Roger
Gonçalves
 *a,
Kaique Afonso
Tozzi
b,
Matheus Colovati
Saccardo
c,
Ariel Gustavo
Zuquello
d,
Rafael
Barbosa
c,
Guilherme Eduardo
de Oliveira Blanco
c,
Laos Alexandre
Hirano
e and
Carlos Henrique
Scuracchio
*a,
Kaique Afonso
Tozzi
b,
Matheus Colovati
Saccardo
c,
Ariel Gustavo
Zuquello
d,
Rafael
Barbosa
c,
Guilherme Eduardo
de Oliveira Blanco
c,
Laos Alexandre
Hirano
e and
Carlos Henrique
Scuracchio
 c
c
aFederal University of São Carlos, Graduate Program in Chemistry, São Carlos, São Paulo, Brazil. E-mail: roger.gabiru@gmail.com
bUniv. Grenoble Alpes, Univ. Savoie Mont Blanc, CNRS, Grenoble INP, LEPMI, UMR5279, 38000 Grenoble, France
cFederal University of Sao Carlos, Graduate Program in Materials Science and Engineering, Rod. Washington Luiz, Km 235, São Carlos – 13565-905, Brazil
dGraduate Program in Technology and Innovation Management, Community University of Chapecó, Chapecó, SC, Brazil
eInstitute of Science and Technology, Federal University of Alfenas (UniFAl), Poços de Caldas, MG, Brazil
First published on 6th February 2024
Abstract
Although efforts to model the electrochemical behavior of ionomeric polymer-metal composite (IPMC) devices through electrochemical impedance spectroscopy (EIS) have been made, there is no equivalent circuit that provides either good data fit or understanding of the electrochemical phenomena when external factors, such as type of counterion and relative humidity, are considered. Most models have either a Warburg element or an ideal capacitor, which results in poor fitting at high frequencies, where the charge motion within the polymer membrane is observed. For the actual application of these devices, a consistent model must be used to comprehend their behavior while working. Furthermore, the models in the literature have limitations as they do not cover the environment and counterion influences. In this manuscript, we review the articles that applied EIS to characterize IPMC devices for different purposes, pointing out the technique's usefulness. At the same time, we use EIS in different relative humidities and counterions to propose a new model based on transmission lines, in which the data obtained have a better adjustment at high frequencies, lower statistical residue value e can also grant robustness regarding the external factors when compared with other five models found in the literature.
1. Introduction
1.1. Ionomeric polymer/metal composites
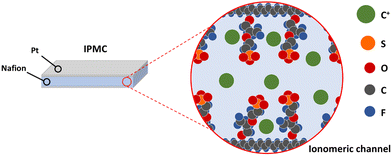
Smart materials are defined as materials that respond to external (chemical or physical) stimuli in a controlled manner to execute a predetermined task, which can be used conveniently. Ionomeric polymer composites (IPMCs) are part of this materials class. They could perform a bending movement as a response to an electrical stimulus and respond with an electrical potential difference when mechanically requested. This property is related to the polymer that composes the device, whose structure can be described as a sandwich structure: electrodes consisting of noble metals are plated on the surfaces of an ion-conductive polymer film (Fig. 1). This type of polymer has a specific structural arrangement in which there is the formation of channels that run through all the material where solvated ions move along. Since these channels result from aggregates with electrical charges, mobile ions are present to guarantee the electrical neutrality of the medium. The formation of these channels and the associated models will be fully explained in a future section. Hence, the smart response of these composites is a consequence of the mobility of ions within the channels.When a potential difference is applied to the electrodes, an electric field is formed through the polymeric film, causing the charged species to migrate towards the electrodes with subsequent migration of water molecules. Since the mobile species are cations, there will be an anisotropic mass accumulation close to the anode, causing the device to bend toward the cathode. On the other hand, if the device is bent, the ionic movement will cause a potential difference that can be measured between the electrodes. In this way, this behavior means that it can be applied both as a sensor and artificial muscle (soft actuator).
Electromechanical characterization of these devices is the most trivial, as it relates to the electrical properties and their mechanical consequences. The most common way to do this is by applying a voltage (typically below 5 V) to the device and then measuring the current passing through it and monitoring the displacement or force performed by the IPMC. The force exerted by the device is measured using a load cell, while the displacement is observed by a couple of methods, such as laser sensors and cameras.1
1.2. Impedance spectroscopy
Impedance spectroscopy is a very versatile electrochemical technique because it allows characterizing, through a semi-stationary measurement, the kinetic process on the electrode surface, the structure of the double-layer, and the transport of charged species.2 This technique is based on the theory of alternating current (AC), which describes the response of an alternating perturbation as a function of the frequency. Therefore, in an uncomplicated way, by applying a potential and measuring the current response, it is possible to obtain the impedance (Z) of the studied system, which is affected by any factor that alters the electron flow.Impedance spectroscopy has been applied for decades in electrochemistry and physics to investigate the electrical properties of conductive materials and their interfaces.3 Among the possible applications of impedance spectroscopy in electrochemical devices, it is worth mentioning: the study of electrodeposition kinetics of polymers,4 electrochemical aging of polymers,5,6 characterization of photoanodes and solar cells photocathodes,7–9 the study of corrosion mechanisms,10–12 study of material doping,13,14etc. This enormous range of applications of this technique is possible due to its versatility and simplicity of execution. However, it is worth noting that the correct interpretation of the impedance data requires a more in-depth study of the system being characterized. This technique and its results are often underestimated. Thus, the present review will address the use of electrochemical impedance spectroscopy to characterize composites of ionomeric polymer and metal and their derivatives.
2. Application of impedance on IPMCs
Since the advent of IPMC devices, many techniques have been used to understand their operating mechanisms. This section will briefly discuss studies that used electrochemical impedance spectroscopy as a form of characterization for a specific purpose, such as obtaining resistivity and capacitance of the device or newly developed electrode and determining the ionic/electronic conductivity of the device and the membrane. Such results had neither a model developed to describe the data nor the obtained data in depth. Among these examples is the determination of the resistivity or capacitance of the device using only the complex impedance data as usual.15–19 The data extracted directly from the Bode graph at a given frequency is still valid in this analysis.Nevertheless, it does not explore the full characterization potential of this technique since one may obtain valuable information about diffusion mechanisms, reactions, and charge transfer processes. Thus, the main objective of this section is to show the range of uses this technique can have and the different information that could be obtained. The studies are organized chronologically; specific uses will be addressed in appropriate subtopics. Fig. 2 shows the primary applications of impedance measurements in IPMC that will be detailed hereafter.
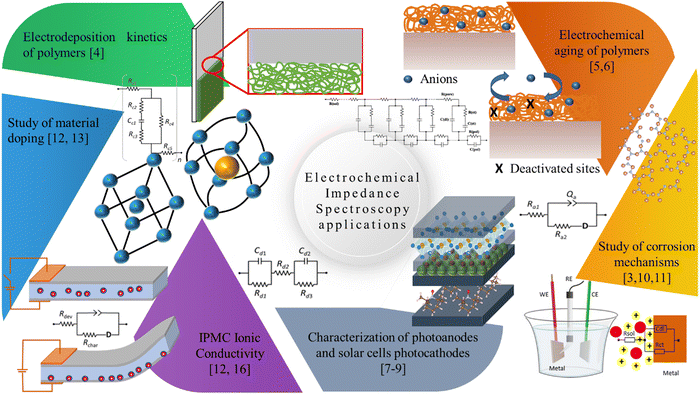 | ||
| Fig. 2 Diagrammatic illustration of the main areas that apply electrochemical impedance spectroscopy in IPMC. | ||
2.1. Widespread use of impedance data
Bar-Cohen et al.20 presented a paper with characterization techniques to quantify the electroactive responses and material properties of EAP materials. The impedance technique was used to observe the magnitude and phase changes as a function of frequency, but its full potential and applications for IPMCs were not explored. In 2002, a subsequent paper21 proposed a new method for gauging EAP mechanical properties via acoustic wave resonators. The technique was based on non-linear curve fitting (non-linear regression using Mason's Model) of impedance data for a thin piezoelectric (PZT) and an acoustic layer (Kapton). In 1999, S. P. Leary, & Y. Bar-Cohen,22 used the Impedance Spectroscopy (EIS) technique to determine the electrical properties of Nafion-based IPMCs with platinum electrodes and Na+ counterions. Samples were immersed in deionized water, and an electrical potential of 0.05 V was applied. The authors assumed that impedance response at low frequencies was governed by space charge effects at the electrodes,23 and no Debye relaxation (dielectric relaxation) was observed. Large displacement occurs only at low frequencies (0.1 Hz). In comparison, at higher frequencies (>5.0 Hz), the device's behavior was similar to a resistor with no mechanical deformation, indicating that ion migration was not ideal. When a higher electrical potential was used (4 V), electrochemical reactions and nonlinear dielectric behavior were observed, associated with water electrolysis, mechanical hysteresis, and power dissipation in the form of heat, respectively.In 2000, Shahinpoor & Kim24 prepared IPMC artificial muscles using Nafion as a perfluorinated ion-exchange membrane, plated with platinum, and exchanged with Nafion/Pt/Li+. Two other samples, one containing copper (Cu) and another containing silver (Ag), deposited electrochemically on the surface of the platinum electrodes, were prepared. EIS was used to report the effects of the electrode surface resistance on the device's performance. An optimized equivalent electric circuit was proposed based on a discrete electrical model described by R. Kanno and S. Tadokoro.24 It is composed of a surface resistance (Rs), a polymer resistance (Rp), a capacitance related to the ionic polymer and the electrical double layer (Cdl), and an impedance (Zw) due to a charge transfer resistance near the electrode surface. However, considering that electrical potential drops along the electrode surface, a simplified series of arbitrary resistances (Rss) was used to represent it. The results suggest that the electrochemical deposition of Cu and Ag produced a continuous metal phase, decreasing the surface resistance considerably and increasing IPMC performance (about 20%). In other words, this thin layer could reduce the surface resistance, Rss, of typical IPMC artificial muscles.
The relation between the layer thickness and the decrease in surface resistance has been experimentally verified by Punning et al.25 The authors developed an innovative experimental apparatus to measure the IPMC surface resistance along its length while performing bending movement. The measurements exhibited that the actuator surface resistance depends on the bending radius, and is more expressive with the increase of the curvature radius. Since the bending motion of the sample was different along its length, the author suggests that the model proposed by Shahinpoor & Kim26 should be modified, replacing the invariant resistors (with time) with variable resistances (variation of electrical resistance as temperature changes). It was the first time that the variable resistor was used to describe the electrical characteristics of the surface of IPMC actuators.
Two similar works were presented by Noh et al.27,28 In their first work,29 a large-surface Nafion-based IPMC actuator was prepared, and the EIS was used to analyze the ion migration capacity of six different cations (H+, Li+, Na+, K+, Mg2+, and Ca2+) on the device performance. The Bode response of impedance analysis suggests that, for monovalent cations, the low-frequency resistance is higher for Li+ when compared to others. In contrast, Ca2+ presented a higher resistance for bivalent cations than Mg2+ at the same frequency range. The authors assume that this increase in resistance is caused by the reduction of ionic migration throughout the material, caused by ion-size (monovalent) and ion–ion (bivalent) interactions. In their second work, Noh et al.28 presented a deeper electrochemical characterization of the interfacial region of the IPMC devices. They prepared a large surface IPMC actuator with a replication technique and investigated increasing the electrode/electrolyte interfacial area on the deformation. Its flexing behavior has also been interpreted with the electrochemical aspects of different Nafion membrane cations. The impedance spectra analysis was carried out using a simple equivalent RC (resistor–capacitor) circuit. The Nyquist plot presented a lower resistance for the large-surface IPMC, indicating that the current density in the replicated Nafion was low, and the charge transfer resistance could be reduced. Using the same proposed circuit, Mukherjee and Gupta30 calculated the capacitance and resistance of IPMC devices to construct a propulsor working underwater where the IPMC device held the actuation.
Kim and Kim31 analyzed the electrochemical behavior of a conventional IPMC with platinum electrodes using cyclic voltammetry, impedance spectroscopy, and quartz crystal microbalance. It was concluded that IPMC has a complex electrochemical behavior due to reactions and phenomena that occur at the interface when electrical potentials are applied. Among these phenomena at the platinum interface, the following are mentioned: change in mass on the electrode surface due to adsorption/desorption of H2O and OH−, formation of platinum oxide, and water electrolysis at a voltage higher than 1.8 V. The equivalent circuit proposed from impedance data is of the RLC (resistor–inductor–capacitor) type, instead of an RC, as suggested in previous works,32,33 with the inductive component being present at high frequencies.
Lee et al.34 used electrical characterization by impedance spectroscopy and surface resistance to investigate the properties of electrodes deposited on Nafion at different reduction temperatures of Pt ions during the reaction. The deposition occurred in two stages, each held at different temperatures (5, 25, and 45 °C). It was reported that electrodes deposited at a higher temperature (45 °C) showed lower impedance and less surface resistance, and the temperature of the first deposition significantly influenced the impedance. It was associated with the interface between the polymer and the metal and with metal penetration in Nafion. The second Pt2+ reduction affected the surface resistance (thickness and density of the platinum layer).
The influence of the roughness of the electrode was studied by impedance spectroscopy simulations using the linearized Poisson–Nernst–Plank (PNP) approach.35,36 Specifically, the polymer is decomposed into a bulk region, where diffusion phenomena occur, and boundary layers in the vicinity of the polymer–electrode interfaces, where charge storage develops as a function of the electrode surface roughness. The authors concluded that IPMC charge storage is enhanced by the increase in effective electrode surface area. On the other hand, bulk diffusion phenomena remain independent of the microscopic topography of the electrode. Thus, the hypothesis of rough electrodes is very well suited to interpreting the abnormal values of IPMC capacitance which scales linearly with the electrode's actual surface area.
Buechler and Leo37 proposed an electromechanical model based on energy, having as background an earlier work by Hagood et al.,38 but including the variation in material properties with frequency. The model requires the empirical determination of three properties of the material: elastic modulus (including viscoelastic effects), dielectric permittivity, and strain coefficient. Electrical impedance measurements obtained the electrical permittivity value. The impedance, in this case, proved to be more capacitive at low frequencies (around 10 to 1 Hz) and more resistive at high frequencies. Finally, the model accurately predicted the free deflection behavior of the IPMC.
Two models to describe the impedance behavior of IPMC have been proposed by Takagi et al.:39 one using transmission lines and another black-box model. The similarity between the models is that they both represent non-rational transfer functions. To calculate the parameters and validate the models, experimental data of impedance spectroscopy of IPMC comprised of Nafion and gold electrodes were used. As counterions, Na+ and TEA+ (tetraethylammonium) were used. The results suggest a good agreement for both models. Two clamp systems were used to investigate the influence of the electrical contact, but it was found that this parameter had little or no influence on the results. On the other hand, the greatest influence on impedance spectroscopy results was the type of cation used, with TEA+ implying greater impedance due to its greater ionic radius and, consequently, less mobility.
Another model, a gray box one, was proposed by Penella et al.40 to study the use of IPMC in energy harvesting. The experimental validation of the model was performed using an IPMC based on Nafion in a free beam configuration. Impedance measurements at frequencies between 0.1 and 100 Hz, made simultaneously with strain measurements, were used to validate the model and choose the best electromechanical coupling function. The model showed good experimental agreement and allowed the authors to estimate the best geometry for energy harvesting and the frequency for the most effective energy conversion.
Chen and Tan41 presented a model based on physical parameters and an infinite-dimensional transfer function. The model relates folding displacement to the applied electrical potential and can simulate the material impedance behavior. The transfer function was applied to developing an open-loop control system for the IPMC actuator's tip positioning problem. Although phenomenological models were not directly studied, the results showed that this strategy could develop open-loop controllers dependent on external parameters. Experimental measurements of mechanical displacement and impedance in an IPMC based on Nafion were used to validate the model. One of the conclusions emphasizes that the resistivity of the electrode must be considered to obtain simulations closer to reality. Another factor of interest is that the proposed model can be scaled to different geometries without defining new adjustment parameters. The same strategy was used to evaluate the influence of the temperature42 and the hydration level43 on the polos and zeros of the transfer function, which is an exciting strategy.
Caponetto et al.44 suggested a compact fractional-order elements (FOEs) fitted model, where the definition of process parameters and strategies can ensure the desired performance. The model was tested for Nafion-based IPMC samples with different Pt electrode thicknesses performed for a fixed electrical potential amplitude to determine the frequency region where the IPMC response could be linear. Then, a frequency analysis is carried out to identify coherent fractional-order dynamics in the Bode diagrams. According to the thickness, the FOE order varied from 0.05 to 0.3. Although this model does not describe the phenomena internal to the IPMC, this strategy provides simplified and valuable parameters for designing control loops.
Tiwari and Kim45,46 studied the performance of IPMC as a sensor and in energy harvesting, varying the types of counterions (Li+, Na+, and H+). The morphology of the platinum electrode was also investigated as follows: 1, 2, and 3 chemical depositions of platinum, formation of grooves by sanding in the transverse direction, and the longitudinal direction of folding and deposition by sputtering. The impedance spectroscopy results showed that IPMCs with only one platinum deposition have a much higher real impedance than 2 or 3 depositions (with a slight difference between the last two conditions). Regarding the induction of cracks in the electrode, the real impedance increases when they are in the transverse direction. Needle-pierced electrodes were also tested and showed the best performance, with the lowest real impedance. The higher impedance values showed a worse performance in the sensitivity of the IPMC in deformation and energy harvesting. Regarding the different cations used, the highest efficiency of IPMCs follows the following order: H+ > Na+ > Li+. Tiwari et al.47 studied the main outputs for IPMC energy harvester devices when altering the thickness and the type of electrode via sputtering, observing that this mechanoelectrical output could be tailored to changing parameters. They used different metal particles to cover the platinum electrode, such as gold, copper, nickel-gold, carbon, and rutile oxide, leading to smoother surfaces less surface resistance, and improved charging.
Using the same approach as another paper of the same group, Cha et al.48 used the PNP system to describe the evaluation of electric potential and counterion concentration in the IPMC in response to large deformations. They concluded that IPMC is electroneutrality during deformation for conductive electrodes if its electrodes are open-circuited and the counterions do not migrate without regarding the IPMC swelling, as a voltage drop arises throughout the electrodes to held equilibrium. On the contrary, boundary layers develop in the interfaces for short-circuited electrodes, so the electroneutrality is lost where charge depletion is provoked by the IPMC deformation (as one can see when reverse relaxation occurs). The conclusion was that the surface resistance directly affects both high and low-frequency responses of the IPMC, increasing resistive effects and altering the formation of the double layer and counterion migration, respectively.
The influence of pH on the electrical and mechanical properties of a Nafion-based IPMC with palladium electrodes was studied by Aoyagi and Omiya.49 The AC impedance measurement results indicate that a lower pH increases the charge transfer resistance and reduces the double-layer capacitance in acid solutions. On the other hand, both parameters were constant with pH in alkaline solutions. The authors related this finding to the mechanical properties of the IPMC.
Using EIS to model the frequency responses of IPMC sensors was the focus of Takagi et al.29 The authors investigated using an IPMC comprised of Nafion 117 and gold electrodes with two different counter ions exchanged: Na+ and TEA+ (tetraethylammonium). They did five gold plating instead of the standard single plating in an unusual approach, creating a large conductor surface area, a convenient path to study sensing materials. Simple measurements of current/electrical potential in the frequency domain were based on data for comparison with EIS data, which can help investigate black box models based on Onsager's equation.50,51 The authors concluded that the electrical potential response is not proportional to the displacement or the velocity in the frequency domain and highly depends on the counter ion species as the differences between Na+ and TEA+ are apparent at higher frequencies. Voltage and current response could only be related through impedance which means that this technique was proper to investigate the black box model proposed for the IPMC sensor.
Disc-shaped IPMC for energy harvesting is still the most used geometry for this application. Based on this proposition, Tiwari52,53 prepared an IPMC based on hot-pressed Nafion 117 pellets and simple silver painting as an electrode with disc-shaped geometry varying its inner radius and thickness to study resistivity and capacitance through EIS. The contribution of these works was the conclusion that the samples with greater thicknesses had high charging, and the inductive behavior was evident. So, they did not use the full potential of the EIS technique.
It is known that ionic liquids as solvents for IPMCs provide better electrochemical stability,54 prevent water electrolysis, and allow these devices to work in dry environments.55–57 So, researching ionic liquids is also becoming a trend in microelectronics. Seeking better electromechanical performance for IPMCs with ionic liquids exchanged at room temperature than those IPMCs with ionic liquids exchanged at 100 °C, Kikuchi and Tsuchitani58 investigated the bending curvature, bending response speed, and electrical properties of an IPMC with ionic liquids [BMIm][BF4], [BMIm]PF6 and [EMIm][BF4] exchanged for 48h at room temperature. The authors used EIS to verify the resistance and capacitance of the devices and an acquisition system with a laser displacement sensor for electromechanical data. They found that the bending curvature became more prominent as the IPMC resistance decreased and that the ionic liquid immiscible with water, BMIMPF6, had the best electromechanical responses. Furthermore, the authors proposed an equivalent circuit for IPMC devices based on the Randles circuit.
To reduce the spike current phenomenon on the IPMC-PWM driving energy amplifier, Takagi et al.59 used a filter on the integrated circuit, which allowed less energy consumption, enhancing the efficiency of this device. To characterize the resistance and capacitance of this circuit, EIS was held, and an equivalent circuit was fitted. The equivalent circuit is a simple RLC circuit with an inductor element between the IPMC and PWM amplifier, where the inductor element represents the filter for large current values. It is an example of a fitted equivalent circuit that does not consider all the phenomena occurring on the device structure. This circuit cannot describe ionic diffusion and the interactions between exchanged counter ions and side chains of the ionomeric membrane.
Diab et al.60 proposed an electromechanical model of Nafion-based IPMC artificial muscle exchanged with Na+. The model is composed of two integrated blocks to describe IPMC actuation. The first part is a simple RC circuit powered by a DC voltage. The second block is the mechanical part determining the amount of deformation in the IPMC for any applied load. The model was simulated using MATLAB and presents the deflection of the device along its length for various input voltages. However, the simulated model has not been compared with experimental data, so it would be useful to compare the results with analytical data obtained from EIS.
Other authors have also presented equivalent circuits to simply represent electrical response data from devices. For example, Feng and Liu61 proposed a novel fabrication process using a microfluidic scheme to construct one arbitrarily shaped planar Nafion-based IPMC device to use as a micromirror actuator. The electrical properties of the swirl-shaped actuator were studied using a simple circuitry designed for acquiring the current flowing through the actuator and the voltage drop between the electrodes. The current response was measured using Ohm's law, while voltage drop was calculated by the difference in voltage that passes through a resistor and the IPMC. A circuit model extracted from62 was used to describe the device's electrical characteristics. Following the same premise, Li et al.63 proposed sensing the Nafion-based IPMC deformation based on the principle that the device's impedance is correlated to its bending curvature. A simple equivalent circuit was proposed, but it was not discussed with the impedance data. In addition, the author assumes a correlation between the impedance and the deformation, but the data is not discussed in detail.
On the other hand, some authors have presented a more elaborate and detailed work correlating the devices’ response with impedance data and equivalent circuit models. In 2014, Palmre et al.64 used palladium (Pd) to develop newly designed Pd–Pt IPMCs with high surface area and thick ionomer membranes (0.5 and 1 mm). They modified the Pd electroless plating process conditions, creating highly dispersed particles at the ionomer surface and inside the membrane. The procedure for fabricating Pd/Pt electrodes was carried out in two stages. First, palladium particles were incorporated into the inner membrane surface, soaking the membrane in a Pd(NH3)4Cl2·H2O solution for 1,5 h. Second, Pt particles were deposited at the outer surface using a traditional chemical deposition method (electroless plating). Samples were exchanged with Li+, and electrochemical characterization was performed using cyclic voltammetry (CV) and electrochemical impedance spectroscopy (EIS). The data indicates that the palladium particles in the electrodes significantly increase the capacitance of IPMC at lower frequencies (<10 Hz), promoting a higher ion migration. For this reason, Pd/Pt-IPMCs exhibit significantly higher electromechanical responses than Pt-IPMCs.
Must et al.65 prepared a three-layer ionic liquid-based actuator using a manufacturing method described by Palmre et al.66 The device was designed using Nafion as the polymeric membrane exchanged with EMI+ counterion. The electrode material was prepared by dispersing titanium carbide-derived carbon powder with 15 wt% Nafion solution. The effect of ambient relative humidity (RH) on the electrical response was investigated by electrochemical impedance spectroscopy. The data were fitted with a simple equivalent circuit that consists of a charge transfer resistance, a Warburg element (electric double-layer), a parallel connection of resistance, and a constant phase element, representing a contact impedance between the n active electrode material and measurement/input terminals. The equivalent circuit presented a good fit in Nyquist plots for the whole frequency tested, giving information about the physical processes occurring in the device. So, the improvement in the actuation performance in a humid environment at low frequencies was described by impedance analysis since the characteristic frequency shifted from 0.3 to 1.3 Hz due to the increased ambient RH, indicating an increase in ionic conductivity.
The migration of ions in perfluorinated membranes also depends on temperature, influencing the deformation behavior of IPMC devices. Based on this fact, Cha et al.67 studied the effect of temperature on the electric impedance of Nafion-based IPMC samples neutralized by sodium counterions. The temperature of the impedance characterization was controlled by immersing the samples in deionized water with the desired temperature (from 25 to 40 °C). In a previous paper,68 a modified Randles circuit was used, for each sample's equivalent resistance, capacitance, and Warburg impedance were measured. It is presented that the resistance and the capacitance decrease as the temperature increases, while the Warburg impedance increases. Such variations are associated with the effect of temperature on the dielectric constant and the diffusivity of the IPMC. Despite an exciting result, the variations are minor, and their impact on electromechanical behavior is not presented.
In subsequent work, the same author69 used the impedance technique to explore the feasibility of enhancing Pt Nafion-based IPMC energy harvesting through impedance matching. The authors used a physics-based model48 to describe the electrical response of 14 Nafion-based IPMC samples exchanged with sodium counterion and designed shunting impedances for four excitation frequencies. Each sample was modeled as a transmission line, in which a shunt impedance was used to represent the counterion motion through the device's thickness. A classical Antoniou's circuit was used to create a match impedance. Results confirm that impedance matching produces a considerable increase in power delivery, with an average performance improvement of more than 60%. It was also suggested that impedance matching should be preferred over a more straightforward resistive loading only for IPMCs with many plating layers or other metal coatings.
In the research from Liu et al., an actuator to operate in air conditions was fabricated using reduced graphene oxide (rGO) with polyaniline (PANI)70 and rGO/CNT71 as the electrode, and a gel electrolyte composed of sulfuric acid and poly(vinyl alcohol) (H2SO4–PVA) as the ionomeric film. That paper aimed to improve the ionic conductivity and increase capacitance through the intercalation of rGO layers with intermediary PANI particles. The EIS measurements showed that the polymerization of PANI on the rGO sheet surfaces improved the ion intercalation and the device capacitance, which was the cause for the enhancement of the actuator's performance. The contact resistance between the electrolyte and electrodes reduced significantly with the intercalation, 657 Ω for rGO and 282 Ω for rGO/PANI electrodes. More impressive, the capacitance increased considerably to 207 F g−1 in the intercalated electrode since the rGO electrode without PANI presented only 79 F g−1 of capacitance.
Silver Cellini et al.72 used EIS measurements to evaluate an air actuator based on polypyrrole-silver electrodes polymerized by photoinduction in the Nafion membrane with Li+ as the counterion. Electrochemical impedance was used to study the mass transport, double-layer capacitance, and resistive phenomena within the electrodes and the ionomer. As an unconventional electrode was used, three different concentrations of pyrrole were studied (0.143 mol L−1, 0.072 mol L−1, and 0.029 mol L−1) while the stoichiometric ratio with silver nitrate was 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (pyrrole
1 (pyrrole![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) silver). The authors found that the initial pyrrole concentration influenced the double-layer phenomena and ion transport. The authors observed a considerable variation of the double-layer capacitance, increasing two orders of magnitude: from 27.0 μF cm−2 when the initial pyrrole concentration was 0.143 mol L−1 to 2.73 mF cm−2 for the initial concentration of 0.029 mol L−1, respectively. The hypothesis in that research was that the higher concentration of initial pyrrole developed a homogeneous distribution of silver particles on electrodes so that a higher electrode surface area is formed, which increases the double-layer capacitance.
silver). The authors found that the initial pyrrole concentration influenced the double-layer phenomena and ion transport. The authors observed a considerable variation of the double-layer capacitance, increasing two orders of magnitude: from 27.0 μF cm−2 when the initial pyrrole concentration was 0.143 mol L−1 to 2.73 mF cm−2 for the initial concentration of 0.029 mol L−1, respectively. The hypothesis in that research was that the higher concentration of initial pyrrole developed a homogeneous distribution of silver particles on electrodes so that a higher electrode surface area is formed, which increases the double-layer capacitance.
Panwar et al.73 developed a polyvinylidene fluoride (PVDF)/polyvinyl pyrrolidone (PVP)/polystyrene sulfonic acid (PSSA) based ionic polymer metal composites (IPMCs) actuator. PVDF is the hydrophobic polymer in the ion exchange membrane, PVP is the basic, water-soluble polymer, and PSSA is the robust and water-soluble polyelectrolyte that provides the free charge carrier. According to the PVDF/PVP/PSSA blend ratio, this novel IPMC presented higher ion exchange capacity (IEC) and water uptake (WUP) than the Nafion membrane and proton conductivity equal to that of the Nafion membrane. The electrochemical impedance spectroscopy analysis showed that the PVDF/PVP/PSSA IPMC had a greater capacitive characteristic than the Nafion-based one.
Rasouli, Naji, and Hosseini74 developed a new device based on Nafion with a non-metallic electrode of polypyrrole (PPy), carbon black (CB), and carbon nanotubes (MWCNT). A conductive paint was prepared by mixing a Nafion solution with CB and MWCNT and then deposited it over the membrane itself. The PPy was deposited electrochemically using cyclic voltammetry and chronoamperometry methods; the electrodeposition media was modified with water and water/acetonitrile solution. Thus, the four different devices were characterized using cyclic voltammetry and impedance spectroscopy, besides the electromechanical response and the water uptake (WUP). The new compounds had ionic conductivity and capacitance eleven and thirty-six times greater than the classic Nafion/Pt composites and a water uptake at least twice that of the conventional Pt/Nafion. Besides, both the synthesis method and solution media used during the synthesis affect the final device's performance since the new composites had lower tip displacement, suggesting that the surface resistance of PPy film, the thickness, and synthesis parameters may all be altered to obtain lower resistance. Since the authors chose cyclic voltammetry and chronopotentiometry to perform the synthesis, it is feasible to try other parameters to bring new compounds, attaining the desired characteristics.
Hong, Almomani, and Montazami75 used the EIS to verify the morphology effects of conductive network composite (CNC) layers in a Nafion-based mechanical strain sensor. The CNC, consisting of Ag nanoparticles dispersed in a poly (allylamine hydrochloride) matrix, was applied as the electrode in the IPMC-like device. It was found that the increase in the number of bilayers decreased the device resistance, leading to a better sensing performance, reaching an 11-fold improvement in the signal.
Aiming to preserve and restore the electroless plated surface is also a practice in the field of soft actuators,76 since the cracking of the electrodes may impair the ionic conductivity. Ming et al.77 proposed a fluid-bed-like reactor to prepare IPMC. This method aims to improve the efficiency of Nafion plating, preserving the etched surface morphology. The sample prepared by this method was compared to the one obtained by the conventional way. The fluid-bed samples exhibited better bending sensing with a sensibility of 2.99 mV for 1% strain and enormous operation stability over 8000 bending cycles. However, the EIS measurements were just used to compare the electrode surface resistance of the conventional method and the new one described. Still, about new methods of IPMC preparation, Kodaira et al.78 described a 3D casting process, which allowed the elaboration of devices with unique formats. The samples obtained exhibited different thicknesses in the same device; thus, the resistance and capacitance were characterized using impedance spectroscopy, relating the values with the membrane thickness. The authors found that both capacitance and resistance increase linearly with the thickness until a value of 400 μm. After that, the relation starts to be nonlinear, an essential characteristic for assembling robots with different morphologies. Guo et al.79 used the dip-coating technique, where IPMCs were put in a solution containing PVP and AgNPs, to restore the cracked electrode surface after actuation through growing Ag particles. They concluded using EIS analysis that the restored IPMCs had higher ionic conductivities and higher Warburg slopes, meaning that the diffusion rate was also higher since the water leaking through the electrode cracks was inhibited. These works represent the basis of EIS use for the characterization of IPMC devices.
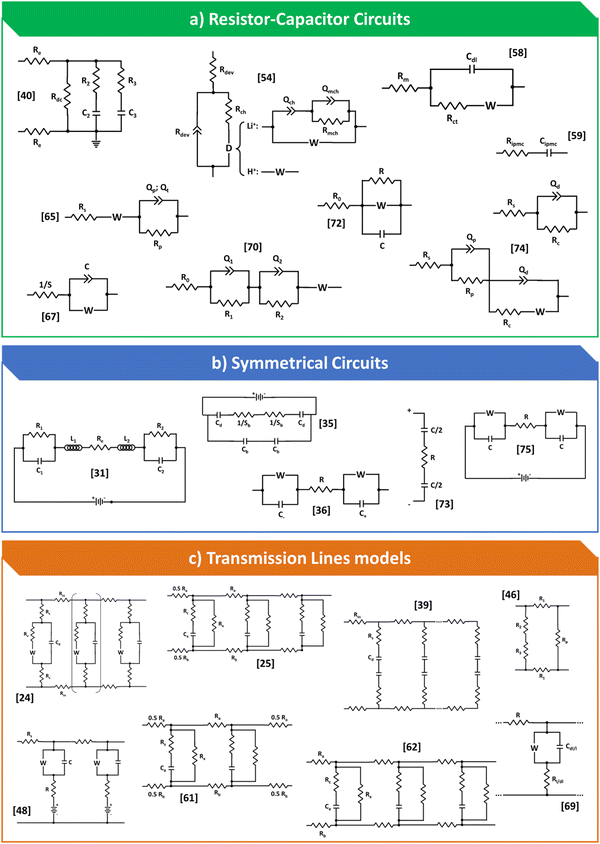
In Fig. 3, was bring together all the models that have been proposed to date for processing impedance data for IPMC-type devices. It is possible to observe that there are an infinite number of models, from the simplest to the most complex, some that consider the symmetrical character of the device and a few transmission lines. In general, there is no or, at least, almost no concern about the internal processes that cations undergo when the device is polarized, a fact that leads to a low representation of each of these models furthermore, failure to consider these processes also leads the model to work in very specific cases, making data comparisons between different authors and devices difficult. Furthermore, the models were divided into equivalent circuits of the RC type, which also include those that take Warburg element, symmetrical circuits and finally, the few representatives that were found of transmission lines.
2.2. Determination of ionic conductivity
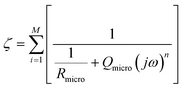
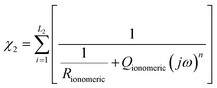
In the case of the development of new ionomeric membranes, the determination of ionic conductivity is essential, as this property is decisive for the characterization of the device. Through eqn (1), it is possible to estimate this parameter from the electrochemical impedance spectroscopy data.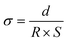 | (1) |
In this sense, Dai, Li, and Zhang80 characterized the ionic conductivity of IPMC made of ethylene vinyl alcohol (EVOH) grafted with sulfonated polyethylene glycol (PEG). Graphitizing PEG synthesized the ionomer into EVOH through the Williamson reaction and subsequent grafting of the sulfonated groups at the end of the PEG side chain. This synthesis method allowed us to vary the number of ethylene glycol (EG) units in the side chains (and, consequently, their length) from 2 to 6 units. The results suggest a decrease in ionic conductivity by increasing the side chain length up to 4 units. On the other hand, an increase of up to 5 and 6 EG units increased the ionic conductivity of the material. The authors explained this behavior considering that, for an EG number ≥5, there is a large enhancement of the hydrophilic domains, which leads to the absorption of water to the point of coalescing and forming a continuous path that contributes to ionic conductivity. AFM confirmed this latter hypothesis. This is a fascinating example of EIS data validated by observing morphology in explaining an electrochemical phenomenon.
Kraton is the commercial name of a block copolymer of styrene and ethylene/butylene with good mechanical properties, being cheaper and easier to obtain than Nafion.81 However, it does not exhibit any electrical or ionic conduction property necessary to modify its polar groups. In this sense, Inamuddin82 prepared a Kraton-based IPMC plated with platinum, exchanged with Na+ counterion, and measured the proton conductivity through impedance measurements. The authors found that its conductivity was 4.25, more significant than the Nafion-IPMC (17.2 S cm−1 against 4.03 S cm−1) at the same testing condition. On the other hand, Khan et al.83,84 studied the ion mobility of Kraton modified with silver nano-powder and Ag-decorated graphene oxide, concluding that the Ag/GO further improves the ionic mobility of the membrane and, consequently, the actuation performance of the device. Still, in another work, Khan et al.,85 besides characterizing the ionic conductivity of IPMC made of sulfonated poly(1,4-phenylene ether-sulfone) membrane modified with carbon nanotubes (SPEES/CNT), also used impedance spectroscopy to evaluate the electrical properties of the device containing different concentrations of sodium sulfate. The authors found better actuation responses due to the increased ionic conductivity of the synthesized membrane.
Tailoring the structure of ionomers to reach desired properties, such as charge accumulation on the interface between the electrodes, is a path to developing new ionomeric polymer transducers. In this sense, Leo et al.86 studied different levels of branching sulfonated polysulfone with phosphine oxide and the doping of electrode with RuO2 particles in a volume fraction varying from 0% to 45% gold films as the outer surface, which reduce the surface resistivity. The EIS data made it possible to infer a percolation threshold as the RuO2 content increased, around 22.5% of particle content. Water absorption from the ambient environment increases the ionic conductivity by two orders of magnitude regardless of the uptake level. Apart from that, the water absorption did not affect the necessary intake of the ionic liquid used as a counter ion (1-ethyl-3-methyl-trifluorosulfonate) [EMIm][Tf]. The magnitude of the impedance versus frequency data for the electrodes suggests a direct relationship between the volumetric content of RuO2 particles and the resistance of the polymer layer. For this unusual IPMC transducer, a standard RC equivalent circuit was fitted through an impedance, which may be hardly criticized by those who consider the variety of nuances that this device has since it has inorganic particles, branching, gold film, and ionic liquid electrolyte.
As mentioned above, doping is one of the techniques applied to enhance the conductivity of IPMC membranes. This practice is not solely done in the electrodes but also in the polymer matrix.87,88 Jung et al.89 doped Nafion membranes with TiO2 anatase particles through the sol–gel method and studied the electromechanical and electrochemical properties of IPMC devices based on this doped polymer and Pt as the electrode. They concluded that the bending deflection decreased with higher TiO2 content in the membrane while the blocking force increased with higher TiO2 content. EIS data shows that the conductivity of doped membranes decreases with increasing TiO2 amount, notwithstanding an internal resistance drop in the samples. The focus of this paper was to use EIS to study ionic conductivity.
Regarding the Nafion modification, Safari et al.90 studied the substitution of water for ionic liquids, changing the counter-ion species (H+ and Li+) and their weight rate. The authors show that the ionic liquid-based actuators incorporating Li+ presented the closest behavior to those of an ideal capacitor and appeared to have the highest charge storage capacity, consequently increasing the tip displacement. However, water-based IPMC actuators with Li+ showed the highest ionic conduction and displacement rate, which is related to the formation of more prominent clusters in comparison with ionic liquid-based actuators.
Ru et al.91,92 developed a different IPMC actuator by doping water-soluble sulfonated multi-walled carbon nanotubes into the Nafion matrix embedded with Li+ and sandwiched between palladium electrodes. This doping tried to overcome some weak points related to conventional IPMCs, like the low ion carrying capacity at low driving voltages. The authors brought up in this research that adding sulfonated MWCNT into the Nafion matrix could effectively shorten the hopping distance, increasing the actuator's ionic conductivity of 8.9 mS cm−1 from the pure Nafion IPMC to 16.65 mS cm−1 of the Nafion doped with 0.5 wt% sulfonated MWCNT actuator. Similarly, Naji et al.93 fabricated Nafion-based IPMC with sulfonated graphene oxide (sGO) doped in the Nafion matrix to improve ion transport and capacitance. Electroless deposition of platinum was used to fabricate the electrodes, and H+ was utilized as the counterion. As the sGO amount increases, the ionic conduction also increases. For example, with 4.0 wt% of sGO, the ionic conductivity is seven times greater than the pure Nafion IPMC. The authors also comment that the ionic conductivity is closely related to the size and number of ionic clusters formed within the swollen Nafion membrane, and Grotthuss describes it (hopping) and vehicular mechanisms.94 Both mechanisms can occur easier in the case of the Nafion doped with sGO actuators than pure Nafion-based actuators since they have higher water uptake content and ion exchange capability.
It is well established in the literature that the type of cation in the Nafion membrane changes its properties as an actuator/sensor. However, it is interesting to mention the work of Aoyagi and Omiya,95 which, in a contrary way, studied the effect of the anion in the Na+ mobility in a conventional IPMC, Anions of different sizes (OH−, Cl−, NO3−, SO42−) were investigated. The authors concluded after the experiments that when ion exchange was performed in solutions containing larger anions, the cation concentration in the membrane tended to increase. Therefore, the extent to which ion conductivity was increased by ion exchange became large, as did the double-layer capacitance at the cathode, indicating that solutions with larger anions increase the tip displacement of the IPMCs actuators.
Even in the most recent works, using EIS to calculate IPMC ionic conductivity is common. No further information is given throughout the data obtained independently if the application is an actuator96–102 or an energy harvesting device.103 Thus, in the following sections, we will present some other features for IPMC devices using EIS.
2.3. Sensor performance evaluation
Assessing the performance of sensor devices with EIS is also a path that one researcher can consider when assembling IPMC devices for actuation, sensing, and energy harvesting. This subchapter presents the central studies that have followed this path.In this way, Cha et al.104 built a ring-shaped device for underwater energy harvesting. This device was studied in five different geometries by varying the inner radius (7 to 15 mm) of the IPMC and maintaining the outer radius constant (30 mm). To predict the IPMC sensing, a Randles circuit was used. In conclusion, it was found that the ratio between the inner and outer radius plays a crucial role in harvesting efficiency. Specifically, it was demonstrated that two orders of magnitude could enhance power delivery by controlling the IPMC geometry.
Gudarzi, Smolinski, and Wang105,106 used impedance data to calculate the maximum frequency to which the pressure sensor could respond. The sensor was a semi-conventional IPMC based on Nafion, whose electrode was made from a conductive paste of RuO2 and ionic liquid of ethyl-methyl-imidazolium, following a technique that the authors called “Direct Assembling Method” (DAP). For the measurement, a coin-sized sensor was placed into a tube, and the air was used to pressure the sensor in some frequencies, compared with a commercial one. The performance and sensibility cut-off of the new device were the analyzed parameters. The authors concluded that sensing could occur both by compression and by shear excitations, whereby shear sensitivity was 1.6 times greater.
Exploring methods to characterize sensors, Mohdisa, Hunt, and Hosseinnia107 worked with active sensing of IPMC-like devices. This paper aimed to compare the frequency responses and noise characteristics of the sensors' voltage, current, and charge measurements. Although the authors did not use impedance itself, they used the concepts of impedance spectroscopy to treat data in the frequency domain, which brought a new perspective on sensing using this kind of device. This is an interesting guide for the design of IPMC sensors because, with the results, it was identified that each type of signal responds better to a specific frequency range. Below 1 Hz, the current is the best signal, while between 1 Hz and 10 Hz, both current and voltage signals are suitable. Finally, at higher frequency ranges, all the signals analyzed become suitable for sensing.
Even in the most recent works using IPMC as a sensor,108 the use of EIS is to calculate the basic properties of the IPMC device, even though the equivalent circuit proposed is simple and doesn’t explain all the complexities of the device as it's composed by a resistor in series with a perfect capacitor that is in parallel with a Warburg element. As the sensor is made of an IPMC, whose main property is the ionic conductivity of the polymer membrane, describing all the device's capacitance with a perfect capacitor is critical.
Fig. 4 illustrates the classification made for the different types of devices that can be found in the literature. Conventional electrodes use any noble or quasi-noble metal deposited on Nafion. The semi-conventional ones use other membranes as polymeric material, or despite using Nafion, they have some important modification in the electrodes used. Finally, the non-conventional ones have only one similarity with the conventional ones, the sandwich structure, with major modifications both in the polymeric material and in the electrodes. These, because they are more complex, represent a great difficulty when it comes to modeling them.
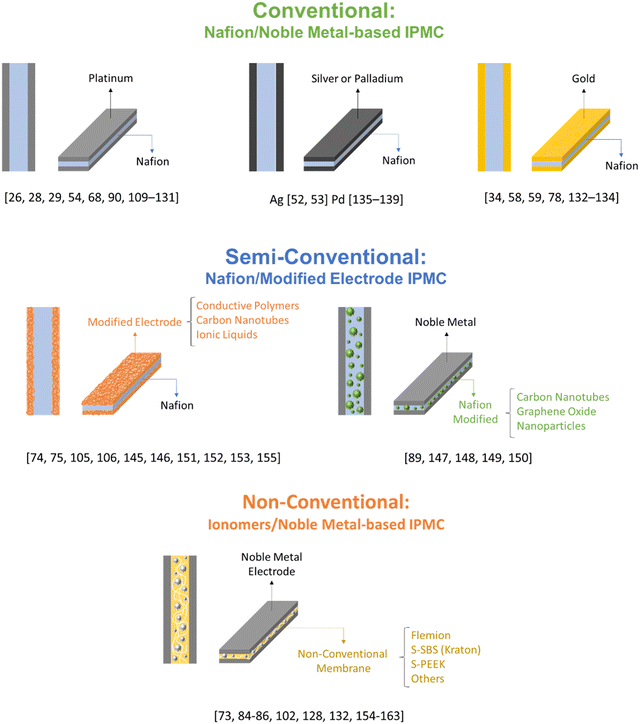 | ||
| Fig. 4 Schematic representation of some of the different types of devices and the classification given to them. | ||
Although many references about the IPMC variety were commented on earlier, Table 1 presents the actual state-of-art of this theme comprising all the literature describing composition of them.
| IPMC | Description | Application | Counter-ion |
|---|---|---|---|
| Conventional | Nafion/Pt26,28,29,54,68,90,109–131 | Actuator26,28,29,54,58,59,68,78,90,109–114,116–119,128,130,131,133,136,138–141 | H+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26,29,54,90,109,112,113,128,130,135,137 26,29,54,90,109,112,113,128,130,135,137 |
| Nafion/Au34,58,59,78,132–134 | Energy Harvesting52,53,115,120,121,129,135,137,142 | Na+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26,29,34,54,59,68,110,116,119,120,129,133,134,137–140,144 26,29,34,54,59,68,110,116,119,120,129,133,134,137–140,144 |
|
| Nafion/Pd135–139 | Sensoring34,122,134,143 | Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26,29,34,54,90,137 26,29,34,54,90,137 |
|
| Nafion/Ag52,53 | K+,26,29 Mg2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 29 |
||
| Nafion/Au–Pt34 | Ca2+,29 TEA+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34,133 34,133 |
||
H+/EG,114 EMIM+,90 BMIM+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 54 |
|||
| BMIMPF6,58 BMIMBF458 | |||
| EMIMBF458,131 | |||
| EMIMOTf131 | |||
| EAN131 | |||
| MAF131 | |||
| Semi-conventional | Nafion/Ppy-CB-MWCNT74 | Actuator74,89,146–151,153,155 | H+,149,150 Na+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 75 |
| Nafion/AuNP-PAH75 | Sensoring75,105,106,152 | Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74,89,105,106,147,148,151–153,155 74,89,105,106,147,148,151–153,155 |
|
| Nafion-TiO2/Pt89 | Transducer145 | EMIM105,106 | |
| Nafion/RuO2-EMI-TF105,106 | EMI-TF/Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 145 145 |
||
| Nafion/RuO2145 | EMI+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 146 |
||
| Nafion/carbon-LI146 | |||
| Nafion/CNT/Pd147,148 | |||
| Nafion/GO/Pt149 | |||
| MCNTs-Nafion/Pt150 | |||
| Nafion/Pt-EGaIn151 | |||
| Nafion/Pt (engineered)152 | |||
| Nafion/Pt-PVP@AgNPs153 | |||
| Nafion/Ppy-Pt155 | |||
| Non-conventional | PVDF-PVP-PSSA/Pt73 | Actuator73,84,85,102,128,154,156,158–163 | H+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73,84,102,128,154,156,158,161–163 73,84,102,128,154,156,158,161–163 |
| Flemion/Au132 | Sensoring132 | Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73,132,157 73,132,157 |
|
| PVA/rGO-PANI154 | Transducer86 | Na+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85,159 85,159 |
|
| PVA/rGO-CNT156 | Unspecified157 | TBA+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 132 |
|
| Pt–Pd (unspecified membrane)157 | EMIM-Tf86 | ||
| EVOH-g-SPEG/Ag/158 | |||
| Kraton/Pt,159 Kraton/Ag160 | |||
| GO-Ag-Kraton/PAni84 | |||
| SPEES-SWNT/Pt85 | |||
| sPSF–phosphine oxide/RuO286 | |||
| SPVC-PTA/Pt/161 | |||
| KR-CuNPs/Pt162 | |||
| GQDs/Pt/128 | |||
| SPVA-PANI-Pt/SA/163 | |||
| Pani – Pt/SPEEK102 |
3. Modeling and fitting
Despite its excellent application versatility, electrochemical impedance spectroscopy often requires complex models to explain and adjust the data obtained. Thus, the topic below deals with the main methods of processing EIS data and some interesting models proposed so far.3.1. Models for impedance treatment
The equivalent circuit model is the most used model to illustrate the obtained impedance spectra. In this model, circuit elements are used to describe the processes that occur on the surface of an electrode.164 This simple representation often suggests a narrow understanding of the electrode vicinity. As an example, it is possible to mention processes controlled by diffusion, which were better explained in an equivalent circuit proposed by Randles,165 where an element that does not have an analogous in electronic systems called Warburg Element (Zw)166 is used. The Warburg element is a constant phase element with an angle equal to 45° and |Z| magnitude inversely proportional to the frequency value. Thus, at low frequencies, when it tends to zero, the transport processes of electroactive species contribute significantly. Similarly, electronic processes, such as charge transfer, have the most significant influence when the frequency tends to infinity.Despite the complexity of equivalent circuits, they work very well to describe homogeneous systems and/or slightly roughened electrode surfaces.167 Porous electrodes and percolated systems, in which the ionomeric polymers fit very well, lack a complete model that can describe the heterogeneities of the system.168,169 As stated, more complete equivalent circuits can solve part of these heterogeneous systems; however, the transmission line model stands out among the possible ways of treating impedance spectra of this type.170,171 As discussed by Levie,172,173 the introduction of constant phase elements (CPE)174 is essential to describe both the roughness of material175–177 and other aspects that may lead to anomalous diffusion,178,179 which is different from that proposed by the diffusion theory.180 In general, for the construction of an impedance spectrum data treatment model, the impedances of the studied material (χ1), the environment (χ2), and the interface between these two (ζ) are considered. In a simple case, like an electrode in a solution with a redox pair, the total impedance of the system is the sum of each of these elements in series (eqn (2)).
| Z = χ1 + ζ + χ2 | (2) |
The current resulting from the AC disturbance at the two interfaces can flow along the two media considered. Thus, the total electrical current of the system is given by the sum of the currents on each side of the interface, which are parallel to the surface. In contrast, the currents associated with electrochemical reactions and/or charging processes flow perpendicularly. Across the surface,183,184 therefore, the elements χ1, χ2, and ζ must be thought of in such a way that the adjustment of the impedance spectra can physically and coherently describe the electrochemical phenomena, and this can be done using elements of an equivalent circuit that are analogous to the processes that may be occurring. In this specific model, the migration process is negligible, and the processes represented here are limited by diffusion transport. It is important because it is possible to apply the 2nd Fick's law185 for diffusion processes to obtain the system's impedance, even if the experimental conditions are different.186,187
3.2. Models for IPMC modeling
Considering the different methods of handling impedance data, the following section deals with the most discussed and used models for modeling and adjusting electrochemical impedance data for IPMCs. The work of MohdIsa, Hunt, and HosseinNia188 is a review of IPMC sensors that, among other things, discusses grey and white box models of electromechanical response modeling of these devices, even discussing some of the works cited in this section. Although many studies have presented mathematical models to describe the electromechanical behavior of IPMC actuators and sensors, the concept of electrical impedance has been used to develop some equations.The first work cited about this is from 2006 when Bonomo et al.140 developed a grey box approach containing electrical impedance concepts to develop a mathematical model composed of two subsystems (electrical and electromechanical transductions) to describe a Nafion-based IPMC actuator bending movement. The model was developed considering the IPMC device as a beam pinned by one end (cantilever). The electrical transduction was modeled using a generalized equivalent lumped nonlinear circuit141,189 to convert the applied voltage into an absorbed current. To aid the development of this model, the electromechanical transduction was resolved using a previous equation190 with the basic concepts of electrical impedance. After applying an electrical stimulus, voltage, current, and tip displacement were obtained and compared with the proposed model. The obtained results show an excellent agreement between the simulated and the real actuator response; hence, they represent a good validation of the proposed model.
Fotsing and Tan191 presented a model for the nonlinear electrical dynamics of IPMC actuators through perturbation analysis of the dynamics-governing partial differential equation (PDE) around a given bias voltage. The PDE was solved by power series expansion, considering a steady-state electric field approximation under the bias with a piecewise linear function for the perturbed charge dynamics. A bias-dependent impedance model obtained from the perturbed electric field and current captures the nonlinear nature of the IPMC electrical dynamics and changes to a linear model when the bias is zero.
In 2013, Moeinkhah et al.192 developed, for the first time, an analytical impedance and actuation model for an IPMC actuator based on the distributed electrical circuit, using the RC transmission line theory. The ionic migration in the polymer membrane was modeled as a double-layer capacitor in an equivalent circuit. In contrast, the energy loss and the stored electrical charge were modeled as resistive and capacitive elements. The resulting RC model was described by a series of similar circuits with single elements. The Laplace transform was used to develop an electrical impedance model based on a simplified equivalent circuit. It was compared with experimental data captured from,193 showing that it was effective in modeling the IPMC actuation. Furthermore, the proposed model can be used for real-time control applications; it can also be applied to other types of ionic polymer actuators, and it provides information about charge density, current, and voltage as a function of the actuator length and frequency.
Since IPMCs can operate under different voltage conditions, Cha and Porfiri144 studied a Nafion-based IPMC impedance in response to an applied DC voltage bias. They suggested an equivalent circuit model for small voltage inputs and an equivalent circuit model under large DC bias voltage should be used. It was proposed that a modified Poisson–Nernst–Planck formulation was to account for the presence of steric effects. The method of matched asymptotic expansions was used to derive a semi-analytical solution for the electric potential, the charge concentration in the IPMC, and a classical Randles circuit model, as presented in a previous paper.68 The model was verified by comparing IPMC counterion concentration and electric potential predictions with finite element results obtained using the commercial software COMSOL Multiphysics. The authors demonstrated that the relative thickness of the composite layer has a major influence on IPMC impedance since increasing the DC bias intensely decreases the double-layer formation and mass transport. In contrast, the DC bias has a secondary effect on IPMC chemoelectrical behavior for thick composite layers.
Similarly, other authors have also studied the effects of variations in metal electrodes on the behavior of IPMCs. In 2014, Nam and Anh194 developed a novel self-sensing technique for an IPMC actuator based on the variation of surface resistance effect during the bending movement, inspired by the results in ref. 195. Therefore, the current equivalent model of an IPMC actuator was based on an impedance model extracted from Chen.196 It consists of a simple equivalent circuit containing only resistive and capacitive elements along the length of the device. Since the surface resistance varies during the bending operation, a variable resistance per unit length was used. Based on this model and mathematical analysis, the self-sensing ability of the IPMC actuator was discussed. It was shown that if the voltage signals on the electrode surfaces can be observed, the bending displacement of the IPMC can be estimated correctly. However, this model is useful for a slightly bent IPMC. As the bending radius increases, the correlation between the resistance variation and the deformation becomes nonlinear, and the proposed method leads to an inaccurate estimation.
A more complex physics-based model proposed by Shen et al.143 was used to investigate the electrical properties of IPMC sensors. The authors assumed that the electrode is composed of two parts. The upper part has resistive characteristics, while the lower part has capacitive properties. Based on the Poisson–Nernst–Planck system of equations, the current in the polymer membrane was modeled. An experimental apparatus was developed to test the impedance and measure the electrodes' resistance, capacitance, and surface electric potential. The experimental data were compared with the developed model, showing that the model can describe the device's resistance, capacitance, and surface electrical potential. Moreover, it was demonstrated that parameters such as the size of the platinum particle, electrode thickness, and defects have a major influence on the electrical properties of the IPMC sensor. However, their influence on sensing and actuating performance has not been completely presented.
A model to describe a practical situation using these devices was presented by Cellini et al.142 The authors prepared a Nafion-based IPMC device with platinum electrodes for energy harvesting induced by a steady fluid flow. The device could transform a paddlewheel rotational movement into a periodic linear motion of radian frequency, promoting large bending movements in the IPMC. The electrical model was proposed based on previous papers197–199 to describe the response of the IPMCs through a single linear lumped circuit composed of a resistor (ion diffusion), a capacitor (double layer formation), and a voltage source (open-circuit IPMC voltage). An external signal acquisition system was used to investigate IPMC energy harvesting feasibility, studying the dependence of the power delivery on both the speed flow and the resistance. Experimental results showed that power harvesting is maximized for a constant speed flow when the resistance matches the IPMC impedance. Also, power harvesting increases with the speed of flow. In general, the model agrees with experimental data, and it can accurately describe IPMC power harvesting.
SamPour, Moeinkhah, and Rahmani200 described an electrochemical viscoelastic model based on an impedance model proposed by Moeinkhah et al.192 Because the sensor signal is proportional to the charge density and the device, this new electromechanical model aims to predict quasi-static and dynamic responses. For this purpose, the electrochemical behavior is described by a transmission line model, which could quantify the ionic charge density as a function of the polymer length. Attention is drawn because the model is easily solved since the current distribution is approximated as isotropic. However, this is not always true, considering different humidities and counterions. In addition, the most essential information extracted from the data adjustment is the capacitance, which is then related to the sensory methods using the IPMC. In conclusion, the authors agreed with the predicted data, covering the back-relaxation phenomenon.
The fractional-order equivalent-circuit model was used by Doregiraei et al.,201 and they had good accuracy with their experimental and fitted data. However, for a model that relies on the physical description of the devices, the local impedance should not be considered the same in the whole molecule since polymers have different chain lengths, which is the main reason for their polydispersity. Furthermore, this model also does not consider that some ionomeric microchannels (that form the ionomeric channels) are open to the electrode, and some are closed, which changes the local impedance of a specific microchannel.
Table 2 summarizes the literature references that apply the cited models and correlates to the applications found in each of them.
| Model | Use of impedance |
|---|---|
| Equivalent circuit | Capacitance106,109,135 |
| “Black box” model140,188 | |
| “Gray box” model188 | |
| Electrode74,75,154,196 | |
| Ionic conductivity80,86,89,90,139,147–149,202 | |
| Device characterization28,54,74,78,85,111–113,115–119,132,138,145,146,152,155,203–206 | |
| Modeling68,141,142,144,207–210 | |
| Performance121 | |
| Sensor limits105 | |
| Equation | Electrode34 |
| Device characterization53 | |
| Capacitance73 | |
| Modeling211 | |
| Ionic conductivity84,160 | |
| Device performance122 | |
| Fractional order equivalent circuit model | Modeling210 |
| Transmission lines | Device26,120,133 |
| Modeling48,192 | |
| PNP modelling/equivalent circuit | Device characterization68 |
| Without description | Device29,110,134,151,212,213 |
| Electrode137 | |
| Capacitance136 | |
| Ionic conductivity102,128,129,131,150,161–163 |
4. Model proposal
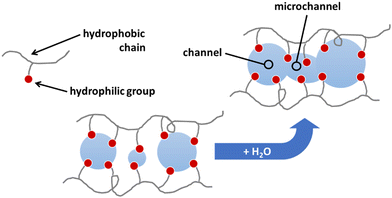
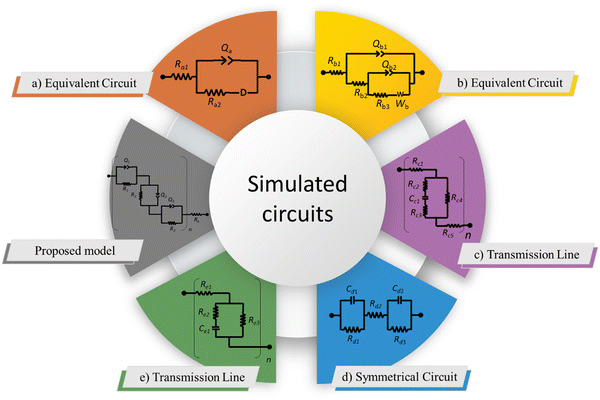
For the proposal of a new model, the morphology of the ionomeric polymer membranes should be considered. Although there is no definitive model on how ionomeric channels are organized, some models can be cited.214 Among them, the Cluster-Network, proposed by Gierke et al.,215,216 and the Phase-separation, proposed by Gebel,217 are the most accepted models. Both agree that after a certain degree of hydration, the structure is a percolated network of channels containing water molecules and solvated mobile ions (Fig. 5).Thus, starting from the definition of the transmission line models, it is easy to use this approach to model these ionomer channels. As both models about ionomeric polymers point out, there are two types of channels: the channels themselves and the microchannels that connect them. They have different contributions to the total impedance of the system since the ion mobility in both is different. In addition, it was also considered that the channels could be opened or closed for the electrodes. Therefore, these two conditions contribute to the electrode interface processes, varying the double-layer capacitance.
The current resulting from the AC disturbance at the different branches can flow in any direction along the two media considered. Besides, the total electrical current that passes through the system is the current sum that passes through each system branch. Thus, following the law of electric current distribution,218 in each position of the transmission line, the currents in each branch vary on opposite sides; consequently, when one increases, the other decreases. Therefore, it only depends on the position being considered on the line. Consequently, the potential distribution will also be a function of the position (length L of the channel). With this in mind, we are applying the two-channel transmission lines model219,220 (eqn (3)).
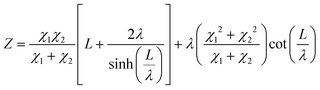 | (3) |
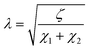 .
.
One of the branches refers to the open channels for the electrode (χ1), and the other branch refers to the closed channels for the electrode (χ2), and connecting both, there are the microchannels (ζ). Figure shows the circuit elements used to describe the impedance in the different channels.
In Fig. 6, it is possible to observe the new transmission line superimposed on our interpretation of the different proposed and accepted models of ionomeric channels. According to this model, there are two types of ionomeric channels, those with a large diameter (6 nm),221 and connecting these, there are micro-channels that are only a fraction of the size of the channels themselves. Furthermore, where considered consider 2 types of ionomeric channels: open and closed. The open ones are located at the edges of the polymer, they have Pt dendritic electrodes inside and consequently, they have greater water availability inside, probably exhibiting a slightly larger diameter. To describe this channel, in addition to the RionomericQionomeric that describes ionic mobility, there is also the resistance attributed to this dendritic electrode (Relec), which because of its tortuous shape, generally results in a delay between its polarization and the arrival of the ion at the active site. In turn, the closed channels are found more in the bulk of the polymer and are therefore described only by RionomericQionomeric, as all their impedance is due to ionic movement in a regime with a smaller amount of solvent than the open ionomeric channel, a higher impedance for this branch. Uniting both there are microchannels, also described only by a RmicroQmicro, whose small width leads to greater impedance.
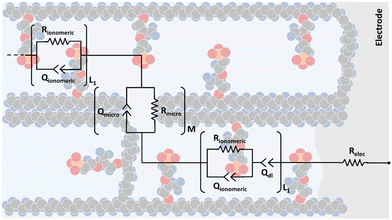 | ||
| Fig. 6 Proposed transmission line model representation considering the morphology of an ionomeric polymer, in this case, Nafion. | ||
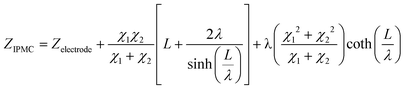
Therefore, elements χ1, χ2, and ζ are represented by eqn (4), (5) and (6), respectively. In turn, the general equation (eqn (7)) that describes the model should also add, in series, the elements that describe the electrode. Resistance is sufficient in a common metallic electrode; more complex electrodes will need more complex circuit elements to be described.
 | (4) |
 | (5) |
 | (6) |
 | (7) |
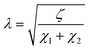 and L = L1 + L2.
and L = L1 + L2.
Each channel is represented by a parallel RC circuit, in which the capacitance is replaced by a constant phase element (Q). This approach was used to represent both the delay in ionic migration and its difficulty in occurring in a hindrance region. As the average size of the microchannels is about 2–3 times smaller than the channels themselves, greater resistance and lower capacitance are expected. In addition, open channels for the electrodes can suffer water loss more easily, either due to cracks in the electrode or electrolysis; thus, resistance and capacitance should be different from closed channels. Therefore, to validate and verify the performance of this model, different conditions of relative humidity and counterions were studied in the next subsection.
4.1. Application and validation
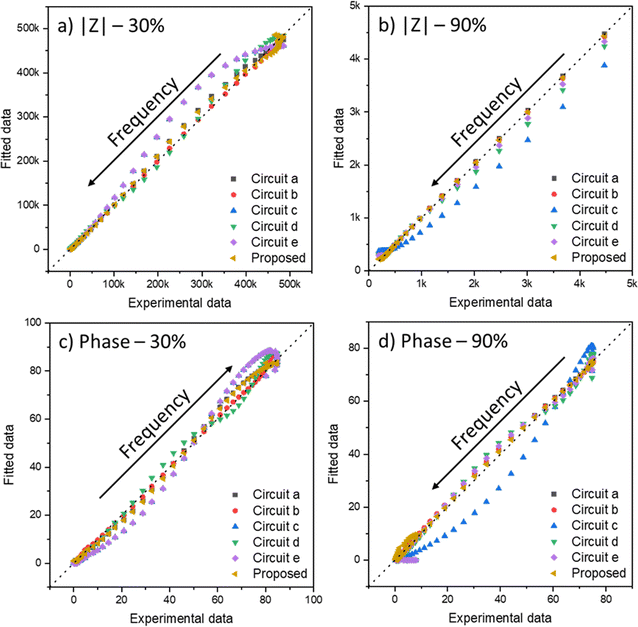
The IPMC assembling method was performed in previous works.54,221 The measurements were carried out in a two-electrode configuration inside a Faraday cage with a controlled atmosphere humidity by an Arduino-based system, also described before.54 The impedance data were obtained using a Solartron frequency response analyzer (model 1260A, from Princeton Applied Research). The frequency was swept from 10 MHz to 400 mHz with an AC perturbation of 10 mV at 0.0 bias potential. Then, the data were adjusted using the least-squares regression approach applied to the proposed equation in a numeric computing platform, MATLAB. Two relative humidities (RH, 30%, and 90%) and three counterions (H+, Li+, and Na+) were compared to verify the model's versatility and applicability.The fit of data with multiple variables is usually done using the least-squares method. This mathematical optimization technique seeks to find the best fit for a data set to minimize the sum of squares of the differences between the estimated value and the observed data. However, depending on the number of variables, it is possible that when adjusting, there is a local minimum; that is, the method does not find the best fit for the data set, but it gets stuck in an adjustment that has good values, but that is still not ideal. Thus, using iterative methods, it is necessary to make several calculations to confirm that the fit found is the absolute minimum of the system. With this care taken, the method is quite robust to deal with any data type, as long as the given equation is valid for the system in question.
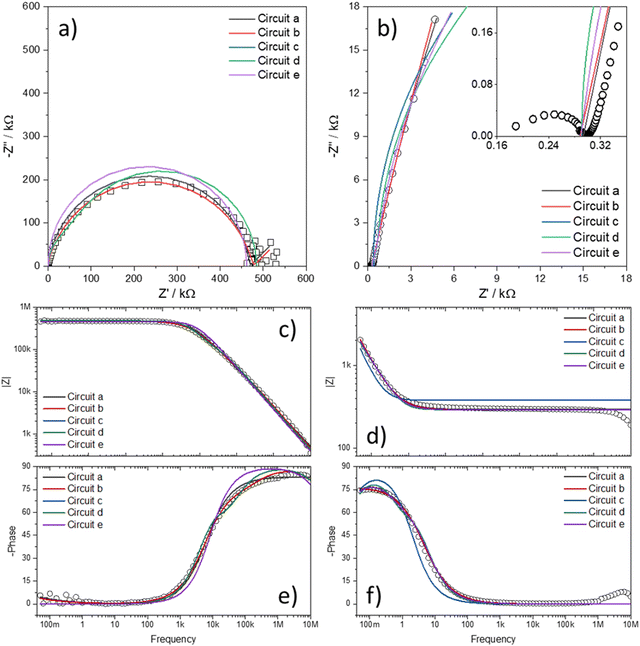
Fig. 7 shows the Nyquist plots of several IPMC samples under different moisture and counter-ion conditions with the proposed model's adjustment. Disregarding the noise presented at low frequencies for a 30% IPMC-H+ sample, the model fits well both in low and high frequencies, as seen in the figures' inset graphics.
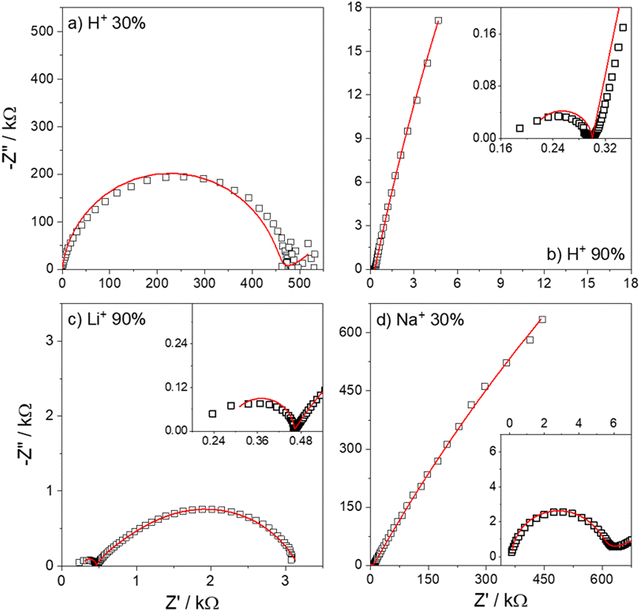 | ||
| Fig. 7 Nyquist spectra of IPMC samples with (a) H+ at 30% RH and (b) H+, (c) Li+, and (d) Na+ at 90% RH. The data is presented in black squares (□) and the fit as the red line (—). | ||
In electrochemical impedance data analysis, it is also possible to attest to the good adjustment of the data by observing the Bode graphs, particularly the Bode Phase, which is more sensitive to the adjustment quality. Thus, in Fig. 8, it is possible to observe the Bode graphs for all IPMC samples. The adjustments are satisfactory throughout the frequency window, even at high frequency, which tends to present many problems, as discussed below. In addition, the χ2, which measures the quality of the fit, was below 1 × 10−4 in all cases. Table 3 shows the fitting statistics.
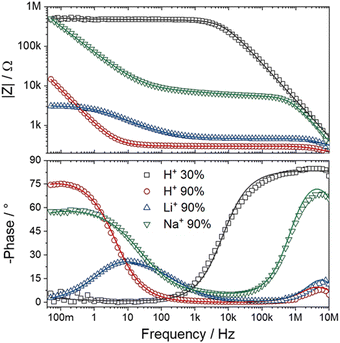 | ||
| Fig. 8 Bode total impedance (above) and Bode phase (below) of each IPMC-cation in 30% and 90% RH (for H+). The data are represented by symbols and the adjustments by lines. | ||
| Data | χ 2 | R 2 | Mean of residues (%) |
|---|---|---|---|
| IPMC-H+ at 30% | 9.87 × 10−5 | 0.9841 | 7.24 |
| IPMC-H+ at 90% | 6.23 × 10−5 | 0.9953 | 3.18 |
| IPMC-Li+ at 90% | 8.12 × 10−5 | 0.9956 | 5.23 |
| IPMC-Na+ at 90% | 2.26 × 10−5 | 0.9991 | 3.51 |
Fig. 9 presents the most frequently cited models in the literature for impedance data adjustment, ranging from equivalent circuits (models a, b, c, and d) to transmission line models (models e and f). In Fig. 9a, a modified Randles circuit is presented. The D element describes the diffusional part of the system and can be either a Warburg, an ideal capacitor, or a constant phase element (CPE).74,78,188Fig. 9b presents a very recurrent model for composite materials in which there is a measurable impedance difference between the different phases of the material.74 Model c and d are symmetric circuits in which the RC in parallel describes both IPMC electrodes' response and the device resistance represented by Rd2 and Rd1, respectively.75 Finally, the e and f models are transmission lines used to predict the response of motion sensors by impedance.141,209 The model is a symmetrical version of the e model. The electrode resistance is respectively Rc1 and Rc5. In contrast, the property of the IPMC charge storage is represented by the capacitance, and the ohmic loss for the electrodes is described by the resistors Rc1 and Rc3. The Rc4, parallel to the capacitor Cc1, is related to the capacitive-resistive response that IPMCs usually exhibit.
It is important to mention that the Randles circuit fits a wide data range very well; however, the Warburg element must be used cautiously, as it is a special and specific case of a CPE. Furthermore, it describes the diffusion process of species free to be transported from the bulk of the solution to the electrode surface and vice versa, which does not occur within the ionomeric channels since space is limited. Also, using an ideal capacitor in the model must be done with a careful analysis of the obtained data. Using a constant phase element is always preferable because when it has a coefficient n = 1, its response is the same as that of an ideal capacitor. When the semicircle in Nyquist has any deformity, that is, it is not a perfect semicircle; the response of the CPE will never be ideal. As shown in Fig. 7, they all have some deformities, so an ideal capacitor would not provide a good fit. Since both capacitor and constant phase element refer to the same electrochemical response type, electron flow delay, and charge separation have the same physical meaning when proposing the model.
With these considerations in mind, the models presented above were used to fit the IPMC-H+ data, the most common cation used in IPMCs, at two extremes: 30% and 90% humidity. It is known that IPMC works best at high relative humidity, with 90% therefore being the most used humidity in the characterization of these devices. Thus, 30% was chosen to make a counterpoint for a better comparison. The models were also fitted using the least-squares regression approach applied to the corresponding equations. Fig. 10a and b present the Nyquist graphs at 30% and 90%, respectively. The adjustments of the different models are represented as lines, in which it is possible to see that the adjustment of 30% was only satisfactory for models a and b.
In comparison, in 90%, no model was able to adjust the data at high frequency, at which the resistive-capacitive response lies. At low frequencies, only models a and b appear to fit successfully. However, observing Fig. 10c and d, where the Bode graphs are shown, it is evident that no model could fit the data at high frequency, especially for the 90% data. However, as mentioned above, circuits a and b adjusted better than the others.
In Fig. 11, the correlation graphs were obtained by the fit versus the experimentally observed values to clarify the performance of the studied models. Thus, as the fit gets better, the closer the calculated points will be to the experimental value, being presented closer to the diagonal dotted line that divides the graph in half. Note that data noise at 30% was disregarded. Although the proposed model showed performance and adjustment much better than the other models, it is remarkable that there are deviations from the best correlation, in the |Z| at 30% low frequency and Phase angle at 90% at high frequency. Also, Table 4 presents the adjustment statistics for better comparison. Note that all have great values of R2 (above 0.96), although the fit is not so good compared to the other values from Table 3. Therefore, the R2 value is not a reliable parameter to judge the quality of the fit.
| Model | IPMC-H+ at 30% | IPMC-H+ at 90% | ||||
|---|---|---|---|---|---|---|
| χ 2 | R 2 | Residuesa (%) | χ 2 | R 2 | Residuesa (%) | |
| a Average of residues. | ||||||
| a | 1.81 × 10−4 | 0.9811 | 8.61 | 1.07 × 10−4 | 0.9945 | 6.16 |
| b | 6.34 × 10−4 | 0.9754 | 8.48 | 1.36 × 10−4 | 0.9968 | 9.62 |
| c | 5.22 × 10−4 | 0.9801 | 15.1 | 7.10 × 10−4 | 0.9562 | 16.6 |
| d | 3.52 × 10−4 | 0.9821 | 16.8 | 4.13 × 10−4 | 0.9952 | 12.8 |
| e | 9.79 × 10−4 | 0.9476 | 9.61 | 2.27 × 10−4 | 0.9842 | 10.5 |
| Proposed | 9.87 × 10−5 | 0.9841 | 7.24 | 6.23 × 10−5 | 0.9953 | 3.18 |
As mentioned during the presentation of the new model, the models found in the literature generally performed very well in adjusting the data for which they were proposed but were not suitable for the data presented in this manuscript, as noted above. Thus, this article proposes this new model and presents the equation that governs it so that more data can be adjusted to explore its robustness or contribute to its refinement.
In this new model, it is possible to perceive the contributions of different branches to the total impedance of the device. As the polymer acquires water molecules, that is, it operates in more humid environments, it is expected that the total impedance of the system will decrease, but in addition, the so-called open ionomeric channels will suffer a much more pronounced reduction in their Z value, mainly in the first moments of change in relative humidity, which are therefore more impactful on the rapid response of the IPMC at high humidity. Likewise, microchannels will have a more significant influence at high humidity, as their existence is closely linked to the formation of a percolated network of ionomeric channels, which is only achieved after a given amount of water is absorbed by Nafion. Furthermore, it will be possible to perceive the influence of the electrode deposited on the Nafion, as it is now possible to see its individual contribution to the total impedance of the device. However, we draw attention to the fact that, depending on the electrode used, a simple resistance may not be enough to overcome its complexity.
5. Final considerations
The fact that composites of the IPMC type are so versatile and have a range of properties that make them great candidates for smooth actuators, strain sensors with great sizing capacity, and energy-collecting devices is due to their unique electromechanical and electrochemical characteristics. However, such features are still far from fully explained and modeled, making gray-box models the furthest away in this regard. Robust electrical and electrochemical models must be developed as mechanical models to simulate and explain IPMCs completely. In this sense, electrochemical impedance spectroscopy is a tool that allows understanding the electrochemical phenomena related to their properties. However, most of the articles found in the literature that mention electrochemical impedance spectroscopy as a characterization technique in IPMCs lack a complete aim to understand this composite's particularities better. On the other hand, the lack of definitive models for fitting EIS data prevents less experienced users of the technique from further using its capabilities.Several models in the literature work very well; however, they have limitations or do not work for a wider range of relative humidities, counterions, or IPMC operating potentials. In this sense, the model presented here intends to be a complete model that works in a wider range of operational possibilities that the IPMC may face. The transmission line method fits very well with the internal structure of the ionomeric polymer. It allows the observation of some interesting phenomena that occur when changing its hydration degree and the counterion.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001 and CNPq. The authors would also like to thank Capes (process #88887.612843/2021-00, #23038.021524/2016-88, #88887.569936/2020-00 and #88887.569936/2020-00) and FAPESP (process #2018/07001-6, #2018/10843-9, #2018/09761-8 and #2020/02696-6) funding agencies.References
- Y. Cha, F. Cellini and M. Porfiri, Electrical impedance controls mechanical sensing in ionic polymer metal composites, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 1–12, DOI:10.1103/PhysRevE.88.062603.
- M. Ates, Review study of electrochemical impedance spectroscopy and equivalent electrical circuits of conducting polymers on carbon surfaces, Prog. Org. Coat., 2011, 71, 1–10, DOI:10.1016/j.porgcoat.2010.12.011.
- H. Herrera Hernández, A. M. Ruiz Reynoso, J. C. Trinidad González, et al., Electrochemical Impedance Spectroscopy (EIS): A Review Study of Basic Aspects of the Corrosion Mechanism Applied to Steels, Electrochemical Impedance Spectroscopy, IntechOpen, 2020 Search PubMed.
- R. Gonçalves, R. S. Paiva and E. C. Pereira, Calculation of real growth current using variable electroactive area obtained during polypyrrole synthesis, J. Solid State Electrochem., 2021, 25, 1567–1577, DOI:10.1007/s10008-021-04938-6.
- R. Gonçalves, A. A. Correa, R. Pereira and E. C. Pereira, Investigation of the electrochemical aging of poly(3-hexiltiophene) using impedance spectroscopy, Electrochim. Acta, 2016, 190, 329–336, DOI:10.1016/j.electacta.2015.12.198.
- W. A. Marmisollé, M. Inés Florit and D. Posadas, Electrochemically induced ageing of polyaniline. An electrochemical impedance spectroscopy study, J. Electroanal. Chem., 2012, 673, 65–71, DOI:10.1016/j.jelechem.2012.03.016.
- A. Pron and P. Rannou, Processible conjugated polymers: from organic semiconductors to organic metals and superconductors, Prog. Polym. Sci., 2002, 27, 135–190, DOI:10.1016/S0079-6700(01)00043-0.
- G. Garcia-Belmonte, A. Munar and E. M. Barea, et al., Charge carrier mobility and lifetime of organic bulk heterojunctions analyzed by impedance spectroscopy, Org. Electron., 2008, 9, 847–851, DOI:10.1016/j.orgel.2008.06.007.
- J. Bisquert, D. Cahen and G. Hodes, et al., Physical chemical principles of photovoltaic conversion with nanoparticulate, mesoporous dye-sensitized solar cells, J. Phys. Chem. B, 2004, 108, 8106–8118, DOI:10.1021/jp0359283.
- D. D. Macdonald, Reflections on the history of electrochemical impedance spectroscopy, Electrochim. Acta, 2006, 51, 1376–1388, DOI:10.1016/j.electacta.2005.02.107.
- D. A. Buttry and M. D. Ward, Measurement of interfacial processes at electrode surfaces with the electrochemical quartz crystal microbalance, Chem. Rev., 1992, 92, 1355–1379, DOI:10.1021/cr00014a006.
- H. H. Hernández, A. M. Ruiz Reynoso, J. C. Trinidad González, et al., Electrochemical Impedance Spectroscopy (EIS): A Review Study of Basic Aspects of the Corrosion Mechanism Applied to Steels, Electrochemical Impedance Spectroscopy, IntechOpen, 2020 Search PubMed.
- Y. Jung, S. J. Kim, K. J. Kim and D. Y. Lee, Characteristics of ionic polymer-metal composite with chemically doped TiO2 particles, Smart Mater. Struct., 2011, 20, 12, DOI:10.1088/0964-1726/20/12/124004.
- L. S. R. Rocha, F. Schipani and C. M. Aldao, Experimental and ab Initio Studies of Deep-Bulk Traps in Doped Rare-Earth Oxide Thick Films, J. Phys. Chem. C, 2019, 124(1), 997–1007, DOI:10.1021/acs.jpcc.9b07217.
- D. Kim and K. J. Kim, Electrochemistry of ionic polymer-metal composite, Smart Structures and Materials 2005: Electroactive Polymer Actuators and Devices (EAPAD), 2005, vol. 5759, p. 464 DOI:10.1117/12.592054.
- R. Tiwari, S.-M. Kim and K. Kim, Variable Thickness IPMC: Capacitance Effect on Energy Harvesting, MRS Proc., 2008, 1129, 1129-V06-05, DOI:10.1557/PROC-1129-V06-05.
- V. Panwar, K. Cha, J. O. Park and S. Park, High actuation response of PVDF/PVP/PSSA based ionic polymer metal composites actuator, Sens. Actuators, B, 2012, 161, 460–470, DOI:10.1016/j.snb.2011.10.062.
- Y. Wang, J. Liu and Y. Zhu, et al., Formation and Characterization of Dendritic Interfacial Electrodes inside an Ionomer, ACS Appl. Mater. Interfaces, 2017, 9, 30258–30262, DOI:10.1021/acsami.7b08012.
- M. Gudarzi, P. Smolinski and Q. M. Wang, Bending mode ionic polymer-metal composite (IPMC) pressure sensors, Measurement, 2017, 103, 250–257, DOI:10.1016/j.measurement.2017.02.029.
- Y. Bar Cohen, S. Sherrit and S.-S. Lih, Characterization of the electromechanical properties of EAP materials, in Smart Structures and Materials 2001: Electroactive Polymer Actuators and Devices, ed. Y. Bar-Cohen, 2001, p 319 Search PubMed.
- Y. Bar-Cohen, X. Bao, S. Sherrit and S.-S. Lih, Characterization of the electromechanical properties of ionomeric polymer-metal composite (IPMC), 2002, vol. 4695, pp. 286–293 DOI:10.1117/12.475173.
- S. P. Leary and Y. Bar-Cohen, Electrical impedence of ionic polymeric metal composites, Smart Structures and Materials 1999: Electroactive Polymer Actuators and Devices, 1999, vol. 3669, pp. 81–86 DOI:10.1117/12.349713.
- M. C. Wintersgill and J. J. Fontanella, Complex impedance measurements on Nafion, Electrochim. Acta, 1998, 43, 1533–1538, DOI:10.1016/S0013-4686(97)10049-4.
- M. Shahinpoor and K. J. Kim, Effect of surface-electrode resistance on the performance of ionic polymer-metal composite (IPMC) artificial muscles, Smart Mater. Struct., 2000, 9, 543–551, DOI:10.1088/0964-1726/9/4/318.
- A. Punning, M. Anton, M. Kruusmaa and A. Aabloo, Empirical model of a bending IPMC actuator, in Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD), ed. Y. Bar-Cohen, 2006, p. 61681V Search PubMed.
- M. Shahinpoor and K. J. Kim, Effect of surface-electrode resistance on the performance of ionic polymer-metal composite (IPMC) artificial muscles, Smart Mater. Struct., 2000, 9, 543–551, DOI:10.1088/0964-1726/9/4/318.
- T. Noh, Y. S. Tak, J. Nam, et al., Development of large-surface Nafion-metal composite actuator and its electrochemical characterization, Smart Structures and Materials 2001: Electroactive Polymer Actuators and Devices, 2001, vol. 4329, p. 458 DOI:10.1117/12.432661.
- T. G. Noh, Y. Tak, J. Do Nam and H. Choi, Electrochemical characterization of polymer actuator with large interfacial area, Electrochim. Acta, 2002, 47, 2341–2346, DOI:10.1016/S0013-4686(02)00089-0.
- T. Noh, Y. S. Tak, J. Nam, et al., Development of large-surface Nafion-metal composite actuator and its electrochemical characterization, Smart Structures and Materials 2001: Electroactive Polymer Actuators and Devices, 2001, vol. 4329, p. 458 DOI:10.1117/12.432661.
- A. Gupta and S. Mukherjee, Dynamic modeling of biomimetic undulatory ribbon fin underwater propulsor actuated by IPMC, Mater. Today: Proc., 2021, 44, 1086–1089, DOI:10.1016/j.matpr.2020.11.183.
- D. Kim and K. J. Kim, Experimental investigation on electrochemical properties of ionic polymer-metal composite, J. Intell. Mater. Syst. Struct., 2006, 17, 449–454, DOI:10.1177/1045389X06058871.
- M. Shahinpoor, in Electromechanics of ionoelastic beams as electrically controllable artificial muscles, ed. Y. Bar-Cohen, 1999, pp. 109–121 Search PubMed.
- S. Tadokoro, M. Konyo and K. Oguro, Modeling IPMC for Design of Actuation Mechanisms, Electroactive Polymer (EAP) Actuators as Artificial Muscles: Reality, Potential, and Challenges, 2nd SPIE, 1000 20th Street, Bellingham, WA 98227-0010 USA, pp. 385–427.
- J.-W. Lee, K. N. Vinh, S. Park and Y. Yoo, in Effect of reduction temperature on electrode formation and performance of ionic polymer metal composites, ed. Y. Bar-Cohen, 2006, p. 616825 Search PubMed.
- M. Aureli and M. Porfiri, Effect of electrode surface roughness on the electrical impedance of ionic polymer-metal composites, Smart Mater. Struct., 2012, 21, 105030, DOI:10.1088/0964-1726/21/10/105030.
- Y. Cha and M. Porfiri, Charge dynamics of ionic polymer metal composites in response to electrical bias, Electroactive Polymer Actuators and Devices (EAPAD), 2013, vol. 8687, p. 868721 DOI:10.1117/12.2009062.
- M. A. Buechler and D. J. Leo, Characterization and Variational Modeling of Ionic Polymer Transducers, J. Vib. Acoust., 2007, 129, 113–120, DOI:10.1115/1.2424973.
- N. W. Hagood, W. H. Chung and A. Von Flotow, Modelling of Piezoelectric Actuator Dynamics for Active Structural Control, J. Intell. Mater. Syst. Struct., 1990, 1, 327–354, DOI:10.1177/1045389X9000100305.
- K. Takagi, Y. Nakabo, Z.-W. Luo and K. Asaka, On a distributed parameter model for electrical impedance of ionic polymer, Electroactive Polymer Actuators and Devices, 2007, vol. 6524, p. 652416 DOI:10.1117/12.715554.
- J. Brufau-Penella, M. Puig-Vidal and P. Giannone, et al., Characterization of the harvesting capabilities of an ionic polymer metal composite device, Smart Mater. Struct., 2008, 17, 015009, DOI:10.1088/0964-1726/17/01/015009.
- Z. Chen and X. Tan, A control-oriented and physics-based model for ionic polymer-metal composite actuators, IEEE/ASME Trans. Mechatron., 2008, 13, 519–529, DOI:10.1109/TMECH.2008.920021.
- R. Dong and X. Tan, Modeling and open-loop control of IPMC actuators under changing ambient temperature, Smart Mater. Struct., 2012, 21, 065014, DOI:10.1088/0964-1726/21/6/065014.
- C. Lim, H. Lei and X. Tan, Characterization and modeling of humidity-dependence of IPMC sensing dynamics, Electroactive Polymer Actuators and Devices (EAPAD), SPIE, 2013, p. 868720 Search PubMed.
- R. Caponetto, S. Graziani, F. L. Pappalardo and F. Sapuppo, Experimental characterization of ionic polymer metal composite as a novel fractional order element, Adv. Math. Phys., 2013, 953695, DOI:10.1155/2013/953695.
- R. Tiwari and K. J. Kim, Improved IPMC sensing by use of cation and through induced nano-to-micro scale surface cracks, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, 2008, vol. 6932, p. 69323H DOI:10.1117/12.776052.
- Z. Chen and X. Tan, A scalable dynamic model for ionic polymer-metal composite actuators, Electroactive Polymer Actuators and Devices (EAPAD), 2008, vol. 6927, p. 69270I DOI:10.1117/12.776508.
- R. Tiwari and K. J. Kim, IPMC as a mechanoelectric energy harvester: tailored properties, Smart Mater. Struct., 2013, 22, 015017, DOI:10.1088/0964-1726/22/1/015017.
- Y. Cha, F. Cellini and M. Porfiri, Electrical impedance controls mechanical sensing in ionic polymer metal composites, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 1–12, DOI:10.1103/PhysRevE.88.062603.
- W. Aoyagi and M. Omiya, Mechanical and electrochemical properties of an IPMC actuator with palladium electrodes in acid and alkaline solutions, Smart Mater. Struct., 2013, 22, 055028, DOI:10.1088/0964-1726/22/5/055028.
- T. Yamaue, H. Mukai, K. Asaka and M. Doi, Electrostress diffusion Coupling Model for Polyelectrolyte Gels, Macromolecules, 2005, 38(4), 1349–1356, DOI:10.1021/ma047944j.
- P. G. De Gennes, K. Okumura, M. Shahinpoor and K. J. Kim, Mechanoelectric effects in ionic gels, Europhys. Lett., 2000, 50, 513–518, DOI:10.1209/epl/i2000-00299-3.
- R. Tiwari and K. J. Kim, Disc-shaped IPMC for use in energy harvesting, Behavior and Mechanics of Multifunctional Materials and Composites, 2009, vol. 7289, p. 72891G DOI:10.1117/12.816100.
- R. Tiwari and K. J. Kim, Disc-shaped ionic polymer metal composites for use in mechano-electrical applications, Smart Mater. Struct., 2010, 19, 065016, DOI:10.1088/0964-1726/19/6/065016.
- R. Gonçalves, K. A. Tozzi and M. C. Saccardo, et al., Nafion-based ionomeric polymer/metal composites operating in the air: theoretical and electrochemical analysis, J. Solid State Electrochem., 2020, 24, 1845–1856, DOI:10.1007/s10008-020-04520-6.
- J. Wang, C. Xu, M. Taya and Y. Kuga, Flemion-based actuator with ionic liquid as solvent. Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD), 2006, vol. 6168, p. 61680R DOI:10.1117/12.658548.
- M. Bennett, D. Leo, V. Tech and D. Hall, Morphological and Electromechanical Characterization of Ionic Liquid/Nafion Polymer Composites, 2005, vol. 5759, pp. 506–517 DOI:10.1117/12.599849.
- M. D. Bennett and D. J. Leo, Ionic liquids as stable solvents for ionic polymer transducers, Sens. Actuators, A, 2004, 115, 79–90, DOI:10.1016/j.sna.2004.03.043.
- K. Kikuchi and S. Tsuchitani, Nafion®-based polymer actuators with ionic liquids as solvent incorporated at room temperature, J. Appl. Phys., 2009, 106, 53519, DOI:10.1063/1.3204961.
- K. Takagi, N. Yamaguchi and K. Asaka, PWM drive of IPMC actuators with the consideration of the capacitive impedance, Electroactive Polymer Actuators and Devices (EAPAD), 2011, vol. 7976, p. 79762L DOI:10.1117/12.880360.
- M. O. Diab, N. F. Al Awar, M. Atiehet al., Electromechanical model of IPMC artificial muscle, in 2014 World Symposium on Computer Applications & Research (WSCAR), IEEE, 2014, pp. 1–5.
- G.-H. Feng and K.-M. Liu, Fabrication and Characterization of a Micromachined Swirl-Shaped Ionic Polymer Metal Composite Actuator with Electrodes Exhibiting Asymmetric Resistance, Sensors, 2014, 14, 8380–8397, DOI:10.3390/s140508380.
- A. Punning, M. Kruusmaa and A. Aabloo, A self-sensing ion conducting polymer metal composite (IPMC) actuator, Sens. Actuators, A, 2007, 136, 656–664, DOI:10.1016/j.sna.2006.12.008.
- S. R. Li, Z. D. Dai and M. Yu, Preliminary study on self-sensing method for ion-conductive polymer metal composite (IPMC) actuator based on current detection, Appl. Mech. Mater., 2014, 461, 967–971, DOI:10.4028/www.scientific.net/AMM.461.967.
- V. Palmre, S. J. Kim, D. Pugal and K. Kim, Improving electromechanical output of IPMC by high surface area Pd-Pt electrodes and tailored ionomer membrane thickness, Int. J. Smart Nano Mater., 2014, 5, 99–113, DOI:10.1080/19475411.2014.914108.
- I. Must, V. Vunder and F. Kaasik, et al., Ionic liquid-based actuators working in air: The effect of ambient humidity, Sens. Actuators, B, 2014, 202, 114–122, DOI:10.1016/j.snb.2014.05.074.
- V. Palmre, D. Brandell and U. Mäeorg, et al., Nanoporous carbon-based electrodes for high strain ionomeric bending actuators, Smart Mater. Struct., 2009, 18, 095028, DOI:10.1088/0964-1726/18/9/095028.
- Y. Cha, H. Kim and M. Porfiri, In fluence of temperature on the impedance of ionic polymer metal composites, Mater. Lett., 2014, 133, 179–182, DOI:10.1016/j.matlet.2014.06.183.
- Y. Cha, M. Aureli and M. Porfiri, A physics-based model of the electrical impedance of ionic polymer metal composites, J. Appl. Phys., 2012, 111, 124901, DOI:10.1063/1.4729051.
- Y. Cha, H. Kim and M. Porfiri, Matching the impedance of ionic polymer metal composites for energy harvesting, Smart Mater. Struct., 2014, 23, 127002, DOI:10.1088/0964-1726/23/12/127002.
- Q. Liu, L. Liu and K. Xie, et al., Synergistic effect of a r-GO/PANI nanocomposite electrode based air working ionic actuator with a large actuation stroke and long-term durability, J. Mater. Chem. A, 2015, 3, 8380–8388, 10.1039/c5ta00669d.
- L. Lu, J. Liu and Y. Hu, et al., Highly Stable Air Working Bimorph Actuator Based on a Graphene Nanosheet/Carbon Nanotube Hybrid Electrode, Adv. Mater., 2012, 24, 4317–4321, DOI:10.1002/adma.201201320.
- F. Cellini, A. Grillo and M. Porfiri, Ionic polymer metal composites with polypyrrole-silver electrodes, Appl. Phys. Lett., 2015, 106, 131902, DOI:10.1063/1.4916672.
- V. Panwar, K. Cha, J. O. Park and S. Park, High actuation response of PVDF/PVP/PSSA based ionic polymer metal composites actuator, Sens. Actuators, B, 2012, 161, 460–470, DOI:10.1016/j.snb.2011.10.062.
- H. Rasouli, L. Naji and M. G. Hosseini, Electrochemical and electromechanical behavior of Nafion-based soft actuators with PPy/CB/MWCNT nanocomposite electrodes, RSC Adv., 2017, 7, 3190–3203, 10.1039/C6RA25771B.
- W. Hong, A. Almomani and R. Montazami, Electrochemical and morphological studies of ionic polymer metal composites as stress sensors, Measurement, 2017, 95, 128–134, DOI:10.1016/j.measurement.2016.09.036.
- Z. He, S. Jiao and Z. Wang, et al., An Antifatigue Liquid Metal Composite Electrode Ionic Polymer-Metal Composite Artificial Muscle with Excellent Electromechanical Properties, ACS Appl. Mater. Interfaces, 2022, 14, 14630–14639, DOI:10.1021/acsami.2c01453.
- Y. Ming, Y. Yang and R. P. Fu, et al., IPMC Sensor Integrated Smart Glove for Pulse Diagnosis, Braille Recognition, and Human–Computer Interaction, Adv. Mater. Technol., 2018, 3, 1800257, DOI:10.1002/admt.201800257.
- A. Kodaira, K. Asaka and T. Horiuchi, et al., IPMC Monolithic Thin Film Robots Fabricated Through a Multi-Layer Casting Process, IEEE Robot Autom. Lett., 2019, 4, 1335–1342, DOI:10.1109/LRA.2019.2895398.
- P. V. P. Agnps, F. Wang and X. Zhang, Facile and effective repair of Pt/Nafion IPMC actuator by dip-coating of Facile and effective repair of Pt/Nafion IPMC actuator by dip-coating of PVP @, AgNPs, 2021 Search PubMed.
- L. Dai, L. Li and Y. Zhang, Microstructure effects on proton conductivity in EVOH based ionic polymer-metal composites actuator, International Conference on Smart Materials and Nanotechnology in Engineering, 2007, vol. 6423, p. 64230X DOI:10.1117/12.779354.
- J. E. Puskas and G. Kaszas, Polyisobutylene-Based Thermoplastic Elastomers: A Review, Rubber Chem. Technol., 1996, 69, 462–475, DOI:10.5254/1.3538381.
- Inamuddin, A. Khan, M. Luqman and A. Dutta, Kraton based ionic polymer metal composite (IPMC) actuator, Sens. Actuators, A, 2014, 216, 295–300, DOI:10.1016/j.sna.2014.04.015.
- A. Khan, R. K. Jain and M. Naushad, Fabrication of a silver nano powder embedded kraton polymer actuator and its characterization, RSC Adv., 2015, 5, 91564–91573, 10.1039/C5RA17776F.
- A. Khan, R. K. Jain and P. Banerjee, Soft actuator based on Kraton with GO/Ag/Pani composite electrodes for robotic applications, Mater. Res. Express, 2017, 4, 115701, DOI:10.1088/2053-1591/aa9394.
- A. Khan, R. K. Jain and P. Banerjee, Development, Characterization and Electromechanical Actuation Behavior of Ionic Polymer Metal Composite Actuator based on Sulfonated Poly(1,4-phenylene ether-ether-sulfone)/Carbon Nanotubes, Sci. Rep., 2018, 8, 1–16, DOI:10.1038/s41598-018-28399-6.
- A. J. Duncan, S. A. Sarles and D. J. Leo, Optimization of active electrodes for novel ionomer-based ionic polymer transducers, Electroactive Polymer Actuators and Devices (EAPAD), 2008, vol. 6927 Search PubMed.
- C. K. Chung, P. K. Fung and Y. Z. Hong, A novel fabrication of ionic polymer-metal composites (IPMC) actuator with silver nano-powders, Sens. Actuators, B, 2006, 117, 367–375, DOI:10.1016/j.snb.2005.11.021.
- B. J. Akle, M. D. Bennett and D. J. Leo, High-strain ionomeric-ionic liquid electroactive actuators, Sens. Actuators, A, 2006, 126, 173–181, DOI:10.1016/j.sna.2005.09.006.
- Y. Jung, S. J. Kim, K. J. Kim and D. Y. Lee, Characteristics of ionic polymer-metal composite with chemically doped TiO2particles, Smart Mater. Struct., 2011, 20, 124004, DOI:10.1088/0964-1726/20/12/124004.
- M. Safari, L. Naji, R. T. Baker and F. A. Taromi, The enhancement effect of lithium ions on actuation performance of ionic liquid-based IPMC soft actuators, Polymer, 2015, 76, 140–149, DOI:10.1016/j.polymer.2015.09.004.
- J. Ru, Y. Wang and L. Chang, Preparation and characterization of water-soluble carbon nanotube reinforced Nafion membranes and so-based ionic polymer metal composite actuators, Smart Mater. Struct., 2016, 25, DOI:10.1088/0964-1726/25/9/095006.
- J. Ru, Y. Wang and L. Chang, Preparation and characterization of sulfonated carbon nanotube/Nafion IPMC actuators, in Electroactive Polymer Actuators and Devices (EAPAD), ed. Y. Bar-Cohen and F. Vidal, 2016, p. 97982Z Search PubMed.
- L. Naji, M. Safari and S. Moaven, Fabrication of SGO/Nafion-based IPMC soft actuators with sea anemone-like Pt electrodes and enhanced actuation performance, Carbon, 2016, 100, 243–257, DOI:10.1016/j.carbon.2016.01.020.
- J. W. Paquette and K. J. Kim, Ionomeric Electroactive Polymer Artificial Muscle for Naval Applications, IEEE J. Ocean. Eng., 2004, 29, 729–737, DOI:10.1109/JOE.2004.833132.
- W. Aoyagi and M. Omiya, Anion effects on the ion exchange process and the deformation property of ionic polymer metal composite actuators, Materials, 2016, 9, 479, DOI:10.3390/ma9060479.
- H. S. Wang, J. Cho and H. W. Park, Ionic polymer–metal composite actuators driven by methylammonium formate for high-voltage and long-term operation, J. Ind. Eng. Chem., 2021, 96, 194–201, DOI:10.1016/j.jiec.2021.01.021.
- M. Luqman, A. Anis and H. M. Shaikh, Development of a Soft Robotic Bending Actuator Based on a Novel Sulfonated Polyvinyl Chloride–Phosphotungstic Acid Ionic Polymer–Metal Composite (IPMC) Membrane, Membranes, 2022, 12, 651, DOI:10.3390/membranes12070651.
- M. Luqman, A. Anis and H. M. Shaikh, Synthesis, Characterization and Fabrication of Copper Nanoparticles Embedded Non-Perfluorintaed Kraton Based Ionic Polymer Metal Composite (IPMC) Actuator, Actuators, 2022, 11, 183, DOI:10.3390/act11070183.
- G. X. Yin, Q. S. He and M. Yu, et al., Ionic polymer metal composites actuators with enhanced driving performance by incorporating graphene quantum dots, J. Cent. South Univ., 2022, 29, 1412–1422, DOI:10.1007/s11771-022-5040-7.
- M. Luqman, H. Shaikh and A. Anis, et al., Platinum-coated silicotungstic acid-sulfonated polyvinyl alcohol-polyaniline based hybrid ionic polymer metal composite membrane for bending actuation applications, Sci. Rep., 2022, 12, 1–9, DOI:10.1038/s41598-022-08402-x.
- X. Zhang, S. Yu and M. Li, et al., Enhanced performance of IPMC actuator based on macroporous multilayer MCNTs/Nafion polymer, Sens. Actuators, A, 2022, 339, 113489, DOI:10.1016/j.sna.2022.113489.
- M. Luqman, H. M. Shaikh and A. Anis, A Convenient and Simple Ionic Polymer-Metal Composite (IPMC) Actuator Based on a Platinum-Coated Sulfonated Poly(Ether Ether Ketone)–Polyaniline Composite Membrane, Polymers, 2022, 14, 668, DOI:10.3390/polym14040668.
- S. N. Patel and S. Mukherjee, Manufacturing, characterization and experimental investigation of the IPMC shoe energy harvester, J. Braz. Soc. Mech. Sci. Eng., 2022, 44, 42, DOI:10.1007/s40430-021-03344-3.
- Y. Cha, S. Abdolhamidi and M. Porfiri, Energy harvesting from underwater vibration of an annular ionic polymer metal composite, Meccanica, 2015, 50, 2675–2690, DOI:10.1007/s11012-015-0165-5.
- M. Gudarzi, P. Smolinski and Q. M. Wang, Compression and shear mode ionic polymer-metal composite (IPMC) pressure sensors, Sens. Actuators, A, 2017, 260, 99–111, DOI:10.1016/j.sna.2017.04.010.
- M. Gudarzi, P. Smolinski and Q. M. Wang, Bending mode ionic polymer-metal composite (IPMC) pressure sensors, Measurement, 2017, 103, 250–257, DOI:10.1016/j.measurement.2017.02.029.
- W. Mohdisa, A. Hunt and S. H. Hosseinnia, Active sensing methods of ionic polymer metal composite (IPMC): Comparative study in frequency domain, RoboSoft 2019 – 2019 IEEE International Conference on Soft Robotics, Institute of Electrical and Electronics Engineers Inc., 2019, pp. 546–551.
- R. Histed, J. Ngo and O. A. Hussain, Ionic polymer metal composite compression sensors with 3D-structured interfaces, Smart Mater. Struct., 2021, 30, 125027, DOI:10.1088/1361-665X/ac3431.
- D. Kim and K. J. Kim, Electrochemistry of ionic polymer-metal composite, Smart Structures and Materials 2005: Electroactive Polymer Actuators and Devices (EAPAD), 2005, vol. 5759, p. 464 DOI:10.1117/12.592054.
- S. P. Leary and Y. Bar-Cohen, Electrical impedence of ionic polymeric metal composites, Smart Structures and Materials 1999: Electroactive Polymer Actuators and Devices, 1999, vol. 3669, pp. 81–86 DOI:10.1117/12.349713.
- A. Punning, M. Anton, M. Kruusmaa and A. Aabloo, Empirical model of a bending IPMC actuator, in Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD), ed. Y. Bar-Cohen, 2006, p. 61681V Search PubMed.
- D. Kim and K. J. Kim, Experimental investigation on electrochemical properties of ionic polymer-metal composite, J. Intell. Mater. Syst. Struct., 2006, 17, 449–454, DOI:10.1177/1045389X06058871.
- J. Brufau-Penella, M. Puig-Vidal and P. Giannone, Characterization of the harvesting capabilities of an ionic polymer metal composite device, Smart Mater. Struct., 2008, 17, 015009, DOI:10.1088/0964-1726/17/01/015009.
- R. Caponetto, S. Graziani, F. L. Pappalardo and F. Sapuppo, Experimental characterization of ionic polymer metal composite as a novel fractional order element, Adv. Math. Phys., 2013, 953695, DOI:10.1155/2013/953695.
- R. Tiwari and K. J. Kim, IPMC as a mechanoelectric energy harvester: tailored properties, Smart Mater. Struct., 2013, 22, 015017, DOI:10.1088/0964-1726/22/1/015017.
- M. O. Diab, N. F. Al Awar, M. Atieh, et al. Electromechanical model of IPMC artificial muscle, in 2014 World Symposium on Computer Applications & Research (WSCAR), IEEE, 2014, pp. 1–5.
- G.-H. Feng and K.-M. Liu, Fabrication and Characterization of a Micromachined Swirl-Shaped Ionic Polymer Metal Composite Actuator with Electrodes Exhibiting Asymmetric Resistance, Sensors, 2014, 14, 8380–8397, DOI:10.3390/s140508380.
- S. R. Li, Z. D. Dai and M. Yu, Preliminary study on self-sensing method for ion-conductive polymer metal composite (IPMC) actuator based on current detection, Appl. Mech. Mater., 2014, 461, 967–971, DOI:10.4028/www.scientific.net/AMM.461.967.
- Y. Cha, H. Kim and M. Porfiri, Influence of temperature on the impedance of ionic polymer metal composites, Mater. Lett., 2014, 133, 179–182, DOI:10.1016/j.matlet.2014.06.183.
- Y. Cha, H. Kim and M. Porfiri, Matching the impedance of ionic polymer metal composites for energy harvesting, Smart Mater. Struct., 2014, 23, 127002, DOI:10.1088/0964-1726/23/12/127002.
- Y. Cha, S. Abdolhamidi and M. Porfiri, Energy harvesting from underwater vibration of an annular ionic polymer metal composite, Meccanica, 2015, 50, 2675–2690, DOI:10.1007/s11012-015-0165-5.
- W. Mohdisa, A. Hunt and S. H. Hosseinnia, Active sensing methods of ionic polymer metal composite (IPMC): Comparative study in frequency domain, in RoboSoft 2019 – 2019 IEEE International Conference on Soft Robotics, Institute of Electrical and Electronics Engineers Inc., 2019, pp. 546–551.
- C. Bonomo, L. Fortuna, P. Giannone, et al., A method to estimate the deformation and the absorbed current of an IPMC actuator, in Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD), ed. Y. Bar-Cohen, 2006, p. 61681W Search PubMed.
- L. Romero, J. Emilio, H. N. Kaniet al. Frequency response of IPMC actuators Physical characterization and identification for control frequency response of ipmc actuators: physical characterization and identification, 2018.
- Y. Cha and M. Porfiri, Bias-dependent model of the electrical impedance of ionic polymer-metal composites, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022403, DOI:10.1103/PhysRevE.87.022403.
- Q. Shen, K. J. Kim and T. Wang, Electrode of ionic polymer-metal composite sensors: Modeling and experimental investigation, J. Appl. Phys., 2014, 115, 0–14, DOI:10.1063/1.4876255.
- F. Cellini, Y. Cha and M. Porfiri, Energy harvesting from fluid-induced buckling of ionic polymer metal composites, J. Intell. Mater. Syst. Struct., 2014, 25, 1496–1510, DOI:10.1177/1045389X13508333.
- G. X. Yin, Q. S. He and M. Yu, et al., Ionic polymer metal composites actuators with enhanced driving performance by incorporating graphene quantum dots, J. Cent. South Univ., 2022, 29, 1412–1422, DOI:10.1007/s11771-022-5040-7.
- S. N. Patel and S. Mukherjee, Manufacturing, characterization and experimental investigation of the IPMC shoe energy harvester, J. Braz. Soc. Mech. Sci. Eng., 2022, 44, 42, DOI:10.1007/s40430-021-03344-3.
- M. J. Doregiraei, H. Moeinkhah and J. Sadeghi, A fractional order model for electrochemical impedance of IPMC actuators based on constant phase element, J. Intell. Mater. Syst. Struct., 2021, 32, 880–888, DOI:10.1177/1045389X20974438.
- H. S. Wang, J. Cho and H. W. Park, et al., Ionic polymer–metal composite actuators driven by methylammonium formate for high-voltage and long-term operation, J. Ind. Eng. Chem., 2021, 96, 194–201, DOI:10.1016/j.jiec.2021.01.021.
- Y. Bar-Cohen, X. Bao, S. Sherrit and S.-S. Lih, Characterization of the electromechanical properties of ionomeric polymer-metal composite (IPMC), 2002, vol. 4695, pp. 286–293 DOI:10.1117/12.475173.
- K. Takagi, Y. Nakabo, Z.-W. Luo and K. Asaka, On a distributed parameter model for electrical impedance of ionic polymer, Electroactive Polymer Actuators and Devices (EAPAD), 2007, vol. 6524, p. 652416 DOI:10.1117/12.715554.
- Y. Ming, Y. Yang and R. P. Fu, et al., IPMC Sensor Integrated Smart Glove for Pulse Diagnosis, Braille Recognition, and Human–Computer Interaction, Adv. Mater. Technol., 2018, 3, 1800257, DOI:10.1002/admt.201800257.
- R. Tiwari, S.-M. Kim and K. Kim, Variable Thickness IPMC: Capacitance Effect on Energy Harvesting, MRS Proc., 2008, 1129, 1129-V06-05, DOI:10.1557/PROC-1129-V06-05.
- Y. Wang, J. Liu and Y. Zhu, et al., Formation and Characterization of Dendritic Interfacial Electrodes inside an Ionomer, ACS Appl. Mater. Interfaces, 2017, 9, 30258–30262, DOI:10.1021/acsami.7b08012.
- R. Tiwari and K. J. Kim, Improved IPMC sensing by use of cation and through induced nano-to-micro scale surface cracks, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, 2008, vol. 6932, p. 69323H DOI:10.1117/12.776052.
- W. Aoyagi and M. Omiya, Mechanical and electrochemical properties of an IPMC actuator with palladium electrodes in acid and alkaline solutions, Smart Mater. Struct., 2013, 22, 055028, DOI:10.1088/0964-1726/22/5/055028.
- W. Aoyagi and M. Omiya, Anion effects on the ion exchange process and the deformation property of ionic polymer metal composite actuators, Materials, 2016, 9, 479, DOI:10.3390/ma9060479.
- C. Bonomo, L. Fortuna, P. Giannone, et al., A method to estimate the deformation and the absorbed current of an IPMC actuator, in Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD), ed. Y. Bar-Cohen, 2006, p. 61681W Search PubMed.
- L. Romero, J. Emilio, H. N. Kani, et al. Frequency response of IPMC actuators Physical characterization and identification for control frequency response of ipmc actuators: physical characterization and identification, 2018.
- F. Cellini, Y. Cha and M. Porfiri, Energy harvesting from fluid-induced buckling of ionic polymer metal composites, J. Intell. Mater. Syst. Struct., 2014, 25, 1496–1510, DOI:10.1177/1045389X13508333.
- Q. Shen, K. J. Kim and T. Wang, Electrode of ionic polymer-metal composite sensors: Modeling and experimental investigation, J. Appl. Phys., 2014, 115, 0–14, DOI:10.1063/1.4876255.
- Y. Cha and M. Porfiri, Bias-dependent model of the electrical impedance of ionic polymer-metal composites, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022403, DOI:10.1103/PhysRevE.87.022403.
- M. A. Buechler and D. J. Leo, Characterization and Variational Modeling of Ionic Polymer Transducers, J Vib. Acoust., 2007, 129, 113–120, DOI:10.1115/1.2424973.
- I. Must, V. Vunder and F. Kaasik, et al., Ionic liquid-based actuators working in air: The effect of ambient humidity, Sens. Actuators, B, 2014, 202, 114–122, DOI:10.1016/j.snb.2014.05.074.
- J. Ru, Y. Wang and L. Chang, et al., Preparation and characterization of water-soluble carbon nanotube reinforced Nafion membranes and so-based ionic polymer metal composite actuators, Smart Mater. Struct., 2016, 25, DOI:10.1088/0964-1726/25/9/095006.
- J. Ru, Y. Wang, L. Chang, et al., Preparation and characterization of sulfonated carbon nanotube/Nafion IPMC actuators, in Electroactive Polymer Actuators and Devices (EAPAD), ed. Y. Bar-Cohen and F. Vidal, 2016, p. 97982Z Search PubMed.
- L. Naji, M. Safari and S. Moaven, Fabrication of SGO/Nafion-based IPMC soft actuators with sea anemone-like Pt electrodes and enhanced actuation performance, Carbon, 2016, 100, 243–257, DOI:10.1016/j.carbon.2016.01.020.
- X. Zhang, S. Yu and M. Li, et al., Enhanced performance of IPMC actuator based on macroporous multilayer MCNTs/Nafion polymer, Sens. Actuators, A, 2022, 339, 113489, DOI:10.1016/j.sna.2022.113489.
- Z. He, S. Jiao and Z. Wang, et al., An Antifatigue Liquid Metal Composite Electrode Ionic Polymer-Metal Composite Artificial Muscle with Excellent Electromechanical Properties, ACS Appl. Mater. Interfaces, 2022, 14, 14630–14639, DOI:10.1021/acsami.2c01453.
- R. Histed, J. Ngo and O. A. Hussain, Ionic polymer metal composite compression sensors with 3D-structured interfaces, Smart Mater. Struct., 2021, 30, 125027, DOI:10.1088/1361-665X/ac3431.
- F. Wang, X. Zhang and L. Ma, Facile and effective repair of Pt/Nafion IPMC actuator by dip-coating of PVP@AgNPs, Nanotechnology, 2021, 32, 385502, DOI:10.1088/1361-6528/ac0cae.
- Q. Liu, L. Liu and K. Xie, et al., Synergistic effect of a r-GO/PANI nanocomposite electrode based air working ionic actuator with a large actuation stroke and long-term durability, J. Mater. Chem. A, 2015, 3, 8380–8388, 10.1039/c5ta00669d.
- F. Cellini, A. Grillo and M. Porfiri, Ionic polymer metal composites with polypyrrole-silver electrodes, Appl. Phys. Lett., 2015, 106, 131902, DOI:10.1063/1.4916672.
- L. Lu, J. Liu and Y. Hu, et al., Highly Stable Air Working Bimorph Actuator Based on a Graphene Nanosheet/Carbon Nanotube Hybrid Electrode, Adv. Mater., 2012, 24, 4317–4321, DOI:10.1002/adma.201201320.
- V. Palmre, S. J. Kim, D. Pugal and K. Kim, Improving electromechanical output of IPMC by high surface area Pd-Pt electrodes and tailored ionomer membrane thickness, Int. J. Smart Nano Mater., 2014, 5, 99–113, DOI:10.1080/19475411.2014.914108.
- L. Dai, L. Li and Y. Zhang, Microstructure effects on proton conductivity in EVOH based ionic polymer-metal composites actuator, International Conference on Smart Materials and Nanotechnology in Engineering, 2007, vol. 6423, p. 64230X DOI:10.1117/12.779354.
- A. Khan, M. Luqman and A. Dutta, Kraton based ionic polymer metal composite (IPMC) actuator, Sens. Actuators, A, 2014, 216, 295–300, DOI:10.1016/j.sna.2014.04.015.
- A. Khan, I. Inamuddin, R. K. Jain and Mu Naushad, Fabrication of a silver nano powder embedded kraton polymer actuator and its characterization, RSC Adv., 2015, 5, 91564–91573, 10.1039/C5RA17776F.
- M. Luqman, A. Anis and H. M. Shaikh, Development of a Soft Robotic Bending Actuator Based on a Novel Sulfonated Polyvinyl Chloride–Phosphotungstic Acid Ionic Polymer–Metal Composite (IPMC) Membrane, Membranes, 2022, 12, 651, DOI:10.3390/membranes12070651.
- M. Luqman, A. Anis and H. M. Shaikh, Synthesis, Characterization and Fabrication of Copper Nanoparticles Embedded Non-Perfluorintaed Kraton Based Ionic Polymer Metal Composite (IPMC) Actuator, Actuators, 2022, 11, 183, DOI:10.3390/act11070183.
- M. Luqman, H. Shaikh and A. Anis, et al., Platinum-coated silicotungstic acid-sulfonated polyvinyl alcohol-polyaniline based hybrid ionic polymer metal composite membrane for bending actuation applications, Sci. Rep., 2022, 12, 1–9, DOI:10.1038/s41598-022-08402-x.
- M. Ates, Review study of electrochemical impedance spectroscopy and equivalent electrical circuits of conducting polymers on carbon surfaces, Prog. Org. Coat., 2011, 71, 1–10, DOI:10.1016/j.porgcoat.2010.12.011.
- J. E. B. Randles, Kinetics of rapid electrode reactions, Discuss. Faraday Soc., 1947, 1, 11, 10.1039/df9470100011.
- D. D. Macdonald, Reflections on the history of electrochemical impedance spectroscopy, Electrochim. Acta, 2006, 51, 1376–1388, DOI:10.1016/j.electacta.2005.02.107.
- J. Macdonald, Impedance spectroscopy: Models, data fitting, and analysis, Solid State Ionics, 2005, 176, 1961–1969, DOI:10.1016/j.ssi.2004.05.035.
- A. J. Terezo, J. Bisquert, E. C. Pereira and G. Garcia-Belmonte, Separation of transport, charge storage and reaction processes of porous electrocatalytic IrO2 and IrO2/Nb2O5 electrodes, J. Electroanal. Chem., 2001, 508, 59–69, DOI:10.1016/S0022-0728(01)00522-8.
- J. Macdonald, Impedance spectroscopy: Models, data fitting, and analysis, Solid State Ionics, 2005, 176, 1961–1969, DOI:10.1016/j.ssi.2004.05.035.
- J. P. Meyers, M. Doyle, R. M. Darling and J. Newman, The Impedance Response of a Porous Electrode Composed of Intercalation Particles, J. Electrochem. Soc., 2000, 147, 2930, DOI:10.1149/1.1393627.
- M. Schlesinger, Modern Aspects of Electrochemistry, Springer New York, New York, NY, 2009, vol. 43 Search PubMed.
- R. De Levie, The influence of surface roughness of solid electrodes on electrochemical measurements, Electrochim. Acta, 1965, 10, 113–130, DOI:10.1016/0013-4686(65)87012-8.
- R. de Levie, Fractals and rough electrodes, J. Electroanal. Chem. Interfacial Electrochem., 1990, 281, 1–21, DOI:10.1016/0022-0728(90)87025-F.
- M. R. Shoar Abouzari, F. Berkemeier, G. Schmitz and D. Wilmer, On the physical interpretation of constant phase elements, Solid State Ionics, 2009, 180, 922–927, DOI:10.1016/j.ssi.2009.04.002.
- G. Láng, K. E. Heusler and A. Sadkowski, et al., Comments on the ideal polarisability of electrodes displaying cpe-type capacitance dispersion, J. Electroanal. Chem., 2000, 481, 227–229, DOI:10.1016/S0022-0728(99)00480-5.
- P. Zoltowski, Comments on the paper ‘On the ideal polarisability of electrodes displaying cpe-type capacitance dispersion’ by A. Sadkowski, J. Electroanal. Chem., 2000, 481, 230–231, DOI:10.1016/S0022-0728(99)00482-9.
- A. Sadkowski, Response to the ‘Comments on the ideal polarisability of electrodes displaying cpe-type capacitance dispersion’ by G. Láng, K.E. Heusler, J. Electroanal. Chem., 2000, 481, 232–236, DOI:10.1016/S0022-0728(99)00483-0.
- P. Zoltowski, On the electrical capacitance of interfaces exhibiting constant phase element behaviour, J. Electroanal. Chem., 1998, 443, 149–154, DOI:10.1016/S0022-0728(97)00490-7.
- G. Láng and K. E. Heusler, Remarks on the energetics of interfaces exhibiting constant phase element behaviour, J. Electroanal. Chem., 1998, 457, 257–260, DOI:10.1016/S0022-0728(98)00301-5.
- J. Bisquert and A. Compte, Theory of the electrochemical impedance of anomalous diffusion, J. Electroanal. Chem., 2001, 499, 112–120, DOI:10.1016/S0022-0728(00)00497-6.
- R. Gonçalves, A. A. A. Correa, R. Pereira and E. C. C. Pereira, Investigation of the electrochemical aging of poly(3-hexiltiophene) using impedance spectroscopy, Electrochim. Acta, 2016, 190, 329–336, DOI:10.1016/j.electacta.2015.12.198.
- G. Paasch, K. Micka and P. Gersdorf, Theory of the electrochemical impedance of macrohomogeneous porous electrodes, Electrochim. Acta, 1993, 38, 2653–2662, DOI:10.1016/0013-4686(93)85083-B.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago and P. R. Bueno, Theoretical models for ac impedance of finite diffusion layers exhibiting low frequency dispersion, J. Electroanal. Chem., 1999, 475, 152–163, DOI:10.1016/S0022-0728(99)00346-0.
- J. Bisquert and A. Compte, Theory of the electrochemical impedance of anomalous diffusion, J. Electroanal. Chem., 2001, 499, 112–120, DOI:10.1016/S0022-0728(00)00497-6.
- A. Fick, Ueber Diffusion, Ann. Phys., 1855, 170, 59–86, DOI:10.1002/andp.18551700105.
- J. Bisquert, G. Garcia-Belmonte and P. Bueno, et al., Impedance of constant phase element (CPE)-blocked diffusion in film electrodes, J. Electroanal. Chem., 1998, 452, 229–234, DOI:10.1016/S0022-0728(98)00115-6.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago and P. R. Bueno, Theoretical models for ac impedance of finite diffusion layers exhibiting low frequency dispersion, J. Electroanal. Chem., 1999, 475, 152–163, DOI:10.1016/S0022-0728(99)00346-0.
- W. H. MohdIsa, A. Hunt and S. H. HosseinNia, Sensing and self-sensing actuation methods for ionic polymer-metal composite (IPMC): A review, Sensors, 2019, 19, 1–36, DOI:10.3390/s19183967.
- J. Paquette, K. J. Kim, J. D. Nam and Y. S. Tak, An equivalent circuit model for ionic polymer-metal composites and their performance improvement by a clay-based polymer nano-composite technique, in ASME International Mechanical Engineering Congress and Exposition, Proceedings, American Society of Mechanical Engineers (ASME), 2002, pp. 27–35.
- K. Newbury, D. J. Leo, D. J. Inman, et al., Characterization, Modeling, and Control of Ionic Polymer Transducers Mechanical Engineering, Virginia Tech, 2002 Search PubMed.
- Y. Kengne Fotsing and X. Tan, Bias-dependent impedance model for ionic polymer-metal composites, J. Appl. Phys., 2012, 111, 124907, DOI:10.1063/1.4730339.
- H. Moeinkhah, J. Rezaeepazhand and A. Akbarzadeh, Analytical dynamic modeling of a cantilever IPMC actuator based on a distributed electrical circuit, Smart Mater. Struct., 2013, 22, 055033, DOI:10.1088/0964-1726/22/5/055033.
- Z. Chen, Ionic polymer-metal composite artificial muscles and sensors: A control systems perspective, Michigan State University, 2009 Search PubMed.
- D. N. C. Nam and K. K. Ahn, Analysis and experiment on a self-sensing ionic polymer–metal composite actuator, Smart Mater. Struct., 2014, 23, 074007, DOI:10.1088/0964-1726/23/7/074007.
- A. Punning, M. Kruusmaa and A. Aabloo, A self-sensing ion conducting polymer metal composite (IPMC) actuator, Sens. Actuators, A, 2007, 136, 656–664, DOI:10.1016/j.sna.2006.12.008.
- Z. Chen and X. Tan, A control-oriented and physics-based model for ionic polymer-metal composite actuators, IEEE/ASME Trans. Mechatron., 2008, 13, 519–529, DOI:10.1109/TMECH.2008.920021.
- M. Aureli and M. Porfiri, Nonlinear sensing of ionic polymer metal composites, Continuum Mech. Thermodyn., 2013, 25, 273–310, DOI:10.1007/s00161-012-0253-x.
- F. Cellini, J. Pounds, S. D. Peterson and M. Porfiri, Underwater energy harvesting from a turbine hosting ionic polymer metal composites, Smart Mater. Struct., 2014, 23, 085023, DOI:10.1088/0964-1726/23/8/085023.
- M. Aureli, V. Kopman and M. Porfiri, Free-locomotion of underwater vehicles actuated by ionic polymer metal composites, IEEE/ASME Trans. Mechatron., 2010, 15, 603–614, DOI:10.1109/TMECH.2009.2030887.
- S. SamPour, H. Moeinkhah and H. Rahmani, Electrochemical viscoelastic modeling to predict quasi-static and dynamic response of IPMC actuators, Mech. Mater., 2019, 138, 103172, DOI:10.1016/j.mechmat.2019.103172.
- M. J. Doregiraei, H. Moeinkhah and J. Sadeghi, A fractional order model for electrochemical impedance of IPMC actuators based on constant phase element, J. Intell. Mater. Syst. Struct., 2021, 32, 880–888, DOI:10.1177/1045389X20974438.
- M. Gudarzi, P. Smolinski and Q. M. Wang, Bending mode ionic polymer-metal composite (IPMC) pressure sensors, Measurement, 2017, 103, 250–257, DOI:10.1016/j.measurement.2017.02.029.
- Z. Chen and X. Tan, A scalable dynamic model for ionic polymer-metal composite actuators, Electroactive Polymer Actuators and Devices (EAPAD), 2008, vol. 6927, p. 69270I DOI:10.1117/12.776508.
- M. Aureli and M. Porfiri, Effect of electrode surface roughness on the electrical impedance of ionic polymer-metal composites, Smart Mater. Struct., 2012, 21, 105030, DOI:10.1088/0964-1726/21/10/105030.
- R. Tiwari and K. J. Kim, Disc-shaped IPMC for use in energy harvesting, Behavior and Mechanics of Multifunctional Materials and Composites, 2009, vol. 7289, p. 72891G DOI:10.1117/12.816100.
- K. Kikuchi and S. Tsuchitani, Nafion®-based polymer actuators with ionic liquids as solvent incorporated at room temperature, J. Appl. Phys., 2009, 106, 53519, DOI:10.1063/1.3204961.
- Y. Cha and M. Porfiri, Charge dynamics of ionic polymer metal composites in response to electrical bias, Electroactive Polymer Actuators and Devices (EAPAD), 2013, vol. 8687, p. 868721 DOI:10.1117/12.2009062.
- D. N. C. Nam and K. K. Ahn, Analysis and experiment on a self-sensing ionic polymer–metal composite actuator, Smart Mater. Struct., 2014, 23, 074007, DOI:10.1088/0964-1726/23/7/074007.
- S. SamPour, H. Moeinkhah and H. Rahmani, Electrochemical viscoelastic modeling to predict quasi-static and dynamic response of IPMC actuators, Mech. Mater., 2019, 138, 103172, DOI:10.1016/j.mechmat.2019.103172.
- A. Gupta and S. Mukherjee, Dynamic modeling of biomimetic undulatory ribbon fin underwater propulsor actuated by IPMC, Mater. Today: Proc., 2021, 44, 1086–1089, DOI:10.1016/j.matpr.2020.11.183.
- Y. Kengne Fotsing and X. Tan, Bias-dependent impedance model for ionic polymer-metal composites, J. Appl. Phys., 2012, 111, 124907, DOI:10.1063/1.4730339.
- Y. Bar-Cohen, S. Sherrit and S.-S. Lih, Characterization of the electromechanical properties of EAP materials, in Smart Structures and Materials 2001: Electroactive Polymer Actuators and Devices, ed. Y. Bar-Cohen, 2001, p. 319 Search PubMed.
- P. V. P. Agnps, F. Wang, X. Zhang, et al. Facile and effective repair of Pt/Nafion IPMC actuator by dip-coating of Facile and effective repair of Pt/Nafion IPMC actuator by dip-coating of PVP@AgNPs, 2021.
- A. Kusoglu and A. Z. Weber, New Insights into Perfluorinated Sulfonic-Acid Ionomers, Chem. Rev., 2017, 117, 987–1104, DOI:10.1021/acs.chemrev.6b00159.
- W. Y. Hsu and T. D. Gierke, Ion transport and clustering in Nafion perfluorinated membranes, J. Membr. Sci., 1983, 13, 307–326, DOI:10.1016/S0376-7388(00)81563-X.
- T. Gierke, G. Munn and F. Wilson, The Morphology in Nafion Perfluorinated Membrane Products, as Determined by WideAngle and Small-Angle X-Ray Studies, J. Polym. Sci., 2003, 19, 1687–1704 Search PubMed.
- G. Gebel, Structural evolution of water swollen perfluorosulfonated ionomers from dry membrane to solution, Polymer, 2000, 41, 5829–5838, DOI:10.1016/S0032-3861(99)00770-3.
- M. Plonus, Circuit Fundamentals, Electronics and Communications for Scientists and Engineers, Elsevier, 2001, pp. 1–48 Search PubMed.
- R. P. Buck and C. Mundt, Origins of finite transmission lines for exact representations of transport by the Nernst–Planck equations for each charge carrier, Electrochim. Acta, 1999, 44, 1999–2018, DOI:10.1016/S0013-4686(98)00309-0.
- G. Paasch, Complete electrochemical transmission line model for conducting polymers, Synth. Met., 2001, 119, 233–234, DOI:10.1016/S0379-6779(00)00865-1.
- M. C. Saccardo, A. G. Zuquello and K. A. Tozzi, et al., Counter-ion and humidity effects on electromechanical properties of Nafion®/Pt composites, Mater. Chem. Phys., 2020, 244, 122674, DOI:10.1016/j.matchemphys.2020.122674.
| This journal is © The Royal Society of Chemistry 2024 |