Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Elucidation of factors shaping reactivity of 5′-deoxyadenosyl – a prominent organic radical in biology†
Zuzanna
Wojdyla
 a,
Mauricio
Maldonado-Domínguez
a,
Mauricio
Maldonado-Domínguez
 a,
Priyam
Bharadwaz
a,
Martin
Culka
b and
Martin
Srnec
a,
Priyam
Bharadwaz
a,
Martin
Culka
b and
Martin
Srnec
 *a
*a
aJ. Heyrovský Institute of Physical Chemistry, Czech Academy of Sciences, Dolejškova 3, 18200 Prague, Czech Republic. E-mail: martin.srnec@jh-inst.cas.cz
bInstitute of Organic Chemistry and Biochemistry, Czech Academy of Sciences, Flemingovo nám. 2, 16610 Prague, Czech Republic
First published on 8th July 2024
Abstract
This study investigates the factors modulating the reactivity of 5′-deoxyadenosyl (5′dAdo˙) radical, a potent hydrogen atom abstractor that forms in the active sites of radical SAM enzymes and that otherwise undergoes a rapid self-decay in aqueous solution. Here, we compare hydrogen atom abstraction (HAA) reactions between native substrates of radical SAM enzymes and 5′dAdo˙ in aqueous solution and in two enzymatic microenvironments. With that we reveal that HAA efficiency of 5′dAdo˙ is due to (i) the in situ formation of 5′dAdo˙ in a pre-ordered complex with a substrate, which attenuates the unfavorable effect of substrate:5′dAdo˙ complex formation, and (ii) the prevention of the conformational changes associated with self-decay by a tight active-site cavity. The enzymatic cavity, however, does not have a strong effect on the HAA activity of 5′dAdo˙. Thus, we performed an analysis of in-water HAA performed by 5′dAdo˙ based on a three-component thermodynamic model incorporating the diagonal effect of the free energy of reaction, and the off-diagonal effect of asynchronicity and frustration. To this aim, we took advantage of the straightforward relationship between the off-diagonal thermodynamic effects and the electronic-structure descriptor – the redistribution of charge between the reactants during the reaction. It allows to access HAA-competent redox and acidobasic properties of 5′dAdo˙ that are otherwise unavailable due to its instability upon one-electron reduction and protonation. The results show that all reactions feature a favourable thermodynamic driving force and tunneling, the latter of which lowers systematically barriers by ∼2 kcal mol−1. In addition, most of the reactions experience a favourable off-diagonal thermodynamic contribution. In HAA reactions, 5′dAdo˙ acts as a weak oxidant as well as a base, also 5′dAdo˙-promoted HAA reactions proceed with a quite low degree of asynchronicity of proton and electron transfer. Finally, the study elucidates the crucial and dual role of asynchronicity. It directly lowers the barrier as a part of the off-diagonal thermodynamic contribution, but also indirectly increases the non-thermodynamic part of the barrier by presumably controlling the adiabatic coupling between proton and electron transfer. The latter signals that the reaction proceeds as a hydrogen atom transfer rather than a proton-coupled electron transfer.
Introduction
An important class of redox-active polynuclear transition-metal catalysts in nature are ubiquitous Fe4S4-dependent radical S-adenosyl-L-methionine (SAM) enzymes.1 These radical SAM enzymes perform a wide range of critical functions in biology and homeostasis.The radical SAM enzymes family comprises of >700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 members that catalyze more than 70 different reactions.1,2 They are involved in post-translational modifications of RNA,3,4 metalloprotein cluster formation,5 DNA repair,6 biosynthesis of various cofactors such as hemes,7 FeMo cofactor,8 chlorophyll9 and many other transformations.
000 members that catalyze more than 70 different reactions.1,2 They are involved in post-translational modifications of RNA,3,4 metalloprotein cluster formation,5 DNA repair,6 biosynthesis of various cofactors such as hemes,7 FeMo cofactor,8 chlorophyll9 and many other transformations.
Most radical SAM enzymes are thought to generate a strongly oxidizing 5′-deoxyadenosyl (5′dAdo˙) radical. The formation of the radical is dependent on a Fe4S4 cluster, which provides electrons for a reductive cleavage of the C–S bond in SAM (see Scheme 1).10–13 After the cleavage, the 5′dAdo˙ radical can form an organometallic complex with the Fe4S4 cluster14 – the so-called Ω intermediate.15,16 It features a labile Fe–C bond between 5′dAdo˙ and the apical Fe ion (Scheme 1). The role of the Ω intermediate has been postulated as an auxiliary reservoir of 5′dAdo˙, suggesting that the reductive cleavage of SAM is effectively irreversible in the enzyme environment and that the intermediate prevents from a potential active site damage by minimizing the time of 5′dAdo˙ radical being unprotected.
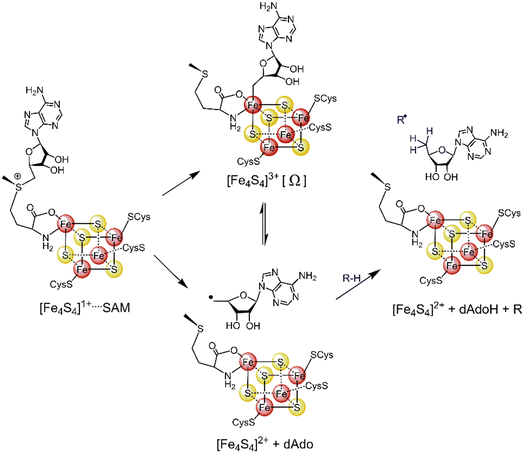 | ||
| Scheme 1 The formation of the 5′dAdo˙ radical-containing intermediate central to the catalytic cycle of all radical SAM enzymes. | ||
The central role of the 5′dAdo˙ radical is the activation of a substrate through H-atom abstraction (HAA), leading to the formation of a substrate-derived radical, which subsequently undergoes further transformations.17,18 Notably, placement of 5′dAdo˙ within the enzymatic cavity is crucial for the utilization of its HAA potential as otherwise it undergoes rapid self-decay in aqueous solution. One possible route for self-decay, established based on photolysis under anaerobic condition of adenosylcobalamin, another biological source of 5′dAdo˙, leads to formation of 8,5′-cycloadenosine – cyc-dAdo˙ (Fig. 1A).19 This transformation likely proceeds through intramolecular addition of the primary 5′dAdo˙ radical at the 5′-position to the C-8 of the adenyl moiety. The formation of cyc-dAdo˙ was also observed during electrochemical reduction of SAM in solution,20 confirming that intramolecular cyclization is a plausible channel for the irreversible decay of 5′dAdo˙. A second potential mechanism for the decomposition of this highly reactive radical was observed during recent synthetic studies on muscarines and isomuscarines.21 It was discovered that the heterocyclic fragment featuring hydroxyl substituents could undergo ring opening (Fig. 1B). The 5′dAdo˙ radical features analogous 2,3-dihydroxylated positions and, therefore, its decay via ring opening is another potential side reaction, which must be suppressed in nature although its relevance has not been investigated hitherto.
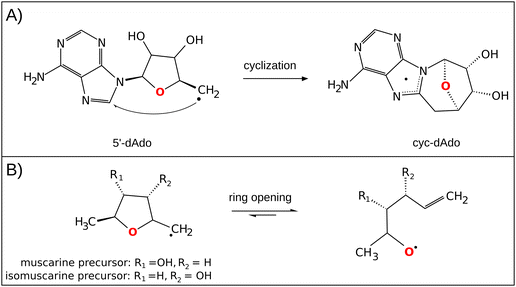 | ||
| Fig. 1 (A) In the cyclization decay mechanism, the 5′dAdo˙ radical undergoes intramolecular radical addition leading to a stable cyclic structure.20 (B) The ring-opening decay mechanism was observed for the radicals similar to 5′dAdo˙.21 | ||
While both mechanisms for unimolecular decay have been observed in related systems in solution, H-atom abstraction has not been observed outside of an enzymatic active site, which raises the questions: is HAA boosted in the active site of 5′dAdo˙-containing enzymes, and/or is the active site suppressing the undesired radical decay routes? To answer them, we investigate the chemical behavior of the 5′dAdo˙ radical in two different media – in aqueous – vs. enzyme-like environment. The latter is represented by two the prototypical radical SAM enzymes, pyruvate formate-lyase activating enzyme (PFL-AE)22–24 and lysine 2,3-aminomutase (LAM)25,26 – with the aim to elucidate how the protein environment tunes the catalytic function of 5′dAdo˙ and suppresses otherwise favorable radical self-decay pathway(s) as depicted in Scheme 2.
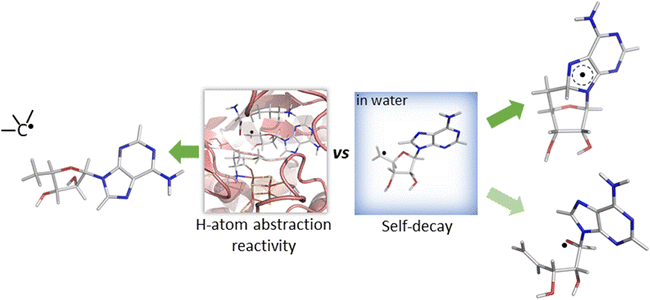 | ||
| Scheme 2 Reactivity of the 5′-deoxyadenosyl radical in water vs. enzymatic environment. While 5′dAdo˙ is well known to be competent as an H-atom abstractor in radical SAM enzymes (the left side of the scheme),17,18 it is unstable in water, undergoing an experimentally documented pathway – cyclization20 (the product of which is shown in the right upper corner of the scheme) or, as suggested by this computational work, rybosyl-ring opening pathway21 depicted in the right lower corner of the scheme. | ||
The HAA reactivity of 5′dAdo˙ can be investigated on the basis of a three-component thermodynamic model, which was developed in our group as a nonempirical link between the reactivity of the system and its redox and acidobasic properties.27,28 In this model, the single-step HAA reaction, during which proton and electron transfer occur concertedly between the reactants, is affected by the energetics of two different states – one associated with electron transfer and one with proton transfer (ET and PT) between the reactants. These states are parts of two (typically) energetically less accessible two-step HAA processes: (i) ET state is formed as an intermediate in the trajectory where ET is followed by PT, whereas PT state is formed in the trajectory where PT is followed by ET. In more detail, it gives rise to two so-called off-diagonal thermodynamic contributions: asynchronicity (η) and frustration (σ), in addition to diagonal thermodynamic driving force for reaction, which is free energy of the reaction. The former measures the energy disproportion between the ET and PT states, and reflects which of the components is dominant in driving the reaction; the latter accounts for the joint (un)availability of the two sequential pathways (for formulas for each of the terms see theoretical background). The implementation of these two factors into a Marcus-type equation demonstrates that a more asynchronous reaction features a lower barrier, whereas a more frustrated process has to overcome a higher barrier. Thus, this concept can be employed to analyze the reactivity of 5′dAdo˙ with respect to different enzymatic substrates as well as look into the mechanism for the reaction in various environments.
In this work, we present that the role of the enzymatic environment is mainly to harness the inherent HAA reactivity of 5′dAdo˙ and to suppress pathways leading to decay (cyclization and ring opening). With this finding, in the following sections, we focus on the analysis of the inherent HAA ability of 5′dAdo˙ with respect to the native substrates of radical SAM enzymes. The decomposition of HAA barriers for 5′dAdo˙-promoted HAA reactions is based on an existing link between an electronic-structure descriptor and off-diagonal thermodynamic contribution to the reaction barriers. Namely, due to a tight relationship between both asynchronicity and the overall off-diagonal thermodynamic term with the redistribution of charge along the reaction coordinate, we could work around the instability of 5′dAdo˙ (and some of the substrates) upon 1e− reduction and protonation and thus gain access to the otherwise unavailable off-diagonal thermodynamic factors shaping the barriers of HAA reactions with 5′dAdo˙. With that, we found the 5′dAdo˙ radical to be a weak oxidant and base, abstracting H-atoms from native substrates with a relatively higher degree of concertedness of H+/e− transfers. Besides that, we found asynchronicity to be a key factor affecting the barrier directly as a part of three-component thermodynamic force and indirectly through its influence on the adiabatic coupling between proton and electron transfer.
Computational details
Structural models for 5′dAdo˙ decay and its HAA reactions in aqueous solution
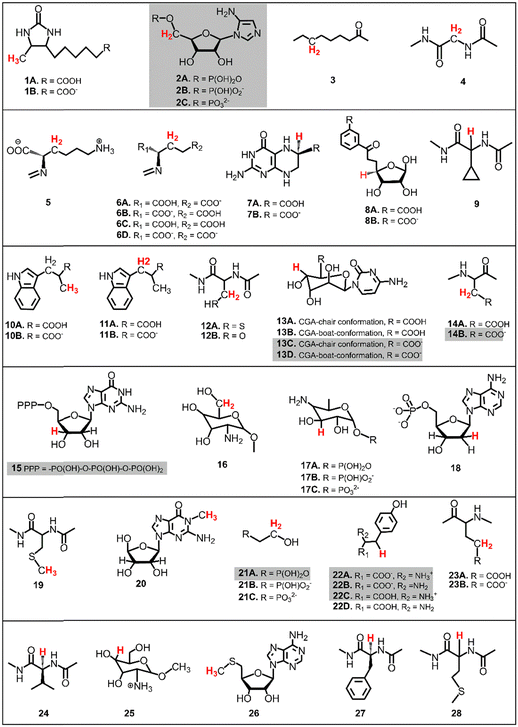
The presented study focuses on energetics of unimolecular decay pathways of 5′dAdo˙ as well as H-atom abstraction reactions between 5′dAdo˙ and 28 different C–H bond substrates, which are known from the literature to be attacked by 5′dAdo˙ in the radical SAM enzymes. Structures of these substrates are listed in Fig. 2; several of them were considered in various protonation states (those with protic groups such as carboxylic acids and/or amine groups). Substrates were obtained from PDB representations of their complexes with radical SAM enzymes (see Table S1, ESI†). The reported structures for the reactant and product complexes are the ones that feature the least changed intra- and intermolecular interactions with respect to the transition state.To additionally study the self-decay reactions, the solvation of 5′dAdo˙ in aqueous solution was determined based on a 10 ns MD simulation in a box of TIP3P water29 with the minimal distance between the atoms of the solute and the wall of the box equal to 10 Å. The simulation was performed with a general Amber force field (GAFF)30,31 using the Amber 22 package.32 Water molecules forming hydrogen bonds with 5′dAdo˙ were selected for further calculations.
Structural models for 5′dAdo˙ decay and its HAA reactions in enzymes
The calculations were performed based on cluster models for the enzymatic cavities, an approach that was shown in numerous studies to yield results consistent with experimental data.33–41 The cluster model of the PFL-AE24 active site comprises 231 atoms, including the SAM-bound Fe4S4 cubane anchored by three cysteines (Cys29, Cys33 and Cys36), along with one sodium cation and second-shell residues Tyr35, His37, Asn38, Asp104, Thr105, Asn106, Asp129, Lys131, Arg166, Val168, Leu199, His202, as well as the fragment of the PFL substrate comprising Gly734 and Ser733 (Fig. 3, top). For LAM,42 the cluster model consists of 205 atoms from the [Fe4S4] cubane coordinated by three cysteines (Cys125, Cys129 and Cys132) and the SAM cofactor, along with the second-shell residues His131, Thr133, Arg134, Ser169, His230, Gln258, Val260, Tyr290, Asp293, and Asp330, as well as the Lys420 acting as the LAM substrate (Fig. 3, bottom). In both models, most of second-shell residues are truncated at the Cα atoms (Cartesian coordinates in ESI†); the fixed atoms are highlighted in Fig. 3 with black circles. The [Fe4S4]2+ was modeled in its ground spin state, featuring anti-ferromagnetic interaction of the two ferromagnetically coupled high-spin iron pairs, as reported in previous study on prototypical radical SAM enzymes.43 The observed antiferromagnetic coupling pattern was also reported for electronic structure of similar Fe4S4 complexes.44–47 The ground-state electronic structures of enzymatic models are shown in Fig. S1 (ESI†).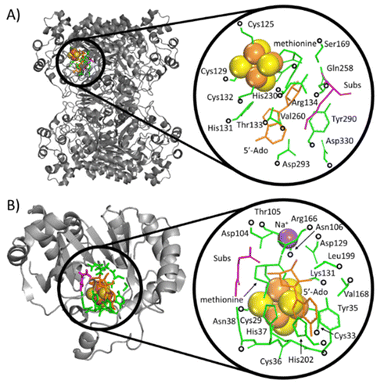 | ||
| Fig. 3 Crystallographic structures of two radical SAM enzymes, LAM (A) PFL-AE (B) [PDB codes: 2A5H42 and 3CB8]24 (left), were used to construct the cluster models representing the enzymatic active sites (right). The Fe and S atoms in these models are displayed as large (orange and yellow) spheres, while the atoms kept fixed during the geometry optimizations are indicated by black circles. SAM (the precursor of 5′dAdo˙) and secondary residues are represented by orange and green sticks, respectively. The substrate for the reaction is shown in magenta. For the sake of clarity, hydrogen atoms are not visualized. | ||
Statistics within the family of radical SAM enzymes
We used a snapshot of the RCSB protein data bank48 acquired on May 3rd 2018 to identify all structures of radical SAM enzymes (43 structures). We specifically looked for structures containing S-adenosylmethionine (SAM) or S-adenosylhomocysteine (SAH), with a coordination bond (distance < 2.5 Å) to an Fe4S4 cluster (residue name SF4 or FS4). In those structures, we measured a dihedral angle within the SAM or SAH, which defines the position of the adenine relative to the ribose ring – Y[O4′–C1′–N9–C8] – see Fig. S2 and Table S2 (ESI†). The scripts for distance and dihedral angle analysis in protein structures were written using the Biopython library.49,50Density functional theory (DFT) calculations
All calculations reported in this study were done using the G16 program.51 Geometry optimizations of water-solvated systems were carried out at the B3LYP+D3/def2-TZVP/CPCM(εr = 78.4) level of theory, which includes the B3LYP52 functional with the Grimme's zero-damping correction to dispersion (D3)53 combined with the def2-TZVP basis set,54 and the CPCM implicit solvation model with the dielectric constant of 78.4.55 Some of the systems were additionally optimized using the M06 functional56 combined with the same basis set and solvation model. Both computational methods yielded comparable results, thus the presented results are based on the B3LYP+D3 level of theory. For the cluster models, an analogous protocol for optimization was employed, only with the def2-SVP basis set for the substrate, Fe4S4 cubane, methionine and 5′dAdo˙ moieties (BS1), and the def2-SV(P)54 basis set for the remaining atoms (BS2); such a protocol is denoted as the B3LYP/BS1-2/CPCM(εr = 10.0) approximation. The single-point energies were recomputed using def2-TZVP instead of BS1. Gibbs free energies were calculated according to the equation:G = Eel,solv + [EZPVE + RT − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q] Q] | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q] corresponds to the thermal enthalpic and entropic contributions to the solute energy with EZPVE and Q being the zero-point vibrational energy and molecular partition function, respectively, and obtained from frequency calculations (at 298 K, 1 atm; ideal-gas approximation) on top of optimized geometries.
Q] corresponds to the thermal enthalpic and entropic contributions to the solute energy with EZPVE and Q being the zero-point vibrational energy and molecular partition function, respectively, and obtained from frequency calculations (at 298 K, 1 atm; ideal-gas approximation) on top of optimized geometries.
In analogy to the protocol from ref. 43, the proton-coupled reduction potentials, reduction potentials and acidity constants (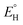 , E° and pKa) associated with species in the thermodynamic half-reaction cycles presented later in the text were calculated as follows:
, E° and pKa) associated with species in the thermodynamic half-reaction cycles presented later in the text were calculated as follows:
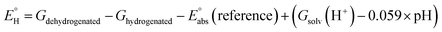 | (2) |
 | (3) |
| pKa = [Gdeprotonated − Gprotonated + Gsolv(H+)]/(RT·ln(10)) | (4) |
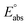 (reference) is the absolute potential of a reference electrode. Specifically, we used −265.9 kcal mol−1 for Gsolv(H+) in water,57 0 for pH and 4.28 eV for
(reference) is the absolute potential of a reference electrode. Specifically, we used −265.9 kcal mol−1 for Gsolv(H+) in water,57 0 for pH and 4.28 eV for 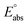 (reference) of the normal hydrogen electrode58 in water. The data is presented in Table S3 (ESI†).
(reference) of the normal hydrogen electrode58 in water. The data is presented in Table S3 (ESI†).
Atoms-in-molecules (AIM) protocol
Atomic charges were determined from wavefunctions of the single-point B3LYP+D3/def2-TZVP/CPCM(εr = 78.4) calculations through the framework of the quantum theory of atoms in molecules, QTAIM,59 using the AIMAll 19.0 suite of programs.60 Atomic charges were obtained using the Proaim method for basin integration, with the “Fine” interatomic surface mesh and outer angular quadrature of 7200 grid points. For atoms with a Lagrangian L(A) > 0.001 a.u., the Promega algorithm was employed instead. The data for the studied reactions is collected in Tables S4 and S5 (ESI†).Theoretical background
The HAA barrier and reaction energy
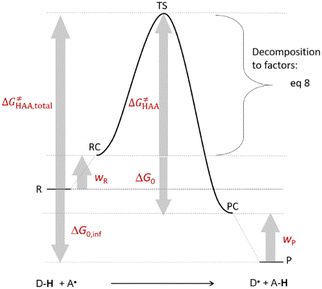
The free-energy barrier of the bimolecular reaction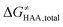 was calculated as the difference between GTS of the transition state (TS) and (Gsubstrate + G5′dAdo˙ + 1.9) kcal mol−1, where Gsubstrate is the free energy of a substrate from Fig. 2 and G5′dAdo˙ is the free energy of the 5′dAdo˙ radical. A value of 1.9 Δn kcal mol−1 has been applied to correct the computed values to the 1 mol L−1 standard state. A value of 1.9 kcal mol−1 corresponds to the conversion of a 1 bar standard state in the gas phase to 1 mol L−1 concentration in solution at 298 K; Δn is the change in the number of moles.
was calculated as the difference between GTS of the transition state (TS) and (Gsubstrate + G5′dAdo˙ + 1.9) kcal mol−1, where Gsubstrate is the free energy of a substrate from Fig. 2 and G5′dAdo˙ is the free energy of the 5′dAdo˙ radical. A value of 1.9 Δn kcal mol−1 has been applied to correct the computed values to the 1 mol L−1 standard state. A value of 1.9 kcal mol−1 corresponds to the conversion of a 1 bar standard state in the gas phase to 1 mol L−1 concentration in solution at 298 K; Δn is the change in the number of moles. 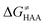 is the free-energy barrier of HAA starting from reactant complex (RC) and equals to
is the free-energy barrier of HAA starting from reactant complex (RC) and equals to 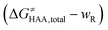 , where wR is the free energy of formation of RC calculated as the difference between GRC of the reactant complex and (Gsubstrate + G5′dAdo˙ + 1.9) kcal mol−1. The free energy of reaction ΔG0 (≡ GPC − GRC) in going from RC to product complex (PC) is related to the free energy of reaction in going from separated reactants to separated products ΔG0,inf (≡ GP − GR) as ΔG0 = ΔG0,inf + wP − wR where wp (in analogy to wR) is the free energy of formation of PC calculated as the difference between GPC of the product complex and (Gsubstrate radical + G5′dAdoH + 1.9) kcal mol−1. This methodology was described in detail previously.61 The key parameters are shown in Scheme 3.
, where wR is the free energy of formation of RC calculated as the difference between GRC of the reactant complex and (Gsubstrate + G5′dAdo˙ + 1.9) kcal mol−1. The free energy of reaction ΔG0 (≡ GPC − GRC) in going from RC to product complex (PC) is related to the free energy of reaction in going from separated reactants to separated products ΔG0,inf (≡ GP − GR) as ΔG0 = ΔG0,inf + wP − wR where wp (in analogy to wR) is the free energy of formation of PC calculated as the difference between GPC of the product complex and (Gsubstrate radical + G5′dAdoH + 1.9) kcal mol−1. This methodology was described in detail previously.61 The key parameters are shown in Scheme 3.
Three-component thermodynamics model of HAA
The model features two so-called off-diagonal thermodynamic factors – asynchronicity (η) and frustration (σ) that together with the diagonal one – free energy of the reaction – form a complete thermodynamic basis for a control of HAA reactivity (see the Introduction and the next section).27,28 All these three thermodynamic components are fully defined based on the combination of two thermodynamic half-reaction cycles – one for the acceptor and one for the donor of the H-atom (Scheme 4). The subtractive combination of two half-reaction diagonals (each of them connecting the radical with its hydrogenated form) defines the reaction energy ΔG0,inf. The effect of the reaction energy on the barrier is well-known: a reaction with more stable products (more negative reaction energy) tends to have a lower barrier.62 The other two thermodynamic factors – η and σ – originate from the subtractive combination of the off-diagonal half-reaction pathways connecting the radical and hydrogenated forms. Asynchronicity accounts for the disparity between the redox and acidobasic component (ΔE° and ΔpKa) of the thermodynamic driving force of the HAA reaction as defined as follows: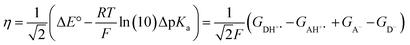 | (5) |
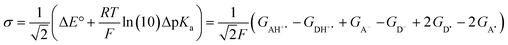 | (6) |
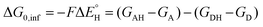 | (7) |
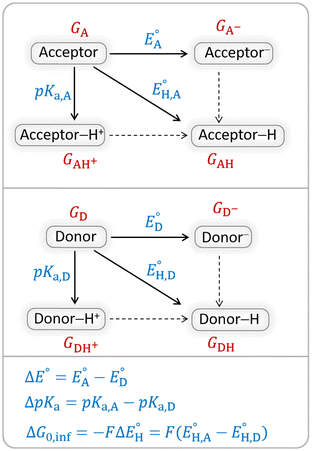 | ||
| Scheme 4 Two half-reaction thermodynamic cycles along with the key thermodynamic characteristics of the H-atom acceptor and donor (also denoted as A and D) – reduction potentials (E°) and acidity constants (pKa). In this study, H-atom donors are the C–H substrates from Fig. 2 and 5′-deoxyadenosine, while H-atom acceptors are the 5′dAdo˙ and CH3˙ radicals. | ||
As a final and important note, the subtractive combination of the two half-reaction cycles to produce three thermodynamic components can be viewed as a tug-of-war between two radicals for three different particles – H-atom (reflected by ΔG0,inf) and two H-atom constituents – electron and proton (reflected together by η and σ).
Analysis of the RC-to-TS HAA barrier components
According to the linearized Marcus-type model for reactivity,27,28 the tunneling-corrected HAA barrier can be decomposed into the four contributions: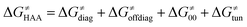 | (8) |
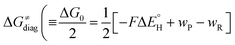 , with quantities defined earlier in the text) is the thermodynamic contribution to the barrier coming from the free energy of reaction going from RC to PC, which is also known as linear free-energy relationship (LFER)62 and
, with quantities defined earlier in the text) is the thermodynamic contribution to the barrier coming from the free energy of reaction going from RC to PC, which is also known as linear free-energy relationship (LFER)62 and 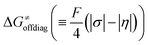 is the thermodynamic contribution to the barrier coming from the frustration (eqn (6)) and asynchronicity (eqn (5)). Altogether, the two barrier contributions can be joined into one thermodynamic term denoted as
is the thermodynamic contribution to the barrier coming from the frustration (eqn (6)) and asynchronicity (eqn (5)). Altogether, the two barrier contributions can be joined into one thermodynamic term denoted as 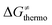 . The third component of the barrier in eqn (8) is
. The third component of the barrier in eqn (8) is 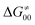 – the term that contains all non-thermodynamic contributions to the barrier, which are specific for a given reaction and depend on the reaction coordinate. Note that
– the term that contains all non-thermodynamic contributions to the barrier, which are specific for a given reaction and depend on the reaction coordinate. Note that 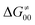 is then determined by subtracting
is then determined by subtracting 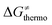 from the tunneling-corrected HAA barrier, using eqn (8). Finally, the fourth component of the barrier is the tunneling correction of the barrier
from the tunneling-corrected HAA barrier, using eqn (8). Finally, the fourth component of the barrier is the tunneling correction of the barrier 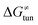 , which may be quite important in reactions such as HAA. It is calculated as
, which may be quite important in reactions such as HAA. It is calculated as 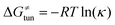 , where κ is the Eckart's tunneling factor for HAA reactions computed using our home-built program (for more details see ESI of ref. 63).
, where κ is the Eckart's tunneling factor for HAA reactions computed using our home-built program (for more details see ESI of ref. 63).
Results and discussion
Referential propensity of 5′dAdo˙ for self-decay reactions and HAA in aqueous environment vs. reactivity in enzymatic microenvironments
The investigation of the three possible reactions of 5′dAdo˙ in aqueous solution, which are cyclization, ring opening or HAA from a substrate, confirms what is known from experiments – HAA activity of the radical is eliminated due to a rapid unimolecular self-decay via either cyclization with a free-energy barrier of 12.0 kcal mol−1 or ring opening with a free-energy barrier of 12.9 kcal mol−1 (Fig. 4, left). The barriers for bimolecular HAA are considerably higher, as exemplified for H-atom abstraction from two (model) radical SAM enzyme substrates – 4 and 5, with the total bimolecular HAA barrier of 21.6 and 19.6 kcal mol−1, respectively (Fig. 4, right). A considerable part of that total barrier corresponds to the formation of RC of 5′dAdo˙ with 4/5, which reaches the respective values of 10.0 and 5.9 kcal mol−1. Thus, the ‘core’ (RC-to-TS) parts of the HAA barriers are then only 11.6 and 13.7 kcal mol−1 (without considering the effect of tunneling) and quite comparable with unimolecular self-decay energetics (cf. the blue and red shaded profiles on the right versus profiles on the left in Fig. 4). Notably, during in-enzyme reactions, the formation of RC does not disfavour HAA relative to the parasitic self-decay reactions as 5′dAdo˙ is generated in situ in the presence of the substrate. This suggests that the enzymatic environment is a crucial ingredient to offset the unfavourable RC formation and effectively directs the reactivity of 5′dAdo˙ toward HAA.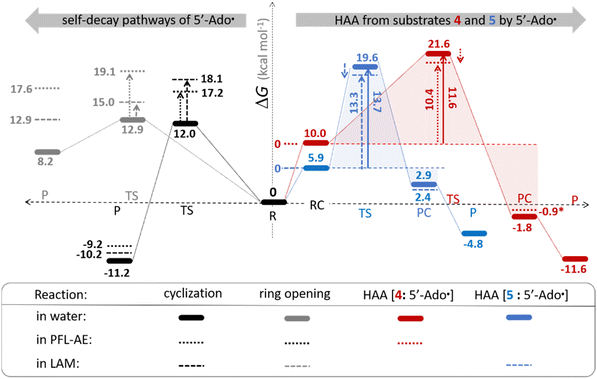 | ||
| Fig. 4 Free-energy reaction profile for the self-decay pathways of 5′dAdo˙ – cyclization and ring opening from Scheme 2 (in black and grey, respectively) vs. free-energy reaction profile for H-atom abstraction from the substrates 4 and 5 by 5′dAdo˙ (in red and blue, respectively) in aqueous solution. The changes in free-energy reaction profiles upon transition from aqueous solution to the enzymatic active site indicated by dotted and dashed lines (for PFL-AE and LAM enzymes, respectively) are also shown. The labels used for the key points in HAA pathways – R, RC, TS, PC and P stand for separated reactants, reactant complex, transition state, product complex and separated products, respectively. The self-decay pathways are unimolecular processes and therefore no RC and PC is present there. Note that the value indicated by * refers to the R-to-PC change of potential energy, considering only the substrate radical and 5′dAdoH moieties taken from the optimized geometry of the cluster model for the PC state of the PFL-AE active site (the R-to-PC free energy of reaction was calculated to be 7 kcal mol−1 due to some changes in interactions between second-shell residues, which are not characteristic of the reaction itself in enzyme). Values for solution were obtained with the B3LYP+D3/def2-TZVP/CPCM(εr = 78.4) protocol, and values for enzyme environment were obtained with the B3LYP/BS1-2/CPCM(εr = 10.0) protocol. For self-decay reactions, addition of water molecules forming hydrogen bonds with 5′dAdo˙ yields comparable results, i.e., the free energy barriers reach 14.3 kcal mol−1 for cyclization and 10.0 kcal mol−1 for ring opening. | ||
In addition, the barriers for H-atom abstraction from 4/5 by 5′dAdo˙ in the cavities of the two prototypic radical SAM enzymes, PLF-AE and LAM, are slightly reduced by only 1.2 and 0.4 kcal mol−1 (dotted and dashed lines in Fig. 4), as compared to their RC-to-TS cognates in water. Thus, the actual enzymatic HAA barriers in the non-tunneling regime are lowered to 10.4 and 13.3 kcal mol−1, whereas the barriers of self-decay pathways are elevated by up to 2–6 kcal mol−1 to reach 15 kcal mol−1 and more. In the majority of radical SAM enzymes, the conformation of 5′dAdo˙ is favourable for self-decay pathways (for details see Fig. S2 in ESI†), indicating that the enzymes must employ other strategies to suppress the otherwise readily accessible self-decay of the H-atom abstracting agent. In more detail, the adenyl group of the 5′dAdo˙ radical is sandwiched in the cavity between vicinal residues (His131, Thr133, Val260, and Asp293 in LAM; Tyr35, His37, Val168, and His202 in PFL-AE; cf.Fig. 2), whose roles are presumably the correct positioning of 5′dAdo˙ for reactivity and, complementarily, the suppression of cyclization by steric means.
Overall, the effect of the enzyme on the RC-to-TS barrier and reaction energy for HAA is probably rather limited (in 1–2 kcal mol−1 relative to barriers in aqueous medium), as witnessed by our calculations on two model enzymatic systems. This indicates that the inherent HAA propensity of 5′dAdo˙ is relatively independent of the environment surrounding the radical and, therefore, valid conclusions regarding the activity of radical SAM enzymes can be made based on investigation of 5′dAdo˙/substrate pairs in aqueous solution, using the three-component thermodynamic model (see the next sections).
H-atom abstraction reactivity of the 5′dAdo˙ radical in aqueous solution
Bearing in mind that a strong H-atom abstraction ability is presumably an inherent property of 5′dAdo˙, we looked into the energetics of HAA reactions in aqueous environment (i) to compare HAA reactivity with the barriers for the self-decay pathways and (ii) to obtain a detailed insight into the mechanism of action of 5′dAdo˙ with the substrates known to be activated via HAA by radical SAM enzymes (substrates listed in Fig. 2). The key energy parameters of the HAA reaction are the free-energy barrier and the thermodynamic driving force, which is the free energy of reaction. From Fig. 5, tunneling-corrected RC-to-TS HAA barriers range from ∼5 to ∼17 kcal mol−1 with ∼30% of them to be higher than the ones corresponding to the ring opening and cyclization pathways with the barrier of 12.0 and 12.9 kcal mol−1, respectively (Fig. 4). Approximately 50% of all calculated tunneling-corrected RC-to-TS barriers are in between 10–12 kcal mol−1 and in only 4 cases above 15 kcal mol−1. Also, almost all of the calculated tunneling-corrected RC-to-PC HAA reactions would eventually be favoured over the self-decay reactions when these parasitic reactions take place in enzymes, where their barriers are shifted up by at least 2 kcal mol−1 (Fig. 4).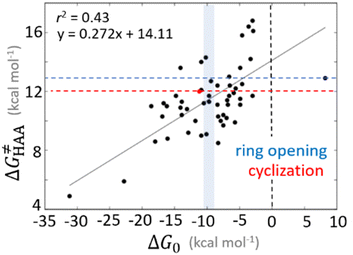 | ||
Fig. 5 Correlation plot between the tunneling-corrected free-energy barrier 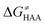 and the free energy of HAA reaction ΔG0 in going from RC to PC (while the two molecules in both RC and PC structures may adopt a considerable amount of conformations/interactions, those consistent with the TS structure were selected). For comparison, the energy parameters for two self-decay reactions are also shown (in red and blue). The grey zone exemplifies points with approximately constant value of ΔG0, diagnosing no effect of the free-energy of reaction on the change of the barrier. All data are also given in Tables S7 and S8 (ESI†) (the subset of reactions modeled with the M06 functional is presented in Tables S9–S11, ESI†). For the sake of comparison, the correlation plot between the tunneling-corrected total free-energy barrier and the free energy of HAA reaction ΔG0 in going from RC to PC (while the two molecules in both RC and PC structures may adopt a considerable amount of conformations/interactions, those consistent with the TS structure were selected). For comparison, the energy parameters for two self-decay reactions are also shown (in red and blue). The grey zone exemplifies points with approximately constant value of ΔG0, diagnosing no effect of the free-energy of reaction on the change of the barrier. All data are also given in Tables S7 and S8 (ESI†) (the subset of reactions modeled with the M06 functional is presented in Tables S9–S11, ESI†). For the sake of comparison, the correlation plot between the tunneling-corrected total free-energy barrier 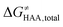 and the free energy of bimolecular HAA reaction ΔG0,inf in going from separated reactants to separated products is given Fig. S3 (ESI†). and the free energy of bimolecular HAA reaction ΔG0,inf in going from separated reactants to separated products is given Fig. S3 (ESI†). | ||
We note in passing that when considering bimolecular HAA reactions from separated reactants to separated products, the barriers are considerably higher. It is ∼75% of all bimolecular HAA reactions that actually have larger barriers than the competitive self-decay pathways (Fig. S3, ESI†), again highlighting the importance of the formation of 5′dAdo˙ in the pre-ordered complex with the substrate in enzyme. All this again suggests that the role of the enzymatic environment might be to suppress the self-decay reactions (but at the same time does not exclude substantial stabilization of the TS for HAA by the binding cavity in some particular cases).
The accessibility of redox and acidobasic properties of 5′dAdo˙
To obtain insight into the mechanism of HAA performed by 5′dAdo˙, we first recall our previous study in ref. 43 where we analyzed redox and basicity properties of the 5′-deoxyadenosyl radical in water vs. enzyme. Therein, the calculations suggested that the basicity of 5′dAdo˙ increases while its reduction potential decreases in passing from solution to enzymatic microenvironment. However, we must emphasize that such redox and acidobasic properties of 5′dAdo˙ in water are coupled with the large geometric and electronic rearrangements upon protonation and reduction. Namely, 1e− reduction of 5′dAdo˙ is connected with the ring cleavage of the ribosyl group, while protonation of 5′dAdo˙ includes the intramolecular ET from adenyl to the ribosyl group (cf. Fig. 7A in ref. 43). These redox and acidobasic properties therefore also reflect energetics involving secondary processes that may not be entirely relevant to HAA reactivity. Alternatively, some other interfering redox centers, as they are present in enzymatic active site (such as Fe4S4), appeared to prohibit the direct characterization of enzymatic 5′dAdo˙ (cf. Fig. 7B in ref. 43). These facts eventually preclude quantitative predictions on how thermodynamics affects the HAA reactivity of 5′dAdo˙ in these two different environments. Nevertheless, from the observed trends in ref. 43, we speculated that enzymatic 5′dAdo˙ is more basic and weaker oxidant than in water solution, and, hence biased toward performing HAA more asynchronously in favor of proton transfer, which may lower enzymatic HAA barrier relative to the referential one in aqueous solution. This conclusion, which we formulated on the basis of the redox and acidobasic properties associated with the accompanying processes, is, inter alia, revised in the present work. As we show later in the text, the mechanism of the reaction (and reactivity thereof) is indeed co-dictated by the redox and acidobasic properties of 5′dAdo˙ vs. substrate but these properties cannot include events that do not occur in HAA. In the next section, we describe the way how such properties are evaluated and linked to off-diagonal thermodynamics contributing to HAA reactivity.Indirect access to the off-diagonal thermodynamic factors based on redistribution of charge during the reaction
The primary challenge in the study of the off-diagonal components of the thermodynamic contribution to the barrier is the instability of 5′dAdo˙ upon its 1e− reduction/protonation, as we already found in our earlier study43 and discussed in the previous section. Also, some of the substrates from Fig. 2 are similarly unstable upon oxidation/deprotonation, i.e., their radical conjugates are unstable upon reduction/protonation. Thus, in order to evaluate the off-diagonal thermodynamics and its effect on the barrier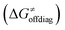 in HAA reactions with 5′dAdo˙, we first identified subset of C–H substrates from Fig. 2, whose off-diagonal thermodynamics can be directly characterized based on the prescription presented in Scheme 4 (the substrates from this subset are listed in Table S1, ESI†).
in HAA reactions with 5′dAdo˙, we first identified subset of C–H substrates from Fig. 2, whose off-diagonal thermodynamics can be directly characterized based on the prescription presented in Scheme 4 (the substrates from this subset are listed in Table S1, ESI†).
For these substrates, we then evaluated the thermodynamic factors η and σ in an accessory set of HAA reactions featuring an auxiliary methyl radical CH3˙ instead of 5′dAdo˙; see the computed data in Fig. 6A and Table S3 (ESI†). In the rest of the text, wherever we refer to the characteristics η and σ for the reaction with CH3˙, we will use the notation η′ and σ′ (and 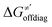 thereof), otherwise η, σ and
thereof), otherwise η, σ and 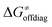 is reserved for reactions with 5′dAdo˙. Employing this set of reactions, we identified an electronic-structure descriptor correlating with asynchronicity η′ (Fig. 6B) as well as with
is reserved for reactions with 5′dAdo˙. Employing this set of reactions, we identified an electronic-structure descriptor correlating with asynchronicity η′ (Fig. 6B) as well as with 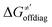 (Fig. 6C); we did not find a descriptor correlating significantly with frustration. Namely, both quantities correlate nicely with the descriptor:
(Fig. 6C); we did not find a descriptor correlating significantly with frustration. Namely, both quantities correlate nicely with the descriptor:
| ΔQ′ = 1/2(|ΔqH| + |ΔqCH3|) | (9) |
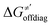 and ΔQ′ is very remarkable (r2 = 0.93), which allows to access
and ΔQ′ is very remarkable (r2 = 0.93), which allows to access 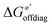 (and η′) for the substrates, for which explicit calculation of the off-diagonal factors was not achievable.
(and η′) for the substrates, for which explicit calculation of the off-diagonal factors was not achievable.
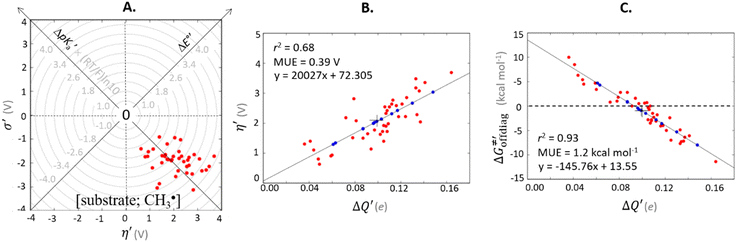 | ||
Fig. 6 (A) Asynchronicity vs. frustration from respective eqn (5) and (6) calculated for the HAA reactions between the C–H bond substrates and the CH3˙ radical. From eqn (5) and (6), the combination of η and σ yields back 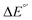 and and 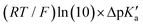 (diagonal axes), which measure differences between CH3˙ and radical conjugate of the substrate in their abilities to be reduced and to be protonated, respectively. As a reference, E° and (RT/F)ln(10) × pKa associated with the CH3˙ radical are calculated to be −1.402 V and −2.786 V, respectively. All the data are shown in Table S3 (ESI†). (B) The correlation between asynchronicity factor and charge redistribution in the transition from separated reactants to TS (ΔQ′) calculated from eqn (9); for a detailed description see Fig. S4 (ESI†). (C) The correlation between the off-diagonal thermodynamic contribution to the barrier from eqn (8) and ΔQ′. Note that red points in all three plots are for substrates, which are directly/explicitly thermodynamically characterized viaScheme 4. The blue points in panels (B) and (C) correspond to the substrates and 5′dAdoH (marked with ‘+’), which are unstable upon oxidation and/or deprotonation and therefore their off-diagonal thermodynamics is approximated using correlation lines in panel (B) and (C). The ΔQ′ values in the panels B and C were obtained using AIM scheme and are explicitly given together with ΔqH and ΔqCH3 in Table S4 (ESI†). (diagonal axes), which measure differences between CH3˙ and radical conjugate of the substrate in their abilities to be reduced and to be protonated, respectively. As a reference, E° and (RT/F)ln(10) × pKa associated with the CH3˙ radical are calculated to be −1.402 V and −2.786 V, respectively. All the data are shown in Table S3 (ESI†). (B) The correlation between asynchronicity factor and charge redistribution in the transition from separated reactants to TS (ΔQ′) calculated from eqn (9); for a detailed description see Fig. S4 (ESI†). (C) The correlation between the off-diagonal thermodynamic contribution to the barrier from eqn (8) and ΔQ′. Note that red points in all three plots are for substrates, which are directly/explicitly thermodynamically characterized viaScheme 4. The blue points in panels (B) and (C) correspond to the substrates and 5′dAdoH (marked with ‘+’), which are unstable upon oxidation and/or deprotonation and therefore their off-diagonal thermodynamics is approximated using correlation lines in panel (B) and (C). The ΔQ′ values in the panels B and C were obtained using AIM scheme and are explicitly given together with ΔqH and ΔqCH3 in Table S4 (ESI†). | ||
Thus, for these C–H substrates as well as the hydrogenated conjugate of 5′dAdo˙ (5′-deoxyadenosine denoted as 5′dAdoH), for which η′ and 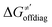 cannot be calculated explicitly, the off-diagonal thermodynamic contributions are estimated based on the respective correlation lines, as presented in Fig. 6B and C. In addition, from the approximated values of η′ and
cannot be calculated explicitly, the off-diagonal thermodynamic contributions are estimated based on the respective correlation lines, as presented in Fig. 6B and C. In addition, from the approximated values of η′ and 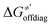 for the reaction between substrate/5′dAdoH and CH3˙, we can eventually determine σ′ as
for the reaction between substrate/5′dAdoH and CH3˙, we can eventually determine σ′ as 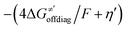 ; this simple combination of η′ and
; this simple combination of η′ and 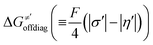 to get σ′ is possible due to the fact that η′ is always positive and σ′ is always negative in presented HAA reactions with CH3˙ (cf.Fig. 6A).
to get σ′ is possible due to the fact that η′ is always positive and σ′ is always negative in presented HAA reactions with CH3˙ (cf.Fig. 6A).
Taking advantage of η′ and σ′ data for all HAA reactions between substrates/5′dAdoH and CH3˙, we can finally evaluate η and σ for reaction between any substrate from Fig. 2 and 5′dAdo˙ as the difference in η′(σ′) between the reaction [substrate; CH3˙] and [5′dAdoH; CH3˙] systems:
| η[substrate; 5′dAdo˙] = η′[substrate; CH3˙] − η′[5′dAdoH; CH3˙] | (10) |
| σ[substrate; 5′dAdo˙] = σ′[substrate; CH3˙] − σ′[5′dAdoH; CH3˙] | (11) |
Analogously, the difference between ΔQ′ of the [substrate; CH3˙] system and ΔQ′ of the [5′dAdoH; CH3˙] system is a measure of the charge redistribution ΔQ′′ in between the substrate and 5′dAdo˙ when going from separated reactants to transition state:
| ΔQ′′[substrate; 5′dAdo˙] = ΔQ′[substrate; CH3˙] − ΔQ′[5′dAdoH; CH3˙] | (12) |
To confirm the relevance of using the radical probe CH3˙ not only to evaluate the off-diagonal thermodynamics of the reactions between the substrate and 5′dAdo˙ (eqn (10) and (11)), but also to faithfully represent the charge redistribution in the [substrate; 5′dAdo˙] reactions, we correlated ΔQ′′ from eqn (12) with
| ΔQ**[substrate; 5′dAdo˙] = ΔQ*[substrate; 5′dAdo˙] − ΔQ*[5′dAdoH; 5′dAdo˙] | (13) |
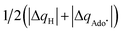 with
with 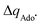 to be always negative and standing for the change of charge on the 5′dAdo˙ moiety, and with ΔqH to be always positive and corresponding to the change of charge of the transferred hydrogen atom in going from separated reactants and to TSHAA. The term ΔqH is again corrected for the charge polarization in the C–H bond upon reactant-to-TS transition of the substrate/5′-deoxyadenosine geometry (cf. Fig. S4 and Table S5, ESI†). In Fig. 7, we show a very nice (almost one-to-one) correlation between ΔQ** from eqn (13) and ΔQ′′ from eqn (12).
to be always negative and standing for the change of charge on the 5′dAdo˙ moiety, and with ΔqH to be always positive and corresponding to the change of charge of the transferred hydrogen atom in going from separated reactants and to TSHAA. The term ΔqH is again corrected for the charge polarization in the C–H bond upon reactant-to-TS transition of the substrate/5′-deoxyadenosine geometry (cf. Fig. S4 and Table S5, ESI†). In Fig. 7, we show a very nice (almost one-to-one) correlation between ΔQ** from eqn (13) and ΔQ′′ from eqn (12).
 | ||
Fig. 7 (A) The correlation of ΔQ** from eqn (13) with ΔQ′′ from eqn (12) and their correlation with asynchronicity η from eqn (10). The interpolation line, mean unsigned error (MUE) and r2 are given for the ΔQ** vs. ΔQ′′ plot. All presented points are for HAA reactions with substrates from Fig. 2. For the data see also Tables S4–S6 (ESI†). Of note, ΔQ* in the [5′dAdoH; 5′dAdo˙] self-exchange reaction in eqn (13) is a constant value of 0.1045e with ΔqH and 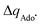 to be 0.137e and −0.072e, respectively. (B) Off-diagonal thermodynamic factors – frustration vs. asynchronicity for HAA by 5′dAdo˙; the points are color coded as in the plot from panel (A). Following eqn (5) and (6), the combination of η and σ yields back ΔE° and (RT/F)ln to be 0.137e and −0.072e, respectively. (B) Off-diagonal thermodynamic factors – frustration vs. asynchronicity for HAA by 5′dAdo˙; the points are color coded as in the plot from panel (A). Following eqn (5) and (6), the combination of η and σ yields back ΔE° and (RT/F)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × ΔpKa (diagonal axes), which measure differences between 5′dAdo˙ and radical conjugate of the substrate in their abilities to be reduced and to be protonated, respectively. Interestingly, ΔQ′′ is almost entirely determined by ΔE°, as evident from the separation and shading of the blue and red points along the ΔE° axis. 10 × ΔpKa (diagonal axes), which measure differences between 5′dAdo˙ and radical conjugate of the substrate in their abilities to be reduced and to be protonated, respectively. Interestingly, ΔQ′′ is almost entirely determined by ΔE°, as evident from the separation and shading of the blue and red points along the ΔE° axis. | ||
Mechanistic interpretation of the ΔQ′′ descriptor and implications on the enzymatic activity of radical SAM enzymes
The reactant-to-TS charge redistribution ΔQ′′ (and ΔQ**) is directly linked to thermodynamically defined asynchronicity (Fig. 7) so that a more asynchronous reaction in favor of ET (more positive η) means more negative ΔQ′′ (and ΔQ**) reflecting more negative charge transferred on the H-atom acceptor 5′dAdo˙ and less positive charge built on H-atom. Conversely, a more asynchronous reaction in favor of PT (more negative η) means more positive ΔQ′′ (and ΔQ**) with less negative charge transferred on the H-atom acceptor 5′dAdo˙ and more positive charge built on H-atom. It is also consistent with the correlations between ΔqH and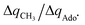 and η presented in Tables S4–S6 (ESI†). In the set of HAAs with 5′dAdo˙, there is a comparable number of reactions asynchronous in favour of PT and ET (∼50% and ∼50% of all reactions, respectively). Also, most of the reactions exhibit a relatively low degree of asynchronicity for H+/e− transfers (65% with |η| less than 700 mV). From that, 5′dAdo˙ appears to be similarly potent as a base and an oxidant in comparison to basicity and one-electron reducibility of radical conjugates of the most studied C–H substrates (cf. relatively low values for ΔE° and (RT/F)ln
and η presented in Tables S4–S6 (ESI†). In the set of HAAs with 5′dAdo˙, there is a comparable number of reactions asynchronous in favour of PT and ET (∼50% and ∼50% of all reactions, respectively). Also, most of the reactions exhibit a relatively low degree of asynchronicity for H+/e− transfers (65% with |η| less than 700 mV). From that, 5′dAdo˙ appears to be similarly potent as a base and an oxidant in comparison to basicity and one-electron reducibility of radical conjugates of the most studied C–H substrates (cf. relatively low values for ΔE° and (RT/F)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × ΔpKa; Fig. 7B and Table S6, ESI†). Since all radical conjugates of the studied substrates, for which E° and pKa could be explicitly calculated, have a (very) negative reduction potential E° (Fig. 6A along with the caption), we conclude that 5′dAdo˙ actually enters HAA as a very weak one-electron oxidant characterized by E° of −1.3 V as well as a very weak base characterized by pKa of −2.2 (i.e., (RT/F)ln
10 × ΔpKa; Fig. 7B and Table S6, ESI†). Since all radical conjugates of the studied substrates, for which E° and pKa could be explicitly calculated, have a (very) negative reduction potential E° (Fig. 6A along with the caption), we conclude that 5′dAdo˙ actually enters HAA as a very weak one-electron oxidant characterized by E° of −1.3 V as well as a very weak base characterized by pKa of −2.2 (i.e., (RT/F)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × pKa of −0.06 V). It should be stressed that the quantification of E° and pKa differs significantly from the 0.28 V and 13 taken from ref. 43. The difference stems from the fact that both the redox and acidobasic values from ref. 43 include processes accompanying the reduction and protonation of water-solvated 5′dAdo˙, such as the ring opening and intramolecular ET, respectively. In contrast, the redox and acidobasic properties of 5′dAdo˙ presented here are devoid of these accompanying and stabilizing processes, indicating that they are closely linked to the methyl-radical group of 5′dAdo˙ and therefore relevant to HAA reactivity.
10 × pKa of −0.06 V). It should be stressed that the quantification of E° and pKa differs significantly from the 0.28 V and 13 taken from ref. 43. The difference stems from the fact that both the redox and acidobasic values from ref. 43 include processes accompanying the reduction and protonation of water-solvated 5′dAdo˙, such as the ring opening and intramolecular ET, respectively. In contrast, the redox and acidobasic properties of 5′dAdo˙ presented here are devoid of these accompanying and stabilizing processes, indicating that they are closely linked to the methyl-radical group of 5′dAdo˙ and therefore relevant to HAA reactivity.
Three-component thermodynamics-based decomposition of barriers for the reaction; the dual role of asynchronicity in hydrogen atom transfer reactions
As noted in the previous sections, the inherent propensity of 5′dAdo˙ for HAA is not strongly affected by the surrounding environment and thus valid conclusions can be made based on the model set of 5′dAdo˙-performed HAA reactions in aqueous solution. From the thermodynamic point of view, we see in Fig. 5 that all studied RC-to-PC HAA reactions are exergonic (i.e., ΔG0 < 0) – likewise in the bimolecular scenario from separated reactants to separated products (cf. Fig. S3, ESI†). It means the 5′dAdo˙ radical forms the stronger C–H bond than any of its native substrates. Although the correlation between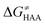 and ΔG0 in Fig. 5 is not so pronounced, it witnesses the effect of the degree of exergonicity on the reaction barrier, i.e., LFER shaping the HAA reactivity of 5′dAdo˙-dependent systems.
and ΔG0 in Fig. 5 is not so pronounced, it witnesses the effect of the degree of exergonicity on the reaction barrier, i.e., LFER shaping the HAA reactivity of 5′dAdo˙-dependent systems.
Nevertheless, it is also apparent that LFER is not the only factor influencing the barrier for HAA as the correlation between ΔG≠ and ΔG0 is not tight and far from an ideal pattern with a slope of ½ (and r2 = 1). In fact, many of the selected subsets cannot be rationalized based on LFER: examples are the points in the grey zone featuring the same ΔG0.
To better understand other factors contributing to the HAA barrier heights along the trajectory going from RC to PC, we performed the analysis based on the eqn (8), which allows to decompose 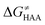 into four contributions (cf. bars in Fig. 8) including the diagonal thermodynamic effect related to the above-discussed LFER
into four contributions (cf. bars in Fig. 8) including the diagonal thermodynamic effect related to the above-discussed LFER 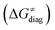 , off-diagonal thermodynamic effect
, off-diagonal thermodynamic effect 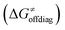 , H-atom tunneling
, H-atom tunneling 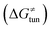 and the reaction-coordinate dependent electronic effects
and the reaction-coordinate dependent electronic effects 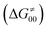 . Of note, the analogous data and analyses for the same reactions but going from separated reactants to separated products are provided in ESI.†
. Of note, the analogous data and analyses for the same reactions but going from separated reactants to separated products are provided in ESI.†
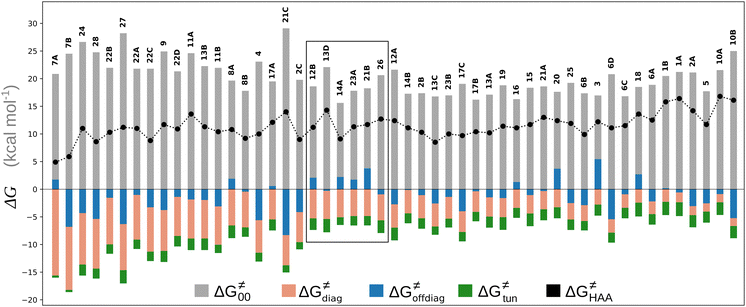 | ||
Fig. 8 The tunneling-corrected free energy barrier for RC-to-PC HAA reactions between 5′dAdo˙ and C–H bond substrates from Fig. 2 (in black), calculated in aqueous solution. The barrier  was decomposed into four terms following eqn (8). HAA reactions are indicated by the labels used for the substrates in Fig. 2. The reactions are ordered following the decrease in the magnitude of RC-to-PC was decomposed into four terms following eqn (8). HAA reactions are indicated by the labels used for the substrates in Fig. 2. The reactions are ordered following the decrease in the magnitude of RC-to-PC 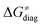 . The reactions in a black frame correspond to the grey zone in Fig. 7. For the sake of comparison, the analogous plot for the HAA reactions going from separated reactants to separated products is given in Fig. S5 (ESI†). . The reactions in a black frame correspond to the grey zone in Fig. 7. For the sake of comparison, the analogous plot for the HAA reactions going from separated reactants to separated products is given in Fig. S5 (ESI†). | ||
First, the LFER term 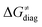 is always negative and decreases the barrier by <10 kcal mol−1 (a few exceptions even more); see the orange part of the bars in the negative region of the vertical axis in Fig. 8.
is always negative and decreases the barrier by <10 kcal mol−1 (a few exceptions even more); see the orange part of the bars in the negative region of the vertical axis in Fig. 8.
Second, the off-diagonal thermodynamic contribution to 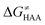 arising from the effect of asynchronicity and frustration is dispersed along the vertical axis in Fig. 8, mostly in the range of −5 to +5 kcal mol−1 as evinced by the blue part of the bars. Despite this variance, 70% of the studied reactions are characterized by a negative contribution
arising from the effect of asynchronicity and frustration is dispersed along the vertical axis in Fig. 8, mostly in the range of −5 to +5 kcal mol−1 as evinced by the blue part of the bars. Despite this variance, 70% of the studied reactions are characterized by a negative contribution 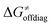 . Thus, for vast majority of these reactions (95%), the sum of the diagonal and off-diagonal contributions remains negative, which means that the overall thermodynamic contribution
. Thus, for vast majority of these reactions (95%), the sum of the diagonal and off-diagonal contributions remains negative, which means that the overall thermodynamic contribution 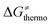 pulls the barrier down in energy.
pulls the barrier down in energy.
Third, the tunneling component of the barrier 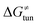 is more or less constant in the presented set of HAA reactions and has a negative contribution to barrier by diminishing it on average by 1.8 kcal mol−1 (the green component of the bars in Fig. 8).
is more or less constant in the presented set of HAA reactions and has a negative contribution to barrier by diminishing it on average by 1.8 kcal mol−1 (the green component of the bars in Fig. 8).
Finally, the 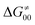 , as the remaining constituent of the HAA barrier, is always positive and has a dominant absolute value in most cases. Notably, it is the factor responsible for the variability of the
, as the remaining constituent of the HAA barrier, is always positive and has a dominant absolute value in most cases. Notably, it is the factor responsible for the variability of the 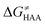 in the grey zone indicated in Fig. 5 (cf. the systems in a black frame in Fig. 8). For better understanding of this term (which by definition absorbs all reaction-coordinate dependent factors), let us rearrange the HAA barrier
in the grey zone indicated in Fig. 5 (cf. the systems in a black frame in Fig. 8). For better understanding of this term (which by definition absorbs all reaction-coordinate dependent factors), let us rearrange the HAA barrier 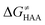 from eqn (8) in an alternative way so that the sum of all contributions to the HAA except for
from eqn (8) in an alternative way so that the sum of all contributions to the HAA except for 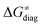 is referred as the intrinsic barrier of the HAA reaction
is referred as the intrinsic barrier of the HAA reaction  . The effect of
. The effect of 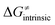 and
and 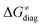 on the HAA barrier is shown in Fig. 9A. The component
on the HAA barrier is shown in Fig. 9A. The component 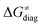 captures what we have already observed in Fig. 5, but it is clear that the complementary component
captures what we have already observed in Fig. 5, but it is clear that the complementary component 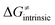 may be even more important in some reaction subsets, as exemplified by the grey region in Fig. 9A. Further decomposition of the intrinsic barrier into off-diagonal thermodynamic
may be even more important in some reaction subsets, as exemplified by the grey region in Fig. 9A. Further decomposition of the intrinsic barrier into off-diagonal thermodynamic 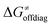 and tunneling-corrected
and tunneling-corrected 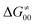 terms reveals the correlation of the two components (Fig. 9B).
terms reveals the correlation of the two components (Fig. 9B).
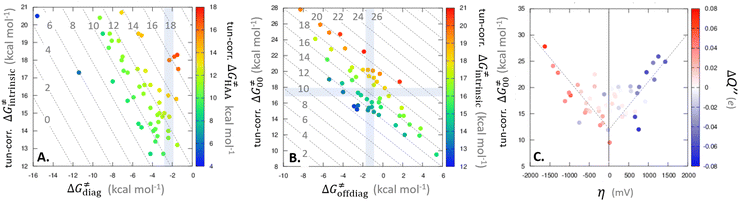 | ||
Fig. 9 (A) The tunneling-corrected  vs. vs. and their effects on the total tunneling-corrected barriers and their effects on the total tunneling-corrected barriers  for RC-to-PC HAA reactions between the C–H substrates from Fig. 2 and the 5′dAdo˙ radical. The iso-contours for tunneling-corrected for RC-to-PC HAA reactions between the C–H substrates from Fig. 2 and the 5′dAdo˙ radical. The iso-contours for tunneling-corrected 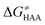 are indicated. (B) The tunneling-corrected are indicated. (B) The tunneling-corrected 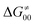 vs. vs.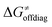 and their effects on and their effects on 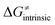 . The iso-contours for tunneling-corrected . The iso-contours for tunneling-corrected 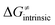 are indicated. (C) are indicated. (C) 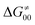 vs. asynchronicity η; the points are color coded according to the charge redistribution ΔQ′′ defined by eqn (12). For the sake of comparison, the analogous plots for the reactions going from separated reactants to separated products is given in Fig. S6 (ESI†). vs. asynchronicity η; the points are color coded according to the charge redistribution ΔQ′′ defined by eqn (12). For the sake of comparison, the analogous plots for the reactions going from separated reactants to separated products is given in Fig. S6 (ESI†). | ||
While there are subsets of reactions characterized by the intrinsic barriers driven solely by 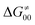 or
or 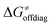 (e.g., the points in the grey zones in Fig. 9B are essentially dependent only on either
(e.g., the points in the grey zones in Fig. 9B are essentially dependent only on either 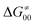 or
or 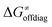 ), overall correlation suggests that
), overall correlation suggests that 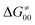 and
and 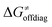 largely compensate each other. Note that neither
largely compensate each other. Note that neither 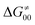 nor
nor 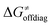 correlate with
correlate with 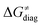 as shown in Table S8 (ESI†). Indeed, the observation that
as shown in Table S8 (ESI†). Indeed, the observation that 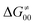 increases as
increases as 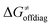 decreases is attributed to the opposite effect of asynchronicity on both HAA barrier components. First,
decreases is attributed to the opposite effect of asynchronicity on both HAA barrier components. First, 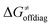 decreases due to an increasing contribution of asynchronicity to
decreases due to an increasing contribution of asynchronicity to 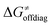 (that is
(that is 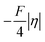 ). Second,
). Second, 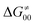 increases as the reaction becomes more asynchronous in favor of either PT or ET component of thermodynamic driving force for reaction. This is evidenced by Fig. 9C, displaying the V-shaped modulation of
increases as the reaction becomes more asynchronous in favor of either PT or ET component of thermodynamic driving force for reaction. This is evidenced by Fig. 9C, displaying the V-shaped modulation of 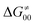 by η, where
by η, where 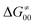 tends to reach its minimum for the most synchronous reactions.
tends to reach its minimum for the most synchronous reactions.
This may seem puzzling as 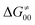 is supposed to be independent of thermodynamic contributions to the overall barrier for the reaction, yet it brings our attention to one crucial characteristic of HAA reactions. Namely,
is supposed to be independent of thermodynamic contributions to the overall barrier for the reaction, yet it brings our attention to one crucial characteristic of HAA reactions. Namely, 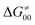 includes the adiabatic coupling (W) between the reactant and product states, which mix along the HAA reaction coordinate and thus contribute to shape the energy profile of the reaction: the stronger the coupling, the greater the mixing and the lower the TS. In other words, the adiabatic coupling also reflects the coupling between PT and ET component in HAA.64–68 Since thermodynamic asynchronicity controls the concertedness of PT and ET in HAA,27,28 the importance of coupling is then expected to decrease when passing from a less asynchronous reaction to a more asynchronous hydrogen atom transfer (HAT) reaction: greater asynchronicity between H+/e− transfers, less coupling and higher
includes the adiabatic coupling (W) between the reactant and product states, which mix along the HAA reaction coordinate and thus contribute to shape the energy profile of the reaction: the stronger the coupling, the greater the mixing and the lower the TS. In other words, the adiabatic coupling also reflects the coupling between PT and ET component in HAA.64–68 Since thermodynamic asynchronicity controls the concertedness of PT and ET in HAA,27,28 the importance of coupling is then expected to decrease when passing from a less asynchronous reaction to a more asynchronous hydrogen atom transfer (HAT) reaction: greater asynchronicity between H+/e− transfers, less coupling and higher 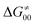 (since the adiabatic coupling must always contribute to
(since the adiabatic coupling must always contribute to 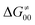 as −|W|). We note in passing that W is strong in HAT reactions, which usually takes place between organic molecules64,66 (as the case of the reaction between C–H substrates and 5′dAdo˙) and therefore, one may expect a relatively large variability of W with changing η. This would contrast to another class of HAA reactions – the related but mechanistically distinct proton-coupled electron transfer (PCET) reactions associated with considerably smaller values of W (usually seen in inorganic chemistry).69–71 In PCET,
as −|W|). We note in passing that W is strong in HAT reactions, which usually takes place between organic molecules64,66 (as the case of the reaction between C–H substrates and 5′dAdo˙) and therefore, one may expect a relatively large variability of W with changing η. This would contrast to another class of HAA reactions – the related but mechanistically distinct proton-coupled electron transfer (PCET) reactions associated with considerably smaller values of W (usually seen in inorganic chemistry).69–71 In PCET, 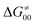 should be therefore effectively independent of η. This was the case that we observed in ref. 27. Of note,
should be therefore effectively independent of η. This was the case that we observed in ref. 27. Of note, 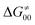 is largely affected by |η| in a strongly adiabatic subspace of radical ligand transfer reactions.72
is largely affected by |η| in a strongly adiabatic subspace of radical ligand transfer reactions.72
In summary, off-diagonal thermodynamics co-determines the HAA barrier directly (as 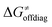 ) and indirectly through modulation of the adiabatic coupling in
) and indirectly through modulation of the adiabatic coupling in 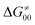 . Because of this indirect effect, these reactions are therefore classified as strongly adiabatic hydrogen-atom transfers.
. Because of this indirect effect, these reactions are therefore classified as strongly adiabatic hydrogen-atom transfers.
Concluding remarks
In this work, we investigated factors modulating reactivity of 5′-deoxyadenosyl radical, a strong hydrogen atom abstractor, which plays a central role for HAA activity of radical SAM enzymes. The study covers HAA reactions with a set of 28 native substrates of radical SAM enzymes as well as two 5′dAdo˙ self-decay processes. The main conclusions of the study are as follows:1. The bimolecular H-atom abstraction from a substrate by 5′dAdo˙ in aqueous environment in most cases indeed features a higher barrier than the competing self-decay reaction. However, a considerable part of this barrier is associated with the formation of a substrate:5′dAdo˙ complex. As a result, the ‘core’ HAA barrier is noticeably lowered and comparable with the barriers for self-decay.
2. The presented HAAs are characterized by a strong (and more or less constant) tunneling factor, which lowers the barrier by ∼2 kcal mol−1 compared to the non-tunneling regime, further favouring HAA compared to the radical self-decay.
3. Nature harnesses the high reactivity of 5′dAdo˙ radical in radical SAM enzymes in two ways: (i) by formation of 5′dAdo˙ in a pre-ordered complex with a substrate present (see point 1), and (ii) by performing the reaction in a tight cavity that hinders radical decay mechanisms by pushing their barriers by 2–5 kcal mol−1, above the referential aqueous solution. In contrast, the transition from water to enzymatic microenvironment does not strongly influence the barrier for HAA in going from reactant complex to transition state. Thus, valuable information can be obtained from the study of the HAA reactivity of 5′dAdo˙ radical based on simplified models in aqueous solution.
4. To analyze HAA reactivity of 5′dAdo˙, we took advantage of the concept of off-diagonal thermodynamics and its effect on reactivity developed in our group. According to this concept, the barrier is not modulated only by the free energy of reaction (the diagonal thermodynamic factor) but also by two off-diagonal thermodynamic factors – frustration and asynchronicity. The two factors arise from combinations of 1e− reduction potentials and basicities of the two radical species that compete over hydrogen atom. To exploit the concept, we had to first deal with the instability of 5′dAdo˙ upon 1e− reduction and protonation, which precluded the direct characterization of the reduction potential and acidity constant of 5′dAdo˙. Instead, we found that off-diagonal thermodynamic factors and hence their contributions to the reaction barriers can be accessed by measuring the change of charge redistribution between the reactants along the reaction coordinate. The descriptor correlates with both asynchronicity and (more remarkably) with the total off-diagonal contribution to the barrier. The methodological aspect of this approach also provides a guide for solving other chemical problems, where the off-diagonal terms are directly unavailable.
5. Examination of HAA-relevant redox and acidobasic properties of 5′dAdo˙ reveals that it is in fact a weak oxidant and a weak base, quite comparable in strength to the radical conjugates of all native substrates under study. This implies a relatively low degree of asynchronicity between proton-transfer and electron-transfer components of HAA reactions between 5′dAdo˙ and most of substrates. This may be one of the ways employed by the radical SAM enzymes to protect themselves from oxidative damage.
6. The decomposition of the HAA barriers into several contributions shows that the diagonal thermodynamic factor (canonical linear free energy relationship) is not the only factor shaping the reactivity of 5′dAdo˙. In the presented set of HAA reactions, it also strongly depends on the intrinsic barrier comprising the off-diagonal thermodynamic component and the non-thermodynamic (reaction-coordinate dependent) component. Globally speaking, the changes of the two contributions across the reaction set are negatively proportional, which can be traced down to the key and dual role of asynchronicity in HAA.
7. Asynchronicity in the presented set of reactions appears to have a two-fold effect on the intrinsic barrier (i) as one of the two components of the direct off-diagonal thermodynamic contribution and (ii) indirectly by affecting the adiabatic coupling, which is a part of the non-thermodynamic component. Since thermodynamic asynchronicity controls the concertedness of the electron and proton transfers, and adiabaticity controls the strength of the coupling between electron and proton transfer, then a larger asychronicity implies smaller adiabatic coupling, which in turn increases the non-thermodynamic component of the HAA barrier. This apparently significant connection between non-thermodynamic component and asynchronicity is likely an imprint of adiabatic hydrogen-atom transfers (HATs), contrasting to proton-coupled electron transfers (PCETs) studied in ref. 27.
Data availability
Data is available in https://zenodo.org/records/11105421 and/or after reasonable request to the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication was supported by the project “The Energy Conversion and Storage”, funded as project no. CZ.02.01.01/00/22_008/0004617 by Programme Johannes Amos Comenius, call Excellent Research and by the Grant Agency of the Czech Republic (Grant No. 24-11247S). MS also acknowledges the Praemium Academiae award by the Czech Academy of Sciences.References
- J. B. Broderick, B. R. Duffus, K. S. Duschene and E. M. Shepard, Chem. Rev., 2014, 114, 4229–4317 CrossRef CAS PubMed.
- B. M. Hoffman, W. E. Broderick and J. B. Broderick, Annu. Rev. Biochem., 2023, 92, 333–349 CrossRef CAS.
- A. K. Boal, T. L. Grove, M. I. McLaughlin, N. H. Yennawar, S. J. Booker and A. C. Rosenzweig, Science, 2011, 332, 1089–1092 CrossRef CAS PubMed.
- E. L. Schwalm, T. L. Grove, S. J. Booker and A. K. Boal, Science, 2016, 352, 309–312 CrossRef CAS.
- P. Dinis, B. M. Wieckowski and P. L. Roach, Curr. Opin. Struct. Biol., 2016, 41, 90–97 CrossRef CAS.
- O. Berteau and A. Benjdia, Photochem. Photobiol., 2017, 93, 67–77 CrossRef CAS.
- A. P. Mehta, S. H. Abdelwahed, N. Mahanta, D. Fedoseyenko, B. Philmus, L. E. Cooper, Y. Liu, I. Jhulki, S. E. Ealick and T. P. Begley, J. Biol. Chem., 2015, 290, 3980–3986 CrossRef CAS.
- J. A. Wiig, Y. Hu, C. C. Lee and M. W. Ribbe, Science, 2012, 337, 1672–1675 CrossRef CAS.
- S. Ouchane, A.-S. Steunou, M. Picaud and C. Astier, J. Biol. Chem., 2004, 279, 6385–6394 CrossRef CAS PubMed.
- A. F. Wagner, M. Frey, F. A. Neugebauer, W. Schäfer and J. Knappe, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 996–1000 Search PubMed.
- S. Ollagnier, E. Mulliez, P. P. Schmidt, R. Eliasson, J. Gaillard, C. Deronzier, T. Bergman, A. Gräslund, P. Reichard and M. Fontecave, J. Biol. Chem., 1997, 272, 24216–24223 CrossRef CAS PubMed.
- K. W. Lieder, S. Booker, F. J. Ruzicka, H. Beinert, G. H. Reed and P. A. Frey, Biochemistry, 1998, 37, 2578–2585 CrossRef CAS PubMed.
- O. T. Magnusson, G. H. Reed and P. A. Frey, J. Am. Chem. Soc., 1999, 121, 9764–9765 CrossRef CAS.
- H. Yang, M. B. Ho, M. N. Lundahl, M. A. Mosquera, W. E. Broderick, J. B. Broderick and B. M. Hoffman, J. Am. Chem. Soc., 2024, 146, 3710–3720 CrossRef CAS PubMed.
- M. Horitani, K. Shisler, W. E. Broderick, R. U. Hutcheson, K. S. Duschene, A. R. Marts, B. M. Hoffman and J. B. Broderick, Science, 2016, 352, 822–825 CrossRef CAS.
- A. S. Byer, H. Yang, E. C. McDaniel, V. Kathiresan, S. Impano, A. Pagnier, H. Watts, C. Denler, A. L. Vagstad, J. Piel, K. S. Duschene, E. M. Shepard, T. P. Shields, L. G. Scott, E. A. Lilla, K. Yokoyama, W. E. Broderick, B. M. Hoffman and J. B. Broderick, J. Am. Chem. Soc., 2018, 140, 8634–8638 CrossRef CAS PubMed.
- M. N. Lundahl, R. Sarksian, H. Yang, R. J. Jodts, A. Pagnier, D. F. Smith, M. A. Mosquera, W. A. van der Donk, B. M. Hoffman, W. E. Broderick and J. B. Broderick, J. Am. Chem. Soc., 2022, 144, 5087–5098 CrossRef CAS PubMed.
- M. N. Lundahl, H. Yang, W. E. Broderick, B. M. Hoffman and J. B. Broderick, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2314696120 CrossRef CAS PubMed.
- H. P. C. Hogenkamp, J. Biol. Chem., 1963, 238, 477–480 CrossRef CAS.
- S. A. Miller and V. Bandarian, J. Am. Chem. Soc., 2019, 141, 11019–11026 CrossRef CAS.
- I. Kempter, B. Frensch, T. Kopf, R. Kluge, R. Csuk, I. Svoboda, H. Fuess and J. Hartung, Tetrahedron, 2014, 70, 1918–1927 CrossRef CAS.
- J. Knappe and A. F. Volker Wagner, Methods in Enzymology, Academic Press, 1995, vol. 258, pp. 343–362 Search PubMed.
- A. Becker, K. Fritz-Wolf, W. Kabsch, J. Knappe, S. Schultz and A. F. Volker Wagner, Nat. Struct. Mol. Biol., 1999, 6, 969–975 CrossRef CAS.
- J. L. Vey, J. Yang, M. Li, W. E. Broderick, J. B. Broderick and C. L. Drennan, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16137–16141 CrossRef CAS.
- M. Moss and P. A. Frey, J. Biol. Chem., 1987, 262, 14859–14862 CrossRef CAS.
- D. J. Aberhart, J. Chem. Soc., Perkin Trans. 1, 1988, 343–350 RSC.
- D. Bím, M. Maldonado-Domínguez, L. Rulíšek and M. Srnec, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E10287–E10294 CrossRef.
- M. Maldonado-Domínguez and M. Srnec, Inorg. Chem., 2022, 61, 18811–18822 CrossRef.
- D. J. Price and C. L. Brooks III, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 Search PubMed.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, J. T. Berryman, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, M. C. Kaymak, E. King, A. K. Valenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O’Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, J. Wang, and H. Wei, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, Amber 2022, University of California, San Francisco, 2022 Search PubMed.
- X. Sheng and F. Himo, Acc. Chem. Res., 2023, 56, 938–947 CrossRef CAS PubMed.
- D. Bím, M. Navrátil, O. Gutten, J. Konvalinka, Z. Kutil, M. Culka, V. Navrátil, A. N. Alexandrova, C. Bařinka and L. Rulíšek, J. Phys. Chem. B, 2022, 126, 132–143 CrossRef.
- M. Prejanò, T. Marino and N. Russo, Front. Chem., 2018, 6, 249 Search PubMed.
- U. Ryde, J. Chem. Theory Comput., 2017, 13, 5745–5752 CrossRef CAS.
- K. M. Merz Jr., Acc. Chem. Res., 2014, 47, 2804–2811 CrossRef PubMed.
- P. E. M. Siegbahn and F. Himo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 323–336 CAS.
- K. H. Hopmann and F. Himo, J. Chem. Theory Comput., 2008, 4, 1129–1137 CrossRef CAS PubMed.
- R. Sevastik and F. Himo, Bioorg. Chem., 2007, 35, 444–457 CrossRef CAS PubMed.
- M. J. Ramos and P. A. Fernandes, Acc. Chem. Res., 2008, 41, 689–698 CrossRef CAS PubMed.
- B. W. Lepore, F. J. Ruzicka, P. A. Frey and D. Ringe, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13819–13824 CrossRef CAS.
- D. Bím, S. Alonso-Gil and M. Srnec, ChemPlusChem, 2020, 85, 2534–2541 CrossRef.
- A. Sato, Y. Hori and Y. Shigeta, Inorg. Chem., 2023, 62, 2040–2048 CrossRef CAS.
- L. Noodleman, T. Lovell, T. Liu, F. Himo and R. A. Torres, Curr. Opin. Chem. Biol., 2002, 6, 259–273 CrossRef CAS.
- A. T. P. Carvalho and M. Swart, J. Chem. Inf. Model., 2014, 54, 613–620 CrossRef CAS PubMed.
- R. A. Torres, T. Lovell, L. Noodleman and D. A. Case, J. Am. Chem. Soc., 2003, 125, 1923–1936 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS.
- T. Hamelryck and B. Manderick, Bioinformatics, 2003, 19, 2308–2310 CrossRef CAS PubMed.
- P. J. A. Cock, T. Antao, J. T. Chang, B. A. Chapman, C. J. Cox, A. Dalke, I. Friedberg, T. Hamelryck, F. Kauff, B. Wilczynski and M. J. L. de Hoon, Bioinformatics, 2009, 25, 1422–1423 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. D. Tissandier, K. A. Cowen, W. Y. Feng, E. Gundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle, J. Phys. Chem. A, 1998, 102, 7787–7794 CrossRef CAS.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066–16081 CrossRef CAS.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019 (http://aim.tkgristmill.com) Search PubMed.
- D. Bím, M. Maldonado-Domínguez, R. Fučík and M. Srnec, J. Phys. Chem. C, 2019, 123, 21422–21428 CrossRef.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS.
- M. Maldonado-Domínguez, D. Bím, R. Fučík, R. Čurík and M. Srnec, Phys. Chem. Chem. Phys., 2019, 21, 24912–24918 RSC.
- S. Hammes-Schiffer, ChemPhysChem., 2002, 3, 33–42 CrossRef CAS PubMed.
- M. Mazzonna, M. Bietti, G. A. DiLabio, O. Lanzalunga and M. Salamone, J. Org. Chem., 2014, 79, 5209–5218 CrossRef CAS PubMed.
- D. Usharani, D. C. Lacy, A. S. Borovik and S. Shaik, J. Am. Chem. Soc., 2013, 135, 17090–17104 CrossRef CAS PubMed.
- O. Tishchenko, D. G. Truhlar, A. Ceulemans and M. T. Nguyen, J. Am. Chem. Soc., 2008, 130, 7000–7010 CrossRef CAS PubMed.
- U. Raucci, M. G. Chiariello, F. Coppola, F. Perrella, M. Savarese, I. Ciofini and N. Rega, J. Comput. Chem., 2020, 41, 1835–1841 CrossRef CAS.
- S. Hammes-Schiffer and A. V. Soudackov, J. Phys. Chem. B, 2008, 112, 14108–14123 CrossRef CAS.
- S. Hammes-Schiffer, J. Am. Chem. Soc., 2015, 137, 8860–8871 CrossRef CAS.
- J. W. Darcy, B. Koronkiewicz, G. A. Parada and J. M. Mayer, Acc. Chem. Res., 2018, 51, 2391–2399 CrossRef CAS PubMed.
- Z. Wojdyla and M. Srnec, Chem. Sci., 2024, 15, 8459–8471 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01725k |
| This journal is © the Owner Societies 2024 |