Open Access Article
Open Access ArticleRecent advances in dynamic modeling and control studies of biomass gasification for production of hydrogen rich syngas
Maham Hussain *a,
Omer Alib,
Nadeem Razacd,
Haslinda Zabirie,
Ashfaq Ahmedf and
Imtiaz Ali
*a,
Omer Alib,
Nadeem Razacd,
Haslinda Zabirie,
Ashfaq Ahmedf and
Imtiaz Ali g
g
aDepartment of Chemical Engineering, NFC Institute of Engineering & Technology, Multan, Pakistan. E-mail: maham.hussain@gmail.com
bDepartment of Electrical Engineering, NFC Institute of Engineering & Technology, Multan, Pakistan
cDepartment of Chemical Engineering Universiti Teknologi PETRONAS, Malaysia
dDepartment of Chemistry, Govt. Alamdar Hussain Islamia Degree College, Multan, Pakistan
eCollege of Science, Department of Chemistry, Imam Muhammad Ibn Saud Islamic University, (IMSIU), Riyadh, Kingdom of Saudi Arabia
fSchool of Engineering, Victoria University Melbourne, Australia
gChemical and Materials Engineering Department, King Abdulaziz University, Rabigh, Saudi Arabia
First published on 8th August 2023
Abstract
The conversion of biomass through thermochemical processes has emerged as a promising approach to meet the demand for alternative renewable fuels. However, these processes are complex, labor-intensive, and time-consuming. To optimize the performance and productivity of these processes, modeling strategies have been developed, with steady-state modeling being the most commonly used approach. However, for precision in biomass gasification, dynamic modeling and control are necessary. Despite efforts to improve modeling accuracy, deviations between experimental and modeling results remain significant due to the steady-state condition assumption. This paper emphasizes the importance of using Aspen Plus® to conduct dynamics and control studies of biomass gasification processes using different feedstocks. As Aspen Plus® is comprising of its Aspen Dynamics environment which provides a valuable tool that can capture the complex interactions between factors that influence gasification performance. It has been widely used in various sectors to simulate chemical processes. This review examines the steady-state and dynamic modeling and control investigations of the gasification process using Aspen Plus®. The software enables the development of dynamic and steady-state models for the gasification process and facilitates the optimization of process parameters by simulating various scenarios. Furthermore, this paper highlights the importance of different control strategies employed in biomass gasification, utilizing various models and software, including the limited review available on model predictive controller, a multivariable MIMO controller.
1 Introduction
Access to energy resources is vital for the survival of human beings, the advancement of social civilization, and the economic prosperity of a nation.1 However, due to population growth and rapid economic development, energy consumption has increased significantly while the supply has become scarce.2 The continuous exploitation of conventional fossil fuels, such as coal, crude oil, and natural gas, has led to depletion and the generation of significant waste,3 resulting in environmental damage and an energy crisis.4,5 As a result, there is an urgent need to develop clean and sustainable alternative energy resources to address these issues. The utilization of renewable energy sources, such as solar, wind, biomass, hydropower, geothermal, and tidal, is becoming increasingly popular due to their potential to mitigate environmental, fossil fuel, and economic issues.6,7 The International Energy Agency (IEA) has recommended transitioning away from fossil fuels due to the increasing demand for energy and the potential scarcity of fossil fuels.8 To reduce emissions and global warming, carbon-neutral sources of energy, such as biomass, are gaining popularity.3In recent decades, there has been increasing attention given to the production of bio-H2 from lignocellulosic biomass through gasification. This process is considered highly efficient, environmentally friendly, and sustainable, as it is a carbon-neutral and renewable energy source.9 Biomass can be converted into hydrogen or syngas using thermochemical and biological methods. Gasification, which is a key thermochemical method, is an important technology for large-scale biomass conversion, and it generates a gaseous mixture consisting of hydrogen, carbon monoxide, carbon dioxide, and methane.10 This syngas can be used as a fuel for power generation and heating or as an intermediate for the production of other chemicals and fuels.10 However, the gasification of biomass requires precise control and management to maintain carbon-free energy systems.10
Mathematical models are necessary for designing, optimizing, and intensifying thermal conversion processes due to their high complexity, involvement of non-linear parameters, and high-dimensional conversion processes.11 These models help in determining optimal operating conditions for a system, as well as in assessing the impact of various features on the outputs. Furthermore, models can be used for real-time process control and optimization, as well as for predicting critical process performance parameters.11
Aspen Plus® is a software tool that can simulate chemical reactions in the petroleum sector, chemical processes, and biomass gasification.12 While steady-state biomass gasification modelling has gained prominence, dynamic modelling and control are essential to evaluate the dynamic operability of the plant under varying environmental conditions.13 Most research employs PI/PID controllers to regulate temperature, flow, pressure, and other process factors,14,15 but modern control research includes multivariate models that incorporate Predictive Model Control (MPC).16 Aspen Plus is a process simulation software that is widely utilized for the modeling and simulation of biomass gasification. Its usefulness lies in the ability to develop both steady-state and dynamic models of the gasification process, enabling various scenarios to be simulated to optimize process parameters. With a comprehensive library of thermodynamic models, Aspen Plus accurately predicts the behavior of gasification reactions. In addition, the software enables the specification of detailed kinetic models that can consider multiple reactions happening simultaneously, and calculate reaction rates. For dynamic and control studies of gasification parameters such as feed rate, temperature, and pressure, Aspen Dynamics is utilized. The software provides a variety of control structures like PID controllers and AMSIMULATION toolboxes, which can be used to link Matlab for model predictive control (MPC) algorithms to achieve optimal process performance. By performing sensitivity analyses, Aspen Plus can determine the impact of changes in process parameters on gasification performance. Therefore, it can be used to identify critical parameters that can be optimized to achieve the desired gasification outcomes. In summary, Aspen Plus® is an essential tool for simulating and modeling biomass gasification, providing accurate predictions of gasification behavior, and allowing for the optimization of process parameters and control strategies.
Several review articles have been published on the steady-state modeling of biomass gasification.17–19 However, most of these studies have focused on steady-state behavior,20–22 with limited attention given to dynamic23–25 and control modeling.26,27 Additionally, some of these articles have only discussed one type of control system, such as decentralized control. Although numerous control strategies have been proposed and evaluated, decentralized control cannot handle the interaction between multiple variables and process constraints, which is crucial for optimal process performance. In contrast, MPC can handle Multiple-Input, Multiple-Output (MIMO) systems consistently and account for explicit constraints acting on a controlled and measured variable. This review article identifies the research gap in the dynamic modelling and control investigations of biomass gasification processes and evaluates the most recent developments and insights. It examines the stoichiometric, non-stoichiometric, and Aspen Plus modelling approaches used in biomass gasification control studies and highlights the best methods reported in the literature.
2 Thermochemical conversion of biomass
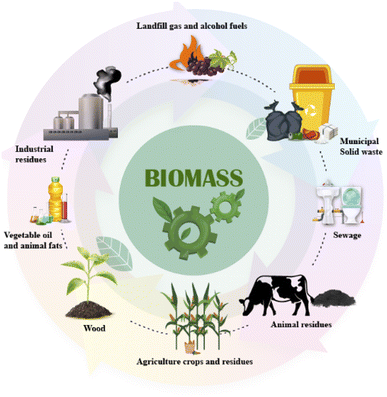
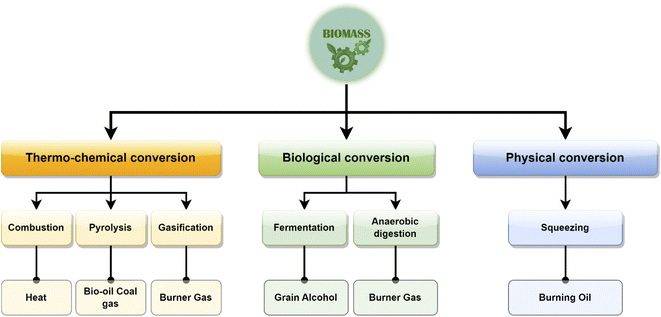
Biomass is described as a renewable carbonaceous resource that exists in a variety of forms and is used to generate heat, power, fuels and other value-added by-products.28 Biomass is classified according to various types of biomass feedstocks from agricultural and forest ecosystem waste (such as animal and plant residues, animal manure) or municipal waste (such as dewatered sludge) as shown in Fig. 1.28 Syngas production, as well as numerous chemical feedstocks, has great potential in the Asian region.29Thermochemical and biochemical conversion are the two basic classes from which syngas can be produced using biomass. The thermochemical conversion process also includes processes such as combustion, pyrolysis, gasification, and liquefaction (hydrothermal upgrading).30 Fermentation, anaerobic digestion, and mechanical extraction are three biochemical conversion processes that convert biomass into energy. The gasification process is a promising method for converting biomass into energy. Gasification has established itself as a potential technology for the development of large-scale biomass-to-syngas production systems. The classification of biomass conversion is shown in Fig. 2.
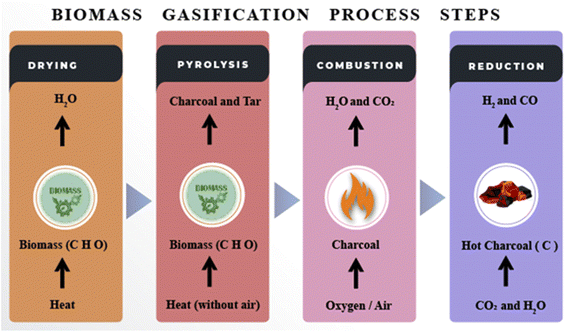
Biomass is converted to a gaseous product, such as H2, CO, CO2, CH4 and N2, using gasifying agents such as air, oxygen, steam or a combination of them, in this process.31 It is useful to use steam as a gasifying agent to produce a better and improved syngas composition.31 Unlike steam, the use of air as a gasifying agent results in an excess of nitrogen in the final gas composition, and the use of pure oxygen has low economic incentives for small-scale operations.32 Typically, biomass with a moisture level of less than 35% by weight is used in the gasification process.33 The steps involved in gasification are shown in Fig. 3.
2.1 Drying and devolatilization
The gasification process starts with a heating and drying step. Initially, the material is dried without any chemical reactions. The amount of time it takes for solids to dry is mainly determined by their particle size and ignition temperature.342.2 Pyrolysis
The thermal decomposition of a solid in the presence of a restricted supply of an oxidizing agent is known as pyrolysis. Eqn (1) can be used to represent the reaction of the pyrolysis process.35
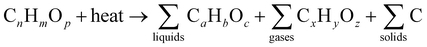 | (1) |
2.3 Combustion
The combustion process is an exothermic reaction that involves oxygen and solid carbon, with CO2 and H2O as the primary combustion products. The combustion process also provides the necessary thermal energy for the endothermic gasification reaction.| C + O2 ⇌ CO2 +401.9 kJ mol−1 | (2) |
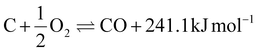 | (3) |
2.4 Gasification
The gasification process involves endothermic reactions that use the heat that is liberated from the combustion reaction. The main product of gasification is the synthesis gas, which comprises gases such as H2, CO, CO2, and CH4.36 The primary reactions involved in the biomass gasification are represented in eqn (4)–(8), respectively:Char gasification reaction
| C + H2O → CO + H2 −131.5 kJ mol−1 | (4) |
Water–gas shift reaction
CO + H2O ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CO2 + H2 +41 kJ mol−1 CO2 + H2 +41 kJ mol−1
| (5) |
Steam methane reforming
CH4 + H2O ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CO + 3H2 −206 kJ mol−1 CO + 3H2 −206 kJ mol−1
| (6) |
Boudouard reaction
| C + CO2 → 2CO −172 kJ mol−1 | (7) |
Methanation reaction
C + 2H2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CH4 +74.8 kJ mol−1 CH4 +74.8 kJ mol−1
| (8) |
The environmental problems associated with carbon dioxide emissions from conventional fossil fuel combustion have increased the development of renewable energy utilization technologies. For sustainable development, biomass as a renewable CO2 neutral energy source provides an increasingly interesting alternative to reduce CO2 emissions. Several conversion technologies, such as biomass pyrolysis, gasification, and liquefaction, are well-known thermochemical conversion processes.37 In this case, biomass gasification provides an option to convert solid biomass into gaseous products, such as hydrogen-rich gases. The product gas quality and quantity would be different depending on the gasifying agent. In recent decades, biomass steam gasification has received a great deal of attention for its ability to use biomass stocks to produce high-quality gas.37 Among all existing hydrogen production technologies, biomass gasification has received significant interest because; (a) the process is fast, (b) the process is efficient, (c) biomass is environmentally friendly, (d) biomass is renewable, etc.38 A biomass gasification process is usually performed with the assistance of a gasification agent, and the most widely used gasification agents are air (air gasification), oxygen (oxygen gasification), steam (steam gasification), etc. Generally, oxygen gasification and steam gasification show better gasification performances and results than air gasification. This is mainly because the dilution of N2 (from the air, about 79 vol% of the air is N2) is avoided during the gasification processes.
Jingjing Zhang et al.39 established an integrated biomass gasification process of catalytic tar steam reforming, methanation and Adsorption Enhanced Reforming (AER) to produce fuel gas rich in hydrogen and methane. A free-fall gasifier followed by a moving-bed upgrading reactor loaded with bed materials was applied as the reaction device. The bed materials consisted of Ni/hematite, calcined limestone, and quartz sand. The Ni/hematite was used to catalyze both tar reforming and methanation, the calcined limestone as a CO2 capturer, and the quartz sand as a diluting agent. In the free-fall reactor, the white pine sawdust was gasified with steam to produce syngas containing tar. The syngas with tar was then introduced upward into the moving-bed reactor and passed through the moving-bed materials. The tar in the syngas was catalytically reformed to produce an H2-rich gas, and the gas then underwent a WGS reaction, CO2 adsorption, and methanation in the upper part of the reactor. The reactions were optimized through a decrease in temperature gradient along with an upward flow of reaction gas in the moving-bed reactor. The influence of the mass ratio of steam-to-biomass (S/B) in the gasifier and the amounts of Ni/hematite and calcined limestone in the bed materials on the reactions was investigated. Under conditions of temperature gradients of 500 to 600 °C, S/B 0.4 and bed materials composed of 20% Ni/hematite, 60% calcined limestone and 20% quartz sand, a mixed fuel gas of H2 and CH4 was obtained with a concentration of over 97 vol%.
Nanou et al.40 added 9.5 wt% KOH to a steam gasification reactor and investigated the kinetics by changing parameters such as steam flow, bed height, and particle size of the char for mass transfer. The reactions followed a first-order rate constant. Alkali metal catalysts significantly enhanced carbon conversion while inhibiting tar formation in biomass gasification processes. Therefore, alkali metal catalysts indicate important effects on the steam reforming process, which improves hydrogen gas production through biomass gasification. Corella et al.41 used small pine wood chips in a fluidized bed gasifier, along with the steam reformer reactor and two shift reactors for hydrogen production. Hydrogen was reported to be 73 vol% with a biomass yield of 140 g kg−1 using a commercial nickel-based catalyst. Furthermore, 90% of the CO was reported to convert to H2 through the water gas shift reaction due to the use of a catalyst in the shift reactors. However, they reported that to achieve the high production rate, the system became increasingly complex; because of the combination of fluidized bed, steam reformer, and two shift reactors, the hydrogen production costs were also very high. But the overall process was technically feasible, which means there were no major technical problems.
3 Modeling of biomass gasification
Several variables, such as feedstock flow rate, gasifying agent, pressure, and temperature, have a significant effect on the gasification process. These factors have a significant impact on the composition of the product gas and the performance of the gasifier.42 Moreover, these parameters are closely related to each other.43 Experimenting to determine the optimal gasifier condition is an expensive and time-consuming process. To optimize the design and operation of a gasifier without experimentation, mathematical modeling has been shown to be a useful technique for analyzing gasifier behavior. Inside the gasifier, mathematical models accurately capture chemical and physical events. The gasifier environment within the gasifier varies from point to point over time.44 As a result of the dynamic changes in the variables that influence the process, the conditions inside the gasifier vary at each stage. The important parameters within the gasifier are temperature, pressure, flow rate, and species concentration, which are interconnected and exhibit dynamic behavior.42,44 In addition, mathematical models have been demonstrated to be effective in providing qualitative guidance on the design, feedstock characteristics, and operating parameters that influence the gasifier's performance. Furthermore, mathematical models have been shown to be effective in providing qualitative guidance on the design, feedstock parameters, and operating parameters that affect the performance of the gasifier.42 Due to the inherent complexity of the biomass gasification process, modeling and simulation for performance prediction are a developing field.45 The mathematical modeling approaches for the gasification process are classified as steady-state modelling or dynamic modelling. In the following sections, a review of recent work by various researchers using dynamic approaches is presented.3.1 Dynamic state modelling & control of biomass gasification
Dynamic modeling is an effective decision-making and policy-making tool for consultants and operators in the design and research of process techno-economics.46 Junxi Jia et al.47 developed a mathematical model of a down-draft gasifier using rubberwood to simulate a steady and transient state of the gasification process. The model is based on the lumped capacitance method, in which the temperature varies with time but always remains uniform, and on the chemical equilibrium. Effects of the equivalence ratio (0.37–0.45), the steam to biomass ratio (0–4), and mass flow rate of biomass (18–25 kg h−1) on the steady and transient characteristics of the gasifier have been studied (Table 1). Robinson P. J. et al.14 present a simple approximation method that uses coal as biomass to develop a gasifier model that can be exported to Aspen Dynamics®. The core concept is to employ a high molecular weight hydrocarbon from the Aspen library as a pseudo fuel. This component should have the same hydrogen to carbon ratio as coal and biomass, which is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Because the dynamics of the gasifier is very fast and the gasifier gas volume is a small proportion of the total volume of the plant, a rigorous high-fidelity dynamic model of the gasifier is not required for many plant-wide dynamic studies. The macroscale thermal, flow, composition, and pressure dynamics are represented by the proposed approximate model. This work does not attempt to optimize the design or control of gasifiers; rather, it gives an idea of how to approximate dynamically simulate coal gasification.
1. Because the dynamics of the gasifier is very fast and the gasifier gas volume is a small proportion of the total volume of the plant, a rigorous high-fidelity dynamic model of the gasifier is not required for many plant-wide dynamic studies. The macroscale thermal, flow, composition, and pressure dynamics are represented by the proposed approximate model. This work does not attempt to optimize the design or control of gasifiers; rather, it gives an idea of how to approximate dynamically simulate coal gasification.
| Authors | Feedstock used | Gasifier type | Model type | Model considerations | Remarks |
|---|---|---|---|---|---|
| Junxi Jia et al.47 | Rubberwood | Downdraft gasifier | Mathematical model | — | — |
| Robinson P. J. et al.14 | Coal | Air | Aspen Dynamics model | — | — |
| Bo Sun et al.48 | Three different coals | Shell gasifier | MATLAB-based model | Flow on walls and accumulation | Step changes in the inlet oxygen-to-coal ratio and steam-to-coal are investigated |
| Baruah D. et al.49 | Woody feedstock | Fixed bed down-draft gasifier | ANN-based model | MLP based ANN model | Biomass composition, reduction temperature is studied |
| Pandey et al.51 | Municipal solid waste (MSW) | Fluidized bed reactor | ANN models | Distribution parameter method | Regulating pump and expander rotating frequency |
| Boujjat H. et al.46 | Beech wood particles | Solar gasification reactor | Mathematical model | Reactor temperature and syngas products | The dynamic control of these solar reactors appears to be feasible and the development of intelligent algorithms plays a key role to cope with solar energy fluctuations |
| J. Salisu et al.56 | Rice husk and plastic | ANN models | Effects of temperature (600–850 °C), steam-to-feed ratio and CaO to feed ratio were examined | A maximum of 69.42 vol% H2 content was obtained at 750 °C from the Aspen plus gasification model | |
| S. Liu et al.57 | Wheat stalk | Integrated supercritical water gasification | ANN models | A process model with 86 types of biomass as raw materials was established, and 4709 samples of power generation indicators were obtained | This work will provide theoretical guidance for the process design and optimization of the ISSCWBPG |
| H. O. Kargbo et al.58 | Waste wood | Fixed bed reactor | Bootstrapped aggregated neural network | Optimal conditions were tested in the laboratory and the experimental results agreed well with the predicted data | Predicted accurately (R2 of 0.999) the gas composition and the 95% confidence bounds for model predictions |
Bo Sun et al.48 investigated the combined cooling, heating, and power (CCHP) systems with condensation heat recovery (CCHP-CHR). The primary energy saving ratio, cost saving ratio, and carbon dioxide emission reduction ratio are all increased by 5.0%, 6.36%, and 2.74%, respectively, by the proposed system. The proposed CCHP-CHR system boosts energy cascade utilisation technology and overall performance. Baruah D. et al.49 developed an ANN-based model for wood gasification using a fixed bed downdraft gasifier and predicted the compositions of gases H2, CO, CO2 and CH4 using input parameters such as C, H, O, ash, moisture content, and the temperature of the reduction zone temperature. Li et al.50 developed a computer-based model based on experimental data to predict the gasification behavior of biomass particles for the production of hydrogen and syngas production. The results showed that an increase in gasification temperature significantly increased the hydrogen yield and Cold Gas Efficiency (CGE). The maximum CGE was also found to have increased by approximately 230% when the reaction temperature increased from 700 to 900 °C. Pandey et al.51 compared MIMO and Multiple Input-Single Output (MISO) ANN models in single and double layer architectures to select the optimal ANN model. Then, the optimal model was applied to predict the performance of Municipal Solid Waste (MSW) gasification in a fluidized bed reactor. Hegazy Rezk et al.52 increased methane production by steam gasification using palm kernel shell and coal bottom ash as a catalyst. Using fuzzy logic and an Adaptive Network-based Duzzy Inference System (ANFIS) framework, a model was developed to simulate methane production by biomass gasification. Additionally, the Marine Predator Algorithm (MPA) is used to calculate the optimal operating parameter for the gasification process. The results indicated that the methane composition reached 52.82 vol% at 678 °C, 0.42 mm, 3.03 and 0.037 wt% for temperature, particle size, CaO/PKS ratio and coal bottom ash, respectively. Using an artificial neural network, Hanif Furqon Hidayat et al.53 examined the control parameters of a gasifier (ANN). The input variables for this model were the combustion temperature, the intake airflow rate, and the discharge airflow rate, while the reactor combustion temperature was the output. The results demonstrated that the two models provide accurate results (R2 = 0.832 and 0.911) with minimal error rates (RMSE values of 0.250 and 0.098). Using the Kalman filter and control, Jinchun Zhang et al.54 suggested a real-time identification model with greater precision. Observations were made of simulation-based studies on gasifier temperature using three fluctuation modes and field application on H2 and CO monitoring for a gasifier with varying starting conditions. The performance of the proposed model is more precise than that of conventional methods. Consequently, the integrated application of the control chart and Kalman filter in monitoring the gasification process parameters has the benefits of high sensitivity to outlier alerts, high identification of variation, and high applicability to multi-mode fluctuations in a variety of settings.
Quoilin et al.55 proposed a dynamic model of the Organic Rankine Cycle (ORC) used to recover energy from a waste heat source with changing flow rate and temperature, focusing on the dynamic performance of heat exchangers, using the distribution parameter technique to describe their transient behavior. Three different PID control schemes were also proposed and compared based on the increase in frequency of the regulator pump and expander. Zhang et al.54 used the moving boundary approach to develop a dynamic control-oriented model for ORC-based waste heat energy conversion systems and then presented a feedback regulation control strategy.
3.2 Identification of biomass gasification system
Using the system identification approach, some researchers have published the empirical linear model of various processes.47,48 The identification method of the subspace system was used by Gatzke et al.49 to establish a quadruple tank system on a laboratory scale. One of the most extensively used laboratory systems in control theory is the 4-Tank System (4TS). It is a well-known MIMO system that may be used to analyze various real-time control systems with nonlinear dynamics. The identification process was carried out without considering any prior knowledge of the process, and no assumptions were made about the state relationships or the number of process states. Only the number of states used in the resulting process model was determined. The developed model was then used for model-based control using Internal Model Control (IMC). Modeling was also performed using step tests and ASPEN software for use with Dynamic Matrix Control (DMC) as shown in Fig. 4.Weyer et al.59 demonstrated the empirical modeling of the water level in an irrigation channel using a system identification technique that considers the previous physical information of the system.59 The structure of the model is derived from mass and momentum balances that employ non-linear equations. The identified process is similar to that of an interacting series process; however, the model only has a single output variable, which is the water level downstream of the irrigation channel. The developed model has a MISO structure. Sotomayor et al.60 presented the multivariable identification of an activated sludge process benchmark using subspace-based algorithms. To overcome the drawbacks of traditional methods in the field of parameter estimation, an evolutionary strategy is proposed. The Genetic Algorithm (GA) technique has proven its effectiveness when applied to identify the parameters of an activated sludge process. Six subspace algorithms were used and their performance was compared to obtain the best model. A discrete-time identification approach based on subspace methods is applied to estimate a nominal MIMO state-space model. The simulation results show that GA can identify the values of the system parameters with high precision. As a result, provide a useful model to be investigated in the control strategies. Despite the very low order of the selected state-space model, it managed to describe the complex dynamics of the process well. However, a drawback of the methods used is that the physical insight of the process in the models is lost, which is characteristic of a black-box model. Wibowo et al.61 developed a MIMO state-space model from input–output data using a linear system identification technique. The subspace identification method using the N4SID algorithm was proposed as a more suitable method for a gaseous pilot plant than Prediction Error Methods (PEM), as indicated by smaller identification and validation errors. In this work, the focus has been on developing a proper procedure and method to construct an empirical model of the interacting series processes from input–output data using a system identification technique. Sivakumar and Mary et al.62 have extended the work using GA to obtain a reduced-order transfer function with a minimum ISE and IAE error.
The ALSTOM gasifier benchmark consists of a 5 input and 4 output systems. The flow rate of extraction of carbon (U1), airflow (U2), coal flow (U3), steam flow (U4), and limestone flow (U5) are inputs, the calorific value of syngas (Y1), the mass of the bed (Y2), the pressure (Y3) and the temperature (Y4) are output. Limestone and coal are added in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. This leaves the gasifier with a 4 × 4 MIMO system. MATLAB has been used to develop the transfer function model. This paper focuses on identifying reduced-order transfer function models for a gasifier with a minimum IAE and ISE error criterion using a GA. The lower order transfer functions obtained using the Genetic Algorithm are found to be superior to those obtained using the RGA loop pairing and the algebraic method proposed, respectively, by Haryanto and Sivakumar et al.63,64
10. This leaves the gasifier with a 4 × 4 MIMO system. MATLAB has been used to develop the transfer function model. This paper focuses on identifying reduced-order transfer function models for a gasifier with a minimum IAE and ISE error criterion using a GA. The lower order transfer functions obtained using the Genetic Algorithm are found to be superior to those obtained using the RGA loop pairing and the algebraic method proposed, respectively, by Haryanto and Sivakumar et al.63,64
3.3 Control strategies for biomass gasification
The main issues and challenges of the 21st century include increased energy consumption, rising energy costs, and climate change caused by greenhouse gases emission into the environment. The international community is increasingly ensuring commitment to sustainability, through increasing use of terms such as renewable bioenergy, renewable bioproducts, and renewable bioeconomy, by proposing the use of renewable energy through effective policymaking and attracting industrial attention. Therefore, a major global priority currently is to increase the use of biomass sources or waste materials containing biomass to generate energy to alleviate and combat problems due to the increasing demand for energy.27 There is a pertinent and emerging requirement for industries to employ newer technologies to efficiently recover biomass and convert it into useful chemicals and fuels of high calorific value. Globally, researchers have been corroborating the growing efforts to promote sustainable growth and zero waste industries by proposing several environmentally friendly processes.27 A. Curcio et al.65 reported on the hybridization strategies of a solar autothermal biomass gasifier for stable and continuous operation under various solar irradiation. The objective of the study was to observe the operational feasibility of the solar biomass conversion process via the oxy-combustion of biomass to control gasification temperature. The purpose of the study was to evaluate the operational viability of a solar biomass conversion process that involves the oxy-combustion of biomass to regulate the gasification temperature. The various hybridizations of the strategies were investigated by thermodynamic analysis and experimental validation. The results showed that controlling the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio above 1 during hybridization required providing high amounts of water steam with oxygen, penalizing efficient heating. However, reducing the water inlet rate changed the H2
CO ratio above 1 during hybridization required providing high amounts of water steam with oxygen, penalizing efficient heating. However, reducing the water inlet rate changed the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio but decreased CO2 production and the solar thermal power requirement. Therefore, control of the flow rate of the outlet H2 + CO volume was demonstrated with respect to the injection of oxygen and wood. Solar-to-fuel efficiencies were maintained around 20%, whereas hybridization decreased the cold-gas efficiency below 80%.
CO ratio but decreased CO2 production and the solar thermal power requirement. Therefore, control of the flow rate of the outlet H2 + CO volume was demonstrated with respect to the injection of oxygen and wood. Solar-to-fuel efficiencies were maintained around 20%, whereas hybridization decreased the cold-gas efficiency below 80%.
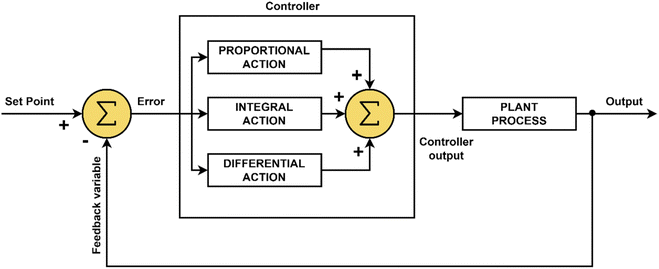
In a biomass gasification plant, the units have non-linearities and high process interactions. The dominance of non-linear behaviour is due to the presence of disturbances and set-point changes, causing the non-linear system to set away from its linear approximation. Therefore, control strategies are crucial in the operational optimization of change and disturbance rejections at the set point of the process, as well as in the reduction in the operational costs of such systems. Control strategies for the biomass gasification process based on decentralized proportional-integral derivative (PID) control could not handle the interaction between multiple controlled and manipulated variables, and the input or control variables have a comparable effect on the outputs. Hence, this will require the implementation of advanced control, such as MPC. Two main advantages of using MPC are that multiple input and multiple output (MIMO) systems are consistently handled.6 Constraints that act on the controlled and measured variables can also be considered explicitly. The ability of MPC to handle constraints makes it more appropriate and preferred than PID control.45 MIMO systems are common in the process industry, where several control objectives and variables are typically available, and the control designer's task is to tune the weighting functions of the optimal control problem to match the objectives. The predictive action of MPC allows future errors to be anticipated, which helps to forecast potential problems in an operation.59
Multiple simultaneous reactions occur within the gasifier, resulting in the formation of several zones, including drying, pyrolysis, oxidation, and reduction zones.71,72 It is extremely challenging to maintain the stable operation of the gasifier to generate syngas with consistent properties at a constant production rate, which is important for subsequent downstream applications.73 The performance of the gasifier could be affected by various factors such as fuel characteristics (particle size, composition, moisture, ash, and energy contents), fuel feed rate, airflow rate, air equivalence ratio, gasifier design, reaction/residence time, gasifying agent, temperature profiles, and pressure.74 Therefore, it is important to simplify the monitoring system to allow accurate control and rapid response to changing operational conditions.75 In addition, one of the key necessities for the control and optimization of a gasification system is the integration of the dynamics of the gasification process and the corresponding scenarios into the actual monitoring and decision-making tool.76 Although much effort has been made to increase the efficiency of the gasification process, improve energy savings, and improve environmental aspects of the gasification process, only partial solutions have been obtained for the partial aspects.76 Many operational parameters related to gasifier and biomass77 such as fuel and airflow rate, composition and moisture content of biomass,78 geometrical configuration and gasifier type,79 reaction/residence time, type of gasifier agent, different sizes of biomass particles,77 different feedstocks,80 gasification temperature and pressure.81 From the process parameters mentioned, the process temperature is one of the most important. It influences the quality of syngas, the reaction rate, and the tar concentration. The low process temperature produces a high tar content,82 low syngas quality, and low cold gas efficiency.83 However, a high process temperature causes unwanted ash to melt. Therefore, the temperature of the process should be controlled.84
Patrick J. Robinson et al.14 performed the dynamic process modelling and control of a coal gasification plant at the National Energy Technology Laboratory (NETL). PI control loops tuned with the Simple Internal Model Control (SIMC) tuning rules are evaluated by disturbing the process with load changes in the flow rate of fuel and changes in the water content of the coal. From the evaluation, it is observed that the dynamics are very fast, with peak temperature deviations taking place about 4 min after the disturbance. The temperature is reported to initially decrease with an increase in fuel flow as a result of the cold temperatures of the feed streams, which lean toward reducing the temperature in the gasifier. However, as more oxygen is fed, the exothermic reaction of CO to CO2 drives the temperature back to the set point. The maximum temperature deviations in the partial oxidizing zone of the gasifier are approximately 25 °F. Vijay Daniel P. et al.85 developed the mathematical modelling and control of a coconut shell biomass gasification process. In this strategy, the control of temperature is studied by manipulating the airflow velocity. The dynamic model is identified as a First-Order-Plus-Time-Delay (FOPTD) process. Comparison between the PI controller and the PID controller showed that the PID controller shows better performance in terms of time-domain specifications and provides better stability. The most important parameter in gasifiers is the need for measurement and control to achieve optimal results for the temperature at which the raw materials react. Kosan Roh et al.10 developed an equation-based dynamic model of the Elevated Pressure Air Separation Unit (EP ASU) system using pulverized coal as a feedstock on the simulation platform of GPROMS. Integrated Gasification Combined Cycle (IGCC) is an alternative power generation system that can use fossil fuels in an eco-friendly way that is in contrast to the conventional pulverized coal-fired plant. An IGCC plant requires an EP ASU that separates air into pure oxygen and nitrogen, which are sent to the gasifier and the gas turbine, respectively. The ASU consumes approximately 10% of the gross power output generated in the IGCC, so economical operation of the ASU is important to lower the overall cost of the power generation cost. In this research, the selection of controlled variables for an EP ASU is studied from the viewpoint of economics, i.e., to maintain an economically (near) optimal operation in the presence of load changes. Instead of full-scale Real-Time Optimization (RTO), they adopted a simpler approach known as Self-Optimizing Control (SOC), which attempts to achieve the objective through a systematic selection of controlled variables. To design and test a self-optimizing control structure, equation-based modelling of EP ASU is carried out using the software platform of GPROMS. Then, the SOC approach is applied based on a model to select the best set of controlled variables, which will lead to the most economical operation in the presence of load changes. Finally, PI control loops are designed, and their dynamic control performances are tested. Furthermore, the economic loss in the presence of load changes is analysed and compared with what was achievable with the use of RTO.
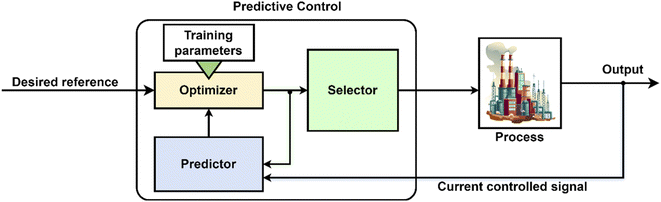
The application of MPC controllers is expected to generally allow for better control performance compared to PI controllers. Gasification is a relatively well-known technology; however, the share of gasification processes that were able to meet general energy demands is small due to current barriers regarding biomass pre-treatment (drying, grinding and densification), gas cleaning (physical, thermal or catalytic), process efficiency, and syngas quality issues.91 Several MPC algorithms have been proposed in the past 30 years.92–94 Examples include Model Predictive Heuristic Control (MPHC), Dynamic Matrix Control (DMC), Generalized Predictive Control (GPC),95 and Internal Model Control (IMC).86 MPC used an optimal control algorithm that incorporates a process model to predict plant behaviour. The MPC algorithm differs in the model used to represent plant dynamics and the cost function.92,96 For gasification control purposes, advanced control concepts have been implemented in several small-scale gasifiers. Elizabeth Saade et al.97 developed a linear Model Predictive Control (MPC) system for a solar thermal reactor for carbon-steam gasification. The controller was designed to minimize the effect of variations in solar irradiation by manipulating the gas and steam flow rates into the reactor. The proposed controller was compared to a multi-loop feedback control strategy comprising two parallel PI controllers. After a four-hour simulation under real conditions, the MPC controller had ISE values of 0.0026 for the synthesis gas fraction and 3819 for the CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio. These values were one order of magnitude smaller than the values obtained with the PI controllers for the same simulation, which were 0.0835 and 37
CO2 ratio. These values were one order of magnitude smaller than the values obtained with the PI controllers for the same simulation, which were 0.0835 and 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 376, respectively. Thus, the MPC controller outperformed the multi-loop feedback control strategy. The results obtained suggest that the proposed controller is suitable for real-world implementation. Rudy Agustriyanto et al.98 tested several multi-loop control structures for the ALSTOM gasifier benchmark process, to determine the most appropriate control structure. The Generalized Relative Disturbance Gain (GRDG) analysis is used to determine the control structure determination. Linear transfer function models are identified from simulated process operation data for five inputs (coal, limestone, air, and steam and char extraction) and four outputs (pressure, temperature, bed mass, and gas quality). Additionally, there is a disturbance input, PSINK, which represents pressure disturbances induced as the gas turbine fuel inlet valve is opened and closed. The Output-Error (OE) method is used in identifying process models because it can lead to models with good long-range prediction (simulation) performance, and hence accurate transfer function models. The results of the GRDG analysis clearly show that the baseline controller proposed by Asmar et al.99 is the preferred multi-loop control structure among their initial designs. This study indicated that the use of RGA analysis is not effective in the selection of control structures for this benchmarking process. It would be possible to find even better control structures using GRDG analysis, and this is under further investigation.
376, respectively. Thus, the MPC controller outperformed the multi-loop feedback control strategy. The results obtained suggest that the proposed controller is suitable for real-world implementation. Rudy Agustriyanto et al.98 tested several multi-loop control structures for the ALSTOM gasifier benchmark process, to determine the most appropriate control structure. The Generalized Relative Disturbance Gain (GRDG) analysis is used to determine the control structure determination. Linear transfer function models are identified from simulated process operation data for five inputs (coal, limestone, air, and steam and char extraction) and four outputs (pressure, temperature, bed mass, and gas quality). Additionally, there is a disturbance input, PSINK, which represents pressure disturbances induced as the gas turbine fuel inlet valve is opened and closed. The Output-Error (OE) method is used in identifying process models because it can lead to models with good long-range prediction (simulation) performance, and hence accurate transfer function models. The results of the GRDG analysis clearly show that the baseline controller proposed by Asmar et al.99 is the preferred multi-loop control structure among their initial designs. This study indicated that the use of RGA analysis is not effective in the selection of control structures for this benchmarking process. It would be possible to find even better control structures using GRDG analysis, and this is under further investigation.
Sidharth Abrol et al.16 developed the methanol synthesis recycle loop model using steady-state and dynamic models to better understand the process behaviour. A linear MPC (4 inputs × 3 outputs) is designed based on a linear process model identified using the data generated from the running of the first-principles models. The model is designed to reject disturbances from a varying upstream syngas production process and to track set-point changes in the desired variables for methanol synthesis. The objective of the controller is to reject any (measured) disturbances observed in the MUG (maximum design rate changed to half the maximum) flow rate, resulting from upstream solar variations over short intervals, and also to track the changes in setpoints corresponding to these disturbances. Wahid et al.100 developed a dynamic model of a steam reformer, which is the main process unit for the production of H2 gas, using the UniSim® process simulator operated in dynamic mode. A First-Order Plus Dead-Time (FOPDT) model is identified and used to design MPC controllers with a sampling-time prediction horizon control horizon of 2 s, 50 s, and 3 s, respectively. The MPC is designed based on two loops that are manipulating; the motor speed and heat of the heat exchanger after the compressor unit, to control the steam pressure that will come to the H2S removal unit; and the inlet and outlet temperatures of the steam reformer. The MPC controller performs better in controlling the pressure and temperature of the steam reformer compressor compared to the PI controller. The MPC shows that it can optimize the system quickly enough, unlike the PI controller, which takes a long time to optimize the system.
The ability of MPC to handle constraints makes it more appropriate and preferred over PID control.101 The predictive action of MPC allows future errors to be predicted, which helps to forecast potential problems in an operation.102 V. Kalaichelvi et al.103 demonstrated that in a biomass boiler combustion system, the boiler drum water level is an important parameter, and it should be measured regardless of whether the boiler steaming water system is in balance or not. For a non-linear process, such as water level control in boilers, conventional control theory is not an appropriate choice. In this study, a neural network-based predictive controller is designed and implemented by simulation in MATLAB software for the control of the water level control. The performance of the neural network controller is compared with that of a conventional PID controller for the water level control system of the boiler drum, and it is observed that the neural network-based approach is more efficient than the conventional PID controller.
Sanjeevi Gandhi et al.68 proposed a MIMO based on experimental data from a wood-based biomass gasification plant. The fuzzy logic controller has been implemented for the transfer function model of the gasifier. The efficiency of a fuzzy controller is compared to conventional controllers for the SISO system gasifier, where the flow is the input and temperature is the output, which has been proposed. A fuzzy logic controller of the MIMO system of gasifiers based on the static model of the gasifier has been proposed, which can be used in controller tuning. The CO/CO2 ratio was well controlled by adjusting the frequency of motion to control the residence time of biomass within the reactor. Similarly, the gasifier temperature control system (SISO) is also effectively controlled with a fuzzy logic controller by adjusting the airflow rate. The performance of the gasifier MIMO system is tested by simulation. Furthermore, the gasifier temperature control system was verified by simulation to ensure that the efficiency of a fuzzy controller was properly verifiable and comparable with that of the conventional controller. Mahapatra and Bequette et al.104 have presented an advanced, centralized, multivariable, predictive control (MPC) model technique to address the controllability of an ASU process (air separations unit) process from integrated gasification combined cycle (IGCC) power plants, and compared the controller performance with decentralized Proportional-Integral (PI) control schemes.104 The ASU model is developed using the Aspen Plus® dynamic simulator, while the MPC is implemented in MATLAB. A 4 × 4 linear transfer function model was developed between each manipulated variable and all controlled variables, and the sample time, prediction, and control horizons were set at 0.1 h, 30 and 3, respectively, based on the time constant values determined from the sensitivity step test. The corresponding weights for the manipulated inputs and controlled variables are set using trial-and-error methods. Constrained linear MPC is considered where upper and lower bounds are imposed on both the manipulated and controlled variables to account for the physical limitations of the plant, including saturation limits in the control valves and operational constraints. Simulation studies based on this design showed the attainment of the desired flow rate and purity levels above acceptable limits within 5–6 h of the 10% step load change demand. It is reported that the linear MPC performed significantly better than the decentralized multi-loop control scheme based on Proportional-Integral (PI controllers), even with absolute and rate-of-change constraints. R. Al Seyab et al.105 developed a simple predictive controller to control an ALSTOM gasifier process using pulverized coal. Using a linear state-space model identified under 0% load condition as the internal model, the controller can achieve all required performance specifications within the input and output constraints. In the predictive controller, a Quadratic Programming (QP) problem is solved online to decide the optimum control moves to steer the output to follow a specified trajectory that keeps the process in the stable operating regions all the time. The novelty of the work is to identify the load condition at 0%, as it is the most difficult case of all three operating conditions of the gasifier to achieve performance specifications. Then, a linear state-space model around 0% load point is used as the internal model for performance prediction. The model works fairly well at other load levels. The controller is implemented using the quadprog function of MATLAB to solve the QP optimization problem. The value of M = 9 s, P = 20 and the sampling time is 1 second (Table 2).
| Authors | Feedstock | Model | Software | PI/PID/MPC | Remarks |
|---|---|---|---|---|---|
| Patrick J. Robinson et al.14 | Coal | Approximate model | Aspen Dynamics | PI | This paper presents an idea of how to dynamically simulate coal gasification approximately |
| Vijay Daniel S. G. et al.106 | Coconut shell | Second-order-plus-time-delay (SOPTD) | MATLAB | PID, PI | It is observed that the PID controller providing less overshoot and settling time during the temperature control process which proves that PID gives better performance for the control of temperature in the biomass gasification process |
| Kosan Roh et al.10 | Pulverized coal | Self-optimizing control | GPROMS | PI | It is verified that self-optimizing control indeed pointed to appropriate choices of cv sets for which economic losses were small (for the chosen load changes) |
| Sidharth Abrol et al.16 | Methanol synthesis | Transfer function models | MATLAB | MPC | By using a linear state-space model identified at 0% load condition as the internal model, the controller can achieve all required performance specifications within the input and output constraints |
| V. Kalaichelvi et al.103 | Biomass boiler combustion system | Neural network controller | MATLAB | PID | It is observed that the neural network-based approach is more efficient than a conventional PID controller. In terms of process stability |
| Mahapatra and Bequette107 | Air separations unit the process from an IGCC power plants | Transfer functions | MATLAB | PI & MPC | MPC controller offers better control performances than the PI controller, especially in multivariable processes |
| R. Al Seyab et al.105 | Pulverized coal | Linear state-space model | MATLAB/SIMULINK | MPC | The new controller meets all the required performance specifications within given input and output constraints during sink pressure disturbance and load change tests and the results show a significant improvement in the process performance |
| Sanjeevi Gandhi et al.68 | Wood | Transfer function model | MATLAB | PID | Disturbance variables: moisture content (Hp) |
| Manipulated variables: airflow rate (FA), and frequency of grate (fg) | |||||
| Controlled variables: throat temperature (T), and CO/CO2 ratio | |||||
| Youssef Karout et al.23 | Biomass | Nonlinear ordinary differential equation | Cantera toolbox | MPC | MPC controller, which is able to find a trade-off between maintaining the reactor's temperature and minimizing oxygen consumption while exploiting the available solar energy, manages to outperform the reference controller |
| Elmaz F. et al.22 | Bio-waste materials | Polynomial regression method | Exogenous neural networks (NARXNN) | MPC | The MPC demonstrated satisfactory performance across all scenarios and exhibited a strong correlation with the experimental data, thereby enhancing its practical applicability |
4 Conclusion
The dynamic nature of biomass gasification involves various stages, including drying, pyrolysis, oxidation, and reduction reactions within the bed and between the solid and gas. While many published studies have focused on steady-state modeling, there have been limited reports on dynamic state modeling, which is essential for control studies. The steady state is simpler, while the dynamic state is more complex due to the different phenomena involved. Therefore, such studies are crucial for future scale-up purposes, especially since the type of feedstock used influences gasification performance. Control strategies play a significant role in optimizing process set point changes, disturbance rejections, and operational cost reduction. However, conventional control structures are not always effective in multivariable systems with higher interactions among variables, such as biomass gasification. This has led to increased interest in modern control algorithms such as model predictive control (MPC), which can handle multiple-inputs multiple-output (MIMO) systems consistently, with constraints explicitly accounted for. Although studies have reported on related applications, there is a research gap in this domain, as there is no concrete framework, architectural model, or middleware platform available. Additionally, there has been no controller study reported for a steam in situ gasification pilot plant model. Aspen Plus is a widely used process simulation software for the modeling and simulation of biomass gasification. Its versatility lies in its capability to create both steady-state and dynamic models of the gasification process, enabling the simulation of various scenarios to optimize process parameters. With a comprehensive library of thermodynamic models, Aspen Plus accurately predicts the behavior of gasification reactions. Moreover, the software allows for the specification of detailed kinetic models that can consider multiple reactions occurring simultaneously and calculate reaction rates. To study the dynamic and control aspects of gasification parameters, such as feed rate, temperature, and pressure, Aspen Dynamics is employed. The software offers an array of control structures, including PID controllers and AMSIMULATION toolboxes, that can link with Matlab for implementing model predictive control (MPC) algorithms to achieve optimal process performance. By conducting sensitivity analyses, Aspen Plus can evaluate the impact of changes in process parameters on gasification performance, allowing for the identification of critical parameters that can be optimized to attain the desired gasification outcomes. In summary, Aspen Plus is an indispensable tool for simulating and modeling biomass gasification, providing precise predictions of gasification behavior, and facilitating the optimization of process parameters and control strategies.Aspen Plus is a prevalent process simulation software that has significant importance in modeling and simulating biomass gasification. It enables the creation of dynamic and steady-state models for the gasification process and facilitates the optimization of process parameters by simulating various scenarios. Additionally, as biomass gasification control studies are crucial, but there is a limited review available on Model Predictive Controller, a multivariable MIMO controller. Moreover, Aspen dynamic is available in Aspen software which helps to estimate the dynamic and control studies of processes. Therefore, it is essential to review and highlight different control strategies employed in biomass gasification, utilizing various models and software.
Aspen Plus is a process simulation software that is widely utilized for the modeling and simulation of biomass gasification. Its usefulness lies in the ability to develop both steady-state and dynamic models of the gasification process, enabling various scenarios to be simulated to optimize process parameters. With a comprehensive library of thermodynamic models, Aspen Plus accurately predicts the behavior of gasification reactions. In addition, the software enables the specification of detailed kinetic models that can consider multiple reactions happening simultaneously, and calculate reaction rates. For dynamic and control studies of gasification parameters such as feed rate, temperature, and pressure, Aspen Dynamics is utilized. The software provides a variety of control structures like PID controllers and AMSIMULATION toolboxes, which can be used to link Matlab for model predictive control (MPC) algorithms to achieve optimal process performance. By performing sensitivity analyses, Aspen Plus can determine the impact of changes in process parameters on gasification performance. Therefore, it can be used to identify critical parameters that can be optimized to achieve the desired gasification outcomes. In summary, Aspen Plus is an essential tool for simulating and modeling biomass gasification, providing accurate predictions of gasification behavior, and allowing for the optimization of process parameters and control strategies.
Nomenclature
| PID | Proportional integral derivative |
| PI | Proportional integral |
| MPC | Model predictive controller |
| Ni | Nickel |
| MIMO | Multiple input multiple output |
| CaO | Calcium oxide |
| PKS | Palm kernel shell |
| MISO | Multiple input single output |
| GA | Genetic algorithm |
| ISE | Internal server error |
| IAE | Integral of absolute error |
| ASU | Air separation unit |
| IGCC | Integrated gasification combined cycle |
| EP ASU | Elevated pressure air separation unit |
| FOPTD | First-order-plus-time-delay |
| RTO | Real-time optimization |
| GRDG | Generalized relative disturbance gain |
| RGA | Relative gain array |
| H2S | Hydrogen sulfide |
| SISO | Single input single output |
| WGS | Water gas shift |
| H2 | Hydrogen |
| CO | Carbon monoxide |
| CO2 | Carbon dioxide |
| CH4 | Methane |
| KOH | Potassium hydroxide |
| ANN | Artificial neural network |
Conflicts of interest
There is no conflict of interest to declare.Acknowledgements
The author would like to acknowledge the coal and renewable energy center at NFC-IET, Multan Pakistan.References
- S. Huseyin, G.-Q. Wei, H.-B. Li, H. Fang and Z. Huang, J. Fuel Chem. Technol., 2014, 42, 922–931 CrossRef CAS.
- P.-C. Kuo, B. Illathukandy, W. Wu and J.-S. Chang, Energy, 2021, 223, 120025 CrossRef CAS.
- F. N. Tubiello, C. Rosenzweig, G. Conchedda, K. Karl, J. Gütschow, P. Xueyao, G. Obli-Laryea, N. Wanner, S. Y. Qiu and J. De Barros, Environ. Res. Lett., 2021, 16, 065007 CrossRef CAS.
- E. Henrich, S. Bürkle, Z. Meza-Renken and S. Rumpel, J. Anal. Appl. Pyrolysis, 1999, 49, 221–241 CrossRef CAS.
- S. Valizadeh, H. Hakimian, A. Farooq, B.-H. Jeon, W.-H. Chen, S. H. Lee, S.-C. Jung, M. W. Seo and Y.-K. Park, Bioresour. Technol., 2022, 128143 CrossRef CAS PubMed.
- A. Rahman, O. Farrok and M. M. Haque, Renewable Sustainable Energy Rev., 2022, 161, 112279 CrossRef.
- T. Güney, Int. J. Sustain. Dev., 2022, 29, 187–194 Search PubMed.
- R. Newell, D. Raimi, S. Villanueva and B. Prest, Global energy outlook 2021: pathways from Paris, Resources for the Future, 2021, vol. 8 Search PubMed.
- C. Guizani, F. E. Sanz and S. Salvador, Fuel, 2013, 108, 812–823 CrossRef CAS.
- K. Roh and J. H. Lee, Ind. Eng. Chem. Res., 2014, 53, 7479–7488 CrossRef CAS.
- Z. A. El-Rub, D. Halawa, I. Alqudah, A. Nasr and M. Naqvi, Fuel, 2023, 346, 128393 CrossRef.
- P. Kamble, Z. Khan, M. Gillespie, J. Mccalmont, I. Donnison and I. Watson, Robust instrumentation and control systems for gasification of biomass, in 26th European Biomass Conference and Exhibition, 2018, pp. 516–520 Search PubMed.
- E. M. B. Aske, Design of plantwide control systems with focus on maximizing throughput, PhD thesis, Norwegian University of Science and Technology (NTNU), 2009.
- P. J. Robinson and W. L. Luyben, Ind. Eng. Chem. Res., 2008, 47, 7784–7792 CrossRef CAS.
- F. Garelli, R. Mantz and H. De Battista, J. Process Control, 2006, 16, 473–483 CrossRef CAS.
- S. Abrol and C. M. Hilton, Comput. Chem. Eng., 2012, 40, 117–131 CrossRef CAS.
- M. Ajorloo, M. Ghodrat, J. Scott and V. Strezov, J. Energy Inst., 2022, 102, 395–419 CrossRef CAS.
- T. Marzoughi, F. Samimi and M. R. Rahimpour, Chem. Eng. Technol., 2022, 45, 620–630 CrossRef CAS.
- N. Mazaheri, A. Akbarzadeh, E. Madadian and M. Lefsrud, Energy Convers. Manage., 2019, 183, 671–688 CrossRef CAS.
- Z. Liu, C. Zhao, L. Cai and X. Long, Energy, 2022, 238, 121616 CrossRef CAS.
- M. Hussain, H. Zabiri, F. Uddin, S. Yusup and L. D. Tufa, Biomass Convers. Biorefin., 2021, 1–14 Search PubMed.
- F. Elmaz, Ö. Yücel and A. Y. Mutlu, Energy, 2020, 191, 116541 CrossRef CAS.
- Y. Karout, A. Curcio, J. Eynard, S. Thil, S. Rodat, S. Abanades, V. Vuillerme and S. Grieu, Clean Technol., 2023, 5, 329–351 CrossRef.
- A. Sachajdak, J. Lappalainen and H. Mikkonen, Energy, 2019, 181, 964–973 CrossRef CAS.
- C. E. Aristizábal-Alzate, P. N. Alvarado and A. F. Vargas, Ing. Invest., 2020, 40, 22–36 CrossRef.
- L. Stanger, A. Schirrer, F. Benedikt, A. Bartik, S. Jankovic, S. Müller and M. Kozek, Energy, 2023, 265, 126378 CrossRef CAS.
- O. P. Verma, G. Manik and S. K. Sethi, Renewable Sustainable Energy Rev., 2019, 100, 90–109 CrossRef.
- K. Yogalakshmi, P. Sivashanmugam, S. Kavitha, Y. Kannah, S. Varjani, S. Adishkumar and G. Kumar, Chemosphere, 2022, 286, 131824 CrossRef PubMed.
- S. H. Shuit, K. T. Tan, K. T. Lee and A. Kamaruddin, Energy, 2009, 34, 1225–1235 CrossRef CAS.
- V. S. Chok, Experimental study of a compartmented fluidized bed gasifier for fuel gas production from oil palm shell biomass, PhD thesis, Curtin University, 2011.
- N. H. Florin and A. T. Harris, Chem. Eng. Sci., 2008, 63, 287–316 CrossRef CAS.
- C. Pfeifer and H. Hofbauer, Powder Technol., 2008, 180, 9–16 CrossRef CAS.
- R. Warnecke, Biomass Bioenergy, 2000, 18, 489–497 CrossRef CAS.
- H. Yang, R. Yan, H. Chen, D. H. Lee and C. Zheng, Fuel, 2007, 86, 1781–1788 CrossRef CAS.
- P. Basue, Biomass Gasification and Pyrolysis Practical Design and Theory, 1st edn, 2010, ISBN: 9780080961620 Search PubMed.
- P. Basu, Combustion And Gasification In Fluidized Beds, Crc Press, 2006 Search PubMed.
- Y. Tursun, S. Xu, A. Abulikemu and T. Dilinuer, Bioresour. Technol., 2019, 272, 241–248 CrossRef CAS PubMed.
- M. Hosseini, I. Dincer and M. A. Rosen, Int. J. Hydrogen Energy, 2012, 37, 16446–16452 CrossRef CAS.
- J. Zhang, M. Wang, S. Xu and Y. Feng, Fuel Process. Technol., 2019, 192, 147–153 CrossRef CAS.
- P. Nanou, H. E. G. Murillo, W. P. Van Swaaij, G. Van Rossum and S. R. Kersten, Chem. Eng. J., 2013, 217, 289–299 CrossRef CAS.
- J. Corella, M. P. Aznar, M. A. Caballero, G. Molina and J. M. Toledo, Int. J. Hydrogen Energy, 2008, 33, 1820–1826 CrossRef CAS.
- P. Basu, Biomass Gasification And Pyrolysis: Practical Design And Theory, Academic Press, 2010 Search PubMed.
- M. Lapuerta, J. J. Hernández, A. Pazo and J. López, Fuel Process. Technol., 2008, 89, 828–837 CrossRef CAS.
- S. Shabbar and I. Janajreh, Energy Convers. Manage., 2013, 65, 755–763 CrossRef CAS.
- J. Warnatz, U. Maas and R. W. Dibble Combustion: Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation, ed. Fizmatlit, Moscow, 2003 Search PubMed.
- H. Boujjat, G. M. Y. Junior, S. Rodat and S. Abanades, Int. J. Hydrogen Energy, 2020, 45, 25827–25837 CrossRef CAS.
- J. Jia, L. Xu, A. Abudula and B. Sun, Energy Convers. Manage., 2018, 155, 138–146 CrossRef CAS.
- B. Sun, Y. Liu, X. Chen, Q. Zhou and M. Su, Fuel Process. Technol., 2011, 92, 1418–1425 CrossRef CAS.
- D. Baruah, D. Baruah and M. Hazarika, Biomass Bioenergy, 2017, 98, 264–271 CrossRef CAS.
- Y. Li, B. Yang, L. Yan and W. Gao, Energy Sources, Part A, 2019, 41, 1336–1343 CrossRef CAS.
- D. S. Pandey, S. Das, I. Pan, J. J. Leahy and W. Kwapinski, Waste Manage., 2016, 58, 202–213 CrossRef CAS PubMed.
- H. Rezk, A. Inayat, M. A. Abdelkareem, A. G. Olabi and A. M. Nassef, Energy, 2022, 239, 122072 CrossRef CAS.
- H. F. Hidayat, R. Setiawan, R. Dhelika, A. Surjosatyo and H. Dafiqurrohman, J. Appl. Eng. Sci., 2022, 1–7 Search PubMed.
- J. Zhang, Y. Zhou, R. Wang, J. Xu and F. Fang, Energy, 2014, 66, 128–138 CrossRef.
- S. Quoilin, R. Aumann, A. Grill, A. Schuster, V. Lemort and H. Spliethoff, Appl. Energy, 2011, 88, 2183–2190 CrossRef CAS.
- J. Salisu, N. Gao, C. Quan, J. Yanik and N. Artioli, J. Energy Inst., 2023, 108, 101239 CrossRef CAS.
- S. Liu, Y. Yang, L. Yu, Y. Cao, X. Liu, A. Yao and Y. Cao, Energy, 2023, 272, 127134 CrossRef.
- H. O. Kargbo, J. Zhang and A. N. Phan, Int. J. Hydrogen Energy, 2023, 48, 10812–10828 CrossRef CAS.
- E. Weyer, Control Eng. Pract., 2001, 9, 1289–1299 CrossRef.
- O. A. Sotomayor, S. W. Park and C. Garcia, Control Eng. Pract., 2003, 11, 961–969 CrossRef.
- T. C. S. Wibowo, N. Saad and M. N. Karsiti, System identification of an interacting series process for real-time model predictive control, in 2009 American control conference, IEEE, 2009, pp. 4384–4389 Search PubMed.
- L. Sivakumar and X. A. Mary, J. Comput. Appl., 2012, 46, 31–38 Search PubMed.
- K. Sivakumar, C. Balamurugan and S. Ramabalan, Comput. Aided Des., 2011, 43, 207–218 CrossRef.
- T. Haryanto, H. Suhartanto and X. Lie, Past, present, and future trend of GPU computing in deep learning on medical images, in 2017 International Conference on Advanced Computer Science and Information Systems (ICACSIS), IEEE, 2017, pp. 21–28 Search PubMed.
- A. Curcio, S. Rodat, V. Vuillerme and S. Abanades, Energy, 2022, 124481 CrossRef CAS.
- O. Marchenko, S. Solomin, A. Kozlov, V. Shamanskiy and I. Donskoy, Appl. Sci., 2020, 10, 7600 CrossRef CAS.
- Y. Muñoz, A. J. Ospino Castro, C. Robles and C. Arizmendi, Int. J. Electr. Comput. Eng., 2019, 66–77 Search PubMed.
- A. S. Gandhi, T. Kannadasan and R. Suresh, Gasification For Practical Applications, 2012, pp. 107–128 Search PubMed.
- B. Gøbel, U. Henriksen, T. K. Jensen, B. Qvale and N. Houbak, Bioresour. Technol., 2007, 98, 2043–2052 CrossRef PubMed.
- S. I. Meramo-Hurtado, P. Puello and A. Cabarcas, ACS Omega, 2020, 5, 19667–19681 CrossRef CAS PubMed.
- I.-S. Antonopoulos, A. Karagiannidis, L. Elefsiniotis, G. Perkoulidis and A. Gkouletsos, Fuel Process. Technol., 2011, 92, 2389–2396 CrossRef CAS.
- J. Watson, Y. Zhang, B. Si, W.-T. Chen and R. De Souza, Renewable Sustainable Energy Rev., 2018, 83, 1–17 CrossRef CAS.
- L. Lombardi, E. Carnevale and A. Corti, Waste Manage., 2015, 37, 26–44 CrossRef PubMed.
- R. Mikulandrić, D. Böhning, R. Böhme, L. Helsen, M. Beckmann and D. Lončar, Energy Convers. Manage., 2016, 125, 264–276 CrossRef.
- Y. Majanne, P. Lautala and R. Lappalainen, Control Eng. Pract., 1995, 3, 1017–1021 CrossRef.
- R. Mikulandrić, D. Lončar, D. Böhning, R. Böhme and M. Beckmann, Energy Convers. Manage., 2015, 104, 135–146 CrossRef.
- T. Y. Ahmed, M. M. Ahmad, S. Yusup, A. Inayat and Z. Khan, Renewable Sustainable Energy Rev., 2012, 16, 2304–2315 CrossRef CAS.
- P. Fowler, G. Krajačić, D. Lončar and N. Duić, Int. J. Hydrogen Energy, 2009, 34, 7027–7040 CrossRef CAS.
- I. Obernberger and G. Thek, Combustion and gasification of solid biomass for heat and power production in Europe-state-of-the-art and relevant future developments, in Proc. of the 8th European Conference on Industrial Furnaces and Boilers (keynote lecture), 2008 Search PubMed.
- M. Aggarwal, B. E. Ydstie, L. R. White and P. Seminar, Modeling Biomass Gasification, in Presentation: PSE Seminar, 2008 Search PubMed.
- H. Boerrigter and R. Rauch, Ecn Biomassa, Kolen En Milieuonderzoek, 2006, vol. 20 Search PubMed.
- M. Puig-Arnavat, J. A. Hernández, J. C. Bruno and A. Coronas, Biomass Bioenergy, 2013, 49, 279–289 CrossRef CAS.
- H. Ghassemi and R. Shahsavan-Markadeh, Energy Convers. Manage., 2014, 79, 18–24 CrossRef CAS.
- L. E. Taba, M. F. Irfan, W. A. M. W. Daud and M. H. Chakrabarti, Renewable Sustainable Energy Rev., 2012, 16, 5584–5596 CrossRef.
- P. Vijay Daniel and A. Sanjeevi Gandhi, Int. J. Control Autom., 2017, 10, 175–184 Search PubMed.
- S. C. Rowe, I. Hischier, A. W. Palumbo, B. A. Chubukov, M. A. Wallace, R. Viger, A. Lewandowski, D. E. Clough and A. W. Weimer, Sol. Energy, 2018, 174, 474–488 CrossRef CAS.
- L. Desborough, Increasing customer value of industrial control performance monitoring-Honeywell’s experience, Preprints of CPC, 2001, pp. 153–186 Search PubMed.
- T. J. Harris, C. Seppala and L. Desborough, J. Process Control, 1999, 9, 1–17 CrossRef CAS.
- S. Padhee and Y. G. Singh, Performance evaluation of different conventional and intelligent controllers for temperature control of shell and tube heat exchanger system, Doctoral dissertation, 2011.
- P. Orukpe, PhD thesis, Imperial College, London, 2005.
- J. A. Ruiz, M. Juárez, M. Morales, P. Muñoz and M. Mendívil, Renewable Sustainable Energy Rev., 2013, 18, 174–183 CrossRef CAS.
- C. Yang, S. Wang, J. Yang, D. Xu, Y. Li, J. Li and Y. Zhang, Green Chem., 2020, 22, 8210–8232 RSC.
- C. Y. Acevedo-Arenas, A. Correcher, C. Sánchez-Díaz, E. Ariza, D. Alfonso-Solar, C. Vargas-Salgado and J. F. Petit-Suárez, Energy Convers. Manage., 2019, 186, 241–257 CrossRef.
- M. A. Nemitallah, A. A. Abdelhafez, A. Ali, I. Mansir and M. A. Habib, Int. J. Energy Res., 2019, 43, 7790–7822 CAS.
- D. W. Clarke, C. Mohtadi and P. Tuffs, Automatica, 1987, 23, 137–148 CrossRef.
- R. Soeterboek, Predictive Control: A Unified Approach, Prentice-Hall, Inc., 1992 Search PubMed.
- E. Saade, D. E. Clough and A. W. Weimer, Sol. Energy, 2014, 102, 31–44 CrossRef CAS.
- R. Agustriyanto and J. Zhang, International Conference on Control, Automation and Systems, IEEE, 2007, pp. 883–888 Search PubMed.
- B. Asmar, W. Jones and J. Wilson, Proc. Inst. Mech. Eng., I: J. Syst. Control Eng., 2000, 214, 441–452 Search PubMed.
- A. Wahid and H. Taqwallah, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 316(1), 012061 Search PubMed.
- E. D. Wilson, Q. Clairon, R. Henderson and C. J. Taylor, Annu. Rev. Control, 2018, 46, 94–106 CrossRef.
- D. E. Seborg, D. A. Mellichamp, T. F. Edgar and F. J. Doyle Iii, Process Dynamics And Control, John Wiley & Sons, 2010 Search PubMed.
- V. Kalaichelvi, R. Ganesh Ram and R. Karthikeyan, Appl. Mech. Mater., 2014, 541, 1260–1265 Search PubMed.
- P. Mahapatra and B. W. Bequette, Ind. Eng. Chem. Res., 2013, 52, 3178–3191 CrossRef CAS.
- R. Al Seyab, Y. Cao and S.-H. Yang, IEE Proc., Control Theory Appl., 2006, 153, 293–301 CrossRef.
- S. G. Vijay Daniel, Int. J. Pure Appl. Math., 2017, 117(10), 13–17 Search PubMed.
- P. Mahapatra and B. W. Bequette, Ind. Eng. Chem. Res., 2012, 52, 3178–3191 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |