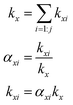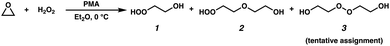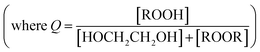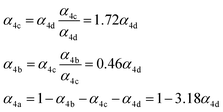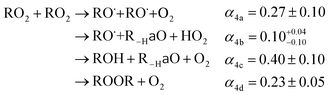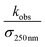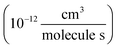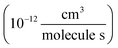Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accretion product formation in the self-reaction of ethene-derived hydroxy peroxy radicals†
Sara E.
Murphy
 *a,
John D.
Crounse
a,
Kristian H.
Møller
*a,
John D.
Crounse
a,
Kristian H.
Møller
 b,
Samir P.
Rezgui
c,
Nicholas J.
Hafeman‡
b,
Samir P.
Rezgui
c,
Nicholas J.
Hafeman‡
 c,
James
Park§
a,
Henrik G.
Kjaergaard
c,
James
Park§
a,
Henrik G.
Kjaergaard
 b,
Brian M.
Stoltz
b,
Brian M.
Stoltz
 c and
Paul O.
Wennberg
c and
Paul O.
Wennberg
 *ad
*ad
aDivision of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA, USA. E-mail: semurphy@caltech.edu
bDepartment of Chemistry, University of Copenhagen, Copenhagen, Denmark
cDivision of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA, USA
dDivision of Engineering and Applied Sciences, California Institute of Technology, Pasadena, CA, USA
First published on 20th March 2023
Abstract
In this study we revisit one of the simplest 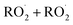 reactions: the self-reaction of the ethene-derived hydroxyperoxy radical formed via sequential addition of ˙OH and O2 to ethene. Previous studies of this reaction suggested that the branching to ‘accretion products’, compounds containing the carbon backbone of both reactants, was minimal. Here, CF3O− GC-CIMS is used to quantify the yields of ethylene glycol, glycolaldehyde, a hydroxy hydroperoxide produced from
reactions: the self-reaction of the ethene-derived hydroxyperoxy radical formed via sequential addition of ˙OH and O2 to ethene. Previous studies of this reaction suggested that the branching to ‘accretion products’, compounds containing the carbon backbone of both reactants, was minimal. Here, CF3O− GC-CIMS is used to quantify the yields of ethylene glycol, glycolaldehyde, a hydroxy hydroperoxide produced from 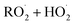 , and a C4O4H10 accretion product. These experiments were performed in an environmental chamber at 993 hPa and 294 K. We provide evidence that the accretion product is likely dihydroxy diethyl peroxide (HOC2H4OOC2H4OH
, and a C4O4H10 accretion product. These experiments were performed in an environmental chamber at 993 hPa and 294 K. We provide evidence that the accretion product is likely dihydroxy diethyl peroxide (HOC2H4OOC2H4OH ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ROOR) and forms in the gas-phase with a branching fraction of 23 ± 5%. We suggest a new channel in the
ROOR) and forms in the gas-phase with a branching fraction of 23 ± 5%. We suggest a new channel in the 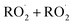 chemistry leading directly to the formation of
chemistry leading directly to the formation of 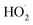 (together with glycolaldehyde and an alkoxy radical). Finally, by varying the ratio of the formation rate of
(together with glycolaldehyde and an alkoxy radical). Finally, by varying the ratio of the formation rate of 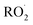 and
and 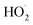 in our chamber, we constrain the ratio of the rate coefficient for the reaction of
in our chamber, we constrain the ratio of the rate coefficient for the reaction of 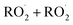 to that of
to that of 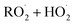 and find that this ratio is 0.22 ± 0.07, consistent with previous flash photolysis studies.
and find that this ratio is 0.22 ± 0.07, consistent with previous flash photolysis studies.
Environmental significancePeroxy radicals formed via oxidation of hydrocarbons in the troposphere play a central role in the radical cycling of the atmosphere. These compounds participate in reactions that terminate radical chemistry and in reactions that propagate the radical chemistry. Quantifying the relative importance of such reactions is important for understanding the impact of hydrocarbon emissions on tropospheric chemistry, including the chemistry that degrades air quality. In this work, we quantify the formation of a C4 accretion product from the self-reaction of ethene-derived hydroxy peroxy radicals. In contrast to previous studies, the radical terminating reaction producing the accretion product is significant. The formation of such accretion products offers a more efficient pathway for peroxy radicals to form secondary organic aerosol. |
1 Introduction
Non-methane hydrocarbons are emitted to the atmosphere by both anthropogenic and biogenic processes at a rate of approximately 1.5 gigatons per year, making their chemistry an essential driver of tropospheric composition.1 In the atmosphere, these compounds are oxidized by reaction with ˙OH,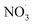 , Cl˙, or O3, often followed by addition of O2 to form organic peroxy radicals
, Cl˙, or O3, often followed by addition of O2 to form organic peroxy radicals 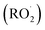 .1–3
.1–3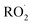 undergo a myriad of bimolecular and unimolecular reactions, including reactions that lead to radical termination or radical propagation. Some
undergo a myriad of bimolecular and unimolecular reactions, including reactions that lead to radical termination or radical propagation. Some 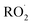 reactions lead to the formation of highly oxidized organic molecules (HOMs) and subsequent particle formation and/or growth. To predict the effects of peroxy radical reactions on tropospheric chemistry, accurate measurements of the rates and products of their uni- and bimolecular reactions are required.
reactions lead to the formation of highly oxidized organic molecules (HOMs) and subsequent particle formation and/or growth. To predict the effects of peroxy radical reactions on tropospheric chemistry, accurate measurements of the rates and products of their uni- and bimolecular reactions are required.
The diverse 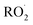 reaction pathways yield products with differing effects on atmospheric chemistry and air quality. In environments with elevated NO˙,
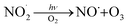
reaction pathways yield products with differing effects on atmospheric chemistry and air quality. In environments with elevated NO˙, 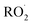 react to form alkoxy radicals (RO˙) (Reaction (1a)) and alkyl nitrates (RONO2) (Reaction (1b)). Reaction (1a) generally propagates the radical chemistry leading to the formation of ozone (Reaction (2)):3,4
react to form alkoxy radicals (RO˙) (Reaction (1a)) and alkyl nitrates (RONO2) (Reaction (1b)). Reaction (1a) generally propagates the radical chemistry leading to the formation of ozone (Reaction (2)):3,4
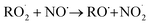 | (1a) |
| →RONO2 | (1b) |
 | (2) |
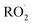 undergo unimolecular5 or bimolecular reactions with
undergo unimolecular5 or bimolecular reactions with 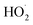 or other
or other 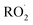 . For β-hydroxyperoxy radicals, reaction with
. For β-hydroxyperoxy radicals, reaction with 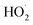 leads to the formation of hydroperoxides (ROOH) (Reaction (3a)) or other products such as RO˙ (Reaction (3b)) or a carbonyl, which in the case of the title reaction will be an aldehyde (R−H
leads to the formation of hydroperoxides (ROOH) (Reaction (3a)) or other products such as RO˙ (Reaction (3b)) or a carbonyl, which in the case of the title reaction will be an aldehyde (R−H![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (Reaction (3c)):3
O) (Reaction (3c)):3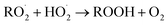 | (3a) |
| →RO˙ + ˙OH + O2 | (3b) |
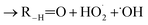 | (3c) |
The 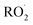 self- and cross-reactions include both radical propagating channels ((4a), (4b)) and radical terminating channels ((4c), (4d)). Reactions (4a), (4c), and (4d) have been observed or proposed previously,3 while Reaction (4b) is proposed here to explain the excess yield of R−H
self- and cross-reactions include both radical propagating channels ((4a), (4b)) and radical terminating channels ((4c), (4d)). Reactions (4a), (4c), and (4d) have been observed or proposed previously,3 while Reaction (4b) is proposed here to explain the excess yield of R−H![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O relative to that of ROH, even in the absence of O2:
O relative to that of ROH, even in the absence of O2:
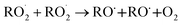 | (4a) |
→RO˙ + R−H![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + HO2 O + HO2 | (4b) |
→ROH + R−H![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + O2 O + O2 | (4c) |
| →ROOR + O2 | (4d) |
The rates and products of Reaction (1) in simple peroxy radical systems have been studied in detail and are generally well known,3 while those of Reaction (3) are more uncertain. Reaction (3a) is the dominant channel for most simple organic peroxy radical reactions. In more substituted 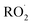 , other channels, such as Reaction (3b) and (3c), become non-negligible.3,6
, other channels, such as Reaction (3b) and (3c), become non-negligible.3,6
The dynamics of Reaction (4) are complex as these pathways require significant electronic rearrangement and/or hydrogen shifts.7 The proposed mechanism of Reaction (4d) requires an intersystem crossing (ISC)7 and was previously believed to be unimportant to the chemistry of the troposphere1,3 (see ESI Appendix A†). Recent studies utilizing chemical ionization mass spectrometry (CIMS) techniques, however, have detected compounds with molecular weights matching the expected products of Reaction (4d), generating renewed interest in quantifying the formation of these peroxides (one of several compounds known as accretion products).1,8,9 In fact, several studies have found that for some 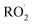 , Reaction (4d) may proceed at rates approaching the collision rate, suggesting a drastic shift from previous assumptions.1,8,10 [While this manuscript was under peer-review, Yue et al. reported11 that a peroxide is produced in the
, Reaction (4d) may proceed at rates approaching the collision rate, suggesting a drastic shift from previous assumptions.1,8,10 [While this manuscript was under peer-review, Yue et al. reported11 that a peroxide is produced in the 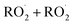 chemistry following H-abstraction from ethane at approximately 10% yield, using VUV photoionization mass spectrometry at 266 Pa and 298 K].
chemistry following H-abstraction from ethane at approximately 10% yield, using VUV photoionization mass spectrometry at 266 Pa and 298 K].
Investigation of the production of peroxides via Reaction (4d) is of additional importance due to their potential to form secondary organic aerosol (SOA).12 Organic aerosols play an important role in climate forcing and have a negative impact on human health, but many routes leading to their formation are poorly quantified. Accretion products formed in Reaction (4d) are much higher in carbon and oxygen numbers than the reactants and therefore have much lower volatility, increasing the likelihood that they condense from the gas phase to the particle phase.4 In both laboratory and field experiments, compounds with masses assigned to such accretion products have been observed in the aerosol and in the gas phase,1,8,9,12 confirming that their production can play an important role in the formation and growth of SOA. However, their identity and mechanism of formation remain unclear.
In this study, we revisit the self-reaction of the ethene-derived hydroxyperoxy radical, 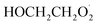 . Previous studies have suggested that the formation of accretion products in this reaction is minimal.13 In contrast, we find that the branching fraction, α4d, is 23 ± 5%. Using H/D exchange experiments, GC techniques, and synthesized standards, we provide evidence that the accretion product is dihydroxy diethyl peroxide (HOCH2CH2OOCH2CH2OH). We propose a new channel leading to direct
. Previous studies have suggested that the formation of accretion products in this reaction is minimal.13 In contrast, we find that the branching fraction, α4d, is 23 ± 5%. Using H/D exchange experiments, GC techniques, and synthesized standards, we provide evidence that the accretion product is dihydroxy diethyl peroxide (HOCH2CH2OOCH2CH2OH). We propose a new channel leading to direct 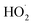 production, Reaction (4b). Finally, we constrain the rate coefficient for Reaction (4) from the ratio of products produced in this reaction to ROOH produced via Reaction (3a).
production, Reaction (4b). Finally, we constrain the rate coefficient for Reaction (4) from the ratio of products produced in this reaction to ROOH produced via Reaction (3a).
2 Experimental
2.1 Experimental design
Our goal in this investigation is to quantify the branching fractions and constrain the rate coefficient for the self-reaction of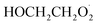 radicals formed following the sequential addition of ˙OH and O2 to ethene:
radicals formed following the sequential addition of ˙OH and O2 to ethene: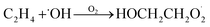 | (5) |
˙OH is produced via the photolysis of H2O2. Eight Sankyo Denki G40T10 254 nm lamps illuminated for 2 min yield a mean photolysis frequency for Reaction (6) of 3.0 ± 0.5 × 10−4 s−1:
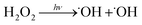 | (6) |
To determine the fraction of ethene reacted, we measured the ˙OH exposure ([OH] × time) from the decay of 2,3-butanediol during the oxidation period in several of our experiments. The primary product of this reaction, 2-hydroxy-3-butanone, is not made elsewhere in our reaction system. The rate coefficient for the reaction of ˙OH with 2,3-butanediol has been reported by Bethel et al. using the relative rate method to be 2.4 ± 0.6 × 10−11 cm3 molecule−1 s−1.14 Bethel et al. measured this rate coefficient relative to that of ˙OH + n-octane, for which they assumed a value of 8.67 ± 0.17 × 10−12 cm3 molecule−1 s−1.15 Current recommendations suggest that the rate coefficient of ˙OH with n-octane at 298 K is somewhat slower (8.11 × 10−12 cm3 molecule−1 s−1)16 so we use 2.25 ± 0.6 × 10−11 cm3 molecule−1 s−1 for the ˙OH + 2,3-butanediol rate constant in this analysis. Approximately 500 ppbv of butanediol was injected during these experiments. When 2,3-butanediol was not injected, we used a photochemical kinetic box model to determine the ˙OH exposure. For the experiments with added butanediol, the modeled and measured ˙OH exposure agree to within 30%. The total ˙OH exposure during our experiments was between 0.8 × 109–4.3 × 109 molecules s cm−3. To minimize secondary chemistry, the lights were turned off before 10% of the initial ethene had reacted, usually after 2 minutes. Specific experimental conditions for each experiment used in this analysis are given in Appendix B of the ESI (Table S1).†
The branching fractions for Reaction (4) are determined from the formation of the products. Note that in this study, we use the following definitions, where j is the total number of possible pathways of Reaction X, αxi is the branching fraction of pathway i of Reaction X, and kx is the rate constant of a Reaction X:
To quantify the ratio of the radical terminating branching channels, 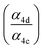 , we measured the yields of ethylene glycol (EG) and dihydroxy diethyl peroxide (ROOR). In the absence of secondary chemistry, the ratio of their concentration is equal to the ratio of their branching fractions. Secondary losses of the products by reaction with ˙OH is calculated to be minimal due to the small fraction of ethene oxidized during the experiment, and the main loss is photolysis. As described in the ESI (Appendix C),† we measured upper limits to the photolysis loss rates for EG, ROOH, glycolaldehyde (GA), and ROOR and find that these losses are also small (negligible for EG, less than 1% of GA, and less than 6% of ROOR and ROOH in a typical experiment). Additionally, we measured the wall loss rates for these compounds as a function of time and find that, over the time period of our experiments, these losses are negligible.
, we measured the yields of ethylene glycol (EG) and dihydroxy diethyl peroxide (ROOR). In the absence of secondary chemistry, the ratio of their concentration is equal to the ratio of their branching fractions. Secondary losses of the products by reaction with ˙OH is calculated to be minimal due to the small fraction of ethene oxidized during the experiment, and the main loss is photolysis. As described in the ESI (Appendix C),† we measured upper limits to the photolysis loss rates for EG, ROOH, glycolaldehyde (GA), and ROOR and find that these losses are also small (negligible for EG, less than 1% of GA, and less than 6% of ROOR and ROOH in a typical experiment). Additionally, we measured the wall loss rates for these compounds as a function of time and find that, over the time period of our experiments, these losses are negligible.
GA is produced in excess of EG in these experiments, consistent with significant additional sources beyond Reaction (4c). In 993 mbar of air, we attribute approximately half of the excess to the reaction of oxygen with the alkoxy radicals formed in Reaction (4a) and (4b):
 | (7a) |
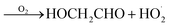 | (7b) |
The fraction of the excess GA that results from Reaction (7b) is well-explained using results from Orlando et al.17 for experiments performed here under both much higher and lower [O2] as discussed in Appendix C of the ESI.† Theoretically, direct hydrogen atom elimination from the initially produced hot alkoxy radical could also explain the excess glycolaldehyde production at low O2, but it is expected that C–C bond scission will be much faster. Thus, we tentatively attribute the remaining excess GA to Reaction (4b).
To further constrain the branching fractions and kinetics of Reaction (4), we perform a series of experiments varying the ratio of the formation rates of 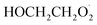 and
and 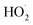 . In the absence of external sources,
. In the absence of external sources, 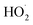 is produced directly in Reaction (4b) and indirectly via the subsequent chemistry of alkoxy radicals, e.g. decomposition (Reaction (7a)) or via their reaction with O2 (Reaction (7b)). We increase the formation rate of
is produced directly in Reaction (4b) and indirectly via the subsequent chemistry of alkoxy radicals, e.g. decomposition (Reaction (7a)) or via their reaction with O2 (Reaction (7b)). We increase the formation rate of 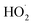 relative to
relative to 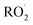 by adding CH3OH to the chamber, which provides an external source of
by adding CH3OH to the chamber, which provides an external source of 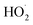 independent of
independent of 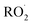 :
:
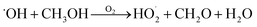 | (8) |
A small amount of additional 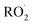 is also produced in our experiments in Reaction (9):
is also produced in our experiments in Reaction (9):
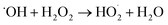 | (9) |
As our independent variable, we define Fexternal, the ratio of the 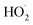 produced externally to Reaction (4)via Reactions (8) and (9) to the amount of
produced externally to Reaction (4)via Reactions (8) and (9) to the amount of 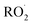 produced via Reaction (5), where the kR are the relevant reaction rate coefficients:
produced via Reaction (5), where the kR are the relevant reaction rate coefficients:
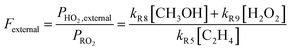 | (10) |
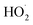 is produced only as a result of Reaction (4). In this ‘high
is produced only as a result of Reaction (4). In this ‘high 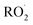 ’ limit, significantly more
’ limit, significantly more 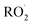 is produced in the chamber than
is produced in the chamber than 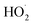 and, according to our box model simulations, more than 90% of the
and, according to our box model simulations, more than 90% of the 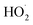 reacts with
reacts with 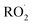 to produce ROOH (the products of Reaction (3) will be discussed further in a later section). As such, the production of ROOH provides a probe of the branching to the radical propagating channels in Reaction (4). To quantify this, we define the dependent variable Q:
to produce ROOH (the products of Reaction (3) will be discussed further in a later section). As such, the production of ROOH provides a probe of the branching to the radical propagating channels in Reaction (4). To quantify this, we define the dependent variable Q: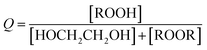 | (11) |
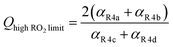 | (12) |
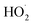 . Therefore, the y-intercept of Q as a function of Fexternal provides a constraint on the ratio of the radical propagating and radical terminating channels of Reaction (4).
. Therefore, the y-intercept of Q as a function of Fexternal provides a constraint on the ratio of the radical propagating and radical terminating channels of Reaction (4).
To further constrain the kinetics of Reaction (4), we explore the ‘high 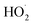 limit’, where Fexternal ≫ 1. In this limit, nearly all the ˙OH produced from the photolysis of H2O2 reacts via Reactions (8) and (9) to produce
limit’, where Fexternal ≫ 1. In this limit, nearly all the ˙OH produced from the photolysis of H2O2 reacts via Reactions (8) and (9) to produce 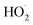 . Because the formation rate of
. Because the formation rate of 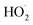 greatly exceeds that of
greatly exceeds that of 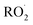 , the
, the 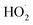 self-reaction is its main loss,
self-reaction is its main loss,
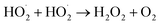 | (13) |
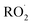 is its reaction with
is its reaction with 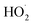 (Reaction (3)).
(Reaction (3)).
Because, as follows from eqn (11):
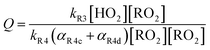 | (14) |
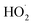 limit is determined by the ratio of their production multiplied by the ratio of their lifetimes:
limit is determined by the ratio of their production multiplied by the ratio of their lifetimes: | (15) |
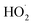 limit, Q is a sensitive measure of the ratio of kR32 to kR4:
limit, Q is a sensitive measure of the ratio of kR32 to kR4: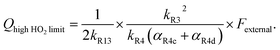 | (16) |
In our experiments, Fexternal ranges from 0.04 to 4.5. The lower limit results from the use of H2O2 as the ˙OH precursor—some external 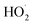 is produced from its reaction with ˙OH even in the absence of methanol addition—while the maximum Fexternal is limited by insufficient production of
is produced from its reaction with ˙OH even in the absence of methanol addition—while the maximum Fexternal is limited by insufficient production of 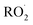 products and the resulting poor quantification of Q.
products and the resulting poor quantification of Q.
The limiting behaviors described by eqn (12) and (16) are useful for designing the experimental methods, for quantifying initial estimates of our parameters, and to perform sensitivity analyses to estimate uncertainty. However, to formally estimate the branching fractions and the rate coefficients, we use a box model that includes all the reactions described above. The complete set of reactions and rate constants used in the box model is given in Appendix D of the ESI (Tables S4, S5 and S6).† The difference between the box model output (the value of Q as a function of Fexternal) and our data is minimized using a least-squares Levenberg–Marquardt (LM) algorithm to optimize the relevant branching fractions and the ratio of the rate coefficients of Reaction (4) to (3). The LM constraints used are provided in Appendix E of the ESI (Table S7).†
2.2 Instrumentation
All measurements were performed with a high-resolution time-of-flight chemical ionization mass spectrometer (HRToF-CIMS) using CF3O− as the reagent ion. The instrument also contains a metal-free, low pressure gas chromatograph (GC). This instrument has been described in detail elsewhere,18 but a brief summary of the critical components is given here. The HRToF-CIMS samples either from the output of the GC or directly from the experimental chamber (direct sampling mode). The CF3O− reagent ion is produced by passing dilute CF3OOCF3 gas in N2 through a polonium-210 ionizer (NRD, P-2021). Sampled chamber gas passes at 180 sccm through a fluorocopolymer-coated critical orifice into a fluorocopolymer-coated glass flow tube maintained at a pressure of 35 mbar, where it is diluted with N2 and mixes with the flow from the ion source. Reagent ions then react with analytes from the chamber to form product ions. CF3O− reacts with many multifunctional organic compounds at the ion–molecule collision rate to yield cluster ions at the mass of the reagent ion (85) plus the mass of the analyte. For example, ethylene glycol, with a molecular weight of 62, is detected at m/z 147. These ion clusters enter the mass spectrometer through a pinhole and a conical hexapole ion guide. In addition to forming clusters, hydroperoxides produce a small fraction (a few %) of characteristic fragmentation ions at m/z 63 and m/z 81, enabling identification of such analytes. For some analytes (e.g. H2O2) the cluster ions are not well bound, such that not all collisions result in a stabilized ion cluster. For these analytes, the resulting sensitivities are therefore lower than estimated based on the ion–molecule collision rate.19 The HRToF-CIMS collected ion signals ranging between m/z 19 and m/z 396 at a mass resolving power of approximately 3000 (m/Δm).The GC consists of a 1 meter fused silica column (Restek RTX-1701) cooled via evaporation and expansion of liquid CO2 and warmed with resistive heating elements connected to a Watlow temperature controller. The sample is diluted by a flow of dry N2 before being cryotrapped on the head of the column at a temperature of −40 °C or below for between 5 and 10 minutes. The specific trapping temperature, time, and dilution for each experiment are chosen to optimize the amount of analyte collected while minimizing the water trapped. When trapping is complete, 5 sccm N2 flows through the column while the temperature of the GC steadily increases at a predetermined ramp rate chosen to best separate analytes of interest in the minimum amount of time. The elution stream from the GC oven is combined with a 200 sccm flow of nitrogen and routed to the mass spectrometer flow tube. Specific conditions for the experiments discussed in this paper are given in Appendix F of the ESI (Table S8).†
2.3 Reagent preparation
H2O2 (30% by mass, Macron Fine Chemicals) was pipetted into a three-way glass vial and weighed for accurate mass determination. Dry air was then passed through the vial into the experiment chamber at 20 SLM until all the reagent was evaporated, as verified by reweighing the vial after injection. 2,3-Butanediol (98%, Sigma-Aldrich) was added to the chamber in a similar manner.Ethene (≥99.5%, Sigma-Aldrich) and methanol (≥99.9%, Sigma-Aldrich) samples were prepared in 500 mL glass bulbs using manometry. The bulb was attached to a vacuum/N2 system and reagent source, and the desired concentration of ethene and methanol was obtained via serial dilution measured with pressure sensors (MKS 1000 and 10 torr Baratron pressure transducers). Concentrations were also determined using FTIR measurements by fitting spectra to absorption cross sections from the PNNL IR Database.20 The manometry and IR determinations agreed to better than 10%.
2.4 CIMS calibration
Quantification of the various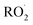 reaction products requires knowledge of their sensitivity in the CIMS instrument. The Caltech CIMS implementation uses a transverse ionization approach where the CF3O− reagent ions travel across the 35 mb gas mixture flow in approximately 5 ms before entering the mass filter. The short reaction time of the reagent ions with the analytes yields a sensitivity for each compound that is proportional to: the ion–molecule collision rate with the analyte, the fraction of such collisions that result in ion products, the transmission efficiency of such ions, and whether there is fragmentation, all modulated by the number of CF3O− produced in the polonium source. As the fraction of reagent ions, here primarily CF3O− and its clusters with H2O and H2O2 (observed at m/z 85, 103, and 119, respectively), that react with the analytes is small, we first normalize the signals at the cluster mass (e.g. the counts at m/z 163 for the hydroxyhydroperoxide) by the sum of signal for the reagent ions. Because the number of reagent ions is very high, to remain in a linear counting regime, we use the reagent ion signal for the sum of the minor isotopologues at m/z + 1 (e.g. 86 for CF3O−). So, the sensitivities listed in Table 1 below are normalized by the sum of m/z 86 + m/z 104 + m/z 120. These normalized signals are proportional to concentration of each analyte ionized in the flow.
reaction products requires knowledge of their sensitivity in the CIMS instrument. The Caltech CIMS implementation uses a transverse ionization approach where the CF3O− reagent ions travel across the 35 mb gas mixture flow in approximately 5 ms before entering the mass filter. The short reaction time of the reagent ions with the analytes yields a sensitivity for each compound that is proportional to: the ion–molecule collision rate with the analyte, the fraction of such collisions that result in ion products, the transmission efficiency of such ions, and whether there is fragmentation, all modulated by the number of CF3O− produced in the polonium source. As the fraction of reagent ions, here primarily CF3O− and its clusters with H2O and H2O2 (observed at m/z 85, 103, and 119, respectively), that react with the analytes is small, we first normalize the signals at the cluster mass (e.g. the counts at m/z 163 for the hydroxyhydroperoxide) by the sum of signal for the reagent ions. Because the number of reagent ions is very high, to remain in a linear counting regime, we use the reagent ion signal for the sum of the minor isotopologues at m/z + 1 (e.g. 86 for CF3O−). So, the sensitivities listed in Table 1 below are normalized by the sum of m/z 86 + m/z 104 + m/z 120. These normalized signals are proportional to concentration of each analyte ionized in the flow.
| Compound | Measured sensitivitya (cts pptv−1) | Calc. CF3O−-molecule collision rateb |
|---|---|---|
| a Signals are normalized to the signal of the 13C isotope of the reagent ion (m/z 86 + m/z 104 + m/z 120). b Relative to ethylene glycol. c The ratio of sensitivity to ethylene glycol is lower than the ratio of the ion–molecule collision rate coefficients due to incomplete stabilization of collisions.19 | ||
| Ethylene glycol | 2.5 ± 0.2 × 10−4 | 1 |
| H2O2c | 1.65 ± 0.06 × 10−4 | 0.94 |
| 2,3-Butanediol | 2.8 ± 1.6 × 10−4 | 1.02 |
| 2-Hydroxy-3-butanone | 1.29 | |
| Glycolaldehyde | 2.7 ± 0.2 × 10−4 | 1.08 |
| HOCH2CH2OOCH2CH2OH | 1.05 | |
| HOCH2CH2OOH | 1.08 | |
To determine the sensitivity of the CIMS to ethylene glycol, we used two methods to produce gas phase standards. In the first, ethylene glycol (Sigma-Aldrich) was evaporated into a 200 L Teflon bag, which was then attached to an FTIR and a flow dilution system in series with our GC-CIMS. The concentration of EG in the Teflon bag was quantified using the FTIR and cross sections from the PNNL IR Database as air from the 200 L bag flowed through a 19 cm pyrex FTIR cell with CaF2 windows at a rate of 484 sccm. The uncertainty in the FTIR cross sections is estimated to be ≤7%. Following the FTIR cell, a subsample (34 sccm) was diluted into a 2 SLM nitrogen flow yielding EG concentrations of approximately 1 ppmv which was directed into the CIMS instrument. In the second method, we prepared a known concentration of EG by flowing 20 sccm of air over a diffusion vial maintained at 30 °C. The diffusion vial containing EG was regularly weighed. The mass loss rate of EG over time, and the flow rate in the CIMS flow tube were used to calculate the mixing ratio of EG in the flow tube. The sensitivity calculated using these two methods agrees within 8%. The sensitivity using the diffusion vial method was repeated often and the average is listed in Table 1.
To estimate the sensitivity for the other 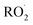 reaction products, we calculate their ion–molecule collision rate relative to that of EG. CF3O− binds strongly to most multifunctional organic compounds21 and as such, the fraction of each product ionized depends linearly on the ion–molecule collision rate. For some analytes, such as H2O2, the ion–molecule complex binding energy is small, and not all collisions lead to stabilized product ions. This dissociation is diagnosed by evaluating the sensitivity as a function of temperature and water vapor. For weakly bound clusters, the sensitivity decreases as a function of temperature and generally has a complex behavior as a function of water—sometimes increasing at low concentrations as the water chaperone increases cluster formation, before decreasing at high water concentrations due to ligand switching.19,21 For the product clusters described in this work, we find that the sensitivity is largely insensitive to temperature and both water and H2O2, consistent with high stability for the ion clusters. Even for well bound clusters, the efficiency of formation of CF3O− clusters following collision can be less than unity if they fragment into smaller ions. The data obtained with the GC enables us to quantify this fragmentation for each analyte, and we observe very little such fragmentation for the species reported here. The hydroxyhydroperoxide (m/z 163) produces a very small signal at m/z 145 (<2%) and m/z 63 + 81 (2–3%). (The latter two ions are diagnostic of organic hydroperoxides.22–24) Given the size and stability of the ion products and the lack of significant fragmentation, we expect that for all the
reaction products, we calculate their ion–molecule collision rate relative to that of EG. CF3O− binds strongly to most multifunctional organic compounds21 and as such, the fraction of each product ionized depends linearly on the ion–molecule collision rate. For some analytes, such as H2O2, the ion–molecule complex binding energy is small, and not all collisions lead to stabilized product ions. This dissociation is diagnosed by evaluating the sensitivity as a function of temperature and water vapor. For weakly bound clusters, the sensitivity decreases as a function of temperature and generally has a complex behavior as a function of water—sometimes increasing at low concentrations as the water chaperone increases cluster formation, before decreasing at high water concentrations due to ligand switching.19,21 For the product clusters described in this work, we find that the sensitivity is largely insensitive to temperature and both water and H2O2, consistent with high stability for the ion clusters. Even for well bound clusters, the efficiency of formation of CF3O− clusters following collision can be less than unity if they fragment into smaller ions. The data obtained with the GC enables us to quantify this fragmentation for each analyte, and we observe very little such fragmentation for the species reported here. The hydroxyhydroperoxide (m/z 163) produces a very small signal at m/z 145 (<2%) and m/z 63 + 81 (2–3%). (The latter two ions are diagnostic of organic hydroperoxides.22–24) Given the size and stability of the ion products and the lack of significant fragmentation, we expect that for all the 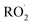 reaction products, the sensitivity of each for its CF3O− cluster will scale with the ion–molecule collision rate to within ±20%.
reaction products, the sensitivity of each for its CF3O− cluster will scale with the ion–molecule collision rate to within ±20%.
To calculate the ion–molecule collision rate, we use the method of Su et al.25 together with calculated dipole moments and polarizabilities using quantum calculations.26 The calculated ion–molecule collision rates, relative to that for ethylene glycol are listed in Table 1.
2.5 Peroxide synthesis
Previous studies of the formation of accretion products have observed compounds at the mass of the peroxides (ROOR) using CIMS techniques,1,8,10 but the identity of these products has not been typically confirmed. Studies by Kenseth et al.27 have, for example, shown that accretion products produced in the ozonolysis of pinenes are not peroxides and do not form in the gas phase. Here, a method for the synthesis of a standard for the C4 dihydroxy peroxide for comparison to our oxidation products is outlined.2.5.1.1 Caution. Although no explosions were experienced in this work, organic peroxides are potentially hazardous compounds and must be handled with great care: avoid direct exposure to strong heat or light, mechanical shock, oxidizable organic materials, or transition-metal ions. A safety shield should be used for all operations involving H2O2.
Unless otherwise stated, reactions were performed in flame-dried glassware under ambient conditions using dry, deoxygenated solvents. Solvents were dried by passage through an activated alumina column under argon. Reagents were purchased from commercial sources and used as received. Reaction temperatures were controlled by an IKAmag temperature modulator. Thin-layer chromatography (TLC) was performed using E. Merck silica gel 60 F254 pre-coated plates (250 μm) and visualized by UV fluorescence quenching, potassium permanganate staining, or p-anisaldehyde staining. Silicycle SiliaFlash P60 Academic Silica gel (particle size 40–63 μm) was used for flash chromatography. Preparative HPLC was performed using an Agilent 1200 HPLC system equipped with an ACE C18 column (5 μm, 21.2 mm × 250 mm). 1H and 13C NMR spectra were recorded on a Varian Inova 500 (500 and 125 MHz, respectively) spectrometer and are reported in terms of chemical shift relative to CHCl3 (δ 7.26 and 77.16 ppm, respectively). Data for 1H NMR are reported as follows: chemical shift (δ ppm) (multiplicity, coupling constant, integration). Abbreviations are used as follows: s = singlet, d = doublet, t = triplet, q = quartet, m = multiplet. IR spectra were obtained from thin films deposited on NaCl plates using a PerkinElmer Spectrum BXII spectrometer and are reported in wavenumbers (cm−1). Optical rotations were measured with a Jasco P-2000 polarimeter operating on the sodium D-line (589 nm) using a 100 mm path-length cell. All of the spectral data can be found in the ESI† (Appendix G).
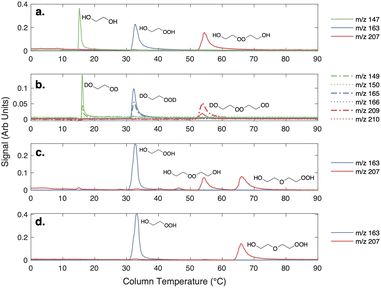
The clear residue was purified via preparatory TLC (5% methanol/ethyl acetate, visualized with p-anisaldehyde). All major bands were collected and were subjected to GC-CIMS analysis. Only two compounds were observed via GC-CIMS analysis: one major compound at m/z 163 and one major compound at m/z 207 (Fig. 2). The chromatograms of both of these compounds contain daughter ions characteristic of –OOH functional groups (m/z 63 and m/z 81).
The two isolated products were identified to be hydroxyhydroperoxide 1 (20.0 mg, 3% yield, colorless oil) and ether 2 (5.4 mg, less than 1% yield, colorless oil). We believe that peroxide 3 forms under the reaction conditions, as a second peak at m/z = 207 is observed in the crude reaction mixture, but is not stable to isolation. Additionally, compound 3 elutes at the same temperature as the putative accretion product in our oxidation experiments.
3 Results and discussion
3.1 The identity of the accretion product
Although several recent studies have reported formation of accretion products in oxidation experiments of organic compounds,1,8,10 the identity of these compounds remains generally unclear. For example, Kenseth et al.27 have recently shown that accretion products formed in the ozonolysis of α- and β-pinene arise not directly in the gas phase but rather from heterogeneous reactions of alcohols and (likely) peroxides produced via O3 and ˙OH chemistry, respectively. Here, in this simplest of systems, we show that the accretion product is likely an organic peroxide, HOCH2CH2OOCH2CH2OH. As shown in Fig. 3, across all our experiments from those with minimal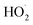 chemistry to those dominated by such reactions, the yield of the accretion product closely tracks the yield of ethylene glycol, a unique gas-phase product of the self-reaction of HOCH2CH2OO˙, suggesting that it is also produced in the gas phase via this self-reaction.
chemistry to those dominated by such reactions, the yield of the accretion product closely tracks the yield of ethylene glycol, a unique gas-phase product of the self-reaction of HOCH2CH2OO˙, suggesting that it is also produced in the gas phase via this self-reaction.
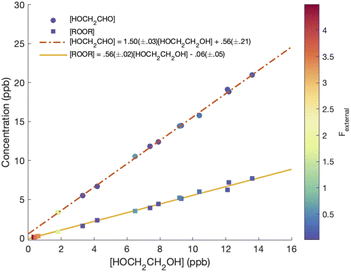 | ||
| Fig. 3 ROOR and glycolaldehyde formation vs. ethylene glycol. Dashed and solid lines are linear fits to the data, with slopes of 0.56 ± 0.02 and 1.50 ± 0.03 for ROOR and glycolaldehyde, respectively. | ||
Shown in the first panel of Fig. 2 are gas chromatograms of the products formed in our ‘high 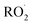 ’ experiments. Due to its high vapor pressure, glycolaldehyde is not efficiently trapped on the column. All the other products – ethylene glycol, the hydroperoxide, and the accretion product – are efficiently collected, separated, and detected at their CF3O− cluster m/z. The average GC transmission efficiencies of all of these species is between 90–100%.
’ experiments. Due to its high vapor pressure, glycolaldehyde is not efficiently trapped on the column. All the other products – ethylene glycol, the hydroperoxide, and the accretion product – are efficiently collected, separated, and detected at their CF3O− cluster m/z. The average GC transmission efficiencies of all of these species is between 90–100%.
Three plausible molecules with the formula C4O4H10 can be postulated to form in the gas-phase chemistry of HOCH2CH2OO˙, and in the condensed-phase synthesis, considering the starting materials: a hydroperoxyhydroxyether, a dihydroxyperoxide, and a triol ether. The last compound can be distinguished from the first two by the number of readily exchangeable hydrogens. To rule out the triol ether, we added D2O to the GC effluent and, as shown in panel b of Fig. 2, ethylene glycol and the C2 hydroxyhydroperoxide shift up 2 m/z, consistent with two exchangeable hydrogens. Likewise, the accretion product shifts up 2 m/z. No +3 m/z isotopologues are observed. As such we eliminate consideration of the triol as a plausible structure for the accretion product.
Also shown in Fig. 2 (panels c and d) is the chromatograph of the synthetic products from the liquid phase condensation of the hydroperoxide (as described above). Two compounds at the m/z of the accretion product (m/z 207, mw 122) are observed in the crude mixture, while only one C4O4H10 compound is stable to prep TLC separation. The isolated compound eluting at approximately 65 °C is identified as the hydroperoxy hydroxy ether, HOCH2CH2OCH2CH2OOH, based on the 1H and 13C NMR spectra (see ESI†) and on the observed fragmentation of m/z 207 to m/z 63 and m/z 81 in CF3O− CIMS, fragments characteristic of hydroperoxides.22,23 The first peak, the peroxide, elutes at the same temperature as the accretion product formed in the gas-phase experiments. Therefore, we conclude by elimination that the accretion product formed in the gas-phase ethene oxidation experiments is likely the dihydroxyperoxide (ROOR).
3.2 Product branching fractions
To calculate the branching fractions of the self-reaction, we quantify the closed-shell end products of these reactions (with the exception of formaldehyde, which does not cluster with CF3O−). Reaction (4) directly produces three products: ethylene glycol, glycolaldehyde, and the accretion product (ROOR).Shown in Fig. 3 are the concentrations of ROOR and glycolaldehyde as a function of the concentration of ethylene glycol. The points are colored by the value of Fexternal. The observed yield of ROOR relative to EG is 0.56 ± 0.02. In 21% O2 at 993 hPa, the yield of GA relative to EG is 1.50 ± 0.03. The ratio of the ROOR to EG is independent of Fexternal. The ratio of GA to EG increases at the highest Fexternal as a result of secondary chemistry of the ROOH, and therefore we do not include these points in the above fit (see ESI Appendix C†).
Absent secondary chemistry, the ratio of the product yields equals the ratio of their production. To accurately determine the ratio of their production, however, secondary losses must be considered. Here, this potentially includes the photolysis of the peroxide product (ROOR), the hydroperoxide (ROOH), and glycolaldehyde. We measured the upper limit of the photolysis rate of these compounds in our chamber as follows: after synthesizing them in the gas phase via an ethene oxidation experiment in the high 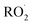 limit, we evacuated the chamber through a coil of Teflon tubing submersed in an ethanol/liquid nitrogen bath maintained at approximately −30 °C, trapping the low volatility products while allowing the remaining ethene and high volatility products to be pumped away. We then flushed out the chamber with clean air and returned the contents of the trap to the Teflon chamber by flowing dry air back through the trap at room temperature (294 K). Finally, we added 50 ppmv methanol to convert any ˙OH produced by subsequent photochemistry to
limit, we evacuated the chamber through a coil of Teflon tubing submersed in an ethanol/liquid nitrogen bath maintained at approximately −30 °C, trapping the low volatility products while allowing the remaining ethene and high volatility products to be pumped away. We then flushed out the chamber with clean air and returned the contents of the trap to the Teflon chamber by flowing dry air back through the trap at room temperature (294 K). Finally, we added 50 ppmv methanol to convert any ˙OH produced by subsequent photochemistry to 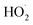 , thereby isolating the loss due to photolysis. We then turned on the UV lights and measured the loss rates of the relevant compounds (Table 2). During a typical 2 min photolysis experiment, we calculate that 1% of the GA is photolyzed and at most 6% of the ROOR was lost. Photolysis of the hydroxyhydroperoxide (ROOH) results in a maximum loss of a few percent. However, these measured photolysis rates are an upper limit to the loss via photolysis, as there may be additional secondary losses during these photolysis experiments – we expect that the true photolysis rates of ROOR and ROOH are likely closer to that of hydrogen peroxide. Therefore, in our subsequent analysis, we assume that over the 120 s time period of our experiments, the average photolysis frequency for the ROOR and ROOH is 3.0 × 10−4 s−1. If instead we use the upper limit to the photolysis frequencies, the estimated branching ratios to ROOR and ROOH increase by approximately a factor of 1.05. We observe no significant photolysis of ethylene glycol over the experiment timescales. In addition to secondary losses, GA is also formed via the reaction of ˙OH with ROOH and EG and via photolysis of ROOH and subsequent reaction of O2 with the generated RO˙. This chemistry is only significant when ROOH is much larger than GA (e.g. at high Fexternal (see ESI Appendix C†)).
, thereby isolating the loss due to photolysis. We then turned on the UV lights and measured the loss rates of the relevant compounds (Table 2). During a typical 2 min photolysis experiment, we calculate that 1% of the GA is photolyzed and at most 6% of the ROOR was lost. Photolysis of the hydroxyhydroperoxide (ROOH) results in a maximum loss of a few percent. However, these measured photolysis rates are an upper limit to the loss via photolysis, as there may be additional secondary losses during these photolysis experiments – we expect that the true photolysis rates of ROOR and ROOH are likely closer to that of hydrogen peroxide. Therefore, in our subsequent analysis, we assume that over the 120 s time period of our experiments, the average photolysis frequency for the ROOR and ROOH is 3.0 × 10−4 s−1. If instead we use the upper limit to the photolysis frequencies, the estimated branching ratios to ROOR and ROOH increase by approximately a factor of 1.05. We observe no significant photolysis of ethylene glycol over the experiment timescales. In addition to secondary losses, GA is also formed via the reaction of ˙OH with ROOH and EG and via photolysis of ROOH and subsequent reaction of O2 with the generated RO˙. This chemistry is only significant when ROOH is much larger than GA (e.g. at high Fexternal (see ESI Appendix C†)).
| Compound | Average photolysis frequency (10−4 s−1) | Literature cross section30 (cm2 molecule−1) |
|---|---|---|
| HOCH2CH2OOCH2CH2OH | <6.1 ± 0.8 | |
| HOCH2CH2OOH | <5.2 ± 0.9 | |
| HOCH2CHO | 1.7 ± 0.05 | 4.0 ± 0.3 × 10−20 |
| H2O2 | 3.0 ± 0.5 | 7.0 ± 1.0 × 10−20 |
Accounting for the photolysis losses and glycolaldehyde production, we find that the ratio of the production of ROOR and GA to ethylene glycol are 0.57 ± 0.10 and 1.55 ± 0.20, respectively, where the uncertainty is derived primarily from the uncertainty in the relative calibration of the CIMS for these compounds. In the first-generation chemistry of this reaction system, Reaction (4) is a unique source of the accretion product and EG, so the ratio of their production is equal to the ratio of the branching in Reaction (4)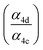 . GA, however, is also produced in the subsequent reactions of the alkoxy radical and O2 (Reaction (7b))17 and, speculatively, via a radical propagating reaction, Reaction (4b). There may be additional GA formed via Reaction (3). The formation of GA in these experiments is discussed further below.
. GA, however, is also produced in the subsequent reactions of the alkoxy radical and O2 (Reaction (7b))17 and, speculatively, via a radical propagating reaction, Reaction (4b). There may be additional GA formed via Reaction (3). The formation of GA in these experiments is discussed further below.
3.3 Glycolaldehyde formation
As shown in Fig. 3, the yield of glycolaldehyde is consistently higher than the yield of ethylene glycol across our experiments. This is true even when oxygen is reduced to 1% of the total volume to minimize the extent of Reaction (7b) (see ESI Appendix C†). This observation is consistent with prior studies of GA formation in the ethene oxidation system. In the FTIR study of the title reaction by Barnes et al.,13 for example, GA yields were 40% higher than EG at low oxygen mixing ratios (5 hPa). At 180 hPa and 200 hPa [O2], similar to the concentrations in our study, GA yields were 70% and 95% larger, respectively.There is no previous estimate for α3c or α3b, both of which would yield glycolaldehyde from the Reaction of 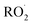 with
with 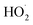 . Shown in Fig. S5† is the ratio of modeled and measured GA to ethylene glycol as a function of the ratio of
. Shown in Fig. S5† is the ratio of modeled and measured GA to ethylene glycol as a function of the ratio of 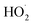 to
to 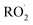 steady state concentration (as simulated by the box model). Using this comparison of the box model with the data, we find that a branching fraction to the formation of GA of more than 1% from the RO2 + HO2 reaction is incompatible with the observations over a wide range of RO2 fate. This in turn suggests that α3c + 5 × α3b is less than 0.01, where the factor of 5 accounts for our determination that in 1 atmosphere of air at 294 K, approximately 20% of alkoxy radicals react via Reaction (7b). In our subsequent analysis we assume both α3c and α3b are zero, producing no GA in our experiments, and attribute excess GA with low partial pressures of O2 to Reaction (4b). We quantify the importance of this reaction pathway by assigning all GA produced in excess of EG in our low [O2] experiments to this reaction channel. It is also a theoretical possibility that this excess GA is formed by the loss of a hydrogen atom from alkoxy radicals with excess energy—however, we do not expect such a reaction to be competitive with C–C bond scission or Reaction (4b). From our experiments, we determine that the branching to pathway (4b) is 26% of the branching to Reaction (4c)
steady state concentration (as simulated by the box model). Using this comparison of the box model with the data, we find that a branching fraction to the formation of GA of more than 1% from the RO2 + HO2 reaction is incompatible with the observations over a wide range of RO2 fate. This in turn suggests that α3c + 5 × α3b is less than 0.01, where the factor of 5 accounts for our determination that in 1 atmosphere of air at 294 K, approximately 20% of alkoxy radicals react via Reaction (7b). In our subsequent analysis we assume both α3c and α3b are zero, producing no GA in our experiments, and attribute excess GA with low partial pressures of O2 to Reaction (4b). We quantify the importance of this reaction pathway by assigning all GA produced in excess of EG in our low [O2] experiments to this reaction channel. It is also a theoretical possibility that this excess GA is formed by the loss of a hydrogen atom from alkoxy radicals with excess energy—however, we do not expect such a reaction to be competitive with C–C bond scission or Reaction (4b). From our experiments, we determine that the branching to pathway (4b) is 26% of the branching to Reaction (4c)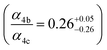 . The large uncertainty in this result reflects the fact that this ratio is determined by the difference between the yield of GA and ethylene glycol at 0% O2 and, as such, is highly sensitive to error in our knowledge of the relative sensitivity of the CIMS to these compounds.
. The large uncertainty in this result reflects the fact that this ratio is determined by the difference between the yield of GA and ethylene glycol at 0% O2 and, as such, is highly sensitive to error in our knowledge of the relative sensitivity of the CIMS to these compounds.
Finally, the extent of Reaction (7b) to the formation of glycolaldehyde is quantified by comparing the relative concentrations of GA and ethylene glycol at varying O2 partial pressures. Fig. S4† shows 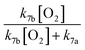 as a function of [O2], which we determine from
as a function of [O2], which we determine from 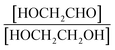 as described in ESI Appendix C.† This figure also shows this ratio as determined from the data of Barnes et al.13 and Orlando et al.17 Direct comparison of these data is complicated by the difference in total pressure between our experiments and those of Orlando et al. and Barnes et al., which may change the relative branching to decomposition and reaction with O2. Additionally, the alkoxy radicals in the experiments of Orlando et al. were generated by the reaction of
as described in ESI Appendix C.† This figure also shows this ratio as determined from the data of Barnes et al.13 and Orlando et al.17 Direct comparison of these data is complicated by the difference in total pressure between our experiments and those of Orlando et al. and Barnes et al., which may change the relative branching to decomposition and reaction with O2. Additionally, the alkoxy radicals in the experiments of Orlando et al. were generated by the reaction of 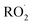 with NO˙. In this system, a temperature-dependent fraction of the alkoxy radicals have excess energy, and undergo prompt decomposition, whereas the rest of the alkoxy radicals are thermalized and can then either undergo decomposition or reaction with O2.17 The fraction of thermalized alkoxy radicals generated in Reaction (4) may differ from that generated by the reaction between
with NO˙. In this system, a temperature-dependent fraction of the alkoxy radicals have excess energy, and undergo prompt decomposition, whereas the rest of the alkoxy radicals are thermalized and can then either undergo decomposition or reaction with O2.17 The fraction of thermalized alkoxy radicals generated in Reaction (4) may differ from that generated by the reaction between 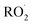 and NO˙. The analysis of our data, as presented in ESI Appendix C,† indicates that approximately 20% of the alkoxy radicals in our system react with O2, whereas 29% of the alkoxy radicals in the system studied by Orlando et al. react with O2 at 298 K. While this difference is well within the uncertainty of our quantification of EG and GA, it may reflect either the difference in pressure or a difference in the fraction of thermalized radicals in our system. The comparison between our data to the data of Orlando et al. and Barnes et al. is discussed further in ESI Appendix C.† In our subsequent analysis, we use a value of 20% for branching to Reaction (7b) in air.
and NO˙. The analysis of our data, as presented in ESI Appendix C,† indicates that approximately 20% of the alkoxy radicals in our system react with O2, whereas 29% of the alkoxy radicals in the system studied by Orlando et al. react with O2 at 298 K. While this difference is well within the uncertainty of our quantification of EG and GA, it may reflect either the difference in pressure or a difference in the fraction of thermalized radicals in our system. The comparison between our data to the data of Orlando et al. and Barnes et al. is discussed further in ESI Appendix C.† In our subsequent analysis, we use a value of 20% for branching to Reaction (7b) in air.
3.4 Radical propagation vs. chain termination in Reaction (4)
As described above, in the limit where Fexternal → 0, Q (eqn (11)) is a measure of the ratio of the radical propagating channels to the radical terminating channels of Reaction (4). In the limit where all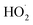 is produced internally to Reaction (4), >90% of the
is produced internally to Reaction (4), >90% of the 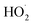 reacts with HOCH2CH2OO˙, and there are no secondary losses,
reacts with HOCH2CH2OO˙, and there are no secondary losses,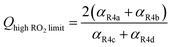 | (17) |
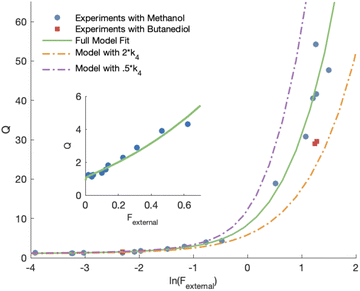
Shown in Fig. 4 is Q plotted as a function of Fexternal. The y-intercept, (Fexternal = 0), is 1.07 suggesting that about half of the 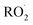 reacting via R4 yields
reacting via R4 yields 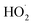 . The solid line shown in Fig. 4 is our box model results optimized to fit these data. The model includes external production of
. The solid line shown in Fig. 4 is our box model results optimized to fit these data. The model includes external production of 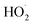 , estimates for the loss of
, estimates for the loss of 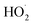 via its self reaction, and photolysis losses of both ROOH and the accretion product. The optimized model suggests that the ratio of the radical recycling channels (αR4a + αR4b) to the radical terminating channels (αR4c + αR4d) is 0.54 ± 0.11. Independent of the subsequent fate of the alkoxy radical, under our reaction conditions two
via its self reaction, and photolysis losses of both ROOH and the accretion product. The optimized model suggests that the ratio of the radical recycling channels (αR4a + αR4b) to the radical terminating channels (αR4c + αR4d) is 0.54 ± 0.11. Independent of the subsequent fate of the alkoxy radical, under our reaction conditions two 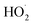 are produced in each of the chain propagating channels. The uncertainty in this ratio represents error in the relative sensitivity of the CIMS to ROOH vs. ethylene glycol and ROOR (±25%) and uncertainty in their photolysis frequencies (±28%). As an additional check on the quantification of ROOH, the box model suggests that in the ‘high
are produced in each of the chain propagating channels. The uncertainty in this ratio represents error in the relative sensitivity of the CIMS to ROOH vs. ethylene glycol and ROOR (±25%) and uncertainty in their photolysis frequencies (±28%). As an additional check on the quantification of ROOH, the box model suggests that in the ‘high 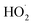 ’ limit, the formation of ROOH should be within a few percent of the reacted ethene. After accounting for the small photolysis losses, we find that the ratio of ROOH to ethene reacted is on average 90% for the high
’ limit, the formation of ROOH should be within a few percent of the reacted ethene. After accounting for the small photolysis losses, we find that the ratio of ROOH to ethene reacted is on average 90% for the high 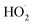 experiments (see Fig. S12†).
experiments (see Fig. S12†).
3.5 The rate coefficient of Reaction (4)
As discussed earlier, when Fexternal is high, Q is proportional to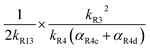 . To estimate k4 and the branching fractions of Reaction (4), we perform a least-squares fit of Q from the box model to Q calculated from our CIMS data. The branching fraction (α4d) to the formation of the accretion product and the self-reaction rate constant (k4) are the only fitted parameters. Other unknown parameters are written in terms of these parameters using the relationships developed in the previous sections, as demonstrated below:
. To estimate k4 and the branching fractions of Reaction (4), we perform a least-squares fit of Q from the box model to Q calculated from our CIMS data. The branching fraction (α4d) to the formation of the accretion product and the self-reaction rate constant (k4) are the only fitted parameters. Other unknown parameters are written in terms of these parameters using the relationships developed in the previous sections, as demonstrated below:In addition to constraining
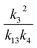 , we report the value of k4 assuming the currently accepted value for k13 (2.5 × 10−12 cm3 molecule−1 s−1 when accounting for both the termolecular and bimolecular pathways – note that in our experiments, the enhancement due to water vapor and methanol is negligible31) and assuming a value of k3 = 1.1 × 10−11 cm3 molecule−1 s−1.32 Additionally, we report the ratio of the radical propagating channels to the radical terminating channels and the fitted results for all of the branching fractions of the self-reaction pathways (Table 3). In summary, we find the following branching fractions for the self-reaction pathways:
, we report the value of k4 assuming the currently accepted value for k13 (2.5 × 10−12 cm3 molecule−1 s−1 when accounting for both the termolecular and bimolecular pathways – note that in our experiments, the enhancement due to water vapor and methanol is negligible31) and assuming a value of k3 = 1.1 × 10−11 cm3 molecule−1 s−1.32 Additionally, we report the ratio of the radical propagating channels to the radical terminating channels and the fitted results for all of the branching fractions of the self-reaction pathways (Table 3). In summary, we find the following branching fractions for the self-reaction pathways:| Quantity | Constraint | Sources of uncertainty | Value |
|---|---|---|---|
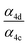
|
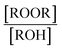
|
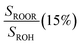 , fit Fig. 3 (3%), secondary chemistry (3%) , fit Fig. 3 (3%), secondary chemistry (3%) |
0.57(±0.09) |
| α 7b (in air) |
|
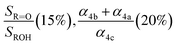
|
0.20(±0.1) |
|
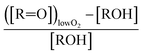
|
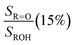
|
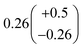
|
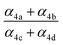
|
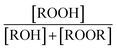
|
Fit Fig. 2 (10%), 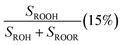 |
0.54(±0.11) |
| α 4a | 1 − α4b − α4c − α4d | α 4b (29%), α4c (25%), α4d (18%) | 0.27(±0.10) |
| α 4b |
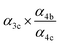
|
α
4c (25%), 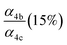 |
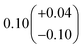
|
| α 4c |
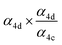
|
α
4d (18%), 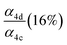 |
0.40(±0.10) |
| α 4d |
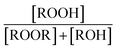
|
Fit Fig. 4 (10%), 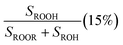 |
0.23(±0.05) |
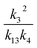
|
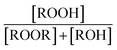
|
Fit Fig. 4 (20%), 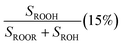 , Fexternal (15%) , Fexternal (15%) |
20.2(±6.1) |
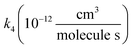
|
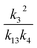
|
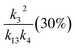 , k3 (30%), k13 (15%) , k3 (30%), k13 (15%) |
2.4(±1.0) |
3.6 Comparison with earlier studies
We find the measured branching fraction to formation of the accretion product, α4d = 0.23 ± 0.05, is much larger than that observed by Barnes et al. who found the ROOR formation to contribute at most 1% of the total products. Barnes et al. performed their experiments in a quartz reaction chamber that included metal mirrors. To evaluate the stability of the peroxide accretion product on quartz (and steel), we performed an ethene oxidation experiment in the high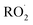 limit and, during direct sampling into the CIMS, replaced a portion of the Teflon sampling line with a length of approximately 60 cm of quartz or metal tubing, which at our flow rate produced a residence time in the quartz/metal tube of <3 s. Despite this very short interaction time, we observed a more than a 50% loss of the accretion product (Fig. S3†). Such wall loss likely limited the ability of Barnes et al.13 to observe the ROOR. Additionally, a recent study published on the reactions of ethyl peroxy radicals11 found a branching ratio to the accretion product of 10 ± 5%, demonstrating that formation of the accretion product is significant even in small unsubstituted peroxy radical systems, lending further support to our results.
limit and, during direct sampling into the CIMS, replaced a portion of the Teflon sampling line with a length of approximately 60 cm of quartz or metal tubing, which at our flow rate produced a residence time in the quartz/metal tube of <3 s. Despite this very short interaction time, we observed a more than a 50% loss of the accretion product (Fig. S3†). Such wall loss likely limited the ability of Barnes et al.13 to observe the ROOR. Additionally, a recent study published on the reactions of ethyl peroxy radicals11 found a branching ratio to the accretion product of 10 ± 5%, demonstrating that formation of the accretion product is significant even in small unsubstituted peroxy radical systems, lending further support to our results.
Our estimate of the ratio of radical propagation to radical termination 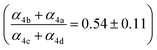 in Reaction (4) is lower than several recent studies.13,36,38 The study most similar to the work presented here is that of Barnes et al.,13 a product study conducted with FTIR, which reports equal contributions of radical propagating and radical terminating channels. In that work, the concentrations of ethylene glycol, glycolaldehyde, and formaldehyde are compared to determine that α4a and α4c are approximately equal (eqn (18)):
in Reaction (4) is lower than several recent studies.13,36,38 The study most similar to the work presented here is that of Barnes et al.,13 a product study conducted with FTIR, which reports equal contributions of radical propagating and radical terminating channels. In that work, the concentrations of ethylene glycol, glycolaldehyde, and formaldehyde are compared to determine that α4a and α4c are approximately equal (eqn (18)):
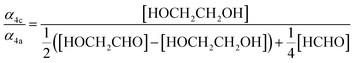 | (18) |
This expression assumes, however, that additional glycolaldehyde is only formed as a result of alkoxy radical chemistry from Reaction (4a) and that no accretion product is formed. Barnes et al. did observe excess GA at low O2 conditions similar to our findings, suggesting an additional source of GA beyond alkoxy chemistry. After accounting for this channel and the formation of ROOR, our optimized box model is fully consistent with the yields of ethylene glycol, GA, and formaldehyde reported by Barnes et al.
The rate coefficient for the title reaction (k4) has been measured in several previous studies (Table 4). These have all been flash photolysis experiments where the decay of HOCH2CH2OO˙ has been monitored by UV spectroscopy. In addition to requiring knowledge of the UV cross sections of this radical, knowledge of the yield and formation timescale of 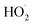 is also needed as the reaction of
is also needed as the reaction of 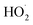 with
with 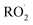 contributes significantly to the observed decay rate of
contributes significantly to the observed decay rate of 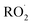 . While the ratio of the decay rate of the
. While the ratio of the decay rate of the 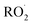 to the assumed
to the assumed 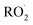 cross sections have been similar in these experiments, the reported rate coefficients have varied due to differences in the inferred cross sections and
cross sections have been similar in these experiments, the reported rate coefficients have varied due to differences in the inferred cross sections and 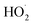 chemistry. Most of these studies determine the absolute rate from the observed decay rate of
chemistry. Most of these studies determine the absolute rate from the observed decay rate of 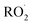 by assuming a steady state of
by assuming a steady state of 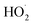 , whereby the following equation holds:
, whereby the following equation holds:
| k4,obs = k4(1 + αradical) = k4(1 + α4a + α4b) | (19) |
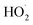 chemistry and the details of how the absorption data are fitted (fitting window and signal-to-noise). Nevertheless, to place these different studies on a similar footing, we use the reported decay rate of the UV absorption at 250 nm and a common value for the UV cross section of the peroxy radical (assumed to be 4.75 × 10−18 cm2 molecule−1)35 and use eqn (19) with the recycling fraction from this work. Finally, we adjust for the difference in the experimental temperature using the temperature dependence for Reaction (4) from Boyd and Lesclaux.36 These are reported in the last column of Table 4.
chemistry and the details of how the absorption data are fitted (fitting window and signal-to-noise). Nevertheless, to place these different studies on a similar footing, we use the reported decay rate of the UV absorption at 250 nm and a common value for the UV cross section of the peroxy radical (assumed to be 4.75 × 10−18 cm2 molecule−1)35 and use eqn (19) with the recycling fraction from this work. Finally, we adjust for the difference in the experimental temperature using the temperature dependence for Reaction (4) from Boyd and Lesclaux.36 These are reported in the last column of Table 4.
| Study | (105 cm s−1)a | α radical | k 4 | T (K) | k 4,recalc |
|---|---|---|---|---|---|
a
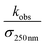 is the reported value in each study, where applicable, for the observed rate of decay of absorption at 250 nm divided by the cross section at 250 nm.
b
k
4,recalc is the value of k4 recalculated given αradical = 0.37 and at 294 K, and σ250 nm = 4.75 × 10−18 cm2 molecule−1, as given in Lightfoot et al.35 The temperature dependence is taken from Boyd et al.36
c Value taken from Barnes et al.13
d Calculated at 294 K using the temperature dependence reported in Boyd et al.36
e Boyd et al. used an explicit non-linear fit of the time dependence of the absorption following the flash and it is difficult to directly compare with the results from the Jenkin laboratory. Here, we use the Arrhenius fits provided by Boyd et al. to extrapolate both k4 and αradical to 294 K. We then multiply the resulting k4 by (0.66/(1 − αradical(294))) to obtain the comparison value. is the reported value in each study, where applicable, for the observed rate of decay of absorption at 250 nm divided by the cross section at 250 nm.
b
k
4,recalc is the value of k4 recalculated given αradical = 0.37 and at 294 K, and σ250 nm = 4.75 × 10−18 cm2 molecule−1, as given in Lightfoot et al.35 The temperature dependence is taken from Boyd et al.36
c Value taken from Barnes et al.13
d Calculated at 294 K using the temperature dependence reported in Boyd et al.36
e Boyd et al. used an explicit non-linear fit of the time dependence of the absorption following the flash and it is difficult to directly compare with the results from the Jenkin laboratory. Here, we use the Arrhenius fits provided by Boyd et al. to extrapolate both k4 and αradical to 294 K. We then multiply the resulting k4 by (0.66/(1 − αradical(294))) to obtain the comparison value.
|
|||||
| This study |
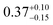
|
2.4 ± 1.0 | 294 | 2.4 ± 1.0 | |
| Jenkin et al.37 | 6.5 ± 0.4 | 0.18 ± 0.2 | 1.4 ± 0.2 | 298 | 2.3 ± 0.6 |
| Murrells et al.34 | 6.6 ± 1.1 | 0.36 ± 0.07 | 2.2 ± 0.5 | 296 | 2.3 ± 1.3 |
| Jenkin et al.38 | 7.1 ± 0.6 | 0.50c | 2.1 ± 0.5 | 298 | 2.5 ± 1.4 |
| Boyd et al.36 | 0.47 ± 0.04d | 2.4 ± 0.2d | 303 | 3.0 ± 0.2e | |
The experiments reported here provide an entirely different constraint on the kinetics. Here, we quantify the relative reaction rate of the 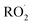 with itself vs. with
with itself vs. with 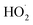 under conditions where the ratio of the production rates of
under conditions where the ratio of the production rates of 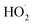 to
to 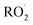 is known, and obtain a value of k4 (294 K) = 2.4 ± 1.0 × 10−12 cm3 molecule−1 s−1. Despite the very different approaches and entirely different error sources, our inferred rate coefficient for Reaction (4) is remarkably similar to the kinetics measurements by flash photolysis.
is known, and obtain a value of k4 (294 K) = 2.4 ± 1.0 × 10−12 cm3 molecule−1 s−1. Despite the very different approaches and entirely different error sources, our inferred rate coefficient for Reaction (4) is remarkably similar to the kinetics measurements by flash photolysis.
4 Conclusions
Bimolecular peroxy radical reactions play an important role in the chemistry of the troposphere, and accurately measuring the rates of these reactions relative to other important loss processes is central to determining their ultimate effect on air quality. In this study, we have shown that the accretion product formed in the reaction of the ethene-derived peroxy radical is likely a peroxide and is produced with a branching fraction of approximately 23%. We have further measured the ratio of radical propagating to radical terminating chemistry as well as the branching to glycolaldehyde, which is produced in both chain propagating and chain terminating channels. Finally, we have constrained the rate coefficient of the title reaction relative to the reaction rate coefficient of the peroxy radical with
loss processes is central to determining their ultimate effect on air quality. In this study, we have shown that the accretion product formed in the reaction of the ethene-derived peroxy radical is likely a peroxide and is produced with a branching fraction of approximately 23%. We have further measured the ratio of radical propagating to radical terminating chemistry as well as the branching to glycolaldehyde, which is produced in both chain propagating and chain terminating channels. Finally, we have constrained the rate coefficient of the title reaction relative to the reaction rate coefficient of the peroxy radical with 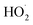 , and obtain a value consistent with those of previous flash photolysis studies. The branching fractions and kinetics along with their uncertainties (derived from comparison of our observations with a box model) are summarized in Table 3. Future studies will extend the methods discussed here to study the
, and obtain a value consistent with those of previous flash photolysis studies. The branching fractions and kinetics along with their uncertainties (derived from comparison of our observations with a box model) are summarized in Table 3. Future studies will extend the methods discussed here to study the 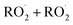 chemistry in more diverse systems.
chemistry in more diverse systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the U. S. National Science Foundation under Grant No. CHE-1905340. This work was also supported by Novo Nordisk Foundation Grant NNF19OC0057374.Notes and references
- T. Berndt, W. Scholz, B. Mentler, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Angew. Chem., Int. Ed. Engl., 2018, 57, 3820–3824 CrossRef CAS PubMed.
- L. Xu, K. H. Møller, J. D. Crounse, R. V. Otkjær, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. A, 2019, 123, 1661–1674 CrossRef CAS PubMed.
- J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317 RSC.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics : from Air Pollution to Climate Change, Wiley, Hoboken, New Jersey, 3rd edn, 2016 Search PubMed.
- J. D. Crounse, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. Lett., 2013, 4, 3513–3520 CrossRef CAS.
- E. Praske, J. D. Crounse, K. H. Bates, T. Kurtén, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. A, 2015, 119, 4562–4572 CrossRef CAS PubMed.
- R. Lee, G. Gryn’ova, K. U. Ingold and M. L. Coote, Phys. Chem. Chem. Phys., 2016, 18, 23673–23679 RSC.
- U. Molteni, M. Simon, M. Heinritzi, C. R. Hoyle, A.-K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, A. Dias, J. Duplissy, C. Frege, H. Gordon, C. Heyn, T. Jokinen, A. Kürten, K. Lehtipalo, V. Makhmutov, T. Petäjä, S. M. Pieber, A. P. Praplan, S. Schobesberger, G. Steiner, Y. Stozhkov, A. Tomé, J. Tröstl, A. C. Wagner, R. Wagner, C. Williamson, C. Yan, U. Baltensperger, J. Curtius, N. M. Donahue, A. Hansel, J. Kirkby, M. Kulmala, D. R. Worsnop and J. Dommen, ACS Earth Space Chem., 2019, 3, 873–883 CrossRef CAS.
- A. J. Kwan, A. W. H. Chan, N. L. Ng, H. G. Kjaergaard, J. H. Seinfeld and P. O. Wennberg, Atmos. Chem. Phys., 2012, 12, 7499–7515 CrossRef CAS.
- T. Berndt, S. Richters, R. Kaethner, J. Voigtländer, F. Stratmann, M. Sipilä, M. Kulmala and H. Herrmann, J. Phys. Chem. A, 2015, 119, 10336–10348 CrossRef CAS PubMed.
- H. Yue, C. Zhang, X. Lin, Z. Wen, W. Zhang, S. Mostafa, P. Luo, Z. Zhang, P. Hemberger, C. Fittschen and X. Tang, Int. J. Mol. Sci., 2023, 24, 3731 CrossRef CAS PubMed.
- B. H. Lee, F. D. Lopez-Hilfiker, E. L. D'Ambro, P. Zhou, M. Boy, T. Petäjä, L. Hao, A. Virtanen and J. A. Thornton, Atmos. Chem. Phys., 2018, 18, 11547–11562 CrossRef CAS.
- I. Barnes, K. H. Becker and L. Ruppert, Chem. Phys. Lett., 1993, 203, 295–301 CrossRef CAS.
- H. L. Bethel, R. Atkinson and J. Arey, Int. J. Chem. Kinet., 2001, 33, 310–316 CrossRef CAS.
- R. Atkinson, J. Phys. Chem. Ref. Data, 1997, 26, 215–290 CrossRef CAS.
- R. Atkinson, Atmos. Chem. Phys., 2003, 3, 2233–2307 CrossRef CAS.
- J. J. Orlando, G. S. Tyndall, M. Bilde, C. Ferronato, T. J. Wallington, L. Vereecken and J. Peeters, J. Phys. Chem. A, 1998, 102, 8116–8123 CrossRef CAS.
- K. T. Vasquez, H. M. Allen, J. D. Crounse, E. Praske, L. Xu, A. C. Noelscher and P. O. Wennberg, Atmos. Meas. Tech., 2018, 11, 6815–6832 CrossRef CAS.
- J. D. Crounse, K. A. McKinney, A. J. Kwan and P. O. Wennberg, Anal. Chem., 2006, 78, 6726–6732 CrossRef CAS PubMed.
- S. W. Sharpe, R. L. Sams and T. J. Johnson, Proceedings of the 31st Applied Image Pattern Recognition Workshop on from Color to Hyperspectral: Advancements in Spectral Imagery Exploitation, USA, 2002, pp. 45–48 Search PubMed.
- N. Hyttinen, R. V. Otkjær, S. Iyer, H. G. Kjaergaard, M. P. Rissanen, P. O. Wennberg and T. Kurtén, J. Phys. Chem. A, 2018, 122, 269–279 CrossRef CAS PubMed.
- F. Paulot, J. D. Crounse, H. G. Kjaergaard, J. H. Kroll, J. H. Seinfeld and P. O. Wennberg, Atmos. Chem. Phys., 2009, 9, 1479–1501 CrossRef CAS.
- J. M. St. Clair, K. M. Spencer, M. R. Beaver, J. D. Crounse, F. Paulot and P. O. Wennberg, Atmos. Chem. Phys., 2014, 14, 4251–4262 CrossRef.
- J. D. Crounse, F. Paulot, H. G. Kjaergaard and P. O. Wennberg, Phys. Chem. Chem. Phys., 2011, 13, 13607–13613 RSC.
- T. Su and W. J. Chesnavich, J. Chem. Phys., 1982, 76, 5183–5185 CrossRef CAS.
- A. L. Garden, F. Paulot, J. D. Crounse, I. J. Maxwell-Cameron, P. O. Wennberg and H. G. Kjaergaard, Chem. Phys. Lett., 2009, 474, 45–50 CrossRef CAS.
- C. M. Kenseth, Y. Huang, R. Zhao, N. F. Dalleska, J. C. Hethcox, B. M. Stoltz and J. H. Seinfeld, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, 8301–8306 CrossRef CAS PubMed.
- Y. Li, H.-D. Hao and Y. Wu, Org. Lett., 2009, 11, 2691–2694 CrossRef CAS PubMed.
- Y. Li, H.-D. Hao, Q. Zhang and Y. Wu, Org. Lett., 2009, 11, 1615–1618 CrossRef CAS PubMed.
- H. Keller-Rudek, G. K. Moortgat, R. Sander and R. Sörensen, Earth Syst. Sci. Data, 2013, 5, 365–373 CrossRef.
- J. B. Burkholder, S. P. Sander, J. Abbatt, J. R. Barker, C. Cappa, J. D. Crounse, T. S. Dibble, R. E. Huie, C. E. Kolb, M. J. Kurylo, V. L. Orkin, C. J. Percival, D. M. Wilmouth and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 19, JPL Publication 19-5, Jet Propulsion Laboratory, Pasadena, 2019, http://jpldataeval.jpl.nasa.gov Search PubMed.
- P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes, M. D. Smarte, J. M. St Clair, A. P. Teng, X. Zhang and J. H. Seinfeld, Chem. Rev., 2018, 118, 3337–3390 CrossRef CAS PubMed.
- C. Anastasi, D. J. Muir, V. J. Simpson and P. Pagsberg, J. Phys. Chem., 1991, 95, 5791–5797 CrossRef CAS.
- T. P. Murrells, M. E. Jenkin, S. J. Shalliker and G. D. Hayman, J. Chem. Soc., Faraday Trans., 1991, 87, 2351–2360 RSC.
- P. D. Lightfoot, R. A. Cox, J. N. Crowley, M. Destriau, G. D. Hayman, M. E. Jenkin, G. K. Moortgat and F. Zabel, Atmos. Environ., Part A, 1992, 26, 1805–1961 CrossRef.
- A. A. Boyd and R. Lesclaux, Int. J. Chem. Kinet., 1997, 29, 323–331 CrossRef CAS.
- M. E. Jenkin and R. A. Cox, J. Phys. Chem., 1991, 95, 3229–3237 CrossRef CAS.
- M. E. Jenkin and G. D. Hayman, J. Chem. Soc., Faraday Trans., 1995, 91, 1911–1922 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ea00020f |
| ‡ Currently at AbbVie. |
| § Currently at Terray Therapeutics. |
| This journal is © The Royal Society of Chemistry 2023 |