Paramagnetic supramolecular mesogens: A new paradigm in self-assembled magnetic materials†
Martin
Lambov
a,
Philipp
Maier
a,
Marcin
Jasiński
 b,
Jacek
Szczytko
b,
Jacek
Szczytko
 c,
Piotr
Kaszyński
c,
Piotr
Kaszyński
 *bde and
Matthias
Lehmann
*bde and
Matthias
Lehmann
 *af
*af
aInstitute of Organic Chemistry, University of Würzburg, Am Hubland, 97074 Würzburg, Germany
bFaculty of Chemistry, University of Łódź, Tamka 12, 91-403 Łódź, Poland
cInstitute of Experimental Physics, Faculty of Physics University of Warsaw, Pasteura 5, 02-093 Warsaw, Poland
dCentre of Molecular and Macromolecular Studies, Polish Academy of Sciences, Sienkiewicza 112, 90363 Łódź, Poland. E-mail: piotrk@cbmm.lodz.pl
eOrganic Materials Research Group, Department of Chemistry, Middle Tennessee State University, Murfreesboro, TN 37132, USA
fCenter for Nanosystems Chemistry and Bavarian Polymer Institute, Theodor-Boveri-Weg 4, 97074 Würzburg, Germany. E-mail: matthias.lehmann@uni-wuerzburg.de
First published on 29th April 2022
Abstract
Sterically crowded, shape-persistent star mesogens with three oligophenylenevinylene arms provide free space in which Blatter radical guests are incorporated by covalent bonds (esters) or supramolecular interactions (hydrogen bonds). The radical guests transform these compounds to paramagnetic liquid crystalline (LC) materials. The LC molecules are demonstrated to self-assemble into several types of columnar phases, a process that is controlled by the binding mode and the size of the star mesogen cavity. The conjugated scaffold remains stable in the presence of these radicals. Magnetic investigations by means of solid-state VT-EPR and SQUID experiments reveal that these materials are paramagnetic with weak antiferromagnetic interactions. In contrast to the covalent mesogens, the supramolecular systems do not only possess much lower clearing temperatures, but also radical guests exhibit mobility independent of the phase transition leading to soft paramagnetic materials with tunable magnetic properties.
Introduction
In recent decades the design of functional liquid crystals (LCs) has been of great interest owing to their structural control at different levels and the stimuli responsiveness based on their molecular mobility.1–3 Some of them have been studied intensively for applications in display technologies,4 organic electronics,5 optical switching,6 and stimuli responsive fluorescence applications.7 There has also been increasing interest in self-organizing paramagnetic molecular materials for technological advances and, in this context, investigation of spininterfaces8 and spintronic phenomena9,10 in thin films,11,12 mesoporous13,14 and in liquid crystalline materials.15–18 In particular, the robust 1,4-dihydrobenzo[e][1,2,4]triazin-4-yl radical19 (Blatter20 radical) has proven to be an attractive building block for the development of novel multi-functional materials21 for organic batteries,22 molecular electronics23,24 and spintronics.13,25Blatter radical derivatives have been designed to self-assemble into photoconductive bent-core26,27 and discotic28,29 LCs. The magnetic properties of the columnar LC phases depend on the molecular design of mesogens,29,30 which, in turn, controls the paramagnetic core overlap and, consequently, the spin–spin exchange interactions in the LC phase.31 Thus, “full disc” Blatter radicals show different magnetic behaviour compared to that of “half discs”. The “half disc” Blatter radicals have also been connected to form isostructural biradicals (“dumbbell” architecture) or triradicals (“superdisc” architecture). However, not all of them are LCs.31
Recently, the rational design of mesogens providing free space in LC phases for the uptake of guest molecules has been studied as a new method to guide the positional order of functional building blocks in mesophases.32 It was shown that shape-persistent star mesogens consisting of an alternating substitution pattern around a benzene core with oligo(phenylenevinylene) arms and pyridyl or hydroxyphenyl groups generate pockets, in which guest molecules can be hosted. These endo-receptors are able to accept up to three guests.33–35 The resulting supramolecular or covalently bonded supermesogens36 self-assemble in highly ordered double or triple nanosegregated structures.37,38 These results prompted us to design new supermesogens 1 and 2 (Fig. 1) containing the Blatter radical guests G1OH and G2OH either covalently or supramolecularily bound to the conjugated sterically crowded star mesogen hosts.
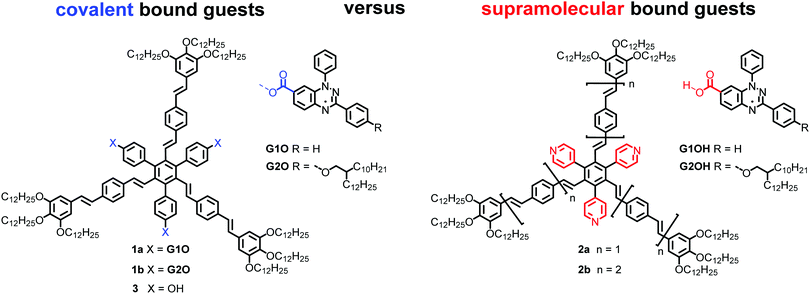 | ||
| Fig. 1 Structures of radical mesogens 1a and 1b, the supramolecular hosts 2a and 2b and the radical guests G1OH and G2OH. | ||
Herein we report on the effect of the covalent vs. the supramolecular binding in the cavity of the host mesogen, the impact of the cavity size (n = 1 and 2) and the substitution of the Blatter radical on the thermotropic and magnetic behaviour of the material. The comprehensive temperature-dependent structural studies by means of polarized optical microscopy (POM), differential scanning calorimetry (DSC), X-ray scattering (XRS) and polarized FT-IR spectroscopy demonstrated low clearing, enantiotropic columnar soft crystalline and columnar liquid crystalline phases of radical supermesogens in a broad temperature range. The magnetic properties have been explored through solid-state SQUID and EPR measurements showing dissimilar behaviour for covalent and supramolecular bound paramagnetic guests. This new paradigm opens up an attractive direction in the design of tailored paramagnetic soft materials.
Results and discussion
Synthesis
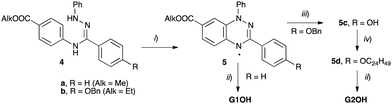
Compounds 1a and 1b were obtained by threefold Steglich esterification of triphenol 3 with carboxylic acids G1OH and G2OH, respectively. Mixtures of star mesogens 2a and 2b with G2OH were prepared in CH2Cl2 solutions followed by removal of the solvent and freeze-drying. Mixtures of 2 with acid G1OH macroscopically segregated owing to the strong crystallization tendency of the acid and were not considered further.The synthesis of the carboxylic acids G1OH and G2OH relied on the classical cyclization of amidrazones,39 as shown in Scheme 1. Thus, the two carboxylic acids were obtained by aerial oxidation of freshly prepared amidrazones 4a and 4b in the presence of Pd and a base to give the esters 5a (71% yield) and 5b (86% yield), respectively. The phenolic group in the latter ester was deprotected under reductive conditions (H2/Pd) and the resulting phenol 5c was alkylated with 2-decyltetradecyl bromide (6) to give the ethyl ester 5d. Both esters, 5a and 5d, were hydrolyzed with KOH in a MeOH/THF/H2O mixture giving acids G1OH and G2OH in 43% and 40% overall yield, respectively.
The requisite amidrazone 4a was prepared in 52% yield by reaction of hydrazonoyl chloride407 with methyl 4-aminobenzoate (Scheme 2). A similar reaction with the 4-benzyloxy analogue of chloride 7 did not yield the desired amidrazone 4b. Instead, the requisite amidrazone was obtained in 24% yield by reacting phenylhydrazine with benzimidoyl chloride 8 (Scheme 2). The chloride 8 was prepared from amide 9 in reaction with SOCl2 (Scheme 3). Mesogens 2 and the tri-hydroxyphenyl mesogen 3 (Fig. 1) were prepared according to literature procedures.33,38,41
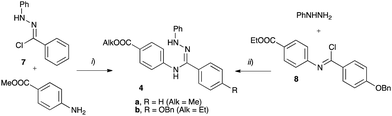 | ||
| Scheme 2 Synthesis of amidrazone 4. Reagents and conditions: (i) EtOH, Et3N, reflux, 2 h; (ii) Et3N, CH2Cl2, rt, overnight. | ||
 | ||
| Scheme 3 Synthesis of benzimidoyl chloride 8. Reagents and conditions: (i) Et3N, CH2Cl2, rt, overnight: (ii) SOCl2, reflux, 24 h. | ||
Thermotropic properties: POM and DSC studies.
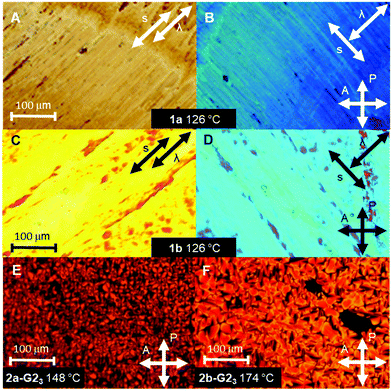
The thermotropic properties of all LC materials were studied by POM and DSC methods. The results are summarized in Table 1 and shown in Fig. 2. The supermesogens 1a and 1b do not reveal any transition to the isotropic phase below 300 °C, consequently, no characteristic LC textures could be obtained from POM observations. Nevertheless, the materials are birefringent under crossed polarizers and can be planar aligned by shearing, demonstrating the LC character of the samples. The supermesogen planes are on average oriented orthogonal to the column direction, which is concluded from the blue colour of the textures (Fig. 2(B) and (D)) originating from the addition of the largest refractive index of the sample and the largest index of the λ-compensation plate inserted perpendicular to the shearing direction and the complete extinction of light when one of the polarizers is parallel to the shearing direction (not shown). Both substances exhibit a reversible transition from a low temperature viscous, highly ordered, soft crystalline phase (Crsoft) for 1a and an oblique columnar phase (Colob) for 1b to more fluid hexagonal columnar phases at 117 °C (1a) and at 114 °C (1b), respectively. The transition to the LC state is accompanied by an increase in birefringence.| Compd | Phase behavior |
|---|---|
| a Transition temperature onset (°C) and transition enthalpy (kJ mol−1)/transition entropy (J K−1 mol−1) in parentheses. First heating and cooling cycles at 10 K min−1: Col columnar LC phase; h hexagonal; hH hexagonal helical; ob oblique; Crsoft soft crystal; g(Colh) glassy hexagonal columnar phase; g(Colorh) glassy orthorhombic columnar phase; Tg glass temperature; I isotropic phase. b Compounds decompose at >300 °C, before clearing. c Data from ref. 33 and 38. d Heating rate 15 K min−1. e POM observations of the growing textures at 187 °C. | |
| 1a | Crsoft(Colob) 117 (19.1/48.9) Colh > 300 °C (dec.)b |
| Colh 109 (−19.3/−49.3) CrSoft (Colob) | |
| 1b | Colob 114 (15.8/40.7) Colh > 300 °C (dec.)b |
| Colh 123 (−16.9/−43.4) Colob | |
| 2a | g(Colh) 89 (Tg) ColhH 138 (5.7/13.8) I |
| 2a-G21 | Colh 145 (7.2/17.2) Id |
| I 141 (−4.9/−11.8) Colh | |
| 2a-G22 | Colh 152 (11.4/26.7) Id |
| I 148 (−7.1/−16.6) Colh | |
| 2a-G23 | Crsoft(Colob) 67 (58.0/173.1) Colh 154 (11.7/27.6) I |
| I 152 (−11.2/−26.2) Colh | |
| 2b | g(Colorh) 153 (Tg) ColhH 194 (9.6/20.5) I |
| 2b-G21 | Crsoft 81 (20.0/56.3) Colh 183 (1.6/3.51) I |
| No visible transition in DSCe | |
| 2b-G22 | Colh 186 (9.2/20.0) I |
| I 182 (−5.1/−11.1) Colh | |
| 2b-G23 | Crsoft(Colob) 74 (−13.4/−38.6) Crsoft(Colob) 117 (8.4/21.5) Colh |
| 183 (11.8/25.8) I | |
| I 179 (−6.8/−14.9) Colh 60 (Tg) g (Colh) | |
The LC properties of the pure hosts 2a and 2b were already reported, and it was concluded that their molecules arrange in hexagonal double helical columnar phases (ColhH).33,38 The clearing temperatures increase with the length of the conjugated arm from 138 °C for 2a (n = 1) to 194 °C for 2b (n = 2).
The existence of mesophases in the presence of the guests G1OH and G2OH was initially investigated with contact samples for 2a and 2b in POM.42 Mixing of 2a with G1OH results only in macroscopic phase separation, owing to the stable crystal phase of G1OH, with a melting point >300 °C. In contrast, the guest G2OH with the branched peripheral chains possesses a much lower melting temperature (168 °C), which allows the formation of stable hydrogen bonded supermesogens with both hosts 2a and 2b and the self-assembly in new functional mesophases. Subsequently, for both hosts mixtures with radical G2OH (2a-G2 and 2b-G2) with an increasing fraction of the radical were prepared (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2a-G21 and 2b-G21; 1
1, 2a-G21 and 2b-G21; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2a-G22 and 2b-G22; 1
2, 2a-G22 and 2b-G22; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 2a-G23 and 2b-G23; Table 1). It was rationalized stochastically that 1
3, 2a-G23 and 2b-G23; Table 1). It was rationalized stochastically that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 systems consist of equilibrium mixtures of different complexes with the 1
2 systems consist of equilibrium mixtures of different complexes with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes, respectively, being the major components. Only for the fully filled cavities (the 1
2 complexes, respectively, being the major components. Only for the fully filled cavities (the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 system) is the material nearly completely composed of the 1
3 system) is the material nearly completely composed of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 supermesogens.38 Interestingly, the clearing transitions (DSC, heating rate 10 K min−1) are well defined with widths of only 4–6 K for the pure hosts and their mixtures. For all mixtures characteristic mosaic textures for columnar phases have been observed (Fig. 2(E) and (F)).37 In the case of 2a, the mesophase stability, i.e. the clearing temperature, increases with the increasing number of guest molecules. The maximum stability of the LC phase is achieved for the 1
3 supermesogens.38 Interestingly, the clearing transitions (DSC, heating rate 10 K min−1) are well defined with widths of only 4–6 K for the pure hosts and their mixtures. For all mixtures characteristic mosaic textures for columnar phases have been observed (Fig. 2(E) and (F)).37 In the case of 2a, the mesophase stability, i.e. the clearing temperature, increases with the increasing number of guest molecules. The maximum stability of the LC phase is achieved for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture (2a-G23) with the completely filled cavities.
3 mixture (2a-G23) with the completely filled cavities.
For this mixture the clearing temperature increases by 15 K to 153 °C relative to that of the pure host. The increase in the clearing temperature is a function of entropy and enthalpy, since at the phase transition ΔH = TΔS.
A LC supermesogen, which can dissociate at least partially into a number of building blocks at the transition to the isotropic liquid, exhibits a stronger increase of entropy, when compared with a system in which the mesogen keeps its integrity (e.g. covalent mesogens 1). According to the above equation, it is therefore expected that the clearing temperature decreases with the increasing number of building blocks constituting the supermesogen. On the other hand, the filling of the free space in the supermesogen results in a larger intermolecular interaction surface leading to higher enthalpies. Consequently, the enthalpy increases with an increasing number of H-bonding guests. For 2a this energy increase overcompensates the entropy change, which results in an increase in the clearing temperatures with increasing number of guests. This finding is in contrast to the previous studies, in which the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures (not 1
2 mixtures (not 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) with smaller guests always formed the most stable phase.38 This was explained by the formation of a completely filled double helix. Contrary to that, the larger π-surface of the guest G2OH prevents the formation of helices, presumably owing to stronger intracolumnar interactions. This suggestion is supported by the increasing transition enthalpy from 5.7 kJ mol−1 for the pure 2a to the maximum value of 11.7 kJ mol−1 for the 1
3) with smaller guests always formed the most stable phase.38 This was explained by the formation of a completely filled double helix. Contrary to that, the larger π-surface of the guest G2OH prevents the formation of helices, presumably owing to stronger intracolumnar interactions. This suggestion is supported by the increasing transition enthalpy from 5.7 kJ mol−1 for the pure 2a to the maximum value of 11.7 kJ mol−1 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture. Eventually, the much-reduced clearing temperature compared with the covalent bonded mesogen 1b can be explained by the entropy effect.
3 mixture. Eventually, the much-reduced clearing temperature compared with the covalent bonded mesogen 1b can be explained by the entropy effect.
A different behaviour is observed for the mesophase stabilities of mixtures 2b-G21–3, which are reduced relative to that of the pure host. Among the supramolecular materials, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture 2b-G22 shows the highest stability with a clearing transition at 186 °C, thus a reduced stability by 8 K relatively to pure 2b. In contrast, both the 1
2 mixture 2b-G22 shows the highest stability with a clearing transition at 186 °C, thus a reduced stability by 8 K relatively to pure 2b. In contrast, both the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the 1
1 and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixtures exhibit a lower stability with transition temperatures at 183 °C, i.e. a reduction of 11 K compared with the pure host. This stability series has also been reproduced by contact samples (see the ESI†). The lower stability of the Colh phases of all binary materials compared with the pure host is in contrast to the previous findings, in which a longer guest forms materials in 1
3 mixtures exhibit a lower stability with transition temperatures at 183 °C, i.e. a reduction of 11 K compared with the pure host. This stability series has also been reproduced by contact samples (see the ESI†). The lower stability of the Colh phases of all binary materials compared with the pure host is in contrast to the previous findings, in which a longer guest forms materials in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio with clearing temperatures exceeding that of the pure host.33 This indicates a mismatch between the pocket size (free space) of the star mesogen 2b and the size of guest G2OH in the present case. The smaller pockets of 2a suit obviously much better the size of the guests and restrict them to better-defined positions. A comparison of the transition enthalpies and entropies (ΔH and ΔS) of the pure hosts 2a and 2b (5.7 kJ mol−1; 13.8 J K−1 mol−1 and 9.6 kJ mol−1; 20.5 J K−1 mol−1) with those for the 1
2 ratio with clearing temperatures exceeding that of the pure host.33 This indicates a mismatch between the pocket size (free space) of the star mesogen 2b and the size of guest G2OH in the present case. The smaller pockets of 2a suit obviously much better the size of the guests and restrict them to better-defined positions. A comparison of the transition enthalpies and entropies (ΔH and ΔS) of the pure hosts 2a and 2b (5.7 kJ mol−1; 13.8 J K−1 mol−1 and 9.6 kJ mol−1; 20.5 J K−1 mol−1) with those for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures 2a-G21 and 2b-G21 (7.2 kJ mol−1; 17.2 J K−1 mol−1 and 1.6 kJ mol−1; 3.5 J K−1 mol−1) demonstrates that the ΔH and ΔS values increase for the mixture of the smaller host and they considerable decrease for the mixture of the larger host 2b. This indicates a higher order in the mesophases of the smaller supramolecular system, when compared with the larger system, in which the guest has much more space to occupy. The radical guest G2OH destabilizes considerably the more ordered helical columnar packing structure of the pure host 2b, which might be attributed to the mixing of the branched aliphatic chain from the small guest with the aromatic building block (vide infra).
1 mixtures 2a-G21 and 2b-G21 (7.2 kJ mol−1; 17.2 J K−1 mol−1 and 1.6 kJ mol−1; 3.5 J K−1 mol−1) demonstrates that the ΔH and ΔS values increase for the mixture of the smaller host and they considerable decrease for the mixture of the larger host 2b. This indicates a higher order in the mesophases of the smaller supramolecular system, when compared with the larger system, in which the guest has much more space to occupy. The radical guest G2OH destabilizes considerably the more ordered helical columnar packing structure of the pure host 2b, which might be attributed to the mixing of the branched aliphatic chain from the small guest with the aromatic building block (vide infra).
Analysis of the data in Table 1 demonstrates that only mixtures 2a-G23, 2b-G21 and 2b-G23 reveal crystalline or soft crystalline phases at low temperatures. However, these phases are observed only for pristine samples in the first heating cycle. The hexagonal columnar phases supercool and persist after the first heating. A glass transition has been detected for 2b-G23 at 60 °C42 rationalizing this stability of the Colh phase, however, even annealing above the glass transition for several hours did not recover the soft crystalline phase. Interestingly, after extrusion of fibres from the Colh phase, the soft crystalline phases can be observed in a subsequent heating cycle by X-ray scattering.42 This can be rationalized with the frozen high temperature phase, which is not in thermodynamic equilibrium after extrusion and thus the non-optimized packing allows structural reorganization.
FT-IR studies
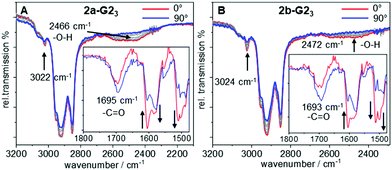
To gain further insight in the H-bonded structures of supermesogens 2a-G23 and 2b-G23, FT-IR studies have been performed on aligned samples, which were obtained by shearing of the Colh phase at 130 °C on a KBr plate. The measurements were then performed in the stable Colh phase at ambient temperature. The polarized FT-IR spectra shown in Fig. 3 demonstrate a broad signal with a maximum at 2466 cm−1 for 2a-G23 and 2472 cm−1 for 2b-G23, when the polarizer is aligned orthogonal to the column direction. This intensity can be attributed to the H-bond between the carboxylic acid and the pyridyl units. When the polarizer is rotated by 90°, the signal almost completely disappears. Similarly, well-defined absorptions at 3022 cm−1/3024 cm−1 for 2a-G23/2b-G23, attributed to aromatic CH-stretching vibrations oriented orthogonal to the column axis, also decrease when the polarization direction is changed. Owing to the steric congestion at the central hexa-substituted benzene ring, only peripheral aromatic building blocks of the host allow such an alignment.Since both stretching vibrations are found predominantly orthogonal to the column direction, this confirms the discotic structure of the supermesogens, with hydrogen-bonded guests in the cavities. These results are consistent with the POM findings. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration is found to be the most intense along the column axis, although it still possesses a considerable intensity orthogonal to the column direction. This shows that the orientation of the carboxyl group in the cavity is not well-defined.
O stretching vibration is found to be the most intense along the column axis, although it still possesses a considerable intensity orthogonal to the column direction. This shows that the orientation of the carboxyl group in the cavity is not well-defined.
XRS investigations
A more detailed picture of the self-assembly of the oligo(phenylenevinylene) scaffolds and the radical building blocks in the LC phases has been established by using XRS techniques. For all temperature-dependent XRS studies, the LC materials were aligned by extrusion to fibres from the respective Colh phases. The results are shown in Table 2 and Fig. 4–6.| Compd | Phase | T/°C | a/Åa | c | ρ | V m,T |
|---|---|---|---|---|---|---|
a Unit cell parameter a for hexagonal structures.
b Thickness of a columnar slice calculated for one molecule in the repeat unit (Z = 1).
c Densities at temperatures T estimated on the basis of the experimental densities obtained by the buoyancy method at 22 °C (see the ESI).
d Molecular volume (Vm,T) at temperature T. It was assumed that there is only a significant volume change for the aliphatic chains, which was calculated according to the literature.43 The molecular volume Vm,T was calculated as the sum of the molecular volume Vm at 22 °C and the volume change of the aliphatic chains. The density was obtained by ρ = M/(Vm,T × NA); NA = Avogadro's constant, M = molecular weight.
e Estimated thickness based on the density of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture.
f The oblique columnar structures could not be indexed with high accuracy. A possible indexation with cell parameters (a, b, γ) for the columnar arrangement is given in the ESI.
g Crsoft2 has been measured during first heating, while the data of the Colh phase has been determined on cooling the sample. 3 mixture.
f The oblique columnar structures could not be indexed with high accuracy. A possible indexation with cell parameters (a, b, γ) for the columnar arrangement is given in the ESI.
g Crsoft2 has been measured during first heating, while the data of the Colh phase has been determined on cooling the sample.
|
||||||
| 1a | Colh | 150 | 42.5 | 4.05 | 0.941 | 6275 |
| 1b | Colob | 25 | ||||
| Colh | 136 | 47.2e | 4.25 | 0.942 | 8135 | |
| 2a-G21 | Colh | 110 | 44.8 | 3.25e | ||
| 2a-G22 | Colh | 110 | 45.5 | 3.81e | ||
| 2a-G23 | Crsoft(Colob) | 66 | ||||
| Colh | 110 | 46.1 | 4.35 | 0.959 | 8009 | |
| 2b-G21 | Colh | 110 | 54.6 | 2.47e | ||
| 2b-G22 | Colh | 110 | 57.9 | 2.62e | ||
| 2b-G23 | Crsoft1 (Colob) | 25 | ||||
| Crsoft2 (Colob) | 110g | |||||
| Colh | 110g | 56.8 | 3.15 | 0.929 | 8815 | |
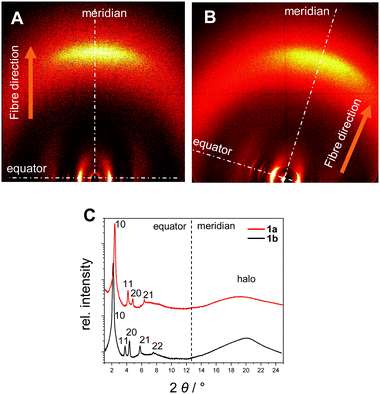 | ||
| Fig. 4 XRS patterns of the oriented samples in the wide-angle region of 1a at 150 °C (A) and of 1b at 136 °C (B). (C) Integration of the diffraction patterns along the equator and the meridian. | ||
The XRS results for the covalent star mesogens 1a at 150 °C and 1b at 136 °C in Fig. 4 show the well-defined equatorial and meridional reflections, which indicate a reasonable good quality of the fibre alignment. The equatorial reflections can be indexed according to a hexagonal columnar phase with a = 42.5 Å (1a) and a = 47.2 Å (1b). The significant difference in the column diameter can be attributed to the additional branched chains on the radical fragment in 1b. In the wide-angle region both materials show diffuse signals at 4.7 Å (1a) and 4.5 Å (1b) with the highest intensity on the meridian. This can be attributed to a superposition of the average distance of liquid-like aliphatic chains and the intracolumnar distance between the disc-like cores. Diffuse intensities are also discerned in the small angle region of 1b, which indicate a further periodicity along the columns.42 However, these signals could not be resolved even with SAXS, thus, no further information could be obtained. With the determined density of 0.942 g cm−3 for 1b, a complete molecule fits into a columnar slice of 4.25 Å height, which is in good agreement with the average distance along the column axis (Table 2).
In the case of 1a the radical fragments possess no aliphatic chains, and consequently the residual free space has to be compensated by the aliphatic chains of the host.32 At lower temperatures the need for efficient space filling leads to a reversible transition to a lower symmetry oblique columnar soft crystal phase for 1a and an oblique columnar LC phase for 1b.
Previous investigation demonstrated that pure hosts 2a and 2b arrange in densely packed helical Colh phases by the formation of discrete propeller-like side-by-side dimers.33,38 This self-assembly is maintained during the uptake of up to two guests, with the size and shape similar to that of the stilbenoid arms. The third guest transforms the supermesogens to a complete disk and thus the dimer and the helical superstructure is lost. We expected to find similar behaviour in complexes 2-G2. XRS experiments revealed however, that complexes of the smaller host 2a give similar XRS patterns at comparable temperatures for all three ratios with guest G2OH (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2a-G21; 1
1, 2a-G21; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2a-G2; 1
2, 2a-G2; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 2a-G23; Fig. 5). The integrated signals on the equator can be assigned to Colh phases. The column diameter slightly increases from 44.8 to 46.1 Å with the increasing number of guests, but is smaller than that for the pure host forming a double helix (46.7 Å).38 The absence of any diffuse meridional signals indicate that the double helical structure is already disfavoured with the first accepted guest, although the dimer structure seems to be maintained for the 1
3, 2a-G23; Fig. 5). The integrated signals on the equator can be assigned to Colh phases. The column diameter slightly increases from 44.8 to 46.1 Å with the increasing number of guests, but is smaller than that for the pure host forming a double helix (46.7 Å).38 The absence of any diffuse meridional signals indicate that the double helical structure is already disfavoured with the first accepted guest, although the dimer structure seems to be maintained for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
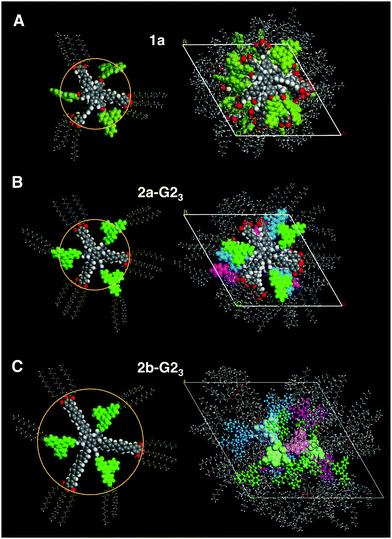
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures. This is rationalised from the c parameters (Table 2), which are calculated to be in the range of 3.3–3.8 Å for one supermolecule within the repeating unit in the column. This small columnar stacking distance is not reasonable for a partially filled sterically crowded core of single hosts with a thickness larger than 4 Å and points to side-by-side dimers as the basic structural units for this columnar self-assembly. The loss of the helical stacking can be attributed to the sterically more demanding Blatter radical guest G2OH possessing a lateral phenyl group, which is turned out of the heterocycle and disc planes. This is based on the experimental results and the previous findings33,38 of the most reasonable model of the phases with less than three guests. Eventually, the radical guests can perfectly fill all three cavities of the host and, as a result, only one mesogen 2a-G23, consisting of the star molecule with three hydrogen-bonded radicals does occupy the average distance of 4.4 Å. This hypothesis is supported by molecular modelling, as highlighted in Fig. 6(B). Note that the radicals are slightly larger than the length of the cavity. This results, however, in additional stabilization of the phase, when compared to the phase behaviour of the pure host or hosts with smaller guests, which frequently destabilize the self-assembly.33,41
2 mixtures. This is rationalised from the c parameters (Table 2), which are calculated to be in the range of 3.3–3.8 Å for one supermolecule within the repeating unit in the column. This small columnar stacking distance is not reasonable for a partially filled sterically crowded core of single hosts with a thickness larger than 4 Å and points to side-by-side dimers as the basic structural units for this columnar self-assembly. The loss of the helical stacking can be attributed to the sterically more demanding Blatter radical guest G2OH possessing a lateral phenyl group, which is turned out of the heterocycle and disc planes. This is based on the experimental results and the previous findings33,38 of the most reasonable model of the phases with less than three guests. Eventually, the radical guests can perfectly fill all three cavities of the host and, as a result, only one mesogen 2a-G23, consisting of the star molecule with three hydrogen-bonded radicals does occupy the average distance of 4.4 Å. This hypothesis is supported by molecular modelling, as highlighted in Fig. 6(B). Note that the radicals are slightly larger than the length of the cavity. This results, however, in additional stabilization of the phase, when compared to the phase behaviour of the pure host or hosts with smaller guests, which frequently destabilize the self-assembly.33,41
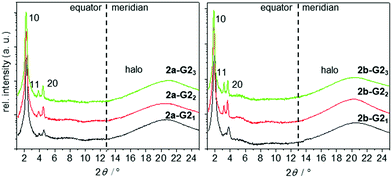 | ||
Fig. 5 2θ-scans along the equator and meridian of WAXS patterns of aligned fibres taken in the hexagonal phase at 150 °C of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1 1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 1 2, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixtures of 2a and 2b with G2. 3 mixtures of 2a and 2b with G2. | ||
With its larger conjugated arms, the star mesogen 2b provides longer cavities relative to those in 2a. This suggests that the steric interactions of the H-bonded radical are not expected to change much, as compared to those in the analogous complexes of the smaller host 2a. Therefore, it is not surprising, that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of radical G2OH with the host 2b exhibits equatorial signals corresponding to a Colh phase. The density ρ and the c parameter indicate for this mixture again mesogenic side-by-side dimers, but, according to the XRS patterns,42 a helical order is absent. Similarly, all data for the 1
1 mixture of radical G2OH with the host 2b exhibits equatorial signals corresponding to a Colh phase. The density ρ and the c parameter indicate for this mixture again mesogenic side-by-side dimers, but, according to the XRS patterns,42 a helical order is absent. Similarly, all data for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture (2b-G22), especially the unreasonable small c parameter for one molecule in the columnar repeating unit, point to a Colh dimer phase over the whole temperature range, while for the 1
2 mixture (2b-G22), especially the unreasonable small c parameter for one molecule in the columnar repeating unit, point to a Colh dimer phase over the whole temperature range, while for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture (2b-G23) the data should be in agreement with an ordinary Colh phase (Table 1, also see the ESI†). Interestingly, although all cavities are filled in the mixture 2b-G23, the height of the repeating unit for one mesogen along the column was calculated to be 3.15 Å (110 °C) at the experimental density of 0.929 g cm−3. This value is smaller than a typical π–π separation, which is about 3.2–3.4 Å44 and much smaller than the thickness of the crowded benzene core (up to 6.6 Å). Therefore, it is reasonable to assume that two molecules occupy the height of 6.3 Å and are not able to stack with their cores on top of each other in the middle of the column. Instead, they must be translationally shifted from the centre. This model is concluded exclusively on the basis of experimental results. In order to gain a better understanding of how such molecules may realise such a stacking in a columnar LC phase, we performed force field geometry optimisation considering all experimental data. A possible geometry optimised model is shown in Fig. 6(C). It demonstrates a higher disorder of the radical fragment in the LC phase. This is in agreement with the XRS results and with the observed small increase of the transition entropy, when compared to that for the pure host 2b (Table 1). As mentioned above, the 1
3 mixture (2b-G23) the data should be in agreement with an ordinary Colh phase (Table 1, also see the ESI†). Interestingly, although all cavities are filled in the mixture 2b-G23, the height of the repeating unit for one mesogen along the column was calculated to be 3.15 Å (110 °C) at the experimental density of 0.929 g cm−3. This value is smaller than a typical π–π separation, which is about 3.2–3.4 Å44 and much smaller than the thickness of the crowded benzene core (up to 6.6 Å). Therefore, it is reasonable to assume that two molecules occupy the height of 6.3 Å and are not able to stack with their cores on top of each other in the middle of the column. Instead, they must be translationally shifted from the centre. This model is concluded exclusively on the basis of experimental results. In order to gain a better understanding of how such molecules may realise such a stacking in a columnar LC phase, we performed force field geometry optimisation considering all experimental data. A possible geometry optimised model is shown in Fig. 6(C). It demonstrates a higher disorder of the radical fragment in the LC phase. This is in agreement with the XRS results and with the observed small increase of the transition entropy, when compared to that for the pure host 2b (Table 1). As mentioned above, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixtures were investigated in their freeze-dried and extruded samples at 25 °C and 110 °C. The soft crystalline phases were observed in these materials only in the first heating, for which the equatorial reflections could be attributed to an oblique packing of columns (Table 2, also see the ESI†).
3 mixtures were investigated in their freeze-dried and extruded samples at 25 °C and 110 °C. The soft crystalline phases were observed in these materials only in the first heating, for which the equatorial reflections could be attributed to an oblique packing of columns (Table 2, also see the ESI†).
Magnetic properties
Magnetic properties of 1a, 2a-G33 and 2b-G23 were investigated with variable temperature EPR spectroscopy and SQUID magnetometry for neat freeze-dried samples. The former method permitted magnetic characterization of the LC phases in broad temperature ranges. In contrast, limitation of the SQUID magnetometer permitted studies only at lower temperatures, in the solid-state. Magnetic characterization of 2b-G23 provides an example of such analysis, which was conducted in the temperature range of 300–2 K and magnetic field of 0.6 T for a pristine freeze-dried solid. Analysis of molar paramagnetic susceptibility, χp, demonstrated weak antiferromagnetic interactions in the solid state (Fig. 7). The amount of uncompensated spin at 2 K is about 32% and it increases to nearly 100% at 300 K. Curie-Weiss analysis of 1/χp(T) plots using eqn (1) revealed a significantly negative Weiss parameter θW = −16.1 K for 2b-G23.| 1/χp = (T − θw)/C | (1) |
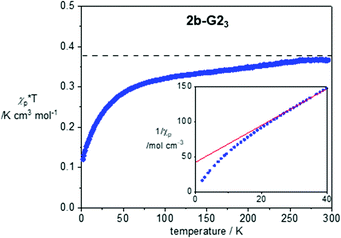 | ||
| Fig. 7 χ p × T vs. T plot for 2b-G23 in the cooling mode after diamagnetic correction χdia = −0.00559 × T K cm3 mol−1. For determination of χdia see the ESI.† The horizontal line marks the Curie constant C = 0.375 cm3 mol−1 K. The inset shows the lower portion of the 1/χpvs. T plot (2–40 K). The red line marks the best-fit line in the range of 30–200 K: 1/χp = 2.684(5) × T + 42.3(5), r2 = 0.9998. | ||
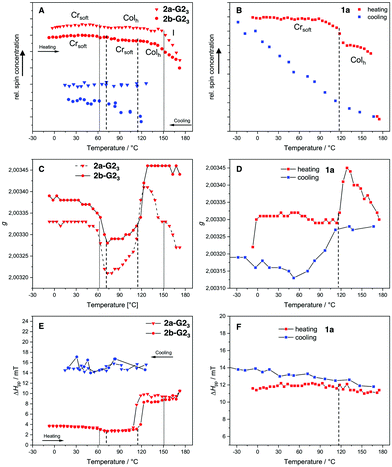
It was expected that the covalent system 1a and the supramolecular systems 2a-G23 and 2b-G23 would exhibit different magnetic behavior in the mesophase temperature range accessible by EPR spectroscopy. Therefore, the temperature dependent EPR spectra for the covalent compound 1a was measured between −30 °C and 180 °C and for the supermesogens 2a-G23 and 2b-G23 between −10 °C and 180 °C. The results for relative spin count, which is related to paramagnetic susceptibility χp,45 the gyromagnetic constant g and the peak-to-peak distance ΔHpp are given in Fig. 8. The changing g-values at the phase transitions in LCs indicate reorientations of the material in the magnetic field, while a change in ΔHpp is a function of spin-spin interactions (increasing value with increasing interactions) and spin-exchange interactions (decreasing value with increasing interactions). It is argued that an increase in ΔHpp with a simultaneous decrease of the number of spins (Ns) points to an increase of antiferromagnetic interactions.46
For the covalent compound 1a the free spin concentration Ns undergoes no significant changes on heating until the transition into the Colh phase at 117 °C, when a steep decrease of 12% is observed (Fig. 8(B), red line). While the ΔHpp is almost constant over the whole temperature range, the change in the g-value indicates that the loss of uncompensated spins can be associated with a reorganisation in the more mobile Colh phase accompanied by an increase of antiferromagnetic interactions. The cooling cycle (Fig. 8(B), blue line) has nearly linear behaviour with a constant increase of free spins and a slight increase of the ΔHpp. The latter becomes slightly steeper at the phase transition to the soft crystalline phase at 109 °C, at which the decreasing g-value points again to reorganisation of the spin environment (Fig. 8(D)). Therefore, the strength of the antiferromagnetic interactions decreases and, as a consequence, the original number of spins Ns is restored. Importantly, it can be noted that the changes in magnetic behaviour for this compound are strongly coupled to the phase transitions.
The EPR curves for 2a-G23 and 2b-G23 behave differently, when compared to those of the covalent compound 1a. Although the LC structures of these two supramolecular materials are evidently distinct, the g-values change similarly at about the same temperatures (50 °C, 115 °C, Fig. 8(C)). After the second change for 2b-G23 the g-value remains high after the transition to the Colh phase, while for 2a-G23 the g-value increases without phase transition starting at 115 °C and falls again starting at 120 °C, even without any phase change. This points to an ongoing reorientation of the paramagnetic units in the increasingly less viscous LC phase. Similarly, the ΔHpp increases at 115 °C (2a-G23) and at 120 °C (2b-G23) pointing to an increase in spin-spin interactions (Fig. 8(E)). This is about 20 K before the Ns value decreases more steeply and it seems that these effects are not related to the phase transition (Fig. 8(A)). At higher temperatures the Ns falls off for both compounds starting in the range of 140–150 °C. For 2a-G23 this might be related to the Colh–I phase transition at 153 °C, however, for 2b-G23 the change starts to take place in the middle of the Colh phase. This is presumably because, in the disordered and less viscous LC phases of 2b-G23 the position of the radical guests G2OH is not fixed and they can rearrange mutually to optimise their communication, resulting in stronger antiferromagnetic exchange interactions. As the magnetic changes do not clearly coincide with the phase transitions, it appears that the paramagnetic guests in the supramolecular materials rearrange independently from the supermesogens in the LC structures. This clearly points to a more autonomous motion of the hydrogen-bonded paramagnetic building blocks. Upon cooling, supermesogen 2a-G23 displays a slightly decreasing Ns with almost constant spin interactions. These results indicate an increasing order of the discs and antiferromagnetic spin interactions with decreasing temperature. In contrast to 2a-G23, Ns values increase continuously for 2b-G23 even though the ΔHpp does not change. These facts may be attributed to the different self-assembly of the supermesogens in the LC phases of 2a-G23 and 2b-G23 (Fig. 8(B) and 8(C)). In the LC material 2a-G23 the radical units are more densely packed with higher order leading, in principle, to stronger spin-spin interactions. In contrast, the supermesogen 2b-G23 deviates from the centre of the column spatially separating the spin units. This separation persists and may even increase during the slow transformation into the soft crystal, explaining the increasing number of independent spins in the paramagnetic material.
Conclusions
The Blatter radical was successfully incorporated into star-shaped, sterically crowded mesogens either by a covalent link (pseudo-supermesogen) or by supramolecular hydrogen bonding (supermesogen) for the first time. Remarkably, these radicals are so stable that even at high temperatures (up to 250 °C) no decomposition or reactions with the conjugated scaffold are observed. The development of a new radical guest with branched peripheral chains and low melting temperature allowed us to obtain supermesogens self-assembling in enantiotropic columnar mesophases with much lower clearing temperatures than their covalent counterparts. All three cavities of the host materials could be completely filled with the radical units. The size of the cavity was crucial for the self-assembly in the LC phase leading to a more ordered structure for the smaller supermesogen (2a-G23) and a more disordered stacking for the larger (2b-G23) supermesogen, in which the host 2b provides more free space. EPR studies of the LC materials showed that the magnetic properties are influenced by the cavity size, but also by the method of radical incorporation – covalent vs supramolecular. While for the covalent system the number of uncompensated spins follows the phase transitions, i.e. the number of uncompensated spins is lower in the LC phases and increases with the separation of the spin units within the soft crystalline phases, in the supramolecular system the changes are largely independent of the phase transitions. This can be attributed to the mobility of radical units in the cavities of the hosts.From these perspectives the radical fragments report structural changes within the different soft columnar phases and thus, can be used as spin probes to explore structural details, e.g. strength of binding, packing and cavity size, in columnar self-assemblies of shape-persistent supermesogens. With respect to materials science, supermesogens with a combination of low clearing temperatures and paramagnetic Blatter radicals represent a fruitful direction in engineering of paramagnetic soft materials with possibly tuneable magnetic properties.
Experimental section
General
Reagents and solvents were used as received without further purification. If not stated otherwise, reactions were carried out under argon in a flame-dried flask with the addition of the reactants by using a syringe; subsequent manipulations were conducted in air. Dichloromethane was dried over CaH2 and distilled just before usage. Products were purified by flash chromatography on silica gel (70–200 mesh). Unless stated otherwise, the reported yields refer to analytically pure samples. The melting points were determined using Mel-Temp II apparatus or with a polarising optical microscope and are uncorrected. NMR spectra of non-radical intermediates were recorded with a Bruker AVIII 600 instrument. Chemical shifts are reported relative to solvent residual peaks (1H NMR: δ = 7.26 [CDCl3]; 13C NMR: δ = 77.0 [CDCl3]). All 13C NMR spectra are proton-decoupled. Multiplicity of the 13C NMR signals was assigned using 2D spectra (the HMQC method). IR spectra were recorded with a Cary 630 FTIR spectrometer. ESI-MS spectra were recorded with a Varian 500-MS LC Ion Trap. Mass spectra were recorded on a Bruker-Daltonics autflex II (MALDI), on a Bruker-Daltonics ultrafleXtreme (HRMS-MALDI), and on a Bruker-Daltonics micrOTOF focus and Synapt G2-Si (HRMS-ESI).The description of other instruments and techniques is provided in the ESI.†
Preparation of compound 1a
Compound 3 (90.0 mg, 34.3 μmol), acid G1OH (45.0 mg, 137 μmol), diisopropylcarbodiimide (DIC, 64.1 μL, 51.9 mg, 411 μmol) and 4-(dimethylamino)pyridinium p-toluenesulfonate (DPTS, 90.1 mg, 308 μmol) were stirred in a mixture of dried CH2Cl2 (40 mL) and dried DMF (10 mL) under nitrogen for 5 days. The reaction mixture was then washed with 1M HCl (3 × 30 mL). The solvent from the organic layer was evaporated under reduced pressure and the crude product was purified by preparative recycling GPC to yield 96.0 mg (269 μmol, 79%) of 1a as a brownish solid: FT-IR v 3026, 2919, 2850, 1725, 1577, 1502, 1465, 1428, 1395, 1291, 1226, 1190, 1161 cm−1; EPR giso = 2.004; aN = 4.4 G, 4.7 G, and 7.8 G; UV-vis (CHCl3) λmax (ε/104) 296 (9.58), 368 (10.52) 518 (0.36) nm; MALDI-HRMS m/z, calcd for C240H306N9O15: 3554.3453, found: 3554.3585. Anal. calcd for C240H306N9O15: C, 81.04; H, 8.67; N, 3.54; found: C, 80.57; H, 8.74; N, 3.48.Preparation of compound 1b
Compound 3 (20.0 mg, 7.62 μmol), acid G2OH (18.2 mg, 26.6 μmol), diisopropylcarbodiimide (DIC, 14.2 μL, 11.5 mg, 91.3 μmol) and 4-(dimethylamino)pyridinium p-toluenesulfonate (DPTS, 22.4 mg, 76.1 μmol) were stirred in a mixture of dried CH2Cl2 (20 mL) and dried DMF (7 mL) under nitrogen for 2 days. The reaction mixture was then washed three times with 1 M HCl (30 mL). The solvent from the organic layer was evaporated under reduced pressure and the crude product was purified by preparative recycling GPC to yield 24.0 mg (5.20 μmol, 68%) of 1b as a dark brown solid: IR v 2919, 2851, 1725, 1606, 1500, 1465, 1428, 1396, 1225, 1115 cm−1; MALDI-HRMS m/z, calcd for C312H450N9O18:4611.456, found: 4611.442. Anal. calcd for C312H450N9O18: C, 81.20; H, 9.83; N, 2.73. Found: C, 80.71; H, 10.00; N, 2.87.Preparation of mixtures 2-G2
Star mesogen 2a or 2b (10 mg) and appropriate amounts of acid G2OH were dissolved in dry CH2Cl2, stirred for 15 min, and the solvent was removed under reduced pressure. Benzene (1 mL) was added and the solution was freeze-dried for 3 h at 1.6 × 10−2 mbar. The resulting spongy material was weighed using a spatula without any rubbing on the flask wall. The stoichiometric data for all mixtures are shown in Table 3.| Mixture | Ratiotheoa2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G2OH G2OH |
Star mesogen 2 | Acid G2OH | Ratioexpb2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G2OH G2OH |
|---|---|---|---|---|
| a Ratiotheo: theoretical mol ratio n(2)/n(G2OH). b Ratioexp: experimental mol ratio n(2)/n(G2OH) based on data in columns 3 and 4; the error was calculated based on a weighting error of 0.01 mg. | ||||
| 2a-G21 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (1.000) 1 (1.000) |
9.98 mg, 3.87 μmol | 2.63 mg, 3.87 μmol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.999 (1.001 ± 0.005) 0.999 (1.001 ± 0.005) |
| 2a-G22 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (0.500) 2 (0.500) |
10.00 mg, 3.89 μmol | 5.29 mg, 7.77 μmol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.005 (0.499 ± 0.001) 2.005 (0.499 ± 0.001) |
| 2a-G23 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (0.333) 3 (0.333) |
9.96 mg, 3.86 μmol | 7.88 mg, 11.60 μmol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.999 (0.333 ± 0.001) 2.999 (0.333 ± 0.001) |
| 2b-G21 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (1.000) 1 (1.000) |
10.10 mg, 3.50 μmol | 2.38 mg, 3.50 μmol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.999 (1.001 ± 0.005) 0.999 (1.001 ± 0.005) |
| 2b-G22 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (0.500) 2 (0.500) |
9.99 mg, 3.46 μmol | 4.71 mg, 6.92 μmol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.999 (0.500 ± 0.002) 0.999 (0.500 ± 0.002) |
| 2b-G23 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (0.333) 3 (0.333) |
9.98 mg, 3.46 μmol | 7.06 mg, 10.40 μmol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.000 (0.333 ± 0.001) 3.000 (0.333 ± 0.001) |
Preparation of carboxylic acids G1OH and G2OH: General procedure
To a solution of the appropriate ester 5a or 5d (0.4 mmol) in THF/H2O (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 6.0 mL) was added methanolic KOH solution (0.1 M, 6.0 mL), and the resulting mixture was refluxed for 8 h. After the mixture was concentrated under reduced pressure to ca. 1/5 volume, excess aq. 1% HCl was added, and the crude acid was filtered off. The product was dissolved in a CH2Cl2/THF (5
1, 6.0 mL) was added methanolic KOH solution (0.1 M, 6.0 mL), and the resulting mixture was refluxed for 8 h. After the mixture was concentrated under reduced pressure to ca. 1/5 volume, excess aq. 1% HCl was added, and the crude acid was filtered off. The product was dissolved in a CH2Cl2/THF (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture, washed with several portions of H2O, the separated organic layer was dried (Na2SO4), filtered, and the solvents were removed. The resulting acid GOH was recrystallized from the THF/MeCN mixture (3×).
1) mixture, washed with several portions of H2O, the separated organic layer was dried (Na2SO4), filtered, and the solvents were removed. The resulting acid GOH was recrystallized from the THF/MeCN mixture (3×).
(1,3-Diphenyl-1,4-dihydrobenzo[e][1,2,4]triazinyl)-7-carboxylic acid (G1OH)
Brown solid, yield: 80 mg (61%); m.p. 309–313 °C (decomp.); IR (neat) v 3421, 1680 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1432, 1395, 1261 cm−1; ESI-MS (m/z): 329.1 (47, [M + H]+), 328.1 (100, [M]+), 77 (44). Anal. calcd for C20H14N3O2 × 0.25H2O: C, 72.17; H, 4.39; N, 12.62. Found: C, 72.13; H, 4.29; N, 12.67.
O), 1432, 1395, 1261 cm−1; ESI-MS (m/z): 329.1 (47, [M + H]+), 328.1 (100, [M]+), 77 (44). Anal. calcd for C20H14N3O2 × 0.25H2O: C, 72.17; H, 4.39; N, 12.62. Found: C, 72.13; H, 4.29; N, 12.67.
{3-[4-(2-Decyl-1-tetradecyloxy)phenyl]-1-phenyl-1,4-dihydrobenzo[e][1,2,4]triazinyl}-7-carboxylic acid (G2OH)
Brown-red solid, yield: 234 mg (86%); m.p. 168–169 °C; IR (neat) v 2920, 1672 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1579, 1394, 1299, 1243, 1165 cm−1; HRMS (ESI-TOF) m/z, calcd for C44H62N3O3: 680.4791, found: 680.4805. Anal. calcd for C44H62N3O3: C, 77.60; H, 9.18; N, 6.17. Found: C, 77.63; H, 9.21; N, 6.15.
O), 1579, 1394, 1299, 1243, 1165 cm−1; HRMS (ESI-TOF) m/z, calcd for C44H62N3O3: 680.4791, found: 680.4805. Anal. calcd for C44H62N3O3: C, 77.60; H, 9.18; N, 6.17. Found: C, 77.63; H, 9.21; N, 6.15.
Preparation of amidrazone 4a
A mixture of N-phenylbenzhydrazonoyl chloride40 (7, 1.15 g, 5.0 mmol), methyl 4-aminobenzoate (0.76 g, 5.0 mmol), and Et3N (0.61g, 0.84 mL, 6.0 mmol) in EtOH (3.0 mL) was refluxed for 2 h. The solvent was removed under reduced pressure, and the resulting mixture was purified by flash column chromatography (SiO2, pet. ether/EtOAc 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to afford 0.90 g (52% yield) of amidrazone 4a as a thick yellow oil, which was immediately used for the next cyclisation step: 1H NMR (CDCl3, 600 MHz) δ 3.87 (s, 3H), 6.33 (sbr, 1H), 6.74 (d, J = 8.7 Hz, 2H), 6.88–6.92 (m, 1H), 7.10–7.16 (m, 2H), 7.24–7.29 (m, 2H), 7.35–7.39 (m, 3H), 7.68–7.71 (m, 2H), 7.79 (brs, 1H), 7.91 (d, J = 8.7 Hz, 2H).
1) to afford 0.90 g (52% yield) of amidrazone 4a as a thick yellow oil, which was immediately used for the next cyclisation step: 1H NMR (CDCl3, 600 MHz) δ 3.87 (s, 3H), 6.33 (sbr, 1H), 6.74 (d, J = 8.7 Hz, 2H), 6.88–6.92 (m, 1H), 7.10–7.16 (m, 2H), 7.24–7.29 (m, 2H), 7.35–7.39 (m, 3H), 7.68–7.71 (m, 2H), 7.79 (brs, 1H), 7.91 (d, J = 8.7 Hz, 2H).
Preparation of amidrazone 4b
A mixture of amide 9 (2.25 g, 6.0 mmol) and SOCl2 (12 mL) was refluxed for 24 h, and the solvent was removed under reduced pressure to dryness. The resulting yellowish benzimidoyl chloride 8 was dissolved in dry CH2Cl2 (30 mL) and Et3N (0.84 mL, 6.0 mmol) followed by phenylhydrazine (0.60 mL, 6.0 mmol) were added dropwise, and the resulting mixture was stirred at ambient temperature overnight under an inert atmosphere (Ar). The reaction was quenched with excess aq 1% HCl, extracted with CH2Cl2 (3 × 15 mL), and the combined organic layers were dried (Na2SO4). The solvent was removed and the resulting mixture was flash chromatographed (SiO2, CH2Cl2/EtOAc 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 gradient to 1
1 gradient to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to give 0.67 g (24% yield) of partially purified amidrazone 4b isolated as a thick yellow oil, and immediately used for the next step without further handling: 1H NMR (CDCl3, 600 MHz) δ 1.36 (t, J = 7.1 Hz, 3H), 4.33 (q, J = 7.1 Hz, 2H), 5.08 (s, 2H), 5.79 (brs, 1H), 6.69 (d, J = 8.6 Hz, 2H), 6.85–6.89 (m, 1H), 6.95 (d, J = 8.7 Hz, 2H), 7.08–7.12 (m, 3H), 7.24–7.27 (m, 2H), 7.32–7.45 (m, 1H), 7.49 (brs, 1H), 7.63 (d, J = 8.7 Hz, 2H), 7.92 (d, J = 8.6 Hz, 2H).
1) to give 0.67 g (24% yield) of partially purified amidrazone 4b isolated as a thick yellow oil, and immediately used for the next step without further handling: 1H NMR (CDCl3, 600 MHz) δ 1.36 (t, J = 7.1 Hz, 3H), 4.33 (q, J = 7.1 Hz, 2H), 5.08 (s, 2H), 5.79 (brs, 1H), 6.69 (d, J = 8.6 Hz, 2H), 6.85–6.89 (m, 1H), 6.95 (d, J = 8.7 Hz, 2H), 7.08–7.12 (m, 3H), 7.24–7.27 (m, 2H), 7.32–7.45 (m, 1H), 7.49 (brs, 1H), 7.63 (d, J = 8.7 Hz, 2H), 7.92 (d, J = 8.6 Hz, 2H).
Preparation of radicals 5a and 5b
To a solution of freshly prepared amidrazone 4 (2.0 mmol) in dry CH2Cl2 (5.0 mL) was added 5% Pd/C (85 mg, 8 mol%) followed by DBU (30 μL, 0.20 mmol), and the resulting mixture was stirred overnight at room temperature. The mixture was filtered through Celite, the solvents were removed under reduced pressure, and the resulting material was purified by column chromatography (SiO2, CH2Cl2 gradient 2.5% MeOH in CH2Cl2) to yield the desired radical 5, which was recrystallized from the AcOEt/EtOH mixture.Methyl (1,3-diphenyl-1,4-dihydrobenzo[e][1,2,4]triazinyl)-7-carboxylate (5a)
Black solid, yield: 486 mg (71%); m.p. 241–243 °C (decomp.); IR (neat) v 1713 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1434, 1392, 1300, 1239, 198 cm−1; ESI-MS m/z 343.2 (100, [M + H]+), 342.2 (71, [M]+). Anal. calcd for C21H16N3O2: C, 73.67; H, 4.71; N, 12.27. Found: C, 73.63; H, 4.93; N, 12.04.
O), 1434, 1392, 1300, 1239, 198 cm−1; ESI-MS m/z 343.2 (100, [M + H]+), 342.2 (71, [M]+). Anal. calcd for C21H16N3O2: C, 73.67; H, 4.71; N, 12.27. Found: C, 73.63; H, 4.93; N, 12.04.
Ethyl {3-(4-benzyloxyphenyl)-1-phenyl-1,4-dihydrobenzo[e][1,2,4]triazinyl}-7-carboxylate (5b)
Black brown solid, yield: 785 mg (85%); m.p. 182–183 °C; IR (neat) v 1694 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1582, 1394, 1230, 1169, 1152, 1012 cm−1; HRMS (ESI-TOF) m/z calcd for C29H25N3O3: 463.1896, found: 463.1903. Anal. calcd for C29H24N3O3: C, 75.31; H, 5.23; N, 9.09. Found: C, 75.30; H, 5.36; N, 9.03.
O), 1582, 1394, 1230, 1169, 1152, 1012 cm−1; HRMS (ESI-TOF) m/z calcd for C29H25N3O3: 463.1896, found: 463.1903. Anal. calcd for C29H24N3O3: C, 75.31; H, 5.23; N, 9.09. Found: C, 75.30; H, 5.36; N, 9.03.
Preparation of ethyl {3-(4-hydroxyphenyl)-1-phenyl-1,4-dihydrobenzo[e]-[1,2,4]triazinyl}-7-carboxylate (5c)
To a suspension of 5% Pd/C (318 mg, 10 mol%) in EtOH (70 mL) a solution of benzyl ether 5b (693 mg, 1.5 mmol) in THF (54 mL) was added, and the resulting mixture was hydrogenated at 3 atm overnight. The mixture was filtered through Celite and oxidized with air until the yellow leuco form of the phenol 5c was fully consumed (TLC monitoring). Solvents were removed in vacuo (cold bath!), and the crude product was purified by flash column chromatography (SiO2, CH2Cl2 gradient CH2Cl2/EtOAc 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to yield 391 mg (70%) of 5c as a back solid: m.p. 215–217 °C; IR (neat) v 3407 (OH), 1683 (C
1) to yield 391 mg (70%) of 5c as a back solid: m.p. 215–217 °C; IR (neat) v 3407 (OH), 1683 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1579, 1394, 1239, 1221, 1150, 1129, 1014 cm−1; HRMS (ESI-TOF) m/z, calcd for C22H19N3O3
O), 1579, 1394, 1239, 1221, 1150, 1129, 1014 cm−1; HRMS (ESI-TOF) m/z, calcd for C22H19N3O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 373.1426, found: 373.1418. Anal. calcd for C22H18N3O3: C, 70.96; H, 4.87; N, 11.28. Found: C, 71.00; H, 4.99; N, 11.09.
373.1426, found: 373.1418. Anal. calcd for C22H18N3O3: C, 70.96; H, 4.87; N, 11.28. Found: C, 71.00; H, 4.99; N, 11.09.
Preparation of ethyl {3-[4-(2-decyl-1-tetradecyloxy)phenyl]-1-phenyl-1,4-dihydrobenzo[e][1,2,4]triazinyl}-7-carboxylate (5d)
A mixture of phenol 5c (223 mg, 0.6 mmol), 2-decyltetradecyl bromide42 (6, 305 mg, 0.73 mmol), solid K2CO3 (126 mg, 0.91 mmol), and DMAP (7 mg, 10 mol%) in dry DMF (9 mL) was stirred at 50 °C for 8 h. The resulting mixture was diluted with H2O (50 mL) and extracted with an Et2O/EtOAc mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 × 30 mL). Combined extracts were dried (Na2SO4), filtered, and the solvents were removed under reduced pressure. The crude product was purified by column chromatography (CH2Cl2/pet. ether 1
1, 3 × 30 mL). Combined extracts were dried (Na2SO4), filtered, and the solvents were removed under reduced pressure. The crude product was purified by column chromatography (CH2Cl2/pet. ether 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 gradient to pure CH2Cl2) to yield 332 mg (78%) of 5d as a brown solid: m.p. 89–90 °C; IR (neat) v 2920, 2851, 1702 (C
2 gradient to pure CH2Cl2) to yield 332 mg (78%) of 5d as a brown solid: m.p. 89–90 °C; IR (neat) v 2920, 2851, 1702 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1586, 1394, 1232, 1169, 1027 cm−1; HRMS (ESI-TOF) m/z calcd for C46H67N3O3
O), 1586, 1394, 1232, 1169, 1027 cm−1; HRMS (ESI-TOF) m/z calcd for C46H67N3O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709.5182, found: 709.5177. Anal. calcd for C46H66N3O3: C, 77.92; H, 9.38; N, 5.93. Found: C, 77.90; H, 9.36; N, 5.99.
709.5182, found: 709.5177. Anal. calcd for C46H66N3O3: C, 77.92; H, 9.38; N, 5.93. Found: C, 77.90; H, 9.36; N, 5.99.
Preparation ethyl 4-[4-(benzyloxy)benzamido]benzoate (9)
To a solution of 4-benzyloxybenzoic acid (2.28 g, 10.0 mmol) in dry CH2Cl2 (23 mL) was added dry DMF (0.12 mL, 1.5 mmol) followed by the dropwise addition of excess oxalyl chloride (1.75 mL, 20.4 mmol) at 0 °C. The mixture was stirred at ambient temperature for 2 h, and the solvents were removed under reduced pressure to dryness. The resulting acid chloride was dissolved in dry CH2Cl2 (20 mL), ethyl 4-aminobenzoate (1.65 g, 10.0 mmol) and Et3N (1.8 mL, 12.9 mmol) were added, and the mixture was stirred at ambient temperature overnight. The reaction was quenched with H2O (40 mL), extracted with CH2Cl2 (3 × 25 mL), combined organic layers were dried (Na2SO4) and the solvents were removed in vacuo. The resulting crude product was purified by column chromatography (SiO2, CH2Cl2/EtOAc 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to afford 3.34 g (89% yield) of amide 9 as a colorless solid: m.p. 203–204 °C; IR (neat) v 3356, 1707 (C
1) to afford 3.34 g (89% yield) of amide 9 as a colorless solid: m.p. 203–204 °C; IR (neat) v 3356, 1707 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1657 (C
O), 1657 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1605, 1600, 1403, 1277, 1243, 1176, 1098, 1008 cm−1; 1H NMR (CDCl3, 600 MHz) δ 1.39 (t, J = 7.1 Hz, 3H), 4.37 (q, J = 7.1 Hz, 2H), 5.13 (s, 2H), 7.04 (d, J = 8.8 Hz, 2H), 7.33–7.44 (m, 5H), 7.72 (d, J = 8.7 Hz, 2H), 7.84 (d, J = 8.8 Hz, 2H), 7.98 (brs 1H), 8.04 (d, J = 8.7 Hz, 2H); 13C NMR (CDCl3, 151 MHz) δ 14.3 (q), 60.9 (t), 70.2 (t), 115.0 (d), 119.0 (d), 126.0 (s), 126.9 (s), 127.5 (d), 128.3 (d), 128.7 (d), 129.0 (d), 130.8 (d), 136.2 (s), 142.2 (s), 161.9 (s), 165.1 (s), 166.1 (s); ESI-MS m/z 398.1 (44, [M + Na]+), 376.1 (100, [M + H]+). Anal. calcd for C23H21NO4: C, 73.58; H, 5.64; N, 3.73. Found: C, 73.61; H, 5.67; N, 3.86.
O), 1605, 1600, 1403, 1277, 1243, 1176, 1098, 1008 cm−1; 1H NMR (CDCl3, 600 MHz) δ 1.39 (t, J = 7.1 Hz, 3H), 4.37 (q, J = 7.1 Hz, 2H), 5.13 (s, 2H), 7.04 (d, J = 8.8 Hz, 2H), 7.33–7.44 (m, 5H), 7.72 (d, J = 8.7 Hz, 2H), 7.84 (d, J = 8.8 Hz, 2H), 7.98 (brs 1H), 8.04 (d, J = 8.7 Hz, 2H); 13C NMR (CDCl3, 151 MHz) δ 14.3 (q), 60.9 (t), 70.2 (t), 115.0 (d), 119.0 (d), 126.0 (s), 126.9 (s), 127.5 (d), 128.3 (d), 128.7 (d), 129.0 (d), 130.8 (d), 136.2 (s), 142.2 (s), 161.9 (s), 165.1 (s), 166.1 (s); ESI-MS m/z 398.1 (44, [M + Na]+), 376.1 (100, [M + H]+). Anal. calcd for C23H21NO4: C, 73.58; H, 5.64; N, 3.73. Found: C, 73.61; H, 5.67; N, 3.86.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support was provided by the German Science Foundation (DFG, LE 1571/5-1) and the National Science Center (NCN, 2017/25/B/ST5/02851). We are especially thankful to Dr Ivo Krummenacher for performing the ESR measurements in solution and to Dr Szymon Kapuściński for his support during the solid-state EPR studies.References
-
P. A. Heiney, in Handbook of Liquid Crystals, eds. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. Gleeson, P. Raynes and H. F. Gleeson, Wiley-WCH, Weinheim, 2014, vol. 4, pp. 521–567 Search PubMed
.
-
H. Bock, in Chirality in Liquid Crystals, eds. H.-S. Kitzerow and C. Bahr, Springer, New York, 2001, pp. 355–374 Search PubMed
.
- T. Kato, J. Uchida, T. Ichikawa and T. Sakamoto, Functional liquid crystals towards the next generation of materials, Angew. Chem., Int. Ed., 2018, 57, 4355–4371 CrossRef CAS PubMed
.
- M. Bremer, P. Kirsch, M. Klasen-Memmer and K. Tarumi, The TV in your pocket: Development of liquid-crystal materials for the new millennium, Angew. Chem., Int. Ed., 2013, 52, 8880–8896 CrossRef CAS PubMed
.
- S. Sergeyev, W. Pisula and Y. H. Geerts, Discotic liquid crystals: A new generation of organic semiconductors, Chem. Soc. Rev., 2007, 36, 1902–1929 RSC
.
-
C. V. Garcìa, I. G. Pérez, P. L. Contreras, B. Vinouze and B. Fracasso, in Optical Switches: Materials and design, eds. B. Li, S. J. Chua, Woodhead Publishing, 2010, pp. 206–240 Search PubMed
.
- Y. Sagara and T. Kato, Stimuli-responsive luminescent liquid crystals: Change of photoluminescent colors triggered by a shear-induced phase transition, Angew. Chem., Int. Ed., 2008, 47, 5175–5178 CrossRef CAS PubMed
.
- M. B. Casu, Nanoscale studies of organic radicals: Surface, interface, and spinterface, Acc. Chem. Res., 2018, 51, 753–760 CrossRef CAS PubMed
.
- M. P. de Jong, Recent progress in organic spintronics, Open Phys., 2016, 14, 337–353 CrossRef CAS
.
- S. Sanvito, Molecular spintronics, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC
.
- M. Mas-Torrent, N. Crivillers, C. Rovira and J. Veciana, Attaching persistent organic free radicals to surfaces: How and why, Chem. Rev., 2012, 112, 2506–2527 CrossRef CAS PubMed
.
- F. Ciccullo, N. M. Gallagher, O. Geladari, T. Chasse, A. Rajca and M. B. Casu, A derivative of the Blatter radical as a potential metal-free magnet for stable thin films and interfaces, ACS Appl. Mater. Interfaces, 2016, 8, 1805–1812 CrossRef CAS PubMed
.
- A. S. Poryvaev, E. Gjuzi, D. M. Polyukhov, F. Hoffmann, M. Froba and M. V. Fedin, Blatter-radical-grafted mesoporous silica as prospective nanoplatform for spin manipulation at ambient conditions, Angew. Chem., Int. Ed., 2021, 60, 8683–8688 CrossRef CAS PubMed
.
- A. S. Poryvaev, D. M. Polyukhov, E. Gjuzi, F. Hoffmann, M. Forba and M. V. Fedin, Radical-doped metal–organic framework: Route to nanoscale defects and magnetostructural functionalities, Inorg. Chem., 2019, 58, 8471–8479 CrossRef CAS PubMed
.
- P. Kaszynski, S. Kapuściński and S. Ciastek-Inskrzycka, Liquid crystalline derivatives of heterocyclic radicals, Adv. Heterocyc. Chem., 2019, 128, 263–331 CrossRef CAS
.
-
R. Tamura, Y. Uchida and K. Suzuki in Handbook of Liquid Crystals, eds. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. F. Gleeson, P. Raynes, Wiley-VCH, Weinheim, 2014, vol. 8, pp. 837–864 Search PubMed
.
- S. Castellanos, F. López-Calahorra, E. Brillas, L. Juliá and D. Velasco, All-organic discotic radical with a spin-carrying rigid-core showing intracolumnar interactions and multifunctional properties, Angew. Chem., Int. Ed., 2009, 48, 6516–6519 CrossRef CAS PubMed
.
- K. Bajzíková, M. Kohout, J. Tarábek, J. Svoboda, V. Novotná, J. Vejpravová, D. Pociecha and E. Gorecka, All-organic liquid crystalline radicals with a spin unit in the outer position of a bent-core system, J. Mater. Chem. C, 2016, 4, 11540–11547 RSC
.
- F. J.-M. Rogers, P. L. Norcott and M. L. Coote, Recent advances in the chemistry of benzo[e][1,2,4]triazinyl radicals, Org. Biomol.
Chem., 2020, 18, 8255–8277 RSC
.
- H. M. Blatter and H. Lukaszewski, A new stable free radical, Tetrahedron Lett., 1968, 9, 2701–2705 CrossRef
.
- I. Ratera and J. Veciana, Playing with organic radicals as building blocks for functional molecular materials, Chem. Soc. Rev., 2012, 41, 303–349 RSC
.
-
Stable radicals: fundamentals and applied aspects of odd-electron compounds, ed. R. Hicks, Wiley & Sons, 2010 Search PubMed
.
- J. Z. Low, G. Kladnik, L. L. Patera, S. Sokolov, G. Lovat, E. Kumarasamy, J. Repp, L. M. Campos, D. Cvetko, A. Morgante and L. Venkataraman, The environment-dependent behavior of the blatter radical at the metal–molecule interface, Nano Lett., 2019, 19, 2543–2548 CrossRef CAS PubMed
.
- F. Bejarano, I. J. Olavarria-Contreras, A. Droghetti, I. Rungger, A. Rudnev, D. Gutiérrez, M. Mas-Torrent, J. Veciana, H. S.-J. van der Zant, C. Rovira, E. Burzurí and N. Crivillers, Robust organic radical molecular junctions using acetylene terminated groups for C–Au bond formation, J. Am. Chem. Soc., 2018, 140, 1691–1696 CrossRef CAS PubMed
.
- F. Ciccullo, A. Calzolari, K. Bader, P. Neugebauer, N. M. Gallagher, A. Rajca, J. van Slageren and M. B. Casu, Interfacing a potential purely organic molecular quantum bit with a real-life surface, ACS Appl. Mater. Interfaces, 2019, 11, 1571–1578 CrossRef CAS PubMed
.
- S. Kapuściński, A. Gardias, D. Pociecha, M. Jasiński, J. Szczytko and P. Kaszyński, Magnetic behaviour of bent-core mesogens derived from the 1,4-dihydrobenzo[e][1,2,4]triazin-4-yl, J. Mater. Chem. C, 2018, 6, 3079–3088 RSC
.
- K. I. Shivakumar, D. Pociecha, J. Szczytko, S. Kapuściński, H. Monobe and P. Kaszyński, Photoconductive bent-core liquid crystalline radicals with a paramagnetic polar switchable phase, J. Mater. Chem. C, 2020, 8, 1083–1088 RSC
.
- M. Jasinski, S. Kapuściński and P. Kaszyński, Stability of a columnar liquid crystalline phase in isomeric derivatives of the 1,4-dihydrobenzo[e][1,2,4]triazin-4-yl: Conformational effects in the core, J. Mol. Liq., 2019, 277, 1054–1059 CrossRef CAS
.
- M. Jasinski, J. Szczytko, D. Pociecha, H. Monobe and P. Kaszyński, Substituent-dependent magnetic behavior of discotic benzo[e][1,2,4]triazinyls, J. Am. Chem. Soc., 2016, 138, 9421–9424 CrossRef CAS PubMed
.
- M. Jasinski, K. Szymańska, A. Gardias, D. Pociecha, H. Monobe, J. Szczytko and P. Kaszyński, Tuning the magnetic properties of columnar benzo[e][1,2,4]triazin-4-yls with the molecular shape, ChemPhysChem, 2019, 20, 636–644 CrossRef CAS PubMed
.
- S. Kapuściński, J. Szczytko, D. Pociecha, M. Jasiński and P. Kaszynski, Discs, dumbbells and superdiscs: Molecular and supermolecular architecture dependent magnetic behavior of mesogenic Blatter radical derivatives, Mater. Chem. Front., 2021, 5, 6512–6521 RSC
.
- M. Lehmann, M. Dechant, M. Lambov and T. Ghosh, Free space in liquid crystals–Molecular design, generation, and usage, Acc. Chem. Res., 2019, 52, 1653–1664 CrossRef CAS PubMed
.
- P. Maier, M. Grüne and M. Lehmann, A star-shaped oligo(phenylenevinylene) liquid crystal host with an anthracene guest–A double nanosegregating supermesogen, Chem. Eur. J., 2017, 23, 1018–1022 CrossRef CAS PubMed
.
- M. Lehmann and M. Hügel, A perfect match: Fullerene guests in star-shaped oligophenylenevinylene mesogens, Angew. Chem., Int. Ed., 2015, 54, 4110–4114 CrossRef CAS PubMed
.
- M. Lambov, N. Hensiek, A. C. Poppler and M. Lehmann, Columnar liquid crystals from star-shaped conjugated mesogens as nano-reservoirs for small acceptors, ChemPlusChem, 2020, 85, 2219–2229 CrossRef CAS PubMed
.
-
J. M. Lehn, in Supramolecular Chemistry, Wiley-VCH, Weinheim, 1995, pp. 81–87 Search PubMed
.
- M. Hügel, M. Dechant, N. Scheuring, T. Ghosh and M. Lehmann, Fullerene-filled stilbene stars: The balance between isolated C60 helices and 3D networks in liquid crystal self-assemblies, Chem. Eur. J., 2019, 25, 3352–3361 Search PubMed
.
- M. Lehmann and P. Maier, Shape-persistent, sterically crowded star mesogens: From exceptional columnar dimer stacks to supermesogens, Angew. Chem., Int. Ed., 2015, 54, 9710–9714 CrossRef CAS PubMed
.
- P. A. Koutentis and D. L. Re, Catalytic oxidation of N-phenylamidrazones to 1,3-diphenyl-1,4-dihydro-1,2,4-benzotriazin-4-yls: An improved synthesis of Blatter's radical, Synthesis, 2010, 2075–2079 CrossRef CAS
.
- C.-Y. Zhang, X.-H. Liu, B.-L. Wang, S.-H. Wang and Z.-M. Li, Synthesis and antifungal activities of new pyrazole derivatives via 1,3-dipolar cycloaddition reaction, Chem. Biol. Drug Des., 2010, 75, 489–493 CrossRef CAS PubMed
.
- M. Lehmann, P. Maier, M. Grüne and M. Hügel, Crowded star mesogens: Guest-controlled stability of meophases from unconventional liquid crystal molecules, Chem. Eur. J., 2017, 23, 1060–1068 CrossRef CAS PubMed
.
- For details see the ESI†.
- B. Donnio, B. Heinrich, H. Allouchi, J. Kain, S. Diele, D. Guillon and D. W. Bruce, A generalized model for the molecular arrangement in the columnar mesophases of polycatenar mesogens. Crystal and molecular structure of two hexacatenar mesogens, J. Am. Chem. Soc., 2004, 126, 15258–15268 CrossRef CAS PubMed
.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, Consistent van der Waals radii for the whole main group, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed
.
-
G. R. Eaton, S. S. Eaton, D. P. Barr and R. T. Weber, Quantitative EPR: A Practitioners Guide, Springer, Vienna, 2010 Search PubMed
.
- K. Suzuki, Y. Uchida, R. Tamura, S. Shimono and J. Yamauchi, Observation of positive and negative magneto-LC effects in all-organic nitroxide radical liquid crystals by EPR spectroscopy, J. Mater. Chem., 2012, 22, 6799–6806 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional synthetic and compound characterization details, POM data, powder XRD analysis, density measurements, FT-IR and EPR spectra, modeling details and magnetization results. See DOI: https://doi.org/10.1039/d2tc00015f |
| This journal is © The Royal Society of Chemistry 2022 |