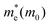Open Access Article
Open Access ArticleUnderstanding the role of spacer cation in 2D layered halide perovskites to achieve stable perovskite solar cells†
Eti
Mahal
 ,
Shyama Charan
Mandal
,
Shyama Charan
Mandal
 and
Biswarup
Pathak
and
Biswarup
Pathak
 *
*
Department of Chemistry, Indian Institute of Technology Indore, Indore 453552, India. E-mail: biswarup@iiti.ac.in
First published on 21st January 2022
Abstract
Intercalation of a large organic cation between metal halide layers provides better energetic stability to the perovskite structure. In this regard large organic cation intercalated two-dimensional layered halide perovskites (2D-LHPs) are receiving research attention due to their improved environmental stability and structural versatility. Here, we present a detailed theoretical investigation on the effect of spacer cations on the structural distortion of the inorganic layer that mainly controls the band edge properties of 2D-LHPs. We have considered pure 2D-LHP systems that include three mono-cation as well as four di-cation spacers. The 2D-LHP systems are A2PbI4 and APbI4 for mono-cation and di-cation spacers, respectively, where A is the ammonium based organic spacer cation. Moreover, the structural, electronic, and optical properties of the 2D-LHPs have been investigated in detail to determine the origin of the spacer cation influence on the properties of 2D-LHPs. In spite of the mono-cationic nature, the 3-APN spacer cation considered in our study provides exceptionally reduced octahedral distortion (Pb–I–Pb angle ∼177° and 172°) and inorganic layer separation (∼10.17 Å) that results in a reduced band gap and good charge carrier masses. Directional anisotropy observed in the transport as well as optical property will guide the fabrication of high-performance photovoltaic devices. The considered di-cationic systems also possess an impressive band gap, carrier effective mass and optical absorption. Our findings expose the scope of mono-cation based systems as an excellent choice of material for applications in photovoltaics. Therefore, our study finds a design approach for 2D-LHPs to tune their properties through spacer cation engineering for application in photovoltaic devices.
Introduction
Hybrid metal halide perovskites have amazing semiconducting properties which have been the focus of renewable energy research in recent times. Despite the remarkable advances in three-dimensional (3D) organic–inorganic hybrid perovskites (formula AMX3, A = CH3NH3+ (methylammonium or MA), NH2CHNH2+ (formamidinium or FA); M = Sn2+, Pb2+; X = Cl−, Br−, I−) in next generation thin film photovoltaics, their large-scale commercialization is still suffering from a lack of environmental stability.1–7 In this context, several studies have reported the instability of a 3D perovskite structure towards water, oxygen, and light. In particular, the metal halide unit interacts with water molecules through H-bonding leading to easy decomposition and the organic cation deprotonates in the presence of light and oxygen.8,9 With the aim of reducing these obstacles, there have been attempts to find new halide perovskites through compositional change, dimensional reduction, and encapsulation. In the search of new materials, two-dimensional layered halide perovskites (2D-LHP) have emerged as potential candidates for application in photovoltaic devices due to their improved environmental stability.10,11 In the case of 3D perovskites, such as CH3NH3PbI3, the PbI3 inorganic part forms corner-sharing PbI6 octahedra and the methylammonium (MA) cation is situated inside the cavity. Like 3D perovskites, the 2D-LHPs are also made of a corner-sharing PbI6 octahedra with an intercalated large organic cation. The hydrophobic nature of large organic cations results in superior moisture stability compared to the 3D systems. Sargent and co-workers have reported energetically stable 2D-LHP-based materials, owing to the appreciable van der Waals forces.12 However, incorporation of a large organic cation between the inorganic layer results in quantum confinement in the hybrid perovskite's structure. Moreover, 2D-LHPs are examples of natural multiple quantum wells (MQW) that result from a large difference in the band gap and dielectric nature of organic and inorganic layers. Because of the smaller dielectric constant value, the organic spacer behaves as the “barrier”, whereas due to the higher dielectric constant value, the inorganic framework behaves as the “well”.13 Even and co-workers reported that variation in the dielectric constant can yield dramatic effects on the quantum well properties of 2D-LHPs.14 In addition to these, the large separation between two inorganic layers shows an increment in the barrier height of the MQW.The compositional design approaches can be made through choice of metal cation, halide anion, organic spacer cation and thickness of inorganic layer to design an effective 2D-LHP based material for photovoltaic applications. In this context, the intercalation of a large hydrophobic organic cation between two inorganic layers makes 2D-LHP versatile towards dimensional and compositional engineering. Based on the charge of the large organic cation of 2D-LHPs, they can be divided into two types: A2MX4 and AMX4 by mono- and di-cations, respectively, which gives an additional choice for material modelling. Several studies have reported that the choice of cation can significantly influence the electronic and optical properties of the 2D-LHPs as the geometries of spacer cations have a considerable effect on the structural distortion and octahedral tilting of the metal halide inorganic layer that determine the band gap and exciton binding energy. Additionally, the restriction of carrier movement can be reduced by incorporating spacer cations that have a better charge transport ability and are able to reduce the inorganic layer separation. Moreover, the introduction of an organic spacer cation that has conjugated functionalities and the ability to form strong H-bonds, increases the possibility of charge transfer between the inorganic and organic layers with improved band alignment. Furthermore, spacer cations that have a compact structure can reduce the inorganic layer separation and distortion of the octahedral geometry. Hence, cation engineering can be a precise way to make the right choice of 2D-LHP, resulting in the improved performance of photovoltaic devices. However, an efficient theoretical study to understand the controlling factors behind the influence of a spacer cation on the geometry of the metal halide layer and the properties of the perovskite system is necessary.
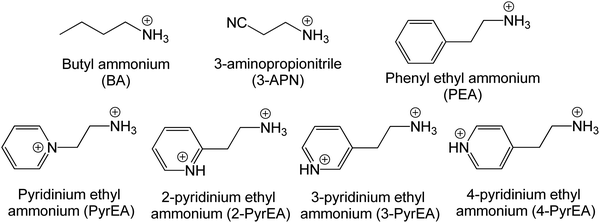
In this article, we present a detailed theoretical investigation of the atomic and electronic structures using a set of 2D-LHP systems to shed light on their tunable optoelectronic properties. We have used density functional theory (DFT) calculations to provide insight on the clear influence of the organic spacers on the structural properties of the 2D-LHPs that can indirectly control the photovoltaic properties of the materials. The inspiration behind the choice of considered systems came from some experimental reports which indicate that functional group modification in organic spacers can guide us to reach a finer photovoltaic property. To execute versatility in 2D-LHPs, our study ranges from aliphatic to aromatic mono- and aromatic di-ammonium based spacer cations. We have started with n-butylammonium (BA) and aromatic phenyl ethyl ammonium (PEA) which have been used extensively in earlier 2D-LHPs (Fig. 1). To explore the scope of aliphatic spacer-based systems we have considered 3-aminopropionitrile (3-APN) containing cyanide group that can form strong H-bonding and acquire rigid geometry. The reason behind choosing this spacer cation was a recent work of Wang and coworkers where they used a 3-APN spacer cation in a pure 2D-LHP and achieved the best performance among pure 2D-LHP based solar cells to the best of our knowledge.15 Even after an excellent experimental report, the underlying reason behind the impact of spacer cations in 2D-LHP is still unknown. Specifically, the sources of structural distortion and the reason behind the improved band edge properties are not fully understood. England and co-workers illustrated in their recent work that the intercalation of di-cations between inorganic layers can be beneficial as it requires single organic layer stacking compared to double organic layer stacking in mono-cation based systems.16 Motivated by their work, we have included a pyridinium based di-cation, pyridinium ethyl amine and its positional isomers (Fig. 1) in our study. The presence of dipositive charge develops cations with more rigid geometry. Also, they reported significant contributions of the di-cations in the band edge states but they are still to be studied to understand their atomistic origin for the same. Here, we have also calculated the effective mass of electrons and holes to understand the optoelectronic device characteristic as this is related to the key properties of semiconductor materials such as charge carrier mobility and diffusion length.
Computational methods
First principles calculations have been performed using the plane wave code, Quantum Espresso (QE).17 The GGA-PBE functional18 has been used with scalar relativistic ultrasoft pseudopotentials19 that include 2s, 2p orbital for O, N, and C; 1s orbital for H; 5s, 5p orbital for I; and 6s, 6p, 5d orbital for Pb ions for geometry optimization. The plane wave basis set cutoffs were set to 25 and 200 Ry for the smooth part of the wave functions and the augmented density, respectively. The cell parameters of the considered systems for relaxation have been taken from the available experimental reports. The optimized cell contains four formula units of the corresponding 2D-LHP such that there are 156 atoms for (BA)2PbI4, 188 atoms for (PEA)2PbI4, 116 atoms for (3-APN)2PbI4 and 104 atoms for all four PyrPbI4 systems. We have used Monkhorst pack k-point sampling22 of 4 × 4 × 1 and 6 × 4 × 1 for the mono-cation ((BA)2PbI4; (PEA)2PbI4; (3-APN)2PbI4) and di-cation spacer-based systems ((PyrEA)PbI4; (2-PyrEA)PbI4; (3-PyrEA)PbI4; (4-PyrEA)PbI4), respectively. For better accuracy in the electronic structure, we carried out single point electronic structure calculations using the HSE06 hybrid functional.20 The Hartree–Fock exchange parameter was set to 43%.21 Keeping in mind the high sensitivity of lead towards relativistic effects, we also included spin orbit coupling (SOC) in our HSE06 calculations. We have used norm-conserving pseudopotentials and electrons from I 5s, 5p; O, N, C 2s, 2p; H 1s; Pb 5s, 5p, 6s, 6p, 5d; and shells explicitly. The plane wave basis set cutoff for the smooth part of the wave functions and Fock energy cutoff have been set to 40 and 80 Ry, respectively, along with a Monkhorst pack k-point sampling of 2 × 2 × 1. Band structure calculations were performed using the GGA-PBE functional with SOC considering relativistic ultrasoft pseudopotentials.For the charge carrier effective mass calculations, we used projector-augmented wave-based (PAW) pseudopotentials along with the plane wave basis set as implemented in the Vienna ab-initio Simulation Package (VASP).23–28 Geometry optimizations were carried out using the GGA-PBE functional18 with a kinetic energy cutoff of 500 eV for the plane waves until the Hellmann–Feynman force on each atom was smaller than 0.01 eV Å−1. The systems considered for relaxation here are the same as earlier. Hence, a similar Γ-centered k-point grid of 4 × 4 × 1 and 6 × 4 × 1 was used for the mono- and di-cation based systems, respectively. To perform the single-point calculations to obtain the electronic structure, we considered the effect of SOC with the GGA-PBE functional. To obtain a more accurate value of the charge carrier effective masses, non-self-consistent calculations were performed using a high k-grid of 30 points between two high-symmetry points. Electron and hole effective masses, 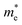 and
and  were calculated around Γ(0,0,0) towards X(0.5, 0, 0) and Γ(0,0,0) towards Y(0,0.5,0) high symmetry points in the Brillouin zone, because the fundamental band gap appears at the Γ-point. Subsequently, the effective masses were calculated using eqn (1),29
were calculated around Γ(0,0,0) towards X(0.5, 0, 0) and Γ(0,0,0) towards Y(0,0.5,0) high symmetry points in the Brillouin zone, because the fundamental band gap appears at the Γ-point. Subsequently, the effective masses were calculated using eqn (1),29
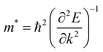 | (1) |
Depending upon the calculated electronic structure, the optical properties were calculated from the real and imaginary part of the dielectric function using eqn (2),30
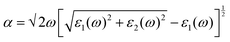 | (2) |
Results and discussion
Structural properties
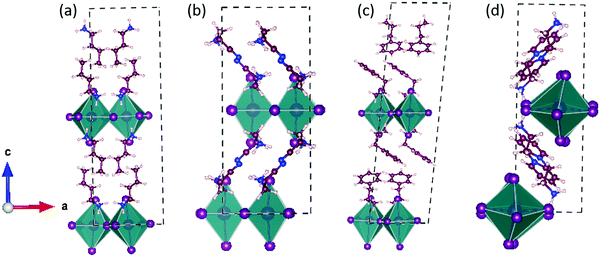
First, we optimized the geometries by taking the experimentally reported crystal structures as the initial guess.16,31–33 The optimized structures are shown in Fig. 2 and Fig. S1 (ESI†).Monovalent spacer cation
In this section, we discuss the three 2D-LHP systems containing mono-cation spacer: (BA)2PbI4, (3-APN)2PbI4, and (PEA)2PbI4. In mono-cation containing systems, interaction of the intercalated large organic cations with the inorganic layer is mainly between hydrogen atoms on the ammonium groups and the I atoms of the inorganic layer. So, the noncovalent interaction can be due to the H-bond formation. Among the three hydrogens of the ammonium group, two interact with nearby axial I atoms and one interacts with equatorial I atoms. In (BA)2PbI4 the distance between H and the axial and equatorial I atom is ∼2.5 Å and ∼2.9 Å, respectively, which indicates the presence of H-bonding interactions. Because of this H-bonding interaction between ammonium H and I of the [PbI6]4− inorganic layer, the lead iodide octahedra get distorted. The octahedral distortion results in a reduction in the Pb–I–Pb bond angles from ideal value (180°) to ∼151° (Table 1 and Fig. S2a, ESI†) and the same has been observed for (PEA)2PbI4 (Fig. S2b, ESI†). An almost similar Pb–I–Pb bond angle and the presence of H-bonding in (BA)2PbI4 was experimentally reported by Kanatzidis and co-workers.11 In the case of (PEA)2PbI4, the two axial Pb–I bond lengths are different, one elongates (3.87 Å) and the other contracts (3.24 Å), whereas all equatorial Pb–I bond lengths (3.19 Å) are the same. For (BA)2PbI4 the axial and equatorial Pb–I bonds have nearly the same lengths (∼3.22 Å). Hence, PEA results in higher octahedral distortion on the PbI6 unit compared to BA. Another candidate we have considered in this section is (3-APN)2PbI4. In general, the two ends of the spacer cations used to be directed in opposite directions i.e., the primary ammonium group is directed towards the lead iodide layer and the other end towards another spacer cation. In the case of (3-APN)2PbI4 both the cyanide and primary ammonium groups of one 3-APN cation is directed towards another 3-APN cation. Due to the presence of the distinct cyanide linkage in 3-APN the orientation of the cation changes i.e., the primary ammonium group in one cation faces the cyanide group of another cation and vice versa. The distance between ammonium H and cyanide N is 1.84 Å which is evidence for the formation of strong intermolecular H-bonding (Fig. 3). Due to this H-bonding interaction two 3-APN cations stacked between the lead iodide layer form a robust dimer pattern. Among the three hydrogens of the primary ammonium functionality, one gets involved in this dimer formation and the other two participate in H-bonding interactions with the two nearest axial iodides. But with equatorial iodides no non-covalent interaction happens which is why the lead iodide layer remains undisturbed where the Pb–I–Pb bond angles in (3-APN)2PbI4 are ∼172° and 177° (Fig. 3a and Table 1) which are close to the ideal (180°) bond angle. As a result of an almost ideal Pb–I–Pb angle, a greater extent of overlap between the Pb and I atomic orbitals pushes valence band maximum (VBM) and conduction band minimum (CBM) closure. Since the 3-APN cation is smaller in size and also forms a dimer inside the inorganic layer via intermolecular H-bonding interactions, the inorganic layer separation (10.17 Å) as well as closest I⋯I contact (4.56 Å) are smaller than other considered mono-cation based systems (Fig. 3a and Table 1). Hence, several factors make (3-APN)2PbI4 distinguishable among other considered systems such as the smaller size of the cation and the presence of electronegative cyanide linkage that is responsible for dimer formation. These factors may result in a reduced band gap in (3-APN)2PbI4 compared to the BA and PEA one and make it the best choice even though it is a mono-cation based system.| Layered perovskite system | Pb–I–Pb Angle-I (deg) | Pb–I–Pb Angle-II (deg) | Closest I⋯I contact (Å) | Inorganic layer separation (Å) |
|---|---|---|---|---|
| (BA)2PbI4 | 151.54 | 151.45 | 8.57 | 13.80 |
| (3-APN)2PbI4 | 171.85 | 177.42 | 4.56 | 10.17 |
| (PEA)2PbI4 | 150.36 | 151.87 | 10.05 | 16.00 |
| (PyrEA)PbI4 | 157.47 | 169.63 | 4.23 | 9.90 |
| (2-PyrEA)PbI4 | 157.73 | 165.45 | 4.21 | 9.98 |
| (3-PyrEA)PbI4 | 156.47 | 168.41 | 4.36 | 10.19 |
| (4-PyrEA)PbI4 | 154.57 | 176.65 | 4.36 | 10.10 |
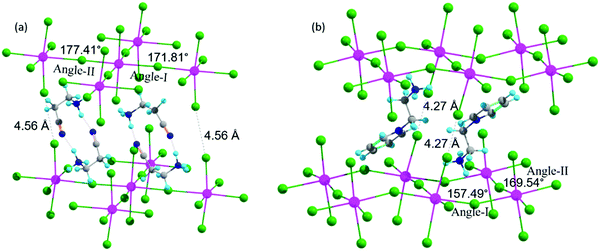 | ||
| Fig. 3 Geometrical features of (a) (3-APN)2PbI4 and (b) (pyridinium)PbI4 (Colors: hydrogen (sky), carbon (grey), nitrogen (blue), iodine (green), and lead (pink). | ||
Divalent spacer cation
In this section we discuss the four di-cation based 2D-LHP systems: (PyrEA)PbI4, (2-PyrEA)PbI4, (3-PyrEA)PbI4 and (4-PyrEA)PbI4 (Fig. 2 and Fig. S1, ESI†). In this case, the divalent nature of the pyridinium ring containing diammonium aromatic spacers results in a less distorted inorganic sheet and smaller inorganic layer separation. As these divalent spacer cations possess dipositive charge, only a single organic layer is present between the two lead iodide layers (Fig. 3b). Di-cations have one primary ammonium linkage and one positive charge centered in the pyridinium ring. Here, one organic spacer cation interacts with two different lead iodide layers, one layer interacts through the primary ammonium functionality and another lead iodide layer comes into contact with the pyridinium ring. Among the three hydrogens of the primary ammonium group two interact with two equatorial iodides and one interacts with one axial iodide. The distances between the interacting hydrogen and iodide are around 2.5–2.9 Å which falls within the H-bonding distance. But this type of H-bond formation happens only in alternative octahedral cavities due to the presence of a pyridinium ring in place of the primary ammonium group in the neighboring cavity. Due to the presence of insufficient H-bonding interactions, the PbI6 octahedral distortion is less with a more ideal Pb–I–Pb bond angle compared to (BA)2PbI4 and (PEA)2PbI4. The extent of distortion depends on the strength of interaction i.e., on the H-bond length. The (PyrEA)PbI4, (2-PyrEA)PbI4, (3-PyrEA)PbI4 and (4-PyrEA)PbI4 2D-LHP have Pb–I–Pb bond angles of ∼170°, 165°, 168° and 177°, respectively (Table 1, Fig. 3b and S2c–S2e, ESI†). Therefore, a substantial overlap between Pb and I atomic orbitals can easily reduce the band gap of di-cation based systems. As the smaller primary ammonium tail and bulkier pyridinium ring are in alternative octahedral cavities, the angle-I of the lead iodide octahedra deviates markedly from the ideal octahedral bond angle. In the case of (2-PyrEA)PbI4, (3-PyrEA)PbI4 and (4-PyrEA)PbI4 there is a secondary ammonium H present in the pyridinium ring which forms H-bonding with I. For this reason, the angle-I (Table 1) of these three systems further distorts and may result in an enhanced band gap in comparison to (PyrEA)PbI4. Single layer intercalation results in inorganic layer separation in the range of 9.9 Å to 10.2 Å (Table 1). The closest I⋯I contact for these systems ranges from 4.21 Å to 4.36 Å (Table 1). This smaller layer separation reduces the barrier of the MQW. Moreover, studying the relaxed structures, we have figured out that the noncovalent interactions between the lead iodide inorganic layer and the large organic spacer cations can strongly affect the geometry of the octahedral moiety. Although the di-cationic systems have one Pb–I–Pb angle close to 180°, due to the bulkiness of the pyridinium cations the overall structural distortion increases but (3-APN)2PbI4 possesses almost ideal octahedral geometry.Electronic structure
Next, we explored the electronic structures of the 2D-LHPs. In general, the PBE functional underestimates the band gap and gives poor agreement with experimental reports. Several theoretical studies have reported hybrid functionals with SOC for the estimation of accurate band gap values.34,35 Therefore, we have also used the HSE06 hybrid functional with SOC for the band gap calculations. We have tabulated the band gap values obtained by using PBE and HSE06-SOC functionals (Table 2). The band gap values obtained using HSE06-SOC are in good agreement with the experimental reports (Table 2). The HSE06-SOC calculated band gap obtained for (BA)2PbI4 is 2.42 eV. Our calculated band gap value for (BA)2PbI4 is very much in agreement with the theoretical value calculated by De Angelis and co-workers.36 Replacing the BA cation with 3-APN, the band gap value changes from 2.42 to 2.22 eV. This observation is anticipated due to the reduction in the inorganic layer separation i.e., closest I⋯I contact distance and reduced octahedral distortion i.e., ideal Pb–I–Pb bonding which results in maximum orbital overlap. On the other hand, in the case of (PEA)2PbI4 no significant changes were found. A similar trend of band gap for BA and PEA based 2D-LHPs has been observed by Tretiak and co-workers.37 This could be due to the aromatic ring impact on the band edge states of (PEA)2PbI4. In spite of having an aliphatic spacer (3-APN)2PbI4 exhibits an extraordinary feature due to the presence of a cyanide group that gives rise to the formation of robust dimers through H-bonding.| Spacer cation | Layered perovskite system | Band gap in eV | ||
|---|---|---|---|---|
| PBE | HSE06 + SOC | Expt. | ||
| n-Butylammonium | (BA)2PbI4 | 2.10 | 2.42 | 2.4311 |
| 3-Aminopropionitrile | (3-APN)2PbI4 | 1.92 | 2.22 | 2.2015 |
| Phenyl ethyl ammonium | (PEA)2PbI4 | 2.10 | 2.41 | 2.5738 |
| Pyridinium ethyl ammonium | (PyrEA)PbI4 | 1.65 | 2.24 | 2.3516 |
| 2-Pyridinium ethyl ammonium | (2-PyrEA)PbI4 | 1.89 | 2.38 | 2.4616 |
| 3-Pyridinium ethyl ammonium | (3-PyrEA)PbI4 | 1.85 | 2.36 | 2.3416 |
| 4-Pyridinium ethyl ammonium | (4-PyrEA)PbI4 | 1.83 | 2.32 | 2.3816 |
In the case of dipositive spacer cation-based 2D-LHPs, reduced band gap values were observed compared to (BA)2PbI4 and (PEA)2PbI4 because of their larger Pb–I–Pb bond angle and smaller inorganic layer separation which have been discussed previously. The trend of the calculated band gap of the four di-cationic systems is a clear consequence of their Pb–I–Pb bond angles discussed earlier. Our calculated band gap values show the smallest band gap value for the (3-APN)2PbI4 (2.22 eV). Although (3-APN)2PbI4 has a comparable inorganic layer separation to (PyrEA)PbI4 and also possesses an aliphatic spacer, its impressive band gap is an example showing that aliphatic mono-cation spacer-based systems are also capable of showing a better performance than aromatic spacer-based as well as di-cation spacer-based systems.
To confirm the position of atomic orbitals on the electronic structure of the system, we have calculated the projected density of states (pDOS) of all the considered 2D-LHPs. The pDOS components of the band edge states indicate that the VBM originates from the I atomic orbitals while the CBM mainly consists of Pb states (Fig. 4 and Fig. S3, ESI†). This clearly suggests that the VBM and CBM mostly spread over the lead iodide inorganic layer and lead and iodine atoms primarily control the mobility of electron and holes in the 2D-LHP. By analyzing the pDOS plots we have observed that the C atomic orbitals of the aromatic spacers remain close to the band edges. In the case of (PEA)2PbI4, the prominent C-pDOS components appear near the valence band and conduction band edges which is because of the high energy of the sp2 carbons in PEA compared to the sp3 carbons in BA. However, in the case of (3-APN)2PbI4, the organic cationic states (C, H, N) appear close to the conduction band edge in comparison to that in (BA)2PbI4. Due to the strong intermolecular H-bonding and dimer formation, the unoccupied orbitals of the organic part are believed to be stabilized and shifted slightly towards the conduction band edge of the perovskite system. Hence, we show that by introducing an electronegative cyanide linkage, we can make the cationic states approach to some extent towards the band edges even in the absence of any aromatic core or sp2 carbons. In the pDOS plot of di-cation based four 2D-LHPs, the cationic states appear close to the conduction band edges (Fig. 4 and Fig. S3, ESI†). In pyridinium ring cations, positive charges are extensively delocalized i.e., the LUMO gets stabilized. This brings the cationic states near the conduction band edge (∼0.77 eV). However, no significant changes have been observed with the change in the position of the ethyl ammonium functionality in the pyridine ring.
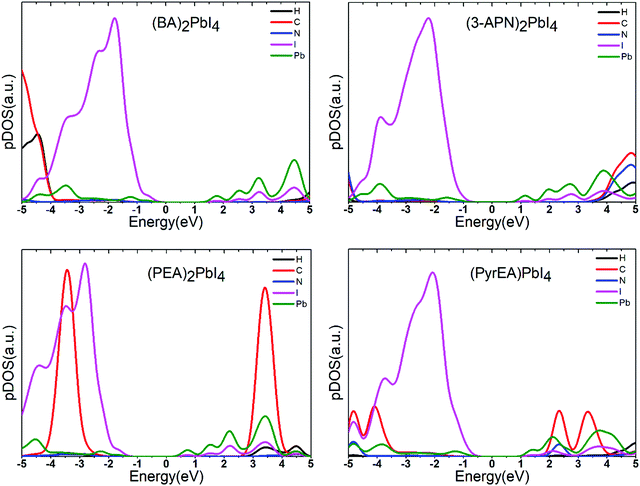 | ||
| Fig. 4 Projected density of states of the 2D-LHP systems using the HSE06 + SOC level of calculations. Here the Fermi level is set to zero. | ||
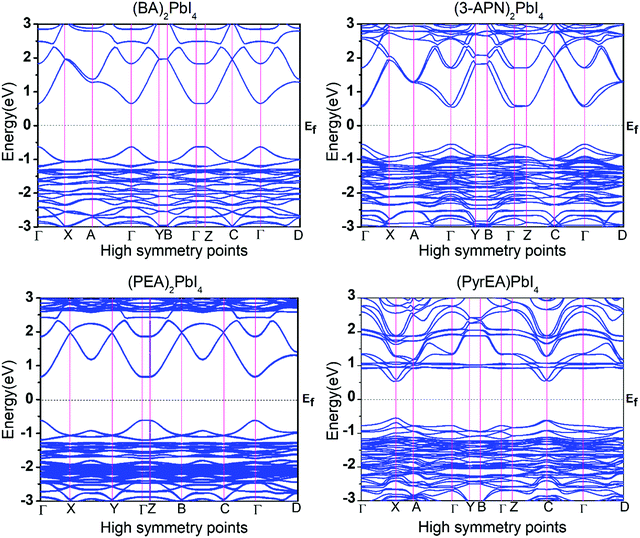
Moreover, we have calculated the band structure of all the 2D-LHP systems to check the dispersion of the energy levels towards the high symmetry points of the Brillouin zone. The band structures of the optimized 2D-LHP (Fig. 5 and Fig. S4, ESI†) structures have been calculated using the PBE+SOC method to reduce the computational costs. All the considered systems were found to show a direct band gap semiconductor property. The top of the valence band predominates an antibonding linear combination of Pb 6s and I 5p orbitals and the bottom of the conduction band is mainly composed of Pb 6p orbitals with minor antibonding contributions of I 5s orbitals (Fig. 4). Similar band edge state properties were distinctly characterized by Umebayashi and co-workers.39 Due to the substantial SOC constant of lead atoms, the effects of SOC on the band structures are significant. For the first three systems we have calculated the band structures both with and without SOC correction (Fig. 5 and Fig. S5, ESI†). The conduction band nature changes exceptionally due to the introduction of the SOC. Specifically, the down shifting of the bottom of the conduction band happens. For all three systems it has been observed that incorporation of SOC reduces the band gap by around 0.8 eV. Here, the conduction band mainly originates from Pb 6p atomic orbitals which are highly sensitive towards the relativistic effect and the introduction of SOC splits the conduction band i.e., reduces the band gap. Even and co-workers also investigated the dominating effect of SOC that mainly acts on the conduction band in hybrid lead halide perovskites.40,41
For monovalent spacer cation containing 2D-LHPs we have observed the fundamental band gap at a Γ high symmetry point whereas in the case of the di-cation based 2D-LHP systems the band gap appears at the X high symmetry point. Moreover, the flat nature of the band has been observed in the Γ–Z direction which is expected due to the presence of organic spacers. Furthermore, the charge carrier effective masses of all the 2D-LHP systems have been investigated to give insight on the carrier mobilities influenced by the choice of organic spacer cations. For the monovalent cationic spacer-based systems, (BA)2PbI4 and (PEA)2PbI4, we have calculated the electron and hole effective masses (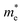 and
and 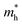 ) in the Γ–X and Γ–Y directions. Towards the Z direction these systems have an infinite value of carrier effective mass because of the low dielectric nature of the organic spacers. (BA)2PbI4 possess equal electron effective mass
) in the Γ–X and Γ–Y directions. Towards the Z direction these systems have an infinite value of carrier effective mass because of the low dielectric nature of the organic spacers. (BA)2PbI4 possess equal electron effective mass 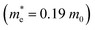 towards the X and Y directions of the Brillouin zone whereas the hole effective mass
towards the X and Y directions of the Brillouin zone whereas the hole effective mass 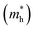 in the Γ–X direction is 0.29 m0 and in the Γ–Y direction it is 0.28 m0 which are almost identical (Table 3). Similar observation has been found for (PEA)2PbI4 where
in the Γ–X direction is 0.29 m0 and in the Γ–Y direction it is 0.28 m0 which are almost identical (Table 3). Similar observation has been found for (PEA)2PbI4 where 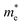 is 0.22 m0 in the Γ–X direction and 0.21 m0 in the Γ–Y direction whereas
is 0.22 m0 in the Γ–X direction and 0.21 m0 in the Γ–Y direction whereas 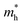 is 0.31 m0 towards both the X and Y directions from the Γ point. Similar effective mass values of (PEA)2PbI4 have been reported in several earlier studies.42,43
is 0.31 m0 towards both the X and Y directions from the Γ point. Similar effective mass values of (PEA)2PbI4 have been reported in several earlier studies.42,43
For (3-APN)2PbI4 we have calculated the electron and hole effective masses towards the Γ–X and Γ–Y directions. In addition, seeing the nature of the valence band near the Γ–Z direction we have crosschecked the hole masses in this direction where we have observed heavy holes. However, in the case of the (3-APN)2PbI4 system, dissimilar effective masses were found towards the X and Y high-symmetry points. The electron effective masses are nearly similar (0.18 m0 in the Γ–X and 0.16 m0 in the Γ–Y directions) while the holes have different effective masses along the Γ–X and Γ–Y directions (0.38 m0 in Γ–X and 0.49 m0 in Γ–Y directions). There shows clear anisotropy of the carrier masses in the X and Y directions. These anisotropic carrier masses are a result of unequal lattice parameters in the X and Y directions. However, for pyridinium di-cation based perovskites we have calculated the carrier effective masses along the X–Γ direction since the fundamental band gap appears at the X high symmetry point. All four pyridinium di-cation based systems have a very small value of electron effective mass ranging from 0.15 m0 to 0.26 m0. Furthermore, we have calculated the hole masses along Γ–Z direction due to the slightly dispersive nature of the valence band near this region. (3-PyrEA)PbI4 possess comparatively small hole effective masses in the vertical direction. Hence, we can comment that with a change in the position of the secondary ammonium nitrogen in the pyridinium ring the electron and hole effective mass is regulated, although the spacer cations have no direct contribution to the upper band edge dispersion. Reviewing the calculated results for the considered 2D-LHPs, we observed lower effective masses for electrons than for holes, which is the effect of the dissimilar hybridization nature of the conduction and valence band edges. The larger values for holes are the result of the Pb 6s orbital contribution in the valence band edges. As the effective mass of electrons and holes is inversely proportional to the mobility of the photoexcited electrons and holes, for a particular system a lower value of electron effective mass will result in a higher mobility for photoexcited electrons. The strong anti-bonding interaction results in a relatively small effective electron mass compared to conventional semiconductors which results in the high mobility of the photo-excited electrons. Moreover, the calculated results of the carrier effective masses demonstrate the strong correlation with the octahedral distortion of 2D-LHP. Octahedral distortion affects the overlapping of the Pb 6s and I 5p orbitals that enables tuning of the effective masses with changing organic spacers. Despite being an aliphatic spacer cation-based system, (3-APN)2PbI4 possess comparable carrier masses to those of aromatic core spacer-based systems and this is an interesting finding for the mono-cationic spacer based 2D-LHP system. Hence, the directional anisotropic behavior expected in the carrier mobility of (3-APN)2PbI4 can be beneficial for the fabrication of vertically oriented perovskite solar cells. Furthermore, we have observed that carrier transport in the X direction will be better than along the Y direction. This observation can also be utilized during the film fabrication of mono-cationic 2D-LHP based systems.
Furthermore, we have calculated the properties of 2D LHPs considering Sn in place of Pb, as well as Br and Cl in place of I, to gain better knowledge of the central metal atom as well as halide anion substitution. As the stability of the +2 state decreases down the group from Pb to Sn to Ge we didn’t consider Ge in our study. These considered systems are as follows: (3-APN)2SnI4, (3-APN)2PbBr4, and (3-APN)2PbCl4. Here, we have fixed the spacer cation to 3-APN as it is the best one among our considered spacer molecules. In Fig. S6 (ESI†) we have presented the relaxed geometries. First, we analysed the geometries of the materials. In (3-APN)2SnI4 we observed strong octahedral distortion that causes the difference in Sn–I bond lengths. The equatorial Sn–I bonds have four different bond lengths that vary from 2.99 to 3.73 Å. Axial Sn–I bonds have a nearly similar length (∼3.20 Å) (Fig. S7, ESI†). However, the Sn–I–Sn bond angles (174° and 179°) do not deviate much from the ideal (180°). On the other hand, (3-APN)2PbBr4 and (3-APN)2PbCl4 have two different equatorial Pb–X bond lengths and similar axial bond lengths (Fig. S7, ESI†). Side by side, the (3-APN)2SnI4 material was found to have a band gap of 2.65 eV which is larger than that of (3-APN)2PbI4. This result is very unlikely in 2D-LHPs as in similar studied systems Sn-based materials are usually reported to have a smaller band gap than Pb based ones.44–46 As we know that the conduction band minima of these 2D-LHPs are composed of mainly central metal atomic orbitals, lowering the energy of the central metal atom should shift the band edge downwards and reduce the gap. The unusual trend of band gap could be due to the octahedral distortion of (3-APN)2SnI4. We have already figured out that this system has different bond lengths for four equatorial Sn–I bonds, where the bond lengths are as large as 3.73 Å and as small as 2.99 Å (Fig. S7, ESI†). This is a unlike behaviour as observed in other Sn based 2D-LHPs where equatorial Sn–I bonds have nearly similar lengths.44–46 Therefore, we can expect that the unusual electronic structure of (3-APN)2SnI4 is a result of its large Sn–I bond lengths that decreases the overlap between Sn and I atomic orbitals. Such anomalous behaviour of Sn based 3D perovskites was previously reported by Malavasi and coworkers.47 In contrast, by changing the halide anion from I to Br and Cl the band gap of the material increases (Table S3, ESI†). This is also due to a similar fact that the valence band of the 2D-LHPs are made up with halogen atomic orbitals. So, lowering the energies of the halogen atomic orbital causes downshifting of the valence band maxima and ultimately an increase in the band gap. The projected density of states plots of (3-APN)2SnI4 and (3-APN)2PbBr4 do not have any significant difference to those observed in (3-APN)2PbI4 (Fig. S8, ESI†). But the pDOS plot of (3-APN)2PbCl4 shows that the carbon components merge with that of chlorine in the valence band edge. This may be due to the close 3p(Cl) and 2p(C) orbital energies. In addition, from the band structure plots we can see these four systems are the direct band gap semiconductors (Fig. S9, ESI†). Moreover, the calculated effective masses show that (3-APN)2SnI4 has different masses towards the X and Y direction of the Brillouin zone (Table S4, ESI†). The charge carrier masses towards the Y direction are much higher in comparison to those in the X direction. Interestingly, (3-APN)2PbBr4 and (3-APN)2PbCl4 possess smaller masses for both the carriers. Therefore, among all of these 2D-LHP systems, (3-APN)2PbI4 is the best one and is a promising choice for photovoltaic applications.
Optical property
We calculated the absorption co-efficient, another factor that dictates the scope of 2D-LHPs for photovoltaic applications. Fig. 6 and Fig. S10 (ESI†) show the optical absorption spectra of the seven studied systems. Our calculated results show that all seven systems have high extinction coefficients in the visible range. Since we have calculated the absorption coefficients using the PBE + SOC method which in general underestimates the band gap of the material, our calculated absorption peaks are somewhat downshifted towards the IR region. For all seven systems, the visible light absorption coefficients in the X and Y directions are significantly higher than those in the Z direction. The absorption coefficients in the X and Y directions are similar for (BA)2PbI4 and (PEA)2PbI4. Similar observations have been reported previously.48,49In the case of (3-APN)2PbI4, the visible light absorption coefficient in the Y direction is a little higher than that in the X direction, which clearly signifies the optical anisotropy in the X and Y directions. Since in the Y direction absorption is higher for (3-APN)2PbI4, more efficient photon absorption is expected in the Y direction compared to that in the X direction. Hence, the observed optical anisotropy in the X and Y directions is an important tool when developing efficient solar cell devices using (3-APN)2PbI4 as the perovskite absorber. In the case of di-cationic systems almost identical visible light absorption coefficients have been observed in the X and Y directions but there is a sharp peak in the X direction. Henceforth, the absorption coefficients in the visible region are higher for (3-APN)2PbI4 than that of (PEA)2PbI4 and are comparable with di-cationic based systems. The 2D-LHP systems show high absorption results due to the direct band gap nature and p–p transition as the VBM of 2D-LHP mainly consists of I 5p states and the CBM mainly comprises Pb 6p states, and the electronic transitions can be ascribed as a p–p transition i.e., from the occupied I(5p) state to the unoccupied Pb(6p) state. Improved visible light absorption properties of the di-cationic systems have also been reported experimentally. As we have already discussed, due to the presence of organic spacer cations in the Z direction the VBM and CBM are mainly located on the inorganic lead iodide layer i.e., in the X and Y directions. Therefore, charge density is expected to be distributed in the XY plane. These facts refer to the fact that the visible light absorption is higher in the X and Y directions and significantly lower in the Z direction.
Conclusion
Here, we have performed a first principles study on the influence of spacer cations in the characteristic property of pure 2D-LHPs. To show the versatility of 2D-LHP, we have studied three mono-cation based (BA)2PbI4 [(3-APN)2PbI4 and (PEA)2PbI4] and four di-cation based systems [(PyrEA)PbI4, (2-PyrEA)PbI4, (3-PyrEA)PbI4 and (4-PyrEA)PbI4]. Among all the studied systems the intermolecular H-bonding between spacer cations in (3-APN)2PbI4 results in an undistorted lead iodide layer and nearly ideal Pb–I–Pb bond angle. The calculated band gap for this system is 2.22 eV which is the lowest among mono-cation based pure 2D-LHPs. In (PyrEA)PbI4 due to the presence of a smaller number of primary ammonium functionalities and the structural rigidity of the spacer cation the lead iodide layer remains less disturbed and an improved band gap is observed. These data indicate that variation in the spacer cation mainly modulates the extent of octahedral distortion in the perovskite systems which is the controlling factor of the band edge states as well as effective mass and carrier mobility. Importantly the lower effective masses found for the systems signify good carrier mobility, the key property of a solar cell material. Implementation of 2D-LHPs with least distorted lead iodide octahedra and reduced I⋯I contact can result the best choice of material. All the studied systems have considerable visible light absorption property in the XY plane. The analyzed properties of (3-APN)2PbI4 clearly state that the aliphatic spacer containing systems can also be a prominent choice of photovoltaic material and the electronegative group attached on the other end of the mono-cation can lead us to a new way. The directional anisotropy characterized in (3-APN)2PbI4 is an important property to be considered during film fabrication. Hence, our study reveals that a nitrile-based mono-cationic spacer-based system can be as good as di-cationic organic spacer based systems for high performance photovoltaic based device applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank IIT Indore for the lab and computing facilities. This work is supported by DST-SERB [Project number: CRG/2018/001131] and SPARC [Project number: SPARC/2018-2019/P116/SL]. E. M. and S. C. M. thank MHRD for the research fellowship.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316 CrossRef CAS PubMed.
- M. Saliba, S. Orlandi, T. Matsui, S. Aghazada, M. Cavazzini, J.-P. Correa-Baena, P. Gao, R. Scopelliti, E. Mosconi, K.-H. Dahmen, F. De Angelis, A. Abate, A. Hagfeldt, G. Pozzi, M. Graetzel and M. K. Nazeeruddin, Nat. Energy, 2016, 1, 15017 CrossRef CAS.
- W. S. Yang, J. H. Noh, N. J. Jeon, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Science, 2015, 348, 1234 CrossRef CAS PubMed.
- K. Yoshikawa, H. Kawasaki, W. Yoshida, T. Irie, K. Konishi, K. Nakano, T. Uto, D. Adachi, M. Kanematsu, H. Uzu and K. Yamamoto, Nat. Energy, 2017, 2, 17032 CrossRef CAS.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS PubMed.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- Y. Zhao and K. Zhu, Chem. Commun., 2014, 50, 1605–1607 RSC.
- I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, Angew. Chem., Int. Ed., 2014, 53, 11232–11235 CrossRef CAS PubMed.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Chem. Mater., 2016, 28, 2852–2867 CrossRef CAS.
- L. N. Quan, M. Yuan, R. Comin, O. Voznyy, E. M. Beauregard, S. Hoogland, A. Buin, A. R. Kirmani, K. Zhao, A. Amassian, D. H. Kim and E. H. Sargent, J. Am. Chem. Soc., 2016, 138, 2649–2655 CrossRef CAS PubMed.
- C. Katan, N. Mercier and J. Even, Chem. Rev., 2019, 119, 3140–3192 CrossRef CAS PubMed.
- D. Sapori, M. Kepenekian, L. Pedesseau, C. Katan and J. Even, Nanoscale, 2016, 8, 6369–6378 RSC.
- Y. Li, Y. Zhao, H. Cheng, K. Zhao and Z. S. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 18590–18595 CrossRef CAS PubMed.
- B. Febriansyah, Y. Lekina, B. Ghosh, P. C. Harikesh, T. M. Koh, Y. Li, Z. Shen, N. Mathews and J. England, ChemSusChem, 2020, 13, 2693–2701 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- M.-H. Du, J. Phys. Chem. Lett., 2015, 6, 1461–1466 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, New York, 1976 Search PubMed.
- M. Fox, Optical Properties of Solids, Oxford University Press, New York, 2001 Search PubMed.
- D. G. Billing and A. Lemmerer, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 735–747 CrossRef CAS PubMed.
- N. Mercier, N. Louvain and W. Bi, CrystEngComm, 2009, 11, 720–734 RSC.
- K.-z. Du, Q. Tu, X. Zhang, Q. Han, J. Liu, S. Zauscher and D. B. Mitzi, Inorg. Chem., 2017, 56, 9291–9302 CrossRef CAS PubMed.
- D. Meggiolaro and F. De Angelis, ACS Energy Lett., 2018, 3, 2206–2222 CrossRef CAS.
- D. Meggiolaro, E. Mosconi, A. H. Proppe, R. Quintero-Bermudez, S. O. Kelley, E. H. Sargent and F. De Angelis, ACS Energy Lett., 2019, 4, 2181–2184 CrossRef CAS.
- A. Mahata, E. Mosconi, D. Meggiolaro and F. De Angelis, Chem. Mater., 2020, 32, 105–113 CrossRef CAS.
- D. Ghosh, A. J. Neukirch and S. Tretiak, J. Phys. Chem. Lett., 2020, 11, 2955–2964 CrossRef CAS PubMed.
- T. Ishihara, J. Lumin., 1994, 60, 269–274 CrossRef.
- T. Umebayashi, K. Asai, T. Kondo and A. Nakao, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155405 CrossRef.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS.
- J. Even, L. Pedesseau, M.-A. Dupertuis, J.-M. Jancu and C. Katan, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205301 CrossRef.
- M. Dyksik, H. Duim, X. Zhu, Z. Yang, M. Gen, Y. Kohama, S. Adjokatse, D. K. Maude, M. A. Loi, D. A. Egger, M. Baranowski and P. Plochocka, ACS Energy Lett., 2020, 5, 3609–3616 CrossRef CAS.
- L. Zhang and W. Liang, J. Phys. Chem. Lett., 2017, 8, 1517–1523 CrossRef CAS PubMed.
- L. Ma, J. Dai and X. C. Zeng, Adv. Energy Mater., 2017, 7, 1601731 CrossRef.
- D. B. Mitzi, Chem. Mater., 1996, 8, 791–800 CrossRef CAS.
- J. L. Knutson and J. D. Martin, Inorg. Chem., 2005, 44, 4699–4705 CrossRef CAS PubMed.
- A. Pisanu, A. Mahata, E. Mosconi, M. Patrini, P. Quadrelli, C. Milanese, F. De Angelis and L. Malavasi, ACS Energy Lett., 2018, 3, 1353–1359 CrossRef CAS.
- Y. Q. Zhao, Q. R. Ma, B. Liu, Z. L. Yu, J. Yang and M. Q. Cai, Nanoscale, 2018, 1, 8677–8688 RSC.
- J. H. Lei, Y. Q. Zhao, Q. Tang, J. G. Lin and M. Q. Cai, Phys. Chem. Chem. Phys., 2018, 20, 13241–13248 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma01135a |
| This journal is © The Royal Society of Chemistry 2022 |