Open Access Article
Open Access ArticleInteractions of limonene with the water dimer†
S. Indira
Murugachandran
and
M. Eugenia
Sanz
 *
*
Department of Chemistry, King's College London, London, SE1 1DB, UK. E-mail: maria.sanz@kcl.ac.uk; Tel: +44 (0)2078487509
First published on 17th October 2022
Abstract
The interactions of two molecules of water with the terpene limonene are characterised by chirped-pulse Fourier transform microwave spectroscopy. Seven isomers of limonene–(H2O)2 have been observed, and identified from the comparison of their experimental spectroscopic parameters with those predicted by computational methods. In all isomers a distorted water dimer binds to limonene through O–H⋯π and C–H⋯O interactions, and shows a strong preference for interacting with equatorial conformations of limonene. O–H⋯π hydrogen bonds to both endocyclic and exocyclic double bonds of limonene are established. In one of the isomers the water dimer forms a bridge between the endocyclic and exocyclic double bonds of limonene. Our results help advance our understanding of the interactions of water with atmospheric compounds.
1. Introduction
Monoterpenes are a large group of natural compounds produced and released by plants to the atmosphere.1,2 They are formed by condensation of two isoprene units, thus having the molecular formula C10H16, and can be open chain, monocyclic or bicyclic. By extension, the term monoterpene is sometimes applied to derivatives including alcohol, carbonyl or aldehyde groups, which are also known as monoterpenoids. Monoterpenes are components of essential oils and many show antifungal, antimicrobial and anti-inflammatory activities, among others.1,2 Therefore, they play a key role in the development of new drugs.1,2 Many monoterpenes are also used as perfumery ingredients due to their volatility.3Once monoterpenes are in the atmosphere, they react quite quickly with ozone and radicals such as OH and NO3, producing a range of oxidised products that are involved in the formation of secondary organic aerosol (SOA).4–6 Water, which is the third most abundant species in the Earth's atmosphere,7 has an active role in atmospheric processes and can modify the formation and composition of SOA.7–13 Water has been found to participate in atmospheric reactions as a reactant, and to influence reaction rates acting as a catalyst or inhibitor through the formation of hydrogen-bonded complexes with other atmospheric molecules.7–10,14 Some reactions may be relevant both in aqueous and gas phases, such as the water hydrolysis of aldehydes and ketones to form gem-diols,15–18 and others may be relevant at the surface of aqueous aerosol droplets, such as those involving ozone.10 Understanding the interactions of water with other atmospheric compounds in the gas phase is essential to accurately modelling its effects and getting insight into the behaviour of more complicated systems like water droplets.
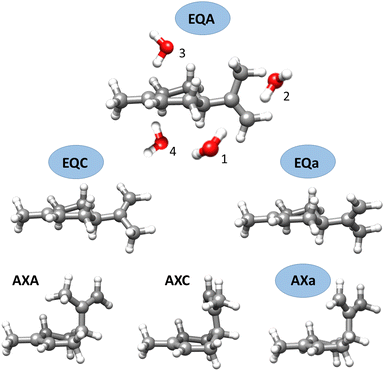
Limonene is one of the most abundant natural monoterpenes and a precursor of SOA.6 It is a major constituent of the emissions of the boreal19 and hemiboreal20 forest, and of various trees used in urban development.21 Limonene is formed of a cyclohexene ring with a methyl and isopropenyl group in para position. Four conformers of limonene, three equatorial and one axial, have been observed in the gas phase22,23 (see Fig. 1). We have recently investigated the interactions of limonene with water using chirped pulse Fourier transform microwave (CP-FTMW) spectroscopy, and identified seven isomers of limonene–H2O involving equatorial and axial limonene conformations and different water configurations.24 Water showed a preference to bind to equatorial limonene through the endocyclic double bond.
Limonene–H2O presented a ridged potential energy surface with many possible low-energy minima that display only small structural changes from one to another. Rotational spectroscopy was key to discriminate between different minima in limonene–H2O thanks to its strong dependence on molecular structure and the use of isotopologue data, which allows determination of the atomic coordinates of the substituted isotopologue.25 In addition, rotational spectroscopy yields the relative arrangement of the molecules in the complex and insight on the non-covalent interactions driving the preferred structures. This information is relevant to understand atmospheric nucleation, which occurs when stable clusters are formed spontaneously from gas-phase molecules. Furthermore, the gas-phase data obtained from rotational spectroscopy is directly comparable with predictions from theory, and can be used to benchmark different computational methods.
Using CP-FTMW spectroscopy in combination with computational calculations, we have examined further the interactions of limonene with water through the study of the limonene–(H2O)2 complex. We aimed to determine its preferred configurations and address several questions: would there be changes in the water binding preferences with respect to limonene–H2O? Would the number of possible minima be reduced or increased when more water molecules bind to limonene? Would two water molecules bind limonene as a water dimer? Interactions of limonene with the water dimer could occur in the atmosphere. The water dimer was predicted to be in significant concentrations in the atmosphere by Goldman et al. in 2001,26 and was observed at atmospherically relevant temperatures in 2013.27 It has been found to react with the simplest Criegee intermediate.28,29
We have observed seven isomers of limonene–(H2O)2, which have been identified by carefully comparing the experimental and theoretical rotational constants, including those of 18O isotopologues. Water maintains a preference to bind to equatorial conformers of limonene. A unique structure has been identified where the two water molecules link the endocyclic and exocyclic double bonds of limonene. Several theoretical methods have been used and benchmarked against the experimental data.
2. Methods
2.1. Experimental
The rotational spectrum of limonene–(H2O)2 was investigated in the 2–8 GHz range with our broadband rotational spectrometer, which has been described previously.30,31 (R)-(+)-limonene (97%) was purchased from Sigma Aldrich and used without further purification. Limonene, in a bespoke reservoir attached to the nozzle heated to ca. 304 K, and water, in an external reservoir in the injection line at room temperature, were seeded in neon at stagnation pressures of 6 bar. Optimal spectral intensities were obtained using molecular pulses of 1000 μs to create an adequate supersonic expansion in our vacuum chamber. The limonene–water complexes in each molecular pulse, formed at the throat of the nozzle by collisions, were polarised with 4 chirped microwave pulses of 4 μs duration varying linearly in frequency from 2–8 GHz and spaced 30 μs. Between microwave pulses, free induction decays (FID) were collected for 20 μs, amplified by a low noise amplifier, and then stored in the time domain in a fast oscilloscope. The final spectrum was obtained by coherently adding 1 M FIDs and using a fast Fourier transform algorithm to convert it to the frequency domain. Further experiments to observe 18O isotopologues were performed with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of H216O
1 mixture of H216O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H218O (97%, Chem-Cruz) to obtain a final spectrum with 2.7 M FIDs.
H218O (97%, Chem-Cruz) to obtain a final spectrum with 2.7 M FIDs.
2.2. Computational
The possible configurations of limonene–(H2O)2 were initially generated by considering the lower-energy limonene–H2O complexes and adding an additional water molecule in different positions. A subsequent exploration of the potential energy surface (PES) of limonene–(H2O)2 was performed using the conformational sampling program CREST.32 Both axial and equatorial conformers of limonene were included as starting structures for different CREST searches. The resulting structures were optimised using the B3LYP33,34-D3BJ35,36 and MP237 methods with the 6-311++G(d,p) basis set within the Gaussian0938 suite of programs, which yielded a total of 85 limonene–(H2O)2 isomers within 12 kJ mol−1. Of these, 39 isomers were predicted within 4 kJ mol−1. Their geometries were also optimised using wB97XD39/6-311++G(d,p), M06-2X40/6-311++G(d,p), and B2PLYP41-D3BJ/def2-TZVP methods. Their predicted rotational constants, dipole moments, relative energies with and without zero-point corrections, and BSSE binding energies (for MP2 and B3LYP-D3BJ) are given in Table 1, and Tables S1–S4 (ESI†).| Parameter | Isomer 1 | EQA-3-II | Isomer 2 | EQA-4-II | Isomer 3 | EQC-4-I | |||
|---|---|---|---|---|---|---|---|---|---|
| Experimental | B3LYPg | MP2h | Experimental | B3LYP | MP2 | Experimental | B3LYP | MP2 | |
| a A, B and C are the rotational constants; κ is Ray's asymmetry parameter, ΔJ, ΔJK, ΔK, δJ and δK are the quartic centrifugal distortion constants. b μ a, μb and μc are the electric dipole moments along the principal inertial axes. Y/N indicates whether a-, b- or c-type transitions have been observed or not. c Rms deviation of the fit. d Number of rotational transitions included in the fit. e Relative energies including zero-point corrections. f Standard error in parentheses in units of the last digit. g B3LYP-D3BJ/6-311++G(d,p) level of theory. h MP2/6-311++G(d,p) level of theory. | |||||||||
| A (MHz) | 947.0945(15)f | 959.3 | 966.6 | 967.27928(59) | 1012.1 | 1001.5 | 922.2727(17) | 964.3 | 962.9 |
| B (MHz) | 597.89778(29) | 607.0 | 606.5 | 578.59179(32) | 570.3 | 577.9 | 604.06009(25) | 605.5 | 603.5 |
| C (MHz) | 432.15280(24) | 441.1 | 444.7 | 461.47508(29) | 471.7 | 472.0 | 436.70875(20) | 445.6 | 450.4 |
| κ | −0.36 | −0.36 | −0.36 | −0.54 | −0.64 | −0.60 | −0.31 | −0.38 | −0.40 |
| Δ J (kHz) | 0.0928(18) | 0.0305 | 0.0375 | 0.1642(35) | 0.0729 | 0.0697 | 0.0595(21) | 0.0304 | 0.0370 |
| Δ JK (kHz) | 0.437(13) | 0.1159 | 0.1534 | 0.943(25) | −0.2085 | −0.0610 | 0.8605(98) | −0.2181 | −0.3059 |
| Δ K (kHz) | — | 0.3506 | 0.3987 | — | 0.5159 | 0.3968 | — | 0.5698 | 0.6088 |
| δ J (kHz) | 0.0350(15) | 0.0034 | 0.0028 | 0.0413(17) | 0.0182 | 0.0147 | −0.0060(12) | −0.0010 | −0.0040 |
| δ K (kHz) | — | 0.1395 | 0.1578 | 0.847(41) | 0.2063 | 0.1974 | 0.440(17) | 0.2776 | 0.2885 |
| μ a (D) | Y | −2.9 | −3.0 | Y | −0.8 | −0.9 | Y | −3.0 | −2.9 |
| μ b (D) | N | 0.3 | 0.2 | Y | −0.8 | −0.5 | N | −0.1 | −0.1 |
| μ c (D | N | 0.5 | 0.0 | Y | −1.3 | −1.5 | N | −0.5 | −0.6 |
| σ (kHz) | 2.6 | — | — | 4.8 | — | — | 2.3 | — | — |
| N | 41 | — | — | 65 | — | — | 46 | — | — |
| ΔE0e (cm−1) | — | 27.2 | 0.0 | — | 88.7 | 62.1 | — | 80.5 | 149.7 |
| Parameter | Isomer 4 | EQC-1-I | Isomer 5 | EQC-2-I | ||
|---|---|---|---|---|---|---|
| Experimental | B3LYPg | MP2h | Experimental | B3LYP | MP2 | |
| A (MHz) | 1019.1339(12)f | 1072.0 | 1058.6 | 1045.9874(58) | 1075.2 | 1081.3 |
| B (MHz) | 580.01176(43) | 579.3 | 581.3 | 535.88202(59) | 541.4 | 538.8 |
| C (MHz) | 463.49138(36) | 477.2 | 475.4 | 423.71543(49) | 431.8 | 436.6 |
| κ | −0.58 | −0.66 | −0.64 | −0.64 | −0.66 | −0.68 |
| Δ J (kHz) | 0.0116(34) | 0.0174 | 0.0174 | 0.1081(25) | 0.0878 | 0.0820 |
| Δ JK (kHz) | 1.048(49) | −0.2319 | −0.2970 | — | 0.6024 | 0.7058 |
| Δ K (kHz) | — | 0.5635 | 0.6684 | — | 0.1786 | 0.1668 |
| δ J (kHz) | — | −0.0018 | −0.0020 | 0.0238(29) | 0.0195 | 0.0134 |
| δ K (kHz) | — | 0.1828 | 0.2237 | — | 0.3885 | 0.3378 |
| μ a (D) | Y | 2.9 | 2.6 | Y | 1.7 | 1.8 |
| μ b (D) | Y | 2.2 | 2.5 | N | −0.4 | 0.0 |
| μ c (D) | N | 0.1 | 0.2 | N | 0.6 | 0.9 |
| σ (kHz) | 6.5 | — | — | 4.7 | — | — |
| N | 41 | — | — | 33 | — | — |
| ΔE0e (cm−1) | — | 70.2 | 304.9 | — | 89.3 | 161.1 |
| Parameter | Isomer 6 | EQa-4-I | Isomer 7 | EQA-2-I | ||
|---|---|---|---|---|---|---|
| Experimental | B3LYPg | MP2h | Experimental | B3LYP | MP2 | |
| A (MHz) | 971.2636(13) | 1010.0 | 1000.1 | 994.4739(14)f | 1010.3 | 990.5 |
| B (MHz) | 585.47084(56) | 578.0 | 589.5 | 556.66918(49) | 565.9 | 566.5 |
| C (MHz) | 472.25591(48) | 482.8 | 479.0 | 415.83179(41) | 422.5 | 418.6 |
| κ | −0.55 | −0.64 | −0.58 | −0.51 | −0.51 | −0.48 |
| Δ J (kHz) | 0.0929(73) | 0.0672 | 0.0539 | 0.1060(60) | 0.0837 | 0.09597 |
| Δ JK (kHz) | 0.531(47) | −0.8438 | −0.1618 | — | 0.9145 | 1.42098 |
| Δ K (kHz) | — | 1.0883 | 0.4189 | 1.40(15) | 0.1069 | −0.02341 |
| δ J (kHz) | — | 0.0113 | 0.0062 | 0.0216(32) | 0.0057 | 0.01959 |
| δ K (kHz) | 0.542(83) | 0.6629 | 0.2880 | 0.147(50) | 0.2026 | 0.19576 |
| μ a (D) | Y | 1.4 | 1.4 | Y | −1.7 | −2.0 |
| μ b (D) | N | 0.2 | 0.1 | Y | 1.0 | 1.2 |
| μ c (D) | Y | −1.0 | −1.4 | Y | 1.1 | 0.8 |
| σ (kHz) | 7.7 | — | — | 7.3 | — | — |
| N | 40 | — | — | 59 | — | — |
| ΔE0e (cm−1) | — | 123.3 | 156.7 | — | 129.5 | 267.1 |
The isomers of limonene–(H2O)2 have been labelled following the same nomenclature we used for the complexes of limonene with one water molecule (see Fig. 1). Limonene conformers are specified by the axial or equatorial position of the isopropenyl group and a letter indicating its dihedral angle with respect to the cyclohexene ring. The binding of the first water molecule to each side of the exocyclic double bond of limonene is indicated with the labels 1 and 2. Labels 3 and 4 indicate binding of the first water to the endocyclic double bond above or below the cyclohexene ring, respectively. Additional suffixes I, II, III, etc. indicate the different positions of the second water molecule in increasing order of energy.
3. Results and discussion
3.1. Potential energy surface
The diverse arrangements adopted by the water molecules, in addition to the configurations arising from limonene's conformations, give rise to a huge number of possible low-energy structures resulting in a very corrugated and intricate PES for limonene–(H2O)2.From our previous investigation of limonene–H2O,24 water primarily interacts with limonene through an O–H⋯π hydrogen bond to either the endocyclic or exocyclic double bonds. The second water molecule can bind to limonene or to the first water molecule. Structures where water binds to limonene without forming a water dimer have an energy penalty of about 18 kJ mol−1, so all low-energy limonene–(H2O)2 complexes involve a water dimer interacting with limonene. Upon binding to limonene, the water dimer can adopt several configurations depending on the arrangement of the hydrogen atoms and the lone pair involved in the O–H⋯O hydrogen bond between the two water molecules (see Table 1). This gives rise to structurally similar sets of isomers, with the same limonene conformation and same location for the O–H⋯π bond but different configurations of the water dimer.
In addition to the O–H⋯π and O–H⋯O hydrogen bonds mentioned above, the lower-energy limonene–(H2O)2 structures show C–H⋯O interactions between the second water molecule and limonene that further anchor the former to the latter. Limonene–(H2O)2 structures without C–H⋯O interactions are predicted above 12.2 kJ mol−1.
The above traits are common to all the calculation methods. However, there are differences in the energy ordering of the isomers (Tables S1–S4, ESI†). Considering the relative energies including zero-point corrections, the global minimum is predicted to be EQA-3-II by MP2 and B2PLYP-D3BJ, EQA-3-I by B3LYP-D3BJ or EQC-1-I by M06-2X and wB97XD. These isomers involve the two most abundant conformers of bare limonene, EQA and EQC.22,23 It should be noted that all calculations methods predict a larger number of low-energy isomers involving EQA, the global minimum of limonene. MP2 consistently predicts isomers involving axial limonene at lower energies, ranging from 115 to 255 cm−1, while M06-2X predict all of them above 400 cm−1.
3.2. Rotational spectrum
The experimental rotational spectrum between 2–8 GHz of limonene–water is quite dense. After removal of the known transition frequencies assigned to bare limonene,22,23 limonene–H2O,24 and water clusters,42–45 many intense lines remained.The majority of the low-energy isomers of limonene–(H2O)2 in Table 1 are prolate asymmetric tops predicted to have a large dipole moment along the a principal inertial axis. Therefore initial searches looked for R-branch a-type transitions of the series 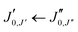 and
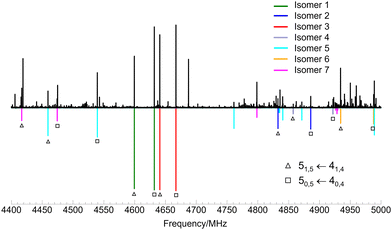
and 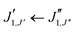 . Identification of experimental isomers was aided by using the spectral simulating and fitting program PGOPHER,46 which incorporates AUTOFIT,47 an automated fitting algorithm for molecular spectra. The computationally predicted A, B and C rotational constants along with the corresponding dipole moment components were used to simulate the rotational spectra of the lower-energy limonene–(H2O)2 isomers within PGOPHER. Initial automated searches yielded the first three isomers of limonene–(H2O)2, all of which were very intense in the spectrum. Removal of their lines from the spectrum and further careful and repeated searches led to the identification of four additional species.
. Identification of experimental isomers was aided by using the spectral simulating and fitting program PGOPHER,46 which incorporates AUTOFIT,47 an automated fitting algorithm for molecular spectra. The computationally predicted A, B and C rotational constants along with the corresponding dipole moment components were used to simulate the rotational spectra of the lower-energy limonene–(H2O)2 isomers within PGOPHER. Initial automated searches yielded the first three isomers of limonene–(H2O)2, all of which were very intense in the spectrum. Removal of their lines from the spectrum and further careful and repeated searches led to the identification of four additional species.
Fits of measured transitions were performed using the semi-rigid rotor Hamiltonian of Watson48 in the A reduction and Ir representation using Pickett's programs.49 The initial sets of experimental rotational constants found using PGOPHER were used to predict and measure more rotational transitions, which were added to the fits. The final spectroscopic constants for the seven observed isomers of limonene–(H2O)2 are shown in Table 1. A section of the experimental spectrum showing lines for the seven complexes is presented in Fig. 2.
No indication of methyl internal rotation splittings due to the two methyl tops of limonene was observed, as for limonene–H2O. Predictions using XIAM50 with B3LYP-D3BJ barrier heights of ca. 700 cm−1 (ring methyl) and 600 cm−1 (isopropenyl methyl) yield splittings of 5–60 kHz for observed transitions, smaller than the resolution of our experiment (ca. 100 kHz).
Assigning the observed isomers to specific dihydrate structures was particularly challenging due to the large number of low-energy structures predicted and the similarity of the experimental rotational constants to one another. Taking into account that the Ray's asymmetry parameters of the detected isomers have values between −0.31 and −0.64 (Table 1), we were able to disregard very prolate structures with −1 < κ < −0.85 and an asymmetric one with κ = −0.15, leaving 21 possible isomers.
In addition to the rotational constants, we considered the observed transition types, theoretical dipole moments, and the coordinates of the water oxygen atoms. For the latter, we ran experiments using enriched 18O water, and observed the possible isotopologues, 18O–16O, 16O–18O and 18O–18O for all isomers, except for isomer 4, for which the 18O–18O isotopologue was not detected. Their experimental spectroscopic parameters are shown in Tables S5–S11 (ESI†). From the differences in the moments of inertia between the parent species and the 18O isotopologues, we obtained the coordinates a, b and c of the oxygen atoms in the principal inertial axis system using Kraitchman's equations51 as implemented in the program KRA52 (Table S12, ESI†).
Systematically considering the observed species, isomers 1 and 3 have very similar A, B and C rotational constants and only presented a-type spectrum. They could correspond to EQA-3-II, EQA-3-I, EQA-3-IV, or EQC-4-I, all of which have similar predicted rotational constants, a sizeable μa value and low μb and μc values. Considering the rs coordinates for the oxygen atoms, isomer 3 can be unambiguously identified as EQC-4-I. Isomer 1 has the best agreement with the oxygen coordinates of EQA-3-II, although it is also very close to those of EQA-3-I. These two isomers differ in the position of the second water molecule, but the change in position causes a change in axes that results in very similar oxygen coordinates. Considering the slightly closer agreement with EQA-3-II, and that this isomer is predicted to be lower in energy by more computational methods (MP2, B2PLYP-D3BJ and wB97XD), we have assigned isomer 1 to EQA-3-II.
Isomer 2 has spectroscopic parameters that could match those predicted for EQA-4-II or EQC-4-I. From the values of the rs coordinates, isomer 2 can be unambiguously identified as EQA-4-II.
Isomer 4 can correspond to EQC-3-I or EQC-1-I, both of which have sizable μa and μb components, consistent with the observation of a- and b-type spectra. The structures of EQC-3-I and EQC-1-I are very similar except for the different direction of the O–H⋯O hydrogen bond, depending on which water molecule acts as a hydrogen bond donor to the other one, and the different positions of the hydrogens of the water molecules. These differences cause minimal changes in the predicted rotational constants and dipole moments. However, considering the oxygen coordinates, we have assigned isomer 4 to EQC-1-I. Moreover, all computational methods predict EQC-1-I as lower in energy.
Isomer 5 presents a similar situation to isomer 1. Comparison of the rotational constants and observed types of transitions points towards either EQC-2-III or EQC-2-I, which only differ in the position of the hydrogen atoms of the water molecule that binds to limonene though a O–H⋯π bond. The rs coordinates of the oxygen atoms do not allow us to distinguish between the two structures, and therefore we have assigned isomer 5 as EQC-2-I as it is the complex predicted to be lowest in energy by all calculations.
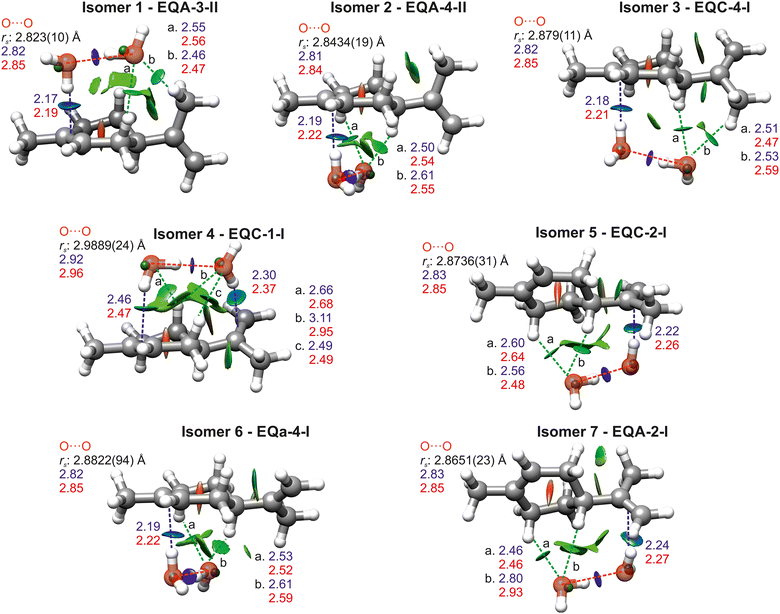
Isomer 6, which shows a- and c-type spectrum, can correspond to EQa-4-I or EQa-4-II, and is assigned to EQa-4-I from the comparison of experimental and theoretical rs coordinates of the oxygen atoms. The observation of a-, b- and c-type lines means that isomer 7 can only be EQA-2-I. The assignment is confirmed by the oxygen rs coordinates. An overlay of the rs coordinates with the equilibrium structures of all isomers are shown in Fig. 3.
Comparing experimental and theoretical rotational constants, MP2/6-311++G(d,p) and B3LYP-D3BJ/6-311++G(d,p) are the best performing methods in predicting the experimental rotational constants, with average deviations of 2.0% and 2.2%, respectively. wB97XD/6-311++G(d,p) and B2PLYP-D3BJ/def2-TZVP are somewhat worse, with average deviations of 2.8% and 3.0%, respectively, and the worst performing method is M06-2X/6-311++G(d,p) with an average deviation of 4.2%. All methods show larger differences for the A rotational constant, ranging from 2.9% for MP2 to 7.2% for M06-2X.
3.3. Isomer abundances and intermolecular interactions
The relative abundances of the seven observed isomers were estimated from measuring the intensities of common a-type transitions considering that line intensity is proportional to the square of the dipole moment in our experiment. The obtained abundances are EQA-4-II ≫ EQA-3-II ≈ EQC-2-I ≈ EQC-4-I ≈ EQa-4-I > EQA-2-I > EQC-1-I.The experimental abundances are not consistent with the theoretical relative energies predicted by the different methods (Tables S1–S4, ESI†), or with ΔE(BSSE) interaction energies (Table S1, ESI†). The isomers with lower abundance, EQC-1-I and EQA-2-I, are predicted to have the higher relative energies of those observed by MP2. However, EQC-1-I is predicted by M06-2X and wB97XD to be the global minimum, and by B3LYP-D3BJ and B2PLYP-D3BJ to be one of the isomers with lower relative energy. EQA-3-II is predicted to be the global minimum by MP2 and B2PLYP-D3BJ, and to have a low relative energy by B3LYP-D3BJ and wB97XD. EQA-4-II, with the highest abundance, is however predicted to have a relative energy intermediate among those of observed isomers. The experimental abundances can be affected by relaxation processes of higher- to lower-energy isomers in the supersonic jet, which can occur if the barriers for interconversion are sufficiently low.53,54 They can also be influenced by the initial abundances of the bare limonene conformers in the jet.
The observed isomers reveal a heavy bias towards structures involving the two most abundant conformers of bare limonene, EQA and EQC. In fact, all isomers have limonene in an equatorial conformation. Despite repeated searches, no limonene–(H2O)2 complexes with limonene in an axial conformation have been observed.
All isomers are stabilised by O–H⋯π hydrogen bonds between water and limonene, O–H⋯O hydrogen bonds between the two water molecules, and C–H⋯O interactions between the hydrogen atoms of limonene and the lone pairs of the oxygen atoms of water. Of the seven observed isomers, four exhibit one water molecule forming an O–H⋯π bond to the endocyclic double bond of limonene and two have one water molecule bonding to the exocyclic double bond. EQC-1-I is unique in that both water molecules bond to limonene, establishing two O–H⋯π hydrogen bonds rather than one and forming a bridge between the endocyclic and exocyclic double bonds. EQC-1-I also has secondary C–H⋯O hydrogen bonds between both water oxygens and the ring, differently to other isomers where only the second water molecule establishes C–H⋯O interactions.
The above non-covalent interactions between limonene and water can be visualised with the NCI method55,56 and are shown in Fig. 3. The O–H⋯O bonds appear as strong attractive interactions with deep blue isosurfaces, and are pill-shaped, indicated their high directionality. In comparison, the O–H⋯π hydrogen bonds show lighter blue isosurfaces spreading along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds, indicating their slightly weaker attractive nature and lower directionality. C–H⋯O hydrogen bonds are less attractive and directional and appear as green isosurfaces.
C double bonds, indicating their slightly weaker attractive nature and lower directionality. C–H⋯O hydrogen bonds are less attractive and directional and appear as green isosurfaces.
To get further insight into the strength of the interactions at play we performed natural bonding orbital (NBO) analysis57 (Tables S13–S19, ESI†) using Gaussian09.38 The NBO results confirm that the strongest interaction in limonene–(H2O)2 is the O–H⋯O hydrogen bond, with values of 42.6–45.4 kJ mol−1, except for EQC-1-I which shows a much weaker interaction of 30.1 kJ mol−1. The second most attractive interaction is the O–H⋯π hydrogen bond, with values of 20.1–21.4 kJ mol−1, again excluding EQC-1-I. EQC-1-I displays two O–H⋯π bonds, of 15.8 kJ mol−1 and 5.7 kJ mol−1 to the exocyclic and endocyclic double bonds of limonene, respectively. The overall energy associated to O–H⋯π interactions is thus 21.5 kJ mol−1 in EQC-1-I. The stronger O–H⋯π is that involving the exocyclic double bond of limonene, which was found to be slightly more electronegative than the endocyclic one.24
All isomers of limonene–(H2O)2 except EQC-1-I show hydrogen bond cooperativity due to the presence of sequential hydrogen bonds running in the same direction (homodromic), where all molecules act as both hydrogen atom donors and acceptors.58,59 This strengthens individual hydrogen bonds by enhancing polarization. The much weaker O–H⋯O and O–H⋯π hydrogen bonds in EQC-1-I can be related to the presence of an antidromic hydrogen bond network where one water molecule acts as a double hydrogen bond donor, and may explain its low abundance.
The effects of hydrogen bond cooperativity in limonene–(H2O)2 are evident if we compare the values of the NBO energies and theoretical bond lengths for the O–H⋯π bonds with those of limonene–H2O.24 The O–H⋯π hydrogen bonds in the monohydrate isomers were predicted by NBO analysis to have energies ranging 11.3–13.8 kJ mol−1, about 63% lower than those in the dihydrates. Additionally, the O–H⋯π bond length in the monohydrates is longer (2.25–2.29 Å from B3LYP-D3BJ and 2.28–2.34 Å from MP2) than in the dihydrates (2.17–2.24 Å from B3LYP-D3BJ and 2.19–2.27 Å from MP2), excluding EQC-1-I.
The effects of cooperativity are also manifest in the O⋯O distances (Fig. 3), shorter than the 2.98(4) Å of the free water dimer,60 except for isomer EQC-1-I, where there are non-sequential hydrogen bonds preventing cooperativity. Similar shortening of the O⋯O distance have been observed in other complexes of terpenoids with the water dimer.61–66 The predicted ∠Ow1Hw2Ow2 angles of all isomers are smaller than 180°, most likely the result of optimising secondary C–H⋯O interactions.
The observation of seven isomers of limonene–(H2O)2 further confirms the ability of water to interact with limonene. No isomers with limonene in an axial conformation have been observed, indicating a stronger preference of the water dimer to bind to equatorial conformers of limonene than in limonene–H2O. In the majority of the isomers observed, the first water molecule prefers to bind to the endocyclic double bond, similarly to limonene–H2O.
4. Conclusions
Seven isomers of limonene–(H2O)2 have been identified from the analysis of its broadband rotational spectrum supported by computational calculations. The two water molecules bind to limonene as a distorted water dimer, establishing O–H⋯π and C–H⋯O hydrogen bonds with limonene, and O–H⋯O bonds between each other. Limonene prefers to adopt an equatorial conformation in the complexes. One limonene–(H2O)2 isomer shows the water dimer binding to both endocyclic and exocyclic double bonds of limonene, forming a bridge between them, but most isomers display O–H⋯π hydrogen bonds to the endocyclic double bond. Our study provides new data on O–H⋯π interactions and their interplay with other hydrogen bonds, of interest to model related clusters.Limonene–(H2O)2 presents a very corrugated PES with many low-energy minima that in some cases only differ by small structural changes involving the water molecules. A combination of manual prediction of possible structures guided by chemical intuition as well as algorithm-driven searches was found optimal for a more complete mapping of the PES. In comparison with limonene–H2O, the addition of a second water molecule greatly increases the complexity of the PES and the number of low-energy isomers with close relative energies.
Several computational methods have been applied to the investigation of limonene–(H2O)2 and benchmarked against experimental data. B3LYP-D3BJ and MP2 with the 6-311++G(d,p) basis set predicted rotational constants closer to the experimental ones. This is with the caveat that we are comparing equilibrium rotational constants (predicted Ae, Be, Ce) with ground vibrational state ones (experimental A0, B0, C0), because of the high computational cost of calculating vibrational corrections for molecular systems like limonene–(H2O)2. Theoretical results were inconsistent with respect to the global minimum structure and the relative energy ordering, which showcases the difficulties in describing a molecular system like limonene–(H2O)2, with a high number of configurations within a small energy range of 4 kJ mol−1.
Humidity has been found to affect the products of limonene ozonolysis, although the mechanism is not clear.12,67 The results presented here show that the water dimer readily interacts with limonene, and prefers to bind to the endocyclic double bond, which is also the preferred site for limonene ozonolysis.68 Limonene–(H2O)2 displays the same preference as limonene–H2O. Our data informs on the initial steps of water microsolvation of limonene and contributes to understanding possible interactions of limonene in the atmosphere.
Author contributions
Conceptualization, M. E. S.; investigation, S. I. M.; formal analysis, S. I. M. and M. E. S.; resources, M. E. S.; writing – original draft preparation, S. I. M. and M. E. S.; writing – review and editing, S. I. M. and M. E. S.; visualization, S. I. M. and M. E. S.; supervision, project administration, and funding acquisition, M. E. S.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank funding from the EU FP7 (grant PCIG12-GA-2012-334525) and King's College London, and acknowledge use of the high performance computing clusters Rosalind (https://rosalind.kcl.ac.uk) and CREATE (King's Computational Research, Engineering and Technology Environment. Retrieved August 31, 2022, from https://doi.org/10.18742/rnvf-m076) at King's College London.Notes and references
- A. Koziol, A. Stryjewska, T. Librowski, K. Salat, M. Gawel, A. Moniczewski and S. Lochynski, An overview of the pharmacological properties and potential applications of natural monoterpenes, Mini-Rev. Med. Chem., 2014, 14, 1156–1168 CrossRef CAS PubMed.
- M. Zielińska-Błajet and J. Feder-Kubis, Monoterpenes and their derivatives-Recent development in biological and medical applications, Int. J. Mol. Sci., 2020, 21, 7078 CrossRef PubMed.
- The Chemistry of Fragrances, ed. D. Pybus and C. Sell, Royal Society of Chemistry, Cambridge, 2nd edn, 2006 Search PubMed.
- M. Hallquist, J. C. Wenger, U. Baltensperger, Y. Rudich, D. Simpson, M. Claeys, J. Dommen, N. M. Donahue, C. George, A. H. Goldstein, J. F. Hamilton, H. Herrmann, T. Hoffmann, Y. Iinuma, M. Jang, M. E. Jenkin, J. L. Jimenez, A. Kiendler-Scharr, W. Maenhaut, G. McFiggans, T. F. Mentel, A. Monod, A. S. H. Prévôt, J. H. Seinfeld, J. D. Surratt, R. Szmigielski and J. Wildt, The formation, properties and impact of secondary organic aerosol: Current and emerging issues, Atmos. Chem. Phys., 2009, 9, 5155–5236 CrossRef CAS.
- J. H. Kroll and J. H. Seinfeld, Chemistry of secondary organic aerosol: Formation and evolution of low-volatility organics in the atmosphere, Atmos. Environ., 2008, 42, 3593–3624 CrossRef CAS.
- M. Kanakidou, J. H. Seinfeld, S. N. Pandis, I. Barnes, F. J. Dentener, M. C. Facchini, R. Van Dingenen, B. Ervens, A. Nenes, C. J. Nielsen, E. Swietlicki, J. P. Putaud, Y. Balkanski, S. Fuzzi, J. Horth, G. K. Moortgat, R. Winterhalter, C. E. L. Myhre, K. Tsigaridis, E. Vignati, E. G. Stephanou and J. Wilson, Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 2005, 5, 1053–1123 CrossRef CAS.
- R. J. Buszek, J. S. Francisco and J. M. Anglada, Water effects on atmospheric reactions, Int. Rev. Phys. Chem., 2011, 30, 335–369 Search PubMed.
- V. Vaida, H. G. Kjaergaard and K. J. Feierabend, Hydrated complexes: relevance to atmospheric chemistry and climate, Int. Rev. Phys. Chem., 2003, 22, 203–219 Search PubMed.
- V. Vaida, Perspective: Water cluster mediated atmospheric chemistry, J. Chem. Phys., 2011, 135, 020901 CrossRef PubMed.
- J. M. Anglada, G. J. Hoffman, L. V. Slipchenko, M. M. Costa, M. F. Ruiz-López and J. S. Francisco, Atmospheric significance of water clusters and ozone–water complexes, J. Phys. Chem. A, 2013, 117, 10381–10396 CrossRef CAS PubMed.
- T. B. Nguyen, P. J. Roach, J. Laskin, A. Laskin and S. A. Nizkorodov, Effect of humidity on the composition of isoprene photooxidation secondary organic aerosol, Atmos. Chem. Phys., 2011, 11, 6931–6944 CrossRef CAS.
- B. Bonn, G. Schuster and G. K. Moortgat, Influence of water vapor on the process of new particle formation during monoterpene ozonolysis, J. Phys. Chem. A, 2002, 106, 2869–2881 CrossRef CAS.
- B. Bonn and G. K. Moortgat, New particle formation during α- and β-pinene oxidation by O3, OH and NO3, and the influence of water vapour: Particle size distribution studies, Atmos. Chem. Phys., 2002, 2, 83–196 CrossRef.
- E. G. Schnitzler, C. Badran and W. Jäger, Contrasting effects of water on the barriers to decarboxylation of two oxalic acid monohydrates: a combined rotational spectroscopic and ab initio study, J. Phys. Chem. Lett., 2016, 7, 1143–1147 CrossRef CAS PubMed.
- J. L. Axson, K. Takahashi, D. O. De Haan and V. Vaida, Gas-phase water-mediated equilibrium between methylglyoxal and its geminal diol, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6687–6692 CrossRef CAS PubMed.
- M. K. Maroń, K. Takahashi, R. K. Shoemaker and V. Vaida, Hydration of pyruvic acid to its geminal-diol, 2,2-dihydroxypropanoic acid, in a water-restricted environment, Chem. Phys. Lett., 2011, 513, 184–190 CrossRef.
- W. Li, A. Maris, C. Calabrese, I. Usabiaga, W. D. Geppert, L. Evangelisti and S. Melandri, Atmospherically relevant acrolein-water complexes: Spectroscopic evidence of aldehyde hydration and oxygen atom exchange, Phys. Chem. Chem. Phys., 2019, 21, 23559–23566 RSC.
- E. Burevschi, I. Peña and M. E. Sanz, Geminal diol formation from the interaction of a ketone with water in the gas phase: structure and reactivity of cyclooctanone-(H2O)1,2 clusters, J. Phys. Chem. Lett., 2021, 12, 12419–12425 CrossRef CAS PubMed.
- H. Hakola, V. Tarvainen, A. P. Praplan, K. Jaars, M. Hemmilä, M. Kulmala, J. Bäck and H. Hellén, Terpenoid and carbonyl emissions from Norway spruce in Finland during the growing season, Atmos. Chem. Phys., 2017, 17, 3357–3370 CrossRef CAS.
- S. M. Noe, K. Hüve, Ü. Niinemets and L. Copolovici, Seasonal variation in vertical volatile compounds air concentrations within a remote hemiboreal mixed forest, Atmos. Chem. Phys., 2012, 12, 3909–3926 CrossRef CAS.
- A. J. Curtis, D. Helmig, C. Baroch, R. Daly and S. Davis, Biogenic volatile organic compound emissions from nine tree species used in an urban tree-planting program, Atmos. Environ., 2014, 95, 634–643 CrossRef CAS.
- J. R. A. Moreno, T. R. Huet and J. J. L. González, Conformational relaxation of S-(+)-carvone and R-(+)-limonene studied by microwave Fourier transform spectroscopy and quantum chemical calculations, Struct. Chem., 2013, 24, 1163–1170 CrossRef CAS.
- D. Loru, A. Vigorito, A. F. M. Santos, J. Tang and M. E. Sanz, The axial/equatorial conformational landscape and intramolecular dispersion: New insights from the rotational spectra of monoterpenoids, Phys. Chem. Chem. Phys., 2019, 21, 26111–26116 RSC.
- S. I. Murugachandran, J. Tang, I. Peña, D. Loru and M. E. Sanz, New insights into secondary organic aerosol formation: water binding to limonene, J. Phys. Chem. Lett., 2021, 1081–1086 CrossRef CAS PubMed.
- D. Loru, I. Peña and M. E. Sanz, The role of secondary interactions on the preferred conformers of the fenchone-ethanol complex, Phys. Chem. Chem. Phys., 2019, 21, 2938–2945 RSC.
- N. Goldman, R. S. Fellers, C. Leforestier and R. J. Saykally, Water dimers in the atmosphere: equilibrium constant for water dimerization from the VRT(ASP-W) potential surface, J. Phys. Chem. A, 2001, 105, 515–519 CrossRef CAS.
- M. Y. Tretyakov, E. A. Serov, M. A. Koshelev, V. V. Parshin and A. F. Krupnov, Water dimer rotationally resolved millimeter-wave spectrum observation at room temperature, Phys. Rev. Lett., 2013, 110, 93001 CrossRef PubMed.
- T. R. Lewis, M. A. Blitz, D. E. Heard and P. W. Seakins, Direct evidence for a substantive reaction between the Criegee intermediate{,} CH2OO{,} and the water vapour dimer, Phys. Chem. Chem. Phys., 2015, 17, 4859–4863 RSC.
- M. C. Smith, C.-H. Chang, W. Chao, L.-C. Lin, K. Takahashi, K. A. Boering and J. J.-M. Lin, Strong Negative Temperature Dependence of the Simplest Criegee Intermediate CH2OO Reaction with Water Dimer, J. Phys. Chem. Lett., 2015, 6, 2708–2713 CrossRef CAS PubMed.
- D. Loru, M. A. Bermúdez and M. E. Sanz, Structure of fenchone by broadband rotational spectroscopy Structure of fenchone by broadband rotational spectroscopy, J. Chem. Phys., 2016, 145, 074311–074318 CrossRef PubMed.
- D. Loru, I. Peña and M. E. Sanz, Ethanol dimer: Observation of three new conformers by broadband rotational spectroscopy, J. Mol. Spectrosc., 2017, 335, 93–101 CrossRef CAS.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Note on an approximation treatment for many-electron systems, Phys. Rev., 1934, 46, 618–622 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revis. E.01, 2010 Search PubMed.
- J. Da Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Structures of cage, prism, and book isomers of water hexamer from broadband rotational spectroscopy, Science, 2012, 336, 897–902 CrossRef.
- C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Broadband Fourier transform rotational spectroscopy for structure determination: The water heptamer, Chem. Phys. Lett., 2013, 571, 1–15 CrossRef.
- C. Pérez, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Hydrogen bond cooperativity and the three-dimensional structures of water nonamers and decamers, Angew. Chem., Int. Ed., 2014, 53, 14368–14372 CrossRef PubMed.
- J. O. Richardson, C. Pérez, S. Lobsiger, A. A. Reid, B. Temelso, G. C. Shields, Z. Kisiel, D. J. Wales, B. H. Pate and S. C. Althorpe, Concerted hydrogen-bond breaking by quantum tunneling in the water hexamer prism, Science, 2016, 351, 1310–1313 CrossRef CAS PubMed.
- C. M. Western and B. E. Billinghurst, Automatic and semi-automatic assignment and fitting of spectra with PGOPHER, Phys. Chem. Chem. Phys., 2019, 21, 13986–13999 RSC.
- N. A. Seifert, I. A. Finneran, C. Perez, D. P. Zaleski, J. L. Neill, A. L. Steber, R. D. Suenram, A. Lesarri, S. T. Shipman and B. H. Pate, AUTOFIT, an automated fitting tool for broadband rotational spectra, and applications to 1-hexanal, J. Mol. Spectrosc., 2015, 312, 13–21 CrossRef CAS.
- J. K. G. Watson, in Vibrational spectra and structure, A series of advances, ed. J. R. Durig, 1977, vol. 6, pp. 1–89 Search PubMed.
- H. M. Pickett, The fitting and prediction of vibration-rotation spectra with spin interactions, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- H. Hartwig and H. Dreizler, The microwave spectrum of trans-2,3-dimethyloxirane in torsional excited states, Z. Naturforsch., A: Phys. Sci., 1996, 51, 923–932 CrossRef CAS.
- J. Kraitchman, Determination of molecular structure from microwave spectroscopic data, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- Z. Kisiel, PROSPE – Programs for ROtational SPEctroscopy, Spectroscopy from Space, 2001, 91–106 CAS.
- R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, Relaxation of conformers and isomers in seeded supersonic jets of inert gases, J. Chem. Phys., 1990, 93, 3142–3150 CrossRef CAS.
- G. M. Florio, R. A. Christie, K. D. Jordan and T. S. Zwier, Conformational preferences of jet-cooled melatonin: Probing trans- and cis-amide regions of the potential energy surface, J. Am. Chem. Soc., 2002, 124, 10236–10247 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing noncovalent interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. Chaudret, B. De Courcy, J. Contreras-García, E. Gloaguen, A. Zehnacker-Rentien, M. Mons and J. P. Piquemal, Unraveling non-covalent interactions within flexible biomolecules: From electron density topology to gas phase spectroscopy, Phys. Chem. Chem. Phys., 2014, 16, 9876–9891 RSC.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- W. Saenger, Circular hydrogen bonds, Nature, 1979, 279, 343–344 CrossRef CAS.
- G. A. Jeffrey, An introduction to hydrogen bonding, Oxford University Press, 1997 Search PubMed.
- T. R. Dyke, K. M. Mack and J. S. Muenter, The structure of water dimer from molecular beam electric resonance spectroscopy, J. Chem. Phys., 1977, 66, 498–510 CrossRef CAS.
- C. Pérez, A. Krin, A. L. Steber, J. C. López, Z. Kisiel and M. Schnell, Wetting camphor: multi-isotopic substitution identifies the complementary roles of hydrogen bonding and dispersive forces, J. Phys. Chem. Lett., 2016, 7, 154–160 CrossRef PubMed.
- M. Chrayteh, A. Savoia, T. R. Huet and P. Dréan, Microhydration of verbenone: How the chain of water molecules adapts its structure to the host molecule, Phys. Chem. Chem. Phys., 2020, 22, 5855–5864 RSC.
- M. Chrayteh, T. R. Huet and P. Dréan, Gas-Phase Hydration of Perillaldehyde Investigated by Microwave Spectroscopy Assisted by Computational Chemistry, J. Phys. Chem. A, 2020, 124, 6511–6520 CrossRef CAS.
- M. Chrayteh, E. Burevschi, D. Loru, T. R. Huet, P. Dréan and M. E. Sanz, Disentangling the complex network of non-covalent interactions in fenchone hydrates via rotational spectroscopy and quantum chemistry, Phys. Chem. Chem. Phys., 2021, 20686–20694 RSC.
- E. M. Neeman, J. R. Aviles Moreno and T. R. Huet, Gas-phase hydration of nopinone: The interplay between theoretical methods and experiments unveils the conformational landscape, Phys. Chem. Chem. Phys., 2021, 23, 18137–18144 RSC.
- M. Chrayteh, T. R. Huet and P. Dréan, Microsolvation of myrtenal studied by microwave spectroscopy highlights the role of quasi-hydrogen bonds in the stabilization of its hydrates, J. Chem. Phys., 2020, 153, 104304 CrossRef CAS PubMed.
- Å. M. Jonsson, M. Hallquist and E. Ljungström, Impact of humidity on the ozone initiated oxidation of limonene, Δ3-carene, and α-pinene, Environ. Sci. Technol., 2006, 40, 188–194 CrossRef PubMed.
- C. S. Maksymiuk, C. Gayahtri, R. R. Gil and N. M. Donahue, Secondary organic aerosol formation from multiphase oxidation of limonene by ozone: Mechanistic constraints via two-dimensional heteronuclear NMR spectroscopy, Phys. Chem. Chem. Phys., 2009, 11, 7810–7818 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Predicted spectroscopic parameters at different levels of theory, cartesian coordinates, measured frequencies, experimental spectroscopic parameters of the isotopic species and substitution coordinates. See DOI: https://doi.org/10.1039/d2cp04174j |
| This journal is © the Owner Societies 2022 |