Reliable prediction of association (free) energies of supramolecular complexes with heavy main group elements – the HS13L benchmark set†
Johannes
Gorges
 ,
Stefan
Grimme
,
Stefan
Grimme
 and
Andreas
Hansen
and
Andreas
Hansen
 *
*
Mulliken Center for Theoretical Chemistry, Clausius-Institute for Physical and Theoretical Chemistry, University of Bonn, Beringstr. 4, 53115 Bonn, Germany. E-mail: hansen@thch.uni-bonn.de
First published on 24th November 2022
Abstract
We introduce a set of 13 supramolecular complexes featuring diverse non-covalent interactions with heavy main group elements (Zn, As, Se, Te, Br, I), high charges (−2 up to +4), and large systems with up to 266 atoms (HS13L). The experimental Gibbs free energies of association cover the typical range (−1.9 to −9.2 kcal mol−1). An efficient automated multilevel theoretical workflow is applied for the determination of the respective minimum structures in solution by conformer ensemble generation with the CREST program at the semiempirical GFN2-xTB level. Subsequent refinement is performed with the r2SCAN-3c composite DFT method including thermostatistical corrections at the GFN2-xTB level and solvation contributions by COSMO-RS using the CENSO free energy ranking algorithm. Various density functional approximations in combination with three London dispersion correction schemes are assessed against “back-corrected” experimental association energies as well as accurate local coupled cluster reference values. Our protocol predicts association free energies with a mean absolute deviation of only 2 kcal mol−1 from the measured values. Thus, it is well suited to generate reference association free energies for assessing theoretical methods on realistically sized supramolecular complexes or to support experimental chemists. For specifically evaluating methods for calculating gas-phase association energies, we recommend using the provided accurate coupled cluster reference values. We propose to use this set as an extension of the S30L benchmark set [Sure et al., J. Chem. Theory Comput., 2015, 11, 3785–3801] with a special focus on the challenging computation of non-covalent interactions of heavy main group elements.
1 Introduction
Non-covalently bound host–guest complexes represent an important research field with many practical applications.1 They are used as reaction containers, for molecular recognition, in template-directed synthesis, biomimetics, and self-assembly.2–7 Due to their unique coordination preferences and electronic properties, heavy main group elements are of special interest to prepare novel structures with new and interesting supramolecular properties.8 Their characteristic interactions, such as halogen bonding, chalcogen bonding, pnictogen bonding, and tetrel bonding are valuable in many areas of chemistry.8For many applications, the stability of supramolecular complexes is decisive, which is directly linked to the Gibbs free energy of association. Thus, it is important to obtain accurate experimental values for this quantity. Among various experimental techniques, Isothermal Titration Calorimetry (ITC) stands out as the most universal one9 and is the method of choice for measuring experimental binding thermodynamics of ligand binding.10 However, the interpretation of the measured energies in terms of specific molecular processes can be difficult if, for example, the stoichiometry of the individual components in the formed complex is not clear.9 Here, a reliable computational protocol is useful to reproduce experimental data for the assumed association mechanism or to predict alternative ones.
The calculation of free energies for the formation of larger supramolecular complexes still poses a challenge to computational chemistry. Since most experimentally synthesized complexes consist of about 100 atoms or more, the computational costs of highly accurate quantum chemical methods are often too large for treating these systems. Furthermore, solvation and entropic effects have to be considered in the binding process, which are generally difficult to predict accurately by computational methods.11 One successful approach was proposed by one of us, in which different ab initio and semiempirical quantum chemical (SQM) methods were combined. For the so-called S12L benchmark set, this procedure yields accurate association free energies with an average deviation from the experimental values of only 2 kcal mol−1.12 The S12L Benchmark set was later extended to 30 complexes (S30L benchmark set), which already covers a broad spectrum of different non-covalent interactions, such as London dispersion (LD), π–π stacking, ion-π interactions, or hydrogen and halogen bonding.13 However, S30L includes heavy main group elements only to a small extent. Benchmark sets focusing on characteristic main group non-covalent interactions (NCI), as the CHAL33614 for chalcogen bonding, or the ATLAS bechmark sets by Rězác for hydrogen bonding (HB300SPXx10),15 σ-hole interactions (SH250x10),16 and LD interactions (D1200 and D442x10)17 contain only small systems, for which canonical coupled cluster reference values can be computed. To the best of our knowledge, no comparable benchmark studies for large supramolecular complexes with heavy elements as significant component exist. Since reliable reference data for such systems are also important, especially for the development of new efficient computational methods, this issue is addressed here with a new benchmark set.
To emphasize the focus on heavy elements it is named “heavy S13L” (HS13L) and covers elements of groups 12 to 17. To demonstrate the accuracy of our approach in direct comparison to experimentally accessible reference values, complexes with available experimental association free energies were selected. Systems with small HOMO–LUMO gaps were consciously not included in HS13L. In metallic-like systems, large electron density fluctuations occur (so-called “type C non-additivity”), which lead to a slower decay of the LD interaction than described by the additive pair-wise approach and thus require special treatment.18 As NCI complexes generally feature many possible binding sites depending on the number and nature of the respective functional groups, it is essential for reliable modeling to determine the most favorable conformer. Therefore, we applied the CREST19 and CENSO workflow20 to screen the large conformational space of the investigated complexes with SQM methods and determine the minimum structure with subsequent refinement at the DFT level of theory. For an accurate calculation of binding thermodynamics of non-rigid systems in solution, it is necessary to consider conformers.20 In this work, we benchmark this workflow for the first time systematically on large supramolecular complexes.
We aim to provide a reliable protocol without any empirical adjustments to predict or validate experimental association free energies of supramolecular complexes including heavy main group elements. First, a short overview of the underlying theory for our approach for the calculation of association free energies in solution is given. After a description of the test set, the computational details are given. Further, we present and discuss the results for the benchmark set. Computer timings are compared for the most accurate methods and evaluated with respect to their cost-accuracy ratio. Finally, we draw general conclusions concerning the proposed workflow and give method recommendations for the computation of association free energies of realistic, experimentally observable, supramolecular complexes.
2 Theory
The association free energy in solution is calculated by| ΔGa = ΔE + ΔGTmRRHO + ΔδGTsolv(X), | (1) |
| ΔE = E(complex) − E(host) − E(guest), |
| ΔE = ΔEDFTel + ΔE(2)disp + ΔE(ATM)disp. | (2) |
For the thermostatistical corrections to the free energy, the modified rigid-rotor-harmonic-oscillator (mRRHO) approach12 is employed here. This approach treats vibrational modes below 50 cm−1, which are notoriously problematic in the harmonic approximation in entropy calculations, as hindered rotations with smooth interpolation to the standard harmonic approach. Due to the large system size in the HS13L, vibrational frequencies are calculated with SQM or force-field (FF) methods. Since the minimum geometry at the SQM level may be distorted with respect to the DFT-optimized structure, the single-point hessian (SPH)34 approach is applied here to compute the mRRHO contribution effectively on DFT geometries. The so-called “conformational” entropy35 is not computed explicitly here, as we do not expect its contribution to the free energy to be significant. Most systems in the HS13L are relatively rigid and do not lose significant conformational freedom upon complexation considering other sources of errors in the calculation of the individual contributions to the free energy. Furthermore, the computational costs for the systems' size in the HS13L for the conformational entropy become unfeasible for larger systems (above 100 atoms) even when using force-field methods in combination with implicit solvation models.36
We calculate the solvation free energy with the continuum solvation models COSMO-RS37,38 and SMD.39 The alternative explicit consideration of solvent molecules, e.g., in our recent so-called quantum cluster growth (QCG) model40 would be too computationally too demanding for this system size. Other physical aspects, such as the pH value and the ionic strength of the reaction solution can be relevant in special cases.41 However, for the complexes included in the HS13L, these effects are expected to be smaller than 0.5 kcal mol−1 and therefore relatively small compared to other sources of errors. These effects are neglected in our approach to retain a fully-automated and generally applicable workflow. For a more throughout discussion of the mentioned and other less important factors contributing to binding free energies, we refer to ref. 41.
3 Description of the HS13L test set
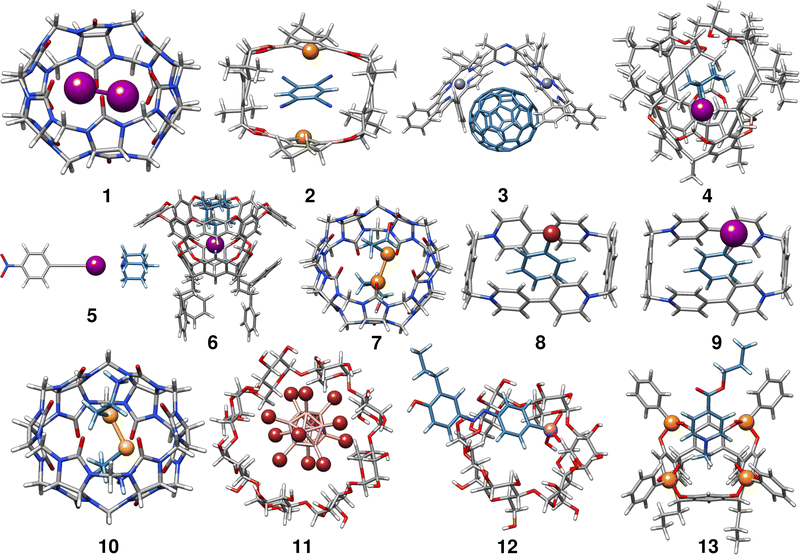
In the following, we provide a short description of the investigated complexes. Fig. 1 depicts the optimized geometries of all complexes included in the HS13L. In Table 1 all complexes are given with their number in this set, their name, their charge, and the experimental conditions at which the association free energy was determined. For an easier interpretation of the results, complexes are sorted according to the most prominent type of interaction and charged complexes are grouped, as it is recommended for NCI complexes by Rězác and Hobza.42| Entry | Complex | Charge | Solvent | T | ΔGexp |
|---|---|---|---|---|---|
| 1 | I2@CB[6]43 | 0 | H2O | 298 | −8.2 |
| 2 | tcb@tellurophene44 | 0 | CHCl3 | 298 | −5.8 |
| 3 | C70@bisZnporphy45 | 0 | Toluene | 296 | −4.8 |
| 4 | Icy@(P)4-AAC46 | 0 | n-Octane | 293 | −5.7 |
| 5 | Iethynyl@quinucli47 | 0 | Benzene | 298 | −1.9 |
| 6 | Iad@cav48 | 0 | DMSO | 298 | −6.8 |
| 7 | (HOC3Te)2@CB[7]49 | 0 | H2O | 298 | −4.7 |
| 8 | Brbenz@CBPQT4+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
4 | H2O | 303 | −5.0 |
| 9 | Ibenz@CBPQT4+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
4 | H2O | 303 | −5.5 |
| 10 | SeCy@CB[6]51 | 2 | H2O | 298 | −9.2 |
| 11 | B12Br122−@γ-CD52 | −2 | H2O | 298 | −8.1 |
| 12 | Asdiazo@α-CD53 | −1 | H2O | 298 | −5.2 |
| 13 | C10H14O2 N@Tiiii54 | 1 | DCE | 303 | −7.6 |
Complex 1 comprises the guest diiodine and the host cucurbit[6]uril (CB[6]). In the crystal structure, halogen bonding was observed,43 whereas in (implicit) aqueous solution this interaction is quenched according to the optimized geometry and was therefore classified as mainly bound by LD. CB[6] is a representative of the cucurbit[n]urils which are important excipients in medical formulations for improving drug delivery.552 is a complex of 1,2,4,5-tetracyanobenzene (TCB) bound via π–π stacking to a macrocyclic boronic ester connecting two tellurophenes, which exhibit advantageous optoelectronic properties44 due to the “heavy-atom effect” of tellurium56 The host of complex 3 is a Zn(II) complex of 2,6-bis(porphyrin)-substituted 3,5-dimethylpyrazine bound to the fullerene C70. The binding motifs are LDs associated with π–π interactions between the electron-rich porphyrin nitrogen atoms and C70.45
Complex 4 is the largest in HS13L with 266 atoms. Two conformers have to be considered as the guest iodocyclohexane can exist in an axial and equatorial conformation, both separately and in the complex. For the isolated guest, the equatorial conformation is the most stable, whereas in the complex the axial conformation is preferred. The binding motif with the host, an enantiopure alleno-acetylenic cage (AAC) with a resorcin[4]arene scaffold, is dominated by dispersion interaction and halogen-bonding.46 With 37 atoms, complex 5 is the smallest one in HS13L. Its binding motif is a single halogen bond between the bond donor iodoethynylbenzene and the bond acceptor quinuclidine. 6 contains a deep cavity host providing four hydrogen atoms pointing into the cavity. It forms unusual hydrogen bonds (C–H⋯X–R) to the guest 1-iodoadamantane.487 is a ditelluride (HOC3Te)2 guest interacting via chalcogen bonding to CB[7].49 Complexes 8 to 13 are charged systems. 8 and 9 both have the +4 charged cyclobis-(paraquat-p-phenylene) host, which is the highest charge considered. This host can form stable complexes through steric complementarity and (assumed) charge transfer mechanisms with the volatile substances bromobenzene and iodobenzene.50 With a value of −9.2 kcal mol−1 for the association free energy, 10 forms the strongest NCI bonds in HS13L. Its bonding motif consists mainly of chalcogen bonds between the selenium atoms of the guest selenocystamine and the carbonyl oxygens of the host CB[6].51 The formation of the double negatively charged dodecaborate boron cluster with γ-cyclodextrin (11) is driven by the so-called chaotropic effect.52 Complexes of cyclodextrin are often used for drug delivery and are therefore of great practical importance.5712 consists of a diazonium compound with an arsenate group which is bound to α-cyclodextrin53 mainly by hydrogen bonding. Last is a tetraphosphonate cavitand, which binds a methylpyridinium cation via cation-dipole and CH3–π interactions.54
In summary, despite the limited number of systems, this benchmark set exhibits a broad range of different non-covalent binding motifs of (heavy) main group elements, such as hydrogen bonding, chalcogen bonding, halogen bonding, π–π stacking, and dispersion interaction. It involves polar as well as non-polar solvents, which are tabulated in Table 1. Furthermore, the complexes are of realistic size (37 up to 266 atoms) and contain a large variety of unusual main group elements (Se, Te, P, As, and Zn).
4 Computational details
Conformer search for the host, guest, and complex structures was performed with CREST19 Version 2.1158 at the GFN2-xTB59 level with the implicit solvation model ALPB60 in xTB version 6.4.0.61 To save computation time, we used GFN-FF62 [ALPB] for larger systems (2, 4, 6, 7, 10, and 11) instead if the optimized structures appeared to be reasonable and showed no deformations compared to the GFN2-xTB geometries. Likewise, we employed the special NCI mode of CREST for some of the larger complexes (2, 3,6,7, and 11) to reduce the number of generated conformers. For rigid systems (1, 12, 13), we utilized the rigid docking mode of the intramolecular force-field xtb-IFF.63Subsequent refinement of the conformer ensembles generated as described above was performed with CENSO64 version 1.2.065 using the default thresholds for Part0 to Part2, as described in ref. 64 and, with stronger focus on NCI complexes, in ref. 66. First, conformers that are more than 4 kcal mol−1 higher in energy than the lowest conformer at the B97-D3(0)67/def2-SV(P)68+gCP69 level of theory were excluded. Solvation effects in Part0 are captured by ALPB(GFN2-xTB). In Part1, we removed conformers above the free energy threshold of 3.5 kcal mol−1 calculated on geometries optimized on the GFN2-xTB[ALPB] level of theory. We performed the free energy ranking in this part already with the r2SCAN-3c composite DFT method including thermostatistical corrections at the GFN2-xTB level in the single-point hessian (SPH)70 approach and solvation contributions with COSMO-RS(16) normal (based on the r2SCAN-3c electron density), which we will refer to in the following as default level. In the last part, we conduct the final geometry optimization at the r2SCAN-3c71 level using the SMD39 continuum solvation model. The geometry optimization was performed with ORCA 5.0.372 employing DefGrid2. Using the default settings in CENSO, i.e. DCOSMO-RS,73 led to severe convergence problems, especially for the larger complexes, and was therefore not applied for this automated workflow. For some of the charged complexes (10, 12, and 13), large deviations from the experimental values were observed. In order to diminish the electrostatic contribution in the solvation free energy and the electronic energies, counterions were added to the charged complexes 10–13 and the resulting set is called HS13L-CI. Chloride counterions were added to the cations and sodium ions to the anions for neutralization with the docking algorithm of the intramolecular force-field xTB-IFF and the lowest found structure was re-optimized at the r2SCAN-3c[SMD] level. We denote these structures with counterions by adding “_CI” to their respective name or number. For the charged complexes 8 and 9, this was not done, as the experimental value was already well reproduced with the standard procedure and the addition of four counterions resulted in massive convergence problems in the SCF iterations, which would be problematic for a benchmark set.
Calculating the ensemble average by Boltzmann weighting all found conformers is not important here compared to other sources of errors and the association free energy can accurately be described by only one distinct minimum structure. Therefore, we investigated the effect of considering also higher conformers only for the default level of theory and applied the other computational methods only for the minimum conformer.
All single-point calculations were performed with ORCA 5.0.3 using the DefGrid3, the TightSCF convergence criteria, and the RIJCOSX74,75 approximation. Ahlrichs def2-QZVP68 basis set with corresponding default ECPs and auxiliary basis sets76 were employed. For the double hybrids, we applied the frozen core approximation and the def2-QZVPP correlation auxiliary basis sets77,78 in the RI-MP2 part. The nonlocal VV10 correction was computed non-self-consistently. The D321,22 and D425 correction were consistently applied with inclusion of the ATM term using the s-dftd379 dft-d480 standalone programs. Becke-Johnson damping81 was applied for all DFAs except for the Minnesota functionals M06L and M06-2x, for which the zero-damping variant was used. Table 2 lists all tested DFAs and dispersion correction combinations. The DFT-C82 basis set superposition error (BSSE) correction was computed for B97M-V/def2-SVPD83 with the Q-Chem 5.4 program package.84 In the following, this combination of small basis set and basis set correction is denoted with a “-C”.
| Functional | D3(BJ) | D4 | VV10/NL | Ref. |
|---|---|---|---|---|
| a Zero-damping was used in the dispersion correction instead of BJ-damping. b Revised D4 parameter taken from ref. 99 were employed (see ESI for details). c 2019 parametrization with unscaled ATM term103 as well as with downscaled ATM term (s9 = 0.5132)104 was employed. | ||||
| GGA | ||||
| PBE | x | x | x | 85 |
| RPBE | x | x | x | 86 |
| meta -GGA | ||||
| r2SCAN | x | x | x | 87 |
| B97M-V | x | x | x | 88–90 |
| M06La | x | x | x | 91 and 92 |
| Hybrid | ||||
| PW6B95 | x | x | x | 93 |
| PBE0 | x | x | x | 94 |
| B3LYP | x | x | x | 95 and 96 |
| M06-2Xa | x | x | x | 97 |
| RS-hybrid | ||||
| ωB97M-V | x | x | x | 89, 90 and 98 |
| ωB97X-Vb | x | x | x | 89, 99 and 100 |
| Double-hybrid | ||||
| PWPB95 | x | x | x | 101 and 102 |
| revDSD-PBEP86c | x | 103 and 104 | ||
| Composite (“3c”) | ||||
| B97-3c | x | 105 | ||
| r2SCAN-3c | x | 106 | ||
| PBEh-3c | x | 107 | ||
Harmonic frequencies for the thermostatistical contributions were calculated on the minimum structure of the respective method. The rotational symmetry numbers of the complexes were obtained with a DESY threshold of 0.1 in TURBOMOLE(V. 7.5.1).108 and used for the calculation of the rotational entropy, see ESI† (Table S7). For the geometry optimization as well as the frequency calculation, an implicit solvation model was consistently applied. GFN2-xTB, GFN1-xTB, and GFN-FF frequencies were calculated with xTB and the ALPB implicit solvation model. PM6-D3H4X and PM7 frequencies were computed with the COSMO109 solvation model with MOPAC2016 (version 19.179L)110 using xtb as driver. Gas-phase single-point calculations with both PM methods were also conducted with the same program combination.
The solvation free energy was calculated with COSMOtherm19.111,112 The default procedure of one single-point calculation in gas-phase and one in continuum solution was performed using r2SCAN-3c with the m4 grid in TURBOMOLE (V. 7.5.1).108 Additionally, we calculated solvation free energies at the default level of theory (BP86113,114/def2-TZVP) and BP86113,114/def2-TZVPD, respectively, for the fine parametrization as the parameters were fitted for this level. The respective solvation free energies with SMD and CPCM115 were calculated with ORCA applying the same procedure.
Furthermore, we generated local coupled-cluster reference association energies for the HS13L and the HS13L-CI set. Due to the large size of the NCI complexes composed in these sets, the “gold-standard” reference level CCSD(T) at the approximate basis set limit116 is computationally impossible without introducing further approximations. Specifically, we applied the domain based, local pair natural orbital coupled cluster method117 in its ORCA 5.0.272 closed-shell, sparse maps non-iterative118 or iterative triples119 implementation (DLPNO-CCSD(T) and DLPNO-CCSD(T1), respectively) together with default TightPNO or special VeryTightPNO threshold settings (i.e., TCutMKN, TCutPNO, and TCutPairs tightened to 10−4, 10−8, and 10−6, respectively). We employed ORCA 5.0.2 TightSCF convergence criteria and default frozen core settings as well as Ahlrich's-type basis sets of different sizes (def2-SVP, def2-TZVPP, def2-QZVPP) together with the corresponding auxiliary basis sets. We used a specially developed correction scheme to minimize the local truncation errors and focal-point analysis120,121 to reduce the BSSE and basis set incompleteness (BSIE) errors (see Section 5.5.1 for details). These so-called “DLPNO-CCSD(T1)/CBS” reference level was computationally unfeasible for complex 3. Therefore, the respective PWPB95-D4/def2-QZVP association energy is used as reference values instead. Based on our experience,122 this double-hybrid represents a very good approximation for coupled cluster association energy in the gas phase (see discussion below).
5 Results and discussion
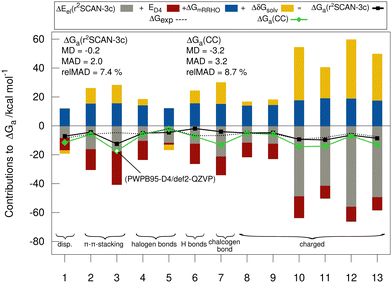
In this section, the performance of all tested methods is presented and discussed with respect to the experimental association free energies. We compare the calculated association energies of the discussed methods by “back-correcting” the experimental values, i.e., subtracting the respective two remaining contributions to the free energy with the default level of theory: r2SCAN-3c energies, GFN2-xTB[ALPB]-SPH thermostatistical contributions, and COSMO-RS(16)-normal(r2SCAN-3c) solvation free energies. For example, “back-corrected” experimental gas-phase association energies are obtained as ΔEexp = ΔGexp − ΔGTmRRHO(GFN2-xTB[ALPB]-SPH) − ΔδGTsolv(X)(COSMO-RS(16)-normal(r2SCAN-3c)) computed at the respective temperature T in solvent X. We calculated the individual contributions to the free energy for the structures of the HS13L and HS13L-CI only for the lowest conformer. Not taking higher-lying conformers into account results in a maximum error of about 0.7 kcal mol−1 and on average 0.2 kcal mol−1 for the HS13L (see ESI†). Details for the statistical measures used, namely mean deviation (MD), mean absolute deviation (MAD) and standard deviation (SD), are given in the ESI.† We conduct the statistical evaluation for the HS13L-CI set, i.e., with counterions, as the deviations to the experimental values are generally smaller than for the HS13L set without counterions (see Section 5.2) and the respective statistics for HS13L can be found in the ESI.† In Section 5.1 the effect of using different methods for calculating the contributions to the free energies are investigated for the HS13L-CI. The use of different solvation models and the addition of counterions is discussed in more detail in Section 5.2. After an evaluation of computational timings (Section 5.3) we discuss the individual contributions to the free energy for each complex in Section 5.4. Furthermore, we evaluate the performance of the DFAs used for the calculation of the gas-phase association energies with respect to the “DLPNO-CCSD(T1)/CBS” reference values in Section 5.5. The computed energies of all assessed methods as well as the conformer ensembles are provided in the ESI.† All DFAs were applied with the quadruple-ζ size basis set def2-QZVP, which is usually sufficient to ensure a diminishing basis set superposition error (BSSE).123 Only for the double hybrids, a significant BSSE of up to 1 kcal mol−1 is expected (for results of the respective counterpoise calculations for the example of 1 see Table S4 in the ESI†).5.1 Finding the best workflow for the calculation of free energies
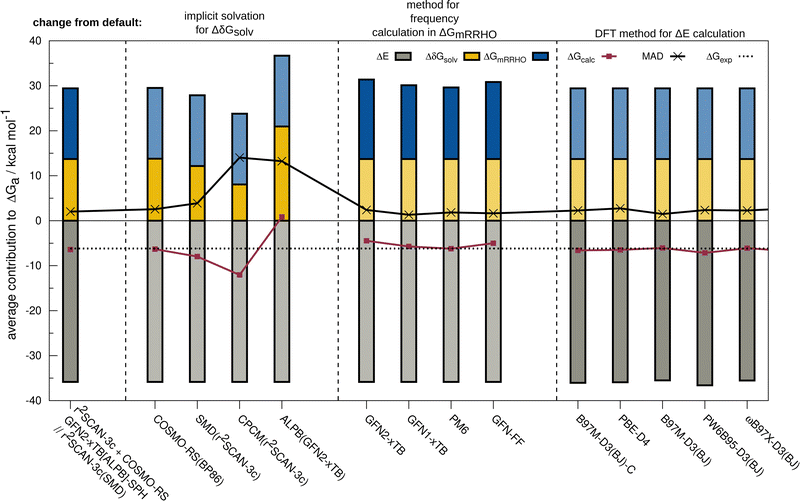
The resulting change of the calculated association free energy upon using other methods than the default theory level (r2SCAN-3c + GFN2-xTB-SPH + COSMO-RS(16)-normal(r2SCAN-3c)) is shown in Fig. 2 for HS13L-CI. Statistical measures are discussed in comparison to the experimental association free energies, whereby only the discussed method is varied and evaluated in combination with the two other components to the association free energy computed at the default level of theory. The default level of theory has a mean absolute deviation (MAD) of only 2.0 kcal mol−1 which is remarkable considering the complexity of the considered property and systems. For the solvation free energy, COSMO-RS 16 with normal parameters yields very similar results with the default BP86/def-TZVP density compared to the r2SCAN-3c density.The deviations when using SMD as solvation model are larger with a MAD of 3.9 kcal mol−1 for HS13L-CI. As expected, the purely electrostatic CPCM solvation model (14 kcal mol−1 MAD) and the semiempirical ALPB(GFN2-xTB) model (13.2 kcal mol−1) show the largest deviations from the assessed solvent models. We investigated the effect of using different solvent models in the geometry optimization on the overall association free energy for the example of complex 8 (see ESI,† for details). SMD and DCOSMO-RS both yield very good geometries for this complex with essentially no deviation for the free energy, validating the choice for the technically more robust SMD model in our workflow. For the GmRRHO contribution, the MAD increases from 2.0 to 2.4 kcal mol−1 when calculating the GFN2-xTB[ALPB] frequencies for the relaxed geometries instead of using the SPH approach. Notably, the MAD is smaller when using GFN1-xTB[ALPB] (1.3 kcal mol−1), PM6[COSMO] (1.8 kcal mol−1), and GFN-FF[ALPB] (1.6 kcal mol−1) indicating some error cancellation between the individual contributions. The comparison to r2SCAN-3c frequencies for a subset composed of the five smallest complexes of HS13L (see ESI†) shows that GFN1-xTB[ALPB] (0.6 kcal mol−1 MAD) and GFN2-xTB[ALPB]-SPH (0.8 kcal mol−1 MAD) give the best results, whereas with PM6[COSMO] (1.1 kcal mol−1), PM7[COSMO] (1.6 kcal mol−1) and GFN-FF[ALPB](1.5 kcal mol−1) the deviations are slightly larger. Since the differences in GmRRHO are for all methods tested small compared to the errors in ΔE and Gsolv, we tentatively conclude that the thermostatistical contribution is not the largest source of error in the workflow. Using a higher level of theory for the computation of frequencies, e.g., DFT, is therefore in most cases not worth the computational costs. For the electronic energy, the best DFAs in each class of functionals and the BSSE corrected B97M-D3(BJ)/def2-SVPD DFA (denoted with B97M-D3(BJ)-C) are shown. Only the meta-GGA B97M-D3(BJ) with a MAD of 1.5 kcal mol−1 yields a better MAD than r2SCAN-3c making it the overall best DFA on HS13L-CI with respect to the “back-corrected” experimental values.
However, as the error of the “back-corrected” experimental values is difficult to estimate, we cannot clearly say here which of both methods is better considering that only 13 systems are statistically evaluated. Even the double-hybrid PWPB95-D3(BJ) shows slightly larger deviations than r2SCAN-3c demonstrating the excellent accuracy of this efficient composite method on this set and validating its use as the default.
5.2 Free energy of solvation and influence of counterions
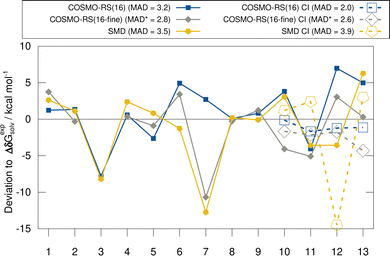
In this section, we discuss the evaluated implicit solvent models for the HS13L and the HS13L-CI benchmark sets. Deviations with respect to the “back-corrected” experimental solvation free energies are shown in Fig. 3. For the HS13L, i.e., without counterions, the fine parametrization of COSMO-RS only performs better for some complexes (2, 5, 12, and 13) than the normal parametrization. However, for complex 3 the SCF did not converge for BP86/def2-SVPD. Removing this outlier, the normal parametrization yields the same MAD of 2.8 kcal mol−1 as COSMO-RS-fine. The addition of counterions reduces the deviations to the experimental values of the COSMO-RS results significantly, especially for the normal parametrization (from 3.2 kcal mol−1 to 2.0 kcal mol−1) making it the overall best solvation model. In contrast, for SMD the errors increase upon the inclusion of counterions. This is consistent with previous observations made for the S30L13 but not a good sign in our opinion regarding the quality of the model itself. However, this is due to the large deviation for complex 12, which may be due to inaccurate atomic radii for arsenic in the SMD model. After excluding this outlier, the MAD for SMD also decreases from 3.5 kcal mol−1 to 3.0 kcal mol−1. As expected, the discrepancies between solvent models are larger for polar solvents than for nonpolar solvents, since polar solvents are generally more challenging for implicit solvation models.38,1245.3 Timing comparison
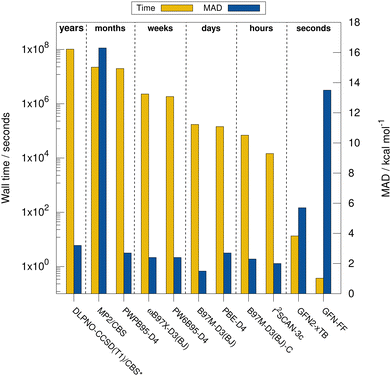
Next, the computational timings are put into perspective. Fig. 4 shows the computational timings for the calculation of the gas-phase association energy for complex 6 including host, guest, and complex scaled down to one CPU core. The most accurate method of each DFA class is shown. For a better discussion of the performance, the MAD to the experimental values of the respective method for HS13L-CI is also given. An upper bound of the serial computation time needed for the complete coupled-cluster based reference value protocol for all complexes (see Section 4) is estimated at 3.3 years, showing how difficult the generation of high-level wave-function theory (WFT) reference values is for such large systems. In practice, the most expensive calculation of the protocol, the coupled-cluster calculation with the def2-TZVPP basis set for complex 4 (265 atoms, 5902 basis functions), took about 18 days wall time on 20 CPU cores. This demonstrates the importance of an efficient computational workflow to calculate “back-corrected” gas-phase association energies from experimental values of large systems for developing new efficient computational methods for this system size. MP2 and double hybrid DFAs require months of computation time. Additionally, a significant BSIE/BSSE even with the large quadruple-ζ size basis set used is indicated by the MAD of 2.7 kcal mol−1 for PWPB95-D3(BJ), which is larger than that of the best meta-GGA methods, such as r2SCAN-3c or B97M-D3(BJ). Hybrid DFAs are already quite expensive with weeks of computation times and are only recommended for cross-checking in difficult cases, i.e., when self-interaction error (artificial charge-transfer effects) is expected to be critical. The BSSE-corrected B97M-D3(BJ)-C method in combination with the def2-SVPD basis set is about 2.5 times faster than B97M-D3(BJ)/def2-QZVP, which comes at the cost of an increase of the MAD by 0.8 kcal mol−1. r2SCAN-3c shows a remarkable performance and gives very accurate results within hours of computation time. GFN2-xTB is very fast providing results in only seconds of computation time. However, considering its relatively large MAD it is only recommended for initial screening steps and for generating accurate geometries. The strength of the very efficient GFN-FF lies in the very low computation time and parametrization for heavier elements which yields reasonable geometries in seconds.5.4 Contributions to the association free energy
Fig. 5 shows the individual contributions of the default level of theory to the calculated free energies. It is remarkable how this diverse set with very different sizes of contributions ranging from −69 to +40 kcal mol−1 depending on the binding motif of the complex lead to very similar and comparably small association energies in the range from −1.9 to −9.2 kcal mol−1. This demonstrates the difficulty of calculating ΔGa for large supramolecular complexes and renders the MAD of our default workflow of only 2 kcal mol−1 even more impressive. The r2SCAN-3c values are in most cases in good agreement with the CC reference values indicating, that the approach mostly gives the right answer for the right physical reasons. Larger differences of over 4 kcal mol−1 between the “DLPNO-CCSD(T1)/CBS” values and the r2SCAN-3c values are obtained for complexes 1, 6, 7, 10, 11, and 13. For 1, 7, 10, 11, and 13 the association free energy obtained with r2SCAN-3c is closer to the experimental value than the coupled cluster result indicating some favorable error compensation in our workflow for these complexes.5.5 Theory benchmark for HS13L-CI
Because of the potential error compensation between the individual energy contributions to the free association energy, we recommend that methods for calculating gas-phase association energies should be evaluated using the provided coupled cluster reference values (see below), for which at least one error range could be estimated, rather than the “back-corrected” experimental association energies. Hence, to further investigate the accuracy of the employed DFAs for the calculation of gas-phase association energies, we compare the calculated DFT to “DLPNO-CCSD(T1)/CBS” reference values for the HS13L-CI. The reference association energies for HS13L-CI range from −10.9 kcal mol−1 to −68.5 kcal mol−1 with an average of −38.9 kcal mol−1 and an estimated error of approximately 2 kcal mol−1 or 5%, respectively (see below). Geometries and all computed energies including the reference values for the HS13L and HS13L-CI are provided in the ESI.† Because of the limited number of systems composed in HS13L-CI and their difficulty, which is reflected in the large error spread of all tested DFAs, we recommend to use this benchmark set as a challenging extension of S30L.13 | (3) |
For the smallest complex from HS13L-CI (system 5), we were also able to calculate reference values without further approximations, supporting the assumptions described above. The comparison of the DLPNO-CCSD(T1)/CBS(def2-TZVPP/def2-QZVPP)/VeryTightPNO association energy of −10.95 kcal mol−1 (i.e., with genuine basis set extrapolation,127,128 iterative triples, and VeryTightPNO threshold settings also for the extended basis sets) with the corresponding “DLPNO-CCSD(T1)/CBS” value of −10.94 kcal mol−1 shows that the additional approximations do not have a large impact on the accuracy of the reference values. Also, the comparison of the CCSD(T)/def2-TZVPP association energy (−10.75 kcal mol−1) with the corresponding “DLPNO-CCSD(T1)/VeryTightPNO/def2-TZVPP” value (−10.48 kcal mol−1) shows that for these conservative threshold settings, the local truncation errors are small compared to the association energies of the complexes in HS13L-CI.
The maximum error in the HS13L-CI reference association energies resulting from the local DLPNO approximations, the BSSE and BSIE, and the additional error from the focal point analysis is therefore estimated to be about ≈5%, which translates to about ±2 kcal mol−1 for a mean association energy of −38.9 kcal mol−1. Nevertheless, this uncertainty in the reference values is largely averaged in the analysis of the statistical descriptors for the entire HS13L-CI set. The square root of the sum of the squares of the estimated maximum error divided by the number of individual association energies, which for HS13L-CI gives ≈1.95 kcal mol−1, can be used as an estimate of statistically distinguishable values of the analyzed descriptors (see 5.5.2). Thus, with the given accuracy of the reference values, we are able to distinguish statistically significant errors of each method above 0.5 kcal mol−1 in the respective MADs.
| MD | MAD | SD | |
|---|---|---|---|
| a Downscaled s9. | |||
| r2SCAN-3c | 3.0 | 3.4 | 3.0 |
| PBEh-3c | 6.2 | 8.0 | 9.4 |
| B97-3c | 3.8 | 5.3 | 9.9 |
| B97M-V-C | -0.7 | 2.5 | 3.2 |
| PBE-NL | 0.6 | 2.7 | 3.3 |
| RPBE-NL | -1.3 | 3.1 | 3.9 |
| r2SCAN-D4 | 2.4 | 2.8 | 2.9 |
| M06L-D3(0) | -1.1 | 3.7 | 4.9 |
| B97M-V | -0.2 | 1.9 | 2.7 |
| PW6B95-NL | 0.5 | 2.5 | 3.5 |
| B3LYP-NL | -0.7 | 2.2 | 3.1 |
| M06-2X-D3(0) | 1.6 | 3.0 | 4.1 |
| PBE0-D4 | 1.9 | 2.3 | 3.2 |
| ωB97X-V | -1.2 | 2.6 | 3.2 |
| ωB97M-V | -2.2 | 3.2 | 3.2 |
| PWPB95-D3 (BJ) | 0.7 | 2.9 | 3.6 |
| rev-DSDPBEP86-D4 | 2.9 | 3.8 | 3.8 |
| rev-DSDPBEP86-D4a | 0.5 | 2.7 | 4.1 |
| MP2-CBS | -13.1 | 13.1 | 12.4 |
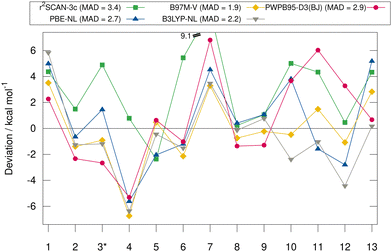
Fig. 6 shows the deviation between the best DFA of each class and the DLPNO-CCSD(T1)/CBS reference values in detail for each complex for the HS13L-CI. For the large halogen-bonded complex 4, all methods except r2SCAN-3c show strong overbinding of over 5 kcal mol−1. Systematic overbinding of all methods is observed for the tellurium containing complex 7 and less pronounced for complex 1 containing I2.
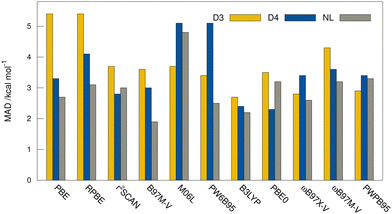
MADs from the “DLPNO-CCSD(T1)/CBS” reference values for the HS13L-CI obtained with the assessed DFAs in combination with D3, D4, and the VV10 correction are shown in Fig. 7. For most DFAs, the VV10 correction yields smaller deviations than the D3 or D4 correction, although higher-order dispersion terms are missing in this model. The NL corrected DFAs tend to overbinding, whereas the D3 and D4 corrected DFAs show the opposite with respect to the “DLPNO-CCSD(T1)/CBS” reference, which can be attributed to the mostly repulsive ATM term in the latter two (see ESI,† for details).
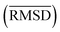 between the geometries optimized with SQM/FF methods and r2SCAN-3c[SMD] for the HS13L is given in Å
between the geometries optimized with SQM/FF methods and r2SCAN-3c[SMD] for the HS13L is given in Å
The large error range of all assessed methods is notable. GFN1-xTB is the best method with a MAD of 6.1 kcal mol−1. GFN2-xTB (MAD of 6.6 kcal mol−1) also yields reasonably good results. PM6 (7.8 kcal mol−1) shows larger deviations than both methods. PM7 (11.9 kcal mol−1) and the force-field GFN-FF (13.6 kcal mol−1) yield a similar accuracy. In summary, this shows that even the most accurate SQM methods tested, namely GFN1- and GFN2-xTB, are only useful in the early stage of screening procedures but with relatively large energy windows for structure selection.
The mean heavy atom 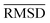 of the optimized geometries in solution are compared to the r2SCAN-3c[SMD] optimized geometries of HS13L, shown in Table 4. GFN2-xTB[ALPB] structures are remarkably accurate with a deviation of only 0.17 Å. Also GFN-FF[ALPB] yields outstanding geometries with an
of the optimized geometries in solution are compared to the r2SCAN-3c[SMD] optimized geometries of HS13L, shown in Table 4. GFN2-xTB[ALPB] structures are remarkably accurate with a deviation of only 0.17 Å. Also GFN-FF[ALPB] yields outstanding geometries with an 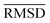 of 0.22 Å, which is better than the SQM methods GFN1-xTB[ALPB] (0.25 Å), PM6-D3H4X [COSMO] (0.30 Å), and PM7[COSMO] (0.29 Å).
of 0.22 Å, which is better than the SQM methods GFN1-xTB[ALPB] (0.25 Å), PM6-D3H4X [COSMO] (0.30 Å), and PM7[COSMO] (0.29 Å).
6 Conclusions
The reliable prediction of association free energies of supramolecular complexes containing (heavy) main group elements is an important yet challenging task for computational methods. Especially for large systems, for which highly accurate reference energies are difficult to obtain with WFT methods, an efficient workflow for the calculation of experimentally accessible association free energies is needed. We assessed the CREST and CENSO workflow of conformer generation with SQM methods and subsequent free energy ranking at DFT level for the first time systematically on large, heavy atom containing supramolecular complexes in direct comparison to experimental values. We introduced a new benchmark set of 13 supramolecular complexes (HS13L or HS13L-CI with counterions added, respectively). By comparison to experimental association free energies, we showed that our protocol reliably predicts this property with a MAD of only 2.0 kcal mol−1.The comparison between various dispersion corrected DFAs and accurate local coupled cluster values shows that in special cases calculations profit from error compensation between the electronic energy and the solvation free energy between the individual contributions to the free energy. Therefore, we recommend to benchmark methods against the “DLPNO-CCSD(T1)/CBS” reference values instead of the “back-corrected” experimental gas-phase association energies. Large deviations of the DFA gas-phase association energy of over 4 kcal mol−1 from the respective coupled cluster values were observed for some complexes of HS13L-CI. Of the assessed methods, the meta-GGA composite method r2SCAN-3c proved to be robust and showed the best cost-accuracy ratio, outperforming some very popular hybrid and double-hybrid DFAs. Also, B97M-D3(BJ) showed a remarkable accuracy. The assessed SQM methods yield large deviations from the “DLPNO-CCSD(T1)/CBS” reference values and are therefore only recommended for initial screening steps. However, GFN2-xTB[ALPB] gives accurate geometries for the HS13L and proves to be a viable tool for the conformer generation of challenging supramolecular complexes. The default structure thresholds in the CENSO workflow are also suitable for these systems. From the assessed solvation models, COSMO-RS is the most accurate for solvation free energies, whereas SMD is the more robust alternative to DCOSMO-RS for the geometry optimization. We propose the HS13L-CI set as test set for the development of new solvation models. GFN2-xTB provides accurate thermostatistical contributions in the SPH approach and can be recommended also for heavy main group systems. We recommend the HS13L-CI benchmark as an extension to the well established S30L set specifically assessing new methods for their robustness and accuracy for systems with heavy main group elements.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Fabian Bohle for technical help regarding the CENSO calculations, fruitful discussions, and helpful suggestions, as well as Thomas Gasevic for providing helpful corrections to the manuscript.References
- I. V. Kolesnichenko and E. V. Anslyn, Chem. Soc. Rev., 2017, 46, 2385–2390 RSC.
- D. Phlip, Adv. Mater., 1996, 8, 866–868 CrossRef.
- I. P. Parkin, Appl. Organomet. Chem., 2001, 15, 236 CrossRef CAS.
- J.-M. Lehn, Angew. Chem., Int. Ed., 1988, 27, 89–112 CrossRef.
- D. J. Cram, Angew. Chem., Int. Ed., 1988, 27, 1009–1020 CrossRef.
- J. M. Lehn, Science, 1993, 260, 1762–1763 CrossRef CAS PubMed.
- Z. Zhang and P. R. Schreiner, Chem. Soc. Rev., 2009, 38, 1187 RSC.
- M. A. Pitt and D. W. Johnson, Chem. Soc. Rev., 2007, 36, 1441–1453 RSC.
- F. P. Schmidtchen, Isothermal Titration Calorimetry in Supramolecular Chemistry, John Wiley & Sons, Ltd, 2012 Search PubMed.
- G. A. Holdgate and W. H. Ward, Drug Discovery Today, 2005, 10, 1543–1550 CrossRef CAS PubMed.
- S. Grimme and P. R. Schreiner, Angew. Chem., Int. Ed., 2018, 57, 4170–4176 CrossRef CAS PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- R. Sure and S. Grimme, J. Chem. Theory Comput., 2015, 11, 3785–3801 CrossRef CAS PubMed.
- N. Mehta, T. Fellowes, J. M. White and L. Goerigk, J. Chem. Theory Comput., 2021, 17, 2783–2806 CrossRef CAS PubMed.
- J. Rězáč, J. Chem. Theory Comput., 2020, 16, 6305–6316 CrossRef PubMed.
- K. Kříž and J. Rězáč, Phys. Chem. Chem. Phys., 2022, 24, 14794–14804 RSC.
- J. Rězáč, Phys. Chem. Chem. Phys., 2022, 24, 14780–14793 RSC.
- J. F. Dobson, Int. J. Quantum Chem., 2014, 114, 1157–1161 CrossRef CAS.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Grimme, F. Bohle, A. Hansen, P. Pracht, S. Spicher and M. Stahn, J. Phys. Chem. A, 2021, 125, 4039–4054 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 124108 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- Y. Muto, J. Phys.-Math. Soc. Jpn, 1943, 17, 629 CAS.
- B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299–300 CrossRef CAS.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 122, 154104 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- R. A. DiStasio, V. V. Gobre and A. Tkatchenko, J. Phys.: Condens. Matter, 2014, 26, 213202 CrossRef PubMed.
- O. A. Vydrov and T. V. Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS PubMed.
- S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 1701–1714 CrossRef CAS PubMed.
- P. Pracht and S. Grimme, Chem. Sci., 2021, 12, 6551–6568 RSC.
- J. Gorges, S. Grimme, A. Hansen and P. Pracht, Phys. Chem. Chem. Phys., 2022, 24, 12249–12259 RSC.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 609–620 CrossRef CAS PubMed.
- S. Spicher, C. Plett, P. Pracht, A. Hansen and S. Grimme, J. Chem. Theory Comput., 2022, 18, 3174–3189 CrossRef CAS PubMed.
- J. H. Jensen, Phys. Chem. Chem. Phys., 2015, 17, 12441–12451 RSC.
- J. Rězáč and P. Hobza, Chem. Rev., 2016, 116, 5038–5071 CrossRef PubMed.
- H. S. El-Sheshtawy, B. S. Bassil, K. I. Assaf, U. Kortz and W. M. Nau, J. Am. Chem. Soc., 2012, 134, 19935–19941 CrossRef CAS PubMed.
- K. Takahashi, S. Shimo, E. Hupf, J. Ochiai, C. A. Braun, W. T. Delgado, L. Xu, G. He, E. Rivard and N. Iwasawa, Chem. – Eur. J., 2019, 25, 8479–8483 CrossRef CAS PubMed.
- Y. Eda, K. Itoh, Y. N. Ito, M. Fujitsuka, T. Majima and T. Kawato, Supramol. Chem., 2010, 22, 517–523 CrossRef CAS.
- C. Gropp, T. Husch, N. Trapp, M. Reiher and F. Diederich, J. Am. Chem. Soc., 2017, 139, 12190–12200 CrossRef CAS PubMed.
- O. Dumele, D. Wu, N. Trapp, N. Goroff and F. Diederich, Org. Lett., 2014, 16, 4722–4725 CrossRef CAS PubMed.
- H. Gan and B. C. Gibb, Supramol. Chem., 2010, 22, 808–814 CrossRef CAS.
- C. Liu, Z. Zhang, Z. Fan, C. He, Y. Tan and H. Xu, Chem. – Asian J., 2020, 15, 4321–4326 CrossRef CAS PubMed.
- P. I. Dron, S. Fourmentin, F. Cazier, D. Landy and G. Surpateanu, Supramol. Chem., 2008, 20, 473–477 CrossRef CAS.
- H. Ren, Z. Huang, H. Yang, H. Xu and X. Zhang, ChemPhysChem, 2015, 16, 523–527 CrossRef CAS PubMed.
- K. I. Assaf, M. S. Ural, F. Pan, T. Georgiev, S. Simova, K. Rissanen, D. Gabel and W. M. Nau, Angew. Chem., Int. Ed., 2015, 54, 6852–6856 CrossRef CAS PubMed.
- N. Yoshida and K. Hayashi, J. Chem. Soc., Perkin Trans. 2, 1994, 1285–1290 RSC.
- D. Menozzi, E. Biavardi, C. Massera, F.-P. Schmidtchen, A. Cornia and E. Dalcanale, Supramol. Chem., 2010, 22, 768–775 CrossRef CAS.
- N. J. Wheate and C. Limantoro, Supramol. Chem., 2016, 28, 849–856 CrossRef CAS.
- M. Zander and G. Kirsch, Z. Naturforsch., A: Phys. Sci., 1989, 44, 205–209 CrossRef CAS.
- M. V. Rekharsky and Y. Inoue, Chem. Rev., 1998, 98, 1875–1918 CrossRef CAS PubMed.
- Conformer-Rotamer Ensemble Sampling Tool based on the xtb Semiempirical Extended Tight-Binding Program Package crest, https://github.com/crest-lab/crest, Accessed: 2021-12-21.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- Semiempirical Extended Tight-Binding Program Package xtb, https://github.com/grimme-lab/xtb, Accessed: 2022-5-15.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 132, 15795–15803 CrossRef.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- S. Grimme, F. Bohle, A. Hansen, P. Pracht, S. Spicher and M. Stahn, J. Phys. Chem. A, 2021, 125, 4039–4054 CrossRef CAS PubMed.
- Commandline ENergetic SOrting of Conformer Rotamer Ensembles censo, https://github.com/grimme-lab/censo, Accessed: 2022-2-11.
- A. H. Markus Bursch, J.-M. Mewes and S. Grimme, Chem. Rev., 2022, 1875–1918 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101 CrossRef PubMed.
- S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 1701–1714 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1606 Search PubMed.
- A. Klamt and M. Diedenhofen, J. Phys. Chem. A, 2015, 119, 5439–5445 CrossRef CAS PubMed.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- Reimplementation of the DFT-D3 program s-DFTD3, https://github.com/awvwgk/simple-dftd3, Accessed: 2022-06-10.
- Generally Applicable Atomic-Charge Dependent London Dispersion Correction DFTD4, https://github.com/dftd4/dftd4, Accessed: 2022-07-06.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- J. Witte, J. B. Neaton and M. Head-Gordon, J. Chem. Phys., 2017, 146, 234105 CrossRef PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al. , J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- A. Najibi and L. Goerigk, J. Chem. Theory Comput., 2018, 14, 5725–5738 CrossRef CAS PubMed.
- A. Najibi and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. Brandenburg, J. Bates, J. Sun and J. Perdew, Phys. Rev. B, 2016, 94, 115144 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- M. Müller, A. Hansen and S. Grimme, ωB97X-3c: A composite range-separated hybrid DFT method with a molecule-optimized polarized valence double-ζ basis set, J. Chem. Phys. Search PubMed , under review.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- F. Yu, J. Chem. Theory Comput., 2014, 10, 4400–4407 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- G. Santra, N. Sylvetsky and J. M. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143 CrossRef CAS PubMed.
- G. Santra, M. Cho and J. M. Martin, J. Phys. Chem. A, 2021, 125, 4614–4627 CrossRef CAS PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- TURBOMOLE V7.5 2020, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.com.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- J. J. P. Stewart, MOPAC2016, Stewart Computational Chemistry, Colorado Springs, CO, USA, 2016 Search PubMed.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- F. Eckert and A. Klamt, COSMOtherm, version C3.0, release 19.01, COSMOlogic GmbH & Co. KG, Leverkusen, Germany, 2019 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- A. Karton and J. M. Martin, J. Chem. Phys., 2012, 136, 124114 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- A. G. Császár, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 1998, 108, 9751–9764 CrossRef.
- M. S. Marshall, L. A. Burns and C. D. Sherrill, J. Chem. Phys., 2011, 135, 194102 CrossRef PubMed.
- S. Spicher, E. Caldeweyher, A. Hansen and S. Grimme, Phys. Chem. Chem. Phys., 2021, 23, 11635–11648 RSC.
- T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591 CrossRef CAS PubMed.
- D. L. Mobley, A. E. Barber, C. J. Fennell and K. A. Dill, J. Phys. Chem. B, 2008, 112, 2405–2414 CrossRef CAS PubMed.
- Y. S. Al-Hamdani, P. R. Nagy, A. Zen, D. Barton, M. Kállay, J. G. Brandenburg and A. Tkatchenko, Nat. Commun., 2021, 12, 1–12 CrossRef PubMed.
- C. Villot, F. Ballesteros, D. Wang and K. U. Lao, J. Phys. Chem. A, 2022, 126, 4326–4341 CrossRef CAS PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Calculated relative energy contributions for all employed methods (HS13Lenergies.xlsx) as well as optimized geometries for the HS13L and HS13L-CI benchmark sets (HS13L.zip) together with the coupled cluster reference association energies are provided. Additional statistical evaluations are provided in the file SI.pdf. See DOI: https://doi.org/10.1039/d2cp04049b |
| This journal is © the Owner Societies 2022 |