Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Site-dependent nuclear dynamics in core-excited butadiene†
Shabnam
Oghbaiee
a,
Mathieu
Gisselbrecht
 a,
Noelle
Walsh
b,
Bart
Oostenrijk
a,
Noelle
Walsh
b,
Bart
Oostenrijk
 a,
Joakim
Laksman‡
a,
Erik P.
Månsson§
a,
Joakim
Laksman‡
a,
Erik P.
Månsson§
 a,
Anna
Sankari
a,
John H. D.
Eland
c and
Stacey L.
Sorensen
a,
Anna
Sankari
a,
John H. D.
Eland
c and
Stacey L.
Sorensen
 *a
*a
aDepartment of Physics, Lund University, Box 118, Lund 221 00, Sweden. E-mail: stacey.sorensen@sljus.lu.se
bMAX IV Laboratory, Lund University, Box 118, 22100 Lund, Sweden
cDepartment of Chemistry, Physical and Theoretical Chemistry Laboratory, Oxford University, South Parks Road, Oxford OX1 3QZ, UK
First published on 16th November 2022
Abstract
Symmetry breaking and competition between electronic decay and nuclear dynamics are major factors determining whether the memory of the initial core-hole localisation in a molecule is retained long enough to affect fragmentation. We investigate the fate of core holes localised at different sites in the free 1,3 trans butadiene molecule by using synchrotron radiation to selectively excite core electrons from different C 1s sites to π* orbitals. Fragmentation involving bonds localised at the site of the core hole provides clear evidence for preferential bond breaking for a core hole located at the terminal carbon site, while the signature of localisation is weak for a vacancy on the central carbon site. The origin of this difference is attributed to out-of-plane vibrations, and statistical evaporation of protons for vacancies located at the central carbon sites.
1 Introduction
Ultra rapid processes in molecules are of fundamental importance for chemical reactions, but the interplay between electron wave-packet dynamics and nuclear motion, including proton transfer, bond rearrangement and dissociation, are found to be at the nexus of a growing number of key processes in photobiology and photochemistry in a wide range of different types of molecules.1–3 New methods involving pump–probe schemes and diffraction are routinely utilized to illuminate processes where electronic states can be connected to dynamics,4–6 but another approach involves excitation of highly localized core electrons in order to initiate dynamics. In the latter approach core-excited states relax to multiply ionized states, allowing for direct imaging studies of molecular dynamics. Since Auger decay, the primary channel for electronic relaxation in hydrocarbons and organic molecules, takes place in less than 10 femtoseconds electronic decay competes directly with nuclear motion.Soft X-ray excitation provides additional insights into dynamics as the site of core-hole creation can be selected by frequency detuning, both to different elements or subshells, but even to identical atoms with chemically-shifted binding energies.7 Early studies identified element-selective bond dissociation over 3 decades ago,8,9 but a growing body of work points at a weak correlation between localized core holes and bond dissociation at the core-hole site,10–13 likely due to population of delocalized valence orbitals via Auger decay which erase the signature of the initial core-hole site.14
1,3 trans butadiene is an important prototype as the smallest π-conjugated system capable of absorbing visible light, with optical properties due to π electrons along the chain and to conformational changes upon photoexcitation.15 Core-electron excitation to the π* orbital is known to induce nuclear dynamics leading to symmetry breaking coupled to conformational changes.16–19 We have shown on the one hand that localization of the core hole is confirmed by selective population of valence states via participator Auger decay originating from the terminal and the central carbon sites.20 On the other hand we find that double ionization from π orbitals selectively triggers a conformational change about the terminal or central C–C bonds21 similar to the result for ethylene.22 This conformational rearrangement is coupled to the population of dication electronic states, and is reflected in the appearance of particular fragmentation channels in the inner-valence region.21 Butadiene thus offers the possibility to gain insight into the correlation between nuclear dynamics and electronic decay of core-excited states in longer π-conjugated systems; whether the symmetry is broken during the core-hole lifetime, and if so, whether hole/charge localisation competes with charge transfer resulting in thermodynamical dissociation.23 The basic principle of our experiment is illustrated in Fig. 1. After core-electron excitation at the terminal or central carbon sites [geometries shown in Fig. 1(a)] electronic relaxation populates dication states. The first electron is ejected within 10 fs, while the second ionization step takes place within picoseconds, but before molecular rotation occurs. These states dissociate preferentially into fragment pairs that reflect the conformer, shown in Fig. 1(b). Dissociation pathways (1), (2), and (3) can be monitored separately as the core-excited state is localized at the central or terminal carbon atom.
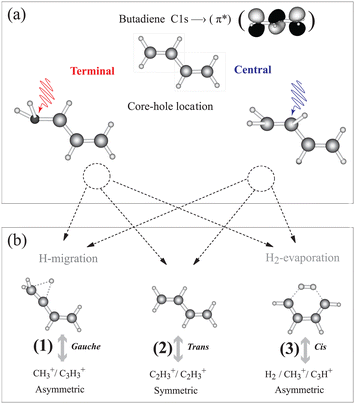 | ||
| Fig. 1 We investigate how core holes localized on the terminal or central carbon atoms in 1,3 trans butadiene influence population of dication states and subsequent fragmentation. (a) Different equilibrium geometries for the terminal and central C 1s-π* excited states are calculated using the “Z + 1” model (see ESI†). (b) Different equilibrium geometries of π−2 dication states and the subsequent dissociation pathways are taken from ref. 21. Measuring the branching ratios of these three dissociation pathways as a function of the photon energy provides a means to probe the effect of core hole localisation on fragmentation. | ||
In the present study we elucidate the connection between symmetry breaking and nuclear dynamics in 1,3 trans butadiene. Site-selective resonant excitation initiates nuclear dynamics at the central and terminal carbon sites and we probe localised bond breaking and hydrogen transfer following C 1s electron excitation. We find clear site-dependent bond dissociation, and trace the origin of these to (a) symmetry breaking at the terminal carbon site (b) out-of-plane bending vibrational modes. The symmetry break motivates the use of the equivalent cores-model, so interpretation of the measured spectra is supported by calculations utilizing the Z + 1 approximation. The equivalent-cores calculation places the core hole at the terminal and central sites with the LUMO occupied.
2 Methods
The measurements were carried out at the soft-X ray beamline I411 at the MAX IV-Laboratory in Lund, Sweden.24,25 A multi-ion coincidence three-dimensional momentum imaging spectrometer was used to perform both ion yield and coincidence measurements.21,26 Synchrotron radiation intersected an effusive gas jet of 1,3 trans butadiene in the center of the spectrometer. Emitted electrons and ions were extracted from the source region with a strong electrical field (∼400 V cm−1) and guided towards position-sensitive detectors. The electrons start the acquisition timing system and all ions are collected in coincidence within an acquisition time window of 10 μs. Three different isotopic sample gases were used. 1,3 trans butadiene was purchased from Air Liquide and the two deuterated isotopes were obtained from Cambridge Isotope Laboratories Inc. (98%), namely C4D6 and C4H2D4. The background pressure in the experimental chamber was maintained at about 10−6 mbar during measurement. The isotopic species were measured separately, and no effects of contamination were visible. We also performed ab initio quantum chemical calculations using the MOLCAS package.27 To infer the dynamics of the resonantly excited core-hole states, we investigated the geometry these states using the (Z + 1) model.16 More information about calculations and data analysis can be found in the ESI,† SM.3 Results and discussion
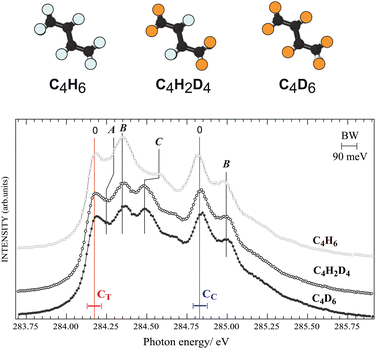
First we investigate nuclear motion in the core-excited states by comparing total ion yield (TIY) spectra of C4H6, C4D6, and C4H2D4 in the region of the C 1s−1π*1 resonance features peaks [see Fig. 2]. The adiabatic excitation energy, labelled as 0, is found to be 284.17(±0.05) eV for the terminal carbon and 284.83(±0.05) eV for the central carbon. Butadiene belongs to the C2h symmetry group, so the C 1s orbitals are of ag and bu symmetries, and features arising from two different unoccupied valence states were identified by de Brito28 in the absorption spectrum. The features in the ion-yield spectrum in Fig. 2 arise from the C 1s-π* (au) transitions for the two chemically-shifted C 1s electrons. Excitations from CC and CT to the π* (bg) state lie at 287.8 and 288.5 eV (not shown). Fine structure is due to vibrational excitations associated with the 1s−1π*1 electronic transition, labelled as A, B, and C. Substitution of hydrogen atoms by deuterium allows us to unambiguously distinguish vibrational excitations involving hydrogen from those of the C–C modes.Feature C, and to a lesser extent feature A, shifts towards lower energy in both deuterated samples, while the energy of feature B for all species is unchanged, in partial agreement with the analysis of de Miranda et al.29 Features A and C are assigned to the excitation of C–H group motions, and feature B is assigned to excitation of C–C stretching vibrations. We can compare to ethylene,30 whose vibrational fine structure resembles structures associated with the butadiene CT 1s core electron. By analogy feature A is associated with a C–H out-of-plane bending (or twisting31) mode, with 100–120 meV vibrational energy, and feature C is related to a C–H stretching mode, with 375–385 meV vibrational energy. The spectra of C4H6, C4D6, and C4H2D4 show no difference in vibrational excitation at the CC 1s−1π*1 transition, suggesting that there is no C–H vibration associated with the CC 1s to π* resonance. This is in line with the interpretation by Sodhi and Brion in their EELS study,32 while de Miranda attributed all vibrations to C–C and C–H stretch vibrational modes.29
In order to support this observation, we calculated the vibrational frequencies of the core-excited states within the “Z + 1” model (see SM, ESI†). As in other alkenes,30 the bonding/antibonding character of the activated π-type orbitals primarily determines the out-of-plane motion around the carbon atoms. Note that the symmetries of the two core-excited states are different, thus dipole allowed excitation is to different valence orbitals. The terminal carbon excitation is to the antibonding π orbital: C 1s (ag)-π*(au) and the central carbon C 1s (bu)-π*(bg) fills the bonding π* orbital. We find that the frequency of transition between trans to gauche conformations increases upon excitation to the π* state.
Although the “Z + 1” model suggests that nuclear relaxation in both the terminal and central core-excited states occurs through the trans–gauche conformation, only the vibrational features associated with the excitation of the terminal carbon exhibit enhancement of the gauche conformation. This does not exclude a trans–gauche conformation in the central carbon excitation, but it must take place on a longer time scale.
In the following we introduce three dication dissociation pathways, connected to gauche, trans and cis conformations.21 They are shown schematically in Fig. 1 for normal butadiene, and the pathways for the fully deuterated butadiene are
1. C4D2+6 → C3D+3 + CD+3 (asymmetric C–C dissociation after deuterium migration)
2. C4D2+6 → C2D+3 + C2D+3 (symmetric C–C dissociation)
3. C4D2+6 → C3D+ + CD+3 + 2D/D2 (asymmetric C–C dissociation after double deuterium evaporation and deuterium migration)
The ion–ion correlation intensity map for the fully deuterated butadiene measured after the terminal C 1s-π* excitation is shown in Fig. 3(a). Asymmetric C–C dissociation (dissociation of a terminal C–C bond) is shown in the upper panel, and symmetric C–C dissociation (central carbon bond dissociation) are shown in the lower panel.
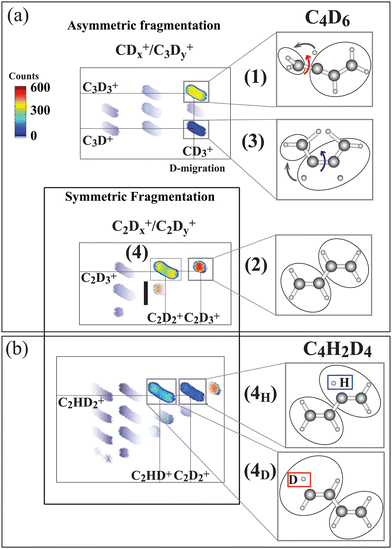 | ||
| Fig. 3 Ion–ion correlation maps measured at 284.17 eV photon energy (terminal carbon excitation) for C4D6 and C4H2D4. In the latter molecule the hydrogen atoms are bonded to central carbons. (a) Asymmetric fragmentation processes, where the carbon bond at the terminal carbon site is broken, and symmetric fragmentation processes, where the central carbon bond is broken, are sketched. In the upper part pathways (1) and (3) are identified as being initiated by C4D2+6 symmetry breaking, as sketched in Fig. 1. Pathways (2) and (4) arise from symmetric fragmentation of C4D2+6. In (b) pathway (4) separates into two (4H) and (4D) pathways for the C4H2D2+6 isotopic species depending upon whether the evaporated hydrogen originates at the terminal or the central carbon site. The hydrogen atoms are initially bonded to the central atoms and the deuterium atoms are bonded to the terminal carbon atoms. Thus 4H indicates evaporation from the central site, and 4D from the terminal carbon. The intensity color scale is shown in the figure. The measured ionic species are shown in the panels to the right. | ||
Furthermore, we include a pathway with C–D bond breaking which leads to the evaporation of a neutral deuterium:
4. C4D2+6 → C2D+3 + C2D+2 + D (symmetric C–C dissociation after deuterium evaporation)
As can be inferred from the momentum analysis (included in SM, ESI†), hydrogen evaporation takes place prior to the symmetric C–C dissociation. Note that this reaction further separates into two mass-distinguished pathways, (4H) and (4D), for the case of the partly deuterated isotope C4H2D4. The (4H) and (4D) pathways are shown in the corresponding correlation map in Fig. 3(b). This isotope has deuterium atoms bonded to CT and hydrogen atoms bonded to CC, allowing us to identify the site of evaporation before the symmetric C–C dissociation.21 In pathway (4D) evaporation from the terminal carbon site is followed by symmetric C–C dissociation in the C2HD2+/C2HD+ ion pair, while in pathway (4H), evaporation from the terminal carbon site is followed by symmetric C–C dissociation creating the C2HD2+/C2D2+ ion pair.
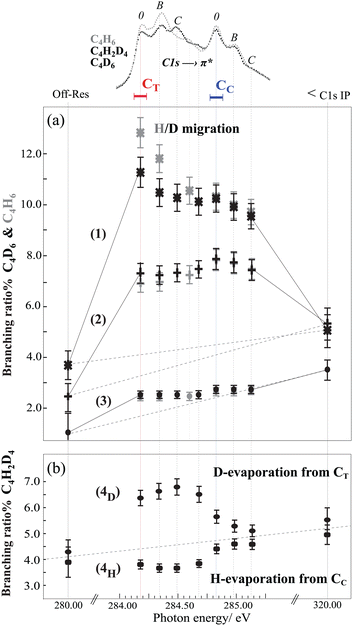
Now we focus on the influence of the core-excited state on the branching ratios for dissociation pathways (1), (2), and (3) for resonant transitions, the off-resonant transition at 280 eV and C 1s ionization at 320 eV photon energies (see Fig. 4(a)). For both samples, C4H6 and C4D6, dissociation pathways (1) and (2) are significantly enhanced for C 1s-π* excitation with respect to the thermodynamic dissociation rate (off-resonance ionization), and the branching ratios are affected by both vibrational excitation and by the site of the core hole. Dissociation pathway (3) is slightly enhanced after excitation of the terminal carbon site, but the branching ratio is essentially flat through the resonance region, and increases slightly upon C 1s ionization at 320 eV with respect to the off-resonance at 280 eV, following the behavior observed for the other pathways.
In an earlier experimental theoretical study we have shown that vacancies in dication states lead to conformational changes, and these states act as gateways to the gauche, trans or cis geometries connected to the dissociation pathways (1), (2) or (3).21 The clear enhancement of the branching ratio observed here points to the connection between the core-hole state and the final-state geometries. From the electronic relaxation point of view, it suggests that resonant excitation to the 2au(π*) enhances the contribution of the 1bg orbital during the electronic relaxation regardless of the site of the initial core hole. Indeed, ionization of the 1bg orbital is involved in both dissociation pathways (1) and (2).21 Furthermore, due to the opposite π-bonding character of the 2au (LUMO) and 1bg (HOMO), the excitation of a core electron to the 2au orbital decreases the binding energy of the 1bg, and could favour certain autoionization channels.
In order to comprehend the underlying connection between the core-hole state and final-state geometries, as evidenced by the site-selective behaviour for the terminal and the central carbon atoms in pathways (1) and (2), the nuclear wave-packet propagation during core hole lifetime (ΔEΔT ≃ h) should be studied. Here, the interplay between the scattering duration time and the characteristic time of wave-packet propagation within the bound core-excited state33 from the Franck-Condon (FC) region to the gauche equilibrium geometry (predicted by the “Z + 1” model) is reflected in the branching ratios of the gauche (1) to the trans (2) pathway. In the case of terminal carbon excitation, the first resonance peak [corresponding to the adiabatic transition and excitation to the twisting/bending vibrational modes (feature 0)] the gauche pathway is at a maximum and the trans pathway is at a minimum. The ratio decreases upon excitation to the C–C and C–H stretching modes (features B and C), indicating less time for the wave-packet to propagate towards the equilibrium geometry, with the result that Auger decay occurs to a greater extent within the FC region.
In order to confirm the importance of the C–H out-of-plane bending motion, we also present the branching ratios in the C4H6 sample in Fig. 4(a). As hydrogen atom motion is faster than deuterium atom motion, we see that the branching ratio for H-migration is higher than D-migration for the terminal carbon 1s excitation. This result constitutes a direct proof of the crucial role of the scattering duration time on H-atom motions (twisting/bending) in core-excited states evolving toward the gauche equilibrium geometry. For the case of central carbon excitation no such effect is visible. This can be understood via slow nuclear motion upon central carbon excitation with respect to the scattering duration time, where Auger decay occurs within the FC region.
Finally to gain further insight into the role of the initial core hole localisation on hydrogen evaporation dynamics, we study the symmetric C–C bond dissociation (pathway 4) as a function of the photon energy. In this pathway, the neutral evaporation takes place prior to dissociation, and the evaporation site can be identified by utilizing the partly deuterated isotope C4H2D4. The branching ratios for evaporation either from the central (4H) or terminal (4D) carbon site reveal clear differences between the intensities of the two pathways, see Fig. 4(b). In pathway (4D) evaporation from the terminal carbon site is enhanced when the core hole is on the terminal carbon, while for CC excitation there is almost no 'memory' of the resonance. In pathway (4H) evaporation from the central carbon site decreases at the terminal core hole, and increases nearly to the off-resonance value at the resonance energy for the central carbon excitation. This indicates that core hole localisation on the central carbon seems to preferentially undergo statistical evaporation, while core hole localisation on the terminal carbon strongly controls the site of evaporation.
4 Conclusions
In summary, inner-shell spectroscopy in butadiene, a prototype for polyene molecules, reveals site-selective dissociation processes in ion-pair fragments after terminal carbon excitation. We find that ultrafast hydrogen evaporation followed by symmetric C–C dissociation is a direct result of the localization of the core hole at the terminal carbon site. We demonstrate that out-of-plane symmetry breaking around the terminal carbon and nuclear wave packet dynamics of the core hole state are mechanisms enhancing the ultrafast hydrogen migration and asymmetric C–C dissociation.The bonding/anti-bonding character of the occupied π* orbital in core excitation primarily determines the out-of-plane nuclear motion in the π-conjugated system. Since in polyene molecules this character alternates between successive carbon atoms, inner-shell spectroscopy studies on larger polyenes will shed light on other factors that can affect symmetry breaking, site-selective or statistical dissociation dynamics.
Author contributions
SO and SLS were responsible for the conception and design of the project, SO carried out analysis and wrote all drafts of the paper. SLS, MG, NW, EPM SO and JL were involved in the data collection, and BO, AS, MG, NW, JHDE and JL, were involved in discussion on data analysis and interpretation with SO and SLS.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the MAX-laboratory staff for support during the measurements, especially Maxim Tchaplyguine. We gratefully acknowledge the support from the Knut and Alice Wallenberg Foundation and the Swedish Research Council (VR).References
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. Robinson, T. J. Lane, D. Ratner, K. Saita, T. Northey, B. Stankus, V. Cofer-Shabica, J. Hastings and P. M. Weber, Faraday Discuss., 2014, 171, 81–91 RSC.
- Y. Dou, B. R. Torralva and R. E. Allen, Chem. Phys. Lett., 2004, 392, 352–357 CrossRef CAS.
- M. N. R. Ashfold, M. Bain, C. S. Hansen, R. A. Ingle, T. N. V. Karsili, B. Marchetti and D. Murdock, J. Phys. Chem. Lett., 2017, 8, 3440–3451 CrossRef CAS PubMed.
- X. J. Liu, G. Prümper, E. Kukk, R. Sankari, M. Hoshino, C. Makochekanwa, M. Kitajima, H. Tanaka, H. Yoshida, Y. Tamenori and K. Ueda, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 042704 CrossRef.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. D. Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martin and M. Nisoli, Science, 2014, 346, 336 CrossRef CAS PubMed.
- J.-C. Liu, C. Nicolas, Y.-P. Sun, R. Flammini, P. O'Keeffe, L. Avaldi, P. Morin, V. Kimberg, N. Kosugi, F. Gel'mukhanov and C. Miron, J. Phys. Chem. B, 2011, 115, 5103–5112 CrossRef CAS PubMed.
- P. Salén, M. Kamińska, R. J. Squibb, R. Richter, M. Alagia, S. Stranges, P. van der Meulen, J. H. D. Eland, R. Feifel and V. Zhaunerchyk, Phys. Chem. Chem. Phys., 2014, 16, 15231 RSC.
- W. Eberhardt, J. Stöhr, J. Feldhaus, E. W. Plummer and F. Sette, Phys. Rev. Lett., 1983, 51, 2370 CrossRef CAS.
- W. Eberhardt, T. K. Sham, R. Carr, S. Krummacher, M. Strongin, S. L. Weng and D. Wesner, Phys. Rev. Lett., 1983, 50, 1038 CrossRef CAS.
- J. Laksman, K. Kooser, H. Levola, E. Itälä, D. T. Ha, E. Rachlew and E. Kukk, J. Phys. Chem. B, 2014, 118, 11688 CrossRef CAS PubMed.
- K. Kooser, D. T. Ha, S. Granroth, E. Itälä, L. Partanen, E. Nõmmiste, H. Aksela and E. Kukk, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 235103 CrossRef.
- L. Inhester, B. Oostenrijk, M. Patanen, E. Kokkonen, S. H. Southworth, C. Bostedt, O. Travnikova, T. Marchenko, S.-K. Son, R. Santra, M. Simon, L. Young and S. L. Sorensen, J. Phys. Chem. Lett., 2018, 9, 1156–1163 CrossRef CAS.
- T. Kierspel, C. Bomme, M. Di Fraia, J. Wiese, D. Anielski, S. Bari, R. Boll, B. Erk, J. S. Kienitz, N. L. M. Müller, D. Rolles, J. Viefhaus, S. Trippel and J. Küpper, Phys. Chem. Chem. Phys., 2018, 20, 20205–20216 RSC.
- L. Cederbaum and J. Zobeley, Chem. Phys. Lett., 1999, 307, 205 CrossRef CAS.
- J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. Mackay, R. H. Friend, P. L. Burns and A. B. Holmes, Nature, 1990, 347, 539 CrossRef CAS.
- N. V. Kryzhevoi, N. V. Dobrodey and L. S. Cederbaum, J. Chem. Phys., 2003, 118, 2081 CrossRef CAS.
- F. X. Gadea, S. Mathieu and L. S. Cederbaum, THEOCHEM, 1997, 401, 15 CrossRef CAS.
- C. Liegener and H. Ågren, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 789–798 CrossRef CAS PubMed.
- M. S. Deleuze and S. Knippenberg, J. Chem. Phys., 2006, 125, 104309 CrossRef CAS PubMed.
- S. L. Sorensen, S. J. Osborne, A. Ausmees, A. Kikas, N. Correia, S. Svensson, A. N. de Brito, P. Persson and S. Lunell, J. Chem. Phys., 1996, 105, 10719 CrossRef CAS.
- S. Oghbaiee, M. Gisselbrecht, J. Laksman, E. P. Månsson, A. Sankari and S. L. Sorensen, J. Chem. Phys., 2015, 143, 114309 CrossRef PubMed.
- G. Nicolas and F. X. Gadea, J. Chem. Phys., 1999, 111, 10537–10549 CrossRef CAS.
- J. Breidbach and L. S. Cederbaum, J. Chem. Phys., 2003, 118, 3983 CrossRef CAS.
- M. Bässler, A. Ausmees, M. Jurvansuu, R. Feifel, J.-O. Forsell, P. de Tarso Fonseca, A. Kivimäki, S. Sundin, S. Sorensen, R. Nyholm, O. Björneholm, S. Aksela and S. Svensson, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 469, 382 CrossRef.
- M. Bassler, J. O. Forsell, O. Björneholm, R. Feifel, M. Jurvansuu, S. Aksela, S. Sundin, S. L. Sorensen, R. Nyholm, A. Ausmees and S. Svensson, J. Electron Spectrosc. Relat. Phenom., 1999, 101–103, 953 CrossRef CAS.
- J. Laksman, D. Céolin, E. P. Månsson, S. L. Sorensen and M. Gisselbrecht, Rev. Sci. Instrum., 2013, 84, 123113 CrossRef CAS PubMed.
- F. Aquilante, L. D. Vico, N. Ferra, G. Ghigo, P. Malmqvist, P. Neogrady, T. B. Pederse, M. Pitoniak, M. Reiher, B. Roos, L. S. Andras, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
- A. Naves de Brito, S. Svensson, N. Correia, M. P. Keane, H. Å gren, O. P. Sairanen, A. Kivimäki and S. Aksela, J. Electron Spectrosc. Relat. Phenom., 1992, 59, 293 CrossRef CAS.
- M. P. de Miranda, J. A. Beswick, P. Parent, C. Laffon, G. Tourillon, A. Cassuto, G. Nicolas and F. X. Gadea, J. Chem. Phys., 1994, 101, 7 CrossRef.
- Y. Ma, F. Sette, G. Meigs, S. Modesti and C. T. Chen, Phys. Rev. Lett., 1989, 63, 2044 CrossRef CAS PubMed.
- F. X. Gadea, H. Köppel, J. Schirmer, L. S. Cederbaum, K. J. Randall, A. M. Bradshaw, Y. Ma, F. Sette and C. T. Chen, Phys. Rev. Lett., 1991, 66, 883 CrossRef CAS PubMed.
- R. N. Sodhi and C. Brion, J. Electron Spectrosc. Relat. Phenom., 1985, 37, 1–21 CrossRef CAS.
- F. Gel'mukhanov, P. Sałek, T. Privalov and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 380–389 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: A PDF file contains supporting material regarding calculations and interpretation of momentum images. Supporting calculation: Ab initio quantum calculation of nuclear dynamics induced by terminal and central C 1s−1π*1 excitation of butadiene using the “Z+1” model. See DOI: https://doi.org/10.1039/d2cp03411e |
| ‡ Present address: Center for Free-Electron Laser Science CFEL, Deutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany. |
| § Present address: European XFEL GmbH, Schenefeld, Germany. |
| This journal is © the Owner Societies 2022 |