Time-dependent density functional theory calculations of electronic friction in non-homogeneous media
Natalia E.
Koval
 *abc,
Daniel
Sánchez-Portal
ab,
Andrei G.
Borisov
d and
Ricardo
Díez Muiño
*ab
*abc,
Daniel
Sánchez-Portal
ab,
Andrei G.
Borisov
d and
Ricardo
Díez Muiño
*ab
aCentro de Física de Materiales (CFM) CSIC-UPV/EHU, Paseo Manuel de Lardizabal 5, E-20018 San Sebastián, Spain. E-mail: natalia.koval.lipina@gmail.com; rdm@ehu.eus
bDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, E-20018 San Sebastián, Spain
cCIC Nanogune BRTA, Tolosa Hiribidea 76, E-20018 San Sebastián, Spain
dInstitut des Sciences Moléculaires d'Orsay (ISMO), UMR 8214, CNRS-Université Paris-Saclay, Bât. 520, F-91405 Orsay CEDEX, France
First published on 12th August 2022
Abstract
The excitation of low-energy electron–hole pairs is one of the most relevant processes in the gas–surface interaction. An efficient tool to account for these excitations in simulations of atomic and molecular dynamics at surfaces is the so-called local density friction approximation (LDFA). The LDFA is based on a strong approximation that simplifies the dynamics of the electronic system: a local friction coefficient is defined using the value of the electronic density for the unperturbed system at each point of the dynamics. In this work, we apply real-time time-dependent density functional theory to the problem of the electronic friction of a negative point charge colliding with spherical jellium metal clusters. Our non-adiabatic, parameter-free results provide a benchmark for the widely used LDFA approximation and allow the discussion of various processes relevant to the electronic response of the system in the presence of the projectile.
1 Introduction
Surfaces can be effective and efficient agents to control, promote, and accelerate chemical reactions.1 The main difficulty in making good use of this attractive quality is the complexity of the gas/solid interface. There are many variables that determine the system's evolution towards its final state, including temperature, gas composition, gas pressure, surface structure, and electronic properties of all species present at the interface. From a theoretical point of view, it is therefore essential to identify what are the key elements that must be accurately described to capture the general features of the problem, as well as those that can be introduced in an approximate manner.For atoms and small molecules of thermal and hyperthermal energies interacting with metallic surfaces, calculations of the potential energy surface based on density functional theory (DFT) are powerful tools to reproduce and understand the process dynamics.2–5 The numerical calculation of interaction energies must be extremely accurate to predict the dynamical paths and chemical outcomes. Such calculations are often performed under the adiabatic Born–Oppenheimer (BO) approximation, assuming that the motion of the nuclei is sufficiently slow to avoid any electronic excitation in the system. The BO approximation provides, in many cases, an excellent description of elementary reactive and non-reactive processes at surfaces.6–8
At metal surfaces, however, the motion of the incoming atoms and molecules and the subsequent coupling with the surface do in fact create electronic excitations.9–14 In metals, there is no energy threshold for these excitations to arise. Otherwise said, there is no minimum kinetic energy of the projectile below which it does not create electronic excitations in the target.15 Ample experimental evidence of the interplay between electronic excitations and nuclear motion can be found in the vibrational linewidths of adsorbates,16–19 in the detection of chemicurrents during atomic and molecular adsorption,20,21 in the scattering of vibrationally excited molecules at surfaces,22,23 or in the photodesorption of molecules,24–27 to name a few cases.
Aside from the electronic excitations, another energy dissipation channel that is frequently neglected is the excitation of phonons at the surface. There is a broad spectrum of theoretical models that have been successfully used to describe the energy exchange between incident atoms and molecules and the surface lattice: semiclassical approximations with atomic interaction potentials,28 stochastic descriptions based on the Generalized Langevin Oscillation model,29 or ab initio molecular dynamics simulations30 are among them.
The relevance of the energy dissipation channels in the description of gas/surface dynamics, as well as the relative importance of each one of the two mentioned mechanisms (electronic excitations versus phonon excitations), very much depend on the particular system under study. For this reason, it is crucial to develop theoretical tools that can reasonably describe the effect of electronic and phononic excitations in the system dynamics without losing the accuracy provided by an ab initio description of the interaction between incident species and surface.
Fortunately, there are many cases in which the non-adiabatic coupling is weak and the most important features of the dynamics can be described within an accurate BO approximation. In the particular case of the excitation of electron–hole (e–h) pairs, it is often the case it can be treated as a small correction. However, even if the coupling is weak, the overall effect of the electronic excitations can be significant for processes that extend over long times, such as the diffusion of H atoms on metal surfaces.30
Several theoretical schemes have been proposed to estimate the effect of e–h pair excitations in molecular dynamics calculations without losing the accuracy offered by DFT potential energy surfaces.31–33 The most successful and widely used is probably the local density friction approximation (LDFA).10,34 The LDFA is based on the linear proportionality between the velocity of an atom moving in a homogeneous electronic system and the dissipative force against its motion, a result which is exact in the zero velocity limit.35 This dissipative force (or friction force) thus depends on a friction coefficient η. In the application of the LDFA to gas/surface problems, η is approximated at each point of any atom trajectory as the friction coefficient of the very same atom moving inside a homogeneous electron gas with an electronic density equal to that of the unperturbed system at this point. Non-local effects due to the inhomogeneity of the electronic density at the surface, as well as the actual dynamics of the system, are therefore neglected.
Because of its success in reproducing experimental outcomes, the LDFA has become a widespread choice to include non-adiabatic effects in molecular dynamics calculations.34,36–40 However, and to the best of our knowledge, there is no direct comparison between the LDFA predictions and results of a more refined theoretical approach, non-perturbative with respect to the velocity. Such comparison is the main purpose of the current article, in which time-dependent density functional theory (TDDFT)41 is used as a touchstone of the LDFA. The use of TDDFT entails a non-perturbative, non-adiabatic description of the interaction between an incoming particle and a metal substrate. The key approximation in TDDFT is that of the utilized exchange–correlation functional. Besides this approximation, in TDDFT simulations the dynamics of all the electrons in the system is treated explicitly. TDDFT is thus an accurate standard that allows us to access various dynamic effects relevant to the gas–surface interaction and discuss the performance of the local description of the projectile energy loss to electronic excitations.42,43
The purpose of this work is, therefore, to advance in some methodological aspects that we consider essential in the theoretical description of the interaction between gas phase atoms and molecules and surfaces. The relevance of electronic excitations in the dissipation of kinetic energy for thermal and hyperthermal incoming species remains under discussion. The LDFA has been proposed as a relatively simple model that can be efficiently implemented in sophisticated molecular dynamics calculations. Our goal in the current study is to show that, despite the strong approximations involved, the LDFA is able to provide a good estimate of the friction force suffered by an atomic particle reaching a metallic surface in this energy regime. Our procedure to do so is a benchmarking in which we make a detailed comparison of LDFA results with TDDFT results for the same system.
Because our goal is purely methodological and in order to distill the essential points of the problem, we focus into a model system: the interaction of a bare negative charge with a metallic jellium cluster. The negative charge can be visualized as an antiproton. With this model system, we ensure that there is no capture or loss of electrons between the bare incident charge and the target. We also warrant that there are no different charge states of the incident particle involved in the calculation.44 Both effects would make much more difficult an exact comparison. Regarding the use of the jellium model, in this energy regime, real-time TDDFT with an atomistic description of the target is computationally very demanding,45,46 needs additional numerical approximations, and prevents a systematic analysis. We therefore simplify the description of the metallic target using the jellium model.
The article is organized as follows: Section 2 describes the details of the TDDFT calculations performed for this work and provides some references for the LDFA calculations. The TDDFT results and the LDFA results are introduced and discussed in Section 3. The summary and conclusions of our work can be found in Section 4.
Atomic units are used throughout the paper unless otherwise stated.
2 Methodology
In order to keep the numerical load within reach we use a simple model for our metallic target and projectile. We thus apply real-time TDDFT to calculate the non-adiabatic, i.e., the force due to electron excitations) force felt by a negative point charge, an antiproton (![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ), traversing spherical free-electron metal (jellium) clusters. The use of an antiproton prevents possible charge transfer from the target to the projectile. The jellium model allows addressing clusters of sufficiently large size so that the friction force inside the cluster is representative of that of the infinite electron gas, an indication that the results are not dominated by finite-size effects. The jellium model combined with TDDFT has been successfully applied to the problem of the electronic excitations created by an antiproton and a proton in metals as the comparison to experiments has shown.47
), traversing spherical free-electron metal (jellium) clusters. The use of an antiproton prevents possible charge transfer from the target to the projectile. The jellium model allows addressing clusters of sufficiently large size so that the friction force inside the cluster is representative of that of the infinite electron gas, an indication that the results are not dominated by finite-size effects. The jellium model combined with TDDFT has been successfully applied to the problem of the electronic excitations created by an antiproton and a proton in metals as the comparison to experiments has shown.47
We consider that the antiproton is a classical particle moving with constant velocity towards the cluster surface. Since the mass of an antiproton is large compared to that of the electrons, we can assume that its velocity does not change while crossing the cluster. The force acting on the moving projectile inside the cluster is calculated at each time step, however is disregarded in the propagation of the antiproton, i.e., the antiproton velocity is not updated due to the force. The constant velocity approximation allows for a clear separation of electronic effects and serves to study the effect of the projectile velocity on the friction coefficient. Actually, our model is also useful to test the conditions under which the non-adiabatic force can be considered a dissipative friction force, i.e., a dissipative force that depends linearly on the projectile velocity.
Within the jellium model, the ions at the metal cluster sites are represented by the uniform positive background with the density 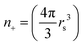 . We use the Wigner–Seitz radius (one electron radius in the electron gas) rs = 448 corresponding to sodium (Na) metal. In order to assess finite-size effects on the electronic friction, closed-shell clusters comprising 106 valence electrons (cluster radius Rcl = 18.93 a.u.) and 1074 valence electrons (Rcl = 40.96 a.u.) are considered in our work. In what follows, we denote the targets as Na106 and Na1074. Prior to the TDDFT runs, the ground state electronic density of the clusters is obtained by performing static DFT49 calculations within the Kohn–Sham (KS) scheme using the local density approximation (LDA) for exchange–correlation potential.50 The response of the electronic density to the
. We use the Wigner–Seitz radius (one electron radius in the electron gas) rs = 448 corresponding to sodium (Na) metal. In order to assess finite-size effects on the electronic friction, closed-shell clusters comprising 106 valence electrons (cluster radius Rcl = 18.93 a.u.) and 1074 valence electrons (Rcl = 40.96 a.u.) are considered in our work. In what follows, we denote the targets as Na106 and Na1074. Prior to the TDDFT runs, the ground state electronic density of the clusters is obtained by performing static DFT49 calculations within the Kohn–Sham (KS) scheme using the local density approximation (LDA) for exchange–correlation potential.50 The response of the electronic density to the ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) motion is obtained by solving time-dependent KS equations, i.e., by propagating the KS orbitals of the cluster in real-time. The time-step of the propagation is 0.05 a.u. (1.2 attoseconds) and 0.2 a.u. of time (4.8 attoseconds) for a smaller cluster Na106 and a larger cluster Na1074, respectively. We use the adiabatic local density approximation of the TDDFT51 with the exchange–correlation functional of Gunnarsson and Lundqvist.52 The incident point charge moves with a constant velocity ν following a straight-line trajectory crossing the spherical cluster through its geometrical center. The initial position of the
motion is obtained by solving time-dependent KS equations, i.e., by propagating the KS orbitals of the cluster in real-time. The time-step of the propagation is 0.05 a.u. (1.2 attoseconds) and 0.2 a.u. of time (4.8 attoseconds) for a smaller cluster Na106 and a larger cluster Na1074, respectively. We use the adiabatic local density approximation of the TDDFT51 with the exchange–correlation functional of Gunnarsson and Lundqvist.52 The incident point charge moves with a constant velocity ν following a straight-line trajectory crossing the spherical cluster through its geometrical center. The initial position of the ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) is set far enough from the cluster surface so that the interaction with the cluster is negligible. The time-dependent electron density obtained by solving the time-dependent KS equations is used to compute the total energy of the system Etot[z
is set far enough from the cluster surface so that the interaction with the cluster is negligible. The time-dependent electron density obtained by solving the time-dependent KS equations is used to compute the total energy of the system Etot[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)] and the total force Ftot[z
(t)] and the total force Ftot[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)] acting on the projectile at each time step of the propagation. Details of the numerical procedure can be found in our previous publications.44,47,53,54
(t)] acting on the projectile at each time step of the propagation. Details of the numerical procedure can be found in our previous publications.44,47,53,54
The total force Ftot[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)] acting on the moving antiproton can be separated into two contributions: adiabatic, Fa[z
(t)] acting on the moving antiproton can be separated into two contributions: adiabatic, Fa[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)] and non-adiabatic, Fna[z
(t)] and non-adiabatic, Fna[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)]. The adiabatic force corresponds to the force acting on the antiproton when the particle is located at the position z
(t)]. The adiabatic force corresponds to the force acting on the antiproton when the particle is located at the position z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t) and the whole system is in its electronic ground state. Here, we are interested in the non-adiabatic component of the force, Fna[z
(t) and the whole system is in its electronic ground state. Here, we are interested in the non-adiabatic component of the force, Fna[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)], that we define according to eqn (2) below as the difference between the actual force experienced by the antiproton in a given instant of time and the adiabatic force felt by the antiproton at that position. In the case of an infinite homogeneous electron gas and for velocities much lower than the Fermi velocity of the electrons νF (for Na, νF = 0.48 a.u.), the non-adiabatic component of the force can be described as a purely dissipative friction force (the so-called stopping power).35,55 A linear dependence on velocity is thus expected, and the friction coefficient is defined as the ratio between the dissipative force and the velocity. For a non-homogeneous finite system, such as the metallic clusters that we are considering here, we can formally define a similar “friction coefficient” η that would vary in time:
(t)], that we define according to eqn (2) below as the difference between the actual force experienced by the antiproton in a given instant of time and the adiabatic force felt by the antiproton at that position. In the case of an infinite homogeneous electron gas and for velocities much lower than the Fermi velocity of the electrons νF (for Na, νF = 0.48 a.u.), the non-adiabatic component of the force can be described as a purely dissipative friction force (the so-called stopping power).35,55 A linear dependence on velocity is thus expected, and the friction coefficient is defined as the ratio between the dissipative force and the velocity. For a non-homogeneous finite system, such as the metallic clusters that we are considering here, we can formally define a similar “friction coefficient” η that would vary in time:
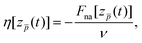 | (1) |
Fna[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)] = Ftot[z (t)] = Ftot[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)] − Fa[z (t)] − Fa[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (t)]. (t)]. | (2) |
The adiabatic force only depends on the position of the projectile and, as far as the process in which the particle appears at that position is sufficiently slow, it should not depend on the precise history of the system. This is the so-called adiabatic switching condition, under which the antiproton + cluster system remains in its ground electronic state for each instantaneous configuration. In our case, to obtain the adiabatic force, we start the TDDFT calculation with the metal cluster in its ground and slowly “switch on” the −1 charge at a given ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) position. The charge variation is set using a sin function:
position. The charge variation is set using a sin function:
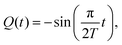 | (3) |
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) . In total, 70 adiabatic points for Na106 and 98 points for Na1074 are calculated. The adiabatic force and energy at every point are subsequently obtained by numerical interpolation.
. In total, 70 adiabatic points for Na106 and 98 points for Na1074 are calculated. The adiabatic force and energy at every point are subsequently obtained by numerical interpolation.
Concerning the LDFA results, the calculations are performed following the lines described in ref. 10. In the LDFA, the friction coefficient of a gas-phase atom moving nearby a surface is a function of the surface electron density at the position of the atom. At each point of the trajectory, the friction coefficient is obtained as the friction coefficient that this atom would have when moving inside a homogeneous electron gas with the same electronic density.10
3 Results and discussion
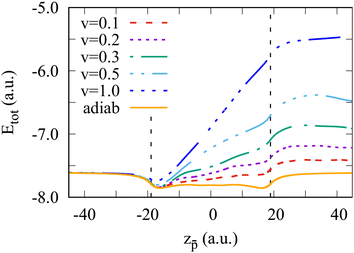
Fig. 1 shows the total energy of the Na106 cluster calculated with TDDFT as a function of the position of a moving antiproton. As indicated in the figure, we consider different antiproton velocities ν ranging from 0.1 to 1 a.u. The moving charge transfers part of its kinetic energy to the excitation of the cluster electrons. This is reflected in the progressive increase of the system's total energy. The effect is velocity-dependent with faster projectiles losing more energy. Note that when the projectile is inside the cluster, the nearly linear increase of the energy as a function of the![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) position reflects a constant dissipative force or stopping power. From energy conservation, the difference between the adiabatic energy and the energy of the cluster at the end of the collision corresponds to the energy loss by the antiproton at a given velocity. Interestingly, in our earlier work,47 we have shown that the energy loss divided by the length of the trajectory inside the cluster (cluster diameter, 2Rcl) provides the velocity-dependent stopping power of the infinite electron gas with the density given by rs = 4. This quantity reproduces the experimental data, and it is nearly independent of the cluster size for the clusters considered here.
position reflects a constant dissipative force or stopping power. From energy conservation, the difference between the adiabatic energy and the energy of the cluster at the end of the collision corresponds to the energy loss by the antiproton at a given velocity. Interestingly, in our earlier work,47 we have shown that the energy loss divided by the length of the trajectory inside the cluster (cluster diameter, 2Rcl) provides the velocity-dependent stopping power of the infinite electron gas with the density given by rs = 4. This quantity reproduces the experimental data, and it is nearly independent of the cluster size for the clusters considered here.
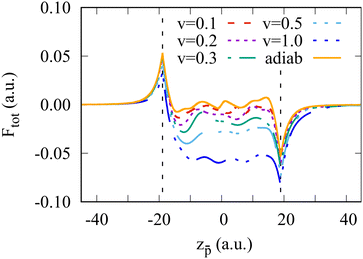
The total force acting on the moving antiproton is presented in Fig. 2 as a function of its position. The singular character of the force at the surface is due to the surface polarization charges and abrupt “switching on” of the positive background charge when the projectile crossing the cluster boundary. Inside the cluster, the force oscillates due to the finite size, i.e., because the electron density is non-homogeneous and the excited electron density waves are reflected by the cluster boundary. A similar behavior of the total energy and force is observed in the larger Na1074 cluster, not shown here.
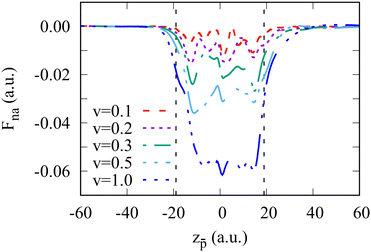
Subtracting the adiabatic force from the total force, we obtain the non-adiabatic force that is shown in Fig. 3 as a function of the antiproton position for several projectile velocities. While Fna oscillates inside the cluster, its mean value is close to the stopping power of the antiproton with a given velocity in the homogeneous electron gas.47 It is interesting to note that the non-adiabatic force is different for the projectile outside the cluster in the in-going or the out-going trajectories. We will return to this issue below.
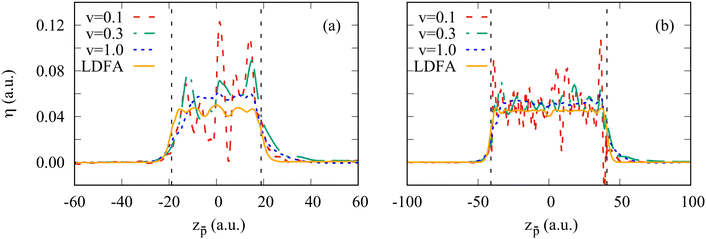
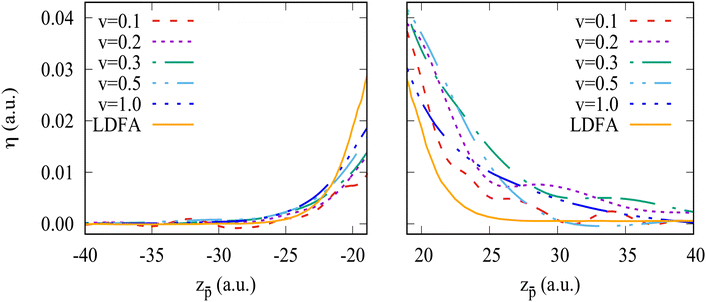
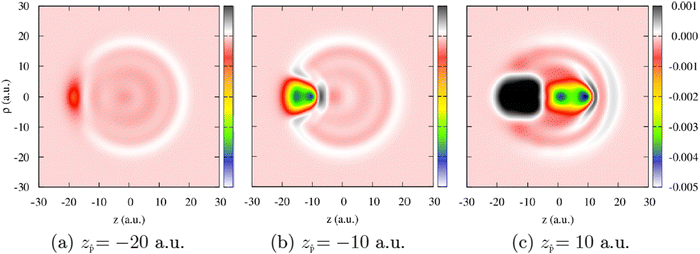
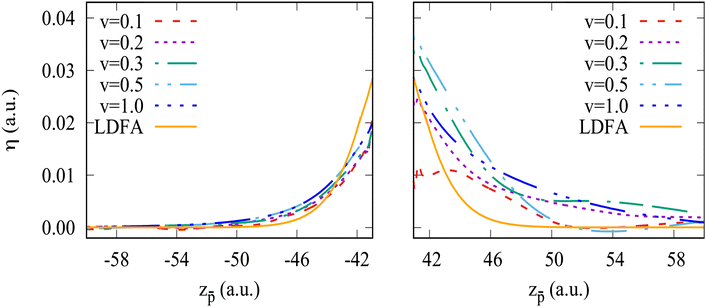
A local friction coefficient calculated from the non-adiabatic force using eqn (1) is shown in Fig. 4 as a function of the antiproton position for two clusters, Na106 (Fig. 4a) and Na1074 (Fig. 4b), and is compared to the LDFA approximation. Inside the cluster, despite the oscillations of the friction coefficient with projectile position, we observe that its mean value is nearly independent of the projectile velocity. Such behavior is consistent with the linear dependence of the stopping power on the projectile velocity within this velocity range47 and reveals the dominant dissipative nature of the non-adiabatic force acting on the projectile inside the cluster. For the larger cluster size, the non-homogeneity of the electron density is smaller (see ground state density profiles of both clusters in Fig. 9 in Appendix A), leading to a better converged mean value of the friction coefficient. Similarly, increasing the cluster size reduces the effect of the reflection of the excited electron density waves from the cluster boundary. In fact, the electrons move away from the antiproton, reflect from the cluster surface, and rebound on the slow antiproton giving rise to the oscillations in the force and thus in the friction coefficient. Noteworthy, this effect strongly reduces for the faster (ν = 1 a.u.) projectile where the η[z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ] dependence is nearly flat. In this situation of the fast antiproton motion, the collision timescale is much shorter, and the antiproton creates a wake behind similar to the one arising in an infinite medium. The effect of velocity can be clearly seen from the induced density plots for fast and slow antiproton motion (see Appendix A, Fig. 10 and 11).
] dependence is nearly flat. In this situation of the fast antiproton motion, the collision timescale is much shorter, and the antiproton creates a wake behind similar to the one arising in an infinite medium. The effect of velocity can be clearly seen from the induced density plots for fast and slow antiproton motion (see Appendix A, Fig. 10 and 11).
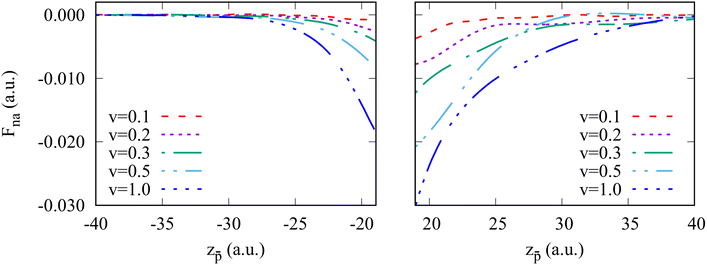
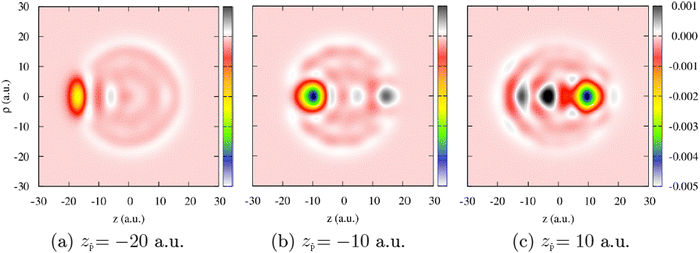
We now turn to the discussion of the asymmetry of the “in” and “out” non-adiabatic force acting on the projectile approaching or leaving the cluster while being outside the cluster. To better visualize this effect, we zoom in on Fig. 5 at the non-adiabatic force at the in-going and out-going trajectory paths. The force is generally larger in the case of the antiproton moving away from the excited cluster for all velocities. To get insights into the observed asymmetry in the non-adiabatic force, we plot the electron density distribution in the Na106 cluster for different positions of the antiproton outside and inside the cluster (Fig. 6). Snapshots correspond to six different projectile positions and velocity ν = 0.3 a.u.
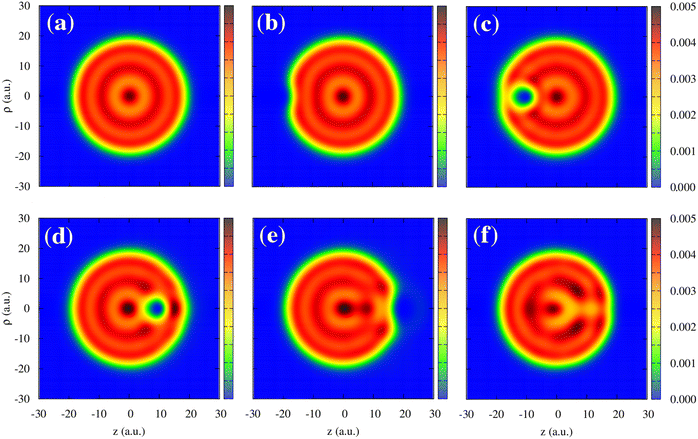 | ||
Fig. 6 Electron density of the Na106 cluster (radius Rcl = 18.93 a.u.) upon collision with antiproton. Results are shown as a function of the cylindrical (z, ρ) coordinates. The projectile moves with the constant velocity ν = 0.3 a.u. along a straight-line trajectory following the symmetry z-axis of the system that passes through the center of the cluster. The snapshots correspond to six different antiproton positions: (a) z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = −30 a.u., (b) z = −30 a.u., (b) z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = −20 a.u., (c) z = −20 a.u., (c) z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = −10 a.u., (d) z = −10 a.u., (d) z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = 10 a.u, (e) z = 10 a.u, (e) z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = 20 a.u., and (f) z = 20 a.u., and (f) z![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = 30 a.u. The color code shows the electron density of the cluster in electrons per (a.u.).3 = 30 a.u. The color code shows the electron density of the cluster in electrons per (a.u.).3 | ||
Before the collision, the cluster features the typical electron density of the small spherical nanoparticle, as can be seen in Fig. 6a. The antiproton polarizes the cluster, which is reflected in the depletion of the electron density in the surface facing the projectile as the electrons in that region are repelled by the antiproton (Fig. 6b). For the moving projectile, the variation of the polarization charge is delayed with respect to the change of the projectile position. Thus the projectile is attracted to the cluster to a lesser extent than in the adiabatic situation. Along with the electronic excitations, because of the scattering at the projectile, this dynamical polarization effect contributes to the non-adiabatic force calculated with TDDFT via subtraction of the adiabatic contribution. Inside the cluster, the screening effect can be observed as a “hole” (i.e., an area of low electronic density) around the projectile (Fig. 6c and d). The screening hole leads to an excess of positive charge once the positive neutralizing background is taken into account and does not adapt instantaneously to the position of the moving antiproton. Therefore, the attraction of the antiproton to the screening hole traveling behind it leads to the stopping force. After the collision (Fig. 6e and 6f), at the out-going trajectory path, the arrival of the delayed screening hole at the surface creates an electron depletion larger than that corresponding to the adiabatic case, leading to an attractive contribution to the non-adiabatic force that slows down the projectile. Thus, while the dominant (stopping) contribution to the non-adiabatic force along the whole trajectory can be understood in terms of the delayed response of the cluster with respect to the adiabatic polarization induced by the projectile at each point in its trajectory, it is interesting to note (Fig. 5) that the effect outside the cluster is larger for out-going than for in-going trajectories. Additionally, one can also state that the projectile excites the plasmon modes of the cluster and dynamically interacts with the associated oscillating charges. In this respect, one can observe the oscillations of the non-adiabatic force shown in Fig. 5. Here, the time scale given by ν−1 has to be compared with the typical plasmon time scale ωDP−1.
A local friction coefficient defined with eqn (1) and calculated on the “in” and “out” trajectory paths from the non-adiabatic force is shown in Fig. 7 and 8 as a function of the antiproton position for the Na106 and Na1074 clusters, respectively. Fig. 7 and 8 zoom the results of Fig. 4a and b at the projectile positions in front of the cluster surface.
 | ||
| Fig. 8 The same as Fig. 7 but for the Na1074 cluster. | ||
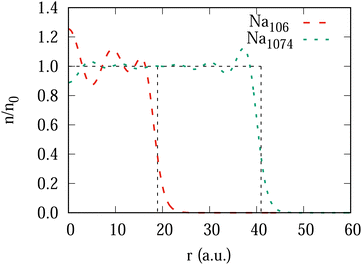 | ||
| Fig. 9 Ground state electron density profile of the spherical clusters Na106 and Na1074 in the units of the constant background density n0 (thin dashed line) as a function of the radial coordinate. | ||
Overall, considering that the non-adiabatic force calculated with TDDFT contains the contributions from complex dynamic polarization effects in finite-size objects, the friction coefficient is reasonably reproduced by the LDFA approximation for the in-going trajectory path. Here, performing the velocity normalization 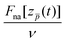 results in a nearly velocity-independent curve. This result seem to indicate that (i) scattering of valence electrons by the projectile is the dominant energy loss process, and (ii) other dynamical screening effects that contribute to the non-adiabatic forces (and, thus, potentially to the energy loss) also scale linearly with the projectile velocity. Further investigations are needed to dissect the effects contributing to the projectile energy losses. As commented above, the out-going trajectories present a larger stopping force than the in-going trajectories. Such difference cannot be reproduced by the LDFA approximation that necessarily produces identical friction coefficients for both types of trajectories. For low velocities, this difference might be due to the fact that the out-going trajectory path is affected by the excitations already created in the cluster and, thus, can not be used for a meaningful comparison with LDFA (which uses the ground-state cluster density as a reference).
results in a nearly velocity-independent curve. This result seem to indicate that (i) scattering of valence electrons by the projectile is the dominant energy loss process, and (ii) other dynamical screening effects that contribute to the non-adiabatic forces (and, thus, potentially to the energy loss) also scale linearly with the projectile velocity. Further investigations are needed to dissect the effects contributing to the projectile energy losses. As commented above, the out-going trajectories present a larger stopping force than the in-going trajectories. Such difference cannot be reproduced by the LDFA approximation that necessarily produces identical friction coefficients for both types of trajectories. For low velocities, this difference might be due to the fact that the out-going trajectory path is affected by the excitations already created in the cluster and, thus, can not be used for a meaningful comparison with LDFA (which uses the ground-state cluster density as a reference).
4 Conclusions
In conclusion, our results show that, for the considered trajectory normal to the cluster surface, the non-adiabatic force acting on an impinging antiproton can be expressed in terms of a position dependent (but velocity independent) friction coefficient to a high level of accuracy. This is the case even when the particle is located outside the metal cluster. This observation holds for a surprisingly large range of velocities below and above νF, and is particularly true for the case of the in-going part of the trajectory. After the collision, there is a higher variation of the friction coefficient with velocity due to the electron dynamics that arose during the interaction of the antiproton with the excited cluster left behind. Notice, however, that this latter effect is related to the finite-size of our targets and might not be relevant in experimental situations in which a surface of a thick target is involved and thus no projectiles are crossing through it. All in all, the extracted friction coefficient shows a remarkable monotonic behavior with a moderate impact of charge oscillations created in the cluster and small velocity dependence in the range of explored velocities.The above observations are necessary prerequisites for a simple approximation like LDFA to provide a reasonable description of non-adiabatic forces during surface collision events. LDFA provides a smooth interpolation, based on the targets ground-state density profile, of the friction coefficient from the known behavior in the bulk to negligible values far from the surface. In fact, our results confirm that LDFA gives a reasonable approximation to the TDDFT friction coefficient outside a metal surface. Important discrepancies between LDFA and TDDFT are only observed in close proximity to the surface and during and after the collision. Such discrepancies can be explained by the fact that the LDFA friction coefficient only depends on the local electronic density. Therefore LDFA does not take into account the asymmetry in the polarization effects observed in our TDDFT results. These conclusions are valid for all cluster sizes due to the local character of the screening process. For the same reason, our results for an antiproton approaching the surface of a metal cluster are expected to be reasonably similar to the case of an infinite metal surface.
The excitation of electron–hole pairs can affect and modulate the dynamics of elementary reactive and non-reactive processes at metal surfaces. Surface electronic excitations are created at the expense of the kinetic energy of the incoming atoms and molecules and the outcome of a given chemical process is very often dependent on this kinetic energy. Although there are some general criteria that may help to evaluate the possible relevance of the electronic excitations (interaction times and interatomic distances reached, for instance), the final effect depends on the particular conditions of the problem under study. The reliability of the LDFA, as shown in this work, will much help in the inclusion of e–h pairs excitation via a friction force in accurate molecular dynamics calculations based on ab initio description of the adiabatic interaction.
Author contributions
All authors contributed to the conceptualization of the problem, and validation and formal analysis of the results. Software: AGB. Simulations and visualization: NEK. Supervision: DSP and RDM. Writing – original draft: NEK and RDM. Writing – review and editing: all authors.Conflicts of interest
The authors declare no competing financial interests.Appendix A
Fig. 9 shows the density profiles of unperturbed clusters Na106 and Na1074.Fig. 10 and 11 show the snapshots of the induced electron density inside the Na106 cluster as a function of the spherical coordinates (z, ρ) for antiproton velocities of 0.1 and 1.0 a.u., respectively. The three panels correspond to different positions of the antiproton as indicated on each plot. From Fig. 10 one can see that at low velocity, the antiproton excites the cluster electrons yet before crossing the surface of the cluster. The oscillations move towards the other side of the cluster and rebound on the slowly moving antiproton, which is reflected in the friction coefficient at this low velocity (Fig. 4a). Therefore, this is a finite size effect that would not be found, in principle, in an infinite system, as our results for the largest cluster suggest (see Fig. 4b). At a higher projectile velocities above νF (Fig. 11), the situation is completely different. There is no wave front moving back because the cluster electrons are slower than the projectile which creates a characteristic wake pattern behind it. The screening cloud surrounding the antiproton is strongly asymmetric, which is a sign of the non-adiabaticity of the process.
Acknowledgements
This work has been supported in part by the Basque Departamento de Educación, Universidades e Investigación, the University of the Basque Country UPV/EHU (Grant No. IT1246-19), the Spanish Ministerio de Ciencia e Innovación (MICIN) Grants No. PID2019-107396GB-I00/AEI/10.13039/501100011033 and PID2019-107338RB-C66/AEI/10.13039/501100011033, as well as the Severo Ochoa Program for Centres of Excellence (CEX-2018-000867-S). NK acknowledges the funding from Spanish MICIN through grant PID2019-107338RB-C61/AEI/10.13039/501100011033, as well as a María de Maeztu award to Nanogune, Grant CEX2020-001038-M funded by MICIN/AEI/10.13039/501100011033. Computational resources were provided by the DIPC computing center.References
- G. A. Somorjai and Y. Li, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 917 CrossRef CAS PubMed.
- In Dynamics of Gas-Surface Interactions: Atomic-level Understanding of Scattering Processes at Surfaces, ed. R. Díez Muiño and H. Busnengo, Springer, 2013 Search PubMed.
- H. F. Busnengo, A. Salin and W. Dong, J. Chem. Phys., 2000, 112, 7641–7651 CrossRef CAS.
- G.-J. Kroes, Phys. Chem. Chem. Phys., 2021, 23, 8962 RSC.
- S. Manzhos and T. Carrington Jr, Chem. Rev., 2021, 121, 10187–10217 CrossRef CAS PubMed.
- C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G.-J. Kroes, Science, 2009, 326, 832–834 CrossRef PubMed.
- I. Goikoetxea, J. I. Juaristi, R. Díez Muiño and M. Alducin, Phys. Rev. Lett., 2014, 113, 066103 CrossRef CAS PubMed.
- A. Rodríguez-Fernández, L. Bonnet, C. Créspos, P. Larrégaray and R. Díez Muiño, J. Phys. Chem. Lett., 2019, 10, 7629–7635 CrossRef PubMed.
- J. C. Tully, Annu. Rev. Phys. Chem., 2000, 51, 153–178 CrossRef CAS PubMed.
- M. Alducin, R. Díez Muiño and J. I. Juaristi, Prog. Surf. Sci., 2017, 92, 317–340 CrossRef CAS.
- S. P. Rittmeyer, V. J. Bukas and K. Reuter, Adv. Phys. X, 2018, 3, 1381574 Search PubMed.
- S. W. Lee, H. Lee, Y. Park, H. Kim, G. A. Somorjai and J. Y. Park, Surf. Sci. Rep., 2021, 76, 100532 CrossRef CAS.
- N. Hertl, A. Kandratsenka and A. M. Wodtke, Phys. Chem. Chem. Phys., 2022, 24, 8738–8748 RSC.
- D. J. Auerbach, J. C. Tully and A. M. Wodtke, Nat. Sci., 2021, 1, e10005 Search PubMed.
- A. A. Correa, Comput. Mater. Sci., 2018, 150, 291–303 CrossRef CAS.
- H. Ueba, Prog. Surf. Sci., 1997, 55, 115–179 CrossRef CAS.
- K.-I. Inoue, K. Watanabe, T. Sugimoto, Y. Matsumoto and T. Yasuike, Phys. Rev. Lett., 2016, 117, 186101 CrossRef PubMed.
- D. Novko, M. Alducin and J. I. Juaristi, Phys. Rev. Lett., 2018, 120, 156804 CrossRef CAS PubMed.
- D. Novko, J. C. Tremblay, M. Alducin and J. I. Juaristi, Phys. Rev. Lett., 2019, 122, 016806 CrossRef CAS PubMed.
- B. Gergen, H. Nienhaus, W. H. Weinberg and E. W. McFarland, Science, 2001, 294, 2521 CrossRef CAS PubMed.
- H. Nienhaus, Surf. Sci. Rep., 2002, 45, 1–78 CrossRef CAS.
- Y. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 2000, 290, 111–114 CrossRef CAS PubMed.
- J. Geweke and A. M. Wodtke, J. Chem. Phys., 2020, 153, 164703 CrossRef CAS PubMed.
- M. Bonn, S. Funk, C. Hess, D. N. Denzler, C. Stampfl, M. Scheffler, M. Wolf and G. Ertl, Science, 1999, 285, 1042–1045 CrossRef CAS PubMed.
- P. Saalfrank, Chem. Rev., 2006, 106, 4116–4159 CrossRef CAS PubMed.
- C. Frischkorn and M. Wolf, Chem. Rev., 2006, 106, 4207–4233 CrossRef CAS PubMed.
- J. I. Juaristi, M. Alducin and P. Saalfrank, Phys. Rev. B, 2017, 95, 125439 CrossRef.
- J. Manson, G. Benedek and S. Miret-Artés, Surf. Sci. Rep., 2022, 77, 100552 CrossRef CAS.
- H. F. Busnengo, W. Dong and A. Salin, Phys. Rev. Lett., 2004, 93, 236103 CrossRef CAS PubMed.
- M. Blanco-Rey, J. I. Juaristi, R. Díez Muiño, H. F. Busnengo, G.-J. Kroes and M. Alducin, Phys. Rev. Lett., 2014, 112, 103203 CrossRef CAS PubMed.
- B. Hellsing and M. Persson, Phys. Scr., 1984, 29, 360 CrossRef CAS.
- J. R. Trail, D. M. Bird, M. Persson and S. Holloway, J. Chem. Phys., 2003, 119, 4539–4549 CrossRef CAS.
- M. Timmer and P. Kratzer, Phys. Rev. B, 2009, 79, 165407 CrossRef.
- J. I. Juaristi, M. Alducin, R. Díez Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CrossRef CAS PubMed.
- A. Salin, A. Arnau, P. M. Echenique and E. Zaremba, Phys. Rev. B, 1999, 59, 2537–2548 CrossRef CAS.
- S. P. Rittmeyer, J. Meyer, J. I. Juaristi and K. Reuter, Phys. Rev. Lett., 2015, 115, 046102 CrossRef PubMed.
- O. Galparsoro, R. Pétuya, F. Busnengo, J. I. Juaristi, C. Crespos, M. Alducin and P. Larregaray, Phys. Chem. Chem. Phys., 2016, 18, 31378–31383 RSC.
- P. Spiering and J. Meyer, J. Phys. Chem. Lett., 2018, 9, 1803–1808 CrossRef CAS PubMed.
- Q. Liu, X. Zhou, L. Zhou, Y. Zhang, X. Luo, H. Guo and B. Jiang, J. Phys. Chem. C, 2018, 122, 1761–1769 CrossRef CAS.
- M. Alducin, N. Camillone III, S.-Y. Hong and J. I. Juaristi, Phys. Rev. Lett., 2019, 123, 246802 CrossRef CAS PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- J. Pruneda, D. Sánchez-Portal, A. Arnau, J. Juaristi and E. Artacho, Phys. Rev. Lett., 2007, 99, 235501 CrossRef CAS PubMed.
- M. Ahsan Zeb, J. Kohanoff, D. Sánchez-Portal, A. Arnau, J. I. Juaristi and E. Artacho, Phys. Rev. Lett., 2012, 108, 225504 CrossRef PubMed.
- N. E. Koval, A. G. Borisov, L. F. S. Rosa, E. M. Stori, J. F. Dias, P. L. Grande, D. Sánchez-Portal and R. Díez Muiño, Phys. Rev. A, 2017, 95, 062707 CrossRef.
- M. Lindenblatt and E. Pehlke, Phys. Rev. Lett., 2006, 97, 216101 CrossRef CAS PubMed.
- L. Deuchler and E. Pehlke, Phys. Rev. B, 2020, 102, 235421 CrossRef CAS.
- M. Quijada, A. G. Borisov, I. Nagy, R. Díez Muiño and P. M. Echenique, Phys. Rev. A, 2007, 75, 042902 CrossRef.
- A. A. Kiejna and K. F. Wojciechowski, Metal Surface Electron Physics, Elsevier Science, 1996 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- E. Gross and W. Kohn, in Density Functional Theory of Many-Fermion Systems, ed. P.-O. Löwdin, Academic Press, 1990, vol. 21 of Advances in Quantum Chemistry, pp. 255–291 Search PubMed.
- O. Gunnarsson and B. I. Lundqvist, Phys. Rev. B, 1976, 13, 4274–4298 CrossRef CAS.
- D. Marinica, A. Kazansky, P. Nordlander, J. Aizpurua and A. G. Borisov, Nano Lett., 2012, 12, 1333–1339 CrossRef CAS PubMed.
- N. E. Koval, D. Sánchez-Portal, A. G. Borisov and R. Díez Muiño, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 317, 56–60 CrossRef CAS.
- P. M. Echenique, R. M. Nieminen, J. C. Ashley and R. H. Ritchie, Phys. Rev. A, 1986, 33, 897 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |