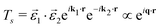Advances in the OCEAN-3 spectroscopy package
John
Vinson

Material Measurement Laboratory, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA. E-mail: john.vinson@nist.gov
First published on 18th May 2022
Abstract
The OCEAN code for calculating valence- and core-level spectra using the Bethe-Salpeter equation is briefly reviewed. OCEAN is capable of calculating optical absorption, near-edge X-ray absorption or non-resonant scattering, and resonant inelastic X-ray scattering, requiring only the structure of the material as input. Improved default behavior and reduced input requirements are detailed as well as new capabilities, such as incorporation of final-state-dependent broadening, finite-temperature dependence, and flexibility in the density-functional theory exchange–correlation potentials. OCEAN is built on top of a plane-wave, pseudopotential, density-functional theory foundation, and calculations are shown for systems ranging in size up to 7 nm3.
1 Introduction
The OCEAN code was introduced several years ago1–3 as a core-level spectroscopy complement to the valence spectroscopy package AI2NBSE.4 The purpose of both codes is to provide predictive calculated electronic response, specifically in the near-edge X-ray or optical/UV energy ranges, respectively. Now, the valence and core-level codes are combined into a single package which retains the name OCEAN.5 In this paper I will detail a number of advances that have been made that improve the accuracy and efficiency of OCEAN as well as extending the scope of materials and spectroscopies that can be simulated. This paper is not intended as a comprehensive review of the underlying theory, but it covers details of the implementation. In particular, I highlight specific approximations made in OCEAN that are not necessarily universal. The OCEAN code is not the only Bethe–Salpeter equation (BSE) based code. For many years BSE has been used for ab initio calculations of both valence6–8 and near-edge X-ray spectra,9 and is now incorporated into many codes.10–13 Nor is BSE the only method for calculated optical or X-ray spectra. A large number of computational tools based on a variety of theoretical methods are available.14,15Before continuing, it is instructive to clarify what is meant when OCEAN is referred to as predictive. I contrast this with approaches that are descriptive, and the important distinction is that of the method's primary purpose. In a descriptive approach a parametrized model, cleverly constructed to capture the relevant effects and excitations, is fit to experimental data. From this fit one infers relative strengths and weights of modeled effects in the system being studied. The OCEAN code is predictive in the sense that the system-dependent adjustable parameters are limited to the structural description. The structure determines the species of atoms and their locations. Parameters that are applicable to a wide variety of systems, such as the choice of density functional (see Section 2.1.1), or to a specific atomic species, such as the core–hole lifetime (see Section 2.1.2), are considered acceptable. Removing these parameters (the universal density functional or reliable decay lifetime calculations) are, of course, goals in the condensed matter community, but will be left to others.
To begin I must clearly define the scope of the problem. As stated above, I am interested in calculating the electronic response to perturbations that range in energy from optical to X-ray. More narrowly, the electronic response of condensed systems, liquids or solids (though gas phase or molecular systems are possible as well). The temperature can range from cold to several times room temperature, subject to the constraint that the temperature be small compared to the Fermi level (metals) or bandgap (insulators), kβT ≪ EF, Eg. This allows the temperature to be treated as a perturbation on top of a 0 K calculation. A pressure range from 0 Pa. to many GPa. is acceptable. These constraints allow for a wide range of possible systems and conditions from battery cathodes to water splitting catalysts to minerals within the Earth's mantle.
The calculation of a material's spectrum involves first the calculation of the ground-state electronic structure of that material. This can be thought of hierarchically. The physical structure of a material, its atoms and their coordinates, determines the electronic structure, and, in turn, the electronic response or spectra. The goal is to provide an overview of how the electronic structure and the electronic response are treated within the OCEAN code.
The format of this paper will continue as follows. After a brief comment on the structure of the code, I give a broad overview of the theoretical underpinnings of OCEAN as well as some implementation details specific to OCEAN and the types of calculations OCEAN is capable of. Then I discuss a number of improvements and advances that have been made to the code before finally presenting a number of examples that showcase the breadth and utility of OCEAN.
1.1 Structure of the OCEAN code
The OCEAN package is a collection of scripts and executable programs. Density-functional theory (DFT) calculations are a vital part of OCEAN, but OCEAN is reliant on external codes for these calculations. After parsing the input file and carrying out initial parameter checks, the OCEAN package runs through several stages. Each stage is controlled by its own script, which allows each stage to be run individually. First is the “OPF” (optimal projector function) stage which calculates details of core-level orbitals (see Section 2.1.2). Next, the “DFT” stage carries out DFT calculations (see Section 2.1.1) to generate electron orbitals which are used in the the BSE calculations. After this is the “PREP” stage which serves as an intermediate step to allow OCEAN to interface with different external DFT codes that might have different output file formats. Next comes the “SCREEN” stage which calculates the dielectric response which screens the electron–hole attraction in the BSE. Finally, the “BSE” stage generates spectra using the BSE.1.2 Measurements and convergence
With OCEAN one is able to make “computational measurements,” that is, probe the theoretical assumptions that are in the code as well as the structural assumptions that are used as input. Unlike reality, where the atomic movement in a system is the dependent variable, changing with applied external forces or conditions, in simulations the atomic positions are the independent (and only free) parameter. This means that one is able to measure how structural changes affect spectra. Additionally, by changing aspects of the underlying theoretical approximations one can observe the effect of that approximation on the electronic structure and response. For instance, the exchange–correlation potentials of DFT are often judged by structural properties, cell volume or bulk modulus, whereas core-level spectroscopy is sensitive to the local shape of the electron orbitals. Computational spectroscopy provides a measurement of the underlying electronic structure beyond energy levels or the density response.The OCEAN code relies on both uncontrolled approximations, such as the use of the Bethe–Salpeter equation to describe excited states or DFT to describe the ground state, and controlled approximations, such as the use of finite sums instead of integrals over electronic states. It is important that calculations are converged with respect to all controllable approximations, irrespective of wether this convergence improves agreement with measured data.
2 Theory overview
2.1 Ground state
Before simulating the electronic response of a system, one must first simulate the system's ground state. This is because the terms needed to solve the response are built diagrammatically out of the ground-state electron wave functions. While a Hamiltonian can be written down for condensed matter systems with only very minor approximations, such a complete description is not tractable. To proceed a number of approximations are made that substantially reduce the size and complexity of the Hamiltonian.First, the nuclei and electrons are decoupled, writing the many-body wave function as
|ξ(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0052_20d1.gif) )〉|Ψ( )〉|Ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0072_20d1.gif) ; ;![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0052_20d1.gif) )〉 )〉 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0072_20d1.gif) , but parametrically on the atomic coordinates
, but parametrically on the atomic coordinates ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0052_20d1.gif) . This is the Born–Oppenheimer approximation. It allows one to treat the nuclei as fixed classical potentials and separately solve the electronic Hamiltonian. Often an argument is made that the nuclei move slowly compared to the timescale of the electronic excitations. Importantly, this approximation treats the vibrational excitations as having negligible energy.16 In what follows spectra are assumed to depend only parametrically on atomic positions, and the atomic positions remain fixed during the excitation.
. This is the Born–Oppenheimer approximation. It allows one to treat the nuclei as fixed classical potentials and separately solve the electronic Hamiltonian. Often an argument is made that the nuclei move slowly compared to the timescale of the electronic excitations. Importantly, this approximation treats the vibrational excitations as having negligible energy.16 In what follows spectra are assumed to depend only parametrically on atomic positions, and the atomic positions remain fixed during the excitation.
Next, the material is treated with periodic boundary conditions. This means that the electron orbitals ψ can be written in terms of bands n, their spin σ, and their crystal momenta k within the Brillouin zone,
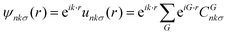 | (2) |
| H [n] = −1/2∇2 + Vext + VH[n] + VKS[n] | (3) |
The OCEAN code relies on external codes to carry out the necessary DFT calculations to generate the electron density n(r) and electron eigenstates {ψnk} and energies {εnk}. At present, OCEAN interfaces with both QUANTUM ESPRESSO21 and ABINIT,10 and it is able to construct their input files, run the codes, and gather and parse their outputs. Adding new plane-wave, psuedopotential DFT code interfaces can be accomplished by writing their output files in a format readable by OCEAN or by extending the OCEAN wave function parser. The examples shown here were calculated with QUANTUM ESPRESSO version 6.7 (version 7.0 for water).
2.1.1.1 Exchange–correlation functionals and DFT+U. While DFT is an exact theory, the exact exchange–correlation functional VKS[n] is not known. The simplest Kohn–Sham exchange–correlation potential is referred to as the local-density approximation (LDA). Within the LDA the value of the Kohn–Sham potential is based on calculations of the homogenous electron gas. More sophisticated exchange–correlation potentials are possible, e.g., taking into account the local gradients of the density as well as is done in the class referred to as generalized gradient approximations (GGA) such as the popular Perdew–Burke–Ernzerhof (PBE) functional.22 One-step further, meta-GGA functionals include terms that depend on the second derivative of the density or the kinetic energy density of the occupied orbitals, like the so-called strongly constrained and appropriately normed (SCAN) functional.23 A different approach for improving the reliability of functionals is to add in some amount of the true exchange interaction in place of the exchange component of the density functional – referred to as exact exchange (EXX).
Lastly, local and semi-local DFT is known to perform poorly for systems with highly-localized states near the valence-band maximum or conduction-band minimum, i.e., 3d and 4d transition metals. This has lead to the use of a Hubbard-U term (DFT+U), where an orbital-specific term is added to the Hamiltonian. In its simplest form, this term is an on-site repulsion that penalizes doubly occupying the d-orbitals, stabilizing high-spin configurations and opening a Hubbard gap.
2.1.1.2 GW corrections. Despite the formalism of DFT designed to produce only the correct ground-state density of a system, DFT orbitals have been widely used in spectroscopy. DFT orbitals often suffer from incorrect relative energies, leading to band gaps and band widths that are too small. Using many-body perturbation theory, the DFT orbitals can be treated as quasiparticles and their energies corrected by the self-energy operator Σ. The first-order energy correction is given by
| εi = εKSi + 〈Ψi|Σ(εi) − VKS|Ψi〉 | (4) |
OCEAN does not carry out GW calculations, but results from external GW codes can be included in an OCEAN calculation. Often calculations keep the DFT orbitals constant and only energy-corrections to the DFT eigenvalues are calculated, the so-called G0W0 approximation. So long as the exchange–correlation functional and pseudopotentials are the same, energy corrections from one code can be applied directly to eigenvalues of another. Energy corrections can be supplied to OCEAN for all states explicitly Σnk, by band Σn, or by energy Σ(ω), and can be either real- or complex-valued. Alternatively, a simple band-gap and stretch can be applied where the valence and conduction band energies are stretched by separate amounts, and the band gap set or changed by a specific value. Quasi-particle self-consistent GW calculations have been used with OCEAN,25 but require inputting the electron orbitals from the GW calculation and this has not yet been automated.
In order to calculate transitions and interactions between core-level orbitals and orbitals from a pseudopotential-based DFT, OCEAN makes use of optimal projector functions (OPFs), a method based upon the projector augmented wave formalism.28 Details of calculating the OPFs and recent improvements are discussed elsewhere.29 The OPFs provide a complete basis set for describing a limited space of DFT orbitals – from the valence bands up to approximately 6 Ryd above the Fermi level and within a small sphere around an atom. The sphere radius is at or slightly larger than the pseudopotential radius, in the range of 1 a.u. to 2.5 a.u. This basis allows the pseudopotential DFT orbitals to be augmented to include the correct all-electron character.
2.1.2.1 Energy alignment. OCEAN and the DFT codes it interfaces with are based on pseudopotentials, and core-levels are ignored. Thus changes in the core-level energy due to chemical surroundings are not available. The energies from the separate, atomic DFT code necessarily cannot account for differences in the electronic structure at the atomic site in a given structure. As an example, an approximately 4 eV energy shift is found experimentally in ammonium nitrate between the N 1s orbitals in the N3− site of ammonium and the N5+ site of nitrate.18
Energy alignments are calculated by first noting that, by using an external atomic code, the calculation is being done within the frozen core approximation. The core-level orbitals are independent of the material. Therefore, the DFT energy of the core orbital γ can be given by some constant Xγ plus the total external electrostatic potential experienced by the orbital VKS. This total external potential is the total potential of the pseudopotential DFT calculation. Finally the adiabatic relaxation of the system is included in response to removing the core orbital
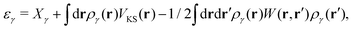 | (5) |
2.2 The Bethe–Salpeter equation method for absorption and related spectroscopies
The Bethe–Salpeter equation (BSE) is a series expansion of the two-particle propagator.33 While originally applied to the ground-state nucleus of a deuteron, it is used widely in condensed matter to describe the behavior of neutral particle–hole excitations. The reader is referred to ref. 34 and 35 and references therein. At present, OCEAN makes use of the Tamm-Dancoff approximation.36 Several additional approximations are required in order to determine the electronic response of a system using the BSE.The first set of approximations is that the electrons are treated either non-relativistically or, at most, in a scalar relativistic manner. The exchange of real or virtual photons is done without accounting for the finite speed of light. Electrons have two-component, up or down spins, not 4-component Dirac spinors. The magnitude of the spin–orbit splitting of core-level electrons is calculated in a scalar relativistic framework and applied perturbatively in the angular momentum and spin, l, ml, σ, basis, e.g., between the 2p3/2 L3 and 2p1/2 L2. The spin–orbit splitting is applied as if it were an interaction term ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) in the BSE Hamiltonian.
in the BSE Hamiltonian.
Importantly, in the BSE only two explicit excited quasi-particles exist at a time – an excited electron and a hole. There is an implicit shift in the crystal momentum between electron and hole that conserves the photon's momentum for absorption or emission. The effective BSE Hamiltonian used by OCEAN can be written in the basis of a pair of occupied (a, b) and unoccupied (i, j) states
HBSEia,jb = (εi − εa)δijδab + ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) abδij − Wia;jb + Xia,jb abδij − Wia;jb + Xia,jb | (6) |
The BSE is evaluated using a finite k-point mesh of electron and hole states in place of an integral over the Brillouin zone. The mesh subdivides the reciprocal lattice vectors, and the number of k-points in each direction should be proportional to the length of that reciprocal lattice vector. Note, that the lengths of the reciprocal lattice vectors depend on both the lengths of the lattice vectors and the angles between them. The number of conduction bands included in the calculation is also limited. This has the effect of limiting the spectral range of the calculation, but, because the DFT single-particle states are not eigenstates of the BSE, convergence of even the low energy part of a calculated spectrum must be checked with respect to the number of conduction bands. As the occupied states at a given k-point are finite they can all be included in the BSE calculation, but this is not done. The core levels are energetically separated enough to be neglected for valence calculations and vice versa, while the core orbitals between atoms have no overlap and are treated independently for core-level spectroscopy.
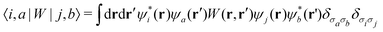 | (7) |
The exchange interaction involves the electron–hole pair combining, emitting a virtual photon, and then reappearing, and it involves the unscreened Coulomb operator
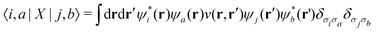 | (8) |
2.2.1.1 Valence-level interactions. For solving the BSE with a valence–hole–conduction–electron excitation, e.g., optical/UV excitations or the final state of RIXS (see Section 2.3.5), the OCEAN code closely follows earlier work,8,38 and I will only briefly summarize it here. The electron and hole states are downsampled from the Fourier coefficients G from the DFT code onto a real-space mesh x. The mesh is aligned with the lattice vectors with a typical spacing of 0.5 a.u. to 1.0 a.u., or a plane-wave energy cut-off range 10 Ryd to 40 Ryd. The direct interaction is evaluated in real-space with a Fourier transform of the k-point mesh defining a supercell in which the exciton is confined. Evaluation of the direct is the most time-consuming part of the valence BSE as both the electron and hole components must be evaluated on the full x-mesh. The direct interaction is evaluated in reciprocal space where it is diagonal.
2.2.1.2 Core-level interactions and the local basis. For the core-level BSE, both the direct and the exchange interaction are evaluated in real-space. Exploiting the locality of the core-level orbital, both the direct and exchange interactions are written as partial wave expansions around the atomic site of interest. It can be immediately seen from eqn (8) that the exchange interaction is limited to the region immediately around the atom because the core orbital must be present at both spatial coordinates. The direct interaction does not have this limitation, and the l = 0 component is very long ranged. Only even powers of l enter into the direct interaction, and by the l = 2 term the interaction decays quickly enough that a local treatment is sufficient. The l = 0 component is broken into two pieces
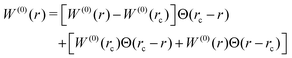 | (9) |
The exchange and short-range components of the direct are evaluated using the OPFs (Section 2.1.2). Between 2 and 5 projectors are constructed per angular momentum channel, and angular momenta up to l = 3 are included, providing a compact basis of no more than 80 OPFs. The long-range component of the direct interaction is evaluated on the x-mesh. It is the long-range component that dominates computational time for large unit cells. The strength of the exchange and short-range, l ≥ 2, components of the direct are typically reduced to 80% of their calculated values.39
2.2.1.3 Spin–orbit splitting. While not an electron–hole interaction, the effects of spin–orbit splitting are treated in OCEAN as part of the interaction Hamiltonian. An electron moving in the electric field of the nucleus will experience an effective magnetic field which, in turn, interacts with the electron's magnetic moment. This is the spin–orbit interaction and takes the form
![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) ∝ (L·S), where L and S are the angular momentum and spin operators respectively. The spin–orbit interaction is not diagonal in the Lz, Sz representation, and the usual practice is to use the total angular momentum basis J2, Jz. The operators L2 and S2 are diagonal in both representations. We take the spin–orbit splitting within first order perturbation theory,
∝ (L·S), where L and S are the angular momentum and spin operators respectively. The spin–orbit interaction is not diagonal in the Lz, Sz representation, and the usual practice is to use the total angular momentum basis J2, Jz. The operators L2 and S2 are diagonal in both representations. We take the spin–orbit splitting within first order perturbation theory,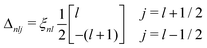 | (10) |
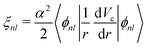 | (11) |
The spin–orbit interaction is not diagonal in the basis vectors used in OCEAN. (The direct and exchange interactions as well as the valence and conduction band states all make use of Sz, and the exchange and local part of the direct interaction make use of Lz.) In the Lz, Sz basis, the dot product is expanded L·S = 1/2(J2 − L2 − S2)
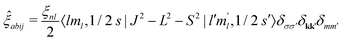 | (12) |
The spin–orbit splitting also leads to a j-dependent lifetime broadening. A hole in the more-bound 2p1/2 state can decay into a less-bound 2p3/2 state, but not the converse. The core–hole lifetime broadening values Γnlj are not calculated by OCEAN. However, experimentally they are seen to be largely independent of the local electronic structure and fairly constant across materials (for a given element and core level). Therefore, they are available in OCEAN as a lookup table based on experimental measurements.40 The state-dependent broadening is included in the spin–orbit Hamiltonian above by dividing the broadening into j-dependent Γnl and j-independent ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) nl components:
nl components:
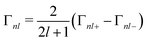 | (13) |
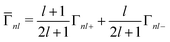 | (14) |
This spin–orbit dependent lifetime broadening is added to the real-valued, spin–orbit splitting interaction giving
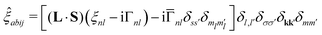 | (15) |
2.3 Calculating spectra
Within OCEAN the BSE Hamiltonian is never explicitly constructed and is not diagonalized. The code calculates the action of the Hamiltonian on a vector in the electron–hole basis. Each of the aforementioned interaction terms is evaluated in a favorable basis: real-space mesh, reciprocal-space mesh, or local basis. Two iterative solvers are available that are capable of calculating the spectra, while the second is also used to generate the exciton wave functions.The macroscopic dielectric function is given by
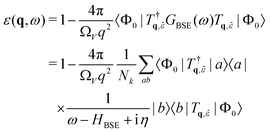 | (16) |
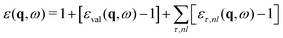 | (17) |
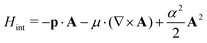 | (18) |
2.3.1.1 Valence. In the case of valence band to conduction band excitations, the matrix elements are proportional to
| Mvck;q = 〈ck|eiq·r|vk − q〉 = 〈vk − q; ck|eiq·r|Φ0〉 | (19) |
2.3.1.2 Core. For core-level excitations the choice of electron-photon interaction is more varied. In all cases the matrix elements can be written
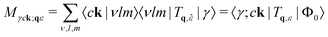 | (20) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , and the OPF basis {νlm} is used to calculate the transitions.
, and the OPF basis {νlm} is used to calculate the transitions.
For scattering, the relevant class of experiments are non-resonant inelastic X-ray scattering (NRIXS) also called X-ray Raman scattering (XRS). Dropping the polarization, this operator is the same as is used to simulate EELS.
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ). The transition operator can be expanded into spherical Bessel functions jl
). The transition operator can be expanded into spherical Bessel functions jl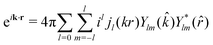 | (21) |
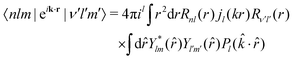 | (22) |
For absorption and emission the matrix elements are also calculated in real space using the localized basis. Interactions are calculated to at most quadrupole order, which includes a single k·r term.
Ta = ![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) ·r − i/2( ·r − i/2(![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) ·r)(k·r) ·r)(k·r) | (23) |
The advantages of using the Haydock recursion method are two-fold. One, the number of iterations required to produce a spectrum (rank of the tridiagonal matrix) is not dependent on the rank of the BSE Hamiltonian. It depends directly on the spectral range included in the BSE (the energy range of the conduction bands) and inversely on the resolution (the core–hole lifetime broadening). While the BSE Hamiltonian can easily be of rank 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, the number of iterations needed to converge the Haydock is typically around 100. Second, though general to any iterative solve, as noted above the BSE Hamiltonian is never explicitly constructed, reducing computational time and memory requirements.
000, the number of iterations needed to converge the Haydock is typically around 100. Second, though general to any iterative solve, as noted above the BSE Hamiltonian is never explicitly constructed, reducing computational time and memory requirements.
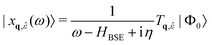 | (24) |
(ω − HBSE + iη)|xq,![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ω)〉 = Tq, (ω)〉 = Tq,![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) |Φ0〉 |Φ0〉 | (25) |
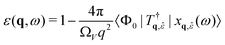 | (26) |
In OCEAN, right preconditioning with a diagonal preconditioner is used,
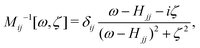 | (27) |
Typically, approximately 100 iterations are required to converge the vector x(ω) for a single energy, making the GMRES method roughly Nω times more computationally expensive than the Haydock recursion. The GMRES method is restarted every 80 iterations to avoid the growing costs of a large Krylov space. If the energy points are sufficiently close compared to the core–hole broadening, |ωi − ωi−1| < 3η, then the previous vector x (ωi−1) is used as an initial guess for x (ω). In all other cases the initial guess is set to 0. Additionally, when the energy points are close compared to the preconditioner broadening ωi − ωi−1 < ζ/4 the Krylov space is recycled from the previous iteration and the preconditioner is held centered at the previous energy until a restart. Together these two modifications can reduce the number of iterations required for repeated energy points significantly.
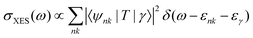 | (28) |
RIXS spectra are calculated by first solving for the initial X-ray absorption exciton vector using GMRES.
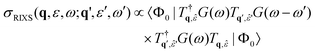 | (29) |
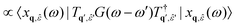 | (30) |
RIXS at spin–orbit-split edges, e.g., L2,3 or M4,5, present the additional complication that spin must be included in the valence-level calculation. This is true even if the valence and conduction bands of the system being studied are degenerate with respect to spin. The core-level spin–orbit splitting mixes the spin of the electron and hole components of the exciton. Previous versions of OCEAN were limited to singlet excitations in the valence solver, but this has now been alleviated, allowing RIXS calculations for spin–orbit-split edges. The computational cost is increased by a factor of four over what is needed for a singlet calculation if the valence and conduction bands are spin degenerate (factor of two if they are not). At present this functionality is only implemented for RIXS calculations.
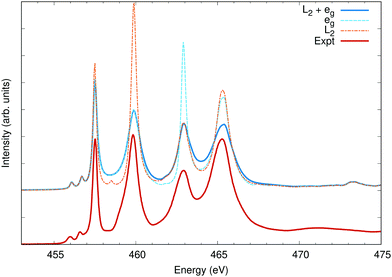
As an example, RIXS calculations have been carried out for the sulfur L2,3 edge of CdS. The energy of the occupied Cd 4d-orbitals was adjusted by applying a Hubbard-U correction of 4.2 eV.48 No valence- or conduction-band spin–orbit was included in the DFT calculation. A uniform broadening of 0.1 eV was used to calculate both the XAS and RIXS. The spin–orbit splitting in sulfur is quite small, around 1 eV, but it is still sufficient to mix the spins. In Fig. 1, the calculated X-ray absorption spectrum (XAS) is shown compared to the experiment from ref. 47. Also shown, is the ratio of spin-aligned electron and hole to the total exciton (both spin-aligned and anti-aligned). It is clear that both singlet and triplet interactions are important for the final-state valence-level BSE when carrying out RIXS at the L2,3 edge.
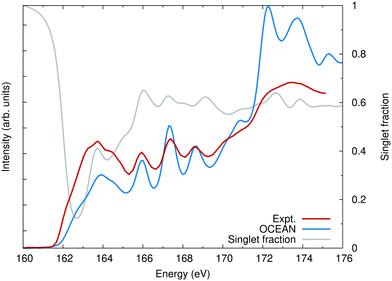 | ||
| Fig. 1 The calculated sulfur L2,3 edge of CdS compared with experiment.47 Also shown, the singlet fraction is the ratio of how much of the exciton is due to a spin-up hole and spin-up electron or a spin-down hole and a spin-down electron as a fraction of the total excitonic weight. Without spin–orbit, linearly polarized X-rays will only populate spin-singlet excitons. | ||
The calculated CdS S L2,3 edge RIXS map is shown in Fig. 2(a) while a comparison to experiment is shown in Fig. 2(b). The CdS RIXS is dominated by the very flat S 3s (emission around 146 eV) and Cd 4d bands (emission around 150 eV), which, other than changes in intensity, show almost no dependence on the incident photon energy. The emission from the upper valence bands (emission above 153 eV) show only slight changes in spectral shape with excitation energy. The overall lack of strong excitonic effects in the measured emission explains the success of previous DFT-based RIXS calculations.47,49 Additionally, the peaks from the sulfur 3s bands are much too narrow in the calculation, resulting in an exaggerated peak intensity. The agreement between the calculation and measurement is good. However, as is typical, the calculated RIXS maps shows more variation with excitation energy than the measured map. This is particularly evident in the upper valence bands, with emission energies above 153 eV. Some of the apparent lack of variation in the experiment is due to incoherent emission. Phonon scattering off of the core hole during the RIXS process has the effect of breaking the momentum dependence between the core hole and excited electron. This in turn allows the final valence hole to occupy any part of the Brillouin zone as in non-resonant X-ray emission. OCEAN is not able to calculate this phonon coupling, and this effect is not accounted for in the calculated spectra.
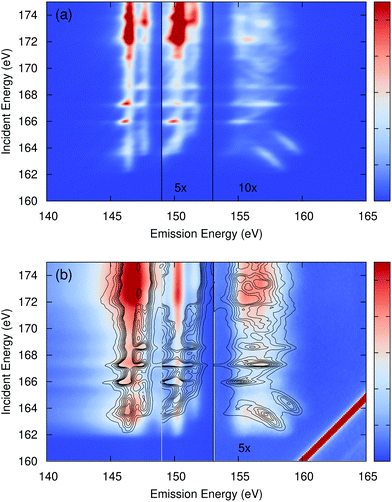 | ||
| Fig. 2 (a) The calculated sulfur L2,3 edge RIXS of CdS as a function of incident and emitted photon energy (intensity in arbitrary units). The region with emission between 149 eV and 153 eV, emission from bands primarily associated with the Cd 4d orbitals, has had the intensity increased by 5×. The region above 153 eV has been increased by 10×. (b) the measured spectra from ref. 47 with contour lines from the calculation overlaid. Above an emission energy of 153 eV the experiment has been increased by 5×. | ||
3 Improvements and developments to OCEAN
In this section I briefly summarize the additions to the OCEAN code over the past 7 years since the previous major version and corresponding publication.2 These improvements cover enhancements to usability, speed, accuracy, and functionality.3.1 Input file and defaults
The input file format has been substantially updated, but OCEAN is still capable of parsing and using an input file from version 2. Input flags have been grouped into hierarchies, and both plain text and JavaScript Object Notation (JSON) formats are supported. During setup, OCEAN automatically writes a single file that contains all of the relevant information needed to recreate a calculation, including both the user-supplied information as well as default values for any optional inputs.The number of required inputs has been reduced as much as possible, as can be seen in Fig. 3. A calculation can be carried out specifying only the DFT program, type of calculation (e.g. XAS) and edge (e.g. Ti 2p), lattice parameters, and atomic coordinates. The k-point mesh for both the BSE final states and screening orbitals is determined by noting that each dimension of the k-point mesh subdivides one of the reciprocal lattice vectors. By default, the spacing of this division is set to be no more than 0.33 a.u.−1 for the BSE and 0.39 a.u.−1 for the screening. This is sufficient to converge the screening calculation in typical systems and provides a reasonable starting point for the BSE. The number of conduction bands included is approximately enough for 50 eV above the Fermi level for the BSE and 100 eV for the screening. These are calculated based on the energy levels of a particle in a box with same volume as the unit cell. The real-space sampling of the orbitals for the BSE, used for all the interactions in a valence-level calculation or the long-range interactions for the core (see Section 2.2.1), is set to divide the lattice vectors by no more than 1 a.u. The other input parameters are not dependent on the unit cell volume.
 | ||
| Fig. 3 A minimal input for calculating the Ti L2,3 XAS of SrTiO3 using QUANTUM ESPRESSO as the external DFT program. | ||
Support for optimized norm-conserving Vanderbilt pseudopotentials has been added by extending the oncvpsp code.26,27 This makes files from two large pseudopotential databases usable, SG1552 and PseudoDojo.53 The input files from version 0.4 of PseudoDojo are included in the OCEAN distribution. A database of all these pseudopotentials can be created and installed with OCEAN, allowing to automatically load the correct pseudopotentials based on the elements in the input file and to set the plane-wave cut-off based on the included pseudopotentials. Previously, OCEAN relied on an internal atomic code, and pseudopotentials had to be supplied following the Fritz-Haber-Institut (FHI) format. Some pseudopotentials following this format could be found on the ABINIT or QUANTUM ESPRESSO websites, or they could be generated by the user using the opium code.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 is used. Accuracy is not needed for conducting systems as the errors scale with the inverse of the dielectric constant. The effect on calculated XAS of incorrect values for the dielectric constant has been discussed elsewhere.29
000 is used. Accuracy is not needed for conducting systems as the errors scale with the inverse of the dielectric constant. The effect on calculated XAS of incorrect values for the dielectric constant has been discussed elsewhere.29
3.2 Screening
Details of the improved method, implementation, and robustness of the screening calculation in OCEAN have been published previously,29 and the main points will be summarized here. The direct interaction is screened using the random phase approximation (RPA) dielectric response. In OCEAN this calculation is carried out in real space using a combination of the RPA response and a model dielectric function. The RPA response is calculated for a neutral excitation consisting of a core hole or point charge surrounded by a neutralizing shell at some radius rS. This approximation is controlled by the shell radius with the contribution of the model going to zero as rS → ∞. This approach can be used for both valence and X-ray excitations.The screening calculation itself scales well, N2log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N where N is system size. However, the calculation requires electron orbitals from a DFT calculation which scales as N3, and for large calculations the total time required is dominated by the DFT calculation. The screening calculation is parallelized both over atomic sites as well as within a single site.
N where N is system size. However, the calculation requires electron orbitals from a DFT calculation which scales as N3, and for large calculations the total time required is dominated by the DFT calculation. The screening calculation is parallelized both over atomic sites as well as within a single site.
3.3 Exciton plotting
At times it is useful to plot out the density of the excited electron or hole that make up the exciton to try and gain insight from the shape of the excitation. Unlike codes that diagonalize the BSE Hamiltonian and can therefore plot excitons from the eigenvectors,11,13,57OCEAN only calculates an exciton vector which includes a projection based on the photon and a finite energy bandwidth (see eqn (24)). In many cases, however, this exciton vector is the physically relevant quantity to plot. The finite energy smearing from iη is set to match the core–hole lifetime broadening and captures the superposition of eigenstates that are populated. The real-space exciton ϕ for a specific x(ω) can be generated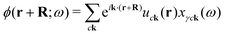 | (31) |
The excitons are localized and need not be generated on an R-grid the same size as the k-point grid. Additionally, the real-space r-mesh need not be the same as the x-mesh used in the BSE calculation to generate x(ω). A user can specify an integer multiple supercell or an explicit right rectangular prism. In the case of the latter, the core site is centered and interpolation is used to transform from the lattice-vector aligned ϕ(r,R) to a regular orthogonal real-space grid. The exciton density is output in the cube file format, allowing plotting with various third-party tools. As an example, the lowest energy exciton at the nitrogen K edge of a single sheet of hexagonal boron nitride is shown in Fig. 4.
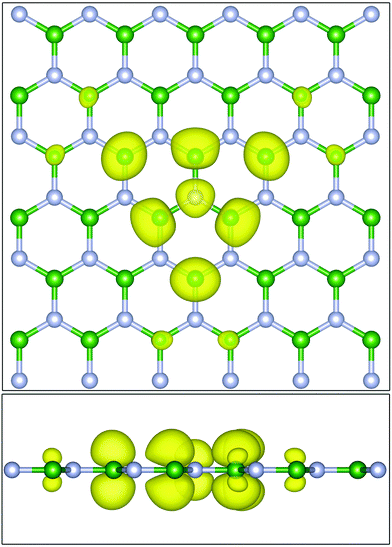 | ||
| Fig. 4 (Top) The excited electron density (yellow) of the lowest energy exciton of a single sheet of hexagonal boron nitride at the nitrogen K edge viewed looking down. (Bottom) the same plot but viewed from the side. The absorbing site is the central nitrogen atom (grey). The majority of the electron density is sitting in pz type states on the first and second nearest neighboring boron atoms (green). Plots generated using VESTA.56 | ||
3.4 Temperature-dependent XAS
At temperatures near or below room temperature, the main effect of temperature on calculated X-ray spectra comes through the motion of the ions. The electronic state occupation numbers can be taken in the T → 0 K limit as either 0 or 1. (As an aid to convergence of the self-consistent DFT calculation, a smearing of the occupation numbers is used to generate the electron density. While this smearing can be treated as a temperature, the goal is to approximate the zero-temperature density while replacing the integral over the Brillouin zone with a coarse sum over k-points.) However, at elevated temperatures or in response to an optical pump, non-integer occupation numbers 0 ≤ n ≤ 1 are possible. If the ions are held fixed, modeling either temperatures below the melting point or short-delay pump–probe experiments which measure before the lattice thermalizes, then the two initial effects on the spectra are due to changes in Fermi blocking and changes to the dielectric screening. The primary effect of the latter is an increase in the long-range dielectric screening of insulating or semiconducting systems due to an increase in charge carriers. Only the first of these effects has been implemented in OCEAN and is described below.Following previous work,59,60 finite temperature has been approximated by modifying the BSE Hamiltonian to include fractional occupation numbers
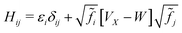 | (32) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) i = |fei − fhi| is the Fermi factor difference between the nominal electron and hole states. The individual Fermi factors are given by the expected f = [exp[(ε − EF)/kBT] + 1]−1, where ε is the energy of the electron or hole state, EF is the Fermi level, kB is Boltzmann's constant, and T the temperature. At T → 0, these factors reduce to 1 or 0, and Eq. 32 is equivalent to algorithmically limiting the space of electrons and holes and neglecting the
i = |fei − fhi| is the Fermi factor difference between the nominal electron and hole states. The individual Fermi factors are given by the expected f = [exp[(ε − EF)/kBT] + 1]−1, where ε is the energy of the electron or hole state, EF is the Fermi level, kB is Boltzmann's constant, and T the temperature. At T → 0, these factors reduce to 1 or 0, and Eq. 32 is equivalent to algorithmically limiting the space of electrons and holes and neglecting the 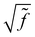 factors. Importantly, the Fermi level itself will shift with temperature as the occupied and unoccupied densities of states are unlikely to be symmetric.
factors. Importantly, the Fermi level itself will shift with temperature as the occupied and unoccupied densities of states are unlikely to be symmetric.
To showcase the effect of temperature of XAS, calculations of bulk copper were carried out at both the L and K edges. Previously, a pump-probe experiment was carried out measuring the changes in the Cu L edge in response to a 400 nm laser pump for probe delay times of 0 ps to 21 ps.58 The laser fluence was sufficient to damage the sample, and previous simulations of the L-edge absorption accounted for this using molecular dynamics to model high-temperature liquid copper.58,61 There is a short delay between the thermalization of the electronic system and that energy being transferred to phonons, heating and then melting the copper lattice. Here, only the electronic temperature is considered. In Fig. 5, calculations at 300 K and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 K are compared with measurements at room temperature and with a 2 ps delay between the laser pump and X-ray probe. The calculations were broadened by 0.305 eV to account for the L3 lifetime broadening and an additional 2.5 eV full-width at half maximum (FWHM) Gaussian. The calculations were both shifted by the same amount to fit the onset of the L3 edge of the room temperature measurement. The redshift with increasing temperature is a direct result of changes to the occupation numbers of states near the Fermi level. The OCEAN calculations agree well with the measured data. The temperature activated features below the L2 (948 eV) and L3 (930 eV) are stronger in the measurement. These are due to transitions into the 3d orbitals which lie just below the Fermi level and are occupied at low temperature. The position and distribution of these orbitals from the DFT calculations may not be correct, and changes in their energy will have a large effect on this part of the spectrum.58 Here, a Hubbard-U correction of 2.0 eV was applied to the copper d orbitals.48 Realistic simulations of high-temperature XAS can be used to measure the electronic temperature of samples in these types of high-fluence pump probe experiments, but proper accounting of the ionic temperature is also necessary.58,61–64
200 K are compared with measurements at room temperature and with a 2 ps delay between the laser pump and X-ray probe. The calculations were broadened by 0.305 eV to account for the L3 lifetime broadening and an additional 2.5 eV full-width at half maximum (FWHM) Gaussian. The calculations were both shifted by the same amount to fit the onset of the L3 edge of the room temperature measurement. The redshift with increasing temperature is a direct result of changes to the occupation numbers of states near the Fermi level. The OCEAN calculations agree well with the measured data. The temperature activated features below the L2 (948 eV) and L3 (930 eV) are stronger in the measurement. These are due to transitions into the 3d orbitals which lie just below the Fermi level and are occupied at low temperature. The position and distribution of these orbitals from the DFT calculations may not be correct, and changes in their energy will have a large effect on this part of the spectrum.58 Here, a Hubbard-U correction of 2.0 eV was applied to the copper d orbitals.48 Realistic simulations of high-temperature XAS can be used to measure the electronic temperature of samples in these types of high-fluence pump probe experiments, but proper accounting of the ionic temperature is also necessary.58,61–64
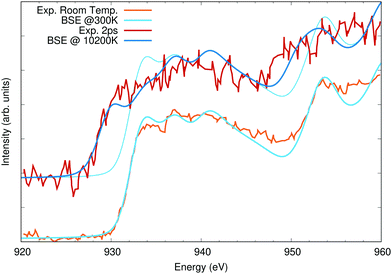 | ||
| Fig. 5 Cu L2,3 edge X-ray absorption calculations compared to measured data taken from ref. 58. The lower spectra were taken and calculated at room temperature, while the upper spectra, offset vertically for clarity, are at elevated temperature (see text for details). The 300 K calculation is shown a second time with the high-temperature spectra to highlight the shifts in spectral weight with temperature. | ||
Finite-temperature effects have also been observed in copper K-edge XAS. A two-photon measurement was carried out using an X-ray laser tuned to half the K-edge energy (4500 eV).65 Unlike standard absorption measurements, which for 3d transition metal K edges are almost entirely within the dipole limit, this measurement explicitly probed quadrupole-like transitions. The first photon excites an electron from the 1s to a highly-non-resonant virtual p-like orbital, and the second from that p orbital into an energetically-allowed s or d state. The two-photon absorption is calculated by assuming that the two photons are absorbed in quick succession with no relaxation in the short-lived intermediate state.
The transition matrix element for this process, following eqn (20), is given by
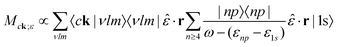 | (33) |
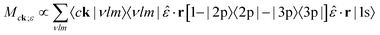 | (34) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ·r takes the place of the photon momentum q·r. For a laser both photons will have identical polarizations,
·r takes the place of the photon momentum q·r. For a laser both photons will have identical polarizations, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ‖
‖![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , while for photons the momentum must be perpendicular,
, while for photons the momentum must be perpendicular, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ⊥q. Like the standard X-ray absorption matrix elements, the terms in eqn (34) were calculated using real-space integration of the all-electron OPFs and core-level orbitals from the atomic all-electron calculation.
⊥q. Like the standard X-ray absorption matrix elements, the terms in eqn (34) were calculated using real-space integration of the all-electron OPFs and core-level orbitals from the atomic all-electron calculation.
In Fig. 6, I show the measured data reproduced from ref. 65 for both standard XAS and two-photon XAS. The two-photon XAS measurement was not explicitly at elevated temperature. However, the high X-ray fluence required for the measurement resulted in inevitable sample heating, and the large 6 eV redshift is evidence of a significant depopulation of the 3d bands. The measured two-photon absorption is not consistent with a single elevated electronic temperature. The redshift can be reproduced with temperatures exceeding 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K but at this temperature a significant white line is predicted. This extreme temperature is also inconsistent with the experimental setup or measurements of the one-photon absorption which show only a slight decrease in intensity around 8980 eV,65 reflecting only a small amount of Fermi blocking due to thermal excitations. Instead, the observed two-photon absorption is consistent with non-thermal depopulation of the 3d band, likely either due to one-photon absorption from the 3d orbitals or far-from resonance excitations from the L2,3 followed by radiative or non-radiative decays involving the 3d states. To approximate this, a constant occupation of 0.91 has been assumed for valence bands (4s and 3d) below the Fermi level. In Fig. 6, calculations using either this reduced valence occupation or 300 K Fermi statistics are compared to the measured two-photon and one-photon absorption, respectively, including an additional 1.5 eV FWHM of Gaussian broadening. The calculated two-photon absorption shows decent agreement with the measured data, but it may be fortuitous. The data is sparse and has relatively large uncertainty in the intensity.
000 K but at this temperature a significant white line is predicted. This extreme temperature is also inconsistent with the experimental setup or measurements of the one-photon absorption which show only a slight decrease in intensity around 8980 eV,65 reflecting only a small amount of Fermi blocking due to thermal excitations. Instead, the observed two-photon absorption is consistent with non-thermal depopulation of the 3d band, likely either due to one-photon absorption from the 3d orbitals or far-from resonance excitations from the L2,3 followed by radiative or non-radiative decays involving the 3d states. To approximate this, a constant occupation of 0.91 has been assumed for valence bands (4s and 3d) below the Fermi level. In Fig. 6, calculations using either this reduced valence occupation or 300 K Fermi statistics are compared to the measured two-photon and one-photon absorption, respectively, including an additional 1.5 eV FWHM of Gaussian broadening. The calculated two-photon absorption shows decent agreement with the measured data, but it may be fortuitous. The data is sparse and has relatively large uncertainty in the intensity.
 | ||
| Fig. 6 Cu K edge X-ray absorption calculations compared to measured data taken from ref. 65 (error bars from the original publication). The two-photon calculated spectra assume a 9% depopulation of the valence bands, leading to the appearance of a strong pre-edge peak from transitions into the otherwise fully occupied 3d states. | ||
4 Further examples
4.1 Dependence on the underlying DFT
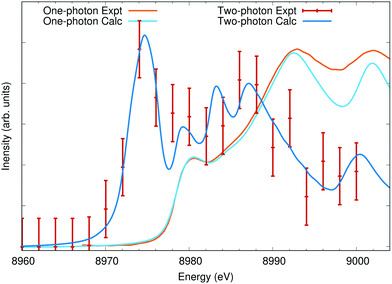
To highlight the effect of the exchange–correlation potential on computed spectra, the O and Fe edges of α-Fe2O3 hematite have been calculated using three different approximations: LDA, PBE, and SCAN. The lattice parameters for α-Fe2O3 hematite were taken from experiment,67 but for each functional the atoms were allowed to relax. No Hubbard-U parameter was included in the calculations. While a +U parameter is capable of reproducing the band gap, it also has the effect of collapsing the two distinct peaks in the O K-edge XAS into a single feature. The band gaps were calculated to be approximately 0.40 eV with LDA, 0.69 eV with PBE, and 1.55 eV with SCAN, as compared to an experimental value of approximately 2 eV.66 The calculated magnetic moments on the Fe sites were found to be 3.4μB, 3.4μB, and 3.7μB, respectively.The Fe L2,3 edge is shown in Fig. 7(a), and all three calculations are normalized and aligned to match the first peak at 707.5 eV. Among the three calculated spectra, only very slight differences in the crystal field splitting is evident between the 3d orbitals: the t2g at 707.5 eV and the eg 709 eV and again at the L2 edge at 721 eV and 722.5 eV. However, there is a significant difference in the spectral weight distribution between the t2g and eg, with PBE giving the smallest eg and SCAN the largest. It is not clear which gives the best agreement with experiment. The BSE does not capture the full multiplet structure of the Fe L2,3 edge and is missing coupling to secondary dd* excitations.68,69 The calculated spin–orbit splitting between the Fe 2p3/2 and 2p1/2 states was scaled by 1.09 to better match the observed spacing between the L3 and L2 edges. The O K edge in Fig. 7(b) provides another view of the same orbitals. The first two peaks in the oxygen XAS of transition metal oxides are due to hybridization between O p and Fe d orbitals. Here the ratio between t2g and eg clearly favors the LDA and PBE over the SCAN calculation, an outcome counter to the performance of the three functionals in reproducing the band gap.
 | ||
| Fig. 7 (a) The iron L2,3 edge and (b) the oxygen K edge of Fe2O3 calculated using three different approximations to the DFT exchange correlation potential and compared with experiment from ref. 66. The iron L edges were aligned and scaled to the lowest feature at 707.5 eV and the O K edge to the second fearture at 530.5 eV. The differences between the three calculations are minor, however the SCAN potential shows a markedly higher intensity in the eg orbitals compared to PBE or LDA as can be noted at 530.5 eV or 709 eV. | ||
4.2 State-dependent lifetime broadening
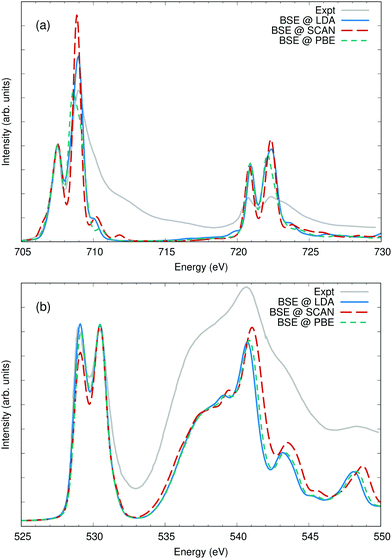
In a number of systems, the lifetime broadening of the excited state cannot be taken as a constant across the spectra. In general, the photoelectron lifetime gets shorter with higher excitation energy, and the broadening steadily increases over an energy scale set by the plasmon energy. It has also been found that valence-band lifetimes can vary widely with orbital, and both conduction and valence band lifetime effects can be included in OCEAN calculations through a complex-valued self-energy correction.18 At L2,3 edges, the 2p3/2 holes have longer lifetimes than the 2p1/2 holes due to Coster-Kronig transitions from a 2p1/2 hole to a 2p3/2 but not vice versa. As noted in Section 2.2.1.3, this effect can be captured by including an imaginary component to the spin–orbit splitting.To showcase this, I examine calculations of the titanium L2,3 edge of strontium titanate and compare to experiment in Fig. 8. The spectra splits into four main peaks. The empty 3d orbitals are divided by symmetry into two groups, the lower-energy t2g (dxy, dxz, dyz) which minimize overlap with the neighboring oxygen atoms and the higher-energy eg (dx2−y2, dz2) which point along the Ti–O bonds. These two 2p → 3d transitions are split into four by the 2p spin–orbit splitting. The Ti 2p spin–orbit splitting parameter ζ2p is calculated to be 3.83 eV, but was lowered to 3.76 eV to better match experiment. The L3 and L2 core–hole lifetime broadening were set to 0.25 eV and 0.52 eV, respectively.40 An additional 0.5 eV broadening factor was added to the the eg orbitals to match the additional vibrational broadening of these states.71 The calculated spectra show agreement with the measured data in line with previous first-principles calculations.70,72,73
 | ||
| Fig. 8 The Ti L2,3 edge of SrTiO3 calculated using three different broadening methods compared to measured data taken from ref. 70. All calculated spectra have a uniform broadening of 0.25 eV full-width at half maximum. Selectively, peaks associated with the L2 edge (2p1/2 holes) are broadened to 0.52 eV, and peaks associated with the 3d eg states are broadened by an additional 0.5 eV. | ||
4.3 Finite momentum transfer
As mentioned in Section 2.3.1.2, OCEAN can calculate non-resonant inelastic X-ray scattering (NRIXS) in which an X-ray photon scatters off of a core-level electron transferring both energy and momentum to the electron. Experimentally, NRIXS gives additional flexibility to X-ray measurements. Soft X-ray transitions below 1000 eV can be probed using hard X-rays with much longer penetration depths. The longer penetration depth allows a variety of sample conditions not possible with soft X-ray such as measuring at high pressures or measuring a component of an operating device like a battery or catalyst. NRIXS also decouples the energy and momentum transfer of the excitation. Measurements at a single X-ray edge can be carried out for several momenta, revealing dipole-forbidden transitions and allowing an investigation of the momentum dependence of the local density of states around the absorbing atom. Here, OCEAN calculations of liquid water have been carried out both in the dipole limit and for several finite momenta.The near-edge X-ray spectra of both liquid water and ice have been studied extensively over the past decade. It is known that the hydrogen bonding network in water affords both low density and high density phases (in part due to the existence of both low-density and high-density amorphous ice). However, debate continues around the coexistence of low and high density liquid water phases and the nature of density fluctuations in liquid water.75–78 Large simulation cells are necessary to capture proposed density fluctuations that reach the scale of ≈1 nm.76 First-principles calculations of the oxygen K-edge spectra have been carried out, including using the BSE,17,31,74,79 but often on small unit cells that might have large artifacts due to artificial periodicity or using various additional approximations to the BSE interactions.
Here, 64-molecule water cells were generated by the Deep Potential Molecular Dynamics model.81–83 This model was trained using the PBE0 functional84 and Tkatchenko-Scheffler approximation to the van der Waals interactions.85 The snapshots were generated using path-integral molecular dynamics with 8 beads and NPT conditions: 64 molecules, 300 K, and 100 kPa. (1 bar).86OCEAN calculations were carried out using the SCAN functional and the LDA approximation to fxc for the core–hole screening29 on 16 snapshots: two time steps separated by 1 ps across all 8 beads. For each snapshot spectra are calculated for 3 orthogonal photon polarizations (for XAS) or momenta (NRIXS) and averaged together to form a single σi. These are averaged to form a single average spectrum ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) with a variance S given by
with a variance S given by 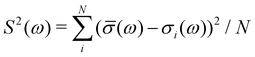 . The resulting spectrum, broadened by an 0.6 eV FWHM Gaussian in addition to the 0.08 eV of core–hole broadening, is shown in Fig. 9 compared with experiment taken from ref. 74.
. The resulting spectrum, broadened by an 0.6 eV FWHM Gaussian in addition to the 0.08 eV of core–hole broadening, is shown in Fig. 9 compared with experiment taken from ref. 74.
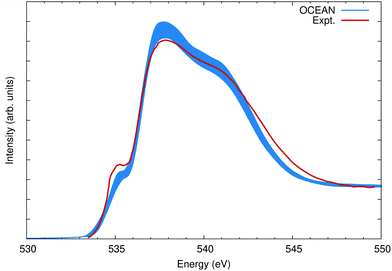 | ||
| Fig. 9 The O K edge of liquid water calculated as an average over 16 snapshots and compared to measurements from ref. 74. The width of the OCEAN line reflects the variance in the mean (see text). Both the calculation and experiment are non-resonant X-ray scattering at a momentum transfer of 3.1 Å−1, which is nearly the same as the dipole absorption [see Fig. 10(b)]. | ||
The photon-momentum dependence is shown in Fig. 10. Again the calculations were aligned to the onset of the main edge, resulting in an 0.3 eV relative shift with respect to Fig. 9. Here the intensity is normalized to the main edge region, between 537 eV and 543 eV, and compared to measurements at q = 2.6 Å−1 and q = 8.2 Å−1.75 The agreement at different momenta and in comparison to different experimental data sets is comparable. Furthermore, by contrasting low-q and high-q NRIXS, it is clear that the relative balance between s-type and p-type final states around the oxygen atoms is similar between the calculation and experiment, see Fig. 10(b). The same discrepancies are seen between the calculation and measurements at all three values of the momentum transfer: a weaker pre-edge at 535 eV, slight overstatement of the main edge at 537 eV, and too narrow overall resulting in reduced spectral weight around 544 eV. It is possible GW corrections would alleviate some of this, though recent GW-BSE calculations show a comparable level of agreement, albeit using a different DFT exchange–correlation and different approximations to the electron–hole interactions.79 It would be instructive to compare calculations of various ice phases to understand if these deficiencies arise due to the structural models used for liquid water or if they are more general to water and ice systems.
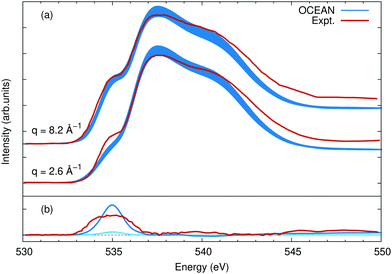 | ||
| Fig. 10 (a) The O K edge of liquid water as seen with NRIXS at momenta of 2.6 Å−1 and 8.2 Å−1. Other than the value of the momentum transfer the details of the calculation are the same as for Fig. 9, and the experimental data is from ref. 75. (b) The difference between the high and low momentum spectra for OCEAN in blue and the measured data in red. For reference, the difference between q = 2.6 Å−1 and a dipole XAS calculation is shown in cyan, showing already a slight increase in the pre-edge feature at finite momentum. While the calculated pre-edge appears to be growing faster with increasing momentum in (a) than the measured pre-edge, in (b) it is clear that in the measured data the pre-edge is wider at higher q. The change in the area of the pre-edge is very similar between OCEAN and experiment. | ||
4.4 Timing
A practical concern with any computational method is the cost – the product of the amount of time and size of computer system required to carry out a calculation. BSE methods have long been considered expensive. The fundamental scaling of the BSE is N3 where N is a measure of the unit cell size. However, the Haydock recursion is only the final step in a BSE calculation, and, despite its poor scaling with system size, usually not the longest step. Pre-computing the dielectric screening for the direct interaction scales as N2log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N,29 and the DFT calculations to generate orbitals for both the screening and BSE calculations scale as N3.
N,29 and the DFT calculations to generate orbitals for both the screening and BSE calculations scale as N3.
The time required to run several of the examples shown so far using a desktop computer3,80 is summarized in Table 1. These are all small systems, under 700 a.u.3 and with 1 to 10 atoms in the unit cell. To compare with previous performance, the timing using OCEAN version 2.0.3 are also shown for hBN and SrTiO3. The DFT times between code versions are not directly comparable as the older version of OCEAN requires an older version of QUANTUM ESPRESSO (5.2.0) and does not support the same PseudoDojo pseudopotentials. However, the times for the DFT stage are similar. The largest difference in timing is seen in the Screen stage, but the time required for the BSE stage has also been substantially reduced.
| System | Edge | Vol. (a.u.3) | N k | N b BSE | N b screen | DFT (s) | Prep (s) | Screen (s) | BSE (s) | Total (min) |
|---|---|---|---|---|---|---|---|---|---|---|
| h-BN | N K | 390.0 | 16 × 16 × 4 | 36 | 271 | 523.6 | 42.0 | 163.2 | 68.1 | 13.3 |
| * v2.0.3 | 628.7 | 53.1 | 913.4 | 120.8 | 28.6 | |||||
| SrTiO3 | Ti L2,3 | 401.9 | 8 × 8 × 8 | 128 | 300 | 777.9 | 34.8 | 350.3 | 115.2 | 21.3 |
| * v2.0.3 | 760.0 | 49.3 | 1827.3 | 161.1 | 46.6 | |||||
| Cu | Cu K | 79.4 | 16 × 16 × 16 | 10 | 90 | 146.8 | 52.5 | 277.2 | 36.1 | 8.5 |
| Fe2O3 | Fe L2,3 | 678.8 | 8 × 8 × 8 | 60 | 257 | 9055.8 | 196.3 | 72.0 | 85.5 | 156.8 |
| CdS | S L2,3 | 674.3 | 12 × 12 × 8 | 40 | 256 | 4576.9 | 136.8 | 415.3 | 247.6 | 89.6 |
To test the performance of OCEAN for large systems the oxygen K edge of water was calculated using 64-, 128-, and 256-molecule cells using a small computer cluster.3,87 The cells were constructed by making super cells of the aforementioned 64-molecule water snapshots. The computational cost of calculating the spectra of various sized water cells is summarized in Table 2. These calculations show that OCEAN is suitable for simulating cells up to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u.3 or around 7 nm3.
000 a.u.3 or around 7 nm3.
| NH2O | Nproc | DFT (m) | Prep (m) | Screen (m) | BSE (m) |
|---|---|---|---|---|---|
| 64 | 256 | 36.1 | 4.7 | 7.6 | 20.2 |
| 128 | 256 | 173.2 | 7.9 | 24.8 | 60.4 |
| 256 | 512 | 576.3 | 23.2 | 60.6 | 162.9 |
5 Outlook and future development
The OCEAN package provides an easy-to-use interface for calculating spectra using the Bethe-Salpeter equation approach. Recent advances have focused on improving the reliability and usefulness of the code for end users by simplifying the inputs and reducing the required information to a minimum. Here a few examples have been shown highlighting new functionality that has been added to OCEAN. Future development of OCEAN will focus in part on increased usability, such as additional pre- and post-processing scripts to facilitate converting structural information such as the Crystallographic Information File (CIF) to an OCEAN input as well as automatically calculating additional ground-state properties such as the projected density of states to aid in interpreting spectra. The DFT stage of OCEAN takes a substantial part of the total computational time due to the large number of unoccupied states required for both the BSE and the screening calculations. Various methods for extrapolation, wave function approximation, or exploiting completeness relations have been suggested in literature and should be investigated for incorporation into OCEAN.There are a number of approximations in OCEAN that can be alleviated through future development. The Tamm-Dancoff approximation is not mandatory in several valence-level BSE codes,11,12 and going beyond it may prove important for simulating momentum-dependent RIXS. The valence BSE solver is now capable of calculating interactions of triplet states in support of L2,3 RIXS, but OCEAN does not support directly calculating spin-triplet valence-level exciton states. For heavier elements or surface states the valence and conduction band spin–orbit coupling can become significant, but currently OCEAN requires collinear spin in the DFT orbitals. Finally, moving beyond the static screening approximation is required to more realistically simulate finite-temperature or non-equilibrium ground states (pump–probe experiments), especially in materials that are semiconductors or insulators in their ground state. Dynamic screening may also be important for transition metal L edges where the 2p splitting is of the same order as the plasmon response, but frequency dependent screening has not yet been investigated for core-level BSE spectra.
At present, OCEAN is limited to simulating excitations that consist of a single electron–hole pair. This ignores the coupling to secondary electron–hole excitations, such as what is seen in the multiplet structure of transition metal L2,3 edges with partial d-band occupancy.39 It also precludes phonon dynamics in response to the creation of the core hole which can influence both absorption and emission spectra. The challenge is extending the BSE approach without a large increase in the size of the Hamiltonian such that calculating spectra of extended systems remains tractable. Some work has been done using a cumulant spectral function to add many-body effects to BSE spectra.70 However, this approach simplifies the spectral function as independent of the photoelectron, and it is not currently applicable if the many-body effects are dependent on symmetry or localization of the photoelectron.
Author contributions
J. V. wrote the manuscript and implemented the changes to the OCEAN code.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The development of what is now OCEAN has taken place over more than 20 years and long predates my involvement and the name OCEAN itself. Much of the work has been carried out by Eric L. Shirley, but I would also like to acknowledge the various contributors and coauthors of earlier versions and earlier efforts: L. X. Benedict, R. B. Bohn, S. D. Dalosto, K. Gilmore, J. J. Kas, A. Krotz, H. M. Lawler, Z. H. Levine, Y. Liang, S. D. Pemmaraju, D. Prendergast, J. J. Rehr, J. A. Soininen, and F. Vila.Notes and references
- J. Vinson, J. J. Rehr, J. J. Kas and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106 CrossRef PubMed.
- K. Gilmore, J. Vinson, E. Shirley, D. Prendergast, C. Pemmaraju, J. Kas, F. Vila and J. Rehr, Comput. Phys. Comm., 2015, 197, 109–117 CrossRef CAS.
- Specific software and hardware are identified for information purposes. Such identification is not intended to imply recommendation or endorsement by NIST, nor is it intended to imply that the software or hardware identified are necessarily the best available for the purpose.
- H. M. Lawler, J. J. Rehr, F. Vila, S. D. Dalosto, E. L. Shirley and Z. H. Levine, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205108 CrossRef.
- The ocean code is available at https://www.ocean-code.com v. 3.0.0.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 80, 3320–3323 CrossRef CAS.
- L. X. Benedict, E. L. Shirley and R. B. Bohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, R9385–R9387 CrossRef CAS.
- L. X. Benedict, E. L. Shirley and R. B. Bohn, Phys. Rev. Lett., 1998, 80, 4514–4517 CrossRef CAS.
- E. L. Shirley, Phys. Rev. Lett., 1998, 80, 794–797 CrossRef CAS.
- X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J.-M. Beuken, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, N. Brouwer, F. Bruneval, G. Brunin, T. Cavignac, J.-B. Charraud, W. Chen, M. Côté, S. Cottenier, J. Denier, G. Geneste, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, X. He, N. Helbig, N. Holzwarth, Y. Jia, F. Jollet, W. Lafargue-Dit-Hauret, K. Lejaeghere, M. A.-L. Marques, A. Martin, C. Martins, H. P.-C. Miranda, F. Naccarato, K. Persson, G. Petretto, V. Planes, Y. Pouillon, S. Prokhorenko, F. Ricci, G.-M. Rignanese, A. H. Romero, M. M. Schmitt, M. Torrent, M. J. van Setten, B. V. Troeye, M. J. Verstraete, G. Zérah and J. W. Zwanziger, Comput. Phys. Commun., 2020, 248, 107042 CrossRef CAS.
- D. Sangalli, A. Ferretti, H. Miranda, C. Attaccalite, I. Marri, E. Cannuccia, P. Melo, M. Marsili, F. Paleari, A. Marrazzo, G. Prandini, P. Bonfà, M. O. Atambo, F. Affinito, M. Palummo, A. Molina-Sánchez, C. Hogan, M. Grüning, D. Varsano and A. Marini, J. Phys.: Condens. Matter, 2019, 31, 325902 CrossRef CAS PubMed.
- J. Deslippe, G. Samsonidze, D. A. Strubbe, M. Jain, M. L. Cohen and S. G. Louie, Comput. Phys. Commun., 2012, 183, 1269–1289 CrossRef CAS.
- C. Vorwerk, B. Aurich, C. Cocchi and C. Draxl, Electronic Structure, 2019, 1, 037001 CrossRef CAS.
- F. M. de Groot, H. Elnaggar, F. Frati, R. Pan Wang, M. U. Delgado-Jaime, M. van Veenendaal, J. Fernandez-Rodriguez, M. W. Haverkort, R. J. Green, G. van der Laan, Y. Kvashnin, A. Hariki, H. Ikeno, H. Ramanantoanina, C. Daul, B. Delley, M. Odelius, M. Lundberg, O. Kuhn, S. I. Bokarev, E. Shirley, J. Vinson, K. Gilmore, M. Stener, G. Fronzoni, P. Decleva, P. Kruger, M. Retegan, Y. Joly, C. Vorwerk, C. Draxl, J. Rehr and A. Tanaka, J. Electron Spectrosc. Relat. Phenom., 2021, 249, 147061 CrossRef CAS.
- in International Tables for Crystallography Volume I, X-ray absorption spectroscopy and related techniques, ed. C. T. Chantler, F. Boscherini and B. Bunker, 2020 Search PubMed.
- C. Brouder, D. Cabaret, A. Juhin and P. Sainctavit, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115125 CrossRef.
- H. Guo, E. Strelcov, A. Yulaev, J. Wang, N. Appathurai, S. Urquhart, J. Vinson, S. Sahu, M. Zwolak and A. Kolmakov, Nano Lett., 2017, 17, 1034–1041 CrossRef CAS PubMed.
- J. Vinson, T. Jach, M. Müller, R. Unterumsberger and B. Beckhoff, Phys. Rev. B, 2016, 94, 035163 CrossRef PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A.-D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- L. Hedin, Phys. Rev., 1965, 139, A796–A823 CrossRef.
- J. Vinson and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195135 CrossRef.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- The open-source code oncvpsp is available at http://www.mat-simresearch.com v. 3.3.1. Modifications for use with ocean are avaiable at https://github.com/jtv3/oncvpsp.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. Vinson and E. L. Shirley, Phys. Rev. B, 2021, 103, 245143 CrossRef CAS.
- W. Zhang, M. Topsakal, C. Cama, C. J. Pelliccione, H. Zhao, S. Ehrlich, L. Wu, Y. Zhu, A. I. Frenkel, K. J. Takeuchi, E. S. Takeuchi, A. C. Marschilok, D. Lu and F. Wang, J. Am. Chem. Soc., 2017, 139, 16591–16603 CrossRef CAS PubMed.
- J. Vinson, J. J. Kas, F. D. Vila, J. J. Rehr and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045101 CrossRef.
- M. Wansleben, J. Vinson, A. Wählisch, K. Bzheumikhova, P. Hönicke, B. Beckhoff and Y. Kayser, J. Anal. At. Spectrom., 2020, 35, 2679–2685 RSC.
- E. E. Salpeter and H. A. Bethe, Phys. Rev., 1951, 84, 1232–1242 CrossRef.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- X. Blase, I. Duchemin, D. Jacquemin and P.-F. Loos, J. Phys. Chem. Lett., 2020, 11, 7371–7382 CrossRef CAS PubMed.
- T. Sander, E. Maggio and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045209 CrossRef.
- M. Rohlfing and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927–4944 CrossRef CAS.
- L. X. Benedict and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 5441–5451 CrossRef CAS.
- F. de Groot, Coord. Chem. Rev., 2005, 249, 31–63 CrossRef CAS.
- J. Campbell and T. Papp, At. Data Nucl. Data Tables, 2001, 77, 1–56 CrossRef CAS.
- R. Haydock, V. Heine and M. J. Kelly, J. Phys. C: Solid State Phys., 1975, 8, 2591–2605 CrossRef.
- C. Lanczos, J. Res. Natl. Bur. Stand., 1952, 49, 33 CrossRef.
- C. Gougoussis, M. Calandra, A. P. Seitsonen and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 075102 CrossRef.
- Y. Saad and M. H. Schultz, SIAM, 1986, 7, 856–869 Search PubMed.
- T. Aoki and K. Ohno, Phys. Rev. B, 2019, 100, 075149 CrossRef CAS.
- C. Vorwerk, F. Sottile and C. Draxl, Phys. Rev. Res., 2020, 2, 042003 CrossRef CAS.
- L. Weinhardt, O. Fuchs, A. Fleszar, M. Bär, M. Blum, M. Weigand, J. D. Denlinger, W. Yang, W. Hanke, E. Umbach and C. Heske, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165305 CrossRef.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- L. Weinhardt, O. Fuchs, E. Umbach, C. Heske, A. Fleszar, W. Hanke and J. D. Denlinger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165207 CrossRef.
- E. Luppi, H.-C. Weissker, S. Bottaro, F. Sottile, V. Veniard, L. Reining and G. Onida, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 245124 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 5414–5416 CrossRef PubMed.
- M. Schlipf and F. Gygi, Comput. Phys. Commun., 2015, 196, 36–44 CrossRef CAS.
- M. van Setten, M. Giantomassi, E. Bousquet, M. Verstraete, D. Hamann, X. Gonze and G.-M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54 CrossRef CAS.
- P. Giannozzi, S. de Gironcoli, P. Pavone and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7231–7242 CrossRef CAS PubMed.
- W. Elam, B. Ravel and J. Sieber, Radiat. Phys. Chem., 2002, 63, 121–128 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. Gulans, S. Kontur, C. Meisenbichler, D. Nabok, P. Pavone, S. Rigamonti, S. Sagmeister, U. Werner and C. Draxl, J. Phys.: Condens. Matter, 2014, 26, 363202 CrossRef PubMed.
- B. I. Cho, K. Engelhorn, A. A. Correa, T. Ogitsu, C. P. Weber, H. J. Lee, J. Feng, P. A. Ni, Y. Ping, A. J. Nelson, D. Prendergast, R. W. Lee, R. W. Falcone and P. A. Heimann, Phys. Rev. Lett., 2011, 106, 167601 CrossRef CAS PubMed.
- A. Schleife, C. Rödl, F. Fuchs, K. Hannewald and F. Bechstedt, Phys. Rev. Lett., 2011, 107, 236405 CrossRef PubMed.
- D. Sangalli, S. Dal Conte, C. Manzoni, G. Cerullo and A. Marini, Phys. Rev. B, 2016, 93, 195205 CrossRef.
- T. S. Tan, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2021, 104, 035144 CrossRef CAS.
- N. Jourdain, L. Lecherbourg, V. Recoules, P. Renaudin and F. Dorchies, Phys. Rev. B, 2018, 97, 075148 CrossRef CAS.
- B. I. Cho, T. Ogitsu, K. Engelhorn, A. A. Correa, Y. Ping, J. W. Lee, L. J. Bae, D. Prendergast, R. W. Falcone and P. A. Heimann, Sci. Rep., 2016, 6, 18843 CrossRef CAS PubMed.
- B. Mahieu, N. Jourdain, K. Ta Phuoc, F. Dorchies, J.-P. Goddet, A. Lifschitz, P. Renaudin and L. Lecherbourg, Nat. Commun., 2018, 9, 3276 CrossRef CAS PubMed.
- K. Tamasaku, E. Shigemasa, Y. Inubushi, I. Inoue, T. Osaka, T. Katayama, M. Yabashi, A. Koide, T. Yokoyama and T. Ishikawa, Phys. Rev. Lett., 2018, 121, 083901 CrossRef CAS PubMed.
- L. W. Finger and R. M. Hazen, J. Appl. Phys., 1980, 51, 5362–5367 CrossRef CAS.
- S. Shen, J. Zhou, C.-L. Dong, Y. Hu, E. N. Tseng, P. Guo, L. Guo and S. S. Mao, Sci. Rep., 2014, 4, 6627 CrossRef CAS PubMed.
- P. S. Miedema and F. M. de Groot, J. Electron Spectrosc. Relat. Phenom., 2013, 187, 32–48 CrossRef CAS.
- P. Kuiper, B. G. Searle, P. Rudolf, L. H. Tjeng and C. T. Chen, Phys. Rev. Lett., 1993, 70, 1549–1552 CrossRef CAS PubMed.
- J. C. Woicik, C. Weiland, C. Jaye, D. A. Fischer, A. K. Rumaiz, E. L. Shirley, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2020, 101, 245119 CrossRef CAS PubMed.
- F. M.-F. de Groot, J. C. Fuggle, B. T. Thole and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 928–937 CrossRef CAS PubMed.
- P. Krüger, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125121 CrossRef.
- R. Laskowski and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205104 CrossRef.
- J. Niskanen, C. J. Sahle, K. Gilmore, F. Uhlig, J. Smiatek and A. Föhlisch, Phys. Rev. E, 2017, 96, 013319 CrossRef PubMed.
- A. Nilsson, D. Nordlund, I. Waluyo, N. Huang, H. Ogasawara, S. Kaya, U. Bergmann, L.-A. Näslund, H. Öström, P. Wernet, K. Andersson, T. Schiros and L. Pettersson, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 99–129 CrossRef CAS.
- C. Huang, K. T. Wikfeldt, T. Tokushima, D. Nordlund, Y. Harada, U. Bergmann, M. Niebuhr, T. M. Weiss, Y. Horikawa, M. Leetmaa, M. P. Ljungberg, O. Takahashi, A. Lenz, L. Ojamäe, A. P. Lyubartsev, S. Shin, L. G.-M. Pettersson and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15214–15218 CrossRef CAS PubMed.
- J. Niskanen, M. Fondell, C. J. Sahle, S. Eckert, R. M. Jay, K. Gilmore, A. Pietzsch, M. Dantz, X. Lu, D. E. McNally, T. Schmitt, V. Vaz da Cruz, V. Kimberg, F. Gel'mukhanov and A. Föhlisch, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4058–4063 CrossRef CAS PubMed.
- L. G.-M. Pettersson, Y. Harada and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17156–17157 CrossRef PubMed.
- F. Tang, Z. Li, C. Zhang, S. G. Louie, R. Car, D. Y. Qiu and X. Wu, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2201258119 CrossRef PubMed.
- MacPro (2017) 3 GHz 10-Core Intel Xeon W with 64 GB RAM. All runs carried out using 8 processors.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- J. Han, L. Zhang, R. Car and W. E, Commun. Comput. Phys., 2018, 23, 629–639 Search PubMed.
- H.-Y. Ko, L. Zhang, B. Santra, H. Wang, W. E, R. A. DiStasio Jr and R. Car, Mol. Phys., 2019, 117, 3269–3281 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- M. Calegari and R. Car, private communication.
- Each node of the cluster has dual 2.1 GHz 16-Core Xeon Silver 4216 with 96 GB RAM.
| This journal is © the Owner Societies 2022 |