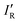Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nucleophilicity of the boron atom in compounds R–B, (R = F, Cl, Br, I, CN, NC, CH3, SiH3, CF3, H): a new look at the inductive effects of the group R†
Ibon
Alkorta
 a and
Anthony
Legon
a and
Anthony
Legon
 *b
*b
aInstituto de Química Médica (IQM-CSIC). Juan de la Cierva, 3, 28006, Madrid, Spain
bSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: a.c.legon@bristol.ac.uk
First published on 13th May 2022
Abstract
Nucleophilicities NR–B of molecules R–B (R = F, Cl, Br, I, CN, NC, CH3, SiH3, CF3, H) are determined from the equilibrium dissociation energies De of 70 hydrogen-bonded complexes R–B⋯HX (X = F, Cl, Br, I, HCN. HCCH, HCP). The change in NR–B relative to NH–B of H–B allows a quantitative measure of the inductive effect IR of each group R because only the group R affects the electron density associated with the axial non-bonding electron pair carried by the boron in R–B. An alternative definition of IR, suggested by the strong correlation of the NR–B values with the minimum value σmin of the molecular electrostatic surface potential on the 0.001 e Bohr−3 iso-surface along the R–B axis leads to excellent agreement between the two definitions.
The molecule fluoroborylene F–B has a
 electronic ground state, is isoelectronic with both CO and N2, and has been characterized experimentally1–3 including via its millimeter wave spectrum.4 It differs from its two isoelectronic analogues both in its chemical stability and in its considerably lower bond order. A generalized valence bond investigation5 concludes that the predominant contribution to the valence-bond description of the molecule is from the Lewis structure that has a single covalent bond, 3 equivalent non-bonding electron pairs on F and one non-bonding pair on the axis at B. The negative end of the electric dipole moment3 is at the B atom, indicating that B is the nucleophilic region of BF. In this article, we report ab initio calculations of the geometries and dissociation energies De of the 70 hydrogen-bonded complexes R–B⋯HX, where R is as listed above and X = F, Cl, Br, I, CN, CP or CCH.
electronic ground state, is isoelectronic with both CO and N2, and has been characterized experimentally1–3 including via its millimeter wave spectrum.4 It differs from its two isoelectronic analogues both in its chemical stability and in its considerably lower bond order. A generalized valence bond investigation5 concludes that the predominant contribution to the valence-bond description of the molecule is from the Lewis structure that has a single covalent bond, 3 equivalent non-bonding electron pairs on F and one non-bonding pair on the axis at B. The negative end of the electric dipole moment3 is at the B atom, indicating that B is the nucleophilic region of BF. In this article, we report ab initio calculations of the geometries and dissociation energies De of the 70 hydrogen-bonded complexes R–B⋯HX, where R is as listed above and X = F, Cl, Br, I, CN, CP or CCH.
The molecules CO and N2 have featured centrally in the identification and characterization of both hydrogen-bonded interactions with Lewis acids6,7 such as HX (X = F, Cl, Br, I, CN, CCH) and of halogen-bonded complexes with Lewis acids such as XY = ClF, Cl2, BrCl, Br2 and ICl.8 The electronic structure of B–F, especially the axial non-bonding pair at B, suggests that B–F, like N2 and CO, will form linear hydrogen-bonded complexes of the type F–B⋯HX.9 Moreover, given that the predominant valence-bond structure of F–B has a single bond, it should be possible to replace F in F–B by other monovalent atoms/groups R, for example, R = H, CH3, SiH3, CF3, Cl, Br, I, CN, NC.
Herein, we examine the effect of the group R on De of the R–B⋯HX complexes and from this determine the nucleophilicity of the boron atom in the various molecules R–B. It has been established elsewhere10–12 that the equilibrium dissociation energy De of a complex formed by a Lewis base with a Lewis acid via a non-covalent interaction (such as a hydrogen bond, a halogen bond, etc.) can be written in terms of the nucleophilicity Nbase of the Lewis base and the electrophilicity Eacid of the Lewis acid according to the expression
| De = c′NbaseEacid | (1) |
For convenience, the constant c′ is chosen to be the unit of energy 1.0 kJ mol−1 so that Nbase and Eacid will be dimensionless when De is measured in kJ mol−1. Through a least-squares analysis of ab initio-calculated De values of 250 complexes involving a range of types of non-covalent interaction, a set of Nbase and Eacid values were determined12 for 11 simple Lewis bases (N2, CO, HC ≡ CH, CH2 = CH2, C3H6, PH3, H2S, HCN, H2O, H2CO and NH3) and 24 Lewis acids (including most of the series of interest here, namely HF, HCl, HBr, HC ≡ CH, HCN, HCP). The values of EHX for these Lewis acids are set out in Table 1. Note that the value EHBr = 3.94 is corrected from the value 4.56 given in ref. 12. It was re-determined from the gradient of the linear regression fit of the Deversus Nbase plot for the series of complexes base⋯HBr, where base = N2, CO, HC≡CH, CH2=CH2, PH3, H2S, HCN, H2O and NH3. This graph is available as Fig. S1 of the ESI.† The previously undetermined value EHI = 2.77 was similarly obtained from the linear regression fit of the corresponding graph for the base⋯HI series, also shown in Fig. S1 (ESI†).
| Lewis acid HX | E HX | H3C–B | H3Si–B | H–B | F–B | Cl–B | Br–B | I–B | NC–B | CN–B | F3C–B |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HF | 6.75 | 40.46 | 35.82 | 33.39 | 21.52 | 25.59 | 24.10 | 23.19 | 23.07 | 24.82 | 21.50 |
| HCl | 4.36 | 26.26 | 22.92 | 20.52 | 12.81 | 15.73 | 14.90 | 14.51 | 13.49 | 14.85 | 12.58 |
| HBr | 3.94 | 23.80 | 20.79 | 18.00 | 10.93 | 13.72 | 13.11 | 12.67 | 11.57 | 12.80 | 10.77 |
| HI | 2.77 | 17.28 | 14.62 | 12.59 | 7.67 | 9.79 | 9.31 | 9.46 | 8.02 | 8.99 | 7.50 |
| HCN | 3.71 | 22.26 | 18.40 | 17.28 | 11.43 | 13.91 | 13.03 | 12.45 | 10.99 | 12.81 | 10.17 |
| HCCH | 2.16 | 11.34 | 9.54 | 9.01 | 6.13 | 7.24 | 6.80 | 6.49 | 6.22 | 6.93 | 5.79 |
| HCP | 2.02 | 11.39 | 9.60 | 8.94 | 6.08 | 7.28 | 6.88 | 6.64 | 6.13 | 6.89 | 5.73 |
The main aim of this report is to the measure the nucleophilicity of the molecule R–B as a function of the group R when acting as a hydrogen-bond acceptor at boron. According to eqn (1), if De/(kJ mol−1) is plotted on the ordinate against EHX along the abscissa for each of the series of hydrogen-bonded complexes R–B⋯HX (X = F, Cl, Br, I, CN,CCH, CP), the result for a given R should be a straight line through the origin. The gradient of each such graph yields NR-B (given that c′ = 1.0 kJ mol−1). The change in NR–B with group R is a measure of the change in electron density at the non-bonding pair carried by the B atom and is presumably caused by the differing inductive effects of groups R. Some quantitative definitions of the inductive effects of the groups R based on this work are presented.
The geometries of the 70 complexes were optimized at the CCSD(T) (F12c) computational level13,14 with the cc-pVDZ-F12 basis set15 using the frozen-core approximation and were constrained to have C∞v or C3v symmetry, as appropriate. The cartesian coordinates of the optimized geometries are available in Table S1 of the ESI.† The dissociation energies De were corrected for basis set superposition error (BSSE) using the full counterpoise method of Boys and Bernadi.16 The calculation were executed with the MOLPRO program.17 The molecular electrostatic surface potentials (MESP) of the isolated R–B molecules were calculated at the MP2/aug-cc-pVTZ level with the GAUSSIAN program18 and analyzed on the 0.001 e Bohr−3 electron density iso-surface with the multiwfn program.19 MESP diagrams for all R–B molecules are available in Table S2 ESI.†
The dissociation energies De calculated at the CCSD(T)(F12c)/cc-pVTZ-F12 level of theory (after counterpoise correction) for the 10 series of hydrogen-bonded complexes R–B⋯HX having R = H, CH3, SiH3, CF3, F, Cl, Br, I, CN, NC, where X is one of F, Cl, Br, CN, I, CCH and CP for each R, are included in Table 1.
Graphs of De plotted against the electrophilicity EHX of the HX molecule (from Table 1) are set out in three separate figures, for clarity, while each contains the line for H–B⋯HX, recognizing that H is the usual reference when the inductive effects of different groups R are compared. Included in Fig. 1 are the plots for R = H, F, Cl, Br, I, while those R = H, H3C and H3Si are in Fig. 2, and those for R = H, CN, NC, F3C are in Fig. S2 (ESI†). The gradients and the values of R2 from linear regression fits of the points for each group are shown in the inset of each figure. The quality of the fit for each group R is excellent (as indicated by R2 > 0.99 in all but one case).
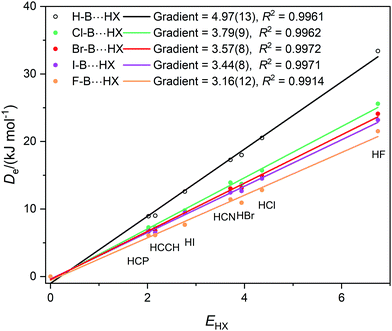 | ||
| Fig. 1 Graphs of dissociation energy De of complexes R–B⋯HX versus the electrophilicity EHX of the Lewis acid HX for R– = H–, F–, Cl–, Br– and I–. | ||
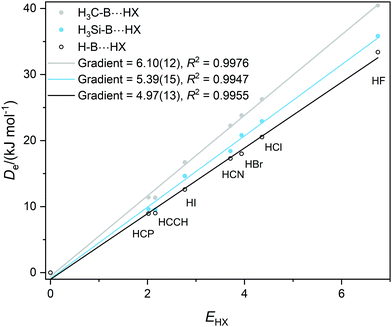 | ||
| Fig. 2 Graphs of dissociation energy De of complexes R–B⋯HX versus the electrophilicity EHX of the Lewis acids HX for R– = H–, H3C– and H3Si–. | ||
Fig. 1 shows clearly that the nucleophilicities NR–B of the R–B molecules- [see eqn (1)] are in the order R = H > Cl > Br ∼ I > F. If the inductive effect IR of a group R relative to H is defined by eqn (2):
| IR = (NR–B − NH–B) | (2) |
Then IH = 0, ICl = −1.18(22), IBr = −1.40(21), II = −1.53(21), and IF = −1.81(25). This definition is consistent with the sign of the inductive effect chosen by Ingold,20 who assigned electron attracting groups, such as halogen atoms, to have a negative inductive effect −I.
It is immediately obvious from Fig. 2 that the gradients of the Deversus EHX graphs for the H3C–B⋯HX and H3Si–B⋯HX series are greater than that for the H–B⋯HX series. This indicates that substitution of H by a methyl or a silyl group pushes electron density onto B relative to H. According to the definition given in eqn (2) the inductive effect IR of the group H3C– is IH3C = +1.13(25) and that of H3Si– is IH3Si = +0.42(28). Thus, both groups exhibit a positive inductive effect, although the range of each value transmitted from the errors in the gradients is larger than ideal.
The corresponding graphs of Deversus EHX for the series R–B⋯HX when R– is H–, CN– (isocyanide), NC– (cyanide), and F3C– (trifluoromethyl) are available in the ESI† as Fig. S2. The last three groups R are electron-withdrawing relative to H. In fact, the gradients of the graphs for R = F3C– (Fig. 3) and R = F– (Fig. 1) are the same. Given the definition IR = NR–B − NH–B in eqn (2) the inductive effects are IF3C = −1.82(27), INC = −1.32(25) and ICN = −1.56(26). Thus, the electron-withdrawing effects of the CF3 group and the F atom are identical, while the cyanide group is a better electron-withdrawing group than isocyanide and has a value ICN comparable with that of Br or I. Unfortunately, the errors in the fitted Deversus the EHX straight lines are sufficient that more precise values of the inductive effects IR of the groups R cannot be obtained by the present approach.
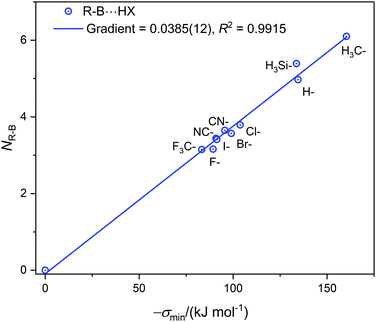 | ||
| Fig. 3 The nucleophilicities NR–B of molecules R–B (determined from the gradient of the Deversus EHX graphs in Fig. 1, 2 and Fig. S2, ESI†) plotted against σmin (the minimum value of the electrostatic potential on the 0.001 e Bohr−3 iso-surface of R–B on the molecular axis at the boron atom). | ||
In conclusion, we have shown that by calculating the equilibrium dissociation energies De for the series of hydrogen-bonded complexes R–B⋯HX, where X = F, Cl, Br, I, HCN, HCCH and HCP, it is possible to determine the nucleophilicity NR–B of the axially symmetric molecules R–B. Repeating this procedure for each group in the series R = H3C, H3Si–, H–, F–, Cl–, Br–, I–, CN– NC–, and F3C– shows that, relative to H–, the groups H3C– and H3Si– increase the nucleophilicity of the B atom in forming hydrogen bonds with HX, while the halogen atoms, the pseudo-halogens CN– and NC–, and the fully fluorinated methyl group, withdraw electronic charge from the non-bonding electron pair carried by boron. The change NR–B − NH–B in the nucleophilicity of the axial, non-bonding electron pair on B in molecules R–B relative to H–B thus, in principle, provides a clean method of assessing the inductive effect IR of the group R. This approach has the advantage that the molecular complexes R–B⋯HX are isolated from solvent effects, that the group R is directly attached to the boron atom and the changes in the De values when R is changed result directly from the changes in electron density in the non-bonding pair carried by B.
Politzer and co-workers21,22 showed some time ago that electrostatic potentials can also be related to nucleophilic processes. A useful, recent general discussion23 of molecular electrostatic surface potentials (MESPs) is available from the same group. We now examine the relationship between MESPs and the inductive effect.
The molecular electrostatic surface potential (MESP) calculated at the MP2/aug-cc-pVTZ level on the 0.001 e Bohr−3 iso-surface (in particular, the value σmin on the R–B molecular axis near to the boron atom) provides a measure of the change in electrostatic potential at the non-bonding electron pair carried by B when the group R is changed.
The values of σmin for the 10 compounds R–B (R = H3C–, H3Si–, H–, F–, Cl–, Br–, I–, CN–, NC–, and F3C–) are collected in Table 2. Fig. 3 displays a graph of NR–Bversus σmin. It is clear from Fig. 3 that there is a strong correlation between the two last-named quantities. Indeed, this suggests another way to express the inductive effect 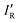 of group R, namely by the equation:
of group R, namely by the equation:
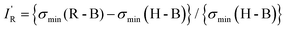 | (3) |
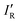 so calculated from the σmin (R–B) are included in Table 2.
so calculated from the σmin (R–B) are included in Table 2.
| Group R | σ min (R–B)a kJ mol−1 | Inductive effect InormRb | Inductive effect c | Hammett σ constantd |
|---|---|---|---|---|
| a Value of the MESP on the 0.001 e Bohr−3 iso-surface on the R–B molecular axis at boron. b As defined in eqn (4). c As defined by eqn (3). d The Hammett σ substituent constants for the para-position of benzoic acid [24]. They are positive for electron withdrawing groups and negative electron donating groups, relative to hydrogen. | ||||
| H3C– | −160.3 | 0.23 | 0.19 | −0.17 |
| H3Si– | −133.7 | 0.08 | -0.01 | 0.10 |
| H– | −134.5 | 0.00 | 0.00 | 0.00 |
| F– | −89.3 | −0.36 | −0.34 | 0.06 |
| Cl– | −103.7 | −0.24 | −0.23 | 0.23 |
| Br– | −99.0 | −0.28 | −0.26 | 0.23 |
| I– | −90.9 | −0.31 | −0.32 | 0.18 |
| NC– | −91.4 | −0.31 | −0.32 | 0.66 |
| CN– | −95.5 | −0.27 | −0.29 | 0.49 |
| F3C– | −83.3 | −0.37 | −0.38 | 0.54 |
The values determined from the nucleophilicities (NR–B − NH–B), but normalised according to the value of NHB, to give
| InormR = (NR–B − NH–B)/NH–B | (4) |
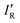 , has R2 = 0.983, a slope close to one (0.90), and an intercept near to zero (−0.032). Finally, the Hammett σ substituent constant is commonly cited24 as a measure of the relative inductive effects of groups R attached to, for example, benzoic acid and is based on how equilibrium constants for dissociation of the acid are affected by substituents R at the para- and meta-positions of the benzene ring. The values for the para-position are included in Table 2 and, after noting they are of opposite sign from the IR proposed here, the magnitudes are in only fair agreement with those of the IR introduced here, but the Hammett constant applies to equilibria/chemical reactions in solvents, and are therefore not strictly comparable.
, has R2 = 0.983, a slope close to one (0.90), and an intercept near to zero (−0.032). Finally, the Hammett σ substituent constant is commonly cited24 as a measure of the relative inductive effects of groups R attached to, for example, benzoic acid and is based on how equilibrium constants for dissociation of the acid are affected by substituents R at the para- and meta-positions of the benzene ring. The values for the para-position are included in Table 2 and, after noting they are of opposite sign from the IR proposed here, the magnitudes are in only fair agreement with those of the IR introduced here, but the Hammett constant applies to equilibria/chemical reactions in solvents, and are therefore not strictly comparable.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
ACL thanks the University of Bristol for a Senior Research Fellowship. IA thanks the Ministerio de Ciencia e Innovación of Spain (PGC2018-094644-B-C22 and PID2021-125207NB-C32) and Comunidad de Madrid (P2018/EMT-4329 AIRTEC-CM) for financial support.Notes and references
- D. L. Hildenbrand and E. Murad, J. Chem. Phys., 1965, 43, 1400–1403 CrossRef CAS.
- P. L. Timms, J. Am. Chem. Soc., 1967, 89, 1629–1632 CrossRef CAS.
- D. Vidovic and S. Aldridge, Chem. Sci., 2011, 2, 601–608 RSC.
- G. Cazzoli, L. Cludi, C. Degli Esposti and L. Dore, J. Mol. Spectrosc., 1989, 134, 159–167 CrossRef CAS.
- F. Fantuzzi, T. M. Cardozo and M. A. C. Nasimento, J. Phys. Chem. A, 2014, 119, 5335–5343 CrossRef PubMed.
- A. C. Legon, P. D. Soper, M. R. Keenan, T. K. Minton, T. J. Balle and W. H. Flygare, J. Chem. Phys., 1980, 73, 583–584 CrossRef CAS.
- P. D. Soper, A. C. Legon, W. G. Read and W. H. Flygare, J. Chem. Phys., 1982, 76, 292–300 CrossRef CAS.
- A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686–2714 CrossRef PubMed.
- I. Rozas, I. Alkorta and J. Elguero, J. Phys. Chem. A, 1999, 103, 8861–8869 CrossRef CAS.
- A. C. Legon and D. J. Millen, J. Am. Chem. Soc., 1987, 109, 356–358 CrossRef CAS.
- A. C. Legon, Phys. Chem. Chem. Phys., 2014, 16, 12415–12421 RSC , see Correction 2014, 16, 25199-25199.
- I. Alkorta and A. C. Legon, Molecules, 2017, 22, 1786–1799 CrossRef PubMed.
- C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74 CrossRef PubMed.
- J. G. Hill and K. A. Peterson, J. Chem. Phys., 2014, 141, 094106 CrossRef PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16; Revision, A.03, Gaussian, Inc.: Wallingford, CT, USA, 2016 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell University Press, Ithaca, New York, 1953, p. 71 Search PubMed.
- J. S. Murray and P. Politzer, Chem. Phys. Lett., 1988, 152, 364–370 CrossRef CAS.
- P. Sjoberg and P. Politzer, J. Chem. Phys., 1990, 94, 3959–3961 CrossRef CAS.
- J. S. Murray and P. Politzer, WIREs Comput. Mol. Sci., 2017, 7, e1326 Search PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Optimised geometries and energies, Molecular electrostatic potential diagrams of molecules R-B. See DOI: https://doi.org/10.1039/d2cp01565j |
| This journal is © the Owner Societies 2022 |