Geometrical picture of the electron–electron correlation at the large-D limit
Kumar J. B.
Ghosh
 ab,
Sabre
Kais
ab,
Sabre
Kais
 b and
Dudley R.
Herschbach
b and
Dudley R.
Herschbach
 *c
*c
aE.ON Digital Technology GmbH, 45131, Essen, Germany. E-mail: jb.ghosh@outlook.com
bDepartment of Chemistry and Physics, Purdue University, West Lafayette, IN 47906, USA. E-mail: kais@purdue.edu
cDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA. E-mail: dherschbach@gmail.com
First published on 30th March 2022
Abstract
In electronic structure calculations, the correlation energy is defined as the difference between the mean field and the exact solution of the non relativistic Schrödinger equation. Such an error in the different calculations is not directly observable as there is no simple quantum mechanical operator, apart from correlation functions, that correspond to such quantity. Here, we use the dimensional scaling approach, in which the electrons are localized at the large-dimensional scaled space, to describe a geometric picture of the electronic correlation. Both, the mean field, and the exact solutions at the large-D limit have distinct geometries. Thus, the difference might be used to describe the correlation effect. Moreover, correlations can be also described and quantified by the entanglement between the electrons, which is a strong correlation without a classical analog. Entanglement is directly observable and it is one of the most striking properties of quantum mechanics and bounded by the area law for local gapped Hamiltonians of interacting many-body systems. This study opens up the possibility of presenting a geometrical picture of the electron–electron correlations and might give a bound on the correlation energy. The results at the large-D limit and at D = 3 indicate the feasibility of using the geometrical picture to get a bound on the electron–electron correlations.
1 Introduction
Dimensional scaling, as applied to electronic structure calculations, offers promising computational strategies and heuristic perspectives with physical insight of the electronic structure of atoms, molecules and extended systems.1–4 Taking the spatial dimension of the physical space as a variable other than D = 3 can make a problem much simpler and then one can use perturbation theory or other techniques to obtain the results at D = 3. The D-scaling technique was used first in quantum chromodynamics5 and then applied to the Helium atom.2–4 In this approach, we solve the problem at the D → ∞ limit and then add terms in powers of δ = 1/D. Using different summation techniques6 can obtain highly accurate results for D = 3. The dimensional scaling approaches were extended to N-electron atoms,7 renormalization with 1/Z expansions,8 random walks,9,10 interpolation of hard sphere virial coefficients,11 resonance states12 and dynamics of many-body systems in external fields.13,14 We refer the reader to the book “Dimensional scaling in chemical physics”15 for more details of the approach and applications.In computational physics and chemistry, the Hartree-Fock (HF) method16 is a self-consistent field approximation to determine the wave function and the energy of a quantum many-body system in a stationary state. This method is based on the idea that we can approximately describe an interacting electronic system in terms of an effective single-particle model. Moreover, this simple approximation remains the starting point for more accurate post Hartree–Fock methods such as coupled clusters and configuration interactions.
The Hartree-Fock method assumes that the exact N-body wave function of the system can be approximated by a single Slater determinant of N spin-orbitals. In quantum chemistry calculations, the correlation energy is defined as the difference between the Hartree-Fock limit energy and the exact solution of the nonrelativistic Schrödinger equation.17 Other measures of electron correlation also exist in the literature, for e.g. the statistical correlation coefficients.18 Recently the Shannon entropy is also described as a measure of the correlation strength.19,20 Electron correlations have wide implications on atomic, molecular,21 and solid state physics.22 Observing the correlation energy for large systems is one of the most challenging problems in quantum chemistry because there is no simple operator in quantum mechanics that its measurement gives the correlation energy. This leads to proposing the entanglement as an alternative measure of the electron correlation for atoms and molecules.23 All the information needed for quantifying the entanglement is contained in the two-electron density matrix. This measure is readily calculated by evaluating the von Neumann entropy of the one electron reduced density operator. As an example, one can see the calculation of the entanglement for He atom and H2 molecule with different basis sets.23 The advantage of this proposal is that entanglement is directly observable, and it is one of the most striking properties of quantum mechanics.
Entanglement is a quantum mechanical property that describes strong correlations between quantum mechanical particles that has no classical analog and has been studied extensively in the field of quantum information and quantum computing.24–29 Moreover, scientists studied numerous properties of the entanglement entropy,30–33 addressing many interesting topics of physics, for example black hole physics,34–36 distribution of quantum correlations in quantum many-body systems in one dimension30,37,38 and higher dimensions,39–42 complexity of quantum many-body systems and their simulation,43,44 and topological entanglement entropy.45–49
In this article we describe a geometric interpretation of correlation energy calculated at large-D limit and at three dimensions and establish a relation between the correlation energy and the area law of entanglement. In Section 2, we describe the area law of entanglement. In Sections 3 and 4, we describe the relation between the area difference and the correlation energy of the atomic/ionic systems and metallic hydrogen at the large-D limit. In Section 5, we consider the helium atom and the metallic hydrogen at D = 3, where the electrons are not localized unlike in the D → ∞ limit. Finally, in Section 6, we make some concluding remarks. We adopt Hartree atomic units for our calculations.
2 Area law of entanglement
In classical physics, concepts of entropy quantify the amount of information that is lacking to identify the microstate of a physical system from all the possibilities compatible with the macrostate of the system. In quantum mechanics, we define the entanglement entropy or geometric entropy,50–52 which arises because of a very fundamental property called entanglement. In quantum many-body systems, for a pure state ρ = |ψ〉 〈ψ|, the von Neumann entropy is a good measure of entanglement and defined as50| S(ρ) = −tr[ρlog2ρ] | (1) |
Generally, a quantum state |ψ〉 of n-qubits (spin ½) is represented as a vector in 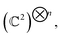
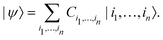 | (2) |
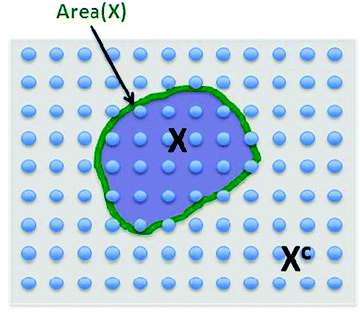
This is a very complex wave function with complex coefficients Ci, in Hilbert space of dimension 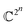 . One way to find a possible efficient representation, is to examine a bipartite system with a local gapped Hamiltonian, summing over nearest neighbor interacting particles, as shown in Fig. 1.53–57 The entanglement entropy between the interior state X and the exterior state Xc scales as the size of the boundary for every region X,
. One way to find a possible efficient representation, is to examine a bipartite system with a local gapped Hamiltonian, summing over nearest neighbor interacting particles, as shown in Fig. 1.53–57 The entanglement entropy between the interior state X and the exterior state Xc scales as the size of the boundary for every region X,
| S(X) ≤ constant × Area(X). | (3) |
Recently, the area law of bounding the entanglement entropy of the ground state energy was examined for local integrating particles with large gapped energy spectrum.53–57 It is shown that the ground state of a chain of d-dimensional spins with a boundary L and spectral gap δ is bounded by an area law
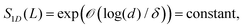 | (4) |
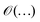 is used to denote a bound up to a numeric constant of order unity. The area law for the entanglement entropy and ground state of local Hamiltonian was further extended to two dimensional lattice.58–62 Here, we use the area law as a heuristic approach to guide us to discuss having a possible bound on the electronic correlation energy as one can obtain a well define geometrical picture of the localized electrons at the large-D limit, for both the mean field and the exact electronic structure.
is used to denote a bound up to a numeric constant of order unity. The area law for the entanglement entropy and ground state of local Hamiltonian was further extended to two dimensional lattice.58–62 Here, we use the area law as a heuristic approach to guide us to discuss having a possible bound on the electronic correlation energy as one can obtain a well define geometrical picture of the localized electrons at the large-D limit, for both the mean field and the exact electronic structure.
3 Correlation energy and the surface area for atomic systems at the large-D limit
At the large-D limit, one can obtain a simple formula for the electronic structure of N-electron atoms.7 At D → ∞ limit, the electrons are localized in the scaled space with equidistant rm from the nucleus and equiangular with respect to each other, which means that there is no shell structure. This simple geometrical picture holds for a wide variety of atoms and ions including all neutral atoms with Z < 14 and all positive ions with N/Z ≲ 0.936.7 In the Hartree–Fock limit all electrons are orthogonal to each other. The electronic energy εHF∞ and distance from the nucleus rHFm of an N-electron atom are described by the following formulas: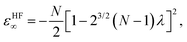 | (5) |
| rHFm = [1 − 23/2 (N − 1) λ]−1, | (6) |
After adding the inter-electronic correlation in the picture the electrons are no more orthogonal to one another. Therefore, the inter-electronic angle θ∞ becomes slightly larger than π/2, although their equi-distance property from the nucleus ρ∞ still holds. At D → ∞ limit the relevant quantities can be calculated by the following formula:
The exact energy is given by
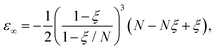 | (7) |
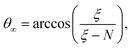 | (8) |
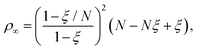 | (9) |
| 8NZ2ξ2 (2 − ξ)2 = (N− ξ)3. | (10) |
We solve the above sets of eqn (5) and (7) numerically and calculate the correlation energy at D → ∞ limit which is defined by
| εCorr∞ = |ε∞ − εHF∞|. | (11) |
For example, from the above eqn (5)–(9), we obtain the following results for the helium-atom rHFm = 1.214737, εHF∞ = −0.6776966, ρ∞ = 1.213927, θ∞ = 1.663309 rad, ε∞ = −0.68444228, and εCorr∞ = 0.0067456.
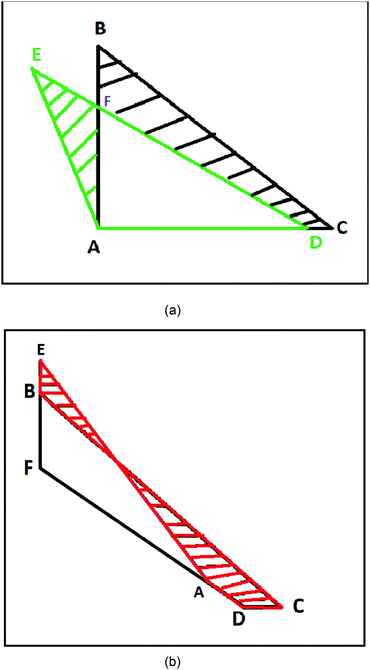
Next, we draw the following geometrical pictures of the two localized electrons of the helium-atom at D → ∞. We first construct a right angle triangle with two equal sides equal to rHFm and another isosceles triangle with two equal sides equal to ρ∞ and the inter-electronic angle θ∞.
In Fig. 2, the nucleus is fixed at the point A. The points B and C describe the positions of the two electrons at HF-limit, whereas the points D and E describe the positions of the two electrons with correlation. At HF-limit ABpAC however the correlation angle ∠EAD > π/2.
The area of the isosceles triangle was calculated with the simple formula 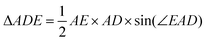 . Then we calculate the magnitude of the area difference (Δarea) between the ΔABC and ΔADE for the helium atom Δarea = 0.00413417. In Fig. 2 we show the area difference as the difference between the stripped areas.
. Then we calculate the magnitude of the area difference (Δarea) between the ΔABC and ΔADE for the helium atom Δarea = 0.00413417. In Fig. 2 we show the area difference as the difference between the stripped areas.
For three-electron atoms we construct the three triangles ΔABC, ΔACD, and ΔADB (see Fig. 3). The point A is the position of nucleus and the points B, C, D are three localized electronic positions. The sides AD = AC = AB. At HF-limit, the angles ∠BAC = ∠CAD = ∠BAD = π/2, whereas, with correlation ∠BAC = ∠CAD = ∠BAD > π/2.
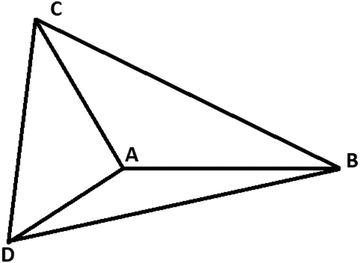 | ||
| Fig. 3 Geometry of a three-electron atom at D → ∞ limit. The point A is the position of nucleus and the points B, C, D are three localized electronic positions. | ||
As an extension of the above, we construct N-triangles for N-electron atoms and compute the total areas for both HF and with inter-electronic correlation. Then we compute the area difference for N-triangles between HF and electronic-correlation.
In Fig. 4, we describe the area difference which is computed from the N-triangles of the N-electron atom.
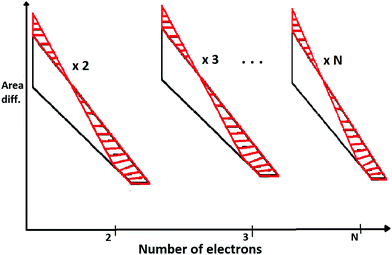 | ||
| Fig. 4 The area differences calculated for N-electron atoms at D → ∞ limit. Because of special symmetry at the large-D limit, area difference per number of electrons is the same. | ||
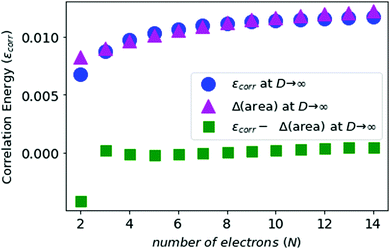
We compute the correlation energies for N-electron atoms, using eqn (5) and (7), and plot this in Fig. 5 along with the area differences obtained above.
We also compute the inverse of the electronic correlation energies and the inverse of the area difference obtained from the above prescription and plot these in Fig. 6.
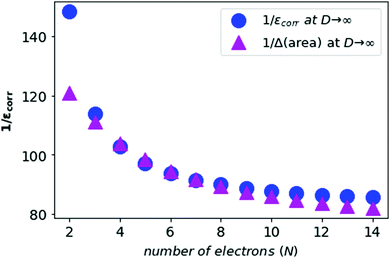 | ||
| Fig. 6 The inverse of the electronic correlation energies for neutral atoms from N = 2 to N = 14 in blue, and the inverse of area difference in purple. | ||
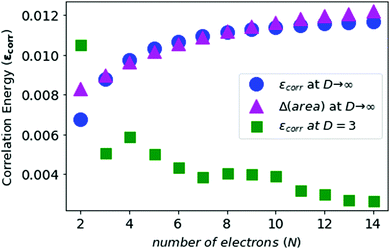
In Fig. 5 and 6, we see that the area difference is a close estimate to the correlation energy at the large-D limit. On the other hand, it was shown by Loeser et al.7 that the correlation energy at D = 3 is a good approximation to the correlation energy at D → ∞. Therefore the correlation energy is bounded by the area difference of the electronic triangles between the HF-limit and with correlation at large-D limit. We plot the known accurate correlation energies at D = 363–66 and with the correlation energies obtained at D = ∞.
In Fig. 7, we see that the correlation energies at D = 3 are bounded by the corresponding area differences at D → ∞ limit, with the only exception for N = 2.
4 Electron correlation and the surface area for metallic hydrogen at the large-D limit
In 1935, Wigner and Huntington predicted the metallization of hydrogen,67 a phase of hydrogen that behaves like an electrical conductor. Ever since this has been a major quest for condensed matter physics, pursuing theory68–72 and extreme high-pressure experiments.73–78 Dimensional scaling and interpolation as applied to metallic hydrogen was investigated in articles.68,79 With appropriate scaling, energies will be in units of 4/(D − 1)2 Hartrees, and distances in units of D (D − 1)/6 Bohr radii. we consider the lattice to be simple cubic (SC). With scaling and simplifications, the Hartree–Fock one-electron Hamiltonian in the D → ∞ limit in a lattice of hydrogen atoms with clamped nuclei can be written as:68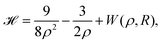 | (12) |
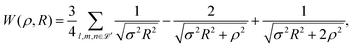 | (13) |
| σ2 = l2 + m2 + n2. | (14) |
For any specified lattice type and scaled lattice constant R, the minimum of eqn (12) with respect to ρ gives the energy per electron. The whole lattice is three-dimensional, noted 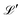 minus the one site (0,0,0). The single variable ρ is the orbit radius and R is the lattice spacing.
minus the one site (0,0,0). The single variable ρ is the orbit radius and R is the lattice spacing.
We introduce the inter-electronic correlation at D → ∞ limit by opening up the dihedral angles from their Hartree–Fock values of exactly π/2 rad. The dihedral angles in the correlated solution is determined by two effects, namely, the centrifugal effects, favoring π/2 rad, and interelectron repulsions, favoring π rad. Although the final effect turns out to be the angles very close to π/2 rad. For the calculation purpose we assume the inter-electronic correlation is up to third nearest neighbor, which is a very legitimate assumption. We assume the lattice structure to be simple cubic (SC).
At D → ∞ limit, the Hamiltonian with inter-electronic correlation can be written as:68
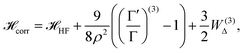 | (15) |
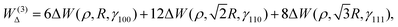 | (16) |
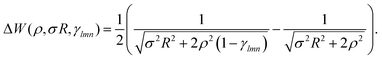 | (17) |
The 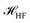 is the Hamiltonian in Hartree–Fock approximation defined in eqn (12). The quantity γlmn = cos
is the Hamiltonian in Hartree–Fock approximation defined in eqn (12). The quantity γlmn = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlmn, with θlmn are the dihedral angles which are very close to π/2. The Gramian ratio
θlmn, with θlmn are the dihedral angles which are very close to π/2. The Gramian ratio 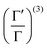 is defined as68
is defined as68
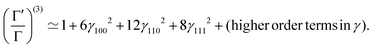 | (18) |
We optimize the above Hamiltonian (15) with respect to the parameters γ100,γ110,γ111, keeping the values of ρ and R from the HF-Hamiltonian.79
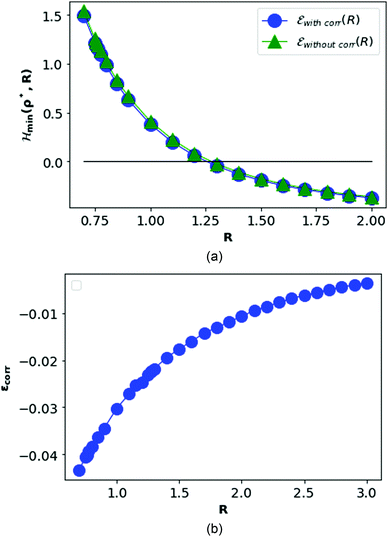
In Fig. 8, we plot the minimum values of the Hamiltonian (15) at D → ∞ limit as function of R and compare with the values obtained from the HF-Hamiltonian. We also plot the correlation energies 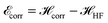 as a function of R. In the left hand side of Fig. 8, we see that the ground state energy becomes positive for R < 1.28, therefore makes the system unstable. Therefore, R > 1.28 can be think of a physically stable region for metallic hydrogen at D → ∞ limit.
as a function of R. In the left hand side of Fig. 8, we see that the ground state energy becomes positive for R < 1.28, therefore makes the system unstable. Therefore, R > 1.28 can be think of a physically stable region for metallic hydrogen at D → ∞ limit.
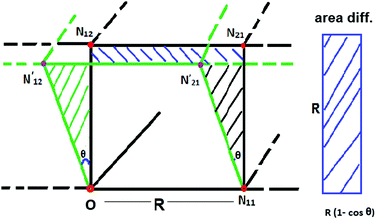
In the simple cubic lattice at D → ∞ limit, the electrons also forms a cubic structure. With each reference electron there are 6 nearest neighbors at a distance R, 12 second nearest neighbors at a distance 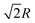 , 8 third nearest neighbors at a distance
, 8 third nearest neighbors at a distance 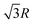 and so on. At HF-limit the nearest neighbours (N1i for i = 1, 2,… 6) are orthogonal to each other with respect to the reference electron (O). For correlation the dihedral angles between the electrons becomes slightly greater than 90°. The following figure describes a cross section of a MH in SC lattice with reference electron O. In HF limit we consider 6 square surfaces for 6 neighbouring electrons at a distance R, 12 square surfaces for 12 neighbouring electrons at a distance
and so on. At HF-limit the nearest neighbours (N1i for i = 1, 2,… 6) are orthogonal to each other with respect to the reference electron (O). For correlation the dihedral angles between the electrons becomes slightly greater than 90°. The following figure describes a cross section of a MH in SC lattice with reference electron O. In HF limit we consider 6 square surfaces for 6 neighbouring electrons at a distance R, 12 square surfaces for 12 neighbouring electrons at a distance 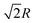 , and 8 square surfaces for 8 neighboring electrons at a distance
, and 8 square surfaces for 8 neighboring electrons at a distance 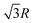 . Whereas, with inter-electronic correlation each square becomes a rhombus.
. Whereas, with inter-electronic correlation each square becomes a rhombus.
In Fig. 9, we plot the area difference due to the electronic correlation. The area difference between the square and the rhombus formed by each nearest neighbor is equal to R2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), where θ = γ100 − 90° is the angle deviation from 90° due to correlation effect. The area difference for each next nearest neighbor is equal to 2R2 (1 − cos
θ), where θ = γ100 − 90° is the angle deviation from 90° due to correlation effect. The area difference for each next nearest neighbor is equal to 2R2 (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2), with θ2 = γ110 − 90°, and so on. The total area difference due to the correlation up to the third nearest neighbor is given by:
θ2), with θ2 = γ110 − 90°, and so on. The total area difference due to the correlation up to the third nearest neighbor is given by:
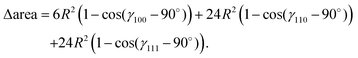 | (19) |
We vary the lattice parameter R and calculate the area difference for each value of R. In Fig. 10, we plot the correlation energy per electron for metallic hydrogen in SC lattice at large-D limit and the area difference described above as a function of the lattice parameter R.
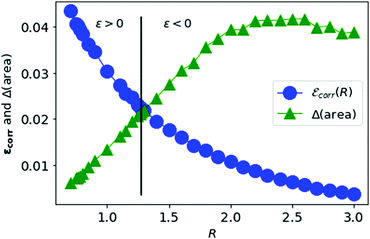 | ||
| Fig. 10 The correlation energy per electron in metallic hydrogen at D → ∞ as a function of R in blue and the area difference in green. | ||
In Fig. 10, we see that the correlation energy per electron is bounded by the area difference in the physically stable region (i.e. total ground state energy ε > 0).
The correlation energy per electron (in Rydberg unit) in metallic hydrogen at D = 3 was calculated by Neece et al.80,81
| εcorr = −0.1303 + 0.0495ln(rs). | (20) |
In the above eqn (20), the lattice constant R is related to rs, the standard solid state parameter, defined as the radius of a sphere (in a0 Bohr units) in which contains on average one electron. For the SC lattice,
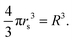 | (21) |
In Fig. 11, we plot the correlation energy of each electron in metallic hydrogen as a function of R at D = 3 and compare with the D = ∞ result.
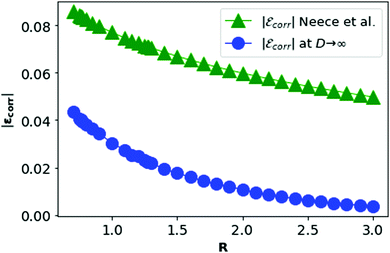 | ||
| Fig. 11 The correlation energy per electron in metallic hydrogen at D → ∞ as a function of R in blue and at D = 3 in green. | ||
In Fig. 11, we see that the correlation energy per electron (εcorr) at D → ∞ is bounded by εcorr at D = 3. Although at D = 3, there is no concept of the dihedral angles between electrons as the electrons are not localized. We shall calculate the corresponding area difference for metallic hydrogen at three dimensions in the next section.
5 Correlation energy and the surface area difference in the three-dimension
In the previous sections, we established that the correlation energies are bounded by the area differences for N-electron atoms and also for metallic hydrogen at the large-D limit. In three dimensions, the picture is different, because at D = 3 the electrons are not localized compared to the D → ∞ limit. To establish the validity of the area law and correlation energy, we consider the helium atom in three-dimensions. The two 1s electrons in the helium atom at 3D are in spherical orbitals with an average electronic radius 〈r〉. The average radius changes from 〈rHF〉 (in HF approximation) to 〈rexact〉 (with inter-electronic correlation). The area difference is the difference between the two spherical surfaces with radii 〈rHF〉 and 〈rexact〉 respectively.In the Hartree–Fock approximation, the average electronic radius82,83 is given by 〈rHF〉 = 0.92724 a.u. On the other hand, with inter-electronic correlation, a very accurate value of 〈rexact〉 = 0.92947 was computed by Thakkar et al.84
The surface area difference between the two spherical orbitals is calculated as
| Δarea = 4π (rHF2 − rexact2) = 0.0520. | (22) |
From DFT calculations the ground state energy (in Rydberg unit) per electron in metallic hydrogen in simple cubic lattice at D = 3 is expressed as86
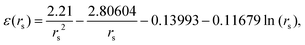 | (23) |
In Fig. 12, we see that the ground state energy becomes positive for rs < 0.68, therefore makes the system unstable. Therefore, rs > 0.68 can be think of a physically stable region for metallic hydrogen at D = 3.
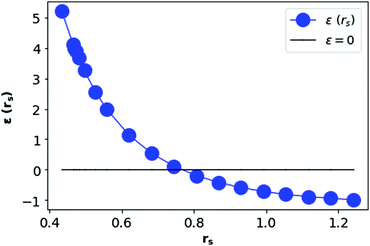 | ||
| Fig. 12 Total ground state energy (in Rydberg unit) per electron in metallic hydrogen at D = 3 as a function of rs. | ||
Now, if we introduce inter-electronic correlation, the average atomic radius in metallic hydrogen will change, i.e. the rs will change. Therefore, we can think of the correlation energy as the change in the ground state energy due to a change in the atomic radius rs, i.e.
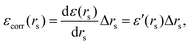 | (24) |
| Δ(area)(rs) = Δ(4πrs2) = 8πrsΔrs = 8πrsεcorr (rs)/ε′ (rs). | (25) |
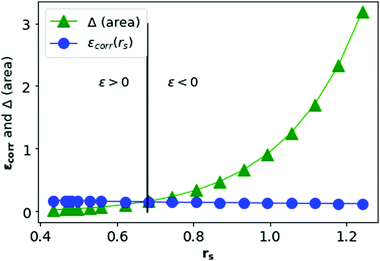
In Fig. 13, we plot the Δ(area) and εcorr as a function of rs. We see that the correlation energy per electron in MH is bounded by the area difference in the physically stable region (i.e. total ground state energy ε > 0) in three-dimension also.
6 Conclusion
Understanding quantum correlation in many-body states of matter, a feature ubiquitous in different problems of physics and chemistry, has gained renewed prominence in recent years. Experimentally, different protocols have been proposed to directly extract spatial correlation functions in phases like in the Mott regime of a Hubbard Hamiltonian87,88 due to single-site resolution and selective spin removal technique afforded by quantum-gas microscopy in platforms like ultracold-atomic lattices. Such techniques have also been used to study response of magnetic field on an spin-imbalanced 2D lattice of fermions wherein there is a competition to maintain the anti-ferromagnetic checkerboard pattern and alignment with the externally applied field leading to canted lattices.89 Even dynamical correlation from retarded Green's function can be obtained experimentally using Ramsey interferometry as illustrated in ref. 90 and in quantum simulator of over 100 trapped ions in a Penning trap through carefully designed echo sequences as illustrated in ref. 91.On the other hand, for atomic and molecular systems as studied in traditional electronic structure as well as in this report, different theoretical measures have also been proposed to quantify the extent of deviation from the mean-field Hartree–Fock state like von Neumann entropy with the eigenvalues of the one-particle reduced density matrix (1-RDM)92 or the Cumulant Expansion of the two-particle reduced density matrix (2-RDM).93,94 The latter in particular affords many useful characterization including its relationship to eigenvalues of the 2-RDM itself and to long-range order,95 its relationship to von Neumann entropy96 and its relationship to various orders of cluster amplitudes for a Couple-Cluster (CC) based wavefunction ansatz.97 It has been successfully used to probe electronic correlation in various problems98–100 and very recently in capturing signatures of van der Waals interaction.101
Akin to the latter, in this paper we propose another metric with a simple geometrical insight which can be theoretically used to detect deviation from mean-field behavior and relate the said quantity through an area law to the correlation energy. This is timely as recently various studies23,102–104 have shown that the entanglement, a quantum observable, can be used in quantifying the correlation energy in atomic and molecular systems. Moreover, a number of studies have shown that the ground state of a local Hamiltonian satisfies an area law and is directly related to the entanglement entropy.53–62 On the other hand, the correlation energy of a system is the difference between the ground state energies in the HF and the accurate calculations. Therefore, the correlation energy is expected be bounded by the area difference when we go beyond the Hartree–Fock approximation to an exact representation. From Fig. 5, we see that the area difference for atomic/ionic systems at large-D limit is a close estimate to the correlation energy of the system. In fact at large-D limit εcorr ≃ Δ(area). In three-dimension, for helium atom, the area difference (0.0520) is close to the correlation energy 0.0420. From eqn (25), the average correlation energy of metallic hydrogen in three dimensions can be described as
| εcorr (rs) = αΔ(area), | (26) |
| εcorr ≤ CΔ(area), | (27) |
In summary, we have shown that the correlation energy might be bounded by an area law which is a close resemblance of the area law conjecture of entanglement entropy. The advantage of this proposal is that we establish a relation between the correlation energy, which is an indirect measure, and the entanglement, which is directly observable, and it is one of the most striking properties of quantum mechanics. Examining the electron correlation in terms of geometry changes between mean field and exact solution might open a new way to observe the correlation effect.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Dr Manas Sajjan and Dr Andrew Hu for useful discussions and their comments on the manuscript. S. K. would like to acknowledge funding by the U.S. Department of Energy (Office of Basic Energy Sciences) under Award No. DE-SC0019215.References
- D. Herrick and F. Stillinger, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 11, 42–53 CrossRef CAS.
- L. Mlodinow and N. Papanicolaou, Ann. Phys., 1980, 128, 314–334 CAS.
- L. Yaffe, Rev. Mod. Phys., 1982, 54, 407 CrossRef CAS.
- D. Herschbach, J. Chem. Phys., 1986, 84, 838–851 CrossRef CAS.
- E. Witten, Phys. Today, 1980, 33, 38–43 CrossRef CAS.
- D. Goodson, M. López-Cabrera, D. Herschbach and J. Morgan III, J. Chem. Phys., 1992, 97, 8481–8496 CrossRef CAS.
- Z. Zhen and J. Loeser, in Large-D Limit for N-Electron Atoms, ed. D. Herschbach, J. Avery and O. Goscinski, Springer Netherlands, Dordrecht, 1993, pp. 83–114 Search PubMed.
- S. Kais and D. Herschbach, J. Chem. Phys., 1994, 100, 4367–4376 CrossRef CAS.
- J. Rudnick and G. Gaspari, Science, 1987, 237, 384–389 CrossRef CAS PubMed.
- K. J. B. Ghosh, S. Kais and D. R. Herschbach, J. Phys. Chem. A, 2021, 125, 7581–7587 CrossRef CAS PubMed.
- J. Loeser, Z. Zhen, S. Kais and D. Herschbach, J. Chem. Phys., 1991, 95, 4525–4544 CrossRef CAS.
- S. Kais and D. Herschbach, J. Chem. Phys., 1993, 98, 3990–3998 CrossRef CAS.
- Q. Wei, S. Kais and D. Herschbach, J. Chem. Phys., 2008, 129, 214110 CrossRef PubMed.
- Q. Wei, S. Kais and D. Herschbach, J. Chem. Phys., 2007, 127, 094301 CrossRef PubMed.
- D. R. Herschbach, J. S. Avery and O. Goscinski, Dimensional scaling in chemical physics, Springer Science & Business Media, 2012 Search PubMed.
- J. C. Slater, Phys. Rev., 1951, 81, 385 CrossRef CAS.
- P. O. Löwdin, Adv. Chem. Phys., 1958, 207–322 Search PubMed.
- W. Kutzelnigg, G. Del Re and G. Berthier, Phys. Rev., 1968, 172, 49 CrossRef.
- N. L. Guevara, R. P. Sagar and R. O. Esquivel, Phys. Rev. A, 2003, 67, 012507 CrossRef.
- Q. Shi and S. Kais, J. Chem. Phys., 2004, 121, 5611–5617 CrossRef CAS PubMed.
- S. Wilson, Electron correlation in molecules, Clarendon Press, Oxford, 1984 Search PubMed.
- N. H. March, Electron Correlations in the Solid State, World Scientific, 1999 Search PubMed.
- Z. Huang and S. Kais, Chem. Phys. Lett., 2005, 413, 1–5 CrossRef CAS.
- C. H. Bennett and D. P. DiVincenzo, Nature, 2000, 404, 247–255 CrossRef CAS PubMed.
- C. Macchiavello, G. M. Palma and A. Zeilinger, Quantum Computation and Quantum Information Theory, World Scientific, 2000 Search PubMed.
- M. Nielsen and I. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press, USA, 10th edn, 2011 Search PubMed.
- J. Gruska et al. , Quantum computing, McGraw-Hill, London, 1999, vol. 2005 Search PubMed.
- E. Schrödinger, Naturwissenschaften, 1935, 23, 823–828 CrossRef.
- D. Bruß, J. Math. Phys., 2002, 43, 4237–4251 CrossRef.
- K. Audenaert, J. Eisert, M. B. Plenio and R. F. Werner, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 042327 CrossRef.
- T. J. Osborne and M. A. Nielsen, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 032110 CrossRef.
- A. Osterloh, L. Amico, G. Falci and R. Fazio, Nature, 2002, 416, 608–610 CrossRef CAS PubMed.
- G. Vidal, J. I. Latorre, E. Rico and A. Kitaev, Phys. Rev. Lett., 2003, 90, 227902 CrossRef CAS PubMed.
- J. D. Bekenstein, JACOB BEKENSTEIN: The Conservative Revolutionary, World Scientific, 2020, pp. 307–320 Search PubMed.
- L. Bombelli, R. K. Koul, J. Lee and R. D. Sorkin, Phys. Rev. D, 1986, 34, 373 CrossRef CAS PubMed.
- M. Srednicki, Phys. Rev. Lett., 1993, 71, 666 CrossRef PubMed.
- L. Amico, R. Fazio, A. Osterloh and V. Vedral, Rev. Mod. Phys., 2008, 80, 517 CrossRef CAS.
- T. Barthel, S. Dusuel and J. Vidal, Phys. Rev. Lett., 2006, 97, 220402 CrossRef PubMed.
- S. Bravyi, M. B. Hastings and F. Verstraete, Phys. Rev. Lett., 2006, 97, 050401 CrossRef CAS PubMed.
- M. Cramer and J. Eisert, New J. Phys., 2006, 8, 71 CrossRef.
- M. Cramer, J. Eisert, M. B. Plenio and J. Dreissig, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 012309 CrossRef.
- M. B. Plenio, J. Eisert, J. Dreissig and M. Cramer, Phys. Rev. Lett., 2005, 94, 060503 CrossRef CAS PubMed.
- U. Schollwöck, Rev. Mod. Phys., 2005, 77, 259 CrossRef.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863 CrossRef PubMed.
- Z. Nussinov and G. Ortiz, Ann. Phys., 2009, 324, 977–1057 CAS.
- X. G. Wen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 7387 CrossRef PubMed.
- E. Witten, Commun. Math. Phys., 1989, 121, 351–399 CrossRef.
- M. Haque, O. Zozulya and K. Schoutens, Phys. Rev. Lett., 2007, 98, 060401 CrossRef PubMed.
- A. Kitaev and J. Preskill, Phys. Rev. Lett., 2006, 96, 110404 CrossRef PubMed.
- J. Eisert, M. Cramer and M. B. Plenio, Rev. Mod. Phys., 2010, 82, 277 CrossRef.
- R. Horodecki, P. Horodecki, M. Horodecki and K. Horodecki, Rev. Mod. Phys., 2009, 81, 865 CrossRef CAS.
- M. B. Plenio and S. S. Virmani, Quantum Inf. Coherence, 2014, 173–209 Search PubMed.
- M. B. Hastings, Journal of statistical mechanics: theory and experiment, 2007, 2007, P08024 Search PubMed.
- M. B. Hastings, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 035114 CrossRef.
- I. Arad, A. Kitaev, Z. Landau and U. Vazirani, arXiv preprint arXiv, 2013, 1301, 1162 Search PubMed.
- F. G. S. L. Brandão and M. Horodecki, Nat. Phys., 2013, 9, 721–726 Search PubMed.
- Z. Landau, U. Vazirani and T. Vidick, arXiv preprint arXiv:1307.5143.
- M. M. Wolf, F. Verstraete, M. B. Hastings and J. I. Cirac, Phys. Rev. Lett., 2008, 100, 070502 CrossRef PubMed.
- L. Masanes, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 052104 CrossRef.
- N. de Beaudrap, T. J. Osborne and J. Eisert, New J. Phys., 2010, 12, 095007 CrossRef.
- S. Michalakis, arXiv preprint arXiv:1206.6900, 2012.
- A. Anshu, I. Arad and D. Gosset, arXiv preprint arXiv:2103.02492, 2021.
- E. R. Davidson, S. A. Hagstrom, S. J. Chakravorty, V. M. Umar and C. F. Fischer, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 7071 CrossRef CAS PubMed.
- A. Veillard and E. Clementi, J. Chem. Phys., 1968, 49, 2415–2421 CrossRef CAS.
- D. Herschbach, J. Loeser and W. Virgo, J. Phys. Chem. A, 2017, 121, 6336–6340 CrossRef CAS PubMed.
- S. Kais, S. Sung and D. Herschbach, Int. J. Quantum Chem., 1994, 49, 657–674 CrossRef CAS.
- E. Wigner and H. B. Huntington, J. Chem. Phys., 1935, 3, 764–770 CrossRef CAS.
- J. G. Loeser, Large-D Limit for Metallic Hydrogen, Dimensional Scaling in Chemical Physics, Springer, 1993, pp. 389–427 Search PubMed.
- H. K. Mao and R. J. Hemley, Rev. Mod. Phys., 1994, 66, 671 CrossRef CAS.
- C. S. Zha, Z. Liu and R. J. Hemley, Phys. Rev. Lett., 2012, 108, 146402 CrossRef PubMed.
- R. P. Dias and I. F. Silvera, Science, 2017, 355, 715–718 CrossRef CAS PubMed.
- J. McMinis, R. C. Clay III, D. Lee and M. A. Morales, Phys. Rev. Lett., 2015, 114, 105305 CrossRef PubMed.
- R. J. Hemley and H. K. Mao, Phys. Rev. Lett., 1988, 61, 857 CrossRef CAS PubMed.
- R. J. Hemley, M. Hanfland and H. K. Mao, Nature, 1991, 350, 488–491 CrossRef CAS.
- R. J. Hemley, H. K. Mao, A. F. Goncharov, M. Hanfland and V. Struzhkin, Phys. Rev. Lett., 1996, 76, 1667 CrossRef CAS PubMed.
- M. Zaghoo, A. Salamat and I. F. Silvera, Phys. Rev. B, 2016, 93, 155128 CrossRef.
- I. F. Silvera and R. Dias, J. Phys.: Condens. Matter, 2018, 30, 254003 CrossRef PubMed.
- P. Loubeyre, F. Occelli and P. Dumas, Nature, 2020, 577, 631–635 CrossRef CAS PubMed.
- K. J. B. Ghosh, S. Kais and D. R. Herschbach, Phys. Chem. Chem. Phys., 2021, 23, 7841–7848 RSC.
- G. Neece, F. Rogers and W. Hoover, J. Comput. Phys., 1971, 7, 621–636 CrossRef CAS.
- M. Ross and C. Shishkevish, Molecular and metallic hydrogen, Tech. Rep. RAND CORP SANTA MONICA CA, 1977 Search PubMed.
- J. B. Mann, Technical Report, Los Alamos Scientific Laboratory, 1968 Search PubMed.
- R. J. Boyd, Can. J. Phys., 1977, 55, 452–455 CrossRef CAS.
- A. J. Thakkar and V. H. Smith, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 15, 1–15 CrossRef CAS.
- L. G. Jiao, L. R. Zan, L. Zhu and Y. K. Ho, Comput. Theor. Chem., 2018, 1135, 1–5 CrossRef CAS.
- B. I. Min, H. J. F. Jansen and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 5076–5083 CrossRef CAS.
- M. F. Parsons, A. Mazurenko, C. S. Chiu, G. Ji, D. Greif and M. Greiner, Science, 2016, 353, 1253–1256 CrossRef CAS PubMed.
- A. Mazurenko, C. S. Chiu, G. Ji, M. F. Parsons, M. Kanász-Nagy, R. R. Schmidt, F. Grusdt, E. A. Demler, D. Greif and M. Greiner, Nature, 2017, 545, 462–466 CrossRef CAS PubMed.
- P. T. Brown, D. Mitra, E. Guardado-Sanchez, P. Schauß, S. S. Kondov, E. Khatami, T. Paiva, N. Trivedi, D. A. Huse and W. S. Bakr, Science, 2017, 357, 1385–1388 CrossRef CAS PubMed.
- M. J. Knap, A. Kantian, T. Giamarchi, I. Bloch, M. D. Lukin and E. A. Demler, Phys. Rev. Lett., 2013, 111(14), 147205 CrossRef PubMed.
- M. Garttner, J. G. Bohnet, A. Safavi-Naini, M. L. Wall, J. J. Bollinger and A. M. Rey, Nat. Phys., 2017, 13, 781–786 Search PubMed.
- K. M. Pelzer, L. Greenman, G. Gidofalvi and D. A. Mazziotti, J. Phys. Chem. A, 2011, 115(22), 5632–5640 CrossRef CAS PubMed.
- W. Kutzelnigg and D. Mukherjee, J. Chem. Phys., 1999, 110, 2800–2809 CrossRef CAS.
- D. A. Mazziotti, in Cumulants and the Contracted Schrödinger Equation, ed. J. Cioslowski, Springer US, Boston, MA, 2000, pp. 139–163 Search PubMed.
- A. Raeber and D. A. Mazziotti, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 052502 CrossRef.
- M. Sajjan, K. Head-Marsden and D. A. Mazziotti, Phys. Rev. A, 2018, 97, 062502 CrossRef CAS.
- L. Kong and E. F. Valeev, J. Chem. Phys., 2011, 134, 214109 CrossRef PubMed.
- T. Juhasz and D. A. Mazziotti, J. Chem. Phys., 2006, 125, 174105 CrossRef PubMed.
- J. W. Hollett and P.-F. Loos, J. Chem. Phys., 2020, 152, 014101 CrossRef CAS PubMed.
- D. R. Alcoba, R. C. Bochicchio, L. Lain and A. Torre, J. Chem. Phys., 2010, 133, 144104 CrossRef CAS PubMed.
- O. Werba, A. Raeber, K. Head-Marsden and D. A. Mazziotti, Phys. Chem. Chem. Phys., 2019, 21, 23900–23905 RSC.
- L. Martina, G. Ruggeri and G. Soliani, Int. J. Quantum Inf., 2011, 9, 843–862 CrossRef.
- M. R. Dowling, A. C. Doherty and S. D. Bartlett, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 062113 CrossRef.
- A. Mohajeri and M. Alipour, Int. J. Quant. Inf., 2009, 7, 801–809 CrossRef.
| This journal is © the Owner Societies 2022 |