Disentangling enantiosensitivity from dichroism using bichromatic fields
Received
21st December 2021
, Accepted 17th February 2022
First published on 11th March 2022
Abstract
We discuss how tensorial observables, available in photoelectron angular distributions resulting from interaction between isotropic chiral samples and cross polarized ω–2ω bichromatic fields, allow for chiral discrimination without chiral light and within the electric-dipole approximation. We extend the concept of chiral setup [A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2018, 98, 063428], which explains how chiral discrimination can be achieved in the absence of chiral light, to the case of tensorial observables. We derive selection rules for the enantiosensitivity and dichroism of the bl,m coefficients describing the photoelectron angular distribution valid for both weak and strong fields and for arbitrary ω–2ω relative phase. Explicit expressions for simple perturbative cases are given. We find that, besides the known dichroic non-enantiosensitive [R. E. Goetz, C. P. Koch and L. Greenman, J. Chem. Phys., 2019, 151, 074106], and dichroic-and-enantiosensitive bl,m coefficients found recently [P. V. Demekhin, Phys. Rev. A, 2019, 99, 063406], there are also enantiosensitive non-dichroic bl,m coefficients. These reveal the molecular enantiomer independently of the relative phase between the two colors and are therefore observable even in the absence of stabilization of the ω–2ω relative phase.
1 Introduction
More than two centuries after the pioneering observations of Biot and Arago,1 the interaction between light and chiral matter2 remains a very active field of research.3–7 This research effort is fueled not only by the interest in finding new ways of manipulating light and matter but also by the homochirality of life. While the molecule–molecule interactions that take place in biological systems are often strongly enantiosensitive,8 the enantiosensitive response in “traditional” light–matter interactions is usually very weak. This weakness, which limits the potential of light-based applications, is prevalent in situations where the electric–dipole approximation is well justified but the chiral effects appear as small corrections such as the magnetic-dipole interaction.9 Besides ingenious methods to cope with such situations,10–12 weakly enantiosensitive responses can be avoided from the outset by relying on chiral effects occurring within the electric–dipole approximation.13,14
Among the chiral electric–dipole effects, photoelectron circular dichroism (PECD)15–19 is very well established and has been shown to consistently yield strongly enantiosensitive signals across many molecular species20 and different photoionization regimes.21,22 In PECD, isotropically oriented chiral molecules are photoionized using circularly polarized light and the photoelectron angular distribution displays a so-called forward–backward asymmetry (asymmetry with respect to the polarization plane). This asymmetry is both enantiosensitive (opposite for opposite enantiomers) and dichroic (opposite for opposite polarizations), and results from the lack of mirror symmetry of the chiral molecules (and thus of the light-matter system) with respect to the plane of polarization. For an isotropically oriented achiral molecule and within the electric-dipole approximation (i.e. ignoring light-propagation effects), the light-matter system is mirror-symmetric with respect to the polarization plane and therefore forward–backward asymmetric observables resulting from a single-molecule response are symmetry-forbidden. For a randomly oriented chiral molecule the mirror symmetry of the light-matter system is absent and there are usually no further symmetries preventing the emergence of forward–backward asymmetric observables. In the one-photon case, the forward–backward asymmetry results from the non-zero molecular rotational invariant describing the average circular polarization of the photoionization-dipole vector field.23
Very recently, the response of chiral molecules to more elaborate field polarizations has been investigated in the multiphoton and strong-field regimes.24–26 In these works, encompassing theory24–26 and experiment,26 a bichromatic field with frequencies ω and 2ω linearly polarized perpendicular to each other yields a new type of enantiosensitive and dichroic asymmetry in the photoelectron angular distribution. The Lissajous figure of this bichromatic field has an eight-like shape for particular phase relations between the two colors, and therefore “rotates” in opposite directions in the first and second halves of its cycle, with the direction of rotation of the field locked to the sign of its ω component. For example, the rotation is clockwise when the ω component is positive and counterclockwise when the ω component is negative. The observed asymmetry in the photoelectron angular distribution corresponds to a correlation between the so-called forward–backward direction and the up-down direction determined by the ω field (see Fig. 1 in ref. 24). So far, this asymmetry has been analyzed on the basis of a subcycle PECD-like picture where electrons detected in the upper hemisphere have an e.g. positive forward–backward asymmetry because they were produced by a field rotating e.g. clockwise, while the electrons detected in the lower hemisphere have a negative forward–backward asymmetry because they were produced by a field rotating counterclockwise.24,26 Extensions of this reasoning to account for non-zero asymmetries for other relative phases between the ω and 2ω components have been considered in ref. 25 and 26.
Here we approach the description of the photoelectron angular distribution taking explicitly into account its tensorial character, the role of tensorial detectors in forming the chiral setup required to distinguish between opposite enantiomers, and the symmetry of the light-matter system. In Section 2 we discuss general considerations regarding how to distinguish between opposite enantiomers in isotropic samples without relying on the chirality of a light field. In Section 3 we discuss how tensorial observables can be used for the construction of chiral setups. In Section 4 we consider the interaction of an ω–2ω cross polarized field with isotropic molecular samples and derive selection rules for multipolar observables. Then we consider the perturbative description of photoionization and exploit the technique presented in ref. 23 to obtain explicit formulas for some representative ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients of the photoelectron angular distribution displaying different combinations of dichroism and enantiosensitivity. Finally, we list our conclusions in Section 5. Analogous results but for the case of charge multipoles induced via excitation of bound states are presented in ref. 27.
l,m coefficients of the photoelectron angular distribution displaying different combinations of dichroism and enantiosensitivity. Finally, we list our conclusions in Section 5. Analogous results but for the case of charge multipoles induced via excitation of bound states are presented in ref. 27.
2 Chiral probes
Distinguishing between the left version (L) and the right version (R) of a chiral object invariably requires interaction with another chiral object (say R′). The difference between the interactions L + R′ and R + R′ is the essence of any enantiosensitive phenomenon. Here we are interested in phenomena where light is used to distinguish between opposite enantiomers of isotropically oriented chiral molecules. In the simplest case, one lets circularly polarized light of a given handedness interact with a chiral sample and measures a scalar, namely the amount of light that is absorbed. In this situation, known as circular dichroism (CD), the chiral probe is the circularly polarized light and its handedness (a pseudoscalar) is given by its helicity, i.e. the projection of the photon spin (the rotation direction of the light at a given point in space, a pseudovector) on the propagation direction of the light (a vector). Another canonical example is optical activity, where one passes linearly polarized light through a chiral sample and measures the rotation of the polarization plane. In this case one measures an angle (a pseudovector). To measure it one must define a positive and a negative direction in the laboratory frame. Although such definition is just as arbitrary as defining what is left and what is right, it is a fundamental step in the measurement process. Once it has been defined, the handedness of the probe is given by the projection of the positive unit angle pseudovector on the propagation direction of the light (see Fig. 8 in ref. 14). That is, the chiral probe in this case is the chiral setup formed by the (achiral) light and the (achiral) detector (which encodes the definition of positive and negative rotations) together. This shows how a chiral setup may probe the handedness of a molecule in the absence of chiral light.
Circular dichroism and optical activity have in common that the handedness of the chiral probe relies on the propagation direction of the light. Since that propagation direction is immaterial within the electric-dipole approximation, unless one considers corrections to the electric-dipole approximation the probe ceases to be chiral and both effects vanish. To the extent that such corrections are typically small at the single molecule level, these effects are also correspondingly small. In order to obtain bigger enantiosensitive signals at the single-molecule level, a probe which is chiral within the electric-dipole approximation is required. Furthermore, if the result of the measurement is a scalar (like in circular dichroism), the light itself must be chiral. The concept of light which is chiral within the electric-dipole approximation, i.e. locally-chiral light, has been recently developed in ref. 6. If the result of the measurement is a polar vector, such as a net photoelectron current along a Cartesian axis, then the detector required to measure the vector must define (again, in an arbitrary fashion) a positive and a negative direction. In addition, if the polarization of the light allows the definition of a pseudovector, as is the case for example for circularly polarized light, where the pseudovector indicates the photon's spin, then one can define a chiral setup with its handedness given by the projection of the light pseudovector on the positive direction defined by the detector. This type of chiral setup is common to a series of recently discovered phenomena that range from rotational dynamics28–30 to photoionization,15–18 and it was recently discussed in ref. 13. In what follows we will extend the concept of chiral setups, to include those that rely on tensors of rank 2 (relevant for the results in ref. 24–26) and higher.
3 Tensor observables and chiral setups
Second and higher-rank tensors emerge naturally for observables which depend on a vector. Charge densities and photoelectron angular distributions (PADs) offer exactly such kind of observable and, as any other function which depends on a vector, they can be expanded as| | 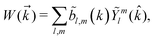 | (1) |
where ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is the photoelectron momentum and we have chosen to do the expansion in terms of real spherical harmonics Ỹml. In the case of a charge distribution we replace the photoelectron momentum
is the photoelectron momentum and we have chosen to do the expansion in terms of real spherical harmonics Ỹml. In the case of a charge distribution we replace the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) by the position
by the position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m could be a time dependent quantity.27 The
l,m could be a time dependent quantity.27 The ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients not only encode all the information contained in W(
l,m coefficients not only encode all the information contained in W(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) but are also examples of tensors of rank l (see e.g. Section 4.10 in ref. 31).
) but are also examples of tensors of rank l (see e.g. Section 4.10 in ref. 31).
In principle, the measurement of a particular ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficient can be performed directly by using a detector with a structure that reflects the corresponding Ỹml. For example, a detector for
l,m coefficient can be performed directly by using a detector with a structure that reflects the corresponding Ỹml. For example, a detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 0,0 would simply sum the counts in all directions. A detector for
0,0 would simply sum the counts in all directions. A detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 would have two plates arranged as in Fig. 1a and b, so that it would add all the counts on one of them (red) and subtract all the counts on the other (blue). The choice of which plate adds and which plate subtracts is what physically defines the ẑ direction of the laboratory frame. A detector for
1,0 would have two plates arranged as in Fig. 1a and b, so that it would add all the counts on one of them (red) and subtract all the counts on the other (blue). The choice of which plate adds and which plate subtracts is what physically defines the ẑ direction of the laboratory frame. A detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 would have four plates arranged as in Fig. 1c, with a pair of opposite plates adding counts and the other pair subtracting counts. In this case, the detector defines the directions that correspond to a positive correlation between x and y, and those that correspond to a negative correlation between x and y. Analogously, a detector for
2,−2 would have four plates arranged as in Fig. 1c, with a pair of opposite plates adding counts and the other pair subtracting counts. In this case, the detector defines the directions that correspond to a positive correlation between x and y, and those that correspond to a negative correlation between x and y. Analogously, a detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 has eight plates arranged as in Fig. 1d, and distinguishes positive from negative correlations of x, y, and z.
3,−2 has eight plates arranged as in Fig. 1d, and distinguishes positive from negative correlations of x, y, and z.
 |
| | Fig. 1 Chiral (a, c and d) and achiral (b) setups consisting of a Lissajous figure and detectors. Counts on red/blue detectors are added/subtracted. The color of the Lissajous figure indicates the phase of the oscillation. (a) A field circularly polarized in the xy plane and a detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0. (b), (c), and (d) A cross-polarized ω–2ω field in the xz plane and a detector for 1,0. (b), (c), and (d) A cross-polarized ω–2ω field in the xz plane and a detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0, 1,0, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 and 2,−2 and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2, respectively. 3,−2, respectively. | |
The combination of a ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m-specific detector and the Lissajous figure of the electric field can make up a chiral setup as shown in Fig. 1a, c and d. These setups are non-superimposable on their mirror images. This is particularly simple to see in Fig. 1a, c and d for reflections with respect to the polarization plane, which do not change the Lissajous figure but do swap blue and red plates. The chirality of these setups allows them to distinguish between opposite enantiomers of a chiral molecule. This is in contrast with the setup in Fig. 1b, which is symmetric with respect to reflection in the polarization plane and thus is not chiral and cannot distinguish between opposite enantiomers of a chiral molecule.
l,m-specific detector and the Lissajous figure of the electric field can make up a chiral setup as shown in Fig. 1a, c and d. These setups are non-superimposable on their mirror images. This is particularly simple to see in Fig. 1a, c and d for reflections with respect to the polarization plane, which do not change the Lissajous figure but do swap blue and red plates. The chirality of these setups allows them to distinguish between opposite enantiomers of a chiral molecule. This is in contrast with the setup in Fig. 1b, which is symmetric with respect to reflection in the polarization plane and thus is not chiral and cannot distinguish between opposite enantiomers of a chiral molecule.
Of course, a chiral setup is only relevant if the light-matter system is indeed asymmetric enough that it can yield a corresponding non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m. In other words, the concept of a chiral setup answers the question of how we can distinguish opposite enantiomers without relying on the chirality of light, but it is the lack of symmetry of the light-matter system itself the deciding factor which determines the emergence of an enantiosensitive observable in the first place (see e.g.Fig. 2 in ref. 13). We now turn to the analysis of a specific family of Lissajous figures to illustrate this in detail.
l,m. In other words, the concept of a chiral setup answers the question of how we can distinguish opposite enantiomers without relying on the chirality of light, but it is the lack of symmetry of the light-matter system itself the deciding factor which determines the emergence of an enantiosensitive observable in the first place (see e.g.Fig. 2 in ref. 13). We now turn to the analysis of a specific family of Lissajous figures to illustrate this in detail.
 |
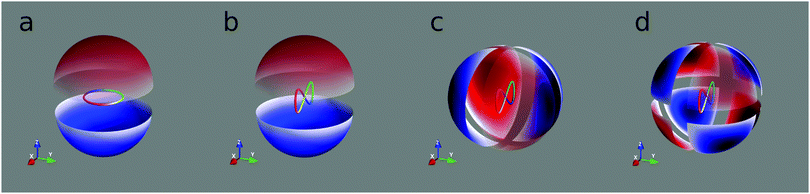
| | Fig. 2 Lissajous curves of the field (2) for different values of ϕ. The position of the red arrow indicates t = 0. | |
4
ω–2ω cross polarized field
Consider a two-color field of the form| | ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) = Eω (t) = Eω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) cos(ωt)![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + E2ω + E2ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt + ϕ)ẑ cos(2ωt + ϕ)ẑ | (2) |
This field is illustrated in Fig. 2 for different phases†ϕ. If we denote rotations by π around the z axis by ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz and time shifts of π/ω by Tπ/ω, then the joint system (field and isotropic chiral molecules) is invariant with respect to
πz and time shifts of π/ω by Tπ/ω, then the joint system (field and isotropic chiral molecules) is invariant with respect to ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz
πz![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π/ω. Clearly, the resulting observables must also be invariant with respect to
π/ω. Clearly, the resulting observables must also be invariant with respect to ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz
πz![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π/ω. That is, the symmetry-allowed
π/ω. That is, the symmetry-allowed ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients must satisfy
l,m coefficients must satisfy ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz
πz![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π/ω
π/ω![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,mỸml =
l,mỸml = ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,mỸml. This corresponds to two scenarios: either
l,mỸml. This corresponds to two scenarios: either ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πzỸml = Ỹml and
πzỸml = Ỹml and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m contains only frequencies 2nω, or
l,m contains only frequencies 2nω, or ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πzỸml = −Ỹml and
πzỸml = −Ỹml and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m contains only frequencies (2n + 1)ω, where n = 0, 1, 2, …. Furthermore, since a reflection
l,m contains only frequencies (2n + 1)ω, where n = 0, 1, 2, …. Furthermore, since a reflection ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y with respect to the y = 0 plane swaps the enantiomers while leaving the field invariant, an enantiosensitive
y with respect to the y = 0 plane swaps the enantiomers while leaving the field invariant, an enantiosensitive ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is associated to a Ỹml satisfying
l,m is associated to a Ỹml satisfying ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yỸml = −Ỹml. And, since a rotation
yỸml = −Ỹml. And, since a rotation ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πx of π around the x axis changes the phase ϕ in the field by π while leaving the molecules invariant, a dichroic‡
πx of π around the x axis changes the phase ϕ in the field by π while leaving the molecules invariant, a dichroic‡![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is associated to a Ỹml satisfying
l,m is associated to a Ỹml satisfying ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πxỸml = −Ỹml. These properties, which are valid independently of the ionization regime, are summarized in Tables 1 and 2.
πxỸml = −Ỹml. These properties, which are valid independently of the ionization regime, are summarized in Tables 1 and 2.
Evidently, the values of l and m that determine whether a given ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is symmetry-allowed and whether it is enantiosensitive and/or dichroic depends on how the field is oriented with respect to the axes. The choice made here [eqn (2)] yields the rather simple conditions in Tables 1 and 2. Conditions corresponding to other choices are given in Appendix A for the sake of comparison with ref. 24–26.
l,m is symmetry-allowed and whether it is enantiosensitive and/or dichroic depends on how the field is oriented with respect to the axes. The choice made here [eqn (2)] yields the rather simple conditions in Tables 1 and 2. Conditions corresponding to other choices are given in Appendix A for the sake of comparison with ref. 24–26.
Tables 1 and 2 reveal two important features. First, the spatial structure of the response depends on whether it oscillates with a frequency which is an even (including zero) or an odd multiple of the fundamental frequency (see also ref. 32). Second, in contrast to a circularly polarized field where dichroism goes hand in hand with enantiosensitivity, the symmetry of the field (2) leads to four types of signals:
Table 1 Conditions imposed by symmetry on the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients describing the photoelectron angular distribution (1) resulting from the interaction between an isotropic molecular sample and the field (2)
l,m coefficients describing the photoelectron angular distribution (1) resulting from the interaction between an isotropic molecular sample and the field (2)
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m
l,m
|
(l,m) condition |
| Symmetry-allowed at 2nω |
Even m |
| Symmetry-allowed at (2n + 1)ω |
Odd m |
| Enantiosensitive |
m < 0 |
| Dichroic |
[(Odd l − m) and (m ≥ 0)] or |
|
|
(even l − m) and (m < 0) |
Table 2 (l,m) conditions derived from Table 1 for non-vanishing enantiosensitive and/or dichroic ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients
l,m coefficients
Symmetry-allowed ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m l,m |
(l,m) condition at 2nω |
(l,m) condition at (2n + 1)ω |
| Enantiosensitive and dichroic |
(Even l) and (even m < 0) |
(Odd l) and (odd m < 0) |
| Enantiosensitive non-dichroic |
(Odd l) and (even m < 0) |
(Even l) and (odd m < 0) |
| Dichroic non-enantiosensitive |
(Odd l) and (even m > 0) |
(Even l) and (odd m > 0) |
(i) Non-dichroic and non-enantiosensitive.
(ii) Dichroic and enantiosensitive.
(iii) Dichroic and non-enantiosensitive.
(iv) Enantiosensitive and non-dichroic.
Type (i) and type (ii) signals are well known from traditional CD and PECD. Type (iii) signals are well known in atoms subject to light fields whose Lissajous figure is not symmetric under spatial inversion.33 They have also been recently calculated for the case of randomly oriented chiral molecules34 for parallel polarizations of ω and 2ω. Here, type (iii) signals are due to the asymmetry of the field (2) along the z direction (see Fig. 2). Type (iv) signals are more exotic but apparently they can also occur in the context of magnetic effects beyond the electric-dipole approximation,35,36 where to the best of our knowledge they remain to be confirmed by experiment. As we will show next, photoionization may prove to be a better candidate for experimentally measuring type (iv) signals.
4.1 Photoionization
The photoelectron angular distribution accumulated over many cycles of the field (2) corresponds to a signal with zero frequency and must satisfy the conditions given in Table 1 for frequencies 2nω. For convenience, we list the properties of the symmetry-allowed ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients for l up to four in Table 3. From this table we can see that e.g.
l,m coefficients for l up to four in Table 3. From this table we can see that e.g. ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is dichroic but not enantiosensitive,
1,0 is dichroic but not enantiosensitive, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is enantiosensitive and dichroic, and
2,−2 is enantiosensitive and dichroic, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is enantiosensitive but not dichroic. Since Ỹ01(
3,−2 is enantiosensitive but not dichroic. Since Ỹ01(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) ∝ kz, Ỹ−22(
) ∝ kz, Ỹ−22(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) ∝ kxky, and Ỹ−23(
) ∝ kxky, and Ỹ−23(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) ∝ kxkykz, then
) ∝ kxkykz, then ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is associated to asymmetry along the direction of the 2ω field (ẑ),
1,0 is associated to asymmetry along the direction of the 2ω field (ẑ), ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is associated to correlations between the direction of the ω field (
2,−2 is associated to correlations between the direction of the ω field (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) and the direction perpendicular to the polarization plane (ŷ), and
) and the direction perpendicular to the polarization plane (ŷ), and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is associated to correlations of the three directions corresponding to the ω field (
3,−2 is associated to correlations of the three directions corresponding to the ω field (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ), the 2ω field (ẑ), and the perpendicular to the polarization plane (ŷ).
), the 2ω field (ẑ), and the perpendicular to the polarization plane (ŷ).
Table 3 Dichroism and enantiosensitivity of symmetry-allowed ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients describing the photoelectron angular distribution (1) resulting from interaction of an isotropic molecular sample and the field (2) for l up to 4. N = No and Y = Yes
l,m coefficients describing the photoelectron angular distribution (1) resulting from interaction of an isotropic molecular sample and the field (2) for l up to 4. N = No and Y = Yes
| Symmetry-allowed |
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 0,0
0,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0
1,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2
2,−2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,0
2,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,2
2,2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2
3,−2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,0
3,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,2
3,2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−4
4,−4
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−2
4,−2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,0
4,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,2
4,2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,4
4,4
|
| Enantiosensitive |
N |
N |
Y |
N |
N |
Y |
N |
N |
Y |
Y |
N |
N |
N |
| Dichroic |
N |
Y |
Y |
N |
N |
N |
Y |
Y |
Y |
Y |
N |
N |
N |
In ref. 23 we showed that, in general, a ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficient is enantiosensitive if and only if it results from interference between pathways with N1 and N2 photons, respectively, and l + N1 + N2 is odd; or if it results from a direct pathway and l is odd. These conditions together with Table 2 tell us that a dichroic non-enantiosensitive
l,m coefficient is enantiosensitive if and only if it results from interference between pathways with N1 and N2 photons, respectively, and l + N1 + N2 is odd; or if it results from a direct pathway and l is odd. These conditions together with Table 2 tell us that a dichroic non-enantiosensitive ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m (with odd l) can only occur as the result of interference between pathways involving an even and an odd number of photons, respectively (so that N1 + N2 is odd and l + N1 + N2 is even). For example,
l,m (with odd l) can only occur as the result of interference between pathways involving an even and an odd number of photons, respectively (so that N1 + N2 is odd and l + N1 + N2 is even). For example, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 contributes to the photoelectron peak where absorption of two ω photons interferes with absorption of one 2ω photon (see Fig. 3a). The same condition (odd N1 + N2) applies for a dichroic and enantiosensitive
1,0 contributes to the photoelectron peak where absorption of two ω photons interferes with absorption of one 2ω photon (see Fig. 3a). The same condition (odd N1 + N2) applies for a dichroic and enantiosensitive ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m (even l) such as
l,m (even l) such as ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2. In contrast, an enantiosensitive non-dichroic
2,−2. In contrast, an enantiosensitive non-dichroic ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m (odd l) can occur as the result of either a direct pathway involving at least one ω photon and one 2ω photon, or as the result of interference between two pathways both with an even or both with an odd number of photons (even N1 + N2). For example,
l,m (odd l) can occur as the result of either a direct pathway involving at least one ω photon and one 2ω photon, or as the result of interference between two pathways both with an even or both with an odd number of photons (even N1 + N2). For example, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 contributes to the photoelectron peak corresponding to absorption of one ω photon followed by absorption of one 2ω photon (see Fig. 3b) and vice versa, or as the result of interference between absorption of two 2ω photons and four ω photons.
3,−2 contributes to the photoelectron peak corresponding to absorption of one ω photon followed by absorption of one 2ω photon (see Fig. 3b) and vice versa, or as the result of interference between absorption of two 2ω photons and four ω photons.
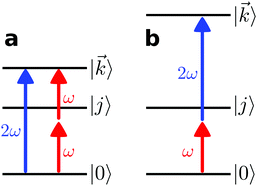 |
| | Fig. 3 (a) Simplest scheme to generate a non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 (dichroic non-enantiosensitive) and 1,0 (dichroic non-enantiosensitive) and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 (dichroic and enantiosensitive) using the field (2). (b) Simplest scheme to generate a non-zero 2,−2 (dichroic and enantiosensitive) using the field (2). (b) Simplest scheme to generate a non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 (enantiosensitive non-dichroic) using the field (2). |0〉 and |j〉 are bound states and | 3,−2 (enantiosensitive non-dichroic) using the field (2). |0〉 and |j〉 are bound states and |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 is a continuum state. 〉 is a continuum state. | |
As an example, let us calculate explicit expressions for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0,
1,0, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2, and
2,−2, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2. For the process depicted in Fig. 3a, the interference between the two pathways gives rise to a non-zero orientation-averaged
3,−2. For the process depicted in Fig. 3a, the interference between the two pathways gives rise to a non-zero orientation-averaged ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 given by (see Appendix B)
1,0 given by (see Appendix B)
| | ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0(k) = A(1)*A(2)g1,0f1,0 + c.c., 1,0(k) = A(1)*A(2)g1,0f1,0 + c.c., | (3) |
where
A(1) and
A(2) are complex-valued constants depending on detunings and pulse envelopes, c.c. denotes the complex conjugate,
g1,0 is a (complex-valued) molecular rotational invariant, and
f1,0 is a setup (
i.e. field + detector) rotational invariant.
g1,0 is a scalar
§ (in contrast to a pseudoscalar) and therefore
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0
1,0 is not enantiosensitive. The expression for
f1,0 reads as
| | 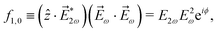 | (4) |
where
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω
2ω ≡
E2ωe
−iϕẑ,
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω
ω ≡
Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
.
Eqn (4) shows that the setup rotational invariant
f1,0 is a scalar involving the field vectors
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω
2ω and
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω
ω, and the
ẑ axis. As discussed in Section 3, the axis vector
ẑ is defined by the detector needed to measure
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0
1,0. From
eqn (4) it is evident that
f1,0 changes sign when
ϕ is shifted by π, and therefore
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0
1,0 is dichroic.
Similarly, the interference between the two pathways in Fig. 3a gives rise to a non-zero orientation-averaged ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 given by (see Appendix C)
2,−2 given by (see Appendix C)
| | ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 = A(1)*A(2)g2,−2f2,−2 + c.c., 2,−2 = A(1)*A(2)g2,−2f2,−2 + c.c., | (5) |
where the molecular rotational invariant
g2,−2 is a (complex-valued) pseudoscalar and therefore
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2
2,−2 is enantiosensitive. The setup rotational invariant, given by
| | 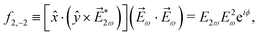 | (6) |
is also a pseudoscalar and it involves the
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
and
ŷ axes, which are defined by the detector needed to measure
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2
2,−2 (see Section 3). Just like
g2,−2 is a pseudoscalar that distinguishes between molecules with opposite handedness,
f2,−2 is a pseudoscalar that distinguishes between chiral setups of opposite handedness. Note that the detector for
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2
2,−2 does not directly tell apart a positive
x from a negative
x, or a positive
y from a negative
y. It only tells apart positive correlations of
x and
y from negative correlations of
x and
y. This is consistent with the invariance of
f2,−2 with respect to a simultaneous inversion of
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
and
ŷ. Furthermore,
eqn (6) shows that
f2,−2 changes sign when
ϕ is shifted by π, and therefore
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2
2,−2 is dichroic. We remark, that although the right hand side of
eqn (4) and (6) look exactly the same after performing the vector operations,
f1,0 and
f2,−2 emerge from different setup rotational invariants of a different physical nature: one is a scalar involving only the
ẑ axis, and the other is a pseudoscalar involving correlation between the
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
and
ŷ axes.
We consider now the simplest process leading to the enantiosensitive but not dichroic term ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2, i.e. we consider the absorption of one ω photon and one 2ω photon, resonantly enhanced through a bound state as shown in Fig. 3b. In this case we get (see Appendix D)
3,−2, i.e. we consider the absorption of one ω photon and one 2ω photon, resonantly enhanced through a bound state as shown in Fig. 3b. In this case we get (see Appendix D)
| | ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2(k) = |A(2)|2g3,−2f3,−2, 3,−2(k) = |A(2)|2g3,−2f3,−2, | (7) |
where the rotational invariant
g3,−2 is a (real-valued) pseudoscalar, which makes
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2
3,−2 enantiosensitive. The setup rotational invariant
f3,−2 is given by
| | 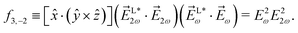 | (8) |
f
3,−2 is also a pseudoscalar, however it does not record ϕ and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is therefore not dichroic. The robustness of f3,−2 against changes of ϕ means that recording
3,−2 is therefore not dichroic. The robustness of f3,−2 against changes of ϕ means that recording ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 allows distinguishing opposite enantiomers in the absence of stabilization of the ω–2ω phase shift ϕ.
3,−2 allows distinguishing opposite enantiomers in the absence of stabilization of the ω–2ω phase shift ϕ.
Eqn (3)–(8) confirm our expectations based on general symmetry arguments according to which ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is dichroic and non-enantiosensitive,
1,0 is dichroic and non-enantiosensitive, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is dichroic and enantiosensitive, and
2,−2 is dichroic and enantiosensitive, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is enantiosensitive and non-dichroic. In addition, these equations show that
3,−2 is enantiosensitive and non-dichroic. In addition, these equations show that ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0,
1,0, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2, and
2,−2, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 are in general not zero for the specific processes considered here. This is important because although a given
3,−2 are in general not zero for the specific processes considered here. This is important because although a given ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m may be symmetry allowed according to the general symmetry analysis above, further “hidden” symmetries¶ involved in a specific process may forbid it. For example, although the geometry of a monochromatic elliptical field allows for a non-zero
l,m may be symmetry allowed according to the general symmetry analysis above, further “hidden” symmetries¶ involved in a specific process may forbid it. For example, although the geometry of a monochromatic elliptical field allows for a non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2, the presence of the triple product in eqn (8) means that opposite photon orderings contribute to
3,−2, the presence of the triple product in eqn (8) means that opposite photon orderings contribute to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 with opposite signs (see Appendix E). Such photon orderings are degenerate in the monochromatic case and thus the two contributions cancel each other out (see Appendix F). However, it must be kept in mind that the hidden symmetry preventing a non-zero
3,−2 with opposite signs (see Appendix E). Such photon orderings are degenerate in the monochromatic case and thus the two contributions cancel each other out (see Appendix F). However, it must be kept in mind that the hidden symmetry preventing a non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 for elliptical fields is specific to the 2-photon process we investigated here, so it may be broken in higher order processes or in the strong field regime. That is, photoionization induced by elliptically polarized strong fields may indeed yield a non-zero enantiosensitive and non-dichroic
3,−2 for elliptical fields is specific to the 2-photon process we investigated here, so it may be broken in higher order processes or in the strong field regime. That is, photoionization induced by elliptically polarized strong fields may indeed yield a non-zero enantiosensitive and non-dichroic ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient. This would be analogous to how
3,−2 coefficient. This would be analogous to how ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is symmetry-forbidden in the elliptical one-photon case23 but it is symmetry allowed in the elliptical strong-field case.38
2,−2 is symmetry-forbidden in the elliptical one-photon case23 but it is symmetry allowed in the elliptical strong-field case.38
5 Conclusions
We discussed how tensorial observables offer new opportunities for constructing chiral setups able to distinguish between opposite enantiomers in isotropic samples without relying on the chirality of light. As a concrete example we considered the interaction of an ω–2ω cross polarized field with isotropic samples and we found selection rules for l and m that specify if a multipole coefficient ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is symmetry allowed, if it is dichroic (sensitive to changes of π in the ω–2ω relative phase), and if it is enantiosensitive. These
l,m is symmetry allowed, if it is dichroic (sensitive to changes of π in the ω–2ω relative phase), and if it is enantiosensitive. These ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients are relevant in the description of photoelectron angular distributions and in the description of induced multipoles of bound charge distributions (discussed in ref. 27). We found that the enantiosensitivity and the dichroism of a
l,m coefficients are relevant in the description of photoelectron angular distributions and in the description of induced multipoles of bound charge distributions (discussed in ref. 27). We found that the enantiosensitivity and the dichroism of a ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficient are in general independent of each other. That is, in addition to the usual types of
l,m coefficient are in general independent of each other. That is, in addition to the usual types of ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients in isotropic samples, namely: (i) non-dichroic and non-enantiosensitive, (ii) dichroic and enantiosensitive, and (iii) dichroic and non-enantiosensitive, we found the more exotic possibility of (iv) enantiosensitive and non-dichroic
l,m coefficients in isotropic samples, namely: (i) non-dichroic and non-enantiosensitive, (ii) dichroic and enantiosensitive, and (iii) dichroic and non-enantiosensitive, we found the more exotic possibility of (iv) enantiosensitive and non-dichroic ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients.
l,m coefficients.
We derived analytic expressions for the lowest rank ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients in photoelectron angular distributions corresponding to types (ii)–(iv) for the case of one- vs. two-photon absorption and for the case of ω + 2ω absorption. Unlike type (ii) coefficients, type (iv) coefficients allow enantiomeric discrimination in the absence of stabilization of the ω–2ω relative phase and remain to be numerically calculated and experimentally observed. Such verification is within reach with current theoretical39 and experimental40,41 capabilities which provide access to the full photoelectron momentum distribution. Imaging of the type (iv) coefficient
l,m coefficients in photoelectron angular distributions corresponding to types (ii)–(iv) for the case of one- vs. two-photon absorption and for the case of ω + 2ω absorption. Unlike type (ii) coefficients, type (iv) coefficients allow enantiomeric discrimination in the absence of stabilization of the ω–2ω relative phase and remain to be numerically calculated and experimentally observed. Such verification is within reach with current theoretical39 and experimental40,41 capabilities which provide access to the full photoelectron momentum distribution. Imaging of the type (iv) coefficient ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 discussed here with a velocity map imaging detector as e.g. in ref. 26 is complicated by two facts: (a) the lack of cylindrical symmetry prevents Abel inversion and (b) projection of the Ỹ3,−2 contribution to the momentum distribution on the xy (or yz) plane cancels exactly (see Fig. 1c). However, re-orientation of the detector so as to project the momentum distribution on e.g. the x = z plane, as shown in Fig. 4, should facilitate imaging the non-zero
3,−2 discussed here with a velocity map imaging detector as e.g. in ref. 26 is complicated by two facts: (a) the lack of cylindrical symmetry prevents Abel inversion and (b) projection of the Ỹ3,−2 contribution to the momentum distribution on the xy (or yz) plane cancels exactly (see Fig. 1c). However, re-orientation of the detector so as to project the momentum distribution on e.g. the x = z plane, as shown in Fig. 4, should facilitate imaging the non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient. Experimentally, one can keep the detector fixed and instead rotate the polarizations of the fields. That is, measurement of the
3,−2 coefficient. Experimentally, one can keep the detector fixed and instead rotate the polarizations of the fields. That is, measurement of the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient only requires rotating ω and 2ω by 45° around their propagation axis in ref. 24 and 26.
3,−2 coefficient only requires rotating ω and 2ω by 45° around their propagation axis in ref. 24 and 26.
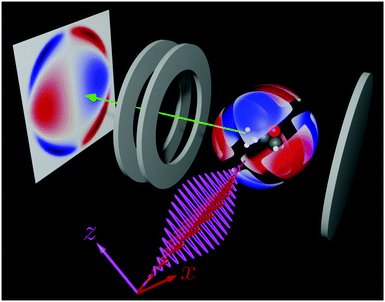 |
| | Fig. 4 Proposed velocity map imaging setup to measure the coefficient ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2: ω (red wave) and 2ω (violet wave) are polarized along x and z, respectively. The detector projects the distribution on the x = z plane. Only the contribution of 3,−2: ω (red wave) and 2ω (violet wave) are polarized along x and z, respectively. The detector projects the distribution on the x = z plane. Only the contribution of ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 to the photoelectron angular distribution is shown. In red/blue regions there is an excess/deficit of photoelectrons. 3,−2 to the photoelectron angular distribution is shown. In red/blue regions there is an excess/deficit of photoelectrons. | |
Finally, it is also possible to obtain the type (iv) coefficient ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 using monochromatic light with elliptical polarization. However, a “hidden” symmetry associated to the degeneracy in photon orderings in the monochromatic case prevents this coefficient in the case of a two-photon process. The possibility of this hidden symmetry to be violated for higher-order or strong-field processes, or in a more refined description of photoionization remains to be investigated.
3,−2 using monochromatic light with elliptical polarization. However, a “hidden” symmetry associated to the degeneracy in photon orderings in the monochromatic case prevents this coefficient in the case of a two-photon process. The possibility of this hidden symmetry to be violated for higher-order or strong-field processes, or in a more refined description of photoionization remains to be investigated.
Conflicts of interest
There are no conflicts to declare.
Appendix
A Selection rules for an alternative orientation of the field
In Section 4 we chose the orientation of the field so as to simplify as much as possible the selection rules for the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients. Here, for the sake of comparison, we consider the alternative orientation|| used in ref. 24–26, namely
l,m coefficients. Here, for the sake of comparison, we consider the alternative orientation|| used in ref. 24–26, namely| | ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) = Eω (t) = Eω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)ŷ + E2ω cos(ωt)ŷ + E2ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt + ϕ) cos(2ωt + ϕ)![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . . | (9) |
Tables 4–6 show the analogues of Tables 1–3 for the orientation in eqn (9). In this case, we see that e.g. ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,1,
1,1, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−1, and
2,−1, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 are dichroic non-enantiosensitive, enantiosensitive and dichroic, and enantiosensitive non-dichroic, respectively. These are just the correspondingly rotated versions of the coefficients in Section 4. Note that
3,−2 are dichroic non-enantiosensitive, enantiosensitive and dichroic, and enantiosensitive non-dichroic, respectively. These are just the correspondingly rotated versions of the coefficients in Section 4. Note that ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−1 ∝ Im{b2,1} is indeed the coefficient discussed in ref. 25.
2,−1 ∝ Im{b2,1} is indeed the coefficient discussed in ref. 25.
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m
l,m
|
(l,m) condition |
| Non-zero 2nω |
(Even l − m and m ≥ 0) or |
| (odd l − m and m < 0) |
| Non-zero (2n + 1)ω |
(Odd l − m and m ≥ 0) or |
| (even l − m and m < 0) |
| Enantiosensitive |
Odd l − m |
| Dichroic |
[(Odd l) and (m ≥ 0)] or |
| [(even l) and m < 0] |
Table 5 Same as Table 2 for the orientation of the field used in eqn (9)
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m
l,m
|
(l,m) condition at 2nω |
(l,m) condition at (2n + 1)ω |
| Enantiosensitive and dichroic |
(Even l) and (odd m < 0) |
(Odd l) and (even m ≥ 0) |
| Enantiosensitive non-dichroic |
(Odd l) and (even m < 0) |
(Even l) and (odd m ≥ 0) |
| Dichroic non-enantiosensitive |
(Odd l) and (odd m ≥ 0) |
(Even l) and (even m < 0) |
Table 6 Same as Table 3 for the orientation of the field used in eqn (9)
| Symmetry-allowed |
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 0,0
0,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,1
1,1
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−1
2,−1
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,0
2,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,2
2,2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2
3,−2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,1
3,1
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,3
3,3
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−3
4,−3
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−1
4,−1
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,0
4,0
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,2
4,2
|
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,4
4,4
|
| Enantiosensitive |
N |
N |
Y |
N |
N |
Y |
N |
N |
Y |
Y |
N |
N |
N |
| Dichroic |
N |
Y |
Y |
N |
N |
N |
Y |
Y |
Y |
Y |
N |
N |
N |
B Derivation of ![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 1,0 in eqn (3)
1,0 in eqn (3)
The process depicted in Fig. 3a yields a ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 coefficient given by23
1,0 coefficient given by23| | 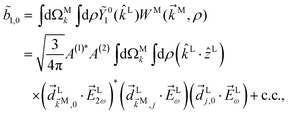 | (10) |
where c.c. denotes the complex conjugate, L and M indicate vectors and functions in the laboratory (L) and molecular (M) frames, ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is the photoelectron momentum,
is the photoelectron momentum, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ≡
≡ ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) /k, ρ ≡ αβγ is the molecular orientation specified by the Euler angles αβγ,
/k, ρ ≡ αβγ is the molecular orientation specified by the Euler angles αβγ, 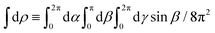 is the normalized integral over all molecular orientations,
is the normalized integral over all molecular orientations, 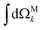 is the integral over all photoelectron directions
is the integral over all photoelectron directions ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M,
M, 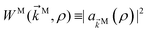 is the photoelectron angular distribution in the molecular frame for a particular orientation ρ.
is the photoelectron angular distribution in the molecular frame for a particular orientation ρ. 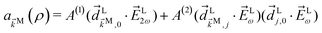 is the probability amplitude of the state |
is the probability amplitude of the state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉, A(1) and A(2) are complex-valued constants depending on detunings and pulse envelopes,
M〉, A(1) and A(2) are complex-valued constants depending on detunings and pulse envelopes, ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i,j ≡ 〈i|
i,j ≡ 〈i|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |j〉 is the dipole transition matrix element between states |i〉 and |j〉, |
|j〉 is the dipole transition matrix element between states |i〉 and |j〉, |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 is the scattering state describing an outgoing plane wave with photoelectron momentum
〉 is the scattering state describing an outgoing plane wave with photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) , and
, and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω = Eω
ω = Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and
and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω = E2ωe−iϕẑ are the Fourier amplitudes of the field (2) at frequencies ω and 2ω, respectively. The vectors
2ω = E2ωe−iϕẑ are the Fourier amplitudes of the field (2) at frequencies ω and 2ω, respectively. The vectors ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L and
L and ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) Li,j, depend on the molecular orientation ρ according to
Li,j, depend on the molecular orientation ρ according to ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) L = S(ρ)
L = S(ρ)![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) M, where S(ρ) is the rotation matrix taking vectors from the molecular frame to the laboratory frame. Note that only the interference between the two pathways in Fig. 3 contributes to
M, where S(ρ) is the rotation matrix taking vectors from the molecular frame to the laboratory frame. Note that only the interference between the two pathways in Fig. 3 contributes to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 (see Section 4).
1,0 (see Section 4).
The integral over orientations yields23,42
| | 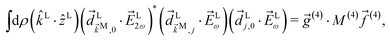 | (11) |
where
![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) (4)
(4) and
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) (4)
(4) are vectors of molecular and setup rotational invariants, respectively,
| | 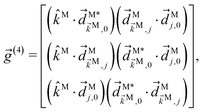 | (12) |
| | 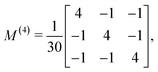 | (13) |
| | 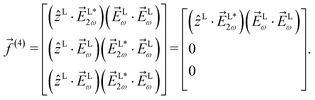 | (14) |
Replacing eqn (11)–(14) in eqn (10) we obtain eqn (3), where f1,0 is given by eqn (4) and g1,0 is given by
| | 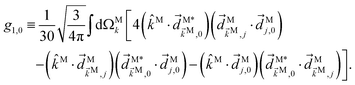 | (15) |
We remark that
eqn (3), (4) and (15) are not valid for arbitrary polarizations of
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω
ω and
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω
2ω. We have kept the vectorial form of the rotational invariant in
eqn (4) to emphasize the scalar
vs. pseudoscalar character (see discussion in Section 4.1). As can be seen from
eqn (14), to derive
eqn (3), (4) and (15) we explicitly used
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω
L2ω‖
ẑL and
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω
Lω‖
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L
L.
C Derivation of ![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 2,−2 in eqn (5)
2,−2 in eqn (5)
Similarly, for the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 coefficient we have23
2,−2 coefficient we have23| | 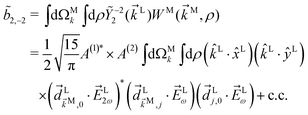 | (16) |
The integral over orientations can be performed analogously to what we did for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0.42 Making explicit use of
1,0.42 Making explicit use of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω‖ẑL and
L2ω‖ẑL and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω‖
Lω‖![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L yields eqn (5), with f2,−2 given by eqn (6) and g2,−2 given by
L yields eqn (5), with f2,−2 given by eqn (6) and g2,−2 given by| | 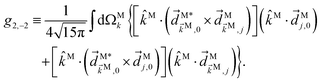 | (17) |
We point out that when dealing with integrals over orientations involving five or more scalar products, the number of rotational invariants that can be formed is such that they are no longer linearly independent from each other.42 As a result it is possible to write the result of the integral in several different ways that, although perfectly equivalent, are not evidently related to each other at first sight. For example, by changing the order of the scalar products in such a way that 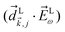 exchanges its position with (
exchanges its position with (![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L·
L·![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L) in eqn (15) one obtains
L) in eqn (15) one obtains
| | 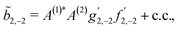 | (18) |
where
| | 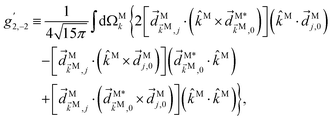 | (19) |
| | 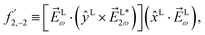 | (20) |
and again we assumed that
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω
L2ω‖
ẑL and
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω
Lω‖
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L
L. Writing the explicit expressions
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω
ω =
Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
and
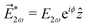
one can show that
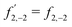
. And using standard vectorial algebra relations one can show that
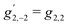
. The latter equality reflects the fact that, for four arbitrary vectors
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)
,
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
,
![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif)
,
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
, the three different rotational invariants
r1 ≡ [
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)
·(
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
×
![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif)
)](
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
·
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
),
r2 ≡ [
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)
·(
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
×
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
)](
![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif)
·
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
), and
r3 ≡ [
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)
·(
![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif)
×
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
)](
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
·
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
) can be written as a linear combination of the
two rotational invariants
r1 and
r4 ≡ [
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
·(
![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif)
×
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
)](
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)
·
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)
). Care must therefore be taken when looking for interpretations that depend on the particular ordering of the vectors appearing in the rotational invariants.
D Derivation of ![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 3,−2 for ω + 2ω [eqn (7)]
3,−2 for ω + 2ω [eqn (7)]
The process depicted in Fig. 3b yields a ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient given by23
3,−2 coefficient given by23| | 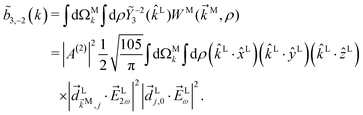 | (21) |
The integral over orientations can be performed analogously to what we did for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0.42 Making explicit use of
1,0.42 Making explicit use of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω‖ẑL and
L2ω‖ẑL and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω‖
Lω‖![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L yields eqn (7), with f3,−2 given by eqn (8) and g3,−2 given by**
L yields eqn (7), with f3,−2 given by eqn (8) and g3,−2 given by**| | 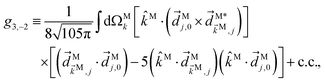 | (22) |
E Derivation of ![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 3,−2 for 2ω + ω: symmetry in photon ordering
3,−2 for 2ω + ω: symmetry in photon ordering
First we rewrite the integral over orientations in eqn (21) as| | 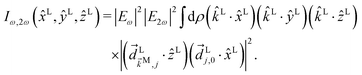 | (23) |
For the opposite photon ordering we have| | 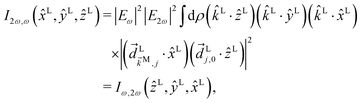 | (24) |
that is, reversing the photon ordering is equivalent to the exchanging ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L and ẑL in eqn (23). On the other hand, from the triple product in eqn (8) it follows that
L and ẑL in eqn (23). On the other hand, from the triple product in eqn (8) it follows that| | Iω,2ω(ẑL,ŷL,![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L) = −Iω,2ω( L) = −Iω,2ω(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L,ŷL,ẑL) L,ŷL,ẑL) | (25) |
and thus| | I2ω,ω(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L,ŷL,ẑL) = −Iω,2ω( L,ŷL,ẑL) = −Iω,2ω(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L,ŷL,ẑL). L,ŷL,ẑL). | (26) |
This means that the expression for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 in the photon ordering 2ω + ω is exactly the same as for the photon ordering ω + 2ω up to a minus sign. However, since for a fixed molecular spectrum the coupling coefficient A(2) strongly depends on detunings (and therefore photon ordering), if one of the photon orderings is resonant it will dominate. Furthermore, in practice each photon ordering might be resonant with different transitions, and one should therefore use different transition dipole matrix elements for each ordering.
3,−2 in the photon ordering 2ω + ω is exactly the same as for the photon ordering ω + 2ω up to a minus sign. However, since for a fixed molecular spectrum the coupling coefficient A(2) strongly depends on detunings (and therefore photon ordering), if one of the photon orderings is resonant it will dominate. Furthermore, in practice each photon ordering might be resonant with different transitions, and one should therefore use different transition dipole matrix elements for each ordering.
Since the derivation we just presented is actually independent of the frequencies, we have that
provided
ω1 and
ω2 have linear polarizations perpendicular to each other. We can therefore conclude that
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2
3,−2 → 0 as
ω1 →
ω2. Note that this is analogous to the corresponding result for the polarization in sum-frequency generation.
43
F Vanishing of ![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 3,−2 for elliptical light
3,−2 for elliptical light
Using relation (27) it is simple to establish why, although a monochromatic elliptical field has a geometry that allows for a non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 in an ω + 2ω process, the “hidden” symmetry in eqn (27) forces it to vanish. To see this, note that for an elliptical field we have
3,−2 in an ω + 2ω process, the “hidden” symmetry in eqn (27) forces it to vanish. To see this, note that for an elliptical field we have| | ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) = (t) = ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ωe−iωt + c.c., ωe−iωt + c.c., | (28) |
with ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω = Eω
ω = Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + iEyŷ and therefore [cf.eqn (21)]
+ iEyŷ and therefore [cf.eqn (21)]| | 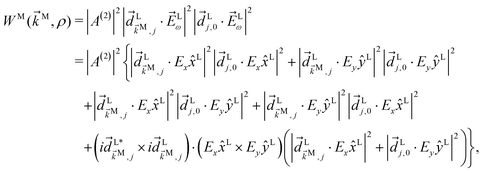 | (29) |
that is, we can decompose the process into six pathways. The first two of them involve either two x-polarized photons or two y-polarized photons and the associated geometrical symmetry prevents them from contributing to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2. The next two terms involve absorption of one x-polarized photon and one y-polarized photon and their lower geometrical symmetry allows for contributions to
3,−2. The next two terms involve absorption of one x-polarized photon and one y-polarized photon and their lower geometrical symmetry allows for contributions to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2. However, since these two terms correspond to opposite photon orderings satisfying ω1 → ω2, the photon-ordering symmetry in eqn (27) implies that their contributions will cancel each other exactly. The remaining terms describe PECD from the state |j〉 [cf. eqn (10) in ref. 13] after excitation via either an x- or a y-polarized photon. These terms make a null contribution to the integral over orientations in
3,−2. However, since these two terms correspond to opposite photon orderings satisfying ω1 → ω2, the photon-ordering symmetry in eqn (27) implies that their contributions will cancel each other exactly. The remaining terms describe PECD from the state |j〉 [cf. eqn (10) in ref. 13] after excitation via either an x- or a y-polarized photon. These terms make a null contribution to the integral over orientations in ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,–2 because all possible setup rotational invariants that can be formed either with the set {
3,–2 because all possible setup rotational invariants that can be formed either with the set {![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L, ŷL, ẑL, (Ex
L, ŷL, ẑL, (Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L × ÊyŷL), Ex
L × ÊyŷL), Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L, Ex
L, Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L} or with the set {
L} or with the set {![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L, ŷL, ẑL, (Ex
L, ŷL, ẑL, (Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L × ÊyŷL), EyŷL, EyŷL} vanish.42
L × ÊyŷL), EyŷL, EyŷL} vanish.42
Acknowledgements
A. F. O. and O. S. gratefully acknowledge the MEDEA Project, which has received funding from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie Grant Agreement No. 641789. A. F. O. and O. S. gratefully acknowledge support from the DFG SPP 1840 “Quantum Dynamics in Tailored Intense Fields” and DFG Grant No. SM 292/5-2. A. F. O. gratefully acknowledges grants supporting his research at ICFO: Agencia Estatal de Investigación (the R&D project CEX2019-000910-S, funded by MCIN/AEI/10.13039/501100011033, Plan Nacional FIDEUA PID2019-106901GB-I00, FPI), Fundació Privada Cellex, Fundació Mir-Puig, Generalitat de Catalunya (AGAUR Grant No. 2017 SGR 1341, CERCA program), and EU Horizon 2020 Marie Skłodowska-Curie grant agreement no. 101029393.
Notes and references
-
T. M. Lowry, Optical Rotatory Power, Dover Publications, New York, 1964 Search PubMed.
-
N. Berova, P. L. Polavarapu, K. Nakanishi and R. W. Woody, Comprehensive Chiroptical Spectroscopy, Wiley, Hoboken, New Jersey, 2012 Search PubMed.
- S. Eibenberger, J. Doyle and D. Patterson, Phys. Rev. Lett., 2017, 118, 123002 CrossRef PubMed.
- A. Yachmenev, J. Onvlee, E. Zak, A. Owens and J. Küpper, Phys. Rev. Lett., 2019, 123, 243202 CrossRef CAS PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, Phys. Rev. Lett., 2019, 122, 013204 CrossRef CAS PubMed.
- D. Ayuso, O. Neufeld, A. F. Ordonez, P. Decleva, G. Lerner, O. Cohen, M. Ivanov and O. Smirnova, Nat. Photonics, 2019, 13, 866 CrossRef CAS.
- T. Cao and Y. Qiu, Nanoscale, 2018, 10, 566–574 RSC.
- R. Noyori, Angew. Chem., Int. Ed., 2002, 41, 2008–2022 CrossRef CAS PubMed.
-
L. D. Barron, Molecular light scattering and optical activity, Cambridge University Press, 2nd edn, 2004 Search PubMed.
- H. Rhee, Y.-G. June, J.-S. Lee, K.-K. Lee, J.-H. Ha, Z. H. Kim, S.-J. Jeon and M. Cho, Nature, 2009, 458, 310–313 CrossRef CAS PubMed.
- Y. Tang and A. E. Cohen, Science, 2011, 332, 333–336 CrossRef CAS PubMed.
- C. Rosales-Guzmán, K. Volke-Sepulveda and J. P. Torres, Opt. Lett., 2012, 37, 3486–3488 CrossRef PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2018, 98, 063428 CrossRef CAS.
-
A. F. Ordonez, PhD thesis, Technische Universität Berlin, Berlin, Germany, 2019.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1411 CrossRef.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190 CrossRef PubMed.
- I. Powis, J. Chem. Phys., 2000, 112, 301–310 CrossRef CAS.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2013, 16, 856–871 RSC.
- L. Nahon, G. A. Garcia and I. Powis, J. Electron Spectrosc. Relat. Phenom., 2015, 204(Part B), 322–334 CrossRef CAS.
- V. Ulrich, S. Barth, S. Joshi, U. Hergenhahn, E. Mikajlo, C. J. Harding and I. Powis, J. Phys. Chem. A, 2008, 112, 3544–3549 CrossRef CAS PubMed.
- S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit, T. Ruchon, V. Blanchet, Y. Mairesse and B. Pons, New J. Phys., 2016, 18, 102002 CrossRef.
-
A. F. Ordonez and O. Smirnova, 2020, arXiv:2009.03660 [physics].
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed.
- P. V. Demekhin, Phys. Rev. A, 2019, 99, 063406 CrossRef CAS.
- S. Rozen, A. Comby, E. Bloch, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, V. Blanchet, B. Pons, N. Dudovich and Y. Mairesse, Phys. Rev. X, 2019, 9, 031004 CAS.
-
A. F. Ordonez and O. Smirnova, in Molecular Beams in Physics and Chemistry: From Otto Stern's Pioneering Exploits to Present-Day Feats, ed. B. Friedrich and H. Schmidt-Böcking, Springer International Publishing, Cham, 2021, pp. 335–352 Search PubMed.
- D. Patterson, M. Schnell and J. M. Doyle, Nature, 2013, 497, 475–477 CrossRef CAS PubMed.
- D. Patterson and J. M. Doyle, Phys. Rev. Lett., 2013, 111, 023008 CrossRef PubMed.
-
K. K. Lehmann, in Frontiers and Advances in Molecular Spectroscopy, ed. J. Laane, Elsevier, 2018, pp. 713–743 Search PubMed.
-
D. M. Brink and G. R. Satchler, Angular Momentum, Clarendon Press, Oxford, 2nd edn, 1968 Search PubMed.
- O. Neufeld, D. Podolsky and O. Cohen, Nat. Commun., 2019, 10, 405 CrossRef PubMed.
- Y.-Y. Yin, C. Chen, D. S. Elliott and A. V. Smith, Phys. Rev. Lett., 1992, 69, 2353–2356 CrossRef CAS PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, J. Chem. Phys., 2019, 151, 074106 CrossRef PubMed.
- G. Wagnière, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 2437–2440 CrossRef PubMed.
- G. H. Wagnière and G. L. J. A. Rikken, Chem. Phys. Lett., 2011, 502, 126–129 CrossRef.
- A. Cisneros and H. V. McIntosh, J. Math. Phys., 1970, 11, 870–895 CrossRef.
- M. Bashkansky, P. H. Bucksbaum and D. W. Schumacher, Phys. Rev. Lett., 1988, 60, 2458–2461 CrossRef CAS PubMed.
- A. D. Müller, E. Kutscher, A. N. Artemyev and P. V. Demekhin, J. Chem. Phys., 2020, 152, 044302 CrossRef PubMed.
- M. Richter, M. Kunitski, M. Schöffler, T. Jahnke, L. P. H. Schmidt and R. Dörner, Phys. Rev. A, 2016, 94, 033416 CrossRef.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, R. Dörner and M. Schöffler, J. Phys. Chem. A, 2019, 123, 6491–6495 CrossRef CAS PubMed.
- D. L. Andrews and T. Thirunamachandran, J. Chem. Phys., 1977, 67, 5026–5033 CrossRef CAS.
- J. A. Giordmaine, Phys. Rev., 1965, 138, A1599–A1606 CrossRef.
Footnotes |
| † Our choice of axes, which differs from ref. 22–24, simplifies Table 1. Our choice of phase coincides with that in ref. 24 and differs from the one in ref. 22 and 23. Note that some of the plots of Fig. 2(a) in ref. 24 are labeled with the wrong phase. |
| ‡ Here we use the word dichroic in analogy to how it is used in the circularly polarized case in PECD, where a change of π in the phase between the two perpendicular components of the field leads to a change of sign of b1,0. |
| § Explicit expressions for the molecular rotational invariants g1,−1, g2,−2, and g3,−2 are given in Appendices B–D. |
| ¶ Symmetries not immediately apparent from the geometric symmetries of the system.37 |
|| Another sensible choice, which slightly reduces the number of non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients, is to take the ω field along the z axis in order to obtain l,m coefficients, is to take the ω field along the z axis in order to obtain ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2N,m = 0 for m ≠ 0 in the signal corresponding to N-photon absorption of the ω field. 2N,m = 0 for m ≠ 0 in the signal corresponding to N-photon absorption of the ω field. |
** This is considerably simplified by ordering the scalar products in the orientation integral as 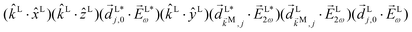 and using Table III in ref. 42. and using Table III in ref. 42. |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab and
Olga
Smirnova
ab and
Olga
Smirnova
 ac
ac
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients of the photoelectron angular distribution displaying different combinations of dichroism and enantiosensitivity. Finally, we list our conclusions in Section 5. Analogous results but for the case of charge multipoles induced via excitation of bound states are presented in ref. 27.
l,m coefficients of the photoelectron angular distribution displaying different combinations of dichroism and enantiosensitivity. Finally, we list our conclusions in Section 5. Analogous results but for the case of charge multipoles induced via excitation of bound states are presented in ref. 27.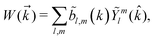
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is the photoelectron momentum and we have chosen to do the expansion in terms of real spherical harmonics Ỹml. In the case of a charge distribution we replace the photoelectron momentum
is the photoelectron momentum and we have chosen to do the expansion in terms of real spherical harmonics Ỹml. In the case of a charge distribution we replace the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) by the position
by the position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m could be a time dependent quantity.27 The
l,m could be a time dependent quantity.27 The ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients not only encode all the information contained in W(
l,m coefficients not only encode all the information contained in W(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) but are also examples of tensors of rank l (see e.g. Section 4.10 in ref. 31).
) but are also examples of tensors of rank l (see e.g. Section 4.10 in ref. 31).
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficient can be performed directly by using a detector with a structure that reflects the corresponding Ỹml. For example, a detector for
l,m coefficient can be performed directly by using a detector with a structure that reflects the corresponding Ỹml. For example, a detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 0,0 would simply sum the counts in all directions. A detector for
0,0 would simply sum the counts in all directions. A detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 would have two plates arranged as in Fig. 1a and b, so that it would add all the counts on one of them (red) and subtract all the counts on the other (blue). The choice of which plate adds and which plate subtracts is what physically defines the ẑ direction of the laboratory frame. A detector for
1,0 would have two plates arranged as in Fig. 1a and b, so that it would add all the counts on one of them (red) and subtract all the counts on the other (blue). The choice of which plate adds and which plate subtracts is what physically defines the ẑ direction of the laboratory frame. A detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 would have four plates arranged as in Fig. 1c, with a pair of opposite plates adding counts and the other pair subtracting counts. In this case, the detector defines the directions that correspond to a positive correlation between x and y, and those that correspond to a negative correlation between x and y. Analogously, a detector for
2,−2 would have four plates arranged as in Fig. 1c, with a pair of opposite plates adding counts and the other pair subtracting counts. In this case, the detector defines the directions that correspond to a positive correlation between x and y, and those that correspond to a negative correlation between x and y. Analogously, a detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 has eight plates arranged as in Fig. 1d, and distinguishes positive from negative correlations of x, y, and z.
3,−2 has eight plates arranged as in Fig. 1d, and distinguishes positive from negative correlations of x, y, and z.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m-specific detector and the Lissajous figure of the electric field can make up a chiral setup as shown in Fig. 1a, c and d. These setups are non-superimposable on their mirror images. This is particularly simple to see in Fig. 1a, c and d for reflections with respect to the polarization plane, which do not change the Lissajous figure but do swap blue and red plates. The chirality of these setups allows them to distinguish between opposite enantiomers of a chiral molecule. This is in contrast with the setup in Fig. 1b, which is symmetric with respect to reflection in the polarization plane and thus is not chiral and cannot distinguish between opposite enantiomers of a chiral molecule.
l,m-specific detector and the Lissajous figure of the electric field can make up a chiral setup as shown in Fig. 1a, c and d. These setups are non-superimposable on their mirror images. This is particularly simple to see in Fig. 1a, c and d for reflections with respect to the polarization plane, which do not change the Lissajous figure but do swap blue and red plates. The chirality of these setups allows them to distinguish between opposite enantiomers of a chiral molecule. This is in contrast with the setup in Fig. 1b, which is symmetric with respect to reflection in the polarization plane and thus is not chiral and cannot distinguish between opposite enantiomers of a chiral molecule.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m. In other words, the concept of a chiral setup answers the question of how we can distinguish opposite enantiomers without relying on the chirality of light, but it is the lack of symmetry of the light-matter system itself the deciding factor which determines the emergence of an enantiosensitive observable in the first place (see e.g.Fig. 2 in ref. 13). We now turn to the analysis of a specific family of Lissajous figures to illustrate this in detail.
l,m. In other words, the concept of a chiral setup answers the question of how we can distinguish opposite enantiomers without relying on the chirality of light, but it is the lack of symmetry of the light-matter system itself the deciding factor which determines the emergence of an enantiosensitive observable in the first place (see e.g.Fig. 2 in ref. 13). We now turn to the analysis of a specific family of Lissajous figures to illustrate this in detail.
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) = Eω
(t) = Eω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)
cos(ωt)![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + E2ω
+ E2ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt + ϕ)ẑ
cos(2ωt + ϕ)ẑ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz and time shifts of π/ω by Tπ/ω, then the joint system (field and isotropic chiral molecules) is invariant with respect to
πz and time shifts of π/ω by Tπ/ω, then the joint system (field and isotropic chiral molecules) is invariant with respect to ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz
πz![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π/ω. Clearly, the resulting observables must also be invariant with respect to
π/ω. Clearly, the resulting observables must also be invariant with respect to ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz
πz![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π/ω. That is, the symmetry-allowed
π/ω. That is, the symmetry-allowed ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients must satisfy
l,m coefficients must satisfy ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πz
πz![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π/ω
π/ω![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,mỸml =
l,mỸml = ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,mỸml. This corresponds to two scenarios: either
l,mỸml. This corresponds to two scenarios: either ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πzỸml = Ỹml and
πzỸml = Ỹml and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m contains only frequencies 2nω, or
l,m contains only frequencies 2nω, or ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πzỸml = −Ỹml and
πzỸml = −Ỹml and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m contains only frequencies (2n + 1)ω, where n = 0, 1, 2, …. Furthermore, since a reflection
l,m contains only frequencies (2n + 1)ω, where n = 0, 1, 2, …. Furthermore, since a reflection ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y with respect to the y = 0 plane swaps the enantiomers while leaving the field invariant, an enantiosensitive
y with respect to the y = 0 plane swaps the enantiomers while leaving the field invariant, an enantiosensitive ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is associated to a Ỹml satisfying
l,m is associated to a Ỹml satisfying ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yỸml = −Ỹml. And, since a rotation
yỸml = −Ỹml. And, since a rotation ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πx of π around the x axis changes the phase ϕ in the field by π while leaving the molecules invariant, a dichroic‡
πx of π around the x axis changes the phase ϕ in the field by π while leaving the molecules invariant, a dichroic‡![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is associated to a Ỹml satisfying
l,m is associated to a Ỹml satisfying ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) πxỸml = −Ỹml. These properties, which are valid independently of the ionization regime, are summarized in Tables 1 and 2.
πxỸml = −Ỹml. These properties, which are valid independently of the ionization regime, are summarized in Tables 1 and 2.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is symmetry-allowed and whether it is enantiosensitive and/or dichroic depends on how the field is oriented with respect to the axes. The choice made here [eqn (2)] yields the rather simple conditions in Tables 1 and 2. Conditions corresponding to other choices are given in Appendix A for the sake of comparison with ref. 24–26.
l,m is symmetry-allowed and whether it is enantiosensitive and/or dichroic depends on how the field is oriented with respect to the axes. The choice made here [eqn (2)] yields the rather simple conditions in Tables 1 and 2. Conditions corresponding to other choices are given in Appendix A for the sake of comparison with ref. 24–26.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients describing the photoelectron angular distribution (1) resulting from the interaction between an isotropic molecular sample and the field (2)
l,m coefficients describing the photoelectron angular distribution (1) resulting from the interaction between an isotropic molecular sample and the field (2)
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m
l,m
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients
l,m coefficients
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m
l,m![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients for l up to four in Table 3. From this table we can see that e.g.
l,m coefficients for l up to four in Table 3. From this table we can see that e.g. ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is dichroic but not enantiosensitive,
1,0 is dichroic but not enantiosensitive, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is enantiosensitive and dichroic, and
2,−2 is enantiosensitive and dichroic, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is enantiosensitive but not dichroic. Since Ỹ01(
3,−2 is enantiosensitive but not dichroic. Since Ỹ01(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) ∝ kz, Ỹ−22(
) ∝ kz, Ỹ−22(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) ∝ kxky, and Ỹ−23(
) ∝ kxky, and Ỹ−23(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) ∝ kxkykz, then
) ∝ kxkykz, then ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is associated to asymmetry along the direction of the 2ω field (ẑ),
1,0 is associated to asymmetry along the direction of the 2ω field (ẑ), ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is associated to correlations between the direction of the ω field (
2,−2 is associated to correlations between the direction of the ω field (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) and the direction perpendicular to the polarization plane (ŷ), and
) and the direction perpendicular to the polarization plane (ŷ), and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is associated to correlations of the three directions corresponding to the ω field (
3,−2 is associated to correlations of the three directions corresponding to the ω field (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ), the 2ω field (ẑ), and the perpendicular to the polarization plane (ŷ).
), the 2ω field (ẑ), and the perpendicular to the polarization plane (ŷ).
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients describing the photoelectron angular distribution (1) resulting from interaction of an isotropic molecular sample and the field (2) for l up to 4. N = No and Y = Yes
l,m coefficients describing the photoelectron angular distribution (1) resulting from interaction of an isotropic molecular sample and the field (2) for l up to 4. N = No and Y = Yes
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 0,0
0,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0
1,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2
2,−2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,0
2,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,2
2,2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2
3,−2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,0
3,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,2
3,2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−4
4,−4
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−2
4,−2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,0
4,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,2
4,2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,4
4,4
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficient is enantiosensitive if and only if it results from interference between pathways with N1 and N2 photons, respectively, and l + N1 + N2 is odd; or if it results from a direct pathway and l is odd. These conditions together with Table 2 tell us that a dichroic non-enantiosensitive
l,m coefficient is enantiosensitive if and only if it results from interference between pathways with N1 and N2 photons, respectively, and l + N1 + N2 is odd; or if it results from a direct pathway and l is odd. These conditions together with Table 2 tell us that a dichroic non-enantiosensitive ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m (with odd l) can only occur as the result of interference between pathways involving an even and an odd number of photons, respectively (so that N1 + N2 is odd and l + N1 + N2 is even). For example,
l,m (with odd l) can only occur as the result of interference between pathways involving an even and an odd number of photons, respectively (so that N1 + N2 is odd and l + N1 + N2 is even). For example, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 contributes to the photoelectron peak where absorption of two ω photons interferes with absorption of one 2ω photon (see Fig. 3a). The same condition (odd N1 + N2) applies for a dichroic and enantiosensitive
1,0 contributes to the photoelectron peak where absorption of two ω photons interferes with absorption of one 2ω photon (see Fig. 3a). The same condition (odd N1 + N2) applies for a dichroic and enantiosensitive ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m (even l) such as
l,m (even l) such as ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2. In contrast, an enantiosensitive non-dichroic
2,−2. In contrast, an enantiosensitive non-dichroic ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m (odd l) can occur as the result of either a direct pathway involving at least one ω photon and one 2ω photon, or as the result of interference between two pathways both with an even or both with an odd number of photons (even N1 + N2). For example,
l,m (odd l) can occur as the result of either a direct pathway involving at least one ω photon and one 2ω photon, or as the result of interference between two pathways both with an even or both with an odd number of photons (even N1 + N2). For example, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 contributes to the photoelectron peak corresponding to absorption of one ω photon followed by absorption of one 2ω photon (see Fig. 3b) and vice versa, or as the result of interference between absorption of two 2ω photons and four ω photons.
3,−2 contributes to the photoelectron peak corresponding to absorption of one ω photon followed by absorption of one 2ω photon (see Fig. 3b) and vice versa, or as the result of interference between absorption of two 2ω photons and four ω photons.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0,
1,0, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2, and
2,−2, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2. For the process depicted in Fig. 3a, the interference between the two pathways gives rise to a non-zero orientation-averaged
3,−2. For the process depicted in Fig. 3a, the interference between the two pathways gives rise to a non-zero orientation-averaged ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 given by (see Appendix B)
1,0 given by (see Appendix B)![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0(k) = A(1)*A(2)g1,0f1,0 + c.c.,
1,0(k) = A(1)*A(2)g1,0f1,0 + c.c.,![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is not enantiosensitive. The expression for f1,0 reads as
1,0 is not enantiosensitive. The expression for f1,0 reads as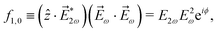
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω ≡ E2ωe−iϕẑ,
2ω ≡ E2ωe−iϕẑ, ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω ≡ Eω
ω ≡ Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . Eqn (4) shows that the setup rotational invariant f1,0 is a scalar involving the field vectors
. Eqn (4) shows that the setup rotational invariant f1,0 is a scalar involving the field vectors ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω and
2ω and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω, and the ẑ axis. As discussed in Section 3, the axis vector ẑ is defined by the detector needed to measure
ω, and the ẑ axis. As discussed in Section 3, the axis vector ẑ is defined by the detector needed to measure ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0. From eqn (4) it is evident that f1,0 changes sign when ϕ is shifted by π, and therefore
1,0. From eqn (4) it is evident that f1,0 changes sign when ϕ is shifted by π, and therefore ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is dichroic.
1,0 is dichroic.
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 given by (see Appendix C)
2,−2 given by (see Appendix C)![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 = A(1)*A(2)g2,−2f2,−2 + c.c.,
2,−2 = A(1)*A(2)g2,−2f2,−2 + c.c.,![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is enantiosensitive. The setup rotational invariant, given by
2,−2 is enantiosensitive. The setup rotational invariant, given by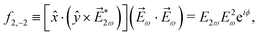
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and ŷ axes, which are defined by the detector needed to measure
and ŷ axes, which are defined by the detector needed to measure ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 (see Section 3). Just like g2,−2 is a pseudoscalar that distinguishes between molecules with opposite handedness, f2,−2 is a pseudoscalar that distinguishes between chiral setups of opposite handedness. Note that the detector for
2,−2 (see Section 3). Just like g2,−2 is a pseudoscalar that distinguishes between molecules with opposite handedness, f2,−2 is a pseudoscalar that distinguishes between chiral setups of opposite handedness. Note that the detector for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 does not directly tell apart a positive x from a negative x, or a positive y from a negative y. It only tells apart positive correlations of x and y from negative correlations of x and y. This is consistent with the invariance of f2,−2 with respect to a simultaneous inversion of
2,−2 does not directly tell apart a positive x from a negative x, or a positive y from a negative y. It only tells apart positive correlations of x and y from negative correlations of x and y. This is consistent with the invariance of f2,−2 with respect to a simultaneous inversion of ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and ŷ. Furthermore, eqn (6) shows that f2,−2 changes sign when ϕ is shifted by π, and therefore
and ŷ. Furthermore, eqn (6) shows that f2,−2 changes sign when ϕ is shifted by π, and therefore ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is dichroic. We remark, that although the right hand side of eqn (4) and (6) look exactly the same after performing the vector operations, f1,0 and f2,−2 emerge from different setup rotational invariants of a different physical nature: one is a scalar involving only the ẑ axis, and the other is a pseudoscalar involving correlation between the
2,−2 is dichroic. We remark, that although the right hand side of eqn (4) and (6) look exactly the same after performing the vector operations, f1,0 and f2,−2 emerge from different setup rotational invariants of a different physical nature: one is a scalar involving only the ẑ axis, and the other is a pseudoscalar involving correlation between the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and ŷ axes.
and ŷ axes.
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2, i.e. we consider the absorption of one ω photon and one 2ω photon, resonantly enhanced through a bound state as shown in Fig. 3b. In this case we get (see Appendix D)
3,−2, i.e. we consider the absorption of one ω photon and one 2ω photon, resonantly enhanced through a bound state as shown in Fig. 3b. In this case we get (see Appendix D)![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2(k) = |A(2)|2g3,−2f3,−2,
3,−2(k) = |A(2)|2g3,−2f3,−2,![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 enantiosensitive. The setup rotational invariant f3,−2 is given by
3,−2 enantiosensitive. The setup rotational invariant f3,−2 is given by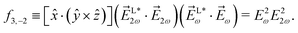
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is therefore not dichroic. The robustness of f3,−2 against changes of ϕ means that recording
3,−2 is therefore not dichroic. The robustness of f3,−2 against changes of ϕ means that recording ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 allows distinguishing opposite enantiomers in the absence of stabilization of the ω–2ω phase shift ϕ.
3,−2 allows distinguishing opposite enantiomers in the absence of stabilization of the ω–2ω phase shift ϕ.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 is dichroic and non-enantiosensitive,
1,0 is dichroic and non-enantiosensitive, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is dichroic and enantiosensitive, and
2,−2 is dichroic and enantiosensitive, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 is enantiosensitive and non-dichroic. In addition, these equations show that
3,−2 is enantiosensitive and non-dichroic. In addition, these equations show that ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0,
1,0, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2, and
2,−2, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 are in general not zero for the specific processes considered here. This is important because although a given
3,−2 are in general not zero for the specific processes considered here. This is important because although a given ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m may be symmetry allowed according to the general symmetry analysis above, further “hidden” symmetries¶ involved in a specific process may forbid it. For example, although the geometry of a monochromatic elliptical field allows for a non-zero
l,m may be symmetry allowed according to the general symmetry analysis above, further “hidden” symmetries¶ involved in a specific process may forbid it. For example, although the geometry of a monochromatic elliptical field allows for a non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2, the presence of the triple product in eqn (8) means that opposite photon orderings contribute to
3,−2, the presence of the triple product in eqn (8) means that opposite photon orderings contribute to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 with opposite signs (see Appendix E). Such photon orderings are degenerate in the monochromatic case and thus the two contributions cancel each other out (see Appendix F). However, it must be kept in mind that the hidden symmetry preventing a non-zero
3,−2 with opposite signs (see Appendix E). Such photon orderings are degenerate in the monochromatic case and thus the two contributions cancel each other out (see Appendix F). However, it must be kept in mind that the hidden symmetry preventing a non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 for elliptical fields is specific to the 2-photon process we investigated here, so it may be broken in higher order processes or in the strong field regime. That is, photoionization induced by elliptically polarized strong fields may indeed yield a non-zero enantiosensitive and non-dichroic
3,−2 for elliptical fields is specific to the 2-photon process we investigated here, so it may be broken in higher order processes or in the strong field regime. That is, photoionization induced by elliptically polarized strong fields may indeed yield a non-zero enantiosensitive and non-dichroic ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient. This would be analogous to how
3,−2 coefficient. This would be analogous to how ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 is symmetry-forbidden in the elliptical one-photon case23 but it is symmetry allowed in the elliptical strong-field case.38
2,−2 is symmetry-forbidden in the elliptical one-photon case23 but it is symmetry allowed in the elliptical strong-field case.38![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m is symmetry allowed, if it is dichroic (sensitive to changes of π in the ω–2ω relative phase), and if it is enantiosensitive. These
l,m is symmetry allowed, if it is dichroic (sensitive to changes of π in the ω–2ω relative phase), and if it is enantiosensitive. These ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients are relevant in the description of photoelectron angular distributions and in the description of induced multipoles of bound charge distributions (discussed in ref. 27). We found that the enantiosensitivity and the dichroism of a
l,m coefficients are relevant in the description of photoelectron angular distributions and in the description of induced multipoles of bound charge distributions (discussed in ref. 27). We found that the enantiosensitivity and the dichroism of a ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficient are in general independent of each other. That is, in addition to the usual types of
l,m coefficient are in general independent of each other. That is, in addition to the usual types of ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients in isotropic samples, namely: (i) non-dichroic and non-enantiosensitive, (ii) dichroic and enantiosensitive, and (iii) dichroic and non-enantiosensitive, we found the more exotic possibility of (iv) enantiosensitive and non-dichroic
l,m coefficients in isotropic samples, namely: (i) non-dichroic and non-enantiosensitive, (ii) dichroic and enantiosensitive, and (iii) dichroic and non-enantiosensitive, we found the more exotic possibility of (iv) enantiosensitive and non-dichroic ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients.
l,m coefficients.
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients in photoelectron angular distributions corresponding to types (ii)–(iv) for the case of one- vs. two-photon absorption and for the case of ω + 2ω absorption. Unlike type (ii) coefficients, type (iv) coefficients allow enantiomeric discrimination in the absence of stabilization of the ω–2ω relative phase and remain to be numerically calculated and experimentally observed. Such verification is within reach with current theoretical39 and experimental40,41 capabilities which provide access to the full photoelectron momentum distribution. Imaging of the type (iv) coefficient
l,m coefficients in photoelectron angular distributions corresponding to types (ii)–(iv) for the case of one- vs. two-photon absorption and for the case of ω + 2ω absorption. Unlike type (ii) coefficients, type (iv) coefficients allow enantiomeric discrimination in the absence of stabilization of the ω–2ω relative phase and remain to be numerically calculated and experimentally observed. Such verification is within reach with current theoretical39 and experimental40,41 capabilities which provide access to the full photoelectron momentum distribution. Imaging of the type (iv) coefficient ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 discussed here with a velocity map imaging detector as e.g. in ref. 26 is complicated by two facts: (a) the lack of cylindrical symmetry prevents Abel inversion and (b) projection of the Ỹ3,−2 contribution to the momentum distribution on the xy (or yz) plane cancels exactly (see Fig. 1c). However, re-orientation of the detector so as to project the momentum distribution on e.g. the x = z plane, as shown in Fig. 4, should facilitate imaging the non-zero
3,−2 discussed here with a velocity map imaging detector as e.g. in ref. 26 is complicated by two facts: (a) the lack of cylindrical symmetry prevents Abel inversion and (b) projection of the Ỹ3,−2 contribution to the momentum distribution on the xy (or yz) plane cancels exactly (see Fig. 1c). However, re-orientation of the detector so as to project the momentum distribution on e.g. the x = z plane, as shown in Fig. 4, should facilitate imaging the non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient. Experimentally, one can keep the detector fixed and instead rotate the polarizations of the fields. That is, measurement of the
3,−2 coefficient. Experimentally, one can keep the detector fixed and instead rotate the polarizations of the fields. That is, measurement of the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient only requires rotating ω and 2ω by 45° around their propagation axis in ref. 24 and 26.
3,−2 coefficient only requires rotating ω and 2ω by 45° around their propagation axis in ref. 24 and 26.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 using monochromatic light with elliptical polarization. However, a “hidden” symmetry associated to the degeneracy in photon orderings in the monochromatic case prevents this coefficient in the case of a two-photon process. The possibility of this hidden symmetry to be violated for higher-order or strong-field processes, or in a more refined description of photoionization remains to be investigated.
3,−2 using monochromatic light with elliptical polarization. However, a “hidden” symmetry associated to the degeneracy in photon orderings in the monochromatic case prevents this coefficient in the case of a two-photon process. The possibility of this hidden symmetry to be violated for higher-order or strong-field processes, or in a more refined description of photoionization remains to be investigated.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients. Here, for the sake of comparison, we consider the alternative orientation|| used in ref. 24–26, namely
l,m coefficients. Here, for the sake of comparison, we consider the alternative orientation|| used in ref. 24–26, namely![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) = Eω
(t) = Eω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)ŷ + E2ω
cos(ωt)ŷ + E2ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt + ϕ)
cos(2ωt + ϕ)![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) .
.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,1,
1,1, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−1, and
2,−1, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 are dichroic non-enantiosensitive, enantiosensitive and dichroic, and enantiosensitive non-dichroic, respectively. These are just the correspondingly rotated versions of the coefficients in Section 4. Note that
3,−2 are dichroic non-enantiosensitive, enantiosensitive and dichroic, and enantiosensitive non-dichroic, respectively. These are just the correspondingly rotated versions of the coefficients in Section 4. Note that ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−1 ∝ Im{b2,1} is indeed the coefficient discussed in ref. 25.
2,−1 ∝ Im{b2,1} is indeed the coefficient discussed in ref. 25.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m
l,m
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m
l,m
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 0,0
0,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,1
1,1
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−1
2,−1
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,0
2,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,2
2,2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2
3,−2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,1
3,1
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,3
3,3
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−3
4,−3
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,−1
4,−1
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,0
4,0
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,2
4,2
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 4,4
4,4
![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 1,0 in eqn (3)
1,0 in eqn (3)![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 coefficient given by23
1,0 coefficient given by23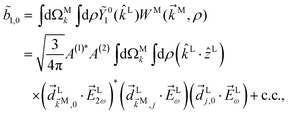
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is the photoelectron momentum,
is the photoelectron momentum, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ≡
≡ ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) /k, ρ ≡ αβγ is the molecular orientation specified by the Euler angles αβγ,
/k, ρ ≡ αβγ is the molecular orientation specified by the Euler angles αβγ,  is the normalized integral over all molecular orientations,
is the normalized integral over all molecular orientations,  is the integral over all photoelectron directions
is the integral over all photoelectron directions ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M,
M, 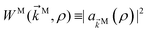 is the photoelectron angular distribution in the molecular frame for a particular orientation ρ.
is the photoelectron angular distribution in the molecular frame for a particular orientation ρ. 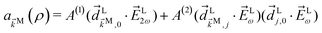 is the probability amplitude of the state |
is the probability amplitude of the state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉, A(1) and A(2) are complex-valued constants depending on detunings and pulse envelopes,
M〉, A(1) and A(2) are complex-valued constants depending on detunings and pulse envelopes, ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i,j ≡ 〈i|
i,j ≡ 〈i|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |j〉 is the dipole transition matrix element between states |i〉 and |j〉, |
|j〉 is the dipole transition matrix element between states |i〉 and |j〉, |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 is the scattering state describing an outgoing plane wave with photoelectron momentum
〉 is the scattering state describing an outgoing plane wave with photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) , and
, and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω = Eω
ω = Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and
and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω = E2ωe−iϕẑ are the Fourier amplitudes of the field (2) at frequencies ω and 2ω, respectively. The vectors
2ω = E2ωe−iϕẑ are the Fourier amplitudes of the field (2) at frequencies ω and 2ω, respectively. The vectors ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L and
L and ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) Li,j, depend on the molecular orientation ρ according to
Li,j, depend on the molecular orientation ρ according to ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) L = S(ρ)
L = S(ρ)![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) M, where S(ρ) is the rotation matrix taking vectors from the molecular frame to the laboratory frame. Note that only the interference between the two pathways in Fig. 3 contributes to
M, where S(ρ) is the rotation matrix taking vectors from the molecular frame to the laboratory frame. Note that only the interference between the two pathways in Fig. 3 contributes to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0 (see Section 4).
1,0 (see Section 4).
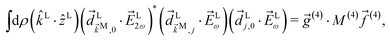
![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) (4) and
(4) and ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) (4) are vectors of molecular and setup rotational invariants, respectively,
(4) are vectors of molecular and setup rotational invariants, respectively,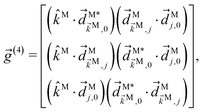
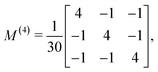
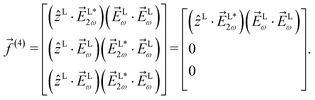
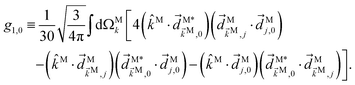
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω and
ω and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω. We have kept the vectorial form of the rotational invariant in eqn (4) to emphasize the scalar vs. pseudoscalar character (see discussion in Section 4.1). As can be seen from eqn (14), to derive eqn (3), (4) and (15) we explicitly used
2ω. We have kept the vectorial form of the rotational invariant in eqn (4) to emphasize the scalar vs. pseudoscalar character (see discussion in Section 4.1). As can be seen from eqn (14), to derive eqn (3), (4) and (15) we explicitly used ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω‖ẑL and
L2ω‖ẑL and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω‖
Lω‖![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L.
L.
![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 2,−2 in eqn (5)
2,−2 in eqn (5)![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 coefficient we have23
2,−2 coefficient we have23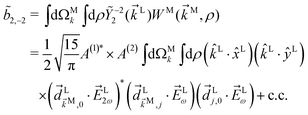
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0.42 Making explicit use of
1,0.42 Making explicit use of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω‖ẑL and
L2ω‖ẑL and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω‖
Lω‖![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L yields eqn (5), with f2,−2 given by eqn (6) and g2,−2 given by
L yields eqn (5), with f2,−2 given by eqn (6) and g2,−2 given by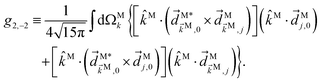
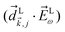 exchanges its position with (
exchanges its position with (![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L·
L·![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L) in eqn (15) one obtains
L) in eqn (15) one obtains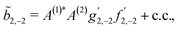
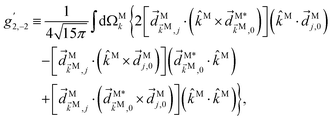
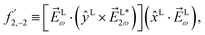
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω‖ẑL and
L2ω‖ẑL and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω‖
Lω‖![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L. Writing the explicit expressions
L. Writing the explicit expressions ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω = Eω
ω = Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and
and 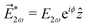 one can show that
one can show that  . And using standard vectorial algebra relations one can show that
. And using standard vectorial algebra relations one can show that  . The latter equality reflects the fact that, for four arbitrary vectors
. The latter equality reflects the fact that, for four arbitrary vectors ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ,
, ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ,
, ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) ,
, ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) , the three different rotational invariants r1 ≡ [
, the three different rotational invariants r1 ≡ [![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ·(
·(![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ×
× ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) )](
)](![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ·
·![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) ), r2 ≡ [
), r2 ≡ [![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ·(
·(![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ×
× ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) )](
)](![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) ·
·![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ), and r3 ≡ [
), and r3 ≡ [![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ·(
·(![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) ×
× ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) )](
)](![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ·
·![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ) can be written as a linear combination of the two rotational invariants r1 and r4 ≡ [
) can be written as a linear combination of the two rotational invariants r1 and r4 ≡ [![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ·(
·(![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) ×
× ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) )](
)](![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ·
·![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ). Care must therefore be taken when looking for interpretations that depend on the particular ordering of the vectors appearing in the rotational invariants.
). Care must therefore be taken when looking for interpretations that depend on the particular ordering of the vectors appearing in the rotational invariants.
![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 3,−2 for ω + 2ω [eqn (7)]
3,−2 for ω + 2ω [eqn (7)]![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 coefficient given by23
3,−2 coefficient given by23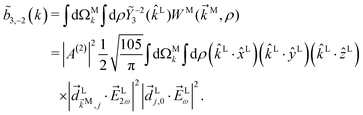
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1,0.42 Making explicit use of
1,0.42 Making explicit use of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L2ω‖ẑL and
L2ω‖ẑL and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) Lω‖
Lω‖![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L yields eqn (7), with f3,−2 given by eqn (8) and g3,−2 given by**
L yields eqn (7), with f3,−2 given by eqn (8) and g3,−2 given by**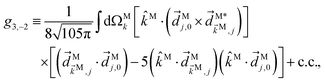
![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 3,−2 for 2ω + ω: symmetry in photon ordering
3,−2 for 2ω + ω: symmetry in photon ordering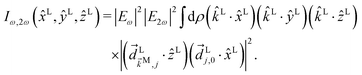
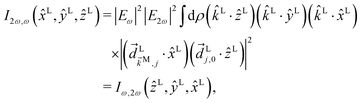
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L and ẑL in eqn (23). On the other hand, from the triple product in eqn (8) it follows that
L and ẑL in eqn (23). On the other hand, from the triple product in eqn (8) it follows that![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L) = −Iω,2ω(
L) = −Iω,2ω(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L,ŷL,ẑL)
L,ŷL,ẑL)![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L,ŷL,ẑL) = −Iω,2ω(
L,ŷL,ẑL) = −Iω,2ω(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L,ŷL,ẑL).
L,ŷL,ẑL).![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 in the photon ordering 2ω + ω is exactly the same as for the photon ordering ω + 2ω up to a minus sign. However, since for a fixed molecular spectrum the coupling coefficient A(2) strongly depends on detunings (and therefore photon ordering), if one of the photon orderings is resonant it will dominate. Furthermore, in practice each photon ordering might be resonant with different transitions, and one should therefore use different transition dipole matrix elements for each ordering.
3,−2 in the photon ordering 2ω + ω is exactly the same as for the photon ordering ω + 2ω up to a minus sign. However, since for a fixed molecular spectrum the coupling coefficient A(2) strongly depends on detunings (and therefore photon ordering), if one of the photon orderings is resonant it will dominate. Furthermore, in practice each photon ordering might be resonant with different transitions, and one should therefore use different transition dipole matrix elements for each ordering.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 → 0 as ω1 → ω2. Note that this is analogous to the corresponding result for the polarization in sum-frequency generation.43
3,−2 → 0 as ω1 → ω2. Note that this is analogous to the corresponding result for the polarization in sum-frequency generation.43
![[b with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0062_0303.gif) 3,−2 for elliptical light
3,−2 for elliptical light![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2 in an ω + 2ω process, the “hidden” symmetry in eqn (27) forces it to vanish. To see this, note that for an elliptical field we have
3,−2 in an ω + 2ω process, the “hidden” symmetry in eqn (27) forces it to vanish. To see this, note that for an elliptical field we have![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) =
(t) = ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ωe−iωt + c.c.,
ωe−iωt + c.c.,![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω = Eω
ω = Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + iEyŷ and therefore [cf.eqn (21)]
+ iEyŷ and therefore [cf.eqn (21)]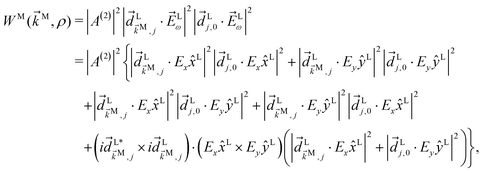
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2. The next two terms involve absorption of one x-polarized photon and one y-polarized photon and their lower geometrical symmetry allows for contributions to
3,−2. The next two terms involve absorption of one x-polarized photon and one y-polarized photon and their lower geometrical symmetry allows for contributions to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,−2. However, since these two terms correspond to opposite photon orderings satisfying ω1 → ω2, the photon-ordering symmetry in eqn (27) implies that their contributions will cancel each other exactly. The remaining terms describe PECD from the state |j〉 [cf. eqn (10) in ref. 13] after excitation via either an x- or a y-polarized photon. These terms make a null contribution to the integral over orientations in
3,−2. However, since these two terms correspond to opposite photon orderings satisfying ω1 → ω2, the photon-ordering symmetry in eqn (27) implies that their contributions will cancel each other exactly. The remaining terms describe PECD from the state |j〉 [cf. eqn (10) in ref. 13] after excitation via either an x- or a y-polarized photon. These terms make a null contribution to the integral over orientations in ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3,–2 because all possible setup rotational invariants that can be formed either with the set {
3,–2 because all possible setup rotational invariants that can be formed either with the set {![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L, ŷL, ẑL, (Ex
L, ŷL, ẑL, (Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L × ÊyŷL), Ex
L × ÊyŷL), Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L, Ex
L, Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L} or with the set {
L} or with the set {![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L, ŷL, ẑL, (Ex
L, ŷL, ẑL, (Ex![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L × ÊyŷL), EyŷL, EyŷL} vanish.42
L × ÊyŷL), EyŷL, EyŷL} vanish.42
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients, is to take the ω field along the z axis in order to obtain
l,m coefficients, is to take the ω field along the z axis in order to obtain ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2N,m = 0 for m ≠ 0 in the signal corresponding to N-photon absorption of the ω field.
2N,m = 0 for m ≠ 0 in the signal corresponding to N-photon absorption of the ω field.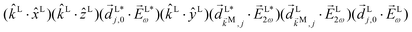 and using Table III in ref. 42.
and using Table III in ref. 42.


