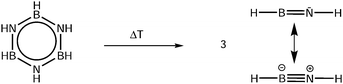
Threshold photoelectron spectroscopy of iminoborane, HBNH
Domenik
Schleier†
a,
Dorothee
Schaffner
a,
Marius
Gerlach
 a,
Patrick
Hemberger
a,
Patrick
Hemberger
 b and
Ingo
Fischer
b and
Ingo
Fischer
 *a
*a
aInstitute of Physical and Theoretical Chemistry, University of Würzburg, Am Hubland, Würzburg D-97074, Germany. E-mail: ingo.fischer@uni-wuerzburg.de
bLaboratory for Femtochemistry and Synchrotron Radiation, Paul Scherrer Institut (PSI), Villigen CH-5232, Switzerland. E-mail: patrick.hemberger@psi.ch
First published on 2nd December 2021
Abstract
We report the mass-selected threshold photoelectron spectrum (ms-TPES) of iminoborane (HBNH), generated by pyrolysis of borazine. The adiabatic ionization energy (IE) of the X+ 2Π ← X 1Σ+ transition was determined to be 11.31 ± 0.02 eV and the wavenumber of the B–N stretching vibration in the cation was measured to be 1550 cm−1. The Renner–Teller splitting in the X+ 2Π state gives rise to two sets of vibrational progressions, separated by 70 meV.
Hydrogen is an alternative energy carrier for the transition away from fossil fuels. It exhibits a large gravimetric-, but very low volumetric energy density, even when compressed at high pressures or liquified.1 Thus, several compounds have been investigated to temporarily store and later release hydrogen when its contained chemical energy is needed.2,3 Among the most promising candidates are ammonia boranes like H3NBH3 (AB).4,5 AB has a very high relative hydrogen content (19.6 wt%), and releases H2 by thermolysis just over 120 °C in a stepwise mechanism, forming H2BNH2, HBNH and BN. For application, this process has to be reversible and consequently reactions must be well defined and thermoneutral. However, both amino borane (H2BNH2) and iminoborane (HBNH) are highly reactive and readily polymerize to polyaminoboranes,6 which can decompose under elimination of H2 to form borazine and other products.7–11 Further interest in iminoboranes R–BN–R′ originates from the isosterism of BN and CC, so substituting CC units by BN is employed to tune the reactivity and the electronic properties of organic molecules.12–14 For example, introducing BN into aromatic molecules can increase the propensity for singlet fission, when the substituent is placed at the right position.15–17 It is thus highly desirable to better understand and characterise the properties of the HBNH intermediate.
Iminoborane is highly reactive, isoelectronic to acetylene and has remained almost elusive so far. First computational studies showed HBNH to be linear (C∞v) with a X 1Σ+ ground state.18,19 Its electronic configuration in the ground state is …(3σ)2(4σ)2(5σ)2(1π)4 with the two HOMOs being a degenerate pair of orthogonal BN-bonding π-orbitals. This results in a bond order of 3 and as a consequence, the B–N bond length RBN = 1.223 Å is similar to a C–C triple bond (1.200 Å).18,19 It was first produced by photolysis of AB in an Ar-matrix using a hydrogen discharge lamp and subsequently identified by IR spectroscopy.20 Later Kawashima et al. generated HBNH in an arc discharge of a diborane/ammonia mixture and reported a rotationally resolved gas-phase IR spectrum.21 A wavenumber of 1786.193 cm−1 for the ν3 fundamental and RBN = 1.2381 Å were determined in this work. HBNH was also detected by mass spectrometry in a crossed beam experiment using beams of boron atoms and ammonia.22 These experiments were supported by computations, which identified HBNH2 as a possible intermediate that releases one hydrogen atom. Iminoborane can also be seen as a structural modification of diborene (HBBH), a prototype inorganic biradical that was recently investigated by our group.23
Accurate properties, like ionization (IE) and appearance energies (AE), are crucial to establish the thermochemistry of the various steps in the H2 release and recovery. Yet, for HBNH these data are only available from computational studies,24 because due to its high reactivity it needs to be generated in situ from a stable precursor. Here we use the pyrolysis of borazine (B3N3H6) as a source of iminoborane, as depicted in Scheme 1.
To avoid interference with side products or residual precursor, we employed photoelectron–photoion coincidence (PEPICO) spectroscopy25 using synchrotron radiation. In this scheme, electrons and ions from a single ionization event are correlated, leading to ion mass-selected threshold photoelectron spectra (ms-TPES). Isomers of the same mass can be distinguished based on the IE and the observed vibrational structure.26 In the past, we applied this approach to record ms-TPE spectra of a number of boron containing molecules, like BH227 or HBBH,23 but also larger species like borylene complexes,28 aza-borinines and aza-boroles.29
Experiments were performed at the X04DB Vacuum Ultraviolet beamline at the SwissLightSource (SLS). The double imaging CRF-PEPICO (combustion reactions followed by PEPICO) spectrometer has been employed.30,31 Borazine has been used as a precursor, synthesized following ref. 32. During the experiments the sample container was cooled to 4 °C. Borazine was seeded in Ar and expanded through a 200 μm nozzle into a SiC pyrolysis tube with 1 mm OD. Here, it was partially converted by resistively heating the SiC to 1100 °C. The molecular beam was skimmed and perpendicularly crossed by synchrotron radiation (SR). The SR was provided by a bending magnet, collimated and diffracted using a plane grating (150 lines per mm) with a resolution of E/ΔE = 1500. Higher harmonics were suppressed by a gas-filter (ptot = 10 mbar) operating with an Ar/Kr mixture. The photon energy was calibrated on the 11 s′–14 s′ autoionization resonances of Ar in the first and second order of the grating. A detailed description of the beamline is given elsewhere.30 Electrons and ions were detected in coincidence using a multiple-start/multiple-stop scheme and both particles were imaged on two position sensitive Roentdeck DLD40 delay line detectors. Threshold electrons were collected with a resolution of 5 meV and contributions of hot electrons were subtracted following the procedure reported by Sztaray and Baer.33
Geometry optimisations followed by calculations of harmonic frequencies in both neutral and cationic states were performed on the B3LYP\6-311G(2d,d,p) level using the CBS-QB3 composite approach in the Gaussian 09 program package.34 The adiabatic ionisation energy was calculated from the difference between the zero-point energies of neutral and cationic species. The threshold photoelectron spectrum was simulated initially in the harmonic approximation using the program ezSpectrum.35 The FC-factors were calculated and the stick spectrum convoluted with a Gaussian with a full-width half maximum (FWHM) of 25 meV. To account for the high temperatures in the pyrolysis, the simulation was performed at 1100 °C. All computed vibrational frequencies have been scaled by a factor of 0.96.
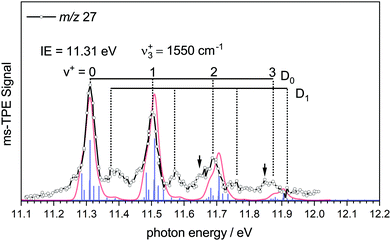
To characterise the pyrolysis products, mass spectra have been recorded at various photon energies and pyrolysis powers. Fig. 1 shows mass spectra at 11.50 eV and three different pyrolysis temperatures of 298 °C, 700 °C and 1100 °C. The signal of borazine, recognisable by the 10B/11B isotope pattern, constantly decreases towards higher pyrolysis temperatures, but remains the most intense peak even at 1100 °C. It is thus very stable with respect to thermal decomposition. A peak at mass 17, identified as ammonia by its ms-TPES, already appears without pyrolysis and increases significantly at higher pyrolysis temperatures. Masses 26 and 27 start to appear at 30 W and also increase with temperature. Their intensities reflect the typical boron isotopic pattern expected for iminoborane HBNH. Upon dissociative photoionization, borazine was found to lose predominately an H-atom and no HBNH+ was observed until 14 eV without pyrolysis. As the best conversion efficiency was achieved at high pyrolysis temperatures, the ms-TPES of HBNH, given in Fig. 2, was recorded at 1100 °C.
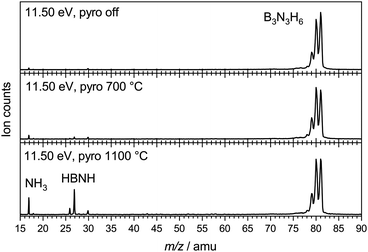 | ||
| Fig. 1 Mass spectra of borazine at different pyrolysis powers, corresponding to estimated temperatures of 700 °C (30 W) and 1100 °C (60 W). | ||
The experimental spectrum is compared to a simulated spectrum based on the calculations. The ms-TPES of HBNH shows four major bands in regular intervals. The first band at 11.31 ± 0.02 eV is assigned as the IE, in excellent agreement with the calculated value of 11.31 eV. The band is due to ejection of an electron from the 1π HOMO, which results in a X+ 2Π ← X 1Σ+ transition. The vibrational progression in the cation with a spacing of 1550 cm−1 can be explained by the removal of an electron from a binding orbital, which reduces the BN bond order. Thus, the computed RBN+ increases to 1.307 Å, resulting in vibrational activity of the ν3+ symmetric BN stretch in the cation. Accordingly, the computed wavenumber of the B–N-stretch decreases from 1780 cm−1 (exp: 1786.193 cm−1)21 to 1533 cm−1 upon ionisation, in agreement with the decrease in bond order. The most important parameters of HBNH are summarised in Table 1. The FC-simulation largely coincides with the experimental spectrum. Towards higher energies the harmonic simulation is increasingly blue-shifted with respect to the spectrum due to the neglect of anharmonicity. The intensities in the experimental spectrum constantly decrease, while the simulation predicts the origin band and the ν3+ fundamental to be equal in intensity, therefore slightly overestimating the B–N bond length in the cation. A slightly better intensity distribution is obtained when RBN+ is reduced by around 0.01 Å in the simulations.
| Parameter | X 1Σ (comp) | X+ 2Π (comp) | Experiment |
|---|---|---|---|
| R BN/Å | 1.234 | 1.307 | ≈1.30 |
| R BH/Å | 1.167 | 1.169 | — |
| R NH/Å | 0.990 | 1.016 | — |
| ∡(H–B–N) | 180° | 180° | — |
| ∡(B–N–H) | 180° | 180° | — |
| ν 3 | 1780 cm−1 | 1533 cm−1 | ν 3 + = 1550 cm−1 |
| IE | 11.31 eV | 11.31 ± 0.02 eV |
Shoulders on the lower energy side of the bands are recognized for v+ = 2 and 3, and marked by arrows, but are also present at the fundamental and origin bands. They represent combinations of ν3+ with sequence band transitions and appear with considerable intensity in the simulation due to the comparably high temperature. By comparing the simulation and the experimental spectrum, one can see, that the broadening of the peaks is well represented by the simulation.
However, further bands arise with significant intensity at 11.39 eV and 11.58 eV that cannot be reasonably assigned to another fundamental. We assign them based on our previous analysis of the TPES of diborene (HBBH). Here ionization occurs from the (1π)2 HOMO, also resulting in a cationic ground state of 2Π symmetry. In both molecules, the cation is subject to a Renner–Teller (RT) splitting. For HBBH, a weak RT interaction was computed and a linear equilibrium geometry was maintained for both components, D0 and D1. Due to the different shape of the potentials along the bending coordinate, different zero-point energies (ZPEs) result, which give rise to slightly displaced vibrational progressions. We assume the same situation for iminoborane and assign the additional bands to the ν3+ progression in the D1 upper Renner–Teller component. From this assignment, the difference in ZPE between D0 and D1 was determined to be 70 meV, which is about twice as much as in diborene (35 meV).
Iminoborane can be compared with two other linear congeners, acetylene and diborene. All three species exhibit a similar orbital structure with a degenerate pair of π-HOMOs. While iminoborane and acetylene display a bond order of 3, diborene is a biradical with a formal bond order of 2 (double bond). Consequently, RBB in HBBH+ is substantially longer than RBN in HBNH+ (1.606 Å compared to 1.307 Å). For comparison, RCC in HCCH was determined to be 1.208 Å36 and increases to 1.257 Å in the cation.37 It has to be noted though that acetylene in its neutral as well as cationic X+ 2Πu ground state38,39 has been investigated in much more detail, because acetylene is a stable molecule. Interestingly, its IE of 11.4006 eV38,40 is very similar to the value determined here for HBNH. The significantly lower IE of HBBH of 9.08 eV can be understood by its open shell character, which results in a destabilised HOMO of the neutral, compared to the closed shell singlet species HBNH and HCCH.
Comparing vibrational frequencies in different molecules is difficult, because in addition to the force constant (bond strength), the reduced mass has to be considered. When HBBH is compared to HBNH and HCCH, both effects work in the same direction for the BB mode, resulting in cationic vibrational wavenumber of 1100 cm−1 (computed 1056 cm−1) more than 400 cm−1 and 700 cm−1 below the BN mode of HBNH+ (1550 cm−1, see above) and the CC mode of HCCH+ (1817.5 cm−1),39 respectively. This contributes to the larger difference in ZPE between the two Renner–Teller components in HBNH. In contrast, the wavenumbers of the B–N stretch modes ν3 and ν3+ of iminoborane are in between the corresponding B–B and C–C modes. This might be explained by the influence of the polarity on the bond strength, because the electronegativity difference between boron and nitrogen in iminoborane weakens the triple bond and thus reduces the wavenumber in comparison to acetylene. This influence of the polarity has been previously recognized by Paetzold and others with respect to the reactivity of iminoboranes and linked to their inherent instability and propensity to oligomerise compared to alkynes.41,42
Conclusions
The highly reactive iminoborane HBNH was generated by pyrolysis of borazine and investigated by photoelectron–photoion coincidence spectroscopy, yielding a mass-selected threshold photoelectron spectrum. Interest in HBNH originates from its role as an intermediate in the hydrogen elimination from ammonia borane, a promising hydrogen storage material. An IE of 11.31 ± 0.02 eV was derived from the data. The spectrum shows a pronounced vibrational progression of the BN stretching mode with a spacing of 1550 cm−1, accompanied by sequence bands at the low energy side of each transition. As the X+ 2Π cationic ground state is subject to a Renner–Teller splitting, the spectrum exhibits an additional series of bands that originate from the upper Renner–Teller component of the 2Π state. Comparing iminoborane to acetylene shows differences that can be explained by the polarity of the BN unit as compared to CC, which reduces orbital overlap and weakens the triple bond. The differences to diborene on the other hand can be explained by the larger formal bond order of 3 in HBNH as compared to 2 in HBBH.Author contributions
Domenik Schleier: investigation, resources, writing – original draft. Dorothee Schaffner, Patrick Hemberger: investigation, resources. Marius Gerlach: investigation. Ingo Fischer: conceptualisation, writing – review and editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The experiments were performed at the VUV beamline of the Swiss Light Source, located at the Paul Scherrer Institute (PSI). The work was financially supported by the Deutsche Forschungsgemeinschaft (DFG), contract FI575/13-2 and GRK 2112. It was also supported by the Swiss Federal Office for Energy (BFE Contract Number SI/501269-01). D. Schaffner acknowledges a fellowship by the Hanns-Seidel foundation. We would like to thank Prof. Holger Braunschweig for insightful discussions on boron chemistry and acknowledge the help of Stephanie Kachel, Carina Brunecker and Alena Haefner from the Institute of Inorganic Chemistry in our department with the analysis of the borazine sample.Notes and references
- H. Kobayashi, A. Hayakawa, K. D. Kunkuma, A. Somarathne and E. C. Okafor, Proc. Combust. Inst., 2019, 37, 109–133 CrossRef CAS.
- P. Jena, J. Phys. Chem. Lett., 2011, 2, 206–211 CrossRef CAS.
- T. B. Marder, Angew. Chem., Int. Ed., 2007, 46, 8116–8118 CrossRef CAS PubMed.
- U. B. Demirci, Energies, 2020, 13, 3071 CrossRef CAS.
- U. B. Demirci, Int. J. Hydrogen Energy, 2017, 42, 9978–10013 CrossRef CAS.
- V. Sit, R. A. Geanangel and W. W. Wendlandt, Thermochim. Acta, 1987, 113, 379–382 CrossRef CAS.
- F. Baitalow, J. Baumann, G. Wolf, K. Jaenicke-Rößler and G. Leitner, Thermochim. Acta, 2002, 391, 159–168 CrossRef CAS.
- R. Benzouaa, U. B. Demirci, R. Chiriac, F. Toche and P. Miele, Thermochim. Acta, 2010, 509, 81–86 CrossRef CAS.
- M. G. Hu, R. A. Geanangel and W. W. Wendlandt, Thermochim. Acta, 1978, 23, 249–255 CrossRef CAS.
- N. Patel, A. Kale and A. Miotello, Appl. Catal., B, 2012, 111-112, 178–184 CrossRef CAS.
- D. Neiner, A. Luedtke, A. Karkamkar, W. Shaw, J. Wang, N. D. Browning, T. Autrey and S. M. Kauzlarich, J. Phys. Chem. C, 2010, 114, 13935–13941 CrossRef CAS.
- H. F. Bettinger and H. Bornemann, J. Am. Chem. Soc., 2006, 128, 11128–11134 CrossRef CAS PubMed.
- H. Braunschweig, A. Damme, J. O. C. Jimenez-Halla, B. Pfaffinger, K. Radacki and J. Wolf, Angew. Chem., Int. Ed., 2012, 51, 10034–10037 CrossRef CAS PubMed.
- H. Braunschweig, W. C. Ewing, K. Geetharani and M. Schäfer, Angew. Chem., Int. Ed., 2015, 54, 1662–1665 CrossRef CAS PubMed.
- A. Singh, A. Humeniuk and M. I. S. Röhr, Phys. Chem. Chem. Phys., 2021, 23, 16525–16536 RSC.
- T. Zeng, N. Ananth and R. Hoffmann, J. Am. Chem. Soc., 2014, 136, 12638–12647 CrossRef CAS.
- M. Pinheiro, F. B. C. Machado, F. Plasser, A. J. A. Aquino and H. Lischka, J. Mater. Chem. C, 2020, 8, 7793–7804 RSC.
- N. C. Baird and R. K. Datta, Inorg. Chem., 1972, 11, 17–19 CrossRef CAS.
- D. R. Armstrong and D. T. Clark, Theor. Chim. Acta, 1972, 24, 307–316 CrossRef CAS.
- E. R. Lory and R. F. Porter, J. Am. Chem. Soc., 1973, 95, 1766–1770 CrossRef CAS.
- Y. Kawashima, K. Kawaguchi and E. Hirota, J. Chem. Phys., 1987, 87, 6331–6333 CrossRef CAS.
- F. Zhang, P. Maksyutenko, R. I. Kaiser, A. M. Mebel, A. Gregušová, S. A. Perera and R. J. Bartlett, J. Phys. Chem. A, 2010, 114, 12148–12154 CrossRef CAS.
- D. Schleier, A. Humeniuk, E. Reusch, F. Holzmeier, D. Nunez-Reyes, C. Alcaraz, G. A. Garcia, J.-C. Loison, I. Fischer and R. Mitric, J. Phys. Chem. Lett., 2018, 9, 5921–5925 CrossRef CAS PubMed.
- M. H. Matus, D. J. Grant, M. T. Nguyen and D. A. Dixon, J. Phys. Chem. C, 2009, 113, 16553–16560 CrossRef CAS.
- T. Baer and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19, 9698–9723 RSC.
- T. Bierkandt, P. Oßwald, N. Gaiser, D. Krüger, M. Köhler, M. Hoener, S. Shaqiri, D. Kaczmarek, Y. Karakaya, P. Hemberger and T. Kasper, Int. J. Chem. Kinet., 2021, 53, 1063–1081 CrossRef CAS.
- D. P. Mukhopadhyay, D. Schleier, I. Fischer, J. C. Loison, C. Alcaraz and G. A. Garcia, Phys. Chem. Chem. Phys., 2020, 22, 1027–1034 RSC.
- K. H. Fischer, M. Schneider, I. Fischer, B. Pfaffinger, H. Braunschweig, B. Sztaray and A. Bodi, Chem. – Eur. J., 2012, 18, 4533 CrossRef CAS PubMed.
- F. Holzmeier, M. Lang, P. Hemberger, A. Bodi, M. Schäfer, R. Dewhurst, H. Braunschweig and I. Fischer, Chem. – Eur. J., 2014, 20, 9683–9692 CrossRef CAS.
- M. Johnson, A. Bodi, L. Schulz and T. Gerber, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 610, 597–603 CrossRef CAS.
- B. Sztáray, K. Voronova, K. G. Torma, K. J. Covert, A. Bodi, P. Hemberger, T. Gerber and D. L. Osborn, J. Chem. Phys., 2017, 147, 013944 CrossRef PubMed.
- T. Wideman, P. J. Fazen, A. T. Lynch, K. Su, E. E. Remsen, L. G. Sneddon, T. Chen and R. T. Paine, Inorganic Syntheses, Wiley, New York, 1998, pp. 232–242 DOI:10.1002/9780470132630.ch39.
- B. Sztáray and T. Baer, Rev. Sci. Instrum., 2003, 74, 3763–3768 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Rev. E.01, Gaussian Inc., Wallingfort, CT, 2009 Search PubMed.
- S. Gozem and A. I. Krylov, Wiley Interdiscip. Rev.: Comput. Mol. Sci. DOI:10.1002/wcms.1546.
- G. Herzberg, Molecular Spectra and Molecular Structure III: Electronic Spectra and Electronic Structure of Polyatomic Molecules, Krieger Publishing, Malabar, FL, 1989 Search PubMed.
- M. F. Jagod, M. Rösslein, C. M. Gabrys, B. D. Rehfuss, F. Scappini, M. W. Crofton and T. Oka, J. Chem. Phys., 1992, 97, 7111–7123 CrossRef CAS.
- S. T. Pratt, P. M. Dehmer and J. L. Dehmer, J. Chem. Phys., 1993, 99, 6233–6244 CrossRef CAS.
- J. Yang and Y. Mo, J. Phys. Chem. A, 2006, 110, 11001–11009 CrossRef CAS.
- P. Rupper and F. Merkt, Rev. Sci. Instrum., 2004, 75, 613–622 CrossRef CAS.
- P. Paetzold, in Advances in Inorganic Chemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1987, vol. 31, pp. 123–170 Search PubMed.
- J. Böhnke, T. Brückner, A. Hermann, O. F. González-Belman, M. Arrowsmith, J. O. C. Jiménez-Halla and H. Braunschweig, Chem. Sci., 2018, 9, 5354–5359 RSC.
Footnote |
| † Present address: Laboratory for Astrophysics, Leiden Observatory, Leiden University, NL 2300 RA Leiden, The Netherlands. |
| This journal is © the Owner Societies 2022 |