Negative valley polarization in doped monolayer MoSe₂

Abstract

Monolayer molybdenum di-selenide (1L-MoSe₂) stands out in the transition metal dichalcogenide family of materials as an outlier where optical generation of valley polarization is inefficient. Here we show that using charge doping in conjunction with an external magnetic field, the valley polarization of 1L-MoSe₂ can be controlled effectively. Most remarkably, the valley polarization can be tuned to negative values, where the higher energy Zeeman mode emission is more intense than the lower energy one. Our experimental observations are interpreted with valley-selective exciton-charge dressing that manifests when gate induced doping populates predominantly one valley in the presence of Zeeman splitting.

---

Introduction

Layered crystals with a hexagonal Brillouin zone (BZ) recently garnered great interest in the development of valleytronics, when both the conduction band minimum and valence band maximum are located at the BZ corner, leading to the presence of low energy quasi-particles in two inequivalent valleys of +K and −K. Prominent examples of such systems are graphene and transition metal dichalcogenides (TMDs).^1–3 While bandgaps in multi-layer TMDs are indirect, they evolve to direct gaps at +K and −K in the monolayer (1L) limit.⁴ In these 1L-TMD crystals, valley polarized excitons and charged excitons have been considered as promising carriers for valleytronics.³ How to reach high valley polarization in TMD in a controllable manner has been a challenging topic that has attracted great attention in recent years.^5–9 In the two valleys, 1L-TMD excitons have opposite angular momentum and are coupled to circularly polarized photons with opposite helicity.³ A popular approach to generate valley polarization is through optical pumping using circularly polarized optical fields.^5,7,10 In TMDs such as MoS₂, WSe₂ and WS₂, decent degree of valley polarization has been achieved with near resonance optical excitation,^5,11,12 application of magnetic field,¹³ charge doping,^6,14 and chiral plasma coupling.¹⁵ The interplay of various depolarization mechanisms, such as large momentum phonon scattering,^10,16 exchange interaction^9,12,17 have been extensively studied to understand valley phenomena in TMDs.

An unusual material in the TMD class is 1L-MoSe₂ where it was found that circularly polarized optical excitation populates both +K and −K valleys and gives rise to very small valley polarization, even when the excitation is close to the optical bandgap.^13,18,19 The exact reason for this behavior is still under debate and recent theoretical studies point to the role of dark excitons in bright exciton valley depolarization.^20–22 With the application of an out-of-plane magnetic field, the two-fold degeneracy of the two valleys are lifted and appreciable valley polarization can be achieved through preferential population of particles in the lower energy valley.²³ Another study further established that with electron doping, the valley polarization of the exciton polarons – quasi-particles arising from interaction of excitons with a Fermi sea of charges – can be greatly improved, an effect that was attributed to interaction induced giant paramagnetism in 1L-MoSe₂.²⁴

In this article, we report that exciton polarons in 1L-MoSe₂ can exhibit a reversed valley polarization in the presence of an external magnetic field, i.e., in the Zeeman-split polaron doublet, the higher energy mode produces more emission than the lower energy mode. This in turn implies that the higher energy mode is more populated than the lower energy one. This counter-intuitive phenomenon can be understood as a result of valley-selective exciton-charge dressing in the presence of Zeeman-split conduction and valence bands. This interpretation is supported by differential reflection measurements from which we derive a similar ‘negative valley polarization’ for oscillator strength. Our work points to a new approach of valleytronics that harnesses doping-controlled valley-dependent oscillator strength distribution.

Experimental

Our device is a 1L-MoSe₂ sample exfoliated from bulk crystals and sandwiched between two hexagonal boron nitride (hBN) flakes via a dry transfer technique.^25–27 The atomic stack is used to pick up a few-layer graphene flake, which serves as the back gate. The device is mounted inside a cryostat with optical access and cooled down to a base temperature of 3.4 K. A tunable Ti-sapphire laser is used to generate excitons in the sample with photon energies detuned 15 to 100 meV above the optical bandgap.

Result and discussion

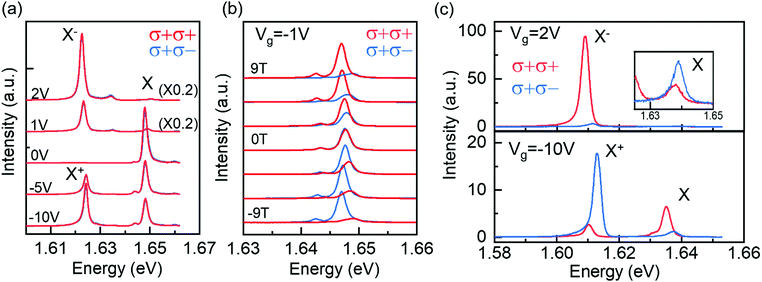
Fig. 1a shows gate dependence of PL emission from our device, where we use σ⁺ circularly polarized light to excite the sample, and collect circular polarization resolved emissions in σ⁺ channel (σ⁺σ⁺ spectra) and σ⁻ channel (σ⁺σ⁻ spectra) respectively. The hBN sandwiched 1L-MoSe₂ has good quality, with the neutral exciton PL at around 1.648 eV exhibiting a full width at half maximum (FWHM) of 1.8 meV, much narrower than typical devices exposed to air and is comparable to MoSe₂ samples of high quality reported so far.^28,29 By tuning the gate voltage between 2 V and −10 V, we can access both the neutral (X) and charged (negative X⁻ and positive X⁺) exciton species, manifested as prominent narrow emission peaks in Fig. 1a. Note that the sample is charge neutral between −2.2 V and 0.2 V (see also Fig. 2a). Our sample exhibits near 0 valley polarization for neutral excitons under a small detuned excitation energy of 15 meV, in line with other studies on monolayer MoSe₂.^13,18,19 Further, even though doping has been shown to improve valley polarization in other TMDs,^6,9 the impact is limited in MoSe₂, as shown in Fig. 1a from measurements of X⁻ and X⁺.

Fig. 1 Circular-polarization resolved PL spectra of gated hBN-encapsulated 1L MoSe₂. The excitation is in σ⁺ circular polarization. Emissions in σ⁺ (red) and σ⁻ (blue) channels are collected separately. (a) Gate dependent emission spectra at zero magnetic field with laser excitation at 1.662 eV. (b) The B field dependency of neutral exciton emission peak (V_g = −1 V, laser excitation: 1.736 eV). (c) PL spectra of electron (upper) and hole (lower) doped device at 9 Tesla with laser excitation at 1.655 eV, showing the intensity of exciton polaron modes. Inset: Magnified repulsive polaron emission at V_g = 2 V.

Fig. 2 Contour map of gate-dependent optical spectra of 1L MoSe₂ at 9 Tesla. (a) Circular-polarization resolved PL with σ⁺ (left column) and σ⁻ (right column) excitation. (b) Differential reflection spectra with σ⁺ (top) and σ⁻ (bottom) excitation. (c) Calculated valley polarization of repulsive polaron (open symbol) and attractive polaron (solid symbol) for σ⁺ (red) and σ⁻ (blue) excitation from PL spectra in (a). (d) Calculated valley polarization of oscillator strength for repulsive polaron (open symbol) and attractive polaron (solid symbol) from reflection spectra in (b).

On the other hand, the application of an external magnetic field, which breaks the degeneracy between +K and −K valleys, has a dramatic impact on the polarization of PL emission from 1L-MoSe₂. As shown in Fig. 1b for the device at charge neutrality, we observe a clear Zeeman splitting between σ⁺ (red, originated from the +K valley) and σ⁻ (blue, from the −K valley) PL emissions. The evolution of the exciton PL as a function of the magnetic field is monotonic: with increasing B, σ⁺ redshifts with increasing intensity, and σ⁻ blueshifts with decreasing intensity. We denote the lower energy state as lower Zeeman (LZ) mode and higher energy state as higher Zeeman (HZ) mode, and assess the valley polarization of the device by comparing the PL intensity in the LZ and the HZ channels, 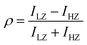. Note that with this definition a positive ρ means that the lower energy mode is more populated. At charge neutrality, the valley polarization to a good approximation is symmetric with respect to the magnetic field, even though we are exciting the device with σ⁺ photons not far from the optical bandgap. This indicates that the excitation polarization of the optical fields has negligible impact on valley polarization even in the presence of a magnetic field.

The combined effects of charge doping and magnetic field are illustrated in Fig. 1c (top: electron doping, V_g = 2 V; bottom, hole doping, V_g = −10 V). With these relatively high doping, the PL emissions are dominated by trions, or more precisely, attractive exciton polarons arising from the dressing of excitons with a Fermi sea of charges.^30–35 The trion/attractive-polaron valley polarization is high, and the emission is almost exclusively in one circular polarization channel. Interestingly, the dominant channel is opposite for X⁺ and X⁻, indicating that at the same 9T magnetic field, X⁻ and X⁺ polaron emission originates mainly from electron–hole recombination in +K (σ⁺, LZ mode) and −K (σ⁻, HZ mode) valleys respectively. We further examine valley polarization for the weaker, but still visible emission of the higher energy repulsive polarons X derived from neutral excitons. Their valley polarization is also relatively good, but the dominant channel is opposite to the attractive polarons: for electron doping σ⁻ (−K valley HZ mode) is more intense, while for hole doping σ⁺ (+K valley LZ mode) emission is stronger.

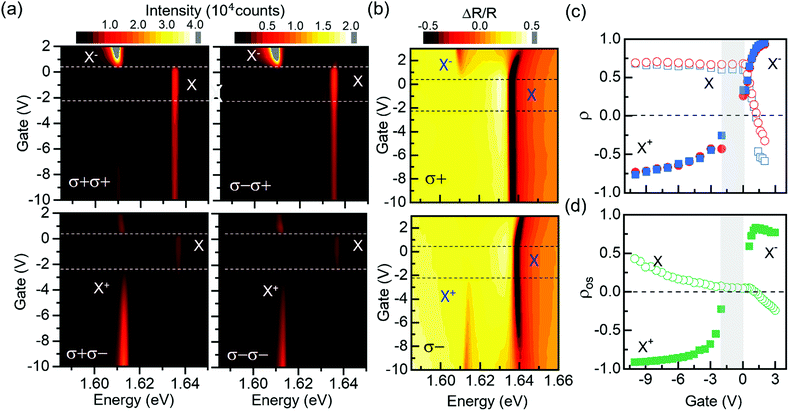
The detailed trend of 1L-MoSe₂ emission at 9 Tesla as a function of gate voltage is shown in Fig. 2(a), where we plot the heat map of circular polarization resolved PL emission with four different circular excitation/emission configurations. Our device is charge neutral for −2.2 < V_g < 0.2 V where the PL emission is dominated by the neutral exciton. Outside this range, charged exciton emission X⁺ and X⁻ are observed. The emission maps acquired with σ⁺ and σ⁻ excitations are quite similar for either σ⁺ (top row) or σ⁻ (bottom row) emission channels. This indicates that the distribution of excitons in the +K and −K valleys is largely independent of the polarization of the initial excitation. We have quantitively calculated the valley polarization ρ from the PL emission map. As shown in Fig. 2c, ρ for σ⁺ and σ⁻ excitation overlaps with each other quite well over almost the whole gate voltage ranges. In the following we focus our discussion on the polarization of emissions.

At charge neutral, the neutral exciton is the main optical feature, and it is more intense in σ⁺ polarization (see also Fig. 1b spectra at 9 T). This larger population of +K valley exciton can be understood with quasi-particle relaxation to lower energy states. The Zeeman shift is negative for the +K valley excitons, which at 9 T is about −1 meV; due to time reversal symmetry, Zeeman shift for −K excitons is about 1 meV. The same argument is applicable to the dominance of σ⁺ polarized emission for attractive polarons under electron doping (X⁻ at ∼1.61 eV for V_g > 0.2 V), and repulsive polarons under hole doping (X at ∼1.64 eV for V_g < −2.2 V), where the positive magnetic field similarly makes the +K valley modes ∼2 meV below the −K valley modes.

In light of the above consideration, the attractive polaron X⁺ at ∼1.612 eV for V_g < −2.2 V shows quite ‘abnormal’ behavior: the higher Zeeman σ⁻ emission from −K valley is visibly more intense, giving rise to a negative valley polarization for X⁺ in Fig. 2c. Note that the effect here is different from previous studies, where negative valley polarization refers to switched handedness of emitted photons after system is excited with circularly-polarized photons.^36,37 To understand this behavior, we performed circular polarization resolved differential reflection for the device as a function of gate voltage at 9 T. From the reflection map in Fig. 2b, we observe that the device is charge neutral for −2.2 < V_g < 0.2 V, consistent with PL map. Outside this range, the attractive polaron X⁻ and X⁺ absorption features are observed dominantly in σ⁺ map (top panel, V_g > 0.2 V) and σ⁻ map (bottom panel, V_g < −2.2 V), respectively. The dominance of absorption at 9 Tesla in only one circular polarization, i.e., one valley, is a result of time reversal symmetry breaking. This effect is most prominent in the presence of charge doping, and it reflects a significant redistribution of polaron oscillator strength between the two valleys.

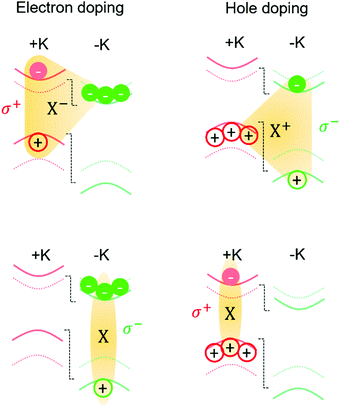
The dominance of electron-dressed attractive polaron X⁻ in +K valley (σ⁺ map in Fig. 2) and hole-dressed attractive polaron X⁺ in −K valley (σ⁻ map in Fig. 2) can be understood as a result of valley selective exciton-charge coupling in the presence of a valley-splitting magnetic field. As illustrated in Fig. 3, in a positive magnetic field, the conduction and valence bands upshift for +K and downshift for −K (dotted: 0 field; solid: 9 Tesla). The shift of the conduction band is smaller than the valence band, leading to a net Zeeman shift for excitons that is negative for +K exciton states and positive for −K exciton states,²³ regardless of electron or hole doping. On the other hand, the opposite shifts of the bands in the two valleys lead to distinct doping effects: electron doping preferentially populates −K valley while hole doping preferentially populates +K valley. The opposite valley population of electrons and holes is the fundamental reason why X⁺ (X⁻) absorption is almost invisible in σ⁺ (σ⁻) map in Fig. 2b. In MoSe₂ with electron–hole mass ratio close to 1, the polaron dressing occurs in an intervalley fashion: excitons in one valley is only dressed by charges residing in the opposite valley,^38,39 as illustrated in Fig. 3, top row. Thus, for electron doping, X⁻ absorption is dominated by σ⁺ photons, and for hole doping, X⁺ absorption is dominated by σ⁻ photons. Correspondingly for repulsive polarons derived from neutral excitons, one anticipates X absorption to favor −K valley for electron doping and +K valley for hole doping (Fig. 3, bottom row). This effect for X, although less prominent than for attractive polarons X⁺ and X⁻, is still visible in Fig. 2b at relatively high doping levels. We quantitatively extract the polaron oscillator strength at +K (lower Zeeman S_LZ) and −K (higher Zeeman S_HZ), and plot in Fig. 2d its valley polarization 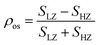as a function of gate voltage. ρ_os exhibits a cross-shaped behavior as a function of V_g, confirming the opposite effects of electron and hole doping for attractive and repulsive polarons discussed above.

Fig. 3 Schematics of valley selective exciton-charge dressing in 1L MoSe₂ in an external magnetic field. Only the lowest conduction and highest valence bands are shown. Dotted curves: 0 field; solid curves: 9 Tesla. Due to Zeeman shift, electrons and holes preferentially populate −K and +K valleys, and dress excitons in +K and −K valleys, respectively.

The overall trend of ρ_os is quite similar to ρ for PL in Fig. 2c: for attractive polarons, both ρ and ρ_os increase from negative values for X⁺ to positive values for X⁻ (solid symbols); for X, both ρ and ρ_os monotonically decrease with V_g and both exhibit a kink near 0 V when we start to introduce electrons into the sample (open symbols). The oscillator strength distribution between the lower Zeeman (S_LZ) and higher Zeeman (S_HZ) modes of 1L-MoSe₂ in the presence of a time reversal breaking magnetic field is indeed a quite prominent factor behind the valley polarization extracted from the PL emission. In particular, it provides a natural explanation for the ‘abnormal’ negative valley polarization of X⁺ attractive polarons. From a trion perspective, the holes in +K valley readily bind to −K excitons (Fig. 3, top right), forming a large population of trions that eventually evolve to −K valley attractive exciton polarons. Hence the larger oscillator strength of X⁺ at −K valley makes the corresponding exciton polaron mode more populated and more emissive, even though it appears energetically unfavorable compared to its +K counterpart. The negative valley polarization indicates that the intervalley charge dressing effect dominates over the Zeeman energy splitting effect for these polarons.

We can also consider the impact of hole doping on the repulsive branch of polarons. In this case X has a larger oscillator strength at +K, i.e., positive ρ_os, as well as a lower energy. Thus the oscillator strength works in tandem with Zeeman splitting to enhance the valley polarization of hole-dressed repulsive polaron. We indeed observe that for V_g < −2.2V, the X valley polarization increases, albeit only mildly, with hole doping. The scenario switches for electron doping where Zeeman splitting and exciton-polaron dressing compete to determine the valley polarization of the repulsive polaron. Thus, with electron doping ρ of X suddenly decreases in Fig. 2c, and it turns negative for V_g > 1 V, attesting the powerful effect of valley-inequivalent Fermi sea dressing. For the attractive polaron under electron doping, the Zeeman splitting and exciton-charge dressing work together to enhance the valley polarization, and we observe that the P of X⁻ increases rapidly with electron doping, reaching values close to unity at V_g = 2 V.

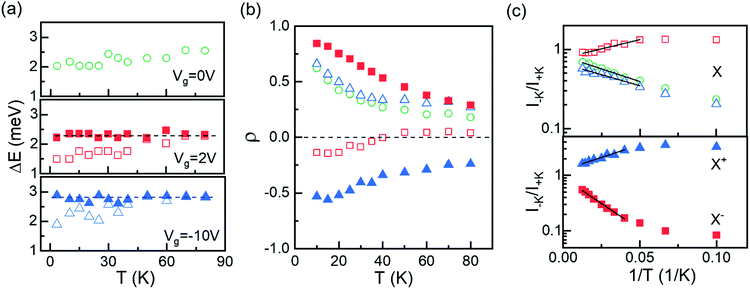
We finally discuss the impact of thermal activation on the valleytronic properties of the exciton polarons. In Fig. 4a and b we plot the energy splitting between σ⁺ and σ⁻ emissions and the valley polarization as a function of temperature for X (open symbols), X⁺ and X⁻ (filled symbols) at V_g = 0, 2 and −10 Volts. All the absolute values of ρ decrease and approach 0 as temperature increases, indicating that thermal activation disrupts the imbalance between +K and −K polaron population and emission. This includes two effects: one is the thermal population of excitonic states, and the other is the thermal activation of doped charges. It is illuminating to plot the intensity ratio I_+K/I_−Kvs. 1/T in a semilog scale, from which a linear fit extracts the activation energy. For V_g = 0 V, the device is charge neutral and the activation is determined by exciton population. We extract an activation energy of 1.2 meV. Note that this is smaller than the Zeeman splitting between the +K and −K excitons (Fig. 4a, top), indicating that not all excitons reach thermal equilibrium in our device. For the hole doping at V_g = −10 V, the activation energy for X is 1.1 meV, similar to the neutral exciton at V_g = 0. This is consistent with Fig. 2c where we observe that although X valley polarization increases with hole doping, the improvement is relatively small. For X⁺ at V_g = −10 V, the activation is 1.7 meV, a value that is significantly smaller than the valence band splitting. Presumably the opposite effect of Zeeman splitting diminishes this value. Simar argument can be put forward for the small 0.9 meV activation for X at V_g = 2 V. Most remarkable is the X⁻ activation at V_g = 2 V where the activation is 3.7 meV, larger than the 2.3 meV splitting between +K and −K polaron energies. This clearly demonstrates that the exciton-charge dressing plays a more important role than Zeeman splitting in improving the valley polarization, and explains why with electron doping the X⁻ valley polarization rapidly increases to near unity.

Fig. 4 Temperature dependency of repulsive polarons (open symbols) and attractive polarons (solid symbols) at V_g = 0 (green), V_g = 2 V (red), and V_g = −10 V (blue) for (a) polaron energy splitting, (b) valley polarization, and (c) intensity ratio of σ⁺ and σ⁻ emission. Spectra were taken with linearly polarized excitation at 1.662 eV. In (c) the solid black lines are fits for extracting thermal activation energy.

Conclusions

In conclusion, we demonstrated valley-selective exciton-charge dressing in 1L MoSe₂, an effect that plays an important role in generating valley-polarized polarons. By controlling charge doping, the dominating exciton-polaron in the device can be tuned from lower-Zeeman to higher-Zeeman states between distinct valleys, as evidenced by the oscillator strength from reflection spectra and the circularly-polarized emission in PL. Our result shows that the valley dressing effect is pivotal in understanding valley phenomena and serves as a viable route for controlling valley polarization in TMDs.

Author contributions

Y.-C. W. and J. Y. designed the experiment; Y.-C. W. performed research; T. T. and K. W. provided high-quality hBN substrates, Y.-C. W. and J. Y. analysed data and wrote the paper. J. Y. supervised the projects.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by National Science Foundation (NSF Grant number: DMR-2004474). K. W. and T. T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan (Grant number JPMXP0112101001) and JSPS KAKENHI (Grant numbers 19H05790 and JP20H00354).

References

1. A. Rycerz, J. Tworzydło and C. W. J. Beenakker, Nat. Phys., 2007, 3, 172–175.
2. D. Xiao, W. Yao and Q. Niu, Phys. Rev. Lett., 2007, 99, 236809.
3. D. Xiao, G.-B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802.
4. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
5. K. F. Mak, K. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494–498.
6. K. Shinokita, X. Wang, Y. Miyauchi, K. Watanabe, T. Taniguchi and K. Matsuda, Adv. Funct. Mater., 2019, 29, 1900260.
7. T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Nat. Commun., 2012, 3, 887.
8. P. Rivera, K. L. Seyler, H. Yu, J. R. Schaibley, J. Yan, D. G. Mandrus, W. Yao and X. Xu, Science, 2016, 351, 688 LP–691 LP.
9. Y.-C. Wu, T. Taniguchi, K. Watanabe and J. Yan, Phys. Rev. B, 2021, 104, L121408.
10. H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490–493.
11. H. Tornatzky, A.-M. M. Kaulitz and J. Maultzsch, Phys. Rev. Lett., 2018, 121, 167401.
12. S.-Y. Chen, T. Goldstein, J. Tong, T. Taniguchi, K. Watanabe and J. Yan, Phys. Rev. Lett., 2018, 120, 046402.
13. D. MacNeill, C. Heikes, K. F. Mak, Z. Anderson, A. Kormányos, V. Zólyomi, J. Park and D. C. Ralph, Phys. Rev. Lett., 2015, 114, 037401.
14. Y. Miyauchi, S. Konabe, F. Wang, W. Zhang, A. Hwang, Y. Hasegawa, L. Zhou, S. Mouri, M. Toh, G. Eda and K. Matsuda, Nat. Commun., 2018, 9, 2598.
15. G. Liu, X. Zheng, H. Liu, J. Yin, C. Ke, W. Yang, Y. Wu, Z. Wu, X. Li, C. Zhang and J. Kang, ACS Appl. Mater. Interfaces, 2021, 13, 35097.
16. B. R. Carvalho, Y. Wang, S. Mignuzzi, D. Roy, M. Terrones, C. Fantini, V. H. Crespi, L. M. Malard and M. A. Pimenta, Nat. Commun., 2017, 8, 14670.
17. T. Yu and M. W. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205303.
18. G. Wang, E. Palleau, T. Amand, S. Tongay, X. Marie and B. Urbaszek, Appl. Phys. Lett., 2015, 106, 112101.
19. G. Kioseoglou, A. T. Hanbicki, M. Currie, A. L. Friedman and B. T. Jonker, Sci. Rep., 2016, 6, 25041.
20. M. Yang, C. Robert, Z. Lu, D. Van Tuan, D. Smirnov, X. Marie and H. Dery, Phys. Rev. B, 2020, 101, 115307.
21. M. Selig, F. Katsch, S. Brem, G. F. Mkrtchian, E. Malic and A. Knorr, Phys. Rev. Res., 2020, 2, 023322.
22. C. Robert, B. Han, P. Kapuscinski, A. Delhomme, C. Faugeras, T. Amand, M. R. Molas, M. Bartos, K. Watanabe, T. Taniguchi, B. Urbaszek, M. Potemski and X. Marie, Nat. Commun., 2020, 11, 4037.
23. Y. Li, J. Ludwig, T. Low, A. Chernikov, X. Cui, G. Arefe, Y. D. Kim, A. M. van der Zande, A. Rigosi, H. M. Hill, S. H. Kim, J. Hone, Z. Li, D. Smirnov and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 266804.
24. P. Back, M. Sidler, O. Cotlet, A. Srivastava, N. Takemura, M. Kroner and A. Imamoğlu, Phys. Rev. Lett., 2017, 118, 237404.
25. S.-Y. Chen, T. Goldstein, T. Taniguchi, K. Watanabe and J. Yan, Nat. Commun., 2018, 9, 3717.
26. S.-Y. Chen, Z. Lu, T. Goldstein, J. Tong, A. Chaves, J. Kunstmann, L. S. R. Cavalcante, T. Woźniak, G. Seifert, D. R. Reichman, T. Taniguchi, K. Watanabe, D. Smirnov and J. Yan, Nano Lett., 2019, 19, 2464–2471.
27. Y.-C. Wu, S. Samudrala, A. McClung, T. Taniguchi, K. Watanabe, A. Arbabi and J. Yan, ACS Nano, 2020, 14, 10503.
28. F. Cadiz, E. Courtade, C. Robert, G. Wang, Y. Shen, H. Cai, T. Taniguchi, K. Watanabe, H. Carrere, D. Lagarde, M. Manca, T. Amand, P. Renucci, S. Tongay, X. Marie and B. Urbaszek, Phys. Rev. X, 2017, 7, 021026.
29. O. A. Ajayi, J. V. Ardelean, G. D. Shepard, J. Wang, A. Antony, T. Taniguchi, K. Watanabe, T. F. Heinz, S. Strauf, X.-Y. Zhu and J. C. Hone, 2D Mater., 2017, 4, 31011.
30. D. K. Efimkin and A. H. MacDonald, Phys. Rev. B, 2017, 95, 035417.
31. D. K. Efimkin and A. H. MacDonald, Phys. Rev. B, 2018, 97, 235432.
32. M. Sidler, P. Back, O. Cotlet, A. Srivastava, T. Fink, M. Kroner, E. Demler and A. Imamoglu, Nat. Phys., 2017, 13, 255–261.
33. J. G. Roch, G. Froehlicher, N. Leisgang, P. Makk, K. Watanabe, T. Taniguchi and R. J. Warburton, Nat. Nanotechnol., 2019, 14, 432–436.
34. T. Goldstein, Y.-C. Wu, S.-Y. Chen, T. Taniguchi, K. Watanabe, K. Varga and J. Yan, J. Chem. Phys., 2020, 153, 071101.
35. J. G. Roch, D. Miserev, G. Froehlicher, N. Leisgang, L. Sponfeldner, K. Watanabe, T. Taniguchi, J. Klinovaja, D. Loss and R. J. Warburton, Phys. Rev. Lett., 2020, 124, 187602.
36. W.-T. Hsu, L.-S. Lu, P.-H. Wu, M.-H. Lee, P.-J. Chen, P.-Y. Wu, Y.-C. Chou, H.-T. Jeng, L.-J. Li, M.-W. Chu and W.-H. Chang, Nat. Commun., 2018, 9, 1356.
37. G. Berghäuser, I. Bernal-Villamil, R. Schmidt, R. Schneider, I. Niehues, P. Erhart, S. Michaelis de Vasconcellos, R. Bratschitsch, A. Knorr and E. Malic, Nat. Commun., 2018, 9, 971.
38. R. A. Sergeev and R. A. Suris, Phys. Status Solidi, 2001, 227, 387–396.
39. J. Yan and K. Varga, Phys. Rev. B, 2020, 101, 235435.

---