Open Access Article
Open Access ArticleGuest induced reversible on–off switching of elastic frustration in a 3D spin crossover coordination polymer with room temperature hysteretic behaviour†
Lucía
Piñeiro-López‡
a,
Francisco-Javier
Valverde-Muñoz‡
 a,
Elzbieta
Trzop
b,
M. Carmen
Muñoz
a,
Elzbieta
Trzop
b,
M. Carmen
Muñoz
 c,
Maksym
Seredyuk
c,
Maksym
Seredyuk
 ad,
Javier
Castells-Gil
ad,
Javier
Castells-Gil
 a,
Iván
da Silva
a,
Iván
da Silva
 e,
Carlos
Martí-Gastaldo
e,
Carlos
Martí-Gastaldo
 a,
Eric
Collet
a,
Eric
Collet
 *b and
José Antonio
Real
*b and
José Antonio
Real
 *a
*a
aDepartamento de Química Inorgánica, Instituto de Ciencia Molecular (ICMol), Universidad de Valencia, Valencia, Spain. E-mail: jose.a.real@uv.es
bUniv Rennes, CNRS, IPR (Institut de Physique de Rennes) - UMR 6251, F-35000 Rennes, France. E-mail: eric.collet@univ-rennes1.fr
cDepartamento de Física Aplicada, Universitat Politècnica de València, Camino de Vera s/n, E-46022, Valencia, Spain
dDepartment of Chemistry, Taras Shevchenko National University of Kyiv, 64/13, Volodymyrska Street, 01601, Kyiv, Ukraine
eISIS Neutron Facility, STFC Rutherford Appleton Laboratory, Chilton, Oxfordshire OX11 0QX, UK
First published on 23rd November 2020
Abstract
A binary reversible switch between low-temperature multi-step spin crossover (SCO), through the evolution of the population γHS(T) with high-spin (HS)-low-spin (LS) sequence: HS1LS0 (state 1) ↔ HS2/3LS1/3 (state 2) ↔ HS1/2LS1/2 (state 3) ↔ HS1/3LS2/3 (state 4) ↔ HS0LS1 (state 5), and complete one step hysteretic spin transition featuring 20 K wide thermal hysteresis centred at 290 K occurs in the three-dimensional (3D) Hofmann-type porous coordination polymer {FeII(3,8phen)[Au(CN)2]2}·xPhNO2 (3,8phen = 3,8-phenanthroline, PhNO2 = nitrobenzene), made up of two identical interpenetrated pcu-type frameworks. The included PhNO2 guest (x = 1, 1·PhNO2) acts as a molecular wedge between the interpenetrated 3D frameworks via PhNO2-3,8phen intermolecular recognition and is the source of the strong elastic frustration responsible for the multi-step regime. Detailed X-ray single crystal analysis reflects competition between spatial periodicities of structurally inequivalent HS and LS SCO centres featuring: (i) symmetry breaking (state 3) with ⋯HS–LS⋯ ordering with γHS = 1/2; and (ii) occurrence of spatial modulation of the structure providing evidence for stabilization of local or aperiodic ordered mixed spin states for states 2 and 4 (with γHS ≈ 2/3) and 4 (with γHS ≈ 1/3), respectively. Below c.a. 20 K, structural and magnetic analyses show the photogeneration of a metastable HS*, state 6. The room-temperature single-step hysteretic regime appears with release of the guest (x = 0, 1) and the elastic frustration, and reversibly switches back to the original four-step behaviour upon guest re-adsorption. Both uncommon relevant SCO events meeting in the same material represent a rare opportunity to compare them in the frame of antiferro- and ferro-elastic transitions.
Introduction
FeII spin crossover (SCO) complexes are relevant switchable molecular materials that reversibly change between the high-spin (HS, t2g4eg2, S = 2) and low-spin (LS, t2g6eg0, S = 0) states by the action of a variety of external stimuli (temperature, pressure, light irradiation or analytes) inducing significant changes in the materials' magnetic, electrical and optical properties. Furthermore, due to the antibonding nature of the eg orbitals, their population–depopulation upon the HS ↔ LS switch is strongly coupled with structural changes primarily affecting the [FeIIN6] coordination sphere and spreading cooperatively from one SCO centre to another across the crystal through intermolecular contacts (π-stacking and hydrogen bonding) and/or covalent and coordination bonds.1 Thus, the thermal dependence of the HS (LS) population, γHS(T), is critically affected by the elastic coupling between the active SCO centres, which is usually assumed to be of purely elastic nature.2–4It has been recently shown that the occurrence of competing elastic interactions in the crystal, i.e. elastic frustration,4–6 is pivotal in the rationalization of most relevant experimentally observed γHS(T) dependences. The lack of significant elastic frustration combined with strong coupling favours highly cooperative bistable hysteretic single-step SCO behaviour conferring a binary on–off nature to the electronic and mechanical properties of the material. In contrast, above a certain threshold elastic frustration, γHS(T) reveals the emergence of an intriguing multistep behaviour. At microscopic level, the steps reflect long-range ordering sequences of HS and LS sites, initially symmetry equivalent, and forming spin-state concentration waves. It results from the competition between local “anti-ferro” elastic interactions, minimizing the elastic energy cost through the alternation of sites of different HS and LS states of high and low volumes, and long-range “ferro” elastic interactions, as a macroscopic volume change will favour the same spin state.4 Both, multistability and room temperature hysteresis are rare events that have raised substantial expectations on the conception of bistable and multiple-bit SCO-based sensors, actuators and memories.7
The control of the coupling between the SCO centres for the design of materials with targeted SCO properties is challenging due to the elusive nature of the intermolecular interactions involved and the extreme sensitivity of the SCO phenomenon to minute structural changes. However, the polymeric approach has revealed to be an important tool to test the coupling between the active centres and its effect on the SCO behaviour. This approach has mitigated in part the dominance of the supramolecular interactions characteristic of discrete SCO compounds by replacing these soft interactions with more controllable covalent and coordination bonds. In this respect, Hofmann-type cyanometallate coordination polymers (CPs) {FeII(L)n[MII(CN)4]} (MII = Ni, Pd, Pt have become excellent testbeds for analysing the coupling between the octahedral SCO [FeIIN6] nodes,8 which are equatorially connected by 4 cyanometallate bridging groups defining robust square grid layers {FeII2[MII(CN)4]2}∞. The remaining axial positions are filled with pyridine-like monodentate (n = 2) or bis-monodentate (n = 1) bridging ligands affording 2D and/or 3D CPs, respectively. For 2D CPs, constructive elastic interactions between consecutive layers can be achieved by π-interactions thanks to the interdigitation of the axial ligands. This is clearly illustrated for the derivatives with L = 3-Xpyridine (X = F,9 NH2;10 MII = Ni, Pd, Pt) and triazole-based ligands thiome11 and proptrz.12 Similar efficient coupling is achieved when connecting the layers through rigid pyrazine ligands to generate 3D porous fsc-type frameworks (MII = Ni, Pd, Pt).13 All these CPs display strong cooperative single-step SCO featuring wide hysteretic behaviour at relatively high temperatures. Comparable efficiency has also been observed for the Hofmann variant {FeII(L)[AuI(CN)2]2}, a 3D system made up of {FeII4[AuI(CN)2]4}∞ grids pillared by L = pyrazine (pz)14 or fluoropyrazine (Fpz)15 defining double interpenetrated pcu-type frameworks. However, this efficient communication and synchronization between the active FeII SCO centres may be modulated or even disrupted by the inclusion of guest molecules since they may act as sources of elastic frustration and multistability. For example, spin-state concentration waves may form at γHS ≈ 1 ↔ 1/2 ↔ 1/3 ↔ 0 as it has been described for the 3D SCO-CP [FeII(dpsme)Pt(CN)4]·2/3dpsme·xEtOH·yH2O and [FeII(Phtrz)2{Pd(CN)4}]·2H2O where dpsme is the non-rigid bridging ligand 4,4′-di(pyridylthio)methane16 and Phtrz = (E)-1-phenyl-N-(1,2,4-triazole-4-yl)-methanimine).17 More recently, a four step SCO behaviour has been described for the 2D CPs [FeII(saltrz)2{M(CN)4}]·8/3H2O (saltrz = (E)-2-(((4H-1,2,4-triazol-4-yl)imino)methyl)phenol, M = PtII, PdII)18 showing steps between plateaus at γHS ≈ 1 ↔ 5/6 ↔ 4/6 ↔ 1/6 ↔ 0. Similarly, four steps have been described for the 3D CPs [FeII(bipydz){Au(CN)2}2]·4EtOH (bipydz = 3,6-bis(4-pyridyl)-1,2-diazine)19 and [FeII(4-abpt){Ag(CN)2}2]·2DMF·EtOH (4-abpt = 4-amino-3,5-bis(4-pyridyl)-1,2,4-triazole)20 with sequences γHS = 1 ↔ 2/3 ↔ 1/2 ↔ 1/3 ↔ 0 and 1 ↔ 3/4 ↔ 1/2 ↔ 1/4 ↔ 0, respectively.
Here we report the synthesis and characterization of an unprecedented dual Hofmann-type SCO-CP formulated {FeII(3,8-phen)[Au(CN)2]2}·xPhNO2 (1·xPhNO2) with low dielectric constant pores capable of discriminating between hydroxylic solvents (i.e. methanol) and benzene derivatives (i.e. PhNO2). The system reversibly switches between a multi-step SCO regime with sequence γHS = 1 ↔ ∼2/3 ↔ 1/2 ↔ ∼1/3 ↔ 0 for x = 1 (1·PhNO2) and a complete single step hysteretic spin transition upon guest removal, x = 0 (1), featuring a c.a. 20 K wide thermal hysteresis centred at room temperature (290 K). The state 3 at γHS = 1/2 features symmetry breaking with an ordered ⋯LS–HS⋯ sequence, forming a spin state concentration wave.
The states 2 and 4 around γHS ≈ 1/3 and 2/3 are associated with aperiodic structural modulations. The modulation of the Fe–N bonds found for state 4 reveals the spatial modulation of γHS.
Preparation
Crystalline samples of 1·PhNO2 were grown by slow liquid–liquid diffusion technique using a modified H-vessel with a third tube added due to the poor solubility of the 3,8-phen ligand in methanol. The peripheral tubes contained Fe(BF4)2·6H2O and K[Au(CN)2] salts, respectively while the central tube contained 3,8-phen ligand (see ESI for more information†). Each tube was partially filled with methanol and then with a solution 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 of PhNO2 in methanol, finally the tubes were sealed. Yellow cube-shaped single crystals were formed two weeks later in the tube which originally contained Fe(BF4)2·6H2O salt with relative high yield (ca. 50%). The presence and quantification of the guest molecule was confirmed by means of single-crystal X-ray diffraction, IR spectroscopy (Fig. S1†), thermogravimetric (Fig. S2†) and elemental analysis. Firmly fastened, the guest PhNO2 molecule desorbs in two consecutive steps centred at ca. 410 and 470 K to give the guest-free derivative 1, which shows remarkable thermal stability in the temperature window 490–550 K. Above 550 K, 1 starts to decompose in two additional steps (Fig. S2†). Consequently, 1 was prepared by controlled thermal treatment of 1·PhNO2 at 480 K for 80 min in a N2 stream. During this process, the crystals deteriorated, thereby preventing us to analyse the structure through single crystal X-ray analysis. However, combination of magnetic and calorimetric measurements together with elemental analysis and room temperature powder X-ray diffraction (PXRD) analysis, show that essentially the framework structure of 1·PhNO2 is retained in 1 (vide infra) (see ESI†).
10 of PhNO2 in methanol, finally the tubes were sealed. Yellow cube-shaped single crystals were formed two weeks later in the tube which originally contained Fe(BF4)2·6H2O salt with relative high yield (ca. 50%). The presence and quantification of the guest molecule was confirmed by means of single-crystal X-ray diffraction, IR spectroscopy (Fig. S1†), thermogravimetric (Fig. S2†) and elemental analysis. Firmly fastened, the guest PhNO2 molecule desorbs in two consecutive steps centred at ca. 410 and 470 K to give the guest-free derivative 1, which shows remarkable thermal stability in the temperature window 490–550 K. Above 550 K, 1 starts to decompose in two additional steps (Fig. S2†). Consequently, 1 was prepared by controlled thermal treatment of 1·PhNO2 at 480 K for 80 min in a N2 stream. During this process, the crystals deteriorated, thereby preventing us to analyse the structure through single crystal X-ray analysis. However, combination of magnetic and calorimetric measurements together with elemental analysis and room temperature powder X-ray diffraction (PXRD) analysis, show that essentially the framework structure of 1·PhNO2 is retained in 1 (vide infra) (see ESI†).
Spin crossover behaviour
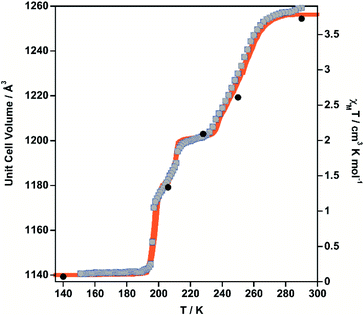
The thermal dependence of the magnetic properties measured at 1 K min−1 and expressed as the product χMT, where χM is the molar magnetic susceptibility and T is the temperature, is displayed in Fig. 1 (left) for 1·PhNO2. The χMT value equal to 3.79 cm3 K mol−1 is consistent with a fully populated FeII–HS state in the range 300–280 K, which corresponds to γHS = 1 (state 1: HS). Below 280 K, χMT decreases in two overlapped steps, a first one gradual followed by a second steeper separated by a narrow inflexion at about 240–245 K with χMT ≈ 2.55 cm3 K mol−1 that corresponds ca. γHS ≈ 2/3 (state 2: HS0.66LS0.33). Then follows a plateau ca. 20 K wide centred at 225 K characterized by a χMT value 2.05 cm3 K mol−1 and γHS = 1/2 (state 3: HS0.5LS0.5). This value, slightly higher than expected for the half of 3.79 cm3 K mol−1, may be the result of an increase of the orbital contribution of the FeII centre remaining HS in state 3. Upon cooling below 214 K, χMT drops again in a third step that leads to a new inclined plateau (206–199 K) with a value 1.30 cm3 K mol−1 at 202 K (state 4: HS0.33LS0.66). Finally, below 199 K a sharp forth step leads the system to the completely populated LS state at 193 K (χMT ≈ 0.1 cm3 K mol−1) (state 5: LS). The heating and cooling modes of the χMT vs. T plot behaviour indicate the lack of any remarkable hysteresis.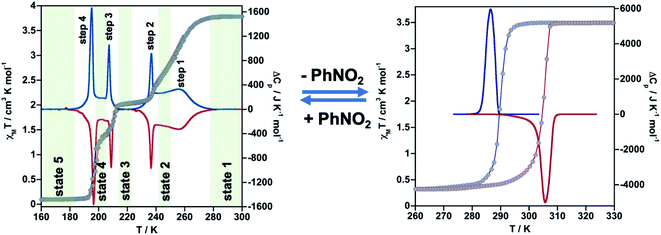 | ||
| Fig. 1 Thermal dependence of magnetic (grey circles) and calorimetric properties of 1·PhNO2 (left) and 1 (right). Blue and red curves correspond to the cooling and heating modes in ΔCp. | ||
The four steps were corroborated by differential scanning calorimetric (DSC) measurements carried out at 5 K min−1 (Fig. 1 left). The critical temperatures associated with the maxima/minima are 258, 236, 208 and 196 K. The associated average enthalpy variations, estimated from the area below each maximum, are ΔHi ≈ 7.60, 3.36, 2.88 and 5.87 kJ mol−1, respectively, and the corresponding average entropy variation being ΔSi = ΔHi/Tci = 29.45, 14.24, 13.85 and 29.94 J K−1 mol−1. These steps correspond well with the sequence of HS molar fraction γHS = 1 (state 1), γHS ≈ 2/3 (state 2), γHS = 1/2 (state 3), γHS ≈ 1/3 (state 4) and γHS = 0 (state 5) with overall ΔHT and ΔST values are 19.8 kJ mol−1 and 87.48 J K−1 mol−1. The entropy change does not correspond exactly to the ratio of spin conversion during the steps, which indicates that other phenomena like structural order may be involved in the transitions.
Photo-generation of the fully populated metastable HS* state (state 6), the so-called light induced excited spin state trapping (LIESST) experiment,21 was carried out at 10 K irradiating a microcrystalline sample of 1·PhNO2 with green light (λ = 532 nm) (Fig. S4†). In these conditions, the sample saturates in 4 h, with values of χMT around 3.45 cm3 K mol−1. Subsequently, the light irradiation was switched off and the temperature increased at a rate of 0.3 K min−1. Then, χMT slightly raises to a value of 3.58 cm3 K mol−1 at 16 K, which practically corresponds to 95% of the maximum value obtained at 300 K. This raise in χMT as well as its value at 16 K reflect the thermal population of different microstates originated from the zero-field splitting of the HS* spin state. At higher temperatures, χMT decreases rapidly until joining the thermal SCO curve at ca. 55 K, indicating that the metastable HS* state has relaxed to the stable LS state. The relaxation is characterized by two distinct slopes with characteristic TLIESST temperatures,22 30.0 K and 48 K, respectively, obtained from ∂χMT/∂T. The low TLIESST temperatures are consistent with the relatively high critical SCO temperatures of 1·PhNO2 and according to the inverse-energy-gap law.23
As mentioned above, controlled thermal desorption of PhNO2 in 1·PhNO2 affords the guest free species 1. Upon desorption, the magnetic properties of 1 correspond to a complete single step spin transition characterized by a square-shaped thermal hysteresis 15 K wide (1 K min−1) centred at room temperature with critical temperatures Tdownc = 290.0 K and Tcup = 305.3 K, which are consistent with those obtained from DSC measurements, 287.0 K and 305.6 K, respectively (Fig. 1 right). The average ΔH and ΔS values are 21.7 kJ mol−1 and 74.1 J K−1 mol−1, respectively. These thermodynamic values for 1 from γHS = 1 to γHS = 0 differ from the sum of the values for 1·PhNO2 over the different steps and confirm that the spin state switching is not the only process coming into play. Interestingly, the original multi-step SCO properties of the as-synthesized derivative 1·PhNO2 are completely recovered when crystals of 1 are soaked in PhNO2 for a week (Fig. S3†). This fact, together with the strong cooperative hysteretic behaviour, are clear proofs confirming the retention of the double interpenetrated porous structure in the desorbed material 1.
Structure
| 290 K | 250 K | 228 K | 206 K | 140 K | 15 K | Photo 15 K | |
|---|---|---|---|---|---|---|---|
| a Spin-state ordering not definitely characterized. | |||||||
| 〈Fe–Nax〉 | 2.231(4) | 2.158(5) | 2.026(5) (LS), 2.219(5) (HS) | 2.068(6) | 2.015(4) | 2.010(7) | 2.203(6) |
| 〈Fe–Neq〉 | 2.133 (4) | 2.070(3) | 1.944(2) (LS), 2.126(2) (HS) | 1.996(4) | 1.933(2) | 1.932(3) | 2.120(3) |
| 〈Fe–N〉 | 2.166(3) | 2.099(2) | 1.971(2) (LS), 2.157(2) (HS) | 2.020(3) | 1.960(2) | 1.958(3) | 2.147(3) |
| ∑ | 3.68(16) | 3.40(16) | 6.66(16) (LS), 5.40(17) (HS) | 3.76(10) | 4.40(15) | 3.2(2) | 4.72(18) |
| γ HS | 1 | 2/3 | 1/2 | 1/3 | 0 | 0 | 1 |
| State | 1 (HS) | 2 (HSHSLS)a | 3 (HSLS) | 4 (LSLSHS)a | 5 (LS) | 5 (LS) | 6 photo(HS) |
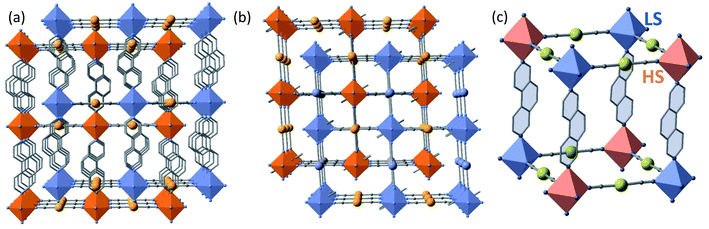
The structures found at 290 K (state 1, γHS = 1), 140 K, 15 K (state 5, γHS ≈ 0) and 15 K after laser irradiation (state 6, γHS ≈ 1) are isostructural and correspond to the monoclinic P2/n space group (Z = 2 (Z′ = 1)) with similar unit cell parameters. In these unit cells, the two Fe sites lie on Wyckoff position with site symmetry 2 and are equivalent by symmetry (n glide plane). The main different features are the changes of Fe–N bond lengths, N–Fe–N angle and unit cell contraction, due to the molecular volume change between LS and HS states. As expected, the linear 3,8-phen and [Au(CN)2]− bridging ligands occupy, respectively, the axial and equatorial positions of the elongated [FeIIN6] octahedral coordination site, thereby defining two identical and mutually interpenetrated 3D porous networks with pcu-type topology made up of {Fe[Au(CN)2]2}n layers pillared by 3,8-phen ligands (Fig. 3a and b). The structures are characterised by positional disorder of the central ring of the 3,8-phen ligand imposed by symmetry (see Fig. S6†). The variation of 〈Fe–N〉 between the 1(HS) and 5 (LS) states, Δ(〈Fe–N〉)1–5 ≈ 0.21 Å is consistent with a complete SCO between the LS and the HS states of FeII. However, the value Δ(〈Fe–N〉)6–5 ≈ 0.19 Å between 5(LS) and 6(HS*) at 15 K is 10% smaller but consistent with an almost complete spin-state conversion.
At 228 K (state 3), the crystal undergoes a symmetry breaking with a change of lattice periodicity from the monoclinic P2/n space group to the monoclinic I2/a (Z = 8 (Z′ = 2)). Therefore, there are now 2 symmetry inequivalent FeII sites in the unit cell, remaining on the 2-fold axis: 4 FeII sites are LS as characterized by 〈Fe–N〉LS = 1.971(2) and the other 4 FeII sites are HS as characterized by 〈Fe–N〉HS = 2.157(2) Å. The average 〈Fe–N〉LS+HS equal to 2.064 Å is ca. 0.1 Å smaller than 〈Fe–N〉 = 2.166 Å at 290 K thus corroborating that γHS = 1/2. This state 3 defines a long-range periodic ⋯LS–HS⋯ ordering in both interpenetrated frameworks. The HS and the LS sites alternate along the 3,8-phen and [Au(CN)2]− groups as shown in Fig. 3c.
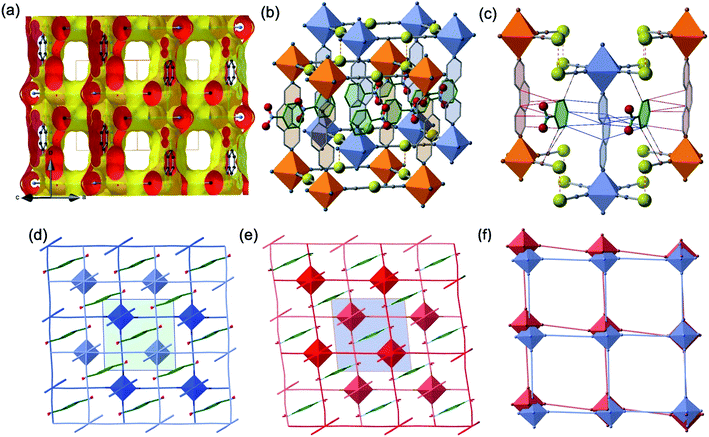
The two interpenetrated pcu-type frameworks interact with each other through strong aurophillic interactions leading to a characteristic 90° criss-cross pattern between the corresponding NC–Au–CN groups. The Au⋯Au distance gradually shortens at lower temperatures due essentially to the spin state change, being 3.0733(4) Å at 290 K and 2.9963(4) Å at 140 K. Interestingly, despite the interpenetration of the two frameworks, channels are formed along a + c direction where the PhNO2 molecules are located (Fig. 4a and b). Within the channels, the disordered PhNO2 molecules are interposed between the two frameworks interacting with the 3,8-phen bridging ligands via π-stacking (Fig. 4b). The number of C(3,8-phen)⋯C(PhNO2) contacts shorter than the sum of the van der Waals radii (ca. 3.70 Å) remains almost constant in number but they shorten as the LS state population increases (γHS decreases) at low temperatures, being in the range 3.39–3.69 Å (Fig. 4c). Furthermore, below 290 K a second type of short C⋯C contacts appear involving PhNO2 molecules and the [Au(CN)2]− bridges (C(Au(CN)2)⋯C(PhNO2) ≈ 3.54–3.68 Å) and weaken at 290 K (C(Au(CN)2)⋯C(PhNO2) > 3.70 Å) (Fig. 4c).
Another relevant observation concerns the pseudo-square {Fe4[Au(CN)2]4} windows. They experience a scissor-like movement changing the acute Au–Fe–Au angle from 88.14° to 84.39° (Δϕ = 3.75°) when moving from the LS state 5 to the HS state 1 (see Fig. 4d–f).
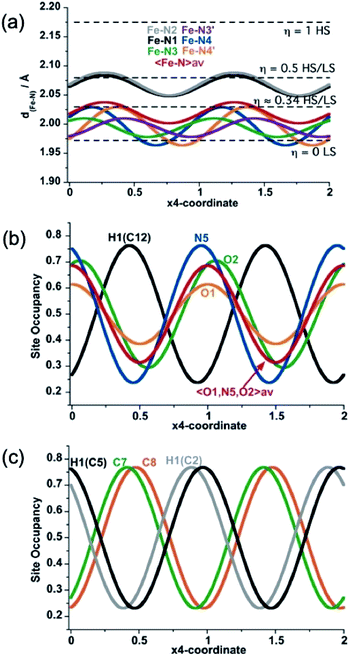
As far as state 2 (250 K) and state 4 (206 K) are concerned, the structure does not change significantly, however, the average 3D space group P2/n has a symmetry different from states 1, 3 and 5 because data shows an aperiodic feature denoted by the presence of satellite diffraction peaks at q-vector ≈ [0.433(5), 0.502(6), 0.359(5)] and [0.433(2), 0.498(2), 0.3689(18)] for state 2 and 4, respectively (see Fig. S7†). The satellite peaks provide evidence of aperiodic order but, unfortunately, we could not solve the structure with superspace approach for state 2 due to the weak signal/noise ratio of the satellites, and we only provide the average 3D periodic structure, where we found 〈Fe–N〉 = 2.099(5) Å, which agrees well with γHS ≈ 2/3. In contrast, for state 4, the structural refinement in the (3 + 1)-dimensional superspace group P2/n (a1|2g)0s (Z = 2 (Z′ = 1)), indicates a spatial modulation of the Fe–N bond lengths (see Fig. 5), which is aperiodic with the (a, b, c) lattice and 〈Fe–N〉=2.020(3) Å providing evidence for an aperiodic modulation of the HS fraction around γHS ≈ 1/3 coupled to the structural reorganization. There is no group–subgroup relationship between states 2 and 3 and between states 3 and 4, consequently, both phase transitions are of first-order nature as shown in Fig. 1. The structure of state 4 is therefore no longer 3D periodic, but incommensurately modulated with respect to the initial (a, b, c) lattice, as it is the case for {Fe[(Hg(SCN)3)2](4,4′-bipy)2}n and [FeH2L2−Me][SbF6]2, where spin state concentration waves also form.24,25
In summary, state 4 (and very likely state 2) corresponds to a long-range aperiodic order close to LS–LS–HS (HS–HS–LS), characterized by the modulation of the Fe–N bonds (Fig. 5a). This modulation also involves modulation of the guest PhNO2 (Fig. 5b) and of the ligand (Fig. 5c). Since some satellite peaks are also observed in the LS state 5 at 140 K, the spatial modulation of HS/LS states is rather driven by the aperiodic ligand/solvent order. Therefore, the steps in γHS during the spin conversion are driven by a subtle balance between the spin crossover centres, ligand order and HS/LS order all influenced by the guest molecule.
Discussion
The four-step SCO behaviour is a rare event so far studied, at the best of our knowledge, in three different FeII Hofmann-type clathrates loaded with hydroxilic solvents (H2O, EtOH and/or DMF) which are stabilised in the pores by host–guest and guest–guest hydrogen bonding interactions facilitated by the presence of acceptor/donor centres associated with the pillar ligands. For example, in the 2D system {FeII(saltrz)2[M(CN)4]}·8/3H2O (M = Pd, Pt) the trapped water molecules interact via hydrogen bonding with the phenyl and triazole groups of the terminal ligand saltrz thereby generating structural constraints leading to four-step SCO behaviour.18 A similar situation has been described for the 3D systems {FeII(bipydz)[Au(CN)2]2}·4EtOH19 and {FeII(4-abpt)[Ag(CN)2]2}·2DMF·EtOH20 where the pillar ligands bipydz and 4-abpt contain 1,2-diazine and aminotriazole moieties, respectively. For the [Au(CN)2]− derivative of the latter compound a seven/eight step behaviour has been recently reported.26Unlike these examples, compound 1·PhNO2 introduces two new relevant features. First, the low dielectric environment of the channels, defined by the aromatic rings of the 3,8-phen ligands, capable of discriminating between hydroxylic solvents such as MeOH or H2O and benzene derivatives like PhNO2, which are easily recognised via π-stacking. Consequently, in the present system, host–guest π–π supramolecular interactions are the relevant promoters of four-step SCO. Second, the guest-free derivative 1 displays a strong cooperative SCO featuring a 20 K wide hysteresis centred at room temperature (290 K), which upon reversible adsorption of PhNO2 regenerates 1·PhNO2 with identical four-step SCO behaviour. The complete single-step bistable SCO behaviour of the guest-free derivative 1 is consistent with that reported for the homologous coordination polymers of general formula {FeII(L)[Au(CN)2]2} with L = pyrazine and 2-fluoropyrazine, which share: (i) the same {FeII4[AuI(CN)2]4}∞ grids connected through rigid axial linear ligands; and (ii) the lack of guest molecules interposed between the two interpenetrated 3D frameworks. These facts ensure efficient communication between the FeII centres in each independent 3D framework favouring “ferro-like” elastic interactions due to the lack of significant local elastic frustration. In contrast, inclusion of PhNO2 as a molecular “wedge” between the two 3D frameworks, introduces two types of host–guest interactions between the interpenetrated frameworks: (i) C⋯C short contacts with the [Au(CN)2]− and (ii) π–π interactions with the 3,8-phen ligands. Clearly opposed to the contraction of the frameworks upon cooling, these interactions may act also as a source of intermolecular “friction” preventing the possible mutual sliding of the 3D frameworks. These facts not only deeply modify the elastic properties of the crystal introducing elastic frustration, clearly seen as a sequence of plateaus with locked fractions of γHS separating the steps,5 but also manifested by an energy cost reflected on the destabilisation of the LS state.
The intermediate plateaus usually reflect ordered populations of HS and LS states, as expected for a succession of “antiferro-like” states.24 Particular relevance has, in the present case, the relative large thermal stability of the state 3 at γHS = 1/2 where the unit cell doubles and the LS–HS FeII centres, connected through 3,8-phen and [Au(CN)2]−, alternate in the two interpenetrated frameworks (Fig. 3c). This thermal stability reflects the extra energy-cost associated with erasing the structural ordering observed in this phase. Indeed, this energy penalisation can be described in terms of structural modifications. The most relevant structural changes to remark are the 〈Fe–N〉 bond lengths and more importantly the large increase of the angular distortion parameter of the [FeN6] when moving to the state 3 (see Σ value Table 1), a fact which is correlated with the noticeable change of the scissor-like angles of the {Fe4[Au(CN)2]4} windows (see Fig. 4d–f). These changes do not impose any toll for 1 since the intermolecular “friction” between the frameworks is minimised. However, the steric hindrance introduced by PhNO2 in 1·PhNO2 between them, reaches a maximum for state 3 (γHS = 1/2). This is clearly illustrated by the increase of the angular distortion (Σ) of the HS and LS FeII octahedrons by ca. 150% in state 3. Apparently, state 2 (γHS ≈ 2/3) and state 4 (γHS ≈ 1/3) can be considered less energy cost symmetric “replicas” paving the way for achieving the state γHS = 1/2, which can be considered the bottleneck of the HS ↔ LS conversion in 1·PhNO2. Detailed crystallographic analysis of state 4 sheds light for the generation of an aperiodic order of HS and LS states, which also could be inferred in a similar aperiodic modulation for state 2.
Conclusions
Here we have reported on a singular FeII Hofmann-type porous coordination polymer whose magnetic, optical and mechanical properties can be reversibly switched between two uncommon SCO behaviours, namely a room temperature single-step strong cooperative spin transition and four-step SCO behaviour. The key of the reversible switch between both behaviours is the absence or presence of a molecule of PhNO2 in the 1D channels. The easy recognition of PhNO2via π-stacking through the aromatic walls of the 1D channels defined by the 3,8-ligands introduces a sort of “molecular wedge” mechanism between the two interpenetrated 3D frameworks which provokes elastic frustration and multistep behaviour. It is worth noting that we have successfully extended these results to other six-membered aromatic guests such as fluoro-, chloro-, bromo- and 1,3-bibromo-benzene, benzaldehyde or benzonitrile among others. These preliminary results, which will be reported elsewhere, show that the new 1·PhX clathrates display similar four-step SCO behaviour, thereby demonstrating the reliability of the dual system here reported.Robust SCO compounds with wide hysteretic behaviour centred at room temperature such as 1, are potentially interesting materials for the construction of sensor, micro/nano electronic and spintronic devices.
Experimental
K[Au(CN)2], and Fe(BF4)2·6H2O were purchased from commercial sources and used as received whereas the synthesis of the 3,8-phen ligand was performed as described in a precedent work.27Materials
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 of PhNO2 in methanol, finally the tubes were sealed. Yield ca. 50%. Calcd for C22H13N7O2FeAu2: C, 30.83; H, 1.53; N, 11.44. Found: C, 31.12; H, 1.59; N, 11.72. IR: ν(C
10 of PhNO2 in methanol, finally the tubes were sealed. Yield ca. 50%. Calcd for C22H13N7O2FeAu2: C, 30.83; H, 1.53; N, 11.44. Found: C, 31.12; H, 1.59; N, 11.72. IR: ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) = 2179.2 cm−1 (vs.), ν(NO2)as = 1523 cm−1 (vs.) and ν(NO2)sym = 1343 cm−1 (vs.). The guest-free derivative 1 was obtained by controlled thermal decomposition under Ar atmosphere. Calcd for C16H8N6FeAu2: C, 26.18; H, 1.10; N, 11.45. Found: C, 26.63; H, 1.16; N, 11.51. This chemical analysis could reflect a residual amount of PhNO2 in the range of ca. 3–4% remaining in the structure, indeed the IR spectrum clearly denoted the lack of significant ν(NO2)as and ν(NO2)sym vibrational modes.
N) = 2179.2 cm−1 (vs.), ν(NO2)as = 1523 cm−1 (vs.) and ν(NO2)sym = 1343 cm−1 (vs.). The guest-free derivative 1 was obtained by controlled thermal decomposition under Ar atmosphere. Calcd for C16H8N6FeAu2: C, 26.18; H, 1.10; N, 11.45. Found: C, 26.63; H, 1.16; N, 11.51. This chemical analysis could reflect a residual amount of PhNO2 in the range of ca. 3–4% remaining in the structure, indeed the IR spectrum clearly denoted the lack of significant ν(NO2)as and ν(NO2)sym vibrational modes.
Physical characterisation
Thermogravimetric analysis was performed on a Mettler Toledo TGA/SDTA 851e, in the 290–800 K temperature range under a nitrogen atmosphere with a rate of 10 K min−1.
A Xcalibur 3 four-circle diffractometer (Oxford Diffraction) equipped with a 2D Sapphire3 CCD detector with Mo Kα radiation (λ = 0.71073 Å), was used for all data collection. An Oxford Cryosystems 700Plus nitrogen-flow cryostat was used for measurements in the temperatures ranging from 290 K down to 140 K; and an Oxford Diffraction Helijet helium-flow cryostat for measurements at 15 K.
The unit cell parameters and the data reduction were obtained with the CrysAlisPro (CrysAlisPro 1.171.38.41, Rigaku OD, 2015) software from Oxford Diffraction. During data processing a data scaling and empirical or multi-scan absorption correction were also performed with CrysAlisPro software. The structures at 290 K, 250 K, 228 K, 140 K, 15 K and 15 K after laser irradiation, with the exception of 206 K data, were solved in P2/n space group by direct methods using SHELXT28 and refined by full-matrix least squares on F2 using SHELXL,29 see Table S1,† with Olex2 GUI.30 All non-hydrogen atoms were refined anisotropically and H-atoms were constrained by geometry. When applicable, DFIX, SIMU and ISOR restraints as well EADP constraints were applied for occupational disorders. For 228 K a cell doubling has been identified; the satellites at Q-vector ∼ 0.5a* + 0.5b* + 0.5c* accompanied with a weak diffuse signal, were found and, since a β-angle is ∼90°, a monoclinic I2/a space group was assigned. Detailed analysis at 206 K revealed a presence of incommensurate satellite peaks with a q-vector ∼ 0.431(2)a* + 0.498(2)b* + 0.3690(18)c*, Fig. S7.† These satellites start to appear already for 250 K data (a weak signal), are stronger at 206 K and tend to slowly diminish with temperature, still present at 140 K, and missing for 290 K and 15 K data. Refinement in (3 + 1)-dimensional superspace: P2/n(a1|2g)0s, has been performed only for 206 K data. Here, the average structure model was solved by charge flipping and used for further least square refinement on F with Jana2006.31 The modulation of the atomic positions for all non-H atoms as well as the first harmonic modulation wave for selected atom sites were refined. All H-atoms were constrained by geometry. A final refinement cycle was stable and allowed refinement of the basic structure parameters along with modulation parameters for all non-H atoms with the exception of PhNO2 site.
The crystal data collection and refinement parameters for all phases are given in Table S1.† CCDC-2010360 (state 1, 290 K), CCDC-2010361 (state 2, 250 K), CCDC-2010362 (state 3, 228 K), CCDC-2010363 (state 4, 206 K), CCDC-2010364 (state 5, 140 K), CCDC-2010365 (state 5, 15 K [dark]) and CCDC-2010366 (state 6, 15 K [532 nm]) contain the ESI crystallographic data for this paper.†
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Spanish Ministerio de Economía y Competitividad (MINECO)/Ministerio de Ciencia e Innovación FEDER (CTQ2016-78341-P/PID2019-106147GB-I00), Unidad de Excelencia María de Maeztu (CEX2019-000919-M), the Generalitat Valenciana through PROMETEO/2016/147 and an EU Framework Programme for Research and Innovation (RISE project number 734322). F. J. V. M. thanks MINECO for a predoctoral (FPI) grant. C. M. G. thanks the funding from the European Research Council (grant agreement No. 714122).Notes and references
- (a) E. König, Struct. Bonding, 1991, 76, 51–152 CrossRef; (b) P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed., 1994, 33, 2024–2054 CrossRef; (c) J. A. Real, A. B. Gaspar, V. Niel and M. C. Muñoz, Coord. Chem. Rev., 2003, 236, 121–141 CrossRef CAS; (d) P. Gütlich and G. Goodwin, Top. Curr. Chem., 2004, 233–235 Search PubMed; (e) J. A. Real, A. B. Gaspar and M. C. Muñoz, Dalton Trans., 2005, 2062–2079 RSC; (f) M. A. Halcrow, Polyhedron, 2007, 26, 3523–3576 CrossRef CAS; (g) A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313–3335 RSC.
- C. Enachescu, M. Nishino and S. Miyashita, in Spin-Crossover Materials Properties and Applications, ed. M. A. Halcrow, Wiley, 2013, pp. 455–474 Search PubMed.
- C. Enachecu and W. Nicolazzi, C. R. Chim., 2018, 21, 1179–1195 CrossRef.
- H. Watanabe, K. Tanaka, N. Bréfuel, H. Cailleau, J.-F. Létard, S. Ravy, P. Fertey, M. Nishino, S. Miyashita and E. Collet, Phys. Rev. B, 2016, 93, 014419 CrossRef.
- M. Paez-Espejo, M. Sy and K. Boukheddaden, J. Am. Chem. Soc., 2016, 138, 3202–3210 CrossRef CAS.
- R. Traiche, M. Sy and K. Boukheddaden, J. Phys. Chem. C, 2018, 122, 4083–4096 CrossRef CAS.
- (a) M. Cavallini, I. Bergenti, S. Milita, J. C. Kengne, D. Gentili, G. Ruani, I. Salitros, V. Meded and M. Ruben, Langmuir, 2011, 27, 4076–4081 CrossRef CAS; (b) P. N. Martinho, C. Rajnak and M. Ruben, in Spin-Crossover Materials: Properties and Applications, ed. M. A. Halcrow, Wiley, 2013, pp. 376–404 Search PubMed; (c) G. Molnar, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 17003862 CrossRef.
- (a) M. C. Muñoz and J. A. Real, Coord. Chem. Rev., 2011, 255, 2068–2093 CrossRef; (b) Z.-P. Ni, J.-L. Liu, Md. N. Hoque, W. Liu, J.-Y. Li, Y.-C. Chen and M. L. Tong, Coord. Chem. Rev., 2017, 335, 28–43 CrossRef CAS.
- V. Martínez, A. B. Gaspar, M. C. Muñoz, G. V. Bukin, G. Levchenko and J. A. Real, Chem.–Eur. J., 2009, 15, 10960–10971 CrossRef.
- W. Liu, L. Wang, Y.-J. Su, Y.-C. Chen, J. Tucek, R. Zboril, Z.-P. Ni and M.-L. Tong, Inorg. Chem., 2015, 54, 8711–8716 CrossRef CAS.
- N. F. Sciortino, F. Ragon, K. A. Zenere, P. D. Southon, G. J. Halder, K. W. Chapman, L. Piñeiro-López, J. A. Real, C. J. Kepert and S. M. Neville, Inorg. Chem., 2016, 55, 10490–10498 CrossRef CAS.
- K. A. Zenere, P. W. Doheny, S. G. Duyker, E. Trzop, E. Collet, B. Chan, P. W. Doheny, C. J. Kepert and S. M. Neville, Chem. Sci., 2018, 9, 5623–5629 RSC.
- (a) V. Niel, J. M. Martinez-Agudo, M. C. Muñoz, A. B. Gaspar and J. A. Real, Inorg. Chem., 2001, 40, 3838–3839 CrossRef CAS; (b) S. Bonhommeau, G. Molnár, A. Galet, A. Zwick, J. A. Real, J. J. McGarvey and A. Bousseksou, Angew. Chem., Int. Ed., 2005, 44, 4069–4073 CrossRef CAS; (c) M. Ohba, K. Yoneda, G. Agustí, M. C. Muñoz, A. B. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 4767–4771 CrossRef CAS; (d) G. Agustí, R. Ohtani, K. Yoneda, A. B. Gaspar, M. Ohba, J. F. Sánchez-Royo, M. C. Muñoz, S. Kitagawa and J. A. Real, Angew. Chem., Int. Ed., 2009, 48, 8944–8947 CrossRef.
- I. A. Gural'skiy, B. O. Golub, S. I. Shylin, V. Ksenofontov, H. J. Shepherd, P. R. Raithby, W. Tremel and I. O. Fritsky, Eur. J. Inorg. Chem., 2016, 3191–3195 CrossRef.
- F. J. Valverde-Muñoz, M. Seredyuk, M. C. Muñoz, K. Znovjyak, I. O. Fritsky and J. A. Real, Inorg. Chem., 2016, 55, 10654–10665 CrossRef.
- N. F. Sciortino, K. R. Scherl-Gruenwald, G. Chastanet, G. J. Halder, K. W. Chapman, J.-F. Létard and C. J. Kepert, Angew. Chem., Int. Ed., 2012, 51, 10154–10158 CrossRef CAS.
- M. J. Murphy, K. A. Zenere, F. Ragon, P. D. Southon, C. J. Kepert and S. M. Neville, J. Am. Chem. Soc., 2017, 139, 1330–1335 CrossRef CAS.
- N. F. Sciortino, K. A. Zenere, M. E. Corrigan, G. J. Halder, G. Chastanet, J.-F. Létard, C. J. Kepert and S. M. Neville, Chem. Sci., 2017, 8, 701–707 RSC.
- J. E. Clements, J. R. Price, S. M. Neville and C. J. Kepert, Angew. Chem., Int. Ed., 2016, 55, 15105–15109 CrossRef CAS.
- W. Liu, Y.-Y. Peng, S.-G. Wu, Y.-C. Chen, Md. N. Hoque, Z.-P. Ni, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2017, 56, 14982–14986 CrossRef CAS.
- S. Decurtins, P. Gütlich, P. C. Köhler, H. Spiering and A. Hauser, Chem. Phys. Lett., 1984, 105, 1–4 CrossRef CAS.
- J. F. Létard, P. Guionneau, L. Rabardel, J. A. K. Howard, A. E. Goeta, D. Chasseau and O. Kahn, Inorg. Chem., 1998, 87, 4432–4441 CrossRef.
- (a) A. Hauser, Coord. Chem. Rev., 1991, 111, 275–290 CrossRef CAS; (b) A. Hauser, C. Enachescu, M. L. Daku, A. Vargas and N. Amstuz, Coord. Chem. Rev., 2006, 250, 1642–1652 CrossRef CAS.
- E. Trzop, D. Zhang, L. Piñeiro-Lopez, F. J. Valverde-Muñoz, M. C. Muñoz, L. Palatinus, L. Guerin, H. Cailleau, J. A. Real and E. Collet, Angew. Chem., Int. Ed., 2016, 55, 8675–8679 CrossRef CAS.
- E. Collet, H. Watanabe, N. Bréfuel, L. Palatinus, L. Roudaut, L. Toupet, K. Tanaka, J.-P. Tuchagues, P. Fertey, S. Ravy, B. Toudic and H. Cailleau, Phys. Rev. Lett., 2012, 109, 257206 CrossRef CAS.
- Y. Y. Peng, S. G. Wu, Y. C. Chen, W. Liu, G. Z. Huang, Z. P. Ni and M. L. Tong, Inorg. Chem. Front., 2020, 7, 1685–1690 RSC.
- E. Botana, E. Da Silva, J. Benet-Buchholz, P. Ballester and J. de Mendoza, Angew. Chem., Int. Ed., 2007, 46, 198–201 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. M. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- V. Petricek, M. Dusek, and L. Palatinus. JANA2006, Institute of Physics, Praha, Czech Republic Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC compound 1·PhNO2: CCDC-2010360 (state 1, 290 K), CCDC-2010361 (state 2, 250 K), CCDC-2010362 (state 3, 228 K), CCDC-2010363 (state 4, 206 K), CCDC-2010364 (state 5, 140 K), CCDC-2010365 (state 5, 15 K [dark]) and CCDC-2010366 (state 6, 15 K [532 nm]). Compound 1: CCDC-2016312. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04420b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |