Open Access Article
Open Access ArticleReductive processing of single walled carbon nanotubes for high volumetric performance supercapacitors†
Pichamon
Sirisinudomkit
 ab,
Evgeny
Senokos
b,
Noelia
Rubio
b and
Milo S. P.
Shaffer
ab,
Evgeny
Senokos
b,
Noelia
Rubio
b and
Milo S. P.
Shaffer
 *ab
*ab
aDepartment of Materials, Imperial College London, SW7 2AZ, UK. E-mail: m.shaffer@imperial.ac.uk
bDepartment of Chemistry, Imperial College London, SW7 2AZ, UK
First published on 2nd February 2021
Abstract
Intrinsically, single walled carbon nanotubes (SWCNTs) are excellent candidates for electrochemical double layer supercapacitor (EDLC) electrodes, owing to their high electrical conductivity, high accessible surface area, and high aspect ratio/connectivity, which provide exceptional intrinsic gravimetric energy and power densities. However, in practice, local bundling due to strong intertube van der Waals interactions reduces the effective surface area; at larger scales, the bundling also creates low density networks that limit the volumetric electrochemical performance of practical electrodes. In this study, reductive charging is used to dissolve individual SWCNTs and assemble them to form relatively dense (0.34 g cm−3), thick (38 μm) ‘buckypaper’ electrodes, with high electrical conductivity (>400 S cm−1). Intermediate charging ratios (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na = 10
Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and carbon concentrations (0.125 M) provide greater SWCNT solubilisation and individualisation, and correlate with maximum volumetric capacitance of 74 F cmelectrode−3 at 10 mV s−1 in 1 M H2SO4. These optimised half-cell electrodes were implemented in full symmetric cell devices, prepared in both aqueous and ionic liquid electrolytes, using a bespoke bacterial cellulose (BC) ultrathin separator (7 microns) to minimize parasitic mass/volume. The full cell performance in ionic liquid reached maximum energy and power densities of 2.6 Wh kg−1 (2.2 mWh cm−3), and 10.2 kW kg−1 (8.3 W cm−3), respectively, normalised by the total mass and volume of device (electrodes, electrolyte, and separator; no separate current collector is needed). The relatively effective transfer of half-cell to full-cell performance is encouraging but could be optimized further in future. Appropriate normalisations for supercapacitor electrodes and devices are discussed in detail. Thin BC-based separators have wide applicability to other electrochemical devices.
1) and carbon concentrations (0.125 M) provide greater SWCNT solubilisation and individualisation, and correlate with maximum volumetric capacitance of 74 F cmelectrode−3 at 10 mV s−1 in 1 M H2SO4. These optimised half-cell electrodes were implemented in full symmetric cell devices, prepared in both aqueous and ionic liquid electrolytes, using a bespoke bacterial cellulose (BC) ultrathin separator (7 microns) to minimize parasitic mass/volume. The full cell performance in ionic liquid reached maximum energy and power densities of 2.6 Wh kg−1 (2.2 mWh cm−3), and 10.2 kW kg−1 (8.3 W cm−3), respectively, normalised by the total mass and volume of device (electrodes, electrolyte, and separator; no separate current collector is needed). The relatively effective transfer of half-cell to full-cell performance is encouraging but could be optimized further in future. Appropriate normalisations for supercapacitor electrodes and devices are discussed in detail. Thin BC-based separators have wide applicability to other electrochemical devices.
Introduction
Carbon-based materials have excellent physical and chemical properties, are abundant, and available in bulk, making them suitable electrodes for supercapacitors.1–3 Amongst this large family, single walled carbon nanotubes (SWCNTs) are particularly promising, owing to their outstanding electron transport, high elastic modulus, tensile strength and excellent thermal properties.4,5 Electrochemical double layer (super)capacitors (EDLCs) based on SWCNTs have high power density due to their high electrical conductivity, chemical stability, accessible porosity and high specific surface area.6 Literature values for the intrinsic gravimetric double layer capacitance of SWCNT electrodes range between 20 to 300 F g−1, relative to the mass of the active carbon in a half-cell electrode.7–9The wide range of capacitive performance reflects the SWCNT type, their purity, and the electrolyte used, as well as the device architecture and the methodology used for measurement.10 A key microstructural factor is that π–π interactions cause strong rebundling of SWCNTs, reducing the active surface area, and associated capacitance. Various methods have been proposed to individualise SWCNTs for application, including intense sonication or other methods of mechanical shear.11 However, these approaches tend to both shorten SWCNTs and degrade their intrinsic properties. Reductive charging provides a means to overcome the van der Waals interactions, without damaging the SWCNT structure, by introducing Coulombic repulsions.12 Negatively-charged SWCNTs (“nanotubides”) form thermodynamically-stable solutions of individual, undamaged species at high concentrations.12,13 There are a wide range of methods to prepare nanotubide solutions, but one of the simplest and most scalable, is the one-pot reduction of SWCNTs in N,N-dimethylacetamide (DMAc), using an organic charge transfer agent (sodium naphthalide, NaNp).13 The resulting solutions are useful both for liquid-phase processing and subsequent reactions with a range of electrophiles. Previously, these nanotubide solutions with concentrations on the order 1 mg ml−1 were cross-linked with dielectrophiles to form gels. The gels were freeze-dried to form aerogel (cryogel) electrodes with high surface area (766 m2 g−1) and reasonable conductivity (9.4 S m−1). These properties are attractive for supercapacitor electrodes with high rate capability and cycling efficiency, and resulted in high gravimetric performance.14
In the literature, supercapacitor performance is frequently reported normalised only to the mass of the active electrode material. From this perspective, both ultra-thin films and porous networks appear to offer a remarkable (gravimetric) performance. Highly porous structures, such as SWCNT aerogels, provide an efficient, lightweight, 3D network structure, with high surface area, and excellent electron/ion transport in energy storage devices.15 However, whilst these data fairly highlight the exceptional intrinsic performance of SWCNTs, they are misleading when it comes to practical application. Ultrathin films (<1 μm) provide negligible active mass compared to the parasitic mass of the remainder of the cells. In addition, SWCNT aerogels have ultralow packing densities, typically consisting of >99% pore volume; in a real device, this volume must be filled with dense electrolyte, dramatically increasing the effective electrode mass. At the same time, the low density implies a poor electrochemical volumetric performance, which is important in many practical applications such as compact electronic devices and power management in electric vehicles.16,17 For example,18 a low density SWCNT aerogel (0.013 g cm−3) shows extremely high gravimetric energy density at ∼40 Wh kg−1 while its volumetric energy density is only ∼0.52 mWh cm−3. Incorporating a practically useful active electrode mass (relative to other cell components, such as the separator or current collector) implies a thick aerogel electrode which may have a high equivalent series resistance (ESR), decreasing the performance further. Whilst it is possible to reduce the thickness of aerogels by capillary collapse or mechanical compression, the SWCNTs tend to rebundle.19 This aggregation reduces surface area and associated EDLC, as well as disrupting ion transport path and increasing charge transfer resistance. For real application, the SWCNT electrode architecture must be designed to maximise volumetric performance, electrical conductivity and ion transport, at high areal mass loadings.20 SWCNT ‘buckypapers’ are dried films, typically prepared by filtration. In principle, they are promising candidates for supercapacitor electrodes, but generally suffer a poor architecture derived from the challenges of solvent processing. There is scope to develop improved ‘buckypapers’, designed to offer individualised SWCNTs, with high aspect ratio, in thick films with high bulk density. Such electrodes should offer lower contact resistance, higher conductivity, and higher volumetric performance than SWCNT aerogels.21
In addition, the integrity and high conductivity of SWCNT buckypaper electrodes means that conventional binders and current collectors can be avoided, in principle increasing specific energy density by reducing the inactive mass and volume of overall device.22,23
Whilst the nature of the active electrodes is critical, the volumetric performance of a full device also depends on the separator. The ideal separator must minimise ionic resistance whilst preventing any electronic short circuit between the two electrodes. Generally, thin highly porous membranes provide the lowest resistive losses, and maximise volumetric performance, but they must remain mechanically robust.24 Cellulose, polytetra-fluoroethylene (PTFE), polyethylene and polypropylene membranes are well-known separators for aqueous supercapacitors. The thickness of commercial separators are roughly around 20–50 μm, including for example, 25 μm for TF4425 (cellulose), 23 μm for GORE (PTFE) and 25 μm for Celgard2400 (polypropylene) separators, respectively.25,26 Reducing the thickness of these established separators may have adverse effects on the mechanical strength, cyclic stability and safety.27 Alternative membranes are needed that can provide reliable mechanical separation at lower thickness.
In this study, we aimed to produce a full supercapacitor cell with excellent overall gravimetric and volumetric performance, by optimising the nanostructure of both electrodes and separator. Since individualised SWCNTs offer maximum electrochemical performance, reductive charging was used to prepare the electrode constructs. SWCNT/DMAc concentration ([C]), charging ratios of carbon to sodium (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na) and/or degree of charge are known to control the level of CNTs solubilisation, therefore the conditions were optimised to maximise effective surface area of the electrodes and consequently capacitance. To fabricate a thinner, highly porous membrane, we explored the use of bacterial cellulose (BC) nanopaper, due to its high surface area (605 m2 g−1), good porosity (65%), light weight (15 g m−2), micrometre-scale thickness and high tensile strength.28 Full cells were then prepared using BC as a separator to maximise performance with an aqueous electrolyte. In order to improve specific energy density, higher voltage cells were produced using an ionic liquid electrolyte.29,30
Na) and/or degree of charge are known to control the level of CNTs solubilisation, therefore the conditions were optimised to maximise effective surface area of the electrodes and consequently capacitance. To fabricate a thinner, highly porous membrane, we explored the use of bacterial cellulose (BC) nanopaper, due to its high surface area (605 m2 g−1), good porosity (65%), light weight (15 g m−2), micrometre-scale thickness and high tensile strength.28 Full cells were then prepared using BC as a separator to maximise performance with an aqueous electrolyte. In order to improve specific energy density, higher voltage cells were produced using an ionic liquid electrolyte.29,30
Experimental
Materials
Tuball75 single walled carbon nanotube powder was supplied by OCSiAl Ltd.13 Sodium (99.95%, ingot), naphthalene (99%), dimethylformamide (DMF, 99.8%), ethyl-methyl-imidazolium bis(trifluoromethylsulfonyl)-imide ([EMIM][TFSI], ≥98% (HPLC), ≤0.5% water) and dimethylactamide (DMAc, 99.8%) were purchased from Sigma-Aldrich UK and sulphuric acid (97%) was purchased from VWR UK Ltd. Naphthalene was dried under vacuum overnight over phosphorus pentoxide (P2O5) before using in a glove box. DMAc was dried over 20% volume, activated molecular sieves (3 Å) before use in the glove box. All gases were supplied by BOC, UK and PTFE membranes were provided by Fisher Scientific Ltd.SWCNT purification via NaNp/DMAc
300 mg of raw SWCNT powder (25 mmol) were reduced with Na/naphthalene solution (1 mg ml−1) in DMAc, following a procedure reported elsewhere.31SWCNT reductive dissolution
250 mg of purified SWCNT powder were dried in a quartz tube, which was sealed and connected to a turbo pump (Leybold PT 70F) using a metal Swagelok joint. The quartz tube was evacuated to approximately 10−6 mbar, and heated up to 500 °C, in a tube furnace, with a ramp rate of 15 °C min−1 and a dwell for 20 min every 100 °C. The temperature was maintained at 500 °C for 10 h, before allowing the quartz tube to cool overnight under vacuum before transferring it into an mBraun glove box (nitrogen atmosphere, <0.1 ppm water, 0.1 ppm oxygen). For preparing reductive stock solution, 50 mg of sodium and 278 mg of naphthalene were stirred in 50 ml of DMAc overnight using a glass stirring bar. The sodium naphthalide (NaNp) was added to purified SWCNTs powder. The ratio between mol C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol Na varied from 5
mol Na varied from 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 15
1 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (molar ratio). The nanotubide solution was stirred for 24 hours.
1 (molar ratio). The nanotubide solution was stirred for 24 hours.
Nanotubide buckypaper
Nanotubide buckypaper was prepared by diluting the nanotubide solution to 1–4 mg ml−1 with additional dry DMAc and using a syringe to dose the nanotubide solution onto a PTFE membrane (0.1 μm) with 3.78 cm diameter placed on a filtration system inside the glove box. The volume was adjusted so that each piece of buckypaper contained 7 mg of SWCNTs. After leaving the solution to settle for 24 hours, the nanotubide buckypaper was taken out from the glove box in a sealed glass flask with a suba-seal stopper and then quenched with dry air (N2/O2, 80/20) to remove the remaining charge. To remove the remaining impurities, and salt by-products, the quenched nanotubide buckypaper was washed with DMF, water and ethanol via solvent exchange. Finally, nanotubide buckypaper was vacuum dried in a vacuum oven at 110 °C overnight.Sonicated SWCNT buckypaper
A control SWCNT buckypaper, used for comparison, was prepared via sonication. 7 mg of raw SWCNT powder were mixed with 4.7 ml DMAc and sonicated for 2 hours using 35 W ultrasonic bath. The resulting suspension was filtered through a PTFE filter membrane (0.1 μm) and washed with DMF, water and ethanol, respectively. Finally, the sonicated SWCNT buckypaper was dried under vacuum at 110 °C overnight.Morphological and structural characterizations
The morphologies of the as-synthesised materials were characterised by field-emission scanning electron microscopy (SEM, Sigma 300). SEM samples were dried at 100 °C overnight in vacuum oven to remove humidity and then fixed on Al stubs using carbon tabs (Agar Scientific Ltd, Essex, UK). The samples were analysed with an InLens detector, using an accelerating voltage of 5 keV, 30 μm standard aperture and 4.5 mm working distance. The chemical composition on the surface of the materials was characterised by X-ray Photoelectron Spectroscopy (XPS). All XPS spectra were recorded using a K-alpha+ XPS spectrometer equipped with a MXR3 Al Kα monochromated X-ray source (hν = 1486.6 eV). The X-ray gun power was set to 72 W (6 mA and 12 kV). Charge compensation was achieved using the FG03 flood gun using a combination of low energy electrons and the ion flood source. Samples were etched using the standard EX06 argon ion source using 500 V accelerating voltage and 1 μA ion gun current. Survey scans were acquired using 200 eV pass energy, 1 eV step size and 100 ms (50 ms × 2 scans) dwell times. All high resolution spectra (C 1s, and O 1s) were acquired using 20 eV pass energy, 0.1 eV step size and 1 second (50 ms × 20 scans = 1000 ms) dwell times. Samples were prepared by pressing the sample onto double side sticky carbon-based tape. Pressure during the measurement of XPS spectra was ≤1 × 10−8 mbar. Casa XPS software (version 2.3.16) was used to process the data. The quantification analysis was carried out after subtracting the baseline using a Shirley or two point linear background. All XPS spectra were corrected by referencing the fitted contribution of C–C graphitic like carbon in the C 1s signal at 284.5 eV. N2 adsorption–desorption analyses were performed with a Micromeritics Tristar 3000 analyser. The surface areas were calculated according to the Brunauer, Emmett and Teller (BET) equation from the adsorption isotherm in p/p0 range between 0.02 and 0.3. The pore-size distribution of the samples was estimated from desorption branch using the Barrett, Joyner, and Halenda (BJH) method. Thermogravimetric analysis (TGA) was run on a Mettler Toledo TGA/DSC1 with lidded 70 μl alumina pans, manually removing a premeasured background. The samples were heated from 30 to 100 °C at 45 °C min−1 before holding for 1 h at 100 °C (to remove residual solvents), then ramped at 10 °C min−1 to 900 °C in a flow of 60 ml min−1 of air. Raman spectra of samples were measured using a Renishaw inVia confocal Raman spectrometer equipped with a 633 nm excitation laser source; mapping measurements were carried out using the Streamline mode (between 500–1000 spectra over at least 3 different areas to reduce the effect of sample heterogeneity). The exposure time was 10 s with a laser intensity of 3.2 mW and grating 1800 l mm−1. WiRe (v4.1, build 4308) software was used to calculated ID/IG ratios after automatic background subtraction, to perform curve fitting of the D and G peaks and plotting the intensity ratio of D peak maximum to G peak maximum. The electrical conductivity was measured using Jandel four point probes with 1 mm needle spacing and 300 μm diameter. The apparatus is connected with Keysight 34410A digital multimeter to interpret the measured resistance.Electrochemical evaluation
The electrochemical properties of the as-synthesised electrodes were evaluated using a Gamry Instruments Interface 1000 potentiostat/galvanostat/ZRA, run with Gamry Instruments Framework™ (v.6.24). For three electrode system measurements, 1 cm2 (1.3 mg) electrodes were tested in 1 M H2SO4 at room temperature using Ag/AgCl as a reference electrode and Pt wire as a counter electrode. Cyclic voltammetry (CV) was performed at various scan rates from 10 to 500 mV s−1 and potentiostatic electrochemical impedance spectroscopy (EIS) performed by applying a sinusoidal signal of 10 mV in the range of frequencies from 1 mHz to 100 kHz. Further details of the data analysis are provided in the ESI.†Fabrication of symmetric device
The BC nanopaper separator was produced from nata de coco, following a procedure reported elsewhere.28,35 BC nanopapers with thicknesses of 7 μm were soaked overnight in 1 M H2SO4 and [EMIM][TFSI] for aqueous and ionic liquid supercapacitors, respectively. A conventional cellulose paper (70 μm), used for comparison with BC nanopaper, was also soaked overnight in 1 M H2SO4. Devices were then assembled by sandwiching the separator between identical circular (10 mm diameter) SWCNT electrodes in Swagelok cell. The electrochemical properties of as-fabricated full cell devices were evaluated by EIS and galvanostatic charge–discharge (GCD) as a two electrode system. GCD was performed at current densities varied from 1 to 100 A g−1 and cyclic stability tests (1–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) were completed via the GCD technique applying current density at 5 A g−1. Further details of the data analysis are provided in the ESI.†
000 cycles) were completed via the GCD technique applying current density at 5 A g−1. Further details of the data analysis are provided in the ESI.†
Results and discussion
Electrode optimisation (half-cell)
In this study, a new type of buckypaper was successfully produced via reductive dissolution and subsequent filtration of charged SWCNTs (here called ‘nanotubide buckypaper’). To optimize the solubilisation and functionalization, nanotubide solutions were prepared with SWCNT/DMAc concentrations [C] in the range of 1 to 4 mg ml−1 and molar carbon to sodium (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na) ratios in the range of 5
Na) ratios in the range of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 15
1 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. SEM images (Fig. S1a–d, ESI†) show that uniform, highly porous networks were formed by filtering nanotubide solutions with concentrations from 1 to 2.5 mg ml−1. However, above 3 mg ml−1, evidence of agglomeration appeared (Fig. S1e and f, ESI†), consistent with the expected solubility limit of Tuball nanotubide in DMAc.13 The SEMs also indicate that the quality of nanotubide dispersions decreased when C
1. SEM images (Fig. S1a–d, ESI†) show that uniform, highly porous networks were formed by filtering nanotubide solutions with concentrations from 1 to 2.5 mg ml−1. However, above 3 mg ml−1, evidence of agglomeration appeared (Fig. S1e and f, ESI†), consistent with the expected solubility limit of Tuball nanotubide in DMAc.13 The SEMs also indicate that the quality of nanotubide dispersions decreased when C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na increased from 5
Na increased from 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 15
1 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, consistent with insufficient Coulombic repulsion and selective dissolution (Fig. S3a–e, ESI†).13 In order to benchmark nanotubide buckypaper against more conventional methods, a control was prepared by dispersing SWCNTs in DMAc using sonication at 1.5 mg ml−1 (0.125 M). This electrode was compared with the purified nanotubide buckypaper prepared at the same concentration ([C] = 1.5 mg ml−1) and an intermediate charge ratio (C
1, consistent with insufficient Coulombic repulsion and selective dissolution (Fig. S3a–e, ESI†).13 In order to benchmark nanotubide buckypaper against more conventional methods, a control was prepared by dispersing SWCNTs in DMAc using sonication at 1.5 mg ml−1 (0.125 M). This electrode was compared with the purified nanotubide buckypaper prepared at the same concentration ([C] = 1.5 mg ml−1) and an intermediate charge ratio (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na = 10
Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Under SEM, the sonicated SWCNT buckypaper showed an agglomerated structure with impurities bound on the surface (Fig. 1a); in sharp contrast, the structure of nanotubide buckypaper contains a network of highly dispersed SWCNTs bundles (Fig. 1b). Nitrogen adsorption isotherms (Fig. 1c) were used to measure the surface area and pore size distribution crucial to EDLC performance. Specific surface areas (SSAs) calculated through the BET model showed an improvement for the nanotubide system (412 m2 g−1) compared to the sonicated control (327 m2 g−1). In addition, the nanotubide paper showed a narrower range of pore sizes (Fig. 1d), predominantly mesopores between 10–50 nm; the sonicated paper showed a broad range of micro-, meso- and macroporous structures. Ion–wall interactions slow ion transport in the micropores, in pore-diameter-dependent fashion.36 Pore diameters larger than 10 nm are considered sufficiently large to neglect ion–wall interactions, leading to fast ion transport, at low resistance, equivalent to bulk electrolyte.36–38 The predominance of the mesopores in the nanotubide buckypaper (maximum PSD peak at 30 nm) therefore implies a low ionic resistance; the narrow mesopore distribution is expected to lead to more efficient pore utilization.39–41 On the other hand, in the sonicated SWCNT buckypaper, the significant fraction of micropores is expected to limit ion transport and hence power storage characteristics.42,43 The electrical conductivity of nanotubide paper (433 S cm−1 at 0.34 g cm−3) was significantly higher than the sonicated SWCNT paper (110 S cm−1 at 0.33 g cm−3) and other SWCNT buckypapers in the literature (Fig. 1f). A higher degree of individualisation, and the retention of longer SWCNTs, is expected to increase conductivity.33,44 Notably, the conductivity is the highest for the optimal dispersion conditions (Fig. S2d and S4a, ESI†). In addition, following reductive purification, the proportion of amorphous carbon and defective nanotubes is lowered.13
1). Under SEM, the sonicated SWCNT buckypaper showed an agglomerated structure with impurities bound on the surface (Fig. 1a); in sharp contrast, the structure of nanotubide buckypaper contains a network of highly dispersed SWCNTs bundles (Fig. 1b). Nitrogen adsorption isotherms (Fig. 1c) were used to measure the surface area and pore size distribution crucial to EDLC performance. Specific surface areas (SSAs) calculated through the BET model showed an improvement for the nanotubide system (412 m2 g−1) compared to the sonicated control (327 m2 g−1). In addition, the nanotubide paper showed a narrower range of pore sizes (Fig. 1d), predominantly mesopores between 10–50 nm; the sonicated paper showed a broad range of micro-, meso- and macroporous structures. Ion–wall interactions slow ion transport in the micropores, in pore-diameter-dependent fashion.36 Pore diameters larger than 10 nm are considered sufficiently large to neglect ion–wall interactions, leading to fast ion transport, at low resistance, equivalent to bulk electrolyte.36–38 The predominance of the mesopores in the nanotubide buckypaper (maximum PSD peak at 30 nm) therefore implies a low ionic resistance; the narrow mesopore distribution is expected to lead to more efficient pore utilization.39–41 On the other hand, in the sonicated SWCNT buckypaper, the significant fraction of micropores is expected to limit ion transport and hence power storage characteristics.42,43 The electrical conductivity of nanotubide paper (433 S cm−1 at 0.34 g cm−3) was significantly higher than the sonicated SWCNT paper (110 S cm−1 at 0.33 g cm−3) and other SWCNT buckypapers in the literature (Fig. 1f). A higher degree of individualisation, and the retention of longer SWCNTs, is expected to increase conductivity.33,44 Notably, the conductivity is the highest for the optimal dispersion conditions (Fig. S2d and S4a, ESI†). In addition, following reductive purification, the proportion of amorphous carbon and defective nanotubes is lowered.13
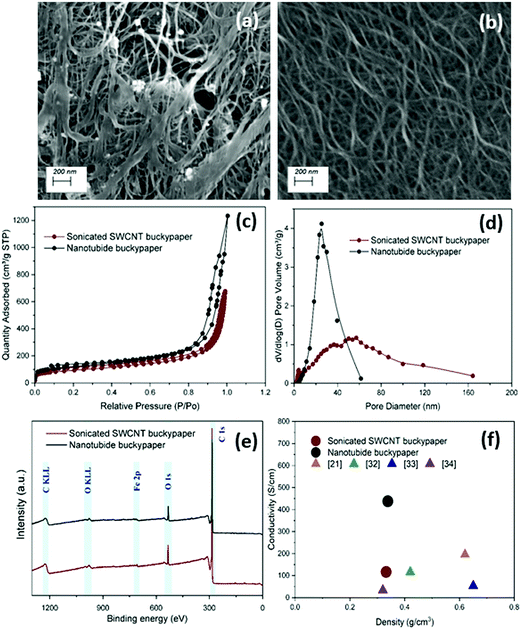 | ||
Fig. 1 SEM images of (a) sonicated SWCNT buckypaper and (b) nanotubide buckypaper ([C] = 1.5 mg ml−1, C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na = 10 Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Comparison of sonicated SWCNT buckypaper and nanotubide buckypaper ([C] = 1.5 mg ml−1, C 1). Comparison of sonicated SWCNT buckypaper and nanotubide buckypaper ([C] = 1.5 mg ml−1, C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na = 10 Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) by (c) BET N2 adsorption–desorption isotherms, (d) pore size distribution (PSD) and (e) XPS survey scans. (f) Electrical conductivity of nanotubide and sonicated SWCNT buckypapers compared to other SWCNT buckypapers in the literature.21,32–34 1) by (c) BET N2 adsorption–desorption isotherms, (d) pore size distribution (PSD) and (e) XPS survey scans. (f) Electrical conductivity of nanotubide and sonicated SWCNT buckypapers compared to other SWCNT buckypapers in the literature.21,32–34 | ||
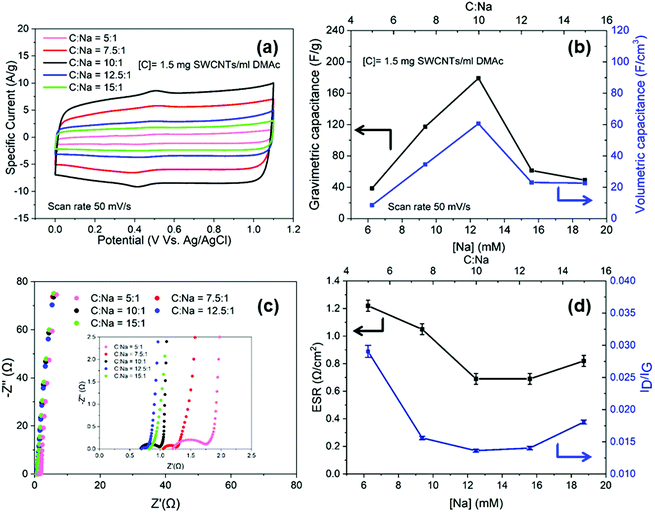
To optimise the electrochemical performance, buckypapers were produced from nanotubide solutions at different charging ratios (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na). Within the aqueous potential window (0 V to 1.1 V), all the electrodes exhibited rectangular CVs, characteristic of EDLC of SWCNTs (Fig. 2a),45 with minor, broad redox peaks around 0.4 V related to the pseudo capacitive behaviour of hydroxyl and carboxylic groups noted in the XPS (Fig. S3f, ESI†). The gravimetric and volumetric capacitances were both maximised for the nanotubide electrode obtained at C
Na). Within the aqueous potential window (0 V to 1.1 V), all the electrodes exhibited rectangular CVs, characteristic of EDLC of SWCNTs (Fig. 2a),45 with minor, broad redox peaks around 0.4 V related to the pseudo capacitive behaviour of hydroxyl and carboxylic groups noted in the XPS (Fig. S3f, ESI†). The gravimetric and volumetric capacitances were both maximised for the nanotubide electrode obtained at C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na = 10
Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 2b). To explore the losses in more detail, characteristic Nyquist plots (Fig. 2c) were derived from EIS. At high-frequency, the semi-circular region denotes a significant resistive contribution where the minimum intercept on the x-axis indicates the equivalent series resistance (ESR) and the diameter of the semicircle relates to charge transfer resistance (Rct).46 The ESR combines resistive contributions from the electrode material, electrolyte and contact resistance.47,48 The optimal (lowest) ESR for the nanotubide electrodes is shown at C
1 (Fig. 2b). To explore the losses in more detail, characteristic Nyquist plots (Fig. 2c) were derived from EIS. At high-frequency, the semi-circular region denotes a significant resistive contribution where the minimum intercept on the x-axis indicates the equivalent series resistance (ESR) and the diameter of the semicircle relates to charge transfer resistance (Rct).46 The ESR combines resistive contributions from the electrode material, electrolyte and contact resistance.47,48 The optimal (lowest) ESR for the nanotubide electrodes is shown at C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na equal to 10
Na equal to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. At other C
1. At other C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na ratios, ESR is increased, presumably due to poorer SWCNT dispersion/individualisation, as inferred from the SEM images (Fig. S3d and e, ESI†), electrical conductivity (Fig. S4a, ESI†) and capacitance data (Fig. 2b). As noted above, networks of individualised SWCNTs offer high conductivity, and minimise resistive losses within agglomerated/bundled regions. The trend may be reinforced by the quality of the SWCNTs,49 since the purification is expected to be most effective around C
Na ratios, ESR is increased, presumably due to poorer SWCNT dispersion/individualisation, as inferred from the SEM images (Fig. S3d and e, ESI†), electrical conductivity (Fig. S4a, ESI†) and capacitance data (Fig. 2b). As noted above, networks of individualised SWCNTs offer high conductivity, and minimise resistive losses within agglomerated/bundled regions. The trend may be reinforced by the quality of the SWCNTs,49 since the purification is expected to be most effective around C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na = 10
Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as confirmed here by the Raman spectroscopy (ID/IG values (Fig. 2d)). The high frequency semicircle was fitted with an equivalent circuit to calculate Rct (Fig. S4b, ESI†) which relates to the ease of electrochemical interactions at the electrode surface.50,51Rct for C
1, as confirmed here by the Raman spectroscopy (ID/IG values (Fig. 2d)). The high frequency semicircle was fitted with an equivalent circuit to calculate Rct (Fig. S4b, ESI†) which relates to the ease of electrochemical interactions at the electrode surface.50,51Rct for C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na at 5
Na at 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is significantly higher than the other electrodes (Table S1, ESI†) and correlates with a higher ID/IG ratio from Raman spectroscopy (Fig. 2d), suggesting that, in the presence of excess NaNp charging agent, the carbon framework begins to be damaged. The optimum nanotubide ([C] = 1.5 mg ml−1, C
1 is significantly higher than the other electrodes (Table S1, ESI†) and correlates with a higher ID/IG ratio from Raman spectroscopy (Fig. 2d), suggesting that, in the presence of excess NaNp charging agent, the carbon framework begins to be damaged. The optimum nanotubide ([C] = 1.5 mg ml−1, C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na = 10
Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
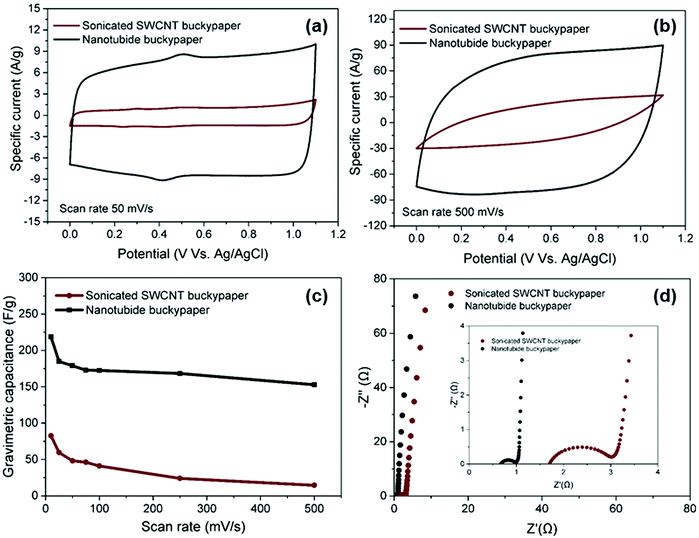
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) electrode was then compared with the sonicated control, under the same conditions, in a 3-electrode cell. Both electrodes exhibited similar rectangular CV curves, typical of classic EDLC behaviour (Fig. 3a), with only a small feature associated with redox of the oxygen-groups already noted in the XPS (Fig. 1e). As the scan rate increased to 500 mV s−1, the CV curve of sonicated SWCNT buckypaper presented a more resistive shape while CV curve of nanotubide buckypaper retains a quasi-rectangular shape with more modest distortion (Fig. 3b), highlighting the desired high power capability.52
1) electrode was then compared with the sonicated control, under the same conditions, in a 3-electrode cell. Both electrodes exhibited similar rectangular CV curves, typical of classic EDLC behaviour (Fig. 3a), with only a small feature associated with redox of the oxygen-groups already noted in the XPS (Fig. 1e). As the scan rate increased to 500 mV s−1, the CV curve of sonicated SWCNT buckypaper presented a more resistive shape while CV curve of nanotubide buckypaper retains a quasi-rectangular shape with more modest distortion (Fig. 3b), highlighting the desired high power capability.52
The much larger area under the CV curve for the nanotubide buckypaper highlights the significantly increased capacitance values, reaching 218 F g−1 (74 F cm−3), as compared to 82 F g−1 (10 F cm−3) for the sonicated SWCNT buckypaper (Fig. 3c). The gravimetric performance of the nanotubide buckypaper, here, is particularly high, compared to previous studies of carbon based buckypaper electrodes (Table S3, ESI†). The improvement is attributed to greater SWCNT individualisation providing larger surface area with suitable mesopores for ion adsorption, within a relatively dense buckpaper, at the same time as retaining a high aspect ratio, graphiticity, and electrical conductivity. Nyquist plots (Fig. 3c), derived from EIS data, show typical, excellent, EDLC responses. At low frequency, the Nyquist plot of nanotubide buckypaper exhibits a nearly vertical line, close to an ideal supercapacitor.53 The ESRs of sonicated SWCNTs and nanotubide buckypapers are 1.71 and 0.69 Ω, respectively, showing a relative trend in good agreement with the electrical conductivity data (Fig. 1f). The lower Rct of nanotubide buckypaper (0.32 Ω) compared to the sonicated SWCNT electrode (1.33 Ω) is consistent with an improved pore structure.
Symmetric supercapacitors (aqueous)
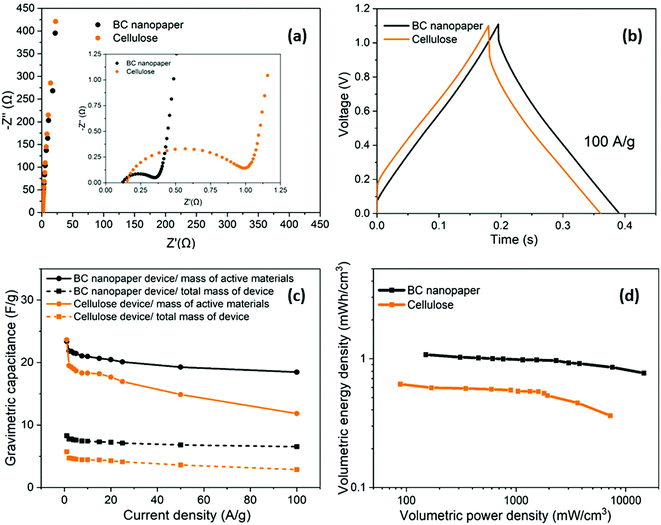
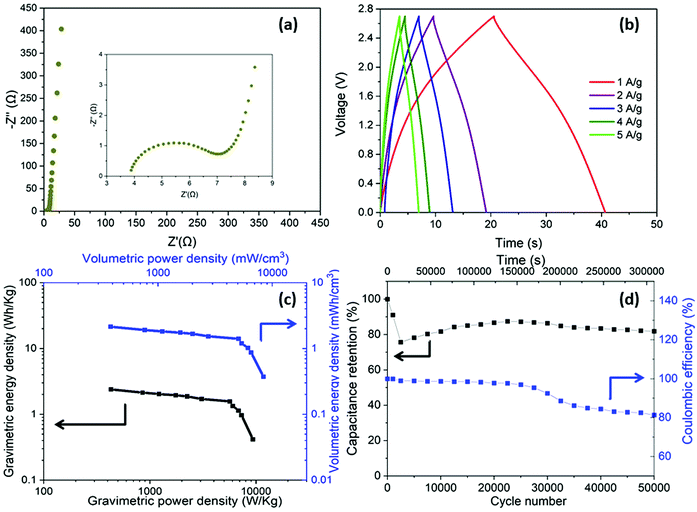
Having optimised the electrode material, using half cell measurements, symmetric full cell devices were assembled in a Swagelok system, using two optimised nanotubide electrodes. Two separators were compared: a bacterial cellulose (BC) nanopaper28 (7 μm thick), produced in-house, and a conventional cellulose paper (70 μm thick). The full cell EIS showed a classic high frequency semi-circle and capacitive response at low frequency (Fig. 4a). The exceptionally thin BC separator, provided a significant reduction in both ESR and Rct of the symmetric device, attributed to a shorter ion diffusion distance through the BC separator, despite a more modest porosity.For the GCD curves at 1 A g−1 (Fig. S5a, ESI†), full cell devices with both BC nanopaper and cellulose separators show an approximately triangular shape typical of EDLC behaviour54 with negligible IR drop (around 0.001 V for BC nanopaper and 0.002 V for cellulose, respectively), correlating with a high coulombic efficiency (>93%, Fig. S5d, ESI†). At high current density (100 A g−1), the IR drop is naturally much more obvious, for the devices with both BC (0.07 V) and cellulose (0.14 V) separators (Fig. 4b). Interestingly, using BC nanopaper as separator significantly reduced the IR drop and associated losses. Many studies calculate the gravimetric capacitance of full cell devices normalised to the total mass of the two active electrodes. This calculation can provide a comparative indication of the intrinsic performance of the active material, where half-cell measurements are not available. In line with the earlier 3-electrode measurements, the performance of the nanotubide buckypaper device remains similar/better than examples in the literature, when compared on a 2-electrode basis (Table S4, ESI†). However, the data (Fig. 4c) again show that the type of separator has a significant effect, especially at higher discharge rates. The intrinsic specific capacitance for electrode materials is best derived from three-electrode measurements involving the reference and counter electrodes. However, it is useful to compare the performance of active materials in the 2-electrode full cell system with the 3-electrode system, in order to establish how much of the intrinsic material performance has been realised. From this perspective, the maximum symmetric cell capacitance should be one quarter that of the half-cell gravimetric performance, where both are normalised to active electrode mass (the multiplier of 4 accounts for the series capacitance of the two electrodes and their combined mass).55 In fact, the full cell capacitance from a two-electrode measurement will be lower due to differential polarisation at the anode and cathode, and other effects such as the higher resistance associated with a separator and limited electrolyte access due to the presence of solid current collectors and a separator.56,57 Here, the full cell performance is around half of the theoretical maximum indicated by the 3-electrode value (Fig. 3c and Fig. S5b, ESI†), which is quite promising given the lack of cell optimisation. There is significant scope for further improvement in the full cell performance, for example, by adjusting relative anode/cathode masses, absolute electrode thickness, and/or the selection of electrolyte.58,59
A more relevant approach to evaluation for practical application, is to normalise the electrochemical performance to the full mass and volume of the cell, as an estimate of the anticipated energy/power density of future devices. The present device is still a lab test cell, but its performance was normalised by the total mass and volume of device. A more developed device would still require current collectors and encapsulation, but these components represent a relatively small additional contribution; in any case, given the high conductivity of the buckypapers, it might be possible to avoid current collectors in certain device geometries. By this measure, the performance of the BC separator device is very encouraging, as summarised by the volumetric (Fig. 4d) and gravimetric (Fig. S5c, ESI†) Ragone plots, reaching an energy density of 1.2 mWh cm−3 (1.4 Wh kg−1) at a power density of 174 mW cm−3 (194 W kg−1). The energy density only drops by 25% at 100 A g−1 maintaining 0.9 mWh cm−3 (1 Wh kg−1) at a power density of 16.4 W cm−3 (18.2 kW kg−1). Note that the power density, here, is derived from the energy density over the discharge time (E/t), which is a more practical measure than the (much larger) theoretical peak power that can be estimated from V2/(4 × ESR); these two measures should be carefully distinguished, although not all literature does so. To illustrate this difference, the peak power here, calculated from V2/(4 × ESR), reaches as high as 303 kW kg−1 when normalized by mass of active materials and 107 kW kg−1 normalized by total mass of the device. Using the more modest, but representative E/t measure, the Ragone plots (Fig. 4d) nevertheless again highlight the advantage of the BC separator over the conventional cellulose, in good agreement with the decreased Rct and IR drop (Fig. 4a and b). The high overall rate capability of the device is attributed to the good ion transport in both the nanotubide buckypaper and the BC separator.
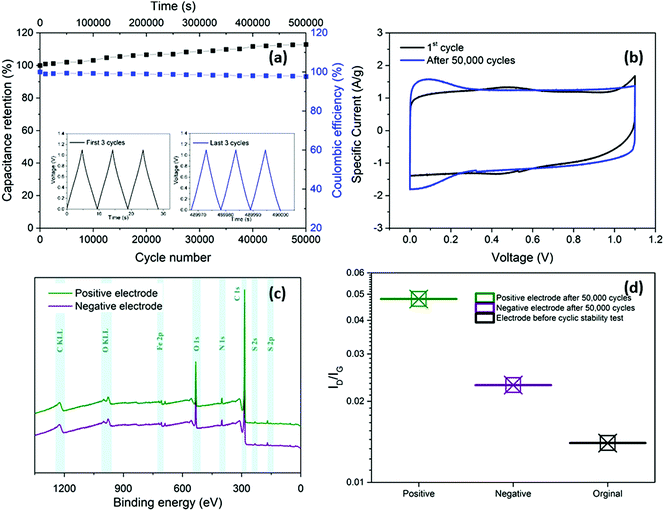
In addition to enhancing transport, the thin separator minimises the parasitic mass and volume associated with the separator and the electrolyte that fills it. To evaluate long-term electrochemical stability of the device based on nanotubide buckypaper, a cyclability GCD test was performed over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles at 5 A g−1 (Fig. 5a). The Coulombic efficiency in the first cycle approached 100% and remained above 98% after 50
000 cycles at 5 A g−1 (Fig. 5a). The Coulombic efficiency in the first cycle approached 100% and remained above 98% after 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, demonstrating a high electrochemical reversibility and structural stability of electrode materials.60,61 Surprisingly, the absolute capacitance continued to increase, reaching 112% of the initial value after 50
000 cycles, demonstrating a high electrochemical reversibility and structural stability of electrode materials.60,61 Surprisingly, the absolute capacitance continued to increase, reaching 112% of the initial value after 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (Fig. 5a). One possible explanation is that electrolyte (electro)wetting of increasingly debundled SWCNTs improves ionic access into the electrode pores.62 However, in the current system, a stronger effect seems to derive from a pseudocapacitive redox contribution.
000 cycles (Fig. 5a). One possible explanation is that electrolyte (electro)wetting of increasingly debundled SWCNTs improves ionic access into the electrode pores.62 However, in the current system, a stronger effect seems to derive from a pseudocapacitive redox contribution.
Comparison of CV curves before and after cyclic stability testing shows a decrease of the small redox peaks around 0.4 V due to deoxygenation (Fig. 5b).46,63 more importantly, redox peaks close to 0 V were observed in the CV curve after 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GCD cycles. To explore the origins of these peaks, the washed and dried positive and negative electrodes were studied with XPS and Raman spectroscopy after the cyclic stability test. The XPS surveys (Fig. 5c) show presence of two peaks at 164 and 229 eV attributed to sulphur (S 2p and S 2s, respectively), detected on both positive and negative electrodes due to possible adsorption of HSO4− and SO42− from the electrolyte.46,64 The ID/IG of both positive (0.048) and negative (0.023) electrodes increased slightly after cycling compared to the initial value before electrochemical test (0.014), which may be related to sulphate functional groups grafting on the electrode surface (Fig. 5d). In addition, to the increased effective area, due to sulphate intercalation, grafted sulphate functional groups may increase the capacitance by contributing pseudocapacitive behaviour.65,66
000 GCD cycles. To explore the origins of these peaks, the washed and dried positive and negative electrodes were studied with XPS and Raman spectroscopy after the cyclic stability test. The XPS surveys (Fig. 5c) show presence of two peaks at 164 and 229 eV attributed to sulphur (S 2p and S 2s, respectively), detected on both positive and negative electrodes due to possible adsorption of HSO4− and SO42− from the electrolyte.46,64 The ID/IG of both positive (0.048) and negative (0.023) electrodes increased slightly after cycling compared to the initial value before electrochemical test (0.014), which may be related to sulphate functional groups grafting on the electrode surface (Fig. 5d). In addition, to the increased effective area, due to sulphate intercalation, grafted sulphate functional groups may increase the capacitance by contributing pseudocapacitive behaviour.65,66
Symmetric supercapacitors (ionic liquid electrolyte)
Given the excellent performance in aqueous electrolyte, the symmetric device based on nanotubide buckypaper and BC nanopaper separator was tested further, in [EMIM][TFSI] ionic liquid electrolyte. The use of ionic liquid was expected to improve the wetting of the SWCNT electrodes, while enhancing electrochemical window of the supercapacitor device.67,68 The Nyquist plot (Fig. 6a) gives ESR and Rct of 3.9 and 3.6 Ω, respectively, confirming good conductivity and ion transport in the nanotubide buckypaper, although with some decrease in performance relative to the aqueous system, as expected due to lower mobility in the ionic liquid.69,70 The CV curves for the as-fabricated device have a stable butterfly shape (Fig. S6, ESI†) and the GCD curves show a complex response (Fig. 6b). Similar behaviour has been previously reported for SWCNTs-based materials, attributed to quantum capacitance contributions: the capacitance follows the density of states (DOS) near the Fermi level which manifests in dependence of capacitance on voltage.71–73 The effect is more obvious in the broader voltage range available in ionic liquid. The calculated electrochemical performance from GCDs, normalised by the total volume and total mass of full device reaches 2.2 mWh cm−3 (2.6 Wh kg−1) of maximum energy density and 8.3 W cm−3 (10.2 kW kg−1) of maximum power density. As-fabricated, the symmetric ionic liquid device has twice the volumetric energy density of the aqueous device, due to the enhanced electrochemical window (Fig. 4d and 6c). Additionally, the electrochemical performance normalised by the mass and volume of the active material remains high, with energy density of 8.8 Wh kg−1 (2.3 mWh cm−3) and specific power of 34 kW kg−1 (9.1 W cm−3). The cyclic stability of symmetric ionic liquid device was good, retaining 81% capacitance after 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (Fig. 6d). However, the stability is lower than the aqueous system due to greater voltage range, combined with the tendency for electrolyte decomposition or other side reactions after long term cycling.74,75 The increase after the first 3000 cycles may again relate to electrochemically driven swelling76 or grafting of redox active species.30,65,66
000 cycles (Fig. 6d). However, the stability is lower than the aqueous system due to greater voltage range, combined with the tendency for electrolyte decomposition or other side reactions after long term cycling.74,75 The increase after the first 3000 cycles may again relate to electrochemically driven swelling76 or grafting of redox active species.30,65,66
Conclusions
In summary, SWCNT buckypapers were successfully synthesised via reductive charging with sodium naphthalide. This method improves the individualisation of SWCNTs without damaging their structure, while contributing additional purification. The carbon and sodium concentrations in the precursor mixture play major role on the dissolution process and hence the resulting buckypaper structure and electrochemical performance. The optimised concentrations of carbon and sodium were 0.125 M and 12.5 mM, respectively, similar to optimums identified for chemical modification. These intermediate values likely reflect the balance of Coulombic repulsion and charge condensation effects, known in more conventional polyelectrolytes.12 The optimised nanotubide buckypaper provided a specific surface area of 412 m2 g−1, good electrical conductivity of 433 S cm−1 and significantly better electrochemical performance, compared to previous studies of carbon-based buckypaper electrodes. In combination with its intrinsic scalability, avoiding ultrasonication or ultracentrifugations, reductive processing is a promising candidate for energy storage applications. The development of BC nanopaper provides a new, simple and thinner separator which decreases resistive loses and maximises volumetric performance in a configured full cell device. The BC separator also readily prevents short circuits between the two electrodes and provides a high device efficiency with long cycle life. BC is widely available as a starting material (the raw material is typically consumed as a foodstuff). BC papers are, therefore, promising electrochemical separators for use in practical applications, in a wide range of devices.The symmetric nanotubide buckypaper supercapacitors in both aqueous and ionic liquid electrolytes achieve high gravimetric and volumetric performances compared to other symmetric devices based on CNT buckpapers, in the literature (Table S4, ESI†). Therefore, the reductive charging strategy is a promising approach for high-performance energy storage devices with simple paper electrodes. Further optimisation of electrode thickness, electrolyte, and cell balance will improve performance further. In addition, the wide range of nanotubide chemistry will provide a convenient route to produce hybrid redox-active SWCNT electrodes in the future, for supercabatteries,77 with enhanced energy density.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author would like to thank Dr Koon-Yang Lee for the supply of BC nanopaper. PS appreciates the financial support from The Ministry of Higher Education, Science, Research and Innovation, Royal Thai Government. NR would like to thank the EU Graphene Flagship under Horizon 2020 Research and Innovation programme grant agreement no. 881603. ES would like to acknowledge the funding provided by the EPSRC Beyond Structural project (EP/P007465/1), the European Office of Aerospace Research and Development (IOE Grant FA9550-17-1-0251) and EU Clean Sky 2 (SORCERER Project #738085).References
- L. L. Zhang and X. S. Zhao, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- L. Miao, Z. Song, D. Zhu, L. Li, L. Gan and M. Liu, Mater. Adv., 2020, 1, 945–966 RSC.
- J. Yan, L. Miao, H. Duan, D. Zhu, Y. Lv, W. Xiong, L. Li, L. Gan and M. Liu, Electrochim. Acta, 2020, 358, 136899 CrossRef CAS.
- B. Arash, Q. Wang and V. K. Varadan, Sci. Rep., 2014, 4, 6479 CrossRef CAS.
- J. N. Coleman, U. Khan, W. J. Blau and Y. K. Gun’ko, Carbon, 2006, 44, 1624–1652 CrossRef CAS.
- O. Kimizuka, O. Tanaike, J. Yamashita, T. Hiraoka, D. N. Futaba, K. Hata, K. Machida, S. Suematsu, K. Tamamitsu, S. Saeki, Y. Yamada and H. Hatori, Carbon, 2008, 46, 1999–2001 CrossRef CAS.
- J. Barisci, G. Wallace and R. Baughman, Faculty of Engineering – Papers, 2000, 147, 4580–4583 CAS.
- Z. Niu, W. Zhou, J. Chen, G. Feng, H. Li, W. Ma, J. Li, H. Dong, Y. Ren, D. Zhao and S. Xie, Energy Environ. Sci., 2011, 4, 1440–1446 RSC.
- S. Perathoner and G. Centi, in Emerging Materials for Energy Conversion and Storage, ed. K. Y. Cheong, G. Impellizzeri and M. A. Fraga, Elsevier, 2018, pp. 305–325 Search PubMed.
- H. Pan, J. Li and Y. Feng, Nanoscale Res. Lett., 2010, 5, 654–668 CrossRef CAS.
- H. Yoon, M. Yamashita, S. Ata, D. N. Futaba, T. Yamada and K. Hata, Sci. Rep., 2014, 4, 3907 CrossRef.
- A. J. Clancy, M. K. Bayazit, S. A. Hodge, N. T. Skipper, C. A. Howard and M. S. P. Shaffer, Chem. Rev., 2018, 118, 7363–7408 CrossRef CAS.
- A. J. Clancy, J. Melbourne and M. S. P. Shaffer, J. Mater. Chem. A, 2015, 3, 16708–16715 RSC.
- M. De Marco, F. Markoulidis, R. Menzel, S. M. Bawaked, M. Mokhtar, S. A. Al-Thabaiti, S. N. Basahel and M. S. P. Shaffer, J. Mater. Chem. A, 2016, 4, 5385–5389 RSC.
- S. Najib and E. Erdem, Nanoscale Adv., 2019, 1, 2817–2827 RSC.
- J. Zhao, Y. Li, G. Wang, T. Wei, Z. Liu, K. Cheng, K. Ye, K. Zhu, D. Cao and Z. Fan, J. Mater. Chem. A, 2017, 5, 23085–23093 RSC.
- Q. Wang, J. Yan and Z. Fan, Energy Environ. Sci., 2016, 9, 729–762 RSC.
- K. L. Van Aken, C. R. Pérez, Y. Oh, M. Beidaghi, Y. Joo Jeong, M. F. Islam and Y. Gogotsi, Nano Energy, 2015, 15, 662–669 CrossRef CAS.
- E. Wilson and M. F. Islam, ACS Appl. Mater. Interfaces, 2015, 7, 5612–5618 CrossRef CAS.
- S.-Y. Lin and X. Zhang, J. Power Sources, 2015, 294, 354–359 CrossRef CAS.
- J. Che, P. Chen and M. B. Chan-Park, J. Mater. Chem. A, 2013, 1, 4057–4066 RSC.
- N. Delaporte, D. B. Ossonon, K. Zaghib and D. Bélanger, Batteries Supercaps, 2020, 3, 638–646 CrossRef CAS.
- B. J. Landi, M. J. Ganter, C. D. Cress, R. A. DiLeo and R. P. Raffaelle, Energy Environ. Sci., 2009, 2, 638–654 RSC.
- T. T. Kerli Liivand, A. Jänes and E. Lust, Electrochem. Soc. Trans., 2015, 64, 41–49 Search PubMed.
- K. Tnurist, T. Thomberg and A. Jänes, Separator Materials Influence on Supercapacitors Performance in Viscous Electrolytes, 2014 Search PubMed.
- K. Jost, D. Stenger, C. R. Perez, J. K. McDonough, K. Lian, Y. Gogotsi and G. Dion, Energy Environ. Sci., 2013, 6, 2698–2705 RSC.
- H. Lee, M. Yanilmaz, O. Toprakci, K. Fu and X. Zhang, Energy Environ. Sci., 2014, 7, 3857–3886 RSC.
- M. Hervy, F. Bock and K.-Y. Lee, Compos. Sci. Technol., 2018, 167, 126–133 CrossRef CAS.
- A. Eftekhari, Energy Storage Mater., 2017, 9, 47–69 CrossRef.
- R. Thangavel, A. G. Kannan, R. Ponraj, V. Thangavel, D.-W. Kim and Y.-S. Lee, J. Power Sources, 2018, 383, 102–109 CrossRef CAS.
- A. J. Clancy, E. R. White, H. H. Tay, H. C. Yau and M. S. P. Shaffer, Carbon, 2016, 108, 423–432 CrossRef CAS.
- M. B. Jakubinek, B. Ashrafi, J. Guan, M. B. Johnson, M. A. White and B. Simard, RSC Adv., 2014, 4, 57564–57573 RSC.
- S. Sakurai, F. Kamada, D. N. Futaba, M. Yumura and K. Hata, Nanoscale Res. Lett., 2013, 8, 546 CrossRef.
- N. Matsumoto, G. Chen, M. Yumura, D. N. Futaba and K. Hata, Nanoscale, 2015, 7, 5126–5133 RSC.
- M. Hervy, A. Santmarti, P. Lahtinen, T. Tammelin and K.-Y. Lee, Mater. Des., 2017, 121, 421–429 CrossRef CAS.
- D.-W. Wang, F. Li, M. Liu, G. Q. Lu and H.-M. Cheng, J. Phys. Chem. C, 2008, 112, 9950–9955 CrossRef CAS.
- F. Xu, R. Cai, Q. Zeng, C. Zou, D. Wu, F. Li, X. Lu, Y. Liang and R. Fu, J. Mater. Chem., 2011, 21, 1970–1976 RSC.
- H.-Q. Li, J.-Y. Luo, X.-F. Zhou, C.-Z. Yu and Y.-Y. Xia, J. Electrochem. Soc., 2007, 154, A731 CrossRef CAS.
- C. Young, J. Lin, J. Wang, B. Ding, X. Zhang, S. M. Alshehri, T. Ahamad, R. R. Salunkhe, S. A. Hossain, J. H. Khan, Y. Ide, J. Kim, J. Henzie, K. C.-W. Wu, N. Kobayashi and Y. Yamauchi, Chem. – Eur. J., 2018, 24, 6127–6132 CrossRef CAS.
- S. Vaquero, R. Díaz, M. Anderson, J. Palma and R. Marcilla, Electrochim. Acta, 2012, 86, 241–247 CrossRef CAS.
- S. Kondrat, C. R. Pérez, V. Presser, Y. Gogotsi and A. A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474–6479 RSC.
- Y. Korenblit, M. Rose, E. Kockrick, L. Borchardt, A. Kvit, S. Kaskel and G. Yushin, ACS Nano, 2010, 4, 1337–1344 CrossRef CAS.
- Z. Song, H. Duan, L. Miao, L. Ruhlmann, Y. Lv, W. Xiong, D. Zhu, L. Li, L. Gan and M. Liu, Carbon, 2020, 168, 499–507 CrossRef CAS.
- P. E. Lyons, S. De, F. Blighe, V. Nicolosi, L. F. C. Pereira, M. S. Ferreira and J. N. Coleman, J. Appl. Phys., 2008, 104, 044302 CrossRef.
- G. Moreno-Fernández, J. L. Gómez-Urbano, M. Enterría, T. Rojo and D. Carriazo, J. Mater. Chem. A, 2019, 7, 14646–14655 RSC.
- S. H. Aboutalebi, A. T. Chidembo, M. Salari, K. Konstantinov, D. Wexler, H. K. Liu and S. X. Dou, Energy Environ. Sci., 2011, 4, 1855–1865 RSC.
- A. Daraghmeh, S. Hussain, I. Saadeddin, L. Servera, E. Xuriguera, A. Cornet and A. Cirera, Nanoscale Res. Lett., 2017, 12, 639 CrossRef.
- C. Y. Lee, H. M. Tsai, H. J. Chuang, S. Y. Li, P. Lin and T. Y. Tseng, J. Electrochem. Soc., 2005, 152, A716–A720 CrossRef CAS.
- M. E. Itkis, D. E. Perea, R. Jung, S. Niyogi and R. C. Haddon, J. Am. Chem. Soc., 2005, 127, 3439–3448 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods, 2001, 2, 580–632 Search PubMed.
- D. P. Dubal, S. H. Lee, J. G. Kim, W. B. Kim and C. D. Lokhande, J. Mater. Chem., 2012, 22, 3044–3052 RSC.
- Y. S. Lim, C. W. Lai and S. B. Abd Hamid, RSC Adv., 2017, 7, 23030–23040 RSC.
- J. Phiri, J. Dou, T. Vuorinen, P. A. C. Gane and T. C. Maloney, ACS Omega, 2019, 4, 18108–18117 CrossRef CAS.
- M. Kebede, Electrochemical Devices for Energy Storage Applications, 2020 Search PubMed.
- M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294–1301 RSC.
- T. Chen and L. Dai, J. Mater. Chem. A, 2014, 2, 10756–10775 RSC.
- M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294–1301 RSC.
- A. Borenstein, R. Attias, O. Hanna, S. Luski, R. B. Kaner and D. Aurbach, ChemElectroChem, 2017, 4, 2660–2668 CrossRef CAS.
- B. Andres, A.-C. Engström, N. Blomquist, S. Forsberg, C. Dahlström and H. Olin, PLoS One, 2016, 11, e0163146 CrossRef.
- Z. Lei, J. Zhang and X. S. Zhao, J. Mater. Chem., 2012, 22, 153–160 RSC.
- T.-W. Chang, L.-Y. Lin, P.-W. Peng, Y. X. Zhang and Y.-Y. Huang, Electrochim. Acta, 2018, 259, 348–354 CrossRef CAS.
- J. Zhou, J. Lian, L. Hou, J. Zhang, H. Gou, M. Xia, Y. Zhao, T. A. Strobel, L. Tao and F. Gao, Nat. Commun., 2015, 6, 8503 CrossRef CAS.
- X. Zhang, D. Zhang, Y. Chen, X. Sun and Y. Ma, Chin. Sci. Bull., 2012, 57, 3045–3050 CrossRef CAS.
- Y. Shao, J. Wang, M. Engelhard, C. Wang and Y. Lin, J. Mater. Chem., 2010, 20, 743–748 RSC.
- R. Singhal and V. Kalra, J. Mater. Chem. A, 2015, 3, 377–385 RSC.
- W. Gu, M. Sevilla, A. Magasinski, A. B. Fuertes and G. Yushin, Energy Environ. Sci., 2013, 6, 2465–2476 RSC.
- L. Yu and G. Z. Chen, Front. Chem., 2019, 7, 272 CrossRef CAS.
- J. M. Klein, E. Panichi and B. Gurkan, Phys. Chem. Chem. Phys., 2019, 21, 3712–3720 RSC.
- Q. Shao, J. Tang, Y. Lin, J. Li, F. Qin, J. Yuan and L.-C. Qin, J. Power Sources, 2015, 278, 751–759 CrossRef CAS.
- K. O. Oyedotun, T. M. Masikhwa, S. Lindberg, A. Matic, P. Johansson and N. Manyala, Chem. Eng. J., 2019, 375, 121906 CrossRef CAS.
- M. J. Biercuk, S. Ilani, C. M. Marcus and P. L. McEuen, Springer, 2008, 11, 455–493 Search PubMed.
- I. Heller, J. Kong, K. Williams, C. Dekker and S. Lemay, J. Am. Chem. Soc., 2006, 128, 7353–7359 CrossRef CAS.
- E. Senokos, V. Reguero, J. Palma, J. J. Vilatela and R. Marcilla, Nanoscale, 2016, 8, 3620–3628 RSC.
- B. Pal, S. Yang, S. Ramesh, V. Thangadurai and R. Jose, Nanoscale Adv., 2019, 1, 3807–3835 RSC.
- M. P. S. Mousavi, B. E. Wilson, S. Kashefolgheta, E. L. Anderson, S. He, P. Bühlmann and A. Stein, ACS Appl. Mater. Interfaces, 2016, 8, 3396–3406 CrossRef CAS.
- S. A. Hodge, M. K. Bayazit, H. H. Tay and M. S. Shaffer, Nat. Commun., 2013, 4, 1989 CrossRef.
- G. Z. Chen, Int. Mater. Rev., 2017, 62, 173–202 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00898b |
| This journal is © The Royal Society of Chemistry 2021 |