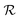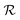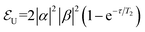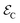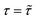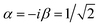Open Access Article
Open Access ArticleA heterometallic [LnLn′Ln] lanthanide complex as a qubit with embedded quantum error correction†
Emilio
Macaluso
ab,
Marcos
Rubín
 cd,
David
Aguilà
cd,
David
Aguilà
 ef,
Alessandro
Chiesa
ef,
Alessandro
Chiesa
 ab,
Leoní A.
Barrios
ab,
Leoní A.
Barrios
 ef,
Jesús I.
Martínez
cd,
Pablo J.
Alonso
ef,
Jesús I.
Martínez
cd,
Pablo J.
Alonso
 cd,
Olivier
Roubeau
cd,
Olivier
Roubeau
 cd,
Fernando
Luis
cd,
Fernando
Luis
 *cd,
Guillem
Aromí
*cd,
Guillem
Aromí
 *ef and
Stefano
Carretta
*ef and
Stefano
Carretta
 *ab
*ab
aDipartimento di Scienze Matematiche, Fisiche e Informatiche, Università di Parma, I-43124 Parma, Italy. E-mail: stefano.carretta@unipr.it
bUdR Parma, INSTM, I-43124 Parma, Italy
cInstituto de Ciencia de Materiales de Aragón (ICMA), CSIC, Universidad de Zaragoza, Zaragoza, Spain. E-mail: fluis@unizar.es
dDepartamento de Física de la Materia Condensada, Universidad de Zaragoza, Zaragoza, Spain
eDepartament de Química Inorgànica, Universitat de Barcelona, Barcelona, Spain. E-mail: guillem.aromi@qi.ub.es
fInstitute of Nanoscience and Nanotechnology of the University of Barcelona (IN2UB), Barcelona, Spain
First published on 20th August 2020
Abstract
We show that a [Er–Ce–Er] molecular trinuclear coordination compound is a promising platform to implement the three-qubit quantum error correction code protecting against pure dephasing, the most important error in magnetic molecules. We characterize it by preparing the [Lu–Ce–Lu] and [Er–La–Er] analogues, which contain only one of the two types of qubit, and by combining magnetometry, low-temperature specific heat and electron paramagnetic resonance measurements on both the elementary constituents and the trimer. Using the resulting parameters, we demonstrate by numerical simulations that the proposed molecular device can efficiently suppress pure dephasing of the spin qubits.
1 Introduction
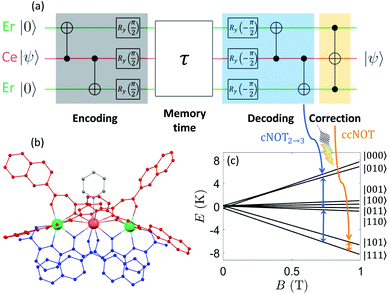
Quantum error correction (QEC) is mandatory for the realization of scalable quantum computing architectures1 going beyond the capabilities of current intermediate scale noisy devices.2–6 Indeed, superposition states are inherently fragile and error-prone, due to unavoidable interactions of the quantum computer with environmental noise. QEC algorithms are based on encoding a single logical qubit into several physical objects, thus often making the implementation and control of such a platform very demanding. In this regard, Molecular Nanomagnets (MNMs) are a particularly attractive class of materials.7–10 Each molecule can host several distinguishable qubits, with chemically tailored magnetic interactions,11–16 and can show remarkably long coherence times.17–27 In addition, they can be characterized and manipulated by radio-frequency26,28,29 and electron paramagnetic resonance (EPR) pulses addressing different transitions,30 as already probed even on individual atoms on surfaces.31 Here, we propose to exploit these peculiarities in order to embed a protected logical unit into the three weakly coupled effective spins 1/2 located within the same molecule.The QEC code we aim to implement is schematically shown in Fig. 1(a) and described in Sec. 2.4.1 below. It corresponds to the three qubit repetition code (TQC) that corrects phase flips,32,33 the most likely source of decoherence in magnetic molecules. Its specific requirements set challenging conditions to chemically design and synthesize a suitable molecular platform. These ingredients include three individually addressable, yet mutually interacting, qubits, the ability to get factorized states, e.g. by applying a sufficiently strong magnetic field, and the existence of suitable coherent transitions linking different states. Lanthanide Ln(III) ions with half-integer spins are particularly well-suited to this end. They often have a well isolated magnetic ground state doublet and therefore behave as effective S − 1/2 systems with large and distinct g values. These provide individually addressable transitions and fast processability, thus making it possible to implement the TQC in times much shorter than the phase memory time T2. In addition, their mutual interactions are weak, mainly dominated by dipolar magnetic couplings. Conversely, total-spin states34 in clusters of strongly interacting ions could yield correlated errors, which are not corrected by these codes.35
Here we show that the heterometallic lanthanide coordination complex [CeEr2(LA)2(LB)2(py)(H2O)2](NO3) (1)36, hereafter referred to as [ErCeEr], meets these stringent conditions and hence can be exploited to encode a logical qubit for the TQC. To fully characterize the system, we prepare two iso-structural compounds in which either Er or Ce are replaced by a diamagnetic analogue. We then combine magnetization, low-temperature specific-heat and continuous-wave electron paramagnetic resonance measurements (CW-EPR) on the different molecules to derive the corresponding Hamiltonian, whose parameters are found to be well within the acceptable range to ensure the feasibility of the QEC algorithm. We finally demonstrate by numerically solving the Lindblad equation (including the full sequence of microwave pulses) that the code can be efficiently implemented on the present system and significantly suppress pure dephasing.
2 Results and discussion
2.1. Synthesis
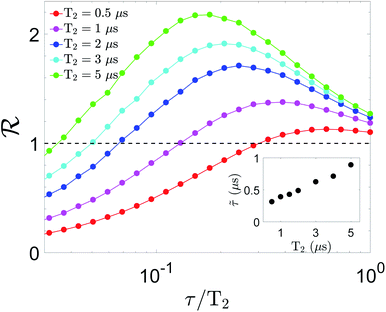
The structure of [CeEr2(LA)2(LB)2(py)(H2O)2] (NO3) is shown in Fig. 1(b). Here H2LA and H2LB are bis-β-diketonate ligands (Fig. S1†). The preparation of this heterometallic molecule, which exhibits a selective distribution of two types of Ln(III) ions, makes use of the remarkable ability of the molecular scaffold provided by donors LA2− and LB2− to generate two different coordination sites that discriminate the metals solely based on their different ionic radii. This allows to locate a Ce(III) ion (rCe = 1.220 Å) at the central site and two Er(III) metals (rEr = 1.040 Å) at the sides. Both ions show strongly different g factors and the ensemble benefits from a minimal influence of nuclear spins as sources of decoherence (Ce has no magnetic nuclear isotopes, while Er features only a small abundance of these). In this cluster, the two Er(III) ions are made inequivalent by the different orientations of their coordination environments within the molecule. This versatile synthetic resource has also enabled the preparation of the new isostructural analogues [LuCeLu] (2, Fig. S2†) and [ErLaEr] (3, Fig. S3†) (rLu = 0.995 Å and rLa = 1.250 Å). These molecules provide model systems to study each type of qubit in the absence of the other (since La(III) and Lu(III), replacing Ce(III) and Er(III), respectively, are both diamagnetic). These two compounds crystallize from a reaction system containing stoichiometric amounts of the Ln(NO3)3 salts involved, together with the corresponding amounts of H2LA and H2LB. The structures of 2 and 3 have been determined (full details in the ESI, Fig. S2 and S3, Tables S1 to S3).†2.2. Requirements for implementation of the scheme
The spin Hamiltonian describing the 8 lowest energy levels of the [ErCeEr] trimer, the only ones being populated at low temperatures and relevant to the QEC, is given by: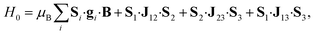 | (1) |
The actual implementation of the QEC code on a molecular hardware requires to meet essentially two criteria. On the one hand, (i) sizeable dipolar (and/or exchange) interactions between the magnetic ions (and in particular its component Jz parallel to the external field), in order to make all transitions well resolved (and hence individually addressable) by pulsed EPR. On the other hand, (ii) a computational basis consisting of direct product states, because most QEC codes are designed to correct independent errors on any of the three qubits. As a consequence, they cannot handle correlated errors which could arise in a basis of entangled states. Condition (i) is accomplished by ensuring that Jz is significantly larger than the finite band-width of the Gaussian pulses used to implement the TQC. Requirement (ii) sets an upper limit to the transverse component of the exchange interaction J⊥, which needs to be much smaller than the difference between the excitation energies of the qubits, which is approximately given by |gzi − gzj|μBB. In particular, thanks to the large |gzi − gzj| probed by EPR (see below), we find that acceptable values for the Er–Ce coupling (enabling the implementation of the code with an error smaller than 3% at short memory times) are |Jz| ≳ 0.1 cm−1 and |J⊥| ≲ 0.3 cm−1.‡ The Er–Er Jz coupling is not strictly required for the implementation of the scheme, but can improve spectral resolution of some transitions if J12 and J23 couplings are not clearly distinguishable. These estimates are done using a magnetic field ≲ 1 T, but can be further relaxed by (i) using longer, thus more selective, microwave pulses (allowing smaller Jz) and/or (ii) tuning the orientation and magnitude of the applied field (thus enabling larger J⊥). Note that the key point is the hierarchy of the interactions in the magnetic Hamiltonian and not their precise value.
Our measurements (reported in the subsection below) show that both requirements (i) and (ii) are fulfilled by 1, even in relatively small magnetic fields, and that a slight uncertainty in the determination of the Hamiltonian parameters does not influence our conclusions about the feasibility of the scheme.
2.3. Characterization
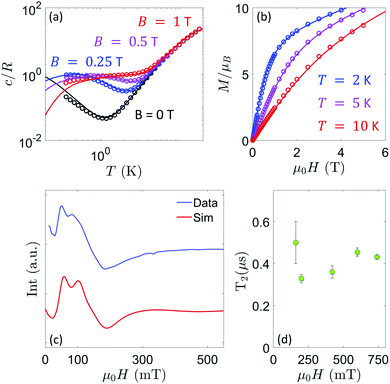
Molecular complexes 1, 2 and 3 have been characterized by thorough magnetization, specific heat and EPR measurements. These experiments allow us to determine all parameters in eqn (1), the effective spin Hamiltonian of 1 that provides the basis to simulate the implementation of the TQC in this system (cf.Fig. 1(c)).The g tensors of the individual Ce(III) and Er(III) ions in 1, which embody the three qubits, have been determined on the isostructural 2 and 3 molecules (Fig. 2) that contain either one or the other. Experimental data for 2 [Fig. 2(a–c)] are satisfactorily reproduced using an isotropic gCe = 1.85. The slight discrepancy in the high-field dependence of the low-temperature magnetization can be fixed by assuming an axially anisotropic gCe = (1.7, 1.7, 2.2), as shown in Fig. S8,† which also improves the agreement of experimental and simulated EPR spectra. However, since this anisotropy produces only a minor improvement of the fit and does not affect our conclusions on the feasibility of the scheme, we prefer to reduce the number of parameters and use an isotropic gCe in the following simulations of the QEC code. Conversely, a good agreement with the experimental data measured on complex 3 is obtained using gEr = (1, 5, 11.5), as shown in Fig. 2(d–f).
 | ||
| Fig. 2 Experimental data for powder samples of 2 (a–c) and 3 (d–f) and corresponding best fit simulations, which characterize the constituent Ce and Er spin qubits, respectively. (a and d) Field dependence of the magnetization measured at different temperatures. (b and e) Temperature dependence of the specific heat at different applied fields. (c and f) CW-EPR spectra at T = 4.5 K. Simulations include inter-molecular dipole–dipole interactions between pairs of nearest-neighboring molecules, as described in the ESI.† | ||
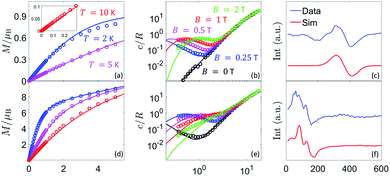
As a second step, the same set of measurements were performed on the full [ErCeEr] molecular trimer 1 in order to assess the Er–Ce interaction. EPR spectra shown in Fig. 3(c) are collected on a frozen solution of 1, in order to reduce the effect of inter-molecular dipole–dipole interactions, leading to broadening of the lines and to a reduction of the corresponding T2. A comparison with the solid state spectrum reported in Fig. S12† shows that the complex is stable in solution and its magnetic properties are not significantly altered. Indeed, we only note a narrowing of the EPR lines due to a reduction of inter-molecular dipole–dipole interactions. The residual width of the lines can be ascribed to several reasons: relatively high concentrations in solution (to keep a sizable signal); the presence of magnetic N nuclei surrounding the magnetic ions and of 167Er isotope (nuclear spin I = 7/2) with 23% natural abundance, hyperfine coupled to Er electronic spin. This latter effect can be reduced by preparing an isotopically purified analogue, as done e.g. in ref. 37 for a Dy compound.
 | ||
| Fig. 3 Experimental data for 1 and corresponding best fit with spin Hamiltonian (1). (a and b) Temperature dependence of the specific heat at different applied fields (a) and field dependence of the magnetization at different temperatures (b). Measurements (dots) have been performed on a concentrated sample, compared with the corresponding simulation (lines) including nearest-neighbour inter-molecular interactions, as described in the ESI.† (c) CW-EPR data on a diluted sample (blue) and simulation (red), showing a good agreement. (d) Phase memory time T2 at different fields, extracted from pulsed EPR measurements on frozen solutions of 1. | ||
A direct comparison between heat capacity data measured, at zero field, on 1 and on 2 and 3 points to an extra contribution in the former, which shows up at low temperatures (below 1 K). This contribution suggests the existence of a non-zero magnetic coupling between the central Ce(III) spin and the two Er(III) spins, which gives rise to an additional energy splitting between the spin levels. This interpretation is confirmed by numerical simulations of the heat capacity, magnetization and EPR spectra, performed on basis of eqn (1). We find that the dipolar couplings calculated from the previously determined gCe and gEr, 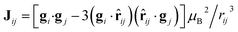 , account well for all data collected on 1, as Fig. 3 shows. These dipole–dipole interaction tensors are calculated in the point-dipole approximation. The principal components of J12 and J23 are (0.01, 0.07, −0.29) cm−1, while for J13 are given by (0.00, 0.02, −0.22) cm−1. Due to the molecular structure of 1 and 3, gEr and gEr2 are not independent but are related via a rotation (see Fig. 1(b) and ESI†). Note that, using the previously determined g tensors, Hamiltonian (1) has no free parameters.
, account well for all data collected on 1, as Fig. 3 shows. These dipole–dipole interaction tensors are calculated in the point-dipole approximation. The principal components of J12 and J23 are (0.01, 0.07, −0.29) cm−1, while for J13 are given by (0.00, 0.02, −0.22) cm−1. Due to the molecular structure of 1 and 3, gEr and gEr2 are not independent but are related via a rotation (see Fig. 1(b) and ESI†). Note that, using the previously determined g tensors, Hamiltonian (1) has no free parameters.
Altogether, the experiments show that the molecular complex 1 perfectly fits the requirements (i) and (ii) for the implementation of the TQC that were defined in Section 2.2. In particular, low-field specific heat results show the existence of sizeable spin–spin interactions, while EPR spectra clearly indicate a large and highly anisotropic g tensor for Er, significantly different from that of Ce. We note, in turn, that the significant gyEr value ensures fast manipulation of the Er ion spin. A further refinement of these values (e.g. with the addition of possible small isotropic exchange contributions) would not alter our conclusions, because their uncertainty is well within the acceptable ranges. We have checked (see Fig. S10 and S11 in the ESI†) that low-field specific heat and EPR measurements fix an upper bound of ∼0.1 cm−1 to the modulus of a possible Er–Ce isotropic exchange, thus leaving Jij well within the acceptable range for the feasibility of the scheme. We stress that this feasibility is determined only by the hierarchy of the interactions in eqn (1) and not by the precise value of these parameters. This, in turn, potentially widens the class of molecular systems that can be of interest for applying our scheme.
The Zeeman energy level scheme derived from eqn (1) is shown in Fig. 1(c) (with a zoom at low field in Fig. S16†). It allows establishing a correspondence between the logical operations of the TQC (cf.Fig. 1(a)) and transition between spin states of 1 induced by resonant microwave pulses. The actual implementation of this code is described in what follows.
2.4. Quantum error correction
The code is schematically shown in the quantum circuit of Fig. 1(a), where each line represents a qubit and time increases from left to right. It is divided in encoding, decoding and correction steps, corresponding to the gray, light blue and yellow areas, respectively. The qubit which carries the logical information (in the form of an initial arbitrary wave function α|0〉 + β|1〉) is indicated by |ψ〉 and corresponds to the central line in the quantum circuit, while the other two qubits need to be initialized into their ground state |0〉. The encoding step consists of two controlled-NOT (cNOT) two-qubit gates inducing a flip of the target qubit (⊕ symbol in Fig. 1(a)) if the control (central qubit, • symbol) is in |1〉. This brings the initial factorized state α|000〉 + β|010〉 to the entangled state α|000〉 + β|111〉, which is protected from a bit flip error. Such protection (and hence our capability of detecting errors) arises indeed from this entanglement.32 The following Ry(π/2) rotations transform σx into σz, i.e. Ry(π/2)σxRy(−π/2) = σz. Hence, they also change bit flip errors (associated to σx) into phase flips (associated to σz), thus making the encoded state robust against pure dephasing.
Encoding is followed by a memory time τ, during which the logical qubit remains stored. This step corresponds to a free evolution of the three qubits subject only to pure dephasing (see below). After the memory time, the TQC includes a decoding part, during which the same gates of the encoding are implemented in reverse order (blue shaded area in Fig. 1(a)). Finally, correction consists of a single controlled-controlled-NOT (ccNOT) gate applied to qubit |ψ〉, i.e. |ψ〉 is flipped conditioned from both the others being in |1〉.
The dipolar couplings in eqn (1) make the excitation energy of the Ce dependent on the state of both ancillary qubits and vice versa. This allow us to implement the necessary quantum gates by means of micro-wave pulses resonant with specific transitions. In particular, the error correcting ccNOT gate is obtained (much more easily than in other implementations) by a single pulse resonant with the |101〉 ↔ |111〉 transition [orange arrow in Fig. 1(c)]. In the cNOT two-qubit gates of the encoding/decoding steps one of the Er(III) ancillas acts as target and Ce(III) acts as the control qubit. Each cNOT is implemented by the application of two resonant pulses (blue arrows in Fig. 1(c)). Finally, Ry(±π/2) rotations of each qubit require four pulses of slightly different frequencies, because they must be performed irrespective of the states of the other two qubits.
In the following, we demonstrate the efficiency of the proposed implementation in fighting phase errors, by means of time-dependent simulations of the TQC, based on realistic parameters. Simulations are done by numerically integrating the Liouville–von Neumann equation of motion for the system density matrix ρ:
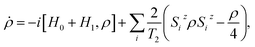 | (2) |
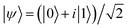 and we apply a magnetic field of 1 T parallel to z axis, in order to get well factorized states. We have checked (see Fig. S20 in the ESI†) that the same experiment could be done using typical X-band fields ∼0.5 T, with only a small increase of the final error. In addition, a tilt of the magnetic field direction with respect to the inter-molecular axis does not affect our simulations. To test that such sequence of pulses correctly implements the code, we have first simulated the coherent time evolution of 1, subject to an instantaneous phase error between encoding and decoding. We find that the ideal text-book performance of the TQC32 is well reproduced by our numerical simulations (see ESI†), indicating that gate errors (which arise from the finite bandwidth of the pulses) are negligible. Besides gate errors, we then include in our realistic simulation the more harmful effect of continuous pure dephasing, acting also during the finite time (TQEC) required to implement the code. To quantify the efficiency of the QEC procedure, we compute the ratio
and we apply a magnetic field of 1 T parallel to z axis, in order to get well factorized states. We have checked (see Fig. S20 in the ESI†) that the same experiment could be done using typical X-band fields ∼0.5 T, with only a small increase of the final error. In addition, a tilt of the magnetic field direction with respect to the inter-molecular axis does not affect our simulations. To test that such sequence of pulses correctly implements the code, we have first simulated the coherent time evolution of 1, subject to an instantaneous phase error between encoding and decoding. We find that the ideal text-book performance of the TQC32 is well reproduced by our numerical simulations (see ESI†), indicating that gate errors (which arise from the finite bandwidth of the pulses) are negligible. Besides gate errors, we then include in our realistic simulation the more harmful effect of continuous pure dephasing, acting also during the finite time (TQEC) required to implement the code. To quantify the efficiency of the QEC procedure, we compute the ratio 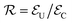 between the error probability on an uncorrected qubit
between the error probability on an uncorrected qubit  and the one after implementation of the TQC
and the one after implementation of the TQC 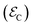 . The error probability is given by
. The error probability is given by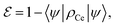 | (3) |
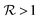 indicates an advantage of the QEC procedure. This is achieved as soon as the error correction overcomes the effect of pure dephasing acting during TQEC.
indicates an advantage of the QEC procedure. This is achieved as soon as the error correction overcomes the effect of pure dephasing acting during TQEC.
As reported in Fig. 4, 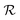 shows a maximum
shows a maximum 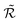 at an intermediate memory time
at an intermediate memory time 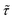 , which we choose as the optimal repetition time of the code. This represents the time before repeating the correction procedure and is therefore related to the number of operations which can be performed between two corrections. Both
, which we choose as the optimal repetition time of the code. This represents the time before repeating the correction procedure and is therefore related to the number of operations which can be performed between two corrections. Both 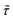 and
and 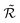 increase with T2 [inset of Fig. 4], with a significant gain of the QEC procedure already shown for T2 of a few μs. Indeed, the error is halved
increase with T2 [inset of Fig. 4], with a significant gain of the QEC procedure already shown for T2 of a few μs. Indeed, the error is halved 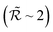 for T2 ∼ 3 μs, meaning that the procedure is efficient in correcting phase errors. In these conditions
for T2 ∼ 3 μs, meaning that the procedure is efficient in correcting phase errors. In these conditions 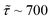 ns, allowing one to implement 50–100 gates before repeating the code. Remarkably, QEC shows an advantage
ns, allowing one to implement 50–100 gates before repeating the code. Remarkably, QEC shows an advantage 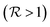 already for T2 = 0.5 μs, thanks to the large and anisotropic g tensors. These lead to well resolved transitions and fast implementation of the pulses, which reduces TQEC to less than 55 ns (see ESI†). Values of T2 ≈ 0.5 μs have been measured by pulsed EPR experiments on 1, [Fig. 3(d)] nearly independently of magnetic field and longer coherence times could be achieved by proper optimization of these samples. We note that the most important sources of decoherence are given by inter-molecular dipole–dipole interactions and by the coupling of the rare-earth ions with the surrounding fluctuating nuclear spins, mainly N and H nuclei. In particular, N nuclear spins are close to Er and Ce in the molecular structure and their dynamics can significantly affect spin coherence times. To reduce the effect of coupling to H nuclei in the solvent, experiments on frozen solutions could be done by using a deuterated solvent. This strategy could significantly improve T2, even of orders of magnitude at low temperature (as reported in ref. 17). A further improvement could be obtained by deuteration of the ligand cage of the magnetic ions, thus practically eliminating the coupling to protons. Moreover, the concentrations could be reduced (we kept them relatively high in order to retain a measurable signal) to diminish inter-molecular couplings. Both sources of decoherence are therefore subject to improvement by removing most of the magnetic nuclei and by reducing concentration.
already for T2 = 0.5 μs, thanks to the large and anisotropic g tensors. These lead to well resolved transitions and fast implementation of the pulses, which reduces TQEC to less than 55 ns (see ESI†). Values of T2 ≈ 0.5 μs have been measured by pulsed EPR experiments on 1, [Fig. 3(d)] nearly independently of magnetic field and longer coherence times could be achieved by proper optimization of these samples. We note that the most important sources of decoherence are given by inter-molecular dipole–dipole interactions and by the coupling of the rare-earth ions with the surrounding fluctuating nuclear spins, mainly N and H nuclei. In particular, N nuclear spins are close to Er and Ce in the molecular structure and their dynamics can significantly affect spin coherence times. To reduce the effect of coupling to H nuclei in the solvent, experiments on frozen solutions could be done by using a deuterated solvent. This strategy could significantly improve T2, even of orders of magnitude at low temperature (as reported in ref. 17). A further improvement could be obtained by deuteration of the ligand cage of the magnetic ions, thus practically eliminating the coupling to protons. Moreover, the concentrations could be reduced (we kept them relatively high in order to retain a measurable signal) to diminish inter-molecular couplings. Both sources of decoherence are therefore subject to improvement by removing most of the magnetic nuclei and by reducing concentration.
We finally note that achieving shorter manipulation times (e.g. by the use of state-of-the-art spectrometers38 or on-chip resonators39–41) could be a viable alternative to the increase of T2, producing similar results on the final error (as shown in the simulations reported in Fig. S21†).
3 Conclusions
In conclusion, we have presented the first concrete proposal for using a molecular nanomagnet to encode a qubit with embedded quantum error correction. To achieve this, we have synthesized a [Er–Ce–Er] trimer consisting of three weakly-interacting lanthanide ions, fulfilling the requirements to implement the three-qubit phase flip code, i.e. a tailored qubit–qubit interaction together with different and highly anisotropic g factors. Access to this molecule is possible by exploiting a remarkably selective synthetic methodology that has been used here to obtain the [LuCeLu] and [ErLaEr] analogues for the full characterization of each type of qubit individually. We have experimentally characterized the system and performed numerical simulations demonstrating that the present platform can efficiently protect the encoded qubit from decoherence. This represents the first step toward the realization of complexes embedding a sizeable number of qubits (thus extending the class of correctable errors) which could constitute the elementary error-protected unit of a forthcoming magnetic quantum processor.39Author contributions
E. M., A. C. and S. C. fit experimental data, derived the spin Hamiltonian parameters and performed numerical simulations of the quantum error correction code. M. R. and F. L. performed magnetic and specific heat measurements and analysed the data. J. I. M. and P. J. A. performed EPR measurements. D. A., L. B., G. A. synthesized and characterized the molecules and determined some of the molecular structures by crystallography. O. R. also determined some of the molecular structures by crystallography. F. L., G. A. and S. C. conceived the work and discussed results with all co-authors. A. C., F. L., G. A. and S. C. wrote the manuscript with inputs from all coauthors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Union's Horizon 2020 research and innovation programme (ERC Starting Grant 258060 FuncMolQIP, COST Action 15128 MOLSPIN, QUANTERA project SUMO, FET-OPEN grant 862893 FATMOLS), the Spanish MICINN (grants CTQ2015-68370-P, CTQ2015-64486-R, RTI2018-096075-B-C21, PCI2018-093116, PGC2018-098630-B-I00, MAT2017-86826-R), the Gobierno de Aragón (grants E09-17R-Q-MAD, and PLATON E31_17R), the Generalitat de Catalunya (ICREA Academia 2018 to GA), and from the Italian Ministry of Education and Research (MIUR) through the co-funding of SUMO and through the PRIN Project 2015 HYFSRT “Quantum Coherence in Nanostructures of Molecular Spin Qubits”. Institució Catalana de Recerca I Estudis Avançats: ICREA Academia Prize 2018.References
- B. Terhal, Rev. Mod. Phys., 2015, 87, 307 CrossRef.
- J. Preskill, Quantum, 2018, 2, 79 CrossRef.
- A. Chiesa, P. Santini, D. Gerace, J. Raftery, A. A. Houck and S. Carretta, Sci. Rep., 2015, 5, 16036 CrossRef.
- F. Tacchino, A. Chiesa, S. Carretta and D. Gerace, Adv. Quantum Technol., 2019, 1900052 Search PubMed.
- F. Arute, et al. , Nature, 2019, 574, 505 CrossRef CAS.
- A. Chiesa, F. Tacchino, M. Grossi, P. Santini, I. Tavernelli, D. Gerace and S. Carretta, Nat. Phys., 2019, 15, 455–459 Search PubMed.
- G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339 CrossRef CAS.
- F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, J. Sesé, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef CAS.
- A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423 CrossRef CAS.
- D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. Alonso, J. Sesé, S. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215 CrossRef.
- J. Ferrando-Soria, E. Moreno-Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. Vitorica-Yrezabal, F. Tuna, E. J. L. McInness and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS.
- J. Ferrando-Soria, S. A. Magee, A. Chiesa, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. F. S. Whitehead, S. Sproules, K. M. Lancaster, A.-L. Barra, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Chem, 2016, 1, 727–752 CAS.
- M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183 RSC.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341 CrossRef CAS.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS.
- C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685 CrossRef CAS.
- M. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344 CrossRef CAS.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef CAS.
- R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. Pedersen, R. D. Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818 CrossRef CAS.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS.
- C. M. Casadei, L. Bordonali, Y. Furukawa, F. Borsa, E. Garlatti, A. Lascialfari, S. Carretta, S. Sanna, G. Timco and R. Winpenny, J. Phys.: Condens. Matter, 2012, 24, 406002 CrossRef CAS.
- F. Adelnia, et al. , J. Chem. Phys., 2015, 143, 244321 CrossRef.
- M. D. Jenkins, Y. Duan, B. Diosdado, J. J. García-Ripoll, A. Gaita-Arino, C. Giménez-Saiz, P. J. Alonso, E. Coronado and F. Luis, Phys. Rev. B, 2017, 95, 064423 CrossRef.
- S. Baumann, W. Paul, T. Choi, C. Lutz, A. Ardavan and A. J. Heinrich, Science, 2015, 350, 417 CrossRef CAS.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, England, 2000 Search PubMed.
- D. G. Cory, M. D. Price, W. Maas, E. Knill, R. Laflamme, W. H. Zurek, T. F. Havel and S. S. Somaroo, Phys. Rev. Lett., 1998, 81, 2152 CrossRef CAS.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, L. Escalera-Moreno, A. Gaita-Ariño and G. Mínguez-Espallargas, Europhys. Lett., 2015, 110, 33001 CrossRef.
- M. H. Michael, M. Silveri, R. Brierley, V. V. Albert, J. Salmilehto, L. Jiang and S. M. Girvin, Phys. Rev. X, 2016, 6, 031006 Search PubMed.
- D. Aguilà, V. Velasco, L. A. Barrios, M. Schütze, O. Roubeau, F. Luis, S. J. Teat and G. Aromí, Chem.–Eur. J., 2019, 25, 15228 CrossRef.
- E. Moreno-Pineda, M. Damjanovic, O. Fuhr, W. Wernsdorfer and M. Ruben, Angew. Chem., Int. Ed., 2017, 56, 9915–9919 CrossRef CAS.
- P. A. S. Cruickshank, D. R. Bolton, D. A. Robertson, R. I. Hunter, R. J. Wylde and G. M. Smith, Rev. Sci. Instrum., 2009, 80, 103102 CrossRef.
- M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682 RSC.
- A. Bienfait, J. J. Pla, Y. Kubo, M. Stern, X. Zhou, C. C. Lo, C. D. Weis, T. Schenkel, M. L. W. Thewalt, D. Vion, D. Esteve, B. Julsgaard, K. Molmer, J. J. L. Morton and P. Bertet, Nat. Nanotechnol., 2016, 11, 253–257 CrossRef CAS.
- B. Sarabi, P. Huang and N. M. Zimmerman, Phys. Rev. Appl., 2019, 11, 014001 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1998121 and 1998122. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03107k |
| ‡ These values are computed using Gaussian pulses of peak amplitude 50 G and keeping the g tensors and the related dipolar interaction J13 fixed. |
| § We assume for simplicity the same T2 for all qubits, but this choice does not affect our conclusions. |
| ¶ ρCe is the reduced density matrix on Ce(III) qubit. |
| This journal is © The Royal Society of Chemistry 2020 |