Open Access Article
Open Access ArticleIndirect-to-direct band gap transition and optical properties of metal alloys of Cs2Te1−xTixI6: a theoretical study
Diwen Liu ab,
Wenying Zhac,
Rusheng Yuan
ab,
Wenying Zhac,
Rusheng Yuan c,
Benyong Lou*d and
Rongjian Sa
c,
Benyong Lou*d and
Rongjian Sa *a
*a
aInstitute of Oceanography, Fujian Key Laboratory of Functional Marine Sensing Materials, Minjiang University, Fuzhou, Fujian 350108, China. E-mail: rjsa@mju.edu.cn
bCollege of Materials and Chemical Engineering, Pingxiang University, Pingxiang 337055, China
cState Key Laboratory of Photocatalysis on Energy and Environment, College of Chemistry, Fuzhou University, Fuzhou 350108, P. R. China
dResearch and Testing Center of Pharmaceutical Formulations, Ocean College, Minjiang University, Fuzhou, Fujian 350108, P. R. China. E-mail: lby@mju.edu.cn
First published on 6th October 2020
Abstract
In recent years, double perovskites have attracted considerable attention as potential candidates for photovoltaic applications. However, most double perovskites are not suitable for single-junction solar cells due to their large band gaps (over 2.0 eV). In the present study, we have investigated the structural, mechanical, electronic and optical properties of the Cs2Te1−xTixI6 solid solutions using first-principles calculations based on density functional theory. These compounds exhibit good structural stability compared to CH3NH3PbI3. The results suggest that Cs2TeI6 is an indirect band gap semiconductor, and it can become a direct band gap semiconductor with the value of 1.09 eV when the doping concentration of Ti4+ is 0.50. Moreover, an ideal direct band gap of 1.31 eV is obtained for Cs2Te0.75Ti0.25I6. The calculated results indicate that all the structures are ductile materials except for Cs2Te0.50Ti0.50I6. Our results also show that these materials possess large absorption coefficients in the visible light region. Our work can provide a route to explore stable, environmentally friendly and high-efficiency light absorbers for use in optoelectronic applications.
1. Introduction
Lead-based halide perovskites have attracted great attention for optoelectronic applications in the past ten years.1–3 The power conversion efficiency (PCE) of lead-based halide perovskite solar cells increased to a high value of 25.2% in 2019.4 However, the toxicity of lead and poor stability still remain significant challenges for commercial applications. Extensive efforts have been paid to exploring lead-free or lead-less and stable halide perovskite materials for solar cells. Sn2+ and Ge2+ metal ions have been expected to replace Pb2+ ions in perovskites.5–9 Sn2+ ion is highly unstable and can be easily oxidized to Sn4+,10 which results in decreased photovoltaic performance. To date, the highest PCE of Ge-based halide perovskites is only 4.94%.11 Two dimensional (2D) layered perovskites have been also explored such as A3B2X9 (A = Cs, Rb; B = Bi, Sb; X = I, Br, Cl).12–17 However, these materials have large band gaps over 2.0 eV, which are not suitable for perovskite solar cells.In recent years, halide double perovskites A2B+B3+X6 have been developed as stable and non-toxic alternatives to lead-based perovskite materials, where two toxic lead ions are substituted by using monovalent B+ and trivalent B3+, such as Ag+, Bi3+, and Sb3+. Although most of the reported double perovskites show excellent stability, their band gaps are too large for application in single-junction solar cells.18–21 A low band gap (1.66 eV) of double perovskites Cs2NaBiI6 has been synthesized, which possesses excellent stability and strong light absorption performance.22 However, its PCE is only 0.42%, which is much lower than those of lead-based hybrid perovskites.
The vacancy-ordered double perovskites with formula of A2BX6 can be regarded as a derivative structure of the traditional ABX3, where two toxic lead ions are substituted by one tetravalent ion to keep charge conservation as the conventional perovskites. Cs2SnI6 is one of the most representative perovskite materials, which belongs to a cubic structure with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.23 The previous study classified Cs2SnI6 as zero dimensional (0D) structure.24 However, this compound still maintains three dimensional (3D) structure and presents 3D materials' properties, so it is still considered as 3D material.25 Cs2SnI6 exhibits air and moisture stability, and strong visible light absorption, which are advantageous properties for photovoltaic applications.26,27 The first tested solar cell using Cs2SnI6 as absorber material in air showed a small PCE of 0.96%.26 Meanwhile, MA2SnI6 was found to have a direct band gap of 1.81 eV with a strong absorption coefficient of ∼7 × 104 cm−1.28 The material properties of Cs2Sn1−xTexI6 were investigated to explore structure–property relationships with potential applications in photovoltaics.29 In 2017, a promising family of all-inorganic based-Ti double perovskites were predicted to possess suitable band gaps, excellent optical absorption, and high stability.30 In particular, the band gap of Cs2TiI6−xBrx can be tuned from 1.38 to 1.78 eV for single-junction and tandem solar cells.30 A comprehensive and systematic study of halide perovskites has been performed by using density functional theory (DFT) calculations.31 The theoretical study on the material properties of Cs2TiX6 (X = I, Br) has been investigated.32–34 The PCE of 3.28% can be obtained for Cs2TiBr6 when it is incorporated into planar-heterojunction PSCs.35 In 2018, Zhou et al. synthesized lead-free all-inorganic Cs2PdBr6 perovskite nanocrystals with a narrow band gap (1.69 eV) for the first time.36 A series of lead-free Te-based double perovskites A2TeX6 (A = MA, FA, or BA; X = Br− or I−; MA = CH3NH3; FA = CH(NH2)2; BA = benzylamine) were reported to be potential materials for optoelectronic devices.37 These Te-based double perovskites exhibited a tunable band gap, a low trap density, and a high mobility. Recently, the structural stability and electronic and optical properties of Te-based double perovskite materials were investigated by using first-principles calculations.38 Therefore, the design of new non-/low-toxic stable halide perovskites for solar cells is inevitable.
m.23 The previous study classified Cs2SnI6 as zero dimensional (0D) structure.24 However, this compound still maintains three dimensional (3D) structure and presents 3D materials' properties, so it is still considered as 3D material.25 Cs2SnI6 exhibits air and moisture stability, and strong visible light absorption, which are advantageous properties for photovoltaic applications.26,27 The first tested solar cell using Cs2SnI6 as absorber material in air showed a small PCE of 0.96%.26 Meanwhile, MA2SnI6 was found to have a direct band gap of 1.81 eV with a strong absorption coefficient of ∼7 × 104 cm−1.28 The material properties of Cs2Sn1−xTexI6 were investigated to explore structure–property relationships with potential applications in photovoltaics.29 In 2017, a promising family of all-inorganic based-Ti double perovskites were predicted to possess suitable band gaps, excellent optical absorption, and high stability.30 In particular, the band gap of Cs2TiI6−xBrx can be tuned from 1.38 to 1.78 eV for single-junction and tandem solar cells.30 A comprehensive and systematic study of halide perovskites has been performed by using density functional theory (DFT) calculations.31 The theoretical study on the material properties of Cs2TiX6 (X = I, Br) has been investigated.32–34 The PCE of 3.28% can be obtained for Cs2TiBr6 when it is incorporated into planar-heterojunction PSCs.35 In 2018, Zhou et al. synthesized lead-free all-inorganic Cs2PdBr6 perovskite nanocrystals with a narrow band gap (1.69 eV) for the first time.36 A series of lead-free Te-based double perovskites A2TeX6 (A = MA, FA, or BA; X = Br− or I−; MA = CH3NH3; FA = CH(NH2)2; BA = benzylamine) were reported to be potential materials for optoelectronic devices.37 These Te-based double perovskites exhibited a tunable band gap, a low trap density, and a high mobility. Recently, the structural stability and electronic and optical properties of Te-based double perovskite materials were investigated by using first-principles calculations.38 Therefore, the design of new non-/low-toxic stable halide perovskites for solar cells is inevitable.
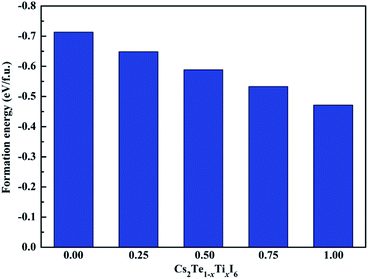
In this work, the structural stability, mechanical properties, electronic and optical properties of double perovskites Cs2Te1−xTixI6 were investigated for the first time. The results show that Cs2Te0.50Ti0.50I6 has excellent stability, suitable direct band gap, and strong optical absorption, which is a promising candidate material for optoelectronic device. The mechanical properties of these materials are discussed in detail, and the results indicate that they are ductile materials except for Cs2Te0.50Ti0.50I6.
2. Computational details
First-principles calculations were performed by using Vienna ab initio simulation package (VASP).39 The interaction between the core and valence electrons was described by the projector-augmented wave (PAW) method.40 The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) was employed to describe the exchange–correlation functional.41 A plane-wave energy cutoff of 500 eV was used. A 4 × 4 × 4 k-point grid was adopted for geometric optimization until the convergence criteria of energy and forces were set to be 10−5 eV and 0.01 eV Å−1, respectively. The structures were fully relaxed without any constraints. A denser 8 × 8 × 8 k-point grid was employed for electronic and optical properties calculations. Four k-points X (0.5, 0, 0), R (0.5, 0.5, 0.5), M (0.5, 0.5, 0), and G (0, 0, 0) were selected for the bandgap calculations. In order to gain accurate lattice parameters of the studied systems, the van der Waals (vdW) interactions were adopted within vdW-DFT in all calculations.42 For Cs2TiI6, considering the underestimation of the band gap in the standard DFT calculation, we used the DFT+U method43 to obtain accurate electronic structure. Various values of U have been tested for Ti 3d orbitals of Cs2TiI6. U = 2 eV was finally chosen for the electronic and optical calculations for the Cs2Te1−xTixI6 solid solutions.3. Results and discussion
3.1 Structure properties
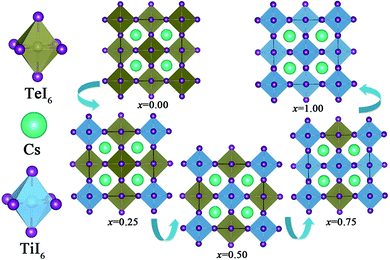
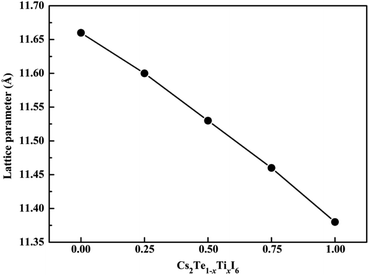
The crystal structures of both Cs2TeI6 and Cs2TiI6 belong to the cubic phase with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.29,30 The calculated lattice constant of Cs2TeI6 is 11.66 Å, which is in good agreement with experimental value (11.71 Å).29 The corresponding lattice constant of Cs2TiI6 is predicted to be 11.38 Å, which is much lower than its experimental value (11.67 Å).30 The ion radii of Te4+ and Ti4+ are 0.97 Å and 0.61 Å, respectively. Interestingly, the experimental lattice constants of Cs2TeI6 and Cs2TiI6 are almost the same. It should be noted that the lattice parameter of Cs2TiI6 is estimated to be 11.67 Å according to the experimental XRD results. The optimized structures of the Cs2Te1−xTixI6 solid solutions are depicted in Fig. 1. x is the concentration of Ti4+. The x values of 0.00, 0.25, 0.50, 0.75, and 1.00 are adopted in this study. For the species with x = 0.25, 0.50, and 0.75, all the possible arrangements are considered in this work. The results show that different structures with the same doping percentage have the same stability, with calculated energy differences within less than 2 meV. The lattice constant of Cs2Te1−xTixI6 decreases gradually when the concentration of Ti4+, as shown in Fig. 2. Moreover, the bond length Te–I (2.96 Å) of Cs2TeI6 is larger than the bond length Ti–I (2.76 Å) of Cs2TiI6.
m.29,30 The calculated lattice constant of Cs2TeI6 is 11.66 Å, which is in good agreement with experimental value (11.71 Å).29 The corresponding lattice constant of Cs2TiI6 is predicted to be 11.38 Å, which is much lower than its experimental value (11.67 Å).30 The ion radii of Te4+ and Ti4+ are 0.97 Å and 0.61 Å, respectively. Interestingly, the experimental lattice constants of Cs2TeI6 and Cs2TiI6 are almost the same. It should be noted that the lattice parameter of Cs2TiI6 is estimated to be 11.67 Å according to the experimental XRD results. The optimized structures of the Cs2Te1−xTixI6 solid solutions are depicted in Fig. 1. x is the concentration of Ti4+. The x values of 0.00, 0.25, 0.50, 0.75, and 1.00 are adopted in this study. For the species with x = 0.25, 0.50, and 0.75, all the possible arrangements are considered in this work. The results show that different structures with the same doping percentage have the same stability, with calculated energy differences within less than 2 meV. The lattice constant of Cs2Te1−xTixI6 decreases gradually when the concentration of Ti4+, as shown in Fig. 2. Moreover, the bond length Te–I (2.96 Å) of Cs2TeI6 is larger than the bond length Ti–I (2.76 Å) of Cs2TiI6.
The tolerance factor (t) has been widely used to predict the structural stability of perovskite material. The formula is defined as follows:44
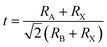 | (1) |
| ΔH = ΔE(Cs2Te1−xTixI6) − 2ΔE(CsI) − (1 − x)ΔE(TeI4) − xΔE(TiI4) | (2) |
3.2 Mechanical properties
To predict the mechanical stability of double perovskite Cs2Te1−xTixI6, the corresponding elastic constants were calculated using the finite strain theory.48 For cubic structure, the Born stability criteria is given as follows:49| C11 − C12 > 0, C11 + 2C > 120, C44 > 0 | (3) |
The calculated results of three independent elastic constants are listed in Table 1. All the compounds satisfy the above Born stability criteria, indicating that they are mechanical stable. The bulk modulus (B) and shear modulus (G) can be obtained by using Hill approximations.50 The Young's modulus (E) and Poisson ratio (ν) can be calculated from the values of bulk modulus and shear modulus by applying the following formula:51
| E = 9BG/(3B + G), ν = (3B − 2G)/(6B + 2G) | (4) |
| C11 | C12 | C44 | B | G | E | B/G | ν | |
|---|---|---|---|---|---|---|---|---|
| Cs2TeI6 | 19.14 | 10.24 | 8.78 | 13.21 | 6.68 | 17.16 | 1.98 | 0.28 |
| Cs2Te0.75Ti0.25I6 | 20.20 | 9.80 | 9.86 | 13.27 | 7.63 | 19.20 | 1.74 | 0.26 |
| Cs2Te0.50Ti0.50I6 | 17.51 | 8.39 | 9.98 | 11.43 | 7.29 | 18.03 | 1.57 | 0.24 |
| Cs2Te0.25Ti0.75I6 | 19.14 | 11.08 | 10.27 | 13.77 | 7.06 | 18.08 | 1.95 | 0.28 |
| Cs2TiI6 | 17.85 | 10.29 | 10.70 | 12.81 | 7.05 | 17.88 | 1.82 | 0.27 |
In order to investigate the ductility and brittleness of the studied double perovskites, we calculated the Pugh's and Poisson ratios. The Pughs's ratio is the ratio between bulk modulus and shear modulus (B/G), which is proposed by Pugh.52 The material is considered as ductile when the value of Pugh's ratio is larger than 1.75, otherwise it is brittle. The Poisson's ratio can also be used to separate the ductile materials from brittle materials. The ductile materials have the Poisson's ratio greater than 0.26, and it is smaller than 0.26 for brittle materials.53 From Table 1, it can be seen that Cs2Te0.50Ti0.50I6 is a brittle material, while other four compounds are ductile materials. It should be noted that the Poisson's ratio values of the studied double perovskites are close to the required lowest limit. The smaller the value of Young's modulus, the better flexibility of a material. The results show that Young's modulus of Cs2TeI6 is the smallest among the five structures, which indicates that it is the most flexible. Moreover, it is beneficial to form high quality film for ductile materials.
3.3 Electronic properties
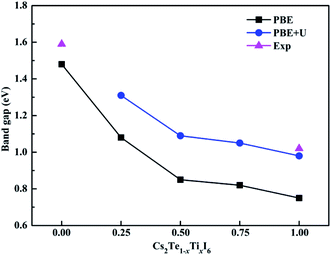
The band structures calculated along high symmetry directions in the Brillouin zone are shown in Fig. 5. Cs2TeI6 has an indirect band gap between G and R point, and a direct band gap at R point. The indirect and direct band gaps of Cs2TeI6 are 1.12 and 1.48 eV, respectively. The previous reported band gap of Cs2TeI6 is about 1.5 eV,54,55 and the recent experimentally observed optical gap is 1.59 eV.29 The band gap of Cs2TiI6 with the PBE method is 0.75 eV, which is lower than its experimental value (1.02 eV).30 Therefore, the DFT+U method is employed to obtain accurate band gap of Cs2TiI6. The result shows that Cs2TiI6 possesses a direct band gap with 0.98 eV at the G point, which is in good agreement with its experimental value.30 The Spin–orbit coupling (SOC) effect on the electronic structures of Te- and Ti-based perovskites is small.30,37 It is observed that Cs2Te0.50Ti0.50I6 is a direct band gap semiconductor with the value of 1.09 eV, while Cs2Te0.75Ti0.25I6 is an indirect band gap semiconductor. The direct band gap of Cs2Te0.25Ti0.75I6 is 1.05 eV. The trend in band gap is displayed in Fig. 6. The band gap of Cs2TeI6 reduces gradually when the ratio of Ti4+ increases. The band gaps of the two calculations with PBE and PBE+U show the same tendency. The variation in band gap is only 0.11 eV when the concentration of Ti4+ changes from 0.50 to 1.00. It should be noted that the direct band gap of Cs2TeI6 is close to the experimental value. The direct band gap of Cs2Te0.75Ti0.25I6 is 1.31 eV, which is a potential candidate for single-junction solar cells according to the Shockley–Queisser theory.56 An indirect-to-direct band gap transition can be observed when the doping content of Ti4+ increases from 0.25 to 0.50. Moreover, the direct band gap is significantly reduced by 0.22 eV. It can be seen that the band gaps of the Cs2Te1−xTixI6 solid solutions are apparently underestimated at the PBE method, as shown in Fig. 6.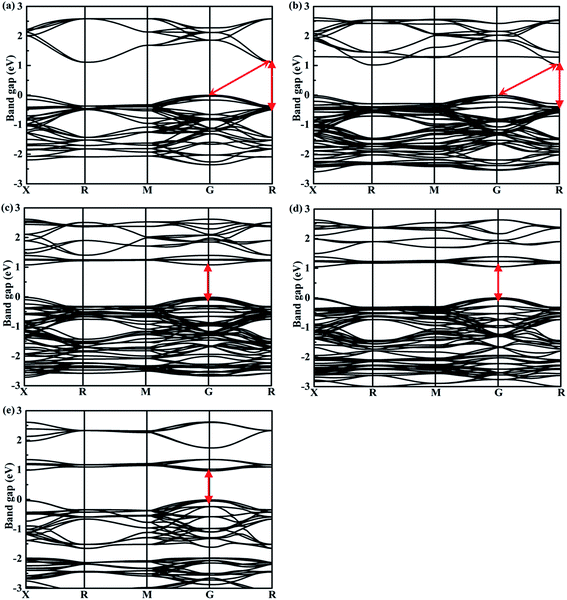 | ||
| Fig. 5 Calculated band structures of double perovskites along the X–R–M–G–R path for (a) Cs2TeI6, (b) Cs2Te0.75Ti0.25I6, (c) Cs2Te0.50Ti0.50I6, (d) Cs2Te0.25Ti0.75I6, and (e) Cs2TiI6. | ||
Fig. 7 shows the calculated density of states of the Cs2Te1−xTixI6 solid solutions. For Cs2TeI6, the valence band maximum (VBM) is mainly contributed by the I-p orbitals, while the conduction band minimum (CBM) is dominated by the Te-p orbitals along with the I-p orbitals. For Cs2TiI6, the VBM is mainly composed of the I-p orbitals, whereas the CBM is composed of the Ti-d orbitals. The similar situation is observed for the mixed Te–Ti double perovskites with respect to Cs2TiI6. It can be seen that Cs+ does not contribute to the band edge states.
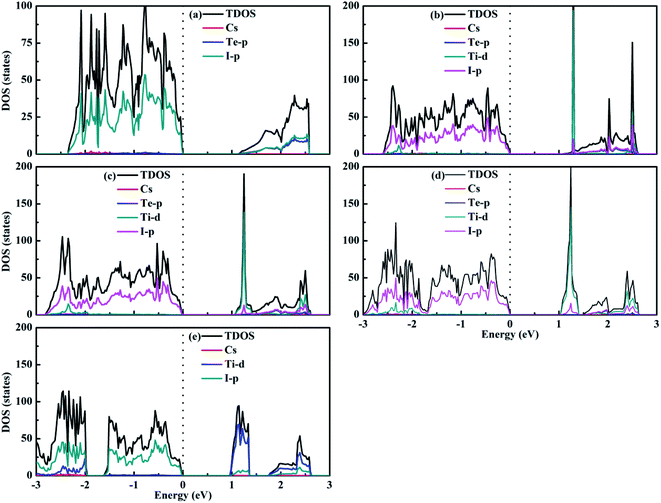 | ||
| Fig. 7 Density of states of (a) Cs2TeI6, (b) Cs2Te0.75Ti0.25I6, (c) Cs2Te0.50Ti0.50I6, (d) Cs2Te0.25Ti0.75I6, and (e) Cs2TiI6. | ||
3.4 Optical properties
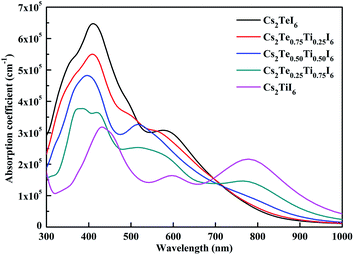
The calculated optical absorption spectrum is given in Fig. 8. Cs2TeI6 shows a large absorption coefficient in the visible light region. The absorption coefficient of Cs2TiI6 is over 10−5 cm−1 in the whole region, but it is lower than that of Cs2TeI6 in the range of 300–700 nm. For Cs2TiI6, two strong absorption peaks are located at about 450 and 800 nm, respectively. The optical absorption ability gradually increases when the proportion of Ti4+ decreases. In general, the Cs2Te1−xTixI6 solid solutions have strong and wide optical absorption in the visible spectrum. Cs2Te0.50Ti0.50I6 is the most promising candidate due to its superior stability, suitable direct band gap, and strong optical absorption.4. Conclusions
In summary, the structural, mechanical, electronic and optical properties for the Cs2Te1−xTixI6 solid solutions have been investigated by using first-principles calculations for the first time. The calculated results show that Cs2TeI6 is an indirect band gap semiconductor, while Cs2TiI6 is a direct band gap semiconductor with the value of 0.98 eV. These compounds show good structural stability compared to CH3NH3PbI3. An indirect–direct band gap transition can be observed when the doping concentration of Ti4+ is 0.50. Cs2Te0.50Ti0.50I6 has a suitable direct band gap (1.09 eV), which is considered as a promising photovoltaic material for single-junction solar cells. Further analysis reveals that all the structures are ductile materials except for Cs2Te0.50Ti0.50I6. Moreover, these materials have large optical absorption coefficients in the visible light region. We expect that this study can provide insights into developing the stable, non-toxic, and high-efficiency perovskite materials for optoelectronic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21872033), the Department of Fujian Science and Technology and Program for Innovative Research Team in Science and Technology in Fujian Province University (No. 2018N2001), and the Fujian Key Laboratory of Functional Marine Sensing Materials (No. MJUKFFMSM201909). The authors thank the Supercomputer environment of Fujian Provincial Key Laboratory of Information Processing and Intelligent Control.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Science, 2017, 356, 1376–1379 CrossRef CAS.
- G. E. Eperon, T. Leijtens, K. A. Bush, R. Prasanna, T. Green, J. T.-W. Wang, D. P. McMeekin, G. Volonakis, R. L. Milot, R. May, A. Palmstrom, D. J. Slotcavage, R. A. Belisle, J. B. Patel, E. S. Parrott, R. J. Sutton, W. Ma, F. Moghadam, B. Conings, A. Babayigit, H.-G. Boyen, S. Bent, F. Giustino, L. M. Herz, M. B. Johnston, M. D. McGehee and H. J. Snaith, Science, 2016, 354, 861–865 CrossRef CAS.
- NREL, Photovoltaic Research. Best Research-Cell Efficiency Chart, 2019, https://www.nrel.gov/pv/cell-efficiency.html Search PubMed.
- N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068 RSC.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Nat. Photonics, 2014, 8, 489–494 CrossRef CAS.
- M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Graetzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122–7127 CrossRef CAS.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta, N. Mathews and S. G. Mhaisalkar, J. Mater. Chem. A, 2015, 3, 23829–23832 RSC.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804–6819 CrossRef CAS.
- M.-G. Ju, G. Sun, Y. Zhao and W. Liang, Phys. Chem. Chem. Phys., 2015, 17, 17679–17687 RSC.
- L.-J. Chen, RSC Adv., 2018, 8, 18396–18399 RSC.
- B. Yang, J. Chen, F. Hong, X. Mao, K. Zheng, S. Yang, Y. Li, T. Pullerits, W. Deng and K. Han, Angew. Chem., Int. Ed., 2017, 56, 12471–12475 CrossRef CAS.
- J. Zhang, Y. Yang, H. Deng, U. Farooq, X. Yang, J. Khan, J. Tang and H. Song, ACS Nano, 2017, 11, 9294–9302 CrossRef CAS.
- M. Leng, Y. Yang, K. Zeng, Z. Chen, Z. Tan, S. Li, J. Li, B. Xu, D. Li, M. P. Hautzinger, Y. Fu, T. Zhai, L. Xu, G. Niu, S. Jin and J. Tang, Adv. Funct. Mater., 2018, 28, 1704446 CrossRef.
- Y. Lou, M. Fang, J. Chen and Y. Zhao, Chem. Commun., 2018, 54, 3779–3782 RSC.
- J. Pal, A. Bhunia, S. Chakraborty, S. Manna, S. Das, A. Dewan, S. Datta and A. Nag, J. Phys. Chem. C, 2018, 122, 10643–10649 CrossRef CAS.
- J. Pal, S. Manna, A. Mondal, S. Das, K. V. Adarsh and A. Nag, Angew. Chem., Int. Ed., 2017, 56, 14187–14191 CrossRef CAS.
- E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Chem. Mater., 2016, 28, 1348–1354 CrossRef CAS.
- F. Wei, Z. Deng, S. Sun, F. Xie, G. Kieslich, D. M. Evans, M. A. Carpenter, P. D. Bristowe and A. K. Cheetham, Mater. Horiz., 2016, 3, 328–332 RSC.
- G. Volonakis, A. A. Haghighirad, R. L. Milot, W. H. Sio, M. R. Filip, B. Wenger, M. B. Johnston, L. M. Herz, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2017, 8, 772–778 CrossRef CAS.
- P. Cheng, T. Wu, Y. Li, L. Jiang, W. Deng and K. Han, New J. Chem., 2017, 41, 9598–9601 RSC.
- C. Zhang, L. Gao, S. Teo, Z. Guo, Z. Xu, S. Zhao and T. Ma, Sustainable Energy Fuels, 2018, 2, 2419–2428 RSC.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS.
- A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141 CrossRef CAS.
- H. Lin, C. Zhou, Y. Tian, T. Siegrist and B. Ma, ACS Energy Lett., 2018, 3, 54–62 CrossRef CAS.
- X. Qiu, B. Cao, S. Yuan, X. Chen, Z. Qiu, Y. Jiang, Q. Ye, H. Wang, H. Zeng, J. Liu and M. G. Kanatzidis, Sol. Energy Mater. Sol. Cells, 2017, 159, 227–234 CrossRef CAS.
- M. Rasukkannu, D. Velauthapillai and P. Vajeeston, Mater. Lett., 2018, 218, 233–236 CrossRef CAS.
- F. Funabiki, Y. Toda and H. Hosono, J. Phys. Chem. C, 2018, 122, 10749–10754 CrossRef CAS.
- A. E. Maughan, A. M. Ganose, M. M. Bordelon, E. M. Miller, D. O. Scanlon and J. R. Neilson, J. Am. Chem. Soc., 2016, 138, 8453–8464 CrossRef CAS.
- M.-G. Ju, M. Chen, Y. Zhou, H. F. Garces, J. Dai, L. Ma, N. P. Padture and X. C. Zeng, ACS Energy Lett., 2018, 3, 297–304 CrossRef CAS.
- N. Hernández-Haro, J. Ortega-Castro, Y. B. Martynov, R. G. Nazmitdinov and A. Frontera, Chem. Phys., 2019, 516, 225–231 CrossRef.
- K. Chakraborty, M. G. Choudhury and S. Paul, Sol. Energy, 2019, 194, 886–892 CrossRef CAS.
- H. Yan, Y. Li, X. Li, B. Wang and M. Li, RSC Adv., 2020, 10, 958–964 RSC.
- M. Tsuyama and S. Suzuki, J. Phys. Soc. Jpn., 2019, 88, 104802 CrossRef.
- M. Chen, M.-G. Ju, A. D. Carl, Y. Zong, R. L. Grimm, J. Gu, X. C. Zeng, Y. Zhou and N. P. Padture, Joule, 2018, 2, 558–570 CrossRef CAS.
- L. Zhou, J.-F. Liao, Z.-G. Huang, X.-D. Wang, Y.-F. Xu, H.-Y. Chen, D.-B. Kuang and C.-Y. Su, ACS Energy Lett., 2018, 3, 2613–2619 CrossRef CAS.
- D. Ju, X. Zheng, J. Yin, Z. Qiu, B. Türedi, X. Liu, Y. Dang, B. Cao, O. F. Mohammed, O. M. Bakr and X. Tao, ACS Energy Lett., 2019, 4, 228–234 CrossRef CAS.
- D. Liu, Q. Li, Z. Zhang and K. Wu, New J. Chem., 2019, 43, 14892–14897 RSC.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- T. Thonhauser, V. R. Cooper, S. Li, A. Puzder, P. Hyldgaard and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125112 CrossRef.
- E. Finazzi, C. Di Valentin, G. Pacchioni and A. Selloni, J. Chem. Phys., 2008, 129, 154113 CrossRef.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- Y. Zhao and K. Zhu, Chem. Soc. Rev., 2016, 45, 655–689 RSC.
- R. Ali, G.-J. Hou, Z.-G. Zhu, Q.-B. Yan, Q.-R. Zheng and G. Su, Chem. Mater., 2018, 30, 718–728 CrossRef CAS.
- O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180301 CrossRef.
- F. D. Murnaghan, Am. J. Math., 1937, 59, 235–260 CrossRef.
- M. Born, Math. Proc. Cambridge Philos. Soc., 2008, 36, 160–172 CrossRef.
- R. Hill, Proc. Phys. Soc., 1952, 65, 349–354 CrossRef.
- M. Roknuzzaman, K. Ostrikov, H. Wang, A. Du and T. Tesfamichael, Sci. Rep., 2017, 7, 14025 CrossRef.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- M. A. Hadi, M. Roknuzzaman, A. Chroneos, S. H. Naqib, A. K. M. A. Islam, R. V. Vovk and K. Ostrikov, Comput. Mater. Sci., 2017, 137, 318–326 CrossRef CAS.
- E. Y. Peresh, V. I. Sidei, N. I. Gaborets, O. V. Zubaka, I. P. Stercho and I. E. Barchii, Inorg. Mater., 2014, 50, 101–106 CrossRef CAS.
- E. Y. Peresh, O. V. Zubaka, V. I. Sidei, I. E. Barchii, S. V. Kun and A. V. Kun, Inorg. Mater., 2002, 38, 859–863 CrossRef CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |