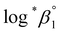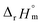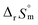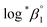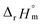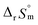Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Studies of aqueous U(IV) equilibrium and nanoparticle formation kinetics using spectrophotometric reaction modeling analysis†
Wansik Cha *a,
Hee-Kyung Kim
*a,
Hee-Kyung Kim a,
Hyejin Choa,
Hye-Ryun Choa,
Euo Chang Junga and
Seung Yeop Leeb
a,
Hyejin Choa,
Hye-Ryun Choa,
Euo Chang Junga and
Seung Yeop Leeb
aNuclear Chemistry Research Laboratory, Korea Atomic Energy Research Institute, 989-111 Daedeok-daero, Yuseong-gu, Daejeon 34057, Republic of Korea. E-mail: wscha@kaeri.re.kr
bRadioactive Waste Management Research Division, Korea Atomic Energy Research Institute, 989-111 Daedeok-daero, Yuseong-gu, Daejeon 34057, Republic of Korea
First published on 6th October 2020
Abstract
Hydrolysis of tetravalent uranium (U(IV)) and U(IV)-nanoparticle formation kinetics were examined over a wide range of temperatures using spectrophotometric reaction modeling analysis. The characteristic absorption bands representing U4+, U(OH)3+, and a proposed oxohydroxo species were newly identified in the UV region (190–300 nm). Dynamic absorption band changes in the UV and visible regions (360–800 nm) were explored to reevaluate the binary ion interaction coefficients for U(IV) ions and the thermodynamic constants of the primary hydrolysis reaction, including complexation constants, enthalpy, and entropy. No further hydrolysis equilibrium beyond the formation of U(OH)3+ was identified. Instead, an irreversible transformation of U(IV) ions to U(IV)-nanoparticles (NPs) was found to occur exclusively via the formation of a new intermediate species possessing characteristic absorption bands. The kinetic analysis, based on a two-step, pseudo-first-order reaction model, revealed that the rate of the initial step producing the intermediates is highly temperature-dependent with the measured kinetic energy barrier of ∼188 kJ mol−1. With additional experimental evidence, we conclude that the intermediates are oligomeric oxohydroxo U(IV) species occurring from the condensation of U(IV) ions and simultaneously participating in the nucleation and growth process of UO2(cr)-NPs.
Introduction
Understanding the physicochemical behaviors of radionuclides, such as the transport, solubility, and speciation in geomedia, is a prerequisite for the reliable safety assessment of nuclear disposal systems.1,2 Tetravalent uranium (U(IV)) is the main component of oxide nuclear fuels and the major reduced form of uranium in the natural environment, particularly under anoxic and reducing conditions of deep groundwater systems. However, understanding U(IV) speciation in solution is still a challenging task. Though efforts have been made to compile thermodynamic data of U(IV), there are relatively few speciation studies reported for aqueous phase reactions.3–7 Easy atmospheric oxidation of soluble U(IV) species and low solubility of U(IV) hydroxides and oxides have imposed experimental difficulties. In addition, the strong Lewis acid property of U(IV) renders U(IV) ions susceptible to being hydrolyzed and to form condensed species through olation and oxolation, depending on pH and temperature.8–10 These processes, as well as other complexations in a given system, often occur simultaneously to release protons. Thus, individual equilibria cannot be readily distinguished by solely monitoring pH changes (e.g., potentiometry) in reaction media. This complication, referred to as “proton ambiguity,” has hampered understanding of the fundamental thermodynamic properties of reaction equilibria involving actinide (An) aqua ions and their hydrolysis products.11 Partly for this reason, among the stability constants of U(IV) hydrolysis the one for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (U(OH)3+) based on spectroscopic measurements is currently accepted in NEA-TDB.3
1 complex (U(OH)3+) based on spectroscopic measurements is currently accepted in NEA-TDB.3
The condensation process can influence the apparent solubility of U(IV) to accelerate its distribution in the environment by producing insoluble uraninite (UO2(cr)) as well as oxo-hydroxo nanoclusters and inorganic colloids.12,13 Recent studies regarding the microbe-mediated redox transformation of U(VI) to U(IV) showed that nanometer- or submicrometer-sized crystalline particles (i.e., uraninite) could be created via both biotic and abiotic pathways.14–16 More recently, Knope et al. identified a series of U(IV) nanoclusters of well-defined structures in the presence of carboxylic ligands by controlling reaction parameters like pH and temperature.8 We have also previously developed a hydrothermal U(IV)-nanoparticle (NP) preparation method directly from aqueous solutions, without organic ligands, to investigate their colloidal properties and interactions with organic molecules.17 It was found that U(IV)-NP formation is a temperature-sensitive process consuming monomeric U(IV) ions and producing pseudo-stable nanoclusters (approximately 20–30 nm) consisting of smaller crystalline-UO2 primary particles (2–6 nm). Inspired by this observation, we are currently interested in understanding the nature of the U(IV)-NP formation kinetics and its formation mechanism.
Spectrophotometry is a versatile detection technique for the speciation of An ions in a wide range of concentrations. The 5f2 electronic configuration of U4+ provides various energy levels that are detectable in the visible (Vis) region (e.g., ϵ(648 nm) ≈ 60 cm−1 M−1).18 It has been shown that, when coupled with a liquid-waveguide capillary cell (LWCC) setup, spectrophotometric analysis is possible for An ions down to μM-levels.19 To minimize the condensation of U(IV) toward polynuclear species, maintaining lower concentrations of uranium is advantageous. The absorption bands of U4+ and U(OH)3+ are distinguishable but often overlap each other. An early study by Cohen and Carnall reported the absorption spectra of U(IV) in DClO4 solution between 200 and 2600 nm.20 Later works for determination of the U(OH)3+ stability constant, including the one reported by Kraus and Nelson, used visible spectral bands (350–1100 nm) and have been reliably referred to date.21,22 The peaks in the visible region are attributed to the f–f electronic transitions from the ground state (3H4) to the upper states (3Pn, 1I6, 1G4, 1D2, n = 0–2) arising from the f2 configuration.23,24 However, no previous work reported applicable absorption bands in the UV region for U(IV) speciation, while the transition to 1S0 at 245 nm has been explored by Kirishima et al. for the luminescence study of aqua U4+ ions.25
The objectives in the present study are threefold: (1) to employ the newly-found strong absorption bands in the UV region for speciation of U(IV) ions, (2) to determine and reevaluate the thermodynamic constants of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis reaction by using both absorption bands in UV and visible regions, and finally (3) to investigate NP formation kinetics and examine spectroscopic evidence for the presence of other U(IV) species, such as 1
1 hydrolysis reaction by using both absorption bands in UV and visible regions, and finally (3) to investigate NP formation kinetics and examine spectroscopic evidence for the presence of other U(IV) species, such as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2–1
2–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 hydrolyzed complexes or condensed polynuclear species. This approach has allowed us to identify new U(IV) species, potentially oxohydroxo intermediates, of which formation kinetics significantly depend on temperature. The thermodynamic constants regarding 1
4 hydrolyzed complexes or condensed polynuclear species. This approach has allowed us to identify new U(IV) species, potentially oxohydroxo intermediates, of which formation kinetics significantly depend on temperature. The thermodynamic constants regarding 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis and the binary ion interaction coefficient for U(IV) ions are also determined. Additionally, a simplified reaction model and the activation energy of the initial step of U(IV)-NP formation reaction are discussed.
1 hydrolysis and the binary ion interaction coefficient for U(IV) ions are also determined. Additionally, a simplified reaction model and the activation energy of the initial step of U(IV)-NP formation reaction are discussed.
Experimental
Sample preparation
A stock solution of U(VI) perchlorate was prepared from uranium dioxide, as described elsewhere.26 Next, U(IV) stock solutions (∼70 mM) were obtained by electrochemically reducing the acidified U(VI) stock solution (<pH 0.5) using a Hg working electrode.20 The U(VI) content in the U(IV) stock solution was monitored using both time-resolved laser fluorescence spectroscopy and inductively coupled plasma atomic emission spectroscopy (ICP-AES) analyses (<1% of the total U content).27 Sodium perchlorate (Sigma-Aldrich, 99%) was purified by recrystallization before use. All chemicals, including NaOH and HClO4, were of ultrapure reagent grade and used as received (Sigma-Aldrich and J.T. Baker for NaOH and HClO4, respectively). Electrolyte stock solutions were filtered through a 0.2 μm syringe filter (PVDF, Millipore) before use. All solution preparations, pH control, and sampling were carried out in an Ar-filled glove box to avoid CO2 dissolution unless otherwise noted.Each sample subjected to spectrophotometric analysis was prepared fresh (daily) and batch-wise to have a fixed ionic strength while the solution pH varied within a series of samples. The ionic strength (I) of individual samples was controlled by adjusting the volume ratio of HClO4 and NaClO4 stock solutions. The addition of NaOH solution was done only into a U(IV) stock solution so that the final pH of each test sample was controlled either by diluting U(IV) stock solutions or by adding a standardized HClO4 solution.
A combination glass electrode (Orion Ross, Fisher Sci.) was used to determine the solution pHc (−log[H+]), typically after the experiment. The electrode was pre-calibrated using standard HClO4 solutions of 0.01 and 0.0001 m (molal concentration) at the designated temperature of a given experiment. The electrode calibration curves yielded near-Nernstian slopes. When the solution pHc was lower than 1.6, at which the electrode shows emf drifting and liquid junction potential, the [H+] of a sample solution was directly calculated with acidity and additive volumes of the U(IV) stock and HClO4 solutions used for sample preparation. Final concentrations of the U(IV) solutions for spectrophotometry were in the range of 0.1–2.5 mM. pHc ranged from 0 to 2.2 and 2.0 to 3.0 for thermodynamic and kinetic analyses, respectively.
UV-Vis spectrophotometry
Absorption spectra were measured using two types of spectrometer systems: a dual-beam UV-Vis spectrophotometer (Cary 100, Agilent), for both UV (190–340 nm) and visible (360–800 nm) regions, and a multi-channel spectrometer (MCS601, Carl Zeiss) for the visible region only. All visible spectra were baseline-corrected against a water blank. For the UV spectra, a series of blank solutions containing the same concentrations of HClO4 and NaClO4 as those of the corresponding samples were used for correction. Samples prepared in an Ar glove box were sealed into screw-capped quartz cells of different optical path-lengths (OPL): 1 mm and 10 mm for UV and Vis absorption measurements, respectively. In addition, an LWCC (WPI) with an OPL of 100 mm was used for visible spectra at room temperature (RT = 26 ± 1 °C). When measured using an LWCC setup, the sample solutions were introduced via a flow-through setup equipped with a syringe pump. Otherwise, the temperature of the quartz cells was precisely controlled in a cell holder (±0.05 °C, qChanger6, and Qpod 2e, Quantum Northwest).Monitoring U(IV)-NP formation kinetics
In this study, the conversion rate from U(IV) ions to U(IV)-NP was measured using sets of spectra collected over time. The relatively fast reaction kinetics at high temperatures were monitored using the multi-channel spectrometer capable of collecting spectra at various time intervals (down to ms-levels). For kinetic studies, an aliquot of U(IV) stock solution was filled into a gas-tight syringe (100 μL, Hamilton). It was then injected into a quartz cell filled with the appropriate electrolyte solution that was pre-equilibrated to the desired temperature (30–80 °C). In this way, the initiation of the reaction and the kinetic data collection began simultaneously.After a hydrothermal reaction, e.g., 5 h at 80 °C, the solution color changed from light blue to dark yellow. The synthesized U(IV)-NPs were characterized by high-resolution transmission electron microscopy (HR-TEM, JEOL, JEM 2001F) and dynamic light scattering (Zetasizer Nano ZS, Malvern Instruments) measurements for analysis of particle size, morphology, and crystalline structure.
Spectrophotometric data analysis
To systemically interpret the multivariate spectrophotometric data, including experimental parameters like pH and concentrations, we employed a global analysis method, i.e., a numerical data fitting procedure involving reaction modeling for both studies of aqueous equilibria and U(IV)-NP formation kinetics. For the analysis of hydrolysis equilibria, a series of absorption spectra of U(IV) as a function of pHc were obtained from the samples prepared at a given condition, i.e., ionic strength and temperature. Then, the conditional stability constant and singular spectra of the absorbing species involved in a given equilibrium model were derived using a commercial spectrophotometric data deconvolution program (HypSpec®2014, Protonic Software). The kinetic reaction analysis was performed similarly; by collecting a series of spectra over time and using a spectral data fitting program (ReactLab®™ Kinetics, JPlus Consulting Ltd.) to obtain the reaction rates and singular spectra of species involved in a given reaction model. For the kinetic data analysis, the molar absorption spectrum of U(OH)3+ was provided as a known parameter. Factor analysis and evaluation of the deconvolution were conducted beforehand to check the validity of the proposed reaction models using the function included in the softwares. Typically, the spectra of a full wavelength range, i.e., 190–340 nm or 360–800 nm, were employed for both thermodynamic and kinetic data analyses. In this work it is assumed that the singular spectra of U(IV) species at a given temperature do not vary depending on the solution ionic strength. Three or more sets of sample series were examined to obtain the statistical results, including standard deviations.Calculation of thermodynamic constants
The thermodynamic constants of the first hydrolysis equilibrium (eqn (1)), including the stability constant log *β1 and the changes in molar enthalpy (ΔrHm) and molar entropy (ΔrSm) of the reaction, were derived from the spectroscopic analysis as shown above.| U4+ + H2O(l) ⇄ U(OH)3+ + H+ | (1) |
The measured conditional stability constant given by
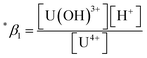 | (2) |
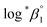 at the standard condition (I = 0, T = 25 °C) using the specific ion interaction theory (SIT).3 Detailed conversion procedures are described in the ESI†. For the correction of I, molar concentrations (M) were converted to molal concentrations (m) using the conversion process described in NEA-TDB.3
at the standard condition (I = 0, T = 25 °C) using the specific ion interaction theory (SIT).3 Detailed conversion procedures are described in the ESI†. For the correction of I, molar concentrations (M) were converted to molal concentrations (m) using the conversion process described in NEA-TDB.3
In this work, we applied the following SIT formula for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 U(IV) hydrolysis to obtain
1 U(IV) hydrolysis to obtain 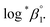
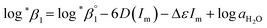 | (3) |
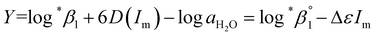 | (3-1) |
The values of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aH2O and the calculation procedure of the Debye–Hückel term (D(Im)) are provided in the ESI (see also Tables S1 and S2†). The binary ion interaction coefficients (ε or Δε) used in this study are provided in Table 1. When a set of log
aH2O and the calculation procedure of the Debye–Hückel term (D(Im)) are provided in the ESI (see also Tables S1 and S2†). The binary ion interaction coefficients (ε or Δε) used in this study are provided in Table 1. When a set of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 values exclusively depending on ionic strength were available,
*β1 values exclusively depending on ionic strength were available, 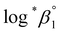 alone or both
alone or both 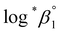 and Δε were measured graphically by analyzing the intercept and slope of the Y vs. Im plot (eqn (3-1)). The limiting values of log
and Δε were measured graphically by analyzing the intercept and slope of the Y vs. Im plot (eqn (3-1)). The limiting values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 at various temperatures are denoted collectively as
*β1 at various temperatures are denoted collectively as 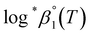 (see ESI†). The uncertainty of the determined thermodynamic constants was expressed with the standard error at a 95% confidence level.
(see ESI†). The uncertainty of the determined thermodynamic constants was expressed with the standard error at a 95% confidence level.
Results and discussion
Monitoring absorption spectra of U(IV) ions
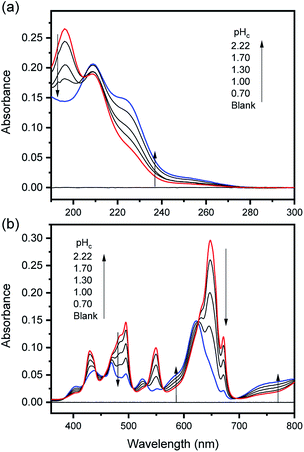
The characteristic absorption spectra of U4+ and U(OH)3+ were confirmed in both UV and visible regions, as shown in Fig. 1 and 2. The absorption peaks in the visible region are almost identical to those reported in the literature.18,20,25 Fig. 1 shows pH-dependent spectral changes in both the UV and visible regions of sample solutions containing U(IV) (I, 0.2 m). At low pHc, U4+ ions are dominant, and the spectra show λmax at 196 nm and 648 nm. As the solution pHc increases, the absorption peaks of U(OH)3+ ions gradually emerge; the λmax of the UV region red-shifts to 209 nm and that of the visible region blue-shifts to 621 nm. We emphasize that the versatile spectral changes in the UV region, depending on U(IV) speciation, is reported here for the first time. It should be noted that these spectral changes are reversible, according to the change of solution pHc in both UV and visible regions, so that the forward and backward reactions of eqn (1) quickly achieve equilibrium.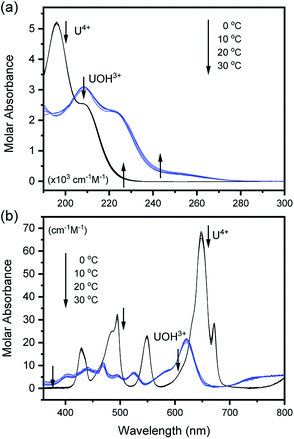 | ||
| Fig. 2 Deconvoluted molar absorption spectra of U4+ and U(OH)3+ in the (a) UV and (b) visible regions at various temperatures. | ||
To examine the thermodynamic properties of eqn (1), a set of spectra was collected from multiple samples (typically four to seven samples) under the same experimental parameters, except pHc, which typically varied from 0–2.2. The spectrum set was then analyzed using a numerical data fitting procedure (see Experimental section). To obtain the best fitting results of low uncertainty, we initially provided a measured spectrum of U4+ as a ‘known’ parameter, which was independently obtained in 2 M HClO4. Then, the molar absorption spectra of U4+ and U(OH)3+ were obtained from the converged outputs of the data fitting iteration process.
Fig. 2 summarizes those molar absorption spectra determined using the aforementioned process. As expected, the factor analysis result of the individual set of spectral data confirmed that no further U(IV) species, other than U4+ and U(OH)3+, is involved in the hydrolytic equilibrium under the given conditions in this work. However, since the reaction products irreversibly occurring at high pH or an elevated temperature can complicate the monitoring of the equilibria (see following sections), the sample solutions for the thermodynamic study were examined only at temperatures ≤ 30 °C. The λmax and molar absorption coefficient (ϵ, Y-axis of Fig. 2) of the observed individual absorption peaks and isosbestic points are summarized in Table 2.
| Species | U4+ | Isosbestic points | U(OH)3+ | Intermediate | |||
|---|---|---|---|---|---|---|---|
| Region | λmax (nm) | ϵ (cm−1 M−1) | λ (nm) | ϵ (cm−1 M−1) | λmax (nm) | ϵ (cm−1 M−1) | λmax (nm) |
| a shIndicating a shoulder peak. | |||||||
| UV | 196 | 5110 ± 90 | 204 | 2730 ± 120 | 209 | 3060 ± 60 | — |
| 210sh | 2500 ± 110 | 225sh | 2200 ± 50 | ||||
| 247sh | 310 ± 40 | 260 ± 3 | |||||
| Vis | 429 | 16.9 ± 0.7 | 419 | 4.5 ± 0.4 | 400sh | 3.9 ± 0.1 | |
| 440 | 7.2 ± 0.5 | 439 | 6.8 ± 0.1 | 429 ± 1 | |||
| 485sh | 24.9 ± 0.9 | 457 | 5.9 ± 0.3 | 468 | 9.4 ± 0.1 | ||
| 495 | 30.7 ± 0.8 | 506 | 3.6 ± 0.3 | 494 | 4.9 ± 0.1 | 468 ± 1 | |
| 533 | 3.9 ± 0.3 | 525 | 5.9 ± 0.1 | ||||
| 549 | 22.2 ± 0.7 | 561 | 3.4 ± 0.2 | 583sh | 7.0 ± 0.1 | 544 ± 1 | |
| 648 | 66.5 ± 1.8 | 625 | 19.0 ± 0.4 | 621 | 20.2 ± 0.3 | 625 ± 1 | |
| 671 | 28.1 ± 0.7 | 695 | 0.9 ± 0.1 | 739sh | 4.4 ± 0.2 | 669 ± 1 | |
As shown in Fig. 1(b) and 2(b), the structure of the visible absorption of the U4+ aqua ion has the characteristic of an electronic transition within the 5f2 configuration (f → f). The characteristic six bands in the visible region are attributed to transitions from the ground state (3H4) to the upper states (3Pn, 1I6, 1G4, 1D2, n = 0–2, see Fig. S1†). The ϵ of these bands is relatively small (<70 cm−1 M−1) because the f–f transition is a Laporte (or parity change)-forbidden transition. In contrast, the broad bands appearing in the UV region are intense (2–5 × 103 cm−1 M−1) since both the 5f2 → 5f16d1 transition and charge-transfer (CT) process, known to be responsible for absorption in the UV region, are Laporte-allowed.18,28,29
Interestingly, Hashem et al. recently reported the spectra in the UV region for UCl5− and UBr5− measured in tetrahydrofuran (THF).30 While more red-shifted, i.e., λmax is at 280–320 nm, those spectra share a similar spectral shape with that of U(OH)3+ (λmax at 209 nm). The possible contribution of the transition to the lowered 5f16d1 energy level and/or the halide-to-uranium CT process was pointed out in the study. In addition, Miles demonstrated the relationship between the wavelength of the CT band edge of aqueous An ions and their redox potentials early on.31 It is considered that H2O or OH− can participate in a CT process as a charge acceptor or donor, respectively. Similarly, we speculate that the electronic transitions responsible for the spectra of U4+ and U(OH)3+ in the UV region (Fig. 2(a)) possess characteristics of the transition from 3H4 (5f2) to 5f16d1 and/or the CT process between H2O/OH− and U(IV). It is further confirmed that mere changing of the isotope (H/D) in the aqueous solutions, i.e., using D2O, has negligible effects on the band positions of the absorption spectra (Fig. S2†). Rather, replacing the aqueous media with organic media such as alcohols induces solvatochromism, i.e., spectral red-shift (data not shown), which probably arises from differences in the dipolarity, polarizability, and hydrogen bond donating (or lone pair donating) capacity of the solvent molecules. These features can be considered typical of a CT process, however, a more in-depth study is needed to elucidate the nature of the U(IV) ion absorption bands in the UV region.
On the other hand, it is noteworthy that the sharp peak at 245 nm, which was assigned to the 3H4 → 1S0 transition in the literature,25 is absent in Fig. 1(a) and 2(a). This phenomenon is probably due to the relatively low ϵ values at 245 nm so that the peak could not be observed in the scale of molar absorbance in Fig. 1(a) and 2(a). In addition, as shown in Fig. 2, there is almost no temperature dependency in the molar absorption spectra, except for a slight decrease in ϵ of the major absorption bands when the temperature increases. Nonetheless, we used the individual molar absorption spectrum, deconvoluted at each temperature, for further analysis of temperature-dependent spectral data.
Evaluation of thermodynamic constants
As described in Experimental section, each value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 derived from the global fitting procedure was converted to
*β1 derived from the global fitting procedure was converted to 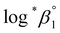 or
or 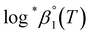 based on the SIT formula, as shown in eqn (3). In all experiments, we acquired two types of log
based on the SIT formula, as shown in eqn (3). In all experiments, we acquired two types of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 in parallel from each data set in the UV and visible regions. As summarized in Test A of Table 3, two
*β1 in parallel from each data set in the UV and visible regions. As summarized in Test A of Table 3, two 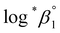 values from UV and visible spectra agreed well with each other within their uncertainty. Thus, the results from UV and visible spectra are combined to produce statistically averaged values for the rest of the thermodynamic study. The average value of
values from UV and visible spectra agreed well with each other within their uncertainty. Thus, the results from UV and visible spectra are combined to produce statistically averaged values for the rest of the thermodynamic study. The average value of 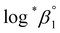 determined is −(0.51 ± 0.05), which is located at the upper boundary of the reported value: −(0.54 ± 0.06).3 Nonetheless, there is a slight but systematic difference between the results from the UV and visible spectra;
determined is −(0.51 ± 0.05), which is located at the upper boundary of the reported value: −(0.54 ± 0.06).3 Nonetheless, there is a slight but systematic difference between the results from the UV and visible spectra; 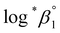 from the UV data is approximately 0.02 higher than those from visible-region data (see Table 3). While the reason is not yet clear, we think that the background correction process applied for UV data may increase the contribution of U(OH)3+ in the final spectrophotometric data.
from the UV data is approximately 0.02 higher than those from visible-region data (see Table 3). While the reason is not yet clear, we think that the background correction process applied for UV data may increase the contribution of U(OH)3+ in the final spectrophotometric data.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis of the aqua U4+ ion
1 hydrolysis of the aqua U4+ ion
| Test | pHc | I (mol kg−1) | T, °C | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 *β1 |
(kJ mol−1) | (J K−1 mol−1) | |
|---|---|---|---|---|---|---|---|
a Each 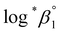 was derived exclusively from one of the spectral data sets (UV or visible region).b Values are was derived exclusively from one of the spectral data sets (UV or visible region).b Values are 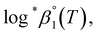 which were obtained at each temperature (see Experimental section).c Conditional constants at I = 0.15 m, i.e., ΔrHm and ΔrSm, as obtained using log*β1. which were obtained at each temperature (see Experimental section).c Conditional constants at I = 0.15 m, i.e., ΔrHm and ΔrSm, as obtained using log*β1. |
|||||||
| A | 1.7–2.2 | 0.02 | RT | −(0.94 ± 0.04) | −(0.51 ± 0.05) | — | — |
| 1.3–2.2 | 0.05 | −(1.05 ± 0.05) | |||||
| 1.0–2.2 | 0.10 | −(1.16 ± 0.04) | |||||
| 0.7–2.2 | 0.20 | −(1.24 ± 0.03) | (−(0.50 ± 0.06)UV, −((0.52 ± 0.08)Vis)a | ||||
| 0.3–2.2 | 0.51 | −(1.38 ± 0.04) | |||||
| 0–2.2 | 1.05 | −(1.48 ± 0.03) | |||||
| 0.8–2.1 | 2.09 | −(1.56 ± 0.02) | |||||
| B | 0.82–2.10 | 0.15 | 0 | −(1.87 ± 0.03) | −(1.17 ± 0.03)b | 43.4 ± 3.0 | 136 ± 11 |
| 5 | −(1.72 ± 0.03) | −(1.02 ± 0.03)b | |||||
| 10 | −(1.58 ± 0.03) | −(0.87 ± 0.03)b | (41.6 ± 2.8)c | (117 ± 10)c | |||
| 15 | −(1.46 ± 0.05) | −(0.75 ± 0.05)b | |||||
| 20 | −(1.32 ± 0.03) | −(0.61 ± 0.03)b | |||||
| 25 | −(1.20 ± 0.02) | −(0.48 ± 0.03)b | |||||
| 30 | −(1.07 ± 0.02) | −(0.34 ± 0.03)b | |||||
| C | 1.70 | 0.02–1.05 | 0–30 | (See Fig. 4(b)) | (See Fig. 4(c)) | (See Table S4 and Fig. S4) | |
| Ref. 3 | 0.02–2.21 | 25 | −(*0.54 ± 0.06) | 46.9 ± 9.0 | 147 ± 30 | ||
Further, we attempted to reevaluate the binary interaction coefficients (ε) of U(IV) ions by using the sets of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 in Table 3. As listed in Table 1, the uncertainty of ε(H+, ClO4−) is relatively small, i.e., ±0.02.3 Therefore, to yield the best result in terms of uncertainty we focused on obtaining Δε′, the direct difference between each ε of U4+ and U(OH)3+, using
*β1 in Table 3. As listed in Table 1, the uncertainty of ε(H+, ClO4−) is relatively small, i.e., ±0.02.3 Therefore, to yield the best result in terms of uncertainty we focused on obtaining Δε′, the direct difference between each ε of U4+ and U(OH)3+, using
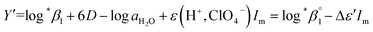 | (4) |
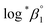 = −(0.51 ± 0.05) from the y-intercept and Δε′ = −(0.35 ± 0.03) from the slope. If we adopt the ε(U4+, ClO4−) = 0.76 ± 0.06 from NEA-TDB, the new ε(U(OH)3+, ClO4−) is estimated as 0.41 ± 0.07, as summarized in Table 1, which is within in the range of previously reported values.3 Also, in Table S3† the reestimated Δε is also compared with those from the literature.3,4
= −(0.51 ± 0.05) from the y-intercept and Δε′ = −(0.35 ± 0.03) from the slope. If we adopt the ε(U4+, ClO4−) = 0.76 ± 0.06 from NEA-TDB, the new ε(U(OH)3+, ClO4−) is estimated as 0.41 ± 0.07, as summarized in Table 1, which is within in the range of previously reported values.3 Also, in Table S3† the reestimated Δε is also compared with those from the literature.3,4
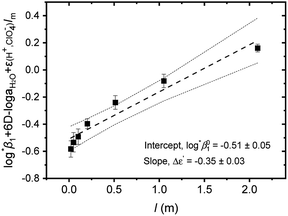 | ||
Fig. 3 Extrapolation to I = 0 of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 data of Test A in Table 3 for the hydrolysis of U4+ to U(OH)3+ using the SIT formula given by eqn (4). (■) experimental data, (---) linear fit, and (⋯) 95% confidence bands. *β1 data of Test A in Table 3 for the hydrolysis of U4+ to U(OH)3+ using the SIT formula given by eqn (4). (■) experimental data, (---) linear fit, and (⋯) 95% confidence bands. | ||
In addition, the changes of reaction enthalpy and entropy were examined by monitoring log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 at various temperatures. As shown in Fig. S3,† the spectra of U(IV) aqueous solution varies significantly upon temperature changes indicating the temperature dependency of log
*β1 at various temperatures. As shown in Fig. S3,† the spectra of U(IV) aqueous solution varies significantly upon temperature changes indicating the temperature dependency of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1. These spectral changes remain reversible at temperatures ≤ ∼30 °C and pH < ∼2, depending on the electrolyte level. For Test B in Table 3, a set of samples having an identical Im (0.15 m) were prepared, but the pHc of individual samples varied in a range of 0.82–2.10. Thus, log
*β1. These spectral changes remain reversible at temperatures ≤ ∼30 °C and pH < ∼2, depending on the electrolyte level. For Test B in Table 3, a set of samples having an identical Im (0.15 m) were prepared, but the pHc of individual samples varied in a range of 0.82–2.10. Thus, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 was calculated at each temperature as implemented in Test A. Subsequently, log
*β1 was calculated at each temperature as implemented in Test A. Subsequently, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 was converted to
*β1 was converted to 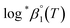 at each temperature by applying the newly determined Δε′ in Table 1 and the SIT formula (eqn (3)).
at each temperature by applying the newly determined Δε′ in Table 1 and the SIT formula (eqn (3)).
On the other hand, for Test C, a set of samples having the same pHc, but differing in Im in a range of 0.02–1.05 m, were examined. In this case, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 was directly extracted from the individual spectra; [U4+] and [U(OH)3+] were directly determined by finding the best combinational fitting of the experimental spectrum using the molar absorption spectra in Fig. 2 and an Excel Solver function-based optimization process developed in this study. The temperature dependences of log
*β1 was directly extracted from the individual spectra; [U4+] and [U(OH)3+] were directly determined by finding the best combinational fitting of the experimental spectrum using the molar absorption spectra in Fig. 2 and an Excel Solver function-based optimization process developed in this study. The temperature dependences of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 from Tests B and C in Table 3 are demonstrated in Fig. 4(a) and (b), respectively, using the van't Hoff equation,
*β1 from Tests B and C in Table 3 are demonstrated in Fig. 4(a) and (b), respectively, using the van't Hoff equation,
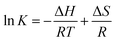 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = ln
K = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × log
10 × log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1).
*β1).
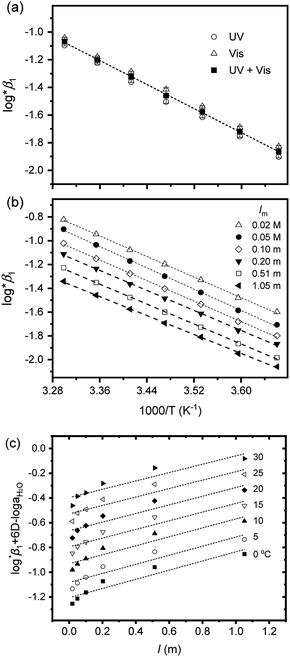 | ||
Fig. 4 Two van't Hoff plots using log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 in Table 3, (a) from Test B at I = 0.15 m and (b) from Test C at pHc 1.70 (ln *β1 in Table 3, (a) from Test B at I = 0.15 m and (b) from Test C at pHc 1.70 (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = ln K = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × log 10 × log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 in eqn (5)). (c) Extrapolation to I = 0 of log *β1 in eqn (5)). (c) Extrapolation to I = 0 of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *β1 data of (b) data using the SIT formula, eqn (3-1), at each temperature. All dotted lines indicate linear fit results. *β1 data of (b) data using the SIT formula, eqn (3-1), at each temperature. All dotted lines indicate linear fit results. | ||
For Test B, two conditional constants, i.e., ΔrHm and ΔrSm at I = 0.15 m, can be determined from the graphical analysis of van't Hoff plots in Fig. 4(a), which correspond to 41.6 ± 2.8 kJ mol−1 and 117 ± 10 J K−1 mol−1, respectively. Further, by employing 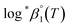 the standard molar thermodynamic constants,
the standard molar thermodynamic constants, 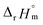 and
and 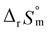 were determined to be 43.4 ± 3.0 kJ mol−1 and 136 ± 11 J K−1 mol−1, respectively, which are all in good agreement with literature values within the uncertainty range.3 Although Fig. 4(a) exhibits a systematic difference in the determined constants depending on the wavelength region (UV or Vis) of spectral data, the differences
were determined to be 43.4 ± 3.0 kJ mol−1 and 136 ± 11 J K−1 mol−1, respectively, which are all in good agreement with literature values within the uncertainty range.3 Although Fig. 4(a) exhibits a systematic difference in the determined constants depending on the wavelength region (UV or Vis) of spectral data, the differences 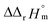 and
and 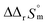 are within the range of measured uncertainty: approximately 1.3 kJ mol−1 and 3 J K−1 mol−1, respectively. The negative slopes of van't Hoff plots in Fig. 4 clearly indicate the endothermic property of the 1
are within the range of measured uncertainty: approximately 1.3 kJ mol−1 and 3 J K−1 mol−1, respectively. The negative slopes of van't Hoff plots in Fig. 4 clearly indicate the endothermic property of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis reaction. The large positive value of
1 hydrolysis reaction. The large positive value of 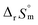 should result from the reduction of total charges upon hydrolysis (+4 → +3) of the U(IV) ion. The less restrained water molecules or the liberation of some from U(IV) ion's hydration shell contribute to increase in the disorder of the system.22
should result from the reduction of total charges upon hydrolysis (+4 → +3) of the U(IV) ion. The less restrained water molecules or the liberation of some from U(IV) ion's hydration shell contribute to increase in the disorder of the system.22
Test C and its corresponding results, as shown in Fig. 4(b), demonstrate the particular importance of the ionic strength correction for the determination of 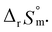 . It is apparent in Fig. 4(b) that the slope of the plot, i.e., ΔrHm, does not fluctuate significantly. However, the intercept, ΔrSm, consistently decreases as Im increases (see also Table S4†). Therefore, by applying the ionic strength correction to the data in Fig. 4(b), the
. It is apparent in Fig. 4(b) that the slope of the plot, i.e., ΔrHm, does not fluctuate significantly. However, the intercept, ΔrSm, consistently decreases as Im increases (see also Table S4†). Therefore, by applying the ionic strength correction to the data in Fig. 4(b), the 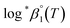 at each temperature was obtained, as displayed in Fig. 4(c). A new van't Hoff plot
at each temperature was obtained, as displayed in Fig. 4(c). A new van't Hoff plot 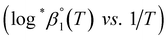 was then used to calculate
was then used to calculate 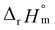 and
and 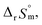 , as shown in Fig. S4.† After the ionic strength correction, the determined values for
, as shown in Fig. S4.† After the ionic strength correction, the determined values for 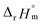 and
and 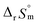 fall well within the uncertainty range of the values from Test B, which are the representative
fall well within the uncertainty range of the values from Test B, which are the representative 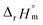 and
and 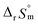 of this work. Also, these measured constants are compared in Table S5† with the selected literature values. Interestingly, Fig. 4(c) also allowed us to estimate the temperature dependency of Δε from the slope analysis of the plots. In fact, Δε at each temperature is similar to each other, and their standard deviation is approximately 0.01. Thus, we conclude that the Δε change over the temperature range (0–30 °C) in this work plays a minor role in the thermodynamics of the 1
of this work. Also, these measured constants are compared in Table S5† with the selected literature values. Interestingly, Fig. 4(c) also allowed us to estimate the temperature dependency of Δε from the slope analysis of the plots. In fact, Δε at each temperature is similar to each other, and their standard deviation is approximately 0.01. Thus, we conclude that the Δε change over the temperature range (0–30 °C) in this work plays a minor role in the thermodynamics of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis reaction.
1 hydrolysis reaction.
Reevaluated thermodynamic constants using literature data
We further attempted to reevaluate the thermodynamic constants that were recently reported by Brown and Ekberg using the selected literature data.4 All the available stability constants at 25 °C in the literature and those in Table 3 were combined and plotted as a function of the ionic strength (see Fig. S5†). The Δε and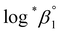 were derived by analyzing the non-linear I-dependence of log*β1 using a two-parameter SIT model (Δε = Δε1 + Δε2
were derived by analyzing the non-linear I-dependence of log*β1 using a two-parameter SIT model (Δε = Δε1 + Δε2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I).4 For the reaction enthalpy and entropy, the stability constants at I = 0 in Table 3 and those selected from the literature (Fig. S6†) were combined, so that the overall temperature varied over a wide range (0–150 °C). The reevaluated constants are listed in Table 4.
I).4 For the reaction enthalpy and entropy, the stability constants at I = 0 in Table 3 and those selected from the literature (Fig. S6†) were combined, so that the overall temperature varied over a wide range (0–150 °C). The reevaluated constants are listed in Table 4.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis of the aqua U4+ ion
1 hydrolysis of the aqua U4+ ion
| Reference | Δε1, Δε2a (kg mol−1) | a | b (kJ mol−1) | b (J K−1 mol−1) |
|---|---|---|---|---|
a Based on the two-term SIT expression in ref. 4; Δε = Δε1 + Δε2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I.b Used values of I.b Used values of 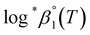 at 0 ≤ T ≤ 150 °C.c See calculation details in Fig. S5 and S6. at 0 ≤ T ≤ 150 °C.c See calculation details in Fig. S5 and S6. |
||||
| Ref. 4 | −(0.28 ± 0.03), 0.28 ± 0.06 | −(0.58 ± 0.08) | 42.7 ± 3.3 | 135 ± 10 |
| This workc | −(0.30 ± 0.05), 0.32 ± 0.08 | −(0.59 ± 0.08) | 43.3 ± 2.2 | 136 ± 7 |
Kinetic analysis at elevated temperatures
One aim of this work is to investigate the hydrolytic reaction of U(IV) at higher pH or temperature. Under such conditions, equilibria involving U(OH)n+4−n (n ≥ 2) species are expected to be established according to their stability constants; for U(OH)22+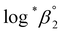 = −(1.1 ± 1) and for U(OH)3+
= −(1.1 ± 1) and for U(OH)3+ 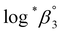 = −(4.7 ± 1).3 As an extension of the 1
= −(4.7 ± 1).3 As an extension of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis equilibrium shown above, we assume that further mononuclear ligations of hydroxide also result in facile and reversible reactions. If so, as soon as an aliquot of the U(IV) stock solution is added into an electrolyte with higher pH or temperature (at t = 0), as shown in Fig. 5 and 6, U(OH)3+ might instantaneously hydrolyze further into U(OH)22+ or other forms to establish a new equilibrium. Fig. 5(a) and 6(a) display the results of spectrophotometric reaction monitoring over time in two different settings; Fig. 5(a) at 26 °C and a pHc of 3 and Fig. 6(a) at 70 °C and a pHc of 2. However, we could not find spectroscopic evidence of the occurrence of such higher hydrolyzed species within our observation window (typically from minutes to days). Despite the difference in the reaction parameters of the two experiments in Fig. 5(a) and 6(a), each initial spectrum is almost identical with that of U(OH)3+ in terms of the spectrum shape and molar absorbance.
1 hydrolysis equilibrium shown above, we assume that further mononuclear ligations of hydroxide also result in facile and reversible reactions. If so, as soon as an aliquot of the U(IV) stock solution is added into an electrolyte with higher pH or temperature (at t = 0), as shown in Fig. 5 and 6, U(OH)3+ might instantaneously hydrolyze further into U(OH)22+ or other forms to establish a new equilibrium. Fig. 5(a) and 6(a) display the results of spectrophotometric reaction monitoring over time in two different settings; Fig. 5(a) at 26 °C and a pHc of 3 and Fig. 6(a) at 70 °C and a pHc of 2. However, we could not find spectroscopic evidence of the occurrence of such higher hydrolyzed species within our observation window (typically from minutes to days). Despite the difference in the reaction parameters of the two experiments in Fig. 5(a) and 6(a), each initial spectrum is almost identical with that of U(OH)3+ in terms of the spectrum shape and molar absorbance.
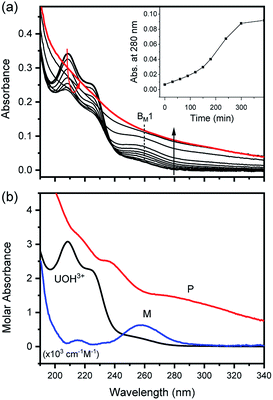
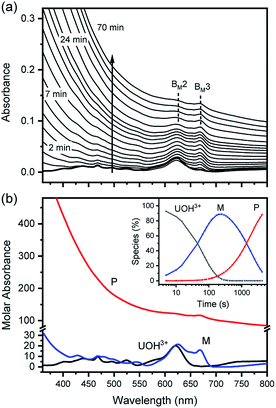
In fact, only an irreversible and slow process of which the final product is U(IV)-NPs from the reactant U(OH)3+ was observed as the reaction proceeded. As shown in Fig. 5(a) and 6(a), the overall spectrum changes exhibit the characteristics of a kinetic process in which reaction rates depend on pH and temperature. The reaction shown in Fig. 6(a) is an example of the hydrothermal U(IV)-NP production process. As we reported previously, the synthesized U(IV)-NP can retain its colloidal stability up to several weeks at pH ∼ 2 and RT.17 Interestingly, the emergence of an intermediate species is discovered in this work during the conversion of aqua U(IV) ions to U(IV)-NPs. The intermediate (M) was first probed due to its characteristic bands in both UV and visible regions, denoted as BM1, BM2, and BM3 in Fig. 5(a) and 6(a). Since it is obvious that the conversion processes to U(IV)-NPs are far from equilibria, we established the simple reaction model
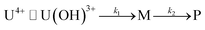 | (6) |
Herein we assume that the two stepwise reactions, U(OH)3+ to M and M to P, are pseudo first-order reactions. It is apparent that, as shown in Fig. 5(b) and 6(b), U(OH)3+ is the predominant species at t = 0 and plays a role as the reactant initiating the process. Therefore, k1 indicates the rate of consumption of U(OH)3+ in the system to possess quantitatively meaningful information. In contrast, since the chemical identity of M and P cannot be defined exactly, there is a limitation that the other outcomes of kinetic analysis will provide only qualitative information. In addition, light-scattering by the nanoparticles probably results in the deviation from the Beer–Lambert law for spectrophotometric analysis. However, despite such limitations, the optimization of kinetic analysis on the two different data sets was conducted successfully. It resulted in reliable converged outputs, e.g., reaction rates and singular spectra of M and P, as shown in Fig. 5(b) and 6(b) (see also Fig. S7,† an example of the residual plot). The inset plot in Fig. 6(b), one of the results of kinetic analysis, clearly shows the evolution and consumption of M over time.
The singular spectra of M clearly exhibit the characteristic major bands at BM1, BM2, and BM3 (∼260, 625, and 669 nm, respectively) in addition to some minor bands (see Table 2). In fact, BM3 plays an important role in this work as it reveals the irreversible nature of the first step (k1). In a separate experiment, we quenched the reaction when [M] reached its maximum level (see the inset of Fig. 6(b)) by lowering the temperature or by adding HClO4 to see if a backward reaction occurs. In any case, M remained in the solution once formed (see Fig. S8†), e.g., up to days at a refrigerated temperature (data not shown). Therefore, we confirm that the backward reaction of M to U(OH)3+ is not facile. On the other hand, the singular spectra of P are characterized by the monotonously decreasing absorption pattern from the UV to the visible region.
Fig. 7(a) and (b) show TEM images, the direct evidences of crystalline primary particles (2–3 nm) of U(IV)-NPs and their clusters (20–30 nm), respectively. We confirmed that both particles possess uraninite-like crystalline structures. The Rayleigh scattering of the incident light by the growing U(IV)-NPs can account for the increasing absorption over time in a wide wavelength range. It is also noted that a few broad undulating features in UV-Vis absorption of P (Fig. 5(b) and 6(b)) can be attributed to the semiconductor properties of U(IV)-NPs, e.g., UO2(cr) possessing optical bandgaps. Previous studies reported that such broad band absorption of UO2 could change by varying the U/O ratio and the oxidation state of U.32,33 Thus, we think that both of the primary particles and the U(IV)-NP clusters are to be responsible for the overall spectral shape of P. Therefore, P in the reaction model (eqn (6)) is used to represent the primary particles and their clusters combined.
 | ||
| Fig. 7 TEM images of (a) primary particles from the sample solution taken at the maximum level of [M] (see the inset of Fig. 6(b)) and (b) U(IV)-NPs (P), i.e., the clusters of primary particles after the reaction (eqn (6)) is completed. Arrows indicate distinctive lattice fringes (d = 0.32 nm) of the nanoscale U(IV) crystallites. | ||
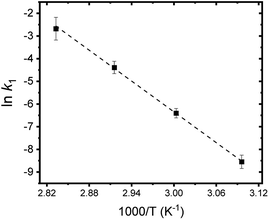
The results of reaction rate analysis also show temperature dependency. Typically, the transformation of aqua U(IV) ions to U(IV)-NPs at RT is a slow process, as shown in the inset of Fig. 5(a), that can take a few hours to days, depending on the I and pH. The k1 and k2 obtained at RT are comparable with each other, ∼1–2 × 10−4 s−1. In contrast, at higher temperatures, as shown in Fig. 6, the overall reaction proceeds much faster and generally k1 > k2; k1 = (1.2 ± 0.3) × 10−2 s−1 and k2 = (5 ± 3) × 10−4 s−1 at 70 °C (pH = 2.0). Thus, in this situation, the last step (k2) of eqn (6) becomes the rate-determining step of the whole process. While both k1 and k2 can be influenced by the solution parameters, like pH, I, and temperature, we found that k1 is more susceptible to temperature changes.
Fig. 8 summarizes the results of monitoring k1 at different temperatures (50–80 °C) as a plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k1 vs. 1/T, an Arrhenius-type plot. Since k1 reflects the consumption rate of soluble U(IV) ions in eqn (6), it can be used to describe the nucleation rate (J) of particles as shown by
k1 vs. 1/T, an Arrhenius-type plot. Since k1 reflects the consumption rate of soluble U(IV) ions in eqn (6), it can be used to describe the nucleation rate (J) of particles as shown by
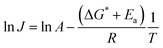 | (7) |
Therefore, combining all the evidences above, it is reasonable to conclude that M represents oligomeric oxohydroxo U(IV) species, e.g., Ux(O)y(OH)z4x−2y−z. Recently, Falaise et al. identified a hexameric U(IV) species (U6O4(OH)412+) in aqueous solutions containing an amino acid under a condition that is similar to that of our study.39 They also reported that the hexamer possesses a traceable absorptivity (λmax at 664 nm) at longer wavelengths than those of U4+ in the visible range. In fact, the overall process is very similar to that of iron oxide NP formation from soluble iron ions following a two-step oxolation mechanism.40 We speculate that the kinetic process represented by k1 and Ea in this study also includes a similar condensation process, as shown in Scheme 1. In this association mechanism, the lability of (coordinated) water molecules should be a key factor determining the reaction rate. Thus, it is very probable that the formation process of M is associated with both the condensation of U(IV) ions and the subsequent nucleation process that eventually creates primary particles.
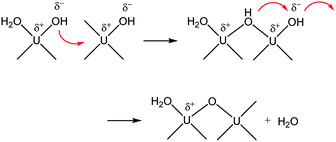 | ||
| Scheme 1 Condensation of U(IV) ions through a two-step associative mechanism as an initiating step of U(IV)-NP nucleation. | ||
In addition, it should be pointed out that in the M-dominant solution, the individual primary particles (crystallites) can exist separately from each other (Fig. 7(a)). However, at the last stage of the reaction (eqn (6)), raspberry-shape U(IV)-NP clusters become prevalent, as shown in Fig. 7(b). As U(OH)3+ and M are depleted in solution, the second step of Scheme 1 seems to prevail and contribute to reducing surface charges via oxo-bridge formation, thereby increasing the surface energy of primary particles and finally induce their aggregation. Therefore, we speculate that M is likely the key species involved in the nucleation and growth of these primary particles via influence on their colloidal stability.
Conclusions
To summarize, we examined the U(IV) hydrolytic reaction at a wide range of temperatures using UV-Vis spectrophotometric analysis. Characteristic absorption bands newly identified in the UV region (190–300 nm) were employed for U(IV) speciation together with those in the visible region. Aided by a numerical global fitting analysis for the collected spectral data, we successfully reevaluated the thermodynamic constants of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrolysis reaction and the ion interaction coefficient for U(IV) ions with ClO4−. The new values reported in this work include
1 hydrolysis reaction and the ion interaction coefficient for U(IV) ions with ClO4−. The new values reported in this work include 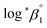 = −(0.51 ± 0.05),
= −(0.51 ± 0.05), 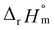 = 43.4 ± 3.0 kJ mol−1, and
= 43.4 ± 3.0 kJ mol−1, and 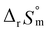 = 136 ± 11 J K−1 mol−1, which are well matched with literature values within the uncertainty range. Further, kinetic studies demonstrate that the increase of pH and/or temperature primarily induces the irreversible formation of reaction intermediates and subsequent production of U(IV)-NPs. The reaction intermediates that are newly observed in this study are suggested to be oligomeric oxohydroxo U(IV) species. This interpretation is strongly supported by other results, such as the confirmed two-step reaction model, the electronic absorption characteristics of the isolated spectrum of the intermediate, and the high energy barrier of the intermediate species generating step. We believe that the formation process of the intermediate is comprised of both the condensation of U(IV) ions and the subsequent nucleation process of U(IV)-NPs, while the interpretation of kinetic data should be considered only in a qualitative manner since the chemical identity of the intermediate and nanoparticles cannot be defined exactly. We expect that the spectroscopic and kinetic properties of various U(IV) species provided in this work will play a crucial role in understanding their speciation and evolution into polymeric oxohydroxo species in aqueous environments.
= 136 ± 11 J K−1 mol−1, which are well matched with literature values within the uncertainty range. Further, kinetic studies demonstrate that the increase of pH and/or temperature primarily induces the irreversible formation of reaction intermediates and subsequent production of U(IV)-NPs. The reaction intermediates that are newly observed in this study are suggested to be oligomeric oxohydroxo U(IV) species. This interpretation is strongly supported by other results, such as the confirmed two-step reaction model, the electronic absorption characteristics of the isolated spectrum of the intermediate, and the high energy barrier of the intermediate species generating step. We believe that the formation process of the intermediate is comprised of both the condensation of U(IV) ions and the subsequent nucleation process of U(IV)-NPs, while the interpretation of kinetic data should be considered only in a qualitative manner since the chemical identity of the intermediate and nanoparticles cannot be defined exactly. We expect that the spectroscopic and kinetic properties of various U(IV) species provided in this work will play a crucial role in understanding their speciation and evolution into polymeric oxohydroxo species in aqueous environments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is supported by the Nuclear Research and Development program of the National Research Foundation of Korea (Grant code: 2017M2A8A-5014719).References
- M. Altmaier, X. Gaona and T. Fanghänel, Chem. Rev., 2013, 113, 901–943 CrossRef CAS.
- K. Maher, J. R. Bargar and G. E. Brown, Inorg. Chem., 2013, 52, 3510–3532 CrossRef CAS.
- R. Guillaumont, T. Fanghänel, J. Fuger, I. Grenthe, V. Neck, D. A. Palmer and M. H. Rand, Update on the chemical thermodynamics of uranium, neptunium, plutonium, americium and technetium, in (OECD, NEA-TDB): Chemical Thermodynamics, Elsevier, North-Holland, Amsterdam, 2003, vol. 5, pp. 187, 707–752 Search PubMed.
- P. L. Brown and C. Ekberg, Actinide Metals, in Hydrolysis of Metal Ions, Wiley-VCH, Germany, Weinheim, 2016, ch. 9, vol. 1, pp. 336–349 Search PubMed.
- I. Grenthe, H. Wanner and I. Forest, Chemical thermodynamics of uranium, in (OECD, NEA-TDB): Chemical Thermodynamics, Elsevier, North-Holland, Amsterdam, 1992, vol. 1, pp. 120–124 Search PubMed.
- D. Rai, A. R. Felmy and J. L. Ryan, Inorg. Chem., 1990, 29, 260–264 CrossRef CAS.
- V. Neck and J. I. Kim, Radiochim. Acta, 2001, 89, 1–16 CAS.
- K. E. Knope and L. Soderholm, Chem. Rev., 2013, 113, 944–994 CrossRef CAS.
- L. S. Natrajan, A. N. Swinburne, M. B. Andrews, S. Randall and S. L. Heath, Coord. Chem. Rev., 2014, 266–267, 171–193 CrossRef CAS.
- H. Zänker and C. Hennig, J. Contam. Hydrol., 2014, 157, 87–105 CrossRef.
- W. Hummel, G. Anderegg, L. Rao, I. Puigdomenech and O. Tochiyama, Chemical Thermodynamics of Compounds and Complexes of U, Np, Pu, Am, Tc, Se, Ni and Zr with Selected Organic Ligands, in (OECD, NEA-TDB): Chemical Thermodynamics, Elsevier, North-Holland, Amsterdam, 2005, vol. 9 Search PubMed.
- C. Walther and M. A. Denecke, Chem. Rev., 2013, 113, 995–1015 CrossRef CAS.
- J.-I. Kim, Nucl. Eng. Technol., 2006, 38, 459–482 CAS.
- S. Y. Lee, W. Cha, J.-G. Kim, M. H. Baik, E. C. Jung, J. T. Jeong, K. Kim, S. Y. Chung and Y. J. Lee, Chem. Geol., 2014, 370, 40–48 CrossRef CAS.
- J. R. Bargar, R. Bernier-Latmani, D. E. Giammar and B. M. Tebo, Elements, 2008, 4, 407–412 CrossRef.
- B.-H. Jeon, B. A. Dempsey, W. D. Burgos, M. O. Barnett and E. E. Roden, Environ. Sci. Technol., 2005, 39, 5642–5649 CrossRef CAS.
- H. Cho and W. Cha, Colloids Interfaces, 2019, 3, 63 CrossRef CAS.
- W. T. Carnall in Gmelin Handbook of Inorganic Chemistry, ed. K.-C. Buschbeck, Springer-Verlag Berlin Heidelberg GmbH, 1989, pp. 69–161 Search PubMed.
- E. W. Richard, H. Yung-Jin and N. Heino, Radiochim. Acta, 2005, 93, 203–206 Search PubMed.
- D. Cohen and W. T. Carnall, J. Phys. Chem., 1960, 64, 1933–1936 CrossRef CAS.
- K. A. Kraus and F. Nelson, J. Am. Chem. Soc., 1950, 72, 3901–3906 CrossRef CAS.
- K. A. Kraus and F. Nelson, J. Am. Chem. Soc., 1955, 77, 3721–3722 CrossRef CAS.
- A. Kirishima, T. Kimura, O. Tochiyama and Z. Yoshida, Chem. Commun., 2003, 910–911 RSC.
- W. T. C. M. Crosswhite, in The Chemistry of the Actinide Elements, ed. J. J. Katz, G. T. Seaborg and L. R. Morss, Springer, Dordrech, 1984, pp. 1235–1277 Search PubMed.
- A. Kirishima, T. Kimura, R. Nagaishi and O. Tochiyama, Radiochim. Acta, 2004, 92, 705–710 CAS.
- E. C. Jung, H.-R. Cho, K. Park, J.-W. Yeon and K. Song, Appl. Phys. B, 2009, 97, 867–875 CrossRef CAS.
- W. Cha, S. Lee, E. Jung, H. R. Cho and M. Baik, J. Radioanal. Nucl. Chem., 2014, 302, 1127 CrossRef CAS.
- J. L. Ryan and C. K. Jørgensen, Mol. Phys., 1964, 7, 17–29 CrossRef CAS.
- C. K. Jørgensen, in Progress in Inorganic Chemistry, ed. S. J. Lippard, New York, 1970, pp. 101–152 Search PubMed.
- E. Hashem, A. N. Swinburne, C. Schulzke, R. C. Evans, J. A. Platts, A. Kerridge, L. S. Natrajan and R. J. Baker, RSC Adv., 2013, 3, 4350–4361 RSC.
- J. H. Miles, J. Inorg. Nucl. Chem., 1965, 27, 1595–1600 CrossRef CAS.
- R. J. Ackermann, R. J. Thorn and G. H. Winslow, J. Opt. Soc. Am., 1959, 49, 1107–1111 CrossRef CAS.
- J. M. Jones and D. G. Murchison, Nature, 1965, 205, 663–665 CrossRef CAS.
- Q. Li and Y.-S. Jun, Commun. Chem., 2018, 1, 56 CrossRef.
- A. C. Lasaga, Kinetic Theory in the Earth Sciences, Princeton University Press, Princeton, New Jersey, 1998 Search PubMed.
- I. Bretos, R. Jiménez, J. Ricote and M. L. Calzada, Chem. Soc. Rev., 2018, 47, 291–308 RSC.
- P. Deb and A. Basumallick, J. Nanopart. Res., 2004, 6, 527–531 CrossRef CAS.
- H. Zhang and J. F. Banfield, Chem. Mater., 2002, 14, 4145–4154 CrossRef CAS.
- C. Falaise, H. A. Neal and M. Nyman, Inorg. Chem., 2017, 56, 6591–6598 CrossRef CAS.
- N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05352j |
| This journal is © The Royal Society of Chemistry 2020 |