Machine learning for renewable energy materials
Geun Ho
Gu
,
Juhwan
Noh
 ,
Inkyung
Kim
,
Inkyung
Kim
 and
Yousung
Jung
and
Yousung
Jung
 *
*
Graduate School of EEWS, Korea Advanced Institute of Science and Technology (KAIST), 291 Daehak-ro 34141, Daejeon, 305-335, South Korea. E-mail: ysjn@kaist.ac.kr
First published on 30th April 2019
Abstract
Achieving the 2016 Paris agreement goal of limiting global warming below 2 °C and securing a sustainable energy future require materials innovations in renewable energy technologies. While the window of opportunity is closing, meeting these goals necessitates deploying new research concepts and strategies to accelerate materials discovery by an order of magnitude. Recent advancements in machine learning have provided the science and engineering community with a flexible and rapid prediction framework, showing a tremendous potential impact. Here we summarize the recent progress in machine learning approaches for developing renewable energy materials. We demonstrate applications of machine learning methods for theoretical approaches in key renewable energy technologies including catalysis, batteries, solar cells, and crystal discovery. We also analyze notable applications resulting in significant real discoveries and discuss critical gaps to further accelerate materials discovery.
1. Introduction
Despite the international effort emerging from the 2016 Paris agreement,1 the international commitment aiming to hold global warming below 2 °C above the pre-industrial level by 2100 is projected to be inadequate to meet the goal2 (Fig. 1). Beyond enforcing policies and supporting non-state actions, the research community can help meet this goal by innovating and deploying new economic materials that produce fuels, chemicals, and energy from renewable resources.2,3 While the carbon budget – the upper limit of CO2 emission to remain under the target temperature – is expected to run out by 2030 with 66 percent probability,2 discovering new materials and their deployment in the market takes on average 10–20 years with a large investment.4,5 Thus, the research community will have to develop new concepts and research approaches that accelerate materials discovery. In this regard, Mission Innovation, a global initiative led by 24 countries to accelerate global clean energy innovation, has advocated combining theoretical physical chemistry and materials science with high-throughput computational data generation, machine learning (ML), and robotics.3 This data-driven approach has the potential to reduce the cost and computation–experiment cycle time in the conventional trial-and-error approach, and is expected to accelerate materials discovery by a factor of ten.5,6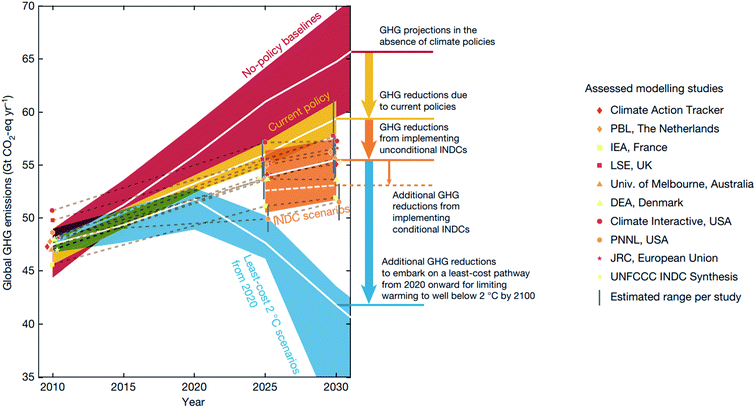 | ||
| Fig. 1 Global greenhouse gas (GHG) emissions as implied by the Intended Nationally Determined Contributions (INDCs) compared to the no-policy baseline, current-policy and 2 °C scenarios reproduced with permission from ref. 2 Copyright 2016 Springer, Nature. White lines show the median, and 20th–80th-percentile ranges are shown for no-policy and least-energy-economy-cost 2 °C scenarios, and the 10th–90th percentile across all studies is shown. | ||
Machine learning-based data-driven approaches have demonstrated tremendous impact in a number of aspects. The advancement in computational power and the emergence of big data have led to the success of machine learning methods in retail,7 medical diagnoses,8 image recognition,9 and speech understanding.10 These successes accompanying the advancement in machine learning have attracted interest in its application to science and engineering led initially by the U.S. Materials Genome Initiative.11
Conventional trial-and-error theoretical and experimental research studies involve an in-depth understanding of interesting, useful phenomena followed by the exploitation of new knowledge to test better materials. Such intuition-based approaches provide insightful knowledge but are not the most efficient approach for discovering new materials. Experimental approaches involve synthesis, characterization and property analysis by manual labor, resulting in a slow turnover. On the other hand, computational simulations can allow easier integration of high-throughput screening through automation. However, finding suitable descriptors or a model for the material's activity of interest is difficult and the ability to bridge the time-and-length scale to obtain macroscale properties is limited due to the large computational cost. In addition, computational simulations alone are not enough to discover materials as the simulations may not be realistic. For this, machine learning and robotics offer a systematic solution to speed up discovery.
Machine learning offers a flexible and accessible framework that correlates the materials' a priori knowledge with the properties of interest with respectable accuracy and speed given a large data set. For the experimental approach, interpreting and designing of the experiment can be delegated to the machine learning algorithms while robotics is used to automate the aforementioned manual labor.12 Notably, the Autonomous Research System, ARES, has used this approach successfully to optimize carbon nanotube synthesis.13 For the computational approach, machine-learning models offer a practical solution for high-throughput screening as theoretically developing a highly flexible model that correlates a priori knowledge with the properties of interest is often difficult. We do note that developing theoretical models and understanding is important for developing machine learning models as it provides insights into effective descriptors and designs.
Machine learning is also useful in coupling the small and large time-and-length scales. For example, molecular dynamics simulations are often performed with a surrogate model such as a force-field, but the accuracy of the energy and force is typically lower than that of the ab initio methods. Machine learning models can provide high accuracy while maintaining the large speed up from ab initio calculations.14 Another exciting and promising area of machine learning is inverse design where the desired properties of the material are given to the model, and materials with those properties are outputted.15 Its application to functional materials discovery has enormous potential in academia and industry, but the inverse design model development for materials is still in its infancy.
The U.S. Department of Energy has identified several major technical advancement goals for realizing a secure and sustainable energy future: (1) production of fuels from sunlight, (2) carbon-neutral electricity generation, and (3) revolutionizing energy efficiency and use.16 Among renewable sources of energy including wind, geothermal heat, and hydropower, solar energy is the most available and practical resource to harness.17 However, with current solar cell technology and its growth rate, solar cells are predicted to supply only 10 percent of the carbon-free energy demand in 2050.18 While the solar cell has grown to be the least expensive technology to produce energy in many countries,12 continued improvements in the cost, solar conversion efficiency, and energy storage are needed to meet the global energy demand sustainably.18
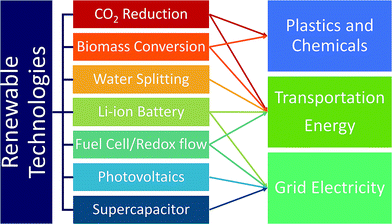
Currently, the transportation sector is almost completely dependent on fossil fuels. Replacing them with renewable and clean-burning fuel is thus essential, and discovering catalysts that convert water, biomass, and CO2 to hydrogen fuels and small hydrocarbons such as methanol and ethanol is critical.16 A large emphasis has been placed on discovering water-splitting catalysts as hydrogen is the cleanest fuel.17 Hydrogen fuel production, delivery and dispensing have become nearly cost-competitive with gasoline, and continued innovation and deployment is key.19 In addition to fuels, developing catalysts for renewable production of chemicals and plastics from biomass and CO2 is widely investigated as well. While renewable fuels can power transportation either by direct burning or generating electricity through fuel-cells, battery-operated cars are another solution to renewable transportation. In this regard, developing better batteries is necessary to increase range, reduce weight and improve efficiency.16 Also, renewable energy sources such as solar and wind energy suffer from inconsistent power output due to the day and night cycles and weather. Thus, developing battery technologies that provide large amounts of electricity over a long period of time is important.16 To address this, improvement of redox flow fuel-cells, which can be thought of as a hybrid of a battery and a fuel cell, to exhibit the potential to store electricity in large quantities, was carried out. In addition, improving electric grid reliability can reduce economic overhead expenses. The Lawrence Berkeley National Laboratory estimated that power outages cost the US about $80 billion annually.20 The materials discovery of high power energy storages to address micro-outages is a critical issue to improve electric grid reliance.16 As briefly discussed above, the trend of replacing the energy supply infrastructure with renewable energy sources is currently not encouraging, and CO2 emission from combustion is likely to continue.17 In this regard, developing CO2 capture materials can negate the CO2 emissions from using fossil fuels.17Fig. 2 summarizes and categorizes these key renewable energy technologies.
These challenges in realizing a renewable society can be addressed to some extent at the manufacturing level and by (non-)state actions, but, in essence, discovering game-changing materials with superior efficiency and low cost offers a fundamental solution. In this review, we aim to provide a broad overview of machine learning research in innovating renewable energy technology with a focus on the computational approaches. We refer to other in-depth reviews of machine learning methods for the physical system,6,21–26 and here we focus on applications of various machine learning techniques towards renewable energy materials development. Section 2 introduces key studies on critical renewable energy technologies discussed above such as solar cells, catalysts, CO2 capture, and batteries. We also summarize the emerging inverse design machine learning and others with large implications in accelerating materials design.27 To move forward, we report the success stories that have led to the real discovery of practical materials in Section 3. Finally, we close this review with the remaining gaps and prospects.
2. Machine learning in renewable energy materials
We begin this section by briefly summarizing the workflow of implementing machine learning. The subsequent sections discuss the literature overview of the applications and are organized by the characteristics of the machine learning applications. Section 2.2 summarizes the most widely used form where materials' properties are predicted from descriptors, and Section 2.3 is dedicated to machine learning potential, where energy and forces of atoms are calculated from atomic coordinates. The last section discusses the machine-learning based inverse modeling applied to materials.2.1. Developing machine learning modelling
Here, we briefly discuss the development of the machine learning model (see ref. 21 for in-depth discussion). The premise of the machine learning model is its ability to automatically learn and predict physical properties given a large enough dataset. As such, the critical steps in developing a successful model are (1) gathering a quality data set, and developing (2) a machine-understandable data representation and (3) a model that correlates the representation with the physical properties.25 The data collection method needs to be designed to minimize noise and to unbiasedly sample the data space, and the dataset needs to be sufficiently large. Data are typically collected experimentally and through ab initio calculations. However, the large resources needed to collect the data often become the bottleneck for machine learning development. In this regard, a number of databases are mostly freely available for molecules (ZINC,28 ChEMBL,29 GDB-13,30 GDB-17,31 and others), as well as for inorganic crystals (International Crystal Structure Database (ICSD),32,33 Materials Project (MP),34 Open Quantum Materials Database (OQMD),35 Atomic-FLOW for materials discovery (AFLOW),36 NOMAD, Pearson's Crystal Data, and others). After collecting data, the data need to be transformed into a mathematical representation that machines can understand, typically involving multi-dimensional matrices of real numbers. This so-called featurization is critical as the better the representation describing the physical properties of interest, the higher the accuracy of the model. In this regard, the field experts are critical as they can advise on suitable descriptors. Most of the research studies introduced here implement descriptors that have been known for some time from previous theoretical and experimental investigations. Lastly, the choice of model determines the model performance. Methods such as ridge regression,37 LASSO,38 elastic net,39 and partial least squares regression40 enhance linear regression by controlling over- and under-fitting and by enabling descriptor selection and so on. Classification methods such as support vector machines,41 decision trees,42 random forests,43 and logistic regression44 categorize data, and researchers have often used them to classify high and low activity of the materials. Kernel ridge regression45 learns a linear function from the similarity between the data point descriptors. In particular, the generalized theory of Kernel ridge regression called the Gaussian process46 offers uncertainty quantification, opening the door to the interesting applications discussed below. Recently, neural network modeling is rapidly entering the field.6,21–26 The type of neural network varies widely, as the framework enables flexible additions and connections between various GPU-optimized operations. The set of operations and the input and output connections between them are called the neural network architecture and are customized to solve the problem of interest. A neural network with a highly complex architecture is often referred to as deep learning.47 Deep learning has become a popular topic in the application of the physical system. Choosing the right model involves careful examination of the underlying physics between the representation and the properties of interest.2.2. Property predictions
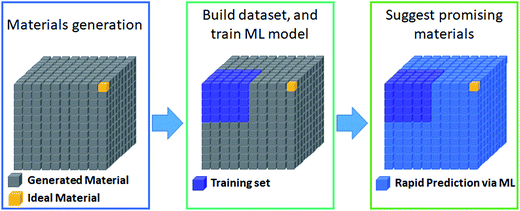
The most prevalent form of the application of machine learning is property prediction in order to rapidly screen materials. Using density functional theory (DFT) to calculate the desired properties remains a bottleneck for computational research due to its high cost; thus machine learning models are used to make rapid predictions. Machine learning model research typically involves the development of effective representation/descriptors. Effective descriptors ideally directly describe the activtiy and stability of materials with minimal calculations. In such a case, large-scale materials screening can be performed as shown in Fig. 3.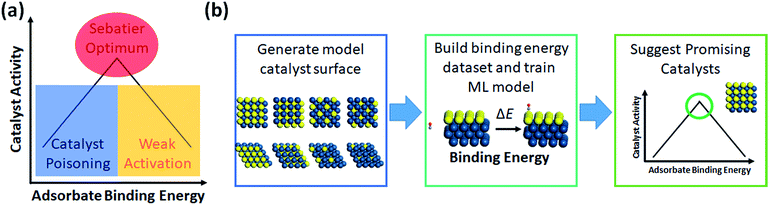 | ||
| Fig. 4 (a) Demonstration of the Sabatier principle for predicting optimal catalyst activity, and (b) workflow chart of catalyst screening via machine learning. | ||
While electronegativity and coordination number descriptors have shown good performance, the reactivity difference among alloys is often derived from d-band characteristics.54 However, the quantifying d-band characteristics for an alloy surface require DFT calculations, and are thus not ideal for high-throughput screening. In order to exploit d-band information without DFT, Noh et al. have introduced the d-band width of the mean-field muffin-tin orbital theory and used it together with electronegativity to compute the CO binding energy. Using the active-learning algorithm to sample the most informative data, the kernel ridge regression model demonstrated the current state-of-the-art performance of 0.05 eV RMSE for CO binding energy on the (100) surface.55 This study also has suggested a number of promising catalyst candidates for the CO2 reduction reaction.
More recently, machine learning is used to guide DFT calculations to find optimal electrocatalysts for CO2 reduction and H2 evolution through binding energy prediction. Here, the TPOT machine learning package is employed to automatically select and run DFT calculations where 80% and 20% of the DFT calculations were dedicated to optimizing the model and finding optimal materials, respectively.56 The automated calculation framework performed for little over a year and resulted in the identification of 131 promising candidate surfaces from various alloys made from a pool of 31 elements. As opposed to the studies above, the binding energy is computed with DFT accuracy as opposed to ML accuracy, thus adding credibility to the suggested candidates.
In a similar vein, Takigawa and co-workers have investigated models predicting the d-band center.57 Ordinary least squares regression, partial least squares regression, Gaussian process regression, and gradient boosting regression are used with nine readily accessible physical descriptors of metal atoms that do not require ab initio calculations. Bimetallic alloys with impure and overlay surfaces are considered. Gradient boosting regression showed the highest accuracy at 0.17 eV and 0.19 eV RMSE for impurity and overlay surfaces, respectively. In the interest of designing catalysts for hydrocarbon selectivity from the conversion of renewably obtained methane, Takigawa and co-workers have employed accessible descriptors to predict the binding energy of CH3, CH2, CH, C and H on Cu-based alloys.58 Out of nine regression methods, extra tree regression demonstrated a RMSE near 0.3 eV. Besides predicting the active components, controlling the structure of the catalyst can improve activity and binding energy, differing based on the facets of the surface. In this regard, Yıldırım and co-workers implemented a neural network to predict the CO binding energy on Au clusters for CO oxidation.59 CO oxidation is an important process for reducing CO emission from transportation and industries. Au catalysts have demonstrated good activity for CO oxidation, but the active site is not well known. Yildirim and co-workers have used the cluster size, overall charge, unpaired-electrons and coordination number to predict binding energies via a neural network. Asahi and co-workers have predicted N, NO and O binding energies and the formation energy of RhAu octahedral nanoparticles with various surface compositions using SOAP kernel regression.60,61 The binding energies and formation energies are predicted at ∼0.1 and 0.02 eV RMSE, respectively. Then, the binding energy and formation energy are used to estimate catalyst activity and predict nanoparticle stability, respectively. This work demonstrates the one-shot approach to directly predict catalyst activity given the composition of the nanoparticle.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 MOF structures is considered, where grand canonical Monte Carlo combined with the Lennard-Jones potential and DFT-derived electrostatic potential is used to model electronic interactions. The model was able to capture most of the known active MOFs. Froudakis and co-workers used the presence or absence of substructure patterns in MOFs as descriptors and “Just Add Data”, an automated machine learning analysis tool, to predict the CO2 and H2 uptake capacity.66 Compared to the earlier study by Woo and co-workers, this model is able to predict the continuous uptake capacity value and is trained using experimental data of 100 MOFs. Similar to Woo and co-workers, Gómez-Gualdrón and co-workers investigated CO2 capture prediction of MOFs using DFT, grand canonical Monte Carlo, and machine learning.67 Here, various storage properties of 400 MOFs are determined which are then used to train six different machine learning models via 13 different electronic and geometric descriptors. Instead of CO2, Woo and co-workers investigated storage capacity prediction for methane using the geometric features, such as pore size and void fraction, of 130
500 MOF structures is considered, where grand canonical Monte Carlo combined with the Lennard-Jones potential and DFT-derived electrostatic potential is used to model electronic interactions. The model was able to capture most of the known active MOFs. Froudakis and co-workers used the presence or absence of substructure patterns in MOFs as descriptors and “Just Add Data”, an automated machine learning analysis tool, to predict the CO2 and H2 uptake capacity.66 Compared to the earlier study by Woo and co-workers, this model is able to predict the continuous uptake capacity value and is trained using experimental data of 100 MOFs. Similar to Woo and co-workers, Gómez-Gualdrón and co-workers investigated CO2 capture prediction of MOFs using DFT, grand canonical Monte Carlo, and machine learning.67 Here, various storage properties of 400 MOFs are determined which are then used to train six different machine learning models via 13 different electronic and geometric descriptors. Instead of CO2, Woo and co-workers investigated storage capacity prediction for methane using the geometric features, such as pore size and void fraction, of 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs with multilinear regression, decision trees, and nonlinear support vector machines.65 Analysis of the model revealed the desired geometric properties of the MOF that could lead to high methane storage.
000 MOFs with multilinear regression, decision trees, and nonlinear support vector machines.65 Analysis of the model revealed the desired geometric properties of the MOF that could lead to high methane storage.
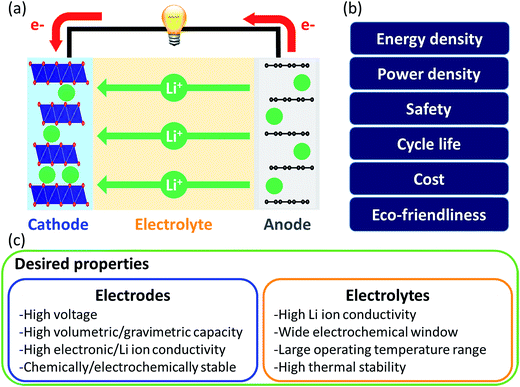
Liquid electrolytes are often based on organic solvents and suffer from flammability. In this regard, solid electrolytes are promising as they are generally less flammable and have a larger electrochemical window than liquid electrolytes. However, solid electrolytes suffer from low Li ion conductivity and thus research on them focuses on finding highly conductive materials. In computational approaches, the Li-ion migration barrier is widely computed as a surrogate measurement of ionic conductivity. Jalem et al. applied the partial least squares algorithm to predict the migration barrier of olivine-type LiMXO4.73 Analyzing the model coefficient plot and variable importance in projection plot revealed that descriptors such as the ionic size of M and local lattice distortion are important for migration barriers and new promising olivine-type solid electrolytes were suggested. Furthermore, Jalem et al. employed the neural network framework for olivine-type LiMXO4 as solid electrolyte candidates to predict the migration barrier and cohesive energy.74 The neural network migration barrier prediction model reported by Jalem et al. was applied to tavorite type LiMTO4F materials as a solid electrolyte.75 The Li migration trajectory has also been widely studied to understand the Li migration mechanism and elucidate the rate determining step which can be improved for ionic conductivity. Chen et al. developed a density-based clustering method to elucidate Li migration trajectories of garnet-type solid electrolytes.76 In addition, Li ion conductivity was directly evaluated using experimental measurements where the support vector regression algorithm with descriptors of diffusivity at 1600 K, average volume of the disordered structure, ordered/disordered phase transition temperature and temperature at which ionic conductivity was measured, were employed to classify the Li ion conductivity of LiSiCON type solid electrolytes77 and garnet-type solid electrolytes.78 Jalem et al. applied the Gaussian process with Bayesian sampling to predict the migration barrier of tavorite type solid electrolytes.79
For electrodes, Li ions intercalate and deintercalate into and from the electrodes to store and release energy. Intercalation characteristics of the electrode are critical for energy and power densities. To achieve high energy density, researchers have focused on understanding structure–performance relationships by controlling the elements and structure of electrode materials. In this regard, Shandiz et al. classified three crystal structures (monoclinic, orthorhombic, and triclinic) from Li–Si–(Mn, Fe, Co)–O compositions using five algorithms.80 Among them, random forests and extremely randomized trees showed the highest accuracy. Wang et al. used partial least squares regression to distinguish the descriptors which described the volume change during delithiation of cathode candidates well.81 Eremin et al. applied ridge regression to predict the energy of LiNiO2 and LiNi0.8Co0.15Al0.05O.82 From the results, common features that (de)stabilize the structure and stabilization effect of doping were discovered. The investigation revealed important descriptors for evaluating the migration barrier of LiMTO4F structures and the model was extended to predict the values of a database containing two structure types, both having the 1D Li path in common. Okamoto employed Kernel ridge regression with Bayesian optimization sampling to evaluate the change in Gibbs free energy before and after Li intercalation into a graphite anode.84
One of the high power energy storage techonology is called, Superconducting Magenetic Energy Storage (SMES). Majority of the SMES cost is in the superconductor materials. Discovering economic superconductors may aid in the SMES distribution. However, machine learning-based research on superconductive materials is preliminary, as the mechanisms behind high-temperature superconductivity are not clear. Stanev et al. applied the random forest method to classify critical temperatures to identify superconductive materials. 35 promising materials and their common characteristics were determined.84 For the redox flow battery, Kim et al. have developed a multiple descriptor multiple kernel method that predicts the solubility of active molecule derivatives of the molecular candidates in an aqueous electrolyte depending on the pH.85
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 perovskites with further analysis of the stability using the DFT calculations. Dey et al. investigated a machine learning approach for predicting the bandgap of chalcopyrite type materials using OLS, SPLS, elastic net, and LASSO coupled with rough set and principal component analysis methods.92 A total of 15 accessible elemental properties are used as descriptors to predict the bandgap, where 28 data points are used for training. The bandgaps of 227 chalcopyrite materials are predicted. Though this study greatly expanded the knowledge of the solar cell performance of chalcopyrite materials, the lack of training data limited the testing of model accuracy. Beyond specific types of materials, Ward et al. developed a flexible framework that can be used for crystalline or amorphous materials.93 Here, the OQMD database is used where properties such as the volume, formation energy, and bandgap were the target properties and 145 attributes were used as descriptors. The algorithms such as partial least squares regression, LASSO, decision tree, kernel ridge regression, Gaussian process regression, and neural networks are used together with an effective data partitioning strategy for high accuracy. On the other hand, the organic solar cell has been gaining popularity due to its accessible electronic property engineering as well as its cheap cost. Aspuru-Guzik and co-workers have used the Harvard Organic Photovoltaic Dataset where molecular fingerprint methods were used together with the Gaussian process to predict properties such as frontier orbital energies, optical gaps, current density, open circuit voltage, and power conversion efficiency. The same strategy is applied to discover non-fullerene acceptors where the molecular fingerprint based Gaussian process is used to leverage the difference between the DFT calculated and experimental frontier molecular orbital energies.94 Schmidt and co-workers have developed the variational autoencoder method where context-free grammar representations of molecules are implemented to predict the LUMO and optical transition energy. The variational autoencoder enables inverse modeling, which is used to identify a number of molecules with desired properties.
000 perovskites with further analysis of the stability using the DFT calculations. Dey et al. investigated a machine learning approach for predicting the bandgap of chalcopyrite type materials using OLS, SPLS, elastic net, and LASSO coupled with rough set and principal component analysis methods.92 A total of 15 accessible elemental properties are used as descriptors to predict the bandgap, where 28 data points are used for training. The bandgaps of 227 chalcopyrite materials are predicted. Though this study greatly expanded the knowledge of the solar cell performance of chalcopyrite materials, the lack of training data limited the testing of model accuracy. Beyond specific types of materials, Ward et al. developed a flexible framework that can be used for crystalline or amorphous materials.93 Here, the OQMD database is used where properties such as the volume, formation energy, and bandgap were the target properties and 145 attributes were used as descriptors. The algorithms such as partial least squares regression, LASSO, decision tree, kernel ridge regression, Gaussian process regression, and neural networks are used together with an effective data partitioning strategy for high accuracy. On the other hand, the organic solar cell has been gaining popularity due to its accessible electronic property engineering as well as its cheap cost. Aspuru-Guzik and co-workers have used the Harvard Organic Photovoltaic Dataset where molecular fingerprint methods were used together with the Gaussian process to predict properties such as frontier orbital energies, optical gaps, current density, open circuit voltage, and power conversion efficiency. The same strategy is applied to discover non-fullerene acceptors where the molecular fingerprint based Gaussian process is used to leverage the difference between the DFT calculated and experimental frontier molecular orbital energies.94 Schmidt and co-workers have developed the variational autoencoder method where context-free grammar representations of molecules are implemented to predict the LUMO and optical transition energy. The variational autoencoder enables inverse modeling, which is used to identify a number of molecules with desired properties.
In addition to the bandgap, the stability of the materials is critical for their longevity. The stability of the materials can be analyzed by calculating the energy above the convex hull (in eV per atom) within the phase diagram constructed from the given elements in a theoretical or experimental manner. We note that the energy above the convex hull is defined as the difference between the enthalpy of the formation of a target material and the most stable enthalpy of formation evaluated from the phase diagram. In this regard, Li et al.95 proposed classification and regression models for predicting the energy of the convex hull of a perovskite oxide material using the elemental property data (the best F1 score for classification is 0.881 and the best RMSE for regression is 28.5 meV per atom). Furthermore, the model was used to discover 15 new promising perovskite materials. In addition, Schmidt et al.96 tested various types of machine learning models including ridge regression, random forests, extremely randomized trees (including adaptive boosting), and neural networks to predict the energy above the hull for 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cubic perovskite materials (ABX3), where extremely randomized trees outperformed all the other models with a mean absolute error of 121 meV per atom.
000 cubic perovskite materials (ABX3), where extremely randomized trees outperformed all the other models with a mean absolute error of 121 meV per atom.
In order to search for sunlight absorbing molecules, Xin and co-workers tested LASSO, kernel ridge regression, support vector machines, and neural networks to predict energy gaps of porphyrin molecules using molecular fingerprints, Coulomb matrices, chemoinformatics, and electro topological-state indices as descriptors.99 The model captures the energy gaps within 0.06 eV RMSE, and its analysis suggests structural motifs that influence energy gaps via sensitivity analysis. Besides utilizing CO2 and splitting water, biomass utilization is another attractive pathway to produce chemicals and fuels. Lignocellulosic monomers are already functionalized as opposed to petrochemicals which need functionalization, and aromatic structures, widely synthesized in the petrochemical industry, are already present. However, theoretical studies of biomass conversion are difficult due to their large reaction network.100 In this regard, Vlachos and co-workers have applied LASSO to predict the thermochemistry of biomass monomer adsorbates on metal surfaces using subgraph descriptors.101 The model demonstrated a RMSE of 0.09 eV for the heat of formation of lignin monomers on the Pt(111) surface. Such a model reinforces the drawbacks of a popular semi-empirical method for predicting energy called group additivity, where manually identifying graph descriptors is difficult.102–104 Metal heterogeneous catalysts are often synthesized by supporting metal particles on oxides, but theoretical metal catalyst studies often use ideal surfaces as a model catalyst. In this regard, Hammer and co-workers introduced a genetic algorithm to globally optimize the metal nanoparticle structure on supports, where the pairing of candidates involved cutting of two candidate particles in half and splicing.105
While a large number of machine learning studies on catalysts focused on metal alloys, several studies addressed homogeneous catalysts. Rothenberg and co-workers investigated cross-coupling reactions via a neural network where steric and electronic descriptors of ligands, substrates, catalyst precursors and 412 Heck reactions are correlated with experimentally computed catalyst activity.106 Also, Kulik and co-workers have been leading the efforts in developing machine learning frameworks for transition metal complexes, which are used often in homogeneous catalysts.107 Kulik and co-workers introduced molSimplify, an automated toolkit for screening and discovery of inorganic and intermolecular complexes.108 The neural network has been implemented to predict important properties such as energetics, metal–ligand bond lengths, spin-states, and oxidation states and the model accounts for DFT functional sensitivities. An example is the redox potential design of octahedral Fe(II/III) redox couples with nitrogen ligands. Furthermore, they have introduced revised autocorrelation functions that encode atomic properties to molecular graphs demonstrating great accuracy (0.26 eV mean absolute error for atomization energies) for various properties of metal complexes.109 Finally, the genetic algorithm and neural network are employed to discover spin-crossover complexes, which have applications as spin-based switches.110 This work demonstrates the accelerated discovery of machine learning augmented screening.
Beyond the specific applications discussed above, machine learning methods have been extensively applied for diverse materials applications due to their flexibility.111 Faber et al.112 proposed the formation energy prediction machine learning model for Elpasolite materials by utilizing kernel ridge regression. The developed model was used to screen all possible candidates suggesting that 90 out of 212 new structures are predicted to be on the convex hull. Legrain et al.113 utilized a random forest machine learning model to predict the force constant of the 121 metastable phase of KZnF3 with a mean absolute error of 0.17 eV Å−2, and the predicted force constant was used to estimate phonon spectral features, heat capacities, vibrational entropies, and vibrational free energies, which were in good agreement with the ab initio calculations. Furthermore, Pilania et al.114 proposed a machine learning model to estimate diverse physical properties (formation energy, bandgap, elastic constants and so on) for more than 1200 binary wurtzite superlattices. Dixon and co-workers have developed a linear model predicting thermochemistry using fragments of ZnO nanoparticles, predicting various phase transitions and providing insights on particle growth for ZnO.115 All of the studies discussed here lead to a concrete conclusion that combining the ab initio calculations with the novel machine learning model can help to accelerate the understanding of novel materials.
2.3. Machine learning potentials
Though DFT has realized simulation-based research, DFT calculation is expensive and, therefore, limited to simulations of small time and length scales. For example, computations of bandgaps and formation energies require a single snapshot calculation of the unit-cell; the macro- and meso/micro-scale simulations such as catalyst surface dynamics, surface–solvent interface dynamics, and lithium diffusion coefficients are difficult. Effectively bridging time and length scales is critical to materials discovery as many properties of interest are not directly accessible from DFT calculations but need multi-scale strategies. For example, catalysis is one of the most complex multi-scale phenomena, where the surface and adsorbates dynamically interact and change. In the simulation of gaseous phase catalysts, micro-kinetic modeling and kinetic Monte Carlo have been used successfully to bridge these gaps116 (similarly for the battery as well117). However, these multi-scale approaches rely on the ordered structure of the materials, and such multi-scaling becomes difficult for disordered structures.118 In such a case, developing a force-field-like model for the complex system could bridge these scales by its fast-prediction ability (see Fig. 6). Force-field modeling has been used typically to address larger-scale simulations, but flexible models that can predict energy and force at ab initio-level accuracy is desired. In this regard, machine learning has been used to correlate atomic coordinates with the potential surface. Machine learning potential directly learns the potential surface from ab initio calculations, and aims to predict the ab initio potential surface at a significantly lower cost.14,119,120 While the non-physical form of machine learning limits model interpretation and extrapolation is difficult, the fast calculation speed and the ab initio comparable accuracy are the combination of the advantages of force-field and DFT.121 We refer to other reviews for an overview of the various machine learning potential methods.119,120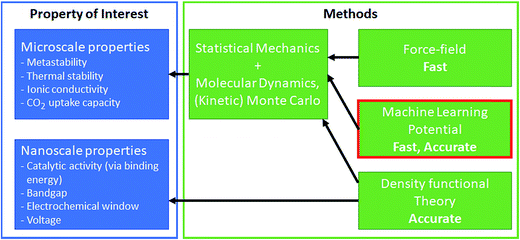 | ||
| Fig. 6 Machine learning potential enables microscale simulations to understand other key properties of interest. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 bulk structures, and 5347 slab geometries is used to achieve a 2 meV per atom RMSE. Such modeling has been applied to copper bulk and surfaces as well.123 The MLP framework of Behler and co-workers has been developed into the Aenet software package that can systematically generate data sets to develop a model.124 Software evaluation demonstrates independence of the CPU time from the number of atoms, attractive for the multi-scale approach. Similarly, Kitchin and co-workers have employed a MLP framework for zirconia to test its ability to predict diverse bulk properties.125 A total of 2178 DFT calculations are used to train the model which demonstrated high accuracy for formation energy, the equation of states, oxygen vacancy formation energies, and diffusion barrier prediction. MLP has also shown great predictive ability for predicting surface energy, palladium vacancy formation, diffusion barriers, and adatom diffusion barriers for palladium particles.126
037 bulk structures, and 5347 slab geometries is used to achieve a 2 meV per atom RMSE. Such modeling has been applied to copper bulk and surfaces as well.123 The MLP framework of Behler and co-workers has been developed into the Aenet software package that can systematically generate data sets to develop a model.124 Software evaluation demonstrates independence of the CPU time from the number of atoms, attractive for the multi-scale approach. Similarly, Kitchin and co-workers have employed a MLP framework for zirconia to test its ability to predict diverse bulk properties.125 A total of 2178 DFT calculations are used to train the model which demonstrated high accuracy for formation energy, the equation of states, oxygen vacancy formation energies, and diffusion barrier prediction. MLP has also shown great predictive ability for predicting surface energy, palladium vacancy formation, diffusion barriers, and adatom diffusion barriers for palladium particles.126
Artrith and co-workers have investigated solvents and Au–Cu alloys using MLP. Au–Cu alloys have shown promising overpotential and stability for CO2 reduction electrochemistry.129 However, identifying the active site for electrochemical reactions is difficult due to the solvent and adsorbate. The MLP model is trained using 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 995 DFT calculations consisting of the Au–Cu alloy bulk, slab, and clusters in a vacuum and in water. The developed model was combined with molecular dynamics and Monte Carlo simulations and predicted a Cu–Au core–shell structure in agreement with experimental results. The temperature dependence of the core–shell structure is observed and a potential strategy for nanoparticle structure control during experimental synthesis is suggested. A computation-based synthesis suggestion is atypical due to the complexity of the synthesis simulation, demonstrating the MLP's ability to couple the time–length-scale. In addition, Artrith and co-workers have shown that the Cu–Au alloy structure changes from the core–shell structure in a vacuum to a mixed surface in an aqueous solvent.130 This demonstrates that MLP can be used to understand the surface structure under reaction conditions in order to perform DFT investigation more in-line with experimental conditions. The MLP predicted nanoparticle structure agreed well with the Wulff-construction predicted structure, validating the neural network potential-based particle prediction. While Artrith and co-workers used a simple frozen water shell model to account for the solvent effect, Behler and co-workers performed water–copper interface dynamics simulations for various surfaces.131 Here, the water–copper interaction strength has been shown to depend on the facets, and structures of the interface hydration layer have been analyzed.
995 DFT calculations consisting of the Au–Cu alloy bulk, slab, and clusters in a vacuum and in water. The developed model was combined with molecular dynamics and Monte Carlo simulations and predicted a Cu–Au core–shell structure in agreement with experimental results. The temperature dependence of the core–shell structure is observed and a potential strategy for nanoparticle structure control during experimental synthesis is suggested. A computation-based synthesis suggestion is atypical due to the complexity of the synthesis simulation, demonstrating the MLP's ability to couple the time–length-scale. In addition, Artrith and co-workers have shown that the Cu–Au alloy structure changes from the core–shell structure in a vacuum to a mixed surface in an aqueous solvent.130 This demonstrates that MLP can be used to understand the surface structure under reaction conditions in order to perform DFT investigation more in-line with experimental conditions. The MLP predicted nanoparticle structure agreed well with the Wulff-construction predicted structure, validating the neural network potential-based particle prediction. While Artrith and co-workers used a simple frozen water shell model to account for the solvent effect, Behler and co-workers performed water–copper interface dynamics simulations for various surfaces.131 Here, the water–copper interaction strength has been shown to depend on the facets, and structures of the interface hydration layer have been analyzed.
MLP has also been applied for the gas phase adsorbate surface system as well. Kroes and co-workers investigated the N2/Ru(0001) system where the phonons, wave-like vibrations of surface atoms, are used to describe dissociative chemisorption of N2 more in-line with the experimental conditions.132 Combining MLP with molecular dynamics allows the computation of a sticking coefficient lower than previously possible using ab initio molecular dynamics, which also shows good agreement with the experiment. Kitchin and co-workers have implemented MLP to predict dynamic interactions between oxygen atoms on the Pd(111) surface which enables molecular dynamics simulation of adsorbates on catalytic surfaces.133
On the other hand, Nørskov and coworkers implemented MLP for classic binding energy calculation problems.134 In the interest of predicting CO2 reduction activity, MLP is used to learn the CO binding energy for various catalytic site environments of the Ni–Ga alloy. The geometries of CO at 583 binding sites were relaxed using neural network potential, and if the neural network potential error rose above 0.2 eV, DFT calculation is performed which is subsequently used as a training set. This modeling revealed the active sites for the Ni–Ga alloy, providing a rationalization for its high activity for CO2 reduction. Compared to full explicit DFT calculations, only 10% of DFT calculations are used, demonstrating computational time efficiency of the machine learning approach.
2.4. Crystal discovery
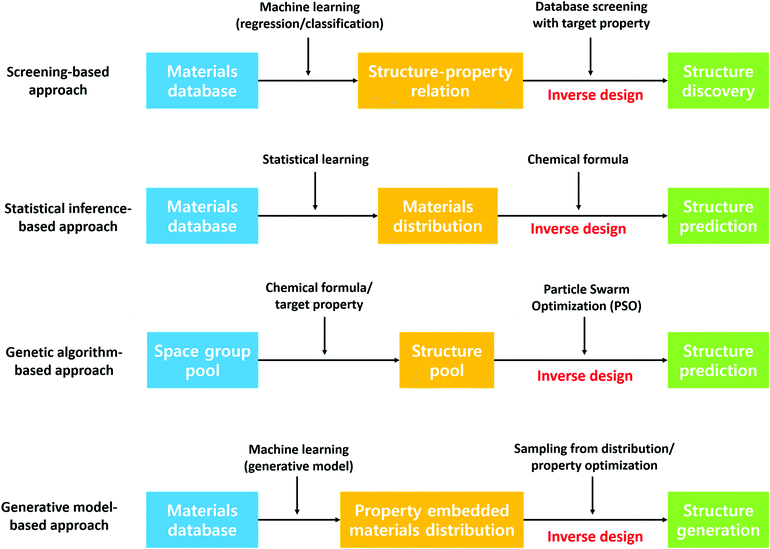
Besides predicting the properties of interest of a defined chemical space, discovering new stable crystal structures is another critical aspect of materials discovery. Leveraging the former approach to discover materials typically involves generation of idealized materials followed by using machine learning to predict target properties. However, generated idealized materials may not be stable materials, may be unsynthesizable or the synthesis routine may not be known. In this regard, the latter approach can provide the community with a database of stable materials which researchers can use as a starting point for searching for new materials. For example, Jeffrey and co-workers have discovered 15 new photoanode materials for splitting water by step-by-step screening.139 This approach has been realized considerably through the Materials Genome Initiative, a result of which is the Materials Project crystal structure database. In addition, designing materials with target properties, the so-called inverse design of materials, has received tremendous attention recently due to its implications of guided materials discovery. Although the theoretical and experimental high-throughput screening has demonstrated success in finding new promising candidates, these approaches omit materials that are not in the screening scope. In this section, we present a literature review on various data-driven models for crystal structure prediction and high-throughput screening as well as inverse designing. Fig. 7 summarizes the methods that are discussed below.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 theoretically calculated diffraction patterns from the 3D atomic arrangement are used to train the deep learning model. Although this model is limited to only 8 crystal systems, the proposed model outperforms other packages significantly regardless of defects in the crystal structures. In the case of an experimental investigation, the extraction of symmetry group information from the spectroscopy data can enhance experimental characterization capability. In this regard, Park et al.141 trained a deep learning model to classify X-ray diffraction patterns into 230 space groups, 101 extinction groups, and 7 crystal systems simultaneously. The model demonstrates a reliable accuracy of 81.14, 83.83 and 94.99% for the space group, extinction group, and crystal system, respectively. On the other hand, a couple of models have been developed to predict the crystal structure type given the fixed chemical formula type such as equiatomic binary (AB)142 and ternary (ABC)143 compounds. Here, the support vector machine was used for the high-throughput classification model. Notably, the model identified a new experimentally validated material, an RhCd compound with the CsCl-type structure.142 Furthermore, Oliynyk et al.143 experimentally confirmed 19-polymorphs between TiNiSi- and ZrNiAl-type structures in agreement with experimental results.
000 theoretically calculated diffraction patterns from the 3D atomic arrangement are used to train the deep learning model. Although this model is limited to only 8 crystal systems, the proposed model outperforms other packages significantly regardless of defects in the crystal structures. In the case of an experimental investigation, the extraction of symmetry group information from the spectroscopy data can enhance experimental characterization capability. In this regard, Park et al.141 trained a deep learning model to classify X-ray diffraction patterns into 230 space groups, 101 extinction groups, and 7 crystal systems simultaneously. The model demonstrates a reliable accuracy of 81.14, 83.83 and 94.99% for the space group, extinction group, and crystal system, respectively. On the other hand, a couple of models have been developed to predict the crystal structure type given the fixed chemical formula type such as equiatomic binary (AB)142 and ternary (ABC)143 compounds. Here, the support vector machine was used for the high-throughput classification model. Notably, the model identified a new experimentally validated material, an RhCd compound with the CsCl-type structure.142 Furthermore, Oliynyk et al.143 experimentally confirmed 19-polymorphs between TiNiSi- and ZrNiAl-type structures in agreement with experimental results.
Fischer et al.144 approached materials discovery using statistics and proposed data mining structure prediction (DMSP), a probability-theory-based model, for binary alloys, and the model was used to predict novel nitrogen-rich nitride materials.145 Furthermore, this concept was extended by Hautier et al.146 to ternary materials where 209 new compounds were discovered with a minimal computational budget. The model predicted two new compounds in the Mg–Mn–O system, MgMnO3 and Mg2Mn3O8, and for MgMnO3, the diffraction pattern matched the experimental diffraction pattern. On the other hand, Ryan et al.147 proposed a neural network based model using the normalized atomic fingerprints to predict crystal structures given alloy compositions.
Besides the supervised-learning models introduced above, DFT-based evolutionary algorithms have been widely employed to predict crystal structures and generate materials with target properties. The software packages Crystal structure analysis by particle swarm optimization148 and XTALOPT149,150 are well known. Zhou et al.151 used XTALOPT to predict host–guest Na–Fe intermetallics at high pressures and Na3Fe and Na4Fe were predicted to be stable at pressures above 120 and 155 GPa, respectively. All the predicted materials have formed a host–guest-like Na sublattice structure. These structures are similar to the host framework of the self-hosting incommensurate phases observed in group I and II elements. In addition, the model is further used to find 2D B2S materials and discover new anisotropic 2D-Dirac cone materials.152 Furthermore, Wang et al.153 used the evolutionary algorithm to predict new metastable allotropes of Li2MnO3 as cathode materials under a high pressure of 20 GPa. Similarly, Shamp et al.154 predicted the most stable hydrides of phosphorus (PHn, n = 1–6) at 100, 150, and 200 GPa, pressure of which the phosphorus hydrides decomposes to elemental phases such as PH2 and H2. Interestingly, three metallic PH2 phases have been found that are dynamically stable and superconducting between 100 and 200 GPa providing new insights on high-pressure-driven materials with properties that cannot be observed at 1 atm.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 candidates. Similarly, Balachandran et al.,157 investigated into perovskite structure classification using the two-step machine learning models: one for classifying perovskite and the other for classifying the cubic perovskite structure. The proposed models were trained with the experimentally known ABO3 compounds. High-throughput screening was performed and revealed 625 ABO3 compounds which were further analyzed using DFT calculations, suggesting 87 highly promising cubic perovskite materials. All the listed results suggest that the data-driven approach can be effectively used to determine the class of the crystal structure.
178 candidates. Similarly, Balachandran et al.,157 investigated into perovskite structure classification using the two-step machine learning models: one for classifying perovskite and the other for classifying the cubic perovskite structure. The proposed models were trained with the experimentally known ABO3 compounds. High-throughput screening was performed and revealed 625 ABO3 compounds which were further analyzed using DFT calculations, suggesting 87 highly promising cubic perovskite materials. All the listed results suggest that the data-driven approach can be effectively used to determine the class of the crystal structure.
Machine learning can also be applied to perform optimization for various materials and device designs. For example, Ma et al.158 proposed a deep learning framework for design parameter prediction for on-demand design of the chiral metamaterials where the developed model enables not only the prediction of light–matter interaction properties of devices but also the proposal of design parameters for nano-photonic devices suggesting that the deep-learning-based model effectively used real world device design. A similar approach was also proposed by Peurifoy et al.159 where the author proposed a neural network model for the inverse design of nanophotonic particle simulation with the analytical gradient method. Furthermore, Liu et al., by combining a forward neural network (property prediction network) and an inverse network (input feature prediction network), overcame non-uniqueness in all inverse scattering problems. Interestingly, the structure of the proposed model is quite similar to that of the novel autoencoder widely used for generative models, but the authors used each part of the autoencoder (i.e. encoder and decoder) as independent regression models to handle the fundamental non-uniqueness of the inverse scattering problem effectively. One interesting study on machine learning for real materials synthesis was conducted by Yuan et al.160 to predict electrostrain of Pb-free BaTiO3 (BTO)-based materials. Here, the author used both exploration (using uncertainty) and exploitation (using only model prediction) to find out the optimal criterion for new novel BTO-based materials, and (Ba0.84Ca0.16) (Ti0.90Zr0.07Sn0.03)O3 was confirmed to be a novel piezoelectric material with large electrostrain both experimentally and theoretically.
3. Successful materials discovery
The summaries above demonstrate that the machine learning strategy is becoming widespread in the materials science and engineering field. While many studies demonstrate significant potential to accelerate research in high-throughput discovery, only some studies discuss the discovery of new economical materials using the machine learning approach. In this section, we summarize these studies to understand their key ingredients to discuss future prospects in Section 4.Aspuru-Guzik and co-workers have been leading a one-shot approach where high-throughput computational screening is performed followed by an experimental demonstration of the discovered materials (Fig. 8). While organic light-emitting diodes (OLEDs) have many industrial applications due to their high efficiency and color properties, blue OLED development has been particularly difficult due to the higher energy needed for excitation. In this regard, Aspuru-Guzik and co-workers have presented a highly integrated design process involving theoretical insight, quantum mechanics, machine learning, industrial expertise, and experiments to discover new highly efficient blue OLEDs.161 Here, the chemical space is defined using a combinatorial enumeration of defined fragments. These fragments are selected using theoretical intuition. Molecules with unstable substructures known from experiments are filtered as well. Then, a neural network is employed to find the best OLED candidate, which is analyzed by time-dependent DFT calculations, resulting in a total of 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 calculations. From the 400
000 calculations. From the 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidates, four candidates were experimentally validated after 2500 human experts voted for property novelty of candidates and synthetic accessibility. The study demonstrated one validated candidate showing 22% external quantum efficiency as well as about one thousand potential candidates with equal or better performance. This study demonstrates that an end-to-end highly integrated approach directly leads to the discovery of new materials.
000 candidates, four candidates were experimentally validated after 2500 human experts voted for property novelty of candidates and synthetic accessibility. The study demonstrated one validated candidate showing 22% external quantum efficiency as well as about one thousand potential candidates with equal or better performance. This study demonstrates that an end-to-end highly integrated approach directly leads to the discovery of new materials.
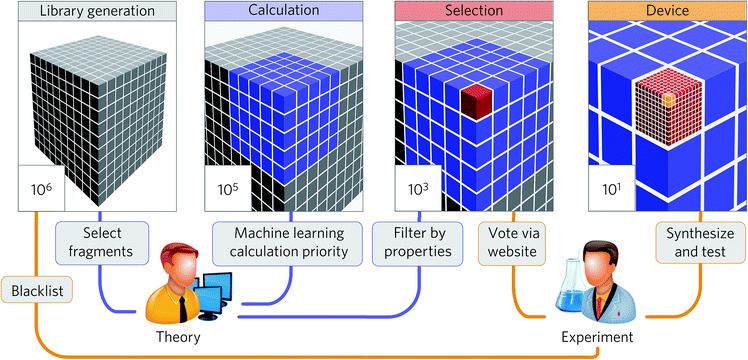 | ||
| Fig. 8 Collaborative discovery approach adopted by Aspuru-Guzik and co-workers to discover blue OLED materials (adapted with permission from ref. 161 Copyright 2016 Springer, Nat. Mater.). The screening stages integrating theoretical and computational approaches and experimental input and testing were the key to successful discovery. | ||
One of the methods to produce white light using LEDs involves phosphor coating on a light emitting diode (LED), where part of the LED emission is absorbed and re-emitted as photons at different wavelengths. The combination of all the photons results in white light. Such engineering simplifies the design and improves the efficiency of the white light LED, but only a handful of phosphor materials have been reported. In this regard, Brgoch and co-workers employed DFT, the support vector machine regression model, and experimental validation to discover NaBaB9O15 which is highly efficient and stable.162 Here, support vector machine regression is trained with 2610 DFT-based Debye temperature from the Materials Project database that correlates with the quantum efficiency of the materials. Then, the model is used to screen 2071 materials (1) that are available in Pearson's crystal database, (2) for which the bandgap is available in the Materials Project database, (3) that are ternary, and (4) that are non-metals. Out of these, NaBaB9O15 shows the most ideal Debye temperature and bandgaps, which are further validated using experiments (see Fig. 9). The key in this study was the screening of materials from the database which contains experimentally observed materials.
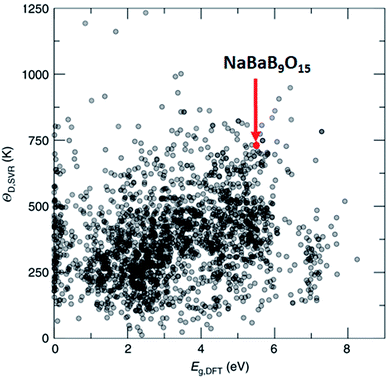 | ||
| Fig. 9 Machine learning predicted Debye temperature against the calculated bandgap. Machine learning predicted Debye temperatures (ΘD,SVR) against the density functional theory calculated bandgaps (Eg,DFT) for 2071 compounds predicted (adapted with permission from ref. 162 Copyright 2018 Springer, Nat. Commun.). | ||
Degradation of battery performance caused by electrolyte decomposition can be improved by adding electrolyte additives as discussed above. Anode additives are reduced prior to electrolyte solvents and cathode additives are oxidized prior to electrolyte solvents to form a stable solid electrolyte interphase layer to reduce the irreversible capacity.163 In this regard, calculating the reduction and oxidation potential can help find promising electrolyte additives. Park et al. used a neural network model to predict the oxidation and reduction potentials for organic additives and solvents using 86 descriptors, such as bonding types, functional groups and so on.164 The relationship between the redox potential and the functional group was proposed as in Fig. 10(a). From the results, it can be seen that organic compounds containing double bonds are prone to reduction and unsusceptible to oxidation, i.e., the compounds can be used as anode additives. Among various candidates that meet these conditions, quinoxaline was tested for full cell applications and validated to improve cycle life as shown in Fig. 10(b).
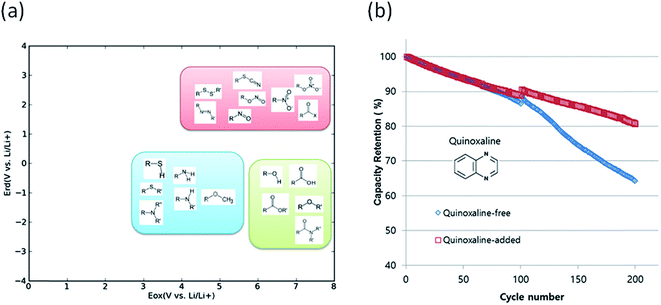 | ||
| Fig. 10 (a) Schematic of the distribution of functional groups on the potential plane, (b) cyclic performance of a Li(Ni0.88Co0.11Al0.01)O2/graphite full cell with and without a quinoxaline additive (adapted with permission from ref. 164 Copyright 2016 Royal Society of Chemistry, Phys. Chem. Chem. Phys.). | ||
Saeki and co-workers applied a similar strategy, where molecular fingerprinting techniques are combined with neural networks and random forests to predict the bandgap, molecular weight and power conversion efficiency for fullerene polymer using approximately a thousand experimentally calculated properties of polymer-fullerene. To demonstrate materials design (see Fig. 11), 2.3 million molecules from the Harvard Clean Energy Project database were screened. A total of 1000 molecules were selected from the database based on the first-principles calculated properties, 149 molecules of which were selected after the screening using a random forest model. One molecule was manually chosen based on its possibility of synthesis. The study identified a new polymer with a power conversion efficiency of ∼5.4%.165 The study shows stage by stage screening starting from the existing large first-principles database, followed by a machine learning model trained using experimental values to narrow the gap between the theory and experiments. Finally, manual consideration was used to decide the synthesis accessibility of the screened material.
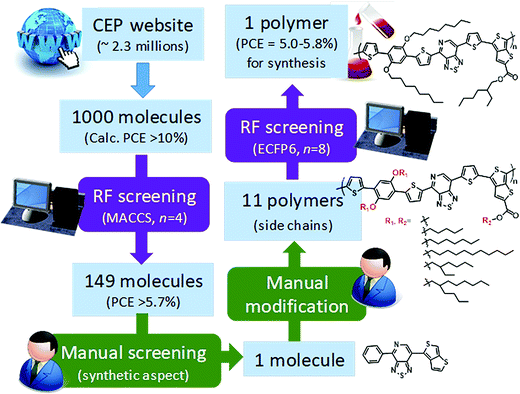 | ||
| Fig. 11 Polymer design scheme combining first-principles, machine learning, and manual consideration to discover a new polymer for organic photovoltaics (adapted with permission from ref. 165 Copyright 2018 ACS publications, J. Phys. Chem. Lett.). | ||
Sun et al.166 used the DMSP scheme, already discussed in the previous section, to expand the chemical space of the various nitride systems since it can be used for various applications such as solid-state lighting, ammonia-synthesis catalysts, superconductors, superinsulators, electrodes and so on. In spite of the aforementioned high potential, the nitride systems (<400) are relatively under-explored in the ICSD compared to the ternary metal oxides (>4000) suggesting that it is important to find new (meta-) stable metal nitrides. Because the DMSP scheme can easily be applied to predict the crystal structure from the given composition of the target metal nitride system, they first constructed a map of the metal nitrides after doing DFT calculations to identify the stability of the predicted materials as shown in Fig. 12. One interesting point is that although there are many previously known metal nitrides in the nitride map, there are still plausible new ternary metal nitrides indicating that machine learning can be effectively used to discover a large materials space compared to the conventional combinatorial explorations.
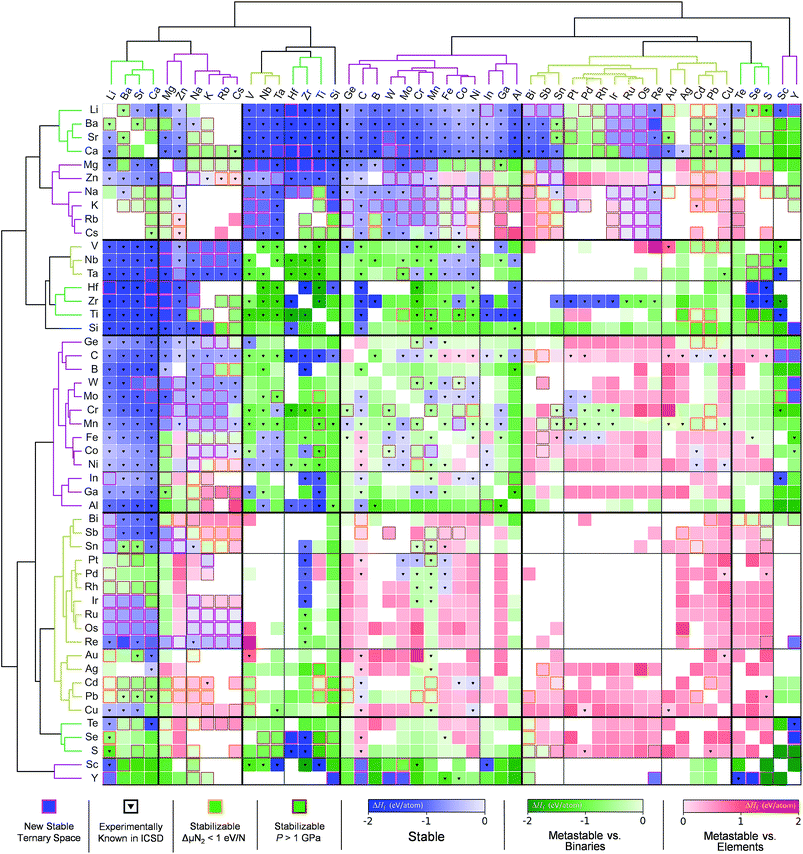 | ||
| Fig. 12 Map of the constructed metal nitrides using the DMSP scheme and DFT calculations to identify stability (adopted with permission from the corresponding author of ref. 166). | ||
The other interesting point is that from the theoretical predictions the authors experimentally identified 7 new phases of Zn- and Mg-based ternary metal nitrides (Zn–Mo–N, Zn–W–N, Zn–Sb–N, Mg–Ti–N, Mg–Zr–N, Mg–Hf–N, and Mg–Nb–N) of which the latter new materials can be classified into the two unique crystal structures (the wurtzite and rocksalt structure; see Fig. 13). Although there is still a need for human intuition in experimental synthesis from the newly discovered materials, one can reduce unnecessary trial and error for exploring un-plausible chemical space by utilizing machine learning models.
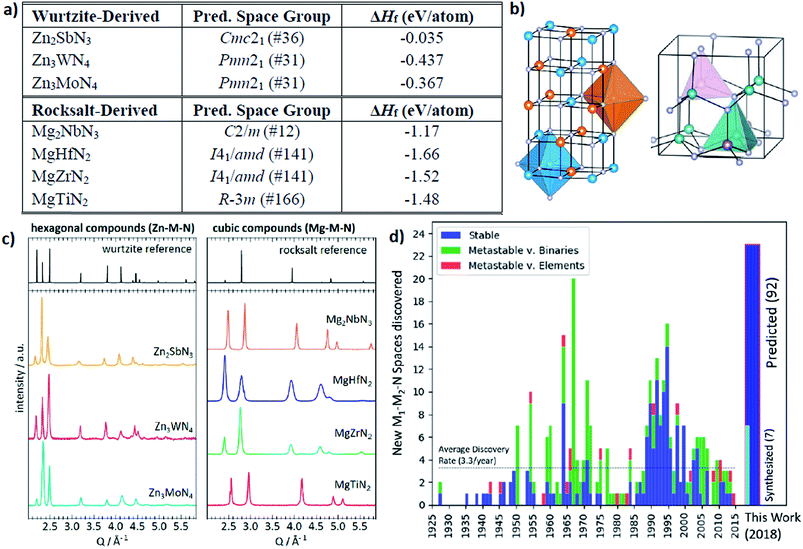 | ||
| Fig. 13 (a) 7 new phases of the ternary metal nitrides with the corresponding space group and formation energies, (b) detailed structures for the newly discovered nitrides, (c) synchrotron measured XRD patterns of new Zn- and Mg-based ternary nitrides and (d) discovery histogram for new ternary nitride spaces, based on entries as cataloged in the ICSD (adopted with permission from the ref. 166). | ||
Reed and co-workers have leveraged machine-learning with experiments to predict Li ion conductivity in order to discover a solid electrolyte for Li-ion batteries.167 Here, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 Li-containing crystal structures from the Materials Project were extracted, and performance-related properties such as electronic conductivity and electrochemical stability were computed using DFT and theory (see Fig. 14). Another critical performance measure is the Li-ion conductivity, but DFT is difficult to use to compute this metric as it is a larger scale phenomenon. However, ionic conductivity for 40 crystal structures was available; thus the authors have implemented logistic regression to classify high and low conductivity via 20 features extracted from the crystal's elemental and structural properties. The screening narrowed the search space down to 21 structures, the performances of which were confirmed by experiments. This work highlights the difficulty of theoretical approaches to simulate larger scale phenomena as well as highlighting the importance of integrating experiments to screen materials.
831 Li-containing crystal structures from the Materials Project were extracted, and performance-related properties such as electronic conductivity and electrochemical stability were computed using DFT and theory (see Fig. 14). Another critical performance measure is the Li-ion conductivity, but DFT is difficult to use to compute this metric as it is a larger scale phenomenon. However, ionic conductivity for 40 crystal structures was available; thus the authors have implemented logistic regression to classify high and low conductivity via 20 features extracted from the crystal's elemental and structural properties. The screening narrowed the search space down to 21 structures, the performances of which were confirmed by experiments. This work highlights the difficulty of theoretical approaches to simulate larger scale phenomena as well as highlighting the importance of integrating experiments to screen materials.
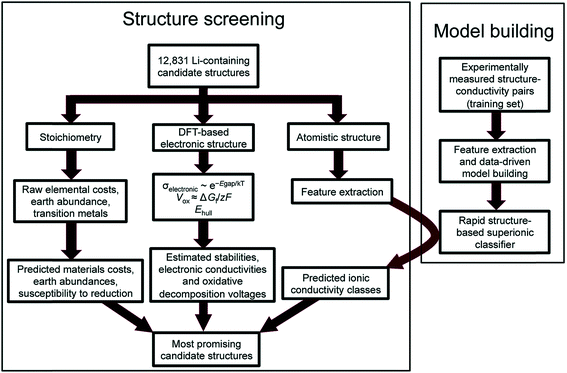 | ||
| Fig. 14 Flowchart of the discovery of a new Li solid electrolyte by integrating DFT, machine learning, and experiments. Machine learning is used to predict Li ion conductivity which is difficult to compute using DFT due to its multi-scale nature (adopted with permission from ref. 167 Copyright 2017 Royal Society of Chemistry, Energy Environ. Sci.). | ||
4. Future prospects
4.1. Summary
Within 5 years of the launch of the Materials Genome Initiative in 2011, some of the machine learning models have shown performances approaching chemical accuracy (1 kcal mol−1 or ∼43 meV) for given training and test cases for electronic energies (within the error of data acquisition methods) from atomic coordinates. Many models are flexible and can achieve respectable accuracy given a large enough data set. A majority of the studies have demonstrated significant potential in terms of accelerating the DFT calculations. This signifies that the machine learning, science, and engineering interdisciplinary community has effectively established a strategy to perform accurate theoretical high-throughput screening. In particular, renewable technologies with accessible activity-descriptors have been widely investigated with ML-based high-throughput screening and promising candidates have been suggested.Machine learning potentials (MLPs) have demonstrated their potential to couple the DFT time–length scale to a larger scale. In particular, much attention has been devoted to understanding the surface and nanocluster dynamics in the interest of catalysis. Notably, MLP has been effectively applied to the multi-scaling phenomenon of the nanocluster structure change under reaction conditions, demonstrating its ability to reveal new catalytic phenomena. Furthermore, MLP shows promise for identifying active sites of an alloy by learning the binding energy activity descriptor.
Discovering new stable crystals is critical to expanding our knowledge of viable materials. In this respect, several studies focused on predicting crystal structures given the materials composition constraint. In addition, a couple of machine learning augmented DFT based materials discovery methods are introduced and suggested as a standard strategy for discovering materials. Another approach has involved stability screening within a defined chemical space. Many of these introduced approaches have successfully identified previously unknown materials, signifying that the community has a good idea in leveraging machine learning to discover new materials.
4.2. Moving forward
Several possible strategies can be suggested. For example, a number of studies leverage the experimental experts to measure the synthesizability. The blue OLED discovery study developed a web interface for experimentalists to vote on the synthesizability of molecules screened using a machine.161 Similarly, manual screening of the synthetic aspect is considered for the discovery of polymers for organic photovoltaics.165 Another popular strategy is to avoid hypothetical materials entirely by defining the screening scope as the experimentally known materials. The discovery of white LED materials introduced above is an example.162 This approach has been one of the most successful strategies for screening studies not involving machine learning. In addition, theoretical screening criteria are often limited to properties that are easily computable due to practical consideration (tractable time–length scale), instead of properties that are more directly relevant to experiments, and for these cases surrogate models are helpful to predict experimentally determined properties. All this shows that close collaboration between the computational and experimental investigators is key. Also, it would be helpful if the theoretical and experimental researchers closely communicate coherently at the beginning of collaboration to improve the success rate of machine prediction followed by experimental validation, instead of performing separate roles of “design” and “validation” by theory and experiments, respectively.
Although, here, we have mainly focused on the application of machine learning in terms of computational prediction of novel functional materials mainly using computational data, utilizing actual experimental data to predict materials properties of unknown compounds or even suggest new materials can be highly impactful. The critical aspect here is to collect a large set of data that have been obtained consistently using the same experimental setup under controlled conditions. Most of the existing experimental data in the literature are sparse and inhomogeneous for use in machine learning. For this reason, the number of quality experimental machine learning studies is limited. Recently, Gregoire and co-workers have demonstrated the potential of high-throughput consistent experiments where 178![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 994 data samples are used to map the visual image of samples and their adsorption spectra.171 Furthermore, compositions and Raman signal data of 1379 BiVO4 alloys have been correlated to their photoelectrochemical activity.172 These promising results demonstrate that the consistent experiments enable end-to-end data science for materials science.
994 data samples are used to map the visual image of samples and their adsorption spectra.171 Furthermore, compositions and Raman signal data of 1379 BiVO4 alloys have been correlated to their photoelectrochemical activity.172 These promising results demonstrate that the consistent experiments enable end-to-end data science for materials science.
Augmenting machine learning with robotics, or the so-called self-driving laboratory, has been emerging as a significant new direction.4,12,124 Developing the self-driving laboratory requires non-human-interrupted closed-loop flow work, where a machine learning model designs the experiments, followed by using robotics to perform the experiments and characterize the sample. Then, the new knowledge is learned by machine learning which can design the next experiment to repeat the cycle. Maruyama and co-workers are the pioneers in this regard via the Autonomous Research System (ARES) where the carbon nanotube growth rate is learned by machine learning model to grow the carbon nanotube at target rates, showing its potential,13 but such an effort is still in its infancy.173,174 The self-driving lab enables robust end-to-end materials search and is expected to revolutionize materials discovery in the future, which can be adopted in industry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the generous support of the Saudi Aramco–KAIST CO2 Management Center and National Research Foundation of Korea (award number 2018M3D1A1089310) to perform this research.References
- Synthesis report on the aggregate effect of INDCs, United Nations Framework Convention on Climate Change, United Nations, 2016, http://https://unfccc.int/sites/default/files/resource/docs/2016/cop22/eng/02.pdf Search PubMed.
- J. Rogelj, M. den Elzen, N. Höhne, T. Fransen, H. Fekete, H. Winkler, R. Schaeffer, F. Sha, K. Riahi and M. Meinshausen, Nature, 2016, 534, 631 CrossRef CAS PubMed.
- Mission Innovation, http://mission-innovation.net/, accessed January, 2019.
- A. Aspuru-Guzik, K. Persson, A. Alexander-Katz, C. Amador, D. Solis-Ibarra, M. Antes, A. Mosby, M. Aykol, E. Chan, S. Dwaraknath, J. Montoya, E. Rotenberg, J. Gregoire, A. HattrickSimpers, D. M. Huang, J. Hein, G. Hutchison, O. Isayev, Y. Jung, J. Kiviaho, C. Kreisbeck, L. Roch, S. Saikin, D. Tabor, J. Lambert, S. Odom, J. Pijpers, M. Ross, J. Schrier, R. Segalman, M. Sfeir, H. Tribukait and T. Vegge, Materials Acceleration Platform: Accelerating Advanced Energy Materials Discovery by Integrating High-Throughput Methods with Artificial Intelligence: Report of the Clean Energy Materials Innovation Challenge Expert Workshop, Mission Innovation, 2018 Search PubMed.
- E. Maine and E. Garnsey, Resour. Policy, 2006, 35, 375–393 CrossRef.
- T. Mueller, A. G. Kusne and R. Ramprasad, in Reviews in Computational Chemistry, ed. A. L. Parrill and K. B. Lipkowitz, John Wiley & Sons, Inc., Hoboken, New Jersey, 2016, vol. 29, ch. 4, pp. 186–273 Search PubMed.
- X. Su and T. M. Khoshgoftaar, Lect. Notes Artif. Int., 2009, vol. 2009, p. 19 Search PubMed.
- I. Kononenko, Artif. Intell. Med., 2001, 23, 89–109 CrossRef CAS PubMed.
- N. M. Nasrabadi, J. Electron. Imaging, 2007, 16, 049901 CrossRef.
- A. Graves, A. Mohamed and G. Hinton, Speech recognition with deep recurrent neural networks, 2013 Search PubMed.
- M. L. Green, C. L. Choi, J. R. Hattrick-Simpers, A. M. Joshi, I. Takeuchi, S. C. Barron, E. Campo, T. Chiang, S. Empedocles, J. M. Gregoire, A. G. Kusne, J. Martin, A. Mehta, K. Persson, Z. Trautt, J. Van Duren and A. Zakutayev, Appl. Phys. Rev., 2017, 4, 011105 Search PubMed.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz, H. Tribukait, C. Amador-Bedolla, C. J. Brabec, B. Maruyama, K. A. Persson and A. Aspuru-Guzik, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker, M. Krein, J. Poleski, R. Barto and B. Maruyama, npj Comput. Mater., 2016, 2, 16031 CrossRef.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- J. Hemminger, G. Crabtree, M. Kastner, S. Bare, B. Nora, C. Sylvia, S. Clark, P. Cummings, F. Disalvo, M. El-sayed, G. Flynn, B. Gates, L. Greene, S. Hammes-Schiffer, M. Hochella, B. Kay, K. Kirby, J. McCurdy, W. D. Morse, M. Moskovits, K. Nagy, J. Richards, J. Spence, K. Taylor, D. Tobias and J. Tranquada, New Science for a Secure and Sustainable Energy Future: A report of a subcommittee to the Basic Energy Science Advisory Committee, U.S. Department of Energy, U.S.A, 2008 Search PubMed.
- J. Stringer, L. Horton, M. Singer, J. Ahearne, G. Crabtree, C. Baker, L. DeJonghe, J. Herbst, M. Dresselhaus, R. Smalley and R. Stoller, Basic Research Needs To Assure A Secure Energy Future: A Report from the Basic Energy Science Advisory Committee, U.S. Department of Energy, Oak Ridge National Laboratory, U.S.A., 2003 Search PubMed.
- SunShot Initiative 2030 Goals, U.S. Department of Energy: Office of Energy Efficiency & Renewable Energy: Solar Energy Technologies Office, U.S.A., 2017, http://https://www.energy.gov/sites/prod/files/2018/05/f51/SunShot%202030%20Fact%20Sheet.pdf Search PubMed.
- Progress in Hydrogen and Fuel Cells, Office of Energy Efficiency & Renewable Energy, U.S. Department of Energy, Fuel Cell Technologies Office, U.S.A., 2017, http://https://www.energy.gov/sites/prod/files/2017/10/f37/fcto-progress-fact-sheet-august-2017.pdf Search PubMed.
- A. Chen, Berkeley Lab Study Estimates $80 Billion Annual Cost of Power Interruptions, https://newscenter.lbl.gov/2005/02/02/berkeley-lab-study-estimates-80-billion-annual-cost-of-power-interruptions/, accessed January, 2019 Search PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS.
- S. V. Kalinin, B. G. Sumpter and R. K. Archibald, Nat. Mater., 2015, 14, 973 CrossRef CAS PubMed.
- L. Ward and C. Wolverton, Curr. Opin. Solid State Mater. Sci., 2017, 21, 167–176 CrossRef CAS.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 54 CrossRef.
- Y. Liu, T. Zhao, W. Ju and S. Shi, J. Materiomics, 2017, 3, 159–177 CrossRef.
- B. R. Goldsmith, J. Esterhuizen, J.-X. Liu, C. J. Bartel and C. Sutton, AIChE J., 2018, 64, 2311–2323 CrossRef CAS.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- J. J. Irwin and B. K. Shoichet, J. Chem. Inf. Model., 2005, 45, 177–182 CrossRef CAS PubMed.
- A. Gaulton, A. Hersey, A. Karlsson, D. Mendez, E. Cibrián-Uhalte, F. Atkinson, G. Papadatos, I. Smit, J. P. Overington, J. Chambers, L. J. Bellis, M. Davies, M. Nowotka, N. Dedman, P. Mutowo, A. R. Leach, A. P. Bento and M. P. Magariños, Nucleic Acids Res., 2016, 45, D945–D954 CrossRef PubMed.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- R. Allmann and R. Hinek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 63, 412–417 CrossRef CAS PubMed.
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- A. E. Hoerl and R. W. Kennard, Technometrics, 1970, 12, 55–67 CrossRef.
- R. Tibshirani, J. R. Stat. Ser. Soc. B Stat. Methodol., 1996, 58, 267–288 Search PubMed.
- H. Zou and T. Hastie, J. R. Stat. Soc. Ser. B, 2005, 67, 301–320 CrossRef.
- S. Wold, M. Sjöström and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109–130 CrossRef CAS.
- J. A. K. Suykens and J. Vandewalle, Neural Process. Lett., 1999, 9, 293–300 CrossRef.
- S. R. Safavian and D. Landgrebe, IEEE Trans. Syst. Man Cybern., 1991, 21, 660–674 CrossRef.
- H. Tin Kam, Random decision forests, Proceedings of 3rd International Conference on Document Analysis and Recognition, 1995, pp. 278–282, DOI:10.1109/ICDAR.1995.598994.
- J. S. Cramer, Stud. Hist. Philos. Sci., 2004, 35, 613–626 CrossRef.
- C. Saunders, A. Gammerman and V. Vovk, Ridge regression learning algorithm in dual variables, International Conference on Machine Learning, 1998, pp. 515–521 Search PubMed.
- C. E. Rasmussen, in Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2–14, 2003, Tübingen, Germany, August 4–16, 2003, Revised Lectures, ed. O. Bousquet, U. von Luxburg and G. Rätsch, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 63–71, DOI:10.1007/978-3-540-28650-9_4.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436 CrossRef CAS PubMed.
- P. Sabatier, La catalyse en chimie organique, Librairie polytechnique, Paris et Liege, 1920 Search PubMed.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- F. S. Roberts, K. P. Kuhl and A. Nilsson, Angew. Chem., Int. Ed., 2015, 54, 5179–5182 CrossRef CAS PubMed.
- X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Nat. Commun., 2017, 8, 15438 CrossRef CAS PubMed.
- X. Ma, Z. Li, L. E. K. Achenie and H. Xin, J. Phys. Chem. Lett., 2015, 6, 3528–3533 CrossRef CAS PubMed.
- Z. Li, X. Ma and H. Xin, Catal. Today, 2017, 280, 232–238 CrossRef CAS.
- B. Hammer and J. K. Nørskov, in Advances in Catalysis, Academic Press, 2000, vol. 45, pp. 71–129 Search PubMed.
- J. Noh, S. Back, J. Kim and Y. Jung, Chem. Sci., 2018, 9, 5152–5159 RSC.
- K. Tran and Z. W. Ulissi, Nat. Catal., 2018, 1, 696–703 CrossRef.
- I. Takigawa, K.-i. Shimizu, K. Tsuda and S. Takakusagi, RSC Adv., 2016, 6, 52587–52595 RSC.
- T. Toyao, K. Suzuki, S. Kikuchi, S. Takakusagi, K.-i. Shimizu and I. Takigawa, J. Phys. Chem. C, 2018, 122, 8315–8326 CrossRef CAS.
- T. Davran-Candan, M. E. Günay and R. Yıldırım, J. Chem. Phys., 2010, 132, 174113 CrossRef PubMed.
- R. Jinnouchi and R. Asahi, J. Phys. Chem. Lett., 2017, 8, 4279–4283 CrossRef CAS PubMed.
- R. Jinnouchi, H. Hirata and R. Asahi, J. Phys. Chem. C, 2017, 121, 26397–26405 CrossRef.
- H. Yarveicy, M. M. Ghiasi and A. H. Mohammadi, J. Mol. Liq., 2018, 255, 375–383 CrossRef CAS.
- Y. Liu, Z. U. Wang and H.-C. Zhou, Greenhouse Gases: Sci. Technol., 2012, 2, 239–259 CrossRef CAS.
- M. Fernandez, N. R. Trefiak and T. K. Woo, J. Phys. Chem. C, 2013, 117, 14095–14105 CrossRef CAS.
- M. Fernandez, T. K. Woo, C. E. Wilmer and R. Q. Snurr, J. Phys. Chem. C, 2013, 117, 7681–7689 CrossRef CAS.
- G. Borboudakis, T. Stergiannakos, M. Frysali, E. Klontzas, I. Tsamardinos and G. E. Froudakis, npj Comput. Mater., 2017, 3, 40 CrossRef.
- R. Anderson, J. Rodgers, E. Argueta, A. Biong and D. A. Gómez-Gualdrón, Chem. Mater., 2018, 30, 6325–6337 CrossRef CAS.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC.
- K. Sodeyama, Y. Igarashi, T. Nakayama, Y. Tateyama and M. Okada, Phys. Chem. Chem. Phys., 2018, 20, 22585–22591 RSC.
- D. Aurbach, E. Pollak, R. Elazari, G. Salitra, C. S. Kelley and J. Affinito, J. Electrochem. Soc., 2009, 156, A694–A702 CrossRef CAS.
- Z. Lin, Z. Liu, W. Fu, N. J. Dudney and C. Liang, Adv. Funct. Mater., 2013, 23, 1064–1069 CrossRef CAS.
- Y. Okamoto and Y. Kubo, ACS Omega, 2018, 3, 7868–7874 CrossRef CAS.
- R. Jalem, T. Aoyama, M. Nakayama and M. Nogami, Chem. Mater., 2012, 24, 1357–1364 CrossRef CAS.
- R. Jalem, M. Nakayama and T. Kasuga, J. Mater. Chem. A, 2014, 2, 720–734 RSC.
- R. Jalem, M. Kimura, M. Nakayama and T. Kasuga, J. Chem. Inf. Model., 2015, 55, 1158–1168 CrossRef CAS PubMed.
- C. Chen, Z. Lu and F. Ciucci, Sci. Rep., 2017, 7, 40769 CrossRef CAS PubMed.
- K. Fujimura, A. Seko, Y. Koyama, A. Kuwabara, I. Kishida, K. Shitara, C. A. J. Fisher, H. Moriwake and I. Tanaka, Adv. Energy Mater., 2013, 3, 980–985 CrossRef CAS.
- N. Kireeva and V. S. Pervov, Phys. Chem. Chem. Phys., 2017, 19, 20904–20918 RSC.
- R. Jalem, K. Kanamori, I. Takeuchi, M. Nakayama, H. Yamasaki and T. Saito, Sci. Rep., 2018, 8, 5845 CrossRef PubMed.
- M. Attarian Shandiz and R. Gauvin, Comput. Mater. Sci., 2016, 117, 270–278 CrossRef CAS.
- X. Wang, R. Xiao, H. Li and L. Chen, J. Materiomics, 2017, 3, 178–183 CrossRef.
- R. A. Eremin, P. N. Zolotarev, O. Y. Ivanshina and I. A. Bobrikov, J. Phys. Chem. C, 2017, 121, 28293–28305 CrossRef CAS.
- Y. Okamoto, J. Phys. Chem. A, 2017, 121, 3299–3304 CrossRef CAS PubMed.
- V. Stanev, C. Oses, A. G. Kusne, E. Rodriguez, J. Paglione, S. Curtarolo and I. Takeuchi, npj Comput. Mater., 2018, 4, 29 CrossRef.
- S. Kim, A. Jinich and A. Aspuru-Guzik, J. Chem. Inf. Model., 2017, 57, 657–668 CrossRef CAS PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506 CrossRef CAS.
- O. Allam, C. Holmes, Z. Greenberg, K. C. Kim and S. S. Jang, ChemPhysChem, 2018, 19, 2559–2565 CrossRef CAS PubMed.
- G. Pilania, A. Mannodi-Kanakkithodi, B. P. Uberuaga, R. Ramprasad, J. E. Gubernatis and T. Lookman, Sci. Rep., 2016, 6, 19375 CrossRef CAS PubMed.
- G. Pilania, J. E. Gubernatis and T. Lookman, Comput. Mater. Sci., 2017, 129, 156–163 CrossRef CAS.
- K. Takahashi, L. Takahashi, I. Miyazato and Y. Tanaka, ACS Photonics, 2018, 5, 771–775 CrossRef CAS.
- P. Dey, J. Bible, S. Datta, S. Broderick, J. Jasinski, M. Sunkara, M. Menon and K. Rajan, Comput. Mater. Sci., 2014, 83, 185–195 CrossRef CAS.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Joule, 2017, 1, 857–870 CrossRef CAS.
- W. Li, R. Jacobs and D. Morgan, Comput. Mater. Sci., 2018, 150, 454–463 CrossRef CAS.
- J. Schmidt, J. Shi, P. Borlido, L. Chen, S. Botti and M. A. L. Marques, Chem. Mater., 2017, 29, 5090–5103 CrossRef CAS.
- Z. W. Ulissi, A. R. Singh, C. Tsai and J. K. Nørskov, J. Phys. Chem. Lett., 2016, 7, 3931–3935 CrossRef CAS PubMed.
- Z. W. Ulissi, A. J. Medford, T. Bligaard and J. K. Nørskov, Nat. Commun., 2017, 8, 14621 CrossRef PubMed.
- Z. Li, N. Omidvar, W. S. Chin, E. Robb, A. Morris, L. Achenie and H. Xin, J. Phys. Chem. A, 2018, 122, 4571–4578 CrossRef CAS PubMed.
- J. E. Sutton and D. G. Vlachos, Chem. Eng. Sci., 2015, 121, 190–199 CrossRef CAS.
- G. H. Gu, P. Plechac and D. G. Vlachos, React. Chem. Eng., 2018, 3, 454–466 RSC.
- G. H. Gu and D. G. Vlachos, J. Phys. Chem. C, 2016, 120, 19234–19241 CrossRef CAS.
- G. H. Gu, B. Schweitzer, C. Michel, S. N. Steinmann, P. Sautet and D. G. Vlachos, J. Phys. Chem. C, 2017, 121, 21510–21519 CrossRef CAS.
- K. Han, A. Jamal, C. A. Grambow, Z. J. Buras and W. H. Green, Int. J. Chem. Kinet., 2018, 50, 294–303 CrossRef CAS.
- L. B. Vilhelmsen and B. Hammer, J. Chem. Phys., 2014, 141, 044711 CrossRef PubMed.
- E. Burello, D. Farrusseng and G. Rothenberg, Adv. Synth. Catal., 2004, 346, 1844–1853 CrossRef CAS.
- J. P. Janet, T. Z. H. Gani, A. H. Steeves, E. I. Ioannidis and H. J. Kulik, Ind. Eng. Chem. Res., 2017, 56, 4898–4910 CrossRef CAS.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed.
- J. P. Janet and H. J. Kulik, J. Phys. Chem. A, 2017, 121, 8939–8954 CrossRef CAS PubMed.
- J. P. Janet, L. Chan and H. J. Kulik, J. Phys. Chem. Lett., 2018, 9, 1064–1071 CrossRef CAS PubMed.
- A. Seko, H. Hayashi, K. Nakayama, A. Takahashi and I. Tanaka, Phys. Rev. B, 2017, 95, 144110 CrossRef.
- F. A. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Phys. Rev. Lett., 2016, 117, 135502 CrossRef PubMed.
- F. Legrain, A. v. Roekeghem, S. Curtarolo, J. Carrete, G. K. H. Madsen and N. Mingo, arXiv:1803.09827, 2018.
- G. Pilania and X. Y. Liu, J. Mater. Sci., 2018, 53, 6652–6664 CrossRef CAS.
- M. Chen and D. A. Dixon, J. Phys. Chem. C, 2018, 122, 18621–18639 CrossRef CAS.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, Chem. Eng. Sci., 2011, 66, 4319–4355 CrossRef CAS.
- A. Van der Ven, G. Ceder, M. Asta and P. D. Tepesch, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 184307 CrossRef.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191 CrossRef CAS PubMed.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- M. Gastegger, C. Kauffmann, J. Behler and P. Marquetand, J. Chem. Phys., 2016, 144, 194110 CrossRef PubMed.
- J. R. Boes, M. C. Groenenboom, J. A. Keith and J. R. Kitchin, Int. J. Quantum Chem., 2016, 116, 979–987 CrossRef CAS.
- N. Artrith, T. Morawietz and J. Behler, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 153101 CrossRef.
- N. Artrith and J. Behler, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045439 CrossRef.
- N. Artrith and A. Urban, Comput. Mater. Sci., 2016, 114, 135–150 CrossRef CAS.
- C. Wang, A. Tharval and J. R. Kitchin, Mol. Simul., 2018, 44, 623–630 CrossRef CAS.
- T. Gao and J. R. Kitchin, Catal. Today, 2018, 312, 132–140 CrossRef CAS.
- R. Ouyang, Y. Xie and D.-e. Jiang, Nanoscale, 2015, 7, 14817–14821 RSC.
- H. Zhai and A. N. Alexandrova, J. Chem. Theory Comput., 2016, 12, 6213–6226 CrossRef CAS PubMed.
- N. Artrith and A. M. Kolpak, Comput. Mater. Sci., 2015, 110, 20–28 CrossRef CAS.
- N. Artrith and A. M. Kolpak, Nano Lett., 2014, 14, 2670–2676 CrossRef CAS PubMed.
- S. K. Natarajan and J. Behler, Phys. Chem. Chem. Phys., 2016, 18, 28704–28725 RSC.
- K. Shakouri, J. Behler, J. Meyer and G.-J. Kroes, J. Phys. Chem. Lett., 2017, 8, 2131–2136 CrossRef CAS PubMed.
- J. R. Boes and J. R. Kitchin, Mol. Simul., 2017, 43, 346–354 CrossRef CAS.
- Z. W. Ulissi, M. T. Tang, J. Xiao, X. Liu, D. A. Torelli, M. Karamad, K. Cummins, C. Hahn, N. S. Lewis, T. F. Jaramillo, K. Chan and J. K. Nørskov, ACS Catal., 2017, 7, 6600–6608 CrossRef CAS.
- A. Ostadhossein, E. D. Cubuk, G. A. Tritsaris, E. Kaxiras, S. Zhang and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2015, 17, 3832–3840 RSC.
- N. Artrith, A. Urban and G. Ceder, J. Chem. Phys., 2018, 148, 241711 CrossRef PubMed.
- B. Onat, E. D. Cubuk, B. D. Malone and E. Kaxiras, Phys. Rev. B, 2018, 97, 094106 CrossRef CAS.
- S. Fujikake, V. L. Deringer, T. H. Lee, M. Krynski, S. R. Elliott and G. Csányi, J. Chem. Phys., 2018, 148, 241714 CrossRef PubMed.
- Q. Yan, J. Yu, S. K. Suram, L. Zhou, A. Shinde, P. F. Newhouse, W. Chen, G. Li, K. A. Persson, J. M. Gregoire and J. B. Neaton, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3040–3043 CrossRef CAS PubMed.
- A. Ziletti, D. Kumar, M. Scheffler and L. M. Ghiringhelli, Nat. Commun., 2018, 9, 2775 CrossRef PubMed.
- W. B. Park, J. Chung, J. Jung, K. Sohn, S. P. Singh, M. Pyo, N. Shin and K.-S. Sohn, IUCrJ, 2017, 4, 486–494 CrossRef CAS PubMed.
- A. O. Oliynyk, L. A. Adutwum, J. J. Harynuk and A. Mar, Chem. Mater., 2016, 28, 6672–6681 CrossRef CAS.
- A. O. Oliynyk, L. A. Adutwum, B. W. Rudyk, H. Pisavadia, S. Lotfi, V. Hlukhyy, J. J. Harynuk, A. Mar and J. Brgoch, J. Am. Chem. Soc., 2017, 139, 17870–17881 CrossRef CAS PubMed.
- C. C. Fischer, K. J. Tibbetts, D. Morgan and G. Ceder, Nat. Mater., 2006, 5, 641 CrossRef CAS PubMed.
- W. Sun, A. Holder, B. Orvañanos, E. Arca, A. Zakutayev, S. Lany and G. Ceder, Chem. Mater., 2017, 29, 6936–6946 CrossRef CAS.
- G. Hautier, C. C. Fischer, A. Jain, T. Mueller and G. Ceder, Chem. Mater., 2010, 22, 3762–3767 CrossRef CAS.
- K. Ryan, J. Lengyel and M. Shatruk, J. Am. Chem. Soc., 2018, 140, 10158–10168 CrossRef PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- D. C. Lonie and E. Zurek, Comput. Phys. Commun., 2011, 182, 372–387 CrossRef CAS.
- D. C. Lonie and E. Zurek, Comput. Phys. Commun., 2011, 182, 2305–2306 CrossRef CAS.
- Y. Zhou, H. Wang, C. Zhu, H. Liu, J. S. Tse and Y. Ma, Inorg. Chem., 2016, 55, 7026–7032 CrossRef CAS PubMed.
- Y. Zhao, X. Li, J. Liu, C. Zhang and Q. Wang, J. Phys. Chem. Lett., 2018, 9, 1815–1820 CrossRef CAS PubMed.
- S. Wang, J. Liu and Q. Sun, J. Mater. Chem. A, 2017, 5, 16936–16943 RSC.
- A. Shamp, T. Terpstra, T. Bi, Z. Falls, P. Avery and E. Zurek, J. Am. Chem. Soc., 2016, 138, 1884–1892 CrossRef CAS PubMed.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- F. Legrain, J. Carrete, A. van Roekeghem, G. K. H. Madsen and N. Mingo, J. Phys. Chem. B, 2018, 122, 625–632 CrossRef PubMed.
- P. V. Balachandran, A. A. Emery, J. E. Gubernatis, T. Lookman, C. Wolverton and A. Zunger, Phys. Rev. Mater., 2018, 2, 043802 CrossRef CAS.
- W. Ma, F. Cheng and Y. Liu, ACS Nano, 2018, 12, 6326–6334 CrossRef CAS PubMed.
- J. Peurifoy, Y. Shen, L. Jing, Y. Yang, F. Cano-Renteria, B. G. DeLacy, J. D. Joannopoulos, M. Tegmark and M. Soljačić, Sci. Adv., 2018, 4, eaar4206 CrossRef PubMed.
- R. Yuan, Z. Liu, P. V. Balachandran, D. Xue, Y. Zhou, X. Ding, J. Sun, D. Xue and T. Lookman, Adv. Mater., 2018, 30, 1702884 CrossRef PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120 CrossRef PubMed.
- Y. Zhuo, A. Mansouri Tehrani, A. O. Oliynyk, A. C. Duke and J. Brgoch, Nat. Commun., 2018, 9, 4377 CrossRef PubMed.
- A. M. Haregewoin, A. S. Wotango and B.-J. Hwang, Energy Environ. Sci., 2016, 9, 1955–1988 RSC.
- M. S. Park, I. Park, Y.-S. Kang, D. Im and S.-G. Doo, Phys. Chem. Chem. Phys., 2016, 18, 26807–26815 RSC.
- S. Nagasawa, E. Al-Naamani and A. Saeki, J. Phys. Chem. Lett., 2018, 9, 2639–2646 CrossRef CAS PubMed.
- W. Sun, C. Bartel, E. Arca, S. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. Holder and G. Ceder, arXiv:1809.09202, 2018.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K. N. Duerloo, Y. Cui and E. J. Reed, Energy. Environ. Sci., 2017, 10, 306–320 RSC.
- P. Ertl and A. Schuffenhauer, J. Cheminf., 2009, 1, 8 Search PubMed.
- P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73 CrossRef CAS PubMed.
- J. S. Hummelshøj, F. Abild-Pedersen, F. Studt, T. Bligaard and J. K. Nørskov, Angew. Chem., Int. Ed., 2012, 51, 272–274 CrossRef PubMed.
- H. S. Stein, D. Guevarra, P. F. Newhouse, E. Soedarmadji and J. M. Gregoire, Chem. Sci., 2019, 10, 47–55 RSC.
- M. Umehara, H. S. Stein, D. Guevarra, P. F. Newhouse, D. A. Boyd and J. M. Gregoire, npj Comput. Mater., 2019, 5, 34 CrossRef.
- L. M. Roch, F. Häse, C. Kreisbeck, T. Tamayo-Mendoza, L. P. E. Yunker, J. E. Hein and A. Aspuru-Guzik, Science Robotics, 2018, 3, eaat5559 CrossRef.
- F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 1134–1145 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2019 |