Open Access Article
Open Access ArticleThe intrinsic volumetric capacitance of conducting polymers: pseudo-capacitors or double-layer supercapacitors?†
Ihor Sahalianov a,
Sandeep Kumar Singha,
Klas Tybrandt
a,
Sandeep Kumar Singha,
Klas Tybrandt ab,
Magnus Berggrenab and
Igor Zozoulenko
ab,
Magnus Berggrenab and
Igor Zozoulenko *ab
*ab
aLaboratory of Organic Electronics, ITN, Linköping University, 60174 Norrköping, Sweden. E-mail: igor.zozoulenko@liu.se
bWallenberg Wood Science Center, Linköping University, 60174 Norrköping, Sweden
First published on 20th December 2019
Abstract
The capacitance of conducting polymers represents one of the most important material parameters that in many cases determines the device and material performances. Despite a vast number of experimental studies, the theoretical understanding of the origin of the capacitance in conducting polymers remains unsatisfactory and appears even controversial. Here, we present a theoretical method, based on first principle capacitance calculations using density functional theory (DFT), and apply it to calculate the volumetric capacitance of two archetypical conducting polymers: poly(3,4-ethylene dioxythiophene) (PEDOT) and polypyrrole (PPy). Our aim is to achieve a quantitate description of the volumetric capacitance and to provide a qualitative understanding of its nature at the atomistic level. We find that the volumetric capacitance of PEDOT and PPy is ≈100 F cm−3 and ≈300 F cm−3, respectively, which is within the range of the corresponding reported experimental results. We demonstrate that the capacitance of conducting polymers originates from charges stored in atomistic Stern layers formed by counterions and doped polymeric chains. The Stern layers have a purely electrostatic origin, since the counterions do not form any bonds with the atoms of the polymeric chains, and no charge transfer between the counterions and conducting polymer takes place. This classifies the conducting polymers as double-layer supercapacitors rather than pseudo-capacitors. Further, we analyze contributions to the total capacitance originating from the classical capacitance CC and the quantum capacitance CQ, respectively, and find that the latter provides a dominant contribution. The method of calculations of the capacitance developed in the present paper is rather general and opens up the way for engineering and optimizing the capacitive response of the conducting polymers.
Introduction
Conducting polymers represent a material of choice for many applications in printed electronics and bioelectronics owing to their low costs, well-developed synthesis protocols, mixed electron-ion conduction, as well as biocompatibility. Among all conducting polymers, poly(3,4-ethylene dioxythiophene) (PEDOT) and its derivatives, is the most widely used and explored material system in the aforementioned applications (for a review on PEDOT see e.g. ref. 1–6). In many applications, the capacitance of PEDOT determines, and even defines, the device performance. This includes, for example, PEDOT-based supercapacitors7–14 with a specific volumetric capacitance, C ≈ 30–300 F cm−3 that approaches the best-ever achieved performance of porous carbon supercapacitors.15 The capacitive response of PEDOT governs the delivery capacity of the organic electronic ion pump, an ionic drug delivery device that translates electronic signals into ion fluxes.16 The specific capacitance C is one of two factors which govern the transconductance g*, which is the-figure-of-merit of PEDOT-based organic electrochemical transistors.17 The switching time of polymeric electrochromic displays is also directly correlated to the volumetric capacitance C of PEDOT.18Electrolyte-based supercapacitors can be divided into two prime types, electric double layer supercapacitors (EDLS) and pseudo-capacitors. In EDLS charge storage occurs in the Helmholtz (and Stern) electrostatic double layers, which are formed at the interface between an electrode (electronic conductivity) and an electrolyte (ionic conductivity). A typical example of EDLS is the graphitic-based supercapacitors that exhibit a high specific capacitance thanks to the high internal surface area, porosity and the high electronic conductivity. The second type of the supercapacitors, the pseudo-capacitors, rely on electron transfer between the active electrode material and the reduction-oxidation materials. One of the most common types of pseudo-capacitors is based on transition metal oxides, typically RuO2.19 In many review papers15,20–23 the conducting polymers, including PEDOT, are classified as pseudo-capacitors with the redox reaction occurring between the conducting polymer (CP) and the oxidant in the electrolyte described as22
| CP + Oxidant → CP+(Anion−) + Oxidant− | (1) |
The point of view of considering conducting polymers being pseudo-capacitors with electron transfer between the polymer and oxidants (or ions) in electrolyte is prevailing within the electrochemical community.20 In the physical community the description of the CP systems, and interpretations of experiments, is usually based on the concept of the coupled electronic and ionic species and does not involve any assumptions regarding redox reactions and electron transfer between polymer and redox-active solutes in electrolyte.9,25–30 (For a recent perspective on how the conducting polymers store charge see ref. 31). This description typically utilizes the Nernst–Plank–Poisson equations (also called drift-diffusion equations) and it successfully describes a variety of systems, based on CP-electrolyte configuration, including standard cyclic voltammetry experiments performed on CP electrodes,9,28 organic electrochemical transistors,28,30 and the “moving front” experiments in the electrochemical conversion from the uncharged to the charged state of conducting polymers.25–27 Within this approach, the oxidation of conducting polymers is given by the scheme,21
| CP + Anion− → CP+(Anion−) + e− | (2) |
This equation, in contrast to eqn (1), does not describe a faradaic reaction involving the electron transfer from the polymer to redox-active solutes in electrolyte. Instead, the polymer becomes oxidized (positively charged) due to that pi-electrons, of the backbone (e−) of the CP, are repelled to the contacts (electrodes) by negative anions that migrates towards the polymer from the electrolyte promoted by the applied voltage. This means that the underlying mechanism of charging the CP is conceptually equivalent to the charging of the active conductive material in EDLS. In fact, eqn (2) equally well describes charge storage in EDLS (where “CP” then is replaced by the corresponding material used in EDLS, e.g. porous carbon). It is noteworthy that a precise nature of conductivity and charge carriers in the material (polarons/bipolarons as in conjugated polymers32 or band electrons as in carbon) is not relevant to the charging of the EDLS.
Several recent studies addressing the capacitance of PEDOT have challenged the view on this material as a redox pseudocapacitor.9,28,29,31 It is important to stress that a quantitate and even qualitative description of various electrochemical phenomena in conducting polymers (such as e.g. cyclic voltammetry) is not possible without introducing a phenomenological parameter corresponding to the intrinsic volumetric capacitance of the conducting polymers.9,33–35 Numerous recent experimental studies reporting volumetric capacitance of PEDOT do not really touch upon its microscopic origin.7,11–14 Without proper understanding on this subject further advancement on the materials and/or tailored design for better device performance remains difficult.
So far, there have been no reports on the first principle calculations of the intrinsic capacitance of conducting polymers, nor any theoretical formalisms presented for these calculations. Our study represents a step in this direction where we present a method for the first principle capacitance calculations based on the density functional theory (DFT) and apply this method to calculate the volumetric capacitance of PEDOT, aiming at understanding the nature of the fundamental capacitance of CPs and its quantitate description on the atomistic level.
The DFT approach is a powerful tool to calculate the capacitance in nano-scaled and molecular systems. It has been used to estimate the capacitance of few-electron semiconductor quantum dots electrostatically defined by split-gates in a two-dimensional electron gas,36,37 the capacitance of carbon nanotubes38 and graphene nanoribbons,39 and the capacitance of molecular clusters and layers.40,41 In this paper, we use this approach for the case of conducting polymers, particularly focusing on PEDOT. For our calculations, we find that the volumetric capacitance of PEDOT is on the order of 100 F cm−3, which is within the range of reported experimental measurements. We analyze the calculated capacitance in terms of contributions from the classical and quantum capacitances, where we find that the latter appears to be the dominant one. We demonstrate that the capacitance of conducting polymers originates from the charges stored in atomistic Stern layers formed by counterions and doped polymeric chains. This classifies the conducting polymers as double-layer supercapacitors rather than pseudo-capacitors relying on charge transfer between polymer and redox-active solutes in electrolyte.
The method of calculations of the capacitance developed in the present paper is rather general and can be applied to any conducting polymer such as polyaniline, polyacetylene, polythiophenes, polyphenylene vinylene and others. We demonstrate this by performing capacitance calculations for another archetypical conducting polymer, polypyrrole (PPy). We hope that our work will motivate further studies on this topic, both theoretical and experimental research focusing on a better understanding of the nature of the capacitance in CPs and material design for improved performance. In particular, we believe that the developed theoretical approach opens up a pathway for engineering and optimization of the capacitance, including the investigation of the effects of water, solvents, ionic liquids, counterions, functional groups and many other factors that can affect the capacitive response of the conducting polymers.
Methods
Basics
Differential volumetric capacitance,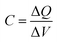 , describes the change of charges, ΔQ, stored in the unit volume of the system at equilibrium in response to the infinitesimal change of the potential of charge carriers, ΔV. The electrochemical potential of the system η = μ − eV at equilibrium is constant, and therefore the changes in the electrical potential are directly related to the changes in the chemical potential μ,
, describes the change of charges, ΔQ, stored in the unit volume of the system at equilibrium in response to the infinitesimal change of the potential of charge carriers, ΔV. The electrochemical potential of the system η = μ − eV at equilibrium is constant, and therefore the changes in the electrical potential are directly related to the changes in the chemical potential μ,| eΔV = Δμ | (3) |
This defines the capacitance in the form,36,37,40,42,43
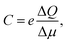 | (4) |
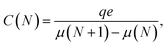 | (5) |
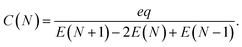 | (6) |
This equation will be our starting point in the calculation of the volumetric capacitance of conducting polymers.
For a quantum system, it is instrumental to represent a change of the chemical potential, eqn (1), as a sum of two terms,39,40,45
| Δμ = eΔV = eΔVC + eΔVQ, | (7) |
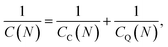 | (8) |
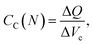 and
and 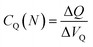 are the corresponding classical and quantum capacitances, respectively, of the N-particle system. Eqn (7), along with a definition of the capacitance, eqn (4), provides an intuitive explanation why the total capacitance can be presented as series coupled classical and quantum capacitances. Note that a concept of the quantum capacitance and a representation of a capacitance of a nanoscaled device as series coupled quantum and classical capacitances, eqn (8), have been put forward in a seminal paper of Luryi.46 The derivation of eqn (8) using the DFT is due to Bueno et al.40 The quantum capacitance CQ(N) is given by40,44
are the corresponding classical and quantum capacitances, respectively, of the N-particle system. Eqn (7), along with a definition of the capacitance, eqn (4), provides an intuitive explanation why the total capacitance can be presented as series coupled classical and quantum capacitances. Note that a concept of the quantum capacitance and a representation of a capacitance of a nanoscaled device as series coupled quantum and classical capacitances, eqn (8), have been put forward in a seminal paper of Luryi.46 The derivation of eqn (8) using the DFT is due to Bueno et al.40 The quantum capacitance CQ(N) is given by40,44
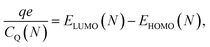 | (9) |
The classical capacitance of the N-particle system in eqn (8) is related to the classical Coulomb electrostatic energy,44
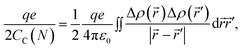 | (10) |
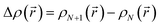 is the change of the charge density in the system when the number of charges changes from N to N + 1. For practical implementations, a more convenient way to compute the electrostatic energy is to relate it to the local electric field
is the change of the charge density in the system when the number of charges changes from N to N + 1. For practical implementations, a more convenient way to compute the electrostatic energy is to relate it to the local electric field 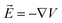 , such that the classical capacitance is
, such that the classical capacitance is
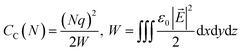 | (11) |
Model
In order to define a model for the capacitance calculations, let us first discuss the morphology of PEDOT. Experimentally the morphology of conducting polymers has been studied using various methods including Grazing Incidence Wide Angle X-ray Scattering (GIWAXS), Atomic Force Microscopy (AFM), and high-resolution transmission electron microscopy (TEM).5 These studies indicate that PEDOT represents largely amorphous materials with a limited crystalline order. In crystallites, the polymeric chains are assembled in small π–π stacked crystallites typically consisting of 3–6 chains.48–51 These findings are also confirmed by molecular dynamics simulations.52–56 We calculate the total energy of the system, E(N), using the DFT approach. Because of the computation limitations of the DFT approach we apparently cannot consider a system of size even comparable to a dimension of the polymeric thin film (10–100 nm). We therefore consider a small part of a realistic system, and average over many configurations, such that eqn (6) transforms into
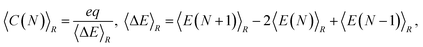 | (12) |
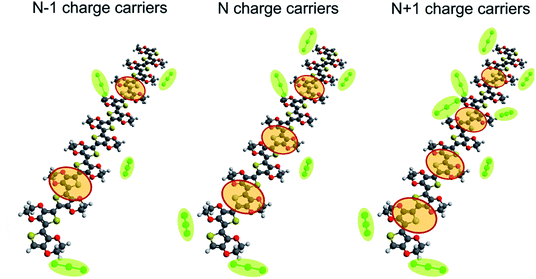
We charge the system by oxidizing the chains by removing/adding electrons as illustrated in Fig. 1. This then corresponds to a typical electrochemical setup where the polymer is oxidized/reduced during cyclic voltammetry. Note that charge carriers in p-type conjugated polymers are positive quasiparticles termed polarons and bipolarons. They represent electronic states that are localized within the polymeric backbone due to a strong electron–lattice interaction. (A detailed analysis of the polaronic and bipolaronic states in PEDOT was recently given in ref. 32). The charging of the polymer chains is accompanied by the addition of the negative counterions to the system to maintain the electroneutrality as prescribed by eqn (2). Note that the above model of capacitive charging of conjugated polymers used in the present study corresponds to the one outlined in ref. 31, as well as presented in ref. 9,28,29. In addition to the calculation of the capacitance as described above, we also perform calculations of the self-capacitance. In this case the charging of the polymeric chains is performed in the same way as for the capacitance calculations, but no counterions are then added to the system (i.e. the charge neutrality is not maintained, and the charge of the total system is therefore equal to the number of removed electrons). A comparison of the capacitance and self-capacitance provides an efficient way to outline the effect of counterions. Details of the calculations of the total capacitance, and the classical and quantum capacitances, are given in the next section.
Calculations of the total, quantum, and classical capacitances
The total capacitance and the self-capacitance are calculated based on eqn (12), and the quantum capacitances are calculated based on eqn (9), where the total energies E(N) and EHOMO(N) and ELUMO(N) are calculated using the DFT method as implemented in the Gaussian16 package.59 The range-separated hybrid exchange–correlation functional ωB97XD is used.60 This functional accounts to 100% Hartree–Fock (HF) at the long range, and 22% of the HF at the short range, and it is particularly suited for description of localized polarons/bipolarons in polymeric conjugated systems.32,61 For the basis set we chose 6-31G(d) since it represents a balance between accuracy and required computational efforts. We also performed test runs with 6-31G(d)+ basis set to ensure that the absence of diffusive functions does not affect the obtained results, see Fig. S4† for details. We find that systems with even numbers of electrons show faster convergence. Hence, to speed up computations we remove two electrons and add two counterions at the time starting from a neutral chain. Because of the even number of electrons in the system at hand we perform the restricted (close-shell) spin calculations corresponding to the singlet (S = 0) spin multiplicity (M = 2S + 1 = 1). (Note however that even with the even numbers of electrons the ground state of the system might be distinct from singlet, in particular for the case of two charges on the chain,32 but in the present calculations we restrict ourselves to the singlet spin multiplicity).In the calculation of the capacitance, a full geometrical optimization of the chain is carried out with frozen positions of Cl−3 counterions which are distributed around the polymer chains. We chose the frozen positions of the counterions because, as described in the Model section, the system that we compute represents a small part of a polymer thin film. Hence, the positions of the counterions are defined not only by their interaction with the given chain, but also with the surrounding chains and counterions (which are apparently not included in the DFT calculations). Thus, in order to account for the effect of surroundings we choose the position of the counterions in accordance with the MD prescription and keep them fixed during calculations.
Calculations of the total capacitance requires averaging over many spatial realizations of counterions. All the results reported in this paper correspond to the averaging over 50 different counterion configurations, see Fig. S5 in ESI† for details.
In experimental studies a volumetric capacitance is typically reported. To obtain the volumetric capacitance we divide the calculated capacitance by the effective volume of each polymer sample, which is calculated as an average volume of the corresponding oligomer (or a crystallite). The same volume is used for the computational boxes in calculation of the classical capacitance. The corresponding details are presented in Sec. S6 in ESI.†
Note that the full optimization of the chain geometry is computationally expensive and represents the most time-consuming step in the calculation of the total energy E(N) for a given counterion configuration. We also performed calculations of the capacitance utilizing the pre-optimized geometry of polymer chains obtained without counterions. For these calculations we first optimize geometry of a chain (or a crystallite) at a given oxidation level without counterions. Then, using this pre-optimized geometry we perform single-point energy calculations for different realizations of counterion configurations. Such calculations are much faster and less accurate than those with the full geometrical optimization. They are however still accurate enough to reproduce the total capacitance even quantitatively, see for detail Sec. S8 and Fig. S8 in ESI.† We therefore use these calculations to calculate capacitance of larger systems such as PEDOT crystallites consisting of two or three chains (Sec. S1 in ESI†).
An important issue of the DFT calculations is the self-interaction problem. In an ideal case each Cl−3 must carry −|e| charge on it. For the case of high oxidation level (>50%), DFT often fails to calculate correctly the charge density in the polymer-counterions system which results in a lesser charge on each counterion. During each simulation we investigate an average charge on each counterion with natural population analysis. Successful production run must fulfill the condition that average charge on Cl−3 is in the range from −0.95|e| to −1|e|; otherwise, the production run is discarded. For further confidence we recalculated some of the main results with the restricted Hartree–Fock method to ensure that the self-interaction does not affect the obtained data, see section Sec. S9 in ESI.†
The classical capacitance is calculated based on eqn (11), where electric field 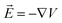 is calculated using the electrostatic potential extracted using the cubegen utility of Gaussian16. Representative electric field (or potential) distributions are shown in Fig. 4, 5 and S1.† The sizes of the simulation boxes for calculation of the potential are depicted in Fig. S7.† The simulation boxes must be large enough to account the major part of the electrostatic potential that decays away from the oligomers. Here, the simulation boxes were consisted of volume of oligomers enlarged with 10 Å in all directions. For numerical integration of the electric field in eqn (11), a cubic grid was used with a step of 0.2 Å in x-, y- and z-directions. For each atom, an atomic cutoff radius Rcutoff was used in the integration, where the electric field for r < Rcutoff is set to zero. Within this approximation, atoms are treated as metallic charged spheres with constant potential and zero electric field inside. A detailed description of the numerical calculations and their validation are presented in Sec. S10 in ESI.†
is calculated using the electrostatic potential extracted using the cubegen utility of Gaussian16. Representative electric field (or potential) distributions are shown in Fig. 4, 5 and S1.† The sizes of the simulation boxes for calculation of the potential are depicted in Fig. S7.† The simulation boxes must be large enough to account the major part of the electrostatic potential that decays away from the oligomers. Here, the simulation boxes were consisted of volume of oligomers enlarged with 10 Å in all directions. For numerical integration of the electric field in eqn (11), a cubic grid was used with a step of 0.2 Å in x-, y- and z-directions. For each atom, an atomic cutoff radius Rcutoff was used in the integration, where the electric field for r < Rcutoff is set to zero. Within this approximation, atoms are treated as metallic charged spheres with constant potential and zero electric field inside. A detailed description of the numerical calculations and their validation are presented in Sec. S10 in ESI.†
Results and discussion
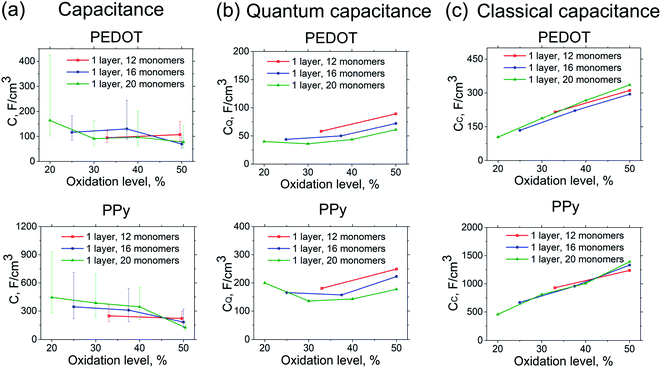
Fig. 2 shows the calculated total capacitance C, quantum capacitance CQ, and classical capacitance CC of PEDOT and PPy for different oxidization levels (defined as a number of charges per monomer). The calculated total capacitance is found to be rather insensitive to the oxidation level. This applies to both PEDOT and PPy (taking into account the large error bars for the latter case). This behaviour is expected for a classical system. However, this is also expected for the present case of a large quantum system where (after averaging over many configurations) the Coulomb potential variation is approximately homogeneous in space when the electron density is changed, and therefore independent on the total charge of the system.40,44 For PEDOT, the calculated total capacitance is CPEDOT ≈ 100 F cm−3, whereas for PPy it is CPPy ≈ 300 F cm−3. (Note that the calculated capacitance of PEDOT and PPy crystallites show similar values as those for monomers in Fig. 2, see Fig. S1 in ESI.†) The difference between the capacitances of PEDOT and PPy is consistent with experimental observations, where most studies reported a PPy capacitance that is higher than the one for PEDOT. Indeed, the reported volumetric capacitances for PEDOT are as follows (values are in F cm−3), 36–40,7 34,9 39,10 327 (ref. 11) (PEDOT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSS); 263 (ref. 12) (nanofibrillar PEDOT); 138,13 115 (ref. 14) (PEDOT
PSS); 263 (ref. 12) (nanofibrillar PEDOT); 138,13 115 (ref. 14) (PEDOT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOS). For PPy the reported volumetric capacitances are (values are in F cm−3), 80,62 60,63 332,64 200–350,65 823–646,66 523,67 1200.68 (Note that many studies report the mass capacitance Cm (in F g−1) as opposed to the volumetric capacitance Cv (in F cm−3). For these cases we converted Cm to Cv using the density ρ = 1.5 g cm−3 for PEDOT and ρ = 2.1 g cm−3 for PPy. Note also that PEDOT
TOS). For PPy the reported volumetric capacitances are (values are in F cm−3), 80,62 60,63 332,64 200–350,65 823–646,66 523,67 1200.68 (Note that many studies report the mass capacitance Cm (in F g−1) as opposed to the volumetric capacitance Cv (in F cm−3). For these cases we converted Cm to Cv using the density ρ = 1.5 g cm−3 for PEDOT and ρ = 2.1 g cm−3 for PPy. Note also that PEDOT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSS usually consists of PEDOT-rich and PSS-rich regions of approximately same size.9,10 Since only PEDOT-rich regions presumably contribute to the capacitive response, thus for the comparison with the theoretical values, the PEDOT
PSS usually consists of PEDOT-rich and PSS-rich regions of approximately same size.9,10 Since only PEDOT-rich regions presumably contribute to the capacitive response, thus for the comparison with the theoretical values, the PEDOT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSS experimental capacitance should be multiplied by a factor of ∼2). Our calculated values are then within the range of the capacitance reported experimentally. However, it should be emphasised that the precise comparison of the calculated and measured values is not possible, because of the vast variation of experimentally measured values of the PEDOT and PPy capacitances. It is not always clear whether the difference in the reported measurements reflects different morphology of materials or different characterization techniques. More systematic experimental studies to clarify these issues are needed.
PSS experimental capacitance should be multiplied by a factor of ∼2). Our calculated values are then within the range of the capacitance reported experimentally. However, it should be emphasised that the precise comparison of the calculated and measured values is not possible, because of the vast variation of experimentally measured values of the PEDOT and PPy capacitances. It is not always clear whether the difference in the reported measurements reflects different morphology of materials or different characterization techniques. More systematic experimental studies to clarify these issues are needed.
In order to get insight into the nature of the capacitance of PEDOT, we then analyse the contributions of the quantum and the classical capacitances to the total capacitance value. (The validity of eqn (8) for the system at hand expressing the total capacitance as classical and quantum capacitances connected in series, as well as the validity of the definition of the quantum capacitance, eqn (9), are discussed at the end of this section). Note that the calculated capacitances show practically identical behaviour for all systems studied, i.e. for the 12-, 16-, 20-oligomer cases as well as for crystallites. Therefore, in the subsequent analysis we will focus on one representative system, the N = 20 PEDOT oligomer. Fig. 3 shows the calculated quantum and classical capacitances and self-capacitances of PEDOT. It is noteworthy that the self-capacitance cannot be measured in a typical electrochemical setup, but the comparison of the self-capacitance and total capacitance provides an important insight into the role of counterions.
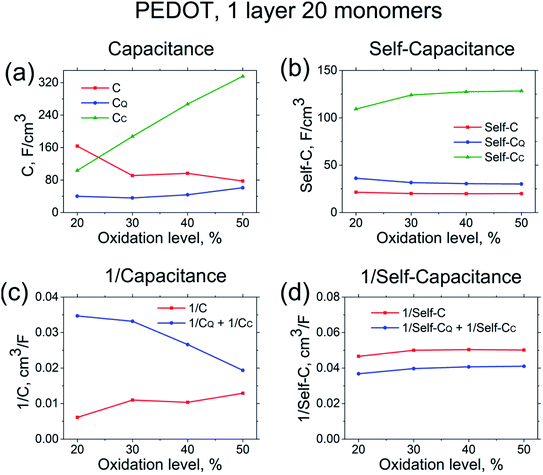 | ||
| Fig. 3 Capacitance and self-capacitance of PEDOT (left and right panels respectively). (a) and (b) show the total capacitance C, quantum capacitance CQ, and classical capacitance CC. Figures (c) and (d) compare 1/C and 1/CQ + 1/CC according to eqn (8). Results correspond to the PEDOT oligomers of the length N = 20. | ||
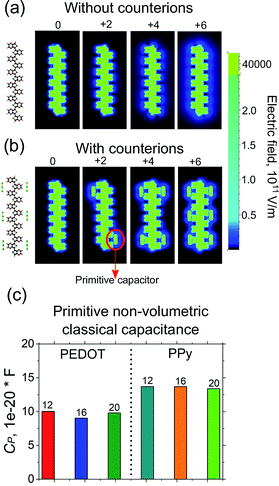
The calculated classical capacitance increases linearly with the increase of the oxidation level, whereas the classical self-capacitance remains more or less constant. This behaviour can be understood from the analysis of the electric field and potential distribution. For the case of the self-capacitance (the systems without counterions), the electric field (and the potential V) increases linearly in the whole domain when the total charge of the system Q is increased, see Fig. 4a. As a result, the self-capacitance, 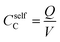 , stays constant. For the case of the capacitance (the systems with counterions), the electric field increases only in the regions in the immediate vicinity of the counterions and rapidly decays outside these regions. Also, when a new counterion is added, the electric field in the vicinity of other counterions is not affected, see Fig. 4b. Thus, as the electric field distribution illustrates (Fig. 4b), each counterion, together with a part of the polymer backbone in its vicinity, can be considered as a primitive capacitor Cp. The whole oligomer can therefore be considered as a system of parallel coupled primitive capacitors, with the capacitance CC = NcounterCp, where Ncounter is a number of counterions surrounding one chain. (Note that the total charge is increased as a new primitive capacitor is added, which corresponds to the case of the parallel coupling Fig. 4c). The calculated primitive capacitance is Cp ≈ 9.6 × 10−19 F for PEDOT and Cp ≈ 1.4 × 10−19 F for PPy. As expected, Cp for each polymer is practically the same for all system studied (i.e. 12-, 16-, 20-oligomers). The primitive capacitance for the case of PPy is larger as compared to PEDOT, because the counterions are located close to the backbone due to a smaller size of monomers. This apparently translates into the larger value of the classical capacitance of PPy, see Fig. 2c.
, stays constant. For the case of the capacitance (the systems with counterions), the electric field increases only in the regions in the immediate vicinity of the counterions and rapidly decays outside these regions. Also, when a new counterion is added, the electric field in the vicinity of other counterions is not affected, see Fig. 4b. Thus, as the electric field distribution illustrates (Fig. 4b), each counterion, together with a part of the polymer backbone in its vicinity, can be considered as a primitive capacitor Cp. The whole oligomer can therefore be considered as a system of parallel coupled primitive capacitors, with the capacitance CC = NcounterCp, where Ncounter is a number of counterions surrounding one chain. (Note that the total charge is increased as a new primitive capacitor is added, which corresponds to the case of the parallel coupling Fig. 4c). The calculated primitive capacitance is Cp ≈ 9.6 × 10−19 F for PEDOT and Cp ≈ 1.4 × 10−19 F for PPy. As expected, Cp for each polymer is practically the same for all system studied (i.e. 12-, 16-, 20-oligomers). The primitive capacitance for the case of PPy is larger as compared to PEDOT, because the counterions are located close to the backbone due to a smaller size of monomers. This apparently translates into the larger value of the classical capacitance of PPy, see Fig. 2c.
We conclude the discussion of the calculated classical capacitances by an important remark. Namely, there is a fundamental ambiguity in the definition of the classical capacitance for a system such as an oligomer, which by definition is essentially the quantum one. Indeed, to calculate the classical capacitance, the contribution from the interatomic potential inside the atoms, due to the electron–nucleus interaction, must be excluded from the simulated system. This is done by introducing the atomic cutoff radius Rcutoff (see Method section for details). Within this approximation, atoms are treated as metallic charged spheres with a constant potential and zero electric field inside. As Fig. S3a† illustrates, the calculated classical capacitance is sensitive to Rcutoff. This is not surprising, since for a quantum system, such as an oligomer, it is impossible to define a volume of the constant potential as opposed to the case of metallic plates in a classical capacitor. In our calculations we use Rcutoff = 1.5Rw, where Rw is the van der Waals radius of the corresponding atoms (which is the radius of a hard sphere defining the distance of the closest approach for another atom). Another factor contributing to the ambiguity in the calculated CC is that the calculated classical capacitance also depends on the size of the computational box, see Fig. 3b. Hence, the obtained values of the classical capacitance should be treated as a qualitative estimation, rather than exact values.
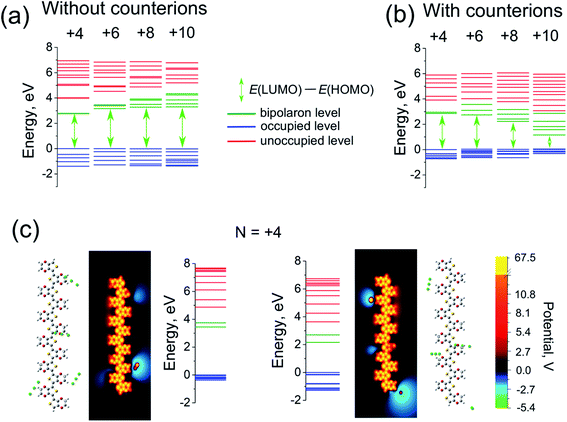
The quantum capacitance and quantum self-capacitance exhibit the opposite trend as compared to the classical ones. Namely, the quantum capacitance increases with the increase of oxidation level, whereas the quantum self-capacitance stays rather constant. This can be understood from the analysis of the evolution of the band structure of the polymer chain as the oxidation level increases. According to eqn (9), the quantum capacitance CQ is inversely proportional to the energy gap between LUMO and HOMO levels, ΔEg = ELUMO(N) − EHOMO(N). For the case without counterions, ΔEg is not sensitive to the oxidation level.32 However, for the case of the counterions the gap between LUMO and HOMO levels gradually decreases as the ion concentration is increased, which is related to the effect of the disorder potential caused by counterions.69,70 This is illustrated in Fig. 5a and b, that shows the evolution of the energy structure as the oxidation level changes.
Let us now discuss the validity of eqn (8), separating the total capacitance into the classical and quantum contributions, as well as the validity of the definition of the quantum capacitance, eqn (9). Fig. 3c and d shows a comparison of the calculated 1/C and 1/CQ + 1/CC for the capacitance and self-capacitance. (We remind that C, CQ and CC are calculated independently based respectively on eqn (9), (11) and (12)). For the case of the self-capacitance, the agreement between 1/Cself and 1/CselfQ + 1/CselfC is very good. The difference between 1/Cself and 1/CselfQ + 1/CselfC can be attributed to the ambiguity in the definition of the classical capacitance as discussed above, where CC is sensitive to the choice of the atomic cutoff radius Rcutoff. However, for the case of the capacitance the agreement between 1/C and 1/CQ + 1/CC is only qualitative, improving as the oxidation level of the system increases. Note also that for two capacitors coupled in series the total capacitance is always smaller than each of the individual capacitances, which is apparently not fulfilled for the present system, see Fig. 3a. The deviation from the ideal behaviour of the series capacitor coupling, eqn (8), can be attributed to the approximations made in derivations of this equation within the DFT approach. In particular, the validity of eqn (8) (as well as eqn (9)) requires that the potential changes smoothly upon an addition of new charges.40,44 This is satisfied for the case of the self-capacitance (the system without counterions), but apparently does not hold for the case of the capacitance, where an addition of each counterion strongly changes the potential landscape, see Fig. 5c. Also, for a given oxidation level the gap ΔEg (and therefore the quantum capacitance), as well as the potential distribution for a given oligomer strongly depends on the ion configuration as Fig. 5c illustrates. This then represents the reason for a strong sample-to sample variation of the calculated capacitances, which necessitates an averaging over many counterion configurations. To conclude, the total capacitance of our system cannot be represented exactly as the series coupled quantum and classical capacitors; nevertheless, eqn (8) holds in an approximate manner, which makes it possible for us to use it as a tool to analyse the total capacitance.
A comparison of the calculated quantum and classical capacitances shows that the quantum capacitance is a factor of ∼2–4 smaller than the classical one, see Fig. 2 and 3. Thus, according to eqn (8), it is the quantum capacitance that limits the resulting total capacitance of the conducting polymers. It is also important to stress that neither electron transfer occurs between the polymer and counterions, nor the counterions form covalent bonds with polymer chains. (A typical distance between the Cl−3 counterions and atoms in the polymers exceeds 3 Å, which is much larger than e.g. C–C bond length, aC–C ≈ 1.5 Å). This means that the capacitance of PEDOT has a purely electrostatic origin and is not related to any redox reactions giving rise to electron transfer. Hence, the capacitive energy storage in conducting polymers can be understood as a result of the formation of atomistic Stern layers composed of respectively polymeric chains and counterions in the vicinity of polymeric chains. Alternative (but very related) view is that a polymeric chain can be regarded as parallel coupled primitive capacitors, each of them representing a negative counterion and a segment of polymer backbone (as illustrated in Fig. 4b). In a typical electrochemical setup, the application of the external potential causes charging or discharging of these layers (or primitive capacitors), in a similar way as charging or discharging takes place in porous carbon supercapacitors.15 Hence, our first principle calculations demonstrate that conducting polymers should be regarded as double layer supercapacitors, where double layers are extended over the whole polymer volume. The difference with carbon supercapacitors is that for the case of conducting polymers the quantum nature of the density of states of polymeric chains limits the total capacitance, whereas for carbon supercapacitor the classical capacitance dominates because of the classical character of the DOS in carbon.
Finally, one comment is in order. In our discussion we tried to avoid terms “faradaic reactions” or “faradaic currents” because this can lead to some misunderstanding, as in the literature these terms are often used in different meanings. Indeed, the International Union of Pure and Applied Chemistry (IUPAC) defines the faradaic current as “a current corresponding to the reduction or oxidation of some chemical substance”.15 Literally following this definition, a current in a carbon-electrode EDLS should be called faradaic, because in this system a chemical substrate (carbon) gets reduced or oxidized (charged or discharged) giving rise to a current. The same applies even to a current in convention silicon metal-oxide-semiconductor field-effect transistors (MOSFETs) where oxidation or reduction (p- and n-doping in semiconductor terminology) of a chemical substrate (Si or GaAs) leads to a current. This apparently contradicts a common viewpoint that EDLSs (not even mentioning the MOSFETs) are never regarded as faradaic systems. Instead, a faradaic current is often considered as a current at the interface of a material (electrode), due to the electron charge transfer through this interface typically resulting from redox reactions at this interface. In contrast, non-faradaic systems are typically associated with the system without redox reaction at the interface, where a transient current arises due to charge accumulation and double layer formation at the electrode interface. (A pedagogical discussion of the difference between faradaic and nonfaradaic processes is recently given by Biesheuvel and Dykstra71). Hence, in order to avoid confusion, in the present paper instead of terms “faradaic” and “non-faradaic” systems we use terms EDLSs and pseudo-capacitors where the former are associated with charge accumulation at the electrode interface, whereas the later correspond to electron transfer between polymer and redox-active solutes in electrolyte.
We conclude this section by stressing once again that using the concept of the intrinsic volumetric capacitance of conducting polymers, one can quantitatively describe cyclic voltammetry experiments,9,28 organic electrochemical transistors,28,30 and the “moving front” experiments25–27 without assuming any redox reaction involving the electron transfer between the polymer and/or redox-active solutes and counterions in electrolyte.
Conclusions
Despite of the wide-spread utilization of conducting polymers as a capacitive material for charge storage, the fundamentals of their intrinsic volumetric capacitance remains controversial. Traditionally, conducting polymers are considered to be redox pseudo-capacitors where electron charge is transfer between the polymer and redox-active solutes in electrolyte. However, several recent studies have challenged this view.9,28,29,31 In the present paper we have developed an approach for the first principle quantum-mechanical calculations of the capacitance of conducting polymers based on the density functional theory. The capacitance is calculated by consecutive charging of the polymer chains by changing the number of charge carriers (and corresponding number of the surrounding counterions) as N − 1 → N → N + 1. Then the total energy of the system is calculated using the DFT, and is subsequently related to the total capacitance via eqn (6). Further, the total capacitance is presented as series coupled classical and quantum capacitances, eqn (8), where the classical capacitance CC corresponds to the classical Coulomb charging, whereas the quantum capacitance CQ describes the effect of the quantum mechanical density of states. The quantum capacitance is calculated via HOMO and LUMO Kohn–Sham orbital energies, eqn (9), and the classical capacitance is computed by integrating the classical electrostatic energy density, eqn (11).We demonstrate that the capacitive energy storage in conducting polymers can be understood as a result of the formation of atomistic Stern layers due to counterions in the vicinity of charged polymeric chains. The counterions together with the corresponding segments of a polymer backbone can be regarded as primitive capacitors coupled in parallel. The Stern layers have a purely electrostatic origin because neither the counterions form bonds with atoms belonging to polymeric chains, nor charge transfer occurs between the counterions and the polymer chains. Our results thus show that the conducting polymers should be considered as double-layer supercapacitors rather than pseudo-capacitors.
For PEDOT, the calculated total capacitance is found to be CPEDOT ≈ 100 F cm−3, whereas for PPy it is CPPy ≈ 300 F cm−3, and these values are rather insensitive to the oxidation levels of the polymers. The calculated values are within the ranges reported experimentally (∼30–300 F cm−3 for PEDOT and ∼60–1200 F cm−3 for PPy, respectively); they are also consistent with the experimental observations, where most studies report PPy capacitance that is higher than the one for PEDOT. We discuss the calculated total capacitance in terms of the series coupled quantum and classical capacitances according to eqn (8). We analyze the validity of eqn (8) and conclude that for our system it holds in an approximate manner, which makes it possible to use it as a tool to analyse the total capacitance. A comparison of the calculated quantum and classical capacitances shows that the quantum capacitance is a factor of ∼2–4 smaller than the classical one. Thus, according to eqn (8), it is the quantum capacitance that limits the calculated total capacitance of the conducting polymers. Thus, the difference with traditional double layer carbon supercapacitors is that for the case of conducting polymers the quantum nature of the density of states of polymeric chains dominates the total capacitance, whereas for carbon supercapacitor the classical capacitance governs because of the classical character of the DOS in carbon.
The method of calculations of the capacitance developed in the present paper is rather general and can be applied to any conducting polymer. We hope that our study would motivate further studies, both theoretical and experimental ones, focusing on better understanding of the nature of the capacitance in conducting polymers, and to develop materials and device configurations with better performance. Because of the computational limitations in our study we were able to calculate rather small systems, consisting of oligomers or small crystallites. It would be interesting to develop computational techniques (based e.g. on tight-binding DFT or first principle molecular dynamics method) allowing to address the capacitance of realistic and larger thin film systems. This would allow to outline the effect of various factors on the capacitance including water content, solvents, ionic liquids, porosity and various counterions. As far as experimental results are concerned, more systematic studies are needed to clarify whether the significant difference in the reported data even for the same polymers reflects different material morphology or different measurement techniques.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Knut and Alice Wallenberg Foundation, Swedish Research Council (2016-05990; 2017-04474), Swedish Energy Agency (43561-1), and Wallenberg Wood Science Center. I. Z. thanks the Advanced Functional Material Center at Linköping University for support. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC and HPC2N.References
- A. Elschner, PEDOT: principles and applications of an intrinsically conductive polymer, CRC Press, Boca Raton, FL, 2011 Search PubMed.
- H. Shi, C. Liu, Q. Jiang and J. Xu, Adv. Electron. Mater., 2015, 1, 1500017 CrossRef.
- K. Sun, S. Zhang, P. Li, Y. Xia, X. Zhang, D. Du, F. H. Isikgor and J. Ouyang, J. Mater. Sci.: Mater. Electron., 2015, 26, 4438–4462 CrossRef CAS.
- M. Berggren, X. Crispin, S. Fabiano, M. P. Jonsson, D. T. Simon, E. Stavrinidou, K. Tybrandt and I. Zozoulenko, Adv. Mater., 2019, e1805813 CrossRef PubMed.
- N. Kim, I. Petsagkourakis, S. Chen, M. Berggren, X. Crispin, M. P. Jonsson and I. Zozoulenko, in Conjugated Polymers: Properties, Processing, and Applications, ed. J. R. Reynolds, B. C. Thompson and T. A. Skotheim, CRC Press 2019, vol. 1 Search PubMed.
- I. Petsagkourakis, N. Kim, K. Tybrandt, I. Zozoulenko and X. Crispin, Adv. Electron. Mater., 2019, 5, 1800918 CrossRef CAS.
- T. Cheng, Y.-Z. Zhang, J.-D. Zhang, W.-Y. Lai and W. Huang, J. Mater. Chem. A, 2016, 4, 10493–10499 RSC.
- A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wågberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305 CrossRef PubMed.
- A. V. Volkov, K. Wijeratne, E. Mitraka, U. Ail, D. Zhao, K. Tybrandt, J. W. Andreasen, M. Berggren, X. Crispin and I. V. Zozoulenko, Adv. Funct. Mater., 2017, 1700329, DOI:10.1002/adfm.201700329.
- J. Rivnay, P. Leleux, M. Ferro, M. Sessolo, A. Williamson, D. A. Koutsouras, D. Khodagholy, M. Ramuz, X. Strakosas, R. M. Owens, C. Benar, J.-M. Badier, C. Bernard and G. G. Malliaras, Sci. Adv., 2015, 1, e1400251 CrossRef PubMed.
- N. Kurra, J. Park and H. N. Alshareef, J. Mater. Chem. A, 2014, 2, 17058–17065 RSC.
- J. M. D'Arcy, M. F. El-Kady, P. P. Khine, L. Zhang, S. H. Lee, N. R. Davis, D. S. Liu, M. T. Yeung, S. Y. Kim, C. L. Turner, A. T. Lech, P. T. Hammond and R. B. Kaner, ACS Nano, 2014, 8, 1500–1510 CrossRef PubMed.
- Y. Yang, L. Zhang, S. Li, W. Yang, J. Xu, Y. Jiang and J. Wen, J. Mater. Sci.: Mater. Electron., 2013, 24, 2245–2253 CrossRef CAS.
- C. Karlsson, J. Nicholas, D. Evans, M. Forsyth, M. Strømme, M. Sjödin, P. C. Howlett and C. Pozo-Gonzalo, ChemSusChem, 2016, 9, 2112–2121 CrossRef CAS PubMed.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- A. Jonsson, Z. Song, D. Nilsson, B. A. Meyerson, D. T. Simon, B. Linderoth and M. Berggren, Sci. Adv., 2015, 1, e1500039 CrossRef PubMed.
- J. Rivnay, S. Inal, A. Salleo, R. M. Owens, M. Berggren and G. G. Malliaras, Nat. Rev. Mater., 2018, 3, 17086 CrossRef CAS.
- P. Tehrani, L.-O. Hennerdal, A. L. Dyer, J. R. Reynolds and M. Berggren, J. Mater. Chem., 2009, 19, 1799–1802 RSC.
- F. Shi, L. Li, X.-l. Wang, C.-d. Gu and J.-p. Tu, RSC Adv., 2014, 4, 41910–41921 RSC.
- J. Heinze, B. A. Frontana-Uribe and S. Ludwigs, Chem. Rev., 2010, 110, 4724–4771 CrossRef CAS PubMed.
- G. A. Snook, P. Kao and A. S. Best, J. Power Sources, 2011, 196, 1–12 CrossRef CAS.
- A. M. Bryan, L. M. Santino, Y. Lu, S. Acharya and J. M. D'Arcy, Chem. Mater., 2016, 28, 5989–5998 CrossRef CAS.
- Q. Meng, K. Cai, Y. Chen and L. Chen, Nano Energy, 2017, 36, 268–285 CrossRef CAS.
- N. Casado, G. Hernández, H. Sardon and D. Mecerreyes, Prog. Polym. Sci., 2016, 52, 107–135 CrossRef CAS.
- X. Wang, B. Shapiro and E. Smela, J. Phys. Chem. C, 2009, 113, 382–401 CrossRef CAS.
- M. Modestov, V. Bychkov, G. Brodin, D. Valiev, M. Marklund, P. Matyba and L. Edman, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 081203 CrossRef.
- E. Stavrinidou, P. Leleux, H. Rajaona, M. Fiocchi, S. Sanaur and G. G. Malliaras, J. Appl. Phys., 2013, 113, 244501 CrossRef.
- K. Tybrandt, I. V. Zozoulenko and M. Berggren, Sci. Adv., 2017, 3, eaao3659 CrossRef PubMed.
- C. M. Proctor, J. Rivnay and G. G. Malliaras, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1433–1436 CrossRef CAS.
- V. N. Prigodin, F. C. Hsu, J. H. Park, O. Waldmann and A. J. Epstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035203 CrossRef.
- M. Berggren and G. G. Malliaras, Science, 2019, 364, 233 CAS.
- I. Zozoulenko, A. Singh, S. K. Singh, V. Gueskine, X. Crispin and M. Berggren, ACS Appl. Polym. Mater., 2019, 1, 83–94 CrossRef CAS.
- S. W. Feldberg, J. Am. Chem. Soc., 1984, 106, 4671–4674 CrossRef CAS.
- B. J. Feldman, P. Burgmayer and R. W. Murray, J. Am. Chem. Soc., 1985, 107, 872–878 CrossRef CAS.
- T. Yeu, K. M. Yin, J. Carbajal and R. E. White, J. Electrochem. Soc., 1991, 138, 2869–2877 CrossRef CAS.
- M. Macucci, K. Hess and G. J. Iafrate, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17354–17363 CrossRef CAS PubMed.
- G. J. Iafrate, K. Hess, J. B. Krieger and M. Macucci, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 10737–10739 CrossRef CAS PubMed.
- P. Pomorski, C. Roland, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 161404 CrossRef.
- A. A. Shylau, J. W. Kłos and I. V. Zozoulenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205402 CrossRef.
- P. R. Bueno, G. T. Feliciano and J. J. Davis, Phys. Chem. Chem. Phys., 2015, 17, 9375–9382 RSC.
- P. R. Bueno and J. J. Davis, Anal. Chem., 2014, 86, 1337–1341 CrossRef CAS PubMed.
- C. E. D. Chidsey and R. W. Murray, J. Phys. Chem., 1986, 90, 1479–1484 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte and J. García-Cañadas, J. Chem. Phys., 2004, 120, 6726–6733 CrossRef CAS PubMed.
- J. Luo, Z. Q. Xue, W. M. Liu, J. L. Wu and Z. Q. Yang, J. Phys. Chem. A, 2006, 110, 12005–12009 CrossRef CAS PubMed.
- J. Fernández-Rossier, J. J. Palacios and L. Brey, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205441 CrossRef.
- S. Luryi, Appl. Phys. Lett., 1988, 52, 501–503 CrossRef.
- P. R. Bueno and J. J. Davis, Anal. Chem., 2014, 86, 1997–2004 CrossRef CAS PubMed.
- T. Takano, H. Masunaga, A. Fujiwara, H. Okuzaki and T. Sasaki, Macromolecules, 2012, 45, 3859–3865 CrossRef CAS.
- J. Rivnay, S. Inal, B. A. Collins, M. Sessolo, E. Stavrinidou, X. Strakosas, C. Tassone, D. M. Delongchamp and G. G. Malliaras, Nat. Commun., 2016, 7, 11287 CrossRef PubMed.
- A. Ugur, F. Katmis, M. Li, L. Wu, Y. Zhu, K. K. Varanasi and K. K. Gleason, Adv. Mater., 2015, 27, 4604–4610 CrossRef CAS PubMed.
- I. Petsagkourakis, E. Pavlopoulou, G. Portale, B. A. Kuropatwa, S. Dilhaire, G. Fleury and G. Hadziioannou, Sci. Rep., 2016, 6, 30501 CrossRef PubMed.
- J. F. Franco-Gonzalez and I. V. Zozoulenko, J. Phys. Chem. B, 2017, 121, 4299–4307 CrossRef CAS PubMed.
- J. F. Franco-Gonzalez, N. Rolland and I. V. Zozoulenko, ACS Appl. Mater. Interfaces, 2018, 10, 29115–29126 CrossRef CAS PubMed.
- M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Phys. Chem. Chem. Phys., 2018, 20, 17188–17198 RSC.
- M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Phys. Chem. Chem. Phys., 2019, 21, 6699–6711 RSC.
- S. Rudd, J. F. Franco-Gonzalez, S. Kumar Singh, Z. Ullah Khan, X. Crispin, J. W. Andreasen, I. Zozoulenko and D. Evans, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 97–104 CrossRef CAS PubMed.
- U. Salzner, J. Phys. Chem. A, 2008, 112, 5458–5466 CrossRef CAS PubMed.
- R. Brooke, J. F. Franco-Gonzalez, K. Wijeratne, E. Pavlopoulou, D. Galliani, X. Liu, R. Valiollahi, I. V. Zozoulenko and X. Crispin, J. Mater. Chem. A, 2018, 6, 21304–21312 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- U. Salzner and A. Aydin, J. Chem. Theory Comput., 2011, 7, 2568–2583 CrossRef CAS PubMed.
- J. D. Madden, P. G. Madden and I. W. Hunter, Polypyrrole actuators: modeling and performance, SPIE, 2001 Search PubMed.
- M. D. Ingram, H. Staesche and K. S. Ryder, Solid State Ionics, 2004, 169, 51–57 CrossRef CAS.
- Y. Han, X. Qing, S. Ye and Y. Lu, Synth. Met., 2010, 160, 1159–1166 CrossRef CAS.
- Y. Wang, F. Chen, Z. Liu, Z. Tang, Q. Yang, Y. Zhao, S. Du, Q. Chen and C. Zhi, Angew. Chem., Int. Ed., 2019, 58, 15707–15711 CrossRef CAS PubMed.
- S. Liu, K. He, X. Wu, X. Luo and B. Li, RSC Adv., 2015, 5, 87266–87276 RSC.
- M. R. Arcila-Velez and M. E. Roberts, Chem. Mater., 2014, 26, 1601–1607 CrossRef CAS.
- M. Li and L. Yang, J. Mater. Sci.: Mater. Electron., 2015, 26, 4875–4879 CrossRef CAS.
- W. A. Muñoz, S. K. Singh, J. F. Franco-Gonzalez, M. Linares, X. Crispin and I. V. Zozoulenko, Phys. Rev. B, 2016, 94, 205202 CrossRef.
- W. A. Munoz, X. Crispin, M. Fahlman and I. V. Zozoulenko, Macromol. Rapid Commun., 2018, 39, 1700533 CrossRef PubMed.
- P. M. Biesheuvel and J. E. Dykstra, The difference between Faradaic and Nonfaradaic processes in Electrochemistry, Report arXiv:1809.02930v1 2018.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10250g |
| This journal is © The Royal Society of Chemistry 2019 |