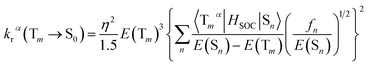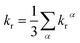DOI:
10.1039/C5RA22754B
(Paper)
RSC Adv., 2016,
6, 11648-11656
Theoretical study and design of highly efficient platinum(II) complexes bearing tetradentate ligands for OLED†
Received
30th October 2015
, Accepted 19th January 2016
First published on 22nd January 2016
Abstract
Density functional theory and time-dependent density functional theory investigations were performed on the geometrical structures, basic photophysical properties, phosphorescence quantum efficiency (Φ PL), and reorganization energy (λ) calculations of a new potential class of tetradentate Pt(II) complexes Pt[ppz-O-Popy] (1) (where ppz = phenyl-pyrazole; Popy = phenoxyl-pyridine), Pt[pmi-O-Popy] (2) (where pmi = phenyl-methylimidazole), Pt[pmi-O-Cbpy] (3) (where Cbpy = carbazolyl-pyridine) and Pt[ppz-O-Cbpy] (4), which show highly efficient (ΦPL > 80%) and deep-blue emission. Nonradiative decay processes were investigated in order to obtain a more reliable nonradiative decay rate comparison. The calculated results confirm that tetradentate Pt(II) complexes are conducive to maintaining the rigidity of the molecules. The extended conjugation complexes with carbazole groups in 3 and 4 can not only improve the structural rigidity but also enhance the capability and balance of charge transfer. Thereupon, the following two designed derivatives Pt[pmi-O-Cbmi] (5) and Pt[pmi-O-Cbbm] (6) which substitute pyridine with imidazole and benzimidazole based on complexes 3 and 4 are also considered for promising materials exploitation and theoretical understanding. The charge transfer balance performance and the radiative decay rate constant (kr) of 5 and 6 are greatly improved compared with 1–4, and the better structural rigidity will weaken nonradiative decay pathways, which may result in a higher phosphorescence quantum efficiency. Therefore, complexes 5 and 6 through judicious molecular design will be promising candidates as highly efficient blue-emitting phosphorescent materials for applications.
1 Introduction
Organic light-emitting diodes (OLEDs) based on transition metal complexes have obtained extensive attention over recent decades for their applications in displays and lighting technologies.1–11 Cyclometalated Pt(II) complexes have been extensively studied and widely applied in OLEDs because (1) the ligand can be designed as bidentate, tridentate, and tetradentate due to the square-planar configuration and these variations can significantly affect the photophysical properties of Pt(II) complexes;12–17 (2) their emission colour can be altered in the visible region flexibly by judicious modification of the ancillary ligand;18–21 (3) high phosphorescence quantum efficiency caused by spin–orbit coupling (SOC) effect.22–24 In the previous investigations, red and green emitters have been successfully developed.25,26 However, the development of a true-blue OLED with high efficiency and good stability is still a challenge.27 So the investigation of the blue emission spectrum and the improvement of the photoluminescence efficiency are the focuses in the current research.
Previous study has demonstrated that the phosphorescence quantum efficiency of Pt(II) complexes consisting of the C^N ligands such as phenyl-methylimidazole (pmi) and phenyl-pyrazole (ppz) was generally lower than that of Ir(III) analogues.12,28 To overcome this issue, a new class of tetradentate Pt(II) complexes of Pt[C^N-O-LL′] (1–4) were synthesized and reported by Li and co-workers, where LL′ is the ligand such as phenoxyl-pyridine (Popy) and carbazolyl-pyridine (Cbpy).16,29 The phosphorescence quantum efficiency of these complexes was significantly improved due to the excellent rigidity of tetradentate structure, since it is well known that better molecular rigidity can weaken nonradiative pathways. In addition, a maximum value of 23.7% for external quantum efficiency (EQE) of complex 3 was achieved by adding a carbazole group in Cbpy chelate, which is also a significant promotion compared to its Pt and Ir analogues. In order to further improve the photophysical properties and device performance, complexes 5 and 6 were designed by replacing the pyridine of Cbpy ligand with imidazole and benzimidazole in complexes 3. The schematic structures of 1–6 are presented in Fig. 1. It has been reported that the emission spectrum of many Ir(III) complexes with benzimidazole ligand have significant blue-shift30 and the complexes based on the bis-carbene (:C^C:) ligand possess higher phosphorescence quantum efficiency than that of C^N ligand.31 Therefore, complexes 5 and 6 are expected to radiate bluer and achieve higher efficiency compared with other complexes investigated previously.
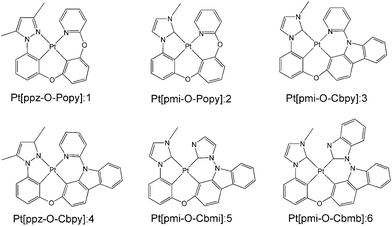 |
| | Fig. 1 Structures of the investigated Pt(II) complexes 1–6. | |
In order to further understand the effects of different ligands on the photophysical properties and phosphorescence quantum efficiency of this class of complexes, the electronic structure, absorption and emission properties of 1–6 were calculated and analyzed by density functional theory and time-dependent density functional theory (DFT/TDDFT) method. The radiative decay rate constant (kr) and reorganization energy (λ) were quantitatively evaluated for comparison of efficiency and charge transfer capability. In addition, the nonradiative decay rate constant (knr) was also qualitatively discussed. We mainly analyzed the effect of molecular rigidity and extend conjugation on phosphorescence quantum efficiency and charge transport performance. The results show that complexes 5 and 6 (especially for 6) would be efficient phosphorescent materials with considerably large efficiency and better charge transfer performance. The reasonable ligand modification significantly improved the photophysical properties and device performance. We hope that this study will be helpful for further design and synthesis of highly efficient blue phosphorescence emitters.
2 Computational details
All the calculations were performed with the Gaussian 09 D01 program.32 The geometry optimization and spectral properties for 1–6 were calculated by DFT and TDDFT method. Vibrational frequency calculations were performed on both the singlet and triplet states optimized geometries and all the optimized structures have no imaginary frequency which confirms that all the optimized geometries are the minimum on the potential energy surface. The stable calculations were also performed for all the optimized structures to ensure all the wavefunctions were stable. The solvent effect of dichloromethane (CH2Cl2) simulated by using the polarized continuum model (PCM)33 was taken into account in the calculation of the geometry optimization, absorption and emission properties. Considering the dynamical solvent effect, the emission wavelengths of 1–6 were calculated via the state-specific (SS) approach. Moreover, the LANL2DZ basis set and the quasi-relativistic effective core potential (ECP) proposed by Hay and Wadt34 with 18 valence electrons were employed for the Pt atom, while the 6-31G(d) basis set was adopted for the light atoms such as C, H, O and N atoms.
In order to ensure the reliability of the selected functional used in the present calculation, five commonly functional levels include B3P86,35 B3LYP,36 PBE0,37 CAM-B3LYP38 and M06-2X39 were performed on the calculation of the singlet state for 1 based on its crystal X-ray structure.40 The calculated ground state geometry parameters and main absorption peaks with rational characters together with the experimental values are collected in Tables 1 and 2, respectively. The results show that the singlet state calculated results of PBE0 are most close to the experimental values. Moreover, due to there is a difference between phenyl-pyrazole (ppz) and phenyl-methylimidazole (pmi) in C^N ligand, we compared some bond lengths of 2 and some similar complexes with pmi ligand. The average deviation between calculated values by PBE0 and experimental values are less than 5%, indicating the PBE0 functional has good performance in the description for these complexes. (The detailed data was summarized in Table S1.†) So the singlet state geometry optimization and absorption properties of 1–6 were carried out with PBE0 functional.
Table 1 The singlet ground state geometries of complex 1 optimized by different functionals together with experiment values
| Item |
Expt |
B3P86 |
B3LYP |
PBE0 |
CAM-B3LYP |
M06-2X |
| Bond length (Å) |
| Pt–N1 |
2.097 |
2.142 |
2.180 |
2.139 |
2.159 |
2.207 |
| Pt–C2 |
1.970 |
1.964 |
1.978 |
1.962 |
1.972 |
1.957 |
| Pt–C3 |
1.980 |
1.979 |
1.993 |
1.977 |
1.987 |
1.969 |
| Pt–N4 |
2.093 |
2.135 |
2.173 |
2.134 |
2.154 |
2.192 |
| N8–C9 |
1.417 |
1.422 |
1.430 |
1.421 |
1.429 |
1.430 |
| C5–O/N6 |
1.357 |
1.332 |
1.339 |
1.330 |
1.333 |
1.337 |
| C10–O11 |
1.374 |
1.361 |
1.368 |
1.359 |
1.363 |
1.363 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Bond angle [degree] |
| N1–Pt–C2 |
80.0 |
79.2 |
79.0 |
79.2 |
79.2 |
79.0 |
| C2–Pt–C3 |
93.0 |
92.1 |
92.1 |
92.0 |
91.8 |
92.4 |
| C3–Pt–N4 |
87.0 |
89.2 |
88.8 |
89.1 |
88.8 |
88.7 |
| N4–Pt–N1 |
102.5 |
101.3 |
101.8 |
101.5 |
102.0 |
101.4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Dihedral angle [degree] |
| N1–C2–Pt–C3 |
167.0 |
170.2 |
170.2 |
170.2 |
170.4 |
171.0 |
| N4–C5–O6–C7 |
32.1 |
40.5 |
41.9 |
41.4 |
43.6 |
44.2 |
Table 2 Calculated main absorption peaks of 1 at different functional levels together with its experimental values (unit in nm)
| |
Expt |
B3P86 |
B3LYP |
PBE0 |
CAM-B3LYP |
M06-2X |
| Peak 1 |
334 |
349 |
348 |
332 |
281 |
269 |
| Peak 2 |
284 |
304 |
306 |
292 |
230 |
226 |
| Peak 3 |
260 |
272 |
277 |
265 |
204 |
203 |
Furthermore, we also checked the reliability of the functional used in the triplet states calculation due to the spin of triplet states flipped. The lowest-lying emission wavelength of triplet states for 1 at five different functional are calculated. The results are 505, 502, 510, 520, and 425 nm at B3P86, B3LYP, PBE0, CAM-B3LYP and M06-2X functional levels, respectively. The lowest-lying emission wavelength calculated by M06-2X functional was best consistent with experimental value of 430 nm compared with other functional. For singlet–triplet transitions, within the selected TD-DFT framework, M06-2X emerges as the most efficient hybrids which allow taking the inner track to accurate estimates with typical mean absolute deviation close to 0.25 eV in many cases.41 Therefore, the M06-2X functional was used in the triplet state geometry optimization and emission properties calculation of 1–6.
3 Results and discussion
3.1 Geometries in the ground and lowest-lying triplet excited state
The optimized ground-state structure of 3 is presented in Fig. 2 along with the numbering of some key atoms. All these complexes show a square-planar geometry because of the d8 electronic configuration of Pt(II) atom. In order to have a better understanding of structural modification from S0 to T1 state, the main optimized geometric parameters of S0 and T1 are summarized in Table 3. At the S0 states, the Pt–C1 bond lengths of 1 and 4 with phenyl-pyrazole (ppz) ligand are elongated by 0.087 Å compared with Pt–N1 bond lengths of 2 and 3 with phenyl-methylimidazole (pmi) ligand, and the Pt–C2 and Pt–C3 bond lengths of 1 and 4 are shortened by 0.014 Å and 0.040 Å compared with those of 2 and 3, which is attributed to the different C^N (ppz and pmi) ligands. The N8–C9 bond lengths of C^N ligand and the C10–O11 bond lengths of all complexes are almost the same. Meanwhile, the introduction of the carbazole group has little effect on the geometric structure except the C5–O/N6 bond lengths. The C5–N6 bond lengths of 3–6 are elongated by 0.035–0.055 Å compared with that of 1 and 2. For the designed complexes 5 (6), the Pt–C4 bond lengths are drastically shortened by 0.109–0.137 Å as a result of the substitution of pyridine by carbene groups, which may facilitate the charge transfer from metal to imidazole or benzimidazole ligands. Additionally, the Pt–C2 bond lengths are elongated by 0.037–0.053 Å, which can be interpreted by trans effect in this class of tetradentate cyclometalated platinum complexes.19,42,43 The dihedral angles of N1–C2–Pt–C3 in 1–4 are about 170° and in 5–6 are about 173°, but the dihedral angles of C/N4–C/N5–N/O6–C7 in all complexes are about 40°, indicating that Pt(II) with the whole ligand is nearly a square-planar configuration except the pyridine part bowed to some extent from LL′ moiety and the introduction of imidazole and benzimidazole can slightly enhance the planarity of the molecules.
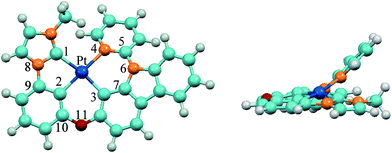 |
| | Fig. 2 Vertical view (left) and side view (right) of the optimized geometrical structure of 3 at the singlet ground state. | |
Table 3 Main geometry parameters for 1–6 in the optimized ground and lowest lying triplet excited states
| Item |
1 |
2 |
3 |
4 |
5 |
6 |
| S0 |
T1 |
S0 |
T1 |
S0 |
T1 |
S0 |
T1 |
S0 |
T1 |
S0 |
T1 |
| Bond length (Å) |
| Pt–C/N1 |
2.139 |
2.109 |
2.052 |
2.032 |
2.052 |
2.058 |
2.138 |
2.133 |
2.045 |
2.051 |
2.045 |
2.049 |
| Pt–C2 |
1.962 |
1.940 |
1.976 |
1.934 |
1.975 |
1.980 |
1.961 |
1.967 |
2.013 |
2.020 |
2.014 |
2.022 |
| Pt–C3 |
1.977 |
1.982 |
2.017 |
2.026 |
2.008 |
1.999 |
1.969 |
1.960 |
2.030 |
2.016 |
2.030 |
2.011 |
| Pt–C/N4 |
2.134 |
2.140 |
2.141 |
2.147 |
2.155 |
2.153 |
2.147 |
2.149 |
2.025 |
2.036 |
2.018 |
2.029 |
| N8–C9 |
1.421 |
1.355 |
1.418 |
1.360 |
1.418 |
1.414 |
1.422 |
1.418 |
1.421 |
1.415 |
1.421 |
1.415 |
| C5–O/N6 |
1.330 |
1.342 |
1.328 |
1.343 |
1.383 |
1.383 |
1.383 |
1.382 |
1.368 |
1.365 |
1.365 |
1.362 |
| C10–O11 |
1.359 |
1.363 |
1.358 |
1.361 |
1.359 |
1.367 |
1.360 |
1.367 |
1.360 |
1.368 |
1.360 |
1.370 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Bond angle [degree] |
| C/N1–Pt–C2 |
79.2 |
79.6 |
79.7 |
81.0 |
79.7 |
79.7 |
79.3 |
79.2 |
79.2 |
79.2 |
79.3 |
79.2 |
| C2–Pt–C3 |
92.0 |
91.8 |
90.4 |
90.2 |
90.2 |
90.6 |
91.8 |
92.3 |
89.3 |
89.9 |
89.1 |
89.6 |
| C3–Pt–C/N4 |
89.1 |
88.8 |
89.0 |
88.4 |
89.5 |
89.2 |
89.7 |
89.3 |
88.9 |
88.9 |
89.2 |
89.2 |
| C/N4–Pt–C/N1 |
101.5 |
101.4 |
102.6 |
101.9 |
102.4 |
102.2 |
101.2 |
101.1 |
103.8 |
103.3 |
103.7 |
103.3 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Dihedral angle [degree] |
| N1–C2–Pt–C3 |
170.2 |
171.7 |
170.4 |
171.5 |
170.4 |
170.4 |
170.2 |
170.2 |
173.0 |
173.0 |
173.2 |
172.7 |
| C/N4–C/N5–N/O6–C7 |
41.4 |
47.5 |
41.5 |
51.3 |
40.4 |
37.1 |
39.2 |
35.8 |
39.2 |
35.5 |
41.0 |
36.5 |
From the S0 to T1 state, the N8–C9 bond lengths of 1 and 2 are shortened by 0.058 Å and 0.066 Å, but there is almost no change in 3–6. So do Pt–C/N1 and Pt–C2. The bond lengths in 3–6 change smaller compared with those of 1 and 2. The bond angles for all complexes have no obvious variation (less than 1°). It is also noted that the dihedral angles of N4–C5–O6–C7 in complexes 1 and 2 increased by 6.1° and 9.8° from S0 to T1 state, but the dihedral angles of C/N4–C/N5–N6–C7 in complexes 3–6 were decreased by 3.3°, 3.4°, 3.7°, and 4.5°, respectively. This difference indicated that the introduction of carbazole groups which could enhance the planarity of the molecule. Overall, complexes 3–6 show better planarity and rigidity compared with 1, 2, which might lead to a smaller nonradiative rate (knr) according to the energy-gap law.
3.2 Frontier molecular orbital properties
The composition of frontier molecular orbital (FMO) is closely related to the electronic absorption properties. So the analysis of FMO at the S0 optimized geometry is important to gain in-depth understanding of photophysical behaviour of complexes 1–6. The energy levels and energy gaps together with the plots of HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) distribution of all complexes are presented in Fig. 3, and the calculated compositions for correlative orbital are summarized in Table S2.†
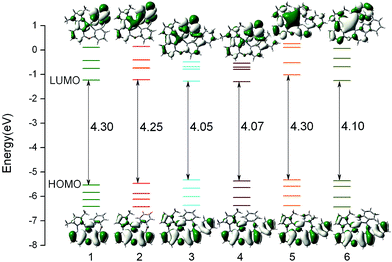 |
| | Fig. 3 Calculated energy levels, energy gaps (in eV), and orbital composition distributions of the HOMO and LUMO for 1–6 at their S0 optimized geometries. | |
For 1 and 2, the HOMO is mostly localized on Pt 5d orbitals (∼30%) and the π orbitals of phenyl part of the whole ligand, while the pyrazole part of the phenyl-pyrazole ligand and the pyridine part of the phenyl-pyridine ligand almost have no contribution to HOMO. The HOMO distributions of 3–6 are similar to that of 1 and extend to the carbazole moiety. It is also noticed that the LUMO distributions of 1–4 are mainly localized on the π* orbitals of pyridine moiety of the LL′ ligand, indicating the C^N ligands and the introduction of carbazole have little influence on the distribution of LUMO. While, the substitution of pyridine by imidazole and benzimidazole of 5 and 6 have significant effect on the distribution of LUMO, which may be effective in altering the photophysical properties of complexes. As shown in Fig. 3, the HOMO energy of 3–6 are slightly increased due to the introduction of carbazole group, hence the HOMO–LUMO energy gaps were narrowed and the higher HOMO energy will cause the better hole-injection ability compared with 1 and 2, which will also make a contribution to the balance between the hole and electron injection when the electron-injection ability is similar. Partial modification of the ligand has little effect on the LUMO energy levels except for complex 5, the LUMO energy is drastically increased due to the substitution of pyridine by imidazole, so that the energy gap is significantly enlarged, which will blue shift the emission wavelength.44 In addition, for all complex, the energy gaps between LUMO and LUMO+1 are large (∼0.50 eV), which indicated that the electron transition to LUMO+1 or higher molecular orbital will be more difficult and we can predict that the dominant configuration for the excitation may be HOMO–LUMO transition. Combining Fig. 3 and Table S2,† the transition from HOMO to LUMO of complexes 1–6 may have mixed metal-to-ligand charge transfer (MLCT) and ligand-to-ligand charge transfer (LLCT) transition characters.
3.3 Absorption spectra
The absorption properties of complexes 1–6 were calculated by TDDFT method with PCM in CH2Cl2 media based on the optimized ground-state geometry. The simulated Gaussian-type absorption curves according to the calculated singlet transition results are plotted in Fig. 4, and the lowest and strongest energy absorption peaks along with the configuration interaction (CI) coefficient, vertical excitation energy, oscillator strengths (f), and assignments are listed in Table 4.
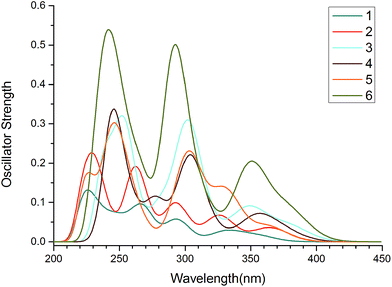 |
| | Fig. 4 Absorption spectra of 1–6 in CH2Cl2 media. | |
Table 4 The calculated strongest and lowest energy absorption properties of 1–6
| |
States |
Main configuration |
λ (nm)/E (eV) |
f |
Assignment |
| 1 |
S1 |
H → L (93%) |
355/3.50 |
0.0548 |
MLCT/LLCT |
| S26 |
H−3 → L+3 (54%) |
225/5.50 |
0.0127 |
MLCT |
| 2 |
S1 |
H → L (87%) |
365/3.40 |
0.0635 |
MLCT/LLCT |
| S24 |
H−2 → L+3 (21%) |
229/5.42 |
0.1241 |
MLCT/ILCT |
| 3 |
S1 |
H → L (93%) |
379/3.27 |
0.0741 |
MLCT/LLCT |
| S20 |
H−6 → L (35%) |
254/4.89 |
0.0348 |
MLCT/LLCT |
| 4 |
S1 |
H → L (93%) |
375/3.31 |
0.0626 |
MLCT/LLCT |
| S24 |
H−5 → L+2 (22%) |
246/5.04 |
0.1514 |
MLCT/LLCT |
| 5 |
S1 |
H → L (87%) |
363/3.41 |
0.0859 |
MLCT/LLCT |
| S15 |
H−3 → L+1 (58%) |
247/5.02 |
0.0103 |
MLCT |
| 6 |
S1 |
H → L (90%) |
379/3.27 |
0.1004 |
MLCT/LLCT |
| S22 |
H−1 → L+4 (23%) |
242/5.12 |
0.125 |
MLCT/LLCT |
In experiment, both 2 and 3 exhibit very strong absorption bands below 300 nm. The intense bands in the 300–420 nm and weaker bands between 420 and 450 nm extend into the visible region.29 The positions, intensities and separations of absorption spectra are consistent with our calculated results. As seen in Fig. 4, 1 and 2 (3, 4 and 5) show very similar absorption curves, indicating that the pmi ligand has similar influence on the absorption spectra compared with that of ppz ligand. For 3–6, the introduction of carbazole significantly improved the intensity of the absorption bands. Notably, the absorption intensity in the lower-energy region of 6 with benzimidazole ligand would enhance the intersystem crossing (ISC) from singlet to triplet excited states and then increase the phosphorescent quantum efficiency.45 As shown in Table 4, the calculated lowest-lying absorption bands are in the following order: 1 (355 nm) < 5 (363 nm) < 2 (365 nm) < 4 (375 nm) < 3 (379 nm)/6 (379 nm), which is almost consistent with the trend of HOMO–LUMO energy gaps for 1–6 because H → L transition is dominant configuration for the excitation. Meanwhile, the lowest-lying absorptions of 1–6 have mixed MLCT/LLCT character. For 1 and 2, the calculated strongest absorption peaks are localized at 225 and 229 nm respectively, with character of MLCT and MLCT/ILCT (intra-ligand charge transfer). For 3–6, they are red-shifted about 20 nm (254, 246, 247, and 242 nm, respectively) and possess stronger intensities which may be due to the extended π-conjugation. Moreover, Pt d-orbitals still give much contribution to the occupied molecular orbital and little contribution to the unoccupied molecular orbital, hence the transition of the strongest absorption of 3–6 can be characterized as MLCT/LLCT character. The comparison of absorption of 1–6, shows that the intermolecular energy transfer process and spectroscopic properties can be tuned by altering ligands.
3.4 IP, EA and reorganization energy
The excellent charge injection, transport abilities, and the balance between the electron and hole transport are crucial to the device performance of OLEDs. To quantitatively evaluate the charge injection abilities, the ionization potential (IP) and electron affinity (EA) both in vertical (v, at the geometry of the neutral molecule) and adiabatic (a, optimized structures for both the neutral and charged molecules) processes have been studied by DFT method. As it is known that a smaller IP value facilitates hole injection, while larger EA value will facilitate electron injection. In addition, the reorganization energy (λ) is also calculated to evaluate the balance properties for all complexes. According to Marcus theory,46 the charge (hole and electron) transfer rate (Ket) can be estimated by the following equation:| |
Ket = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λ/4KBT) exp(−λ/4KBT)
| (1) |
where A is a correlation factor of the electronic coupling between adjacent molecules, λ is the reorganization energy, KB is the Boltzmann constant, and T is the temperature. Seen from eqn (1), a smaller λ value means faster charge transport process, and the reorganization energy for hole/electron transfer can be expressed as follows:47
All the calculated values including the vertical IP (IPv), adiabatic IP (IPa), hole extraction potential (HEP), vertical EA (EAv), adiabatic EA (EAa), electron extraction potential (EEP), and reorganization energy for hole/electron (λh/λe) are listed in Table 5.
Table 5 The calculated ionization potentials (IPs), electron affinity (EAs), and reorganization energy (λ) by DFT for 1–6 (unit in eV)
| |
IP(v) |
IP (a) |
HEP |
EA (v) |
EA (a) |
EEP |
λhole |
λelectron |
| 1 |
6.42 |
6.34 |
6.26 |
−0.13 |
0.06 |
0.25 |
0.16 |
0.38 |
| 2 |
6.33 |
6.24 |
6.16 |
−0.18 |
0.01 |
0.21 |
0.17 |
0.39 |
| 3 |
6.09 |
6.00 |
5.91 |
−0.05 |
0.13 |
0.34 |
0.18 |
0.39 |
| 4 |
6.17 |
6.07 |
5.97 |
0.01 |
0.17 |
0.36 |
0.20 |
0.35 |
| 5 |
6.07 |
5.98 |
5.90 |
−0.42 |
−0.31 |
−0.19 |
0.17 |
0.23 |
| 6 |
6.08 |
5.98 |
5.88 |
−0.02 |
0.09 |
0.22 |
0.20 |
0.24 |
The results confirm that 3–6 have smaller IP values and their associated HOMO energy levels are higher than that of 1, 2 as expected. That is, they have better hole injection ability than other complexes. This is attributed to the introduction of imidazole and benzimidazole. Meanwhile, 4, 3, and 6 have better electron injection ability indicated by their larger EA values, which is also consistent with their lower LUMO energy levels. In addition, for 1–6, the reorganization energies for hole transport (λh) are all smaller than electron (λe), thus this series of complexes have better hole transport performance. In general, 5, 6 give better charge transfer balance performance due to their smaller λh and λe values and their smaller deviations (0.06 and 0.04 eV) between λh and λe values.
3.5 Phosphorescence properties
The calculated lowest energy emission and transition natures together with some experimental data are listed in Table 6. Moreover, the molecular orbital energy level diagrams and orbital composition distribution at the triplet excited state geometries for 1–6 are collected in Fig. S1 and Table S3,† respectively.
Table 6 The calculated phosphorescent emissions in CH2Cl2 media of 1–6
| |
States |
λ (nm)/E (eV) |
λexpt (nm) |
Main configuration |
Assignment |
| 1 |
T1 |
425/2.92 |
430 |
H−1 → L (57%) |
MLCT/ILCT |
| 2 |
T1 |
431/2.87 |
442 |
H → L (55%) |
MLCT/ILCT |
| 3 |
T1 |
437/2.84 |
452 |
H → L (47%) |
MLCT/LLCT |
| H → L+1 (28%) |
MLCT/ILCT |
| 4 |
T1 |
436/2.84 |
449 |
H → L (45%) |
MLCT/LLCT |
| H → L+1 (34%) |
MLCT/ILCT |
| 5 |
T1 |
431/2.88 |
|
H → L (60%) |
ILCT/MLCT |
| H → L+1 (25%) |
MLCT/ILCT |
| 6 |
T1 |
432/2.87 |
|
H → L+1 (44%) |
MLCT/ILCT |
| H → L (38%) |
LLCT/MLCT |
In Table 6, the calculated lowest-energy emission wavelengths for 1–4 are 425, 431, 437, and 436 nm, which agree well with the experimental values. In addition, the phosphorescence emission of 5, 6 at 431 and 432 nm have slightly hypochromatic shifted compared with 3 and 4. All complexes are deep-blue emitting. The T1 state of 1 is mainly from HOMO−1 → LUMO (57%) transition with 3MLCT/3ILCT transition characters, which may be attributed to the small difference of energies between HOMO and HOMO−1. Besides, the important transitions of 3–6 are all attributed to the HOMO → LUMO and HOMO → LUMO+1 transition with 3MLCT/3ILCT transition characters. As shown in Table S3,† the HOMOs of all complexes are localized on atom Pt, pmi and Cb ligands. For 1, and 2, the LUMO and LUMO+1 are both localized on pmi and LL′ ligands; for 3, and 4, the LUMO and LUMO+1 are both localized on Cb and LL′ ligands. Hence, the transition characters for 1 and 2, 3 and 4 are identical, causing very close emission wavelengths of 1 and 2, as well as 3 and 4. For 5 and 6, the LUMO are mainly localized on pmi and Cb ligands; the LUMO+1 are mainly localized on Cb ligand. The pyridine part of LL′ ligand for all complexes have little composition on the HOMO orbital but have large composition on the LUMO and LUMO+1 orbital, which reveals that the pyridine part of LL′ ligand is significant for the transition from HOMO to LUMO/LUMO+1. Therefore, changing the LL′ ligand may effectively impact the phosphorescence properties.
3.6 Phosphorescence quantum efficiency analysis
3.6.1 Nonradiative decay rate. The smaller structural distortion and larger energy difference between T1 and S0 states lead to slower temperature-independent nonradiative decay rate according to the energy gap law.48 The degree of structural distortion can be described by Stokes shift.49 In this research, the calculated Stokes shifts for 1–6 are 0.58, 0.53, 0.43, 0.47, 0.53, and 0.40 eV, respectively, which suggests that complexes 3, 4 and 6 with carbazole group have better rigidity and show smaller structural distortion compared with 1 and 2. The energy differences between Tm and S0 states for 1–6 are 2.38, 2.26, 2.09, 2.18, 2.02, and 2.05 eV, respectively. The energy differences in complexes 1–4 is larger than that in 5 and 6 slightly. As described above, the temperature-independent nonradiative decay rate of 1–6 will not have too much difference.There is another important process, the temperature-dependent nonradiative decay process, needs to be considered. In general, the triplet excited state (3ES) converts to 3MC state and then back to ground state (1GS) via the minimum energy crossing points (MECPs) between the 3MC and 1GS potential surfaces. Therefore, a larger activation barrier of 3ES → 3MC and a relatively higher energy of MECPs will decrease the temperature-dependent nonradiative decay rate.50,51 The spin density plots of MECPs for 1–6 are shown in Fig. S2.† We found that optimizing the geometry of the MECP will directly reach to the triplet excited state and the intrinsic reaction coordinate (IRC) calculation shows a smooth path (Fig. S3†). There is no obvious low energy 3MC state of these complexes. This may be due to the better geometrical rigidity. The calculated energy gaps between the 3ES and MECP of 1–6 are 22.7, 25.6, 37.5, 49.7, 35.1, and 62.1 kcal mol−1, respectively. The introduction of carbazole in 3–6 significantly increased the energy gaps between MECP and 3ES, which means the 3ES → MECP → 1GS decay path of 3–6 will be more difficult than that of 1, 2. Hence, the nonradiative decay rate of 3–6 will be smaller than that of 1, 2 due to the introduction of carbazole group enhanced the rigidity of the molecules. The MECP between the 3ES and 1GS were optimized using Gaussian09 together with the code developed by Harvey et al.52,53
3.6.2 Radiative decay rate. Within the Born–Oppenheimer approximation and perturbation theory and frozen core calculation, the simplified equation for kr from Tm state to S0 state can be expressed as follows:54–56| |
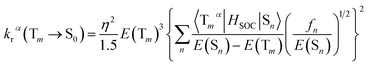 | (4) |
| |
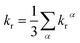 | (5) |
where η is the refractive index of the medium, which of CH2Cl2 solution is taken to be 1.424, and the 〈Tmα|HSOC|Sn〉 is the SOC matrix elements between the mth triplet excited state (Tm) and the nth singlet excited (Sn), α is the spin sublevel of the triplet excited state Tm (α = x, y, or z), and fn is the oscillator strength. Based on eqn (4) the value of kr is determined by the SOC matrix elements 〈Tmα|HSOC|Sn〉, the oscillator strength fn, and the energy gap between the coupled Sn and Tm. The calculated krα (α = x, y, z) and the average kr of the Tm → S0 transition [eqn (5)]54,57 are listed in Table 7.
Table 7 Calculated radiative decay rate constants kr (105 s−1) of 1–6 at the optimized T1 geometry
| Complexes |
States |
krz |
kry |
krx |
kr |
kr,exp |
| 1 |
T1 |
0.20 |
— |
0.12 |
|
|
| T2 |
4.16 |
0.10 |
0.08 |
1.45 |
1.3 |
| 2 |
T1 |
0.28 |
0.23 |
0.08 |
0.51 |
2.3 |
| 3 |
T1 |
0.05 |
0.03 |
— |
|
|
| T2 |
1.57 |
0.49 |
0.01 |
|
|
| T3 |
11.83 |
2.71 |
0.13 |
4.90 |
2.1 |
| 4 |
T1 |
0.10 |
0.03 |
— |
|
|
| T2 |
3.32 |
— |
0.42 |
|
|
| T3 |
7.07 |
0.15 |
0.04 |
2.42 |
1.9 |
| 5 |
T1 |
— |
0.03 |
— |
|
|
| T2 |
1.04 |
1.12 |
— |
|
|
| T3 |
24.27 |
— |
0.43 |
8.23 |
|
| 6 |
T1 |
0.01 |
0.09 |
0.01 |
|
|
| T2 |
0.08 |
0.76 |
0.63 |
|
|
| T3 |
25.75 |
— |
65.21 |
30.32 |
|
In order to make the calculation results more accurate, we considered ten singlet excited states from S1 to S10 and the low-lying triplet excited state below the first singlet excited state S1. Only when the 1MLCT and 3MLCT excitation configurations of the coupling singlet and triplet states have the same unoccupied ligand π* orbital and different Pt d orbitals can have effective SOC. The available coupling energy levels between the singlet excited states and triplet excited states of 1–6 are shown in Fig. S4† and the corresponding data are listed in Tables S4–S9.† Complex 2 has the least available singlet excited states (S2, S3, S5, S6, S9, and S10) coupling with T1 state and the energy gap between the coupled T1 and Sn states is much larger than that of the other complexes else in this work. It is also noted that most of the available Sn states of 2 have smaller oscillator strengths. Therefore, the kr of complex 2 is the minimum. The difference between calculated result and measured result in complex 2 may be due to other factors out of single molecule model. In addition, the experimental results show that the phosphorescence quantum efficiency of complex 2 is the lowest in these complexes, which is consistent with our calculation results. The trend of calculated results of 1, 3, and 4 is consistent with the experimental values, which proved that the method we used to calculate the kr is reliable. The two designed complexes 5 and 6 have considerable kr compared with 1–4. The replacing of the imidazole and benzimidazole groups are conducive to the radiative decay process, which may be attributed to the fact that shorten bond length between the metal Pt and the ligand LL′ would be advantageous to the transition from metal to ligand. Combined with previous discussion on knr, we can draw the conclusion that complex 6 has the maximum phosphorescence quantum efficiency and would be the most suitable emitting material for the application in OLED.
4 Conclusions
In this work, the electronic structures, absorption properties, charge transfer performance, and phosphorescence properties of six cyclometalated tetradentate Pt(II) complexes 1–6 are investigated by DFT/TDDFT methods. Compared with 1 and 2, complexes 3–6 with carbazole segment have greater oscillator strength especially for 6. The lowest-lying absorption of 3, 4, and 6 have a little red-shift. The investigation of two designed complexes 5 and 6 based on the structure of 3 and 4 confirms that partial modification of the large ligand can affect the photophysical properties of the complexes. The lowest-lying energy emission of 5 and 6 have a little blue-shift compared with 3–4. Carbazole group in 3–6 can enhance the rigidity of the molecules and thus decrease the nonradiative rate. As the conclusion, the complex 6 has the best charge transport properties and the highest phosphorescence quantum efficiency in all complexes, which could be used in OLEDs as a high efficiency blue-emitting material. All of the above analysis shows that judicious molecular design will be helpful in improving luminescent properties of complexes for highly efficient phosphorescent emitter in OLED application.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21173096 and 21203071) and the State Key Development Program for Basic Research of China (Grant No. 2013CB834801) and Young Scholar Training Program of Jilin University.
Notes and references
- E. Holder, B. M. Langeveld and U. S. Schubert, Adv. Mater., 2005, 17, 1109–1121 CrossRef.
- F. So, B. Krummacher, M. K. Mathai, D. Poplavskyy, S. A. Choulis and V.-E. Choong, J. Appl. Phys., 2007, 102, 091101 CrossRef.
- Y. You and W. Nam, Chem. Soc. Rev., 2012, 41, 7061–7084 RSC.
- S. Moromizato, Y. Hisamatsu, T. Suzuki, Y. Matsuo, R. Abe and S. Aoki, Inorg. Chem., 2012, 51, 12697–12706 CrossRef CAS PubMed.
- C. Schildknecht, C. Lennartz, K. Kahle, O. Molt, E. Fuchs, N. Moonen, J. Rudolph, G. Wagenblast, P. Amrhein, J. Proelss and I. Muenster, in Organic Light Emitting Materials and Devices Xi, ed. Z. H. Kafafi and F. So, 2007, vol. 6655, pp. 65502–65502 Search PubMed.
- P. T. Chou and Y. Chi, Chem.–Eur. J., 2007, 13, 380–395 CrossRef CAS PubMed.
- M. K. Nazeeruddin and M. Gratzel, in Photofunctional Transition Metals Complexes, ed. V. W. W. Yam, 2007, vol. 123, pp. 113–175 Search PubMed.
- W. Y. Wong, Dalton Trans., 2007, 4495–4510, 10.1039/b711478h.
- Y. Shirota and H. Kageyama, Chem. Rev., 2007, 107, 953–1010 CrossRef CAS PubMed.
- R. C. Evans, P. Douglas and C. J. Winscom, Coord. Chem. Rev., 2006, 250, 2093–2126 CrossRef CAS.
- F. Q. Bai, J. Wang, B. H. Xia, Q. J. Pan and H. X. Zhang, Dalton Trans., 2012, 41, 8441–8446 RSC.
- Y. Unger, D. Meyer, O. Molt, C. Schildknecht, I. Münster, G. Wagenblast and T. Strassner, Angew. Chem., 2010, 122, 10412–10414 CrossRef.
- T. Fleetham, Z. Wang and J. Li, Org. Electron., 2012, 13, 1430–1435 CrossRef CAS.
- D. A. Vezzu, J. C. Deaton, J. S. Jones, L. Bartolotti, C. F. Harris, A. P. Marchetti, M. Kondakova, R. D. Pike and S. Huo, Inorg. Chem., 2010, 49, 5107–5119 CrossRef CAS PubMed.
- S. C. F. Kui, P. K. Chow, G. S. M. Tong, S. L. Lai, G. Cheng, C. C. Kwok, K. H. Low, M. Y. Ko and C. M. Che, Chem.–Eur. J., 2013, 19, 69–73 CrossRef CAS PubMed.
- E. Turner, N. Bakken and J. Li, Inorg. Chem., 2013, 52, 7344–7351 CrossRef CAS PubMed.
- J. Kalinowski, V. Fattori, M. Cocchi and J. A. G. Williams, Coord. Chem. Rev., 2011, 255, 2401–2425 CrossRef CAS.
- G.-J. Zhou, Q. Wang, W.-Y. Wong, D. Ma, L. Wang and Z. Lin, J. Mater. Chem., 2009, 19, 1872–1883 RSC.
- F.-M. Hwang, H.-Y. Chen, P.-S. Chen, C.-S. Liu, Y. Chi, C.-F. Shu, F.-I. Wu, P.-T. Chou, S.-M. Peng and G.-H. Lee, Inorg. Chem., 2005, 44, 1344–1353 CrossRef CAS PubMed.
- M. Tanaka and H. Mori, J. Phys. Chem. C, 2014, 118, 12443–12449 CAS.
- H. Tsujimoto, S. Yagi, Y. Honda, H. Terao, T. Maeda, H. Nakazumi and Y. Sakurai, J. Lumin., 2010, 130, 217–221 CrossRef CAS.
- M. G. Colombo, A. Hauser and H. U. Guedel, Inorg. Chem., 1993, 32, 3088–3092 CrossRef CAS.
- F.-Q. Bai, J. Wang, B.-H. Xia, Q.-J. Pan and H.-X. Zhang, Dalton Trans., 2012, 41, 8441–8446 RSC.
- L.-M. Xie, F.-Q. Bai, W. Li, Z.-X. Zhang and H.-X. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 10014–10021 RSC.
- S. Lamansky, P. Djurovich, D. Murphy, F. Abdel-Razzaq, H.-E. Lee, C. Adachi, P. E. Burrows, S. R. Forrest and M. E. Thompson, J. Am. Chem. Soc., 2001, 123, 4304–4312 CrossRef CAS PubMed.
- M. K. Nazeeruddin, R. Humphry-Baker, D. Berner, S. Rivier, L. Zuppiroli and M. Graetzel, J. Am. Chem. Soc., 2003, 125, 8790–8797 CrossRef CAS PubMed.
- S.-C. Lo, C. P. Shipley, R. N. Bera, R. E. Harding, A. R. Cowley, P. L. Burn and I. D. Samuel, Chem. Mater., 2006, 18, 5119–5129 CrossRef CAS.
- S. Haneder, E. Da Como, J. Feldmann, J. M. Lupton, C. Lennartz, P. Erk, E. Fuchs, O. Molt, I. Münster, C. Schildknecht and G. Wagenblast, Adv. Mater., 2008, 20, 3325–3330 CrossRef CAS.
- X. C. Hang, T. Fleetham, E. Turner, J. Brooks and J. Li, Angew. Chem., Int. Ed., 2013, 52, 6753–6756 CrossRef CAS PubMed.
- R. J. Holmes, S. R. Forrest, T. Sajoto, A. Tamayo, P. I. Djurovich, M. E. Thompson, J. Brooks, Y. J. Tung, B. W. D'Andrade, M. S. Weaver, R. C. Kwong and J. J. Brown, Appl. Phys. Lett., 2005, 87, 243507 CrossRef.
- F. Monti, F. Kessler, M. Delgado, J. Frey, F. Bazzanini, G. Accorsi, N. Armaroli, H. J. Bolink, E. Ortí and R. Scopelliti, Inorg. Chem., 2013, 52, 10292–10305 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- J. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- R. A. Friesner, Annu. Rev. Phys. Chem., 1991, 42, 341–367 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- E. Turner, N. Bakken and J. Li, Inorg. Chem., 2013, 52, 7344–7351 CrossRef CAS PubMed.
- D. Jacquemin, E. A. Perpète, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2010, 6, 1532–1537 CrossRef CAS PubMed.
- A. Tsuboyama, H. Iwawaki, M. Furugori, T. Mukaide, J. Kamatani, S. Igawa, T. Moriyama, S. Miura, T. Takiguchi and S. Okada, J. Am. Chem. Soc., 2003, 125, 12971–12979 CrossRef CAS PubMed.
- T. Sajoto, P. I. Djurovich, A. Tamayo, M. Yousufuddin, R. Bau, M. E. Thompson, R. J. Holmes and S. R. Forrest, Inorg. Chem., 2005, 44, 7992–8003 CrossRef CAS PubMed.
- T. Ran, Q. Juan, D. Lian and Q. Yong, Prog. Chem., 2010, 22, 2255–2267 Search PubMed.
- X.-Y. Ren, Y. Wu, L. Wang, L. Zhao, M. Zhang, Y. Geng and Z.-M. Su, J. Mol. Graphics Modell., 2014, 51, 149–157 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- N. F. Mott and E. A. Davis, Electronic processes in non-crystalline materials, Oxford University Press, 2012 Search PubMed.
- J. S. Wilson, N. Chawdhury, M. R. A. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Kohler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412–9417 CrossRef CAS PubMed.
- N. Nijegorodov and W. Downey, J. Phys. Chem., 1994, 98, 5639–5643 CrossRef CAS.
- B.-Z. Yang, S. Huang, J. Zhong and H. Zhang, Org. Electron., 2015, 19, 7–14 CrossRef CAS.
- W. H. Lam, E. S. Lam and V. W. Yam, J. Am. Chem. Soc., 2013, 135, 15135–15143 CrossRef CAS PubMed.
- J. N. Harvey and M. Aschi, Phys. Chem. Chem. Phys., 1999, 1, 5555–5563 RSC.
- J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99 CrossRef CAS.
- G. S. M. Tong and C. M. Che, Chem.–Eur. J., 2009, 15, 7225–7237 CrossRef CAS PubMed.
- Z. A. Siddique, Y. Yamamoto, T. Ohno and K. Nozaki, Inorg. Chem., 2003, 42, 6366–6378 CrossRef CAS PubMed.
- K. Nozaki, J. Chin. Chem. Soc., 2006, 53, 101–112 CrossRef CAS.
- J. M. Younker and K. D. Dobbs, J. Phys. Chem. C, 2013, 117, 25714–25723 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of calculated molecular orbital (MO) compositions, transition characters analysis and the corresponding coupling energy levels between singlet excited states and triplet excited states for complexes 1–6. See DOI: 10.1039/c5ra22754b |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λ/4KBT)
exp(−λ/4KBT)