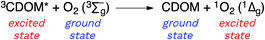Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Triplet state dissolved organic matter in aquatic photochemistry: reaction mechanisms, substrate scope, and photophysical properties
Kristopher
McNeill
 *a and
Silvio
Canonica
b
*a and
Silvio
Canonica
b
aInstitute for Biogeochemistry and Pollutant Dynamics, ETH Zurich, Universitaetstrasse 16, 8092 Zurich, Switzerland. E-mail: kris.mcneill@env.ethz.ch
bEawag, Swiss Federal Institute of Aquatic Science and Technology, Überlandstrasse 133, 8600 Dübendorf, Switzerland
First published on 22nd September 2016
Abstract
Excited triplet states of chromophoric dissolved organic matter (3CDOM*) play a major role among the reactive intermediates produced upon absorption of sunlight by surface waters. After more than two decades of research on the aquatic photochemistry of 3CDOM*, the need for improving the knowledge about the photophysical and photochemical properties of these elusive reactive species remains considerable. This critical review examines the efforts to date to characterize 3CDOM*. Information on 3CDOM* relies mainly on the use of probe compounds because of the difficulties associated with directly observing 3CDOM* using transient spectroscopic methods. Singlet molecular oxygen (1O2), which is a product of the reaction between 3CDOM* and dissolved oxygen, is probably the simplest indicator that can be used to estimate steady-state concentrations of 3CDOM*. There are two major modes of reaction of 3CDOM* with substrates, namely triplet energy transfer or oxidation (via electron transfer, proton-coupled electron transfer or related mechanisms). Organic molecules, including several environmental contaminants, that are susceptible to degradation by these two different reaction modes are reviewed. It is proposed that through the use of appropriate sets of probe compounds and model photosensitizers an improved estimation of the distribution of triplet energies and one-electron reduction potentials of 3CDOM* can be achieved.
Environmental impactPhotochemical processes are critically important in driving biogeochemical element cycling and in the breakdown of contaminants in surface waters. One of the most important and least understood sets of photochemical pathways involves triplet chromophoric dissolved organic matter (3CDOM*), a form of electronically excited DOM. There has been a recent surge in the study of the properties and reactivity of 3CDOM* and this review article is an attempt to organize and synthesize what has been discovered about 3CDOM* over the past few decades. |
Introduction
Sunlight-driven processes are central to both the buildup of complex molecules through photosynthesis and their breakdown through photodegradation reactions. These photodegradation processes may be initiated not only directly by the absorption of light, but also indirectly through reactions involving a menagerie of exotic chemical species such as free radicals and electronically excited molecules, referred to here collectively as photochemically produced reactive intermediates (PPRI).1–4 Triplet excited states of chromophoric dissolved organic matter (3CDOM*) are an important subset of the larger pool of PPRI formed in sunlit waters that also include singlet oxygen (1O2, 1Δg), superoxide (O2−˙), hydrogen peroxide, hydroxyl radical (OH˙), and others.1–43CDOM* has been implicated in the degradation of contaminants, such as pesticides5 and pharmaceuticals,6,7 and holds a special position among the PPRI for at least two reasons. First, 3CDOM* is known or suspected to be a precursor of other PPRI.1–4 For example, 3CDOM* is the primary source for 1O2 in sunlit natural waters.8,9 Second, unlike other PPRI, 3CDOM* is not a well-defined species; rather, it is an infamously ill-defined mixture of triplet states, which vary in their excited state energies and excited state redox potentials.The goal of this review article is to outline the reactivity modes of 3CDOM* and to summarize what is known or can be reasonably inferred about both the triplet energy and redox potential of 3CDOM*. In addition, some back-of-the-envelope calculations are presented that give rough answers to questions that often arise when discussing 3CDOM*: why are triplet states more important than singlet states in CDOM-sensitized processes? And, what is the steady-state concentration of 3CDOM*?
Steady-state concentration of 3CDOM* in natural waters
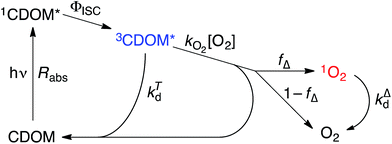
Attempting to quantify the steady-state concentration of 3CDOM* in an aquatic system would seem to be more challenging than other PPRI, due to the abovementioned problem that 3CDOM* is a mixture of triplet states of diverse molecules. Therefore, it may seem surprising that we can actually estimate the steady-state concentration of 3CDOM* within about a factor of two with a high degree of confidence. This is thanks to the inextricable link between 1O2 and 3CDOM*.To understand this, it is helpful to consider the simplified kinetic scheme that connects 3CDOM* and 1O2 (Fig. 1). CDOM is excited by the absorption of a photon (symbolized by hν) to form the excited singlet state of CDOM, 1CDOM*. Under optically thin conditions, the rate of light absorbance (Rabs), in units of M s−1, is given by the product of the irradiance (mmol photons cm−2 s−1), the Naperian absorption coefficient of CDOM (natural log-based absorption coefficient in units of cm−1), and a conversion factor (mol L−1 (mmol cm−3)−1 = 1). The efficiency of the conversion of 1CDOM* to 3CDOM* (i.e., the intersystem crossing efficiency) is given by ΦISC. The rate constants for the O2-independent and O2-dependent deactivation pathways of 3CDOM* are given by kTd and kO2[O2], respectively. Under normal air-saturated surface–water conditions, O2-dependent relaxation almost certainly dominates over O2-independent relaxation. Sharpless has estimated the O2-independent lifetime of triplets through O2-dependent formation kinetics of 1O2 using Suwannee River and Pony Lake isolates, and determined a lifetime around 20 μs (kTd ≈ 5 × 104 s−1).10 Zepp has made a reasonable estimate of kO2 = 2 × 109 M−1 s−1, based on O2 quenching rate constants of well-defined sensitizers.9 While there is certainly some variation in the individual kO2 values among the numerous sensitizers that comprise 3CDOM*, they are all expected to be quite high and near the diffusion-controlled limit. For air-saturated freshwater at 25 °C (258 μM O2), kO2[O2] is thus approximately 5 × 105 s−1 (τ = 2 μs), which suggests that the O2-dependent relaxation pathway is an order of magnitude more important than the O2-independent pathway.
The quenching of triplet states by O2 produces 1O2, but the yield for this process (fΔ) is different for each sensitizer. It has often been assumed that fΔ is close to unity,9 but studies with a range of well-defined triplet sensitizers have shown that this value can vary from near 0 (e.g., coumarin11) to near 1 (e.g., perinaphthenone12), depending on the sensitizer.11 Indeed, the value of fΔ varies with the sensitizer's triplet energy and sensitizer's excited state oxidation potential (i.e., how strong a reductant the sensitizer is in the excited state), with high energy and strongly reducing triplet species generally being poorer 1O2 sensitizers.13,14 Once formed, 1O2 mainly undergoes unimolecular deactivation, kΔd.15
Expressions for the steady-state concentrations of 3CDOM* and 1O2 based on the scheme depicted in Fig. 1 are given by eqn (1) and (2).
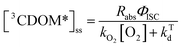 | (1) |
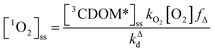 | (2) |
One can rearrange eqn (2) to arrive at an expression for the ratio of the steady-state concentrations of 1O2 and 3CDOM* (eqn (3)).
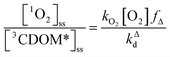 | (3) |
Substituting values for kΔd (2.5 × 105 s−1 for H2O),15kO2 (2 × 109 M−1 s−1),9 and [O2] (258 μM at 298 K), one arrives at eqn (4).
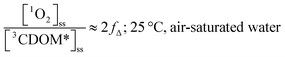 | (4) |
This result indicates that for 25 °C, air-saturated water, the ratio of 1O2 to 3CDOM* is linearly dependent on the yield of 1O2 from the O2-dependent quenching of 3CDOM* (fΔ) with a maximum [1O2]ss value of two times [3CDOM*]ss. While we do not know the value of fΔ for 3CDOM*, eqn (4) nevertheless suggests a useful rule-of-thumb of [3CDOM*]ss ≈ [1O2]ss. To reiterate, this will hold when the value for kO2 is close to the estimate of 2 × 109 M−1 s−1 and the average fΔ value is near 0.5. Under noon-time clear summer sky conditions, [1O2]ss, has been found to be between 10−14 and 10−12 M in natural waters, depending on the concentration of DOM (1–100 mgC L−1; see for example Peterson et al.16). Based on the above argumentation, we can therefore adopt this same concentration range for [3CDOM*]ss.
Why triplet states and not singlet states?
Could singlet excited state CDOM moieties (1CDOM*) act as reactive intermediates in a similar manner to 3CDOM*? After all, the lowest lying singlet excited state of a given sensitizer is higher in energy than its lowest lying triplet state and would therefore be expected to be more reactive than the triplet. While this is true, it is counteracted by the fact that the steady-state concentration of 1CDOM* is much lower than that of 3CDOM*.To determine exactly how much lower [1CDOM*]ss is than [3CDOM*]ss, we need estimates of the relative formation and decay rate constants for both species. Formation quantum yields for 3CDOM* have been estimated to be in the range of 1–2%,9,17 but could be as high as 6% or higher for some DOM samples, based on 1O2 quantum yield measurements.16,18 This indicates that 1CDOM* formation rates are 15–100 times faster than those for 3CDOM*. On the decay side, the 1CDOM* lifetime is much shorter than that of 3CDOM*, which has a lifetime of about 2 μs (i.e., the inverse of kO2[O2]; see previous section). Fluorescence lifetime studies give a direct measurement of the decay of 1CDOM*, and, as expected, the mixture of fluorophores do not display a single lifetime. Rather, the data suggest a dominant pool of short lifetime 1CDOM* species (τ < 150 ps), with contributions from two other pools of 1CDOM* (τ ≈ 1 and 3 ns).19 For simplicity, we consider 100 ps to be the typical lifetime of 1CDOM*.
Taken together, we see that while 1CDOM* is formed 15–100 times faster than 3CDOM*, it decays approximately 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster, giving 200- to 1300-fold lower steady-state concentrations than 3CDOM*. This corresponds to [1CDOM*]ss of 10−17 to 10−14 M in sunlit surface waters, compared to [3CDOM*]ss of 10−14 to 10−12 M. To put this into context of another PPRI, [1CDOM*]ss is expected to be similar to [OH˙]ss. Thus, 3CDOM* is expected generally to be the more important species, but 1CDOM* could also play a role under the right circumstances. For example, we speculate that this could occur with CDOM samples that have low intersystem crossing quantum yields (i.e., low rates of 3CDOM* production) or when the rate constant for reaction with 1CDOM* is orders of magnitude faster than with 3CDOM*. Another case where 1CDOM* could conceivably participate in bimolecular reactions despite being so short-lived is when its reaction partner is already associated with CDOM. Such intra-humic photosensitization reactions have been proposed for the photoreduction of mirex,20,21 reactions involving 1O2 with a highly hydrophobic probe molecule,22,23 and the 3CDOM*-sensitized degradation of amoxicillin.24
000 times faster, giving 200- to 1300-fold lower steady-state concentrations than 3CDOM*. This corresponds to [1CDOM*]ss of 10−17 to 10−14 M in sunlit surface waters, compared to [3CDOM*]ss of 10−14 to 10−12 M. To put this into context of another PPRI, [1CDOM*]ss is expected to be similar to [OH˙]ss. Thus, 3CDOM* is expected generally to be the more important species, but 1CDOM* could also play a role under the right circumstances. For example, we speculate that this could occur with CDOM samples that have low intersystem crossing quantum yields (i.e., low rates of 3CDOM* production) or when the rate constant for reaction with 1CDOM* is orders of magnitude faster than with 3CDOM*. Another case where 1CDOM* could conceivably participate in bimolecular reactions despite being so short-lived is when its reaction partner is already associated with CDOM. Such intra-humic photosensitization reactions have been proposed for the photoreduction of mirex,20,21 reactions involving 1O2 with a highly hydrophobic probe molecule,22,23 and the 3CDOM*-sensitized degradation of amoxicillin.24
Energy transfer reactions
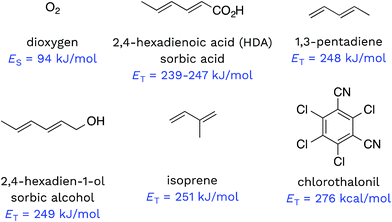
Triplet excited states of CDOM have been shown to undergo energy transfer reactions with selected substrates (Fig. 2). The best studied of these energy transfer processes is the formation of 1O2 from the interaction of triplet ground state O2 with 3CDOM*, which was first reported by Zepp in 1977.8The energy required to promote ground state O2 to 1O2 is 94 kJ mol−1 (980 meV).11 Since most triplet excited states of organic chromophores are much higher (typically 180–320 kJ mol−1), O2 has been proposed to be a universal energy acceptor, capable of accepting energy from all 3CDOM* moieties.9 This is an oversimplification as discussed above in the section on the concentration of 3CDOM* in natural waters, but to a first approximation, it is a reasonable statement.
Dienes have also been reported to participate in energy transfer reactions with 3CDOM*. Zepp first demonstrated this with pentadiene (ET = 248 kJ mol−1)25 and 2,4-hexadien-1-ol (sorbic alcohol, ET = 249 kJ mol−1),25 showing that various natural organic matter isolates could sensitize the reversible photoisomerization of the cis- and trans-forms.9 Zepp26 extended this reaction type to include 2,4-hexadienoate (HDA, also known as sorbic acid, ET = 239–247 kJ mol−1).27 More recently, Grebel et al.17 made an in depth study of the reaction of HDA with 3CDOM*, and this work has sparked the use of HDA as both a quencher of 3CDOM* and a molecular probe to quantify its concentration.28–42 In a similar way, isoprene (ET = 251 kJ mol−1)25,43 has been effectively used as a triplet quencher, providing evidence for the involvement of 3CDOM* in the oxidation of mefenamic acid,44 some sulfa drugs,45,46 and the amino acids tryptophan, methionine, and tyrosine.47 Dienes have not only been used as probe molecules. Domoic acid, a naturally occurring diene and potent marine toxin, has been shown to undergo 3CDOM*-sensitized isomerization, among other indirect photoprocesses.48
There are very few well-characterized energy transfer reactions between 3CDOM* and non-diene organic substrates. A notable exception is chlorothalonil, which is promoted to its triplet state through a CDOM-sensitized process.49,50 Porras et al. tested for the involvement of energy transfer between 3CDOM* and chlorothalonil through quenching experiments.49 In addition, they determined the triplet energy of chlorothalonil by low temperature phosphorescence measurements to be 276 kJ mol−1 and verified that excitation of CDOM with wavelengths longer than 450 nm (<266 kJ mol−1) gave very little sensitized photoreaction.49
Triplet energy of 3CDOM*
Given the heterogeneous nature of the components of 3CDOM*, there is no one triplet energy, ET, that can be used to describe it. Rather, there is a distribution of triplet energies. Using the energy transfer reactions between 3CDOM* and either O2 (ES = 94 kJ mol−1)11 or dienes 1,3-pentadiene (ET = 248 kJ mol−1)25 and 2,4-hexadien-1-ol (ET = 249 kJ mol−1),25 Zepp concluded that 3CDOM* comprised both high-energy triplets (ET ≥ 250 kJ mol−1) and low-energy triplets (94 ≤ ET ≤ 250 kJ mol−1).9 The high-energy triplets were able to sensitize the isomerization of the 1,3-pentadiene and produce 1O2, while the low energy triplets could only produce 1O2. One conclusion of this study was that the high-energy triplets accounted for about 15–53% (mean = 37%) of the total triplet pool, depending on the DOM sample.9 To visualize this result, a hypothetical normal (Gaussian) distribution of triplet energies with 37% of the triplet energies being greater than or equal to 250 kJ mol−1 is shown in Fig. 3. Also plotted in Fig. 3 are ranges of triplet energies found for representative compounds (Table 1) that contain chromophoric functional groups believed to be present in DOM. The data in Fig. 3 suggest that PAH-like moieties and quinones are most likely not major contributors to the high-energy triplet pool, whereas aromatic ketones and other carbonyl-containing compounds (e.g., coumarins and chromones) are better candidates for high-energy triplets. However, it is not only the triplet energy that is important, but also the triplet yield (i.e., intersystem crossing quantum yield). For example, aromatic ketones have triplet yields near unity,51,52 while coumarins typically have poor triplet yields.53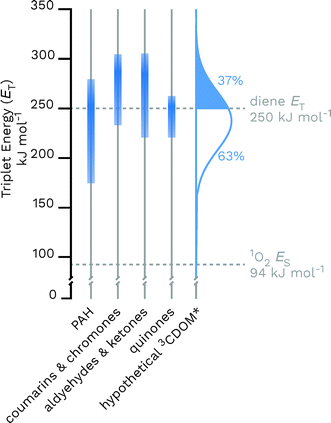 | ||
| Fig. 3 Distributions of triplet energies found for different classes of organic molecules containing functional groups that are thought to be present in CDOM and a hypothetical normal distribution of 3CDOM* triplet energies that fit the observation of 37% having ET ≥ 250 kJ mol−1.9 The data used for this figure is compiled in Table 1. | ||
| Entry | Sensitizer (S) | E°(S/S−) V (SHE) | Solventa,b | E T (kJ mol−1) | Matrixb | E°*(3S*/S−) V (SHE) | Φ Δ | Solventb |
|---|---|---|---|---|---|---|---|---|
a Balance is H2O when a percentage co-solvent is specified.
b Abbreviations: CBBP = 4-carboxybenzophenone; 3MAP = 3-methoxyacetophenone; EtOH = ethanol; MeOH = methanol; iPrOH = isopropanol; DMF = N,N-dimethylformamide; MCIP = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methylcyclohexane 1 methylcyclohexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) isopentane; EPA = 5 isopentane; EPA = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 diethyl ether 2 diethyl ether![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) isopentane isopentane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol; PMMA = polymethylmethacrylate; EtOAc = ethyl acetate; EA = 3 ethanol; PMMA = polymethylmethacrylate; EtOAc = ethyl acetate; EA = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 diethyl ether 1 diethyl ether![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol; MTHF = 2-methyltetrahydrofuran; IPMC = 5 ethanol; MTHF = 2-methyltetrahydrofuran; IPMC = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 isopentane 1 isopentane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methylcyclohexane; CFC–EA = mixture of CFC-113 (1,1,2-trichlorotrifluoroethane) and EtOAc; EM = 9 methylcyclohexane; CFC–EA = mixture of CFC-113 (1,1,2-trichlorotrifluoroethane) and EtOAc; EM = 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol 1 ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol; MeCf = 3 methanol; MeCf = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol 1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHCl3.
c Matrix not specified.
d No reported value found. CHCl3.
c Matrix not specified.
d No reported value found.
|
||||||||
| Quinones | ||||||||
| 1 | Benzoquinone | 0.099 (ref. 139) | H2O | 224 (ref. 140) | Ne solid | 2.42 | 0.13 (ref. 141) | H2O (pH 7) |
| 2 | Naphthoquinone | −0.12 (ref. 142) | H2O | 241 (ref. 143) | MCIP | 2.38 | 0.27 (ref. 141) | H2O (pH 7) |
| 3 | Anthraquinone | −0.52 (ref. 144) | H2O | 265 (ref. 145 and 146) | EPA | 2.23 | 0.62 (ref. 147) | CH3CN |
| 4 | Duroquinone | −0.24 (ref. 139) | H2O | 235 (ref. 148) | PMMA | 2.19 | 0.89 (ref. 147) | CH3CN |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Aldehydes and ketones | ||||||||
| 5 | Benzil | −0.47 (ref. 149) | 50% EtOH | 230 (ref. 150) | EtOAc | 1.92 | 0.58 (ref. 151) | C6H6 |
| 6 | CBBPb | −1.13 (ref. 152) | H2O (pH 11) | 286 (ref. 152) | EA | 1.84 | — | |
| 7 | Acetophenone | −1.42 (ref. 149) | 50% EtOH | 308 (ref. 153) | MTHF | 1.77 | 0.33 (ref. 151) | C6H6 |
| 8 | Biacetyl | −0.79 (ref. 149) | 50% EtOH | 239 (ref. 146) | EPA | 1.69 | 0.29 (ref. 151) | C6H6 |
| 9 | Benzophenone | −1.31 (ref. 149) | 50% EtOH | 288 (ref. 150) | EtOAc | 1.67 | 0.37 (ref. 11) | CH3CN |
| 10 | 3MAP | −1.50 (ref. 149) | 50% EtOH | 303 (ref. 149) | 1.64 | 0.27 (ref. 154) | C6H6 | |
| 11 | 2-Naphthaldehyde | −1.10 (ref. 149) | 50% EtOH | 249 (ref. 146) | MCIP | 1.48 | — | |
| 12 | 9-Fluorenone | −0.97 (ref. 149) | 50% EtOH | 223 (ref. 146) | MCIP | 1.34 | 0.82 (ref. 11) | C6H6 |
| 13 | 2-Acetylnaphthone (2AN) | −1.48 (ref. 149) | 50% EtOH | 249 (ref. 146) | EPA | 1.10 | 0.71 (ref. 11) | C6H6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Coumarins, chromones, and related | ||||||||
| 14 | Xanthone | −1.21 (ref. 155) | 25% EtOH | 306 (ref. 150) | EtOAc | 1.96 | 0.27 (ref. 11) | C6H6 |
| 15 | Coumarin | −1.16 (ref. 156) | 75% MeOH | 267 (ref. 157) | H2O | 1.61 | 0.01 (ref. 11) | D2O |
| 16 | Flavone | −1.18 (ref. 158) | 50% iPrOH | 260 (ref. 146) | IPMC | 1.51 | 0.16 (ref. 159) | MeCf |
| 17 | Umbelliferone | −1.23 (ref. 156) | 75% MeOH | 255 (ref. 157) | EtOH | 1.42 | — | |
| 18 | Cinnamic acid | −1.14 (ref. 156) | 75% MeOH | 235 (ref. 160) | 1.29 | — | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Polycyclic aromatic hydrocarbons | ||||||||
| 19 | Triphenylene | −2.22 (ref. 161) | DMF | 281 (ref. 146 and 162) | EPA | 0.69 | 0.40 (ref. 163) | C6H6 |
| 20 | Phenanthrene | −2.22 (ref. 164) | 75% dioxane | 259 (ref. 146 and 162) | EPA | 0.46 | 0.33 (ref. 163) | C6H6 |
| 21 | Naphthalene | −2.25 (ref. 164) | 75% dioxane | 253 (ref. 150) | CFC–EA | 0.37 | 0.50 (ref. 163) | C6H6 |
| 22 | Pyrene | −1.86 (ref. 164) | 75% dioxane | 204 (ref. 146) | MCIP | 0.25 | 0.38 (ref. 163) | C6H6 |
| 23 | Anthracene | −1.70 (ref. 164) | 75% dioxane | 178 (ref. 165) | EPA | 0.15 | 0.61 (ref. 163) | C6H6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Other sensitizers | ||||||||
| AQ2S | Anthraquinone-2-sulfonate | −0.39 (ref. 166) | H2O | 258 (ref. 167) | CH3CN | 2.28 | ∼0 (ref. 125 and 147) | H2O |
| LC | Lumichrome | −0.50 (ref. 168) | H2O | 232 (ref. 169) | EM | 1.91 | 0.63 (ref. 170) | H2O (pH 7.4) |
| RF | Riboflavin | −0.29 (ref. 171) | H2O | 209 (ref. 169) | EM | 1.88 | 0.49 (ref. 11) | H2O (pH 7.4) |
| MB | Methylene blue | 0.024 (ref. 172) | H2O | 142 (ref. 133) | 1.50 | 0.37–0.56 (ref. 173) | H2O | |
| RB | Rose bengal | −0.54 (ref. 93) | H2O | 171 (ref. 93) | EPA | 1.23 | 0.75 (ref. 11) | D2O (pD 8.2) |
| PN | Perinaphthenone | −0.67 (ref. 174 and 175) | 50% EtOH | 164 (ref. 176) | CH3CN | 1.03 | 0.98 (ref. 12) | H2O |
Another piece of information that could be obtained by Zepp and coworkers in the CDOM-sensitized isomerization of 1,3-pentadiene was the apparent ET of CDOM from the final cis–trans ratio, or the photostationary state, of 1,3-pentadiene.9 This photostationary state was shown to reflect the sensitizer's ET, and the values obtained for CDOM solutions were consistent with an apparent ET of 250 kJ mol−1.9 Similar experiments conducted with functionalized carbon nanotubes41 and petroleum54 found the apparent ET values to be lower and higher than CDOM, respectively. The petroleum value was estimated to be 288–303 kJ mol−1, suggesting that the triplet photochemistry relevant to oil spills may differ substantially from CDOM-based photochemistry.54 The high average ET value found in petroleum stands in contrast to the low average triplet energies of PAH molecules in Table 1 and Fig. 3. This may mean that the small selection of PAHs (triphenylene, phenanthrene, naphthalene, pyrene, and anthracene) is not representative of the PAH mixture in petroleum or that other higher ET species present in petroleum (e.g., ketones formed from oxidation)55,56 are dominating the sensitization of the diene probes.
At least two spectroscopic estimates of the ET value of 3CDOM* have been made. Bruccoleri et al. applied magnetic circular dichroism (MCD) spectroscopy to an organic matter isolate and assigned an absorbance transition as S0 → T1, and the wavelength for this transition (714 nm; 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) corresponded to an energy of 170 kJ mol−1.57,58 Mazhul et al. used room temperature phosphorescence spectroscopy to identify the opposite transition (T1 → S0), with an onset near 405 nm, corresponding to the highest energy (phosphorescing) triplets having an ET value of 300 kJ mol−1.59 In both of these studies, the estimates of ET must be viewed with caution, as both techniques are almost certainly confounded by the complex mixture of DOM. Indeed, Mazhul et al. explicitly point out that they believe they are only observing phosphorescence from a minority of the 3CDOM* components in their mixture.59 Additionally, these spectroscopic values do not seem reasonable as average or representative values, since one is at the extreme low end and one is at the far high end of the range of triplet energies normally found for organic sensitizers.
000 cm−1) corresponded to an energy of 170 kJ mol−1.57,58 Mazhul et al. used room temperature phosphorescence spectroscopy to identify the opposite transition (T1 → S0), with an onset near 405 nm, corresponding to the highest energy (phosphorescing) triplets having an ET value of 300 kJ mol−1.59 In both of these studies, the estimates of ET must be viewed with caution, as both techniques are almost certainly confounded by the complex mixture of DOM. Indeed, Mazhul et al. explicitly point out that they believe they are only observing phosphorescence from a minority of the 3CDOM* components in their mixture.59 Additionally, these spectroscopic values do not seem reasonable as average or representative values, since one is at the extreme low end and one is at the far high end of the range of triplet energies normally found for organic sensitizers.
3CDOM* oxidation reactions
Redox reactions are the dominant reaction type between organic substrates and 3CDOM*, with 3CDOM* primarily acting as the oxidant. The oxidation reactions have been reviewed elsewhere60 and the discussion here will be mostly confined to the substrate scope and the reduction potential of 3CDOM*.Some patterns are revealed by examining the structures of compounds for which triplet states have been established as playing a role in their organic matter-sensitized degradation. In Fig. 4, selected structures of compounds are presented that have been shown to react with 3CDOM*. Excluded from this group are compounds that are suspected to be reactive toward 3CDOM*, based on their reactivity toward model sensitizers (e.g., anthraquinone-2-sulfonate; AQ2S), but that have not yet been investigated with CDOM.61–65
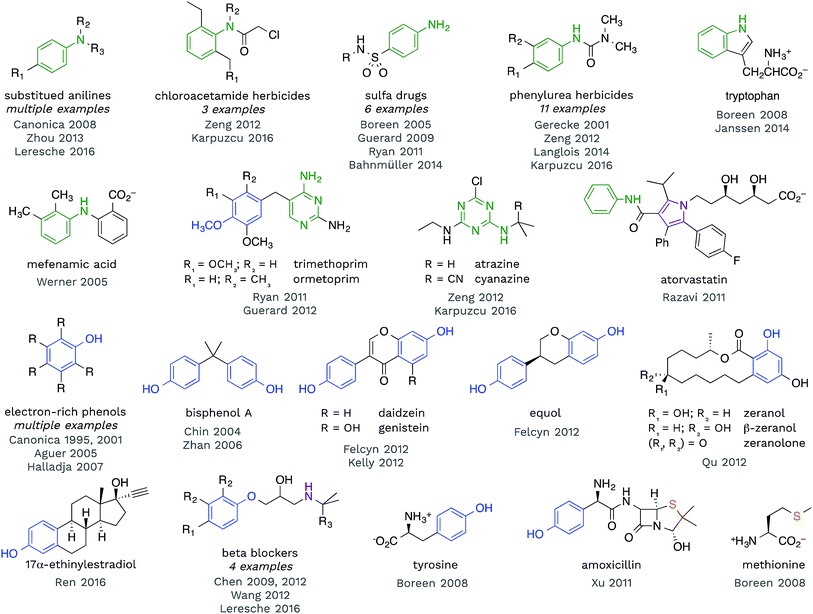 | ||
| Fig. 4 Selected compounds that have been shown to react with 3CDOM*. Aniline (and other aminoarene), phenol (and aryl ether), sulfide and related substructures are highlighted. | ||
Examining the structures in Fig. 4, one can see that anilines and phenols are well represented. Anilines and compounds containing aniline substructures are especially susceptible to oxidation by 3CDOM*. This includes simple aniline structures, such as N,N-dimethylaniline,66p-aminobenzoic acid,67 and p-cyano-N,N-dimethylaniline,68 but also more complex structures, such as found in phenylurea herbicides,28,69–72 sulfa drugs,45,46,73–75 chloroacetamide herbicides,28,72 diarylamines (e.g., mefenamic acid44), and arguably within the structure of tryptophan47,76 and indole77 (Fig. 4). There is also some evidence that this reactivity extends to aniline analogues that are amino-substituted aromatic heterocycles. For example, triazine herbicides atrazine and cyanazine have been shown to react with 3CDOM*, and both of these compounds contain a diaminotriazine functional group.28,72 The structurally similar diaminopyrimidine group in trimethoprim45 and ormetoprim78 may be responsible for the reactivity of these compounds toward 3CDOM*, but these compounds also contain electron-rich methoxy-substituted benzene rings that could instead be the locus of reactivity. 3CDOM* is capable of oxidizing both electron-rich and electron-poor anilines, although the rates of aniline oxidation are clearly modulated by their electron-richness.60,69 By contrast, only electron-rich phenols appear to be susceptible to oxidation by 3CDOM*.
Relatively simple alkyl- and methoxy-substituted phenols, such as p-cresol, 3,4-dimethoxyphenol, tyrosine, and 2,4,6-trimethylphenol, have been shown to be oxidized by 3CDOM* (Fig. 4).47,79–81 This reactivity has been found in more complicated phenol-containing compounds, including the polycarbonate constituent bisphenol A,82,83 the oral contraceptive 17α-ethinylestradiol,42 agricultural hormones zeranol, β-zeranol, and zeranolone,84 and phytoestrogens daidzein, genistein, and equol32,85 (Fig. 4). Presumably, the phenol functionality is the site of reactivity toward 3CDOM* in these compounds.
The mechanism of oxidation of phenols to phenoxy radicals can be either electron transfer followed by proton transfer (2 steps) or proton-coupled electron transfer (PCET; 1 step), and one critical piece of evidence supporting PCET is the presence of a kinetic isotope effect when O–H is changed to O–D.86 Canonica found weak isotope effects for oxidation of phenols by 3CDOM*, favoring a two-step electron transfer-proton transfer mechanism being operative.79
For some of the polyfunctional compounds shown in Fig. 4, the primary target of 3CDOM* oxidation is not clear. Atorvastatin contains an anilide functional group (aniline amide), but also contains a pentasubstituted pyrrole that could be the preferred site of oxidation. Indeed, the pyrrole has been proposed as the site of electrochemical oxidation of atorvastatin.87 Amoxicillin reacts with 3CDOM* and contains both phenol and sulfide functional groups.24 While the reaction could be occurring at the phenol, S-containing compounds, such as methionine,47 are also believed to be oxidized by 3CDOM*. Beta blockers, atenolol, metoprolol, nadolol, and propranolol, have all been shown to react with 3CDOM*.29,68,88 While the initial site of reactivity is likely the electron-rich alkoxy-substituted benzene, analogous to phenol oxidation, Chen et al. have shown evidence for oxidation at the alkyl amine as the ultimate product.88,89
We have focused on the oxidation of organic molecules, but there is also evidence that 3CDOM* can also oxidize inorganic species. Canonica demonstrated that triplet ketone sensitizers with similar reactivity to 3CDOM* were capable of oxidizing carbonate, CO32−, to carbonate radical, CO3−˙.90 Recent work by Parker and Mitch has implicated 3CDOM* in the oxidation of halides to dihalogen radical anions, X2− (X = Cl, Br).48 The production of these reactive halogen species (RHS) could have major implications for the photochemical fate of organic contaminants in seawater. Brigante, Vione and coworkers previously showed the possibility of sensitized photochemical production of dihalogen radical anions X2− from Br− and Cl−, using AQ2S as a sensitizer.91,92 AQ2S is a powerful oxidant (see below), and while it can be used to establish the viability of triplet-sensitized oxidation reactions, it may not be an ideal surrogate for quantitative predictions of CDOM-sensitized oxidation rates. For example, using authentic CDOM, Parker and Mitch estimate steady-state concentrations of RHS in surface seawater orders of magnitude lower than the estimates gained from AQ2S halide oxidation kinetics.48,91,92
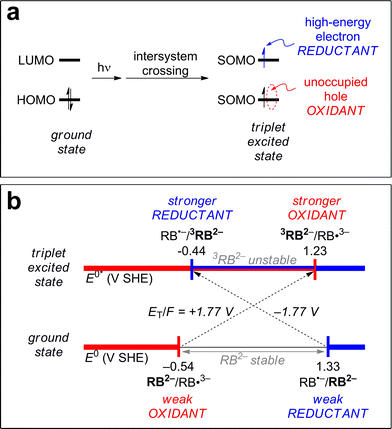
3CDOM* reduction reactions
Excited triplet states are both better oxidants and better reductants than their ground states. The reason for this can be seen visually in Fig. 5a, which shows the ground state and lowest triplet state electronic configurations of the frontier orbitals of a generic molecule. One can see that for the molecule to act as an oxidant (receive an electron), it requires less energy in the excited state than the ground state. Instead of the incoming electron having to occupy the high-energy lowest unoccupied molecular orbital (LUMO) in the ground state, it can occupy the lower energy singly occupied molecular orbital (SOMO) (formerly the highest unoccupied molecular orbital [HOMO]) in the excited state. Similarly, to act as a reductant (release an electron), it requires less energy for this process in the excited state than the ground state as one electron has already been promoted to the higher SOMO (former LUMO).A concrete example is shown in Fig. 5b for the case of rose bengal dianion (RB2−). RB2− in its triplet state has been shown to act as both a reductant and an oxidant.93 The potential associated with RB2− as a reductant, E°(RB˙−/RB2−), decreases by 1.77 V (from 1.33 to −0.44 V SHE) upon excitation to its triplet state, 3RB2−.93 The potential associated with RB2− as an oxidant, E°(RB2−/RB˙3−), increases by 1.77 V (from −0.54 to 1.23 V SHE).93 The value 1.77 V is the triplet energy converted to potential, ET(RB2−)/F = 1.77 V, and the reason this is combined with the ground state potential is discussed further in the next section. Note that RB2− in its ground state exhibits a window of redox stability between −0.54 and 1.33 V SHE, but has no such window in its triplet state. Triplet state RB2− is thermodynamically unstable with respect to oxidation above −0.44 V SHE and to reduction below 1.23 V SHE. Between these values, 3RB is thermodynamically unstable with respect to both processes, and can thus act as both an oxidant and a reductant.
The most important photoreduction reaction involving 3CDOM* is almost certainly reduction of O2 (E°(O2,1 M/O2˙−) = −0.18 V)94 to superoxide (O2−˙). Superoxide production has not been definitively linked to 3CDOM*, but it is logical that a subset of these 3CDOM* species would reduce dissolved O2, given the foregoing discussion and the fact that O2 is the dominant oxidant present in surface waters. A sense of the maximum quantum yield for such a process comes from H2O2 production quantum yields, since the primary formation pathway involves dismutation of O2˙−. H2O2 production quantum yields are strongly wavelength dependent,95–97 but are in the range of 0.5 × 10−4 to 10−3, with typical quantum yields being about 10−4.95–99 Considering that two equivalents of O2˙− are needed to produce H2O2 and that only a fraction of O2˙− goes down the dismutation pathway,100–102 the quantum yield for superoxide production is higher, perhaps by a factor of four98 or six,100 giving 10−3 as a rough upper limit on the quantum yield of O2˙− production. Of the superoxide-producing photoreductants, the fraction that is 3CDOM* is unknown and, in fact, 3CDOM* may not be involved at all. For example, Blough and others have argued that charge-transfer states of CDOM are more important photoreductants than 3CDOM*.98,100,103
How strong are these 3CDOM* reductants? Some information potentially comes from Krogh who examined the photoreduction of a suite of halogenated compounds sensitized by CDOM.104 CCl4 (E°(CCl4/CCl3˙,Cl−) ≈ −0.1 V)105 underwent facile photoreduction sensitized by Christina River water (18 mgC L−1) exposed to 310 nm radiation. This makes sense given that CCl4 is thermodynamically easier to reduce than O2 (−0.18 V).94 Importantly, however, tetrachloroethylene (PCE) (E°(PCE/C2Cl3˙,Cl−) ≈ −0.60 V)105 was not reduced under the same conditions. This gives an effective oxidation potential of the photoreductants produced by 310 nm radiation between the reduction potentials of O2 (−0.18) and PCE (−0.60 V SHE).
Reduction potential of 3CDOM*
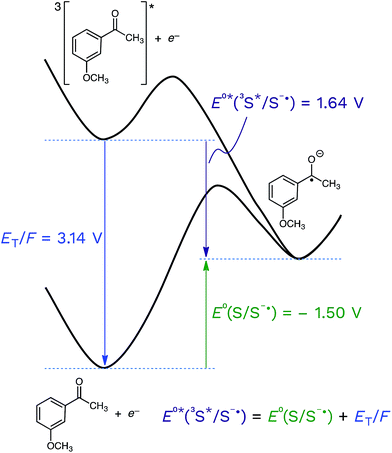
Returning to the topic of 3CDOM* as an oxidant, the excited state reduction potential of 3CDOM* (E°*(3S*/S−˙)) is a critical value that determines not only the thermodynamics, but also the kinetics of its electron transfer reactions.105 The connection between the thermodynamics and kinetics of electron transfer are discussed in the following section. As with all other parameters involving DOM, there is no single value for E°*(3S*/S−˙), but rather a distribution. It is important to realize that the excited state potential is a sum of the ground state potential and the excited state energy, divided by the Faraday constant (F = 96.485 kJ V−1) to convert from energy to potential (eqn (5)).| E°*(3S*/S−˙) = E°(S/S−˙) + ET/F | (5) |
This is shown visually in Fig. 6 for the half-wave reduction of an example aromatic ketone, 3-methoxyacetophenone (3MAP). While the ground-state reduction reaction is unfavorable in this example (E°(S/S−˙) = −1.50 V), the excited-state reaction is favorable (E°*(3S*/S−˙) = +1.64 V), and the difference between the two is the triplet energy of the ketone (ET = 303 kJ mol−1; ET/F = 3.14 V) (see Table 1). This means that compounds that are good oxidizers in the ground state (e.g., quinones) and compounds that have high triplet energies (e.g., ketones) are often powerful oxidants in their triplet state. We will return to this point below.
There have been some experimental attempts to put a value on the reduction potential of 3CDOM*.79,106 Using a set of phenols that vary in their electron richness, Canonica compared their relative rates of oxidation by both well-defined sensitizers (2-acetonaphthone, 2AN; 3MAP; and, benzophenone, BP) and by DOM (filtered Greifensee water, GSW; Suwannee River fulvic acid; Fluka humic acid; and, Contech humic acid).79 The DOM solutions showed very similar kinetic selectivity for the various phenols, meaning that the ranges of relative rate constants krel (normalized to the reference compound TMP) observed for the set of phenols were almost equal. To compare selectivities, the slopes of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel (DOM isolate or sensitizer) vs. log
krel (DOM isolate or sensitizer) vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel (GSW) plots were used. For all of the isolates as well as 3MAP (E°*(3S*/S−˙) = 1.64 V SHE) compared to GSW, the slope was approximately 1, indicating equal selectivity. However, with BP (E°*(3S*/S−˙) = 1.69 V SHE), the slope was lower than 1, indicating lower selectivity than 3CDOM*, and with 2AN (E°*(3S*/S−˙) = 1.10 V SHE), the slope was higher than 1, indicating higher selectivity than 3CDOM*. Insofar as the kinetics of the phenol oxidation reaction are controlled by the E°*(3S*/S−˙) value of the oxidant (see following section), this argues that the reduction potentials for the 3CDOM* systems are centered near 1.64 V.79 In a second study, in which the kinetics of phenol photooxidation by 2AN, 3MAP, and BP were followed using transient absorbance spectroscopy, E°*(3CDOM*/CDOM−˙) was estimated to be between 1.36 and 1.90 V.106 Parker and Mitch came to a similar conclusion using the sensitized photoproduction of halide radicals from bromide and chloride ions.48 They found Suwannee River DOM to have halide radical production rates consistent with model ketone sensitizers in the E°*(3S*/S−˙) range of 1.6 to 1.8 V.48
krel (GSW) plots were used. For all of the isolates as well as 3MAP (E°*(3S*/S−˙) = 1.64 V SHE) compared to GSW, the slope was approximately 1, indicating equal selectivity. However, with BP (E°*(3S*/S−˙) = 1.69 V SHE), the slope was lower than 1, indicating lower selectivity than 3CDOM*, and with 2AN (E°*(3S*/S−˙) = 1.10 V SHE), the slope was higher than 1, indicating higher selectivity than 3CDOM*. Insofar as the kinetics of the phenol oxidation reaction are controlled by the E°*(3S*/S−˙) value of the oxidant (see following section), this argues that the reduction potentials for the 3CDOM* systems are centered near 1.64 V.79 In a second study, in which the kinetics of phenol photooxidation by 2AN, 3MAP, and BP were followed using transient absorbance spectroscopy, E°*(3CDOM*/CDOM−˙) was estimated to be between 1.36 and 1.90 V.106 Parker and Mitch came to a similar conclusion using the sensitized photoproduction of halide radicals from bromide and chloride ions.48 They found Suwannee River DOM to have halide radical production rates consistent with model ketone sensitizers in the E°*(3S*/S−˙) range of 1.6 to 1.8 V.48
Connecting excited state reduction potential to electron transfer kinetics
To assess whether or not 3CDOM* will oxidize a substrate molecule at an appreciable rate, the standard molar Gibbs free energy change for the electron transfer reaction (ΔrG0et) can be taken as a proxy. As a rough estimate, the reaction will be relevant when ΔrG0et ≤ 0. However, a detailed quantitative assessment of reaction rates requires kinetic considerations. Although kinetics and thermodynamics are not a priori connected, there are established approaches to correlate the rate of a reaction with the Gibbs free energy change of the reaction. For reactions involving the transfer of an electron from a donor (e.g., a contaminant) to an acceptor (specifically 3CDOM*) second-order rate constants, ket, depend on ΔrG0et following characteristic relationships that were developed in the frame of theoretical models. Electron transfer theories, originally developed for unimolecular reactions, are applied to bimolecular reactions by assuming the formation of an encounter complex of the electron donor and acceptor, called a precursor complex, which is in equilibrium with the reactants and for which a steady-state assumption can be made.105 We consider here the Rehm–Weller relationship (eqn (6)),105–107 which was found to be successful in explaining fluorescence quenching data: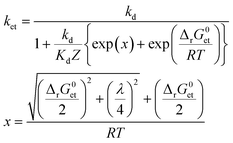 | (6) |
Both ΔrG0et and λ determine the activation energy of the electron transfer process. A basic qualitative feature of eqn (6) (see the thin lines in Fig. 7) is that for highly exergonic electron transfer reactions, ket approaches the diffusion-controlled rate constant kd. For highly endergonic reactions, the denominator of eqn (6) simplifies and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ket decreases linearly with increasing ΔrG0et, with a slope of −(2.3 × RT)−1 (corresponding to −(5.7 kJ mol−1)−1 or −(0.059 eV)−1 at 25 °C). The Rehm–Weller, Marcus or Sandros–Boltzmann equations were found to adequately fit sets of second-order rate constants obtained in aqueous solution for the quenching of the excited triplet state of individual acceptor photosensitizers using series of electron donor quenchers.106,110 Moreover, in the case of electron-rich phenols as the electron donor quenchers, such triplet quenching rate constants106 were almost equal to the second-order rate constants measured for phototransformation.79 Thus, provided that each quenching event leads to transformation of the quencher, Rehm–Weller relationships of the type of eqn (6) could be used to predict the photooxidation rate constants of any organic contaminant in the aquatic environment.
ket decreases linearly with increasing ΔrG0et, with a slope of −(2.3 × RT)−1 (corresponding to −(5.7 kJ mol−1)−1 or −(0.059 eV)−1 at 25 °C). The Rehm–Weller, Marcus or Sandros–Boltzmann equations were found to adequately fit sets of second-order rate constants obtained in aqueous solution for the quenching of the excited triplet state of individual acceptor photosensitizers using series of electron donor quenchers.106,110 Moreover, in the case of electron-rich phenols as the electron donor quenchers, such triplet quenching rate constants106 were almost equal to the second-order rate constants measured for phototransformation.79 Thus, provided that each quenching event leads to transformation of the quencher, Rehm–Weller relationships of the type of eqn (6) could be used to predict the photooxidation rate constants of any organic contaminant in the aquatic environment.
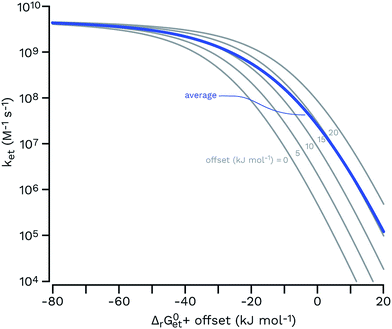 | ||
| Fig. 7 Rehm–Weller plots (gray thin curves) for a set of five functions having the same parameters (eqn (6); kd = 6.2 × 109 M−1 s−1; kd/(KdZ) = 0.1; λ = 65 kJ mol−1; values from a typical fit in ref. 106 were used) and an offset of 0, 5, 10, 15 and 20 kJ mol−1 (from left to right) for ΔrG0et. The arithmetic average of these curves is shown as a thick blue line, showing that a hypothetical equimolar mixture of five sensitizers would be expected to show a smoother transition from the diffusion-controlled plateau to the log-linear kinetic regime. | ||
The estimates for E°*(3S*/S−˙) of 3CDOM* that have been made so far79,106 suffer from the simplification that 3CDOM* is assigned a single “average” value of E°*(3S*/S−˙), that is determined by comparison with the E°*(3S*/S−˙) values of the model photosensitizers. Actually, a whole distribution of reduction potentials should be considered to account for the great variety of chromophores present in the CDOM. Let us assume that an ensemble of triplet excited chromophoric units of the CDOM, defined here as 3CDOM*i (i = 1…N), contributes to the photosensitized oxidation of a target compound (TC). The pseudo-first-order rate constant for this reaction, ksensTC, can then be expressed as:
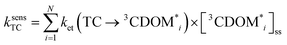 | (7) |
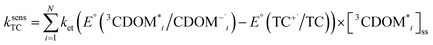 | (8) |
Unfortunately the distributions of one-electron reduction potentials in excited triplet CDOM are not known, and one has to rely on model calculations to predict the impact of such distributions on ksensTC. Let us assume that ket for the electron transfer reaction between TC and 3CDOM*i can be expressed by eqn (6) using constant values for kd and λ. In Fig. 7, Rehm–Weller plots are shown for five hypothetical 3CDOM*i having F × E°*(3CDOM*i/CDOM−˙i) that differ by 5 kJ mol−1 (ΔE°* = 52 mV). Assuming equal [3CDOM*i]ss for all chromophoric units, one can use the average of these five curves to represent ket for this group of five chromophores. The resulting curve (in the logarithmic representation, see thick line in Fig. 7) has a similar shape but a smoother transition between the diffusion-controlled plateau and the steep linear decrease compared to the single Rehm–Weller curves. We therefore refer to this as a pseudo-Rehm–Weller curve. With these considerations in mind, one can conclude that the determination of E°*(3S*/S−˙) for CDOM will remain fuzzy.
A possible approach to empirically determine the shape of the pseudo-Rehm–Weller curve for 3CDOM* consists of using a suite of probe compounds (PCs) with different (and exactly known) oxidation potentials and unit product yield for excited triplet state quenching, as recently proposed elsewhere.111 Thereby, it is suitable to define an “effective” concentration of 3CDOM* capable of oxidizing a given PC by dividing an experimentally determined ksensPC through the best guess for the maximum second-order rate constant for the electron-transfer reaction from the PC to 3CDOM* (e.g., ≈3 × 109 M−1 s−1, but an optimized value might be obtained from a consistent set of quenching data for model photosensitizers in aqueous solution). The “effective” concentration of 3CDOM* obviously decreases with increasing PC oxidation potential. In such a way, a function of [3CDOM*] vs. oxidation potential of PC can be constructed and used for the prediction of the “effective” concentration of 3CDOM*, and consequently of a pseudo-first-order transformation rate constant, for the transformation of any TC by 3CDOM* (provided that the one-electron oxidation potential of the TC is known).
After the kinetic considerations made in this section, one might ask why a corresponding analysis is not available for triplet energy transfer rate constants. Indeed, energy transfer kinetics can be treated in the frame of analogous models, which lead to equations of the same or similar form as those derived for electron transfer processes.112,113 Thereby, the difference in triplet energy between donor and acceptor assumes the same role as ΔrG0et in electron transfer processes. To our knowledge, there has been no application of these concepts to the photochemistry of CDOM to date, but this approach appears to be promising.
Comparison to well-defined triplet oxidants
Another way to look at the question of the triplet state one-electron reduction potential of CDOM is to consider known values from well-defined compounds. Table 1 gives E°*(3S*/S−˙) values for a series of compounds that have structures that could plausibly be similar to constituents of CDOM. These E°*(3S*/S−˙) values come from the compounds triplet energies (ET) and ground state reduction potentials (E°(S/S−˙)) (eqn (5)), which are also listed in Table 1. These data are visualized in Fig. 8, with a plot of ETvs. E°*(3S*/S−˙).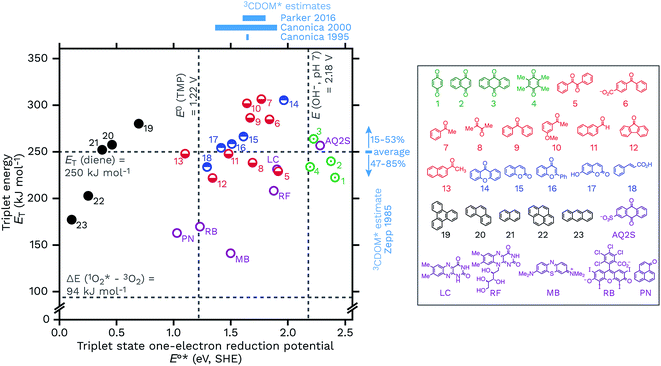 | ||
| Fig. 8 Triplet energies (ET, kJ mol−1) vs. triplet state one-electron reduction potentials (E°*(3S*/S−˙), V SHE) for a selection of 23 DOM-like model compounds and a selection of widely used sensitizers. The horizontal lines correspond to the triplet excited state energy of a typical diene energy transfer probe and the singlet state energy of O2. The vertical lines correspond to the one-electron oxidation potentials of TMP, E°(ArOH+˙/ArOH), and hydroxide at pH 7, E°′(OH˙/OH−). Selected estimates for 3CDOM* values from Zepp,9 Canonica,79,106 and Parker and Mitch48 are also shown. The data used for this figure is compiled in Table 1 along with the abbreviation definitions. | ||
A word of caution about excited state redox potentials is in order. There are several difficulties associated with obtaining accurate (ground state) aqueous one-electron reduction potentials for the various compounds listed, which lead directly to difficulties in calculating accurate excited state reduction potentials.105 First, most of the compounds (excluding the quinones) are poorly behaved electrochemically, displaying irreversible redox couples, which necessitates some estimation of the true reduction potential. Second, the observed couples are also often not associated with pure one-electron transfers, but rather have an associated protonation process. For predicting the kinetics of electron transfer, the potential associated with just the one-electron process is needed. Third, the compounds are often poorly soluble, leading to the use of co-solvents or non-aqueous conditions, which can drastically alter the potentials. In compiling the data for Table 1, every effort was made to find values in water or water–alcohol mixtures. In the case of the polycyclic aromatic hydrocarbons, one value was only found in DMF and the others were from experiments in 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 dioxane
25 dioxane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water mixtures. Additionally, for reduction potentials of the ketones and other carbonyl-containing compounds, values from the highest pH conditions were taken to get as close to the pure one-electron potential as possible. The values collected here differ somewhat from other compilations, for example the excellent compilation of Loeff, et al.114 All of this is to say that, while we believe the values in Table 1 are the best available, they should be used with some caution.
water mixtures. Additionally, for reduction potentials of the ketones and other carbonyl-containing compounds, values from the highest pH conditions were taken to get as close to the pure one-electron potential as possible. The values collected here differ somewhat from other compilations, for example the excellent compilation of Loeff, et al.114 All of this is to say that, while we believe the values in Table 1 are the best available, they should be used with some caution.
Caveats aside, it can be seen that this relatively small selection of compounds covers a wide range of E°*(3S*/S−˙), from 0.15 V for anthracene to 2.42 V for benzoquinone, suggesting that triplet CDOM oxidants will be found across the entire range of possible potentials in aqueous solution.
There are some other notable observations that can be made by examining this collection of representative triplets. One is that the E°*(3S*/S−˙) values of different functional group classes are somewhat distinct, with polycyclic aromatic hydrocarbons having the lowest reduction potentials (i.e., relatively weak oxidants, E°*(3S*/S−˙) ≤ 0.69 V) of this set and quinones having the highest (i.e., strong oxidants, E°*(3S*/S−˙) ≥ 2.19 V). Indeed, excited state triplet quinones are such strong oxidants that they are above the one-electron reduction potential for water at pH 7 (E°′(OH˙/OH−) = 2.18 V), which is actually the oxidation of hydroxide ion (E°(OH˙/OH−) = 1.77 V) corrected for its activity at pH 7.115,116 Incidentally, the one-electron oxidation of water itself requires a much higher potential of E°(H2O+˙/H2O) = 2.65 V.117 This makes quinones one of the prime suspects in the CDOM-sensitized formation of hydroxyl radical or lower-energy hydroxyl radical-like species.118–120 Whether or not quinones actually oxidize hydroxide ion (or water) to produce hydroxyl radical has been a controversial topic.118,121–124 To give just two concrete examples, both methylbenzoquinone and AQ2S give positive results when challenged with hydroxyl radical probes, but deeper investigations suggest very little if any free hydroxyl radical involvement in these processes.118,119,124,125
Carbonyl-containing compounds fill the middle of the series with potentials ranging from 1.10 V (13, 2AN) to 1.96 V (14, xanthone). Among the carbonyl-containing compounds, aromatic ketones and aldehydes in particular, represented by compounds 5–13 in Table 1 and Fig. 8, have been considered an especially important sensitizer type in CDOM.9,10,60,70,79,98,106,126–128
Further support for the importance of ketone- and aldehyde-containing sensitizers in CDOM comes from experiments in which the CDOM-sensitized photooxidation rates of trimethylphenol (TMP, a probe molecule for triplet oxidants) were significantly reduced following removal of the ketone and aldehyde functional groups by treatment of the CDOM samples with sodium borohydride.128 Similarly, Sharpless showed that borohydride-treated DOM formed 1O2 at lower rates than (but with the same quantum efficiency as) untreated DOM.10 In most cases, treatment with borohydride led to incomplete loss of photosensitization ability, suggesting that non-ketone and -aldehyde photosensitizers are also involved.10,128 Quinones, which are reduced by borohydride but quickly revert under aerated conditions, are candidates for a part of this other pool of photosensitizers. Flavones, which are not easily reduced by borohydride129 and have similar triplet state properties to aromatic ketones (Table 1 and Fig. 8), are also possible candidates.
A second observation concerns a potential noted in Fig. 8 as a vertical line at 1.22 V. The line corresponds to the one-electron oxidation potential for TMP, E°(ArOH+˙/ArOH),106 which is a popular probe molecule for 3CDOM*.130 One-electron transfer reactions between TMP and any of the triplets to the right of this line are exergonic. This does not necessarily forbid reactions between TMP and the triplets with E°*(3S*/S−˙) < 1.22 V, but rather means that strict one-electron transfer oxidations of TMP by these sensitizers will be thermodynamically unfavorable. The way around this problem for weaker oxidants is to oxidize TMP via hydrogen atom transfer or some other proton-coupled electron transfer (PCET) reaction that yields a phenoxy radical directly. For example, 2AN (E°*(3S*/S−˙) = 1.10) oxidizes TMP and one strong piece of evidence favoring PCET as the oxidation mechanism comes from the isotope effect on this reaction. Photooxidation of TMP by 2AN in D2O was 3.4 times slower than in H2O, which can be interpreted as a result of the phenolic O–H/D bond being broken in the rate-determining step.79 When Suwannee River fulvic acid or Fluka humic acid was used as the sensitizer for TMP photooxidation, isotope effects of only kH/kD = 1.1 ± 0.1 and 1.2 ± 0.1, respectively, were observed.79 This suggests that the majority of the oxidants responsible for the oxidation of TMP in these two DOM isolates did not undergo PCET, and the most obvious reason is that their E°*(3S*/S−˙) values were significantly greater than 1.22 V.
Another observation is that triplet quenchers based on energy transfer, such as isoprene, HDA, and other dienes, are only able to capture a subset of the total triplet pool. One might be tempted to conclude from eqn (5) that using a diene quencher would lead to preferential quenching of the highly oxidizing triplets, but even with the small set of triplet states shown in Fig. 8, it is clear that some highly oxidizing triplets could be missed. For example, low-energy triplet species that are strong oxidants include benzil (5), diacetyl (8), and 9-fluorenone (12). On the other hand, the data in Fig. 8 suggest that energy transfer quenching by O2 is thermodynamically feasible for essentially all triplet states. If this is true, a potentially surprising finding was that high concentrations of TMP were shown to inhibit the production of 1O2 completely, indicating that nearly all of the 1O2-sensitizing triplets in 3CDOM* (Elliot Soil humic and fulvic acid, in this case) have a sufficiently high E°*(3S*/S−˙) to oxidize TMP.81
A final set of observations regards the sensitizers that are commonly used in laboratory studies. Perinaphthenone (PN), rose bengal (RB), and methylene blue (MB) are widely employed for generating 1O2, but all three have also been found to be triplet oxidants, with E°*(3S*/S−˙) ranging from 1.03 to 1.50 V (Table 1). Flavin-type photosensitizers, such as riboflavin (E°*(3S*/S−˙) = 1.88 V) and lumichrome (E°*(3S*/S−˙) = 1.91 V), are even stronger triplet oxidants, with potentials near the most oxidizing triplet ketone sensitizers. Near the far end of the spectrum is AQ2S, a powerful triplet oxidant (E°*(3S*/S−˙) = 2.28 V), which has been reported to give very low yields of either 1O2 or hydroxyl radical.125 Thus AQ2S might model some of the most oxidizing triplet states found in 3CDOM*, but is a considerably stronger oxidant than the average 3CDOM* species.
It would be remiss not to mention that there is often a discussion in the chemistry of triplet excited states of whether the triplet is an nπ* triplet (strong sensitizer) or ππ* triplet (weak sensitizer).114,131 The difference has to do with the electronic configuration of the triplet, in which the lower energy SOMO has more non-bonding (n) or π-bonding (π) character. For example, many triplet aromatic ketones are classified as nπ*, while triplet PAHs are ππ*. We have not included discussion of nπ* and ππ* classifications in this review for a few reasons. First, and foremost, we are mostly concerned with 3CDOM* and, while there seems to be some hope in the near term of determining the average and spread of excited state energies (ET) and excited state reduction potentials (E°*), assessing the distribution of nπ* and ππ* triplets in 3CDOM* is beyond the currently visible horizon. Second, assigning a triplet as nπ* or ππ* is not trivial, as the SOMO in question may have mixed character. For example, duroquinone has been taken as a prototypical nπ* triplet and ππ* triplet in different studies.114,132 Finally, while some have found the nπ*/ππ* framework useful for interpreting reactivity, other models have also been used. For instance, the variation in 1O2 yields from O2 quenching of triplet states has not only been interpreted using the nπ*/ππ* concept (where ππ* triplet states give higher 1O2 yields),132 but also in terms of ET and excited state oxidation potential (E°*(3S*/S+˙)) (where low ET and low E°* triplet states give higher 1O2 yields), without considering the electronic configuration.13,14,133
Outlook
Despite the importance of 3CDOM* in the transformation of organic molecules, its study has lagged behind other important PPRI, especially 1O2, ˙OH, H2O2, and O2−˙. This is clearly because 3CDOM* is a complex mixture, and its complexity confounds both direct (i.e., spectroscopic) and indirect (i.e., molecular probe methods) methods to observe and/or quantify these states. While this certainly provides a challenge, the situation is far from hopeless. Some strategies for attaining a clearer picture of 3CDOM* are outlined below along with some of the most pressing research problems.A critical strategy for studying a complex mixture like 3CDOM* is to use methods that integrate the disparate signals arising from the mixture's components and give a single signal that is more easily detected. The best and most accessible example is the use of 1O2 as a proxy for 3CDOM*. As mentioned above, quenching of triplet states by O2 to yield 1O2 is not quantitative, but it is the best universal triplet detection method of any available. Singlet oxygen formation quantum yields provide solid lower bounds for 3CDOM* formation quantum yields. Additionally, the steady-state concentrations of 1O2 and 3CDOM* must be within a factor of two of each other (when 0.25 < fΔ < 1; see eqn (4)).
While O2 quenching of 3CDOM* gives a picture of essentially all of the component triplets, using energy transfer quenchers of different energies is a clear way to probe the distribution of triplet energies in 3CDOM*. For example, HDA (sorbic acid), being a diene, is an excellent probe for quantifying the high energy triplet states capable of transferring energy to diene-containing contaminants such as domoic acid.48 At the moment, there is a large gap between the energy of 1O2 (94 kJ mol−1) and the diene quenchers that have been employed (ET ≈ 250 kJ mol−1; see Fig. 2), giving us only a rudimentary idea of the distribution (e.g., Fig. 3). While triplet energy acceptors with intermediate energies are certainly known, such as 1,3-cyclohexadiene (ET = 221 kJ mol−1), anthracene (178 kJ mol−1), ferrocene (167 kJ mol−1), azulene (163 kJ mol−1), and tetracene (123 kJ mol−1), they pose technical challenges including long wavelength absorbance, poor aqueous solubility, and/or susceptibility to photooxidation. All of these challenges can and will eventually be overcome.
The use of HDA isomerization and TMP oxidation as probe reactions for 3CDOM* is gaining in popularity. The fact that these methods are based on different mechanisms (energy transfer and oxidation, respectively) is not widely discussed in the aquatic photochemistry literature. This is potentially problematic as energy transfer- and oxidation-based probe methods are reporting on different, but overlapping, subpopulations of 3CDOM*. This will hopefully change in the future as a more nuanced and detailed view of 3CDOM* is brought into focus by further research. This also brings up the larger issue of the correct use of probe molecules and quenchers in photochemical studies. As essentially all probe molecules react by different pathways (e.g., with triplet states and with 1O2), care must be taken in both conducting the proper control experiments and in interpreting the outcome. We refer the interested reader to a recent review on the use of molecular probes for studying PPRI.111
Finally, the composition of 3CDOM* is clearly different for different sources of organic matter. In particular, there has been growing evidence of significant variability in the nature of 3CDOM in DOM of terrestrial origin (e.g., surface waters with input from soil organic matter) and of microbial origin (e.g., surface waters dominated by algal DOM or wastewater effluent DOM).134 The photochemistry of sulfa drugs serves to illustrate the point. Sulfa drugs are widespread contaminants in wastewater-impacted surface waters that have been the subject of several recent studies seeking to understand their phototransformation.45,46,73,74,135,136 In three separate studies, with three different sulfa drugs, significantly better photosensitization by autochthonous (algal) than allochthonous (terrestrial) CDOM has been observed. Chin observed that sulfadimethoxine undergoes enhanced degradation when sensitized by Pony Lake (Antarctica) fulvic acid (PLFA, a standard for microbially derived organic matter) and eutrophic lake water, but not terrestrial isolates (e.g., Suwannee River fulvic acid, SRFA).73,135 Arnold found that sulfamethoxazole degraded much more rapidly in the presence of effluent organic matter than with CDOM from other sources.45 Canonica found that sulfadiazine undergoes more rapid degradation when sensitized by PLFA than SRFA.74 In each case, convincing evidence that 3CDOM was responsible for the indirect transformation was obtained.
Why do autochthonous-dominated DOM samples (e.g., PLFA) seem to show increased reactivity compared to SRFA and other terrestrially derived organic matter samples? One possibility is that both PLFA and SRFA photooxidize compounds similarly, but SRFA contains many more antioxidants which repair some of the photooxidation damage (intermolecular or intramolecular) and slow down the macroscopic transformation rate. This idea definitely has support from studies showing the antioxidant properties of DOM in photoreactions.66,137,138 Another possibility is that the PLFA-derived 3CDOM* is a stronger oxidant (higher E°*(3S*/S−˙)) than the SFRA-derived 3CDOM*. The only way to answer the question is to determine the fundamental photophysical properties of both terrestrially derived and microbially (algal) derived CDOM.
It is clear that the study of 3CDOM* is both important and difficult. Despite the challenges, a fair amount of information about its reactivity, steady-state concentrations, and physical properties can already be inferred from existing data. Future studies, taking advantage of energy transfer-based probe methods (e.g., O2 and HDA) and oxidation-based probe methods (e.g., TMP) will only further our understanding of the scope, reactivity, and variability of 3CDOM*. There is an especially important link between 1O2 and 3CDOM* that makes 1O2 probe methods (both spectroscopic and reaction-based) particularly useful in this regard. With additional study, a clearer and more detailed picture of the components contributing to 3CDOM* and their reactivity patterns will come into view, which will in turn allow a better understanding of the role of 3CDOM* in the photochemical fate of contaminants and sunlight-driven biogeochemical processes.
Acknowledgements
We thank Caroline Davis, Paul Erickson, Elisabeth Janssen, Douglas Latch, Vivian Lin, Rachele Ossola, Kimberly Parker, Fernando Rosario-Ortiz, and Markus Schmitt for helpful feedback on the manuscript. We gratefully acknowledge funding from the Swiss National Science Foundation (Grant number 200021_156198).References
- O. C. Zafiriou, Marine organic photochemistry previewed, Mar. Chem., 1977, 5(4), 497–522 CrossRef CAS.
- O. C. Zafiriou, J. Joussot-Dubien, R. G. Zepp and R. G. Zika, Photochemistry of natural waters, Environ. Sci. Technol., 1984, 18(12), 358A–371A CrossRef CAS.
- N. V. Blough and R. G. Zepp, Reactive oxygen species in natural waters, in Active oxygen in chemistry, Springer, 1995, pp. 280–333 Search PubMed.
- D. Vione, M. Minella, V. Maurino and C. Minero, Indirect photochemistry in sunlit surface waters: photoinduced production of reactive transient species, Chem.–Eur. J., 2014, 20(34), 10590–10606 CrossRef CAS PubMed.
- C. K. Remucal, The role of indirect photochemical degradation in the environmental fate of pesticides: a review, Environ. Sci.: Processes Impacts, 2014, 16(4), 628–653 CAS.
- J. K. Challis, M. L. Hanson, K. J. Friesen and C. S. Wong, A critical assessment of the photodegradation of pharmaceuticals in aquatic environments: defining our current understanding and identifying knowledge gaps, Environ. Sci.: Processes Impacts, 2014, 16(4), 672–696 CAS.
- S. Yan and W. Song, Photo-transformation of pharmaceutically active compounds in the aqueous environment: a review, Environ. Sci.: Processes Impacts, 2014, 16(4), 697–720 CAS.
- R. G. Zepp, N. L. Wolfe, G. L. Baughman and R. C. Hollis, Singlet oxygen in natural waters, Nature, 1977, 267(5610), 421–423 CrossRef CAS.
- R. G. Zepp, P. F. Schlotzhauer and R. M. Sink, Photosensitized transformations involving electronic energy transfer in natural waters: role of humic substances, Environ. Sci. Technol., 1985, 19(1), 74–81 CrossRef.
- C. M. Sharpless, Lifetimes of triplet dissolved natural organic matter (DOM) and the effect of NaBH4 reduction on singlet oxygen quantum yields: implications for DOM photophysics, Environ. Sci. Technol., 2012, 46(8), 4466–4473 CrossRef CAS PubMed.
- F. Wilkinson, W. P. Helman and A. B. Ross, Quantum yields for the photosensitized formation of the lowest electronically excited singlet state of molecular oxygen in solution, J. Phys. Chem. Ref. Data, 1993, 22(1), 113–262 CrossRef CAS.
- R. Schmidt, C. Tanielian, R. Dunsbach and C. Wolff, Phenalenone, a universal reference compound for the determination of quantum yields of singlet oxygen O2 (1Δg) sensitization, J. Photochem. Photobiol., A, 1994, 79(1), 11–17 CrossRef CAS.
- M. Bodesheim, M. Schütz and R. Schmidt, Triplet state energy dependence of the competitive formation of O2 (1Σ+g), O2 (1Δg) and O2 (3Σ−g) in the sensitization of O2 by triplet states, Chem. Phys. Lett., 1994, 221(1), 7–14 CrossRef CAS.
- C. Schweitzer, Z. Mehrdad, A. Noll, E.-W. Grabner and R. Schmidt, Mechanism of photosensitized generation of singlet oxygen during oxygen quenching of triplet states and the general dependence of the rate constants and efficiencies of O2 (1Σg+), O2 (1Δg), and O2 (3Σg−) formation on sensitizer triplet state energy and oxidation potential, J. Phys. Chem. A, 2003, 107(13), 2192–2198 CrossRef CAS.
- F. Wilkinson, W. P. Helman and A. B. Ross, Rate constants for the decay and reactions of the lowest electronically excited singlet state of molecular oxygen in solution. An expanded and revised compilation, J. Phys. Chem. Ref. Data, 1995, 24(2), 663–677 CrossRef CAS.
- B. M. Peterson, A. M. McNally, R. M. Cory, J. D. Thoemke, J. B. Cotner and K. McNeill, Spatial and temporal distribution of singlet oxygen in Lake Superior, Environ. Sci. Technol., 2012, 46(13), 7222–7229 CrossRef CAS PubMed.
- J. E. Grebel, J. J. Pignatello and W. A. Mitch, Sorbic acid as a quantitative probe for the formation, scavenging and steady-state concentrations of the triplet-excited state of organic compounds, Water Res., 2011, 45(19), 6535–6544 CrossRef CAS PubMed.
- S. L. H. Sandvik, P. Bilski, J. D. Pakulski, C. F. Chignell and R. B. Coffin, Photogeneration of singlet oxygen and free radicals in dissolved organic matter isolated from the Mississippi and Atchafalaya River plumes, Mar. Chem., 2000, 69(1), 139–152 CrossRef CAS.
- E. S. Boyle, N. Guerriero, A. Thiallet, R. D. Vecchio and N. V. Blough, Optical properties of humic substances and CDOM: relation to structure, Environ. Sci. Technol., 2009, 43(7), 2262–2268 CrossRef CAS PubMed.
- S. E. Burns, J. P. Hassett and M. V. Rossi, Binding effects on humic-mediated photoreaction: intrahumic dechlorination of mirex in water, Environ. Sci. Technol., 1996, 30(10), 2934–2941 CrossRef CAS.
- S. E. Burns, J. P. Hassett and M. V. Rossi, Mechanistic implications of the intrahumic dechlorination of mirex, Environ. Sci. Technol., 1997, 31(5), 1365–1371 CrossRef CAS.
- D. E. Latch and K. McNeill, Microheterogeneity of singlet oxygen distributions in irradiated humic acid solutions, Science, 2006, 311(5768), 1743–1747 CrossRef CAS PubMed.
- M. Grandbois, D. E. Latch and K. McNeill, Microheterogeneous concentrations of singlet oxygen in natural organic matter isolate solutions, Environ. Sci. Technol., 2008, 42(24), 9184–9190 CrossRef CAS PubMed.
- H. Xu, W. J. Cooper, J. Jung and W. Song, Photosensitized degradation of amoxicillin in natural organic matter isolate solutions, Water Res., 2011, 45(2), 632–638 CrossRef CAS PubMed.
- R. E. Kellogg and W. T. Simpson, Perturbation of Singlet–Triplet Transition Energies, J. Am. Chem. Soc., 1965, 87(19), 4230–4234 CAS.
- R. G. Zepp, M. M. Gumz, W. L. Miller and H. Gao, Photoreaction of valerophenone in aqueous solution, J. Phys. Chem. A, 1998, 102(28), 5716–5723 CrossRef CAS.
- J. Morrison, H. Osthoff and P. Wan, Photoredox, photodecarboxylation, and photo-retro-aldol chemistry of p-nitrobiphenyls, Photochem. Photobiol. Sci., 2002, 1(6), 384–394 CAS.
- T. Zeng and W. A. Arnold, Pesticide photolysis in prairie potholes: probing photosensitized processes, Environ. Sci. Technol., 2013, 47(13), 6735–6745 CAS.
- L. Wang, H. Xu, W. J. Cooper and W. Song, Photochemical fate of beta-blockers in NOM enriched waters, Sci. Total Environ., 2012, 426, 289–295 CrossRef CAS PubMed.
- S. L. Rosado-Lausell, H. Wang, L. Gutiérrez, O. C. Romero-Maraccini, X.-Z. Niu, K. Y. Gin, J.-P. Croué and T. H. Nguyen, Roles of singlet oxygen and triplet excited state of dissolved organic matter formed by different organic matters in bacteriophage MS2 inactivation, Water Res., 2013, 47(14), 4869–4879 CrossRef CAS PubMed.
- J. E. Grebel, J. J. Pignatello and W. A. Mitch, Impact of halide ions on natural organic matter-sensitized photolysis of 17β-estradiol in saline waters, Environ. Sci. Technol., 2012, 46(13), 7128–7134 CrossRef CAS PubMed.
- J. R. Felcyn, J. C. Davis, L. H. Tran, J. C. Berude and D. E. Latch, Aquatic photochemistry of isoflavone phytoestrogens: degradation kinetics and pathways, Environ. Sci. Technol., 2012, 46(12), 6698–6704 CAS.
- B. A. Cottrell, S. A. Timko, L. Devera, A. K. Robinson, M. Gonsior, A. E. Vizenor, A. J. Simpson and W. J. Cooper, Photochemistry of excited-state species in natural waters: a role for particulate organic matter, Water Res., 2013, 47(14), 5189–5199 CAS.
- O. C. Romero-Maraccini, N. J. Sadik, S. L. Rosado-Lausell, C. R. Pugh, X.-Z. Niu, J.-P. Croué and T. H. Nguyen, Sunlight-induced inactivation of human Wa and porcine OSU rotaviruses in the presence of exogenous photosensitizers, Environ. Sci. Technol., 2013, 47(19), 11004–11012 CrossRef CAS PubMed.
- K. M. Parker, J. J. Pignatello and W. A. Mitch, Influence of ionic strength on triplet-state natural organic matter loss by energy transfer and electron transfer pathways, Environ. Sci. Technol., 2013, 47(19), 10987–10994 CAS.
- W. A. Arnold, One electron oxidation potential as a predictor of rate constants of N-containing compounds with carbonate radical and triplet excited state organic matter, Environ. Sci.: Processes Impacts, 2014, 16(4), 832–838 CAS.
- S. A. Timko, C. Romera-Castillo, R. Jaffé and W. J. Cooper, Photo-reactivity of natural dissolved organic matter from fresh to marine waters in the Florida Everglades, USA, Environ. Sci.: Processes Impacts, 2014, 16(4), 866–878 CAS.
- M. Antonopoulou, C. G. Skoutelis, C. Daikopoulos, Y. Deligiannakis and I. K. Konstantinou, Probing the photolytic–photocatalytic degradation mechanism of DEET in the presence of natural or synthetic humic macromolecules using molecular-scavenging techniques and EPR spectroscopy, J. Environ. Chem. Eng., 2015, 3(4), 3005–3014 CAS.
- A. P. S. Batista, A. C. S. Teixeira, W. J. Cooper and B. A. Cottrell, Correlating the chemical and spectroscopic characteristics of natural organic matter with the photodegradation of sulfamerazine, Water Res., 2016, 93, 20–29 CrossRef CAS PubMed.
- C. Prasse, J. Wenk, J. T. Jasper, T. A. Ternes and D. L. Sedlak, Co-occurrence of photochemical and microbiological transformation processes in open-water unit process wetlands, Environ. Sci. Technol., 2015, 49(24), 14136–14145 CAS.
- C.-Y. Chen and R. G. Zepp, Probing photosensitization by functionalized carbon nanotubes, Environ. Sci. Technol., 2015, 49(23), 13835–13843 CAS.
- D. Ren, B. Huang, T. Bi, D. Xiong and X. Pan, Effects of pH and dissolved oxygen on the photodegradation of 17α-ethynylestradiol in dissolved humic acid solution, Environ. Sci.: Processes Impacts, 2016, 18(1), 78–86 CAS.
- R. S. H. Liu, N. J. Turro and G. S. Hammond, Mechanisms of Photochemical Reactions in Solution. XXXI. Activation and Deactivation of Conjugated Dienes by Energy Transfer, J. Am. Chem. Soc., 1965, 87(15), 3406–3412 CAS.
- J. J. Werner, K. McNeill and W. A. Arnold, Environmental photodegradation of mefenamic acid, Chemosphere, 2005, 58(10), 1339–1346 CAS.
- C. C. Ryan, D. T. Tan and W. A. Arnold, Direct and indirect photolysis of sulfamethoxazole and trimethoprim in wastewater treatment plant effluent, Water Res., 2011, 45(3), 1280–1286 CrossRef CAS PubMed.
- A. L. Boreen, W. A. Arnold and K. McNeill, Triplet-Sensitized Photodegradation of Sulfa Drugs Containing Six-Membered Heterocyclic Groups: Identification of an SO2 Extrusion Photoproduct, Environ. Sci. Technol., 2005, 39(10), 3630–3638 CAS.
- A. L. Boreen, B. L. Edhlund, J. B. Cotner and K. McNeill, Indirect photodegradation of dissolved free amino acids: the contribution of singlet oxygen and the differential reactivity of DOM from various sources, Environ. Sci. Technol., 2008, 42(15), 5492–5498 CAS.
- K. M. Parker and W. A. Mitch, Halogen radicals contribute to photooxidation in coastal and estuarine waters, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(21), 5868–5873 CAS.
- J. Porras, J. J. Fernández, R. A. Torres-Palma and C. Richard, Humic Substances Enhance Chlorothalonil Phototransformation via Photoreduction and Energy Transfer, Environ. Sci. Technol., 2014, 48(4), 2218–2225 CrossRef CAS PubMed.
- S. Bouchama, P. de Sainte-Claire, E. Arzoumanian, E. Oliveros, A. Boulkamh and C. Richard, Photoreactivity of the fungicide chlorothalonil in aqueous medium, Environ. Sci.: Processes Impacts, 2014, 16(4), 839–847 CAS.
- A. A. Lamola and G. S. Hammond, Mechanisms of photochemical reactions in solution. XXXIII. Intersystem crossing efficiencies, J. Chem. Phys., 1965, 43(6), 2129–2135 CrossRef CAS.
- P. J. Wagner and G. S. Hammond, Mechanisms of Photochemical Reactions in Solution. XXXVIII. 1 Quenching of the Type II Photoelimination Reaction, J. Am. Chem. Soc., 1966, 88(6), 1245–1251 CAS.
- N. A. Kuznetsova and O. L. Kaliya, The photochemistry of coumarins, Russ. Chem. Rev., 1992, 61(7), 683–696 Search PubMed.
- P. Z. Ray and M. A. Tarr, Formation of organic triplets from solar irradiation of petroleum, Mar. Chem., 2015, 168, 135–139 CAS.
- D. E. Nicodem, C. L. Guedes, M. C. Z. Fernandes, D. Severino, R. J. Correa, M. C. Coutinho and J. Silva, Photochemistry of petroleum, Prog. React. Kinet. Mech., 2001, 26(2–3), 219–238 CrossRef CAS.
- J. R. Payne and C. R. Phillips, Photochemistry of petroleum in water, Environ. Sci. Technol., 1985, 19(7), 569–579 CrossRef CAS PubMed.
- A. Bruccoleri, C. H. Langford and C. Arbour, Pulsed photo acoustic evaluation of intersystem crossing quantum yields in fulvic acid, Environ. Technol., 1990, 11(2), 169–172 CAS.
- A. Bruccoleri, B. C. Pant, D. K. Sharma and C. H. Langford, Evaluation of primary photoproduct quantum yields in fulvic acid, Environ. Sci. Technol., 1993, 27(5), 889–894 CAS.
- V. M. Mazhul, L. S. Ivashkevich, D. G. Shcherbin, N. A. Pavlovskaya, G. V. Naumova and T. F. Ovchinnikova, Luminescence properties of humic substances, J. Appl. Spectrosc., 1997, 64(4), 503–508 CAS.
- S. Canonica, Oxidation of aquatic organic contaminants induced by excited triplet states, Chim. Int. J. Chem., 2007, 61(10), 641–644 CAS.
- D. Vione, P. R. Maddigapu, E. De Laurentiis, M. Minella, M. Pazzi, V. Maurino, C. Minero, S. Kouras and C. Richard, Modelling the photochemical fate of ibuprofen in surface waters, Water Res., 2011, 45(20), 6725–6736 CrossRef CAS PubMed.
- E. De Laurentiis, S. Chiron, S. Kouras-Hadef, C. Richard, M. Minella, V. Maurino, C. Minero and D. Vione, Photochemical fate of carbamazepine in surface freshwaters: laboratory measures and modeling, Environ. Sci. Technol., 2012, 46(15), 8164–8173 CAS.
- B. Sur, E. De Laurentiis, M. Minella, V. Maurino, C. Minero and D. Vione, Photochemical transformation of anionic 2-nitro-4-chlorophenol in surface waters: laboratory and model assessment of the degradation kinetics, and comparison with field data, Sci. Total Environ., 2012, 426, 296–303 CAS.
- G. Marchetti, M. Minella, V. Maurino, C. Minero and D. Vione, Photochemical transformation of atrazine and formation of photointermediates under conditions relevant to sunlit surface waters: laboratory measures and modelling, Water Res., 2013, 47(16), 6211–6222 CAS.
- E. De Laurentiis, C. Prasse, T. A. Ternes, M. Minella, V. Maurino, C. Minero, M. Sarakha, M. Brigante and D. Vione, Assessing the photochemical transformation pathways of acetaminophen relevant to surface waters: transformation kinetics, intermediates, and modelling, Water Res., 2014, 53, 235–248 CrossRef CAS PubMed.
- S. Canonica and H.-U. Laubscher, Inhibitory effect of dissolved organic matter on triplet-induced oxidation of aquatic contaminants, Photochem. Photobiol. Sci., 2008, 7(5), 547–551 CAS.
- L. Zhou, Y. Ji, C. Zeng, Y. Zhang, Z. Wang and X. Yang, Aquatic photodegradation of sunscreen agent p-aminobenzoic acid in the presence of dissolved organic matter, Water Res., 2013, 47(1), 153–162 CAS.
- F. Leresche, U. von Gunten and S. Canonica, Probing the photosensitizing and inhibitory effects of dissolved organic matter by using N,N-dimethyl-4-cyanoaniline (DMABN), Environ. Sci. Technol. DOI:10.1021/acs.est.6b02868.
- A. C. Gerecke, S. Canonica, S. R. Müller, M. Schärer and R. P. Schwarzenbach, Quantification of dissolved natural organic matter (DOM) mediated phototransformation of phenylurea herbicides in lakes, Environ. Sci. Technol., 2001, 35(19), 3915–3923 CAS.
- S. Canonica, B. Hellrung, P. Müller and J. Wirz, Aqueous oxidation of phenylurea herbicides by triplet aromatic ketones, Environ. Sci. Technol., 2006, 40(21), 6636–6641 CAS.
- M. C. Langlois, L. K. Weavers and Y.-P. Chin, Contaminant-mediated photobleaching of wetland chromophoric dissolved organic matter, Environ. Sci.: Processes Impacts, 2014, 16(9), 2098–2107 Search PubMed.
- M. E. Karpuzcu, A. J. McCabe and W. A. Arnold, Phototransformation of pesticides in prairie potholes: effect of dissolved organic matter in triplet-induced oxidation, Environ. Sci.: Processes Impacts, 2016, 18(2), 237–245 CAS.
- J. J. Guerard, Y.-P. Chin, H. Mash and C. M. Hadad, Photochemical fate of sulfadimethoxine in aquaculture waters, Environ. Sci. Technol., 2009, 43(22), 8587–8592 CAS.
- S. Bahnmüller, U. von Gunten and S. Canonica, Sunlight-induced transformation of sulfadiazine and sulfamethoxazole in surface waters and wastewater effluents, Water Res., 2014, 57, 183–192 Search PubMed.
- Y. Li, J. Chen, X. Qiao, H. Zhang, Y. Zhang and C. Zhou, Insights into photolytic mechanism of sulfapyridine induced by triplet-excited dissolved organic matter, Chemosphere, 2016, 147, 305–310 CAS.
- E. M.-L. Janssen, P. R. Erickson and K. McNeill, Dual roles of dissolved organic matter as sensitizer and quencher in the photooxidation of tryptophan, Environ. Sci. Technol., 2014, 48(9), 4916–4924 CrossRef CAS PubMed.
- E. M. Janssen, E. Marron and K. McNeill, Aquatic photochemical kinetics of benzotriazole and structurally related compounds, Environ. Sci.: Processes Impacts, 2015, 17(5), 939–946 CAS.
- J. J. Guerard and Y.-P. Chin, Photodegradation of ormetoprim in aquaculture and stream-derived dissolved organic matter, J. Agric. Food Chem., 2012, 60(39), 9801–9806 CrossRef CAS PubMed.
- S. Canonica, U. Jans, K. Stemmler and J. Hoigné, Transformation kinetics of phenols in water: photosensitization by dissolved natural organic material and aromatic ketones, Environ. Sci. Technol., 1995, 29(7), 1822–1831 CAS.
- J.-P. Aguer and C. Richard, Humic substances mediated phototransformation of 2,4,6-trimethylphenol: a catalytic reaction, Photochem. Photobiol. Sci., 2005, 4(6), 451–453 CAS.
- S. Halladja, A. Ter Halle, J.-P. Aguer, A. Boulkamh and C. Richard, Inhibition of humic substances mediated photooxygenation of furfuryl alcohol by 2,4,6-trimethylphenol. Evidence for reactivity of the phenol with humic triplet excited states, Environ. Sci. Technol., 2007, 41(17), 6066–6073 CAS.
- Y.-P. Chin, P. L. Miller, L. Zeng, K. Cawley and L. K. Weavers, Photosensitized degradation of bisphenol A by dissolved organic matter, Environ. Sci. Technol., 2004, 38(22), 5888–5894 CrossRef CAS PubMed.
- M. Zhan, X. Yang, Q. Xian and L. Kong, Photosensitized degradation of bisphenol A involving reactive oxygen species in the presence of humic substances, Chemosphere, 2006, 63(3), 378–386 CrossRef CAS PubMed.
- S. Qu, E. P. Kolodziej and D. M. Cwiertny, Phototransformation rates and mechanisms for synthetic hormone growth promoters used in animal agriculture, Environ. Sci. Technol., 2012, 46(24), 13202–13211 CAS.
- M. M. Kelly and W. A. Arnold, Direct and indirect photolysis of the phytoestrogens genistein and daidzein, Environ. Sci. Technol., 2012, 46(10), 5396–5403 CAS.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Proton-coupled electron transfer, Chem. Rev., 2012, 112(7), 4016–4093 CrossRef CAS PubMed.
- D. Eskiköy, Z. Durmuş and E. Kiliç, Electrochemical oxidation of atorvastatin and its adsorptive stripping determination in pharmaceutical dosage forms and biological fluids, Collect. Czech. Chem. Commun., 2012, 76(12), 1633–1649 Search PubMed.
- Y. Chen, C. Hu, X. Hu and J. Qu, Indirect photodegradation of amine drugs in aqueous solution under simulated sunlight, Environ. Sci. Technol., 2009, 43(8), 2760–2765 CrossRef CAS PubMed.
- Y. Chen, H. Li, Z. Wang, H. Li, T. Tao and Y. Zuo, Photodegradation of selected β-blockers in aqueous fulvic acid solutions: kinetics, mechanism, and product analysis, Water Res., 2012, 46(9), 2965–2972 CrossRef CAS PubMed.
- S. Canonica, T. Kohn, M. Mac, F. J. Real, J. Wirz and U. von Gunten, Photosensitizer method to determine rate constants for the reaction of carbonate radical with organic compounds, Environ. Sci. Technol., 2005, 39(23), 9182–9188 CAS.
- E. De Laurentiis, M. Minella, V. Maurino, C. Minero, G. Mailhot, M. Sarakha, M. Brigante and D. Vione, Assessing the occurrence of the dibromide radical (Br2−) in natural waters: measures of triplet-sensitised formation, reactivity, and modelling, Sci. Total Environ., 2012, 439, 299–306 CrossRef CAS PubMed.
- M. Brigante, M. Minella, G. Mailhot, V. Maurino, C. Minero and D. Vione, Formation and reactivity of the dichloride radical (Cl2−˙) in surface waters: a modelling approach, Chemosphere, 2014, 95, 464–469 CrossRef CAS PubMed.
- C. R. Lambert and I. E. Kochevar, Electron transfer quenching of the rose bengal triplet state, Photochem. Photobiol., 1997, 66(1), 15–25 CrossRef CAS PubMed.
- W. H. Koppenol, D. M. Stanbury and P. L. Bounds, Electrode potentials of partially reduced oxygen species, from dioxygen to water, Free Radical Biol. Med., 2010, 49(3), 317–322 CrossRef CAS PubMed.
- W. J. Cooper, R. G. Zika, R. G. Petasne and J. M. Plane, Photochemical formation of hydrogen peroxide in natural waters exposed to sunlight, Environ. Sci. Technol., 1988, 22(10), 1156–1160 CrossRef CAS PubMed.
- L. C. Powers and W. L. Miller, Blending remote sensing data products to estimate photochemical production of hydrogen peroxide and superoxide in the surface ocean, Environ. Sci.: Processes Impacts, 2014, 16(4), 792–806 CAS.
- D. J. Kieber, G. W. Miller, P. J. Neale and K. Mopper, Wavelength and temperature-dependent apparent quantum yields for photochemical formation of hydrogen peroxide in seawater, Environ. Sci.: Processes Impacts, 2014, 16(4), 777–791 CAS.
- C. M. Sharpless and N. V. Blough, The importance of charge-transfer interactions in determining chromophoric dissolved organic matter (CDOM) optical and photochemical properties, Environ. Sci.: Processes Impacts, 2014, 16(4), 654–671 CAS.
- N. M. Scully, D. J. McQueen, D. R. S. Lean and W. J. Cooper, Photochemical formation of hydrogen peroxide in lakes: effects of dissolved organic carbon and ultraviolet radiation, Can. J. Fish. Aquat. Sci., 1995, 52(12), 2675–2681 CAS.
- Y. Zhang and N. V. Blough, Photoproduction of one-electron reducing intermediates by chromophoric dissolved organic matter (CDOM): relation to O2− and H2O2 photoproduction and CDOM photooxidation, Environ. Sci. Technol. DOI:10.1021/acs.est.6b02919.
- R. G. Petasne and R. G. Zika, Fate of superoxide in coastal sea water, Nature, 1987, 325, 516–518 CAS.
- S. Garg, A. L. Rose and T. D. Waite, Photochemical production of superoxide and hydrogen peroxide from natural organic matter, Geochim. Cosmochim. Acta, 2011, 75(15), 4310–4320 CAS.
- Y. Zhang, K. A. Simon, A. A. Andrew, R. Del Vecchio and N. V. Blough, Enhanced photoproduction of hydrogen peroxide by humic substances in the presence of phenol electron donors, Environ. Sci. Technol., 2014, 48(21), 12679–12688 CAS.
- D. R. Letourneau, C. G. Gill and E. T. Krogh, Photosensitized degradation kinetics of trace halogenated contaminants in natural waters using membrane introduction mass spectrometry as an in situ reaction monitor, Photochem. Photobiol. Sci., 2015, 14(11), 2108–2118 CAS.
- L. Eberson, Electron transfer reactions in organic chemistry, Springer-Verlag, 1987 Search PubMed.
- S. Canonica, B. Hellrung and J. Wirz, Oxidation of phenols by triplet aromatic ketones in aqueous solution, J. Phys. Chem. A, 2000, 104(6), 1226–1232 CAS.
- D. Rehm and A. Weller, Kinetics of fluorescence quenching by electron and H-atom transfer, Isr. J. Chem., 1970, 8(2), 259–271 CAS.
- S. Farid, J. P. Dinnocenzo, P. B. Merkel, R. H. Young and D. Shukla, Bimolecular Electron Transfers That Follow a Sandros–Boltzmann Dependence on Free Energy, J. Am. Chem. Soc., 2011, 133(13), 4791–4801 CrossRef CAS PubMed.
- S. Farid, J. P. Dinnocenzo, P. B. Merkel, R. H. Young, D. Shukla and G. Guirado, Reexamination of the Rehm–Weller data set reveals electron transfer quenching that follows a Sandros–Boltzmann dependence on free energy, J. Am. Chem. Soc., 2011, 133(30), 11580–11587 CAS.
- P. R. Erickson, N. Walpen, J. J. Guerard, S. N. Eustis, J. S. Arey and K. McNeill, Controlling factors in the rates of oxidation of anilines and phenols by triplet methylene blue in aqueous solution, J. Phys. Chem. A, 2015, 119(13), 3233–3243 CrossRef CAS PubMed.
- F. Rosario-Ortiz and S. Canonica, Probe molecules to assess the photochemical activity of natural organic matter, Environ. Sci. Technol. Search PubMed , in revision.
- K. Sandros, Transfer of triplet state energy in fluid solutions III. Reversible energy transfer, Acta Chem. Scand., 1964, 18(10), 2355–2374 Search PubMed.
- V. Balzani, F. Bolletta and F. Scandola, Vertical and “nonvertical” energy transfer processes. A general classical treatment, J. Am. Chem. Soc., 1980, 102(7), 2152–2163 CrossRef CAS.
- I. Loeff, J. Rabani, A. Treinin and H. Linschitz, Charge transfer and reactivity of nπ* and ππ* organic triplets, including anthraquinonesulfonates, in interactions with inorganic anions: a comparative study based on classical Marcus theory, J. Am. Chem. Soc., 1993, 115(20), 8933–8942 CrossRef CAS.
- W. H. Koppenol and J. F. Liebman, The oxidizing nature of the hydroxyl radical. A comparison with the ferryl ion (FeO2+), J. Phys. Chem., 1984, 88(1), 99–101 CrossRef CAS.
- G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, Critical review of rate constants for reactions of hydrated electrons, hydrogen atoms and hydroxyl radicals (˙OH/˙O−) in aqueous solution, J. Phys. Chem. Ref. Data, 1988, 17(2), 513–886 CrossRef CAS.
- H. A. Schwarz, Free radicals generated by radiolysis of aqueous solutions, J. Chem. Educ., 1981, 58(2), 101 CrossRef CAS.
- A. Pochon, P. P. Vaughan, D. Gan, P. Vath, N. V. Blough and D. E. Falvey, Photochemical oxidation of water by 2-methyl-1,4-benzoquinone: evidence against the formation of free hydroxyl radical, J. Phys. Chem. A, 2002, 106(12), 2889–2894 CrossRef CAS.
- D. Gan, M. Jia, P. P. Vaughan, D. E. Falvey and N. V. Blough, Aqueous photochemistry of methyl-benzoquinone, J. Phys. Chem. A, 2008, 112(13), 2803–2812 CrossRef CAS PubMed.
- S. E. Page, W. A. Arnold and K. McNeill, Assessing the contribution of free hydroxyl radical in organic matter-sensitized photohydroxylation reactions, Environ. Sci. Technol., 2011, 45(7), 2818–2825 CrossRef CAS PubMed.
- O. Brahmia and C. Richard, Phototransformation of 1,4-naphthoquinone in aqueous solution, Photochem. Photobiol. Sci., 2003, 2(10), 1038–1043 CAS.
- H. Görner, Photoprocesses of p-benzoquinones in aqueous solution, J. Phys. Chem. A, 2003, 107(51), 11587–11595 CrossRef.
- J. von Sonntag, E. Mvula, K. Hildenbrand and C. von Sonntag, Photohydroxylation of 1,4-Benzoquinone in Aqueous Solution Revisited, Chem.–Eur. J., 2004, 10(2), 440–451 CrossRef CAS PubMed.
- D. Vione, M. Ponzo, D. Bagnus, V. Maurino, C. Minero and M. E. Carlotti, Comparison of different probe molecules for the quantification of hydroxyl radicals in aqueous solution, Environ. Chem. Lett., 2010, 8(1), 95–100 CrossRef CAS.
- P. R. Maddigapu, A. Bedini, C. Minero, V. Maurino, D. Vione, M. Brigante, G. Mailhot and M. Sarakha, The pH-dependent photochemistry of anthraquinone-2-sulfonate, Photochem. Photobiol. Sci., 2010, 9(3), 323–330 CAS.
- J. Wenk, S. N. Eustis, K. McNeill and S. Canonica, Quenching of excited triplet states by dissolved natural organic matter, Environ. Sci. Technol., 2013, 47(22), 12802–12810 CrossRef CAS PubMed.
- J. Ma, R. Del Vecchio, K. S. Golanoski, E. S. Boyle and N. V. Blough, Optical properties of humic substances and CDOM: effects of borohydride reduction, Environ. Sci. Technol., 2010, 44(14), 5395–5402 CrossRef CAS PubMed.
- K. S. Golanoski, S. Fang, R. Del Vecchio and N. V. Blough, Investigating the mechanism of phenol photooxidation by humic substances, Environ. Sci. Technol., 2012, 46(7), 3912–3920 CrossRef CAS PubMed.
- K. Pratibha, Poonam and S. M. S. Chauhan, Efficient cobalt(II) phthalocyanine-catalyzed reduction of flavones with sodium borohydride, Chem. Commun., 2009, 42, 6397–6399 Search PubMed.
- S. Canonica and M. Freiburghaus, Electron-rich phenols for probing the photochemical reactivity of freshwaters, Environ. Sci. Technol., 2001, 35(4), 690–695 CrossRef CAS PubMed.
- J. N. Moore, D. Phillips, N. Nakashima and K. Yoshihara, Photophysics and photochemistry of sulphonated derivatives of 9,10-anthraquinone. “Strong” versus “weak” sensitisers, J. Chem. Soc., Faraday Trans. 2, 1987, 83(8), 1487–1508 RSC.
- A. P. Darmanyan and C. S. Foote, Solvent effects on singlet oxygen yield from nπ* and ππ* triplet carbonyl compounds, J. Phys. Chem., 1993, 97(19), 5032–5035 CrossRef CAS.
- K. Gollnick, T. Franken, G. Schade and G. Dörhöfer, Photosensitized oxygenation as a function of the triplet energy of sensitizers, Ann. N. Y. Acad. Sci., 1970, 171(1), 89–107 CrossRef CAS.
- L. C. Bodhipaksha, C. M. Sharpless, Y.-P. Chin, M. Sander, W. K. Langston and A. A. MacKay, Triplet Photochemistry of Effluent and Natural Organic Matter in Whole Water and Isolates from Effluent-Receiving Rivers, Environ. Sci. Technol., 2015, 49(6), 3453–3463 CrossRef CAS PubMed.
- J. J. Guerard, P. L. Miller, T. D. Trouts and Y.-P. Chin, The role of fulvic acid composition in the photosensitized degradation of aquatic contaminants, Aquat. Sci., 2009, 71(2), 160–169 CrossRef CAS.
- P. R. Tentscher, S. N. Eustis, K. McNeill and J. S. Arey, Aqueous oxidation of sulfonamide antibiotics: aromatic nucleophilic substitution of an aniline radical cation, Chem.–Eur. J., 2013, 19(34), 11216–11223 CrossRef CAS PubMed.
- J. Wenk, U. Von Gunten and S. Canonica, Effect of dissolved organic matter on the transformation of contaminants induced by excited triplet states and the hydroxyl radical, Environ. Sci. Technol., 2011, 45(4), 1334–1340 CrossRef CAS PubMed.
- J. Wenk and S. Canonica, Phenolic antioxidants inhibit the triplet-induced transformation of anilines and sulfonamide antibiotics in aqueous solution, Environ. Sci. Technol., 2012, 46(10), 5455–5462 CrossRef CAS PubMed.
- Y. A. Ilan, G. Czapski and D. Meisel, The one-electron transfer redox potentials of free radicals. I. The oxygen/superoxide system, Biochim. Biophys. Acta, Bioenerg., 1976, 430(2), 209–224 CrossRef CAS.
- J. Goodman and L. E. Brus, Distant intramolecular interaction between identical chromophores: the n–π* excited states of p-benzoquinone, J. Chem. Phys., 1978, 69(4), 1604–1612 CrossRef CAS.
- A. E. Alegrıa, A. Ferrer, G. Santiago, E. Sepúlveda and W. Flores, Photochemistry of water-soluble quinones. Production of the hydroxyl radical, singlet oxygen and the superoxide ion, J. Photochem. Photobiol., A, 1999, 127(1), 57–65 CrossRef.
- I. Loeff, S. Goldstein, A. Treinin and H. Linschitz, Interactions of formate ion with triplets of anthraquinone-2-sulfonate, 1,4-naphthoquinone, benzophenone-4-carboxylate and benzophenone-4-sulfonate, J. Phys. Chem., 1991, 95(11), 4423–4430 CrossRef CAS.
- T. Vo-Dinh and U. P. Wild, Luminescence of 1,4-naphthoquinone and the vitamin K system in Shpolskii matrices at 4 K, Spectrochim. Acta, Part A, 1984, 40(5), 411–418 CrossRef.
- S. Hayano and M. Fujihira, The effect of water on the reduction potentials of some aromatic compounds in the DMF–water system, Bull. Chem. Soc. Jpn., 1971, 44(8), 2051–2055 CrossRef CAS.
- C. A. Parker and C. G. Hatchard, The possibilities of phosphorescence measurement in chemical analysis: tests with a new instrument, Analyst, 1962, 87(1037), 664–676 RSC.
- W. G. Herkstroeter, A. A. Lamola and G. S. Hammond, Mechanisms of Photochemical Reactions in Solution. XXVIII. 1 Values of Triplet Excitation Energies of Selected Sensitizers, J. Am. Chem. Soc., 1964, 86(21), 4537–4540 CrossRef CAS.
- I. Gutiérrez, S. G. Bertolotti, M. A. Biasutti, A. T. Soltermann and N. A. García, Quinones and hydroxyquinones as generators and quenchers of singlet molecular oxygen, Can. J. Chem., 1997, 75(4), 423–428 CrossRef.
- J. Nafisi-Movaghar and F. Wilkinson, Photochemical reactions of duroquinone. Part 2—Flash photolytic investigations, Trans. Faraday Soc., 1970, 66, 2268–2278 RSC.
- A. J. G. Barwise, A. A. Gorman, R. L. Leyland, P. G. Smith and M. A. J. Rodgers, A pulse radiolysis study of the quenching of aromatic carbonyl triplets by norbornadienes and quadricyclenes. The mechanism of interconversion, J. Am. Chem. Soc., 1978, 100(6), 1814–1820 CrossRef CAS.
- P. B. Merkel and J. P. Dinnocenzo, Thermodynamic energies of donor and acceptor triplet states, J. Photochem. Photobiol., A, 2008, 193(2), 110–121 CrossRef CAS.
- W. M. Nau and J. C. Scaiano, Oxygen quenching of excited aliphatic ketones and diketones, J. Phys. Chem., 1996, 100(27), 11360–11367 CrossRef CAS.
- J. K. Hurley, H. Linschitz and A. Treinin, Interaction of halide and pseudohalide ions with triplet benzophenone-4-carboxylate: kinetics and radical yields, J. Phys. Chem., 1988, 92(18), 5151–5159 CrossRef CAS.
- P. J. Wagner, R. J. Truman, A. E. Puchalski and R. Wake, Extent of charge transfer in the photoreduction of phenyl ketones by alkylbenzenes, J. Am. Chem. Soc., 1986, 108(24), 7727–7738 CrossRef CAS PubMed.
- A. A. Gorman and M. A. J. Rodgers, The quenching of aromatic ketone triplets by oxygen: competing singlet oxygen and biradical formation?, J. Am. Chem. Soc., 1986, 108(17), 5074–5078 CrossRef CAS.
- R. A. Day Jr and R. E. Biggers, Polarography of p-Chlorobenzophenone and Xanthone, J. Am. Chem. Soc., 1953, 75(3), 738–739 CrossRef.
- Y. E. Orlov, Polarography of Coumarins (Chromen-2-ones), Russ. Chem. Rev., 1977, 46(7), 671 CrossRef.
- W. W. Mantulin and P.-S. Song, Excited states of skin-sensitizing coumarins and psoralens. Spectroscopic studies, J. Am. Chem. Soc., 1973, 95(16), 5122–5129 CrossRef CAS PubMed.
- T. A. Geissman and S. L. Friess, Flavanones and related compounds. VI. The polarographic reduction of some substituted chalcones, flavones and flavanones, J. Am. Chem. Soc., 1949, 71(12), 3893–3902 CrossRef CAS.
- S. Criado, S. G. Bertolotti, A. T. Soltermann, V. Avila and N. A. Garcia, Effect of flavonoids on the photooxidation of fats. A study on their activity as singlet molecular oxygen [O2 (1Δ)] generators and quenchers, Fat Sci. Technol., 1995, 97(7–8), 265–269 CAS.
- M. Tsuda, S. Oikawa and R. Miyake, Phosphorescence and Excitation Spectra of Cinnamic Acid, Bull. Soc. Sci. Photogr. Jpn., 1972, 35(2), 90–93 CAS.
- R. S. Ruoff, K. M. Kadish, P. Boulas and E. C. M. Chen, Relationship between the electron affinities and half-wave reduction potentials of fullerenes, aromatic hydrocarbons, and metal complexes, J. Phys. Chem., 1995, 99(21), 8843–8850 CrossRef CAS.
- D. S. McClure, Triplet–Singlet Transitions in Organic Molecules. Lifetime Measurements of the Triplet State, J. Chem. Phys., 1949, 17(10), 905–913 CrossRef CAS.
- A. A. Abdel-Shafi and F. Wilkinson, Charge transfer effects on the efficiency of singlet oxygen production following oxygen quenching of excited singlet and triplet states of aromatic hydrocarbons in acetonitrile, J. Phys. Chem. A, 2000, 104(24), 5747–5757 CrossRef CAS.
- S. Wawzonek and H. A. Laitinen, The Reduction of Unsaturated Hydrocarbons at the Dropping Mercury Electrode. II. Aromatic Polynuclear Hydrocarbons, J. Am. Chem. Soc., 1942, 64(10), 2365–2368 CrossRef CAS.
- W. G. Herkstroeter and G. S. Hammond, Mechanisms of Photochemical Reactions in Solution. XXXIX. 1 Study of Energy Transfer by Kinetic Spectrophotometry, J. Am. Chem. Soc., 1966, 88(21), 4769–4777 CrossRef CAS.
- P. Wardman, Reduction potentials of one-electron couples involving free radicals in aqueous solution, J. Phys. Chem. Ref. Data, 1989, 18(4), 1637–1755 CrossRef CAS.
- I. Loeff, A. Treinin and H. Linschitz, Photochemistry of 9,10-anthraquinone-2-sulfonate in solution. 1. Intermediates and mechanism, J. Phys. Chem., 1983, 87(14), 2536–2544 CrossRef CAS.
- P. F. Heelis, B. J. Parsons, G. O. Phillips, E. J. Land and A. J. Swallow, Pulse-radiolysis study of the effect of pH on the one-electron reduction potentials of lumichrome derivatives, J. Chem. Soc., Faraday Trans. 1, 1985, 81(5), 1225–1235 RSC.
- R. W. Chambers and D. R. Kearns, Triplet states of some common photosensitizing dyes, Photochem. Photobiol., 1969, 10(3), 215–219 CrossRef CAS PubMed.
- C. K. Remucal and K. McNeill, Photosensitized amino acid degradation in the presence of riboflavin and its derivatives, Environ. Sci. Technol., 2011, 45(12), 5230–5237 CrossRef CAS PubMed.
- D. Meisel and P. Neta, One-electron reduction potential of riboflavine studied by pulse radiolysis, J. Phys. Chem., 1975, 79(23), 2459–2461 CrossRef CAS.
- S. O. Kelley, J. K. Barton, N. M. Jackson and M. G. Hill, Electrochemistry of methylene blue bound to a DNA-modified electrode, Bioconjugate Chem., 1997, 8(1), 31–37 CrossRef CAS PubMed.
- R. W. Redmond and J. N. Gamlin, A compilation of singlet oxygen yields from biologically relevant molecules, Photochem. Photobiol., 1999, 70(4), 391–475 CrossRef CAS PubMed.
- P. Beckmann, A Polarographic Investigation of Perinaphthenone, Aust. J. Chem., 1961, 14(2), 229–236 CrossRef CAS.
- A. J. Wain, L. Drouin and R. G. Compton, Voltammetric reduction of perinaphthenone in aqueous and non-aqueous media: an electrochemical ESR investigation, J. Electroanal. Chem., 2006, 589(1), 128–138 CrossRef CAS.
- T. Okutsu, S. Noda, S. Tanaka, A. Kawai, K. Obi and H. Hiratsuka, Nature of excited singlet and non-phosphorescent triplet states of perinaphthenone, J. Photochem. Photobiol., A, 2000, 132(1), 37–41 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |