Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microjets and coated wheels: versatile tools for exploring collisions and reactions at gas–liquid interfaces
Jennifer A.
Faust
and
Gilbert M.
Nathanson
*
Department of Chemistry, University of Wisconsin-Madison, 1101 University Avenue, Madison, Wisconsin 53706-1322, USA. E-mail: gmnathan@wisc.edu
First published on 29th April 2016
Abstract
This tutorial review describes experimental aspects of two techniques for investigating collisions and reactions at the surfaces of liquids in vacuum. These gas–liquid scattering experiments provide insights into the dynamics of interfacial processes while minimizing interference from vapor-phase collisions. We begin with a historical survey and then compare attributes of the microjet and coated-wheel techniques, developed by Manfred Faubel and John Fenn, respectively, for studies of high- and low-vapor pressure liquids in vacuum. Our objective is to highlight the strengths and shortcomings of each technique and summarize lessons we have learned in using them for scattering and evaporation experiments. We conclude by describing recent microjet studies of energy transfer between O2 and liquid hydrocarbons, HCl dissociation in salty water, and super-Maxwellian helium evaporation.
Key learning points(1) A backward glance: the history of jets, coated wheels, and the scientists behind them(2) Breakup, cooling, and vapor clouds: working with liquids in vacuum (3) Tradeoffs and lessons learned using coated wheels and microjets (4) Examples of scattering and evaporation experiments and what we learn from them (5) The Tortoise and the Hare: utilizing low and high-vapor pressure techniques together |
Introduction – Hickman, Fenn, and Faubel
Gas–liquid interfaces abound within us and around us. They occur in natural settings, from the alveoli coatings inside our lungs to the sea surface microlayer, and they are harnessed in settings we create, from the industrial production of sulfuric acid and surfactants to the evaporation of fuel droplets in combustion engines. Perhaps the earliest recorded queries about gas–liquid interfaces date to Greek philosophers in the sixth century B.C., who described how seawater distilled by the sun fell back as rain.1 Even earlier, sailors poured oil onto the sea and smeared it around their eyes to “calm troubled waters”, a wave-stilling phenomenon later investigated by Benjamin Franklin.2 These oil and surfactant-coated surfaces have more recently generated intense interest for their ability to limit water evaporation from reservoirs3 and to alter gas–liquid reactions in sea-spray aerosols and at the surface of the ocean.4The first systematic study of gas–liquid interfaces in vacuum, however, might be credited to Kenneth Hickman of the Kodak Research Labs, who in 1952 invented the “Falling Stream Tensimeter” to measure the evaporation coefficient of pure liquids and mixtures.5 Hickman was fascinated with distillation and wondered if liquids evaporated at the maximum rate allowed by their finite speeds, equal to Jevap = α〈v〉nvap/4, where Jevap is the evaporation flux, 〈v〉 is the average speed, and nvap = Pvap/RT is the vapor density. In this expression, α is the evaporation coefficient, ranging from 0 to 1. Hickman's research was not driven purely by curiosity; he was measuring α in the hope of perfecting his large-scale distillation of vitamins A and D from fish oil, first publicized by Time magazine in 1937 as the “vitamin still”.
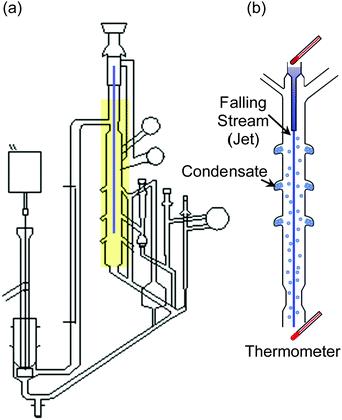
Hickman, as had Irving Langmuir before him, recognized that the surface of the liquid must be clean and continuously renewed, “free of dross”, to evaporate at its maximum rate. Hickman's tensimeter, shown in Fig. 1a, is made entirely of glass and is evacuated to ∼10−3 Torr by a mechanical pump and a liquid CO2 condensation trap. It is a marvel of ingenuity. A liquid jet, or falling stream, is formed by gravity through a 1–10 mm diameter opening and internally recirculated. As the stream of liquid falls through the open space under vacuum (Fig. 1b), some of it evaporates and collects in air-cooled traps surrounding the jet. The collected liquid is then weighed in order to calculate α. Hickman and his coworkers D. J. Travoy and J. R. Maa measured α for many liquids, including water, and observed values close to one. Even today, the value of α for water is a subject of much interest in the scientific literature.6
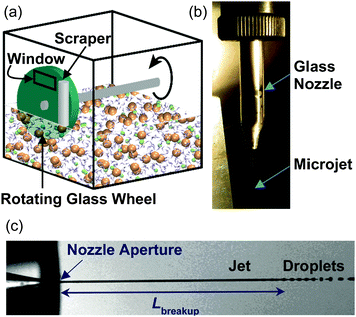
Sandra Lednovich and John Fenn made the next great experimental advance in 1972 by developing a robust technique to generate flat liquid films in vacuum.7 As depicted in Fig. 2a, a continuously renewed, vertical film is formed by rotating a partially submerged ∼5 cm diameter glass wheel through liquid contained in a temperature-controlled reservoir. The coated wheel is then skimmed by a metal or glass blade or a Teflon cylinder to a uniform thickness, typically 0.5 mm or less (corresponding to ∼106 molecular layers). This scraping process removes the outer portion of the liquid, including contaminants, and returns the excess liquid to the reservoir. The freshly skimmed film is then exposed to vacuum through a ∼1 cm2 circular or rectangular hole for 0.1 to 1 s at wheel speeds of 1 to 0.1 Hz. Lednovich and Fenn first used their trough to continue measurements of α, and Sinha and Fenn then measured the angular distributions of argon atoms scattering from liquid glycerol.8 This coated-wheel technique is currently used by us and by other groups as a means to provide clean, stable, and continuously renewed surfaces of low vapor pressure liquids, with interaction areas of 1–10 mm2 that are equivalent to areas used in studies of gas–solid interfaces.9–11 Among the liquids that have been investigated are hydrocarbons such as squalane, perfluorinated ethers, bare and surfactant-coated sulfuric acid and formamide, pure and salty glycerol, ionic liquids, and even salty water at 212 K. These liquids are generally limited to vapor pressures below 5 mTorr in order to avoid gas–vapor collisions just outside the liquid film.
Static crucibles of liquids have also been employed, particularly by Olander and coworkers to investigate reactions of Cl2 with liquid metals.12 These horizontal puddles may be coated with oxides or organic impurities, but can be cleaned in vacuum by stirring, scraping, ion sputtering, or neutral atom etching, allowing even reactive liquids such as molten alkali hydroxides, alkali carbonates, and metal alloys to be investigated.
The main subject of this review is our recent application of liquid microjets to explore helium evaporation and collisions of inert and reactive gases with high-vapor pressure liquids, including hydrocarbon fuels and pure and salty water, which were previously inaccessible with the coated-wheel technique. This narrow radius jet, as thin as 3 μm (∼1/10 the thickness of a strand of hair), was introduced by Manfred Faubel and coworkers in 1988.13 The microjet is a precisely fabricated glass tube pulled to a narrow open tip, as shown in Fig. 2b, that is deceptively challenging to maintain straight and unclogged for experiments spanning several days. As described below, Faubel recognized that gas–vapor collisions surrounding the jet are suppressed if the jet diameter is chosen to be smaller than the gas-phase mean free path. Faubel used this microjet technique to make the first collision-free measurements of the evaporation of liquid water. Several groups have since employed the microjet for spectroscopic measurements of both interfacial and bulk-phase aqueous solutions, opening an entirely new field of experimental research.14–19
Most recently, Yang et al. have adapted microfluidic channels to introduce aqueous solutions into vacuum by drilling a 2–3 μm wide hole in the top of the channel and exposing the circulating liquid.20 This technique offers fascinating opportunities for investigating gas–surface collisions with volatile liquids.
Scope of this tutorial review
This tutorial benefits from prior reviews of methods to prepare liquids in vacuum, including those by Seigbahn,21 Faubel,22 Wilson and Saykally,14 Winter and Faubel,15 Minton and McKendrick,11 Andersson,9 and Nathanson.23 In addition, reviews by the Boston College-Aerodyne group24 and by Hanson and Lovejoy25 provide excellent surveys of the droplet train and aerosol methods to explore the kinetics of gas uptake and reactivity, which have contributed greatly to our understanding of multiphase atmospheric chemistry.6 While this tutorial focuses on methods to generate clean liquids in vacuum coupled with mass spectrometric detection of the scattered and desorbing molecules, we note that significant advances in spectroscopic detection of molecules such as CO2 and NO by the Nesbitt group and OH by the McKendrick group have provided tremendous insights.10,11,26–29 These laser-based techniques can measure the rotational, vibrational, and electronic states of the outgoing molecules in addition to their velocity and direction.Why do we pursue gas–liquid scattering experiments in vacuum? Under very low pressures, gas-phase collisions are absent that would otherwise scramble velocities, directions, and appearance times of the products, and perhaps also destroy evaporating reaction intermediates. By suppressing collisions in the region surrounding the liquid, we can glean a wealth of information: the identity and relative amounts of nascent products as a function of collision energy, internal state, and incoming direction; the translational and internal energies of the product molecules and the reagent molecules that escape; and residence times indicating when and where reactions take place (within the interfacial region or the bulk). The velocities and directions of the scattered molecules often reflect the corrugation and motion of the surface molecules and even their identity and orientation. Gas–liquid scattering experiments, in concert with deep insights from simulations, provide us with a dynamical, “blow-by-blow” picture of collisions and interfacial reactions. In a sense, surface molecules are at the “frontier”: they are the first molecules under attack by reactive species approaching from the gas phase, and they act as gatekeepers for entry into and out of the bulk. Gas–liquid scattering experiments deploy powerful tools developed for gas-phase studies to interrogate the structure and reactivity of the interface, where molecules are asymmetrically distributed yet intrinsically cooperative. In future work, it may even be possible to couple scattering experiments with interfacial spectroscopic probes, following earlier experiments investigating structural changes in liquid crystals upon bombardment by helium atoms.30
As described above, the development of vacuum-liquid techniques builds on two key criteria: (1) the production of clean and continuously renewed surfaces of pure liquids and mixtures, including solutions with surfactant coatings, and (2) the suppression of gas–vapor collisions just above the solution that would otherwise distort the speeds and directions of incoming and outgoing molecules. In addition, it is important to evaluate the effects of evaporative cooling and to be aware of the size, stability, shape, and exposure times of the liquid sample itself. In the paragraphs below, we describe basic features of the microjet and coated-wheel techniques for scattering experiments, along with lessons we have learned, and then survey three experiments from our lab: (1) inert gas scattering from hydrocarbon fuels, (2) acid dissociation at the surface of water, and (3) non-Maxwellian helium evaporation from water and hydrocarbons.
Microjet and coated wheel experimental setups: scattering and evaporation
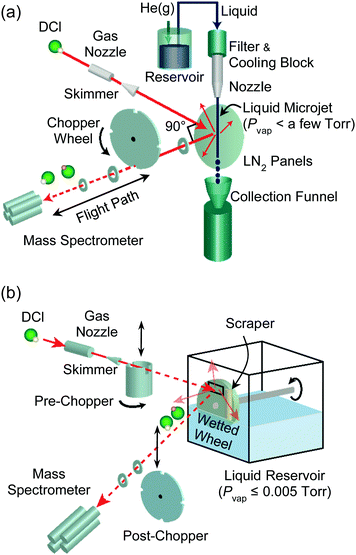
The experimental setups used in our laboratory are illustrated in Fig. 3. We generate microjets (panel a) by pressurizing a solution inside a stainless steel reservoir with 1–20 bar of inert gas, but microjets are more typically produced using a HPLC or screw pump to push the solution through the nozzle. Three nozzle types are currently in use, each with nozzle radii in the range of 5 μm or greater. These are fused silica capillaries14 drawn by a CO2 laser puller and quartz31 and borosilicate tubes drawn in a flame and then polished. Our own borosilicate nozzles have a lip at the top that serves as a bumper, preventing the nozzle from ejecting out of its stainless steel holder under high pressures. The liquid travels from the nozzle through the vacuum chamber and is collected in a chilled bottle, typically submerged in a dry ice–ethanol bath. Liquid nitrogen-cooled steel panels inside the chamber trap solvent molecules evaporating from the jet, lowering the background pressure to <10−5 Torr when the chamber is additionally evacuated by a 2000 L s−1 diffusion pump.In evaporation experiments (Fig. 3a without the gas nozzle and beam), a solute gas such as helium or argon is dissolved in the solution within the stainless steel reservoir through vigorous shaking. The evaporating solute and solvent species emerging from the jet are then monitored by a differentially-pumped quadrupole mass spectrometer. A spinning slotted wheel (“post-chopper”) divides the desorbing molecules into packets whose arrival times t over a flight path L are monitored by the mass spectrometer, yielding a time-of-flight (TOF) distribution. The velocities of the desorbing molecules are given by v = L/t, and the translational energies are calculated from 1/2mgasv2.
We can perform scattering experiments to explore collisions and interfacial reactions by introducing a gas beam, as shown in Fig. 3. These studies rely on differentially-pumped supersonic gas expansions (also developed by John Fenn) from a pinhole nozzle to generate reagent atoms or molecules at precisely controlled translational energies and fluxes.32 Many collisions occur as the gas exits the nozzle, channeling random thermal motions into directed motion of the gas molecules. For a ∼100 μm diameter pinhole nozzle at ∼1 bar pressure of pure argon, the ratio of the mean free path λ to the orifice diameter D (Knudsen number) is λ/D ≈ 0.001, so the gas expands adiabatically and the speed distribution narrows. While we harness these gas–gas collisions in the gas nozzle to produce supersonic expansions, we assiduously avoid the analogous vapor-phase collisions when preparing liquid surfaces in vacuum by increasing λ and decreasing D. These criteria are discussed in detail later.
Molecules in the incident gas beam (shown in Fig. 3 as DCl) strike the surface of the jet or coated wheel, and the reagent DCl and product HCl molecules scatter or desorb in all directions. The detection method remains the same as in evaporation, but the fixed geometry of our machine limits the view of the mass spectrometer to those molecules exiting through a 90° deflection angle. As described later, the identities, velocities, and fluxes of the outgoing molecules reveal how DCl molecules dissociate, undergo proton exchange, and even escape reaction in collisions with water.
Fig. 3b illustrates one method to directly measure solvation and reaction times of solutes in liquids. When the post-chopper wheel is removed from its position after the surface and a pre-chopper wheel (shown here as a cylinder) is placed between the incident beam and surface, the rotating cylinder creates short bursts of reagent molecules that strike the liquid. In this case, the arrival time of the reagent or product molecule at the mass spectrometer is a sum of its residence time in the liquid and its flight time to the mass spectrometer. Average residence times on the order of one microsecond or longer can then be extracted from the spectrum. See ref. 33 for more details.
In order to generate sufficient scattering signal, the incident gas beam is designed to intersect the liquid jet over a ∼3 mm length, considerably longer than in spectroscopic or photoemission experiments. This overlap requires the jet to run steady and straight over many hours. Our current gas beam is significantly broader than the jet, but it should ultimately be possible to match the width of a rectangular gas beam to the narrow size of the jet in order to minimize the background gas load.
Microjet and coated-wheel parameters, trade-offs, and lessons learned
Microjets and coated wheels both produce continuously renewed liquid samples, but with very different variables that can be controlled. We outline below several of these parameters and trade-offs and lessons they have taught us.Jet breakup
The cylindrical jet is inherently unstable and ultimately breaks up into droplets, as photographed in Fig. 2c.22 Disturbances in the jet pinch off the liquid stream, minimizing the surface area and the surface free energy. The length of the cylindrical jet prior to droplet conversion increases with the jet diameter djet, velocity vjet, viscosity η, and density ρ, but decreases with surface tension γ: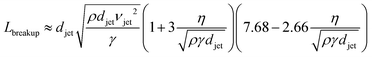 | (1) |
The comparable breakup phenomenon for the coated wheel occurs when the wheel rotates so slowly that the liquid drains from the surface. This time can be long if the fluid is viscous and fully wets the glass or metal wheel: in the case of supercooled sulfuric acid at 212 K (1800 mPa s viscosity), we found that the glass wheel remains coated even when it is stationary for 6 s.
Evaporative cooling
As the microjet travels through the vacuum chamber, evaporating molecules remove heat, and the temperature decreases. Evaporative cooling from a cylindrical jet can be predicted from the expression:13,14,35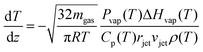 | (2) |
In the case of the coated wheel, solvent evaporation also cools the patch of liquid as it rotates in front of the hole in the reservoir and molecules evaporate into vacuum. The heat supplied for this evaporation comes from thermal conduction of the underlying liquid, yielding a change in surface temperature of ΔT ≈ (ΔHvapnvap〈vvap〉/4)(texp/(κnliqCp))1/2, where κ is the thermal conductivity and texp is the exposure time of the liquid to vacuum.7 For texp = 0.5 s, ΔT is much less than 1 K for glycerol at 295 K (Pvap = 0.1 mTorr) and about 1 K for 8 molal LiBr/H2O at 212 K (Pvap = 5 mTorr).
Gas–vapor collisions
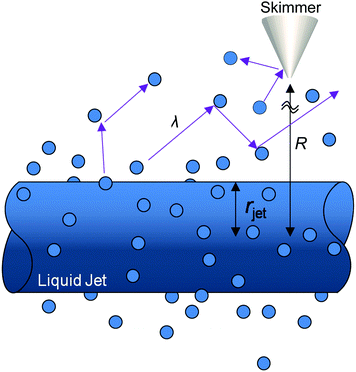
The high vapor pressure of water, fuels, and many other solvents implies that these molecules travel only a short distance in the vapor phase before colliding into each other, altering their speed and direction. This collision distance, or mean free path λ, can be expressed as (cσngas)−1, where σ is the collision cross section (about 30 Å2 for water) and c = 〈vrel/v〉 is the ratio of relative and gas velocities, equal to √2 in a uniform gas sample. It is difficult to estimate λ precisely because the value of σ depends on the process observed. The constant c is also difficult to calculate for molecules striking and leaving a cylinder or flat surface of finite dimensions. Useful approximate values include c → 1 for solute molecules traveling much faster than solvent molecules and c ≈ 3/4 for evaporating solvent molecules colliding with each other.36 For these reasons, we can only roughly estimate the number of collisions Ncoll in the vapor phase above the surface, as depicted in Fig. 4. Faubel originally calculated Ncoll by counting the number of mean free paths over the radial distance r from the jet:13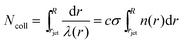 | (3) |
 | (4) |
It is helpful to compare this infinite cylinder calculation of Ncoll to expressions for other geometries calculated by Sadtchenko,37 Faubel,22 and us:38
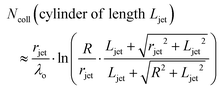 | (5) |
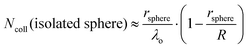 | (6) |
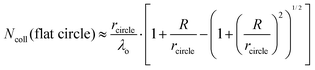 | (7) |
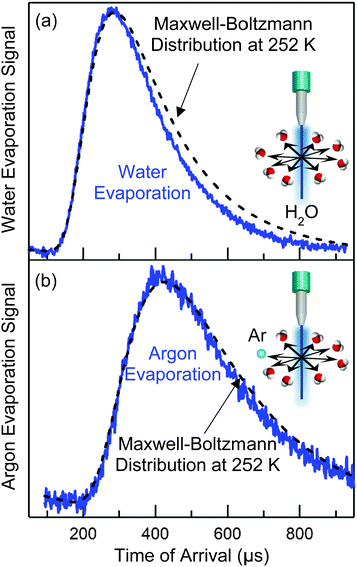
As an example, let's calculate Ncoll for water evaporating from a 5 μm radius jet of supercooled water at 252 K, where vapor-phase collisions are cut off by a skimmer at R = 1 mm from the surface. At this temperature, Pvap equals 0.9 Torr and λo is ∼250 μm. Eqn (4) yields Ncoll ≈ 0.1 when treating the jet as infinitely long. We can also calculate the fraction of unperturbed evaporation trajectories, given by Beer's law, of e−Ncoll = 0.9. The corresponding TOF spectrum of water molecules evaporating from the jet is shown in Fig. 5a, where it is compared with a Maxwell–Boltzmann distribution at the 252 K temperature of the water. (This distribution is expected when the evaporation coefficient is near one or is independent of collision energy.39,40) The observed spectrum is slightly narrower, most likely reflecting a weak supersonic expansion arising from the few collisions that do occur near the jet surface. As calculated above, however, this jet breaks up into a string of droplets less than 1 mm from the nozzle, and Ncoll likely falls between the cylinder and isolated sphere values of 0.1 and 0.04. We note that there is no “magic” threshold value of Ncoll to guarantee successful experiments, but we generally find that we can record TOF spectra with minimal distortion for Ncoll < 0.1. This limit may be superseded by higher values as more volatile liquids are investigated.
We can use eqn (7) to estimate the useful maximum vapor pressure for the coated-wheel technique. Consider water evaporating through a 1 cm diameter circular hole that exposes the coated wheel to vacuum, with an aperture placed 2 cm from the wheel to cut off further gas–vapor collisions. The second term in eqn (7) has a value close to one, and λo is about 4 cm for 8 molal LiBr/H2O at 212 K and Pvap = 0.005 Torr. In this case, Ncoll ≈ rcircle/λo = 0.05, and in accord with this small value we find that water evaporation is slightly supersonic.38
Argon thermometry
As stated above, the temperature of the pure water jet is 252 K, cooling about 30 K by the time it reaches a distance 4.5 mm below the nozzle. But how do we know this? While evaporative cooling calculations provide valuable guidance in both the cylinder and droplet regimes,35 we can also measure the temperature directly in the observation region.41Fig. 5b displays the TOF spectrum of dissolved argon atoms evaporating through the water vapor cloud. This distribution is even closer to Maxwellian than is the H2O spectrum in Fig. 5a because the scattering cross section is smaller for Ar–H2O than for H2O–H2O, and Ncoll drops to a negligible value. This evaporation acts as an “Argon Thermometer”: in practice, we fit the Ar TOF spectrum to a Maxwell–Boltzmann distribution at a temperature T, which if fit well, is then used as the temperature of the jet in the observation region in all subsequent analyses. The fitting uncertainty is typically less than ±5 K. Although we cannot know a priori that Ar atoms evaporate in a Maxwell–Boltzmann distribution at the temperature of every liquid, we find that argon temperatures and those predicted by eqn (2) are typically closer than the fitting uncertainty for all liquids investigated so far. We can further test the validity of the thermometer by monitoring Ar evaporation from squalane (10−8 Torr vapor pressure), which does not measurably cool and is not surrounded by a thick vapor cloud. In this case, the Ar and thermostatted liquid temperatures are again identical within the fitting uncertainty.Trade-offs between the microjet and coated wheel
Despite the extraordinary access to higher vapor pressures provided by the microjet, experimentalists face substantial tradeoffs when switching from the wetted wheel to the jet. First, the jet provides a much smaller scattering target. We typically utilize nozzles for scattering experiments that are 15 μm or larger in radius in order to increase the signal, while simultaneously lowering the temperature to maintain a thin vapor cloud. For a 15 μm radius jet, the ratio of wetted wheel to microjet surface areas is given approximately by rcircle/rjet ≈ 3 mm/15 μm = 200! This large area ratio highlights the challenges of microjet scattering and implies that experiments must be chosen judiciously because they require much longer signal averaging times. The small size of the jet also means that artifacts can contribute substantially to the measured signal. Molecules in the incident beam and those evaporating from the jet can scatter off the chamber walls, apertures, liquid nitrogen shields, and the back of the post-chopper wheel, ultimately contributing to the TOF spectrum. We subtract these spurious signals by recording spectra with the jet out of the scattering region and without the incident beam. We also note that the mismatch in size between the incident gas beam and the jet makes it much more difficult to carry out measurements of the absolute uptake of gas into the jet. These entry probabilities can be readily measured when the incident gas beam is contained within the larger exposed area of the coated wheel.33,38Second, the typical velocity of a 15 μm radius jet is 30 m s−1, permitting a viewing time of 100 μs over a 3 mm wide detection window. In contrast, the wetted wheel rotates slowly, allowing measurements of desorbing species over times of 0.05 to 1 s, or up to 104 times longer than for the microjet.33 These longer times are especially useful for observing soluble products that slowly evaporate, such as gaseous HCl produced after recombination of dissolved H+ and Cl−. As mentioned above, shorter solvation times between 10−6 and 10−3 s may be measured using the short gas bursts created by a pre-chopper, shown in Fig. 3b for the coated wheel.33
The more slowly moving wheel also allows surfactants sufficient time to diffuse from the bulk to the surface when the solution is intentionally doped with amphiphiles.42 The time for a bulk surfactant to populate the surface is roughly τsurfactant ≈ (csurf/cbulk)2/D, where csurf and cbulk are the surface and bulk surfactant concentrations and D is the diffusion constant. For D ≈ 10−6 cm2 s−1, cbulk must exceed 0.01 M to generate csurf of 1014 cm2 (∼1/10 monolayer) over 100 μs. This is certainly achievable for smaller and more soluble surfactants in low-viscosity fluids, but denser monolayers require much longer times to form.43
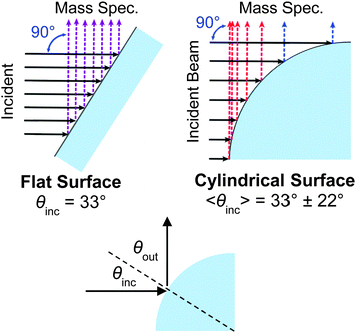
Third, the cylindrical jet and flat wheel generate potentially different angular distributions of scattered molecules, although this effect may be mitigated by the intrinsic surface roughness of molecular liquids. Fig. 6 compares collisions from a flat film and a cylindrical jet at a 90° configuration between the incident beam and mass spectrometer detector. A uniform incident beam strikes the cylinder at different local angles along the quadrant, with an average angle of incidence 〈θinc〉 = 33° ± 22° (one standard deviation). The flat film is oriented at this same incident angle for comparison. When the outgoing direction θout monitored by the mass spectrometer is constrained to be 90° − θinc, as it is in our experiments, then 〈θout〉 = 57° ± 22°. The differences in angular distributions and scattering patterns from a flat film and a cylindrical jet are not yet firmly known, but can hopefully be mapped out using a rotatable mass spectrometer or other spectroscopic technique to sample different deflection angles and out-of-plane scattering. Fig. 7 (discussed later) suggests that the scattering patterns can be quite similar.
Fourth, we note a useful complementarity among low and high vapor pressure liquids used in the coated wheel and microjet techniques. Many low vapor pressure liquids, such as squalane (20 mPa s), glycerol (103 mPa s), and supercooled sulfuric acid (102–104 mPa s), are viscous fluids that thickly coat the rotating wheel and retain a uniform fidelity of the skimmed film even at low rotation speeds and long exposure times. In contrast, higher vapor pressure liquids, including short-chain hydrocarbons (0.3 to 1.3 mPa s) and pure and salty water (1–10 mPa s), are well suited to the microjet technique because they are often less viscous, and therefore require lower backing pressures to reach operational jet speeds.
Lessons in generating microjets in vacuum
The goal when designing liquid microjet experiments is always to minimize vapor-phase collisions, but practical considerations also govern the selection of experimental parameters. In particular, the flow rate through the nozzle must be carefully balanced to prevent freezing and clogging at any given radius and temperature combination. Typical backing pressures in our experiments range from 1 to 20 bar, generating jet velocities between 5 and 30 m s−1, though speeds up to 150 m s−1 have been achieved at backing pressure greater than 100 bar.22Icicles are a concern when operating at temperatures close to the freezing point of the solution because solvent evaporation from the jet leads to supercooling (see Fig. 3 of ref. 44). If the flow rate is too low, the jet will freeze right at the tip of the nozzle. Alternatively, if the flow rate is too high, icicles grow up from the bottom of the collection bottle as the jet strikes the pool of frozen solution. A small hoop can be manually spun above the neck of the collection bottle to break the emerging icicle rods. Ultimately, the choice of flow rate affects not only the temperature of the jet within the interaction zone, but also the jet speed and the breakup length. From a practical standpoint, high flow rates are discouraged when working with expensive solvents. Whereas wetted-wheel experiments can be conducted for several weeks with less than 50 mL of solution, the tiny microjet can require up to 2 L of solution per day, which must be replaced or filtered before reuse.
Perhaps the greatest practical challenge posed by microjets is clogging. Common culprits are dust, air bubbles, salt, and corrosion, and the best recourse is sonication with a healthy dose of patience or a large supply of replacement nozzles. In our setup, solutions are filtered upon preparation and then pass through two in-line filters (15 μm and 2 μm pore sizes) between the reservoir and the nozzle to eliminate dust particles. To keep the jet running smoothly, liquid should flow through the nozzle at all times. This precaution also prevents salt deposits from collecting at the tip of the nozzle. The vacuum chamber is vented overnight (to avoid extensive consumption of the solution and of liquid nitrogen), and the nozzle is continuously flushed with pure water to prevent clogging. The sum of our experience has taught us to group experiments by jet radius to minimize the time spent changing nozzles.
The complementary nature of the coated wheel and microjet may be captured by the fable of the Tortoise and the Hare. While the coated wheel rotates slowly, it provides data quickly for low vapor pressure liquids because the surface area struck by the incident gas beam is so large. Conversely, the microjet moves quickly, but its narrow diameter requires long signal averaging times. The race may best be won by the Tortoise and the Hare holding hands: initial experiments with a low vapor pressure mimic (such as glycerol for water) using the coated wheel can provide invaluable guidance for designing the low signal-to-noise microjet experiments, as described below.
The microjet in practice: jet fuel heating, interfacial acid dissociation, and super-Maxwellian helium evaporation
We describe three recent experiments that utilize microjets in vacuum: collisions of Ar and O2 with hydrocarbon liquids to measure fuel droplet heating, interfacial dissociation of HCl in salty water, and non-Maxwellian helium evaporation to probe interfacial solute–solvent forces.A striking comparison: scattering from the microjet and wetted wheel
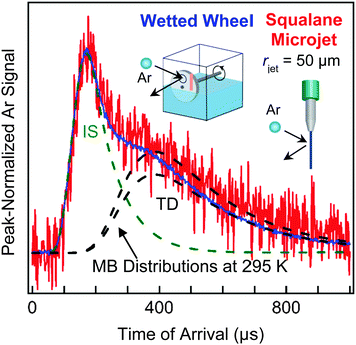
Fig. 7 highlights the different signal levels we obtained in our initial experiments from a cylindrical microjet and a flat wetted wheel when we scattered high-energy (90 kJ mol−1) argon atoms from liquid squalane, whose 10−8 Torr vapor pressure and moderate viscosity make both techniques possible.45 The TOF spectra reveal two distinct features at short and long arrival times. Some Ar atoms undergo direct inelastic or impulsive scattering (IS) and recoil from the surface after one or a few bounces, losing only a fraction of their translational energy. The remaining Ar atoms fully dissipate their energy through multiple collisions and are momentarily trapped at the surface; they undergo thermal desorption (TD) in a characteristic Maxwell–Boltzmann distribution at the temperature of the liquid. (We note that “TD” refers to both “trapping and desorption”, a two-step process, and “thermal desorption”, just the second step, which may follow adsorption, dissolution, and/or reaction. “IS” is used to refer to both “inelastic scattering” and “impulsive scattering”, and is sometimes called “DR” for “direct recoil”. These three terms refer to the same short-time single or multi-bounce collision.32) The branching between the IS and TD channels for the microjet and flat film TOF spectra are remarkably similar despite the different geometries.Perhaps the most striking aspect of Fig. 7 is that the signal-to-noise is significantly lower for the 50 μm radius jet (8 hour recording time) versus the wetted wheel (10 minute recording time). We have recently increased the microjet signal tenfold by moving the gas nozzle closer to the jet and reduced the background twofold by adding more cold panels to freeze out background gases. Nevertheless, Fig. 7 emphasizes the great challenges involved in microjet scattering experiments.
Droplet fuel heating: collisions of O2 with dodecane
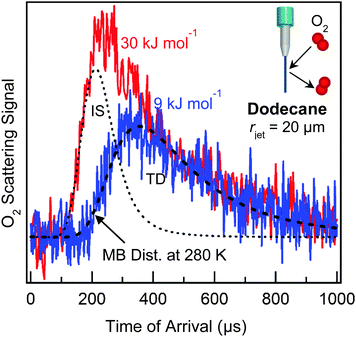
The combustion of liquid fuel presents one very practical application of gas–liquid interfacial chemistry. In order for combustion to occur, gasoline and jet fuel must first evaporate into the gas phase. The energy required to rapidly heat and vaporize the fuel droplets is provided by collisions with ambient gases, primarily N2 and O2, at temperatures and pressures up to 2000 K and 20 atm. Our first microjet scattering experiments focused on collisions of O2 with liquid dodecane, often the largest single component in kerosene jet fuel.45 We directed beams of O2 molecules at a 20 μm radius jet of dodecane (Pvap = 0.1 Torr) at collision energies of 9 and 30 kJ mol−1, which are the average translational energies at gas temperatures of ∼500 and ∼1800 K. The TOF spectra in Fig. 8 illustrate that, at low collision energy, nearly all impinging O2 molecules become momentarily trapped at the surface and then desorb in a Maxwell–Boltzmann distribution at Tliq = 280 K, while at higher collision energy, both impulsive scattering and thermal desorption occur. Overall, O2 collisions with dodecane and squalane (not shown) transfer ∼70% of their translational energy to the surface molecules. These studies indicate that gas-hydrocarbon energy transfer is very efficient and further imply that short-chain hydrocarbons like dodecane and long-chain hydrocarbons like squalane absorb similar amounts of energy. It will be intriguing to extend these measurements to narrower jets of gasoline, where the mix of alkanes and aromatics may roughen the surface and thereby promote multiple bounces and even larger energy transfers.Interfacial acid dissociation and reactive scattering
Fig. 9 shows one example of our efforts to address a reactive gas–liquid system: how do acidic gases such as HCl dissolve in water and other protic liquids? We chose the deuterated isotope DCl so that DCl → HCl exchange may be used as a signature of reaction. Fig. 9 illustrates several fundamental pathways following collisions of the acid DCl with salty water: (1) direct inelastic scattering of DCl molecules from the surface in one or a few bounces; (2) full energy dissipation through several energy-exchanging collisions, leading to momentary DCl trapping and hydrogen bonding at the surface, followed by thermal desorption of DCl before it dissolves or reacts; (3) DCl dissociation into D+ and Cl− in the interfacial region; (4) diffusion of these ions into solution (uptake), followed by slow evaporation of D → H exchanged HCl; and (5) perhaps most fascinating, rapid D+ → H+ exchange with H2O and immediate desorption of HCl from the interfacial region.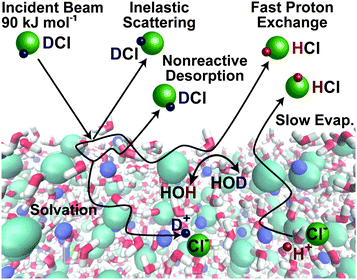 | ||
| Fig. 9 Pathways following collisions of DCl molecules with the surface of a 8 molal LiBr/H2O solution. Simulation of salty solution by Zachary R. Kann and James L. Skinner. Adapted from ref. 38 with permission from the PCCP Owner Societies. | ||
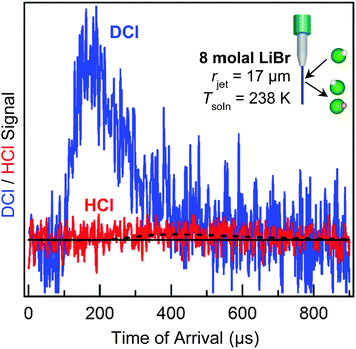
All five processes listed above have been observed when DCl molecules strike a wetted wheel coated with liquid glycerol, HOCH2CH(OH)CH2OH, at 295 K (Pvap = 10−4 Torr).46 In contrast, longtime uptake dominates when DCl collides with 8 molal LiBr/H2O at 212 K (Pvap = 0.005 Torr) due to the enormous solubility of D+/H+ and Cl− in the cold solution.38 More recently, we have extended these measurements to 238 K using a 17 μm radius jet, where the water vapor pressure rises to 0.1 Torr (a 20-fold increase).47 Collisions of 90 kJ mol−1 DCl with the LiBr/H2O jet generate the TOF spectrum shown in Fig. 10, which has been corrected for spurious background scattering of DCl in the absence of the microjet. This spectrum is dominated by direct scattering, with minimal thermal desorption of intact DCl molecules. In parallel, the signal from D → H exchanged HCl is very weak. These observations imply that momentarily trapped DCl molecules only infrequently desorb and instead mostly dissolve and dissociate, as also observed in simulations.48 A major experimental challenge is to use even narrower jets to reach higher temperatures and vapor pressures while preserving strong enough scattering signals to detect.
The example above illustrates one type of reactive scattering experiment. Studies by other groups and collaborators include collisions of reactive species such as O, Cl, F, and Na atoms with many liquids, all investigated using the wetted-wheel technique.49–52 We note the remarkable discovery by Garton et al. that collisions of high-energy O atoms with squalane produce consecutive OH and H2O products through direct “pick-off” reactions of H atoms from the hydrocarbon chain, bypassing thermalization of the O atom reagent and OH and H2O products.49 In a beautiful application of gas-phase ideas to gas–surface interactions, these studies also led to the creation of the “surface Newton diagram” to determine the effective mass of the surface molecules and energy deposition into their internal motions.50 Hydrogen atom abstraction by O atoms from hydrocarbon and organic ionic liquids may even become a general analytical tool to determine the propensity for organic ions to segregate to the surface.11,29
Non-Maxwellian helium evaporation from protic and hydrocarbon liquids
A unique feature of the microjet is that it can carry dissolved gases into vacuum, enabling studies of the evaporation of weakly soluble gases. The backing gas that pressurizes the jet also dissolves within the liquid and then evaporates once the jet emerges into vacuum. Helium, which is often used as the backing gas, has the lowest solubility among all gases due to its very low polarizability, and this trait leads to remarkable consequences.40,41,53–55Fig. 11b shows the TOF spectrum of evaporating He atoms dissolved in a cold salty water jet in comparison with a Maxwell–Boltzmann distribution. The spectrum is shifted to shorter arrival times and therefore higher He kinetic energies. This super-Maxwellian He evaporation appears to be universal: we have observed this behavior from every liquid jet investigated, including dodecane, octane, jet fuel, ethylene glycol, and pure water. The average kinetic energies of the evaporating He atoms range from 1.05 to 1.70 × 2RTliq, where 2RTliq is the flux-weighted kinetic energy of molecules evaporating in a Maxwell–Boltzmann distribution. In contrast, more soluble and polarizable gases such as Ar, O2, N2, CO2, Cl2, HCl, HNO3, and H2O all evaporate from liquid microjets with velocities that are very close to Maxwell–Boltzmann distributions at Tliq.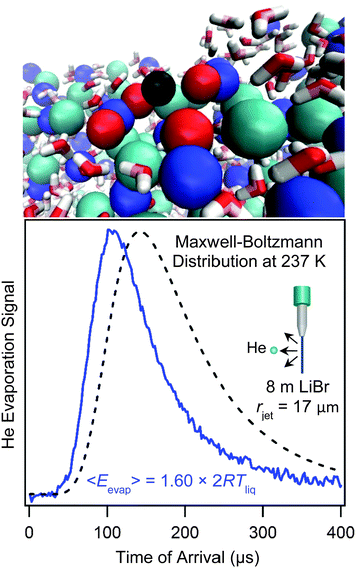 | ||
| Fig. 11 Bottom panel: Helium evaporation from 8 molal LiBr/H2O. The black dashed line is a Maxwell–Boltzmann distribution at Tliq = 237 K. The He atoms' velocities are faster than Maxwellian, corresponding to an average evaporation energy of 1.60 × 2RTliq. See ref. 41. Top panel: Simulation of a He atom (black) evaporating from the salty solution. Li+ = dark blue, Br− = light blue, H2O directly solvating the He atom = red. Simulation provided by Zachary R. Kann and James L. Skinner. | ||
The super-Maxwellian evaporation of He has two surprising implications. First, microscopic reversibility allow us to reverse the trajectories of the outgoing He atoms and view them as approaching the liquid—these trajectories all lead to dissolution because the He atoms began in the liquid in the original trajectories.32,39 In this time-reversed picture, He atoms at higher kinetic energies preferentially dissolve—they “ballistically” deposit in the liquid—while those that approach the surface more slowly are likely to bounce off.53 In this way, we can exploit evaporation from microjets to explore collisions that lead to gas dissolution, which are such rare events for He that they are exceedingly difficult to probe experimentally.
Second, we find that the kinetic energy of the evaporating He atoms scales approximately with the (positive) free energy of solvation of He. Atomistic simulations by Kann and Skinner show that the correlation reflects the sharply decreasing potential of mean force as the interloping He atom passes through the interfacial region (as shown in Fig. 11a).41,55 The gradient of this potential is the force acting on the He atom by the neighboring water molecules as they reconfigure and return to their unperturbed state. The He atom is accelerated by this repulsive force, and because He binds so weakly to water, it does not dissipate all of its excess energy through additional He–H2O collisions before its last collision with the surface molecules. We hope soon to investigate He evaporation from solutions containing surface-active species in order to learn how they alter the final collisions of the He atom as it is propelled through the interface.
Future directions
Microjet scattering offers the possibility to explore collisions and reactions at the surfaces of water and hydrocarbon fuels under conditions closer to room temperature. The results described above imply that jet radii no larger than a few microns, along with careful detection schemes, will be required to perform scattering experiments free of gas–gas collisions at vapor pressures of several Torr. We believe that these jets will be useful for investigating atmospherically important reactions with actual seawater and sea spray, fuel evaporation in gasoline engines, and even electrochemical reactions at the vacuum/water/electrode interface. In combination with theoretical efforts and spectroscopic characterization, these scattering experiments hold great promise to reveal a microscopic picture of everyday gas–liquid processes.Acknowledgements
We delight in honoring the remarkable creativity of Kenneth Hickman, John Fenn, and Manfred Faubel in laying the groundwork for experimental studies of the dynamics of gas–liquid interfaces. We would also like to thank Kevin Wilson, Bernd Winter, Manfred Faubel, Christopher Cappa, Richard Saykally, Josephina Werner, John Hemminger, and Daniel Neumark for sharing their microjet expertise with us and Zachary Kann and James Skinner for providing the simulation snapshots in Fig. 9 and 11. This work would not have been possible without the tireless efforts of Alexis Johnson, Diane Lancaster, Daniel Burden, Christine Hahn, and Thomas Sobyra, who transformed initial microjet failures into working experiments. We are grateful to the Air Force Office of Scientific Research (FA9550-10-0176) and to the National Science Foundation (CHE-1152737 to GMN and DGE-0718123 for a fellowship to JAF) for making it possible to carry out this research.References
- W. Brustaert, Evaporation into the Atmosphere, Reidel, Dordecht, 1982, ch. 2.1 Search PubMed.
- A. B. Wyckoff, Proc. Am. Philos. Soc., 1886, 23, 383–388 Search PubMed.
- G. T. Barnes, Agric. Water Manag., 2008, 95, 339–353 CrossRef.
- D. J. Donaldson and V. Vaida, Chem. Rev., 2006, 106, 1445–1461 CrossRef CAS PubMed.
- K. C. D. Hickman and D. J. Trevoy, Ind. Eng. Chem., 1952, 44, 1882–1888 CrossRef CAS.
- C. E. Kolb, R. A. Cox, J. P. D. Abbatt, M. Ammann, E. J. Davis, D. J. Donaldson, B. C. Garrett, C. George, P. T. Griffiths, D. R. Hanson, M. Kulmala, G. McFiggans, U. Pöschl, I. Riipinen, M. J. Rossi, Y. Rudich, P. E. Wagner, P. M. Winkler, D. R. Worsnop and C. D. O'Dowd, Atmos. Chem. Phys., 2010, 10, 10561–10605 CrossRef CAS.
- S. L. Lednovich and J. B. Fenn, AIChE J., 1977, 23, 454–459 CrossRef CAS.
- M. P. Sinha and J. B. Fenn, Proceedings of the 5th International Symposium on Molecular Beams, Nice, 1975 Search PubMed.
- G. Andersson and C. Ridings, Chem. Rev., 2014, 114, 8361–8387 CrossRef CAS PubMed.
- B. G. Perkins and D. J. Nesbitt, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12684–12689 CrossRef CAS PubMed.
- M. A. Tesa-Serrate, E. J. Small, T. K. Minton and K. G. McKendrick, Annu. Rev. Phys. Chem., 2016, 67 DOI:10.1146/annurev-physchem-040215-112355.
- M. Balooch, W. J. Siekhaus and D. R. Olander, J. Phys. Chem., 1984, 88, 3521–3528 CrossRef CAS.
- M. Faubel, S. Schlemmer and J. P. Toennies, Z. Phys. D: At., Mol. Clusters, 1988, 10, 269–277 CrossRef CAS.
- K. R. Wilson, B. S. Rude, J. Smith, C. Cappa, D. T. Co, R. D. Schaller, M. Larsson, T. Catalano and R. J. Saykally, Rev. Sci. Instrum., 2004, 75, 725–736 CrossRef CAS.
- B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176–1211 CrossRef CAS PubMed.
- M. A. Brown, R. D'Auria, I.-F. W. Kuo, M. J. Kirsch, D. E. Starr, H. Bluhm, D. J. Tobias and J. C. Hemminger, Phys. Chem. Chem. Phys., 2008, 10, 4778–4784 RSC.
- M. A. Brown, A. B. Redondo, I. Jordan, N. Dduyckaerts, M.-T. Lee, M. Ammann, F. Nolting, A. Kleibert, T. Huthwelker, J.-P. Mächler, J. Birrer, R. Wetter, H. J. Wörner and J. A. van Bokhoven, Rev. Sci. Instrum., 2013, 84, 073904 CrossRef PubMed.
- M. H. Elkins, H. L. Williams and D. M. Neumark, J. Chem. Phys., 2015, 142, 234501 CrossRef PubMed.
- O. J. Maselli, J. R. Gascooke, W. D. Lawrance and M. A. Buntine, Chem. Phys. Lett., 2011, 513, 1–11 CrossRef CAS.
- L. Yang, Z. Zhu, X.-Y. Yu, S. Thevuthasan and J. P. Cowin, Anal. Methods, 2013, 5, 2515–2522 RSC.
- H. Siegbahn, J. Phys. Chem., 1985, 89, 897–909 CrossRef CAS.
- M. Faubel, in Photoionization and Photodetachment: Part I, ed. C.-Y. Ng, World Scientific, Singapore, 2000, vol. 10A, pp. 634–690 Search PubMed.
- G. M. Nathanson, Annu. Rev. Phys. Chem., 2004, 55, 231–255 CrossRef CAS PubMed.
- P. Davidovits, C. E. Kolb, L. R. Williams, J. T. Jayne and D. R. Worsnop, Chem. Rev., 2006, 106, 1323–1354 CrossRef CAS PubMed , updated 2011.
- D. R. Hanson and E. R. Lovejoy, J. Phys. Chem., 1996, 100, 6397–6405 CrossRef CAS.
- A. J. Kenyon, A. J. McCaffery, C. M. Quintella and M. D. Zidan, J. Chem. Soc., Faraday Trans., 1993, 89, 3877–3884 RSC.
- B. G. Perkins and D. J. Nesbitt, J. Phys. Chem. B, 2006, 110, 17126–17137 CrossRef CAS PubMed.
- A. Zutz and D. J. Nesbitt, J. Phys. Chem. C, 2015, 119, 8596–8607 CAS.
- C. Waring, P. A. J. Bagot, M. L. Costen and K. G. McKendrick, J. Phys. Chem. Lett., 2010, 2, 12–18 CrossRef PubMed.
- K. Y. Randall, Y. B. Fan, O. Michel, M. C. Goh and D. J. Donaldson, Phys. Rev. Lett., 1996, 77, 310–313 CrossRef CAS PubMed.
- A. Charvat, E. Lugovoj, M. Faubel and B. Abel, Rev. Sci. Instrum., 2004, 75, 1209–1218 CrossRef CAS.
- K. W. Kolasinski, Surface Science, Wiley, United Kingdom, 3rd edn, 2012, ch. 2.3, 3.7, and 3.8 Search PubMed.
- A. H. Muenter, J. L. DeZwaan and G. M. Nathanson, J. Phys. Chem. B, 2006, 110, 4881–4891 CrossRef CAS PubMed.
- A. H. Lefebvre, Atomization and Sprays, Hemisphere Pub. Corp., New York, 1989, p. 51 Search PubMed.
- J. D. Smith, C. D. Cappa, W. S. Drisdell, R. C. Cohen and R. J. Saykally, J. Am. Chem. Soc., 2006, 128, 12892–12898 CrossRef CAS PubMed.
- The value of c = 3/4 was estimated using Clausius's assumption of a single speed. L. B. Loeb, The Kinetic Theory of Gases, Dover, New York, 1961, ch. 2 Search PubMed.
- V. Sadtchenko, M. Brindza, M. Chonde, B. Palmore and R. Eom, J. Chem. Phys., 2004, 121, 11980–11992 CrossRef CAS PubMed.
- S. M. Brastad and G. M. Nathanson, Phys. Chem. Chem. Phys., 2011, 13, 8284–8295 RSC.
- C. T. Rettner, E. K. Schweizer and C. B. Mullins, J. Chem. Phys., 1989, 90, 3800–3813 CrossRef CAS.
- D. K. Lancaster, A. M. Johnson, K. Kappes and G. M. Nathanson, J. Phys. Chem. C, 2015, 119, 14613–14623 CAS.
- C. Hahn, Z. R. Kann, J. A. Faust, J. L. Skinner and G. M. Nathanson, J. Chem. Phys., 2016, 144, 044707 CrossRef PubMed.
- S.-C. Park, D. K. Burden and G. M. Nathanson, Acc. Chem. Res., 2009, 42, 379–387 CrossRef CAS PubMed.
- J. K. Ferri and K. J. Stebe, Adv. Colloid Interface Sci., 2000, 85, 61–97 CrossRef CAS PubMed.
- B. Winter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601, 139–150 CrossRef CAS.
- D. K. Lancaster, A. M. Johnson, D. K. Burden, J. P. Wiens and G. M. Nathanson, J. Phys. Chem. Lett., 2013, 4, 3045–3049 CrossRef CAS.
- L. P. Dempsey, S. M. Brastad and G. M. Nathanson, J. Phys. Chem. Lett., 2011, 2, 622–627 CrossRef CAS.
- J. A. Faust, T. B. Sobyra and G. M. Nathanson, J. Phys. Chem. Lett., 2016, 7, 730–735 CrossRef CAS PubMed.
- L. Halonen, L. J. Partanen, G. Murdachaew and R. B. Gerber, Phys. Chem. Chem. Phys., 2016 10.1039/C6CP00597G.
- J. Zhang, D. J. Garton and T. K. Minton, J. Chem. Phys., 2002, 117, 6239–6251 CrossRef CAS.
- D. J. Garton, T. K. Minton, M. Alagia, N. Balucani, P. Casavecchia and G. G. Volpi, J. Chem. Phys., 2000, 112, 5975–5984 CrossRef CAS.
- A. M. Zolot, P. J. Dagdigian and D. J. Nesbitt, J. Chem. Phys., 2008, 129, 194705 CrossRef PubMed.
- W. A. Alexander, J. P. Wiens, T. K. Minton and G. M. Nathanson, Science, 2012, 335, 1072–1075 CrossRef CAS PubMed.
- A. M. Johnson, D. K. Lancaster, J. A. Faust, C. Hahn, A. Reznickova and G. M. Nathanson, J. Phys. Chem. Lett., 2014, 5, 3914–3918 CrossRef CAS PubMed.
- S. P. K. Koehler and M. A. Williams, Chem. Phys. Lett., 2015, 629, 53–57 CrossRef.
- Z. R. Kann and J. L. Skinner, J. Chem. Phys., 2016, 144, 154701 Search PubMed.
| This journal is © The Royal Society of Chemistry 2016 |