Gas storage in porous metal–organic frameworks for clean energy applications
Shengqian
Ma
*a and
Hong-Cai
Zhou
b
aChemical Sciences and Engineering Division, Argonne National Laboratory, 9700 S. Cass Avenue, Argonne, IL 60439, USA. E-mail: sma@anl.gov; Fax: +1 630 252 9917; Tel: +1 630 252 5917
bDepartment of Chemistry, Texas A&M University, PO Box 30012, College Station, TX 77842, USA. Fax: +1 979 845 4719; Tel: +1 979 845 4034
First published on 2nd November 2009
Abstract
Depletion of fossil oil deposits and the escalating threat of global warming have put clean energy research, which includes the search for clean energy carriers such as hydrogen and methane as well as the reduction of carbon dioxide emissions, on the urgent agenda. A significant technical challenge has been recognized as the development of a viable method to efficiently trap hydrogen, methane and carbon dioxide gas molecules in a confined space for various applications. This issue can be addressed by employing highly porous materials as storage media, and porous metal–organic frameworks (MOFs) which have exceptionally high surface areas as well as chemically-tunable structures are playing an unusual role in this respect. In this feature article we provide an overview of the current status of clean energy applications of porous MOFs, including hydrogen storage, methane storage and carbon dioxide capture.
 Shengqian Ma | Shengqian Ma received his BS degree from Jilin University, China in 2003, and obtained his PhD degree in 2008 from Miami University (Ohio) under the supervision of Hong-Cai “Joe” Zhou. Currently he is the Director’s Postdoctoral Fellow at Argonne National Laboratory. His research interest focuses on developing functional porous MOFs and other nanostructured materials for clean energy applications. |
 Hong-Cai Zhou | Hong-Cai “Joe” Zhou obtained his PhD in 2000 from Texas A&M University under the supervision of F. A. Cotton. After a postdoctoral stint at Harvard University with R. H. Holm, he joined the faculty of Miami University, Ohio in 2002. Since the fall of 2008, he has been a Professor of Chemistry at Texas A&M University. His research interest focuses on hydrogen/methane storage and gas separation that are relevant to clean energy technologies. |
1. Introduction
Emerging as a new type of porous materials, porous metal–organic frameworks (MOFs), also known as porous coordination polymers, have been one of the fastest growing fields in chemistry during the past decade.1 Porous MOFs are highly crystalline inorganic–organic hybrids, and they are constructed by assembling metal-containing clusters known as secondary building units (SBUs) with multidentate organic ligands (such as carboxylates, tetrazolates, sulfonates) via coordination bonds into a three-dimensional structure.2,3 The drive behind the rapid development of this field lies in the superior characteristics and properties of porous MOFs4 compared to traditional inorganic zeolites and porous carbon materials5 as well as their wide applications in catalysis,6 magnetism,7 luminescence,8 and particularly in gas storage9/separation.10Under the concept of “reticular synthesis”,11,12 the pore sizes of porous MOFs can be easily tuned from several angstroms to a few nanometers just by controlling the length of the organic ligands.13 In addition, their pore walls can also be functionalized for specific applications via ligand design.14–17 These two aspects, however, are usually hardly attainable in inorganic zeolites and porous carbon materials.5
The most intriguing characteristic of porous MOFs is their exceptional specific surface area.14 Landmarks in this respect are MOF-177 with a high surface area of 5640 m2/g18 followed by MIL-101 having an even higher surface area of 5900 m2/g,19 and the current record for surface area is held by UMCM-2 which possesses an exceptional surface area of over 6000 m2/g.20 The unprecedentedly high surface areas of porous MOFs make them stand out from other porous materials, and the nanospace inside their frameworks allows them to efficiently trap various gas molecules. This also pushes porous MOFs to the frontier of clean energy research, which has been particularly driven by the increasing threat of global warming together with decreasing stockpiles of fossil oil.
The aim of this feature article is to summarize recent developments in porous MOFs for clean energy applications, which include hydrogen storage, methane storage and carbon dioxide capture.
2. Hydrogen storage in porous MOFs
Hydrogen has long been considered an ideal clean energy carrier because of its ubiquitous merits. It is carbon free, and oxidation of hydrogen in an engine or fuel cell releases only water as a byproduct thus generating “zero emission”. In addition, it has an almost inexhaustible resource of water. Moreover, hydrogen has a high energy density which can nearly triple that of gasoline per mass unit; and in addition the performance of fuel cells is more than twice as efficient as that of internal combustion engines.21,22Despite the attractive concept of “Hydrogen Economy” on the basis of replacing current fossil oil powered vehicles with clean hydrogen fuel cell driven ones, the biggest bottleneck for its success lies in the lack of a safe, efficient, and economical on-board hydrogen storage system.23 It has been claimed that if a breakthrough in hydrogen storage could be realized, a complementary impetus would be applied to resolving other issues of hydrogen production and delivery.23 Several years ago, the US Department of Energy (DOE) set a number of very aggressive targets for the hydrogen storage system (including the container and necessary components): 6.0 wt% or 0.045 kg/L by the year 2010, and 9.0 wt% or 0.081 kg/L by the year 2015 at near-ambient temperatures and applicable pressures. Additionally, hydrogen adsorption and desorption should be totally reversible and the refueling of hydrogen should be completed within minutes.24,25 By noting that the density of liquid hydrogen is 0.0708 kg/L, the achievement of those targets is absolutely intimidating if not impossible.23 In February 2009, DOE revised the targets as shown in Table 1. By 2010, the target for system gravimetric capacity is lowered to 0.045 kg/kg, and that for system volumetric capacity is lowered to 0.028 kg/L; by 2015, the system gravimetric storage target is 0.055 kg/kg coupled with the volumetric one of 0.040 kg/L; the ultimate targets are 0.075 kg/kg and 0.070 kg/L for gravimetric storage and volumetric storage, respectively. In addition, the lifetime of the storage system is targeted at 1000 cycles by 2010, and it needs to be improved to 1500 cycles as the ultimate number by 2015; the storage (or delivery) temperature should range from −40 to 85 °C, and the storage (or delivery) pressure should be less than 100 bar.26 It must be borne in mind that those targets are for the entire storage system, meaning the performance of a storage material must be even higher in order to account for the storage container and other necessary components.27 Another important criterion for on-board hydrogen storage, which has not been adopted by DOE yet but should be worthy of attention, is the deliverable H2 storage capacity, which can be defined as the deliverable amount of H2 assuming that recharge starts at 1.5 bar of pressure.28,29
| Storage Parameters | Units | 2010 | 2015 | Ultimate |
|---|---|---|---|---|
| System Gravimetric Capacity (net useful energy/max. system mass) | kg H2/kg system | 0.045 | 0.055 | 0.075 |
| System Volumetric Capacity (net useful energy/max. system volume) | kg H2/L system | 0.028 | 0.040 | 0.070 |
| Min./max. delivery temperature | °C | −40/85 | −40/85 | −40/85 |
| Cycle life (1/4 tank to full) | Cycles | 1000 | 1500 | 1500 |
| Max. delivery pressure from storage system | Atm (abs) | 100 | 100 | 100 |
| System fill time (for 5 kg H2) | min | 4.2 | 3.3 | 2.5 |
Since the first report of hydrogen adsorption on a porous MOF in 2003,30 about 200 porous MOFs have been evaluated as physi-sorbents for hydrogen storage applications and they have shown superior performances compared to other porous materials.23,31–36 Great efforts have been dedicated to the exploration of various strategies to enhance hydrogen uptake in porous MOFs at 77 K and 1 atm, and these studies can be very useful and instructive at this early stage of exploration for hydrogen storage materials.27,31–36 However, DOE targets for hydrogen storage are for systems operating at near-ambient temperatures and high pressures,23 and herein we will mainly summarize the current status of high-pressure hydrogen storage in porous MOFs.
In high-pressure studies, two concepts, excess and absolute (or total) adsorption, are frequently used to describe hydrogen adsorption in porous MOFs.21,22,27 In brief, excess adsorption is the amount of adsorbed gas interacting with the frameworks, whereas absolute (or total) adsorption is the amount of gas both interacting with the frameworks and staying in pores in the absence of gas–solid interaction.37 The majority of the experimental adsorption data reported in the literature are excess adsorption isotherms. From the viewpoint of hydrogen storage, however, the total amount that a material can store or its absolute adsorption is also an important criterion. Fortunately, the framework density of a porous MOF derived from single crystal X-ray diffraction data allows the estimation of its absolute adsorption capacity based on the excess adsorption data. Nevertheless, it is important to note that the framework density is the ideally maximum packing density of a porous MOF material, and the mass and volume of a storage tank must be taken into account as well for determining the overall density of a storage system in real applications.27 It should also be noted that the units for revised DOE gravimetric targets are in units of mass/mass instead of the previous wt%. The unit of wt%, which should be equal to (mass H2)/(mass sample + mass H2), has unfortunately been frequently misused by neglecting the second term in the determinator leading to complications in comparing hydrogen uptake capacities of different materials.27 Thus, it is highly recommended that the DOE revised targets’ units of kg/kg and kg/L be used for gravimetric capacity and volumetric capacity, respectively, when reporting hydrogen uptakes in porous materials either of excess adsorption or absolute (or total) adsorption.
Current research on high-pressure hydrogen storage on porous MOFs has been focused at a liquid nitrogen temperature of 77 K, at which the excess uptake usually can reach saturation in the pressure range of 20 to 80 bar.27,31,36 Assuming cryogenic hydrogen-storage could be adopted in near-term mobile applications, as enumerated in Table 2, more than twenty reported porous MOFs could achieve or even surpass the values of DOE 2010 targets for both gravimetric and volumetric system storage, and some even would have the potential to meet the values of 2015 targets when total adsorption capacities are considered.
| Compoundsa | Surface area (m2/g) | P/bar Excess (Absolute) | Gravimetric H2 uptake (kg/kg) | Volumetric H2 uptake (kg/L) | Ref. | |||
|---|---|---|---|---|---|---|---|---|
| BET | Langmuir | Excess | Absolute | Excess | Absolute | |||
| a abtc4− = azobenzene-3,3′,5,5′-tetracarboxylate; adip4− = 5,5′-(9,10-anthracenediyl)di-isophthalate; adc2− = 9,10-anthracenedicarboxylate; aobtc4− = azoxybenzene-3,3′,5,5′-tetracarboxylate; bdc2− = 1,4-benzenedicarboxylate; BDP2− = 1,4-benzenedipyrazolate; bhtc3− = biphenyl-3,4′,5-tricarboxylate; bpdc2− = 4,4′-biphenyldicarboxylate; bpe = 4,4′-trans-bis(4-pyridyl)-ethylene; bpndc2− = benzophenone-4,4′-dicarboxylate; bptc4− = 3,3′,5,5′-biphenyltetracarboxylate; bpy = 4,4′-bipyridine; H3BTB = 1,3,5-tri(4-carboxyphenyl)benzene; BTC = benzenetricarboxylate; BTT3− = 1,3,5-benzenetristetrazolate; dabco = 1,4-diazabicyclo[2.2.2]octane; dbdc2− = 1,2-dihydrocyclobutabenzene-3,6-dicarboxylate; H4dhtp = 2,5-dihydroxyterephthalic acid; DMF = N,N′-dimethylformamide; FMA2− = fumarate; hpdc2− = 4,5,9,10-tetrahydropyrene-2,7-dicarboxylate; MeIM− = 2-methylimidazole; NDC2− = 2,6-naphthalenedicarboxylate; oxdc2− = oxydiacetate; pbpc2− = pyridine-3,5-bis(phenyl-4-carboxylate); qptc4− = quaterphenyl-3,3‴,5,5‴-tetracarboxylate; sbtc4− = trans-stilbene-3,3′,5,5′-tetracarboxylic acid; tatb3− = 4,4′,4″-s-triazine-2,4,6-triyltribenzoate; T2DC = thieno[3,2-b]thiophene-2,5-dicarboxylate; tptc4− = terphenyl-3,3″,5,5″-tetracarboxylate; H3tpb-3tz = 1,3,5-tri-p-(tetrazol-5-yl)phenylbenzene; H3tpt-3tz = 2,4,6-tri-p-(tetrazol-5-yl)phenyl-s-triazine; trz− = 1,2,4-triazolate; ttdc2− = thieno[3,2-b]thiophene-2,5-dicarboxylate; ttpm4− = tetrakis(4-tetrazolylphenyl)methane; ttca = triphenylene-2,6,10-tricarboxylate. | ||||||||
| Ag2[Ag4(trz)6], FMOF-1 | 810 | 77 | 0.0233 | 0.041 | 38 | |||
| Al(OH)(BDC), MIL-53 (Al) | 1100 | 1590 | 16 | 0.038 | 0.037 | 39 | ||
| Cr(OH)(BDC), MIL-53 (Cr) | 1100 | 1500 | 16 | 0.031 | 39 | |||
| Cr3OF(BTC)2, MIL-100 | 2700 | 90 | 0.0328 | 0.023 | 40 | |||
| Cr3OF(BDC)3, MIL-101 | 5900 | 80 | 0.061 | 0.0261 | 40 | |||
| Co(BDP) | 2670 | 30 | 0.031 | 41 | ||||
| Co2(BDC)2(dabco) | 1595 | 2120 | 44 | 0.0411 | 42 | |||
| HCu[(Cu4Cl)3(BTT)8], Cu-BTT | 1710 | 1770 | 30 (90) | 0.042 | 0.057 | 0.038 | 0.053 | 43 |
| Cu(dccptp)(NO3) | 268 | 20 | 0.0191 | 0.0239 | 44 | |||
| Cu2(abtc), SNU-5 | 2850 | 50(50) | 0.0522 | 0.0676 | 0.0378 | 0.0458 | 45 | |
| Cu2(abtc), JUC-62 | 40 | 0.0471 | 0.0384 | 46 | ||||
| Cu2(aobtc), PCN-10 | 1407 | 1779 | 45(45) | 0.042 | 0.0523 | 0.0322 | 0.0392 | 47 |
| Cu2(sbtc), PCN-11 | 1931 | 2442 | 45(45) | 0.0504 | 0.0597 | 0.0378 | 0.0447 | 47 |
| Cu2(adip), PCN-14 | 1753 | 2176 | 45 | 0.0442 | 0.0366 | 48 | ||
| Cu2(BDC)2(dabco) | 1300 | 1703 | 33.7 | 0.027 | 42 | |||
| Cu2(bpndc)2(bpy), SNU-6 | 2910 | 70(70) | 0.0487 | 0.1 | 0.0154 | 0.0316 | 49 | |
| Cu2(bptc), MOF-505 | 1670 | 1830 | 20 | 0.0402 | 0.0373 | 50 | ||
| Cu2(qptc), NOTT-101 | 2247 | 20 (60) | 0.0607 | 0.06 | 0.0411 | 0.0431 | 50 | |
| Cu2(tptc), NOTT-102 | 2942 | 20 (60) | 0.0606 | 0.072 | 0.0436 | 0.0423 | 50 | |
| Cu2(C26O8H12), NOTT-103 | 2929 | 20 (60) | 0.0651 | 0.0778 | 0.05 | 51 | ||
| Cu2(C30O8H14), NOTT-110 | 2960 | 55 (55) | 0.0543 | 0.0762 | 0.0468 | 52 | ||
| Cu2(C30O8H16), NOTT-111 | 2930 | 48 (48) | 0.0547 | 0.0736 | 0.0454 | 52 | ||
| Cu3(tdbb), NOTT-112 | 3800 | 40 (77) | 0.0707 | 0.1 | 0.0503 | 53 | ||
| Cu3(bhtc)2, UMCM-150 | 2300 | 3100 | 45 | 0.057 | 0.036 | 54 | ||
| Cu3(BTC)2, HKUST-1 | 1154 | 1958 | 50 | 0.036 | 55 | |||
| Cu3(tatb)2 (catenated), PCN-6 | 3800 | 50 (50) | 0.072 | 0.095 | 0.0402 | 0.0528 | 29 | |
| Cu3(tatb)2 (non-catenated), PCN-6′ | 2700 | 50 (50) | 0.042 | 0.058 | 0.0118 | 0.0162 | 29 | |
| Cu3(ttca)2, PCN-20 | 3525 | 4237 | 50 | 0.062 | 56 | |||
| Cu3[(Cu4Cl)3(tpb-3tz)8]2·11CuCl2 | 1120 | 1200 | 30 | 0.028 | 57 | |||
| Cu4(TTPM)2·0.7CuCl2 | 2560 | 2745 | 20 (70) | 0.041 | 0.056 | 0.041 | 58 | |
| Cd3(bpdc)3, JUC-48 | 880 | 40 | 0.028 | 0.02 | 59 | |||
| Fe3(OH)(pbpc)3 | 1200 | 20 | 0.0305 | 0.0331 | 60 | |||
| Mn3[(Mn4Cl)3(tpt-3tz)8]2 | 1580 | 1700 | 25 (80) | 0.037 | 0.045 | 0.037 | 57 | |
| Mn3[(Mn4Cl)3(BTT)8]2, Mn-BTT | 2100 | 50 (90) | 0.051 | 0.069 | 0.06 | 61 | ||
| Ni(dhtp)2 | 1083 | 70 | 0.018 | 62 | ||||
| Ni3(OH)(pbpc)3 | 1553 | 20 | 0.0415 | 0.0439 | 60 | |||
| Ni3O(adc)3·2(C4H10NO+), PCN-19 | 723 | 823 | 48 (48) | 0.0167 | 0.022 | 0.0159 | 0.021 | 63 |
| Sm2Zn3(oxdc)6 | 719 | 34 | 0.0119 | 0.0186 | 64 | |||
| Zn(MeIM)2, ZIF-8 | 1630 | 1810 | 55 | 0.0301 | 65 | |||
| Zn2(abtc)(DMF)2, SNU-4 | 1460 | 50 | 0.037 | 45 | ||||
| Zn(NDC)(bpe)0.5 | 303 | 40 | 0.02 | 66 | ||||
| Zn2(dhtp), MOF-74, COP-27-Zn | 950 | 1072 | 26 | 0.0221 | 0.0276 | 67 | ||
| Zn2(BDC)2(dabco) | 1165 | 1488 | 83.2 | 0.0317 | 42 | |||
| Zn4O(FMA)3 | 1120 | 1618 | 39 | 0.052 | 68 | |||
| Zn4O(BDC)3, MOF-5, IRMOF-1 | 3800 | 4400 | 40 (100) | 0.076 | 0.1 | 0.0421 | 0.066 | 69 |
| Zn4O(BTB)3, MOF-177 | 4750 | 5640 | 66 (72) | 0.076 | 0.112 | 0.032 | 0.048 | 28 |
| Zn4O(dbdc)3, IRMOF-6 | 2804 | 3305 | 45 | 0.0463 | 0.0317 | 67 | ||
| Zn4O(hpdc)3, IRMOF-11 | 1984 | 2337 | 33.7 | 0.034 | 0.0267 | 67 | ||
| Zn4O(NDC)3, IRMOF-8 | 1818 | 15 | 0.036 | 0.0209 | 70 | |||
| Zn4O(ttdc)3, IRMOF-20 | 4024 | 4593 | 77.6 | 0.0625 | 0.0341 | 67 | ||
| Zn4O(T2DC)(BTB)4/3, UMCM-2 | 5200 | 6060 | 46 | 0.0688 | 20 | |||
Existing studies have revealed that the gravimetric excess hydrogen saturation uptakes of porous MOFs at 77 K generally scale up with their Langmuir surface areas, and it is also widely recognized that a high surface area is the first prerequisite for cryogenic hydrogen-storage application of porous MOFs.21,22,27,31–36 Nonetheless, high surface area is not the sole factor determining high hydrogen uptake capacity of a porous MOF. For example, MOF-5 with a Langmuir surface area of 4400 m2/g exhibits a record excess hydrogen uptake of 0.076 kg/kg at saturation,69 which is much higher than MIL-101 (0.061 kg/kg)40 and UMCM-2 (0.069 kg/kg)20 although they have much larger surface areas of close to 6000 m2/g. Another example is a recently reported copper porous MOF, PCN-6, which can adsorb 0.072 kg/kg hydrogen at 77 K and 50 bar despite its relatively lower Langmuir surface area of 3800 m2/g.29 Particularly, in terms of volumetric hydrogen uptake, high surface area does not guarantee a high volumetric storage density. This is because a porous MOF with a very high surface area usually has low framework density, which decreases the volumetric uptake in spite of its high gravimetric uptake value.27 A typical example is MOF-177, which at 77 K has a maximal excess gravimetric uptake of 0.076 kg/kg and an exceptional total capacity of 0.112 kg/kg at 78 bar benefiting from its high Langmuir surface area of 5640 m2/g.28 Its low crystallographic density of 0.427 g cm−3, however, leads to the volumetric storage densities of just 0.032 kg/L (excess) and 0.048 kg/L (total),28 which are significantly lower than those of PCN-6 (0.042 kg/L for excess uptake and 0.053 kg/L for total uptake at 77 K, 50 bar) despite the much lower surface area of PCN-6 compared to MOF-177.29 A compromise between the surface area and crystal density should be met when seeking porous MOFs with both high gravimetric and volumetric hydrogen uptakes.21,22 This necessitates more extensive and insightful studies of hydrogen adsorption in porous MOFs to elucidate structure–performance correlations.27 Taking advantage of the single crystallinity of porous MOFs, computational methods have played a useful role in this aspect.71 For detailed understanding of the location of H2 and the energetics of H2-framework interactions within porous MOFs, however, one can turn to neutron diffraction and inelastic neutron scattering (INS), respectively.27,29,72–74
Single-crystal neutron diffraction studies of MOF-5 indicated two hydrogen-binding sites, one higher-energy site over the center of the Zn4(μ4-O)(CO2)8 SBU and a second site over the face of a ZnO4 tetrahedron.75 This is in agreement with neutron powder diffraction studies76 on MOF-5, which located two additional sites with the increase of D2 loading: one above the oxygen atoms of the carboxylate group and the other over the phenyl ring of the BDC ligand. Neutron powder diffraction studies on a D2-loaded HKUST-177 sample identified six distinct D2 adsorption sites within the nanoporous structure, as shown in Fig. 1. The first occupied and highest-energy site resides at the axial sites of the dinuclear Cu center, and the remaining sites are located near the benzene ring and carboxylate moieties of the ligand, which are occupied progressively. The short Cu⋯H2 distance of 2.39 Å at 4 K indicates appreciable interaction between a dihydrogen molecule and the d9 Cu(II) center. Generally, the neutron diffraction studies agree with the INS experiments performed on the same materials, all revealing that the hydrogen molecules will occupy the sites around the inorganic metal cluster first. As a complementary tool to neutron diffraction, INS29,30,72–74 can provide useful information on the energetics of H2-framework interactions in addition to identifying the specific hydrogen binding sites. INS studies on MOF-530 and HKUST-173 have revealed that the metal centers have higher hydrogen binding energy than the organic linkers.21,22,36
![D2 binding sites in HKUST-1, identified via neutron powder diffraction, numbered in order of occupation with increased D2 loading. Top: shown along [001] direction (left) and [111] direction (right). Bottom: axial Cu(ii) paddlewheel UMC site (left), along [111] direction in the 5 Å small pore with 3.5 Å side windows (middle), and along [100] direction showing the 9 Å pore. Reprinted with permission from ref. 77. Copyright 2006, American Chemical Society.](/image/article/2010/CC/b916295j/b916295j-f1.gif) | ||
| Fig. 1 D2 binding sites in HKUST-1, identified via neutron powder diffraction, numbered in order of occupation with increased D2 loading. Top: shown along [001] direction (left) and [111] direction (right). Bottom: axial Cu(II) paddlewheel UMC site (left), along [111] direction in the 5 Å small pore with 3.5 Å side windows (middle), and along [100] direction showing the 9 Å pore. Reprinted with permission from ref. 77. Copyright 2006, American Chemical Society. | ||
Unfortunately, at non-cryogenic temperatures, the interaction energy of just a few kJ/mol between the frameworks and the dihydrogen molecules within porous MOFs is overwhelmed by the thermal energy of the hydrogen gas resulting in very low hydrogen uptake at room temperature even under high pressure.21,22 As indicated in Table 3, reports of high-pressure hydrogen storage in porous MOFs at room temperature to date are still far away from DOE targets.
| Compoundsa | Surface area (m2/g) |
P/bar
Excess (Absolute) |
Gravimetric H2 uptake (kg/kg) | Volumetric H2 uptake (kg/L) | Ref. | |||
|---|---|---|---|---|---|---|---|---|
| BET | Langmuir | Excess | Absolute | Excess | Absolute | |||
| a aobtc4− = azoxybenzene-3,3′,5,5′-tetracarboxylate; bdc2− = 1,4-benzenedicarboxylate; H3BTB = 1,3,5-tri(4-carboxyphenyl)benzene; BTC = benzenetricarboxylate; BTT3− = 1,3,5-benzenetristetrazolate; dabco = 1,4-diazabicyclo[2.2.2]octane; H4dhtp = 2,5-dihydroxyterephthalic acid; dcdBn2− = 6,6′-dichloro-2,2′-dibenzyloxy-1,1′-binaphthyl-4,4′-dibenzoate; dcdEt2− = 6,6′-dichloro-2,2′-diethoxy-1,1′-binaphthyl-4,4′-dibenzoate; H2hfipbb = 4,4-(hexafluoroisopropylidene)bis(benzoic acid); NDC2− = 2,6-naphthalenedicarboxylate; oxdc2− = oxydiacetate; sbtc4− = trans-stilbene-3,3′,5,5′-tetracarboxylic acid; tatb3− = 4,4′,4″-s-triazine-2,4,6-triyltribenzoate. | ||||||||
| Cr3OF(BTC)2, MIL-100 | 2700 | 90 | 0.0015 | 0.00104 | 40 | |||
| Cr3OF(BDC)3, MIL-101 | 5900 | 80 | 0.0043 | 0.00184 | 40 | |||
| Co2(BDC)2(dabco) | 1595 | 2120 | 100 | 0.0032 | 42 | |||
| HCu[(Cu4Cl)3(BTT)8], Cu-BTT | 1710 | 1770 | (80) | 0.0046 | 43 | |||
| Cu2(aobtc), PCN-10 | 1407 | 1779 | 45 | 0.0025 | 47 | |||
| Cu2(sbtc), PCN-11 | 1931 | 2442 | 45 | 0.0034 | 47 | |||
| Cu2(BDC)2(dabco) | 1300 | 1703 | 100 | 0.0042 | 42 | |||
| Cu3(BTC)2, HKUST-1 | 1154 | 1958 | 65 | 0.0035 | 55 | |||
| Cu3(tatb)2 (catenated), PCN-6 | 3800 | 50 (50) | 0.0093 | 0.015 | 29 | |||
| Cu3(tatb)2 (non-catenated), PCN-6′ | 2700 | 50 (50) | 0.004 | 0.081 | 29 | |||
| Cu(hfipbb)(h2hfipbb)0.5 | 1120 | 1200 | 48 | 0.010 | 0.0147 | 78 | ||
| Mn3[(Mn4Cl)3(BTT)8]2, Mn-BTT | 2100 | (90) | 0.0094 | 0.0079 | 61 | |||
| Ni(dhtp)2 | 1083 | 70 | 0.003 | 62 | ||||
| Sm2Zn3(oxdc)6 | 719 | 35 | 0.0054 | 0.0084 | 64 | |||
| Zn4O(BDC)3, MOF-5, IRMOF-1 | 3800 | 4400 | (100) | 0.0057 | 69 | |||
| Zn4O(NDC)3, IRMOF-8 | 1818 | 30 | 0.004 | 0.00232 | 70 | |||
| Zn4O(dcbBn)3 | 396 | 48 | 0.0098 | 79 | ||||
| Zn4O(dcdEt)3 | 502 | 48 | 0.0112 | 79 | ||||
| IRMOF-1 + Pt/AC | 100 | 0.03 | 80 | |||||
| IRMOF-8 + Pt/AC | 100 | 0.04 | 80 | |||||
A desired binding energy of ca. 20 kJ/mol in the overall hydrogen loading range has been proposed for room temperature hydrogen storage.27,81 Ongoing efforts have been devoted to exploiting viable means to increase hydrogen adsorption enthalpies in porous MOFs with attention particularly drawn to the introduction of coordinatively unsaturated metal centers (UMCs) on the surfaces.23,27,31,58,82–84 This method has been proved very attractive in enhancing the adsorption enthalpies. Recent systematic investigation85 of hydrogen affinities of different UMCs in a series of isomorphous structures revealed that open nickel centers possess the highest hydrogen binding energy compared to other first transition metals and magnesium. Although high adsorption enthalpies up to 13.5 kJ/mol have been achieved in some porous MOFs at very low hydrogen coverage,85 the adsorption enthalpies abruptly decline to 5–6 kJ/mol with the increase of hydrogen loadings and no significant improvement of hydrogen uptakes could be observed at room temperature under high pressure.27,31 In order to enhance the room temperature hydrogen storage capacities, it is believed that high concentrations of UMCs on the surfaces within porous MOFs must be generated, and this may require more rational design and some new synthetic methods in future development of porous MOFs.27,31,58
A very intriguing method recently reported for hydrogen adsorption enhancement at room temperature is the secondary hydrogen spillover. It comprises the dissociative chemisorption of hydrogen on a metal catalyst with the subsequent migration of atomic hydrogen to the surface of a carrier contacting the metal (primary hydrogen receptor) and then to the second carrier (secondary receptor).21,22,31 Li and Yang80 demonstrated that mechanically mixing 5% Pt on activated carbon with a MOF, followed by melting and subsequent carbonization of an amount of sucrose with the porous MOF, could give rise to materials with hydrogen adsorption capacities up to 0.03–0.04 kg/kg at 298 K and 10 MPa. Meanwhile, the hydrogen adsorption enthalpies were enhanced to 20–23 kJ/mol, which reaches the desired enthalpy of 20 kJ/mol. These results are very encouraging, and the secondary hydrogen spillover technique seems to show great potential for achieving the 2010 DOE gravimetric target of 0.045 kg/kg for hydrogen storage. However, the cost of expensive Pt casts a shadow on its widespead application in practice, and the search for alternative cheap catalysts to replace Pt deserves future efforts.
Nonetheless, to reach the 2015 and particularly the ultimate DOE targets for on-board hydrogen storage systems, there is still a long way to go for porous MOF materials.
3. Methane storage in porous MOFs
As with hydrogen, methane is also considered a clean energy gas. Compared to petroleum oil, it can provide much more energy because of its higher hydrogen-to-carbon ratio, and has much lower carbon emission. In addition, deposits of methane-containing natural gas are more widespread globally than those of petroleum oil, and its refinement (purification) to an energy fuel is much simpler than that of crude petroleum oil to gasoline or diesel fuels. Methane is also produced by decomposition of organic waste and by bacteria in the guts of ruminants and termites. In terms of near-term practical utilization and innovations necessary for commercialization, methane appears to be a more promising alternative for mobile applications.21,86Although compressed natural gas (CNG) vehicles already exist, current vehicles store the methane CNG in high-pressure (greater than 200 atm) tanks which are heavy and potentially explosive. To address the need for better methane-storage technology, the US DOE has set the target for methane storage systems at 180 v(STP)/v(STP equivalent of methane per volume of adsorbent material storage system) under 35 bar and near ambient temperature, with the energy density of adsorbed natural gas comparable to that of current CNG technology.21,87
The first reported measurement of methane uptake by a porous MOF could date back to as early as 1997 reported by Kitagawa and coworkers but with very limited methane uptake.88 However, the field of methane storage on MOFs has not developed as quickly as the hydrogen-storage field, and studies on methane storage in porous MOFs are far less numerous than hydrogen (Table 4).21
| Compoundsa | Surface area (m2/g) | P/bar | Excess gravimetric CH4 uptake (absolute), (cm3(STP)/g) | Excess volumetric CH4 uptake (absolute), (v(STP)/v) | Ref. | |
|---|---|---|---|---|---|---|
| BET | Langmuir | |||||
| a adip4− = 5,5′-(9,10-anthracenediyl)di-isophthalate; azpy = 4,4′-azopyridine; BDC2− = 1,4-benzenedicarboxylate; 4,4′-bpy = 4,4′-bipyridine; BTC = benzenetricarboxylate; dabco = 1,4-diazabicyclo[2.2.2]octane; dbdc2− = 1,2-dihydrocyclobutabenzene-3,6-dicarboxylate; H4dhtp = 2,5-dihydroxyterephthalic acid; 2,7-ndc = 2,7-naphthalenedicarboxylate; pia = N-(pyridin-4-yl)isonicotinamide; sbtc4− = trans-stilbene-3,3′,5,5′-tetracarboxylic acid. b Measured at 290 K. | ||||||
| Al(BDC)(OH), MIL-53-Al | 1500 | 35 | 155 | 100 | ||
| Cd2(azpy)3(NO3)4 | 36 | 40 | 60 | 89 | ||
| Cr(BDC)(OH), MIL-53-Cr | 1500 | 35 | 165 | 100 | ||
| Cr3OF(BTC)2, MIL-100 | 1900 | 2700 | 35 | 169 | 119 | 97 |
| Cr3OF(BDC)3, MIL-101 | 4230 | 5900 | 35 | 224 | 110 | 97 |
| Co2(BDC)2(dabco) | 1600 | 2300 | 35 | 171 | 140 | 101 |
| Co2(4,4′-bpy)2(NO3)4 | 30 | 56 | 88 | |||
| Co2(dhtp) | 35 | 149 | 174 | 99 | ||
| Cu2(BDC)2(dabco) | 1819 | 35 | 212 | 153 | 95 | |
| Cu2(sbtc), PCN-11 | 1931 | 2442 | 228 | 171 | 47 | |
| Cu2(adip), PCN-14b | 1753 | 2176 | 35 | 252 (264) | 220 (230) | 92 |
| Cu3(BTC)2, HKUST-1 | 1502 | 2216 | 36 | 200 | 109 | 96 |
| CuSiF6(4,4′-bpy) | 1337 | 36 | 146 | 159 | 102 | |
| Cu2(pia)2(NO3)4 | 31 | 65 | 103 | |||
| Mg2(dhtp) | 35 | 164 | 149 | 99 | ||
| Mn2(dhtp) | 35 | 146 | 158 | 99 | ||
| Ni2(dhtp) | 35 | 157 | 190 | 99 | ||
| Zn2(BDC)2(dabco) | 35 | 175 | 137 | 95 | ||
| Zn4O(BDC)3, MOF-5, | 2296 | 3840 | 36 | 135 | 13 | |
| Zn4O(dbdc)3, IRMOF-3 | 2446 | 3062 | 36 | 120 | 13 | |
| Zn4O(dbdc)3, IRMOF-6 | 2804 | 3305 | 36 | 240 | 155 | 13 |
| Zn9O3(2,7-ndc)6 | 901 | 1281 | 50 | 107 | 104 | |
| Zn2(dhtp) | 35 | 139 | 171 | 99 | ||
Different from hydrogen storage, the US DOE methane storage target is only for volumetric capacity in the unit of v(STP)/v.87 Nonetheless, gravimetric capacities in units of cm3/g or mmol/g have been frequently reported, and these values are very informative and useful for the exploration of high-capacity methane storage materials. To date, the reported volumetric storage capacity of a porous MOF is usually calculated from the gravimetric value using the crystallographic density of the material.
As in the case of hydrogen storage, a variety of factors influence the ability of porous MOFs to adsorb methane, such as surface areas, pore sizes, ligand functionalization, and heat of adsorption etc.21 For example, the contribution of interpenetration was demonstrated by Kitagawa and coworkers for a series of azopyridine-based MOFs, with the highest of the series adsorbing ∼60 v(STP)/v.89
The ability of IRMOF-6 to uptake a higher amount of methane compared to the other members of the IRMOF series was ascribed to both the high accessible surface area and the functionality of the ligand: in IRMOF-6, the phenyl ring of the typical bdc ligand was modified to generate 1,2-cyclobutane-3,6-benzenedicarboxylate. The resulting porous MOF was found to adsorb 155 v(STP)/v (or 240 cm3/g) methane at 298 K and 36 atm,13 significantly higher than any zeolite material or any other porous MOF at the time, particularly in terms of gravimetric capacity. Theoretical simulations90 indicated that further functionalization of the ligand by insertion of an anthracene ring would improve methane uptake further, perhaps within reach of the DOE goal. Attempts to synthesize this proposed porous MOF, however, resulted in a material with very limited methane uptake, due to the ultramicroporous nature of the porous MOF, with pores too small to accommodate methane molecules.91
Recently, our research group21 endeavored to continue to pursue this proposed anthracene-based porous MOF with high methane uptake; in an effort to triumph over the problems associated with extremely small pores, the ligand was extended by adding additional phenyl rings to form 5,5′-(9,10-anthracenediyl)-diisophthalate (adip). The resulting porous MOF, dubbed PCN-14, was found to contain nanoscopic cages of a size (Fig. 2) suitable for methane accommodation, with an absolute uptake capacity of 230 v(STP)/v(excess: 220 v(STP)/v) 28% higher than the US DOE target, at 290 K and 35 bar. Additionally, the heat of adsorption of methane on the framework is ∼30 kJ/mol, higher than any other reported porous MOF—this indicates the validity of using ΔHads as a benchmark for evaluating potential saturation uptake at room temperature. PCN-14 holds the current record for methane storage, and represents the first case surpassing the US DOE target for porous MOFs.92
 | ||
| Fig. 2 Nanoscopic cages in PCN-14. Reprinted with permission from ref. 92. Copyright 2008, American Chemical Society. | ||
Although in 2001 Seki claimed an estimated value of 225 v(STP)/v for a copper porous MOF which has a gravimetric capacity of 213 cm3(STP)/g,93 the number was miscalculated and the corrected one was supposed to be 213 × 0.983 (the apparent density) = 209 v(STP)/v. Nonetheless, the volumetric value of 209 v(STP)/v is still much overestimated, because the apparent density, 0.983 g/cm3, of the primary particles calculated from the mercury porosimetry result is much higher than its real crystallographic framework density.94 The copper porous MOF is isostructural with Cu2(bdc)2(dabco) which has a BET surface area of 1891 m2/g, a pore volume of 0.70 cm3/g, and crystal density of 0.87 g/cm3,95 and the extension from benzene dicarboxylate ligand to the longer styrene dicarboxylate ligand results in its much higher BET surface area of 3265 m2/g and pore volume of 1.26 cm3/g.93,94 It can be inferred that its crystal density should be much lower than that of Cu2(bdc)2(dabco), and a gravimetric capacity of 175 v(STP)/v could be estimated assuming it has a crystal density of 0.80 g/cm3.
It is worth noting that the volumetric capacity of a porous MOF calculated from the gravimetric value by using its crystallographic density is the ideally maximium number it can reach in reality, because the crystallographic density is higher than the effective packing density of the material due to the voids between the particles caused by particle packing. Nevertheless, packing efficiencies of over 90% have recently been demonstrated for some porous MOFs in methane storage studies.96 Assuming a packing efficiency of 90% could be achieved for PCN-14 in real application, its absolute methane storage capacity is then lowered to 207 v(STP)/v. However, this value still makes it stand out from other porous materials, and promises porous MOFs great potential for on-board methane storage application.21
Reports of methane storage in porous MOFs to date indicate that high surface area is necessary but not a decisive factor for high methane storage either in volumetric capacity or gravimetric capacity. For example, PCN-14 with a Langmuir surface area of 2176 m2/g has by far the highest excess volumetric methane uptake capacity of 220 v(STP)/v corresponding to a gravimetric value of 252 cm3/g at 290 K, 35 bar;93 in contrast, under similar conditions, the excess volumetric capacity of MIL-101 which has an exceptionally high Langmuir surface area of 5900 m2/g is just about 110 v(STP)/v and the gravimetric value is about 224 cm3/g,97 both of which are lower than those of PCN-14.
The locations of methane adsorption sites together with methane-framework interactions in porous MOFs have recently been elucidated by neutron powder diffraction studies of CD4 adsorption in MOF-598 and a series of isomorphous porous MOFs with different UMCs.99 Information derived from these studies is very instructive for future design of new porous MOFs with high methane storage capacities. However, to further illustrate structure–performance correlations, systematic investigation of the effects of other factors such as pore size, ligand functionalization etc. on methane uptakes in porous MOFs is still needed, and this demands more studies to screen existing porous MOFs as well as to develop more new structures.
4. Carbon dioxide capture in porous MOFs
The concern of global warming has drawn unprecedented public attention to the issue of CO2 emission. Carbon dioxide, generated mainly through combustion of fossil fuel, accumulates at an alarming pace due to the rapid expansion of the energy consumption worldwide. To stabilize CO2 levels in the atmosphere, it is imperative to develop viable carbon dioxide capture and sequestration technologies. Current technologies are dominated by amine-based web-scrubbing systems, which are costly and inefficient.105 Adsorption of CO2 using highly porous solids has been of increasing interest for carbon dioxide capture applications,106 and porous MOFs have been positioned at the forefront due to their high surface areas together with functionalizable pore walls.14The seminal work107 by Yaghi et al. revealed that CO2 uptakes in porous MOFs scale up with their surface areas, and MOF-177 with a high Langmuir surface area of 5640 m2/g could surpass the benchmark materials zeolites 13X and activated carbon MAXSORB by a factor of over 1.5 in both gravimetric and volumetric capcities (Fig. 3). A record capacity of 40 mmol/g or 390 cm3(STP)/cm3 has been achieved in NH4F-treated MIL-101 with an even higher surface area of 5900 m2/g.97
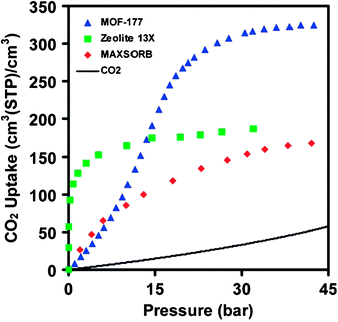 | ||
| Fig. 3 Comparison of the volumetric CO2 capacity of MOF-177 relative to zeolite 13X pellets, MAXSORB carbon powder, and pressurized CO2. Reprinted with permission from ref. 107. Copyright 2005, American Chemical Society. | ||
Although MOF-177 and MIL-101 have comparable surface areas and carbon dioxide uptake capacities, the shapes of their CO2 adsorption istherms are quite different. MOF-177 presents a sigmoid shape, but MIL-101 does not.14 The usual shape of the CO2 adsorption isotherm in MOF-177 and some other porous MOFs can be attributed to attractive electrostatic interactions between CO2 molecules together with changes in the porous MOF crystal structure as illustrated by a recent theoretical simulation.108
To enhance CO2 uptake in porous MOFs, the incorporation of pendant alkylamine functionalities within the pores has recently been pursued either by the direct use of an amine-based bridging ligand,109 or via postsynthetic approaches110 which can be achieved by covalently modifying a bridging ligand or grafting an alkylamine functionality onto a UMC. This latter strategy has been proved an effective way to improve CO2 adsorption capacity as well as to increase CO2 binding energy in porous MOFs.111
No doubt, results reported thus far (Table 5) have demonstrated that porous MOFs are superior to conventional inorganic zeolites and activated carbons in CO2 uptake,97 and also pioneered them as the most promising sorbent-based candidates for carbon dioxide capture application.
| Compoundsa | Surface area (m2/g) | P/bar | Excess gravimetric CO2 uptake (mmol/g) | Excess volumetric CO2 uptake (cm3/cm3) | Ref. | |
|---|---|---|---|---|---|---|
| BET | Langmuir | |||||
| a BDC2− = 1,4-benzenedicarboxylate; 4,4′-bpy = 4,4′-bipyridine; BTC = benzenetricarboxylate; dbdc2− = 1,2-dihydrocyclobutabenzene-3,6-dicarboxylate; 2,7-ndc = 2,7-naphthalenedicarboxylate; H3BTB = 1,3,5-tri(4-carboxyphenyl)benzene. b Measured at 302 K. c Measured at 304 K. | ||||||
| Al(BDC)(OH), MIL-53-Alb | 1500 | 25 | 10 | 225 | 100 | |
| Cr(BDC)(OH), MIL-53-Crb | 1500 | 25 | 10 | 225 | 100 | |
| Cr3OF(BTC)2, MIL-100c | 1900 | 50 | 18 | 280 | 97 | |
| Cr3OF(BDC)3, MIL-101c | 4230 | 5900 | 50 | 40 | 390 | 97 |
| V(BDC)(O), MIL-47b | 1500 | 20 | 111 | 250 | 100 | |
| Zn4O(BDC)3, IRMOF-1, | 2296 | 3840 | 35 | 21.7 | 290 | 107 |
| Zn4O(dbdc)3, IRMOF-6 | 2804 | 3305 | 40 | 19.8 | 286 | 107 |
| Zn9O3(2,7-ndc)6 | 901 | 1281 | 50 | 171 | 104 | |
| Zn4O(BTB)3, MOF-177 | 4750 | 5640 | 42 | 33.5 | 320 | 107 |
5. Conclusions
As a relatively new class of materials, porous MOFs will continue to draw interest and inquiry by both academia and industry. They have shown great promise for the adsorptive storage of hydrogen, methane, and carbon dioxide in clean energy applications. The emerging ability to tune pore size and pore wall functionality allows researchers to focus on those factors which hold the most promise, increasing both the volume available for storage and the affinity of the network for the stored gas molecules. Particularly, as alternative clean fuels such as hydrogen and methane continue to be developed in automotive and other applications and as the emission of carbon dioxide won’t be reduced significantly in the short term, the need for effective storage technologies will continue to increase, and porous MOFs are well-positioned to play an important role at the forefront of this research.Acknowledgements
S. Ma acknowledges the Director’s Postdoctoral Fellowship from Argonne National Laboratory for the support of this work. H.-C. Zhou acknowledges financial support from the Department of Energy (DE-FC36-07GO17033) and the National Science Foundation (CHE-0449634) for this work.Notes and references
- J. R. Long and O. M. Yaghi, Chem. Soc. Rev., 2009, 38, 1213–1214 RSC.
- M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319–330 CrossRef CAS.
- D. J. Tranchemontagne, J. L. Mendoza-Cortes, M. O'Keeffe and O. M. Yaghi, Chem. Soc. Rev., 2009, 38, 1257–1283 RSC.
- S. Kitagawa, R. Kitaura and S.-i. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375 CrossRef CAS.
- M. E. Davis, Nature, 2002, 417, 813–821 CrossRef CAS.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450–1459 RSC.
- M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379 RSC.
- M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330–1352 RSC.
- R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966–4981 CrossRef.
- J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS.
- M. O'Keeffe, Chem. Soc. Rev., 2009, 38, 1215–1217 RSC.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef.
- G. Férey, Chem. Soc. Rev., 2008, 37, 191–214 RSC.
- M. P. Suh, Y. E. Cheon and E. Y. Lee, Coord. Chem. Rev., 2008, 252, 1007–1026 CrossRef CAS.
- S. Kitagawa, S.-i. Noro and T. Nakamura, Chem. Commun., 2006, 701–707 RSC.
- S. Kitagawa and R. Matsuda, Coord. Chem. Rev., 2007, 251, 2490–2509 CrossRef CAS.
- H. K. Chae, D. Y. Siberio-Perez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523–527 CrossRef CAS.
- G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surble and I. Margiolaki, Science, 2005, 309, 2040–2042 CrossRef CAS.
- K. Koh, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2009, 131, 4184–4185 CrossRef CAS.
- D. J. Collins, S. Ma and H.-C. Zhou, Metal-Organic Frameworks Design and Application, ed. L. MacGillivray, Wiley-VCH, Hoboken, New Jersey, USA, 2009 Search PubMed.
- S. Ma, C. D. Collier and H.-C. Zhou, Design and Construction of Metal-Organic Frameworks for Hydrogen Storage and Selective Gas Adsorption, ed. M. Hong, Wiley, Hoboken, New Jersey, USA, 2009 Search PubMed.
- J. L. C. Rowsell and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4670–4679 CrossRef CAS.
- DOE Office of Energy Efficiency and Renewable Energy Hydrogen, Fuel Cells & Infrastructure Technologies Program Multi-Year Research, Development and Demonstration Plan, available at: http://www.eere.energy.gov/hydrogenandfuelcells/mypp.
- Hydrogen, Fuel Cells & Infrastructure Technologies Program Multi-Year Research, Development and Demonstration Plan, ed. U. D. o. Energy, 2007.
- U.S. Department of Energy, Targets for on-board hydrogen storage systems: Current R&D focus is on 2015 targets with potential to meet ultimate targets (http://www1.eere.energy.gov/hydrogenandfuelcells/storage/current_technology.html).
- L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314 RSC.
- H. Furukawa, M. A. Miller and O. M. Yaghi, J. Mater. Chem., 2007, 17, 3197–3204 RSC.
- S. Ma, J. Eckert, P. M. Forster, J. W. Yoon, Y. K. Hwang, J.-S. Chang, C. D. Collier, J. B. Parise and H.-C. Zhou, J. Am. Chem. Soc., 2008, 130, 15896–15902 CrossRef CAS.
- N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keefe and O. M. Yaghi, Science, 2003, 300, 1127–1129 CrossRef CAS.
- D. J. Collins and H.-C. Zhou, J. Mater. Chem., 2007, 17, 3154–3160 RSC.
- K. M. Thomas, Dalton Trans., 2009, 120, 1487–1505 Search PubMed.
- V. I. Isaeva and L. M. Kustov, Russ. J. Gen. Chem., 2007, 77, 721–739 CrossRef CAS.
- X. Lin, J. Jia, P. Hubberstey, M. Schroder and N. R. Champness, CrystEngComm, 2007, 9, 438–448 RSC.
- K. M. Thomas, Catal. Today, 2007, 120, 389–398 CrossRef CAS.
- D. Zhao, D. Yuan and H.-C. Zhou, Energy Environ. Sci., 2008, 1, 222–235 RSC.
- W. Zhou, H. Wu, M. R. Hartman and T. Yildirim, J. Phys. Chem. C, 2007, 111, 16131–16137 CrossRef CAS.
- C. Yang, X. Wang and M. A. Omary, J. Am. Chem. Soc., 2007, 129, 15454–15455 CrossRef CAS.
- G. Férey, M. Latroche, C. Serre, F. Millange, T. Loiseau and A. Percheron-Guégan, Chem. Commun., 2003, 2976–2977 RSC.
- M. Latroche, S. Surblé, C. Serre, C. Mellot-Draznieks, P. L. Llewellyn, J.-H. Lee, J.-S. Chang, S. H. Jhung and G. Férey, Angew. Chem., Int. Ed., 2006, 45, 8227–8231 CrossRef CAS.
- H. J. Choi, M. Dincă and J. R. Long, J. Am. Chem. Soc., 2008, 130, 7848–7850 CrossRef CAS.
- T. Takei, J. Kawashima, T. Ii, A. Maeda, M. Hasegawa, T. Kitagawa, T. Ohmura, M. Ichikawa, M. Hosoe, I. Kanoya and W. Mori, Bull. Chem. Soc. Jpn., 2008, 81, 847–856 CrossRef CAS.
- M. Dincă, W. S. Han, Y. Liu, A. Dailly, C. M. Brown and J. R. Long, Angew. Chem., Int. Ed., 2007, 46, 1419–1422 CrossRef CAS.
- W. Yang, X. Lin, J. Jia, A. J. Blake, C. Wilson, P. Hubberstey, N. R. Champness and M. Schröder, Chem. Commun., 2008, 359–361 RSC.
- Y.-G. Lee, H. R. Moon, Y. E. Cheon and M. P. Suh, Angew. Chem., Int. Ed., 2008, 47, 7741–7745 CrossRef CAS.
- M. Xue, G. Zhu, Y. Li, X. Zhao, Z. Jin, E. Kang and S. Qiu, Cryst. Growth Des., 2008, 8, 2478–2483 CrossRef CAS.
- X.-S. Wang, S. Ma, K. Rauch, J. M. Simmons, D. Yuan, X. Wang, T. Yildirim, W. C. Cole, J. J. López, A. de Meijere and H.-C. Zhou, Chem. Mater., 2008, 20, 3145–3152 CrossRef CAS.
- S. Ma, J. M. Simmons, D. Sun, D. Yuan and H. C. Zhou, Inorg. Chem., 2009, 48, 5263–5268 CrossRef CAS.
- H. J. Park and M. P. Suh, Chem.–Eur. J., 2008, 14, 8812–8821 CrossRef CAS.
- X. Lin, J. Jia, X. Zhao, K. M. Thomas, A. J. Blake, G. S. Walker, N. R. Champness, P. Hubberstey and M. Schröder, Angew. Chem., Int. Ed., 2006, 45, 7358–7364 CrossRef.
- X. Lin, I. Telepeni, A. J. Blake, A. Dailly, C. M. Brown, J. M. Simmons, M. Zoppi, G. S. Walker, K. M. Thomas, T. J. Mays, P. Hubberstey, N. R. Champness and M. Schröder, J. Am. Chem. Soc., 2009, 131, 2159–2169 CrossRef CAS.
- S. Yang, X. Lin, A. Dailly, A. J. Blake, P. Hubberstey, N. R. Champness and M. Schröder, Chem.–Eur. J., 2009, 15, 4829–4835 CrossRef CAS.
- Y. Yan, X. Lin, A. Dailly, A. J. Blake, P. Hubberstey, N. R. Champness and M. Schröder, Chem. Commun., 2009, 1025–1027 RSC.
- A. G. Wong-Foy, O. Lebel and A. J. Matzger, J. Am. Chem. Soc., 2007, 129, 15740–15741 CrossRef CAS.
- B. Panella, M. Hirscher, H. Putter and U. Muller, Adv. Funct. Mater., 2006, 16, 520–524 CrossRef CAS.
- X.-S. Wang, S. Ma, D. Yuan, J. Yoon, Y. Hwang, J.-S. Chang, X. Wang, M. Jørgensen, Y.-S. Chen and H.-C. Zhou, Inorg. Chem., 2009, 48, 7519–7521 CrossRef CAS.
- M. Dincă, A. Dailly, C. Tsay and J. R. Long, Inorg. Chem., 2008, 47, 11–13 CrossRef CAS.
- M. Dincă and J. R. Long, Angew. Chem., Int. Ed., 2008, 47, 6766–6779 CrossRef CAS.
- Q. R. Fang, G. S. Zhu, Z. Jin, Y. Y. Ji, J. W. Ye, M. Xue, H. Yang, Y. Wang and S. L. Qiu, Angew. Chem., Int. Ed., 2007, 46, 6638–6642 CrossRef CAS.
- J. Jia, X. Lin, C. Wilson, A. J. Blake, N. R. Champness, P. Hubberstey, G. Walker, E. J. Cussen and M. Schroder, Chem. Commun., 2007, 840–842 RSC.
- M. Dincă, A. Dailly, Y. Liu, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128, 16876–16883 CrossRef CAS.
- P. D. C. Dietzel, B. Panella, M. Hirscher, R. Blom and H. Fjellvag, Chem. Commun., 2006, 959–961 RSC.
- S. Ma, J. M. Simmons, D. Yuan, J.-R. Li, W. Weng, D.-J. Liu and H.-C. Zhou, Chem. Commun., 2009, 4049–4051 RSC.
- Y. Wang, P. Cheng, J. Chen, D.-Z. Liao and S.-P. Yan, Inorg. Chem., 2007, 46, 4530–4534 CrossRef CAS.
- K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191 CrossRef CAS.
- B. Chen, S. Ma, F. Zapata, E. B. Lobkovsky and J. Yang, Inorg. Chem., 2006, 45, 5718–5720 CrossRef CAS.
- A. G. Wong-Foy, A. J. Matzger and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 3494–3495 CrossRef CAS.
- M. Xue, Y. Liu, R. M. Schaffino, S. C. Xiang, X. J. Zhao, G. S. Zhu, S.-L. Qiu and B. Chen, Inorg. Chem., 2009, 48, 4649–4651 CrossRef CAS.
- S. S. Kaye, A. Dailly, O. M. Yaghi and J. R. Long, J. Am. Chem. Soc., 2007, 129, 14176–14177 CrossRef CAS.
- A. Dailly, J. J. Vajo and C. C. Ahn, J. Phys. Chem. B, 2006, 110, 1099–1101 CrossRef CAS.
- S. S. Han, J. L. Mendoza-Cortes and W. A. Goddard III, Chem. Soc. Rev., 2009, 38, 1460–1476 RSC.
- J. L. C. Rowsell, J. Eckert and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 14904–14910 CrossRef CAS.
- Y. Liu, C. M. Brown, D. A. Neumann, V. K. Peterson and C. J. Kepert, J. Alloys Compd., 2007, 446–447, 385–388 CrossRef CAS.
- Y. Liu, H. Kabbour, C. M. Brown, D. A. Neumann and C. C. Ahn, Langmuir, 2008, 24, 4772–4777 CrossRef CAS.
- E. C. Spencer, J. A. K. Howard, G. J. McIntyre, J. L. C. Rowsell and O. M. Yaghi, Chem. Commun., 2006, 278–280 RSC.
- T. Yildirim and M. R. Hartman, Phys. Rev. Lett., 2005, 95, 215504 CrossRef CAS.
- V. K. Peterson, Y. Liu, C. M. Brown and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 15578–15579 CrossRef CAS.
- L. Pan, M. B. Sander, X. Huang, J. Li, M. R. Smith, E. W. Bittner, B. C. Bockrath and J. K. Johnson, J. Am. Chem. Soc., 2004, 126, 1308–1309 CrossRef CAS.
- B. Kesanli, Y. Cui, M. R. Smith, E. W. Bittner, B. C. Bockrath and W. Lin, Angew. Chem., Int. Ed., 2005, 44, 72–75 CrossRef CAS.
- Y. Li and R. T. Yang, J. Am. Chem. Soc., 2006, 128, 8136–8137 CrossRef CAS.
- S. K. Bhatia and A. L. Myers, Langmuir, 2006, 22, 1688–1700 CrossRef CAS.
- S. Ma and H.-C. Zhou, J. Am. Chem. Soc., 2006, 128, 11734–11735 CrossRef CAS.
- P. M. Forster, J. Eckert, B. D. Heiken, J. B. Parise, J. W. Yoon, S. H. Jhung, J. S. Chang and A. K. Cheetham, J. Am. Chem. Soc., 2006, 128, 16846–16850 CrossRef CAS.
- S. Ma, D. Yuan, J. S. Chang and H.-C. Zhou, Inorg. Chem., 2009, 48, 5398–5402 CrossRef CAS.
- W. Zhou, H. Wu and T. Yildirim, J. Am. Chem. Soc., 2008, 130, 15268–15269 CrossRef CAS.
- S. Ma, PhD Dissertation “Gas Adsorption Applications of Porous Metal-Organic Frameworks”, Miami University, 2008 Search PubMed.
- T. Burchell and M. Rogers, SAE Tech. Pap. Ser., 2000, 2000–2205 Search PubMed.
- M. Kondo, T. Yoshitomi, K. Seki, H. Matsuzaka and S. Kitagawa, Angew. Chem., Int. Ed. Engl., 1997, 36, 1725–1727 CrossRef CAS.
- M. Kondo, M. Shimamura, S.-i. Noro, S. Minakoshi, A. Asami, K. Seki and S. Kitagawa, Chem. Mater., 2000, 12, 1288–1299 CrossRef CAS.
- T. Düren, L. Sarkisov, O. M. Yaghi and R. Q. Snurr, Langmuir, 2004, 20, 2683–2689 CrossRef CAS.
- S. Ma, X. S. Wang, C. D. Collier, E. S. Manis and H. C. Zhou, Inorg. Chem., 2007, 46, 8499–8501 CrossRef CAS.
- S. Ma, D. Sun, J. M. Simmons, C. D. Collier, D. Yuan and H.-C. Zhou, J. Am. Chem. Soc., 2008, 130, 1012–1016 CrossRef CAS.
- K. Seki, Chem. Commun., 2001, 1496–1497 RSC.
- K. Seki and W. Mori, J. Phys. Chem. B, 2002, 106, 1380–1385 CrossRef CAS.
- H. Kim, D. G. Samsonenko, S. Das, G. H. Kim, H. S. Lee, D. N. Dybtsev, E. A. Berdonosova and K. Kim, Chem.–Asian J., 2009, 4, 886–891 CrossRef CAS.
- I. Senkovska and S. Kaskel, Microporous Mesoporous Mater., 2008, 112, 108–115 CrossRef CAS.
- P. L. Llewellyn, S. Bourrely, C. Serre, A. Vimont, M. Daturi, L. Hamon, G. D. Weireld, J.-S. Chang, D.-Y. Hong, Y. K. Hwang, S. H. Jhung and G. Férey, Langmuir, 2008, 24, 7245–7250 CrossRef.
- H. Wu, W. Zhou and T. Yildirim, J. Phys. Chem. C, 2009, 113, 3029–3035 CAS.
- H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2009, 131, 4995–5000 CrossRef CAS.
- S. Bourrelly, P. L. Llewellyn, C. Serre, F. Millange, T. Loiseau and G. Ferey, J. Am. Chem. Soc., 2005, 127, 13519–13521 CrossRef CAS.
- H. Wang, J. Getzschmann, I. Senkovska and S. Kaskel, Microporous Mesoporous Mater., 2008, 116, 653–657 CrossRef CAS.
- S.-i. Noro, S. Kitagawa, M. Kondo and K. Seki, Angew. Chem., Int. Ed., 2000, 39, 2081–2084 CrossRef.
- M. Kondo, T. Okubo, A. Asami, S.-i. Noro, T. Yoshitomi, S. Kitagawa, T. Ishii, H. Matsuzaka and K. Seki, Angew. Chem., Int. Ed., 1999, 38, 140–143 CrossRef CAS.
- M. Park, D. Moon, J. W. Yoon, J.-S. Chang and M. S. Lah, Chem. Commun., 2009, 2026–2027 RSC.
- J. Johnson, Chem. Eng. News, 2004, 82, 36–42.
- Z. Yong, V. Mata and A. E. Rodrigues, Sep. Purif. Technol., 2002, 26, 195–205 CrossRef CAS.
- A. R. Millward and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 17998–17999 CrossRef CAS.
- K. S. Walton, A. R. Millward, D. Dubbeldam, H. Frost, J. J. Low, O. M. Yaghi and R. Q. Snurr, J. Am. Chem. Soc., 2008, 130, 406–407 CrossRef CAS.
- Y. S. Bae, O. K. Farha, J. T. Hupp and R. Q. Snurr, J. Mater. Chem., 2009, 19, 2131–2134 RSC.
- Z. Wang and S. M. Cohen, Chem. Soc. Rev., 2009, 38, 1315–1329 RSC.
- A. Demessence, D. M. D'Alessandro, M. L. Foo and J. R. Long, J. Am. Chem. Soc., 2009, 131, 8784–8786 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2010 |
