Open Access Article
Open Access ArticleProfiling single-molecule reaction kinetics under nanopore confinement†
Wei
Liu
a,
Zhong-Lin
Yang
a,
Chao-Nan
Yang
a,
Yi-Lun
Ying
 *ab and
Yi-Tao
Long
*ab and
Yi-Tao
Long
 a
a
aState Key Laboratory of Analytical Chemistry for Life Science, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing, 210023, P. R. China. E-mail: yilunying@nju.edu.cn
bChemistry and Biomedicine Innovation Center, Nanjing University, Nanjing, 210023, P. R. China
First published on 14th March 2022
Abstract
The study of a single-molecule reaction under nanoconfinement is beneficial for understanding the reactive intermediates and reaction pathways. However, the kinetics model of the single-molecule reaction under confinement remains elusive. Herein we engineered an aerolysin nanopore reactor to elaborate the single-molecule reaction kinetics under nanoconfinement. By identifying the bond-forming and non-bond-forming events directly, a four-state kinetics model is proposed for the first time. Our results demonstrated that the single-molecule reaction kinetics inside a nanopore depends on the frequency of individual reactants captured and the fraction of effective collision inside the nanopore confined space. This insight will guide the design of confined nanopore reactors for resolving the single-molecule chemistry, and shed light on the mechanistic understanding of dynamic covalent chemistry inside confined systems such as supramolecular cages, coordination cages, and micelles.
Introduction
In nature, nanoconfinement is the key feature of the enzymatic reaction, where the substrates selectively encounter reactive sites.1 The confined intermolecular interactions between enzymes and substrates facilitate the pre-organization of reagents, giving exceptional reaction efficiency. Inspired by enzyme confinement, reaction vessels at the micro/nanoscale are engineered to capture and organize the reagent, which is formed by nanoparticles,2 micelles,3 supramolecular cages,4 coordination cages,5 and proteins.6–8 In this way, confined space is further designed to isolate a single reactant from the bulk, which is beneficial for studying the reactive intermediates and reaction pathways.Biological nanopores utilize membrane proteins to form nanoconfinement for accommodating single molecules.9–13 Reactive groups could be spatially designed alone in the polypeptide chain of a protein nanopore. Under bias voltages, a single reactant is confined inside a nanopore with controllable movement and direction. The covalent bond formation can be triggered at a specific reactive site, leading to the ionic current modulation through a nanopore.14,15 Coupled with a high bandwidth current recording system, the nanopore could report reactive intermediates in real time,16–18 study the reaction kinetics,19–21 and explore reaction trajectory22–24 at the single-molecule level.
Generally, the reaction between a single reactant molecule and reactive site inside a nanopore is proposed as a pseudo first order process.25 Their reaction rate is calculated by a concentration-dependent experiment.26 This kinetics model has also been expanded to study interactions between the transported analyte and the nanopore, including the electrostatic interaction between ssDNA and DNA polymerase,27 the hydrophobic interaction between DNA and a graphene nanopore28 and even the hydrogen bond of paired bases inside a nanopore.29 Continuous efforts have been made to understand the contribution of driving force on the interaction kinetics under nanopore confinement.30–33 But questions remain, for example, how does the driving force of the reactant affect the interaction kinetics? Why does the bulk concentration of the reactant affect the single-molecule reaction kinetics under nanopore confinement? How does the capture frequency regulate the reactive kinetics? In the enzyme-catalysis process, the reaction pathway is divided into the binding/unbinding of the substrate and the conversion of the reactant to a product, which is supported by the Michaelis–Menten equation. Inspired by this model,34 we classify the single-molecule reaction process inside a nanopore into three steps which are (1) capture of a single reactant, (2) trigger of the single-molecule reaction at a specific site and (3) possible dissociation of the single reactant from the reactive site inside a nanopore. To profile the kinetics of this reaction, the rapid translocation of the single reactant should be slowed down to clearly record the above three processes.
Herein we designed a series of thiol-containing peptides (R1–R5) as reactants to bond with cysteine mutant aerolysin (AeL) nanopore. A previous study demonstrated that the cysteine mutants at the 238 site could prolong the residence of single molecules under nanoconfinement.35 Therefore, K238C AeL was designed for simultaneously probing reaction events and non-reaction events, producing the distinguishable ionic current signatures. This model system ensures the study of the single-molecule reaction kinetics. Our results demonstrated that the reaction kinetics inside a nanopore depends on the reactant capture frequency and a fraction of effective collision between a single reactant and the active site under nanopore confinement.
Results and discussion
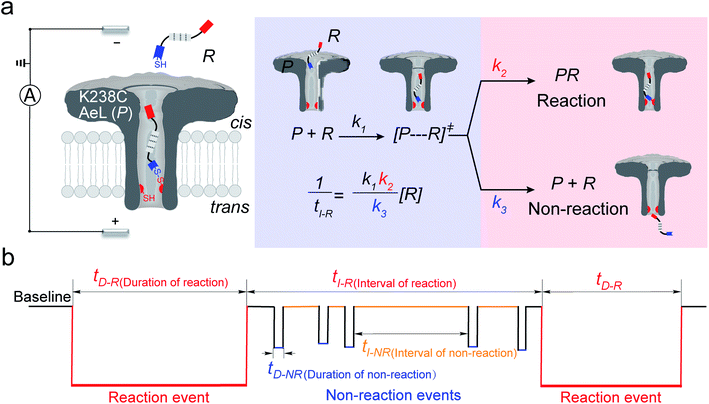
In the first step, a K238C AeL nanopore reactor with seven inward-facing cysteines at position 238 was employed to real-time monitor a disulfide formatting and breaking reaction (Fig. 1a). The constriction of AeL is around 1 nm and the length of the whole channel is approximated to 10 nm, which provides nanoconfinement for studying the single-molecule reaction.36 The conductance of K238C AeL is 0.52 ± 0.02 nS in 1 M KCl (n = 5) at 20.0 ± 2.0 °C (Fig. S1 and S2†). Under the positive potential (cis side is grounded) from +60 mV to +120 mV, K238C AeL shows a stable open pore current with rare gating events.The thiol derivative, thiol-containing peptide (R), is designed and contains a glutamic acid (E) segment as the guiding sequence at the N-terminal and a reactive cysteine at the C-terminal. We use R1 (EEESGSGSGSGSGSC) as a model reactant to demonstrate our proposed kinetics model. The ionic events of R1 could be classified into type I for reaction events with long durations (>120 ms) and type II for non-reaction events with short durations. The bumping events were excluded from further analysis (Fig. S3–S5, see details in ESI 2.2†).
Both the reaction and non-reaction events were observed under the whole bias voltage ranging from +60 mV to +110 mV (with respect to the cis chamber, Fig. S6†). These results reveal that the single reactant could undergo either the reaction or non-reaction (translocation or bumping out) pathway as it approaches reactive site of the nanopore. Therefore, we proposed a four-state kinetic model to describe single-molecule reactions inside a nanopore as shown in Fig. 1a and eqn (1)–(3). When the reactant peptide (R) is confined into K238C AeL (P) from the cis side, it continuously moves and collides along the inner surface of K238C AeL under the bias voltage. Then, R reaches the reactive thiol groups at the 238 site, and interacts with the cysteine residues, giving an intermediate state of [P⋯R]‡ (eqn (1)), similar to the enzyme–substrate binding. Due to the confinement effect, [P⋯R]‡ acquires sufficient energy to enable the covalent bond formation, resulting in a disulfide product of PR (eqn (2)). This process of P + R → [P⋯R]‡ → PR yields reaction events. Alternatively, [P⋯R]‡ would be dissociated after a rapid interaction but not form the bond with the K238C site (eqn (3)). If the driving force of R is larger than the repelling force from the translocation energy barrier, R translocates through the nanopore. Otherwise, R escapes from the cis side of the nanopore. The second pathway P + R → [P⋯R]‡ → P + R generates non-reaction events.
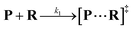 | (1) |
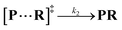 | (2) |
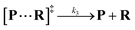 | (3) |
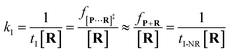 | (4) |
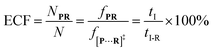 | (5) |
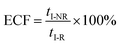 | (6) |
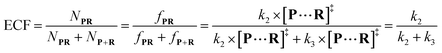 | (7) |
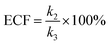 | (8) |
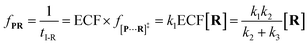 | (9) |
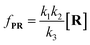 | (10) |
To verify the proposed kinetics we initially analyzed the frequency of reaction events at various concentrations. As expected, the ECF gives a constant value of (17.0 ± 2.0)% while fPR is linearly increased with the increase in the [R1] concentration (Fig. 2a). These results demonstrate that the ECF is nearly irrelevant to the R1 concentration. The high possibility for effective trapping of R1, giving the high occurrence of formation of [P⋯R1].
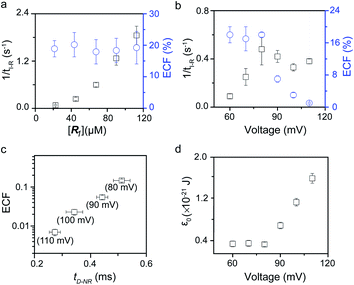 | ||
| Fig. 2 Kinetics evaluation of R1 reacting with the K238C AeL nanopore. (a) The reaction rate (fPR = 1/tI-R) and fraction of effective collision (ECF) at different R1 concentrations. (b) Reaction rate (fPR) and ECF under different voltages from +60 mV to +110 mV. (c) The relationship between the ECF and non-reaction event duration (tD-NR). The voltage dependent results of tD-NR and tI-NR are shown in Fig. S5a and b,† respectively. (d) The collision threshold energy (ε0) under different voltages from +60 mV to +110 mV. All data were acquired at 20.0 ± 2.0 °C in 1.0 M KCl, 10.0 mM Tris, and 1.0 mM EDTA solution buffered at pH 8.0 in the presence of 50.0 μM R1. | ||
The results from voltage-dependent studies show that the higher voltage provides a larger k1 due to the stronger driving force for the negatively charge R1 (Fig. S5b†). Consequently, fPR gradually increases from +60 mV to +80 mV (Fig. 2b). However, fPR does not show significant change at the bias voltage from +80 mV to +110 mV. When the bias voltage increased from +60 mV to +80 mV, the ECF showed a constant value of (18.0 ± 2.0)% (Fig. 2b). Then, it decreased rapidly as the bias voltage exceeds the threshold of +80 mV. The low bias voltage (<+80 mV) is in favor of the formation pathway of the disulfide bond. However, the high bias voltage (>+80 mV) is prone to deactivation of [P⋯R1]‡ to release R1 from the trans side. At +110 mV, fP+R is over 100 times larger than fPR, which suggests that most of the R1 molecules undergo ineffective bonding at a high bias voltage (Table S1†). In our four-state kinetics model, the reaction rate is controlled by the reactant captured and the result of two parallel reaction pathways of the process of eqn (2) and (3). At a defined temperature and pH, the reaction rate is mainly restricted by the process of eqn (3) rather than eqn (2). More interestingly, at a low voltage (<+80 mV), fPR is increased from +60 mV to +80 mV, which is mainly dominated by the process of eqn (1). At a high voltage (>+80 mV), the destabilization of [P⋯R1]‡ significantly shifts the reaction pathway to the non-reaction pathway, thereby inhibiting the eqn (2) process.
We assume that k3 is correlated with the velocity of R1 reaching and escaping from the 238 site. Our previous studies demonstrated that the 238 site is located at the energy barrier of the single-molecule translocation.38 Compared with WT AeL, K238C prolongs the duration of poly(dA)4 for about 7 times.34 Therefore, K238C AeL could decrease the velocity of R1. The increasing residence time of single reactants at the reaction site can effectively improve the reaction efficiency. Moreover, the linear relationship between lg(ECF) and duration time of the non-reaction event (tD-NR) further supports our hypothesis (Fig. 2c).
The collision threshold energy (ε0) between AeL and R1 can be calculated from the ECF for the formation of the disulfide bond under nanopore confinement according to the previous study37 (eqn (11), see details in ESI 2.3†):
| ε0 = −ln(ECF)kBT | (11) |
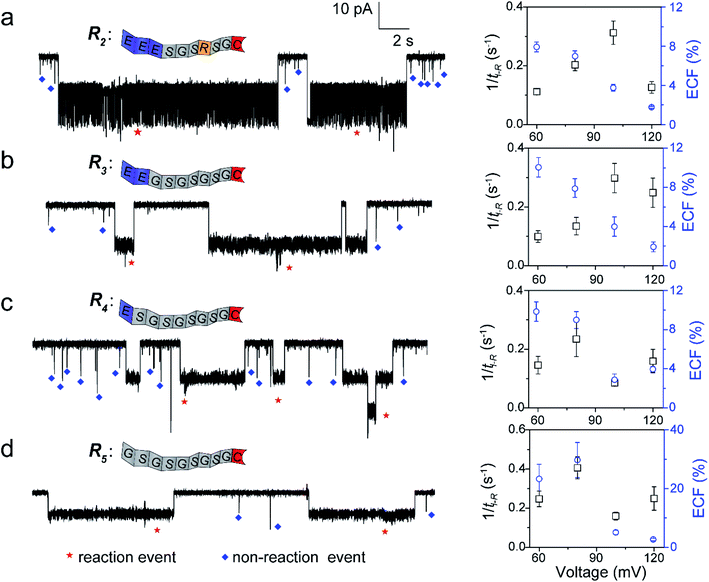
To further confirm our kinetics model, we designed a series of cysteine-containing peptides. As shown in Fig. 3a and b, two peptides (R2 and R3) exhibit the same length and same net charge but different charge distributions. Two types of events with a distinguishable duration difference are shown in Fig. S8a and b.† For R2 and R3, fPR, ECF and the relationship between tD-NR and the ECF show similar voltage-dependent tendencies (Fig. 3a, b, S10a and b†). Since both R2 and R3 carry two negative charges under pH 8.0, their k1 values increase with increasing positive voltage (Fig. S8a and b†). At a voltage >+100 mV, the reaction rate is mainly affected by decreasing ECF. Note that the heterogeneous charge distribution of R2 and R3 affects the capture possibility and duration, resulting in the difference of k1 and ECF (Table S1†).
For modulating the residence time, another two peptides, R4 and R5 were designed (Fig. 3c and d), which remove the one (R4) and two (R5) negatively charged amino acids from the guiding segment, respectively. As expected, the order of the ECF is R5 > R4 at the lower voltages (≤+80 mV). The uncharged R5 threads through the pore at the slowest rate of about 20.0 nm ms−1 compared with R3 and R4, leading to the largest ECF (Fig. S10c, d, and Table S1†). For all the four peptides, their trends of fPR in voltage are diverse and irregular, however, the voltage-dependent trends of the ECF are similar to that of R1. The results confirm that the ECF is decreased with the enhanced translocation speed of non-reaction events at high voltages.
In our experiments, all reaction events could return to the initial open-pore state, illustrating that the disulfide bond could be cleaved without additional reducing agents under nanoconfinement. To analyze the single bond-breaking process, we prepared a three-state kinetics model for describing the disulfide bond breaking under nanopore confinement (Fig. S11†). The breaking of a single disulfide bond is divided into two steps: (1) PR → [P⋯R]‡ for a single disulfide bond breaks down with a rate constant of 1/k2. (2) Then [R] escapes from the trans side of the pore, that is, [P⋯R]‡ → P + R gives a rate constant of 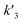 . 1/tD-R could be calculated by using eqn (12):
. 1/tD-R could be calculated by using eqn (12):
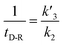 | (12) |
Conclusions
In conclusion, the nanopore confined effect provokes the “four-state kinetics module” for a single-molecule reaction. The kinetics of bond-forming is decided by both the possibility of the captured molecule (k1[R]) and fraction of effective collision (ECF) inside a nanopore. According to concentration and bias voltage-dependent experiments, the ECF is dominated by the bond active rate constant k2 and deactivation rate constant of [P⋯R]‡ (k3). Moreover, the charge and composition effects could affect the values of fP+R and ECF, leading to the differences of reaction constants. This reaction kinetics model provides a new basis for the design of nanopore reactors. We anticipate that this model could be extended to a wide range of organic and inorganic nanoconfinements for promoting multiple single-molecule reactions and interactions.Data availability
All experimental supporting data and procedures are available in the ESI.†Author contributions
YLY and YTL conceived the idea. WL and ZLY conducted the experiments and analysed the data. WL and CNY prepared the manuscript. WL and YLY wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the National Natural Science Foundation of China (21922405, 22027806 and 21834001). YLY is sponsored by National Ten Thousand Talent Program for young top-notch talent. We thank Dr Shaochuang Liu for data analysis and Dr Xueyuan Wu for nanopore preparation.Notes and references
- A. B. Grommet, M. Feller and R. Klajn, Nat. Nanotechnol., 2020, 15, 256–271 CrossRef CAS PubMed.
- T. Zdobinsky, P. S. Maiti and R. Klajn, J. Am. Chem. Soc., 2014, 136, 2711–2714 CrossRef PubMed.
- J. Lee, D. Samanta, H. Nam and R. Zare, J. Am. Chem. Soc., 2019, 141, 10585–10589 CrossRef CAS PubMed.
- A. Palma, M. Artelsmair, G. Wu, X. Lu and O. A. Scherman, Angew. Chem., Int. Ed., 2017, 129, 15894–15898 CrossRef.
- H. Takezawa, K. Shitozawa and M. Fujita, Nat. Chem., 2020, 12, 574–578 CrossRef CAS PubMed.
- S. Dutta, J. R. Whicher and D. A. Hansen, et al. , Nature, 2014, 510, 512–517 CrossRef CAS PubMed.
- J. A. Mindell, H. J. Zhan, P. D. Huynh, R. J. Collier and A. P. Finkelstein, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 5272–5276 CrossRef CAS PubMed.
- Y. Qing, H. Tamagaki-Asahina, S. A. Ionescu, M. D. Liu and H. Bayley, Nat. Nanotechnol., 2019, 14, 1135–1142 CrossRef CAS PubMed.
- Y.-L. Ying and Y.-T. Long, J. Am. Chem. Soc., 2019, 141, 15720–15729 CrossRef CAS PubMed.
- L. Xue, H. Yamazaki, R. Ren, M. Wanunu, A. P. Ivanov and J. B. Edel, Nat. Rev. Mater., 2020, 5, 931–951 CrossRef CAS.
- N. S. Galenkamp, A. Biesemans and G. Maglia, Nat. Chem., 2020, 12, 481–488 CrossRef CAS PubMed.
- P. Tripathi, A. Benabbas, B. Mehrafrooz, H. Yamazaki and M. P. Wanunu, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 1–10 CrossRef PubMed.
- L. Liu and H.-C. Wu, Angew. Chem., Int. Ed., 2016, 55, 15216–15220 CrossRef CAS PubMed.
- S. Shin, T. Luchian, S. Cheley, O. B. And and H. Bayley, Angew. Chem., Int. Ed., 2002, 114, 3859–3861 CrossRef.
- K.-P. Qiu, T. P. Fato, B. Yuan and Y.-T. Long, Small, 2019, 15, 1805426 CrossRef PubMed.
- W. J. Ramsay, N. A. W. Bell, Y. Qing and H. Bayley, J. Am. Chem. Soc., 2018, 140, 17538–17546 CrossRef CAS PubMed.
- M. M. Haugland, S. Borsley, D. F. Cairns-Gibson, A. Elmi and S. L. Cockroft, ACS Nano, 2019, 13, 4101–4110 CrossRef CAS PubMed.
- T. Luchian, S. H. Shin and H. Bayley, Angew. Chem., Int. Ed., 2003, 42, 1925–1929 Search PubMed.
- G. S. Pulcu, N. S. Galenkamp, Y. Qing, G. Gasparini, E. Mikhailova, S. Matile and H. Bayley, J. Am. Chem. Soc., 2019, 141, 12444–12447 CrossRef CAS PubMed.
- Y.-J. Qing, G. S. Pulcu, N. A. W. Bell and H. Bayley, Angew. Chem., Int. Ed., 2018, 57, 1218–1221 CrossRef CAS PubMed.
- Y.-J. Qing, S. A. Ionescu, G. S. Pulcu and H. Bayley, Science, 2018, 361, 908–912 CrossRef CAS PubMed.
- M. B. Steffensen, D. Rotem and H. Bayley, Nat. Chem., 2014, 6, 604–608 CrossRef PubMed.
- B. Zhou, Y. Wang, C. Cao, D. Li and Y.-T. Long, Sci. China: Chem., 2018, 61, 1385–1388 CrossRef CAS.
- J. Lee and H. Bayley, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13768–13773 CrossRef CAS PubMed.
- L. Q. Gu, O. Braha, S. Conlan, S. Cheley and H. Bayley, Nature, 1999, 398, 686–690 CrossRef CAS PubMed.
- H. Bayley, Single Molecules and Nanotechnology, Single-molecule covalent chemistry in a protein nanoreactor, 2008, ch. 10, pp. 251–277 Search PubMed.
- M. Palla, S. Punthambaker and B. Stranges, et al. , ACS Nano, 2020, 15, 489–502 CrossRef PubMed.
- S. Banerjee, J. Wilson, J. Shim, M. Shankla, E. A. Corbin, A. Aksimentiev and R. Bashir, Adv. Funct. Mater., 2014, 25, 936–946 CrossRef PubMed.
- R. Hang, C. G. Cheyne, A. M. Fleming, C. J. Burrows and H. S. White, J. Am. Chem. Soc., 2018, 140, 5153–5160 CrossRef PubMed.
- J. E. Reiner, J. J. Kasianowicz, B. J. Nablo and R. N. J. Turro, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12080–12085 CrossRef CAS PubMed.
- B. Luan and A. Aksimentiev, J. Phys.: Condens. Matter, 2010, 22, 454123 CrossRef PubMed.
- B. Cressiot, A. Oukhaled and G. Patriarche, et al. , ACS Nano, 2012, 6, 6236–6243 CrossRef CAS PubMed.
- M. Richard, T. Susana and K. Syma, Nanomaterials, 2015, 5, 144–153 CrossRef PubMed.
- X. Xie and H. Lu, J. Biol. Chem., 1999, 274, 15967–15970 CrossRef CAS PubMed.
- M.-Y. Li, Y.-Q. Wang, Y. Lu, Y.-L. Ying and Y.-T. Long, Front. Chem., 2019, 7, 258–264 CrossRef PubMed.
- I. Iacovache, S. De Carlo, N. Cirauqui, M. D. Peraro, F. Goot and B. Zuber, Nat. Commun., 2016, 7, 12062 CrossRef CAS PubMed.
- S.-K. Upadhyay, Chemical Kinetics and Reaction Dynamics, Theories of Reaction Rate, 2007, ch. 4, pp. 83–89 Search PubMed.
- Y.-Q. Wang, C. Cao, Y.-L. Ying, S. Li, M. B. Wang, J. Huang and Y.-T. Long, ACS Sens., 2018, 3, 779–783 CrossRef CAS PubMed.
- S. Borsley, M. M. Haugland and S. Oldknow, et al. , Chem, 2019, 5, 1275–1292 CAS.
- A. Wiita, S. Ainavarapu, H. Huang and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7222–7227 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc06837g |
| This journal is © The Royal Society of Chemistry 2022 |